Abstract
This research identified the types of wave breaker on a non-overtoppable, smooth and impermeable 1:10 slope under regular waves. Experimental tests were carried out in the Atmosphere-Ocean Interaction Flume of the Andalusian Institute for Earth System Research (University of Granada). Using the experimental space [log(h/L)–log(H/L)] and the alternate slope similarity parameter [χ = log (h/L H/L)], a complete set of breaker types was identified. Four types of wave breaker were then added to Galvin’s classification. Our results showed that the value of the Iribarren number was not sufficient to predict the expected type of wave breaker on the slope. Except for spilling and early plunging breakers, no biunivocal relationship was found between Ir and the type of breaker. The data obtained in the physical model were further enriched with the results of the flow characteristics and the wave energy transformation coefficients obtained with the IH-2VOF numerical model on a 1:10 impermeable slope. This research study, presented in this paper, showed that the Iribarren number is not a convenient wave breaking similarity parameter.
1. Introduction
Sloping breakwaters are the most common coastal structure for the protection of ports and beaches, because of their capacity to dissipate incident wave energy when interacting with the structure.
The transformation of the wave train propagating on an impermeable slope depends, among other things, on the transport of turbulent kinetic energy (TKE) from the following sources: (a) wave breaking causing advection and diffusion of turbulence, generating a vortex dependent on the breaking type; (b) the armor layer whose vortex depends on the characteristic diameter of the armor unit; and (c) the porous core whose turbulence scale depends on the grain size.
The research in [1] is based on the hypothesis that the Iribarren number () [2] helps to address the questions of whether a wave train will break on a slope, by decaying, voluting, collapsing, or oscillating [3,4]. However, surprisingly, in the case of breakwaters, very little attention has been paid to calculating wave dissipation as a function of the type of wave breaking on the slope.
In recent decades, several numerical and physical studies have studied the different types of wave breaking on an impermeable slope. References [5,6,7,8,9] developed numerical models based on the volume-averaged Reynolds average Navier–Stokes (VARANS) equations and using the volume of fluid (VOF) method for measuring the free surface. References [7,8] performed an in-depth study of plunging and spilling breakers. On the other hand, using numerical and mathematical models, ref. [9] studied the differences between weak and strong plunging; Ref. [10] investigated the bore type of breakers; Ref. [11] researched breaking waves on steep impermeable slopes for measuring run-up, and ref. [12] studied plunging breakers.
These studies provided the spatial-temporal progression of the wave, which is key information to analyze the source of the experimental uncertainty, and to identify the transitions between the types of wave breakers [3,4]. Particularly relevant for this research was the distinction between weak and strong bore [13] and weak and strong plunging [7,12].
Nowadays, in coastal engineering, the flow characteristics of the waves (energy transformation, stability, run-up, etc.) are determined by the application of semi-empirical formulas, most of which are based on the Iribarren number [2]. It is implicitly conjectured that the value of the Iribarren number determines the type of wave breaker [1,3,4] on the slope.
Following [14,15], the first aim of this paper was to verify that conjecture. The second was to describe and analyze the dependence of the type of wave breaker on the relative depth (h/L) and wave steepness (H/L), while propagating on a smooth, impermeable slope under regular wave train. For this purpose, a physical test was carried out in the Atmosphere-Ocean Interaction Flume (CIAO) of the Andalusian Institute for Earth System Research (IISTA-University of Granada).
The rest of the paper is organized as follows. Firstly, the experimental set-up and space are described. Next, a series of pictures defining the types of wave breaker are shown. The types of breakers are presented as a function of the relative depth and wave steepness. In addition, these results are discussed and compared with the Iribarren number. Finally, the paper ends with the conclusions that can be derived from this research.
2. Methodology
To study the influence of the different wave parameters and test conditions in the breaking processes, tests were carried out in the Atmosphere-Ocean Interaction Flume (CIAO) of the Andalusian Institute for Earth System Research (IISTA-University of Granada). This wave flume facilitates the combined study of marine and atmospheric processes. The facility has two opposing piston-type generating paddles, equipped with active systems to absorb reflection, and a closed circuit for wind generation. A detailed description of the CIAO facility is given in Appendix A.
For this study, an impermeable ramp made of wood, with a slope angle of 1:10 (in the study area, Figure 1) was used. Regular waves were generated with paddle 2. Two water depths were used, and . A total of 19 tests were done, of which the conditions are summarized in Table 1. Test conditions were chosen to cover the maximum experimental space to analyze the maximum types of breakers, with combinations of H and T, and then Ir was calculated. Pictures of the waves were taken from the first waves approaching the slope.

Figure 1.
Diagram of the Atmosphere-Ocean Interaction Flume (CIAO) and wave gauge position (measured in meters).

Table 1.
Summarized test conditions. Parameters H and T are input values, namely, the values given to the generation system. Tz, L, HI and Ir represent the zero-upcrossing mean wave period, wavelength, incident wave height, and Iribarren number, respectively, from the statistical analysis of the surface elevation data.
The free surface elevation was measured using four UltraLab ULS 80D acoustic wave gauges placed along the flume before the ramp (Figure 1). These gauges have a maximum repetition rate of 75 Hz, a space resolution of 0.18 mm, a working range of 350 mm and a reproducibility of ±0.15%. Video cameras were used in the study section for recording and photographing the breaking waves.
The values of HI and Tz used in the results were the r.m.s. wave height and the mean wave period at the toe of the ramp. Those values were obtained from the statistical analysis of the recorded free surface elevation time series by wave gauges 1, 2 and 3. In the analysis, the zero-upcrossing technique of the time series was applied to obtain the individual wave heights and periods of the signal [16].
While the mean period coincided with the input period, the incident wave height was usually lower than the input value [14]. L is the wavelength, calculated with the linear dispersion equation, , where σ is the angular frequency (); g is the gravity acceleration; k is the wavenumber ().
3. Results
3.1. Log-Transformed Experimental Space
Firstly, it was necessary to analyze the limits of wave generation in the flume tests. For that purpose, Figure 2 shows the tests carried out on a 1:10 slope, plotted in the log-transformed experimental space [14]. The logarithmic axes were used to assist in the visualization of the data. The sides of the parallelepiped indicated the wave generation limits of the wave flume (maximum and minimum wave height and period). This figure also shows the maximum wave steepness in the intermediate water depth (constant depth) given by Miche’s equation (Equation (1)) [17].
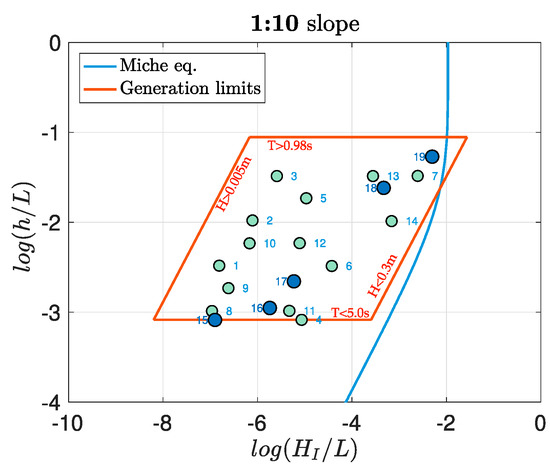
Figure 2.
Experimental data (blue dots) in the log-transformed experimental space (darker dots are the breakers shown in Figure 3), as well as the generation limits (red lines) and Miche’s law for wave breaking (blue line).
3.2. Breakers Photographs
In what follows, the sequence of the type of wave breaker observed is shown with the pictures taken during the experiments. The ID of each picture indicates the number of the test in the log-transformed experimental space. Each test is represented by two pictures of the wave.
The sequence of the five photographs shows the transition between five types of wave breaker observed on the plane impermeable 1:10 slope:
- −
- ID 15: Surging—weak bore
- −
- ID 16: Weak bore—strong bore
- −
- ID 17: Strong bore—strong plunging
- −
- ID 18: Strong plunging—weak plunging
- −
- ID 19: Weak plunging—spilling
As can be observed, the difference between the weak and strong bore found by [13] (their Figure 5 and Figure A1) are also observed in the physical test. In a weak bore, the front of the wave is unbalanced and starts breaking from the bottom or nearby it. In a strong bore, there is an attempt to plunge, but, before it can finish the plunge, the front “collapses”, thus developing a forward volume of water and bubbles, which are highly turbulent.
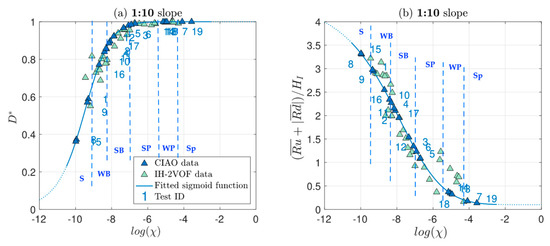
Figure 5.
Fitted sigmoid functions to the (a) bulk dissipation and (b) total water excursion versus . Light blue dots are data from the IH-2VOF, to which the sigmoid function was fitted. Dark blue dots are the tests conducted at the CIAO flume and their value of D* and [(Ru + |Rd|)/HI] in the sigmoid. Vertical lines show the transition between breaker types.
For plunging breakers, the top of the front wave turns over. In the strong plunging, the water falls on the slope (or on a tongue of water), splashing and losing energy. In the weak plunging, the water lands on the main wave, building a roller which propagates with the wave [18].
3.3. The Experimental Space and the Types of Wave Breaker
Figure 4 shows the same log-transformed experimental space with the experimental data, but in this case, the other information is the following: (1) the different types of wave breaker: (2) vertical red lines indicating constant values of the Iribarren number; and (3) slanting blue lines, showing the transition between breaking types, following the constant relationship between h/L and H/L. This relationship was found after analyzing the pictures and organizing the breaker types. Figure 4 clearly illustrates that for a constant value of Ir, different types of breaking wave can be expected. For , surging, weak bore, strong bore and strong plunging breakers could be possible. Thus, it cannot be assumed that there is a biunivocal relationship between the Iribarren number and the types of wave breaker.
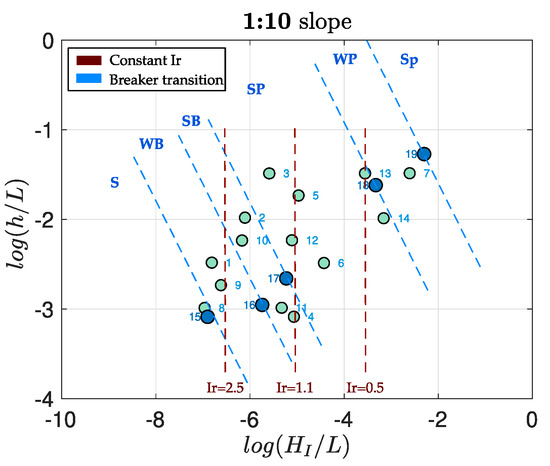
Figure 4.
Breaking types (blue lines) vs. Iribarren number (red lines), plotted in the log-transformed experimental space. S: surging, WB: weak bore, SB: strong bore, SP: strong plunging, WP: weak plunging, Sp: spilling.
3.4. Influence of the Breaker Types in the Flow Characteristics
Figure 5 shows sigmoid functions fitted to the values of the bulk dissipation (D*) and the total water excursion [(Ru + |Rd|)/HI], being Ru and Rd the run-up and run-down respectively, versus the alternate slope similarity parameter . Those data were calculated numerically using the IH-2VOF numerical model [5] on a smooth impermeable 1:10 slope (further information of the model and the test can be found in Appendix B. The tests are fully described in [14,15]). A sigmoid function was fitted to the numerical data and then, with the value of the experimental tests, the value of the dissipation was obtained from the sigmoid function. The figure highlights the relationships between the types of wave breaker and the flow characteristics and the wave energy transformation on the slope. The relationship with the reflection coefficient can be estimated from the bulk dissipation . For impermeable and non-overtoppable slopes, it mimics the wave energy dissipation behavior.
4. Discussion
The previously mentioned results showed that small changes in the relative depth and wave steepness can alter the type of wave breaker, and consequently change the flow characteristics on the slope. It is important to highlight that the types of wave breaker were found to be strongly dependent on the slope angle ([14,15]) and thus their location in the experimental space, (h/L) and (H/L). The results in Figure 3 are representative of the types of breaker on an impermeable 1:10 slope.

Figure 3.
Types of breaker transitions at the CIAO flume for a 1:10 impermeable slope. ID Numbers are used in Figure 2, Figure 4 and Figure 5 to identify the types of wave breaker in the experimental space. The pairs of figures show the transition between: (a,b) surging and weak bore; (c,d) weak bore and strong bore; (e,f) strong bore and strong plunging; (g,h) strong plunging and weak plunging; and (i,j) weak plunging and spilling.
The analysis of the photographs and videos taken at the wave flume showed that the characteristics of each transition between the different breakers were the following:
- 1)
- Surging—Weak bore: The wave trains oscillates (like a standing wave), generating no turbulence in the profile. The period of the water rising and falling along the slope is considerably larger than the wave period.
- 2)
- Weak bore—Strong bore: The inclined plane becomes more vertical and collapses in the middle or bottom of the water column.
- 3)
- Strong bore—Strong plunging: There is no volute. There is an inclined plane, mixing water and air bubbles.
- 4)
- Strong plunging—Weak plunging: The wave volute impacts the slope, hits it and bounces back.
- 5)
- Weak plunging—Spilling: The wave volute begins, but disappears in turbulence before it impacts the slope.
As reflected in the results, the wave breaking process determined the flow characteristics (run-up, run-down, stability…), as well as wave energy transformation on the slope. Three regimens were found: (i) a reflective regime caused by surging breakers; (ii) a dissipative domain caused by spilling and weak plunging breakers; (iii) a transition regime where strong and weak bores, and strong plunging are the most plausible type of wave breaker.
Reference [2] proposed the value of to identify the change of wave energy transformation: for Ir >2.3, the flux of reflected wave energy was larger than the energy dissipation. Later, [19] showed that for Ir ≈ 2.3, the period of the up-rush and down-rush on the slope and the period of the incident wave were approximately equal. In the experiments in this study, these “quasi-resonant” conditions occurred during the transition between strong plunging and strong bore. The variability of the observed flow characteristics was significant, depending on the type of wave breaker [15].
The use of the experimental space could help to develop the experimental design. It made it possible to forecast the types of breaker, as well as the variability of the flow characteristics, wave energy transformation, and structure stability. The types of wave breaker identified previously in the numerical computation [15] were verified with the physical breakers observed in the CIAO flume. For that purpose, the application of the alternative slope parameter () was relevant. Thus, with a smaller number of tests, a wide range of results were obtained. The time of the physical experiments was also decreased; and even more importantly, costs were lowered.
5. Conclusions
The objective of this research was to identify the types of wave breaker on a non-overtoppable, smooth, and impermeable 1:10 slope under regular waves. Experimental tests were carried out in the CIAO flume of the IISTA. From this study, the following conclusions can be drawn:
- 1)
- Six types of wave breaker were observed in the flume experiments: surging, weak bore, strong bore, strong plunging, weak plunging and spilling. Four of them were classified as follows [4]: surging, bore (collapsing), plunging, and spilling. The differences between weak—strong bore [13] and strong—weak plunging were explained by [8,12].
- 2)
- 3)
- It was found that the value of the Iribarren number is not sufficient to forecast the expected type of wave breaker on the slope. Except for spilling and early plunging breakers, there is not a biunivocal relationship between Ir and the type of breaker.
- 4)
- A relationship was found between the breaker types and flow characteristics and the wave energy dissipation on the slope. These results could be useful and relevant information for the design of mound breakwaters.
Author Contributions
All authors conceptualized the study. M.V.M. did the physical tests with the help of M.C. M.V.M. did the analysis of the data with the guidance of M.Á.L. All authors contributed to the preparation of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the research group TEP-209 (Junta de Andalucía) and by two projects: (1) “Protection of coastal urban fronts against global warming–PROTOCOL” (917PTE0538), (2) “Integrated verification of the hydrodynamic and structural behavior of a breakwater and its implications on the investment project–VIVALDI” (BIA2015-65598-P) and (3) “Laboratory testing and knowledge transfer for the development of sustainable strategies for marine energy harvesting (SUSME)” (PCI2019-103565).
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Appendix A. Atmosphere-Ocean Interaction Flume
The Atmosphere-Ocean Interaction Flume (CIAO) is part of the Environmental Fluid Dynamics Laboratory and focuses on the study of the coupling processes between the sea and the atmosphere. The marine atmospheric boundary layer (ABL) and the oceanic boundary layer (OBL) are full of small and large scale flow processes. The vertical dimensions of the ABL (on the order of 500 m), the OBL (on the order of 50 m) and the swell (on the order of 5 m) are small compared to the general height of the atmosphere and ocean. In contrast, boundary layer turbulence and waves play a major role on a large scale, as they regulate the functioning of the earth’s climate and weather systems. The coupling of the atmosphere and the ocean through these processes is particularly important and affects many scientific disciplines: climate prediction, wave breaking, bubble and spray generation, etc.
This is why the CIAO flume covers a large part of the processes involved in the coupling between the ABL and the OBL, and therefore has the capacity to simulate them:
- 1)
- Wave generation:
- -
- By means of a generation system with paddles and electric actuators, in both directions
- -
- By wind, either in the direction of the swell or in the opposite direction
- 2)
- Generation of currents, in both directions
- 3)
- Wave breakage
- 4)
- Rain generation
- 5)
- Heat exchange processes in the air-water interface
- 6)
- Behavior of different density biphasic fluids: lagoons and reservoirs
Thus, the new facility will provide the ability to study:
- 1)
- Consequences on ABL and OBL of processes such as wave generation or breaking
- 2)
- Heat balances in the boundary layers
- 3)
- Particle dynamics, droplet formation
- 4)
- Wave and wind actions on structures: offshore platforms, wind farms and offshore wind turbines
- 5)
- Wave power generation
- 6)
- Relations between heat exchange and life development: formation of ecosystems
Characteristics of the Flume
The CIAO flume has three main components:
- 1)
- A wave generation system (wave flume), of 1 m width and 0.70 m water depth design, 15 m length and the possibility of generating waves of a period of 1–5 s and up to 25 cm high.
- 2)
- A closed circuit wind generation system (wind tunnel), 24 m long and capable of generating winds of up to 12 m/s.
- 3)
- A double current generation system, to generate currents at double height, with a maximum generated current speed of 0.75 m/s.
The three components are reversible and independent, so that all phenomena can be simulated in equal or opposite directions of propagation, giving the equipment great versatility.
In addition, the equipment has a series of auxiliary systems that make it unique worldwide:
- 1)
- Rain generation system, from 75 to 300 mm/h, with water temperature variation between 10 and 30 °C.
- 2)
- Sediment collector for transport tests.

Figure A1.
Atmosphere-Ocean Interaction Flume (CIAO) pictures. (a) Inside of the flume with the ramp installed without water; (b) Scheme of the flume provided by the manufacturer (VTI S.L.).
Appendix B. Numerical Model IH-2VOF
The IH-2VOF numerical model [5] is based on the volume-averaged/Reynolds averaged Navier–Stokes equations (VARANS) in a two-dimensional domain. These equations are obtained when the RANS equations are integrated in a control volume. The volume of fluid (VOF) method is followed to compute free surface. Wave conditions are introduced in the model, imposing a velocity field and a free surface time evolution on one side of the numerical domain. The IH-2VOF model has been widely validated [20,21,22,23,24,25].
The current-wave flume of the IISTA laboratory was reproduced in the numerical model. The numerical set-up was calibrated by [24] and it is formed by a uniform grid on the y-axis, with a grid cell size of 0.5 cm, and horizontally (on the x-axis) grid with three regions: (i) a center region, 5 m long, containing the breakwater section with the finest resolution and a cell size of 1 cm; two regions (ii) at the beginning and (iii) at the end of the numerical wave flow, with a cell size of 2 cm. The total number of cells in the numerical domain was 1304 × 162. Active wave absorption was used at the generation boundary.
A non-overtoppable, smooth and impermeable 1:10 slope was tested under regular waves (Figure A2). Tests were performed, setting the value of T and increasing H to cover the maximum number of Iribarren numbers (always Ir > 1.5). Water depth was kept constant at h = 0.35 m. Tests conditions are summarized in Table A1.

Figure A2.
Diagram of the wave flume and position of wave gauges (dimensions in meters) in the numerical tests IH-2VOF.

Table A1.
Summarized test conditions for the numerical model.
Table A1.
Summarized test conditions for the numerical model.
| tan(α) | H(m) | T(s) | Tz(s) | h/L | HI/L | Ir |
|---|---|---|---|---|---|---|
| 1:10 | 0.002–0.14 | 1–2.2 | 0.8–2.19 | 0.09–0.36 | 0.0008–0.06 | 0.45–4.007 |
References
- Battjes, J.A. Surf similarity. Coast. Eng. 1974, 466–480. [Google Scholar] [CrossRef]
- Irribarren, C.R.; Nogales, C. Protection des ports. XVII Int. Navig. Congr. Sect. II Comm. 1949, 4, 27–47. [Google Scholar]
- Iversen, H.W. Laboratory study of breakers. Gravity Waves Circ. 1952, 52, 9–32. [Google Scholar]
- Galvin, C.J., Jr. Breaker type classification on three laboratory beaches. J. Geophys. Res. 1968, 73, 3651–3659. [Google Scholar] [CrossRef]
- Lara, J.L.; Losada, I.J.; Guanche, R. Wave interaction with low-mound breakwaters using a RANS model. Ocean Eng. 2008, 35, 1388–1400. [Google Scholar] [CrossRef]
- Lin, P.; Liu, P.L.-F. A numerical study of breaking waves in the surf zone. J. Fluid Mech. 1998, 359, 239–264. [Google Scholar] [CrossRef]
- Ting, F.C.; Kirby, J.T. Dynamics of surf-zone turbulence in a strong plunging breaker. Coast. Eng. 1995, 24, 177–204. [Google Scholar] [CrossRef]
- Ting, F.C.; Kirby, J.T. Dynamics of surf-zone turbulence in a spilling breaker. Coast. Eng. 1996, 27, 131–160. [Google Scholar] [CrossRef]
- Christensen, E.D.; Deigaard, R. Large eddy simulation of breaking waves. Coast. Eng. 2001, 42, 53–86. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, P.L.-F. A numerical study of bore runup a slope. Adv. Eng. Mech. Reflect. Outlooks 2005, 265–285. [Google Scholar] [CrossRef]
- Madsen, P.A.; Fuhrman, D.R. Run-up of tsunamis and long waves in terms of surf-similarity. Coast. Eng. 2008, 55, 209–223. [Google Scholar] [CrossRef]
- Lakehal, D.; Liovic, P. Turbulence structure and interaction with steep breaking waves. J. Fluid Mech. 2011, 674, 522–577. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, P.L.-F. A numerical study of swash flows generated by bores. Coast. Eng. 2008, 55, 1113–1134. [Google Scholar] [CrossRef]
- Díaz-Carrasco, P.; Moragues, M.V.; Clavero, M.; Losada, M.A. 2D water-wave interaction with permeable and impermeable slopes: Dimensional analysis and experimental overview. Coast. Eng. 2020. [Google Scholar] [CrossRef]
- Moragues, M.V.; Clavero, M.; Losada, M.A. Flow characteristics on plane slopes: An alternate similarity parameter. Impermeable and non-overtoppable case. Coast. Eng. 2020. under review. [Google Scholar]
- Goda, Y. Random Seas and Design of Maritime Structures; World Scientific: Singapore, 2010; ISBN 981-4282-39-1. [Google Scholar]
- Miche, R. Mouvements ondulatoirs des mers en profondeur constante on decroissant. Ann. Ponts Chaussées 1944, 2, 25–78. [Google Scholar]
- Svendsen, I.A. Wave heights and set-up in a surf zone. Coast. Eng. 1984, 8, 303–329. [Google Scholar] [CrossRef]
- Bruun, P.; Johannesson, P. A Critical Review of the Hydraulics of Rubble Mound Structures; Report no. 3; Division of Port and Harbour Engineering, Norwegian Institute of Technology: Trondheim, Norway, 1974. [Google Scholar]
- Pérez-Romero, D.M.; Ortega-Sánchez, M.; Moñino, A.; Losada, M.A. Characteristic friction coefficient and scale effects in oscillatory porous flow. Coast. Eng. 2009, 56, 931–939. [Google Scholar] [CrossRef]
- Lara, J.L.; Losada, I.J.; Maza, M.; Guanche, R. Breaking solitary wave evolution over a porous underwater step. Coast. Eng. 2011, 58, 837–850. [Google Scholar] [CrossRef]
- Maza, M.; Lara, J.L.; Losada, I.J. A coupled model of submerged vegetation under oscillatory flow using Navier–Stokes equations. Coast. Eng. 2013, 80, 16–34. [Google Scholar] [CrossRef]
- Guanche, R.; Iturrioz, A.; Losada, I.J. Hybrid modeling of pore pressure damping in rubble mound breakwaters. Coast. Eng. 2015, 99, 82–95. [Google Scholar] [CrossRef]
- Vílchez, M.; Clavero, M.; Lara, J.L.; Losada, M.A. A characteristic friction diagram for the numerical quantification of the hydraulic performance of different breakwater types. Coast. Eng. 2016, 114, 86–98. [Google Scholar] [CrossRef]
- Formentin, S.M.; Zanuttigh, B. A new method to estimate the overtopping and overflow discharge at over-washed and breached dikes. Coast. Eng. 2018, 140, 240–256. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).