A DES-SST Based Assessment of Hydrodynamic Performances of the Wetted and Cavitating PPTC Propeller

Abstract

The paper describes an investigation of the hydrodynamic performances of a five-bladed controllable pitch propeller, whose geometry was provided by Schiffbau-Versuchsanstalt (SVA) Potsdam GmbH Model Basin. Both cavitating and non-cavitating regimes are numerically simulated for different advance ratio coefficients. The numerical approach is based on a finite volume approach in which closure to the turbulence is achieved through detached eddy simulation (DES). Propeller open water (POW) characteristics are computed, and the numerical solutions are validated through extensive comparisons with experimental data. In addition, the bi-phasic flow for the cavitating regime is simulated, for which comparisons with the cavitation sketches are performed to check the ability of the solver to estimate the cavitation extent. Grid convergence tests are performed for both working regimes together with validation and verification checks, not only to size the level of the numerical errors, but also to prove the robustness of the chosen numerical approach. Finally, a set of final remarks will conclude the present research.

1. Introduction

For a ship propeller the cavitation initiation may lead to a significant performance degradation and can produce vibration and noise. In the early days of the past century, the propeller design milestones focused on cavitation avoidance for the widest possible range of working conditions. Larger blade areas for propellers operating at low revolutions seemed to be a proper choice in spite of the fact that in many cases the propulsive efficiency was lowered due to the significant frictional losses associated with a large blade surface. Reducing ship operating costs as well as lowering pollution determined an overall enhancement of the efforts devoted to heightening the efficiency of the propulsion. Under such circumstances, it became clear that a decrease of the margin of cavitation-free operation as well as the allowance for some controlled amounts of cavitation on the propeller blades were expressly required. Nevertheless, this new task had to be achieved only if the negative impacts of noise production and propagation and vibration and erosion could be efficiently controlled.

Obviously, an accurate prediction of the cavitation behavior of the propeller, as a function of loading conditions, is crucial in balancing difficult constraints in demanding design tasks. A propeller should preferably be ensured that meets the requirements relating not only to its economic operation, but also from the point of view of the comfort conditions on board in terms of noise and vibration levels, prior to the ship construction. In failing to meet these conditions, the cost of manufacture and repair can easily increase the cost of a ship project. Having these circumstances given, the propeller design represents a challenging task in balancing properly different pros and cons within which it is crucially important to accurately estimate the characteristics of cavitation and not only its existence or extent. When analyzing numerically the cavitation, one should be aware of the co-existence of phase change and vortical structures that create a complex flow structure on the propeller since they both involve very small-scale dynamics in time and space. From this viewpoint, a complete understanding of the underlying physics becomes of crucial importance, either in preventing or in controlling its occurrence and development on the propeller blades.

Historically, theoretical investigation of propeller behavior and its associated hydrodynamic performances originates in the beginning of the previous century with the lifting line theory approaches based on the concept of circulation and the Kutta-Joukowski theorem. Although not a straightforward approach, the method was successfully used for predicting the lift and drag forces which were developed by a series of wing sections that geometrically describe a propeller blade. Although based on many assumptions which lowered its accuracy, the method provided more accurate predictions than those based on the use of the empirical propeller diagrams. A step ahead was taken in addressing the shortages of the lifting line-based methods in the 1950s by the lifting surface approaches, even though the approaches could not be used for real ship propeller geometries due to insufficient computing power at that time. The earliest lifting surface approaches were based on mode functions which prescribed continuous distributions of surface singularities. At that time, the mode function approach was the common procedure for solving lifting-line or two-dimensional common wing section problems. For lifting surfaces that had to fit the propeller blades, the mode functions required a complicated mathematical treatment, therefore their ability to describe arbitrary geometries was rather poor. The second generation of lifting surface methods was developed around the late 1970s when sufficient computer power became available. Mostly, these methods could handle arbitrary geometries, but could not physically consider the true blade thickness, nor the propeller hub. Despite a theoretical inferiority, vortex-lattice methods gave results of comparable quality to latter panel methods in benchmark tests of the International Towing Tank Conference (ITTC) for propellers with moderate skew. A valuable introspection of the lifting line and lifting surface theories as well as a comprehensive analysis of the relation between the two is given in [1].

Real progress was made in the community when the boundary element methods (BEM) began to be used to solve the problem. Because of its certain merits, the panel method seen as an implementation of the BEM, quickly became a prevailing industry standard since it is simple to implement and accurate enough in most of the predictions. Marine propellers operate behind the ship and are subject to a non-uniform inflow due to the ship wake. Due to the spatial variation of the upstream conditions, the propeller blades are subject to time-dependent inflow conditions causing an unsteady flow field around the blades. This flow field is responsible for unsteady loads and often for the occurrence of unsteady cavitation phenomena. The unsteady loads are important in the analysis of shaft vibrations, and the unsteady pressure field is important for cavitation analysis and pressure fluctuations. Hsin [2] was one of the first authors to carry out this analysis with a low-order BEM code. The method was also applied to ducted propellers by Kinnas et al. [3]. The various approaches developed since then may differ in the detailed numerical implementations, surface discretization used and, more importantly, in the assumptions made for modeling the wakes behind the propeller blades. One of the most serious problems that usually occurs when the BEM method is used is the accuracy with which the propeller and wake surfaces can be reproduced by the panels used for discretization.

The most convenient way to represent a propeller is to use rectangular panels [4], which are simple and easy to calculate, in spite of the fact that there will always be gaps between adjacent rectangular panels. Obviously, poor panelization affects the accuracy of the calculations. As a remedy, several improvements based on the B-spline schemes were gradually proposed to make the spatial interpolation of the singular point of the panel elements more accurate and generate reasonable surface meshes [5,6,7]. The hydrodynamic performance prediction when using the B-spline high-order panel method led to a lower number of panels, therefore a higher computational efficiency. However, the effect of the singularities on the numerical instability proved to be difficult to overcome in the high-order methods. In contrast, a constant potential strength with an equal singularity density on a panel seems more stable in the numerical computation, therefore more studies are still required to find the most appropriate, as comprehensively shown in [8].

With the advent of both hardware power and new numerical methods, computational fluid dynamics (CFD) research was focused on finding a solution for the Navier‒Stokes and conservation of mass equations written for the viscous flow. Although less efficient than the potential methods because of the higher CPU costs, the viscous solvers proved to be by far more accurate. Moreover, they could provide more information concerning the local flow features in areas otherwise impossible to be treated in the potential-based methods. Different numerical techniques were sequentially developed to solve the partial differential equations which describe the flow, out of which the finite volume seems to be the most popular for the time being. An important issue of all these methods is the turbulence treatment. Although the direct numerical simulation, in which the whole range of spatial and temporal scales of the turbulence are resolved, is by far the most accurate, it still remains the least attractive one because of its prohibitive computational costs. As an alternative, large eddy simulation (LES), in which the smallest length scales, which are the most computationally expensive to resolve, are simply ignored by filtering the governing equations, gained in popularity recently [9,10,11].

The easiest to implement and the cheapest method is based on averaging the turbulence characteristics; the Reynolds averaged Navier-Stokes equations (RANS) differ only by the turbulence model employed. Algebraic, zero- one- and two-equation models were proposed as a closure to the RANS equations. The most popular ones are the explicit algebraic Reynolds stress model EARSM [12] and the $k-\omega$ SST, which is based on the Menter’s model proposed in [13]. A special class between the LES and the RANS approaches are the detached eddy simulation (DES) and delayed detached eddy simulation (DDES) methods, which combine the advantages of the two [14,15]. The main advantage of the viscous flow solution method is the possibility of a complete description of the flow features for a wide spectrum of applications, ranging from simple propeller analyses at both model and full scales [16,17,18] to self-propulsion in waves [19] or during maneuvers [20]. They can be relatively easy to apply for various problems such as ventilation of the propellers [21,22,23], oblique flow [24,25,26], wake analysis [27,28,29] and cavitation [30,31,32,33].

Within the above context, the present paper describes a numerical investigation aimed at clarifying the details of the flow around the VP 1304 controllable pitch propeller, known in the naval architecture community as the Potsdam propeller test case (PPTC). The work continues a previous study of the author [34] which was devoted to the assessment of the scale effects on the P1727 (PPTC II) propeller. In the present study, the numerical simulations are performed for both wetted and cavitating regimes for a series of eight different advance ratio coefficients. The software package used to solve the task of the present research is Fine^TM/Marine, whose main solver is ISIS-CFD, which is a finite volume based one. Closure to turbulence is achieved through the DES model. A grid convergence test as well as verification and validation computation will be provided. Comparisons with the experimental data will also be given to size the appropriateness of the numerical approach and the robustness of the flow solver.

2. Geometric Setup and Computational Meshes

2.1. Propeller Characteristics and Computational Conditions

The VP 1304 propeller is a five blades, significantly skewed, controllable pitch propeller designed at Potsdam Model Basin and proposed as a benchmark case for the 2011 Symposium on Marine Propulsors for which the experimental conditions as well as the measurement data were publicly provided by the organizers. Two sets of complete computations are performed in the present study, i.e., firstly the non-cavitation regime then the cavitation one. In the first case, the fluid domain is unbounded, whereas in the second one the propeller is placed in a cavitation tunnel with a square cross-section of 0.85 m × 0.85 m with rounded corners, as Figure 1b–e bear out. To help the reader easily understand the computation settings, the figure also depicts the boundary condition formulations that will be discussed later in the paper. As Figure 1 shows, the whole propeller is considered in the numerical simulations, regardless of the associated higher CPU costs. The reason for not considering only a single blade is the need to avoid the periodic boundary condition, which leads to an unwanted slight distortion of the solution, especially for the heavy loading working regimes. Seemingly, the solution distortion is due to the periodic boundary condition, which is only first order accurate while the solution at interior nodes is of a second order of accuracy.

Being a controllable pitch propeller, the experimental model has a gap of 0.3 mm between the roots of the blades and the hub. For reasons related to discretization convenience, that gap was simply neglected in the numerical approach reported here.

The main geometric particulars of the PPTC propeller are tabulated in

Table 1. Main particulars of the Potsdam propeller test case (PPTC) propeller.

Parameter	Symbol	Units	Values
Diameter	D	[m]	0.250
Pitch ratio	P0.7/D	[–]	1.635
Area ratio	AE/A0	[–]	0.779
Chord length	c0.7	[m]	0.1042
Skew angle	θ	[°]	18.837
Hub ratio	dh/D	[–]	0.300

, whereas the computational conditions for both the non-cavitating and cavitating regimes are provided in

Table 2. Experimental and computational conditions.

Computation	Parameter	Units	Values
W/O cavitation	${\rho }_w$	kg/m3	998.2
	${\mu }_w$	kg/m·s	1.003 × 10−3
W cavitation	${\rho }_w$	kg/m3	997.44
	${\rho }_v$	kg/m3	0.01927
	${\mu }_w$	kg/m·s	1.003 × 10−3
	${\mu }_v$	kg/m·s	8.8 × 10−6

, in which $\rho$ and $\mu$ are the density and dynamic viscosity of the working fluids, whereas the subscripts “w” and “v” stand for water and vapor, respectively. The fluid properties correspond to a temperature of 15.6 °C for the open water propeller (POW) computations. For the cavitation computations the water temperature was 23.2 °C.

For open water performance calculations, the propeller is arranged in a pulling configuration, the same as in the open water experimental tests. The computational domain depicted in Figure 1a is of a cylindrical geometry, whose diameter is five times the propeller diameter, while its length is 13.5 times the propeller diameter, out of which 4.5 diameters are upstream of the propeller, which is considered as being enough to avoid the influence of the inflow boundary condition imposition on the flow around the propeller. For all the calculations of the flow inside the tunnel, the propeller is arranged in a pushing configuration. As said above, the cross-section of the computational domain is 0.85mx0.85m and the domain extends 4.5 propeller diameters at the upstream and 9 times the propeller diameter at the downstream, as shown in Figure 1e.

2.2. Computational Grids

Several computational meshes are generated in the Hexpress mesh builder, which is an integrated part of the Fine^TM/Marine software suite. Since the computations refer to two distinctive regimes, the minimal grid generation requirements are substantially different. That is, because of the differences between the non-cavitating and cavitating flow set-up, in the first case only restrictions related to the propeller surface and its potentially relevant surroundings are imposed. However, for the simulation of the propeller placed inside the cavitation tunnel, the conditions change since the tunnel solid walls must be taken into consideration as well. Four different grids are generated for each computational case, so that the grid convergence test can be performed. The finest grid for the non-cavitation computations consists of 63.48 M cells, whereas the coarsest consists of 8.27 M cells. In the following, the four grids will be identified as coarse, medium, fine and very fine, respectively.

The finest grid for the cavitation computation consists of 73.148 M cells, while the coarsest contains 11.927 M cells. They will be identified similarly with the first set of computations. For the sake of consistency, the discretization settings around the propeller are maintained at the same values as for the open water grid. The only difference that is allowed between the two computational cases regards the boundary layer close to the solid walls of the tunnel when the cavitation case is computed. Figure 2 depicts six different views: the grids around the open water propeller, Figure 2a‒c, and around the propeller working in the cavitation tunnel, Figure 2d‒f. As shown in the figure, the grid is mostly unstructured in both cases, a fact that simplified the discretization in the areas where the geometry is either discontinuous, see Figure 1a,b, or in the proximity of the edges and the tips of the blades. Special requirements such as smoothness, clustering and orthogonality inside the viscous boundary layer are imposed. Aside from that, in certain regions of the computational domain, such as the wake of the tips and the roots, additional refinement is imposed so that the accuracy of released vortices not be affected by the numerical dissipation. Computations in the wetted propeller case are performed by using a rotating frame method, whereas the cavitation simulations employ a sliding grid technique. The sliding grid denoted by SG in Figure 2e was built so that the grids near the sliding interface are almost structured. The grid refinement around the interface was carefully controlled so that no jump in cell size across the interface was allowed.

In both cases the minimum grid size is chosen so that the resulting y⁺ remains below 0.25 everywhere on the propeller surfaces. This condition led to a maximum cell dimension of 10⁻⁶ m measured normal to the solid walls. A number of 41 layers of cells are placed inside the viscous boundary layer of the propeller in both computational cases, whereas on the solid walls of the cavitation tunnel only 22 layers are used because of the limitations imposed by the existing hardware resources, as depicted in Figure 2d. The growth ratio of the cells through the inflation layers is 1.15 for all solid surfaces of the propeller in both cases, whereas a ratio of 1.2 is imposed for the tunnel walls.

3. Numerical Approach

The ISIS-CFD viscous flow solver, part of the Numeca Fine-Marine^TM software package, is employed in the present research. The solver is based on the finite-volume method for constructing the spatial discretization of the transport equations on mostly unstructured grids. The simulation is performed in a global approach in which the momentum and mass conservation equations are solved. Closure to the turbulence is achieved through the shear stress transport DES model, which provides the accuracy of LES for highly separated flow regions and computational efficiency of RANS in the near-wall regions. Fluxes are built using the AVLSMART bounded difference scheme, which is based on the third order QUICK scheme. The velocity field is obtained from the momentum conservation equation and the pressure field is then solved from the mass conservation constraint transformed into a pressure equation. The entire discretization is fully implicit and second order accurate both in space and time, according to which an implicit scheme is applied for the discretization in time, whereas a second order three-level time scheme is used for the time-accurate unsteady computation. Computations are performed in two successive steps. At first, the viscous flow is computed based on the $k-\omega$ SST turbulence model and it runs until the solution stabilizes within 1% limit of variation in the last 10% of the computational time. Six iterations for a time step are imposed for this first set of runs. Secondly, the computation is restarted after the turbulence model is switched to the DES for a few more seconds until the final convergence. At this stage, the imposed number of iterations per time step is augmented to 16.

For the open water simulations, the boundary conditions are of Dirichlet type. That is, a Dirichlet condition is imposed for the incoming velocity at the upstream boundary and on the exterior boundary, as well as for the pressure at the outlet. However, when the flow around the propeller placed in the tunnel is computed, the Neumann condition, in terms of the pressure $\left(\partial p/\partial n=0\right)$, is imposed at the downstream boundary, as shown in Figure 1d. The no-slip condition is used on all the solid boundaries of the propeller, whereas the wall function is imposed on the cavitation tunnel walls. In ISIS-CFD the choice of default free-stream values is ${\omega }_{\infty }=\lambda U_{\infty }/D$, ${\mu }_{t\infty }={10}^{-3}{\mu }_t$, $K_{\infty }={\mu }_{t\infty }{\omega }_{\infty }/\rho$, where $D$ is the propeller diameter and $U_{\infty }$ is the incoming velocity at the far inlet. $\lambda$ is a factor of proportionality, which is recommended to be between 1 and 10. These limits are compatible with the values recommended for boundary layer flows, therefore $\lambda =10$ was chosen [34]. Since free-shear layers are more sensitive to small free-stream values of ${\omega }_{\infty }$ and larger values of $\omega$ are imposed in the free-stream, at least $\lambda =40$ for mixing layers, increasing up to $\lambda =80$ for round jets. Wall boundary conditions are taken as $K=0$ and $\omega =60\mu /\beta \rho {\left(\mathsf{\Delta }y\right)}^2$, where $\mathsf{\Delta }y$ is the distance of the first point away from the wall and such that $y^{+}<1$.

Various approaches to cavitation modeling have been proposed so far. Obviously, the most commonly used ones are based on the volume of fluids (VOF) approach, coupled with a model for the exchange from a liquid to vapor phase (vaporization) and vice versa (condensation). These models are commonly referred to as homogenous multiphase models. In the present case, the numerical model is based on the resolution of a transport equation in which source terms are added to model the vaporization and condensation of the liquid/vapour co-existent phases.

The Sauer, Merkle and Kunz models are implemented in the ISIS-CFD solver. Since in the Sauer model the nuclei density, which is unknown a-priori, has to be provided, the model has been disregarded. The justification for the choice resides in the fact that the accuracy of the inputs is significantly subject to a fortunate choice rather than to a consistently motivated reason. Under such circumstances, the only remaining choice was between the Merkle and Kunz models for which the input data are the liquid product coefficient, liquid destination coefficient and cavitation reference length. Based on previous numerical simulation achievements of the author [32], the Kunz model is chosen for the numerical simulation [35]. Basically, the ISIS-CFD solver considers the cavitation as being based on the resolution of a transport equation similarly to what is done for free surface, although the significance of the sheet surface is completely different to that which concerns the water waves. In this particular case, the source terms, whose mathematical expression is given in [35], are used in modelling the vaporization and condensation of the two phases.

4. Results and Discussion

In the following, the computed solutions will be presented and discussed separately for each of the two cases considered, i.e., non-cavitating (wetted) and cavitating working regimes.

4.1. Wetted Propeller

4.1.1. Grid Convergence Test

Four different computational grids consisting of 8.27, 15.98, 31.09 and 63.48 million cells respectively, are considered in the following to host the grid convergence test computations. Let these grids be denoted by coarse, medium, fine and very fine for the convenience of a proper identification of each computational case. The thrust and torque coefficients are computed for a series of eight advance ratios ranging from 0.6418 to 1.6563 and compared with the corresponding experimental data [36], as tabulated in

Table 3. Grid convergence test for the thrust coefficient. Wetted propeller case.

Parameter		KT
J		0.6418	0.8021	0.961	1.1212	1.283	1.4422	1.6021	1.6563
EFD		0.6084	0.517	0.4293	0.3354	0.246	0.1576	0.0491	0.009
CFD	Coarse	0.5772	0.4906	0.4085	0.3215	0.2364	0.1514	0.0471	0.0086
	│ε│ %	5.12	5.11	4.84	4.14	3.89	3.93	4.02	4.47
	Medium	0.5821	0.4960	0.4123	0.3235	0.2392	0.1533	0.0476	0.0087
	│ε│ %	4.32	4.07	3.95	3.54	2.77	2.72	2.98	3.35
	Fine	0.5891	0.5010	0.4165	0.3267	0.2417	0.1546	0.0480	0.0087
	│ε│ %	3.17	3.09	2.98	2.58	1.76	1.91	2.17	2.91
	Very fine	0.5973	0.5271	0.4198	0.3397	0.2435	0.1551	0.0483	0.0092
	│ε│ %	1.82	1.95	2.21	1.28	1.02	1.59	1.63	2.22

and

Table 4. Grid convergence test for the torque coefficient. Wetted propeller case.

Parameter		10 KQ
J		0.6418	0.8021	0.961	1.1212	1.283	1.4422	1.6021	1.6563
EFD		1.3669	1.1994	1.0399	0.8606	0.6832	0.5029	0.2678	0.1786
CFD	Coarse	1.2973	1.1397	0.9876	0.8235	0.6505	0.4801	0.2563	0.1693
	│ε│ %	5.09	4.98	5.03	4.31	4.78	4.54	4.28	5.23
	Medium	4.8645	4.7624	4.8127	4.1410	4.5998	4.3788	4.1336	5.0140
	│ε│ %	4.43	4.37	4.32	3.92	3.77	3.55	3.42	4.13
	Fine	1.3221	1.1615	1.0065	0.8342	0.6620	0.4879	0.2600	0.1725
	│ε│ %	3.28	3.16	3.21	3.07	3.11	2.99	2.92	3.42
	Very fine	1.3291	1.1682	1.0111	0.8412	0.6657	0.48845	0.2607	0.1731
	│ε│ %	2.77	2.60	2.77	2.25	2.56	2.87	2.65	3.08

. In all computations the rate of revolution is kept constant at a value of 600 rpm, whereas the inflow speed corrected at experiments with idle torque and gap force is varied to achieve the different advance ratios.

For the sake of consistency, all the computations employ the DES turbulence model and all the reported solutions are computed for 25 s physical time when the propeller has already performed 250 complete rotations. All the parallel computations are performed on 120 processors, which means that for the finest grid case, a number of about 529,000 cells are computed on each processor.

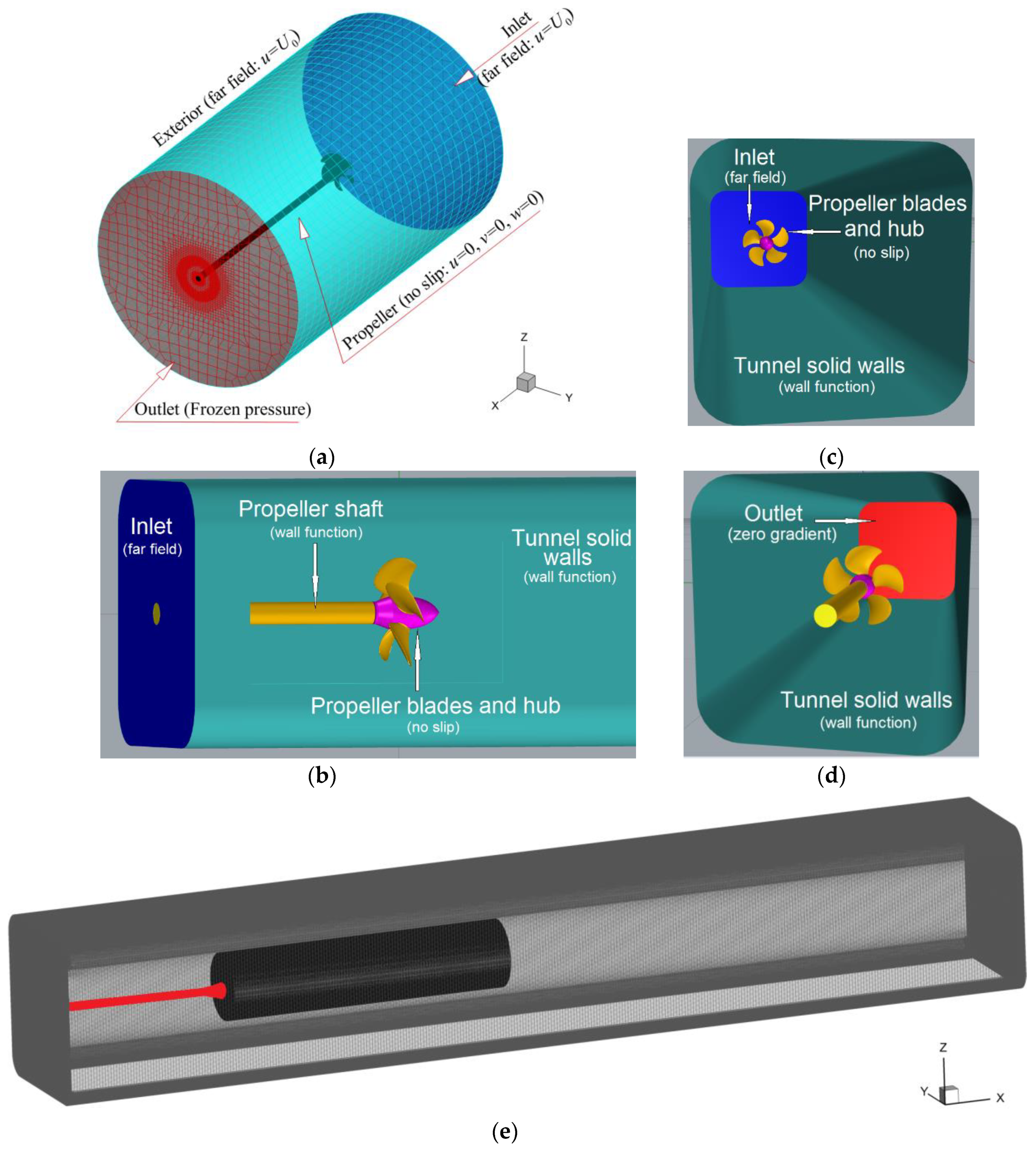
Automatic mesh refinement is performed based on sensors placed next to solid walls and inside the wake. Special attention to the quality criteria such as orthogonality, smoothness and clustering inside the areas next to the solid boundaries is paid during the generation process. Areas of rather heavy clustering are placed around the blade edges and tips and hub and shaft, as depicted in Figure 2. Aside from that, an annular volume of grid refinement is generated in the wake of the propeller, therefore in the region where large gradients of the flow parameters are expected to occur. In the immediate proximity of the propeller, the grid lines perpendicular to the wall are refined substantially to maintain a $y^{+}$ value less than unity for the first layer of grid cells.

All the computations are performed on a high-performance computer with 624 Intel E5 2680 v3 processors with 12 cores with a frequency of 2.5 GHz and 3.3 GHz for the turbo boost regime. In the very fine mesh computational case, an average of 0.205 millisecond per mesh point was necessary. As said before, each simulation is performed for 25 s, out of which the rotational acceleration time done on a half sinusoidal law is imposed for two seconds. A time of 15 to 17 s is sufficient to achieve the convergence of both thrust and torque computed coefficients.

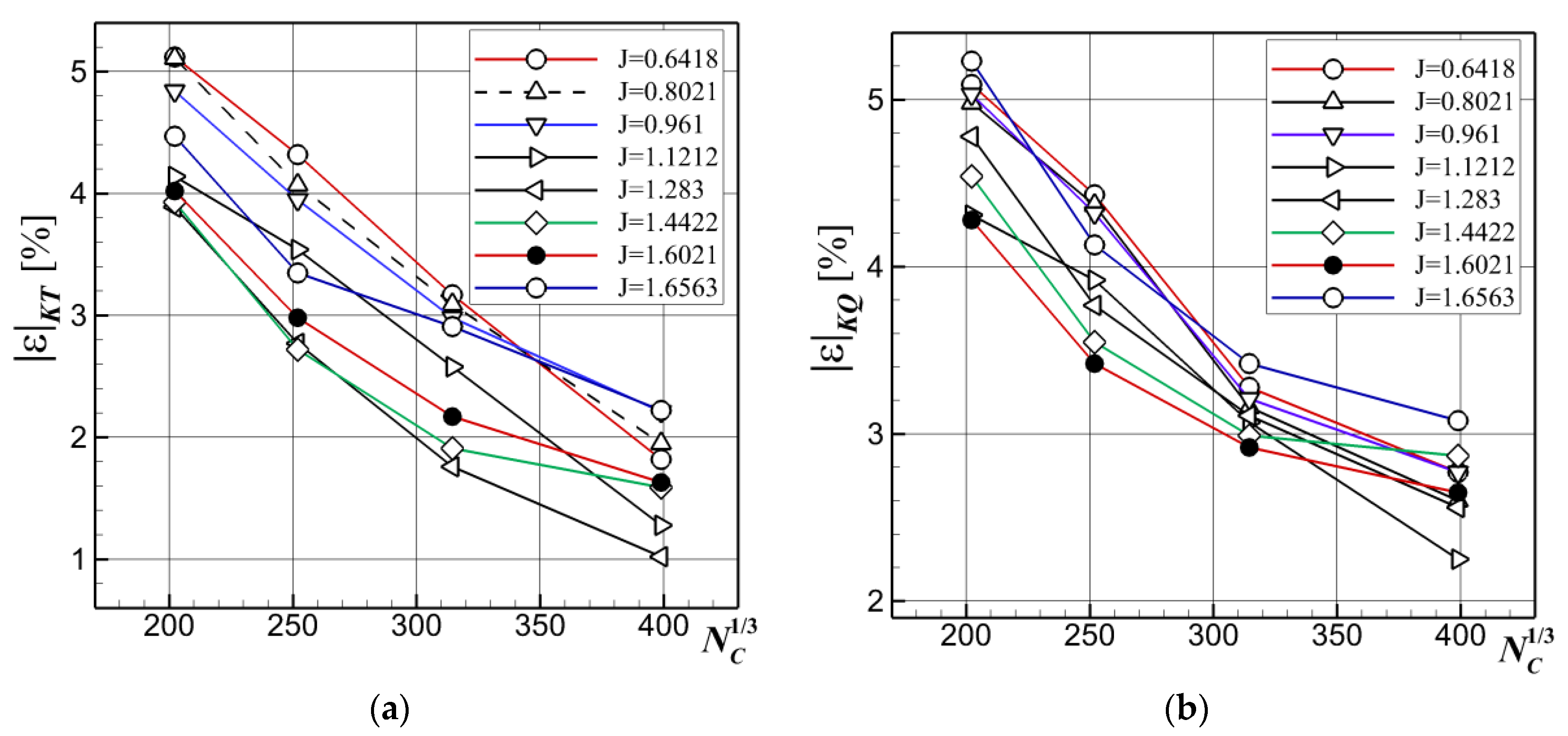
The variation of the computed errors of the numerical solutions compared to the experimental data [36] is depicted in Figure 3a for the thrust coefficient and Figure 3b for the torque coefficient. The reason for reporting the solutions in the abscissae to the cubic root of the number of cells of a given computation is that when using an unstructured grid it is difficult to define another relevant parameter to describe locally the grid resolution.

Obviously, the general trend of the solutions shows that with the increase of the accuracy of the discretization, the errors are monotonically decreasing, a fact that is sustained by the theory of numerics. Nevertheless, there are some advance coefficients for which variation slope does not wholly sustain the above statement, a fact which is not generally in conflict with the general rule of the monotonic decrease of the computational error with the increase of the discretization accuracy. As an overall conclusion based on Figure 3, the reader may notice that the grid convergence test sustains not only the consistency of the numerical model used in the present study, but also the robustness of the solver.

The grid uncertainty is further evaluated by following the methodology described in [37] for monotonic convergence. The verification and validation will be carried out only for the J=1.283 case, which produced the smallest error of the thrust coefficient compared to the experimental data. Let the four meshes considered in the grid convergence computations be denoted by M1…M4, where M1 corresponds to the coarse mesh and M4 to the very fine one. The grid ratio (r_G), the associated relative error between the K_T computed on the very fine mesh M4 and the fine mesh M3, ${\epsilon }_{43}\%K_{T4}$, the ratio between the estimated order of convergence and the theoretical order of convergence, p_G/p_Gth, the grid uncertainty, U_G%M₄, the experimental uncertainty, U_D%D, and the validation uncertainty, U_v%, are tabulated in

Table 5. Verification and validation for the thrust and torque coefficients computed for J = 1.283.

Parameters	${\mathit{r}}_{\mathit{G}}$	${\mathit{\epsilon }}_{43}\mathit{\%}{\mathit{K}}_{\mathit{T}4}$$\mathbf{or}{\mathit{\epsilon }}_{43}\mathit{\%}{\mathit{K}}_{\mathit{Q}4}$	${\mathit{p}}_{\mathit{G}}/{\mathit{p}}_{\mathit{G}, \mathit{t}\mathit{h}}$	${\mathit{U}}_{\mathit{G}}\mathit{\%}{\mathit{M}}_4$	${\mathit{U}}_{\mathit{D}}\mathit{\%}\mathit{D}$	${\mathit{U}}_{\mathit{V}}\mathit{\%}$
$K_T$	2.042	0.740	1.023	1.583	1.0	1.872
$10 K_Q$	2.042	0.550	1.023	1.583	1.0	1.872

. p_G,th in Table 5 is the theoretical order of accuracy, which is the order of convection scheme, whereas the validation uncertainty is $U_V=\sqrt{{\left(U_G\%M_4\right)}^2+{\left(U_D\%D\right)}^2}$. The relative error between the solution computed on the finest mesh M4 and the experimental data for the thrust coefficient is smaller than the Richardson-based validation numerical uncertainty, therefore the K_T prediction can be considered as being validated. A similar conclusion can be withdrawn for K_Q.

4.1.2. Propeller Performances and Flow Analysis

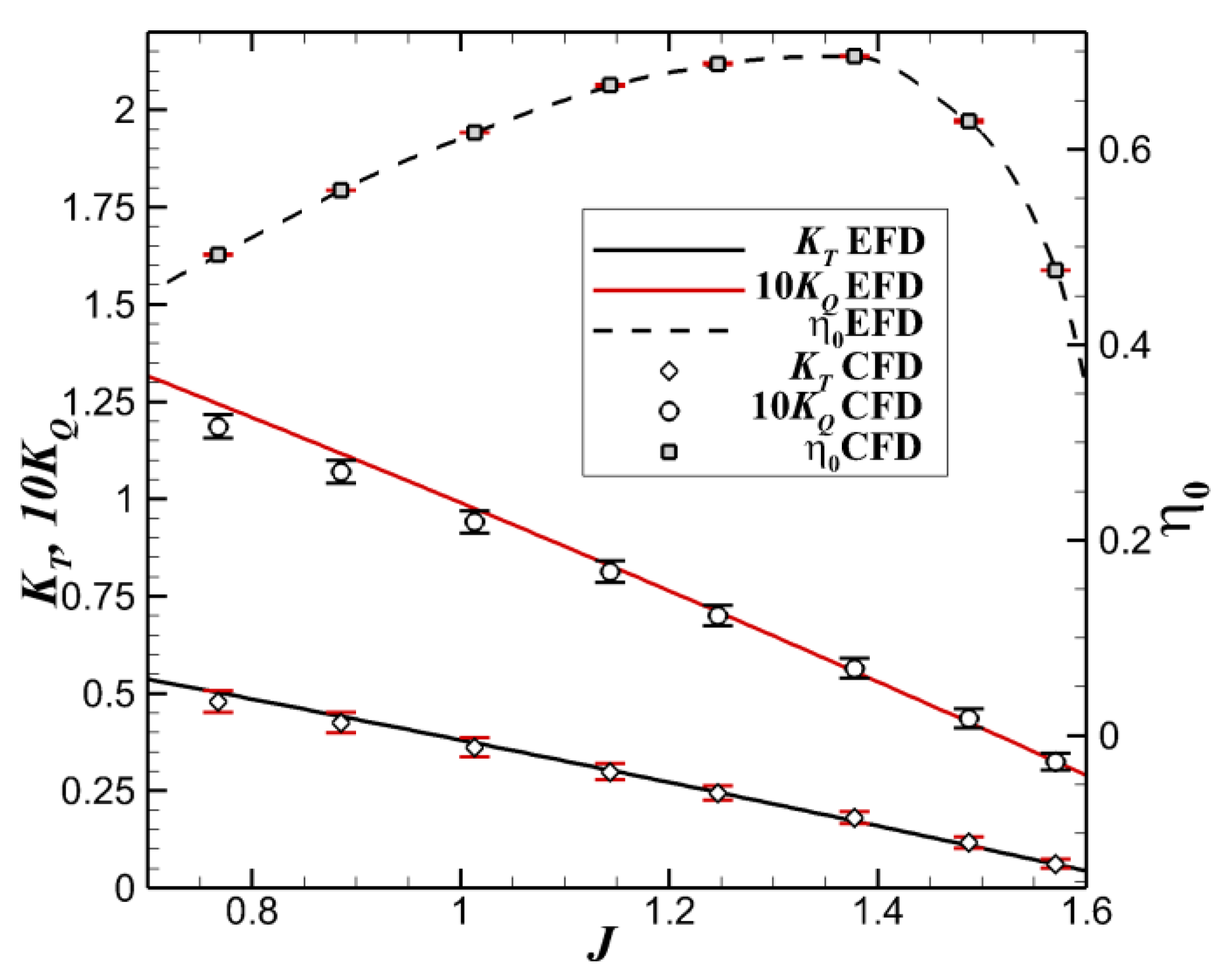
Having carried out the grid convergence test, in the following only the solutions computed on the very fine grid will be reported and discussed. Prediction of thrust and torque realized by the propeller is performed first. The computed propeller performance coefficients are tabulated in

Table 6. Comparison between the open water propeller performance coefficients measured and computed.

J	KT		│ε│ %	10KQ		│ε│ %	ηO		│ε│ %
	EFD	CFD		EFD	CFD		EFD	CFD
0.6418	0.6084	0.5973	1.8245	1.3669	1.3291	2.7654	0.4550	0.4593	0.9451
0.8021	0.5170	0.5271	1.9536	1.1994	1.1682	2.6013	0.5500	0.5763	4.5636
0.9610	0.4293	0.4198	2.2129	1.0399	1.0111	2.7695	0.6310	0.6353	0.6768
1.1212	0.3354	0.3397	1.2821	0.8606	0.8412	2.2542	0.6950	0.7210	3.6061
1.2830	0.2460	0.2435	1.0163	0.6832	0.6657	2.5615	0.7350	0.7473	1.6459
1.4422	0.1576	0.1551	1.5863	0.5029	0.4884	2.8733	0.7190	0.7292	1.3853
1.6021	0.0491	0.0483	1.6293	0.2678	0.2607	2.6512	0.4670	0.4726	1.1849
1.6563	0.0090	0.0092	2.2222	0.1786	0.1731	3.0795	0.1330	0.1402	5.1355

for all the advance ratios and compared with the corresponding experimental data reported in [36]. The level of errors is limited to 2.22% for the thrust coefficient and to 3.08% for the torque coefficient. A slight underestimation of the thrust may be seen for almost all the advance ratios. In spite of that fact, it is worth mentioning that the computed and experimental curves almost overlap and their slopes are practically coincident, as depicted in Figure 4. Things are rather similar for the torque coefficient, although the level of the errors is slightly higher. Seemingly, the reason behind the differences is related to the small values of the torque, a fact that sometimes brings numerical difficulties, although all the computations reported here were performed in double precision. The highest level of errors for the open water efficiency coefficients reaches a value slightly larger than 5% for the highest advance ratio, at which the thrust and torque have the lowest values over the domain, as Figure 4 bears out.

The numerical solutions reported here are very similar to those reported in [38], even though the solvers were different and the closure to turbulence was achieved by using different models. Moreover, the present solutions are in a good agreement with most of those reported in [39], where various solvers were used to solve the benchmark case of the PPTC propeller by 14 attendees of the symposium. That is, the same trend was noticed in the concluding remarks of the final report of the symposium, which noticed that the numerical solutions reported by most of the participants slightly underestimated the thrust and torque coefficients as well.

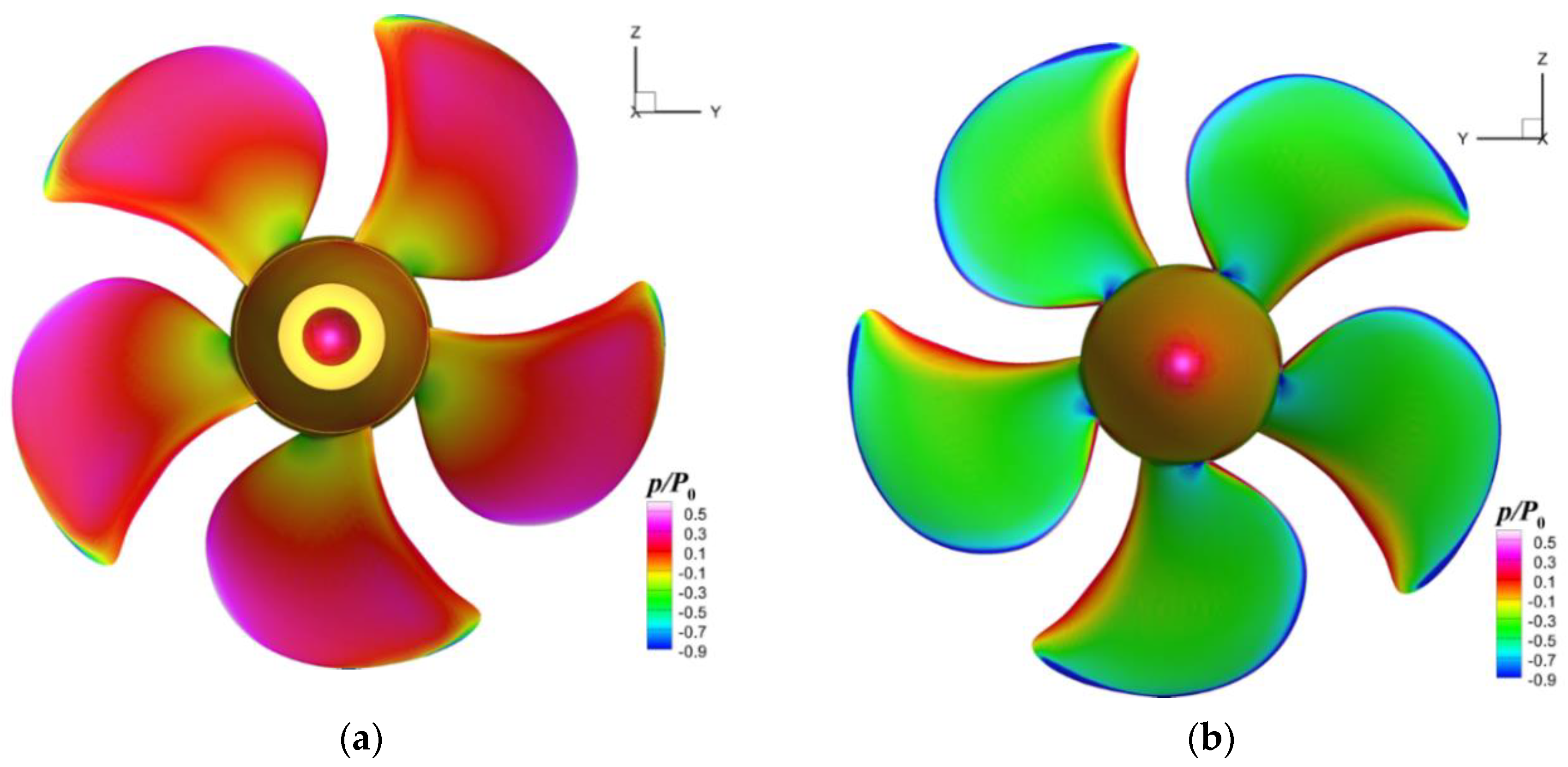
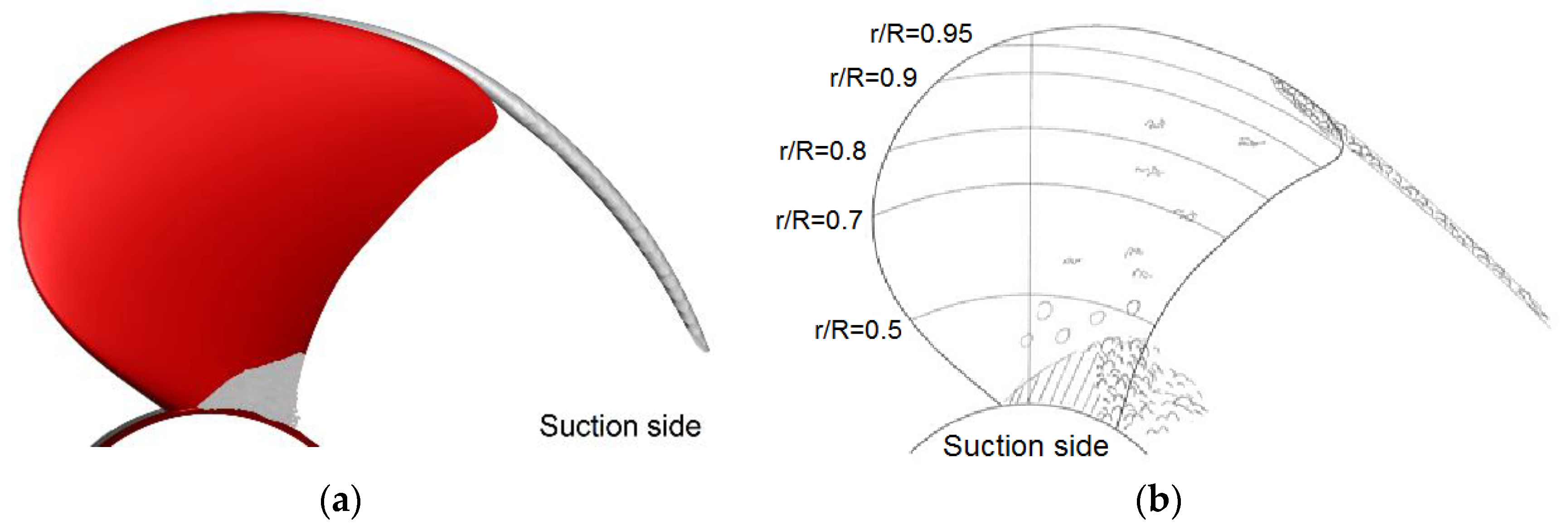
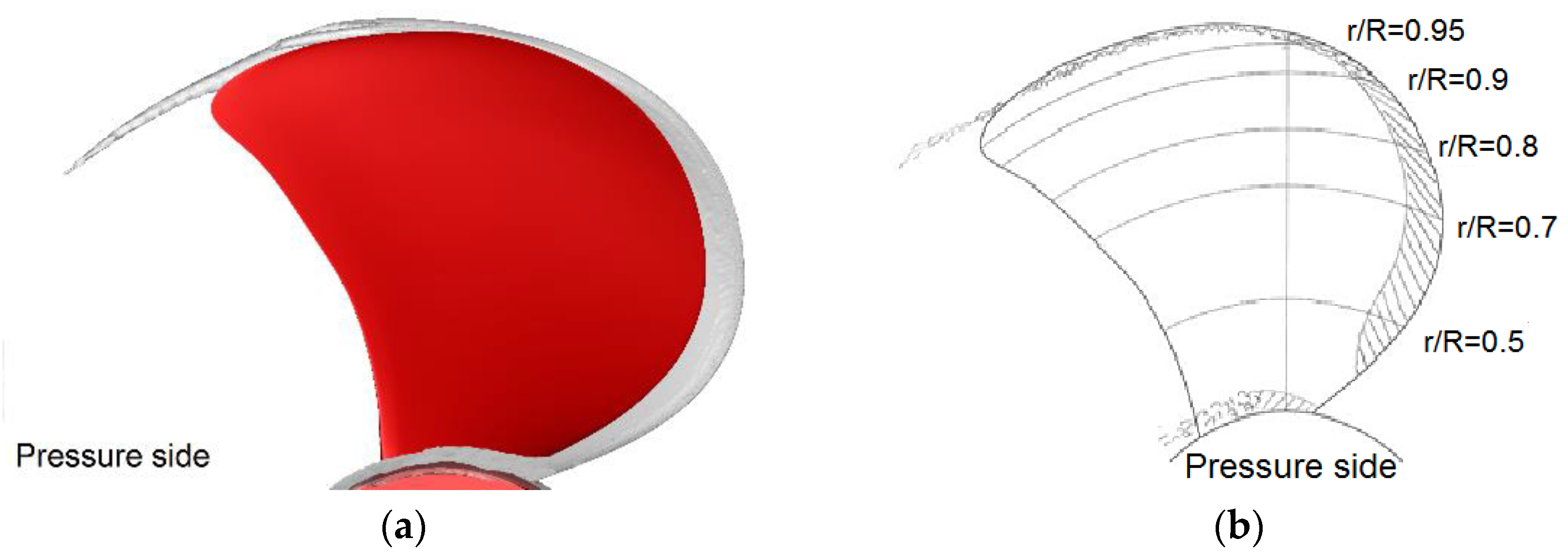
In terms of pressure distribution on the blades, the present computation revealed that the highest values correspond to lower advance ratios, i.e., for heavier loading conditions, as expected. For instance, the non-dimensional pressure computed for $J=0.6418$ depicted in Figure 5 unveils rather strong gradients inside the regions around the tips and mid chord of the roots on both sides of the propeller. The same high gradients are located on both leading and trailing edges of the suction side, shown in Figure 5b, which is not the case on the pressure side where the distribution looks more uniform, except for a limited area which extends between the relative radii of 0.6 and 0.7.

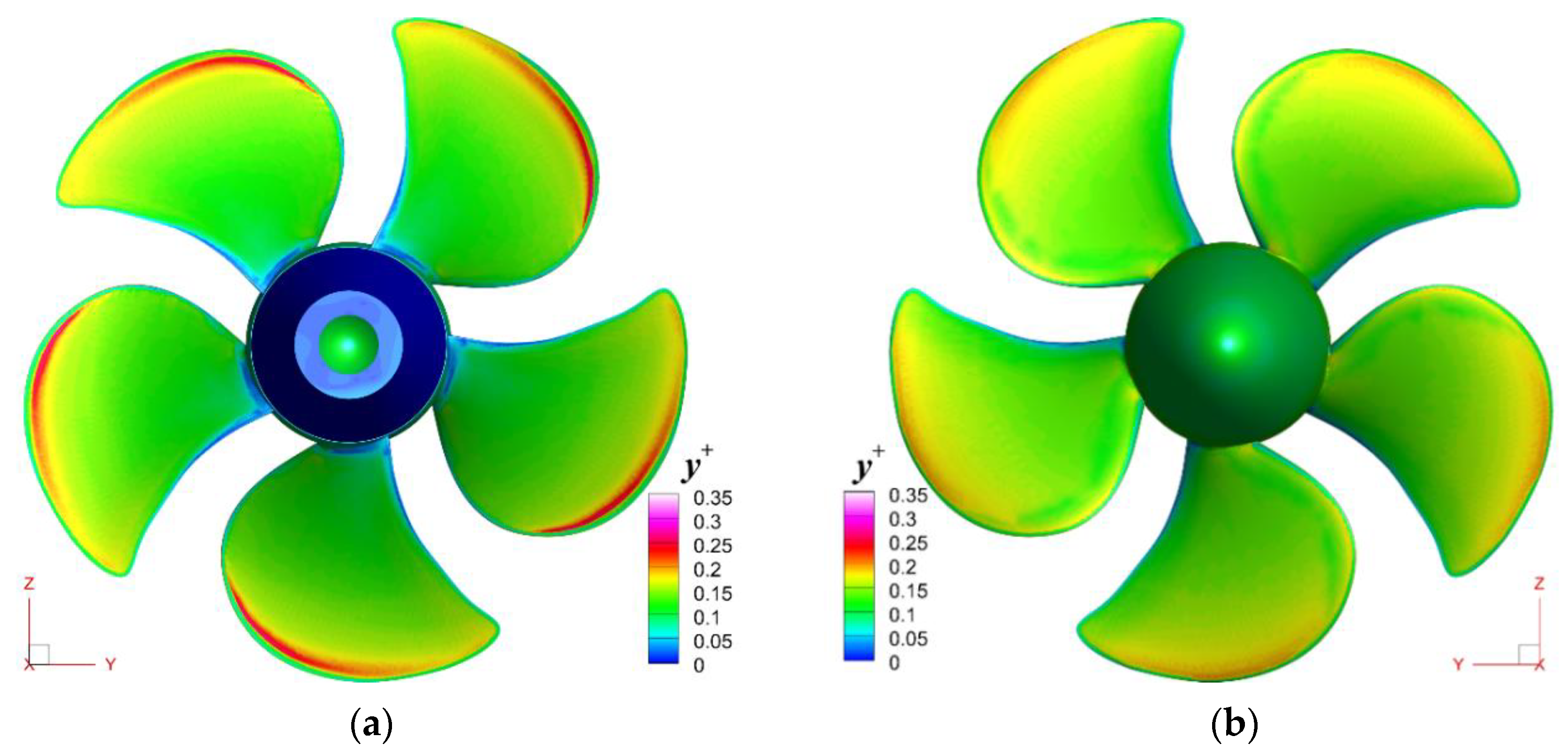
Obviously, the accuracy of the numerical solution strongly depends of the fineness of the spatial discretization. Although not presented here because of limited space reasons, systematic computations have proven that the best matching between the measured and computed pressure coefficients at all the relative radii between the hub and the tip of the propeller were obtained on the finest grids. As mentioned above, the severe restrictions imposed on the cells clustering on the solid surfaces, required by the DES turbulence model, led to a $y^{+}$ well below unity, as proven in Figure 6, which bears out its distribution on each side of the propeller. A maximum value for around the upper part of the leading edge, in the order of 0.3, can be distinguished in the figure. The high resolution of the discretization had to be correlated with small enough time-stepping so that the Courant-Friedrichs-Lewy condition is satisfied. The time-step size for all the simulations reported here is less than 5 × 10⁻⁵ s, so that the Courant numbers could be kept below unity regardless of the value of the oncoming flow velocity. Needless to say, the small time-step value led to high CPU time costs. However, they were finally justified by the good agreement with the available experimental data provided in [36].

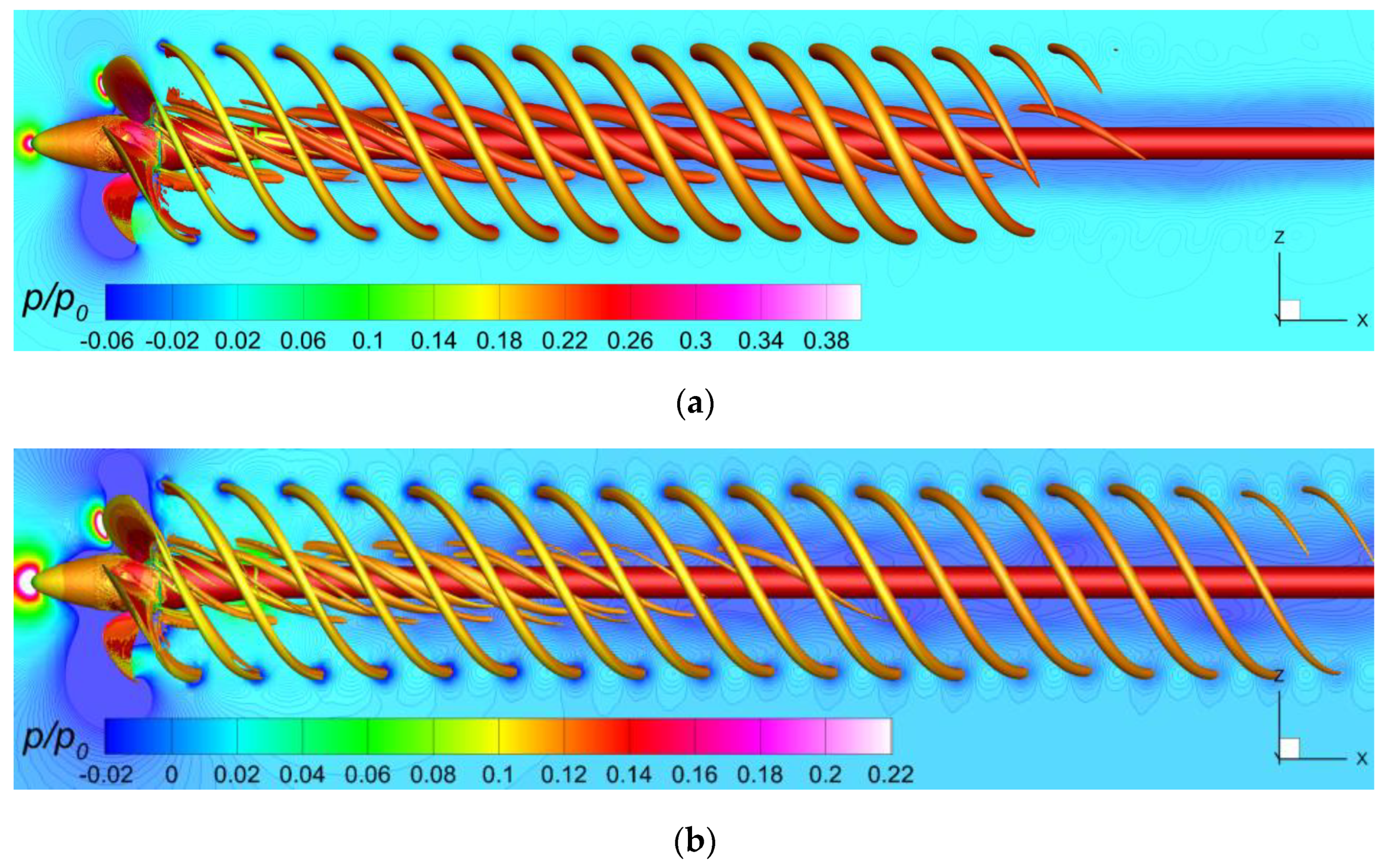
Definitely, the pressure field developed in the wake is always strictly related not only to the pressure distribution on the propeller blades and hub, but also to the vortical structures released by them downstream. This can be clearly seen in Figure 7, which shows the non-dimensional pressure field computed in the longitudinal plane of symmetry of the computational domain for $J=0.6418$ and $J=1.4422$, respectively. $p$ and $p_0$ in Figure 7 are the instantaneous and atmospheric pressure, respectively.

The vortices are represented by the non-dimensional iso-surfaces of the second invariant of the velocity gradient colored by the normalized streamwise velocity, i.e., the component parallel to the free-stream velocity. The locations of the cores, regardless of their intensities, correspond to areas of lower local pressures, as expected. In terms of intensity, Figure 7 proves that the propagation is dependent on the advance coefficients, i.e., as the advance coefficient increases, the extension of the vortices increases, and the wake remains co-linear with the incoming flow. It is also observed that the pressure intensity in the surrounding areas of the core of the vortex slightly decreases for higher advance coefficients.

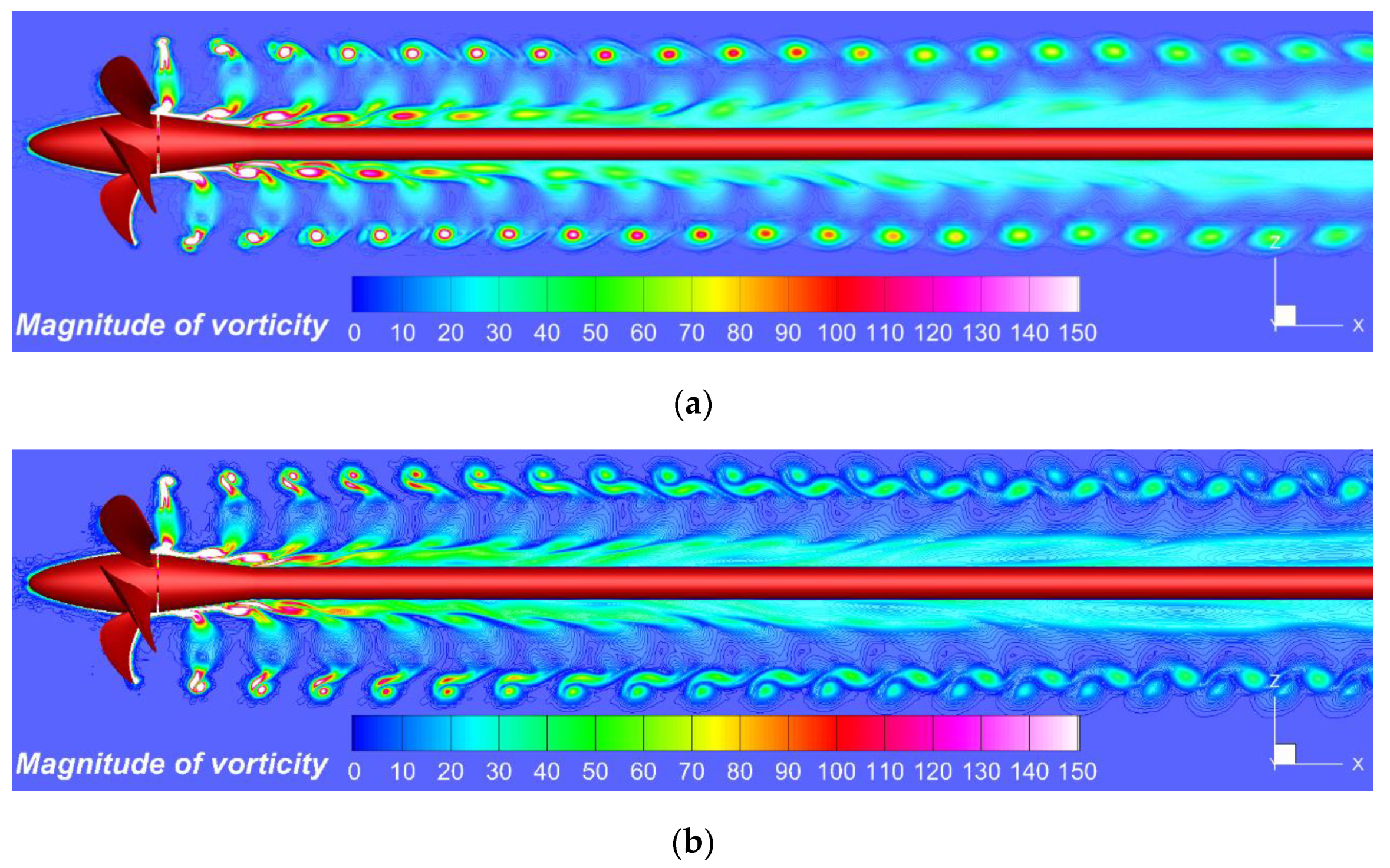
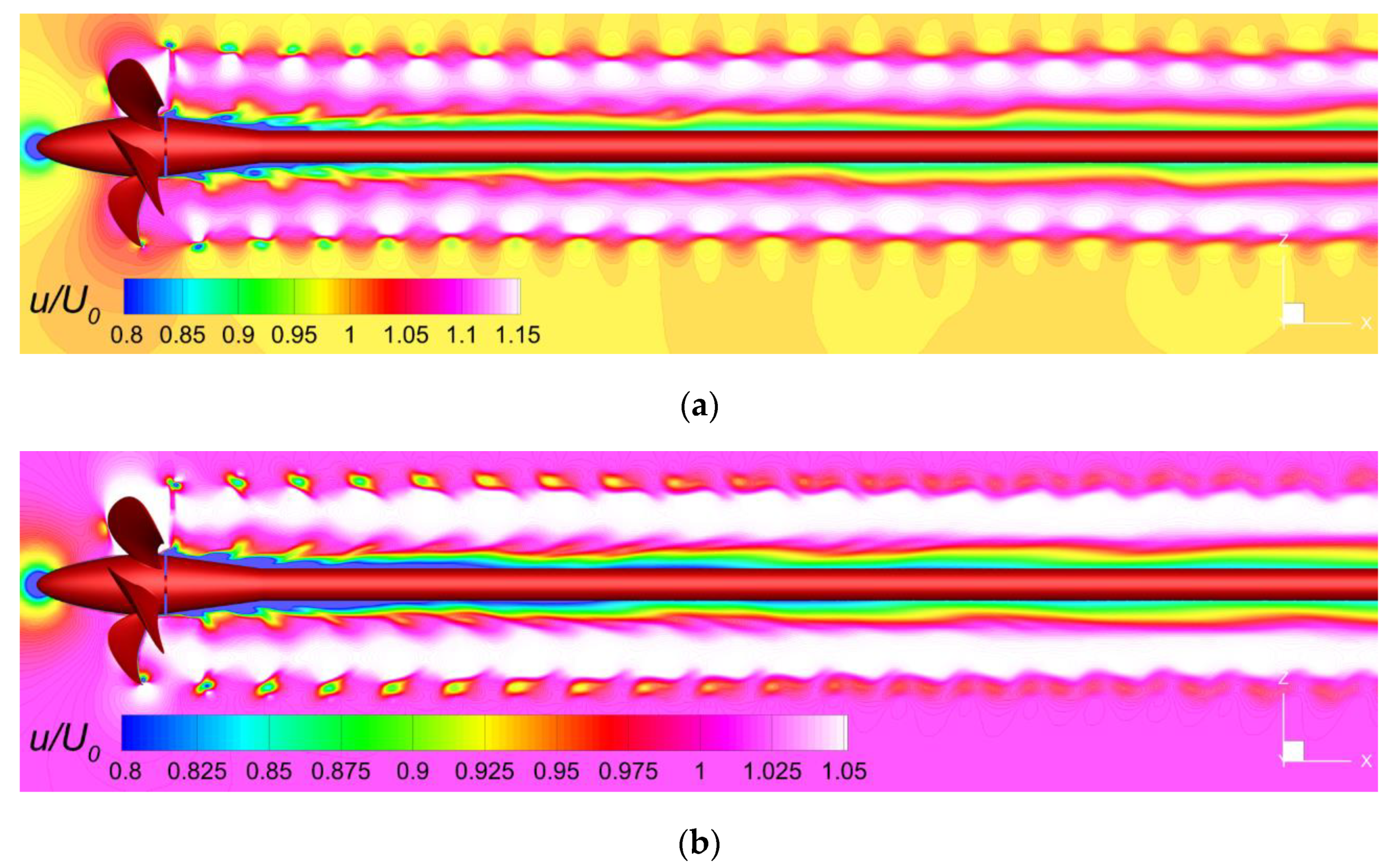
The pressure distribution on the longitudinal plane of symmetry has to be related to the other hydrodynamic parameters that describe the flow mechanism. In order to do that, Figure 8 proposes a comparison of the vorticity fields, whereas Figure 9 shows the non-dimensional streamwise velocities drawn for the same two advance coefficients of $J=0.6418$ and $J=1.602$, respectively. $u$ and $U_0$ in Figure 9 represent the instantaneous axial velocity and the incoming flow velocity. The comparison between these figures supports a primary conclusion. To simulate the onset and progression of the vortical structures it is mandatory to use a very fine grid around and in the wake of the propeller. Otherwise, the numerical diffusion will be so large that the onset and progression of these vortices is destroyed by the artificial numerical diffusion. To reduce the need for prohibitive computational resources, an automatic grid refinement based on a regularized version of the Hessian of the pressure is employed in this study.

It has been shown by the author in [16,17] that the anisotropic two-equation EARSM non-linear turbulence closure performs better than the linear isotropic $k-\omega$ closure with a significant increase of the vorticity and extension of the vortices predicted, with even new structures detected. However, the DES-SST model which is employed in this research proves to behave better since it is able to predict more intense and sustainable vortices, as also mentioned in [40]. This statement is sustained by Figure 8 and Figure 9. The magnitude of vorticity shown in Figure 8 is expressed in s⁻¹. Both the axial velocity and vorticity manifest periodic pulses that correspond to the cores of the vortices. Their intensity decreases in the wake because of the viscous dissipation. Strong tip-released structures are shed in the wake, correlating with local maxima of turbulent kinetic energy. The good agreement between the velocity and vorticity is explainable since they derive from the other. Because the hybrid LES model DES-SST only works with no-slip conditions for velocity on the solid boundaries, it proves to be more reliable since it does not employ any wall functions.

The acceleration of the flow right behind the propeller determines a slight reduction of the radial position of the vortex cores. Further downstream, the helices formed by the tip vortices become stable and remain located on a circular cylinder. In the DES-SST approach, the tip vortices are maintained much further in the wake, which is not the case with the RANS models, which yields tip vortices but they vanish more or less rapidly in the wake depending on the level of anisotropy associated with the turbulence model. These remarks were also made in [40,41].

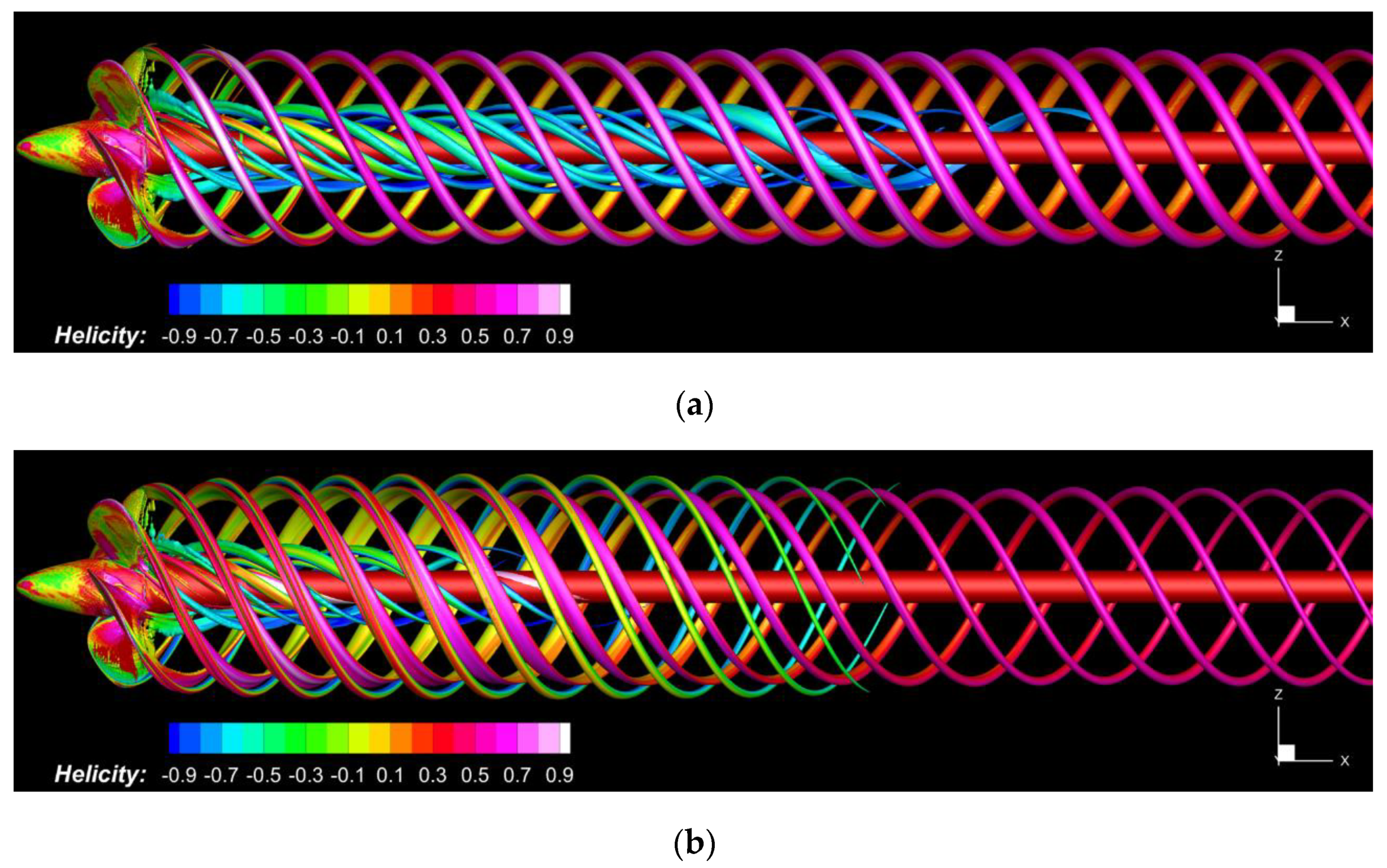
Regardless of the advance ratio, the trajectory of the tip vortex in the longitudinal plane inclines towards the hub on the whole, suggesting a contraction of the trajectories of the tip vortices, which becomes more significant when the advance ratio decreases. The helical pitch of the vortices is constant, a fact that suggests that no numerical dissipation takes place. This is a merit of the solver, which indicates suitable conservation properties, and also of the mesh clustering downstream of the tips, which proves to be non-dissipative. The intensity of the vortices gets weaker further in the propeller wake, a fact which is seemingly due to the viscous interaction with the rest of the fluid. As a result, the vortical structures either vanish, as Figure 10 bears out, or simply collapse into each other within an area of distortion. Figure 10a shows the vortices computed at an advance coefficient of $J=1.4422$, whereas Figure 10b shows the solution computed for $J=1.602$. Both solutions are drawn at $T=25$ sec., therefore when the propeller has already made 250 complete rotations. For higher advance coefficients, with the increase of the downstream distance, the propeller trailing vortex wake restores gradually to the free-stream flow and the fluctuation of the circumferential distribution of axial velocities becomes weaker, as depicted in Figure 9. A secondary vortex system is released by the trailing edges of the blade roots. The junction between the blade and hub determines the occurrence of a horseshoe-like vortex of a lower intensity than the tip vortex, which is therefore washed away in the downstream. The mechanism of its generation and development was formerly described in detail in [42,43], therefore no more discussion will be made herein.

In the following, an analysis of the wake based on several detailed comparisons with the LDV measurements reported in [44] is proposed as an additional validation of the computational method. Five relative radii ranging from $r/R=0.7$ to $r/R=1$ are considered in the polar representation of the wake depicted in Figure 11 for two different distances measured from the propeller center towards the downstream, namely $x/D=0.1$, shown in Figure 11a, and $x/D=0.2$ in Figure 11b.

The figure shows the angular variation of the axial wake computed as $w=u/U_o$, whereas ${\theta }^o$ is the rotation angle of the propeller. Both numerical solutions refer to $T=25$ sec. The experimental data are represented by solid lines, whereas the numerical solutions by symbols. At first glance, one may notice that the agreement with the LDV data is rather good despite the differences induced by the data filtering. This statement is valid for most of the data. Seemingly, this is the merit of the fine discretization around the blades as well as of the efficiency with which the automatic mesh refinement works.

Nevertheless, there are some differences which can be seen in the correspondence of the blade tips. This may suggest the need of extending the comparative analysis to the other wake components. Consequently, the tangential and radial wake distributions will be subjected to study in the following figures.

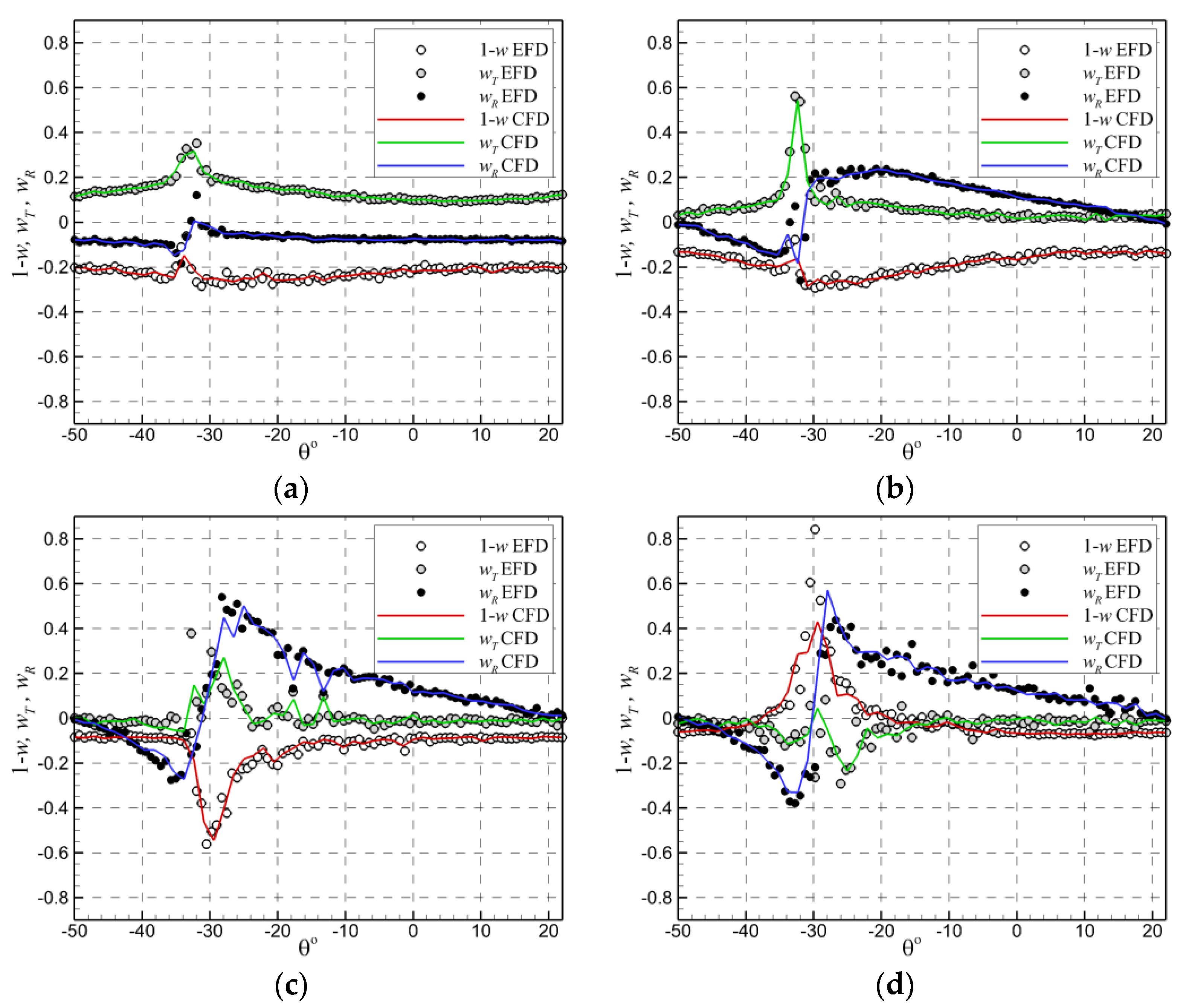
Figure 12 and Figure 13 show comparisons between the computed and measured tangential and radial wakes computed for a blade at two different axial locations, i.e., x/D = 0.1 and x/D = 0.2, respectively. Numerical solutions are drawn with lines, whereas the experimental data provided in [44] with symbols. For the sake of similarity with the experimental data, the circumferential wake distribution is given within the range of $-50°\le \theta \le 22°$ only, which is a sector that completely covers the first blade. The tangential wake is defined as $w_{\tau }=U_t/U_0$, whereas the radial one as $w_r=U_r/U_0$. $U_t$ and $U_r$ are the tangential and radial components of velocity. Axial velocities are positive in flow directions and radial velocities are positive for increasing radii, while tangential velocities are positive for the direction of rotation. The solutions are reported for the relative radii of 0.7, 0.9, 0.97 and 1.0 for both axial locations. They all refer to $T=25$ sec.

The comparisons made for x/D = 0.1 shown in Figure 12 reveal an overall satisfactory agreement between the numerical solution and the experimental data [44]. However, small differences can be observed around the tip of the blade for the axial wake computed at r/R = 1.0. Although the experimental data show some spare points due probably to the filtering, the numerical solution seems to slightly under-predict the wake intensity. This fact may suggest either an insufficiency of the grid resolution in that region or a failure of the solver in capturing properly the separation that takes place there. In either case, more detailed investigations are obviously required to get a better understanding of the reason for that local discrepancy.

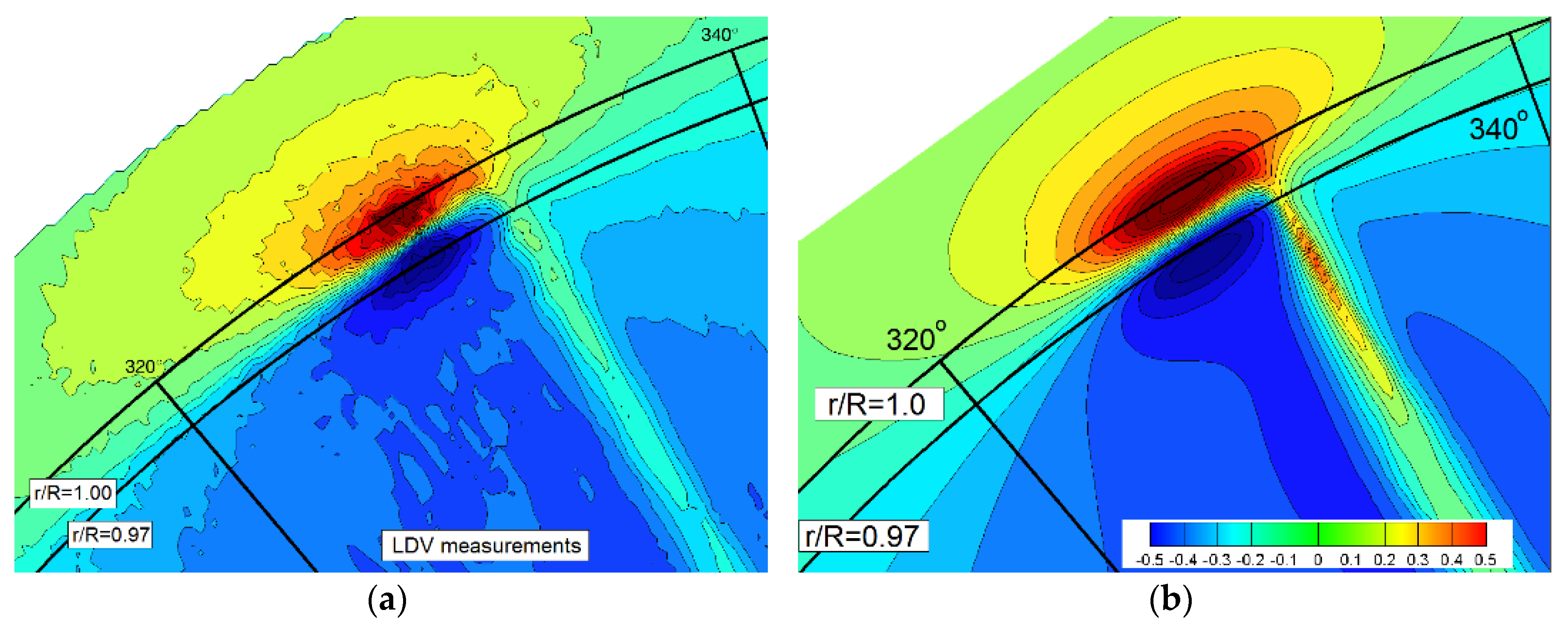
A similar conclusion may be drawn from Figure 13, which depicts the same comparisons of the wake components measured [44] and computed at x/D = 0.2. Comparing Figure 12 with Figure 13, one may notice that because of the viscous dissipation, the wake intensity decreases as the distance from the propeller increases, a fact that confirms the expectations. The conclusions above are sustained by the comparisons of the normalized axial velocities computed and measured [44] (pictures provided courtesy of Lars Lubke at Schiffbau-Versuchsanstalt (SVA) Potsdam [45]) at x/D = 0.1 and x/D = 0.2, shown in Figure 14 and Figure 15, respectively. It is worth emphasizing that the agreement is satisfactory although both comparisons reveal that the numerical solution is slightly over-predicting the extension of the axial wake at both locations considered. Nonetheless, the magnitude of the numerical solution is below the measured data within a limited region strictly confined to the blade tip, as also seen in Figure 12d and Figure 13d.

4.2. Cavitating Propeller

The simulations reported in the present subsection will be performed in a cavitation tunnel (see Figure 1b–e), which is based on a numerical model that differs from the one used previously in terms of the boundary condition formulation. Simulating the flow on a new computational domain, a new grid convergence test is therefore required. Moreover, since additional equations that describe the bi-phasic flow are to be solved, the discretization requirements are rather different from those above. For the validation of POW performances of the propeller working in the cavitation tunnel, four more computational grids with a number of cells varying from 12.98 M to 97.34 M are further generated at this step. Aside from the clustering criteria imposed on the walls of the cavitation tunnel, the present grids are also clustered inside the areas where the cavitation is expected to occur. For the simulations reported in the present section of the paper the no-slip boundary condition is imposed for all the solid walls of the cavitation tunnel. The thickness of the first layer of cells is chosen so that the $y^{+}<1$ on the propeller surfaces, and the adaptive mesh refinement is used in all cases. The time-step value is set to 10⁻⁵ s so that the Courant number should be less than 0.3. Eight advance coefficients ranging from 0.7676 to 1.5708 are considered for the grid convergence test, as tabulated in

Table 7. Grid convergence test for the thrust coefficient. Propeller working in cavitation tunnel.

Parameter		KT
J		0.7676	0.8851	1.0132	1.1432	1.2467	1.3776	1.4875	1.5708
EFD		0.493	0.4363	0.3708	0.3057	0.2492	0.1837	0.1187	0.0633
CFD	Coarse	0.4697	0.4140	0.3529	0.2930	0.2395	0.1765	0.1139	0.0611
	│ε│ %	4.72	5.11	4.84	4.14	3.89	3.93	4.02	3.47
	Medium	0.4712	0.4188	0.3568	0.2947	0.2413	0.1783	0.1155	0.0616
	│ε│ %	4.42	4.02	3.78	3.61	3.17	2.93	2.72	2.61
	Fine	0.4744	0.4225	0.3603	0.2980	0.2433	0.1796	0.1162	0.0620
	│ε│ %	3.77	3.17	2.84	2.53	2.38	2.21	2.14	2.02
	Very fine	0.4791	0.4247	0.3619	0.2992	0.2447	0.1808	0.1169	0.0626
	│ε│ %	2.82	2.65	2.41	2.12	1.82	1.59	1.53	1.13

and

Table 8. Grid convergence test for the torque coefficient. Propeller working in cavitation tunnel.

Parameter		10 KQ
J		0.7676	0.8851	1.0132	1.1432	1.2467	1.3776	1.4875	1.5708
EFD		1.224	1.1018	0.9693	0.8361	0.7194	0.5795	0.4472	0.3326
CFD	Coarse	1.1668	1.0524	0.9273	0.8009	0.6893	0.5555	0.4297	0.3202
	│ε│ %	4.67	4.48	4.33	4.21	4.18	4.14	3.91	3.73
	Medium	1.1698	1.0537	0.9307	0.8042	0.6930	0.5589	0.4319	0.3215
	│ε│ %	4.43	4.37	3.98	3.82	3.67	3.55	3.42	3.35
	Fine	1.1839	1.0670	0.9401	0.8113	0.6988	0.5633	0.4355	0.3245
	│ε│ %	3.28	3.16	3.01	2.97	2.86	2.79	2.62	2.43
	Very fine	1.1864	1.0697	0.9415	0.8131	0.7004	0.5650	0.4362	0.3253
	│ε│ %	3.07	2.91	2.87	2.75	2.64	2.51	2.45	2.18

. Table 7 contains the validations for the thrust coefficients, while Table 8 tabulates the corresponding data for the torque coefficients. All the computations are performed for a rotation speed of 1500 rpm, therefore the advance coefficients result from the variable advance velocity which is imposed for each computation. The experimental data used for comparisons are provided in [46].

As far as the thrust coefficient is concerned, the absolute errors vary from 1.13%, which corresponds to $J=1.5708$ for the very fine grid, to 5.11% for $J=0.8851$ on the coarse grid. The situation is similar for the torque coefficient. Thus, the absolute errors vary from 2.18%, which corresponds to $J=1.5708$ for the very fine grid, to 4.67% for the $J=0.7676$ flow regime computed on the coarse grid. The variation of the computed errors of the numerical solutions compared to the experimental data [46] is depicted in Figure 16a for the thrust coefficient and Figure 16b for the torque coefficient, in which the trend of the monotonic decrease of the error levels with the increase of resolution is straightforward.

The computed propeller performance coefficients are tabulated in

Table 9. Comparison between the open water performance coefficients measured and computed for the propeller working in the cavitation tunnel.

J	KT		│ε│ %	10KQ		│ε│ %	ηO		│ε│ %
	EFD	CFD		EFD	CFD		EFD	CFD
0.7676	0.4930	0.4791	2.82	1.224	1.1864	3.07	0.492	0.4923	0.06
0.8851	0.4363	0.4247	2.65	1.1018	1.0697	2.91	0.558	0.5581	0.02
1.0132	0.3708	0.3619	2.41	0.9693	0.9415	2.87	0.617	0.6172	0.03
1.1432	0.3057	0.2992	2.12	0.8361	0.8131	2.75	0.665	0.6656	0.09
1.2467	0.2492	0.2447	1.82	0.7194	0.7004	2.64	0.687	0.6877	0.10
1.3776	0.1837	0.1808	1.59	0.5795	0.5650	2.51	0.695	0.6954	0.05
1.4875	0.1187	0.1169	1.53	0.4472	0.4362	2.45	0.628	0.6287	0.11
1.5708	0.0633	0.0626	1.13	0.3326	0.3253	2.18	0.476	0.4760	0.01

for all the advance ratios and compared with the corresponding experimental data reported in [46]. The level of errors is limited to 2.82% for the thrust coefficient and to 3.07% for the torque coefficient. Based on the grid convergence test, the propeller diagram for the finest grid is proposed in Figure 17, in which the good agreement between the experimental data and the solutions reported here is shown. Nonetheless, it is worth noticing that for all the values of the advance coefficient the numerical solution is below the measured data.

For a better accuracy of the numerical solution of the cavitating working condition, in the following, all the computations will be performed on the very fine grid only. Propeller performances and cavitation extension evaluations are carried out for three different cavitation numbers. Computed solutions will be compared with the cavitation sketches drawn at SVA Potsdam and provided courtesy of L. Lubke. Thrust identity is imposed in order to replicate the same tunnel measured flow conditions. The non-cavitating thrust coefficients are imposed at 0.387, 0.245 and 0.167, with prescribed cavitation numbers, respectively 2.024, 1.424 and 2.000. The cavitation number is defined as

$${\sigma }_n=\frac{p_{ref}-p_{sat}}{0.5·{\rho }_l·{\left(nD\right)}^2}$$

where $p_{ref}$ is the reference pressure, i.e., the pressure at the outlet, $p_{sat}$ is the saturation pressure, ${\rho }_l$ is the liquid density and $n$ and $D$ are the rotational velocity and the diameter of the propeller, respectively. The three different cavitating flow regimes determined by the cavitation number ${\sigma }_n$ are defined by varying the value of $p_v$ because $p_{ref}$ and ${\rho }_l$ are kept constant. For reasons related to the similarity with the experiments [46], all the simulations reported here will be referred to as 2.3.1–2.2.3. In all the cases, the inflow velocity is left free to alter for matching the thrust equivalence.

4.2.1. Propeller Cavitation Simulation for ${\sigma }_n=2.024$ (test case 2.3.1 in [46])

The first simulation is performed for a cavitation number of 2.024, for which the input data used for experiments [46] are tabulated in

Table 10. Cavitation observations. Test case 2.3.1 in [46].

Parameter	Symbol	UM	Value
Advanced coefficient	J	[-]	1.019
Thrust coefficient (non-cavitating)	$K_T$	[-]	0.387
Cavitation number	${\sigma }_n$	[-]	2.024
Number of revolutions	n	[s−1]	24.987

.

A comparison between the numerical solution and the cavitation sketch of the experiment reported in [46] is depicted in Figure 18. For the computed solution, the comparison reveals that a stable and narrow sheet cavity is observed on the suction side of the blade, a fact which is confirmed by the experiment. At the outmost radius, the sheet cavity merges into a tip vortex cavity. In addition, a cavitation sheet is observed along the blade root with a maximal extension which corresponds to the mid-chord of the root, as observed in the experiments. No hub cavitation is numerically detected. The mean shape and extent of the root cavitation, as well as the tip and hub vortex cavitation, are captured well. The tip vortex cavitation extending far behind the propeller is successfully captured. Despite the good resemblance between the simulation and the experiment, one may notice that an additional thin cavitation sheet, which was not seen during the experiments, develops around the higher relative radii of the trailing edge of the numerical solution. Moreover, the numerical model seems to be unable to predict the bubble cavitation at the trailing edge of the root.

4.2.2. Propeller Cavitation Simulation for ${\sigma }_n=1.424$ (test case 2.3.2 in [46])

The second simulation is performed for a cavitation number of 1.424, for which the input data used for experiments [46] are tabulated in

Table 11. Cavitation observations. Test case 2.3.2 in [46].

Parameter	Symbol	UM	Value
Advanced coefficient	J	[-]	1.269
Thrust coefficient (non-cavitating)	$K_T$	[-]	0.245
Cavitation number	${\sigma }_n$	[-]	1.424
Number of revolutions	n	[s−1]	24.986

.

The computed solution reveals a tip vortex cavity which is released by the trailing part of the blade and a substantial root cavitation which starts around the mid-chord on the suction side, as depicted in Figure 19. The comparison with the experimental cavitation sketch emphasizes a satisfactory agreement between the theoretical and experimental approaches. Nevertheless, one may notice again the inability of the numerical solver to capture the cavitation bubbles, neither on the blade nor in the wake of the trailing edge of the root. This could be due either to the cavitation model employed or to an insufficient grid resolution in those areas. Obviously, more systematic studies are required to clarify the reasons for the difference.

4.2.3. Propeller Cavitation Simulation for ${\sigma }_n=2.000$ (test case 2.3.3 in [46])

The last numerical simulation is performed for a cavitation number of 2.200, for which the input data used for experiments [46] are tabulated in

Table 12. Cavitation observations. Test case 2.3.3 in [46].

Parameter	Symbol	UM	Value
Advanced coefficient	J	[-]	1.408
Thrust coefficient (non-cavitating)	$K_T$	[-]	0.167
Cavitation number	${\sigma }_n$	[-]	2.000
Number of revolutions	n	[s−1]	25.014

.

At this loading and cavitation number, a narrow stable sheet cavity is observed on the pressure side of the blade around its leading edge, together with a rather weak root cavitation, as shown in Figure 20a. A rather short pigtail vortex tip cavitation develops in the blade trail. Aside from that, a slight hub cavitation is detected around the trailing edge of the blade root. Comparing the numerical solution with the experimental sketch, it may be noticed that the computed cavitation sheet extends to the root of the blade, more than was observed in the cavitation tunnel. In spite of this fact, the overall agreement is more than satisfactory.

5. Concluding Remarks

The paper describes a thorough investigation of the hydrodynamic performances of the PPTC I propeller. The flow is numerically simulated by integrating in time the unsteady Navier‒Stokes equations in which closure to the turbulence is achieved by means of a modified DES-SST approach. The ISIS-CFD solver, part of the Numeca Fine^TM/Marine package, uses the finite volume of fluid approach. All the parallel computations were performed on 120 processers. Non-cavitating and cavitating flow regimes were computed for a significant range of advance coefficients, and the comparisons with the available experimental data validated the numerical solutions. Grid convergence tests were performed, and the computed solutions proved not only a satisfactory accuracy of the numerical approach, but also the solver robustness. Based on the discussions provided in the preceding sections, the following conclusions may be put forward:

−

extensive comparisons with the available experimental data have proven the accuracy of the numerical treatment;

−

the automatic grid refinement based on a regularized version of the Hessian of the pressure allowed convergence achievement at a reasonable CPU cost;

−

flow analysis of the non-cavitating propeller working regime revealed that the hybrid DES-SST turbulence model allows very good progression of the vortical structures in the wake;

−

comparisons of the numerical solution with the LDV measurements revealed that the numerical solution slightly under-predicted the intensity of the radial and tangential wake components and, on the other hand, it insignificantly over-predicted its axial component;

−

the Kunz cavitation model was able to provide a satisfactory estimation of the cavitation sheet extension but failed in capturing the bubble cavitation.