Risk Assessment Framework for Structural Failures of Polar Ship Under Ice Loads

Abstract

For polar ships, navigation in ice-covered regions can lead to high risk to structural safety. To study the structural risk induced by ice loads, a risk assessment framework is proposed based on a probabilistic analysis. The fatigue failure probability is derived with the first-order second-moment (FOSM) method. Typical ice load cases are extracted as a joint probability distribution of ice thickness and ship speed, based on shipboard measurements. Equivalent fatigue stresses for each case are calculated using a coupled discrete element method (DEM) and finite element method (FEM), and fatigue failure probabilities are obtained via linear cumulative damage theory. The ultimate strength failure probability is derived from the reliability theory. The probabilistic distribution of load-carrying capacity for the bow structure, determined by the moment estimation method, is used as the structural resistance, while the ice load distribution identified from shipboard monitoring is treated as the external load. Considering both the likelihood and consequence of failure, a risk matrix is constructed to assess structural failure risk. Inspection and maintenance intervals are then proposed according to the assessed risk levels. This approach offers a quantitative basis for structural risk management, supporting safe navigation and efficient maintenance planning for polar ships.

1. Introduction

In polar regions, ice loads are the primary external cause of hull vibration and damage to polar ships [1]. Several safety incidents in recent years involving ship collisions with sea ice have resulted in severe hull damage and economic losses [2,3]. Under long-term ice-structure interaction, ice loads may lead to structural fatigue failure. The failure risk of polar ship structures increases over time as their service life extends, while extreme ice conditions such as icebergs and ice ridges further elevate this risk. Risk assessment has been widely applied in the maritime industry [4,5], but its application to polar ship structures remains limited. Therefore, a systematic assessment based on polar environmental conditions and the characteristics of ice loads is essential.

Accurate identification of ice loads on polar ship structures is fundamental to failure risk assessment. This is typically achieved through numerical methods such as the discrete element method (DEM) and finite element method (FEM) [6,7]. Shipboard monitor database coupling machine learning and influence coefficient matrix approaches have also been utilized to support ice load identification on hulls [8,9].

Under long-term service conditions, fatigue damage in hull components significantly elevates the risk of structural failure [10,11]. This is typically assessed using S–N curves combined with linear cumulative damage theory, which can be adapted to reflect the specific characteristics of ice loads [12]. FEM is commonly used to calculate stress at critical hotspots, providing a basis for estimating the fatigue life of polar ship structures [13,14]. Given the stochastic nature of ship–ice interactions, reliability analysis based on probabilistic methods is essential. The statistical characteristics of ice loads are typically represented by Weibull or lognormal distributions [15,16,17]. Among various approaches, the first-order second-moment (FOSM) method is commonly employed to estimate the probabilities of both fatigue failure and ultimate strength failure [18].

To address the lack of practical tools for quantitatively assessing structural failure risks in polar ships, this paper proposes a risk matrix approach that integrates fatigue reliability and ultimate strength analysis to evaluate hull structural safety in ice-covered regions. A polar transport vessel is used as a case study. A DEM model is established to calculate the ice loads acting on the vessel, from which the local ice loads on the loading patch of the ship bow are extracted. These local ice loads are then applied to the corresponding position in the FEM model of the bow structure, ensuring consistent data transfer between the DEM and FEM analyses. Based on the statistical distribution of equivalent stresses at fatigue hotspots, the probability of fatigue failure is calculated using the FOSM method. Then the probability of ultimate strength failure is also determined. These results are then used to construct a structural failure risk matrix, enabling a quantitative assessment of failure risks across different components of the hull structure. The schematic representation of this proposed method is illustrated in Figure 1.

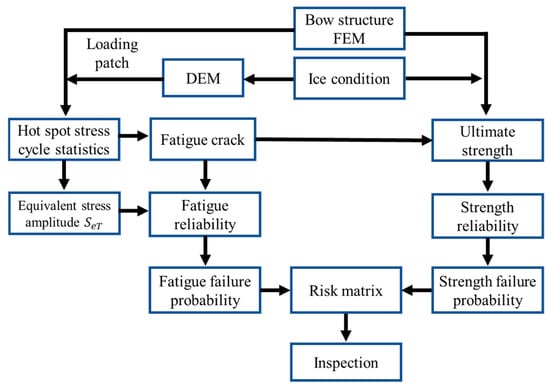
Figure 1. The schematic of the proposed method illustrates a probabilistic risk assessment framework for evaluating the structural failure risk of polar ships under ice loads. It integrates FOSM-based fatigue and ultimate strength reliability analyses with a risk matrix approach to guide inspection strategies.

2. Probability of Fatigue Failure

Fatigue damage in hull structures is a complex process influenced by numerous random factors. It is generally evaluated using the S–N (stress–number of cycles) curve, as recommended by design codes and classification society standards [19,20]. The S–N curve describes the relationship between the applied stress amplitude and the number of cycles to failure, providing a basis for estimating fatigue life under cyclic loading. Furthermore, fatigue performance can be analyzed through probabilistic approaches to account for uncertainties in loading conditions and material properties.

2.1. Methodology of Fatigue Reliability

The FOSM method is a widely used reliability-based approximation technique, named for its use of linear terms (first-order) and standard deviations (second-moment) in the calculation [21]. Based on the FOSM method, a failure function can be established as follows:

$$Z={T_{\mathrm{f}}-T}_{\mathrm{d}}$$

(1)

where $Z$ is the failure function. When $Z$ > 0, the structure is in a positive safety margin station. In contrast, the structure is in danger when $Z$ < 0. $T_{\mathrm{d}}$ is the service life or the design life, which is a constant parameter based on ship design requirements. $T_{\mathrm{f}}$ is the predicted fatigue life of the structure, which is a random variable.

Under random ice loads, the local stress in polar ship structures also behaves as a random variable. According to the linear damage accumulation theory, the total damage $D_j$ caused by a series of random fatigue stress amplitudes $S_{ij}$ (i = 1, 2, 3, …, $N_j$) can be equivalently expressed as the damage $D_{\mathrm{e}j}$ caused by a constant stress amplitude $S_{\mathrm{e}j}$ applied over the same number of cycles [22]. Therefore, the equivalent stress amplitude $S_{\mathrm{e}j}$ can be calculated as follows:

$$D_j=\sum _{i=1}^{N_j}{\displaystyle \frac{S_{ij}^m}{K}}={\displaystyle \frac{S_{\mathrm{e}j}^m{N}_j}{K}}=D_{\mathrm{e}j}$$

(2)

$$S_{\mathrm{e}j}={[{\displaystyle \frac{1}{N_j}}\sum _{i=1}^{N_j}{S}_{ij}^m]}^{{\displaystyle \frac{1}{m}}}={\left[E\right(S_{ij}^m\left)\right]}^{{\displaystyle \frac{1}{m}}}$$

(3)

where $N_j$ is the number of stress cycles for the j-th load case; m and K are parameters of the S–N curve, typically obtained through a fatigue test. $E$ is the mathematical expectation.

Assuming there are $n$ load cases, with $a_j$ representing the probability weight of the j-th case, the total equivalent fatigue stress amplitude $S_{\mathrm{e}\mathrm{T}}$ for the polar ship structure can be calculated as follows:

$$S_{\mathrm{e}\mathrm{T}}=\sum _{j=1}^n{a}_j{S}_{\mathrm{e}j}$$

(4)

According to the S–N curve method [21], if the total fatigue damage under the equivalent stress amplitude is $D$, and the total number of cycles (the predicted fatigue life) is $T_{\mathrm{f}}$, which can be expressed as follows:

$$T_{\mathrm{f}}={\displaystyle \frac{KD}{S_{\mathrm{e}\mathrm{T}}^m}}$$

(5)

where $T_{\mathrm{f}}$ can be treated as a random variable to analyze the influence of each parameter. The parameter $K$, obtained from fatigue tests, is subject to significant uncertainty due to material manufacturing variability, and it should be treated as a random variable. Since the actual fatigue damage $D$ is not always equal to 1, it can also be treated as a random variable, denoted by $\Delta$. To account for errors in the calculation of equivalent stress amplitude, a random error coefficient $B$ is introduced. Accordingly, Equation (5) can be rewritten as follows:

$$T_{\mathrm{f}}={\displaystyle \frac{K\Delta }{B^m{S}_{\mathrm{e}\mathrm{T}}^m}}$$

(6)

As $T_{\mathrm{d}}$ is a constant parameter, the probabilistic characteristic of the failure function Z is governed by the distribution of $T_{\mathrm{f}}$. To simplify the analysis, the random variables $\Delta$, $B$ and $K$ are typically assumed to follow lognormal distributions. Then $T_{\mathrm{f}}$ also follows a lognormal distribution, and its probability density function $f\left(T_{\mathrm{f}}\right)$ is given as follows:

$$f(T_{\mathrm{f}})={\displaystyle \frac{1}{\sqrt{2\pi }{\sigma }_{\mathrm{T}}}}\mathrm{e}\mathrm{x}\mathrm{p}[-{\displaystyle \frac{1}{2}}{({\displaystyle \frac{\mathrm{l}\mathrm{g}{T}_{\mathrm{f}}-{\mu }_T}{{\sigma }_{\mathrm{T}}}})}^2]$$

(7)

where ${\mu }_T$ and ${\sigma }_{\mathrm{T}}$ are the mean and standard deviation of $\mathrm{l}\mathrm{g}{T}_{\mathrm{f}}$, which is the logarithm of $T_{\mathrm{f}}$. The coefficients of variation of $\Delta$, $B$ and $K$ are denoted by $C_{\Delta }$, $C_B$ and $C_K$, respectively. According to the Taylor series expansion, the coefficient of variation of $\mathrm{l}\mathrm{g}{T}_{\mathrm{f}}$, denoted as $C_T$, can be expressed as follows:

$$C_T^2=\mathrm{l}\mathrm{g}\left[\right(1+C_{\Delta }^2\left)\right(1+C_K^2\left)\right(1+C_B^2\left)\right]$$

(8)

The mean value of $\mathrm{l}\mathrm{g}{T}_{\mathrm{f}}$ can be determined by Equation (6), denoted as ${\mu }_{\mathrm{T}}$, can be expressed as follows:

$${\mu }_T={\displaystyle \frac{{\mu }_{\Delta }\cdot {\mu }_K}{{\left({\mu }_B\right)}^m{\left(\mathrm{l}\mathrm{g}{S}_{\mathrm{e}\mathrm{T}}\right)}^m}}$$

(9)

where ${\mu }_{\Delta }$, ${\mu }_B$ and ${\mu }_K$ are the means of $\mathrm{l}\mathrm{g}\Delta$, $\mathrm{l}\mathrm{g}B$ and $\mathrm{l}\mathrm{g}K$. And the standard deviation of $\mathrm{l}\mathrm{g}{T}_{\mathrm{f}}$ can be expressed as ${\sigma }_T=C_T·{\mu }_T$.

The reliability P_r is the probability that the failure function $Z$ > 0, which can be expressed as follows [21]:

$$P_{\mathrm{r}}=P(Z>0)={\displaystyle \frac{1}{\sqrt{2\pi }{\sigma }_Z}}{\int }_0^{\mathrm{\infty }}{\mathrm{e}}^{-{\displaystyle \frac{1}{2}}{({\displaystyle \frac{Z-{\mu }_Z}{{\sigma }_Z}})}^2}\mathrm{d}Z$$

(10)

where ${\mu }_Z$ and ${\sigma }_Z$ are the mean and standard deviation of the failure function $Z$. By standardizing the random variable, let ${\displaystyle \frac{Z-{\mu }_Z}{{\sigma }_Z}}=Y$, then Equation (10) can be rewritten as

$$P_{\mathrm{r}}={\displaystyle \frac{1}{\sqrt{2\pi }}}{\int }_{-{\displaystyle \frac{{\mu }_Z}{{\sigma }_Z}}}^{\mathrm{\infty }}{\mathrm{e}}^{-{\displaystyle \frac{1}{2}}{Y}^2}\mathrm{d}Y=1-\Phi \left(Y\right)=1-\Phi (-\beta )$$

(11)

where $\beta$ is the safety index, and $\beta =-Y$. When the limit state $Z$ = 0, $Y=-{\displaystyle \frac{{\mu }_Z}{{\sigma }_Z}}$. Since $T_{\mathrm{f}}$ follows a lognormal distribution and $T_{\mathrm{d}}$ is a constant variable, the failure function Z also follows a lognormal distribution. Therefore, ${\mu }_Z$ and ${\sigma }_Z$ can be expressed as follows:

$${\mu }_Z={\mu }_T-T_{\mathrm{d}}$$

(12)

$${\sigma }_Z=\sqrt{{\sigma }_T^2+0}={\sigma }_T$$

(13)

The safety index $\beta$ can be expressed as follows:

$$\beta =-Y={\displaystyle \frac{{\mu }_T-T_{\mathrm{d}}}{{\sigma }_T}}$$

(14)

Then the reliability $P_{\mathrm{r}}$ can be calculated by Equation (11). And the failure probability is

$$P_{\mathrm{f}}=1-P_{\mathrm{r}}$$

(15)

2.2. Determination of Parameter Values

As shown in Equations (1) and (6), the fatigue reliability is determined by three random variables ($\Delta$, $B$ and $K$) and three constant parameters ($T_{\mathrm{d}}$, $m$ and $S_{\mathrm{e}\mathrm{T}}$).

The statistical characteristics of random variables typically require extensive experimental analysis and summarization. For example, $\Delta$ represents the uncertainty in the cumulative fatigue damage at the point of structural failure. This uncertainty arises from various sources, including material properties, load sequence effects, stress concentrations, temperature, and environmental conditions. Based on an analysis of a large amount of experimental data, Wirsching [22] recommended modeling $\Delta$ as a normally distributed variable in the fatigue life prediction of ship and offshore structures, with a mean value of 1.0 and a coefficient of variation of 0.30. In this study, the statistical characteristics of three random variables are adopted from the data provided by Wirsching and Chen [23], as shown in Table 1.

Table 1. Characteristic of random variables for fatigue reliability [23].

Random Variable	Mean		Coefficient of Variation
	Symbol	Value	Symbol	Value
$\Delta$	${\mu }_{\Delta }$	1.0	$C_{\Delta }$	0.3
$B$	${\mu }_B$	0.7	$C_B$	0.5
$K$	${\mu }_K$	12.6	$C_K$	0.512

As for the constant parameter, $T_{\mathrm{d}}$ denotes the service life or the design life of the ship structure. The parameter m is the slope of bilogarithmic S–N curve, which is selected according to the specifications of the International Association of Classification Societies (IACS). For welded joints, the D-curve is commonly adopted, with a typical value $m$ = 3 [19].

The equivalent fatigue stress amplitude $S_{\mathrm{e}\mathrm{T}}$ is obtained based on the probability distribution of load cases and the statistical analysis of stress cycles. The following section provides a detailed description of the calculation procedure.

2.3. Load Cases for Fatigue Assessment

Load cases form the basis of fatigue assessment. In this study, load cases are established using the shipboard sensor–image acquisition and analysis method. This method collects key environmental parameters in polar regions using shipboard sensors and imaging devices (e.g., accelerometers, strain gauges, and temperature sensors) and constructs a database through statistical analysis. It provides a realistic and accurate representation of ship operating conditions in polar environments and has been widely applied in polar navigation research and forecasting [24]. Since 1995, China has conducted 12 Arctic scientific expeditions. This study uses shipboard monitoring data from the 7th, 8th, 9th, and 12th expeditions to perform statistical analysis of ice-induced fatigue load cases for polar ship structures.

The main factors affecting ice loads include sea ice thickness, ice concentration, hull form, and ship speed [25]. To simplify, ice concentration is assumed as 100%. This assumption leads to safer fatigue life estimates. The case study in this paper is based on a predetermined hull form of a polar transport vessel. At last, sea ice thickness and ship speed are selected as the primary parameters for defining ice-induced fatigue load cases.

It is important to note that sea ice thickness and ship speed are not independent variables. When navigating through thicker ice, ship speed is typically reduced to ensure operational safety, whereas in areas with thinner ice, speed is often increased to reduce transit time. Therefore, the construction of environmental load cases for polar navigation should be based on the joint probability distribution of sea ice thickness and ship speed.

In this study, the measured ranges of ice thickness (0.3~2.3 m) and ship speed (3~13 knots) are, respectively, divided into 10 intervals, resulting in 100 combined load cases, as shown in Figure 2. It indicates that most operational conditions are concentrated in the region where ice thickness ranges from 0.5 to 1.3 m and ship speed ranges from 5 to 8 knots. Based on this distribution, nine typical fatigue load cases with a joint probability density greater than 2.5% are selected for subsequent analysis, as listed in Table 2.

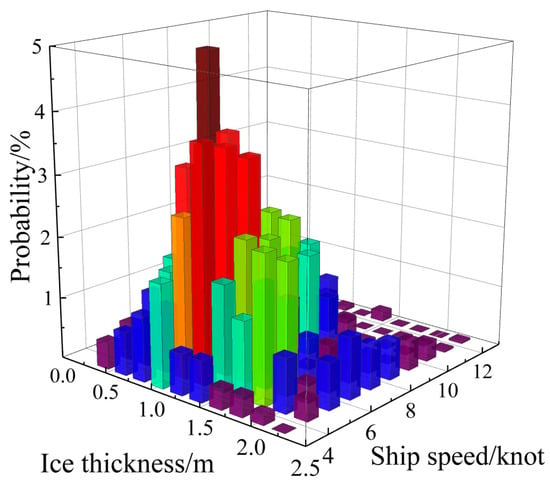
Figure 2. Joint probability distribution of ice thickness and ship speed.

Table 2. Load cases and equivalent fatigue stress amplitude.

Load Case	Ice Thickness (m)	Speed (knot)	Probability (%)	${\mathit{S}}_{\mathbf{e}}$ (MPa)
1	0.5~0.7	6~7	7.90	23.08
2	0.5~0.7	7~8	13.50	30.05
3	0.7~0.9	5~6	8.32	38.33
4	0.7~0.9	6~7	11.10	41.92
5	0.7~0.9	7~8	12.90	50.00
6	0.9~1.1	5~6	12.90	41.31
7	0.9~1.1	6~7	11.40	52.14
8	0.9~1.1	7~8	12.00	60.44
9	1.1~1.3	6~7	9.98	71.55
$S_{\mathrm{e}\mathrm{T}}$ (MPa)				45.84

2.4. Calculation of Equivalent Fatigue Stress Amplitude

Then the DEM is employed to calculate ice loads on the ship hull. DEM is commonly used to simulate the failure processes of brittle materials and has been widely applied in studies of sea ice drift and accumulation, ridge formation, and ice–structure interactions [26].

To calculate the ice loads, it is necessary to define the characteristics of sea ice and the ship hull, as shown in Table 3. In this study, a polar transport vessel is adopted as a case study, and the mechanical properties of sea ice are determined based on an experimental study [27]. The simulation with DEM of load case 1.0 m ice thickness (0.9~1.1 m) and 7.5 knots ship speed (7~8 knots) is shown in Figure 3a [28,29].

Table 3. Characteristics of sea ice and ship hull in DEM.

Ice Mechanics		Ship Hull Information
Density (kg/m3)	920.0	Length (m)	190.0
Elasticity modulus (GPa)	1.0	Breadth (m)	28.5
Bending strength (MPa)	0.7	Waterline (m)	11.0
Compressive strength (MPa)	2.0	Stem angle (°)	10.0

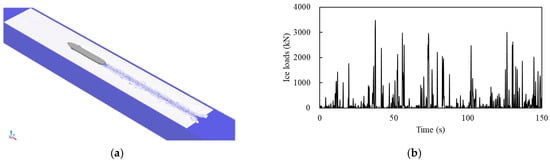
Figure 3. (a) Simulation of ship navigation in a level-ice region using the DEM. (b) Time history of ice loads acting on the designated loading patch extracted from the DEM simulation under the load case of 1.0 m ice thickness (0.9–1.1 m) and 7.5 knots ship speed (7–8 knots).

The area subjected to the most intense ship–ice interactions is designated as the loading patch. The area from the stem to the shoulder experiences significantly higher ice loads and collision frequencies compared with other parts of the hull and is therefore commonly regarded as a critical zone for ice-induced fatigue analysis [30]. Since sea ice remains afloat on the water surface, ice–structure collisions are concentrated near the waterline. As shown in Figure 4, the green-marked area on the bow model represents the loading patch. The time history of ice loads for the loading patch extracted from DEM in this case is presented in Figure 3b.

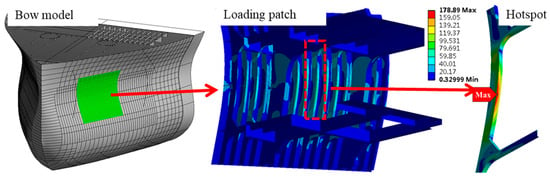
Figure 4. Finite element model of ship bow structure. The green-marked area is loading patch. The red bracket is the frame containing hotspot.

The local ice loads are applied to the loading patch in the finite element model to compute the structural stress distribution, as shown in Figure 4. In the bow structure model, the outer plate has a thickness of 12 mm, the frame spacing is 73 mm, and the frame’s thickness and height are 10 mm and 130 mm, respectively.

The results show that the maximum stress occurs at the midpoint of the frame, which is therefore selected as the fatigue analysis hotspot. Its stress time history is shown in Figure 5a. The corresponding stress cycle histogram is obtained by the rain flow counting method, as shown in Figure 5b. According to Equation (3), the equivalent fatigue stress amplitude $S_{\mathrm{e}}$ at the bow hotspot under the selected load case is calculated to be 60.44 MPa. Then the $S_{\mathrm{e}}$ for all typical load cases are calculated and listed in Table 2. The equivalent fatigue stress amplitude $S_{\mathrm{e}\mathrm{T}}$ for the entire voyage is calculated by Equation (4) as 45.84 MPa.

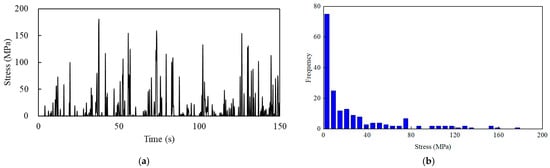
Figure 5. (a) Time history of stress amplitude for bow structure. (b) Statistics of stress amplitude.

2.5. Results of Fatigue Failure Probability

By substituting the random variables and constant parameters into Equations (9) and (10), the mean and coefficient of variation in the predicted fatigue life in logarithmic form are calculated as ${\mu }_T=33.83$ and $C_T=0.485$, respectively. According to Equations (15) and (16), for the service life $T_{\mathrm{d}}=20$ years, the fatigue failure probability of the bow hotspot is calculated to be 4.09 × 10⁻², with the corresponding parameters summarized in Table 4.

Table 4. Fatigue failure probability for service life of 20 years.

Reliability Parameter	$\mathbf{Safety} \mathbf{Index} \mathit{\beta }$	$\mathbf{Reliability} {\mathit{P}}_{\mathbf{r}}$	$\mathbf{Failure} \mathbf{Probability} {\mathit{P}}_{\mathbf{F}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{g}\mathbf{u}\mathbf{e}}$
Value	1.74	0.9591	4.09 × 10−2

3. Probability of Ultimate Strength Failure

Under extreme environments, polar ships may experience ultimate limit states (ULSs). Reliability analysis of ultimate strength requires the probabilistic distributions for both the structural loading capacity and the external loads.

3.1. Probabilistic Distribution of Structural Load-Carrying Capacity

The load-carrying capacity of polar ship structures is primarily influenced by factors of material properties and structural dimensions. Among these, the elastic modulus and Poisson’s ratio have a relatively minor effect, whereas the yield strength has a significant impact [31]. The statistical characteristics of the yield strength of marine-grade steel are generally assumed to follow either a normal or a lognormal distribution [32]. The primary construction material of the polar transport vessel is EH36 steel, which is a high-strength, corrosion-resistant, and low-temperature-tolerant material [33]. The hull plate thickness also has a notable influence and is typically assumed to follow a normal distribution [31,34]. In this study, the statistics of yield strength and plate thickness for EH36 steel are adopted as shown in Table 5.

Table 5. Statistics of random variables for load-carrying capacity [34,35].

Random Variable	Probabilistic Distribution	Mean	Coefficient of Variation
Yield strength	Normal	355 MPa	0.06
Plate thickness	Normal	(1 + 2%) nominal value	0.04

The structure’s ultimate strength decreases with fatigue damage. In this study, based on the fatigue assessment results, a through-thickness fatigue crack with a width of 15 mm is introduced at the hot spot, as shown in Figure 6a. Loads are applied to both the integrated structure and the structure with a crack. The corresponding load–displacement curves are shown in Figure 6b. The twice elastic slope method is applied [36]. The load-carrying capacity is determined to be 4.20 MPa for the integrated structure and 3.25 MPa for the structure with fatigue crack. The results indicate that the presence of crack significantly reduces the ultimate strength.

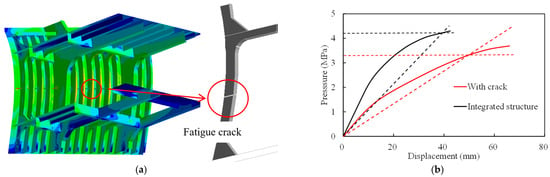
Figure 6. (a) Bow structure with fatigue crack. (b) Calculation of load-carrying capacity by twice elastic slope method. The dashed lines represent the baseline of the method.

According to the method of moment estimation [37], the mean values of yield strength and plate thickness in the ship bow model are adjusted by adding or subtracting standard deviation, respectively. With only five times of FEM calculation, the probabilistic distribution of load-carrying capacity can be obtained. The results follow a normal distribution, with a mean of 4.20 MPa and a standard deviation of 0.319 for the integrated structure, while the structure with a fatigue crack has a mean of 3.25 MPa and a standard deviation of 0.231.

3.2. Probabilistic Distribution of Ice Pressure

Ice loads are the primary external loads acting on polar ships during navigation in ice-covered regions. Therefore, the probabilistic distribution of ice loads is adopted as the representation of external loads. The statistical characteristics of local ice pressure on the ship bow are obtained based on the results of Li et al. by full-scale monitoring [38]. The 2018/19 Antarctic voyage of the Polar Supply and Research Vessel (PSRV) S.A. Agulhas II gathered considerable data on the ship in floe ice fields under various thicknesses, concentrations, and floe sizes. The probability density function (PDF) of extreme load among 10,000 ice pressure samples with a Weibull distribution is shown in Figure 7. To simplify reliability calculation, the ice pressure is assumed to follow a normal distribution. Based on the statistical data, the mean and standard deviation of the ice pressure distribution are 2.16MPa and 0.609, respectively.

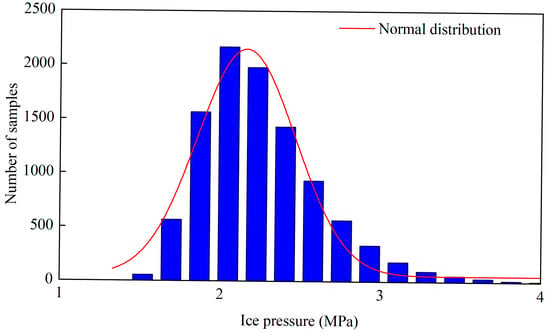
Figure 7. Probabilistic distribution of ice pressure.

3.3. Results of Ultimate Strength Failure Probability

For the reliability analysis, the failure function in Equation (1) can be reformulated as follows:

$$Z=R-S$$

(16)

where $R$ is the load-carrying capacity of the ship bow structure, and $S$ is the external loads (ice pressure). The probabilistic distributions of $R$ and $S$ are illustrated in Figure 8. According to the definition of structural reliability, the ultimate strength failure probability of the bow structure corresponds to the probability that $R$ is less than $S$.

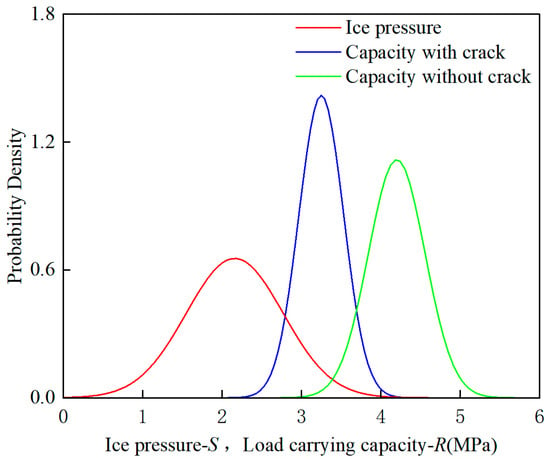
Figure 8. Probability of ultimate strength failure.

When R and S are independent normally distributed random variables, the reliability index β can be expressed as follows [39]:

$$\beta ={\displaystyle \frac{{\mu }_Z}{{\sigma }_Z}}={\displaystyle \frac{{\mu }_R-{\mu }_S}{\sqrt{{{\sigma }_R}^2-{{\sigma }_S}^2}}}$$

(17)

where ${\mu }_R$ and ${\sigma }_R$ represent the mean and standard deviation of the load-carrying capacity. Based on the analysis results in Section 3.1, for the structure with a fatigue crack, ${\mu }_{R\_with}=3.25 \mathrm{M}\mathrm{P}\mathrm{a}$ and ${\sigma }_{R\_with}=0.231$; for the structure without a fatigue crack, ${\mu }_{R\_without}=4.20 \mathrm{M}\mathrm{P}\mathrm{a}$ and ${\sigma }_{R\_without}=0.319$. Based on the analysis results in Section 3.2, the mean and standard deviation of the external load are ${\mu }_S=2.16 \mathrm{M}\mathrm{P}\mathrm{a}$ and ${\sigma }_S=0.609$, respectively. Based on Equation (11), the reliability and failure probability of the bow structure’s ultimate strength are determined, and the results are summarized in Table 6.

Table 6. Ultimate strength failure probability of ship bow structure.

Reliability Parameter	$\mathbf{Safety} \mathbf{Index} \mathit{\beta }$	$\mathbf{Reliability} {\mathit{P}}_{\mathbf{r}}$	$\mathbf{Failure} \mathbf{Probability} {\mathit{P}}_{\mathbf{S}\mathbf{t}\mathbf{r}\mathbf{e}\mathbf{n}\mathbf{g}\mathbf{t}\mathbf{h}}$
With crack	1.673	0.9529	4.71 × 10−2
Without crack	2.385	0.9915	8.54 × 10−3

To validate the proposed method, results are compared with Mikko’s [40] study, whose model is similar to the without-crack model used here. Both studies indicate that the probability of structural failure in the bow region under local ice loads is on the order of 10⁻³ to 10⁻⁴, demonstrating the reliability of the present approach.

4. Risk Assessment

Risk assessment methods are generally categorized into scenario analysis, hazard and operability analysis (HAZOP), event tree analysis (ETA), and fault tree analysis (FTA) [41]. Among these, the risk matrix method is a widely used tool for visualizing and ranking risks by defining the range of failure consequences and their likelihood [42].

4.1. Risk Matrix Method

When assessing and evaluating uncertainties associated with an event, risk is defined as the potential for loss as a result of a system failure. It can be measured as a pair of factors, one being the probability of occurrence of an event, also called a failure scenario. And the other is the potential outcome or consequence associated with the event’s occurrence [43]. Accordingly, the structural failure risk index is defined as follows:

$$\mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}=\mathrm{L}\mathrm{i}\mathrm{k}\mathrm{e}\mathrm{l}\mathrm{i}\mathrm{h}\mathrm{o}\mathrm{o}\mathrm{d}\left(\mathrm{E}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{t}\right)\times \mathrm{I}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}\left(\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{e}\mathrm{q}\mathrm{u}\mathrm{e}\mathrm{n}\mathrm{c}\mathrm{e}\right|\mathrm{E}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{t})$$

(18)

In this study, the likelihood can be expressed as the probability of fatigue failure, which is described as a numeric value. The consequence included in the present risk analysis can be defined as the ultimate strength failure of the polar ship structure, given that fatigue failure (the initiating event) has already occurred. Then Equation (18) can be expressed as follows:

$$P_{\mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}}=P_{\mathrm{F}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{e}}\times P_{\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}|\mathrm{F}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{e}}$$

(19)

where $P_{\mathrm{R}\mathrm{i}\mathrm{s}\mathrm{k}}$ is the structural failure risk, $P_{\mathrm{F}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{e}}$ is the fatigue failure probability, and $P_{\mathrm{S}\mathrm{t}\mathrm{r}\mathrm{e}\mathrm{n}\mathrm{g}\mathrm{t}\mathrm{h}|\mathrm{F}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{g}\mathrm{u}\mathrm{e}}$ is the ultimate strength failure probability under the condition of the structure with fatigue crack.

4.2. Results of Risk Assessment

To enhance the reliability of the risk analysis, it is necessary to evaluate the risk levels of multiple critical locations within the ship structure. In this study, three representative structural components of ship bow were selected, as shown in Figure 9. To analyze the evolution of structural failure risk over time, the fatigue failure probabilities of the structure were also calculated for service lives of 5, 10, 20, and 50 years. The corresponding results were calculated by the aforementioned method and are presented in Table 7.

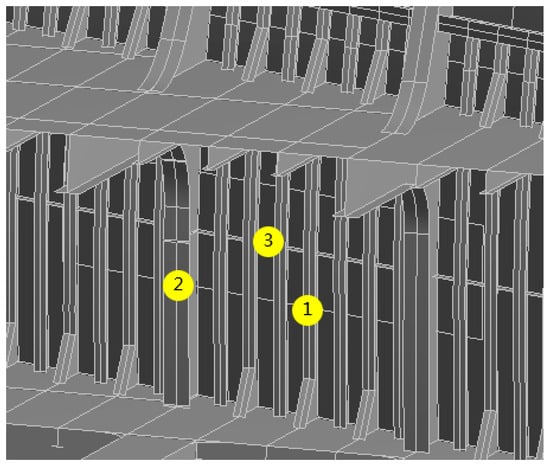
Figure 9. Typical components of ship bow structure for risk assessment. ① indicates the hotspot on the frame, ② indicates the hotspot on the web frame, ③ indicates the hotspot on the stringer.

Table 7. Results of risk assessment.

Component	$\mathbf{Fatigue} \mathbf{Failure} \mathbf{Probability} {\mathit{P}}_{\mathbf{F}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{g}\mathbf{u}\mathbf{e}}$				Strength Failure Probability ${\mathit{P}}_{\mathbf{S}\mathbf{t}\mathbf{r}\mathbf{e}\mathbf{n}\mathbf{g}\mathbf{t}\mathbf{h}|\mathbf{F}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{g}\mathbf{u}\mathbf{e}}$
	5 Years	10 Years	20 Years	50 Years
Frame ①	3.11 × 10−3	1.30 × 10−2	4.09 × 10−2	9.70 × 10−2	4.71 × 10−2
Web frame ②	2.48 × 10−3	8.43 × 10−3	2.74 × 10−2	6.10 × 10−2	2.36 × 10−1
Stringer ③	3.30 × 10−3	1.25 × 10−2	3.60 × 10−2	8.30 × 10−2	4.40 × 10−2

Based on Table 7, a risk matrix was constructed using the strength failure probability and fatigue failure probability as the horizontal and vertical axes, respectively, as shown in Figure 10. The blue line in the figure is the risk target, which was determined by multiple factors, such as potential economic loss, personnel safety, risk quantification methods and failure modes. A reliable target value must be derived from extensive statistical analysis of existing data. Currently, no explicit guidelines are provided for polar ship structures. In this study, the risk target value is set to 1.00 × 10⁻³. It should be noted that this target is not fixed and can be adjusted based on safety requirements and cost considerations. When a high level of safety is required and cost constraints are less critical, the target risk level may be increased. In practice, an upper risk target of 3.16 × 10⁻³ and a lower risk target of 3.16 × 10⁻⁴ are often set to define acceptable risk bounds. Then the risk matrix is divided into three risk levels: low, medium and high.

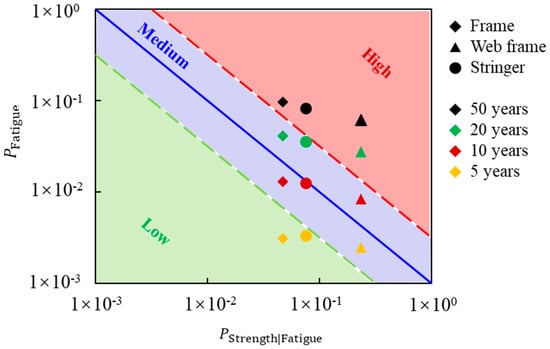
Figure 10. Risk matrix of bow structure.

4.3. Discussions

The results of risk assessment listed in Table 7 are mapped on the risk matrix. A comparative analysis was conducted to evaluate the failure risks of the components after 20 years of service. It is observed that the web frame exceeds the upper risk target and is in the high-risk zone. The frame and the stringer, while exceeding the risk target, remain below the upper target and are classified as medium risk. Although the fatigue failure probability of the web frame is relatively low in this study, it plays a critical role in the overall structural integrity. Consequently, its ultimate strength failure probability is much higher with the existence of fatigue crack, leading to a greater failure risk. This component should therefore be prioritized in maintenance activities.

These findings highlight that assessing structural safety solely based on fatigue life or ultimate strength is insufficient. The risk matrix method offers a more comprehensive and rational framework for evaluating structural failure risk.

In addition, the failure risks are compared across different service durations. When the service life reaches 5 years, only the web frame reaches a medium-risk level, while the other components remain in the low-risk zone. By 10 years, all components fall into the medium-risk zone. After 20 years of service, the web frame reaches the high-risk level. Without inspection and maintenance, all components will exceed the upper risk target and fall into the high-risk zone after 50 years of service. This trend is attributed to the continuous accumulation of fatigue damage, which increases the probability of fatigue failure and leads to a gradual rise in structural failure risk with longer service time.

According to the risk-based inspection (RBI) methodology, structural risk assessment enables targeted inspection planning based on the risk status of individual components. In the present risk evaluation, the failure probability of each component is used as the basis for determining inspection intervals. If the upper target of the risk matrix is adopted as the inspection threshold, then, among the three components, the web frame should be inspected at 18 years of service, the stringer at 23 years, and the frame at 32 years. This method enables a rational prioritization of structural risks through systematic analysis and forms the basis of an optimized inspection strategy that balances safety and economic considerations.

4.4. Limitations and Future Work

Although the proposed risk matrix approach provides a systematic and quantitative framework for assessing the structural failure risks of polar ships under ice loads, several limitations should be acknowledged.

(1)

The present study focuses on local structural components in the bow region, and the complex interactions between global hull responses and spatially varying ice loads were not fully considered.

(2)

The ice load simulations and fatigue analyses are based on idealized assumptions and a limited range of operational and environmental parameters, which may not capture all realistic ice–ship interaction scenarios.

(3)

The probabilistic models adopted for fatigue and ultimate strength evaluations employ simplified statistical distributions, and the effects of uncertainties such as material degradation, crack growth behavior, and repair actions were not explicitly incorporated.

Future research will aim to overcome these limitations. Efforts will be made to extend the methodology to full-ship structural systems and to integrate stochastic representations of environmental and operational conditions. The incorporation of real-time monitoring data and dynamic risk updating will also be explored to enhance the practical applicability of the framework. Furthermore, combining the proposed approach with event tree analysis (ETA) and fault tree analysis (FTA) may enable a more comprehensive understanding of risk propagation and system-level failure mechanisms. Experimental validation and long-term service data analysis will be key priorities for improving the reliability and engineering relevance of future studies.

5. Conclusions

Based on the risk matrix framework, this study proposes a quantitative risk assessment method for evaluating the structural failure of polar ships under ice loads. The approach integrates fatigue reliability and ultimate strength analysis to establish a comprehensive understanding of failure risks. The most important conclusions are listed as follows:

(1)

Based on full-scale measurements, DEM and FEM analyses were used to quantify fatigue and ultimate strength failure probabilities of the ship bow, providing a reliable basis for polar ship structural safety assessment.

(2)

A risk matrix was constructed by defining fatigue failure as the probability of failure and ultimate strength failure as the consequence. Through this matrix, the structural failure risks of three typical components were assessed and classified into low, medium and high-risk levels under varying service durations.

(3)

The results show that neither fatigue nor strength analysis alone is sufficient for robust safety evaluation. The proposed risk matrix approach offers a rational and practical framework that supports RBI strategies, enhancing both the safety and cost effectiveness of polar ship operations in ice-covered regions.