Abstract
In the Shenhu Area of the South China Sea, although some numerical studies are conducted on the gas production at well SHSC-4, the geomechanical responses have not been taken into account, and the associated impact of permeability enhancement on gas production has not been thoroughly investigated. In this study, pTOUGH+HYDRATE V1.5 coupled with the RGMS is applied to account for geomechanical responses. Based on actual geological conditions, the reservoir model has five layers: the hydrate-bearing layer (HBL), the three-phase layer (TPL), the free gas layer (FGL), the overburden, and the underburden. The numerical results match the trial production data, validating the numerical model. The analysis shows that gas production from the FGL contributed the most (72.17%) to the cumulative gas production (Vg), followed by the TPL (23.54%) and the HBL (4.29%). The cumulative water-to-gas ratio (RwgT) gradually decreased during gas production, with the HBL exhibiting the highest value. Permeability enhancement can improve gas production, with the FGL being the most responsive to such enhancement. It increased Vg by 87% and reduced RwgT to 85%. To achieve more realistic production schemes and better enhance energy recovery, it is advisable to conduct numerical investigations that incorporate geomechanical considerations due to the intricate nature of hydrate-bearing sediments.
1. Introduction
1.1. Background
Natural gas hydrates (NGHs) are commonly referred to as combustible ice, which is a non-stoichiometric cage crystalline compound [1], because of their ice-like appearance and ability to be burned. NGH, being an unconventional source of clean energy, produces the least amount of CO2 per unit of energy [2]. The potential reserves of hydrated gas are over 1.5 × 1016 m3 and are widely distributed throughout the earth [3], with over 230 hydrate deposits discovered globally in ocean floors and permafrost zones. To extract methane gas from hydrate reservoirs, the in-situ equilibrium condition (high pressure and low temperature) of NGH must be broken, allowing it to decompose and be produced as fluid. Four methods can be used for gas recovery from hydrate-bearing sediments, including depressurization [4,5], thermal stimulation [6], inhibitor injection [7], and CO2–CH4 replacement [8,9,10,11]. National programs exist in many countries to research and produce natural gas from gas hydrate deposits in order to discover the commercialization possibility of methane hydrate resources, leading to various studies on the Alaska North Slope [12,13,14,15], the Mallik site in Canada [4,16,17], the Black Sea [18,19], the Krishna–Godavari basin in India [20,21], the Ulleung basin in Korea [22,23], the Nankai Trough in Japan [24,25,26], and the South China Sea [27,28,29] and Qilian Mountain [30] in China.
In general, both marine and terrestrial gas hydrate accumulations are targeted for exploitation. Extracting methane from hydrates can provide a significant global energy supply as long as the operation is controlled to prevent any leakage. Concerns about potential environmental risks are increasing, particularly regarding methane escape to the seafloor during hydrate exploitation in marine region [31]. In addition to production leakage, the warming atmosphere can disrupt the stability of hydrate fields, leading to the release of sequestered methane into the sediments and soils above. The methane, along with methane-derived carbon, can further contribute to greenhouse warming when it reaches the atmosphere [32]. If this happens in the terrestrial region, it has the potential to cause a catastrophic disaster, even with only around 1% of the global gas-in-place estimated to be in the permafrost-associated NGH [33]. This topic has sparked interest in studies that aim to quantify natural gas hydrates from ice [34] and understand how gas hydrate-bearing permafrost sediments respond to changes in environmental temperature [35]. While both NGH exploitation and global warming can have environmental effects, the focus of this study is to evaluate the production potential of offshore hydrate accumulations in the South China Sea.
The main focus of this study is on the Shenhu area located in the northern part of the South China Sea. Between the years 2007 and 2016, the Guangzhou Marine Geological Survey (GMGS) conducted three gas hydrate drilling expeditions, namely, GMGS1, GMGS3, and GMGS4 [36]. During GMGS3, the team drilled a total of 23 sites for logging-while-drilling (LWD) and 4 sites for core drilling. The results indicated that the average hydrate saturation ranged from 13.7% to 45.2% [36]. Among these drilling sites, the first gas hydrate production site, W17, was selected [29]. This was a significant accomplishment since hydrates in the Shenhu area exist in clayey silt sediments, which pose production challenges due to their low permeability and high levels of clays. The W17 well test demonstrated the possibility of production in such a location, which accounts for 90% of total hydrate reservoirs [37]. In 2017, the China Geological Survey set a new world record for gas hydrate production by performing a successful offshore methane hydrate production test in the Shenhu Area. The team used a single vertical well and depressurization for a production period of 60 days, resulting in a total gas production of 3.09 × 105 ST m3, averaging 5.15 × 103 ST m3/d [29]. This achievement marked the most significant amount of gas production and the longest production period in history. Recently, the China Geological Survey performed another production test using a horizontal well for the first time in the Shenhu Area, achieving a 30-day continuous gas production process. The total gas production reached 8.614 × 105 ST m3, averaging 2.87 × 104 ST m3/d [27]. The gas production rates in both production tests remain significantly below 5.00 × 105 ST m3/d, which is necessary for the commercial exploitation of NGHs [1].
The commercialization of methane hydrate resources is a crucial challenge, necessitating the need for enhanced gas recovery from methane hydrate deposits and leading to the exploration of various methods to increase gas production. The second production test in the Shenhu area indicates that horizontal wells have been found to enhance gas production by increasing the contact area between the well and the reservoir. However, the cost of horizontal wells is 1.5 to 2.5 times more than vertical wells [38]. In addition to horizontal wells, permeability enhancement (e.g., hydraulic fracturing), allowing gas to flow more freely towards the wellbore, might be a cost-effective option for methane hydrate reservoirs to stimulate gas production, resulting in a significant increase in gas recovery. This enhanced gas recovery can maximize the productivity of wells and boost overall production rates, ultimately paving the way for the commercialization of methane hydrate resources. Previous studies in the eastern Nankai Trough have demonstrated that permeability anisotropy and permeability improvement can enhance gas recovery [24,39]. Therefore, it appears feasible to improve gas recovery in the South China Sea via permeability enhancement as well.
Conducting field tests to determine gas recovery via different production schemes is impossible, thus necessitating the use of a numerical simulator to simulate production performance. The most commonly used simulator for studying production behavior in gas-hydrate-bearing sediments is TOUGH+HYDRATE (T+H). T+H is capable of describing mass and heat flows, hydrate formation and dissociation, and the inhibitor effect [40]. When compared to other simulators available for hydrate simulations, T+H demonstrates superior predictive results when assessing production feasibility for permafrost and marine hydrates [41]. T+H has been utilized to identify gas recovery from low-permeability hydrate reservoirs via depressurization [42], as well as natural gas hydrate reservoirs in the eastern Nankai Trough [26]. Some studies have also incorporated a geomechanical simulator to analyze geomechanical responses [43,44,45]. By utilizing these simulators, the effectiveness of permeability enhancement can be determined.
In order to evaluate the potential for gas production resulting from permeability enhancement in the South China Sea, various numerical simulations have been carried out. In the Liwan 3 Area, Zhang et al. [46] focused on a methane hydrate reservoir with the conditions of low permeability located at site LW3-H4-2. Their approach involved the use of an enlarged, highly permeable well wall, which was proposed as a means of promoting gas production. At site SH2 in the Shenhu Area, Li et al. [47] and Sun et al. [48] suggested the stratification split grouting foam mortar method and hydraulic fracturing, respectively, as methods to improve permeability for production enhancement. The latter study demonstrated the influences of horizontal and vertical fractures. Despite the different methods used for permeability enhancement, Yu et al. [49] conducted a study showing that gas production can be significantly enhanced by the complex mechanisms associated with permeability enhancement at well SHSC-4. These models were based on various geological conditions in the South China Sea and explored the impact of different parameters, including permeability, on gas recovery.
Despite the progress made in enhancing gas production from methane hydrate deposits, the effect of permeability associated with geomechanical responses on gas production enhancement has not been thoroughly investigated. Previous studies have predominantly relied on simplistic adjustments of formation porosity and permeability based on pressure and temperature, with a primary focus on understanding the interplay between system flow and thermal aspects. Unfortunately, these studies have overlooked the crucial factors of media deformations and changes in stress fields. Geomechanics is a critical factor in understanding the behavior of hydrate behavior because of the state and phase changes, leading to changes in its porosity, permeability, and flow characteristics [4,50,51]. Specifically, changes in stress and pressure can cause the rock to compact or expand, affecting the pore structure and connectivity. These changes in permeability can significantly impact the flow of gas within the reservoir, influencing production rates and overall productivity.
Before commercial gas production from hydrate deposits can be developed, it is essential to address and understand the geomechanical response of hydrate-bearing sediments. Particularly, potential wellbore instability and casing deformation are significant concerns that must be tackled [52]. The application of mechanical loads to sediments containing hydrates can cause hydrate dissociation and result in a substantial increase in pressure. This pressure increase can negatively impact the wellbore assembly, the hydrate-bearing sediments, and the surrounding formations, posing risks to their integrity and stability [50]. To prevent failures like tensile or buckling failure in the well assembly, it becomes crucial to implement appropriate well design based on numerical simulations accounting for the geomechanical response [53].
To evaluate the production potential in the South China Sea, it is crucial to have a comprehensive understanding of the intricate interactions between permeability, geomechanical responses, and gas production enhancement. To gain a more accurate and holistic understanding of these phenomena, it is imperative to consider the influence of media deformations and stress field changes. Only a geomechanical model can accurately capture the mechanical behavior of subsurface rocks, including (a) the deformation and potential failure of the reservoir media and well assembly; (b) the effects of changes in stresses, fluid pressures, and temperatures on flow properties like porosity and permeability that control production; and (c) the interdependence of system flow, thermal, and geomechanical properties. Hence, the accurate determination of (a) the impact of permeability enhancement associated with geomechanical responses on hydrate development and (b) the effectiveness of permeability enhancement can be achieved.
1.2. Targeted Accumulation
This study focuses on the oceanic hydrate accumulation at well SHSC-4 in the Shenhu area (Figure 1), which is located in the northern South China Sea between the Xisha Trough and Dongsha Islands and is structurally part of the Baiyun Sag of the Zhuer Depression [29]. The seafloor exhibits a complex topography, including various features such as eroded channels, sea valleys, sea mounts, steep slopes, reverse slopes, plateaus, alluvial fans, and slide fans [54]. The continental slope in the northern South China Sea displays both passive and active continental features due to interactions between the Eurasian, Pacific, and Indochina plates. The reservoir lithology is composed of clayey silt, with montmorillonite and illite constituting over a quarter of the total minerals [29]. Based on the logging interpretation and core analysis of SHSC-4, the overlying formation extends from the sea bottom to a depth of 1495 m (201 m below seafloor (mbsf), with a water depth of 1266 m). The NGH system at the test site comprises three intervals, with the first interval ranging from 1495 to 1530 m (201–236 mbsf), and its pore space is filled with solid NGH and liquid water. The second interval spans from 1530 to 1545 m (236–251 mbsf), and its pore space is filled with three phases: solid NGH, free hydrocarbon gas, and liquid water. The third interval spans from 1545 to 1572 m (251–278 mbsf), and its pore space is filled with two phases: free hydrocarbon gas and liquid water.
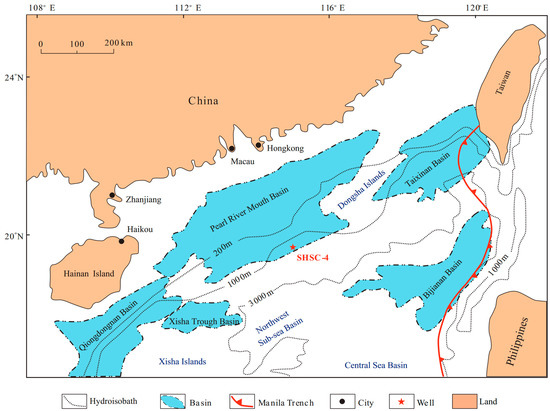
Figure 1.
Structural units in the northern South China Sea and the location of SHSC-4 (modified from Li et al. [29]).
1.3. Objectives
The objective of this study is to assess the technical feasibility of gas production and production enhancement by the numerical simulation of oceanic hydrate accumulation in the Shenhu Area of the South China Sea. Specifically, the study evaluates the impact of increased permeabilities in the near-wellbore region on gas production associated with the geomechanical responses. The analysis considers the properties and conditions obtained at well SHSC-4; studies the gas production behavior at well SHSC-4 using a single vertical well by depressurization; assesses the contribution of different layers to gas production; and investigates the feasibility of permeability enhancement, the potential of increased gas production, and the geomechanical response of the geological system during production. To validate the accuracy of the numerical model used in the study, a 60-day simulation result is compared against the actual trial production test conducted at well SHSC-4. The impact of permeability enhancement is evaluated by quantifying the ratios of the cumulative gas production and cumulative water-to-gas ratio, comparing them to the original conditions.
2. Methodology
2.1. Coupled Numerical Simulators
Two parallel simulators, pTOUGH+HYDRATE (pT+H) V1.5 and the Reservoir GeoMechanics Simulator (RGMS) [55,56], based on an MPI (message passing interface) were utilized in this study to simulate the coupled processes of flow, thermal, chemical, and geomechanical processes associated with gas production induced by depressurization. pT+H V1.5 is a parallel version of TOUGH+HYDRATE V1.5 used for conducting numerical investigations of flow and thermal behavior in hydrate-bearing geologic media. The code uses the integral finite difference method (IFDM) [57,58] for space discretization and the Newton–Raphson (NR) iteration for a fully implicit solution. The computational domain is decomposed into subdomains for efficient workload distribution to multiple processes. The RGMS is a parallel geomechanical simulator that accurately characterizes deformations and stresses in subsurface systems by employing parallel strategies in conjunction with the finite element method (FEM). It has the capability to handle grids with Cartesian (2D and 3D) and cylindrical (2D) coordinates. Additionally, the simulator can be used either as a standalone or coupled with T+H, pT+H, and other simulators describing flow and thermal behavior. To explore the geomechanical responses to gas production from hydrate reservoirs, pT+H V1.5 and the RGMS are coupled via the fixed-stress split iterative scheme. The coupling scheme was validated in previous studies [55,56].
2.2. Governing Equations
2.2.1. Flows of Fluid and Heat
The mass and energy balance equation includes the accumulation, flux, and source/sink terms through a control volume in a porous medium [40], which is expressed as
where is the time, is the volume of subdomain n, is the differential volume, is the accumulation of component in terms of mass or heat, is the surface area of subdomain n, is the differential surface area, is the flux vector of component in terms of mass or heat, denotes the inward unit normal vector, and is the source/sink term of component .
For component , the mass accumulation is calculated by
where indicates phase (A refers to aqueous, G refers to gaseous, I refers to solid ice, and H refers to solid hydrate), indicates component (w refers to H2O, m refers to CH4, and i refers to water-soluble inhibitor), represents the porosity, represents the saturation of phase , represents the density of phase , and represents the mass fraction of component in phase .
The heat accumulation comprises contributions from both the rock matrix and all the phases and is expressed by
where is the density of the rock, CR is the heat capacity of the dry rock, T is the temperature, and is the specific internal energy of phase . The energy change of hydrate dissociation Qdiss is
where denotes the quantity change during a given timestep, and is the specific enthalpy of hydrate dissociation, which can be calculated by Equation (5) from [59]:
where the conversion factor Cf is 33.72995 J∙gmol∙kg−1∙cal−1,
It is important to note that hydrate dissociation can be treated in two ways: (a) a chemical equilibrium reaction (the hydrate is considered a thermodynamic state of the CH4 and H2O system) or (b) a kinetic reaction (the hydrate is regarded as a distinct component) [60]. The former was employed in this study. Interested readers can refer to Moridis [40,61] for in-depth information on the specifics of the two models and the associated thermodynamics.
The mass flux of component (e.g., H2O, CH4, and inhibitor) contributed by the aqueous and gaseous phases is defined as
Following Darcy’s law, the mass flux of phase is defined as
in which, for phase β, is the relative permeability, is the viscosity, and is the fluid pressure. Additionally, k is the absolute permeability tensor, and g is the gravity vector.
The heat flux is defined as
where is the specific enthalpy of phase , and is the composite thermal conductivity considering the properties of medium and fluid.
2.2.2. Geomechanics
The quasi-static momentum conservation equation is based on the underlying assumption that there is always equilibrium between the fluid and rock, which is calculated by
where is the total stress tensor. The bulk density is found using
in which ρf is the saturation-weighted fluid density, which is calculated using
In accordance with convention, the equations below always consider tensile stress as positive. The relationship that defines the stresses associated with the rock skeleton is expressed as
where C is the elasticity tensor, is the effective stress tensor, I is the identity matrix, and is the strain tensor. Biot’s coefficient α [62] is defined as
where Ks is the skeletal grain modulus, and Kdr is the drained bulk modulus. The average mobile fluid pressure Pt is calculated using
By utilizing the assumption of infinitesimal deformation, the strain tensor is determined using
in which u is the displacement vector.
2.2.3. The Coupling Method between Geomechanics and Flows of Fluid and Heat
To investigate the geomechanical response during production, pT+H and the RGMS were coupled with the fixed-stress split iterative scheme so that the changes in fluid pressure, temperature, phase saturations, and associated stresses can be found. The accuracy and reliability of the scheme were verified by comparing its numerical results and the analytical solutions of Terzaghi’s problem [63] and McNamee–Gibson’s problem [64,65] in prior research [55].
The scheme operates in a sequential manner as shown in Figure 2, where pT+H solves the problem when the stress field is frozen. The strongly nonlinear equations are solved via the NR iteration, and the porosity is calculated using
in which k is the number of the NR iterations, Kdr is the drained modulus, εv is the volumetric strain, and is the difference at the NR iteration k and k − 1.
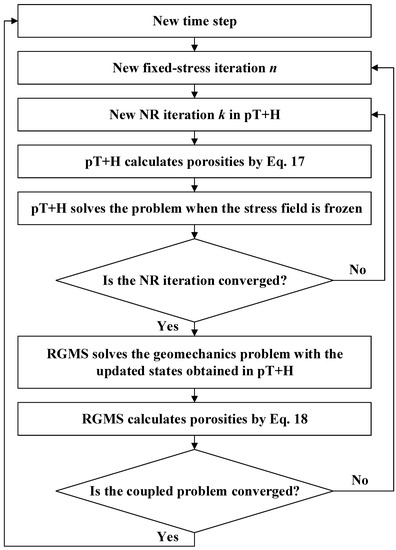
Figure 2.
Flow chart of the coupling method between geomechanics and flows of fluid and heat.
Subsequently, the porosity in the RGMS is calculated using
where subscript n denotes the initial states.
pT+H and the RGMS solve the problem sequentially; do not proceed to the next time step until is lower than a predetermined tolerance level.
The mechanical properties of the hydrate are influenced by the existence of hydrate, which is more pronounced when SH has a higher value. However, there is a scarcity of research on how the properties are related to the hydrate phase. Rutqvist and Moridis [50] proposed a standard approach that utilizes linear interpolation equations as follows:
and
where G is the shear modulus, subscript 0 denotes SH = 0, and subscript 1 denotes SH = 1.
3. Numerical Model
3.1. The Geologic Model
The geological model was developed from a combination of geophysical surveys and an analysis of core samples retrieved from the well. The model consists of five units: the overburden (OB), the hydrate-bearing layer (HBL), the three-phase layer (TPL), the free gas layer (FGL), and the underburden (UB). The computational domain used in both the production and geomechanical studies accurately represents the geological model, encompassing the entire OB to the ocean floor and a portion of the UB that was thick enough to fully account for the necessary heat and water exchange with the reservoir, and provides a true zero-displacement boundary for geomechanical computations.
Combining geophysical surveys and core sample analysis from the well, the geological model was developed (Figure 3), comprising five units: the overburden (OB), the hydrate-bearing layer (HBL), the three-phase layer (TPL), the free gas layer (FGL), and the underburden (UB). In pT+H V1.5 and the RGMS, the same computational domain was utilized to represent the geological model, covering the entire OB to the ocean floor and a thick enough portion of the UB to account for water and heat exchange within the reservoir, and to make sure there was no displacement occurring at the bottom boundary for geomechanical computations.
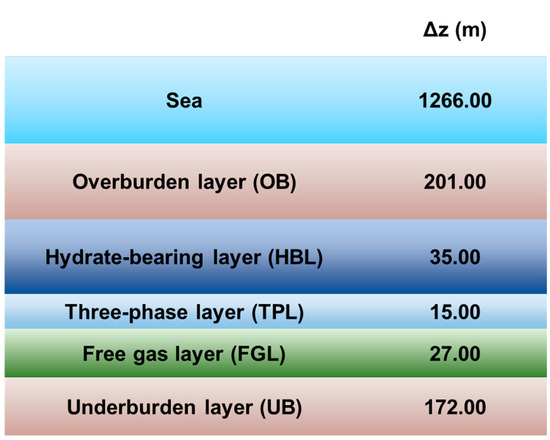
Figure 3.
The geological model with layered geometries.
3.2. Domain Discretization
A 2D cylindrical domain with an outer radius of 300 m, as presented in Figure 4, was utilized to investigate gas production with a single vertical well. The domain was divided into 412 segments radially and 232 segments vertically, leading to 95,584 gridblocks. Gridblocks with different lengths were produced due to the high-resolution radial discretization in the vicinity of the well; specifically, the segment length in the radial direction (Δr) of 0.10 m was used for rw < r ≤ 1 m, while that of 0.20 m was used for 1 m ≤ r ≤ 21 m. For distances greater than 21 m but less than 300 m (rmax), Δr increased logarithmically for r > 0.20 m. The segment length in the vertical direction (Δz) was 0.5 m in the hydrate accumulation area and was larger in OB and UB. A mesh representation of the domain used in this study is presented in Figure 5a, while a more detailed representation of the grid near the wellbore is given in Figure 5b.
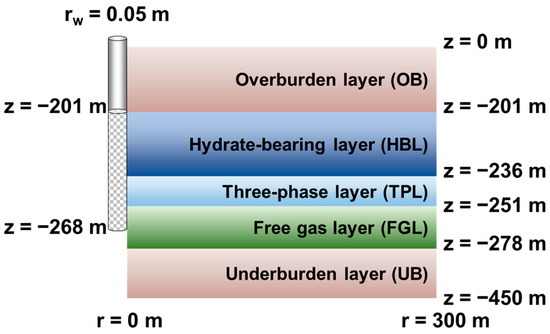
Figure 4.
System geometry and configuration of the single vertical well with a radius of 0.05 m, which is perforated from 201 mbsf to 268 mbsf as shown in the checkboard pattern, produced from a cylindrical section at well SHSC-4.
Figure 5.
Discretization of (a) the entire domain and (b) the region near the well.
For each element, four equations were designed to account for the mass balance of three components (H2O, CH4, and NaCl) as well as the heat balance of the system. Previous research has demonstrated that a chemical equilibrium reaction provides an accurate result during hydrate formation/dissociation in gas production [60]. To account for the scale of the problem, a total of 560,000 equations were formulated, consisting of approximately 380,000 equations in pT+H V1.5 and 180,000 equations in the RGMS. Consequently, the problem sizes necessitated the use of pT+H V1.5 and the RGMS to provide practical solutions.
3.3. Well Description
At the center of the cylindrical domain, the vertical production well was perforated from 201 mbsf to 268 mbsf, covering the HBL, the TPL, and a portion of the FGL (Figure 4). The well was treated as a pseudo-porous medium to use Darcy’s flow concepts within the wellbore, of which the properties are as follows: the vertical permeability was 5 × 10−9 m2, the porosity was 1, the capillary pressure was 0, the irreducible gas saturation was 0.005, and the relative permeabilities had linear relationships with phase saturations. This approach was able to simulate the pressure drop in a steel wellbore, which was validated in a previous study [66]. The bottomhole pressure (Pbh) was 3 MPa [67] at a gridblock above the topmost well gridblock.
3.4. System Properties
Table 1 provides the properties used in pT+H V1.5 that are based on the previous studies [29,49,67,68]. The properties used in the RGMS are based on the previous studies [53,69] as shown in Table 2.

Table 1.
Properties, conditions, and models used in pT+H V1.5.

Table 2.
Properties used in RGMS.
3.5. Initial Conditions
Table 1 presents the temperature and pressure values at the bottom boundary of the TPL, which conform to the geothermal and hydrostatic gradients, respectively, as is typical of most hydrate deposits. Following the initialization process outlined by Moridis and Reagan [66], the simulation with the initial conditions continued until the entire domain reached a steady state without any change in various distributions. For geomechanical simulation, the initial total stress field was obtained by assuming that the initial effective stress field was zero, without requiring the application of the overburden pressure.
3.6. Model Validation
In order to guarantee the prediction accuracy of gas production at well SHSC-4, it is imperative to first validate the numerical model built earlier. As stated in the Introduction section, a trial production test was conducted at well SHSC-4, lasting 60 days, with a total gas production of 3.09 × 105 ST m3 [29]. Using the constructed model, a simulation was performed to replicate the 60-day production, taking into account the geomechanical responses. The simulation resulted in a total gas production of 3.08 × 105 ST m3, as depicted in Figure 6. This successful replication serves as validation for the constructed model.
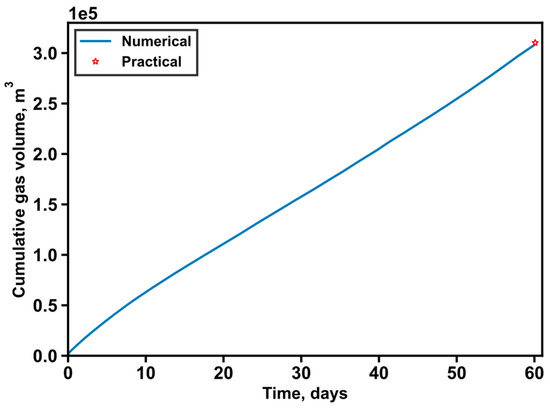
Figure 6.
Comparisons of numerical simulation result and field test data.
3.7. Simulations Cases
The base case was based on the original formation information obtained from the first test production at well SHSC-4 (Figure 4). In addition to the base case, this study investigates whether the cumulative gas production can be improved by increasing the permeabilities of the HBL, TPL, and FGL, individually. As illustrated in Figure 7, the permeability was increased to ks within the region from 0 to the stimulated radius (rs) within a specific layer. To assess the effectiveness of permeability enhancement, a permeability enhancement ratio (fk = ks/k0) was proposed, in which k0 is the original permeability of the layer. There are four different values of rs (0.3 m, 0.5 m, 1 m, and 2 m) and three different values of fk (2, 4, and 8), combined with three layers, resulting in a total of thirty-six cases.
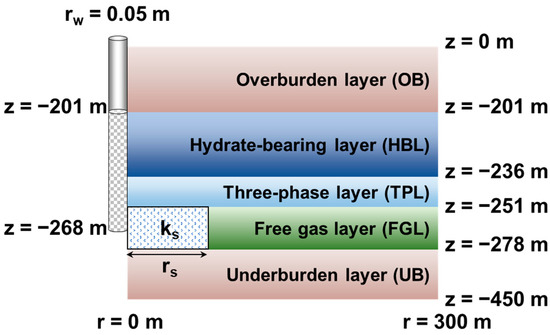
Figure 7.
The illustration of the permeability enhancement region within a layer.
4. Results and Discussion
In the analysis of the production potential associated with the geomechanical response at well SHSC-4, the monitoring included various parameters related to flow and geomechanics both with and without permeability enhancement, which were obtained from pT+H and the RGMS. The monitored flow-related parameters were pressure (P), temperature (T), gas saturation (SG), hydrate saturation (SH), the production rates of CH4 and H2O (Qg and Qw, respectively), and the cumulative production of CH4 and H2O (Vg and Mw, respectively), The water-to-gas ratio was also monitored, both instantaneously (Rwg = Qw/Qg) and cumulatively (RwgT = Mw/Vg). Geomechanics-related parameters monitored were radial and vertical displacements (ur and uz, respectively) at key locations. To evaluate the influence of permeability enhancement, the key parameters are Vg and RwgT. Specifically, more gas and less water are desired after permeability enhancement, so larger Vg and smaller RwgT values are better.
4.1. Base Case
4.1.1. Fluid Production
Figure 8a shows Qg produced at the well from the HBL, TPL, and FGL and all layers in the base case. The value of Qg has an initial peak after production begins, followed by a decline and minor fluctuations within a certain range in the subsequent production period. The initial peak is caused by the rapid dissociation of hydrates near the wellbore region and a subsequent surge in gas production rate after the bottomhole pressure drops. In addition, the free gas in the TPL and FGL contributes to the initial peak of Qg. The average gas production over the entire production period is 0.074 ST m3/s, which is far below the gas production rate of 0.579 ST m3/s (=5.00 × 105 ST m3/d) required for the commercial exploitation of NGHs [1]. Compared with hydrate deposits in Mount Elbert, Alaska North Slope, where there exists a lag time before substantial gas production [14], the hydrate deposit at well SHSC-4 does not exhibit such a lag phenomenon but instead has the highest gas production rate in the early stage of production, indicating that this class of hydrate deposit is conducive to exploitation. The contribution of each layer to the total gas production rate was ranked from highest to lowest as FGL, TPL, and HBL, indicating that the FGL is the primary source of gas production. This suggests that the FGL is the most important layer for gas production in the studied area.
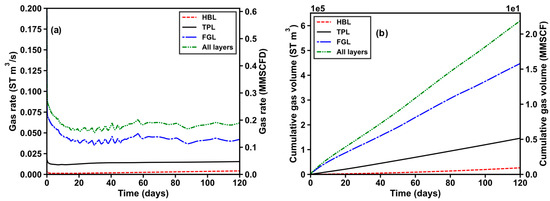
Figure 8.
Evolution of (a) the volumetric rate of the total CH4 production (Qg) and (b) the cumulative volumes of CH4 produced at the well (Vg) in the base case.
Figure 8b shows Vg produced at the well from the HBL, TPL, and FGL and all layers in the base case. As shown in the figure, in the later production period, since Qg fluctuates within a certain range, Vg, which is the integral of gas production over time, shows a nearly linear relationship with time. After 120 days of production, the FGL, TPL, and HBL accounted for 72.17%, 23.54%, and 4.29% of the total cumulative gas production, respectively. This also indicates that the FGL is the most important layer for gas production because it has the highest contribution to the total cumulative gas production. It is anticipated that the FGL will exhibit the most pronounced response to permeability enhancement.
Figure 9 shows Rwg and RwgT produced at the well from the HBL, TPL, and FGL and all layers in the base case. Apart from directly evaluating production via Qg and Vg, Rwg and RwgT can also be used to indirectly characterize production performance. In real practice, more gas and less water are desired, so smaller Rwg and RwgT values are better. Rwg produced from the HBL, TPL, and FGL and all layers decreased gradually during production. Among the three layers, the HBL has the highest Rwg with the smallest contribution to gas production observed in Figure 8. Moreover, Rwg produced from the HBL is tens of times higher than those from TPL and FGL. If permeability enhancement is carried out within HBL, gas production may increase, while water production may also increase. RwgT reaches a short-term peak in the first two days of production and then shows a decreasing trend throughout the entire production period. RwgT produced from the FGL and all layers tends to stabilize in the later period of production. Due to the large RwgT produced from HBL, the total RwgT was far higher than those from TPL and FGL.
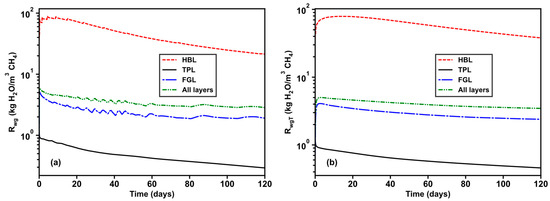
Figure 9.
Evolution of (a) the instantaneous water-to-gas ratio at the well (Rwg) and (b) the cumulative water-to-gas ratio at the well (RwgT) in the base case.
Figure 10 shows ur and uz at key locations in the base case. As Pbh is lower than the pressure of the formation, the reservoir is “squeezed” and moves toward the vertical well in the radial direction, but the compaction is not significant. Although the location with the largest radial displacement occurs at (r, z) = (1 m, −201 m), the absolute value does not exceed 0.01 m when the simulation ends. In the vertical direction, the subsidence at the top of the HBL and the uplift at the bottom are observed. As the gridblock that was set to the bottomhole pressure is closer to the top of the HBL, the subsidence at the top of HBL is more obvious, with a maximum level of no more than 0.08 m. Overall, the displacement within the formation is not significant.
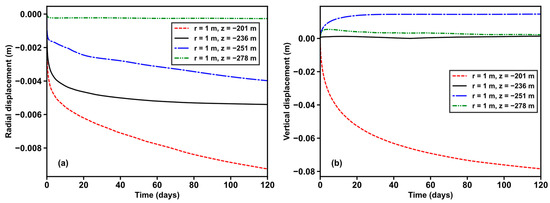
Figure 10.
Evolution of (a) ur and (b) uz at key locations in the base case.
4.1.2. Spatial Distributions
Figure 11 illustrates the spatial evolution of P in the base case. The cylindrical region of pressure drop gradually expands over production time, with those in the HBL and FGL being larger than that in the TPL. This is mainly due to the higher permeability of the HBL and FGL compared to that of the TPL. Additionally, as the hydrate saturation is highest in the hydrate layer and the effective permeability is lower, fluid replenishment becomes difficult, resulting in the most significant pressure drop. Although the cylindrical region of the pressure drops in the TPL and FGL is relatively small during production, the rates of pressure drop are faster than that in the HBL. Particularly, the pressure drops in the FGL and the lower part of the TPL are very significant. In previous studies [49,67], the pressure drop area obtained using T+H was only not significant in the FGL, which differs from the results in this study. It is evident that considering mechanical response leads to different hydrate production mechanisms.
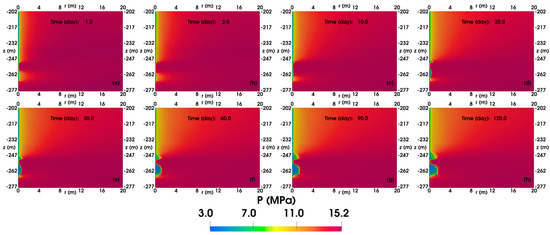
Figure 11.
Evolution of the spatial distributions of pressure (MPa) in the reservoir of the base case. (a) 1-day production, (b) 3-day production, (c) 10-day production, (d) 20-day production, (e) 30-day production, (f) 60-day production, (g) 90-day production, and (h) 120-day production.
Figure 12 illustrates the spatial evolution of T in the base case. As hydrate dissociation is endothermic, the low-temperature region generally indicates the location of hydrate dissociation. In this figure, the low-temperature region is found in the FGL and the lower part of the TPL, coinciding with the significant pressure drop area and indicating a large amount of hydrate dissociates. Unlike production lasting over 1000 days in previous studies [49,67], the numerical simulation in this study was halted due to the temperature in the low-temperature region reaching 0.01 °C after 120 days of production.
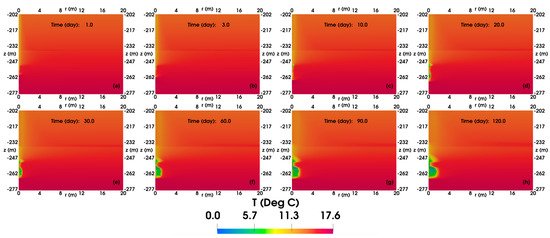
Figure 12.
Evolution of the spatial distributions of temperature (°C) in the reservoir of the base case. (a) 1-day production, (b) 3-day production, (c) 10-day production, (d) 20-day production, (e) 30-day production, (f) 60-day production, (g) 90-day production, and (h) 120-day production.
Figure 13 illustrates the spatial evolution of SH in the base case. Hydrate dissociation occurs in the area where the significant pressure drop is shown in Figure 11 and the low temperature is presented in Figure 12. Hydrates gradually dissociate during production, but the unevenness of hydrate dissociation progress in each layer becomes apparent. The dissociation rate of the HBL is relatively uniform, while the lower part of the TPL undergoes hydrate dissociation, followed by hydrate formation. Moreover, in the FGL, the hydrate forms and dissociates alternatively. This phenomenon may be caused by the Joule–Thomson cooling effect, the capillary effect, the “upstream weighting” approach applied in the simulator [72], and the equilibrium model used in this study. The cyclic process of hydrate formation and dissociation in the FGL ultimately led to the temperature reaching 0.01 °C, resulting in the simulation stopping.
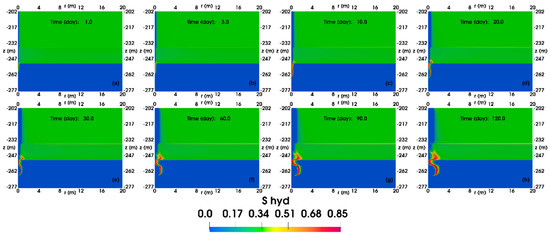
Figure 13.
Evolution of the spatial distributions of hydrate saturation in the reservoir of the base case. (a) 1-day production, (b) 3-day production, (c) 10-day production, (d) 20-day production, (e) 30-day production, (f) 60-day production, (g) 90-day production, and (h) 120-day production.
Figure 14 illustrates the spatial evolution of SG in the base case. The evolution of gas saturation in the base case is also presented. The gas saturation in the HBL and TPL gradually expands, and some gas migrates from the TPL to the HBL. Gas dissociated from hydrate in the lower part of the TPL migrates toward the wellbore radially and toward the HBL vertically at a very slow rate due to the low permeability of the TPL (1.5 mD), resulting in gas accumulation in the lower part of the TPL. In the FGL, a large amount of gas flows into the wellbore because of the significantly lower wellbore pressure compared to the formation pressure and higher formation permeability. The Joule–Thomson effect caused by the rapidly migrating gas may have caused the low temperature in the FGL, meeting the conditions for hydrate generation. Thus, hydrates are formed, hindering the radial gas migration in the FGL and causing the gas to accumulate on the side away from the wellbore.
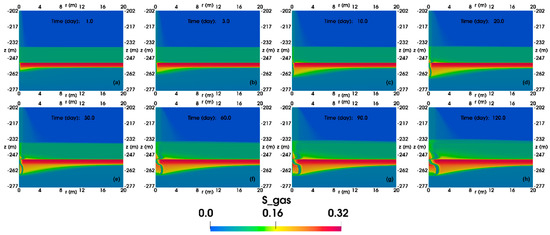
Figure 14.
Evolution of the spatial distributions of gas saturation in the reservoir of the base case. (a) 1-day production, (b) 3-day production, (c) 10-day production, (d) 20-day production, (e) 30-day production, (f) 60-day production, (g) 90-day production, and (h) 120-day production.
4.2. Effect of Permeability Enhancement
4.2.1. Fluid Production
In the following tables, the values marked in green are the minimum, while the values marked in red are the maximum. Table 3 and Table 4 present Vg with permeability enhancement and its ratio relative to that in the base case after 120-day production, respectively. For reference, the Vg in the base case (Vg,0) is 620,668 ST m3 following 120 days of production. The permeability enhancement of three different layers (i.e., the HBL, TPL, and FGL) shows that the larger the values of rs and kf, the more significant the increase in gas production. When (kf, rs) = (8, 2 m), the Vg values, predicted by improving the permeabilities of the HBL, TPL, and FGL, are 711,590, 706,541, and 1,160,649 ST m3, respectively. Compared to the base case, the production was increased by 15%, 15%, and 87% corresponding to the modification in the HBL, TPL, and FGL, respectively. In order to reach higher production, the permeability of the FGL should be enhanced.

Table 3.
The cumulative gas production with permeability enhancement (Vg) after 120-day production.

Table 4.
The ratios of cumulative gas production with permeability enhancement (Vg) to that in the base case (Vg,0) after 120-day production.
Table 5 and Table 6 present RwgT with permeability enhancement and its ratio relative to that in the base case after 120-day production, respectively. For reference, the cumulative water–gas ratio (RwgT,0) is 2.84 kg H2O/m3 CH4 following 120 days of production. The results of permeability enhancement in the HBL show that the larger the values of rs and kf, the larger the RwgT. The increase in permeability near the wellbore area in the HBL results in a greater increase in water production than gas production, leading to a larger RwgT. The results of permeability enhancement in the TPL and FGL show that the larger the values of rs and kf, the smaller the RwgT. When (kf, rs) = (8, 2 m), the RwgT values, determined by permeability enhancement in the HBL, TPL, and FGL are 4.03, 3.17, and 2.41 kg H2O/m3 CH4, respectively. The resulting ratios of RwgT to RwgT,0 are 1.42, 1.12, and 0.85 when the permeabilities of the HBL, TPL, and FGL are increased, respectively. To reduce the amount of separated water required for unit gas production, the FGL should be treated to enhance its permeability.

Table 5.
The cumulative water-to-gas ratio with permeability enhancement (Rwg) after 120-day production.

Table 6.
The ratios of cumulative water-to-gas ratio with permeability enhancement (RwgT) to that in the base case (RwgT,0) after 120-day production.
The radial and vertical displacements with permeability enhancement are not significant, and therefore, further discussion is not included in this section.
4.2.2. Spatial Distributions
In this section, the figures depicting the spatial distributions of P, T, SH, and SG with permeability enhancement after 120 days of production are arranged in a manner where the rs values increase from left to right and the kf values increase from top to bottom. The highest Vg and the lowest RwgT are achieved after increasing the permeabilities of the FGL, and only the spatial distributions with permeability enhancement in the FGL are discussed.
Figure 15 shows the spatial distributions of P with permeability enhancement in the FGL after 120 days of production.
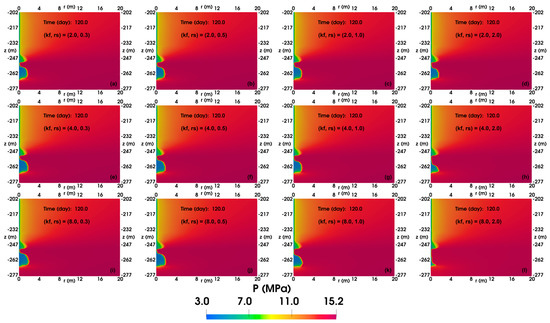
Figure 15.
The spatial distributions of pressure (MPa) in the reservoir with permeability enhancement in FGL after 120-day production. (a) (kf, rs) = (2, 0.3 m), (b) (kf, rs) = (2, 0.5 m), (c) (kf, rs) = (2, 1.0 m), (d) (kf, rs) = (2, 2.0 m), (e) (kf, rs) = (4, 0.3 m), (f) (kf, rs) = (4, 0.5 m), (g) (kf, rs) = (4, 1.0 m), (h) (kf, rs) = (4, 2.0 m), (i) (kf, rs) = (8, 0.3 m), (j) (kf, rs) = (8, 0.5 m), (k) (kf, rs) = (8, 1.0 m), and (l) (kf, rs) = (8, 2.0 m).
In cases where the value of kf is small, augmenting rs has an insignificant effect on the area of pressure drop, and the spatial distributions of P remain relatively unchanged compared to the base case. Conversely, when the value of kf is large, the increasing rs results in a narrower area of pressure drop in the upper section of the FGL and the lower section of the TPL, which is closer to the wellbore.
Figure 16 shows the spatial distributions of T with permeability enhancement in the FGL after 120 days of production. When the value of kf is small, the varying rs has a negligible effect on the spatial distributions of T compared to the base case, which is comparable to the area of pressure drop presented in Figure 15. However, when kf equals 4, an increase in rs results in a shrinkage of the low-temperature area within the FGL, with a gradual shift of the lowest temperature from the upper to the middle section of the FGL. Furthermore, when (kf, rs) = (8, 2 m), the low-temperature region within the FGL becomes exceedingly small.
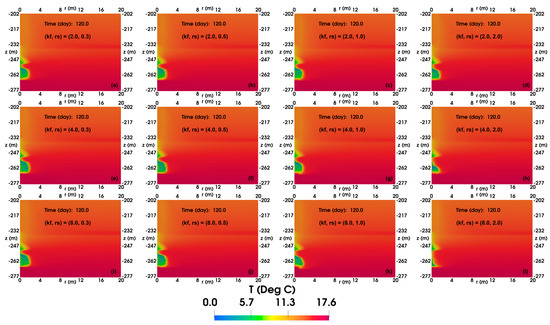
Figure 16.
The spatial distributions of temperature (°C) in the reservoir with permeability enhancement in FGL after 120-day production. (a) (kf, rs) = (2, 0.3 m), (b) (kf, rs) = (2, 0.5 m), (c) (kf, rs) = (2, 1.0 m), (d) (kf, rs) = (2, 2.0 m), (e) (kf, rs) = (4, 0.3 m), (f) (kf, rs) = (4, 0.5 m), (g) (kf, rs) = (4, 1.0 m), (h) (kf, rs) = (4, 2.0 m), (i) (kf, rs) = (8, 0.3 m), (j) (kf, rs) = (8, 0.5 m), (k) (kf, rs) = (8, 1.0 m), and (l) (kf, rs) = (8, 2.0 m).
Figure 17 and Figure 18 show the spatial distributions of SH and SG with permeability enhancement in the FGL after 120 days of production, respectively. In Figure 17, as the kf and rs values increase, the formation and dissociation of gas hydrate transpire in closer proximity to the wellbore, thereby facilitating the production of gas dissociated from gas hydrate. Furthermore, Figure 18 demonstrates that the formation of gas hydrate is less likely to obstruct the flow of gas, resulting in less gas accumulating on the side of the gas hydrate that is farther from the wellbore. These two figures collectively suggest that augmenting kf and rs values is more conducive to gas production. This assertion is supported by Table 3 and Table 4, which indicate that larger kf and rs values yield higher cumulative gas production.
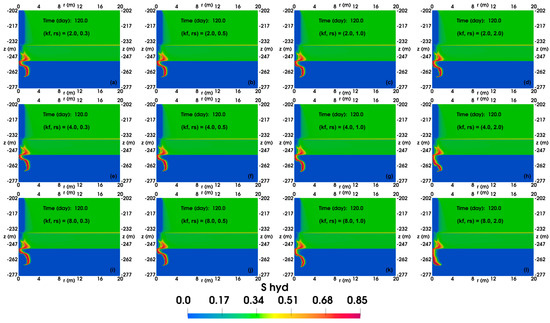
Figure 17.
The spatial distributions of hydrate saturation in the reservoir with permeability enhancement in FGL after 120-day production. (a) (kf, rs) = (2, 0.3 m), (b) (kf, rs) = (2, 0.5 m), (c) (kf, rs) = (2, 1.0 m), (d) (kf, rs) = (2, 2.0 m), (e) (kf, rs) = (4, 0.3 m), (f) (kf, rs) = (4, 0.5 m), (g) (kf, rs) = (4, 1.0 m), (h) (kf, rs) = (4, 2.0 m), (i) (kf, rs) = (8, 0.3 m), (j) (kf, rs) = (8, 0.5 m), (k) (kf, rs) = (8, 1.0 m), and (l) (kf, rs) = (8, 2.0 m).
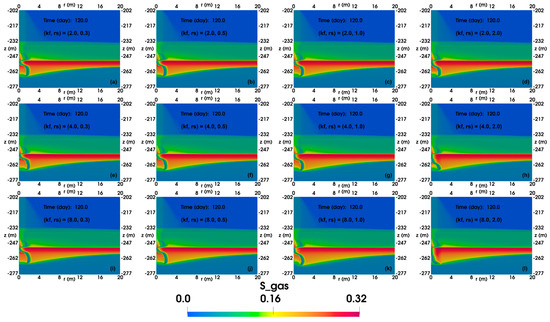
Figure 18.
The spatial distributions of gas saturation in the reservoir with permeability enhancement in FGL after 120-day production. (a) (kf, rs) = (2, 0.3 m), (b) (kf, rs) = (2, 0.5 m), (c) (kf, rs) = (2, 1.0 m), (d) (kf, rs) = (2, 2.0 m), (e) (kf, rs) = (4, 0.3 m), (f) (kf, rs) = (4, 0.5 m), (g) (kf, rs) = (4, 1.0 m), (h) (kf, rs) = (4, 2.0 m), (i) (kf, rs) = (8, 0.3 m), (j) (kf, rs) = (8, 0.5 m), (k) (kf, rs) = (8, 1.0 m), and (l) (kf, rs) = (8, 2.0 m).
5. Conclusions
The following conclusions can be drawn from this study:
- To evaluate the effectiveness of permeability enhancement considering the geomechanical responses in the Shenhu area, a coupled simulation using pTOUGH+HYDRATE V1.5 and the RGMS (Reservoir Geomechanics Simulator) is implemented.
- Based on the geophysical surveys and analysis of core samples at well SHSC-4 located in the Shenhu area of the northern South China Sea, the established numerical simulation model is accurate, and the simulation results are highly consistent with the trial production data, ensuring the reliability of the outcomes obtained in this study.
- In the base case, the formation and dissociation of gas hydrates in the free gas layer (FGL) alternate, ultimately resulting in a low-temperature region near 0 °C and leading to the cessation of the simulation after 120 days of production. The cumulative gas production reached 6.2 × 105 ST m3.
- In the base case, the FGL contributes the most to gas production, accounting for 72.17% of the cumulative gas production (Vg), followed by the three-phase layer (TPL), accounting for 23.54% of the cumulative gas production, and the hydrate-bearing layer (HBL) contributes the least, accounting for only 4.29% of the cumulative gas production.
- In the base case, the cumulative water-to-gas ratio (Rwg) from the HBL, TPL, and FGL gradually decreases during the production of gas hydrates. RwgT from the HBL, which contributes the least to gas production, is the highest, with a value several times those from TPL and FGL.
- In the base case, the gas production obtained without permeability enhancement is insufficient for commercial production. Permeability enhancement can be an option used to increase gas production.
- After increasing the permeabilities of the HBL, TPL, and FGL with the same permeability enhancement ratio (fk) and the same simulated radius (rs), the improvement effect of modifying the FGL is the best, with a maximum increase of 87%. The required mass of water separated from a unit of gas is the lowest when applying permeability enhancement in the FGL, with a minimum value of 85% of the original separation mass.
- The results of modifying the FGL show that the higher the degree of permeability enhancement, the deeper the impact of permeability enhancement and the closer the formation and dissociation of gas hydrates are to the wellbore, making it more difficult for gas to be obstructed by the formation of gas hydrates, which is more conducive to production.
- Although permeability enhancement is attempted in this study, it did not extend the production period as the simulation still ends due to low temperature in the FGL. Future research should focus on exploring methods to prevent such low temperatures from occurring in the FGL.
- The results obtained by considering geomechanical responses differ from previous numerical studies that only considered flow and thermal behaviors. This indicates that neglecting geomechanical responses may result in an incorrect natural gas hydrate production scheme. Therefore, future numerical studies should take geomechanical responses into consideration to obtain more realistic results.
- In future work, it is imperative to discover production schemes that effectively mitigate the occurrence of a low-temperature region after 120 days of production, which currently causes disruptions in numerical simulations, thus enabling the extension of the observation period. Moreover, new production schemes combined with permeability enhancement should be explored to facilitate the achievement of production rates that meet the necessary threshold for the commercial exploitation of natural gas hydrates.
Author Contributions
Conceptualization, J.Z.; methodology, J.Z.; software, J.Z.; formal analysis, J.Z.; writing—original draft preparation, J.Z.; writing—review and editing, R.W., T.W., and H.L.; supervision, H.L.; funding acquisition, H.L.; project administration, R.W. and T.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by CNPC Engineering Technology R&D Company Limited, grant number 2021DJ4902.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Change in the quantity in parentheses | |
| Specific enthalpy of hydrate dissociation/formation (J∙kg−1) | |
| Del operator | |
| CR | Heat capacity of the dry rock (J∙kg−1∙K−1) |
| dA | Differential surface (m2) |
| dV | Differential volume (m3) |
| E | Young’s modulus (Pa) |
| G | Shear modulus (Pa) |
| G0 | Shear modulus when the hydrate saturation is zero (Pa) |
| G1 | Shear modulus when the hydrate saturation is one (Pa) |
| hβ | Specific enthalpy of phase (J∙kg−1) |
| Kdr | Drained bulk modulus (Pa) |
| Kdr0 | Drained modulus when the hydrate saturation is zero (Pa) |
| Kdr1 | Drained modulus when the hydrate saturation is one (Pa) |
| Skeletal grain modulus (Pa) | |
| Radial permeability (m2) | |
| Relative permeability of phase | |
| Vertical permeability (m2) | |
| Composite thermal conductivity of the medium/fluid ensemble (W∙m−1∙K−1) | |
| Formation thermal conductivity under desaturated conditions (W∙m−1∙K−1) | |
| Formation thermal conductivity under fully liquid-saturated conditions (W∙m−1∙K−1) | |
| Thermal conductivity of ice phase (W∙m−1∙K−1) | |
| MA | Cumulative mass of aqueous phase |
| MG | Cumulative mass of gaseous phase |
| Mθ | Heat accumulation term |
| Mκ | Mass accumulation of component κ (kg∙m−3) |
| P | Pressure (Pa) |
| Pt | Average mobile fluid pressure (Pa) |
| Pt,0 | Initial equivalent pore pressure (Pa) |
| Pβ | Pressure of phase (Pa) |
| Qg | Volumetric rate of CH4 well production |
| Qw | Water mass production rate |
| qκ | Source/sink term of component κ (kg∙m−3∙s−1) |
| r | Radial direction |
| Rwg | Instantaneous water-to-gas ratio |
| RwgT | Cumulative water-to-gas ratio |
| Saturation of phase | |
| T | Temperature (K or °C) |
| t | Time (s) |
| ur | Radial displacement (m) |
| uz | Vertical displacement (m) |
| Specific internal energy of phase (J∙kg−1) | |
| Vg | Cumulative volume of CH4 produced at the well |
| Vn | Volume of the subdomain (m3) |
| Mass fraction of component κ in phase | |
| z | Direction along the z-axis |
| Biot’s coefficient | |
| Γn | Surface of subdomain n (m2) |
| γ | Empirical permeability reduction factor |
| εv | Current volumetric strain |
| εv,0 | Initial volumetric strain |
| Viscosity of phase (Pa∙s) | |
| ν | Poisson’s ratio |
| Bulk density (kg∙m−3) | |
| Fluid density (kg∙m−3) | |
| Rock density (kg∙m−3) | |
| Density of phase (kg∙m−3) | |
| Reservoir porosity | |
| Initial porosity | |
| Flux vector of component κ (kg∙m−2∙s−1) | |
| Flux vector of phase (kg∙m−2∙s−1) | |
| Flux vector of component κ in phase (kg∙m−2∙s−1) | |
| g | Gravitational acceleration vector (m∙s−2) |
| k | Absolute permeability tensor (m2) |
| u | Displacement vector (m) |
| Strain tensor | |
| Total stress tensor (Pa) | |
| Effective stress tensor (Pa) |
References
- Sloan, E.D. Fundamental Principles and Applications of Natural Gas Hydrates. Nature 2003, 426, 353–359. [Google Scholar] [CrossRef]
- Chong, Z.R.; Yang, S.H.B.; Babu, P.; Linga, P.; Li, X.-S. Review of Natural Gas Hydrates as an Energy Resource: Prospects and Challenges. Appl. Energy 2016, 162, 1633–1652. [Google Scholar] [CrossRef]
- Makogon, Y.F.; Holditch, S.A.; Makogon, T.Y. Natural Gas-Hydrates—A Potential Energy Source for the 21st Century. J. Pet. Sci. Eng. 2007, 56, 14–31. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.J.; Grover, T.; Collett, T. Geomechanical Response of Permafrost-Associated Hydrate Deposits to Depressurization-Induced Gas Production. J. Pet. Sci. Eng. 2009, 67, 1–12. [Google Scholar] [CrossRef]
- Sun, J.; Ning, F.; Li, S.; Zhang, K.; Liu, T.; Zhang, L.; Jiang, G.; Wu, N. Numerical Simulation of Gas Production from Hydrate-Bearing Sediments in the Shenhu Area by Depressurising: The Effect of Burden Permeability. J. Unconv. Oil Gas Resour. 2015, 12, 23–33. [Google Scholar] [CrossRef]
- Yin, Z.; Moridis, G.; Chong, Z.R.; Tan, H.K.; Linga, P. Numerical Analysis of Experiments on Thermally Induced Dissociation of Methane Hydrates in Porous Media. Ind. Eng. Chem. Res. 2018, 57, 5776–5791. [Google Scholar] [CrossRef]
- Li, G.; Li, X.-S.; Tang, L.-G.; Zhang, Y. Experimental Investigation of Production Behavior of Methane Hydrate under Ethylene Glycol Injection in Unconsolidated Sediment. Energy Fuels 2007, 21, 3388–3393. [Google Scholar] [CrossRef]
- Ohgaki, K.; Takano, K.; Sangawa, H.; Matsubara, T.; Nakano, S. Methane Exploitation by Carbon Dioxide from Gas Hydrates—Phase Equilibria for CO2-CH4 Mixed Hydrate System. J. Chem. Eng. Jpn. 1996, 29, 478–483. [Google Scholar] [CrossRef]
- Kvamme, B.; Zhao, J.; Wei, N.; Sun, W.; Saeidi, N.; Pei, J.; Kuznetsova, T. Hydrate Production Philosophy and Thermodynamic Calculations. Energies 2020, 13, 672. [Google Scholar] [CrossRef]
- Kvamme, B. Mechanisms for CH4/CO2 Swapping in Natural Sediments. Fluids 2022, 7, 260. [Google Scholar] [CrossRef]
- Kvamme, B. Thermodynamics and Kinetic Mechanisms for CH4/CO2 Swapping in Natural Sediments. Energy Fuels 2022, 36, 6374–6396. [Google Scholar] [CrossRef]
- Moridis, G.J.; Silpngarmlert, S.; Reagan, M.T.; Collett, T.; Zhang, K. Gas Production from a Cold, Stratigraphically-Bounded Gas Hydrate Deposit at the Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope: Implications of Uncertainties. Mar. Pet. Geol. 2011, 28, 517–534. [Google Scholar] [CrossRef]
- Collett, T.S.; Lee, M.W.; Agena, W.F.; Miller, J.J.; Lewis, K.A.; Zyrianova, M.V.; Boswell, R.; Inks, T.L. Permafrost-Associated Natural Gas Hydrate Occurrences on the Alaska North Slope. Mar. Pet. Geol. 2011, 28, 279–294. [Google Scholar] [CrossRef]
- Myshakin, E.M.; Ajayi, T.; Anderson, B.J.; Seol, Y.; Boswell, R. Numerical Simulations of Depressurization-Induced Gas Production from Gas Hydrates Using 3-D Heterogeneous Models of L-Pad, Prudhoe Bay Unit, North Slope Alaska. J. Nat. Gas Sci. Eng. 2016, 35, 1336–1352. [Google Scholar] [CrossRef]
- Anderson, B.J.; Kurihara, M.; White, M.D.; Moridis, G.J.; Wilson, S.J.; Pooladi-Darvish, M.; Gaddipati, M.; Masuda, Y.; Collett, T.S.; Hunter, R.B.; et al. Regional Long-Term Production Modeling from a Single Well Test, Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope. Mar. Pet. Geol. 2011, 28, 493–501. [Google Scholar] [CrossRef]
- Moridis, G.J.; Collett, T.S.; Dallimore, S.R.; Satoh, T.; Hancock, S.; Weatherill, B. Numerical Studies of Gas Production from Several CH4 Hydrate Zones at the Mallik Site, Mackenzie Delta, Canada. J. Pet. Sci. Eng. 2004, 43, 219–238. [Google Scholar] [CrossRef]
- Uddin, M.; Wright, F.; Dallimore, S.; Coombe, D. Gas Hydrate Dissociations in Mallik Hydrate Bearing Zones A, B, and C by Depressurization: Effect of Salinity and Hydration Number in Hydrate Dissociation. J. Nat. Gas Sci. Eng. 2014, 21, 40–63. [Google Scholar] [CrossRef]
- Bazaluk, O.; Sai, K.; Lozynskyi, V.; Petlovanyi, M.; Saik, P. Research into Dissociation Zones of Gas Hydrate Deposits with a Heterogeneous Structure in the Black Sea. Energies 2021, 14, 1345. [Google Scholar] [CrossRef]
- Klymenko, V.; Ovetskyi, S.; Martynenko, V.; Vytyaz, O.; Uhrynovskyi, A. An Alternative Method of Methane Production from Deposits of Subaquatic Gas Hydrates. Min. Miner. Depos. 2022, 16, 11–17. [Google Scholar] [CrossRef]
- Lin, J.-S.; Uchida, S.; Myshakin, E.M.; Seol, Y.; Rutqvist, J.; Boswell, R. Assessing the Geomechanical Stability of Interbedded Hydrate-Bearing Sediments under Gas Production by Depressurization at NGHP-02 Site 16. Mar. Pet. Geol. 2019, 108, 648–659. [Google Scholar] [CrossRef]
- Moridis, G.J.; Reagan, M.T.; Queiruga, A.F.; Boswell, R. Evaluation of the Performance of the Oceanic Hydrate Accumulation at Site NGHP-02-09 in the Krishna-Godavari Basin during a Production Test and during Single and Multi-Well Production Scenarios. Mar. Pet. Geol. 2019, 108, 660–696. [Google Scholar] [CrossRef]
- Zhang, J.; Moridis, G.J.; Blasingame, T.A. Effect of Geomechanics and of Grid Discretization on the Predictions of Production from Natural Hydrate Deposits and of the Associated Geomechanical System Response. Gas Sci. Eng. 2023, 112, 204942. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kim, J.; Reagan, M.T.; Kim, S.-J. Analysis of Short- and Long-Term System Response During Gas Production from a Gas Hydrate Deposit at the UBGH2-6 Site of the Ulleung Basin in the Korean East Sea. Can. J. Chem. Eng. 2023, 101, 735–763. [Google Scholar] [CrossRef]
- Yu, T.; Guan, G.; Abudula, A.; Yoshida, A.; Wang, D.; Song, Y. Enhanced Gas Recovery from Methane Hydrate Reservoir in the Nankai Trough, Japan. Energy Procedia 2019, 158, 5213–5218. [Google Scholar] [CrossRef]
- Zhu, H.; Xu, T.; Yuan, Y.; Xia, Y.; Xin, X. Numerical Investigation of the Natural Gas Hydrate Production Tests in the Nankai Trough by Incorporating Sand Migration. Appl. Energy 2020, 275, 115384. [Google Scholar] [CrossRef]
- Gu, Y.; Sun, J.; Qin, F.; Ning, F.; Cao, X.; Liu, T.; Qin, S.; Zhang, L.; Jiang, G. Enhancing Gas Recovery from Natural Gas Hydrate Reservoirs in the Eastern Nankai Trough: Deep Depressurization and Underburden Sealing. Energy 2023, 262, 125510. [Google Scholar] [CrossRef]
- Ye, J.; Qin, X.; Xie, W.; Lu, H.; Ma, B.; Qiu, H.; Liang, J.; Lu, J.; Kuang, Z.; Lu, C.; et al. The Second Natural Gas Hydrate Production Test in the South China Sea. China Geol. 2020, 3, 197–209. [Google Scholar] [CrossRef]
- Wu, N.; Li, Y.; Wan, Y.; Sun, J.; Huang, L.; Mao, P. Prospect of Marine Natural Gas Hydrate Stimulation Theory and Technology System. Nat. Gas Ind. B 2021, 8, 173–187. [Google Scholar] [CrossRef]
- Li, J.; Ye, J.; Qin, X.; Qiu, H.; Wu, N.; Lu, H.; Xie, W.; Lu, J.; Peng, F.; Xu, Z.; et al. The First Offshore Natural Gas Hydrate Production Test in South China Sea. China Geol. 2018, 1, 5–16. [Google Scholar] [CrossRef]
- Sun, Y.; Li, B.; Guo, W.; Lü, X.; Zhang, Y.; Li, K.; Wang, P.; Jin, G.; Jia, R.; Qu, L. Comparative Analysis of the Production Trial and Numerical Simulations of Gas Production from Multilayer Hydrate Deposits in the Qilian Mountain Permafrost. J. Nat. Gas Sci. Eng. 2014, 21, 456–466. [Google Scholar] [CrossRef]
- Liu, H.; Zhan, L.; Zhang, J.; Shang, S.; Lu, H. Numerical Investigation on Environmental Effect Associated with Gas-Hydrate Exploitation. Geoenergy Sci. Eng. 2023, 227, 211857. [Google Scholar] [CrossRef]
- Ruppel, C.D.; Kessler, J.D. The Interaction of Climate Change and Methane Hydrates. Rev. Geophys. 2017, 55, 126–168. [Google Scholar] [CrossRef]
- Ruppel, C. Permafrost-Associated Gas Hydrate: Is It Really Approximately 1 % of the Global System? J. Chem. Eng. Data 2015, 60, 429–436. [Google Scholar] [CrossRef]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Development of a Coupled Geophysical–Geothermal Scheme for Quantification of Hydrates in Gas Hydrate-Bearing Permafrost Sediments. Phys. Chem. Chem. Phys. 2021, 23, 24249–24264. [Google Scholar] [CrossRef] [PubMed]
- Farahani, M.V.; Hassanpouryouzband, A.; Yang, J.; Tohidi, B. Insights into the Climate-Driven Evolution of Gas Hydrate-Bearing Permafrost Sediments: Implications for Prediction of Environmental Impacts and Security of Energy in Cold Regions. RSC Adv. 2021, 11, 14334–14346. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.; Wang, J. On the China′s Successful Gas Production Test from Marine Gas Hydrate Reservoirs. Chin. Sci. Bull. 2018, 63, 2–8. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S. Current Perspectives on Gas Hydrate Resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Joshi, S.D. Cost/Benefits of Horizontal Wells. In Proceedings of the SPE Western Regional/AAPG Pacific Section Joint Meeting, Long Beach, CA, USA, 19–24 May 2003; p. 2. [Google Scholar] [CrossRef]
- Feng, Y.; Chen, L.; Suzuki, A.; Kogawa, T.; Okajima, J.; Komiya, A.; Maruyama, S. Enhancement of Gas Production from Methane Hydrate Reservoirs by the Combination of Hydraulic Fracturing and Depressurization Method. Energy Convers. Manag. 2019, 184, 194–204. [Google Scholar] [CrossRef]
- Moridis, G. User’s Manual of the TOUGH+ Core Code v1.5: A General-Purpose Simulator of Non-Isothermal Flow and Transport through Porous and Fractured Media; LBNL-6871E.; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2014. [Google Scholar] [CrossRef]
- Chibura, P.E.; Zhang, W.; Luo, A.; Wang, J. A Review on Gas Hydrate Production Feasibility for Permafrost and Marine Hydrates. J. Nat. Gas Sci. Eng. 2022, 100, 104441. [Google Scholar] [CrossRef]
- Sun, X.; Luo, T.; Wang, L.; Wang, H.; Song, Y.; Li, Y. Numerical Simulation of Gas Recovery from a Low-Permeability Hydrate Reservoir by Depressurization. Appl. Energy 2019, 250, 7–18. [Google Scholar] [CrossRef]
- Yuan, Y.; Gong, Y.; Xu, T.; Zhu, H. Multiphase Flow and Geomechanical Responses of Interbedded Hydrate Reservoirs during Depressurization Gas Production for Deepwater Environment. Energy 2023, 262, 125603. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, Z.; Zhao, Y.; Zuo, J.; Li, P.; Liang, W.; Wang, B.; Chen, X.; Lei, H.; Jin, G. Coupled Thermal–Hydrodynamic–Mechanical Numerical Simulation of Natural Gas Hydrate Horizontal Well Depressurization Production: Method and Application in the South China Sea. Nat. Gas Ind. B 2022, 9, 548–560. [Google Scholar] [CrossRef]
- Xia, Y.; Xu, T.; Yuan, Y.; Xin, X.; Zhu, H. Geomechanical Response Induced by Multiphase (Gas/Water) Flow in the Mallik Hydrate Reservoir of Canada. SPE J. 2022, 27, 434–451. [Google Scholar] [CrossRef]
- Zhang, J.; Li, X.; Chen, Z.; Li, Q.; Li, G.; Lv, T. Numerical Simulation of the Improved Gas Production from Low Permeability Hydrate Reservoirs by Using an Enlarged Highly Permeable Well Wall. J. Pet. Sci. Eng. 2019, 183, 106404. [Google Scholar] [CrossRef]
- Li, B.; Ma, X.; Zhang, G.; Guo, W.; Xu, T.; Yuan, Y.; Sun, Y. Enhancement of Gas Production from Natural Gas Hydrate Reservoir by Reservoir Stimulation with the Stratification Split Grouting Foam Mortar Method. J. Nat. Gas Sci. Eng. 2020, 81, 103473. [Google Scholar] [CrossRef]
- Sun, J.; Ning, F.; Liu, T.; Liu, C.; Chen, Q.; Li, Y.; Cao, X.; Mao, P.; Zhang, L.; Jiang, G. Gas Production from a Silty Hydrate Reservoir in the South China Sea Using Hydraulic Fracturing: A Numerical Simulation. Energy Sci. Eng. 2019, 7, 1106–1122. [Google Scholar] [CrossRef]
- Yu, T.; Guan, G.; Wang, D.; Song, Y.; Abudula, A. Numerical Investigation on the Long-Term Gas Production Behavior at the 2017 Shenhu Methane Hydrate Production Site. Appl. Energy 2021, 285, 116466. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.J. Numerical Studies on the Geomechanical Stability of Hydrate-Bearing Sediments. SPE J. 2009, 14, 267–282. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kim, J.; Reagan, M.T.; Kim, S.-J. Feasibility of Gas Production from a Gas Hydrate Accumulation at the UBGH2-6 Site of the Ulleung Basin in the Korean East Sea. J. Pet. Sci. Eng. 2013, 108, 180–210. [Google Scholar] [CrossRef]
- Moridis, G.J.J.; Collett, T.S.S.; Pooladi-Darvish, M.; Hancock, S.; Santamarina, C.; Boswell, R.; Kneafsey, T.; Rutqvist, J.; Kowalsky, M.B.B.; Reagan, M.T.T.; et al. Challenges, Uncertainties, and Issues Facing Gas Production from Gas-Hydrate Deposits. SPE Reserv. Eval. Eng. 2011, 14, 76–112. [Google Scholar] [CrossRef]
- Rutqvist, J.; Moridis, G.J.; Grover, T.; Silpngarmlert, S.; Collett, T.S.; Holdich, S.A. Coupled Multiphase Fluid Flow and Wellbore Stability Analysis Associated with Gas Production from Oceanic Hydrate-Bearing Sediments. J. Pet. Sci. Eng. 2012, 92–93, 65–81. [Google Scholar] [CrossRef]
- Wang, J.; Liang, J.; Zong, X.; Gong, Y.; Wan, T. Differentiated distribution of methane hydrate in the Shenhu area of the northern South China Sea and controlling factors. Mar. Geol. Front. 2015, 31, 24. [Google Scholar]
- Zhang, J.; Moridis, G.J.; Blasingame, T.A. Message Passing Interface (MPI) Parallelization of Iteratively Coupled Fluid Flow and Geomechanics Codes for the Simulation of System Behavior in Hydrate-Bearing Geologic Media. Part 1: Methodology and Validation. SPE Reserv. Eval. Eng. 2022, 25, 600–620. [Google Scholar] [CrossRef]
- Zhang, J.; Moridis, G.J.; Blasingame, T.A. Message Passing Interface (MPI) Parallelization of Iteratively Coupled Fluid Flow and Geomechanics Codes for the Simulation of System Behavior in Hydrate-Bearing Geologic Media. Part 2: Parallel Performance and Application. SPE Reserv. Eval. Eng. 2022, 25, 621–640. [Google Scholar] [CrossRef]
- Narasimhan, T.N.; Witherspoon, P.A. An Integrated Finite Difference Method for Analyzing Fluid Flow in Porous Media. Water Resour. Res. 1976, 12, 57–64. [Google Scholar] [CrossRef]
- Narasimhan, T.N.; Witherspoon, P.A.; Edwards, A.L. Numerical Model for Saturated-Unsaturated Flow in Deformable Porous Media: 2. The Algorithm. Water Resour. Res. 1978, 14, 255–261. [Google Scholar] [CrossRef]
- Kamath, V.A. Study of Heat Transfer Characteristics during Dissociation of Gas Hydrates in Porous Media; University of Pittsburgh: Pittsburgh, PA, USA, 1984. [Google Scholar]
- Kowalsky, M.B.; Moridis, G.J. Comparison of Kinetic and Equilibrium Reaction Models in Simulating Gas Hydrate Behavior in Porous Media. Energy Convers. Manag. 2007, 48, 1850–1863. [Google Scholar] [CrossRef]
- Moridis, G.J. User’s Manual for the Hydrate v1.5 Option of TOUGH+ v1.5: A Code for the Simulation of System Behavior in Hydrate-Bearing Geologic Media; LBNL-6869E; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA, 2014. [Google Scholar] [CrossRef]
- Biot, M.A. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Terzaghi, K.; Peck, R.B.; Mesri, G. Soil Mechanics in Engineering Practice, 3rd ed.; John Wiley & Sons: New York, NY, USA, 1996. [Google Scholar]
- Mcnamee, J.; Gibson, R.E. Displacement functions and linear transforms applied to diffusion through porous elastic media. Q. J. Mech. Appl. Math. 1960, 13, 98–111. [Google Scholar] [CrossRef]
- Mcnamee, J.; Gibson, R.E. Plane strain and axially symmetric problems of the consolidation of a semi-infinite clay stratum. Q. J. Mech. Appl. Math. 1960, 13, 210–227. [Google Scholar] [CrossRef]
- Moridis, G.J.; Reagan, M.T. Strategies for Gas Production from Oceanic Class 3 Hydrate Accumulations. In Proceedings of the Offshore Technology Conference, Houston, Texas, USA, 30 April–3 May 2007. [Google Scholar] [CrossRef]
- Qin, X.; Liang, Q.; Ye, J.; Yang, L.; Qiu, H.; Xie, W.; Liang, J.; Lu, J.; Lu, C.; Lu, H.; et al. The Response of Temperature and Pressure of Hydrate Reservoirs in the First Gas Hydrate Production Test in South China Sea. Appl. Energy 2020, 278, 115649. [Google Scholar] [CrossRef]
- Shang, S.; Gu, L.; Zhan, L.; Qiu, H.; Lu, H. Application of Horizontal Well to Gas Production from a Hydrate Reservoir with Free Gas and High Irreducible Water. J. Nat. Gas Sci. Eng. 2021, 94, 104102. [Google Scholar] [CrossRef]
- Sun, J.; Zhang, L.; Ning, F.; Lei, H.; Liu, T.; Hu, G.; Lu, H.; Lu, J.; Liu, C.; Jiang, G.; et al. Production Potential and Stability of Hydrate-Bearing Sediments at the Site GMGS3-W19 in the South China Sea: A Preliminary Feasibility Study. Mar. Pet. Geol. 2017, 86, 447–473. [Google Scholar] [CrossRef]
- van Genuchten, M.T. A Closed-Form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Rutqvist, J.; Wu, Y.; Tsang, C.; Bodvarsson, G. A Modeling Approach for Analysis of Coupled Multiphase Fluid Flow, Heat Transfer, and Deformation in Fractured Porous Rock. Int. J. Rock Mech. Min. Sci. 2002, 39, 429–442. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kowalsky, M.B.; Pruess, K. Depressurization-Induced Gas Production from Class 1 Hydrate Deposits. SPE Reserv. Eval. Eng. 2007, 10, 458–481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).