Analysis of FPSO Motion Response under Different Wave Spectra
Abstract
1. Introduction
2. Mathematical Model
2.1. Time Domain Model of Wave–Body Interaction
2.1.1. Coordinate System
2.1.2. Governing Equation
2.1.3. Boundary Condition
- 1.
- Free water surface boundary conditions
- 2.
- Body surface and seafloor fixed wall boundary conditions
- 3.
- Incident boundary condition
2.1.4. Initial Condition
2.1.5. Motion Equation
2.2. Mathematical Model of Irregular Waves
2.2.1. Ocean Wave Spectra
- 1.
- The ITTC two-parameters spectrum
- 2.
- The JONSWAP spectrum
- 3.
- The Ochi-Hubble spectrum
2.2.2. A Simulation Method of the Long-Crested Irregular Waves
2.2.3. A Simulation Method of the Short-Crested Irregular Waves
3. Numerical Model and Verification of FPSO
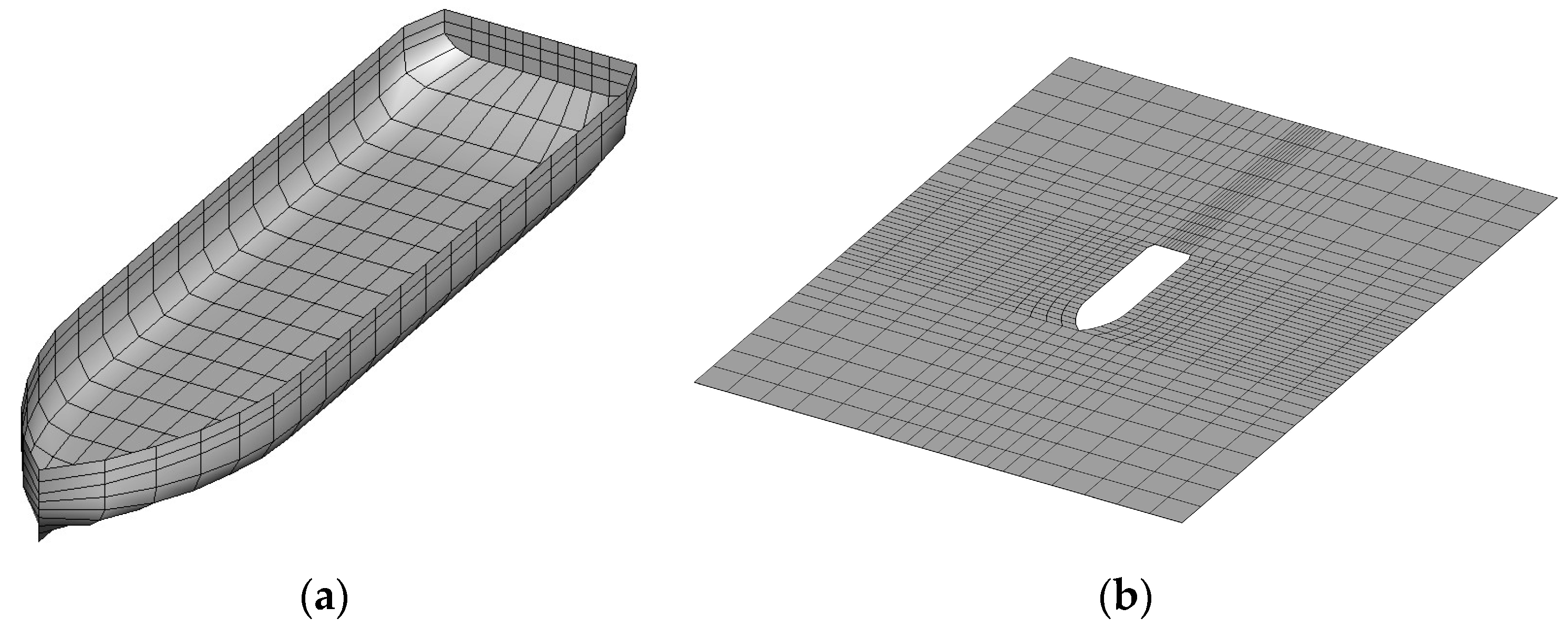
3.1. Model Parameters of FPSO
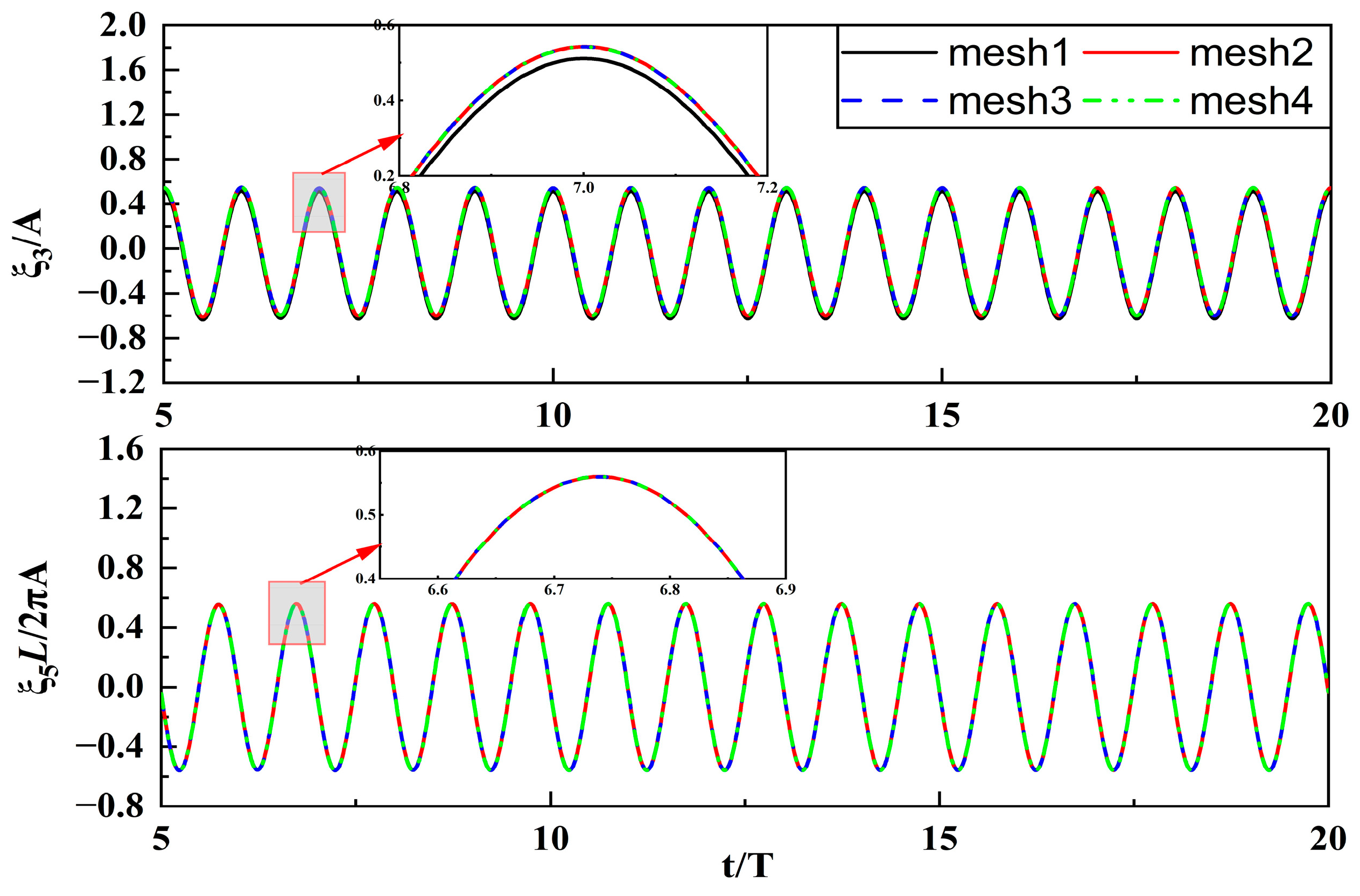
3.2. Verification of Time Step and Grid Convergence
3.3. Damping Matrix
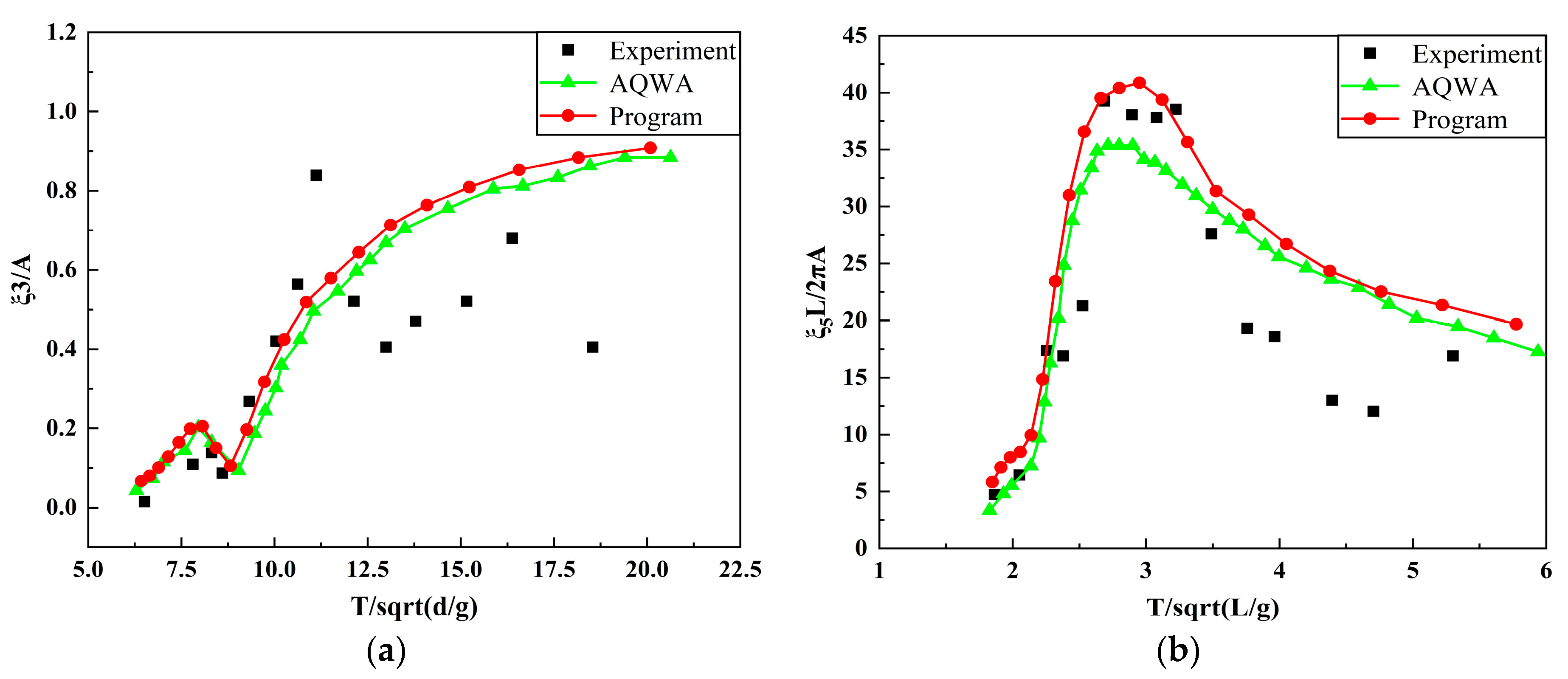
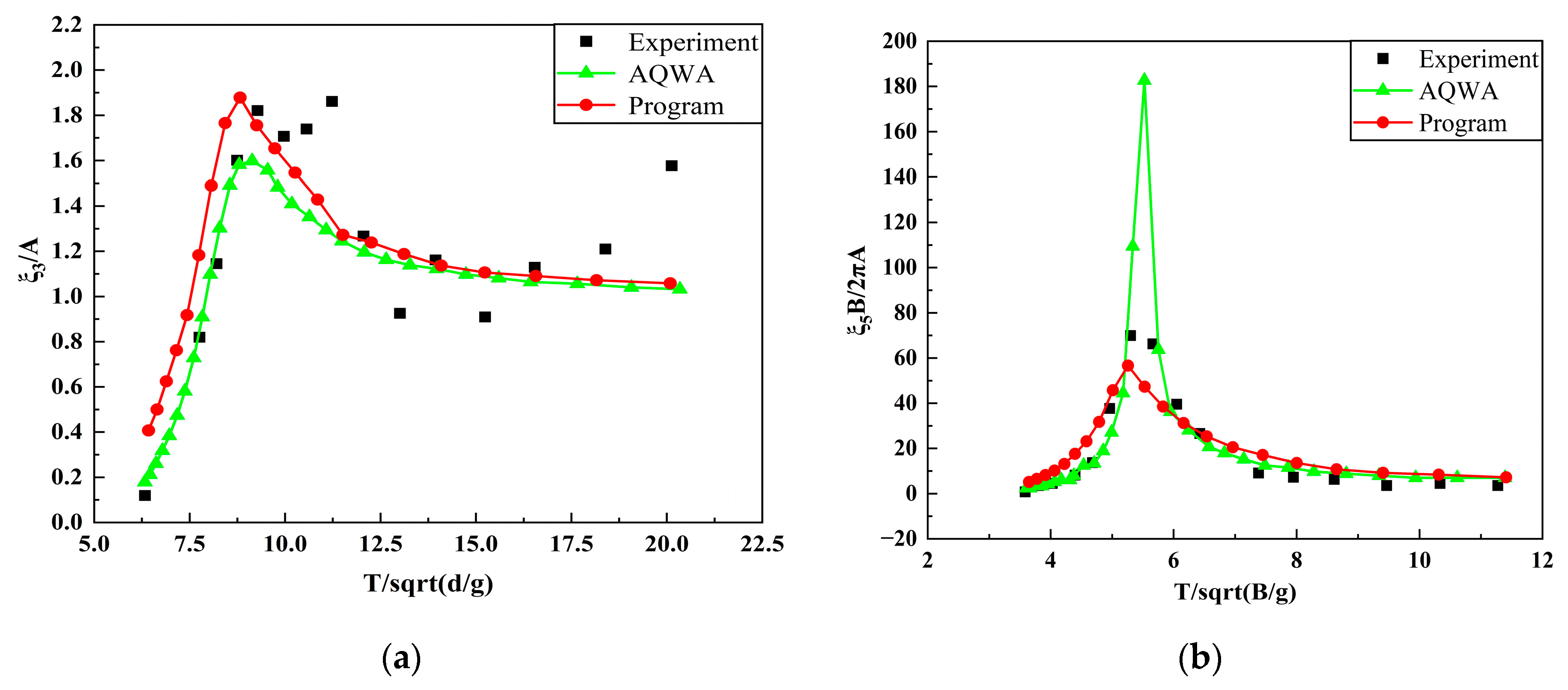
3.4. The Validation of Numerical Model
4. The Impact of Irregular Waves on FPSO under Different Wave Spectra
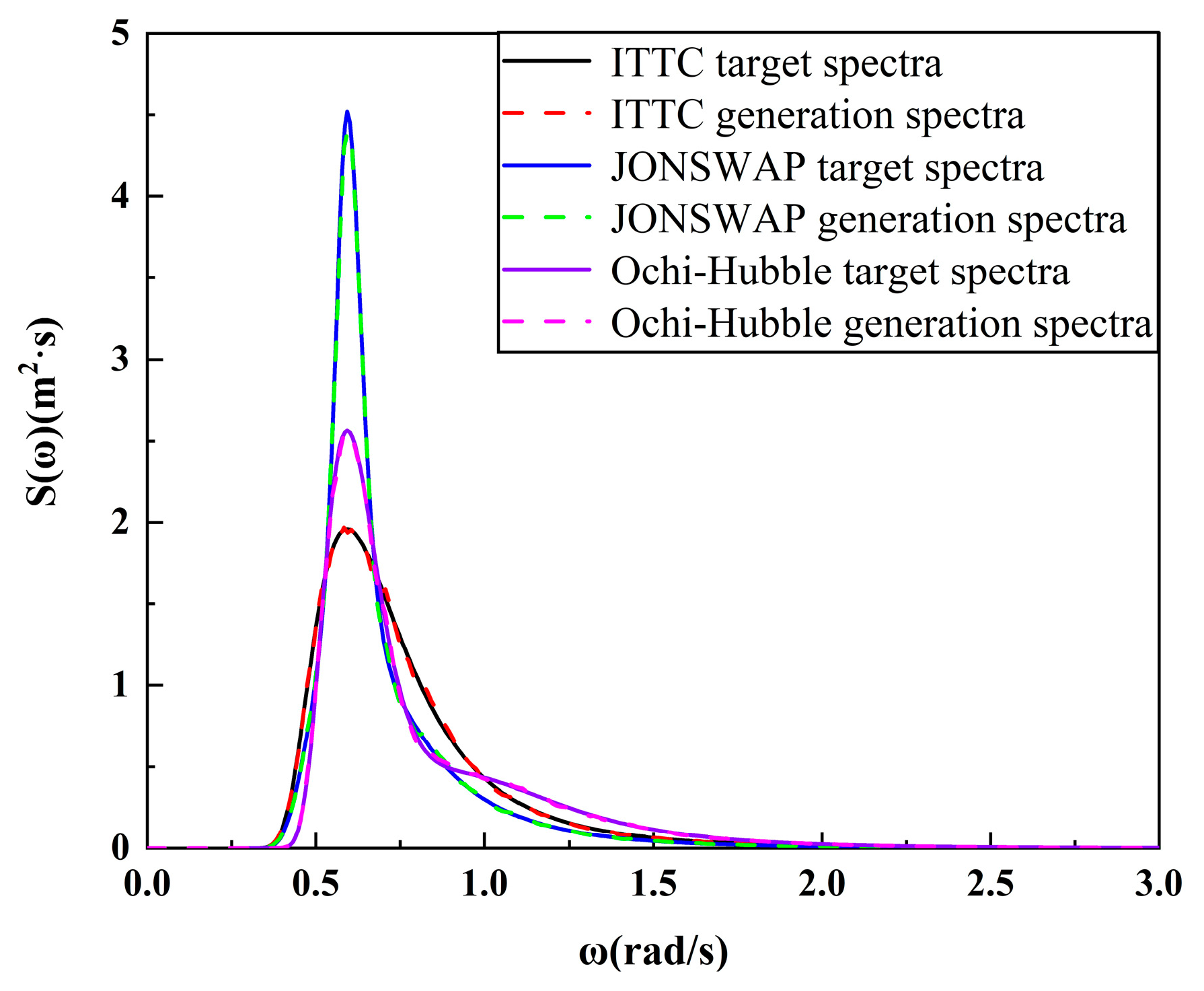
4.1. Simulation and Verification of Irregular Waves
4.1.1. Operating Conditions
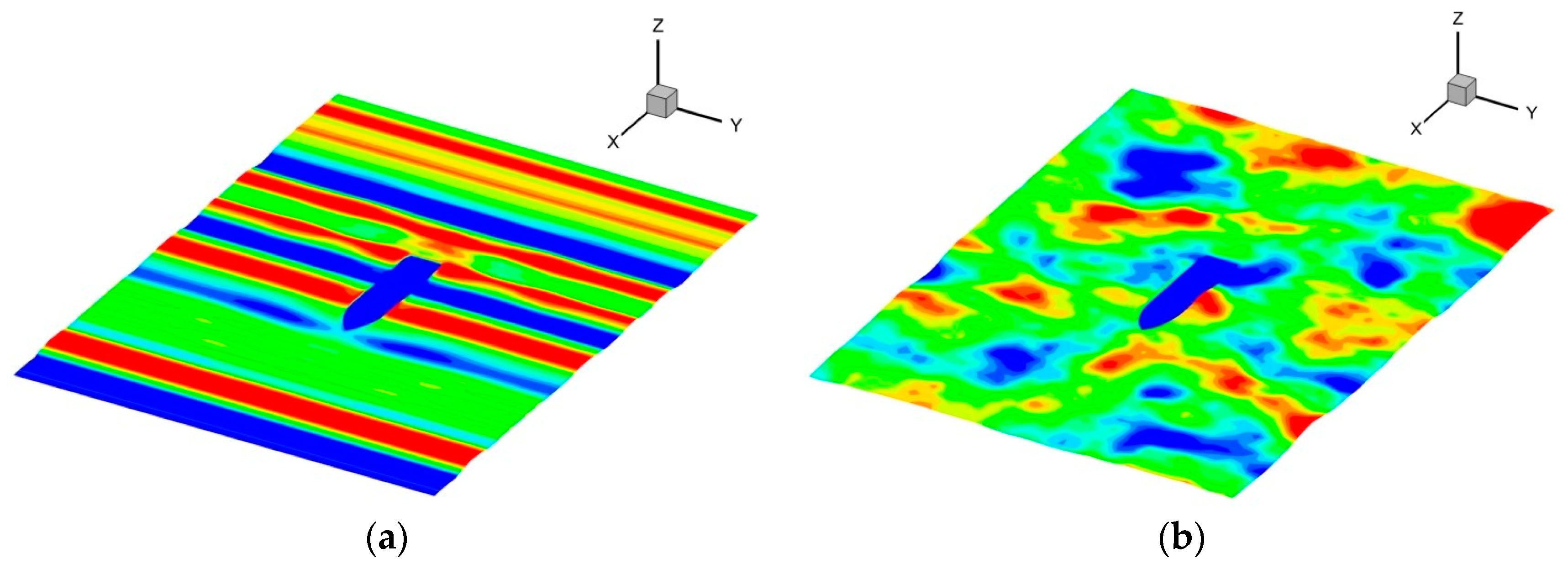
4.1.2. Long-Crested Irregular Waves
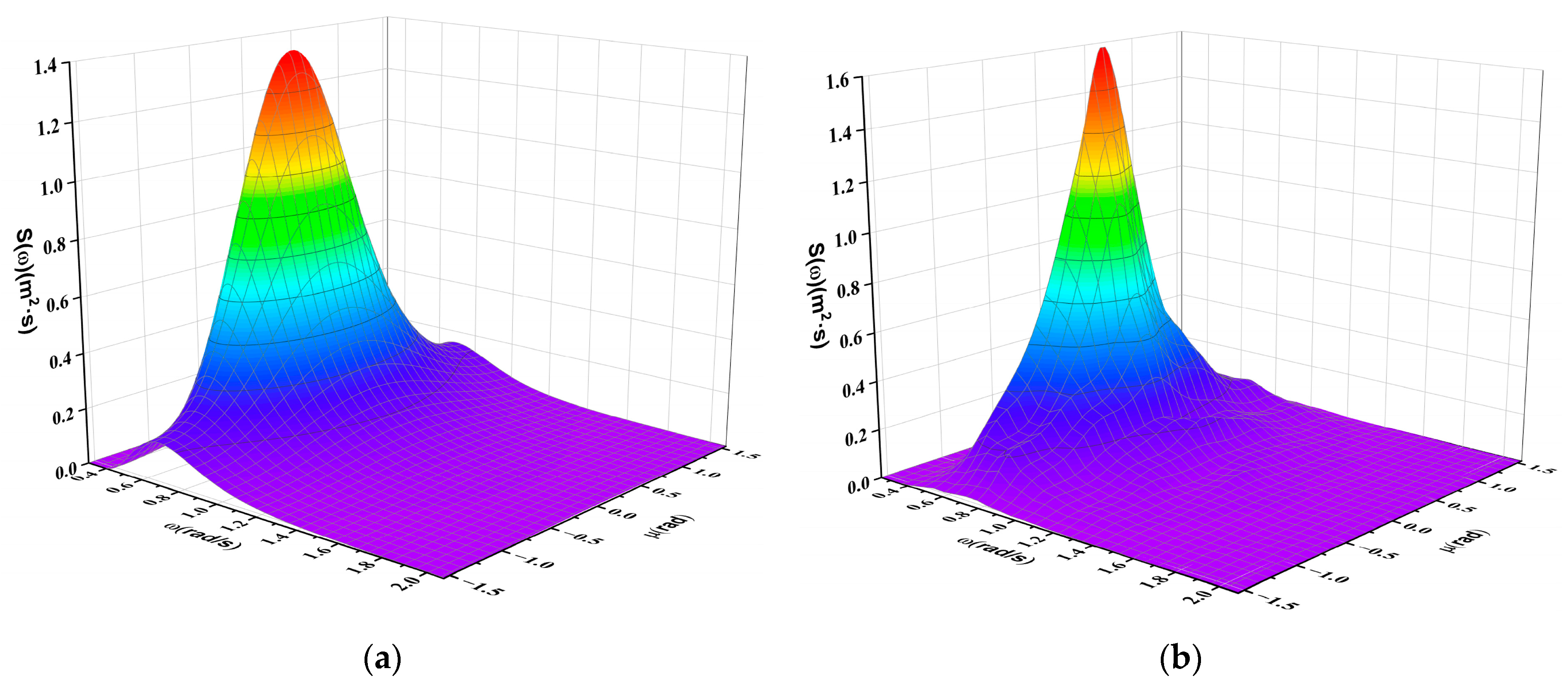
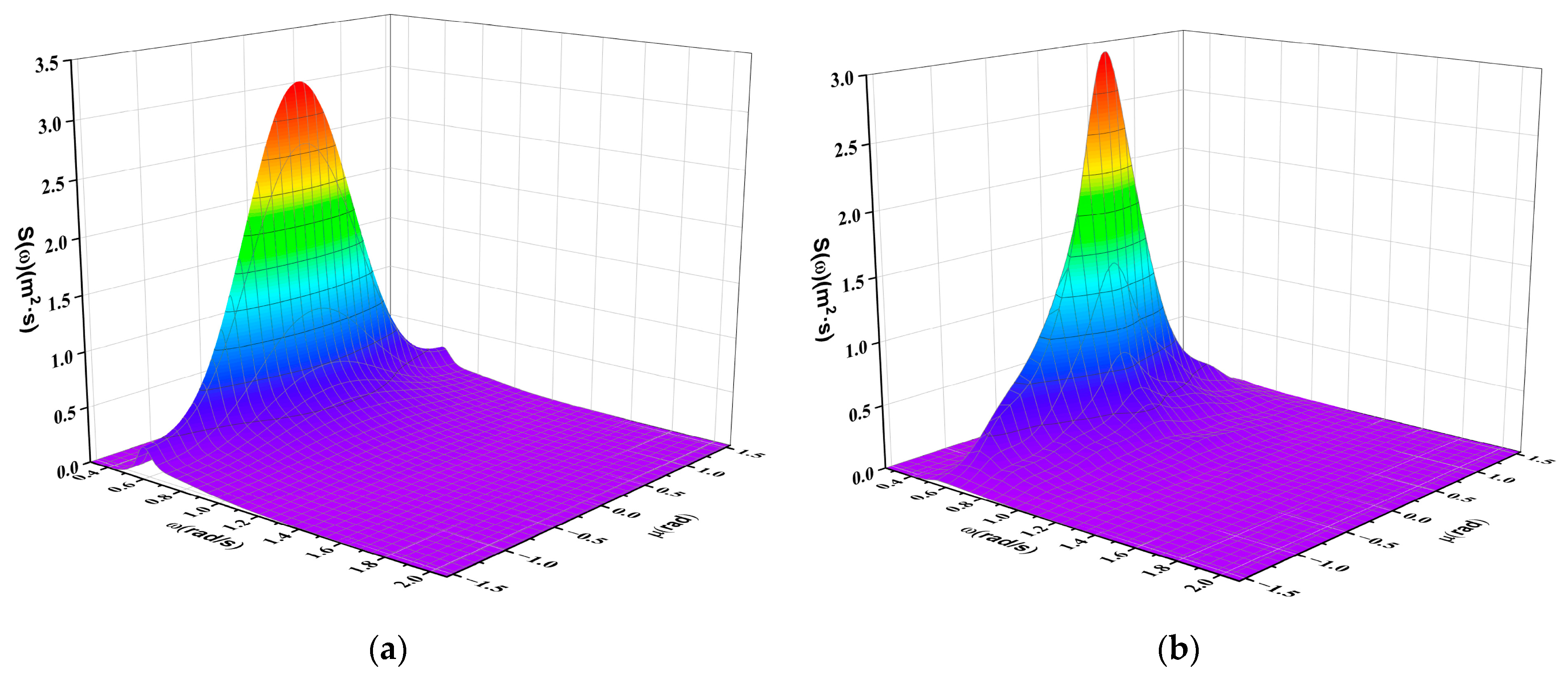
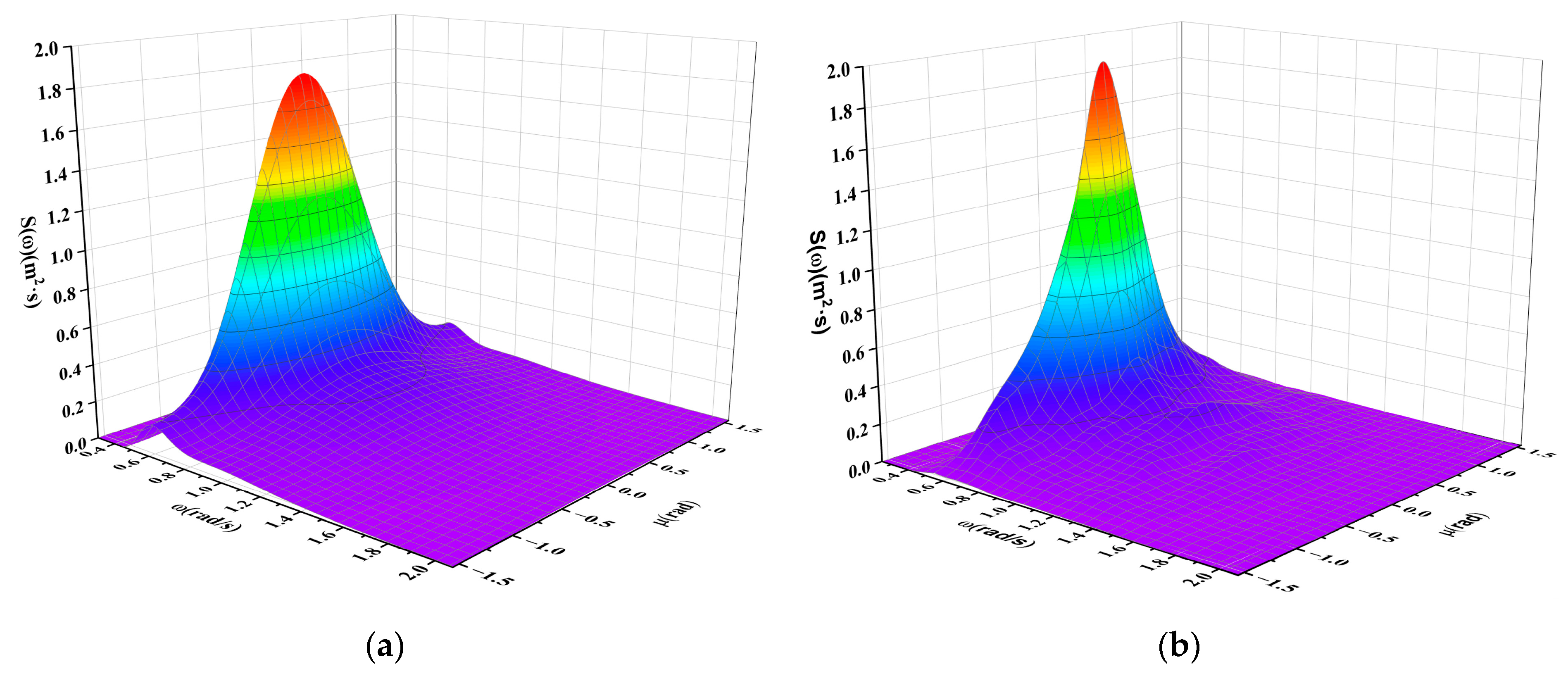
4.1.3. Short-Crested Irregular Waves
4.2. The Effect of Long-Crested Waves on FPSO under Different Wave Spectra
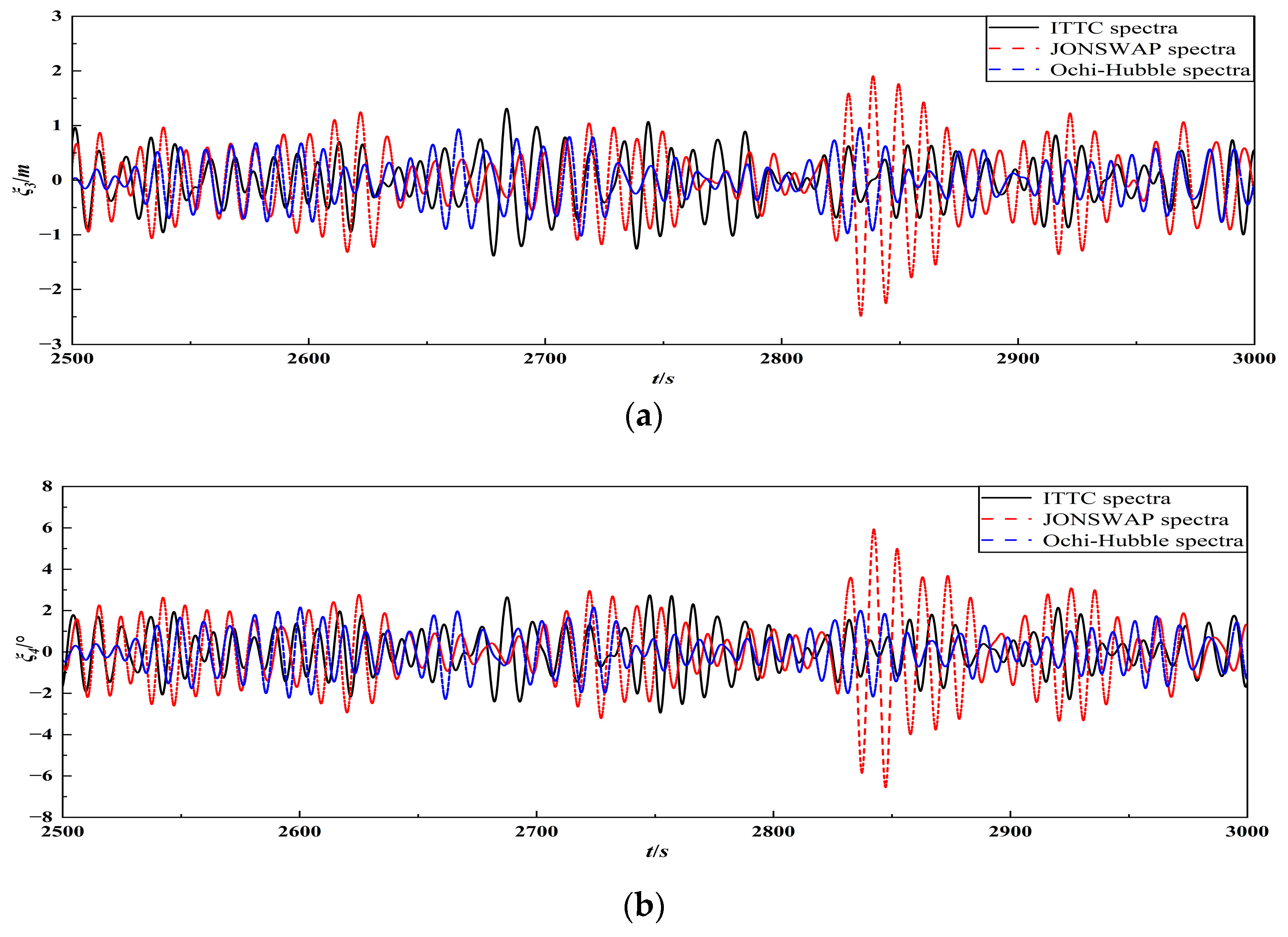
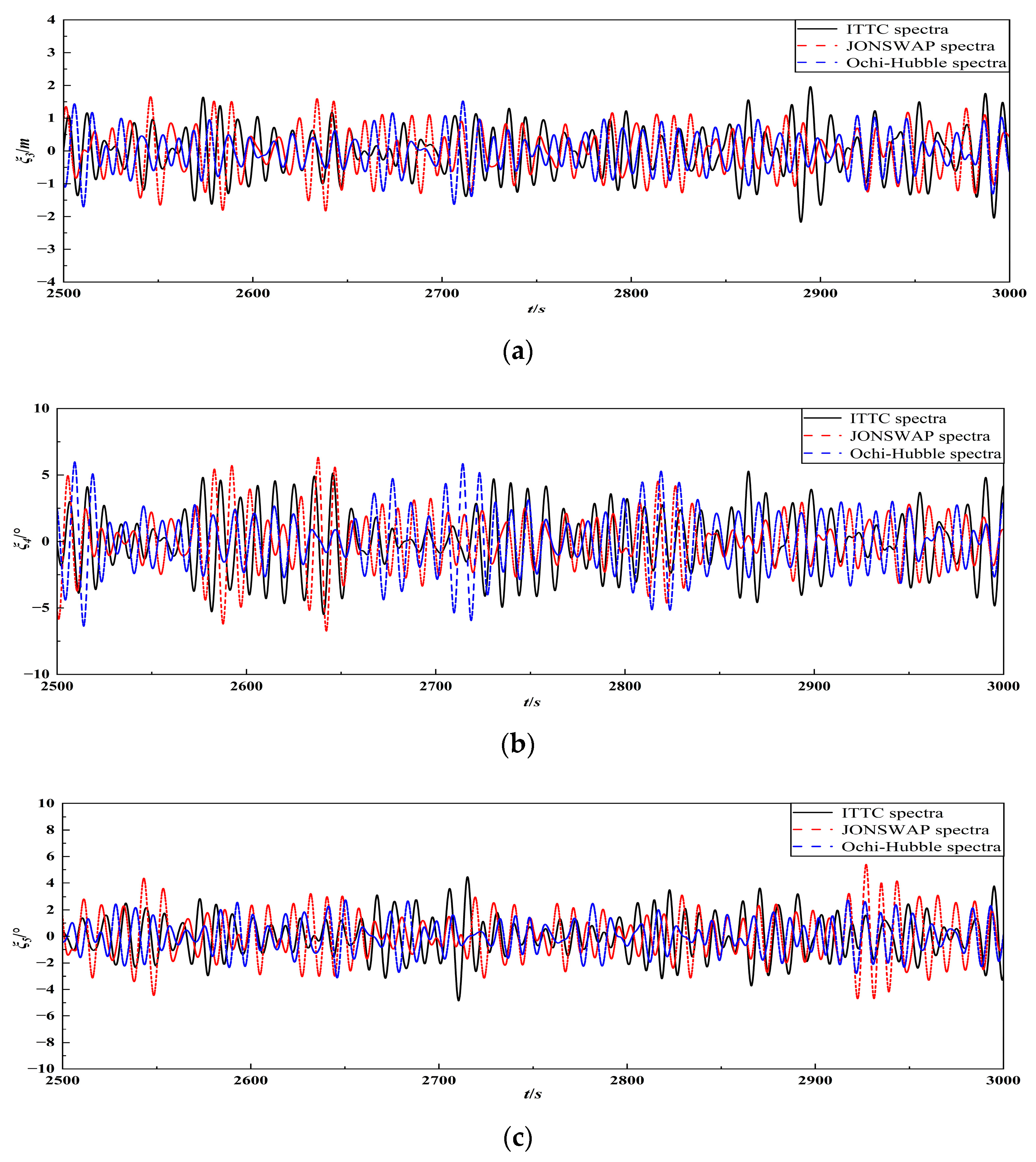
4.2.1. Analysis of the Time History of FPSO Motion Response
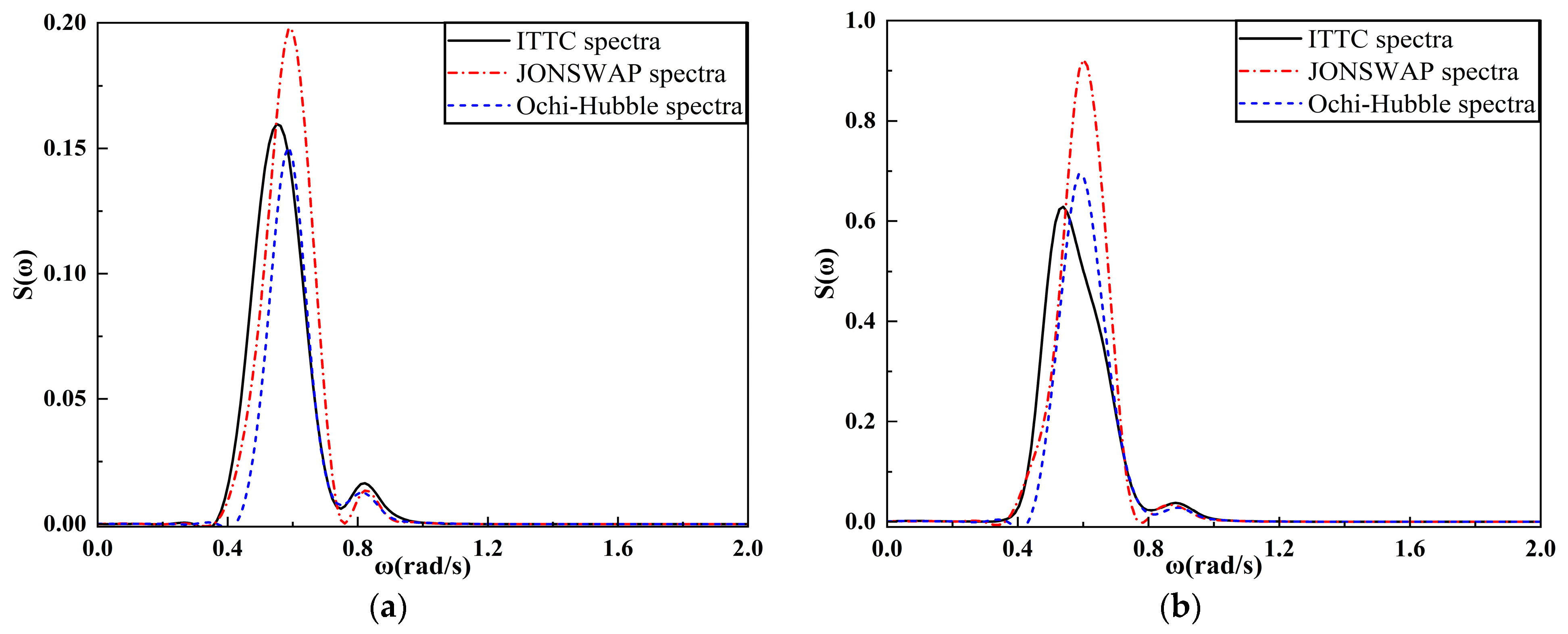
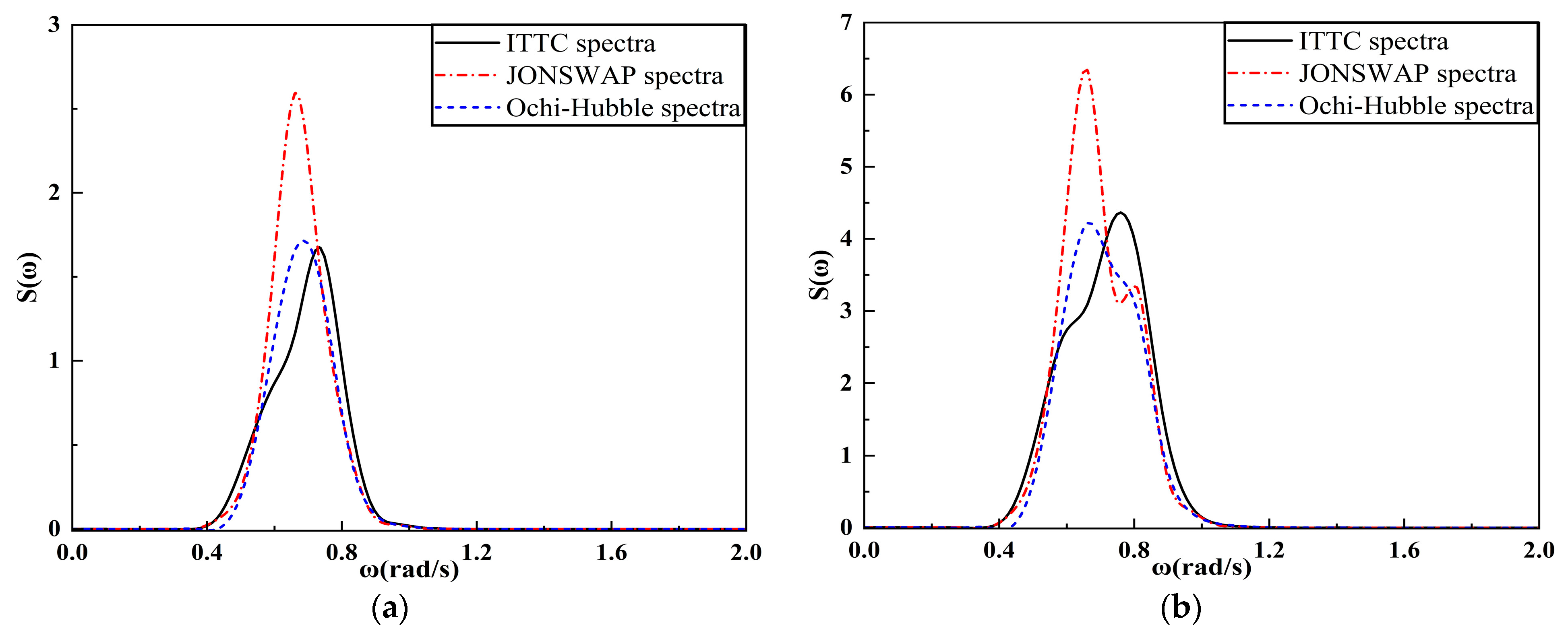
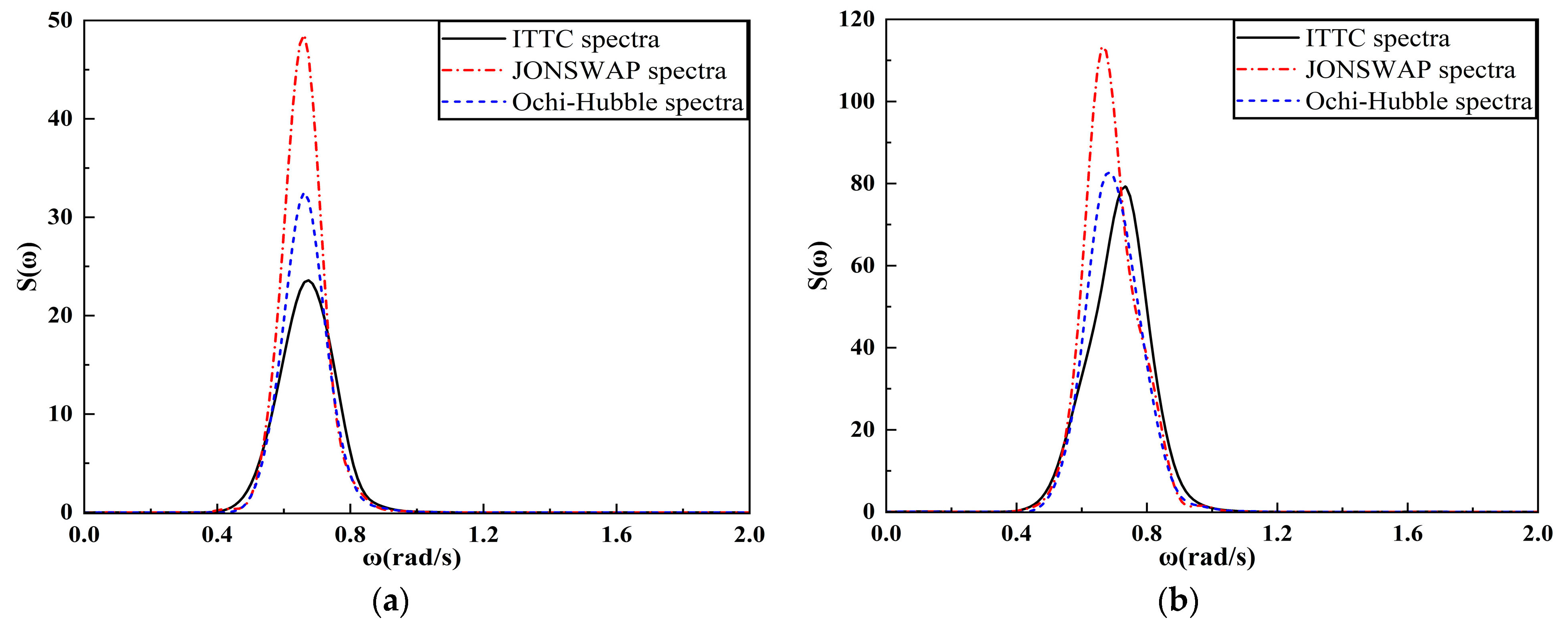
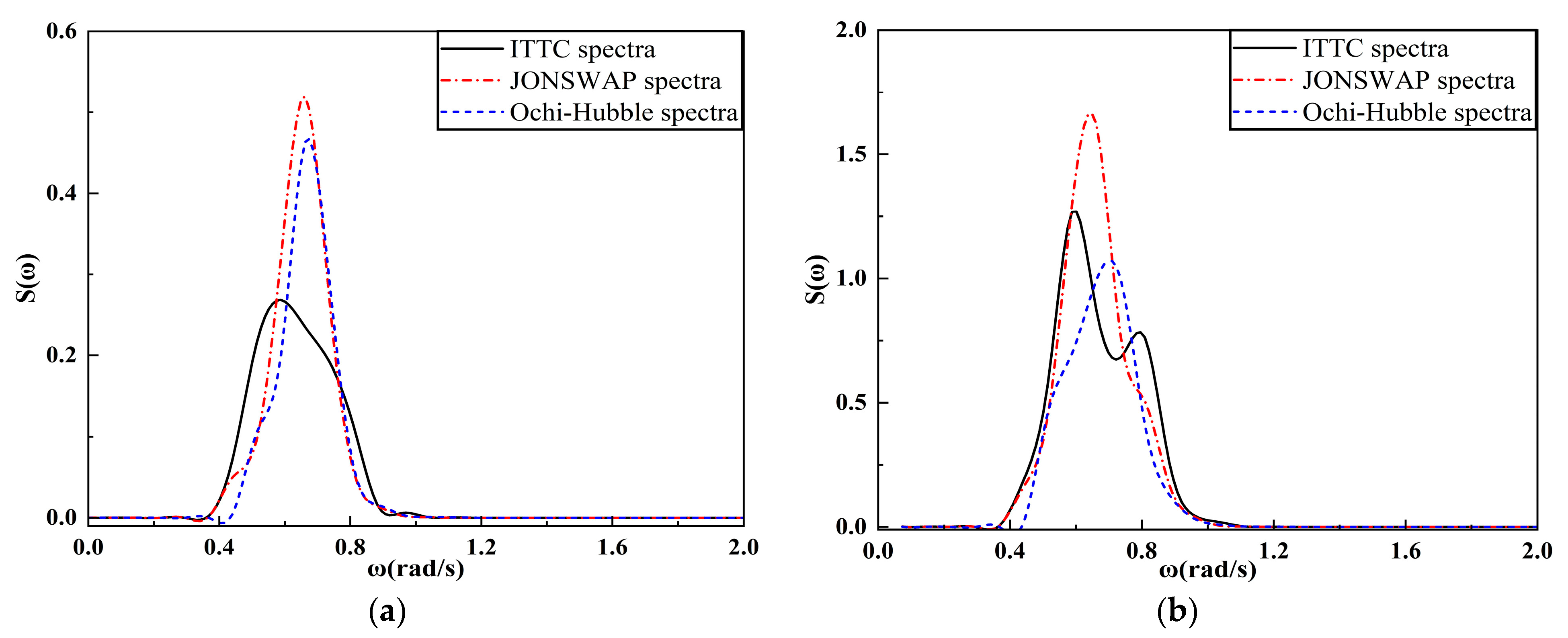
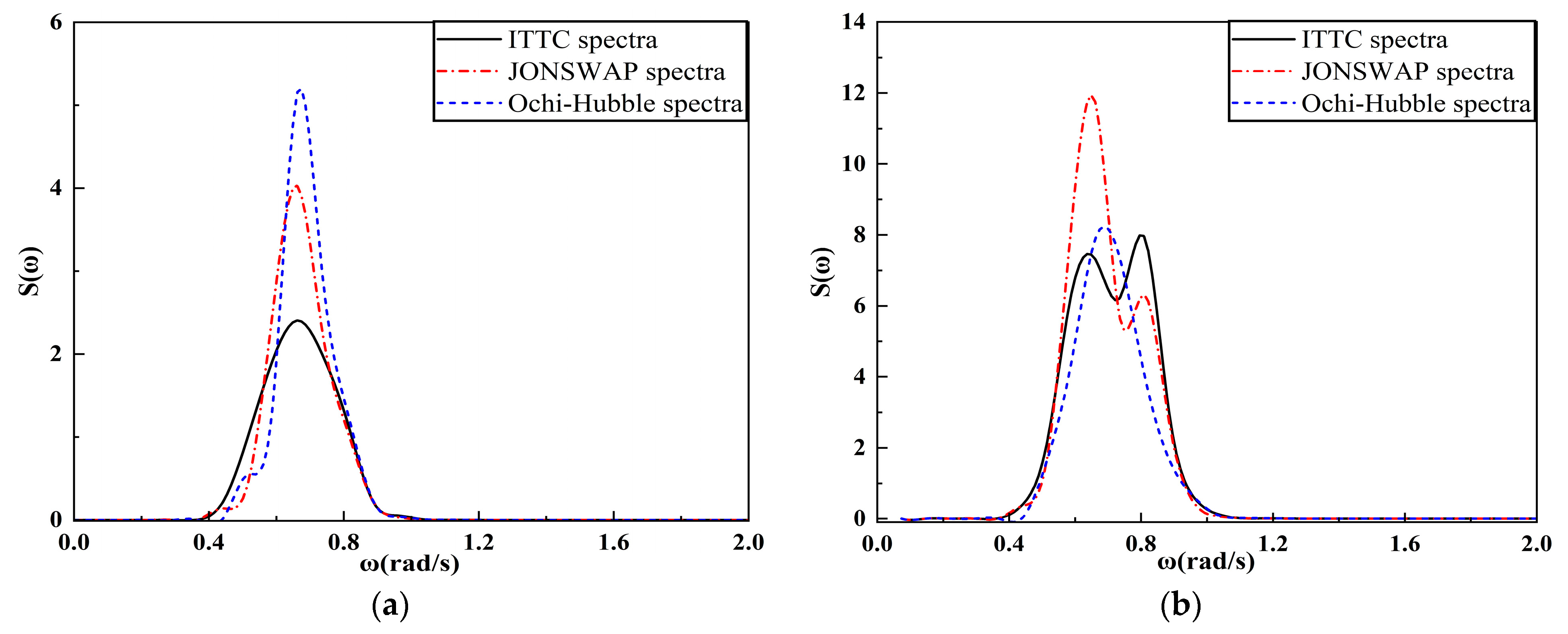
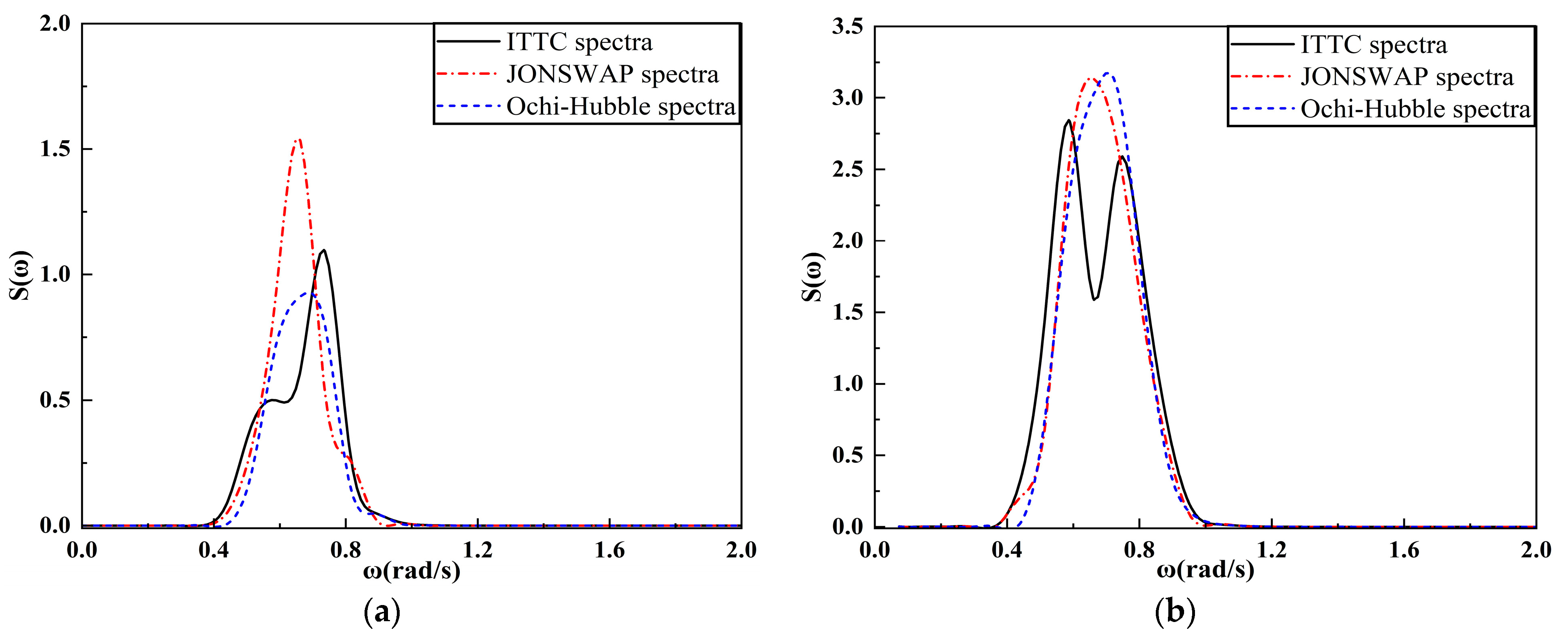
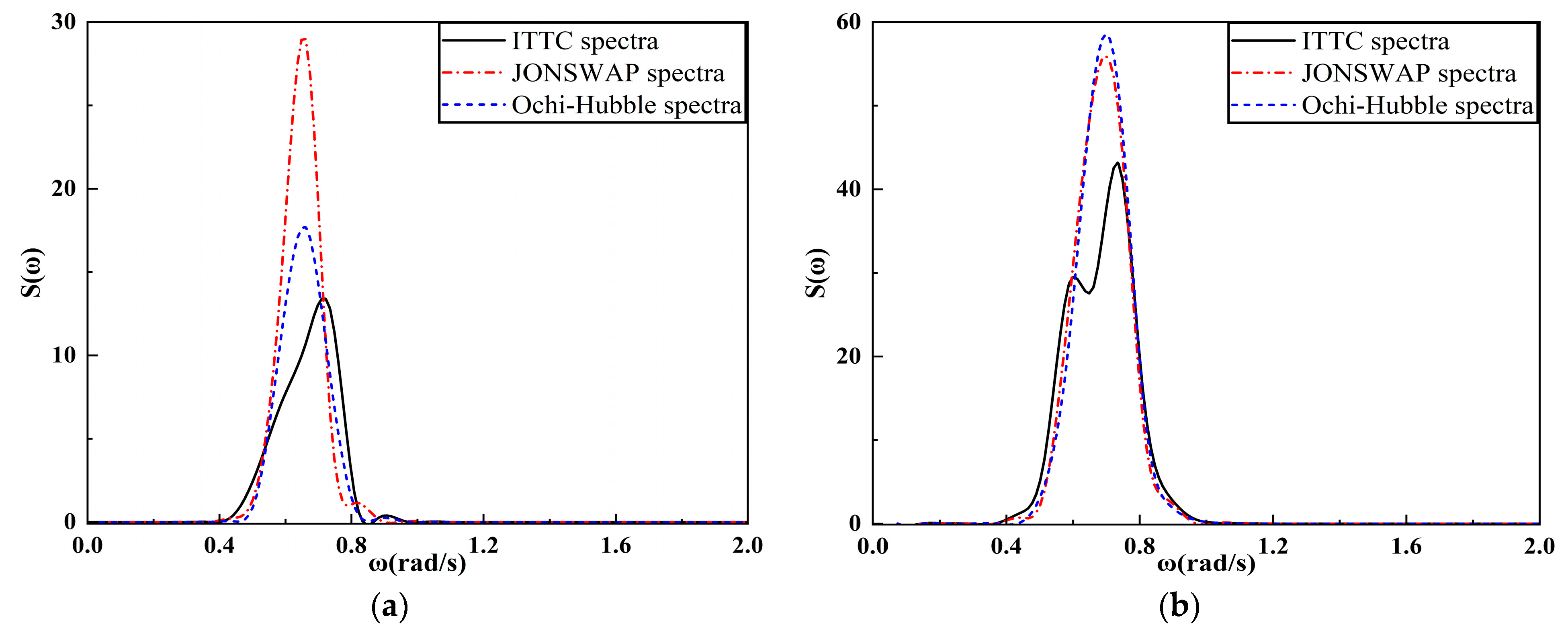
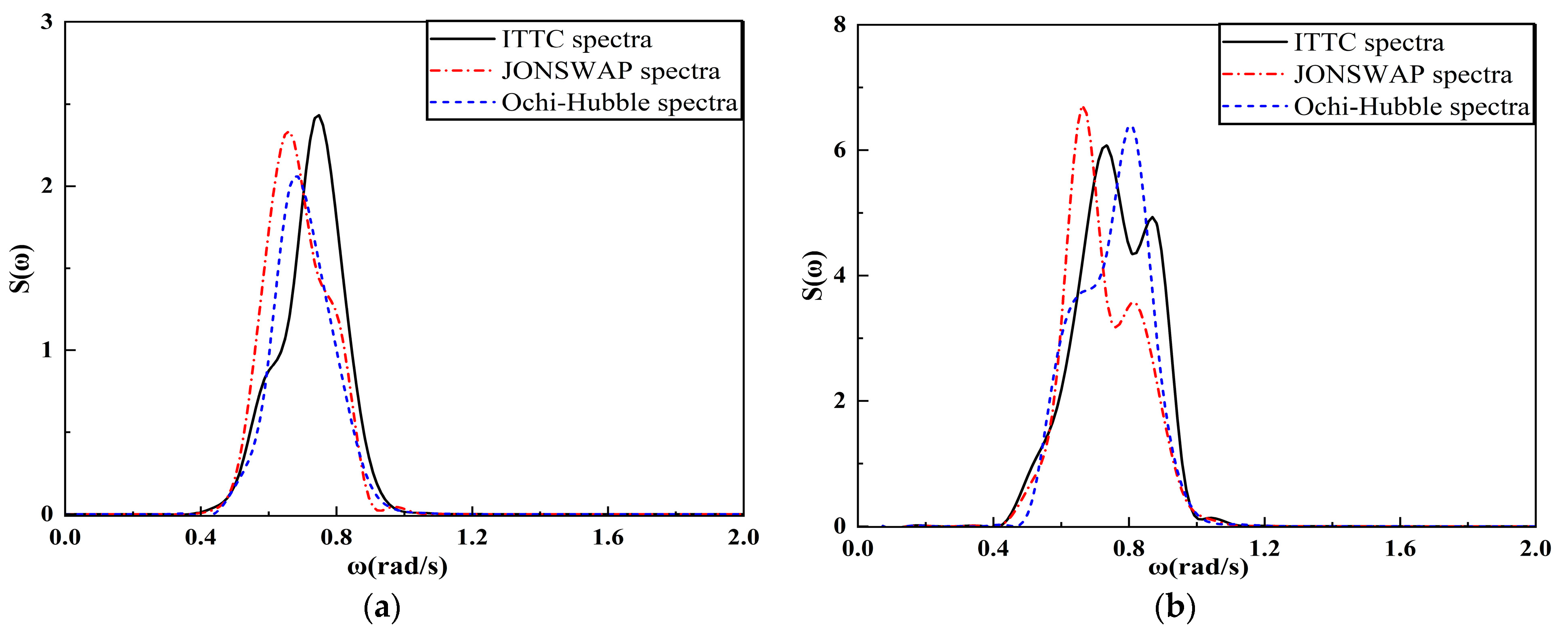
4.2.2. Analysis of the Frequency Spectrum of FPSO Motion Response
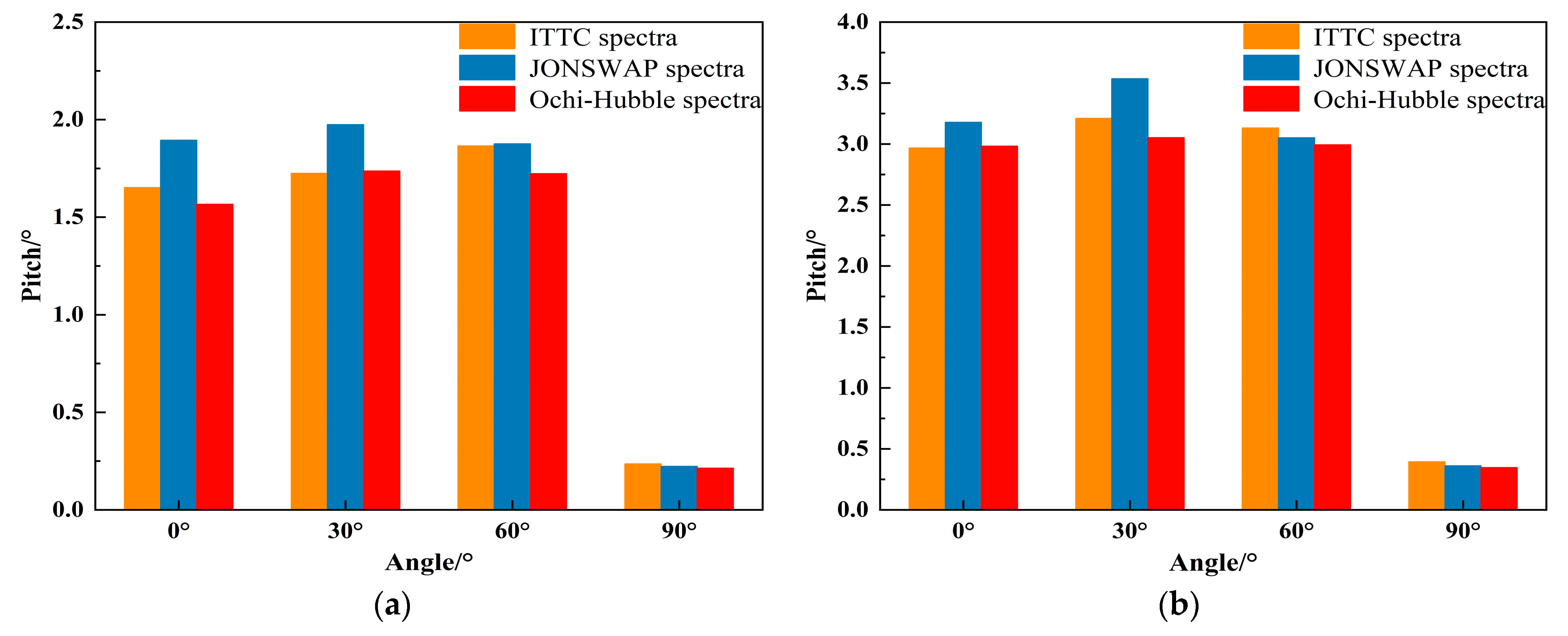
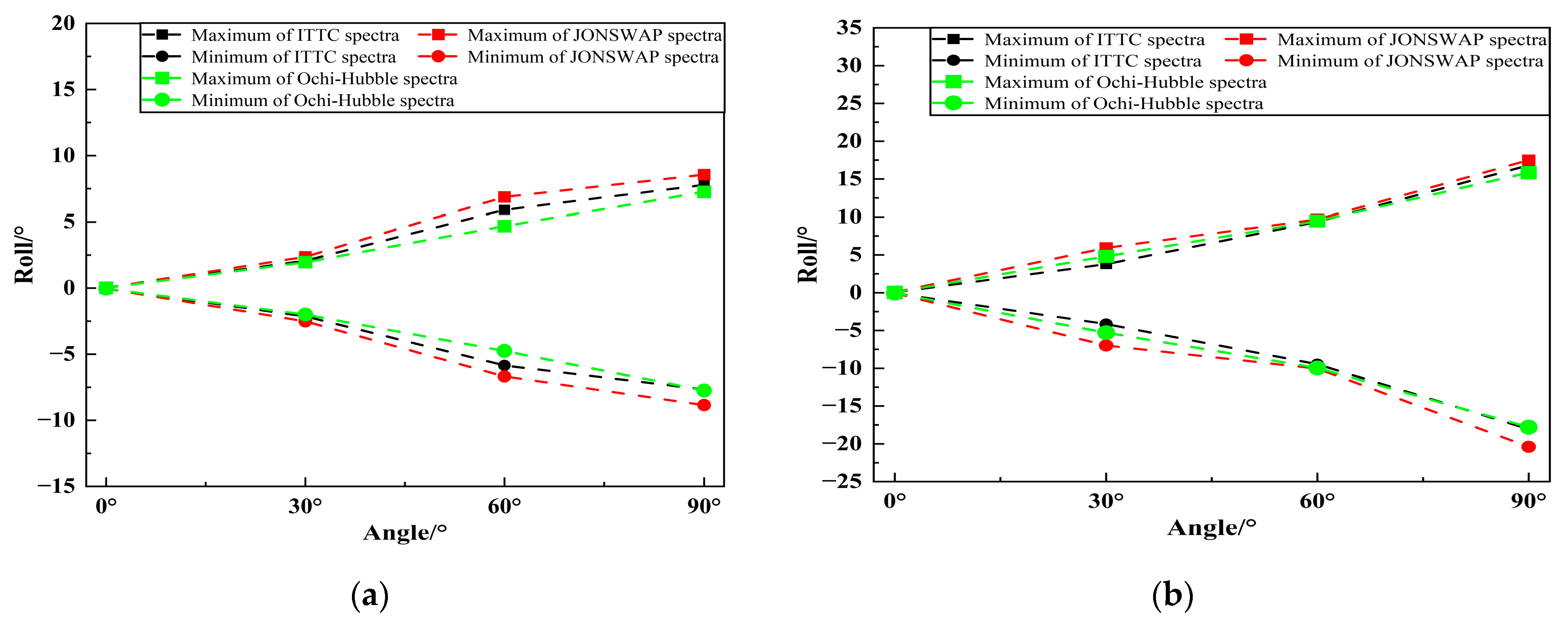
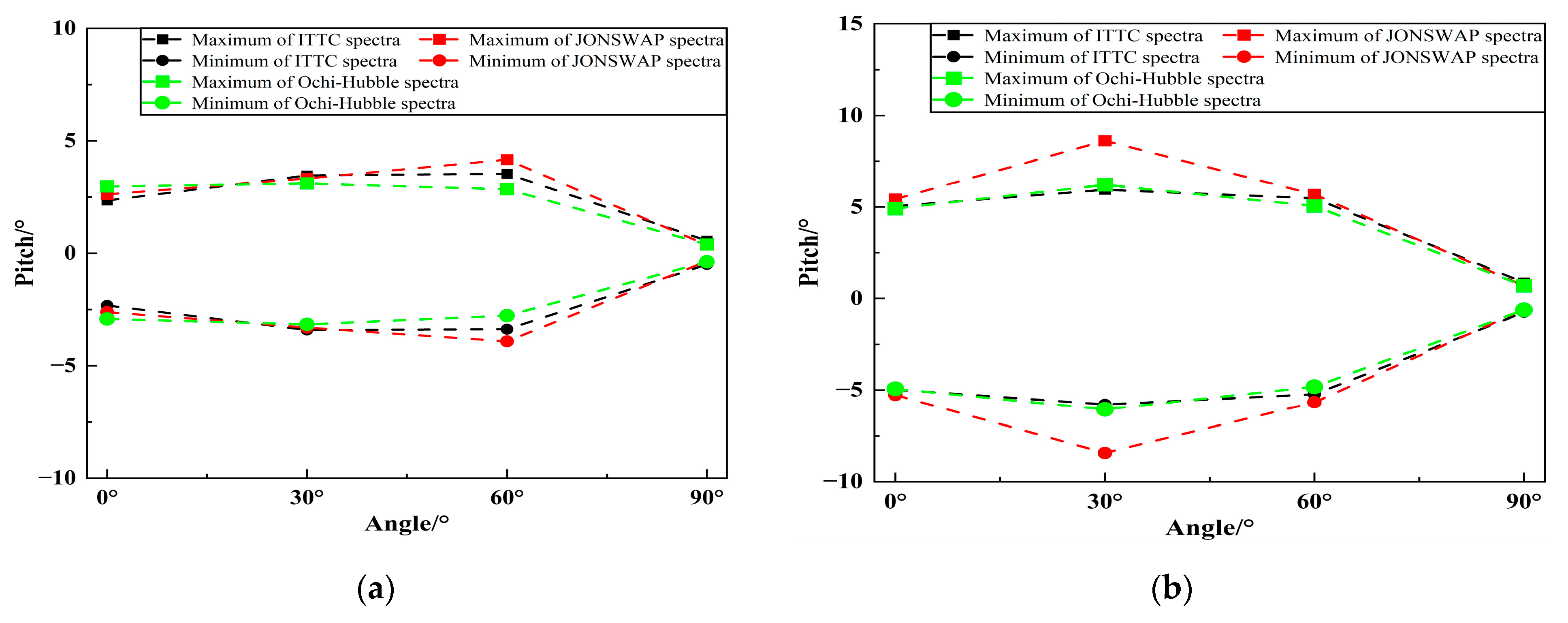
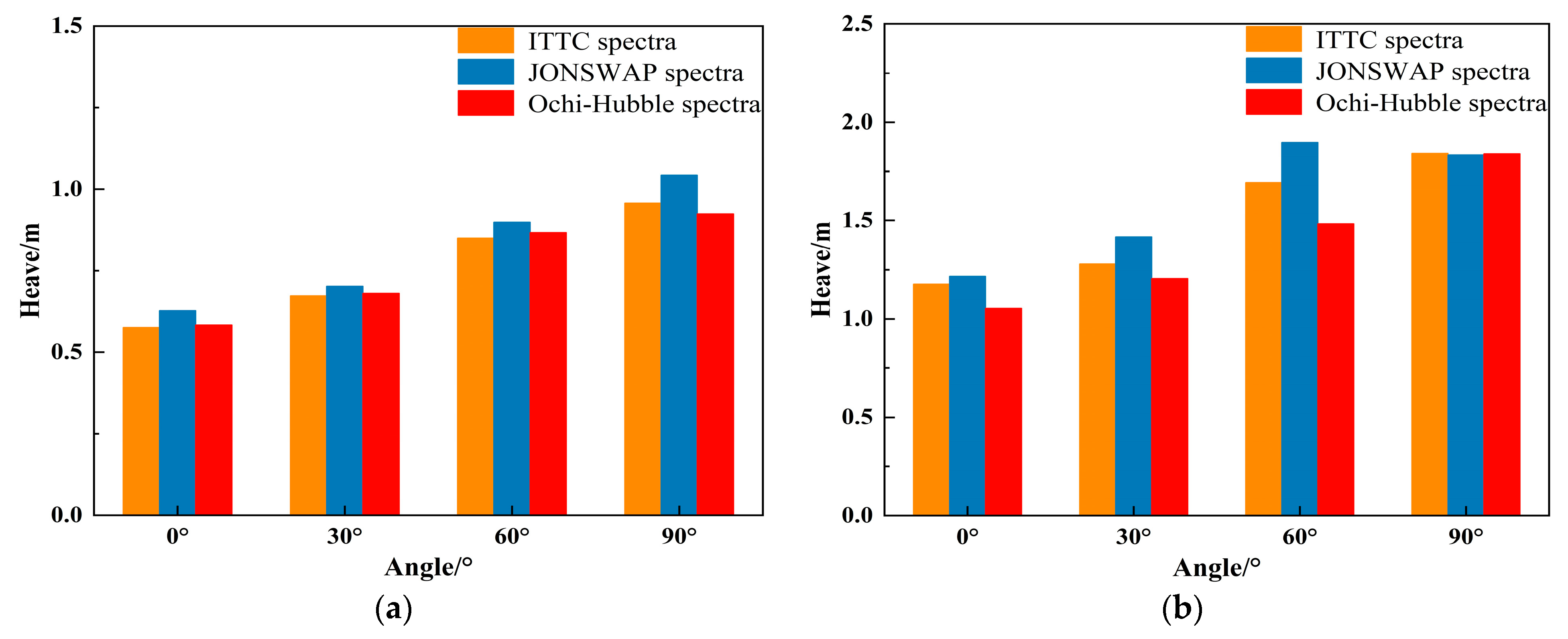
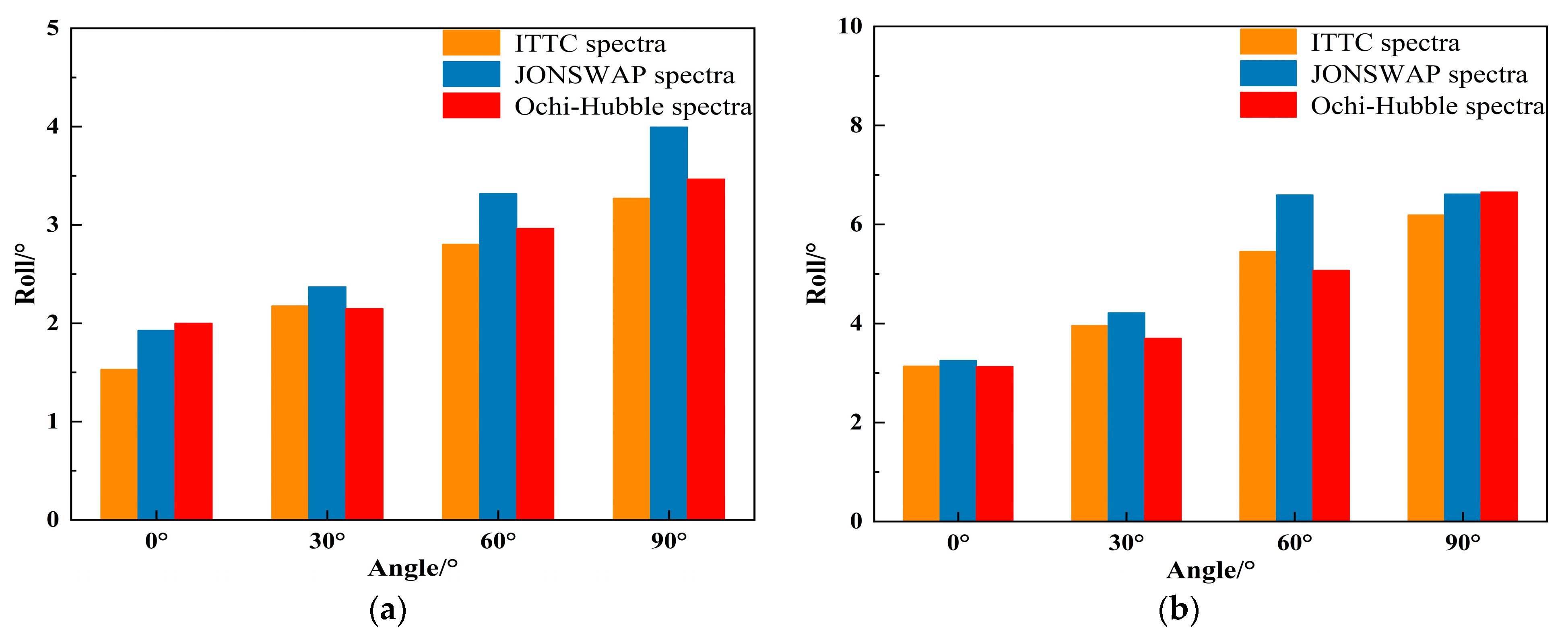
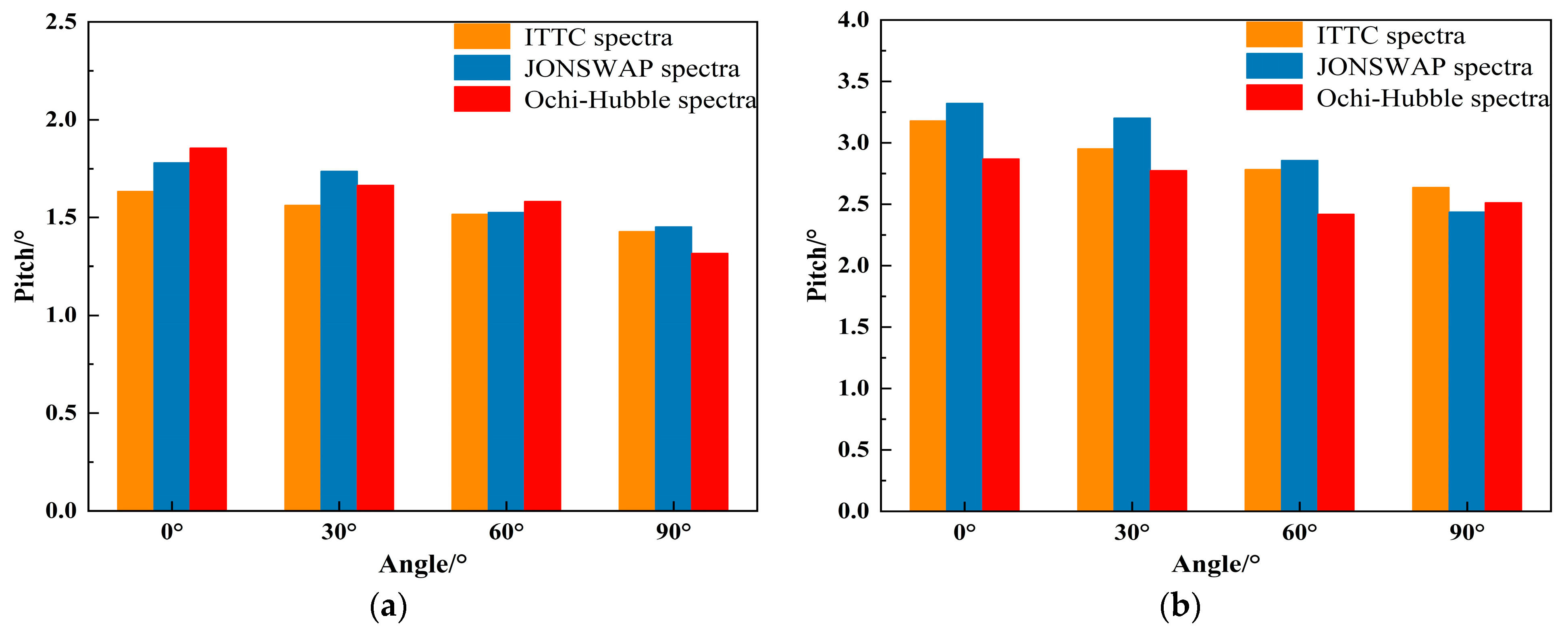
4.2.3. Analysis of the Significant Value of FPSO Motion Response
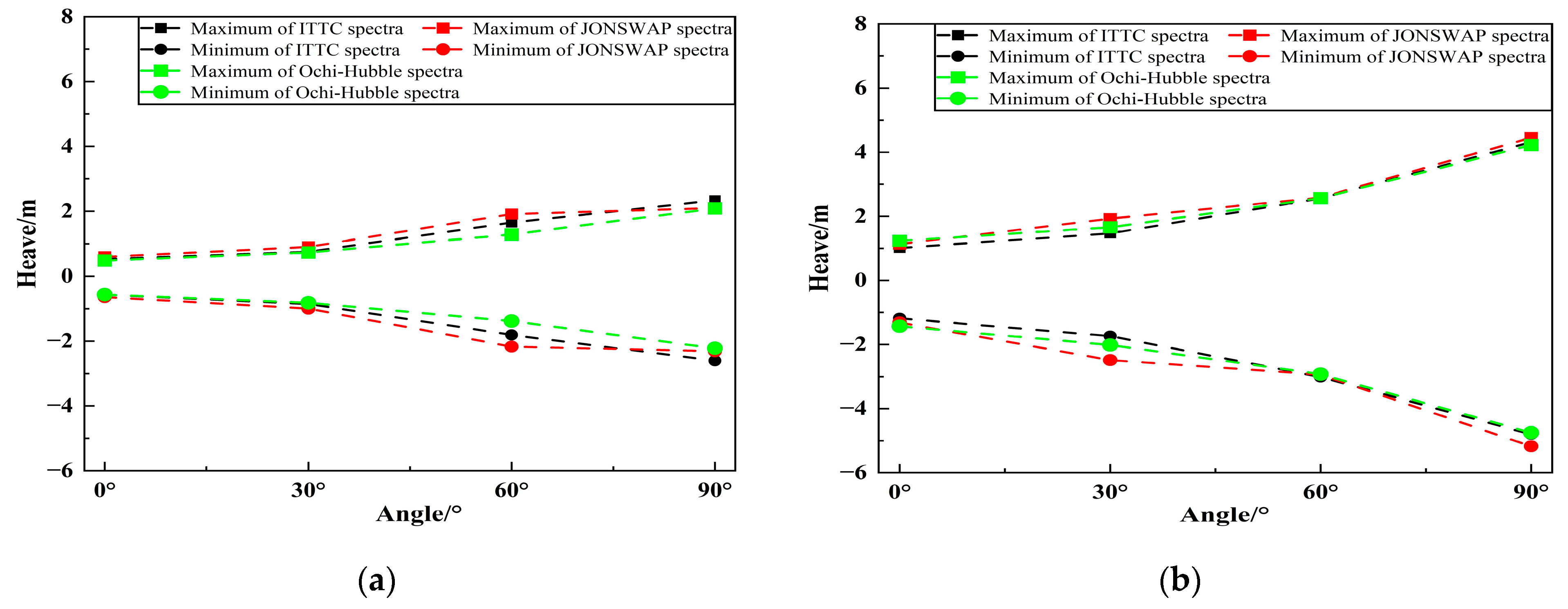
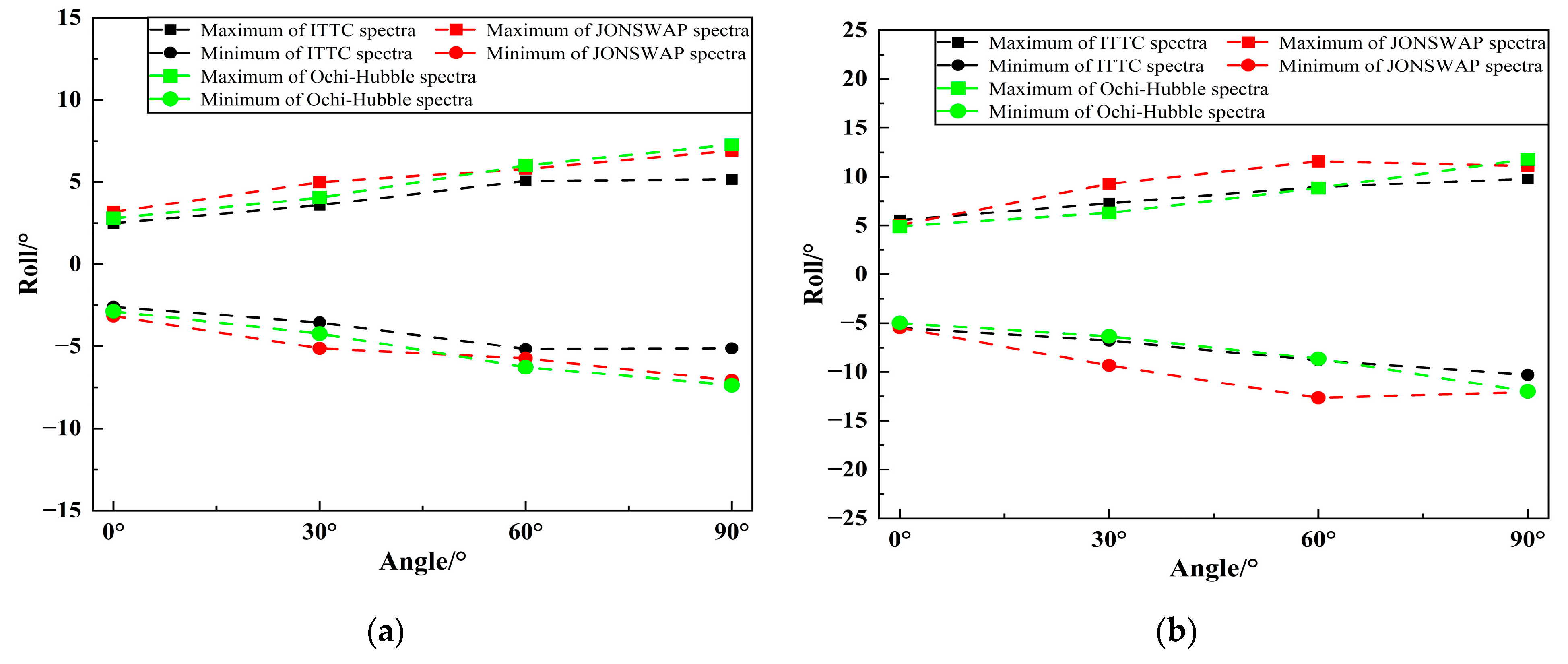
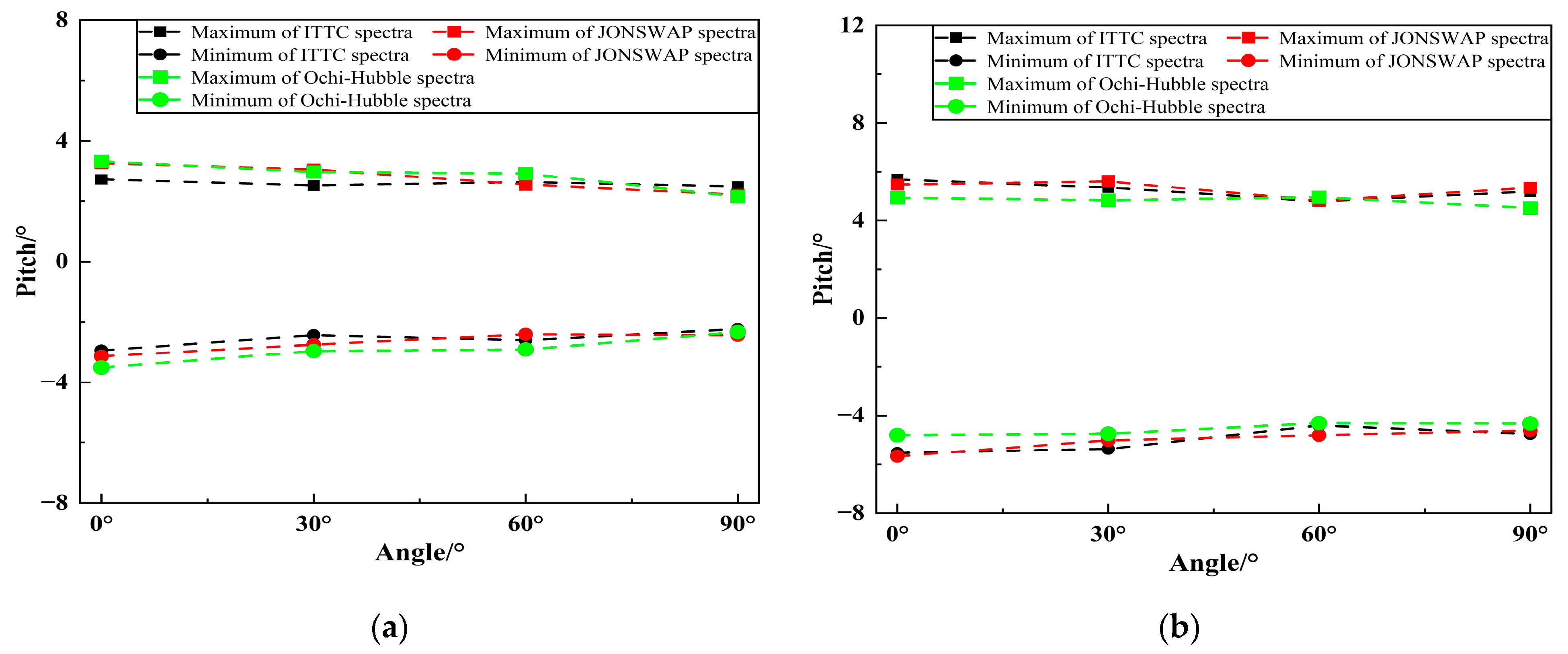
4.2.4. Analysis of the Range of FPSO Motion Response
4.3. The Effect of Short-Crested Waves on FPSO under Different Wave Spectra
4.3.1. Analysis of the Time History of FPSO Motion Response
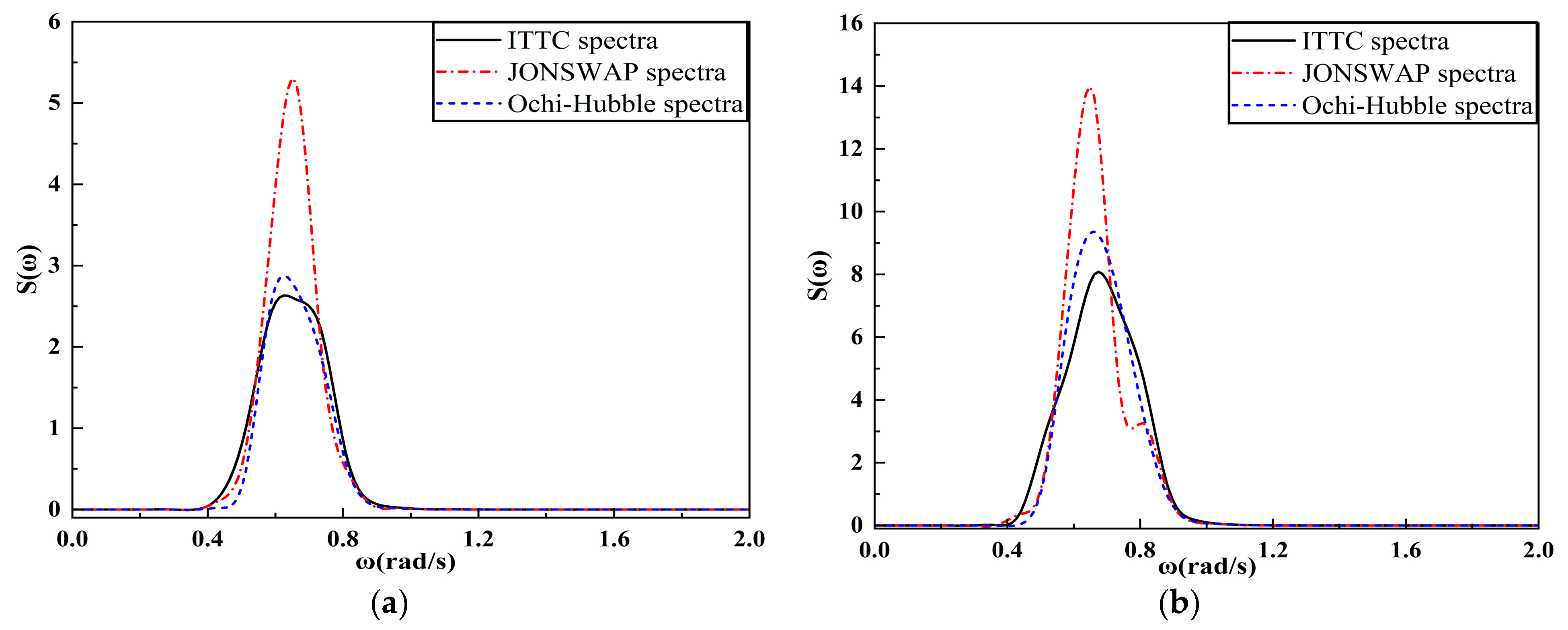
4.3.2. Analysis of the Frequency Spectrum of FPSO Motion Response
4.3.3. Analysis of the Significant Value of FPSO Motion Response
4.3.4. Analysis of the Range of FPSO Motion Response
5. Conclusions
- 1.
- When the incident wave is the long-crested irregular wave, the spectral peak frequencies of the motion spectrum under three types of wave spectra is mainly near the spectral peak frequencies of the incident wave or near the natural frequencies of the vessel. Under two types of sea conditions, the heave and roll motions of FPSO under three types of wave spectra increase with the increase of the incident angle, reaching the peak value at an incident angle of 90°. The pitch motion increases first and then decreases with the increase in the incident angle, reaching the peak value at an incident angle of 30°. The significant values and ranges of heave and roll motions under JONSWAP spectrum are larger than those under the other two wave spectra. When the incident angle is 0° and 30°, the significant values and ranges of pitch motion under JONSWAP spectrum are the largest, and the range difference compared with the pitch motion under the other two wave spectra reaches about 6°. The significant values and ranges of pitch motion under the three types of wave spectra are basically the same when the incident angle is 60°.
- 2.
- When the incident wave is the short-crested irregular wave, the spectral peak frequencies of the motion spectrum under three types of wave spectra is mainly located near the spectral peak frequencies of incident wave or near the natural frequencies of the vessel, presenting a bimodal spectrum with the main peak near the incident wave frequency and the secondary peak near the natural frequency of the vessel. Under both types of sea conditions, the heave and roll motions of FPSO under three types of wave spectra increase with the increase in incident angle and reach the peak value at an incident angle of 90°. The pitch motion decreases with the increase in incident angle, and the motion amplitude of FPSO in short-crested waves is smaller than that in long-crested waves. In the fourth-level sea state, the significant values of FPSO’s heave motion are essentially the same under three different wave spectra, and the ranges of motion are also similar. In the fifth-level sea state, when the incident angle is 60°, the significant values and ranges of FPSO’s heave motion under JONSWAP spectrum are larger than the other two wave spectra, with a difference in amplitude of 0.41 m and a difference in moving range of about 2.0 m. Under both sea states, there are significant differences in the roll motion of the FPSO under the three wave spectra at incident angles of 30°, 60° and 90°. In the fourth level sea state, the FPSO’s roll motion with the significant values and ranges occurs under the JONSWAP spectrum with an incident angle of 30°, while under the Ochi-Hubble spectrum, the FPSO’s roll motion with the significant values and ranges occurs with incident angles of 60° and 90°. In fifth level sea state, the FPSO’s roll motion with the significant values and ranges occurs under the JONSWAP spectrum with incident angles of 30° and 60°, while under the Ochi-Hubble spectrum, the FPSO’s roll motion with the significant values and ranges occurs with an incident angle of 90°. The significant values and ranges of pitch motions of the FPSO under the three wave spectra are basically similar.
Author Contributions
Funding
Informed Consent Statement
Conflicts of Interest
References
- Russo, S.; Contestabile, P.; Bardazzi, A.; Leone, E.; Iglesias, G.; Tomasicchio, G.R.; Vicinanza, D. Dynamic Loads and Response of a Spar Buoy Wind Turbine with Pitch-Controlled Rotating Blades: An Experimental Study. Energies 2021, 14, 3598. [Google Scholar] [CrossRef]
- Pierson, W.J.; Marks, W. The power spectrum analysis of ocean Wave records. Eos Trans. Am. Geophys. Union 1952, 33, 834–844. [Google Scholar] [CrossRef]
- Longuet-Higgins, M.S. The statistical analysis of a random, moving surface. Philos. Trans. R. Soc. Lond Ser. A Math. Phys. Sci. 1957, 249, 321–387. [Google Scholar] [CrossRef]
- Jiao, J.L.; Chen, C.H.; Ren, H.L. A comprehensive study on ship motion and load responses in short-crested irregular waves. Int. J. Nav. Archit. Ocean. Eng. 2019, 11, 364–379. [Google Scholar] [CrossRef]
- Neumann, G.M. On ocean wave spectra and a new method of forecasting wind generated sea. Tech. Memo. Beach Eros. Board 1953, 42. [Google Scholar]
- Pierson, W.J.; Moskowitz, L. A Proposed Spectral form for fully developed wind Seas. J. Geophys. Res. 1964, 69, 5181–5203. [Google Scholar] [CrossRef]
- Hasselmann, K. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergaenzungsheft Dtsch. Hydrogr. Z. Reihe A 1973, 12. [Google Scholar]
- Report of Seakeeping Committee. In Proceedings of the 15th International Towing Tank Conference, The Hague, The Netherlands, 3–10 September 1978.
- Hua, J.B. Fast simulation of nonlinear GM-variation of a ship in irregular waves. J. Ship Mech. 2000, 3, 25–34. [Google Scholar]
- Carrica, P.M.; Wilson, R.V.; Noack, R. A dynamic overset, single-phase Level-set approach for viscous ship flows and large amplitude motions and maneuvering. In Proceedings of the 26th Symposium on Naval Hydrodynamics, Rome, Italy, 17–22 September 2006; pp. 17–22. [Google Scholar]
- Carrica, P.M.; Paik, K.J.; Hosseini, H.S. URANS analysis of a broaching event in irregular quartering seas. J. Mar. Sci. Technol. 2008, 13, 395–407. [Google Scholar] [CrossRef]
- Renaud, M.; Rezende, F.; Waals, O.; Chen, X.B.; Dijk, R.V. Second-order wave loads on a LNG Carrier in multi-directional waves. In Proceedings of the ASME 2008 27th International Conference on Offshore Mechanics and Arctic Engineering, Estoril, Portugal, 15–20 June 2008; pp. 363–370. [Google Scholar] [CrossRef]
- Zheng, W.T.; Kuang, X.F.; Miao, Q.M.; Zhou, D.C. Model test study of ship motions in long-crested and short-crested irregular waves. In Proceedings of the 9th National Congress on Hydrodynamics and the 22nd National Conference on Hydrodynamics, Chengdu, China, 17–20 August 2009; pp. 359–364. (In Chinese). [Google Scholar]
- Chen, J.P.; Wei, J.F.; Zhu, D.X. Numerical simulations of ship motions in long-crested and short-crested irregular waves by a 3D time domain method. Chin. J. Hydrodyn. 2011, 26, 589–596. (In Chinese) [Google Scholar]
- Cao, H.J.; Wan, D.C. Development of multidirectional nonlinear numerical wave tank by Naoe-FOAM-SJTU solver. Int. J. Ocean Syst. Eng. 2014, 4, 49–56. [Google Scholar] [CrossRef]
- Shen, Z.R.; Ye, H.X.; Wan, D.C. URANS simulations of ship motion responses in long-crest irregular waves. J. Hydrodyn. 2014, 26, 436–446. [Google Scholar] [CrossRef]
- Ji, X.R.; Liu, S.X.; Harry, B.B.; Li, J.X. Multi-directional random wave interaction with an array of cylinders. Ocean Eng. 2015, 110 Pt A, 62–77. [Google Scholar] [CrossRef]
- Ducrozet, G.; Bonnefoy, F.; Touzé, D.L.; Ferrant, P. HOS-ocean: Open-source solver for nonlinear waves in open ocean based on High-Order Spectral method. Comput. Phys. Commun. 2016, 203, 245–254. [Google Scholar] [CrossRef]
- Wang, W.; Bihs, H.; Kamath, A. Multi-directional irregular wave modelling with CFD. In Proceedings of the Fourth International Conference in Ocean Engineering (ICOE2018), Chennai, India, 18–21 February 2018; Volume 22. [Google Scholar]
- Jiao, J.L.; Yu, H.C.; Chen, C.H.; Ren, H.L. Time-domain numerical and segmented model experimental study on ship hydroelastic responses and whipping loads in harsh irregular seaways. Ocean Eng. 2019, 185, 59–81. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.N.; Shang, Y.C. A practical direct URANS CFD approach for the speed loss and propulsion performance evaluation in short-crested irregular head waves. Ocean Eng. 2021, 219, 108287. [Google Scholar] [CrossRef]
- Zhang, H.C.; Liu, S.X.; Li, J.X. Multi-directional irregular wave forces acting on a tandem pile group. Appl. Ocean Res. 2023, 135, 103542. [Google Scholar] [CrossRef]
- Goda, Y. A comparative review on the functional forms of directional wave spectrum. Coast. Eng. J. 1999, 41, 1–20. [Google Scholar] [CrossRef]
- Ochi, M.K.; Hubble, E.N. Six-parameter wave spectra. In Proceedings of the 15th International Conference on Coastal Engineering, Honolulu, HI, USA, 11–17 July 1976; pp. 301–328. [Google Scholar] [CrossRef]
- Zhang, X.; Wu, L.; Zhang, L.; Long, L. Ocean wave simulation based on JONSWAP spectrum. Infrared Laser Eng. 2018, 47, 162–167. [Google Scholar]
- Goda, Y. Numerical experiments on wave statistics with spectral simulation. Rep. Port Harb. Res. Inst. 1970, 9, 3–57. [Google Scholar]
- Tessendorf, J. Simulating ocean water. In Proceedings of the ACM SIGRAPH, New York, NY, USA, 8–13 August 1999; pp. 348–367. [Google Scholar]
- Wang, H.T. Temporal and spatial simulation of random ocean wave. In Proceedings of the Fourth International Offshore Mechanics and Arctic Engineering Symposium, Dallas, TX, USA, 17–21 February 1985; pp. 72–80. [Google Scholar]







| Units | Value | |
|---|---|---|
| Length overall | m | 112 |
| Length between perpendiculars | m | 109 |
| Breath | m | 28 |
| Draft | m | 9 |
| Displacement | t | 24,610 |
| Longitudinal center of gravity (to the stern of the ship) | m | 51 |
| Vertical center of gravity (to the hull baseline) | m | 7.2 |
| Roll radius of inertia | m | 8.037 |
| Pitch radius of inertia | m | 28.149 |
| Yaw radius of inertia | m | 29.027 |
| Ocean Wave Spectra | The Significant Wave Height | The Spectral Peak Period | The Peak Elevation Parameter |
|---|---|---|---|
| ITTC two-parameters spectra | 3.6 m/2.0 m | 10.59 s/9.84 s | / |
| JONSWAP spectra | 3.3 | ||
| Ochi-Hubble spectra | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Yang, X.-Q.; Bu, S.-X.; Zheng, W.-T.; Ma, Y.-X.; Jiao, Z.-L. Analysis of FPSO Motion Response under Different Wave Spectra. J. Mar. Sci. Eng. 2023, 11, 1467. https://doi.org/10.3390/jmse11071467
Sun L, Yang X-Q, Bu S-X, Zheng W-T, Ma Y-X, Jiao Z-L. Analysis of FPSO Motion Response under Different Wave Spectra. Journal of Marine Science and Engineering. 2023; 11(7):1467. https://doi.org/10.3390/jmse11071467
Chicago/Turabian StyleSun, Lei, Xing-Quan Yang, Shu-Xia Bu, Wen-Tao Zheng, Yu-Xiang Ma, and Zi-Lu Jiao. 2023. "Analysis of FPSO Motion Response under Different Wave Spectra" Journal of Marine Science and Engineering 11, no. 7: 1467. https://doi.org/10.3390/jmse11071467
APA StyleSun, L., Yang, X.-Q., Bu, S.-X., Zheng, W.-T., Ma, Y.-X., & Jiao, Z.-L. (2023). Analysis of FPSO Motion Response under Different Wave Spectra. Journal of Marine Science and Engineering, 11(7), 1467. https://doi.org/10.3390/jmse11071467





