Dual-Drive Window Control Method for Continuous Grain Drying Based on Water Potential Accumulation
Abstract
1. Introduction
2. Materials and Methods
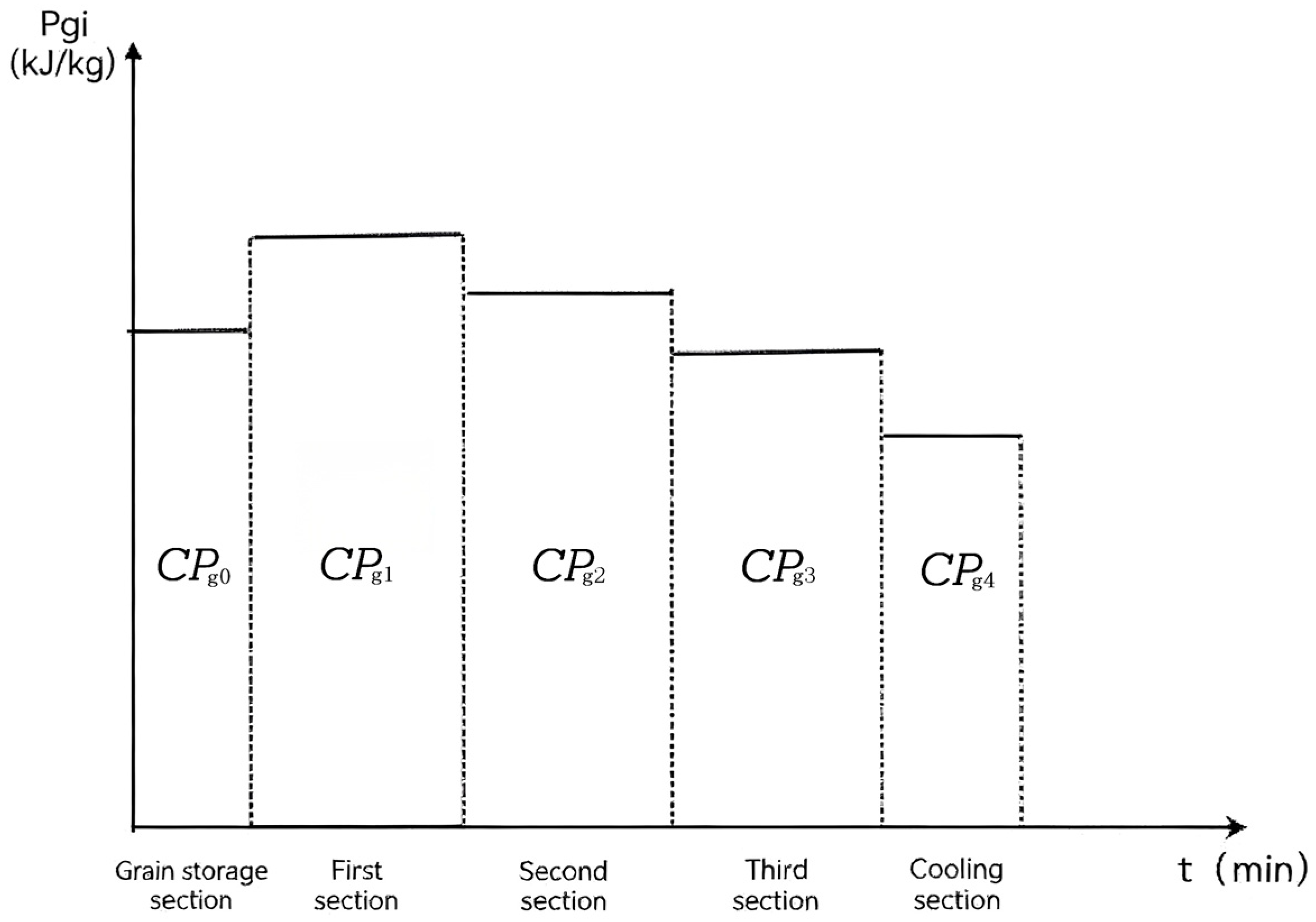
2.1. Water Potential and Water Potential Accumulation for Continuous Grain Drying
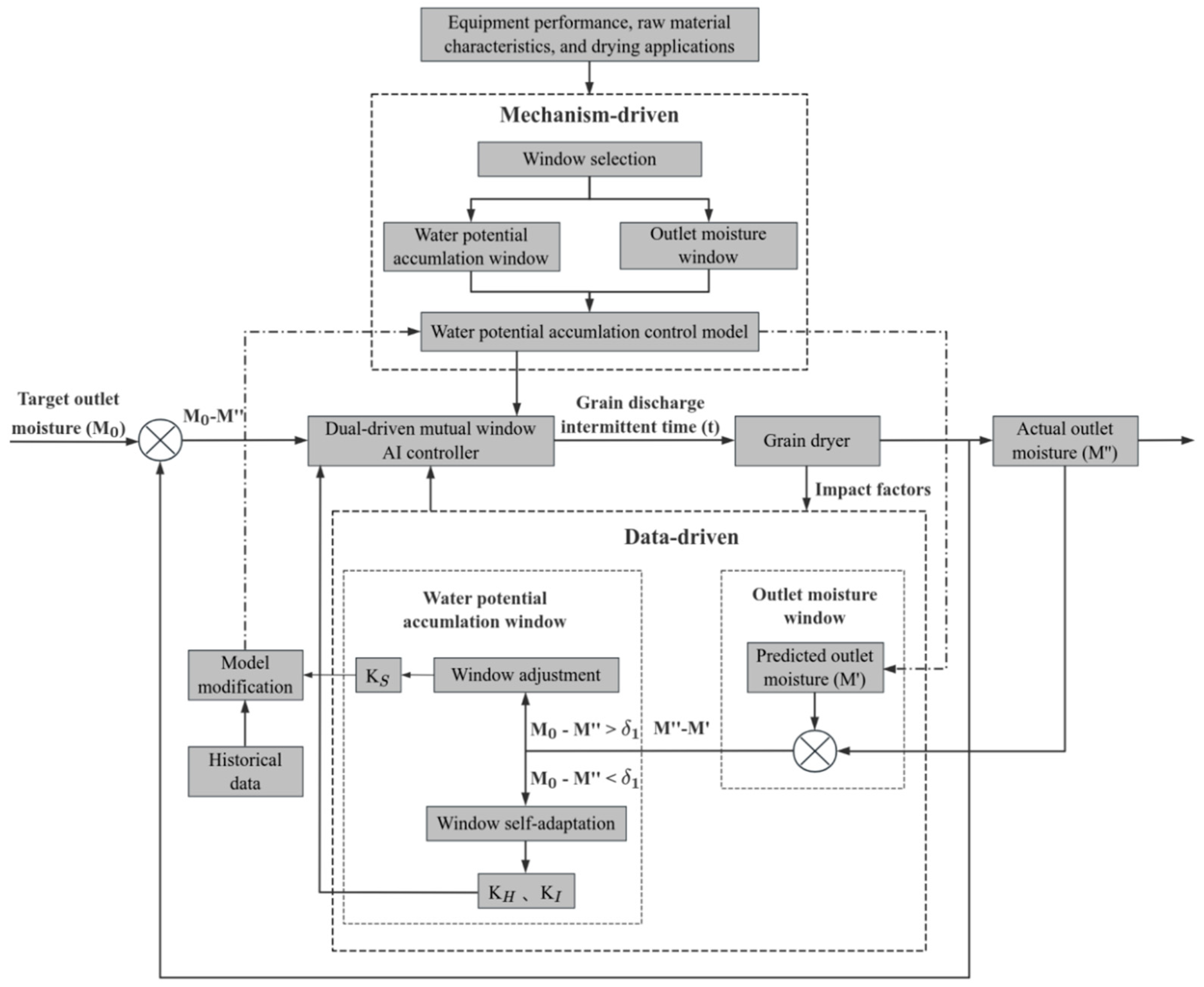
2.2. The Dual-Driven Window AI Control Method for Continuous Grain Drying
2.2.1. Window Selection Based on Mechanism-Driven Control
2.2.2. Window Adjustment and Window Self-Adaptation Based on Data-Driven Control
Window Adjustment
Window Self-Adaptation
2.2.3. Mechanism and Data Dual-Driven Mutual Window Control Method Diagram
2.3. Small Continuous Drying Test System
2.4. Absolute Water Potential Accumulation Model for Small Continuous Dryer
2.5. Experimental Method
2.6. Experimental Indicators
2.6.1. Outlet Moisture Content
2.6.2. Quality Indicators
3. Results
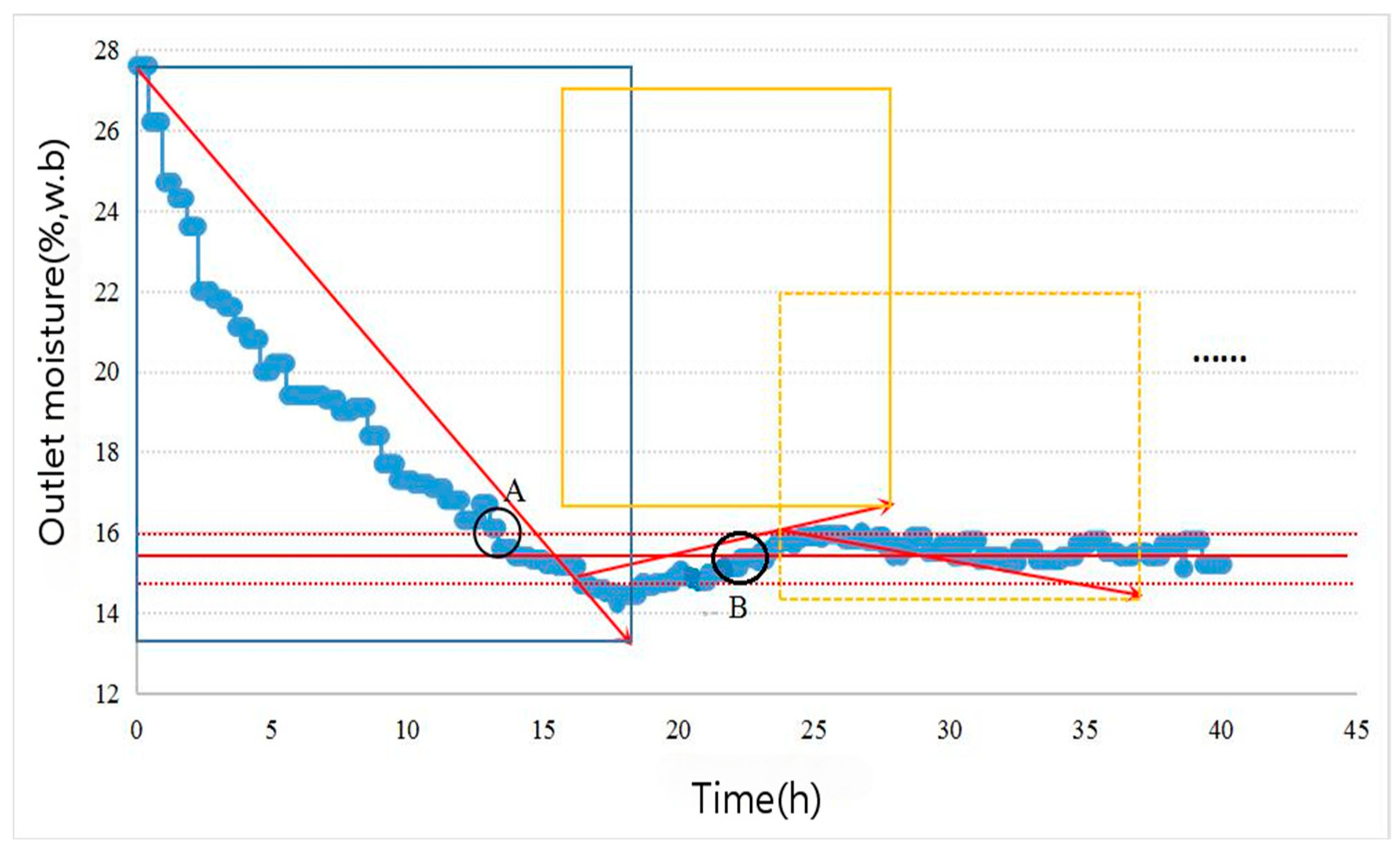
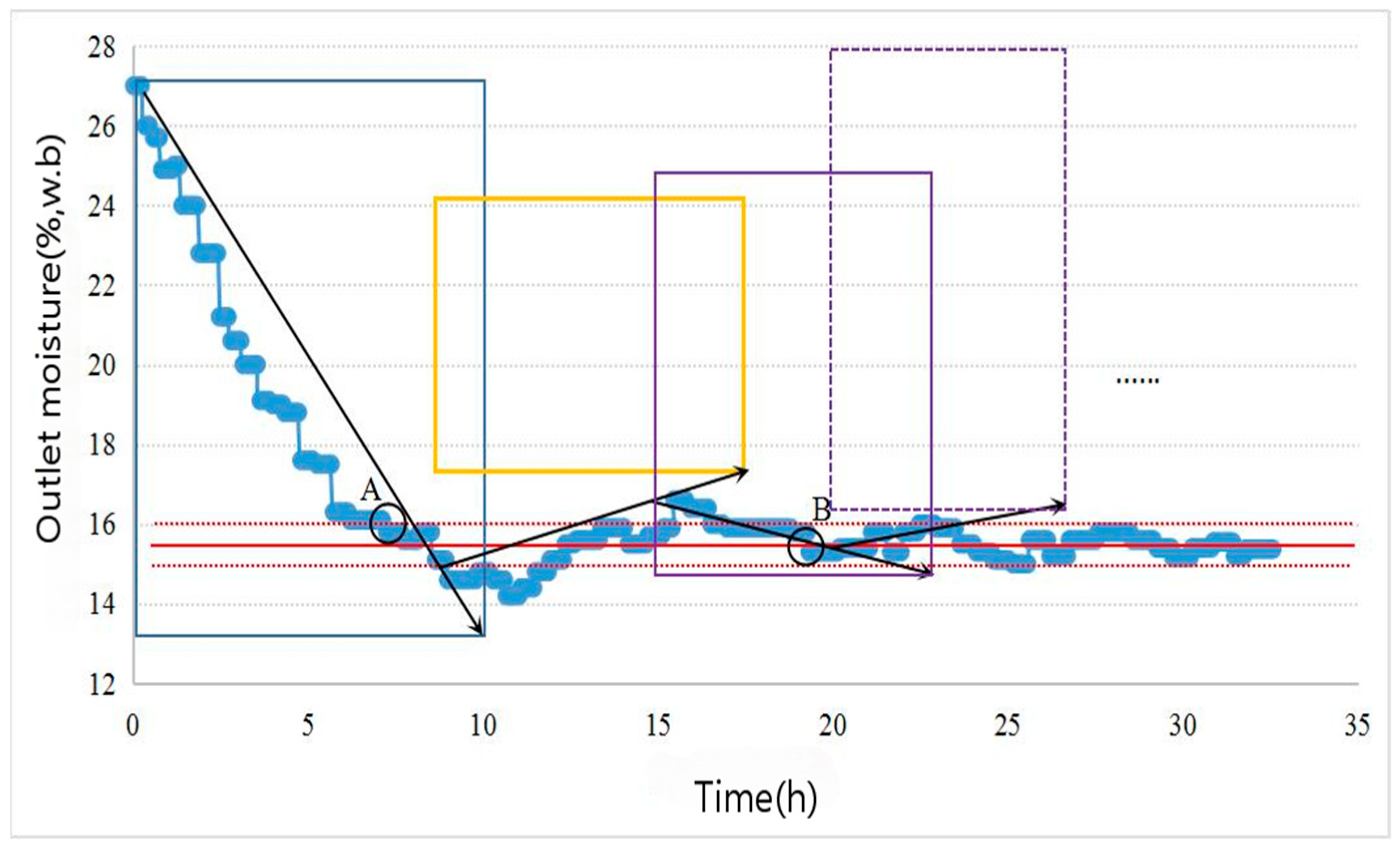
3.1. Analysis and Comparison of Outlet Moisture Control Accuracy
3.2. Analysis and Comparison of Quality Indicators
3.3. Microscopic Structure Observation and Comparison
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bakker-Arkema, F.W.; Bickert, W.G.; Patterson, R.J. Simultaneous heat and mass transfer during the cooling of a deep bed of biological products under varying inlet conditions. J. Agric. Eng. Res. 1967, 12, 297–307. [Google Scholar] [CrossRef]
- Spencer, H.B. A mathematical simulation of grain drying. J. Agric. Eng. Res. 1969, 14, 226–235. [Google Scholar] [CrossRef]
- Sun, Y.; Pantelides, C.C.; Chalabi, Z.S. Mathematical modelling and simulation of near-ambient grain drying. Comput. Electron. Agric. 1995, 13, 243–271. [Google Scholar] [CrossRef]
- Srivastava, V.K.; John, J. Deep bed grain drying modelling. Energy Convers. Manag. 2002, 43, 1689–1708. [Google Scholar] [CrossRef]
- Setty, Y.P.; Murthy, J. Development of a model for drying of solids in a continuous fluidized bed dryer. Indian J. Chem. Technol. 2003, 10, 477–482. [Google Scholar]
- Liu, Q.; Bakker-Arkema, F.W. PH-Postharvest Technology: Automatic Control of Cross-flow Grain Dryers, Part 1: Development of a Process Model. J. Agric. Eng. Res. 2001, 80, 81–86. [Google Scholar] [CrossRef]
- Liu, Q.; Bakker-Arkema, F.W. PH-Postharvest Technology: Automatic Control of Cross-flow Grain Dryers, Part 2: Design of a Model-Predictive Controller. J. Agric. Eng. Res. 2001, 80, 173–181. [Google Scholar] [CrossRef]
- Liu, Q.; Bakker-Arkema, F.W. PH-Postharvest Technology: Automatic Control of Cross-flow Grain Dryers, Part 3: Field Testing of a Model-Predictive Controller. J. Agric. Eng. Res. 2001, 80, 245–250. [Google Scholar] [CrossRef]
- Liu, X.; Chen, X.; Wu, W.; Zhang, Y. Process control based on principal component analysis for maize drying. Food Control 2006, 17, 894–899. [Google Scholar] [CrossRef]
- Prakash, B.; Siebenmorgen, T.J. Single-parameter thin-layer drying equations for long-grain rice. Trans. ASABE 2018, 61, 733–742. [Google Scholar] [CrossRef]
- Forbes, J.F.; Jacobson, B.A. Model based control strategies for commercial grain drying systems. Can. J. Chem. Eng. 1984, 62, 773–779. [Google Scholar] [CrossRef]
- Nybrant, T.G. Modelling and adaptive-control of continuous grain driers. J. Agric. Eng. Res. 1989, 40, 165–173. [Google Scholar] [CrossRef]
- Whitfield, R.D. An unsteady-state simulation to study the control of concurrent and counter-flow dryers. J. Agric. Eng. Res. 2006, 32, 171–178. [Google Scholar]
- Atthajariyaku, S.; Leephakpreeda, T. Fluidized bed paddy drying in optimal conditions via adaptive fuzzy logic control. J. Food Eng. 2006, 75, 104–114. [Google Scholar] [CrossRef]
- Alvinika, Y.; Setyohadi, D.B.; Sulistyoningsih, M. IoT-Based Monitoring and Design of Automatic Fish Drying Equipment Using Fuzzy Logic. IOP Conf. Ser. Earth Environ. Sci. 2021, 704, 012042. [Google Scholar] [CrossRef]
- Soleiman, H.; Alex, M. An adaptive fuzzy logic controller for intelligent drying. Dry. Technol. 2023, 41, 1110–1132. [Google Scholar]
- Kang, C.; Zhang, G.; Zhang, Q.; Gang, M.; Guo, H.; Tong, Y.; Ran, L.; Li, X.; Cheng, Z. Control of multi-energy drying system: Optimal weighted combination prediction of moisture content and fuzzy compensation of wind speed. Therm. Sci. Eng. Prog. 2024, 50, 102503. [Google Scholar] [CrossRef]
- Dai, A.; Zhou, X.; Liu, X.; Liu, J.; Zhang, C. Model of Drying Process for Combined Side-heat Infrared Radiation and Convection Grain Dryer Based on BP Neural Network. Trans. Chin. Soc. Agric. Mach. 2017, 48, 351–360. [Google Scholar]
- Dai, A.; Zhou, X.; Dang, H.; Sun, M.; Wu, Z. Intelligent Modeling Method for a Combined Radiation-Convection Grain Dryer: A Support Vector Regression Algorithm Based on an Improved Particle Swarm Optimization Algorithm. IEEE Access 2018, 6, 14285–14297. [Google Scholar] [CrossRef]
- Dai, A.; Zhou, X.; Liu, X.; Liu, J.; Zhang, C. Intelligent control of a grain drying system using a GA-SVM-IMPC controller. Dry. Technol. 2018, 36, 1413–1435. [Google Scholar] [CrossRef]
- Simonic, M.; Fícko, M.; Klancnik, S. Predicting Corn Moisture Content in Continuous Drying Systems Using LSTM Neural Networks. Foods 2025, 14, 1051. [Google Scholar] [CrossRef]
- Zuo, Y.; Jibril, A.N.; Yan, J.; Xia, Y.; Liu, R.; Chen, K. Optimization of Online Moisture Prediction Model for Paddy in Low-Temperature Circulating Heat Pump Drying System with Artificial Neural Network. Sensors 2025, 25, 2308. [Google Scholar] [CrossRef]
- Jin, Y.; Xie, H.; Yin, J.; Zhang, Z. Research On Intelligent Control Method of Grain Drying Based On LSTM-MPC. Sci. Technol. Cereals Oils Foods 2023, 31, 25–34. [Google Scholar]
- Wu, Y. Study on Temperature-Accumulation Quality Properties of Grain with Measurement and Control Method in Drying Process. Ph.D. Thesis, Jilin University, Changchun, China, 2017. [Google Scholar]
- Liu, Z.; Wu, W.; Han, F.; Xu, Y.; Jin, Y.; Wu, Z. A Control Method for Continuous Grain Drying Based on Equivalent Accumulated Temperature Window. Chinese patent CN110347197A, 18 October 2019. [Google Scholar]
- Wu, W.; Liu, Z.; Han, F.; Zhang, Y.; Chen, J. Dual-Driven Mutual Window Control Method for Continuous Grain Drying Based on Equivalent Water Potential Accumulation. Chinese patent CN113778153A, 10 December 2021. [Google Scholar]
- Liu, Z.; Xu, Y.; Han, F.; Zhang, Y.; Wang, G.; Wu, Z.; Wu, W. Control Method for Continuous Grain Drying Based on Equivalent Accumulated Temperature Mechanism and Artificial Intelligence. Foods 2022, 11, 834. [Google Scholar] [CrossRef] [PubMed]
- Mujumdar, A.S. Editorial: The Making of the Handbook of Industrial Drying. Dry. Technol. 2014, 32, 627–628. [Google Scholar] [CrossRef]
- Wu, W.; Chen, J.; Cheng, R.; Jin, Y.; Wei, X.; Xiao, B.; Xu, Y. Coupling relationship between content of unsaturated fatty acid and drying system of corn grain after variable temperature and humidity drying. Trans. Chin. Soc. Agric. Eng. 2019, 35, 328–333. [Google Scholar]
- Che, G.; Wang, H.; Wan, L.; Wang, X.; Tang, H.; Zhang, C. Design and Test of Varying Temperature Mixing Device on Paddy Rice Drying. Trans. Chin. Soc. Agric. Mach. 2022, 53, 386–392. [Google Scholar]
- Wu, W. Study on Quality Control Principles and Methods of Drying Maize. Ph.D. Thesis, Jilin University, Changchun, China, 2002. [Google Scholar]
- Wu, W.; Chen, S.; Han, F.; Zhang, Y.; Zhang, Z.; Wu, Z. The Moisture Migration of Heat and Humidity Grain Bulk and Granary Aeration Management. J. Chin. Cereals Oils Assoc. 2017, 32, 100–107. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Sugiura, N. Further analysts of the data by akaike’s information criterion and the finite corrections. Commun. Stat.-Theory Methods 1978, 7, 13–26. [Google Scholar] [CrossRef]
- Weakliem, D.L. A Critique of the Bayesian Information Criterion for Model Selection. Sociol. Methods Res. 1999, 27, 359–397. [Google Scholar] [CrossRef]
- Wang, S.; Liu, G.; Qi, Z. BIC Scoring Bayesian Network Model and Its Application. Comput. Eng. 2008, 34, 229–230. [Google Scholar]
- Jin, Y.; Wong, K.; Wu, Z.; Qi, D.; Wang, R.; Han, F.; Wu, W. Relationship between accumulated temperature and quality of paddy. Int. J. Food Prop. 2019, 22, 19–33. [Google Scholar] [CrossRef]
- Liu, Z.; Wu, W.; Shen, W.; Chen, Z.; Han, F.; Xu, Y.; Wu, Z. A Differential Capacitive Moisture Detection Structure and Method Suitable for Bulk Material Flow. Chinese patent CN110779964A, 11 February 2020. [Google Scholar]
- GB 1350; Paddy. China Standards Press: Beijing, China, 2009.
- Ren, Q.; Jiang, P.; Zhang, L.; Li, X. Biochemical method for evaluation of grain damage with fast green FCF dye. Sci. Technol. Food Ind. 2016, 3, 49–53. [Google Scholar]
- Li, S.; Yuan, M.; Ren, Y.; Yu, S. Rapid Method of Testing Germination Percentage in Peanut. J. Peanut Sci. 2004, 33, 30–32. [Google Scholar]
- Wang, Y. Discussion on influence factors on determination of corn fatty acid value. Cereal Food Ind. 2009, 16, 52–53. [Google Scholar]
- GB/T 5510; Inspection of grain and oils—Determination of fat acidity value of grain and oilseeds. China Standards Press: Beijing, China, 2011.
- Zheng, X.; Liu, H.; Shen, L.; Wang, J.; Wang, L.; Zhu, Y. Hot-air Drying Technology of Changing Temperature for Paddy Rice Based on Glass Transition Theory. Trans. Chin. Soc. Agric. Mach. 2020, 51, 331–340. [Google Scholar]
- Sarker, N.N.; Kunze, O.R.; Strouboulis, T. Strouboulis, Transient moisture gradients in rough rice mapped with finite element model and related to fissures after heated air drying. Trans. Am. Soc. Agric. Eng. 1996, 39, 625–631. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, W.; Zhao, T.; Lu, M.; Wu, H.; Cao, D. Drying temperature regulates vigor of high moisture rice seeds via involvement in phytohormone, ROS, and relevant gene expression. J. Sci. Food Agric. 2021, 101, 2143–2155. [Google Scholar] [CrossRef]
- Craufurd, R.Q. Sorption and desorption in raw and parboiled paddy. J. Sci. Food Agric. 1963, 14, 744–750. [Google Scholar] [CrossRef]
- Feng, S.; Tian, Y.; Cao, X.; Fang, K. Microstructure Analysis of Brown Rice Based on Mechanical Force Action. J. Henan Univ. Technol. 2019, 40, 70–74. [Google Scholar]
- Huang, B.; Chu, X.; Zhang, L.; Ge, Y.; Xue, X. Study on the Mechanism of Stress Cracks in Rice Drying Process. Agric. Sci. Technol. Equip. 2014, 6, 24–25. [Google Scholar]
- Zhou, X.; Cheng, J.; Zhang, Y.; Liu, N.; Li, Y. Research on stress crack changes of maize by hot-air and vacuum drying. J. Henan Univ. Technol. (Nat. Sci. Ed.) 2011, 32, 1–4+17. [Google Scholar]
- Lan, Y.; Kunze, O.R. Relative humidity effects on the development of fissures in rice. Cereal Chem. 1996, 73, 222–224. [Google Scholar]
- Shao, X.; Xu, W.; Wang, X.; Yang, X.; Shen, F.; Liu, Q. Fissure Development of Three Japonica Rice Grain during Water Desorption. Sci. Agric. Sin. 2022, 55, 390–402. [Google Scholar]
- Wei, S.; Chen, P.; Xie, W.; Wang, F.; Yang, D. Prediction of stress cracks in corn kernels drying based on three-dimensional heat and mass transfer. Trans. Chin. Soc. Agric. Eng. 2019, 35, 296–304. [Google Scholar]
- Li, D.; Mao, Z. Microscopic structure of rough rice after sun drying. Trans. Chin. Soc. Agric. Eng. 2003, 19, 156–159. [Google Scholar]
- Perez, J.H.; Tanaka, F.; Uchino, T. Modeling of mass transfer and initiation of hygroscopically induced cracks in rice grains in a thermally controlled soaking condition: With dependency of diffusion coefficient to moisture content and temperature—A 3D finite element approach. J. Food Eng. 2012, 111, 519–627. [Google Scholar] [CrossRef]







| Levels | Factors | |
|---|---|---|
| Temperature Variation Gradient of Hot Air (β1/℃) | Relative Humidity Variation Gradient (β2/%) | |
| −2 | −10 (40–30–20) | −30 (70–40–10) |
| −1 | −5 (35–30–25) | −15 (55–40–25) |
| 0 | 0 (30–30–30) | 0 (40–40–40) |
| 1 | 5 (25–30–45) | 15 (25–40–55) |
| 2 | 10 (20–30–40) | 30 (10–40–70) |
| Experiment Parameters | Experiment 1 | Experiment 2 | Experiment 3 |
|---|---|---|---|
| Initial moisture content (%, w.b.) of grain (%, w.b) | 26~27 | 26~27 | 26~27 |
| Tempering ratio | 3:1 | 3:1 | 3:1 |
| Hot air temperature 1 (°C) | 40 | 35 | 40 |
| Hot air temperature 2 (°C) | 40 | 40 | 40 |
| Hot air temperature 3 (°C) | 40 | 45 | 40 |
| Hot air relative humidity (%) | 35~40 | 35~40 | 35~40 |
| Environmental temperature (°C) | 13.9~16.3 | 16.2~19.6 | 15.0~18.9 |
| Environmental relative humidity (%) | 31.4~44.6 | 31.1~43.2 | 26.3~35.6 |
| Hot air velocity (m/s) | 0.8~1.3 | 0.8~1.3 | 0.8~1.3 |
| Target outlet moisture content (%, w.b.) | 15.5 | 15.5 | 15.5 |
| Outlet moisture content threshold (%, w.b.) | 0.5 | 0.5 | 0.5 |
| Experiment | Grain State | Damage Percentage (%) | Germination Percentage (%) | Fatty Acid Value NaOH (mg/100 g) |
|---|---|---|---|---|
| 1 | Raw grain | 1.5 | 83.0 | 8.2 |
| After drying | 5.3 | 73.2 | 14.9 | |
| Change ratio | 2.53 | −0.12 | 0.82 | |
| 2 | Raw grain | 1.5 | 83.0 | 8.2 |
| After drying | 4.2 | 79.0 | 11.94 | |
| Change ratio | 1.80 | −0.05 | 0.46 | |
| 3 | Raw grain | 1.5 | 83.0 | 8.2 |
| After drying | 5.6 | 72.0 | 16.4 | |
| Change ratio | 2.73 | −0.13 | 1.00 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Jin, X.; Chen, J.; Wu, W.; Han, F.; Xu, Y. Dual-Drive Window Control Method for Continuous Grain Drying Based on Water Potential Accumulation. Agriculture 2025, 15, 2355. https://doi.org/10.3390/agriculture15222355
Liu Z, Jin X, Chen J, Wu W, Han F, Xu Y. Dual-Drive Window Control Method for Continuous Grain Drying Based on Water Potential Accumulation. Agriculture. 2025; 15(22):2355. https://doi.org/10.3390/agriculture15222355
Chicago/Turabian StyleLiu, Zhe, Xing Jin, Junyi Chen, Wenfu Wu, Feng Han, and Yan Xu. 2025. "Dual-Drive Window Control Method for Continuous Grain Drying Based on Water Potential Accumulation" Agriculture 15, no. 22: 2355. https://doi.org/10.3390/agriculture15222355
APA StyleLiu, Z., Jin, X., Chen, J., Wu, W., Han, F., & Xu, Y. (2025). Dual-Drive Window Control Method for Continuous Grain Drying Based on Water Potential Accumulation. Agriculture, 15(22), 2355. https://doi.org/10.3390/agriculture15222355







