Decentralized Robust Direct MRAC via e-Modification for the Pose of a Quadrotor UAV

Abstract

In this work, a decentralized robust direct model reference adaptive controller (MRAC) via e-modification is suggested for the pose control of a quadrotor to prevent parameter drift. The governing equations of motion referred to the rotational system of the quadrotor are parameterized involving matched uncertainties through the control input channel in a decentralized way from the angles of motion, where bounded perturbations are also considered. An error-dependent damping term in the update law is added to enforce robustness. Uniform ultimate boundedness of the tracking error signal is ensured. The translational dynamics are governed through a linear proportional–integral–derivative (PID) control. The performance of the decentralized robust MRAC scheme proposed here is assessed via simulation and compared with that from decentralized robust MRACs using smooth dead-zone modification and $\sigma$-modification.

1. Introduction

From experience, it is well-known that when the system output is influenced by uncontrolled inputs, and not only by the control input, such inputs cause disturbances affecting the system in unpredictable ways although these may be present for a limited time.

The design of stable adaptive controllers is the main issue when trying to achieve asymptotic model following. Unbounded solutions could emerge with unmodeled dynamics and time-varying parameters as perturbations [1]. To this last eventuality, certain performance conditions must be satisfied through the control design task having as a main goal the boundedness for all the signals from the closed-loop system [2,3,4,5].

In this work, in order to assure stability in presence of uncontrolled inputs and modeling errors in the decentralized adaptive control for the pose of a quadrotor unmanned aerial vehicle (UAV), modifications to the parametric estimation algorithm (update law) are examined, which leads to robust learning algorithms. A robust learning algorithm is characterized by preserving, within some specifications of design, stability properties under external perturbations and model uncertainties [2,3,6]. It is well known that conventional adaptive (update) laws show parameter drift in the presence of external perturbations, unmodeled dynamics, measurement noise and time variations. The parameter drift is an anomaly in which the parametric estimates go far from their ideal values, possibly to infinity. Parameter drift may be an eventuality when the online parametric estimator does not have any value for the parameters from a matching condition. Also, in the presence of a small amount of measurement noise and high-frequency unmodeled dynamics, if the input signal does not satisfy the so-called persistency of excitation property, in other words, if it is not sufficiently rich, the parametric estimates do not converge to their ideal values, which could mean that these may also drift with output of the system suddenly diverging abruptly [7].

Two alternatives can be addressed in order to evade parameter drift. The first one, the well-known dead-zone modification [4], is suggested when the training error is too small, which consists of not performing parametric adaptation. The last one, through the use of the so-called e-modification [8,9], $\sigma$-modification [5], also known as the leakage factor [2], and projection algorithms [2,10,11,12] shifts the online parametric estimator such that the parametric estimates are constrained from the drift to infinity.

The e-modification has been developed [8] in order to overcome a limitation with the $\sigma$-modification in that it can achieve asymptotic tracking under certain conditions while improving robustness. The aim of the e-modification is to reduce the damping term proportionally to the tracking error norm. The damping term is reduced to zero as the tracking error tends to zero, giving back the asymptotic tracking property of the ideal case with model reference adaptive control (MRAC). Nevertheless, the e-modification only achieves bounded tracking in accordance with the stability analysis, so the ideal property of the MRAC is not preserved. Moreover, asymptotic tracking is not attained in general with increased robustness.

In [13], HIL simulation and flight test results were shown about the performance from both conventional MRAC and MRAC with e-modification in the control of a SIG Rascal 110 UAV. It should be noticed that for flight tests, the commands from the adaptive controller were limited by the autopilot to avoid undesirable attitudes that might lead to the loss of the UAV. Flight test results showed a similar performance as that from HIL results, i.e., degradation of the performance of the closed-loop system was exhibited when adding the damping term in the update law, although parameter drift was avoided. Authors claim that similar results were observed for the MRAC with $\sigma$-modification and a projection operator, although these results were not shown in their work. Also, authors claim that the performance of the MRAC with e-modification could be improved via further tuning of the parameters of the controller. In their study, the analysis stems from the representation of the frequency response for the nominal plant and modeling uncertainties. In [14], under partial feedback linearization and function approximation by Fourier series, an adaptive multiple-surface sliding controller (AMSSC) was proposed. A $\sigma$-modification term was used in the parametric update law. The performance of the AMSSC was validated via numerical simulation for a pendubot, cart-pole system, overhead crane, TORA system, and rotary inverted pendulum; all these latter underactuated mechanical systems are subject to uncertainties and external disturbances. However, it must be highlighted that for all cases, the $\sigma$ constant was set to zero, turning off the $\sigma$-modification in the update law. In [15], an MRAC with integral action is used for the control of an aircraft wing-rock model, whose performance shows slowly varying tracking error at the beginning of the transient response. With the adding of a $\sigma$-modification damping term in the update law, simulation results show that the tracking error gets worse for $\sigma \ge 0.1$. Authors claim that a similar behavior is obtained when using an e-modification, although the corresponding results were not included. In [16], a Linear Quadratic Regulator (LQR) combined with a so-called enhanced MRAC (EMRAC) scheme, namely, a LQ-EMRAC, with $\sigma$-modification was proposed for attitude control of a quadrotor and tested via real-time hardware-in-the-loop (HIL) simulated experiments. A switching control term, as well as an integral feedback action, were included in the LQ-EMRAC to cope with high-frequency and slow-varying disturbances, respectively. The $\sigma$-modification was employed to prevent the drift of the integral of the tracking error. The performance of the LQ-EMRAC was evaluated through the tracking of a helix trajectory, and compared with that from a PID controller and an LQ-MRAC. In [17], a robust hybrid MRAC for the control of a quadrotor was reported. Under the output-feedback linearization framework, the six degrees of freedom (DOF) of the quadrotor were decoupled. The system was augmented due to the use of integral feedback interconnections and also the reference model. Robust learning algorithms, namely e-modification, $\sigma$-modification, and projection operator, were extended to nonlinear, time-varying, uncertain plants. The performance of the hybrid MRAC was validated via numerical simulation, where the trajectory tracking tasks were carried out via an algorithm called the multi-output feedback linearization algorithm, which commutes among the linearized outputs. The simulation results shown were only those using $\sigma$-modification.

In this work, decentralized direct MRACs were used for the pose of a quadrotor UAV with e-modification and smooth dead-zone modification in the update law, in order to evade parameter drift proposed here. The rotational dynamics of the quadrotor UAV are parameterized in the form of a decentralized model with matched uncertainties via control channels. This parametrization is preferred due to the matched uncertainties supplying an extra realism to the ideal system. Also, MRACs are designed from each subsystem that constitutes the whole rotational system. Simulation results validate the proposals.

The manuscript is organized as follows. In Section 2, the nonlinear dynamic model of the quadrotor is described. The parameterized model for the quadrotor and the design of the decentralized robust MRAC via e-modification are developed in Section 3. In Section 4, simulation results for the validation of the proposal are shown. The findings and their implications are discussed in Section 5. The conclusions are drawn in Section 6.

2. Quadrotor’s Dynamics

The rotational dynamics of a rigid body are more complicated than the translational dynamics since the mass of a rigid body is a scalar, but the moment of inertia is given in terms of a matrix. However, the main complication is in the description of the pose of the body in space. The dynamics of a quadrotor is described through the equations of motion derived from the rigid body theory with six degrees of freedom [18], which can be decoupled into translational and rotational dynamics [19].

The dynamic equations

$$\begin{array}{cc}\hfill F_{\mathrm{ext}}& =m_q{\dot{V}}_b+\omega \times m_q{V}_b,\hfill \end{array}$$

(1)

$$\begin{array}{cc}\hfill T_{\mathrm{ext}}& =J\dot{\omega }+\omega \times J\omega ,\hfill \end{array}$$

(2)

are derived from the center of mass, with $m_q$ denoting the quadrotor mass, $V_b$ and $\omega$ are the linear and angular velocities in the body-fixed frame, respectively, $J=\mathrm{diag}\{J_x,J_y,J_z\}$ is the inertia matrix, the external force $F_{\mathrm{ext}}\in {\mathbb{R}}^3$ takes into account the total thrust, the quadrotor weight, and the aerodynamic force, whereas the external torque $T_{\mathrm{ext}}\in {\mathbb{R}}^3$ considers the aerodynamic moment vector and the difference of torque and thrust wielded by the two pairs of rotors. From the standard sequence of rotations Z-Y-X, the rotation matrix is as follows [20]

$$\mathcal{R}\left(\begin{array}{ccc}\psi ,\hfill & \theta ,\hfill & \varphi \hfill \end{array}\right)=\left(\begin{array}{ccc}\mathrm{c}\theta \mathrm{c}\psi & \mathrm{c}\psi \mathrm{s}\theta \mathrm{s}\varphi -\mathrm{c}\varphi \mathrm{s}\psi & \mathrm{c}\varphi \mathrm{c}\psi \mathrm{s}\theta +\mathrm{s}\varphi \mathrm{s}\psi \\ \mathrm{c}\theta \mathrm{s}\psi & \mathrm{s}\theta \mathrm{s}\varphi \mathrm{s}\psi +\mathrm{c}\varphi \mathrm{c}\psi & \mathrm{c}\varphi \mathrm{s}\theta \mathrm{s}\psi -\mathrm{c}\psi \mathrm{s}\varphi \\ -\mathrm{s}\theta & \mathrm{c}\theta \mathrm{s}\varphi & \mathrm{c}\theta \mathrm{c}\varphi \end{array}\right)$$

(3)

with $\psi$, $\theta$ and $\varphi$ the Euler angles denoting yaw, pitch and roll, respectively, where the $sin(·)$ and $cos(·)$ functions are abbreviated by $\mathrm{s}(·)$ and $\mathrm{c}(·)$, respectively. The vector of Euler angles and the angular velocity vector are related by

$$\left(\begin{array}{c}\dot{\psi }\\ \dot{\theta }\\ \dot{\varphi }\end{array}\right)=\mathcal{M}\begin{array}{ccc}(\psi ,& \theta ,& \varphi )\omega \end{array}$$

(4)

with $\theta \in (-\pi /2,\pi /2),\varphi \in (-\pi /2,\pi /2),\psi \in [-\pi ,\pi )$, and

$$\mathcal{M}\begin{array}{ccc}(\psi ,& \theta ,& \varphi )\end{array}=\left(\begin{array}{ccc}0& \mathrm{s}\varphi sec\theta & \mathrm{c}\varphi sec\theta \\ 0& \mathrm{c}\varphi & -\mathrm{s}\varphi \\ 1& \mathrm{s}\varphi tan\theta & \mathrm{c}\varphi tan\theta \end{array}\right.$$

(5)

nonsingular inside the region where the Euler angles take permissible values.

The propeller dynamics are modeled through linear relationships between the force and moment of the propellers and the squared rotor angular rate, given as

$$\begin{array}{cc}\hfill F_{zi}& =-b{\varpi }_i^2,\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill {\tau }_{zi}& =\kappa {\varpi }_i^2,\hfill \end{array}$$

(7)

with ${\varpi }_i$ the rotor angular rate, and $\kappa$ and b denoting drag and thrust coefficients, respectively, where i is the motor index. Under the fact that the motors are aligned with the vertical axis of the body frame, force and moments arise in the z-direction of the body frame, with $F_z$ being negative in compliance with the downward z-axis convention. The motor torque inputs are linked to the rigid body dynamics through the mapping

$$\left(\begin{array}{c}F\\ {\tau }_x\\ {\tau }_y\\ {\tau }_z\end{array}\right)=\left(\begin{array}{cccc}-b& -b& -b& -b\\ 0& bl& 0& -bl\\ bl& 0& -bl& 0\\ \kappa & -\kappa & \kappa & -\kappa \end{array}\right)\left(\begin{array}{c}{\varpi }_1^2\\ {\varpi }_2^2\\ {\varpi }_3^2\\ {\varpi }_4^2\end{array}\right)$$

(8)

where l denotes the distance between the center of mass (center of gravity) and the rotors from the quadrotor. The sum of angular velocity of the rotors ${\varpi }_r=-{\varpi }_1+{\varpi }_2-{\varpi }_3+{\varpi }_4$ and the rotational velocity $\omega$ of the quadrotor settles the resultant gyroscopic moment $M_g=\omega \times J_r{\varpi }_r$. $J_r$ denotes the inertia of the rotating rotors, having the same parametric value for each of the four rotors.

Under the assumption of low speeds, the governing equations for the quadrotor in terms of the rotation angles are given by [21,22]

$$\begin{array}{cc}\hfill \ddot{\theta }& =\left({\displaystyle \frac{J_z-J_x}{J_y}}\right)\dot{\varphi }\dot{\psi }+{\displaystyle \frac{J_r}{J_y}}{\varpi }_r\dot{\varphi }+{\displaystyle \frac{l}{J_y}}{\tau }_y,\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill \ddot{\varphi }& =\left({\displaystyle \frac{J_y-J_z}{J_x}}\right)\dot{\theta }\dot{\psi }-{\displaystyle \frac{J_r}{J_x}}{\varpi }_r\dot{\theta }+{\displaystyle \frac{l}{J_x}}{\tau }_x,\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill \ddot{\psi }& =\left({\displaystyle \frac{J_x-J_y}{J_z}}\right)\dot{\theta }\dot{\varphi }+{\displaystyle \frac{1}{J_z}}{\tau }_z,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \ddot{z}& =-g+\left(\mathrm{c}\theta \mathrm{c}\varphi \right){\displaystyle \frac{F}{m_q}},\hfill \end{array}$$

(12)

where z is the altitude and $J_x$, $J_y$, $J_z$ are the moments of inertia in the Cartesian coordinate system. From (9)–(11), the well-known Euler equations, it is evident that the rotational dynamics are intrinsically highly coupled by the angles of motion, i.e., cyclic permutation of the inertia and rate components are engaged, so angular rates over any two axes produce an angular acceleration over the third.

3. Decentralized Robust MRAC Design

3.1. Quadrotor’s Parametric Model

In this work, the design of a robust MRAC for the pose of a quadrotor is addressed in a decentralized way.

Consider the set of state variables as given by

$$\begin{array}{cccc}{x}_1=\varphi ,\hfill & x_3=\theta ,\hfill & x_5=\psi ,\hfill & x_7=z,\hfill \\ x_2={\dot{x}}_1=\dot{\varphi },\hfill & x_4={\dot{x}}_3=\dot{\theta },\hfill & x_6={\dot{x}}_5=\dot{\psi },\hfill & x_8={\dot{x}}_7=\dot{z}.\hfill \end{array}$$

(13)

In the state-space representation, the model from Equations (9)–(12) is then written as

$$\dot{x}=\left(\begin{array}{c}{x}_2\\ \left({\displaystyle \frac{J_y-J_z}{J_x}}\right)x_4{x}_6-{\displaystyle \frac{J_r}{J_x}}{\varpi }_r{x}_4+{\displaystyle \frac{l}{J_x}}{\tau }_x\\ x_4\\ \left({\displaystyle \frac{J_z-J_x}{J_y}}\right)x_2{x}_6+{\displaystyle \frac{J_r}{J_y}}{\varpi }_r{x}_2+{\displaystyle \frac{l}{J_y}}{\tau }_y\\ x_6\\ \left({\displaystyle \frac{J_x-J_y}{J_z}}\right)x_2{x}_4+{\displaystyle \frac{1}{J_z}}{\tau }_z\\ x_8\\ -g+\left(\mathrm{c}{x}_1\mathrm{c}{x}_3\right){\displaystyle \frac{F}{m_q}}\end{array}\right).$$

(14)

Under the assumption that Euler angles change slightly during flying, the gyroscopic effects are neglected, and the rotational dynamics are divided into

$${\dot{x}}^1=\left(\begin{array}{c}{x}_2\\ \left({\displaystyle \frac{J_y-J_z}{J_x}}\right)x_4{x}_6+{\displaystyle \frac{l}{J_x}}{\tau }_x\end{array}\right),$$

(15)

$${\dot{x}}^2=\left(\begin{array}{c}{x}_4\\ \left({\displaystyle \frac{J_z-J_x}{J_y}}\right)x_2{x}_6+{\displaystyle \frac{l}{J_y}}{\tau }_y\end{array}\right),$$

(16)

$${\dot{x}}^3=\left(\begin{array}{c}{x}_6\\ \left({\displaystyle \frac{J_x-J_y}{J_z}}\right)x_2{x}_4+{\displaystyle \frac{1}{J_z}}{\tau }_z\end{array}\right),$$

(17)

with ${\dot{x}}^1={\left({\dot{x}}_1{\dot{x}}_2\right)}^T,{\dot{x}}^2={\left({\dot{x}}_3{\dot{x}}_4\right)}^T,$ and ${\dot{x}}^3={\left({\dot{x}}_5{\dot{x}}_6\right)}^T$.

Thus, the subsystem (15) is parameterized in the form

$${\dot{x}}^1=A_1{x}^1+B_1{\Lambda }_1\left(u^1+{\mathsf{\Theta }}_1{\Phi }_1\left(x\right)\right)+{\zeta }_1$$

(18)

with $x^1={\left(x_1{x}_2\right)}^T$, $a_1=(J_y-J_z)/J_x$, $b_1=l/J_x$, ${\Lambda }_1=b_1$, ${\mathsf{\Theta }}_1=a_1/b_1$, ${\Phi }_1\left(x\right)=x_4{x}_6$, $u^1={\tau }_x$, and

$$\begin{array}{cc}\hfill A_1=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right],& B_1=\left[\begin{array}{c}0\\ 1\end{array}\right].\hfill \end{array}$$

Similarly, (16) takes the form

$${\dot{x}}^2=A_2{x}^2+B_2{\Lambda }_2\left(u^2+{\mathsf{\Theta }}_2{\Phi }_2\left(x\right)\right)+{\zeta }_2$$

(19)

with $x^2={\left(x_3{x}_4\right)}^T$, $a_2=(J_z-J_x)/J_y$, $b_2=l/J_y$, ${\Lambda }_2=b_2$, ${\mathsf{\Theta }}_2=a_2/b_2,$${\Phi }_2\left(x\right)=x_2{x}_6$, $u^2={\tau }_y$, $A_2=A_1$ and $B_2=B_1$. From (17),

$${\dot{x}}^3=A_3{x}^3+B_3{\Lambda }_3\left(u^3+{\mathsf{\Theta }}_3{\Phi }_3\left(x\right)\right)+{\zeta }_3$$

(20)

where $x^3={\left(x_5{x}_6\right)}^T$, $a_3=(J_x-J_y)/J_z$, $b_3=1/J_z$, ${\Lambda }_3=b_3$, ${\mathsf{\Theta }}_3=a_3/b_3,$${\Phi }_3\left(x\right)=x_2{x}_4$, $u^3={\tau }_z$, $A_3=A_1$ and $B_3=B_1$.

From the decentralized parametric model for the rotational dynamics of the quadrotor, it must be noticed that since the rotational dynamics are intrinsically highly coupled (interconnected) by the angles of motion, an interconnection matrix is not defined, in contrast to the decentralized adaptive control strategy from [5,23].

3.2. MRAC Design from Unmatched External Perturbations

Consider a nonlinear multiple–input/multiple–output (MIMO) system of the form [3]

$$\dot{x}=Ax+B\Lambda (u+f\left(x\right)),$$

(21)

where $x\in {\mathbb{R}}^n$ is the system state, $B\in {\mathbb{R}}^{n\times m}$ is the known control matrix, $u\in {\mathbb{R}}^m$ is the control input, $A\in {\mathbb{R}}^{n\times n}$ and $\Lambda \in {\mathbb{R}}^{m\times m}$ are unknown constant matrices. The pair ($A,B\Lambda$) is controllable with $\Lambda$, a diagonal matrix with elements ${\lambda }_i$ strictly positive. The uncertainty $\Lambda$ is introduced for modeling errors or to model control failures. $f\left(x\right):{\mathbb{R}}^n\to {\mathbb{R}}^m$ accounts for an unknown vector function of the system matched uncertainty. Therefore, $f\left(x\right)$ can be viewed as a linear combination of N known locally as the Lipschitz–continuous basis functions ${\phi }_i\left(x\right)$ with unknown constant coefficients, i.e.,

$$f\left(x\right)={\mathsf{\Theta }}^T\Phi \left(x\right)$$

(22)

with $\mathsf{\Theta }\in {\mathbb{R}}^{N\times m}$ a constant matrix of the unknown coefficients and $\Phi \left(x\right)=({\phi }_1\left(x\right){\phi }_2\left(x\right)$$\cdots {\phi }_N{\left(x\right))}^T\in {\mathbb{R}}^N$ is the measurable signals (regressor) vector [6]. From (21), the uncertainties are matched in the sense that these enter the system dynamics through the control channels. Therefore, the system controllability property is not affected as long as $\Lambda$ is invertible. More even, the matched uncertainty assumption implies the existence of at least one control solution capable of steering the system state along the desired trajectories [3]. Since $f\left(x\right)$ appears in the range space of the control input matrix B, it is termed parametric matched uncertainty. When a parametric uncertainty is matched, the control input can cancel out the uncertainty when the adaptation is perfect.

This study is centered on the design of a MIMO state feedback adaptive controller such that the system state x globally uniformly asymptotically follows the state $x_{\mathit{m}}\in {\mathbb{R}}^n$ of the reference model

$${\dot{x}}_{\mathit{m}}=A_{\mathit{m}}{x}_{\mathit{m}}+B_{\mathit{m}}r$$

(23)

where $A_{\mathit{m}}\in {\mathbb{R}}^{n\times n}$ is Hurwitz, $B_{\mathit{m}}\in {\mathbb{R}}^{n\times m}$ and $r\in {\mathbb{R}}^m$ is the bounded command vector. It is also required that during tracking, all signals in the closed-loop system remain uniformly bounded.

Given $(A,B,\Lambda ,A_{\mathit{m}},B_{\mathit{m}})$, in general, from the matching conditions

$$\begin{array}{cc}\hfill A+B\Lambda K_x^T& =A_{\mathit{m}},\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill B\Lambda K_r^T& =B_{\mathit{m}},\hfill \end{array}$$

(25)

there is no guarantee that ideal gains $K_x$ and $K_r$ exist. Additionally, the pair ($A_{\mathit{m}},B_{\mathit{m}})$ can be selected such that (24) and (25) have one solution pair $(K_x,K_r)$ from the premise that the structure of A may be known.

Thus, given any bounded command, the control input needs to be chosen such that the tracking error

$$e=x-x_{\mathit{m}}$$

(26)

globally uniformly asymptotically tends to zero, i.e.,

$${\lim }_{t\to \infty }\parallel x-x_{\mathit{m}}\parallel =0.$$

(27)

From every subsystem (18)–(20), it is desirable that the closed-loop dynamics take the form

$$\begin{array}{c}\hfill \dot{x}=A_{m}x+B\Lambda (u+{\mathsf{\Theta }}^T\Phi \left(x\right))+B_{m}r+\zeta \left(t\right)\end{array}$$

(28)

with $\zeta \left(t\right)$ a perturbation term. Thus, selecting the control input

$$u=-{\hat{\mathsf{\Theta }}}^T\Phi \left(x\right)$$

(29)

and substituting (29) in (28) results

$$\dot{x}=A_{m}x-B\Lambda {\tilde{\mathsf{\Theta }}}^T\Phi \left(x\right)+B_{m}r+\zeta \left(t\right)$$

(30)

with

$${\tilde{\mathsf{\Theta }}}^T={\hat{\mathsf{\Theta }}}^T-{\mathsf{\Theta }}^T$$

(31)

the parametric estimation error, and

$$e=x-x_m$$

(32)

the tracking error equation.

Subtracting the reference model dynamics (23) from (28) yields the tracking error dynamics

$$\dot{e}=A_{m}e-B\Lambda {\tilde{\mathsf{\Theta }}}^T\Phi \left(x\right)+\zeta \left(t\right).$$

(33)

To guarantee uniform ultimate boundedness (UUB) of all signals in the closed-loop system, consider the Lyapunov function candidate

$$V(e,\tilde{\mathsf{\Theta }})=e^{T}Pe+\mathrm{tr}({\tilde{\mathsf{\Theta }}}^T{\Gamma }_{\mathsf{\Theta }}^{-1}\tilde{\mathsf{\Theta }}\Lambda ),$$

(34)

with $\mathrm{tr}(·)$ the trace operator, ${\Gamma }_{\mathsf{\Theta }}={\Gamma }_{\mathsf{\Theta }}^T>0$ the adaptation gain matrix, and $P=P^T>0$ the symmetric positive-definite solution from the algebraic Lyapunov equation

$$P{A}_{\mathit{m}}+A_{\mathit{m}}^{T}P=-Q$$

(35)

for some $Q=Q^T>0$.

Its time derivative along the error dynamics (33) results

$$\dot{V}(e,\tilde{\mathsf{\Theta }})=-e^{T}Qe-2e^{T}PB\Lambda {\tilde{\mathsf{\Theta }}}^T\Phi \left(x\right)+2e^{T}P\zeta \left(x\right)+2\mathrm{tr}({\tilde{\mathsf{\Theta }}}^T{\Gamma }_{\mathsf{\Theta }}^{-1}\dot{\hat{\mathsf{\Theta }}}\Lambda ),$$

(36)

which can be rewritten as

$$\dot{V}(e,\tilde{\mathsf{\Theta }})=-e^{T}Qe+2\mathrm{tr}\left({\tilde{\mathsf{\Theta }}}^T\left\{{\Gamma }_{\mathsf{\Theta }}^{-1}\dot{\hat{\mathsf{\Theta }}}-\Phi e^{T}PB\right\}\Lambda \right)+2e^{T}P\zeta \left(t\right).$$

(37)

To gain robustness, the update law

$$\dot{\hat{\mathsf{\Theta }}}={\Gamma }_{\mathsf{\Theta }}(\Phi \left(x\right)e^{T}PB-\sigma \parallel e^{T}PB\parallel \hat{\mathsf{\Theta }})$$

(38)

is selected, which includes an extra term adding a tracking error-dependent damping, which tends to zero as the tracking error signal decreases, to the adaptive dynamics with $\sigma$, a design parameter that is a strictly positive constant.

Substituting (38) in (37), it yields to

$$\dot{V}(e,\tilde{\mathsf{\Theta }})=-e^{T}Qe-2\sigma \parallel e^{T}PB\parallel \mathrm{tr}({\tilde{\mathsf{\Theta }}}^T\hat{\mathsf{\Theta }}\Lambda )+2e^{T}P\zeta \left(t\right).$$

(39)

From (31), (39) can be rewritten as

$$\dot{V}(e,\tilde{\mathsf{\Theta }})=-e^{T}Qe-2\sigma \parallel e^{T}PB\parallel \mathrm{tr}({\tilde{\mathsf{\Theta }}}^T\tilde{\mathsf{\Theta }}\Lambda )-2\sigma \parallel e^{T}PB\parallel \mathrm{tr}({\tilde{\mathsf{\Theta }}}^T\mathsf{\Theta }\Lambda )+2e^{T}P\zeta \left(t\right).$$

(40)

By definition,

$$\mathrm{tr}({\tilde{\mathsf{\Theta }}}^T\tilde{\mathsf{\Theta }}\Lambda )=\sum _{i=1}^N\sum _{j=1}^m{\tilde{\mathsf{\Theta }}}_{ij}^2{\Lambda }_{ii}\ge {\parallel \tilde{\mathsf{\Theta }}\parallel }_F^2{\Lambda }_{\min }$$

(41)

with ${\Lambda }_{\min }$ and $\parallel \tilde{\mathsf{\Theta }}{\parallel }_F^2={\sum }_{i=1}^N{\sum }_{j=1}^m{\tilde{\mathsf{\Theta }}}_{ij}^2$, the minimum diagonal element of $\Lambda$ and the Frobenius norm, respectively. From the Schwarz inequality,

$$|\mathrm{tr}({\tilde{\mathsf{\Theta }}}^T\mathsf{\Theta }\Lambda )|\le \parallel {\tilde{\mathsf{\Theta }}}^T{\mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F\le \parallel \tilde{\mathsf{\Theta }}{\parallel }_F{\parallel \mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F.$$

(42)

Replacing (41) and (42) into (40) yields

$$\begin{array}{cc}\hfill \dot{V}(e,\tilde{\mathsf{\Theta }})\le & -{\lambda }_{\min }{\left\{Q\right\}\parallel e\parallel }^2+2\parallel e\parallel {\lambda }_{\max }\left\{P\right\}{\zeta }_{\max }-2\sigma \parallel e\parallel \parallel PB\parallel \parallel \tilde{\mathsf{\Theta }}{\parallel }_F^2{\Lambda }_{\min }\hfill \\ \hfill & +2\sigma \parallel e\parallel \parallel PB\parallel \parallel \tilde{\mathsf{\Theta }}{\parallel }_F{\parallel \mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F.\hfill \end{array}$$

(43)

By completion of squares, the first terms can be written as

$$\begin{array}{c}-{\lambda }_{\min }{\left\{Q\right\}\parallel e\parallel }^2+2\parallel e\parallel {\lambda }_{\max }\left\{P\right\}{\zeta }_{\max }\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=-{\lambda }_{\min }\left\{Q\right\}{\left(\parallel e\parallel -{\displaystyle \frac{{\lambda }_{\max }\left\{P\right\}}{{\lambda }_{\min }\left\{Q\right\}}}{\zeta }_{\max }\right)}^2+{\displaystyle \frac{{\lambda }_{\max }^2\left\{P\right\}}{{\lambda }_{\min }\left\{Q\right\}}}{\zeta }_{\max }^2.\end{array}$$

(44)

Also, the remaining terms, by completion of squares, can be written as

$$\begin{array}{c}-2\sigma \parallel e\parallel \parallel PB\parallel \parallel \tilde{\mathsf{\Theta }}{\parallel }_F^2{\Lambda }_{\min }+2\sigma \parallel e\parallel \parallel PB\parallel \parallel \tilde{\mathsf{\Theta }}{\parallel }_F{\parallel \mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F\hfill \\ \hfill \hspace{1em}\hspace{1em}\hspace{1em}=-2\sigma \parallel e\parallel \parallel PB\parallel {\Lambda }_{\min }{\left(\parallel \tilde{\mathsf{\Theta }}{\parallel }_F-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F}{{\Lambda }_{\min }}}\right)}^2+{\displaystyle \frac{1}{2}}\sigma \parallel e\parallel \parallel PB\parallel {\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F^2{\parallel \Lambda \parallel }_F^2}{{\Lambda }_{\min }}}.\end{array}$$

(45)

Then, (43) can be rewritten as

$$\begin{array}{cc}\hfill \dot{V}(e,\tilde{\mathsf{\Theta }})\le & -{\lambda }_{\min }\left\{Q\right\}{\left(\parallel e\parallel -{\displaystyle \frac{{\lambda }_{\max }\left\{P\right\}}{{\lambda }_{\min }\left\{Q\right\}}}{\zeta }_{\max }\right)}^2+{\displaystyle \frac{{\lambda }_{\max }^2\left\{P\right\}}{{\lambda }_{\min }\left\{Q\right\}}}{\zeta }_{\max }^2\hfill \\ \hfill & -2\sigma \parallel e\parallel \parallel PB\parallel {\Lambda }_{\min }{\left(\parallel \tilde{\mathsf{\Theta }}{\parallel }_F-{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F}{{\Lambda }_{\min }}}\right)}^2+{\displaystyle \frac{1}{2}}\sigma \parallel e\parallel \parallel PB\parallel {\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F^2{\parallel \Lambda \parallel }_F^2}{{\Lambda }_{\min }}}.\hfill \end{array}$$

(46)

Consequently, $\dot{V}(e,\tilde{\mathsf{\Theta }})<0$ if

$$\parallel e\parallel >{\displaystyle \frac{1}{2}}\sigma \parallel PB\parallel {\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F^2{\parallel \Lambda \parallel }_F^2}{{\lambda }_{\min }\left\{Q\right\}{\Lambda }_{\min }}}+2{\displaystyle \frac{{\lambda }_{\max }\left\{P\right\}}{{\lambda }_{\min }\left\{Q\right\}}}{\zeta }_{\max }=c_1$$

(47)

or

$$\parallel \tilde{\mathsf{\Theta }}{\parallel }_F>\sqrt{{\displaystyle \frac{{\lambda }_{\max }\left\{P\right\}}{\sigma \parallel PB\parallel {\Lambda }_{\min }}}{\zeta }_{\max }+{\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F^2{\parallel \Lambda \parallel }_F^2}{4{\Lambda }_{\min }^2}}}+{\displaystyle \frac{1}{2}}{\displaystyle \frac{{\parallel \mathsf{\Theta }\parallel }_F{\parallel \Lambda \parallel }_F}{{\Lambda }_{\min }}}=c_2$$

(48)

Hence, outside of the compact set

$$\mathsf{\Omega }=\{(e,\tilde{\mathsf{\Theta }}):(\parallel e\parallel \le c_1)\wedge (\parallel \tilde{\mathsf{\Theta }}{\parallel }_F\le c_2\left)\right\}\subset R^n\times R^{N\times m},$$

(49)

closed and bounded, so $\dot{V}(e,\tilde{\mathsf{\Theta }})<0$.

Thus, (49) proves UUB tracking of the external command r by the output $y\left(t\right)$. Thus, in the presence of bounded time-varying perturbations $\zeta \left(t\right)$ and parametric uncertainties $(\Lambda ,\mathsf{\Theta })$, command tracking is accomplished. Moreover, the command tracking problem for the MIMO system dynamics (28) is solved, which can be summarized as follows.

Theorem 1.

Given the MIMO dynamics (18) with control uncertainty ${\Lambda }_1$ and matched unknown function $f_1\left(x\right)={\mathsf{\Theta }}_1^T{\Phi }_1\left(x\right)$, the MRAC subsystem (29), (31), (32), (38) imposes uniform ultimate bounded tracking of the reference model (23), driven by any bounded time-varying command $r\left(t\right)$. Also, all signals from the respective closed-loop subsystem are UUB in time.

For robustness comparison purposes, let us consider the adaptive law with dead-zone modification [4]

$$\dot{\hat{\mathsf{\Theta }}}=\left\{\begin{array}{cc}\hfill {\Gamma }_{\mathsf{\Theta }}\Phi \left(x\right)e^{T}PB,& \mathrm{if}\parallel e\parallel >e_0\hfill \\ \hfill 0,& \mathrm{if}\parallel e\parallel \le e_0.\hfill \end{array}\right.$$

(50)

The dead-zone modification consists of stopping the adaptation process when the norm of the tracking error becomes smaller than a prescribed value $e_0$, assuring UUB of $\tilde{\mathsf{\Theta }}$ in addition to e. In other words, suppose that $\parallel e\parallel >e_0$, then the adaptive law is defined by (Equation (50)) which results in the upper bound (Equation (44)). Therefore, $e\left(t\right)$ enters ${\mathsf{\Omega }}_0$ in finite time T residing within the set for all $t\ge T$ and then the adaptive parameter dynamics are frozen, i.e., $\hat{\mathsf{\Theta }}(t+T)=0$. This proves the UUB of the error dynamics (Equation (33)), proving boundedness, but not necessarily UUB, of the parameter estimation errors $\parallel \tilde{\mathsf{\Theta }}\parallel$ uniformly in time.

The tracking error bound $e_0$ is dependent on the eigenvalue ratio ${\lambda }_{\max }\left(P\right)$/${\lambda }_{\min }\left(Q\right)$, for which the minimum is achieved for $Q=I$ [1]. The tracking error upper bound is proportional to $2{\lambda }_{\max }\left(P\right){\zeta }_{\max }$. However, even when the disturbance vanishes, asymptotic stability of the tracking error cannot be recovered. Since the dead-zone modification is not Lipschitz, it may cause chattering (high-frequency oscillations) and undesirable effects when the tracking error is at or near the dead-zone boundary.

A smooth version of the dead-zone modification has been introduced in [10], where an adaptive law with the continuous dead-zone modification is defined as

$$\dot{\hat{\mathsf{\Theta }}}={\Gamma }_{\mathsf{\Theta }}\Phi \left(x\right)\mu (\parallel e\parallel )e^{T}PB$$

(51)

with

$$\mu (\parallel e\parallel )=\max \left(0,\min \left(1,{\displaystyle \frac{\parallel e\parallel -\delta e_0}{(1-\delta )e_0}}\right)\right)$$

(52)

a Lipschitz-continuous modulation function where $0<\delta <1$. Lyapunov-based arguments from [4] can be used to prove bounded tracking and UUB with this latter adaptation law [3].

4. Simulation Results

Simulation results for the performance of the decentralized robust MRAC with e-modification are presented. Both the absence and presence of perturbations are considered when evaluating the proposal. A Gaussian noise source for each of the attitude angles is considered as a source of perturbations. The command signal to be tracked is a non-smooth one, namely a square wave, and the simulation time is extended to 50 s in order to demand parameter drift. The inertial parameters are taken from a real platform whose values are given by $m=1.79\mathrm{kg}$, $l=0.2\mathrm{m}$, $J_x=0.03\mathrm{kg}{\mathrm{m}}^2$, $J_y=0.03\mathrm{kg}{\mathrm{m}}^2$, and $J_z=0.04\mathrm{kg}{\mathrm{m}}^2$ [24]. Ideal gains $K_{x^1}={(-4.89795-1.2)}^T$ and $K_{r^1}=4.89795$ come from solving the matching conditions (24) and (25), with $\xi =0.7$ and ${\omega }_n^2=32.653\mathrm{rad}/\mathrm{s}$ [25].

The symmetric positive-definite matrix

$$P=\left(\begin{array}{cc}20.5931& 0.0153\\ 0.0153& 0.6269\end{array}\right)$$

(53)

results from solving the Lyapunov Equation (35) for

$$Q=\left(\begin{array}{cc}1& 0\\ 0& 10\end{array}\right).$$

(54)

The adaptation gain for the update law (38) is chosen as ${\Gamma }_{{\mathsf{\Theta }}_1}=9500$. The same design procedure is followed for the pitch and yaw angles subsystems, so only that for the roll angle is detailed. The adaptation gains for the update laws of the remaining subsystems are chosen as ${\Gamma }_{{\mathsf{\Theta }}_2}=9430$ and ${\Gamma }_{{\mathsf{\Theta }}_3}=9500$.

A proportional–integral–derivative (PID) controller is used for the control of the altitude [26,27].

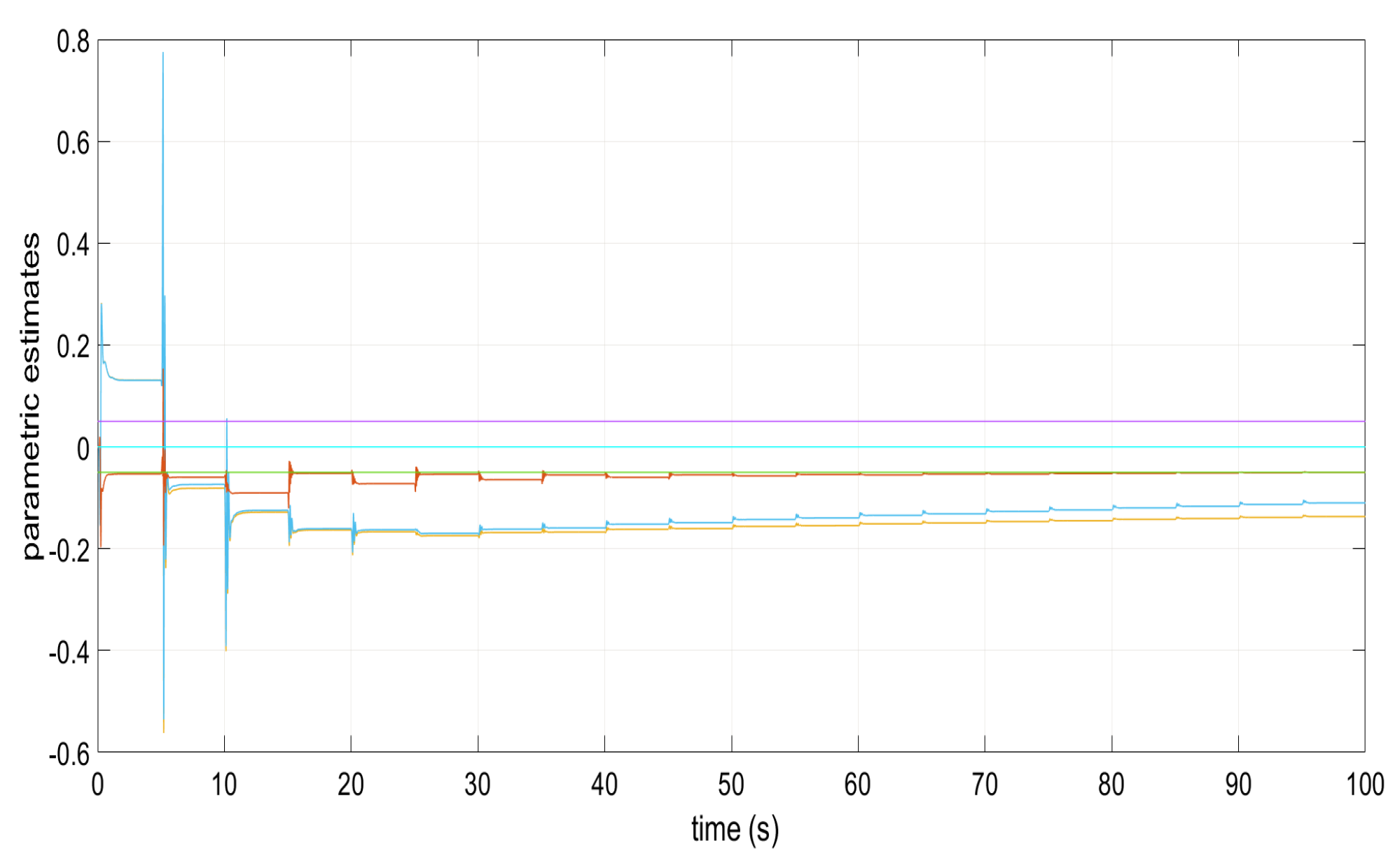
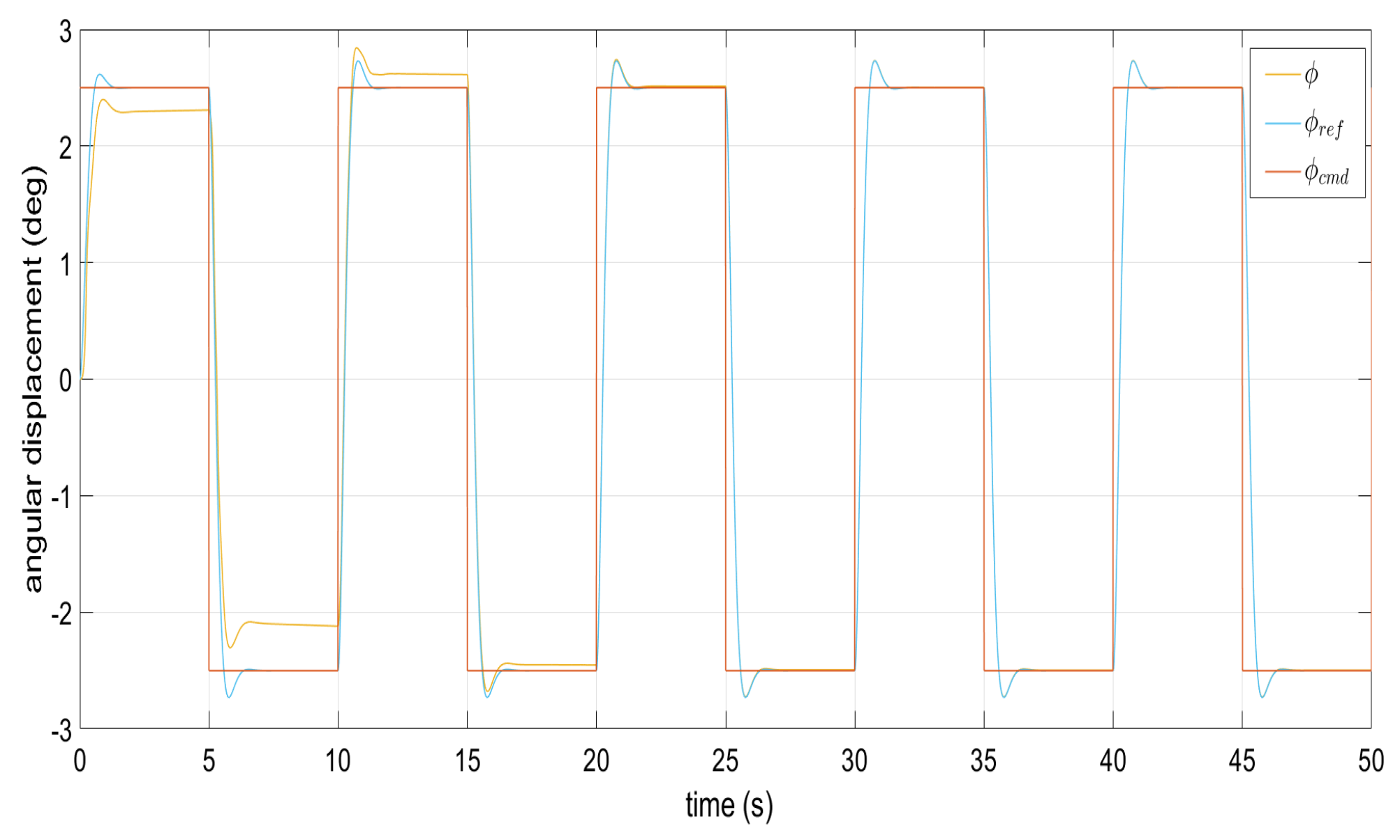
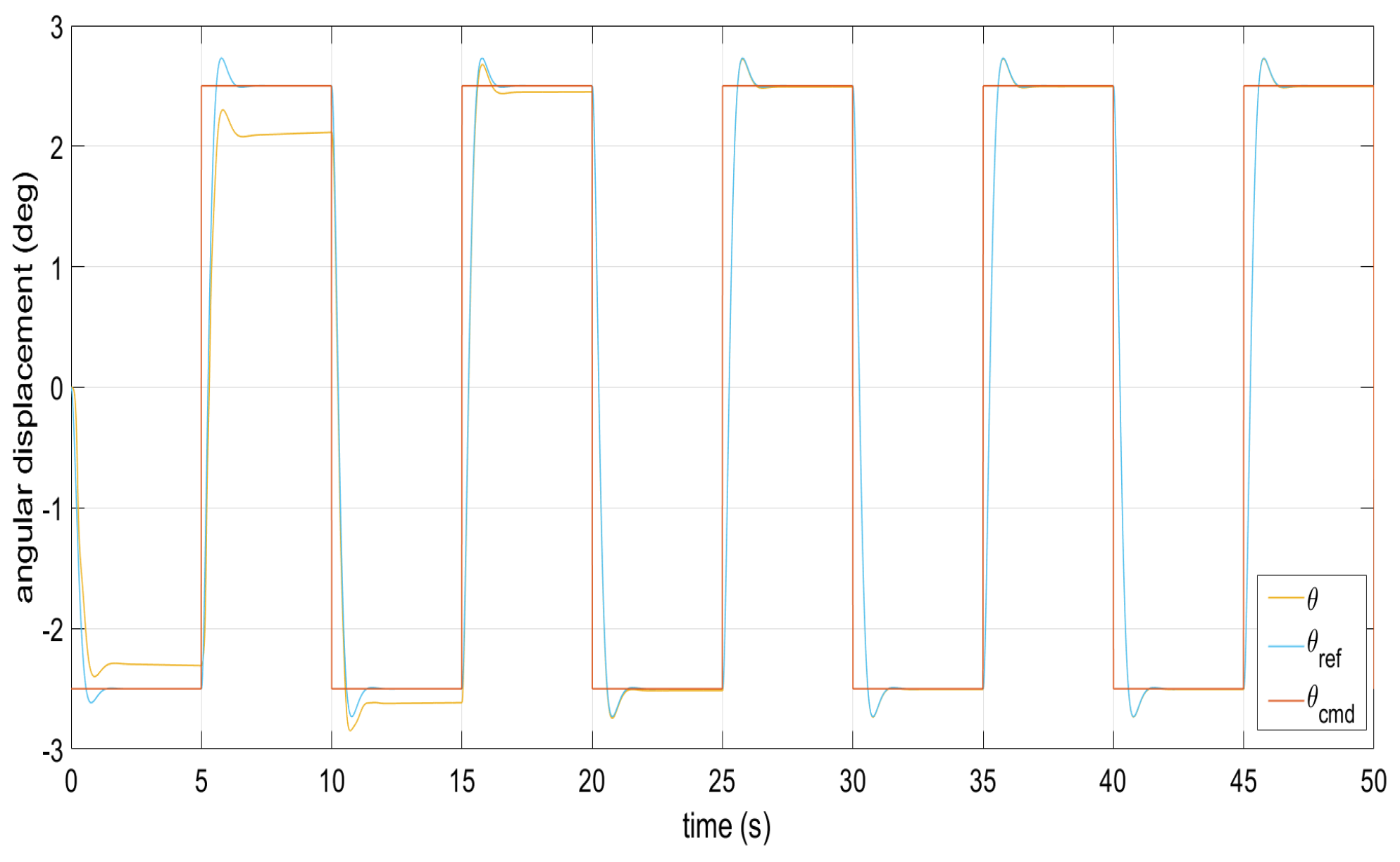
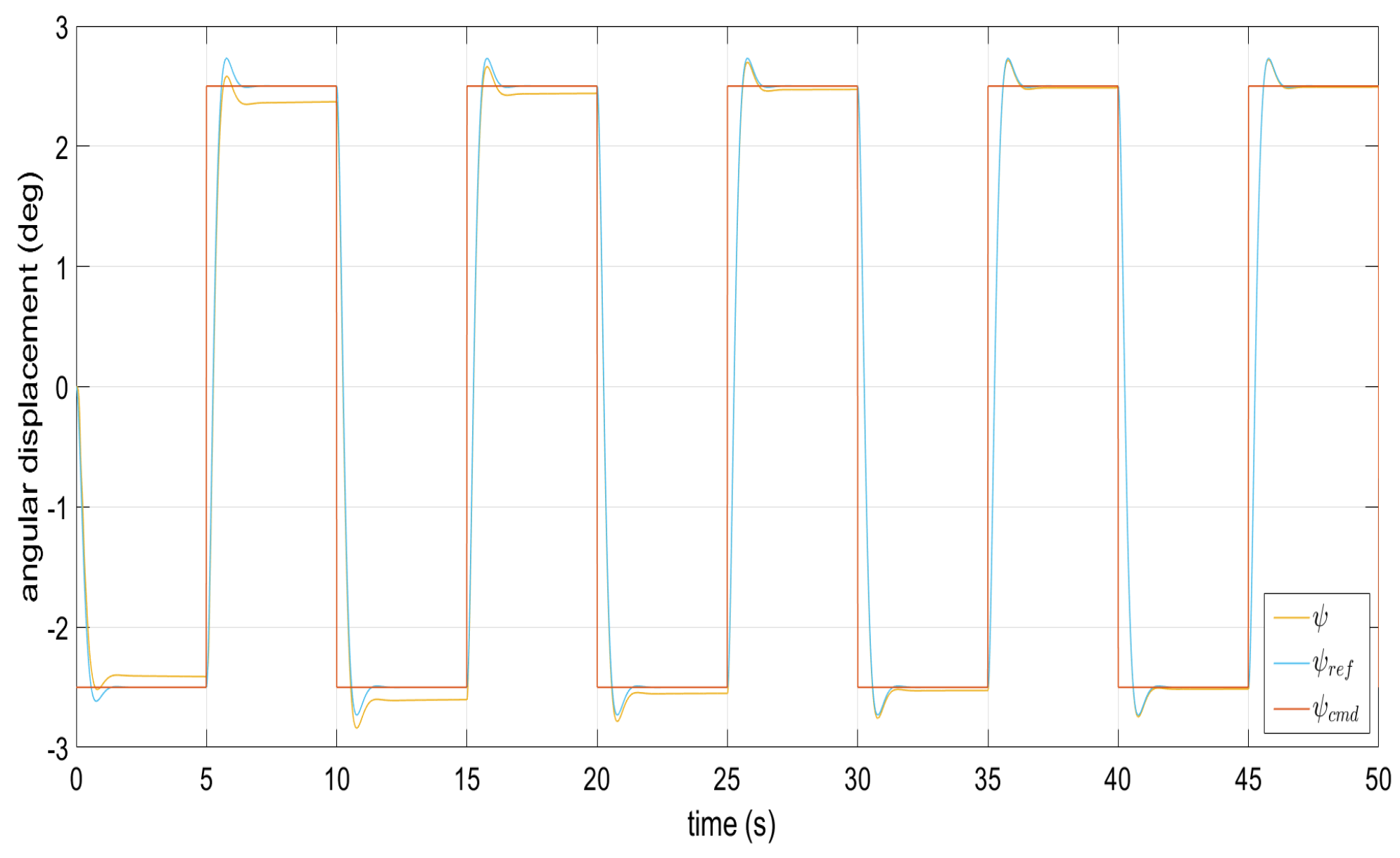
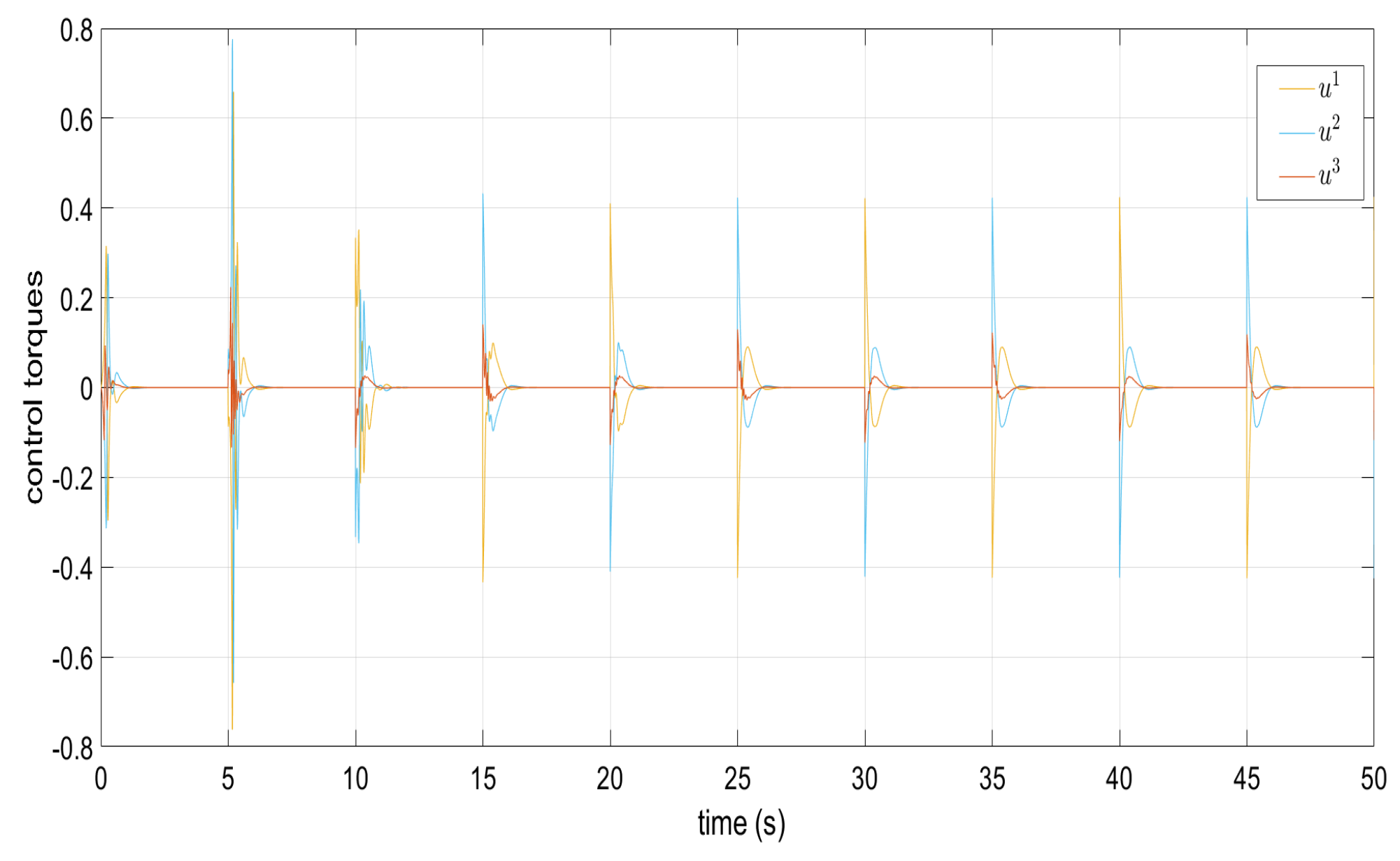
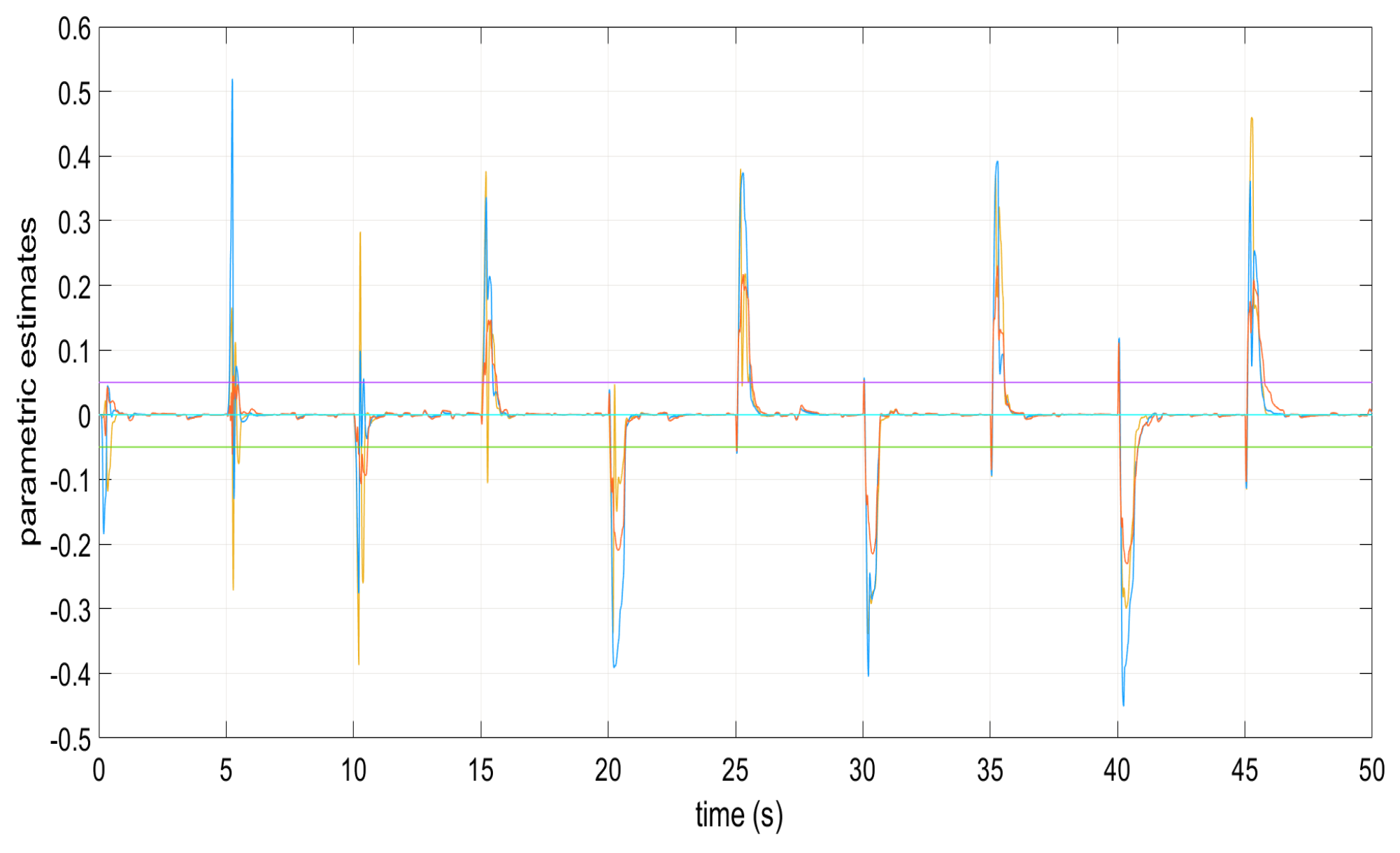
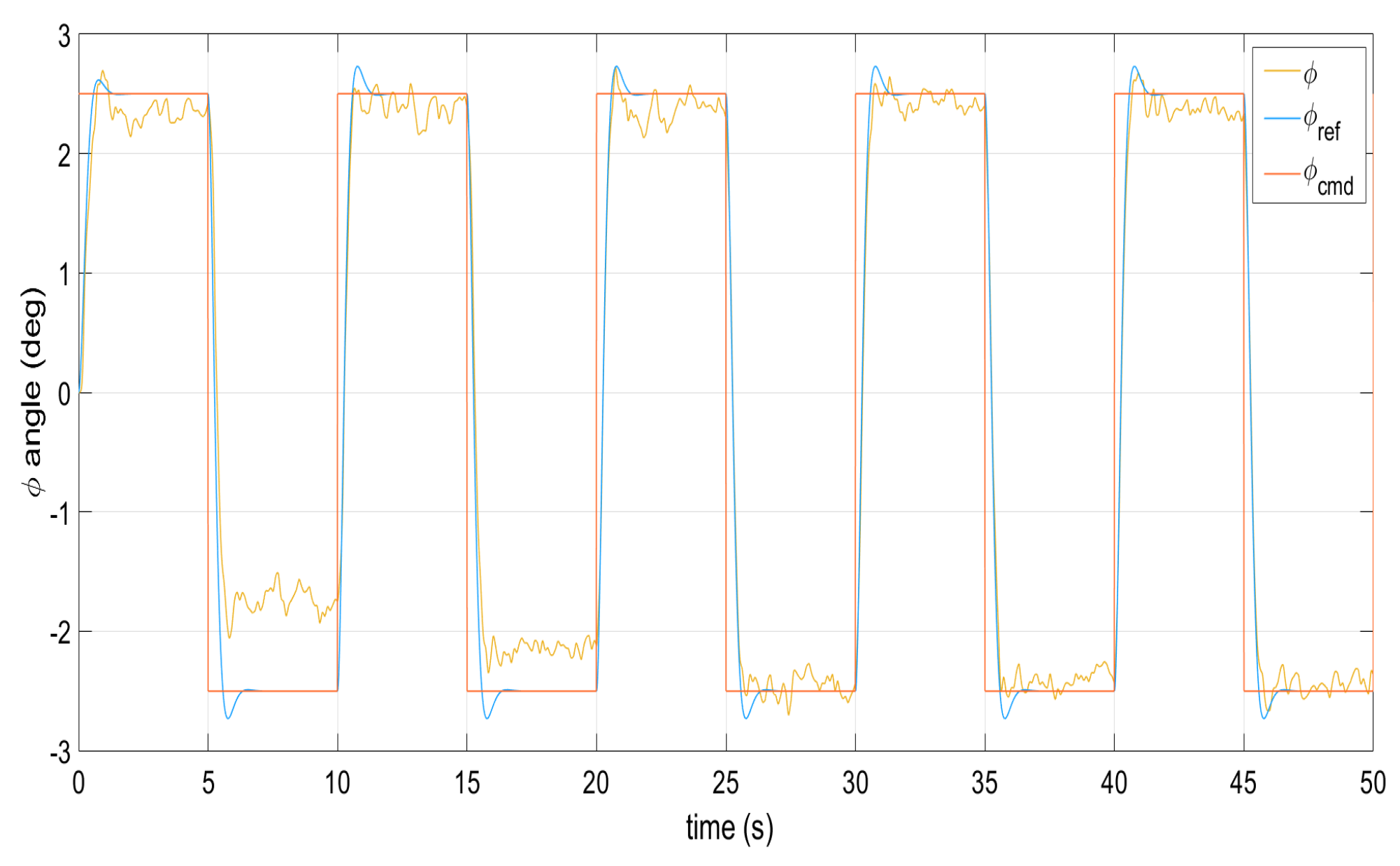
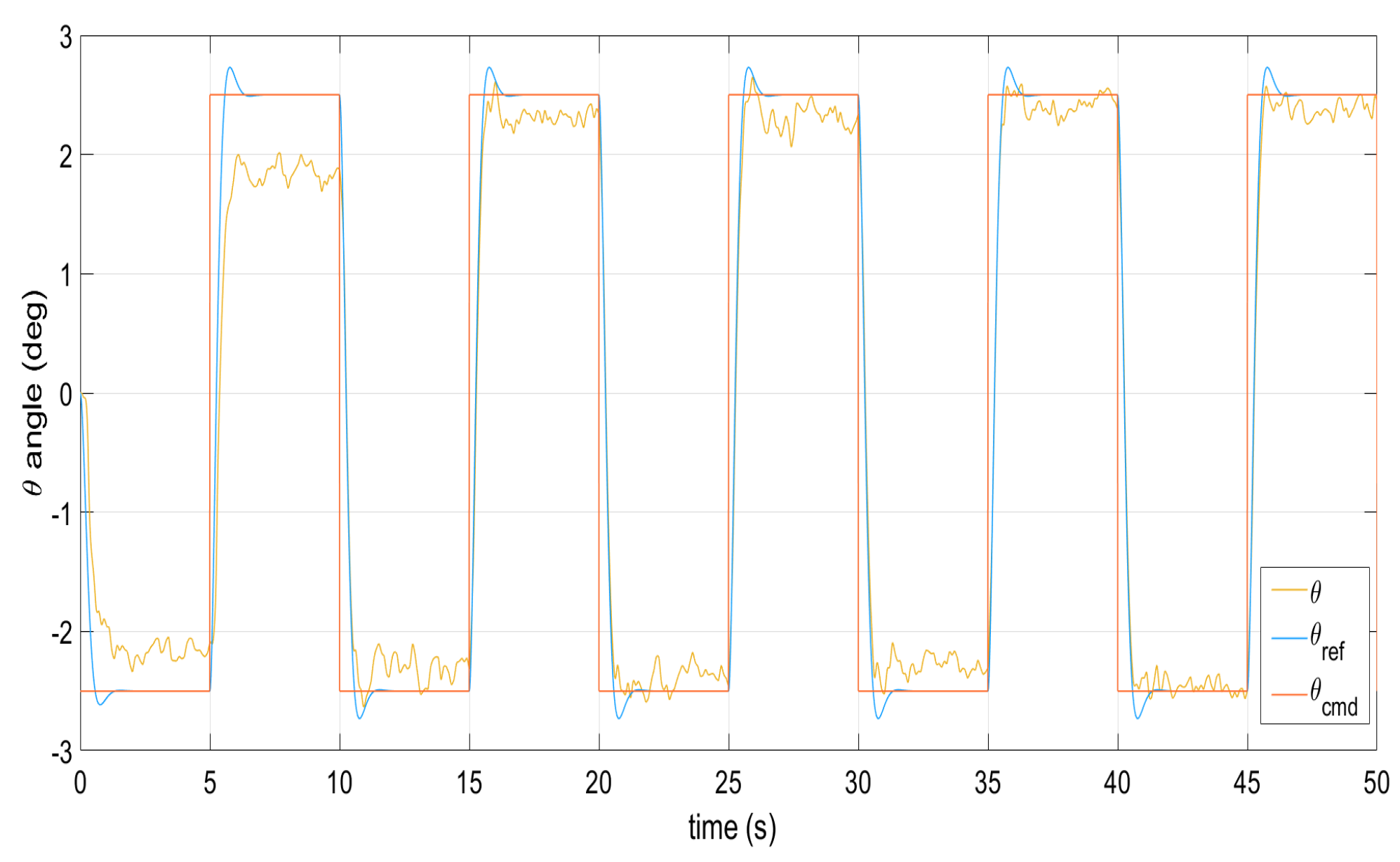
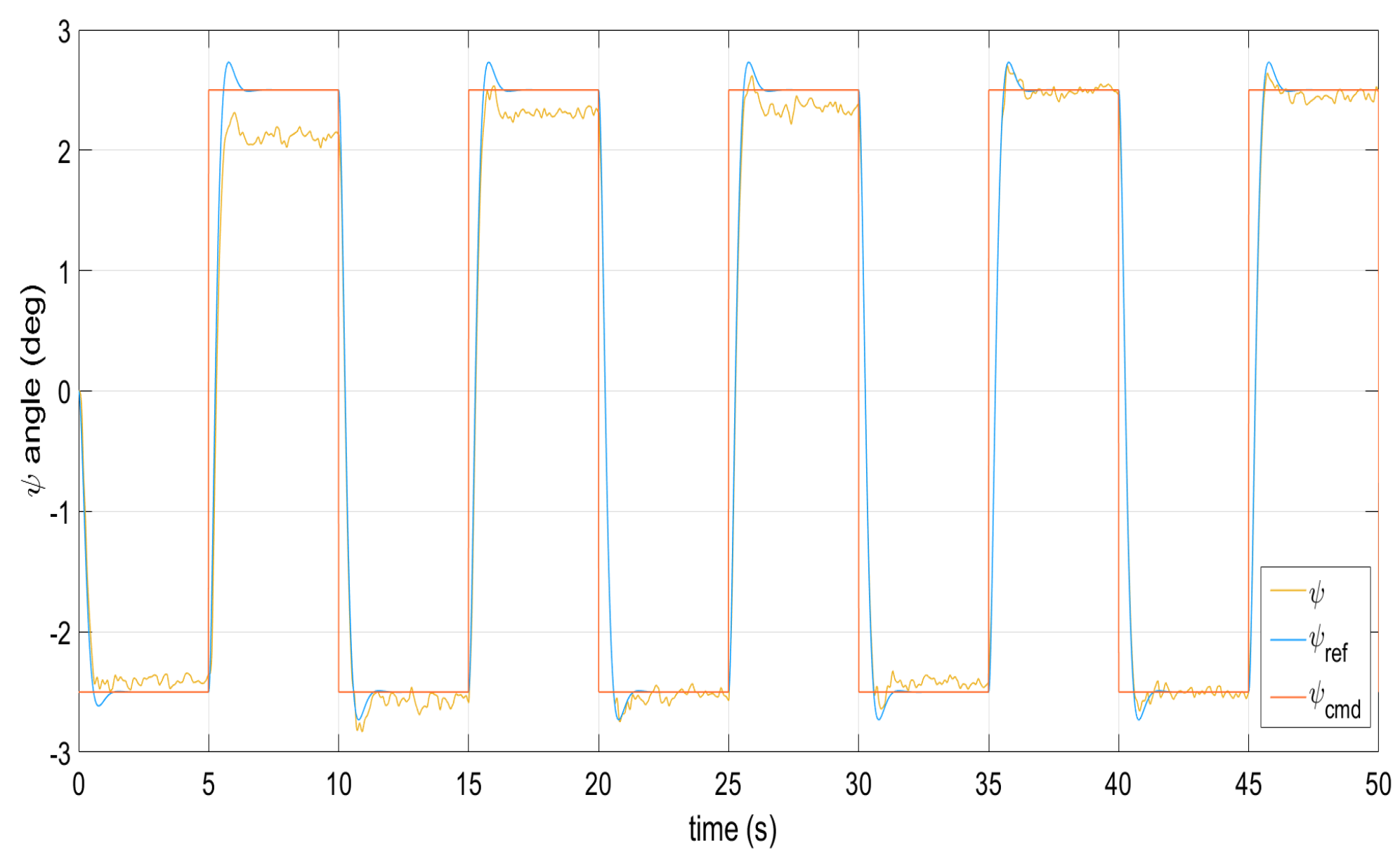
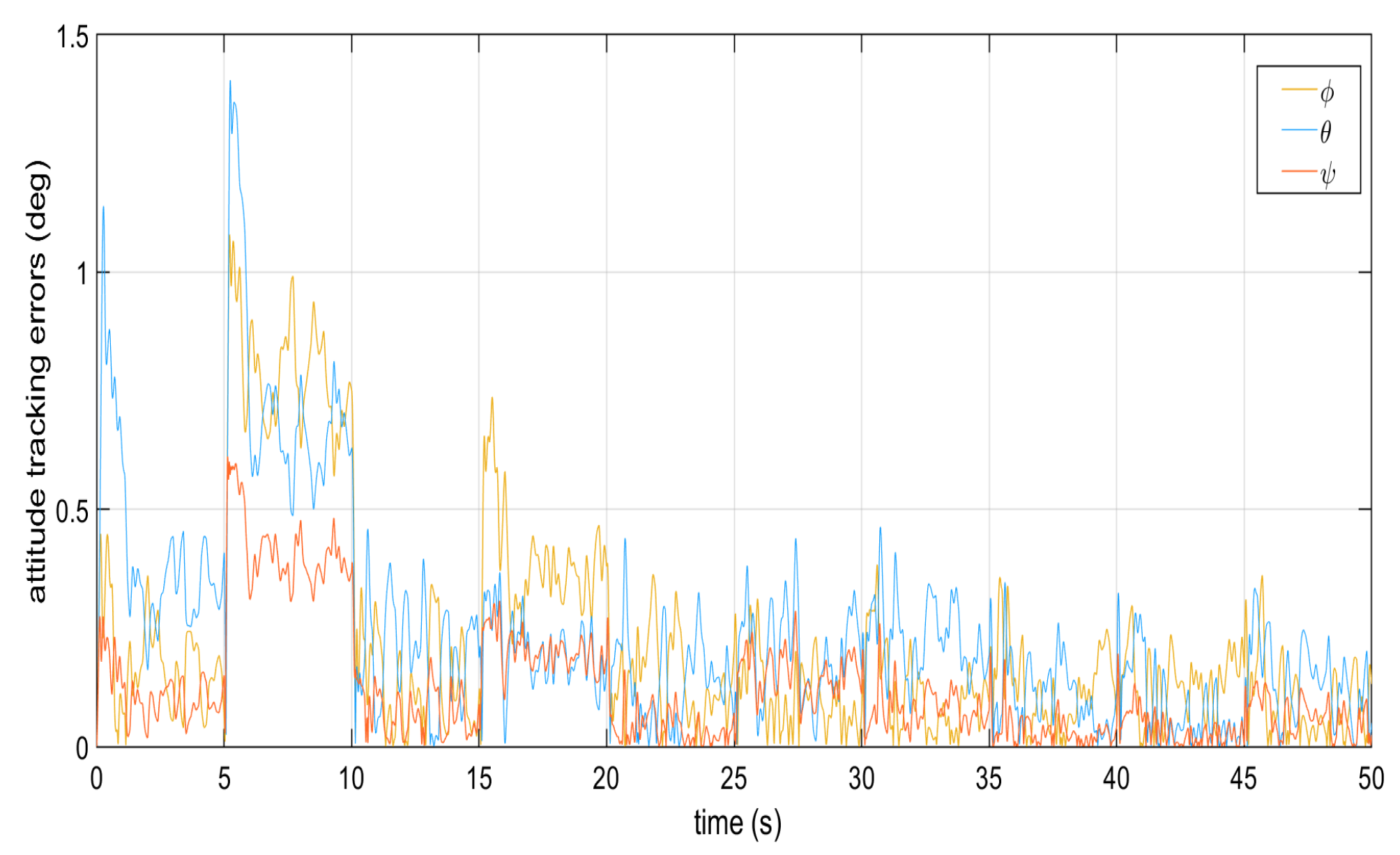
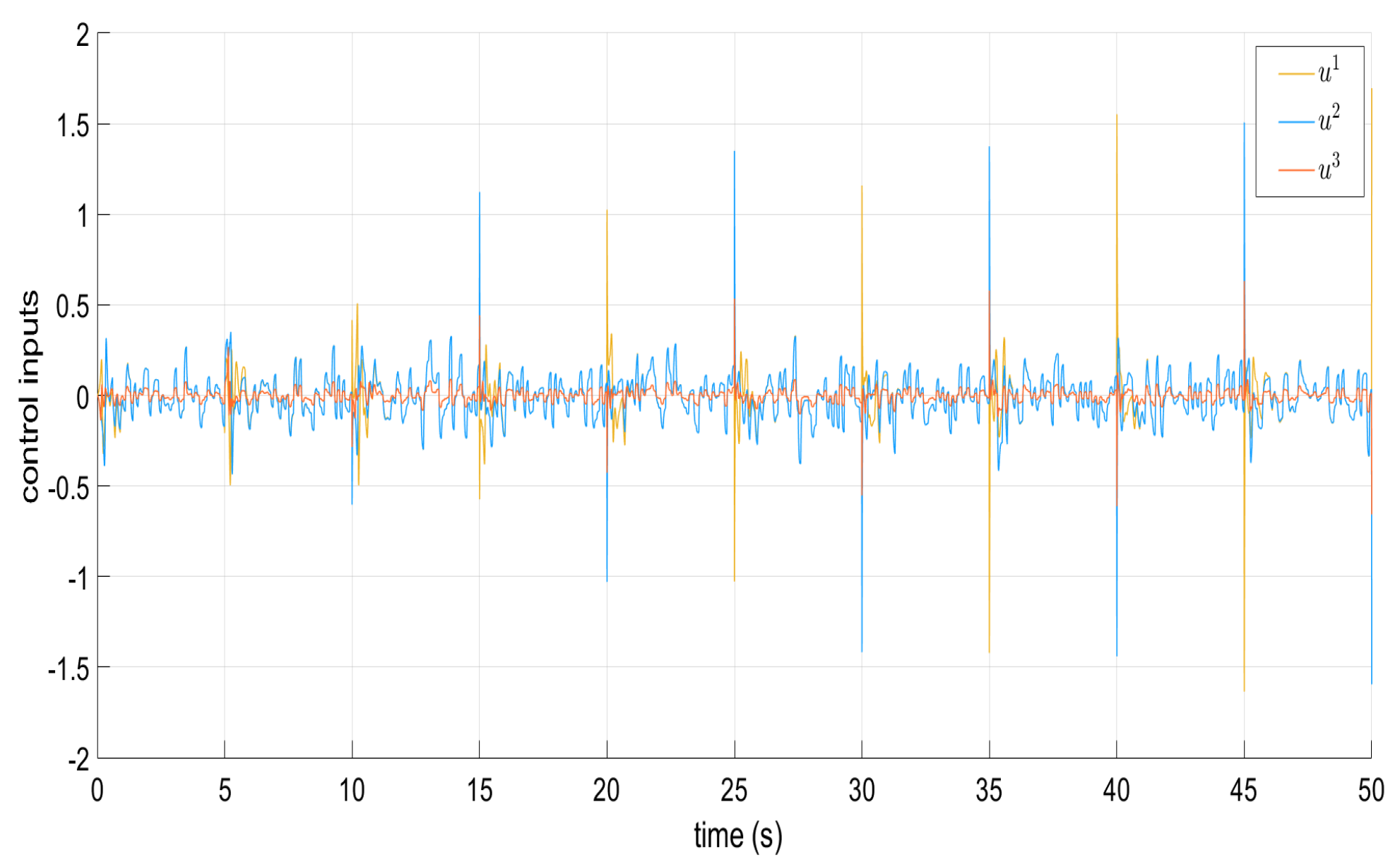
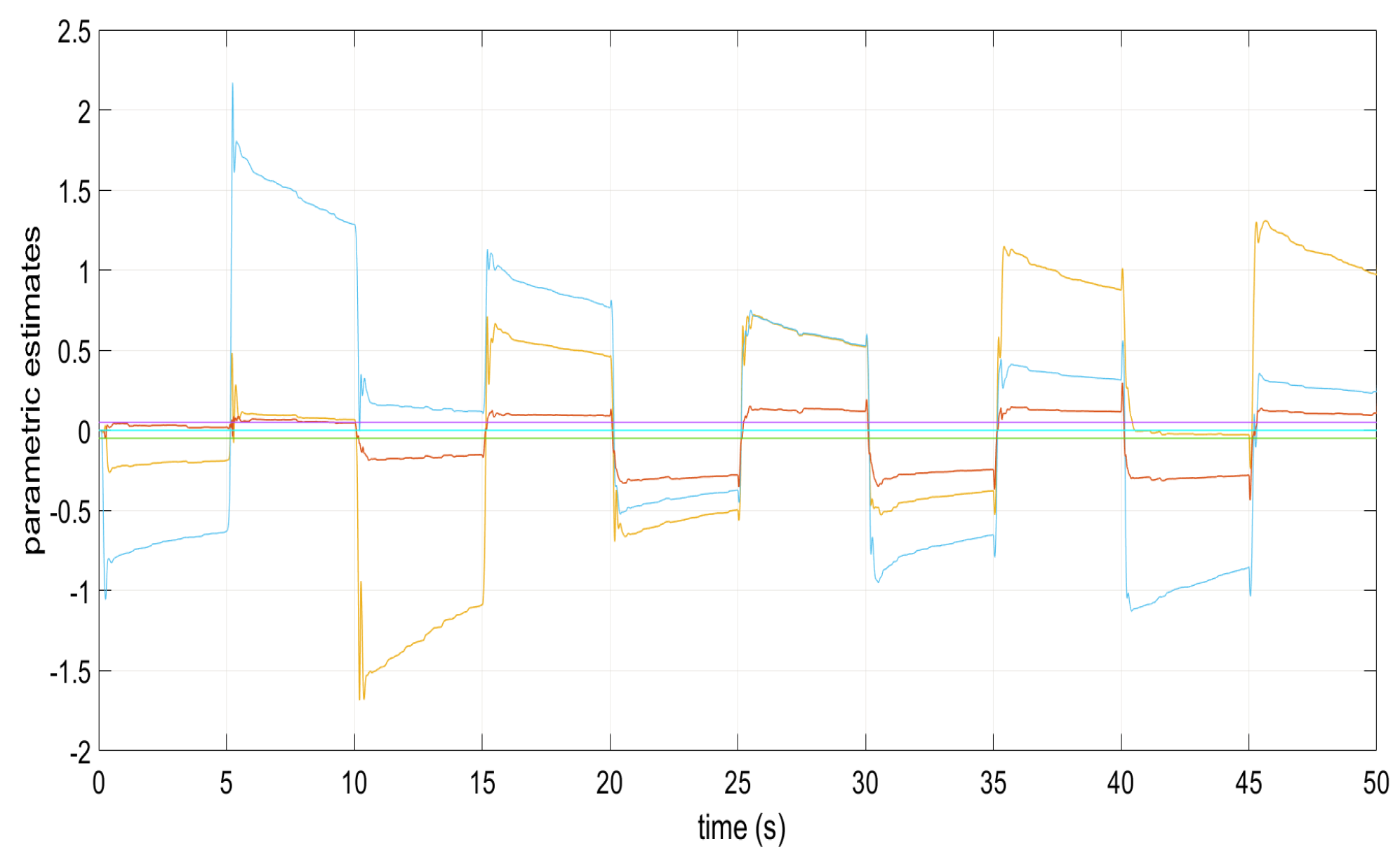
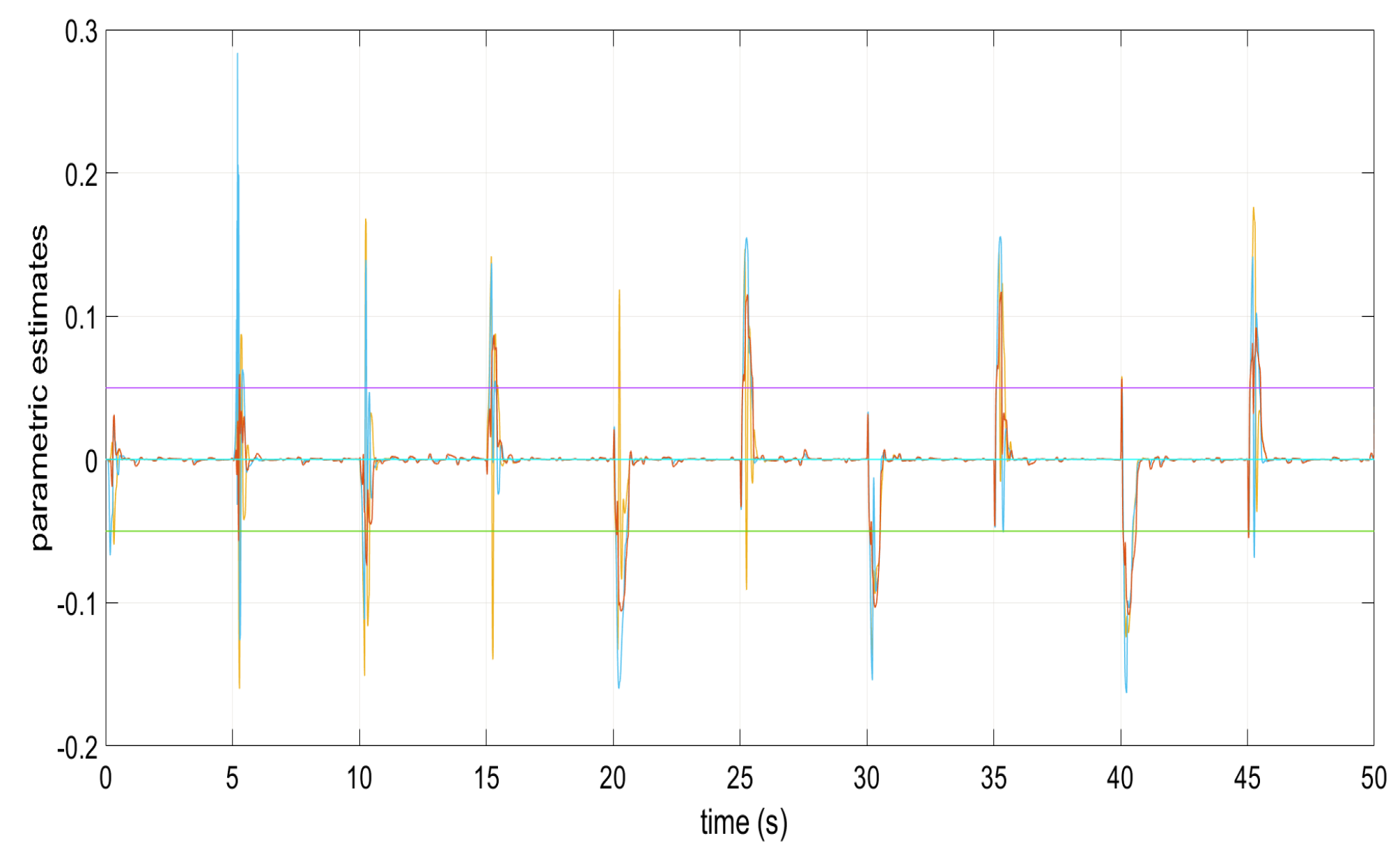
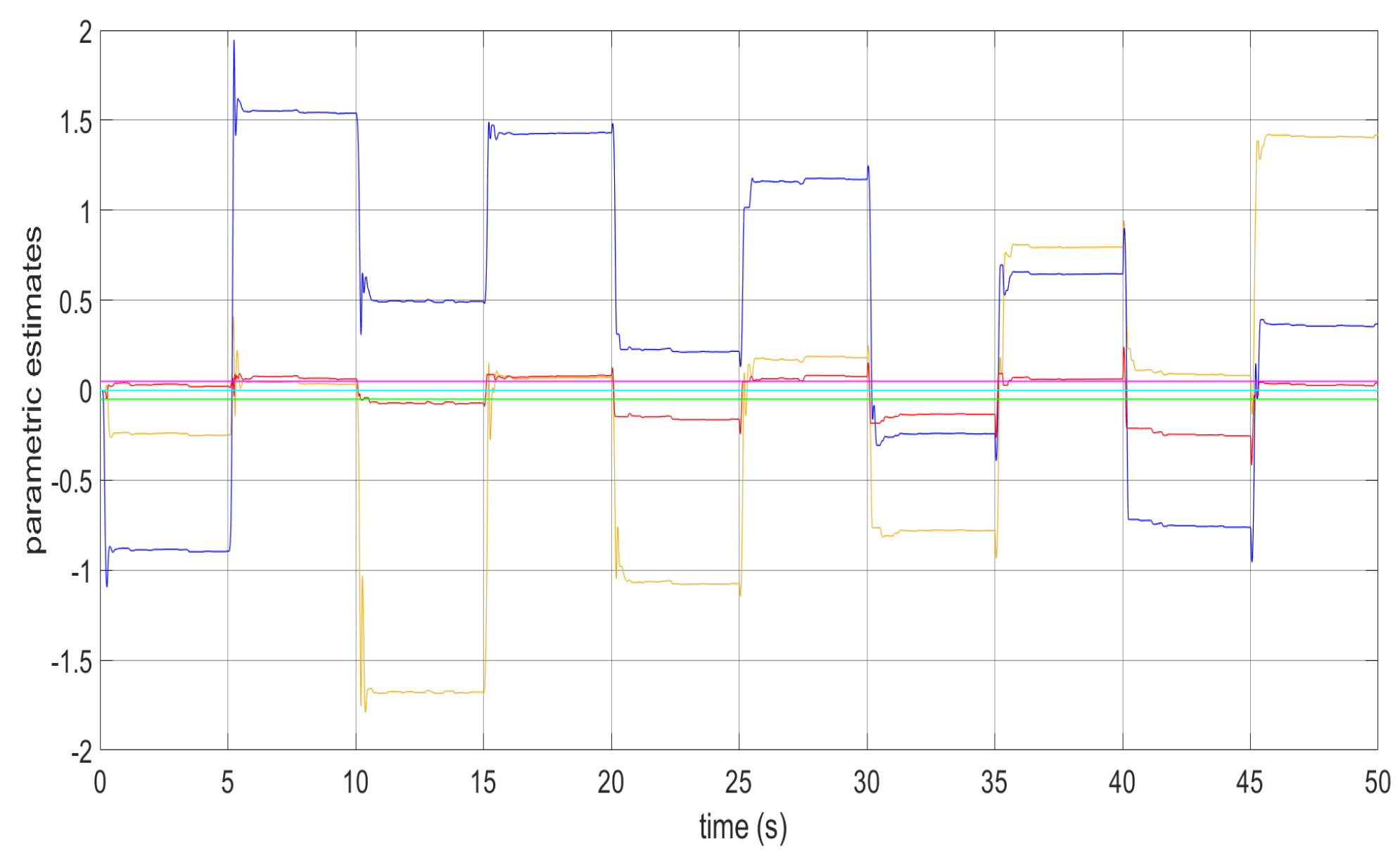
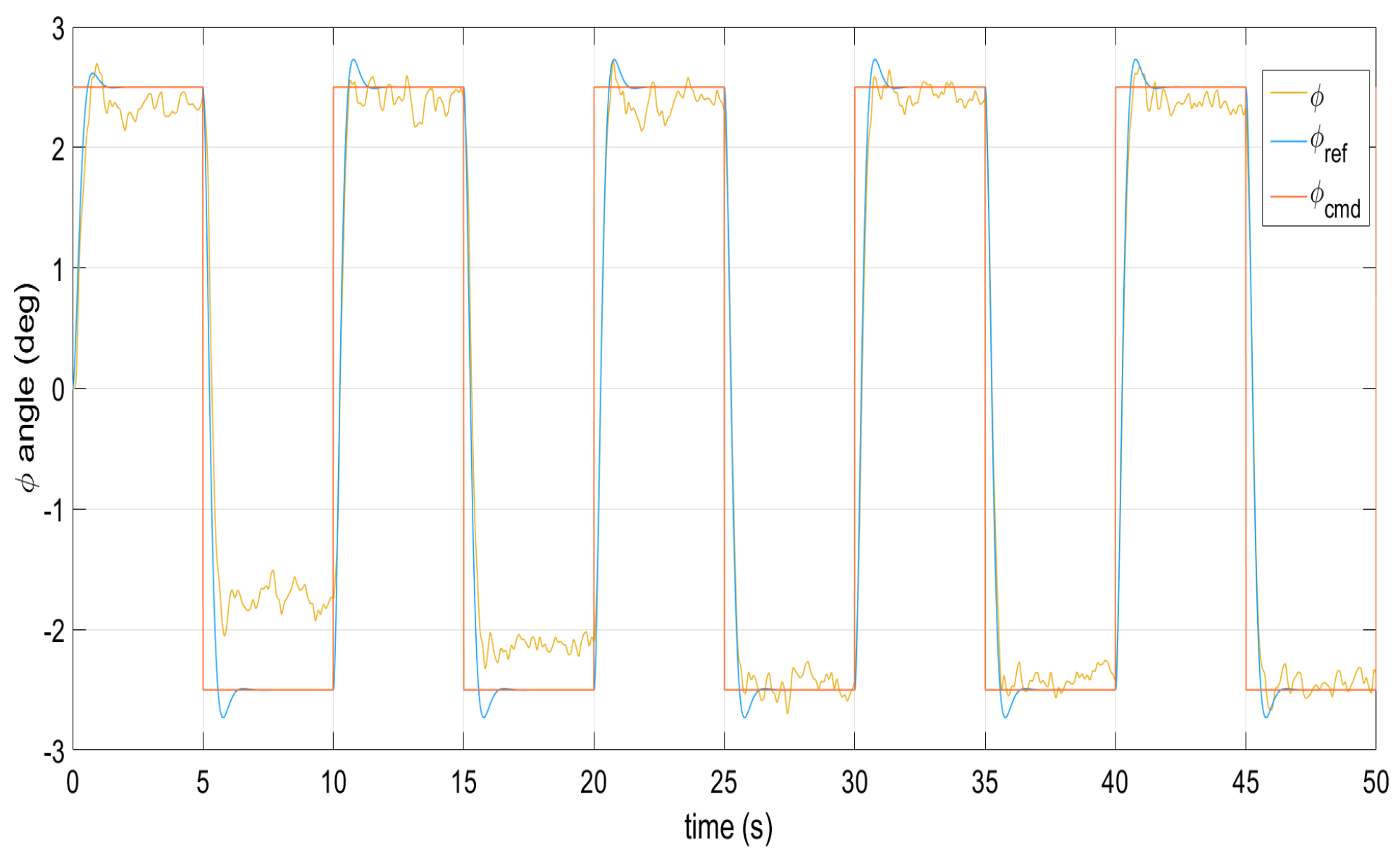
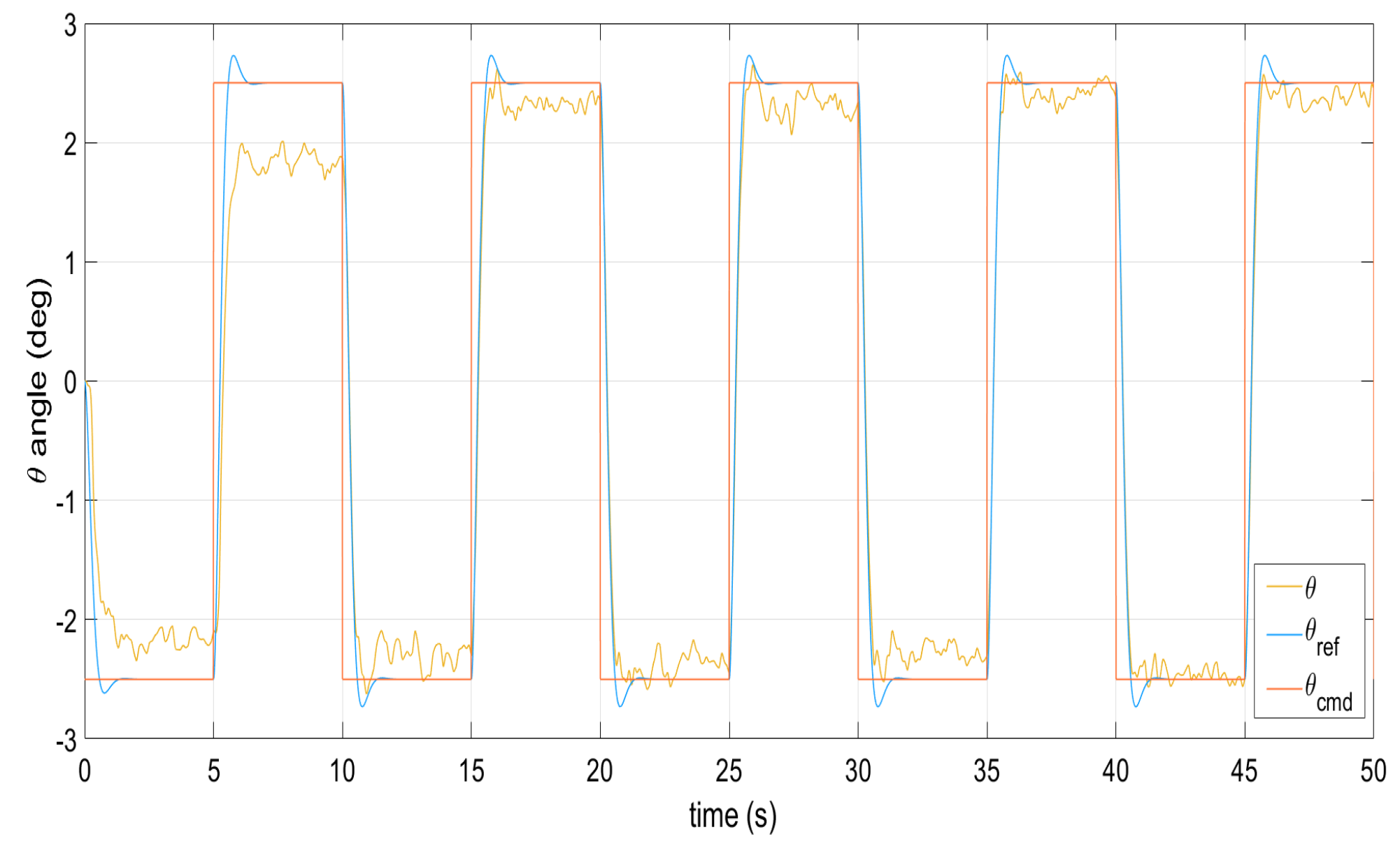
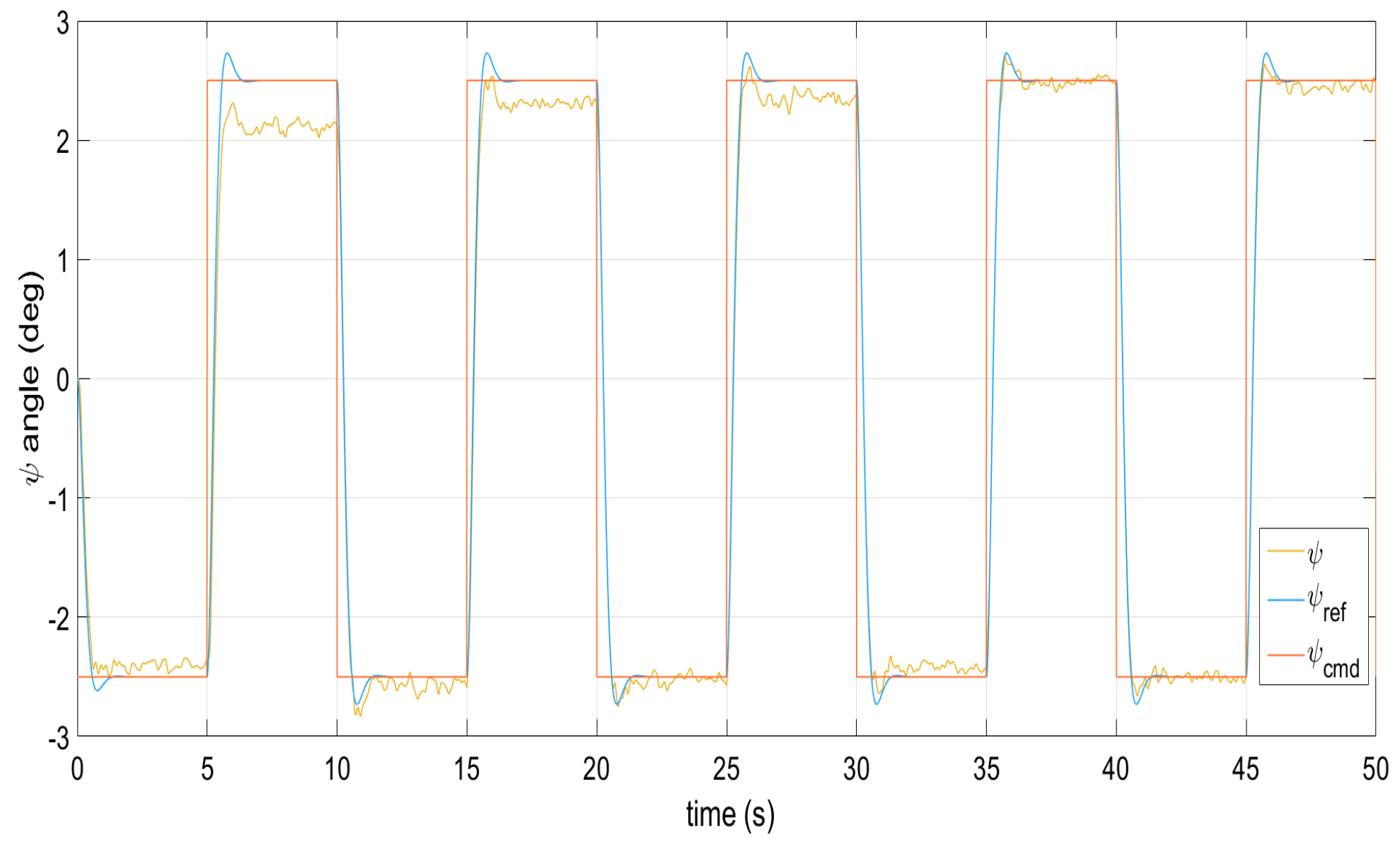
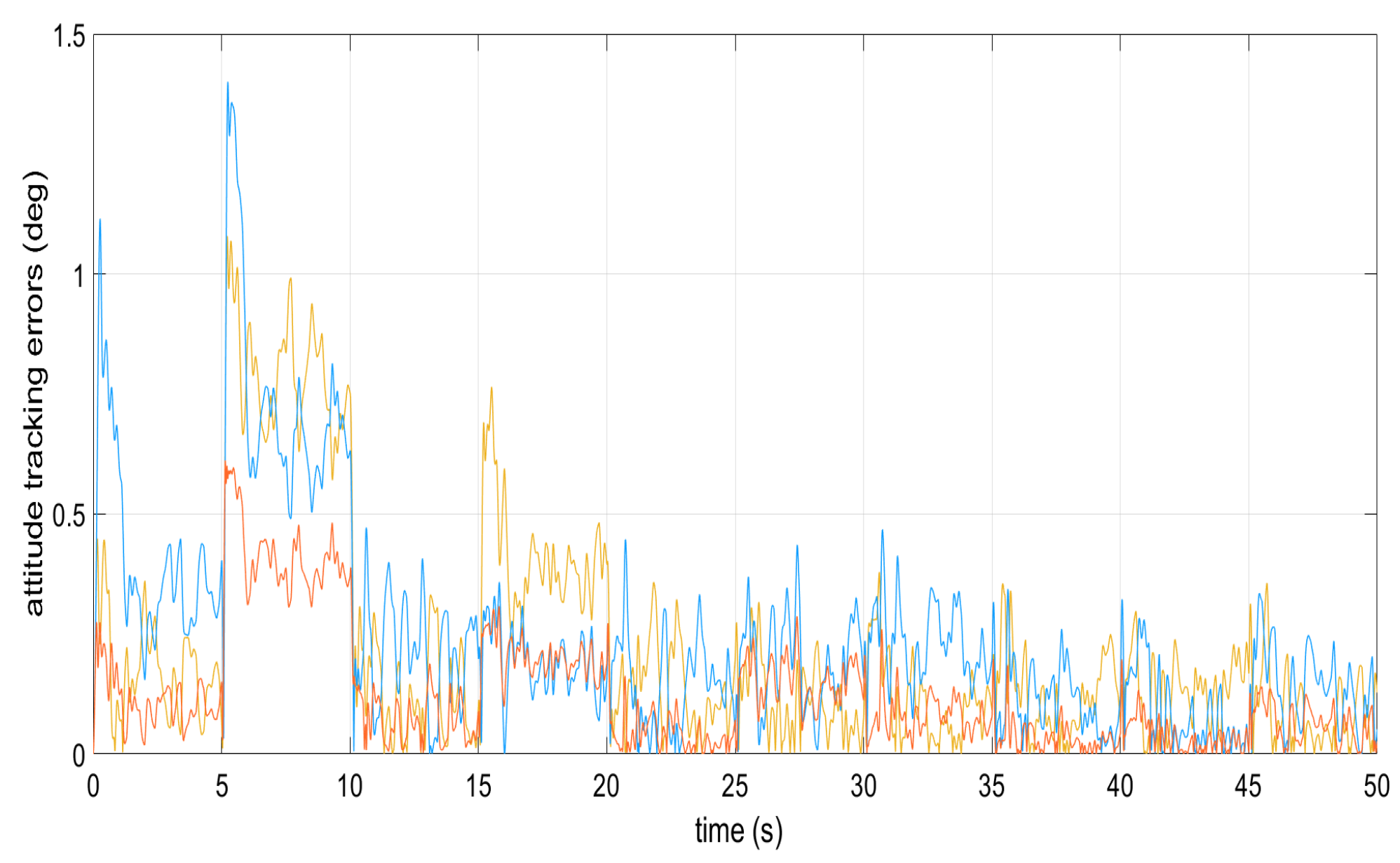
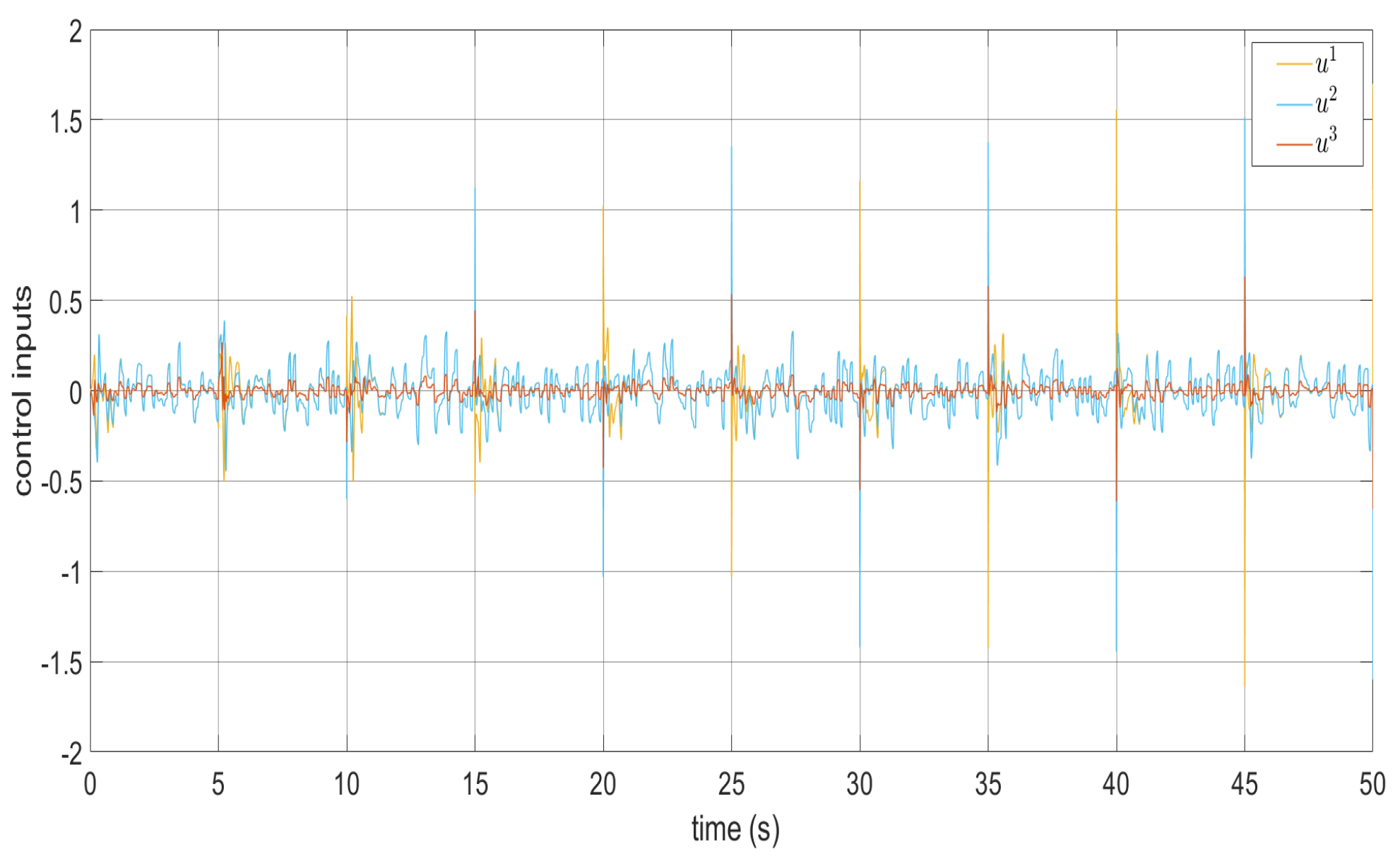
Figure 1, Figure 2, Figure 3, Figure 4 and Figure 5 show the performance of the decentralized robust MRAC with e-modification (38), and $\sigma =0.1$, in the absence of disturbances when performing reference tracking to the pose of the quadrotor UAV. It can be noticed that in the absence of perturbations, the parametric estimates tend to their ideal values in contrast with that proposal in [28], where the parametric estimates from the adaptive law with $\sigma$-modification tend to zero. Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11 show that the decentralized robust MRAC with e-modification (38) is capable of confronting perturbations. Figure 12 and Figure 13 show that the parametric estimates dynamics from the adaptive law with e-modification (38) but with different values for $\sigma$; this latter case is also compared to the case when the quadrotor UAV is under the influence of external perturbations. It must be noticed that the results about reference tracking by the decentralized MRAC with e-modification (38) for these latter cases are not included since they are similar to those shown in Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11.

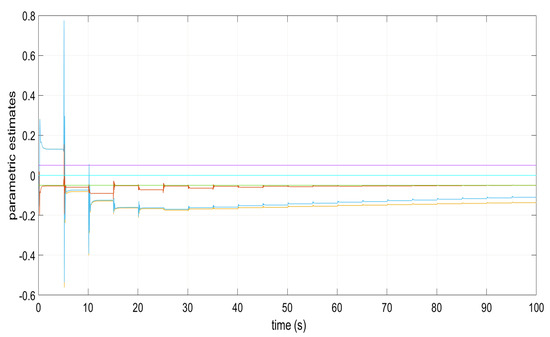
Figure 1. Parametric estimates ${\hat{\mathsf{\Theta }}}_1,{\hat{\mathsf{\Theta }}}_2$ and ${\hat{\mathsf{\Theta }}}_3$ in the absence of disturbances.

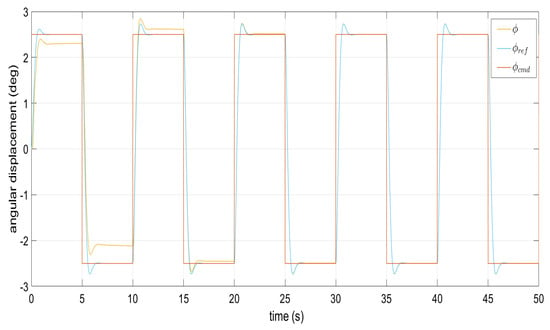
Figure 2. Command signal tracking from the roll angle in the absence of perturbations.

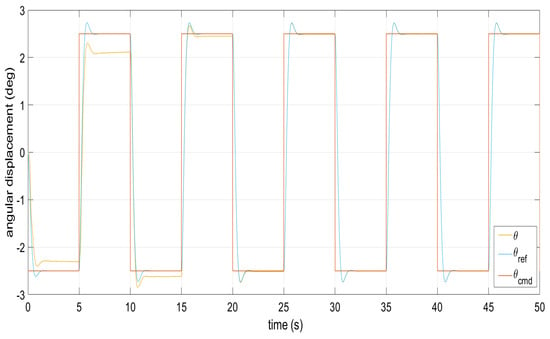
Figure 3. Command signal tracking from the pitch angle in the absence of perturbations.

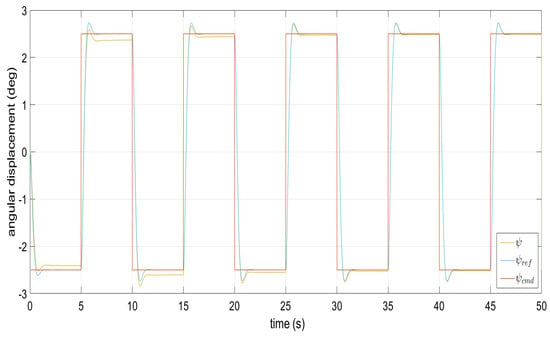
Figure 4. Reference model following the yaw angle in the absence of perturbation.

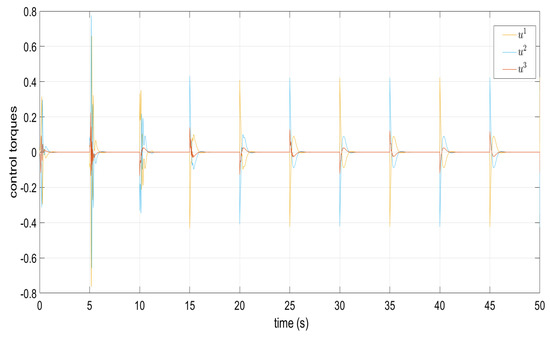
Figure 5. Torque signals $u^1,u^2$ and $u^3$ in the absence of perturbations.

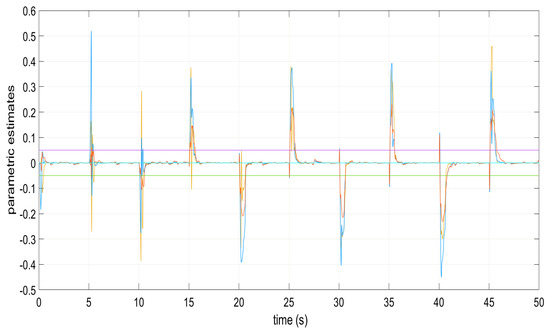
Figure 6. Parametric estimates ${\hat{\mathsf{\Theta }}}_1,{\hat{\mathsf{\Theta }}}_2$ and ${\hat{\mathsf{\Theta }}}_3$ in the appearance of perturbations.

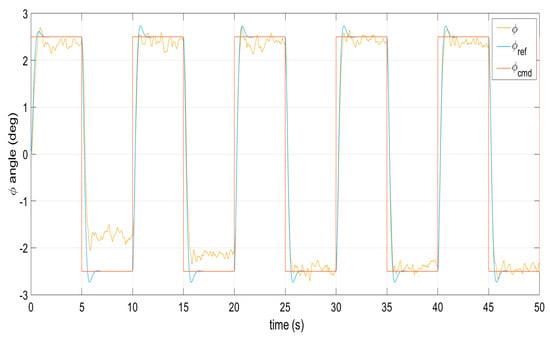
Figure 7. Command signal tracking by the roll angle under perturbations.

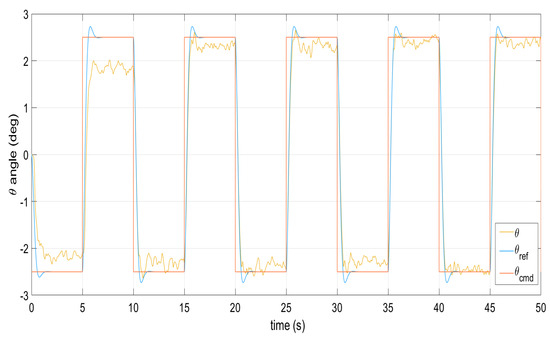
Figure 8. Command signal tracking by the pitch angle under perturbations.

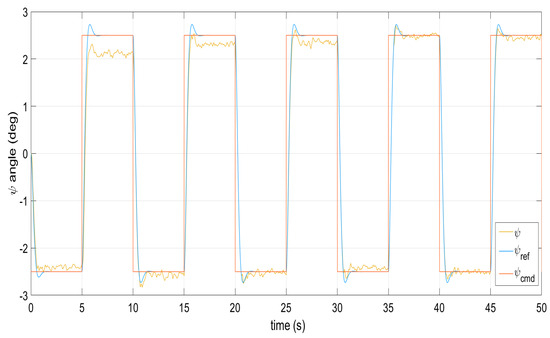
Figure 9. Reference model following the yaw angle under external perturbations.

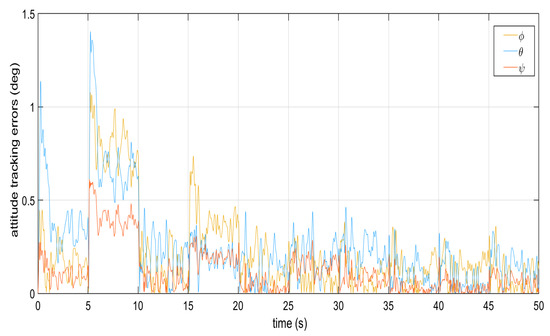
Figure 10. Tracking errors from the dynamics of the attitude angles.

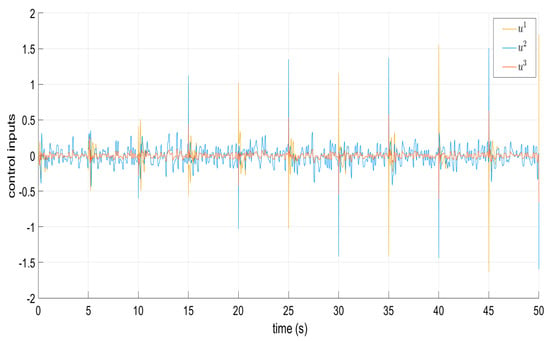
Figure 11. Torque signals $u^1,u^2$ and $u^3$ when confronting perturbations.

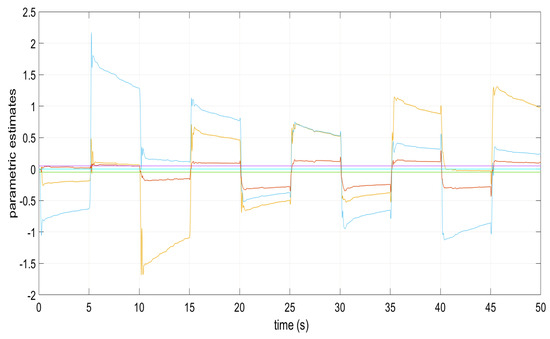
Figure 12. Parametric estimates ${\hat{\mathsf{\Theta }}}_1,{\hat{\mathsf{\Theta }}}_2$ and ${\hat{\mathsf{\Theta }}}_3$ under perturbations for $\sigma =0.001$.

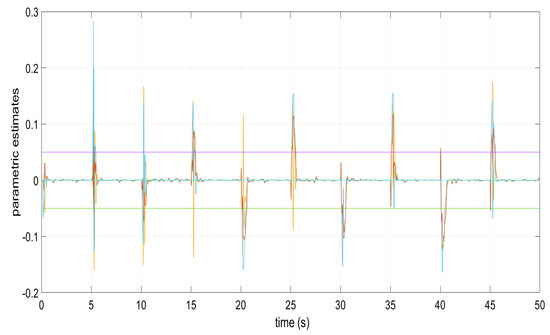
Figure 13. Parametric estimates ${\hat{\mathsf{\Theta }}}_1,{\hat{\mathsf{\Theta }}}_2$ and ${\hat{\mathsf{\Theta }}}_3$ in the appearance of perturbations for $\sigma =0.3$.

The norms and bounds of the error signal and parametric error from the decentralized MRAC with e-modification (38) are exhibited from Table 1, Table 2 and Table 3 for different values of $\sigma$. The best values for the error norm are highlighted in bold font. Therefore, it can be seen that the inequality (47) is satisfied. Thus, from Theorem 1, the robust model reference tracking problem under external unmatched perturbations for the MIMO system is solved.

Table 1. Norms and bounds of the error signals and parametric error from the decentralized MRAC with e-modification for $\sigma =0.01$.

Subsystem	$\parallel \mathbf{e}\parallel$	${\mathbf{c}}_1$	$\parallel \tilde{\mathbf{\Theta }}\parallel$	${\mathbf{c}}_2$
Roll motion	22.2595	10.2967	24.1888	14.0219
Pitch motion	23.1711	10.2967	27.2698	14.0219
Yaw motion	12.0338	10.2965	9.6264	7.2366

For ${\zeta }_{\max }=0.25$.

Table 2. Norms and bounds from the error signals and parametric error from the decentralized MRAC with e-modification for $\sigma =0.001$.

Subsystem	$\parallel \mathbf{e}\parallel$	${\mathbf{c}}_1$	$\parallel \tilde{\mathbf{\Theta }}\parallel$	${\mathbf{c}}_2$
Roll motion	22.3711	10.2966	50.8247	44.3231
Pitch motion	23.2681	10.2966	53.4610	44.3231
Yaw motion	12.0469	10.2965	12.8072	22.8841

For ${\zeta }_{\max }=0.25$.

Table 3. Norms and bounds of the error signal and parametric error from the decentralized MRAC via e-modification for $\sigma =0.0001$.

Subsystem	$\parallel \mathbf{e}\parallel$	${\mathbf{c}}_1$	$\parallel \tilde{\mathbf{\Theta }}\parallel$	${\mathbf{c}}_2$
Roll motion	22.4298	10.2966	57.1221	140.1441
Pitch motion	23.3342	10.2966	60.4800	140.1441
Yaw motion	12.0506	10.2965	14.5524	72.3658

For ${\zeta }_{\max }=0.25$.

Figure 14, Figure 15, Figure 16, Figure 17, Figure 18 and Figure 19 exhibit the dynamics from the decentralized MRAC via smooth dead-zone modification (51) with $\delta =0.9$ and $e_0=0.01$. It can be seen that the decentralized MRAC with smooth dead-zone modification (51) also faces, in a good measure, external perturbations when performing the reference tracking task. Table 4 shows the error signal norm whose values are not far from those for the decentralized MRAC with e-modification (38).

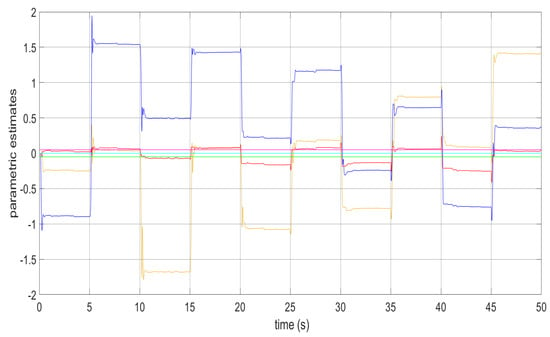
Figure 14. Parametric estimates ${\hat{\mathsf{\Theta }}}_1,{\hat{\mathsf{\Theta }}}_2$ and ${\hat{\mathsf{\Theta }}}_3$ in the appearance of perturbations.

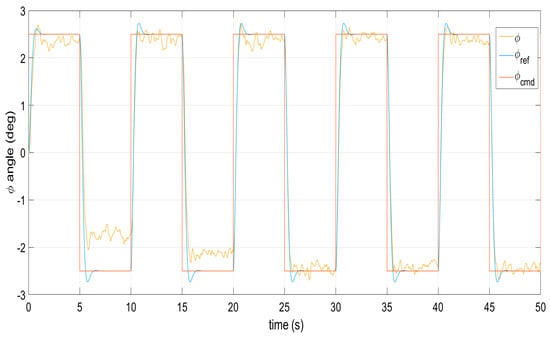
Figure 15. Command signal tracking by the roll angle under perturbations.

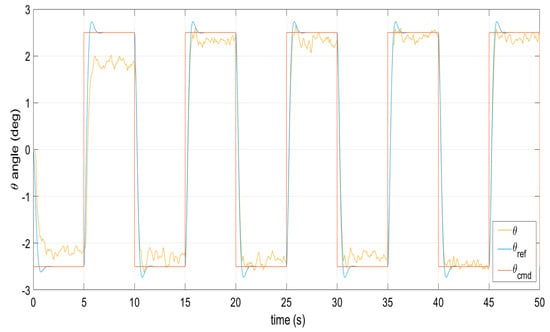
Figure 16. Command signal tracking by the pitch angle under perturbations.

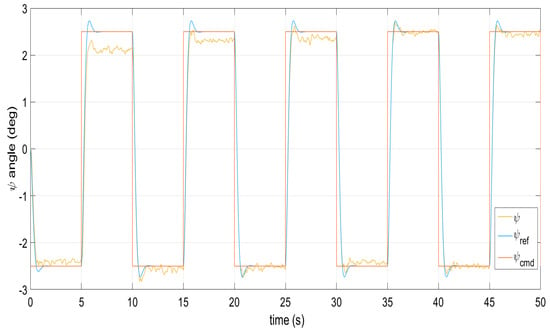
Figure 17. Reference model following the yaw angle under external perturbations.

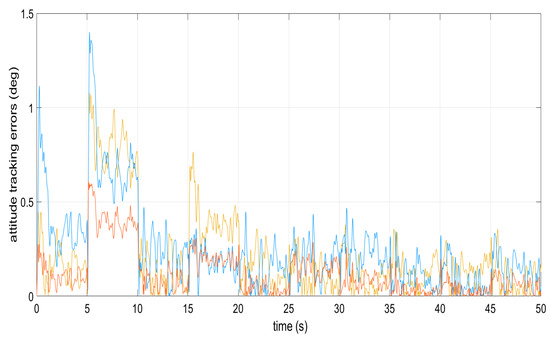
Figure 18. Tracking errors from the dynamics of the attitude angles.

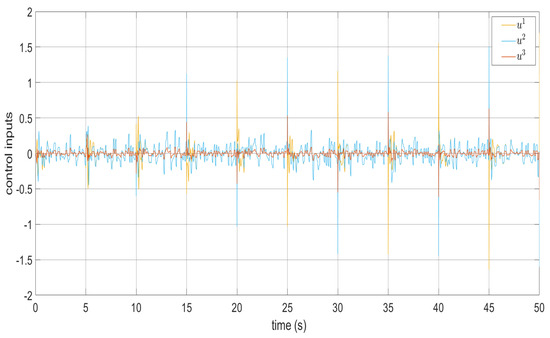
Figure 19. Torque signals $u^1,u^2$ and $u^3$ when confronting perturbations.

Table 4. Error signal norm from the decentralized MRAC via smooth dead-zone modification.

Subsystem	$\parallel \mathbf{e}\parallel$
Roll motion	22.4368
Pitch motion	23.3421
Yaw motion	12.0394

For $e_0=0.01$ and $\delta =0.9$.

Table 5 shows the error signal norm from the decentralized MRAC with $\sigma$-modification, which was proposed in [28], for different values of $\sigma$. The best values are highlighted in bold font, which are those arising from using $\sigma =0.0001$. Figures exhibiting the dynamics from this latter robust MRAC are not included here since its performance is very similar to that reported in [28].

Table 5. Error signal norm from the decentralized MRAC with $\sigma$-modification.

		$\parallel \mathbf{e}\parallel$
	$\sigma =0.01$	$\sigma =0.001$	$\sigma =0.0001$
Subsystem
Roll motion	53.6054	24.8979	24.4003
Pitch motion	47.8176	22.1182	21.8824
Yaw motion	23.8182	11.1669	11.0644

5. Discussion

In the search for the design of a decentralized robust MRAC for the pose of a quadrotor UAV, the e-modification approach is investigated. It must be noticed that the development of this work was also conducted to the proposal of a decentralized robust MRAC via smooth dead-zone modification. For comparison purposes, their performance is contrasted with that from a decentralized robust MRAC previously reported in the literature but designed under the approach of $\sigma$-modification. From experimental simulation results, it can be seen that, through the decentralized MRAC via e-modification, it is possible to obtain the smallest values for the error signal norm between this latter approach and that via smooth dead-zone modification. Also, values from the error signal norm of the decentralized MRAC via smooth dead-zone modification show a good performance from this latter since they are very near those of the decentralized MRAC via e-modification. Moreover, it is interesting to note that the decentralized robust MRAC via $\sigma$-modification exhibits the smallest values of the error signal norm between pitch motion and yaw motion subsystems. Likewise, from this work, it can be seen that the decentralized MRACs for the pose of a quadrotor UAV are robust under the effect of external perturbations since the parametric estimates do not drift to infinity. Additionally, the purpose of most control system designs is to regulate small motions rather than to control absolute position, as is the case with spacecraft attitude dynamics control, where the disturbance (gravitational) torques are of a very low order. Thus, it is worthwhile to note that our proposal could be exploited in the satellite attitude control.

6. Conclusions

It can be seen that, from simulation results, the parametric estimates from the adaptive laws converge to their ideal values in the absence of perturbations for the decentralized MRAC via e-modification. In contrast, in the presence of external perturbations, the parametric estimates tend to the origin, i.e., the parametric estimates from the adaptive laws do not drift to infinity when the decentralized MRAC via e-modification for the pose of the quadrotor UAV has to confront external perturbations. From the above, it can be concluded that the decentralized MRAC via e-modification is robust. Also, the parametric estimation errors do not converge to the origin when the decentralized MRAC with e-modification is under the influence of external perturbations. Moreover, the decentralized MRAC via smooth dead-zone modification is a good option when confronting perturbations. Additionally, it must be noted that the quadrotor UAV arrives at the reference for the altitude in both scenarios. Likewise, our proposal allows us to combine the decentralized robust MRACs, like those from the pitch motion and yaw motion from the $\sigma$-modification, with that for the roll motion from the e-modification, in the achievement of the best performance to the model reference tracking task. Furthermore, the yaw motion subsystem, as it has been shown through experience, demands the minimum control effort in comparison with those from the remaining subsystems.