An Optimal Scheduling Technique for Smart Grid Communications over 5G Networks

Abstract

The latest wireless network technology, Fifth Generation (5G) new radio (NR), is considered to be an emerging wireless network solution for smart grid (SG) communications owing to its ultra-reliable low latency and larger bandwidth properties. Packet scheduling is one of the mechanisms that plays a vital function in the performance of smart grid communications since it is highly responsible for the bandwidth resource allocation processes. The union of a scheduling approach and a beamforming technique can, however, boost the performance of multi-users in the communication system. Since 5G communication is not intended for smart grid communications, the performance of a scheduling approach must be properly utilized and effectively optimized. This paper evaluates and examines the Deadline Scheduling with Commitment (DSC) scheduling approach and further demonstrates that the performance of the popular Earliest Deadline First (EDF) scheduling approach can be richly enhanced by our modification and improvement of the approach. A novel Optimal Usage and Dropping Scheduling (OUD) approach for proper utilization and assigning of Resource Blocks (RBs) is also proposed to meet the stringent requirements of smart grid communications. Several performance indexes are employed to ascertain the performance of these scheduling approaches, and the results indicate that our proposed OUD approach shows a superior scheduling performance. It is concluded that 5G communications can be effectively employed in smart grids while utilizing the proposed OUD scheduling approach.

1. Introduction

The conventional power system is gradually being substituted with a modern-based technological infrastructure that utilizes a recent and emerging communication system known as smart grid (SG). Smart grids ensure more secure distributed generation options, adequate power storage, and state-of-the-art communication technologies. Smart grid also fuses and combines several technological advancements like sensor measurement technologies, computer technologies, control technologies, and communication technologies with the conventional grid facilities to form an innovative type of electric grid that represents a developmental stride of the upcoming power grid [1]. In modern times, smart grids have proven to be self-healing, economically viable, clean, safe, and armed with the capabilities of delivering high-grade power networks suited for the digital age. Unlike the conventional electric power grids that only allow a single passage flow of electricity, smart grids permit a two-way electricity passage between electricity customers and power grids. Furthermore, and most significantly, the integration of Information Communication Technologies (ICTs) into the grid presents a two-way passage of information, thereby enabling the grid to possess digital capabilities and transforming electricity consumers to become active contributors and participators.

The diagram in Figure 1 depicts an ideal model of a typical smart grid, as considered in [2]. It comprises seven different sectional domains with information flowing between them. The four main domains below practically depict the physical facilities of a conventional power grid representing the generating, transmitting, and distributing sectors coupled with the customers. There is also a flow of energy that exists between them which is denoted by the solid red line in the figure. The three other domains located at the top are primarily associated with the information communication technology infrastructure and other electricity facilities comprising service providers, power markets, and operations. The flow of information is represented by dashed blue lines in the figure serving as a source of interaction between the domains, thereby arming the power grid with smartness and intelligence.

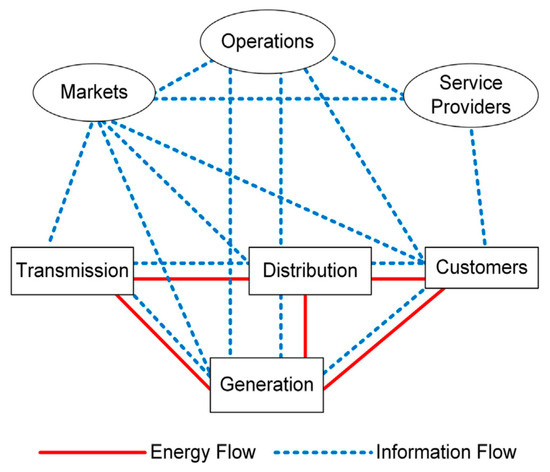
Figure 1. A typical smart grid model [2].

Developing an adaptable communication infrastructure with the existing wireless communication technologies can be very beneficial and favorable to smart grids. This will no doubt provide advanced technological infrastructure, thereby avoiding extra cost and time and will further provide growth in communication technologies and the inclusion of additional applications.

Wireless communication technologies have become a significant part of smart grids since they are largely responsible for monitoring, controlling, and delivering commands amongst power-generating processes, substations, and the end user [3]. Regardless, numerous communication networks can be deployed in smart grids, for instance, Long-Term Evolution, WiMAX, and 5G networks. In a practical scenario, a single wireless communication network cannot successfully cater for the whole entirety of smart grid applications [4]. The 5G network is, however, perceived to be one of the most ideal wireless communication technologies for the next generation of electrical grids owing to its ultra-low latency, high security, data rates, and high performance [5].

The emergence of fifth-generation mobile networks (5G) as a technological means of communication in smart grids can, however, bring about an unparalleled opportunity to proffer and improve on a countless number of promising applications like Demand Response, Smart Homes, Vehicle-to-Grid (V2G), and Advanced Metering Infrastructure (AMI) [6,7]. Fifth Generation is a revolutionary mobile communication that delivers a ubiquitous and ultra-broadband fiber-like experience to customers to utilize emerging swift mobile services such as ultrahigh definition video sharing, Intelligent Transportation Systems (ITSs) [8], machine-type communications [9], and low latency. Fifth-Generation technology will no doubt offer smart and suitable servicing support for real-time applications necessary for the functional operation of an organization just like the ones envisaged for smart grids in evaluating performance [10].

In addition to the basic 20 Gbps downlink and the 10 Gbps uplink data rate that 5G promises, it can also successfully accommodate 1000 times more data traffic while hosting 60 billion or more “online things” such as smart home appliances, sensors, wearable devices, vehicles, and many more. This, however, makes 5G a suitable candidate to successfully introduce Internet of Things (IoTs) to smart grids where multiple devices can serve every user [11]. To ensure more than enough bandwidth, 5G is moving towards the mmWave spectrum and also opportunistically utilizing WiFi’s unlicensed spectrum in the 5 GHz band and also making use of MIMO technologies to ensure adequate spectral efficiency for more bits/s/Hz per node.

One of the most crucial but challenging aspects of smart grid communications over 5G networks is usually task (resource) scheduling. Tasks (user request) submitted by a user equipment to the communication network are processed by a scheduling algorithm and distributed immediately for execution. This article aims to propose a novel algorithm called the Optimal Usage and Dropping Scheduling technique, and the motivation behind this work is as follows:

-

When static scheduling techniques are employed, the network load becomes quite heavy, rendering the resource utilization process less effective.

-

In smart grid communications, the priority of data flow is that the essence and service requirements must be met to avoid packet delay and ensure the reliable scheduling of packets.

-

As much as 5G networks aim to offer high-speed data transfer with low latency, the gradual increase in the number of active users, however, puts a strain on the resource distribution and allocation processes when employing conventional resource allocation techniques.

-

In assigning dedicated resources for transmissions and retransmissions in a typical smart grid, the unstable signal quality causes the resources required for retransmission to be uncertain. This can be a cause of great concern, especially when high-criticality packets or high-priority data cannot be transmitted.

These, therefore, motivate the need to develop an optimal scheduling technique to increase the probability of assigning available Resource Blocks (RBs) to smart grid users. In a typical 5G-enabled network, the least allocatable resource unit in the network is known as a resource block which spans through the sub-1 GHz to millimeter wave bands with a frame duration of 10 ms consisting of 10 subframes, as seen in Figure 2, with scheduling decisions updated at each Transmission Time Interval (TTI). From the figure, the left-hand side depicts the waveform, numerology, and frame structure, while the right-hand side illustrates the resource carrier and bandwidth. It is seen that the duration of the slots of a subframe in milliseconds is dependent on the network numerology. Hence, for a 15 kHz subcarrier, a slot has the same structure as a typical 5G subframe. Each of the sub-frames consists of $2^{\mu }$ slots of 14 OFDM symbols each. Resource management in a 5G-enabled network can be improved by enabling transmission to begin at any OFDM symbol and only last as many symbols as is needed for a specified communication. This no doubt brings about low latency for data and also minimal interference in the network. It is noteworthy to mention that the operation of 5G in millimeter wave bands benefits significantly when complemented by a low-frequency carrier to ensure good coverage, especially in the uplink (UL). In as much as that, the poor management of the resources of 5G can also lead to performance degradation in a communication system. Hence, supplementary UL can be used as low bands complement to the cell’s UL when operating in high-frequency bands and a supplementary DL in a cell’s DL in the spectrum [12]. Radio resource scheduling and management play a vital role in a typical smart grid communication system since it is responsible for allocating radio spectrum resources while guaranteeing the several types of available services. Since 5G networks are not particularly intended for smart grids and because requirements are different amongst devices in a typical smart grid network, it is imperative to formulate and develop efficient scheduling algorithms to meet the requirements of smart grids.

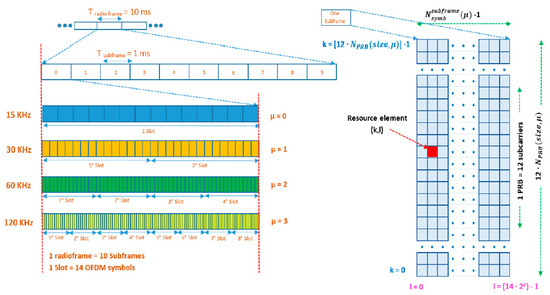
Figure 2. Typical illustration of 5G new radio frame structure and resource block [12].

In this paper, the best possible packet scheduling approaches are proposed and examined, and their suitability for smart grid communications is ascertained and established. The main contributions and highlights of this study are as follows:

-

Elucidate the differences between the operation mode and execution of different scheduling algorithms employed in various environments, including computing, process systems, and smart grid environment.

-

Develop a Deadline Scheduling with Commitment algorithm and evaluate the DSC technique as a possible scheduling candidate for smart grid communications over 5G networks.

-

EDF scheduler is a popular scheduling approach employed in various queuing models; however, its performance has not been too superior due to its inability to prioritize packets. In this work, the present EDF scheduling technique (I-EDF) is improved and modified by including an optimal queuing technique and the knowledge of servicing time upon arrival and other favorable characteristics to enhance its performance.

-

Propose an optimal usage and dropping scheduler that can conveniently accommodate smart grid communications and allocate resources to achieve maximum rewards.

-

Develop a suitable RB allocator that is responsible for allocating the available channels to packets.

The rest of this paper is organized as follows: In Section 2, a review of the works that are related to this area is conducted. Section 3 presents the system model, and Section 4 illustrates the packet scheduling architecture. The simulation results obtained are discussed in Section 5, while Section 6 concludes the work.

2. Related Works

Several research efforts have been made to incorporate efficient scheduling techniques for both real-time and non-real-time applications. The role of 5G in smart grid communications networks has also been investigated recently. For instance, [13] explored the use of 5G slicing technology in which a carrying method based on a neural network is proposed to dynamically predict traffic in the slicing network. A GSM triplexer for 5G-enabled IoT is also designed and evaluated in [14] for smart grid edge computing and the Metaverse. The proposed triplexer is, however, seen to possess low insertion losses.

It is the primary aim of the scheduling technique in a communication network to effectively and conveniently share resources among all tasks and processes in a fair manner [15]. Several scheduling techniques exist depending on how it is implemented and its suitability to improve the system’s communications. In a work by the authors in [16], a fair share scheduler is proposed in which each process is given a weight of the user’s share of the resources in the system as a fraction of the overall resource usage. An algorithm is used to partition the system’s asset into different portions and then allotted to the different fair-share groups by the process schedulers. Also, in [17], the authors proposed a multi-core migration and placement technique to manage resource fairness amongst the processes in a system which eventually enhances its performance by default. A hybrid scheduling algorithm comprising a primary and secondary phase is proposed in [18]. The primary phase aims to limit information conditions amongst subtasks and adjust loads, while the secondary phase limits the “makes-span” without abusing user priorities. The technique employs an elective processor that utilizes a higher capacity to perform subtasks inside a certain cut-off time.

Emerging and developed applications in smart grids, for instance, autonomous cars, require low latency to transmit their packets. That means that implementing low-latency communications will result in each packet having deadline needs that are to be met. In a typical real-time system, if a packet does not deliver before the stipulated deadline, it will be regarded as lost packets. These real-time system issues have been extensively studied in [19,20,21]. A scheduler algorithm known as the Earliest Deadline First (EDF) scheduling algorithm is one of the most popular scheduling techniques employed in a real-time system. EDF is ideal amongst several queuing approaches [22,23,24], yet, amid in prioritized packets, it might not be the ideal technique [25]. In a bid to improve the EDF technique, a controlled pre-emptive EDF (CP-EDF) scheduling approach is proposed in [26] to avoid the occurrence of pre-emption in the system. When the pre-emptions are high in the system, the algorithm behaves like a non-pre-emptive EDF where each of the tasks are computed based on having a task with the least deadline. But when pre-emptions are low, it behaves like a full pre-emptive algorithm where pre-emption is due to occur when the deadline of other processes is lower than the deadline of the task presently being executed.

Quite a few other scheduling techniques have also been proposed to ensure a better performance of resource allocation in systems. Although the complexity of these algorithms is low, most of them are channel-unaware strategies and do not pay much attention to the channel quality, such as the First-In–First-Out strategy in [27] and the Round Robin scheduling method in [28]. A channel-aware strategy that takes into consideration the user’s channel quality so as to boost the system’s throughput is proposed in [29] using the Max C/I algorithm. However, the Quality of Service (QoS) is not taken into consideration. Scheduling policies that take serving priority and rewards as a major importance in their algorithms are presented in [30,31,32], in which packets are placed in a queue and a cost function system is utilized to ascertain the amounts of packets in the queue. As much as packet scheduling with various rewards has been examined, the issue of collaboratively scheduling data packets and the less effective allocation of spectrum resources still needs to be solved when beamforming techniques are applied at the physical layer. With the aim of achieving effective resource allocation and utilization, in this work, there is an improvement in and modification of the existing EDF algorithms in [22,23,24,25] and also presents a proposed scheduling approach that utilizes a mechanism based on scheduling and dropping to schedule packets for transmission, effective resource elements utilization, and allocation so as to achieve optimal rewards and finally meet the requirements of smart grid communications.

3. System Model

In this work, a typical smart grid communication model that is primarily based on a 5G network system is considered. We also consider a sub-system in the network, which is composed of a cellular access network, Next Generation Node B (gNodeB), a radio bearer, and user equipment (UE), as shown in Figure 3. The smart grid user or UE as the case maybe is meant to establish a wireless link with the gNodeB to secure direct access to the evolved packet core, and in a smart grid communication setting, the UEs are considered as AMI devices. In our system model, the following assumptions have been made:

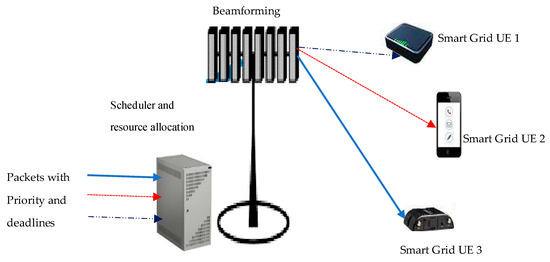
Figure 3. System model architecture.

-

That the gNodeB employs a static beam-forming technique;

-

That each of the UEs can be served by a lone optimal beam;

-

That each of the packets is specifically targeted to a particular UE;

-

That the number of UEs in the system is finite;

-

That the UEs are randomly distributed around the gNodeB.

3.1. Packet Arrival Model

In this packet arrival model, a renewal reward process is employed as defined in [33]. Every packet possesses a time of arrival, a UE, priority and deadline, and a packet size. The parameter $K_i$ is taken to be the data packet arriving in the cell at time $t_i$, while $B_i$ is taken to be the time of inter-arrival of the reward renewal process $\mathcal{B}$, $t_i=t_{i-1}+B_i=\sum _{j=1}^i{B}_j$. The size of the packet is denoted as $S_i$, and the deadline is denoted as $D_i$. The time $t_i$ is calculated from the time of arrival to the end of when a packet is successfully delivered. The priority of the packet $K_i$ is represented as $P_i$, and upon a successful packet delivery, the priority becomes the reward, while $C_i$ is the designated UE. The n-tuple representing a single packet with its random parameter is taken as $K_i=\left(b_i, s_i, d_i, p_i, q_i, r_i\right)$. Let $b_i, s_i, d_i$, and $p_i$ be the realizations of $B_i$, $S_i, D_i$, and $P_i$, and let $q_i=t_i+d_i$, which is considered as the reward. Let ${\acute{J}}_t^{\sigma }$ represent the set of already processed tasks by the policy $\sigma$ up to the time $t$.

The renewal reward process which is a recurrent event process with independent identically distributed interevent times is employed as a strategy to effectively analyze the system’s performance. The cumulative rewards function is one of the simplest ways to correlate the performance of various algorithms.

Definition 1.

The cumulative rewards function for time $t$ and policy $\sigma$ can be defined as:

$$F_t^{\sigma }={\sum }_{K_i\in J_t^{\sigma }}{p}_i$$

(1)

Let$t={\acute{t}}_n$ and $\widehat{t}$= ${\acute{t}}_{n-1}$; then, the rewards difference function is computed as:

$$∆F_t^{\sigma }=F_t^{\sigma }-F_{\widehat{t}}^{\sigma }$$

(2)

The objective is to locate the policy $\sigma$ that tends to maximize the cumulative rewards function. If the reward is deterministic and $P_i=1$, the cumulative reward function then calculates the number of tasks that were serviced.

3.2. Resource Blocks and Structure

Fifth Generation NR is highly dependent on Orthogonal Frequency-Division Multiplexing (OFDM) and can also coexist with LTE on the same frequency band. The 5G NR frame has a time length of 10 ms consisting of 10 subframes, each having a time length of 1 ms. In an OFDM network, 5G NR can enable transmission to begin at any OFDM symbol and will continue on several symbols that are required for the communication, and the data transmitted in the downlink (DL) are split into RBs. The amount of radio resources in a subframe of 1 ms in a specific sub-carrier spacing of a carrier can be perceived as a resource grid composed of subcarriers in frequency and OFDM symbol in time. Hence, each resource element in the resource grid occupies a subcarrier in frequency and another in OFDM symbol in time, which is often regarded as the Transmission Time Interval (TTI). A sub-frame is also regarded as the frequency blocks at a given TTI.

In a 5G NR frame structure, each sub-frame comprises $2^{\eta }$ time slots to handle a broad variety of applications for which it was created for and of course the large spectrum availability. Each TTI contains 14 OFDM symbols or resource elements (12 resource elements in the event of when extended cyclic prefix is used). Consequently, symbol duration is equal to ${(14\times 2^{\eta })}^{-1} \mathrm{m}\mathrm{s}$ or ${(12\times 2^{\eta })}^{-1} \mathrm{m}\mathrm{s}$ if extended cyclic prefix is used [12]. Therefore, the number of symbols constituting each subframe greatly depends on $\eta$. This means a larger value of $\eta$ will lead to more sub-carrier spacing. The RB spacing and period ensure that there is feedback on the quality of the channel and also ensures that the DL scheduler optimizes the utilization of the channel. RBs are the scheduling units in a 5G NR system and are devoted to a particular UE. The RB scheduler ensures that RBs are allocated to connections between the cells and the UEs while maximizing the bearer’s utilization [34].

The antenna system of the cell comprises the an array of $Y_a$ elements consisting of $Y_b$ static beam. For simplicity of our system model, we employ 14 sub-carriers in a single resource block, assuming that they all possess the same characteristics.

-

The parameter $n$ is considered to be the number of user equipment, the number of antennas involved in the beamforming is considered to be $Y_a$, while the number of sub-channels is taken as $u$.

-

${\mathit{g}}_{n,k}={\left[g_1^{n,k} \dots g_{Y_a}^{n,k}\right]}^T\in {\complement }^{Y_a\times 1}$ is considered to be the gain vector.

-

While ${\mathit{z}}_{n,k}={\left[g_1^{n,k} \dots g_{Y_a}^{n,k}\right]}^T\in {\complement }^{Y_a\times 1}$ is considered to be the steering vector.

-

$w_{n,k}\in \complement$ is considered to be the information signal and $P_{n,k}=A\left[{\left|w_{n,k}\right|}^2\right]$ to be the transmission power.

-

$l_{n,k}\in \complement$ is considered as the additive noise under the assumption that the noise is white additive Gaussian noise (AWGN) with a variance of $N_0$.

-

With the assumption that the channel coefficients for the different UEs are independent, the received signal by a specific UE $n$ on a particular subcarrier $k$, $r_{n,k}\in \complement$, is given by:

$$r_{n,k}={\mathit{g}}_{n,k}^G{\mathit{z}}_{n,k}{w}_{n,k}+{\sum }_{m\ne n}{\mathit{g}}_{n,k}^G{\mathit{z}}_{m,k}{w}_{m,k}+l_{n,k}$$

(3)

The signal-to-interference and noise ratio (SINR) of the UE is given by:

$${SNIR}_{n,k}=\frac{{\left|{\mathit{g}}_{n,k}^G{\mathit{z}}_{n,k}\right|}^2{P}_n}{{\sum }_{m\ne n}{\left|{\mathit{g}}_{n,k}^G{\mathit{z}}_{m,k}\right|}^2{P}_m+N_0}$$

(4)

While the achievable bit rate $R_{n,k}$ is expressed by the following equation

$$R_{n,k}={log}_2(1+{SNIR}_{n,k})$$

(5)

Attenuation matrixes permit the sending of one or multiple signals to one or multiple outputs, while changing the power level of each of the signals. The attenuation matrix ${\left\{A_n\right\}}_{n=1}^N\in R^{K\times Y_a}$ is, however, computed as

$$A_n=\left[\begin{array}{ccc}{\left|{\mathit{g}}_{n,1}^G{\mathit{z}}_1\right|}^2& \cdots & {\left|{\mathit{g}}_{n,1}^G{\mathit{z}}_{Y_a}\right|}^2\\ ⋮& \ddots & ⋮\\ {\left|{\mathit{g}}_{n,K}^G{\mathit{z}}_1\right|}^2& \cdots & {\left|{\mathit{g}}_{n,K}^G{\mathit{z}}_{Y_a}\right|}^2\end{array}\right]$$

(6)

The selection of beams is, however, decided based on the attenuation matrix for each of the users in the smart grid.

4. The Scheduler Architecture

The packet scheduling architecture in the 5G NR system is depicted in Figure 4. The system is characterized by selecting a beam, a queue management system, deadline possibility check, and RB allocation before the packet is finally transmitted. During the initial stage, the system picks the ideal beam that will serve the UE. A queue management system is organized in which priority scheduling is decided based on the priority of users (priority level 1 (PL1) and priority level 2 (PL2)). For instance, in smart grid communication, when PL2 users occur, regardless of their channel quality, they will occupy the system resources first before users are placed at PL1. Priority Level 1 users will be scheduled when there are no PL2 users in buffer. Data are transmitted by gNodeB through the downlink time-varying channel. Data packets from the upper layer of gNodeB are taken through the queue management system before the packets are delivered to the several UEs based on priority levels with the aid of the resource block allocation controller. Just before scheduling, the system also goes through a deadline possibility check to determine whether to transmit the packet or not. To ascertain which UE is to be scheduled in the scheduler, the scheduler can employ a scheduling technique coupled with additional information, including channel quality information or any other important information. After the packet is transmitted, the reward is, however, collected if the deadline is met. The UE measures the SNIR of the DL channel between the gNodeB and the UE as the basis of the state of the quality of the channel at the next allocation of resources.

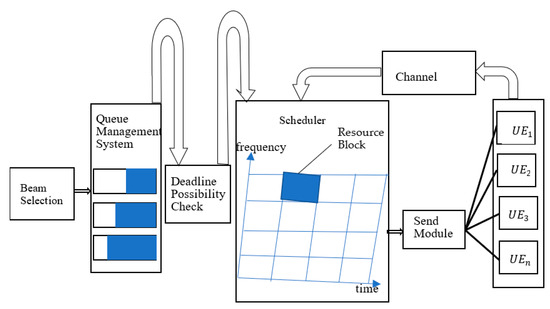
Figure 4. The scheduling architectural in 5G NR system.

4.1. Queue Management System

In this section, we put forward modern scheduling techniques which are modeled for the scheduling of packets with deadlines and rewards. The Deadline Scheduling with Commitment (DSC) and improved and upgraded EDF scheduling techniques are examined here as the reference techniques for the proposed Optimal Usage and Dropping (OUD) scheduling technique, which is also analyzed in this paper.

4.1.1. Reference Scheduling Technique

The primary reason behind the DSC technique [32] is to maximize profit as it evaluates the decision on admission on the basis of comparing the potential profits relating to the acceptance or declining of a task. There is a difference between this technique and other previously existing and related algorithms [35,36,37], in which it processes a situation without commitment, and the job values are subtracted from the penalties. The DSC scheduling technique upholds a tentative schedule most of the time. During the processing of a task request, the DSC scheduler ascertains if there is a possibility of appending a new task at the end of the ongoing tentative schedule while trying to meet its deadline. The task is, however, admitted and appended should the deadline be met; if not, the scheduler calculates if it is reasonable in admitting the task based on the profit of either to accept and decline the task. Should the profit that is related with acceptance not be sufficient enough, then the task is, however, rejected. If it is sufficiently large, then the task is scheduled to another time interval. The DSC algorithm is defined as seen in the pseudocode in Algorithm 1 below. Let the $T_a$ be the tasks to be released and the threshold as $(1+\alpha )$. As in line 4, $T_a$ gets added and appended to the current schedule if appendable. Otherwise, the ${Profit}_{accept}$ and ${Profit}_{decline}$ related to admitting or declining $T_a$ are compared. In line 6, if a better profit is yielded in admitting $T_a$, then $T_a$ is admitted at the end by $d_a$, and the current schedule after $d_a-p_a$ is moved and adjusted accordingly. Otherwise, if admitting $T_a$ does not yield a better profit, $T_a$ is a declined service. The threshold $1+\alpha$ will be optimized after deriving the competitive ratio as a function of $\alpha$.

Algorithm 1 DSC Scheduling Algorithm

1: $\mathbf{l}\mathbf{o}\mathbf{o}\mathbf{p}$ 2: $\mathrm{u}\mathrm{p}\mathrm{o}\mathrm{n} \mathrm{e}\mathrm{v}\mathrm{e}\mathrm{n}\mathrm{t}: \mathrm{T}\mathrm{a}\mathrm{s}\mathrm{k} T_a \mathrm{i}\mathrm{s} \mathrm{r}\mathrm{e}\mathrm{l}\mathrm{e}\mathrm{a}\mathrm{s}\mathrm{e}\mathrm{d}$ 3: $\mathbf{i}\mathbf{f} T_a \mathrm{i}\mathrm{s} \mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d}\mathrm{a}\mathrm{b}\mathrm{l}\mathrm{e} \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}$ 4: $\mathrm{A}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d} T_a \mathrm{t}\mathrm{o} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{e}\mathrm{n}\mathrm{d} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{v}\mathrm{e} \mathrm{s}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{l}\mathrm{e}$ 5: $\mathbf{e}\mathbf{l}\mathbf{s}\mathbf{e}$6: $\mathbf{i}\mathbf{f} {Profit}_{accept}>{(1+\alpha )Profit}_{decline} \mathbf{t}\mathbf{h}\mathbf{e}\mathbf{n}$ 7: $\mathrm{a}\mathrm{p}\mathrm{p}\mathrm{e}\mathrm{n}\mathrm{d} T_a \mathrm{a}\mathrm{t} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{e}\mathrm{n}\mathrm{d} \mathrm{b}\mathrm{y} d_a$ 8: $\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{e} \mathrm{a}\mathrm{n}\mathrm{d} \mathrm{m}\mathrm{o}\mathrm{d}\mathrm{i}\mathrm{f}\mathrm{y} \mathrm{t}\mathrm{h}\mathrm{e} \mathrm{s}\mathrm{c}\mathrm{h}\mathrm{e}\mathrm{d}\mathrm{u}\mathrm{l}\mathrm{e} \mathrm{a}\mathrm{f}\mathrm{t}\mathrm{e}\mathrm{r} d_a-p_a \mathrm{a}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{r}\mathrm{d}\mathrm{i}\mathrm{n}\mathrm{g}\mathrm{l}\mathrm{y}$ 9: $\mathbf{e}\mathbf{l}\mathbf{s}\mathbf{e}$ 10: drop $T_a$ 11: end if 12: end if 13: $\mathbf{e}\mathbf{n}\mathbf{d} \mathbf{l}\mathbf{o}\mathbf{o}\mathbf{p}$

EDF scheduling is a popular policy and has consistently been employed for most scheduling policies, showing itself to be quite optimal under different matrices [20,22,25]. When executing any task in EDF, the task can be pre-empted if any other periodic instance with an earlier deadline is ready for execution and becomes active. EDF is also priority driven and dynamic. Hence, priorities are calculated and changed while the processes are running. Another scheduling mechanism that can be utilized as a standard for comparison purposes is the $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ scheduling mechanism in [38]. This technique assumes there are $J$ queues in the system in which a selection must be made from the queue to be served. It is also assumed that there are $J$ groups or levels of rewards each against a queue. Two essential steps make up the $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ scheduling technique, which are

-

Inserting the new task to $j$ according to its rewards in the first come first serve order upon arrival.

-

When the server is not in use, the mechanism chooses the queue to be served according to $\raisebox{1ex}{${c\mu }_k$}\!\left/ \!\raisebox{-1ex}{${\theta }_k$}\right.$ and processes the task that is in front of the queue.

In the case of EDF scheduling, is it assumed that there is no prior information about the servicing times, while $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ scheduling assumes that the deadline is statistically known based on the probability of abandonment. This, however, is very key in terms of the case of non-deterministic service time. Therefore, there is a possibility case that shows the advantage of employing the knowledge of servicing time upon arrival in the EDF case presented. We fuse the EDF scheduling technique with the $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ policy to propose a new and improved EDF technique that takes advantage of the knowledge of deadline information as presented in Algorithm 2. In the case of the $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ mechanism, when the deadlines are known upon arrival, it allows the modification of the queue order to adequately utilize the EDF policy.

Algorithm 2 An Improved EDF version (I-EDF)

Arrival of new task $A_i$ $k :=w_i$ Insert the $A_i$ at the end of queue $k$ Initialize $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ service $k_0 :=\underset{k=1\dots K}{\mathrm{argmax}}\left(\sum \raisebox{1ex}{${c_k\mu }_k$}\!\left/ \!\raisebox{-1ex}{${\theta }_k$}\right.\right)$ $P_i=\underset{A_j\in {\widehat{J}}_t^{k_0}}{\mathrm{argmin}}\left(q_j\right)$ If ${(q}_i<t)$ then drop $A_i$ Else provide service to $A_i$ Return to 1

4.1.2. Optimal Usage and Dropping (OUD) Scheduling Technique

In this segment, a scheduling technique called the Optimal Usage and Dropping technique (OUD) is proposed and presented. This technique incorporates a schedule and drop mechanism into the system. During scheduling, the following approach is followed. Upon arrival, the technique places the new task into the queue while maintaining the predefined order. If placing a task in the queue results in the task missing its deadline, the technique drops the data packet with the lowest throughput ratio $\left(\frac{p_i}{s_i}\right)$ in the queue. The task that should be eventually selected is one that possesses the highest throughput ratio in as much as it will not cause the succeeding task to miss its deadline. The complexity of adding a new job to the queue is made straightforward by the OUD technique. The technique employs its dropping approach to maintain the queue by using $J_{t_i}^O=\frac{R_{max}}{S_{min}}$, where $S_{min}\le S_i\le S_{max}$ is the processing time required by $A_i$, and $R_{min}\le R_i\le R_{max}$ is the deadline of $A_i$. Time is measured from the arrival time to the beginning of the service. The symbol $J_t^O$ is employed to introduce the OUD parameter with the assumption that $h\left(A_i, t\right)$ and $y\left(A_i, t\right)$ are the functions that describe the predefined order of $A_i$ in the queue potential at time $t$.

-

$h\left(A_i, t\right)$ is the index of task $A_i$ in $J_t^O. h\left(A_i, t\right)=1$ indicates that $A_i$ is at the front of the queue.

-

$y\left(A_i, t\right):=$ $\sum _{A_{k:h(A_k, t)<h\left(A_i, t\right)}}{s}_i$ is the time a task is put on hold before processing with the assumption that no new task arrives until processing starts.

Algorithm 3 below describes how the OUD technique manages a task arrival. The new task is taken as $A_i$, which is introduced to the queue $J_{t_{i-1}}^O$ at time a $t_i$.

It is worth noting that the values of $h\left(A_k,t_i\right)$ and $y\left(A_k,t_i\right)$ change after introducing a new task $A_i$ at time $t_i$ as follows. If $h\left(A_k,t_i\right)>h\left(A_i,t_i\right)$, then $y\left(A_k,t_i\right)≔y\left(A_k,t_{i-1}\right)+s_i$ and $h\left(A_k,t_i\right)=h\left(A_k,t_{i-1}\right)+1$; otherwise, no change exists.

Algorithm 3 OUD Scheduling

1: Arrival of a new task $\left(A_i\right)$ 2: If $J_{t_i}^O=\varnothing$ and the server is not busy, then $A_i$ is processed and return to 1. 3: $A_i$ added to the queue using the order of shortest time of expiry. If there exist task with the same time of expiry, order is taken in descending manner of their rewards. 4: Locate the first task ($A_k$) that will miss its deadline as a result of the inserting $A_i$ into the queue $\left(h\right(A_k, t)\ge h\left(A_i, t\right))$

$h_k≔\left\{\begin{array}{c}\underset{q_{j<y\left(A_j, t_i\right)}}{\min }\left(h\left(A_j, t_i\right)\right) \exists j:q_j\le y\left(A_i, t\right)\\ \infty otherwise. \end{array}\right.$

5: If $h_k≔\infty$ then return to 1. 6: Locate the task $A_r$ that has the lowest reward per servicing time. If there exist several, select the one that has the shortest time of expiry. $A_r≔\underset{h(A_j,t_i)\le h_k}{\min }\left(\frac{p_i}{s_i}\right)$ 7: $\mathrm{Drop} \mathrm{task} A_r$ from queue 8: Go to 1

Table 1 below shows the summary of different scheduling algorithms, the type of workflow scheduling employed, and the tools and objectives of the algorithms.

Table 1. Scheduling Algorithms employed in Different Environments.

Reference	Algorithm Employed	Complexity	Description	Environment
[20,22,23]	Early Deadline First Scheduling Algorithm	Simple scheduling algorithm	Prioritize task scheduling by searching for the queue for the job closest to its deadline	Various Systems including smart grid environment
[32]	Optimal deadline scheduling algorithm with commitment	Simple scheduling algorithm	To maximize the overall profit, which is the total value of the admitted task completed before their deadlines, while taking into consideration the penalty paid for the admitted jobs that miss their deadlines.	Energy Systems, especially EVs.
[39]	Priority fair algorithm with First come first serve as base algorithm	Complexity depends on the task scheduled.	Using priority fair algorithm combined with three other algorithms to reduce overheads and the distribution of scheduled jobs on the Edge	Edge Computing
[40]	Highest Level First with Estimated Times Algorithm	Simple scheduling algorithm	It is a priority-based algorithm that uses the static b-level for assigning priorities to tasks.	Various Systems, including smart grid environment
[41]	New Fuzzy Scheduling Algorithm	Performance heavily depends on computational time	The algorithm assigns priorities to tasks using a single fuzzy inference engine (FIS). The inputs to the FIS are the task’s arrival time, deadline, and computation time, while the output is the runtime priority of the task which is used to schedule tasks on the system.	Various Systems, including smart grid environment
[42]	Priority-Fuzzy-B-Level Algorithm	Complexity depends on the task to scheduled	Employs a single of fuzzy inference engine along with the bottom-level parameter to solve the scheduling algorithm for real-time systems with non-preemptive tasks that have precedence relations and timing constraints.	Processing systems
Proposed	Optimal Usage and Dropping (OUD) Scheduling	Simple Scheduling Algorithm	Employs an approach that utilizes the highest throughput ratio to schedule tasks while maintaining a predefined queue order and avoid missing deadlines.	Smart grid environment

4.2. Checking the Possibility of Deadline

This is where the system takes a decision on whether to transmit packets or not or if the packets meet their deadline upon transmission. The main reason for dropping a packet that misses its deadline is to conserve RF bearer resources. Prior to commencing transmission, the transmission throughput is unknown up till the end of the transmission. Therefore, the possibility of a deadline check needs to be against a throughput estimate. These assumptions can be the maximum interference from neighboring transmitting beams, the average throughput, or the highest theoretical throughput calculated in the system. Each of these approaches has its pros and cons since in the scenario of a false positive, the system drops packets that are unable to reach the UE on time or, conversely, the packets consume resources that are put to waste.

4.3. Allocation of Resource Blocks

In the system, a beam is needed to be selected for the purpose of packets transmission. In this work, the beams are taken to be static while each of the beams possesses at least one or several queues that store packets that are meant for transmission. The mechanism responsible for selection automatically selects the beam that delivers the optimal channel performance. The metric employed to determine the optimal beam is the one that delivers the maximum SINR as amply illustrated in equation 4. The Resource Block Allocator oversees allocating available channels to the packets. Channels with a higher bit rate are usually allocated before channels with lower bit rates. The process is then brought to a halt when the UE transmission is allocated to $Y_{RB}$ sub-channels. When the transmission of packets ends, the resource blocks is then vacated. These RBs are then assigned to the packet that has the shortest deadline.

Algorithm 4 describes the module in charge of the resource block allocation process of the system. The matrix $\mathit{E}$ characterizes the allocation of Resource Blocks; that is, each element $E_{k, { p}_j}$ demonstrates if the sub-channel and the corresponding beam are available $(E_{k, { p}_j}=0)$ or if it is in use by a UE, $n (E_{k, { p}_j}=u)$. At every iteration, the RB allocation process for the transmission of packet $A_i$ is carried out until $Y_{RB}$ subchannels have been allocated for transmitting packets. ${\chi }_{A_i}$ is considered as the number of subchannels which are allocated for transmitting packet $A_i$.

Algorithm 4 RBA Algorithm

1: $\mathrm{For} k=1\dots K$ 2: $\mathrm{If} \left({\mathit{E}}_{k, {\mathit{p}}_j}=0\right)$ and $\left(\left|{\chi }_{A_i}\right|<Y_{RB}\right)$ 3: $\mathrm{then} {\mathit{E}}_{k, {\mathit{p}}_j}=n$ 4: End for

5. Evaluation and Results

In this section, numerical results are presented from the simulations by evaluating and comparing the performance of the presented scheduling techniques. The parameter for the cell with a radius of transmission $r$ is taken as $50 \mathrm{m}$, with $Y_n$ taken as $30$, which is the UEs randomly distributed inside the cell and sub-channels $Y_s$ of 12, with a $BW$ of 3 MHz. The cell also contains $Y_b=8$ one-dimensional antenna arrays in the sense that each of the arrays comprises $Y_a=32$ antennas. For the DL transmission with beamforming, the number of static beams $Y_b$ is set at 8 for each of the antenna arrays, with $0.15 \mathrm{m}$ as the distance between $Y_a$ and a departure angle of $\frac{\sigma }{12}$. In simulating the channel coefficient for each user, the Winner II+ channel model is employed. The power spectral density of the additive white Gaussian noise is taken as $-170 \mathrm{d}\mathrm{B}\mathrm{m}/\mathrm{H}\mathrm{z}$. Algorithm 4 is employed for the RB allocation process, in which four sub-channels are allocated to each transmission of packet. In total, 2500 packets were run with their times of arrival distributed exponentially and their packet destinations distributed uniformly over a finite number of UEs.

Since in [25], the EDF algorithm has been proven not to be an ideal technique in scheduling; we then compare the performances of the improved EDF (I-EDF) algorithm, which was upgraded earlier, and proposed the DSC algorithm [32] as well as our proposed OUD algorithm. In Figure 5, the number of packets that were received over the rate of arrival is presented, while the total reward collection for the various techniques is presented in Figure 6. In both figures, it is observed that the techniques behave differently in terms of employing their respective scheduling decisions. There are more packets received by the OUD technique when compared to the DSC and the improved EDF algorithms, and this is attributed to the fact that the task parameters are already known upon arrival and jobs are selected based on the highest output ratio. It is also seen that the total reward collected is considerably higher for the OUD technique than the other two techniques.

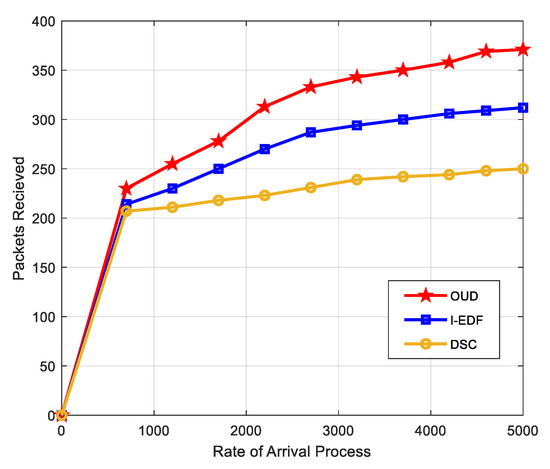
Figure 5. Total number of received packets.

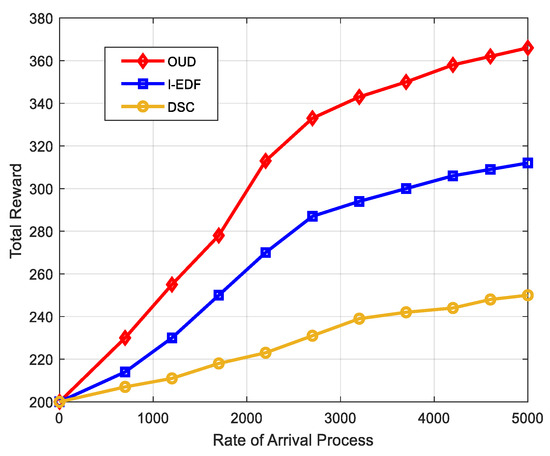
Figure 6. Total number of rewards collected.

Figure 7 displays the average throughput for different amounts of users in the system. By throughput, it simply means the average rate of successful packet delivery over a dedicated communication channel. It is noticed from the figure that the average throughput is almost the same for all the techniques when the number of UEs is lower than 30. However, the OUD technique indicates an improved performance compared to the other two techniques when the number of UEs exceeds a certain range of 30. This is because there are more data packets transmitted utilizing this technique since it has already picked priority users based on the algorithm. The OUD technique also proved superior since tasks are being selected using the shortest time to expiry approach.

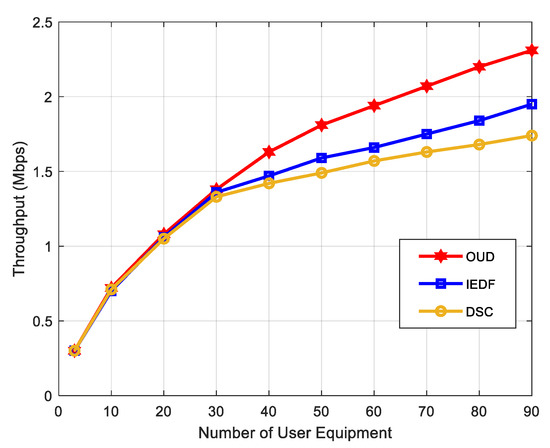
Figure 7. The average throughput for the techniques.

To assess the performance of the schedulability of the techniques, we verify if some of the jobs miss their deadlines during execution. Hence, the schedulability of the technique is measured by the success ratio, which is taken as

$$\mathrm{S}\mathrm{u}\mathrm{c}\mathrm{c}\mathrm{e}\mathrm{s}\mathrm{s} \mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}=\frac{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{t}\mathrm{a}\mathrm{s}\mathrm{k}\mathrm{s} \mathrm{w}\mathrm{i}\mathrm{t}\mathrm{h} \mathrm{n}\mathrm{o} \mathrm{m}\mathrm{i}\mathrm{s}\mathrm{s}\mathrm{e}\mathrm{d} \mathrm{d}\mathrm{e}\mathrm{a}\mathrm{d}\mathrm{l}\mathrm{i}\mathrm{n}\mathrm{e}\mathrm{s}}{\mathrm{n}\mathrm{u}\mathrm{m}\mathrm{b}\mathrm{e}\mathrm{r} \mathrm{o}\mathrm{f} \mathrm{g}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{d} \mathrm{t}\mathrm{a}\mathrm{s}\mathrm{k}}$$

In Figure 8, the results for the success ratio for the various techniques are shown. From the figure, all three scheduling approaches can successfully manage up to 30 tasks sets before their performance begins to plummet as deadline misses start to appear for increasing task sets. With the drop in the success ratio, the OUD technique still manages to outperform the other two techniques due to the fact that handling the scheduling overheads becomes a bottleneck for the I-EDF and DSC techniques. In other words, an additional set of tasks that are not readily deemed schedulable by I-EDF and DSC are gradually schedulable by OUD. Even so, the OUD technique is seen to improve schedulability, and it can be maximized when the number of task sets is not loaded.

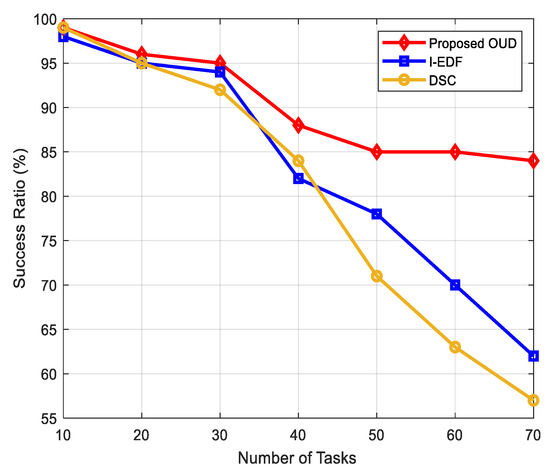
Figure 8. Schedulability for the different number of tasks.

Lastly, the scheduling techniques are also evaluated based on the percentage of jobs executed when set at different priority levels in different scenarios. The jobs submitted to the schedulers are assigned to two different priority levels, in which PL1 is a lower priority that can be assigned to a job when compared to a higher priority level PL2. Figure 9a considers a scenario in which there is an equal job distribution and displays the jobs that have been executed at priority levels (PL) 1 and 2. It is observed that jobs executed based on a higher priority yield more than 50% of total job executed for the various techniques. Since there is an equal number of jobs requests, the various techniques at PL1 processes less jobs due to the fact that there is less capability in differentiating these jobs into priorities and more overhead in determining which job to execute in the queue.

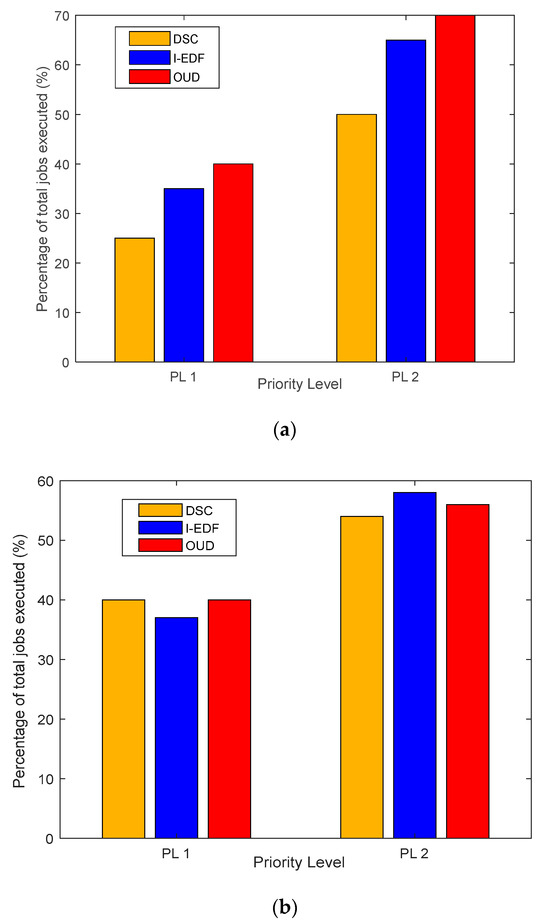
Figure 9. (a) Scenario 1—Percentage of jobs executed based on priority level. (b) Scenario 2—Percentage of jobs executed based on priority level.

From Figure 9b, the percentage of jobs executed in the two priority levels when there is a random job distribution is displayed. In this scenario, there is no prior knowledge of the rate of arrival of jobs. The DSC scheduling does not schedule jobs in a fair manner; hence, it selects the first job request and executes it regardless of its main priority, thereby having more jobs to execute but not taking into consideration its optimal priority before execution. Most of the techniques perform almost equally with a minimal difference owing to the fair manner in which the jobs are being processed. Although more jobs are being processed in priority level 2, most of the processed jobs might not be the optimal ones in the queue.

In summary, the OUD technique has shown itself to be the best implementation choice in all the performance indexes considered and hence recommended to be suitable for implementation in 5G-based smart grid communications.

6. Conclusions

The 5G communication network is currently one of the best wireless transmission platforms, that would be a part of future cellular networks and can be incorporated in other communication systems. The employment of 5G in a typical smart grid communication system will offer high-speed data transfer with low latency and ensure enough bandwidth for various users. However, scheduling data packets and resource distribution and allocation processes are some of the major issues that must be overcome to ensure the efficient assigning of available Resource Blocks (RB) to smart grid users. Although several scheduling techniques have been employed to carry out these tasks, most of them fall short of maintaining an efficient scheduling approach that ensures that a series of tasks need to be executed before their deadlines. Amongst the most popular scheduling techniques is the EDF (Earliest Deadline First) technique, which is employed to meet the timing constraints of a given set of tasks. It unfortunately does not meet time constraints when the system is unaware of the future release patterns of the tasks. In order to improve the efficacy of the EDF scheduling technique, we improved on this technique by fusing a $\raisebox{1ex}{$c\mu $}\!\left/ \!\raisebox{-1ex}{$\theta $}\right.$ policy into an existing EDF scheduling technique to ensure that the deadlines are known upon arrival and also boost its performance. A DSC scheduling approach is also evaluated in this paper, while a novel Optimal Usage and Dropping Scheduling (OUD) technique is proposed. The proposed technique utilizes a smart schedule and drop mechanism in the system and ensures that the needed task remains in the queue while maintaining a predefined order.

The OUD scheduling technique is compared with the DSC technique as well as the improved EDF scheduling technique over several performance indexes so as to evaluate their performance. Simulation results show that the OUD scheduling technique gives a better performance when compared to the improved EDF technique and the DSC scheduling approach. However, the DSC scheduling technique displays poorer schedulability performance when compared to the improved EDF scheduling technique. It is expected that the OUD scheduling approach can be employed in actual smart grid communication systems that require real-time guarantees. When employed in these systems, it will improve its schedulable performance, and the system can accommodate more sets of tasks in real-time.

In the future, artificial intelligence tools like the Genetic Algorithm may be used to modify the proposed OUD algorithm so as to make the proposed algorithm more general, flexible, and smarter.