Clustering and Characterization of the Lactation Curves of Dairy Cows Using K-Medoids Clustering Algorithm
Simple Summary
Abstract
1. Introduction
2. Backgrounds
3. Materials and Methods
3.1. Dataset
3.2. Clustering
- : Distance between lactation dataset A and B
- : Amount of milk yield on day in lactation dataset A
- : Amount of milk yield on day in lactation dataset B
- N: The total number of milking days
- : A median dataset of a cluster A
- : Euclidean distance between lactation datasets and
3.3. Characterization and Comparison of the Clusters
3.4. Statistical Analysis
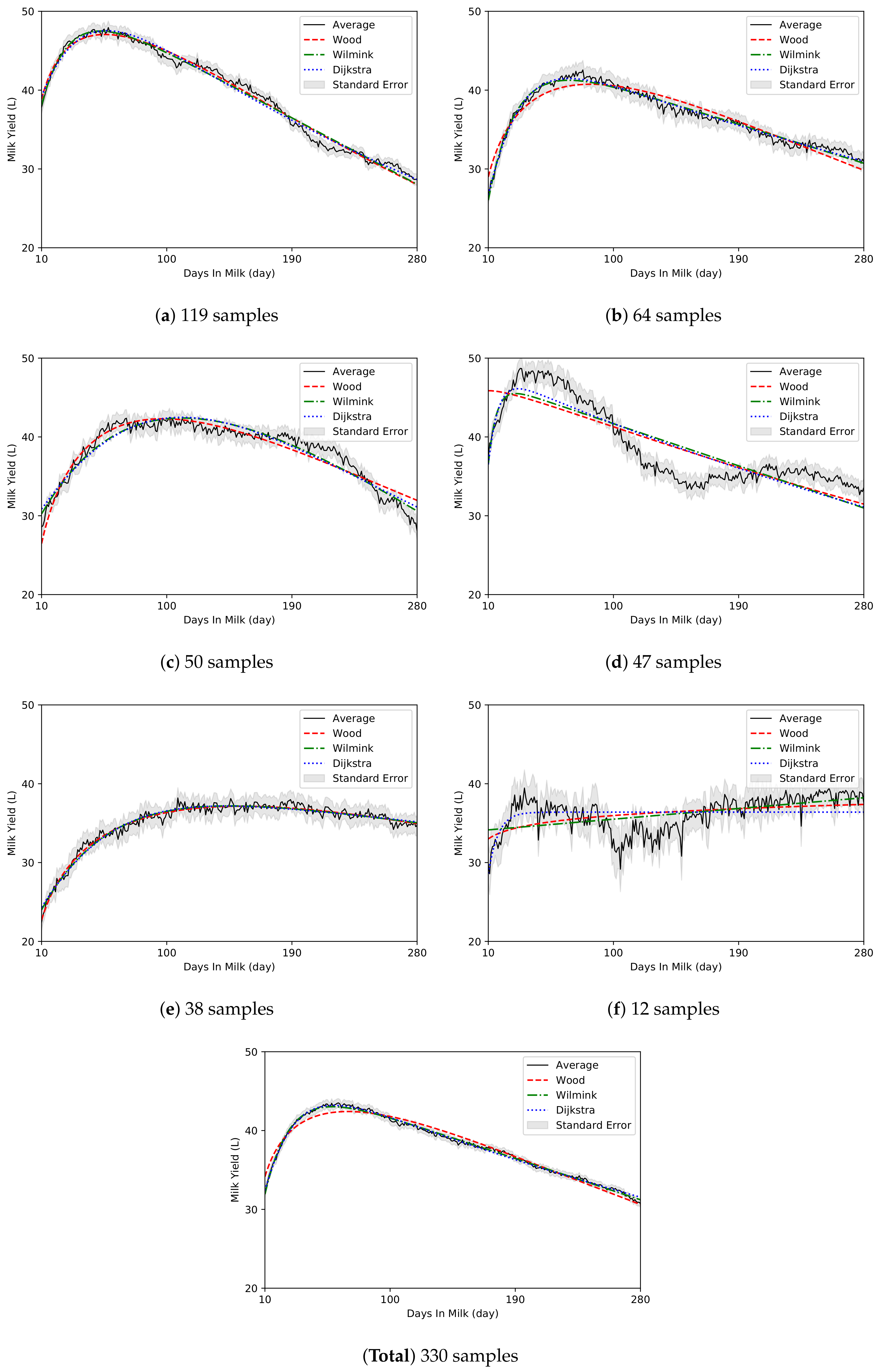
4. Results
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Papajcsik, I.A.; Bodero, J. Modelling lactation curves of Friesian cows in a subtropical climate. Anim. Sci. 1988, 47, 201–207. [Google Scholar] [CrossRef]
- Olori, V.; Brotherstone, S.; Hill, W.; McGuirk, B. Fit of standard models of the lactation curve to weekly records of milk production of cows in a single herd. Livest. Prod. Sci. 1999, 58, 55–63. [Google Scholar] [CrossRef]
- Sherchand, L.; Mcnew, R.W.; Kellogg, D.W.; Johnson, Z.B. Selection of a mathematical model to generate lactation curves using daily milk yields of Holstein cows. J. Dairy Sci. 1995, 78, 2507–2513. [Google Scholar] [CrossRef]
- Brody, S.; Ragsdale, A.C.; Turner, C.W. The rate of decline of milk secretion with the advance of the period of lactation. J. Gen. Physiol. 1923, 5, 441–444. [Google Scholar] [CrossRef]
- Wood, P.D.P. Algebraic model of the lactation curve in cattle. Nature 1967, 216, 164–165. [Google Scholar] [CrossRef]
- Wilmink, J. Adjustment of test-day milk, fat and protein yield for age, season and stage of lactation. Livest. Prod. Sci. 1987, 16, 335–348. [Google Scholar] [CrossRef]
- Dijkstra, J.; France, J.; Dhanoa, M.; Maas, J.; Hanigan, M.; Rook, A.; Beever, D. A model to describe growth patterns of the mammary gland during pregnancy and lactation. J. Dairy Sci. 1997, 80, 2340–2354. [Google Scholar] [CrossRef]
- Pollott, G. A biological approach to lactation curve analysis for milk yield. J. Dairy Sci. 2000, 83, 2448–2458. [Google Scholar] [CrossRef]
- Macciotta, N.; Vicario, D.; Cappio-Borlino, A. Detection of different shapes of lactation curve for milk yield in dairy cattle by empirical mathematical models. J. Dairy Sci. 2005, 88, 1178–1191. [Google Scholar] [CrossRef]
- Ferris, T.; Mao, I.; Anderson, C. Selecting for lactation curve and milk yield in dairy cattle. J. Dairy Sci. 1985, 68, 1438–1448. [Google Scholar] [CrossRef]
- Tassell, C.V.; Jones, L.; Eicker, S. Production evaluation techniques based on lactation curves. J. Dairy Sci. 1995, 78, 457–465. [Google Scholar] [CrossRef]
- Pérochon, L.; Coulon, J.B.; Lescourret, F. Modelling lactation curves of dairy cows with emphasis on individual variability. Anim. Sci. 1996, 63, 189–200. [Google Scholar] [CrossRef]
- Tekerli, M.; Akinci, Z.; Dogan, I.; Akcan, A. Factors affecting the shape of lactation curves of Holstein cows from the balikesir province of Turkey. J. Dairy Sci. 2000, 83, 1381–1386. [Google Scholar] [CrossRef]
- Congleton, W.R.J.; Everett, R.W. Error and bias in using the incomplete gamma function to describe lactation curves. J. Dairy Sci. 1980, 63, 101–108. [Google Scholar] [CrossRef]
- Rekik, B.; Gara, A. Factors affecting the occurrence of atypical lactations for Holstein–Friesian cows. Livest. Prod. Sci. 2004, 87, 245–250. [Google Scholar] [CrossRef]
- Daniel, J.B.; Friggens, N.C.; van Laar, H.; Ingvartsen, K.L.; Sauvant, D. Modeling homeorhetic trajectories of milk component yields, body composition and dry–matter intake in dairy cows: Influence of parity, milk production potential and breed. Animal 2018, 12, 1182–1195. [Google Scholar] [CrossRef]
- Jeretina, J.; Babnik, D.; Škorjanc, D. Modeling lactation curve standards for test–day milk yield in Holstein, Brown Swiss and Simmental cows. J. Anim. Plant Sci. 2013, 23, 754–762. [Google Scholar]
- Pietersma, D.; Lacroix, R.; Lefebvre, D.; Block, E.; Wade, K. A case–acquisition and decision–support system for the analysis of group–average lactation curves. J. Dairy Sci. 2001, 84, 730–739. [Google Scholar] [CrossRef]
- Cunha, D.D.N.F.V.D.; Pereira, J.C.; Silva, F.F.e.; Silva, O.F.d.; Campos, J.L.; Braga, J.A.M. Selection of models of lactation curves to use in milk production simulation systems. Rev. Bras. De Zootec. 2010, 39, 891–902. [Google Scholar] [CrossRef]
- Andersen, F.; Østerås, O.; Reksen, O.; Gröhn, Y.T. Mastitis and the shape of the lactation curve in Norwegian dairy cows. J. Dairy Res. 2011, 78, 23–31. [Google Scholar] [CrossRef]
- Hostens, M.; Ehrlich, J.; Ranst, B.V.; Opsomer, G. On–Farm evaluation of the effect of metabolic diseases on the shape of the lactation curve in dairy cows through the MilkBot lactation model. J. Dairy Sci. 2012, 95, 2988–3007. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z. Extensions to the k-means algorithm for clustering large data sets with categorical values. Data Min. Knowl. Discov. 1998, 2, 283–304. [Google Scholar] [CrossRef]
- Park, H.S.; Jun, C.H. A simple and fast algorithm for k-medoids clustering. Expert Syst. Appl. 2009, 36, 3336–3341. [Google Scholar] [CrossRef]
- Huquet, B.; Leclerc, H.; Ducrocq, V. Characterization of French dairy farm environments from herd–test–day profiles. J. Dairy Sci. 2012, 95, 4085–4098. [Google Scholar] [CrossRef]
- Savegnago, R.P.; do Nascimento, G.B.; de Magalhães Rosa, G.J.; de Carneiro, R.L.R.; Sesana, R.C.; Faro, L.E.; Munari, D.P. Cluster analyses to explore the genetic curve pattern for milk yield of Holstein. Livest. Sci. 2016, 183, 28–32. [Google Scholar] [CrossRef]
- Koster, J.D.; Salavati, M.; Grelet, C.; Crowe, M.; Matthews, E.; O’Flaherty, R.; Opsomer, G.; Foldager, L.; Hostens, M. Prediction of metabolic clusters in early–lactation dairy cows using models based on milk biomarkers. J. Dairy Sci. 2019, 102, 2631–2644. [Google Scholar] [CrossRef]
- Grelet, C.; Vanlierde, A.; Hostens, M.; Foldager, L.; Salavati, M.; Ingvartsen, K.L.; Crowe, M.; Sorensen, M.T.; Froidmont, E.; Ferris, C.P.; et al. Potential of milk mid–IR spectra to predict metabolic status of cows through blood components and an innovative clustering approach. Animal 2019, 13, 649–658. [Google Scholar] [CrossRef]
- Liao, T.W. Clustering of time series data–A survey. Pattern Recognit. 2005, 38, 1857–1874. [Google Scholar] [CrossRef]
- Chung Fu, T. A review on time series data mining. Eng. Appl. Artif. Intell. 2011, 24, 164–181. [Google Scholar] [CrossRef]
- Halkidi, M.; Batistakis, Y.; Vazirgiannis, M. On clustering validation techniques. J. Intell. Inf. Syst. 2001, 17, 107–145. [Google Scholar] [CrossRef]
- Aghabozorgi, S.; Shirkhorshidi, A.S.; Wah, T.Y. Time-series clustering—A decade review. Inf. Syst. 2015, 53, 16–38. [Google Scholar] [CrossRef]
- Xu, D.; Tian, Y. A comprehensive survey of clustering algorithms. Ann. Data Sci. 2015, 2, 165–193. [Google Scholar] [CrossRef]
- Keogh, E.; Lin, J. Clustering of time-series subsequences is meaningless: Implications for previous and future research. Knowl. Inf. Syst. 2005, 8, 154–177. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms; Society for Industrial and Applied Mathematics, Philadelphia, PA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Madhulatha, T.S. Comparison between k-means and k-medoids clustering algorithms. In Advances in Computing and Information Technology; Wyld, D.C., Wozniak, M., Chaki, N., Meghanathan, N., Nagamalai, D., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; pp. 472–481. [Google Scholar]
- Sauder, C.; Cardot, H.; Disenhaus, C.; Le Cozler, Y. Non–parametric approaches to the impact of Holstein heifer growth from birth to insemination on their dairy performance at lactation one. J. Agric. Sci. 2013, 151, 578–589. [Google Scholar] [CrossRef]
- National Research Council. Nutrient Requirements of Dairy Cattle: Seventh Revised Edition, 2001; The National Academies Press: Washington, DC, USA, 2001. [CrossRef]
- Ministry of Agriculture, Food and Rural Affairs. 2018 DHI Annual Report in Korea; Dairy Cattle Improvement Center, National Agricultural Cooperative Federation: Gyeonggi-do, Goyang-si, Korea, 2018.
- Meijering, E. A chronology of interpolation: From ancient astronomy to modern signal and image processing. Proc. IEEE 2002, 90, 319–342. [Google Scholar] [CrossRef]
- Velmurugan, T.; Santhanam, T. Computational complexity between k-means and k-medoids clustering algorithms for normal and uniform distributions of data points. J. Comput. Sci. 2010, 6. [Google Scholar] [CrossRef]
- Ketchen, D.J.; Shook, C.L. The Application of cluster analysis in strategic management research: An analysis and critique. Strateg. Manag. J. 1996, 17, 441–458. [Google Scholar] [CrossRef]
- Thornley, J.; France, J. Mathematical Models in Agriculture. Quantitative Methods for the Plant, Animal and Ecological Sciences, 2nd ed.; CABI: Wallingford, CT, USA, 2007. [Google Scholar]
- Wood, P. Factors affecting the shape of the lactation curve in cattle. Anim. Sci. 1969, 11, 307–316. [Google Scholar] [CrossRef]
- Arbel, R.; Bigun, Y.; Ezra, E.; Sturman, H.; Hojman, D. The effect of extended calving intervals in high lactating cows on milk production and profitability. J. Dairy Sci. 2001, 84, 600–608. [Google Scholar] [CrossRef]
- Dematawewa, C.; Berger, P. Genetic and phenotypic parameters for 305–day yield, fertility, and survival in Holsteins. J. Dairy Sci. 1998, 81, 2700–2709. [Google Scholar] [CrossRef]
- Lee, J.Y.; Kim, I.H. Advancing parity is associated with high milk production at the cost of body condition and increased periparturient disorders in dairy herds. J. Vet. Sci. 2006, 7, 161–166. [Google Scholar] [CrossRef] [PubMed]
- López, S.; France, J.; Odongo, N.; McBride, R.; Kebreab, E.; AlZahal, O.; McBride, B.; Dijkstra, J. On the analysis of canadian holstein dairy cow lactation curves using standard growth functions. J. Dairy Sci. 2015, 98, 2701–2712. [Google Scholar] [CrossRef] [PubMed]
- Weller, J.; Ezra, E. Genetic and phenotypic analysis of daily Israeli Holstein milk, fat, and protein production as determined by a real–time milk analyzer. J. Dairy Sci. 2016, 99, 9782–9795. [Google Scholar] [CrossRef] [PubMed]
- Ray, D.; Halbach, T.; Armstrong, D. Season and lactation number effects on milk production and reproduction of dairy cattle in arizona. J. Dairy Sci. 1992, 75, 2976–2983. [Google Scholar] [CrossRef]
- Weber, M.; Purup, S.; Vestergaard, M.; Akers, R.; Sejrsen, K. Regulation of local synthesis of insulin-like growth factor–I and binding proteins in mammary tissue. J. Dairy Sci. 2000, 83, 30–37. [Google Scholar] [CrossRef]
- Sorensen, A.; Knight, C. Endocrine profiles of cows undergoing extended lactation in relation to the control of lactation persistency. Domest. Anim. Endocrinol. 2002, 23, 111–123. [Google Scholar] [CrossRef]
- Miller, N.; Delbecchi, L.; Petitclerc, D.; Wagner, G.; Talbot, B.; Lacasse, P. Effect of stage of lactation and parity on mammary gland cell renewal. J. Dairy Sci. 2006, 89, 4669–4677. [Google Scholar] [CrossRef]
- Coffey, M.; Hickey, J.; Brotherstone, S. Genetic aspects of growth of Holstein–Friesian dairy cows from birth to maturity. J. Dairy Sci. 2006, 89, 322–329. [Google Scholar] [CrossRef]
- Wathes, D.; Cheng, Z.; Bourne, N.; Taylor, V.; Coffey, M.; Brotherstone, S. Differences between primiparous and multiparous dairy cows in the inter–relationships between metabolic traits, milk yield and body condition score in the periparturient period. Domest. Anim. Endocrinol. 2007, 33, 203–225. [Google Scholar] [CrossRef]
- Swalve, H.H. Theoretical basis and computational methods for different test—Day genetic evaluation methods. J. Dairy Sci. 2000, 83, 1115–1124. [Google Scholar] [CrossRef]
- Jakobsen, J.; Rekaya, R.; Jensen, J.; Sorensen, D.; Madsen, P.; Gianola, D.; Christensen, L.; Pedersen, J. Bayesian estimates of covariance components between lactation curve parameters and disease liability in Danish Holstein cows. J. Dairy Sci. 2003, 86, 3000–3007. [Google Scholar] [CrossRef]
- Lassen, J.; Hansen, M.; Sørensen, M.K.; Aamand, G.P.; Christensen, L.G.; Madsen, P. Genetic relationship between body condition score, dairy character, mastitis, and diseases other than mastitis in first—Parity Danish Holstein cows. J. Dairy Sci. 2003, 86, 3730–3735. [Google Scholar] [CrossRef]
- Hansen, J.; Friggens, N.; Højsgaard, S. The influence of breed and parity on milk yield, and milk yield acceleration curves. Livest. Sci. 2006, 104, 53–62. [Google Scholar] [CrossRef]
- Yamazaki, T.; Takeda, H.; Nishira, A.; Togashi, K. Relationship between the lactation curve and udder disease incidence in different lactation stages in first–lactation Holstein cows. Anim. Sci. J. 2009, 80, 636–643. [Google Scholar] [CrossRef]
- Silvestre, A.; Petim-Batista, F.; Colaço, J. The accuracy of seven mathematical functions in modeling dairy cattle lactation curves based on test-day records from varying sample schemes. J. Dairy Sci. 2006, 89, 1813–1821. [Google Scholar] [CrossRef]
- Arnal, M.; Robert-Granié, C.; Larroque, H. Diversity of dairy goat lactation curves in France. J. Dairy Sci. 2018, 101, 11040–11051. [Google Scholar] [CrossRef]
- Silvestre, A.; Martins, A.; Santos, V.; Ginja, M.; Colaço, J. Lactation curves for milk, fat and protein in dairy cows: A full approach. Livest. Sci. 2009, 122, 308–313. [Google Scholar] [CrossRef]

| Conventional | Automatic | Total | ||||
|---|---|---|---|---|---|---|
| Milking System | Milking System | |||||
| Mean | SE | Mean | SE | Mean | SE | |
| Total milking days (day) | 103,086 | 203,444 | 306,530 | |||
| Milking days (day/lactation) | 207.00 | 5.99 | 243.94 | 5.20 | 230.13 | 3.98 |
| Number of animals | 287 | 437 | 724 | |||
| Number of total lactations | 498 | 834 | 1332 | |||
| - Number of primiparous cows | 191 | 269 | 460 | |||
| - Number of multiparous cows | 307 | 565 | 872 | |||
| Parity | 2.24 | 0.06 | 2.58 | 0.06 | 2.45 | 0.04 |
| Daily milk yield (L/day/lactation) | 30.75 | 0.52 | 32.82 | 0.39 | 32.06 | 0.31 |
| Total milk yield (L/lactation) | 7056 | 224 | 8349 | 189 | 7876 | 146 |
| Parity | Number of Lactations | Milking Days | Daily MY | Total MY | |||
|---|---|---|---|---|---|---|---|
| (Cows) | (Day) | (L/Day/Cow) | (L/Cow/Lactation) | ||||
| Mean | SD | Mean | SD | Mean | SD | ||
| 1 | 111 | 358.95 | 73.55 | 31.65 | 4.86 | 11,303 | 2649 |
| 2 | 101 | 377.30 | 78.56 | 36.00 | 5.41 | 13,545 | 3403 |
| 3 | 61 | 375.21 | 69.06 | 36.89 | 6.12 | 13,786 | 3310 |
| ≥4 | 57 | 406.58 | 81.59 | 37.09 | 6.60 | 14,981 | 3601 |
| Model | Lactation Curve | |
|---|---|---|
| Wood (1967) | [5] | |
| Wilmink (1987) | [6] | |
| Dijkstra (1997) | [7] |
| Cluster | Total | p-Value | ||||||
|---|---|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |||
| No. of lactations | 119 | 64 | 50 | 47 | 38 | 12 | 330 | |
| Primiparous | 17 | 28 | 18 | 10 | 28 | 10 | 111 | |
| Multiparous | 102 | 36 | 32 | 37 | 10 | 2 | 219 | |
| Parity | 2.61 a | 2.16 c | 2.30 b | 2.57 a | 1.63 d | 1.25 e | 2.31 | <0.001 |
| (0.12) | (0.17) | (0.19) | (0.20) | (0.20) | (0.18) | (0.07) | (0.16) | |
| 70 DIM | Aug. 1. | Sep. 29. | Oct. 10. | Aug. 20. | Sep. 30. | Jun. 30. | Aug. 31. | 0.272 |
| in a lactation (days) | (21.79) | (24.92) | (26.28) | (37.73) | (32.88) | (90.25) | (12.47) | (28.93) |
| MY (L/day) | 39.53 a | 36.64 d | 38.20 c | 38.76 b | 35.09 e | 36.18 d | 38.03 | 0.006 |
| (0.61) | (0.96) | (0.93) | (1.02) | (1.13) | (1.69) | (0.39) | (0.88) | |
| MY (L) | 10,713 a | 9930 d | 10,351 c | 10,504 b | 9509 e | 9806 d | 10,305 | 0.006 |
| (164.73) | (261.38) | (252.30) | (274.96) | (305.46) | (459.28) | (104.65) | (238.49) | |
| Peak DIM (days) | 59.92 d | 86.25 c | 119.68 b | 54.94 e | 144.00 a | 119.92 b | 85.24 | <0.001 |
| (2.73) | (4.61) | (8.42) | (6.11) | (9.67) | (25.73) | (3.01) | (6.01) | |
| Peak MY (L) | 53.08 b | 46.39 d | 47.14 c | 54.25 a | 42.70 e | 45.82 d | 49.59 | <0.001 |
| (0.83) | (1.24) | (1.08) | (1.34) | (1.33) | (2.26) | (0.54) | (1.13) | |
| Model | Parameter | Cluster | Total | |||||
|---|---|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | |||
| Wood | a | 24.6645 | 15.9437 | 12.5155 | 44.8198 | 12.2953 | 30.2838 | 22.1761 |
| (0.3161) | (0.3522) | (0.3401) | (2.1754) | (0.1697) | (1.3543) | (0.2843) | ||
| b | 0.2142 | 0.2738 | 0.3406 | 0.0170 | 0.2743 | 0.0374 | 0.2000 | |
| (0.0037) | (0.0063) | (0.0076) | (0.0143) | (0.0038) | (0.0127) | (0.0037) | ||
| c | 0.0039 | 0.0033 | 0.0035 | 0.0016 | 0.0018 | ≈0 | 0.0029 | |
| (≈0) | (0.0001) | (0.0001) | (0.0001) | (≈0) | (0.0001) | (≈0) | ||
| (L) | 0.6680 | 0.9529 | 1.1474 | 2.6746 | 0.5068 * | 1.9778 | 0.6090 | |
| 0.6125 | 0.8121 | 0.8298 | 0.8827 | 0.8343 * | 1.2126 | 0.9087 | ||
| Wilmink | a | 54.2924 | 46.0936 | 65.3834 | 47.6263 | 42.0509 | 6604.6668 | 47.5097 |
| (0.1707) | (0.1337) | (2.2023) | (0.3927) | (0.4718) | (0.1981) | (0.0581) | ||
| b | −24.9865 | −31.9822 | −38.4509 | −58.5113 | −21.6106 | −6570.6721 | −25.8178 | |
| (0.7756) | (0.6105) | (1.9260) | (35.6232) | (0.3697) | (0.1981) | (0.3245) | ||
| c | −0.0937 | −0.0549 | −0.1200 | −0.0594 | −0.0247 | ≈0 | −0.0582 | |
| (0.0009) | (0.0007) | (0.0072) | (0.0023) | (0.0019) | (9.1156) | (0.0003) | ||
| k | 0.0494 | 0.0495 | 0.0124 | 0.1715 | 0.0195 | ≈0 | 0.0543 | |
| (0.0020) | (0.0012) | (0.0009) | (0.0496) | (0.0008) | (0.0014) | (0.0008) | ||
| (L) | 0.6676 * | 0.5240 | 1.0063 * | 2.5458 | 0.5509 | 1.8807 * | 0.2436 * | |
| 0.6119 * | 0.7866 | 0.8230 * | 0.8682 | 0.8359 | 1.1974 * | 0.9006 * | ||
| Dijkstra | a | 34.0962 | 18.8021 | 28.2765 | 13.6532 | 21.3504 | 12.0427 | 25.1318 |
| (0.5020) | (0.3568) | (0.4192) | (8.0760) | (0.2697) | (7.7063) | (0.2315) | ||
| b | 0.0197 | 0.0467 | 0.0126 | 0.1950 | 0.0152 | 0.1686 | 0.0346 | |
| (0.0011) | (0.0018) | (0.0005) | (0.1342) | (0.0007) | (0.1449) | (0.0009) | ||
| c | 0.0357 | 0.0506 | 0.0124 | 0.1525 | 0.0230 | 0.1525 | 0.0520 | |
| (0.0015) | (0.0011) | (0.0010) | (0.0356) | (0.0009) | (0.0443) | (0.0008) | ||
| d | 0.0026 | 0.0015 | 0.0032 | 0.0016 | 0.0006 | ≈0 | 0.0016 | |
| (≈0) | (≈0) | (0.0002) | (0.0001) | (≈0) | (0.0001) | (≈0) | ||
| (L) | 0.6933 | 0.4644 * | 1.1214 | 2.3680 * | 0.5784 | 2.0179 | 0.2479 | |
| 0.6131 | 0.7852 * | 0.8316 | 0.8510 * | 0.8371 | 1.2012 | 0.9010 | ||
| Cluster | Total | ||||||
|---|---|---|---|---|---|---|---|
| (a) | (b) | (c) | (d) | (e) | (f) | ||
| Wood model 1 | |||||||
| Peak yield (L) | 46.96 | 40.65 | 42.34 | 45.87 | 37.10 | N/A | 42.34 |
| Peak DIM (days) | 54.92 | 82.97 | 97.31 | 10.63 | 152.39 | N/A | 68.97 |
| Persistency | −0.0026 | −0.0017 | −0.0016 | −0.0015 | −0.0005 | N/A | −0.0017 |
| Dijkstra model 2 | |||||||
| Peak yield (L) | 47.50 | 41.48 | 42.37 | 46.14 | 37.02 | N/A | 43.13 |
| Peak DIM (days) | 56.73 | 67.95 | 110.53 | 31.50 | 140.53 | N/A | 59.11 |
| Persistency | −0.0025 | −0.0015 | −0.0020 | −0.0016 | −0.0005 | N/A | −0.0016 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, M.; Lee, S.; Park, J.; Seo, S. Clustering and Characterization of the Lactation Curves of Dairy Cows Using K-Medoids Clustering Algorithm. Animals 2020, 10, 1348. https://doi.org/10.3390/ani10081348
Lee M, Lee S, Park J, Seo S. Clustering and Characterization of the Lactation Curves of Dairy Cows Using K-Medoids Clustering Algorithm. Animals. 2020; 10(8):1348. https://doi.org/10.3390/ani10081348
Chicago/Turabian StyleLee, Mingyung, Seonghun Lee, Jaehwa Park, and Seongwon Seo. 2020. "Clustering and Characterization of the Lactation Curves of Dairy Cows Using K-Medoids Clustering Algorithm" Animals 10, no. 8: 1348. https://doi.org/10.3390/ani10081348
APA StyleLee, M., Lee, S., Park, J., & Seo, S. (2020). Clustering and Characterization of the Lactation Curves of Dairy Cows Using K-Medoids Clustering Algorithm. Animals, 10(8), 1348. https://doi.org/10.3390/ani10081348





