Abstract
Shape memory polymers (SMPs) are smart materials capable of changing their shapes in a predefined manner under a proper applied stimulus and have gained considerable interest in several application fields. Particularly, two-way and multiple-way SMPs offer unique opportunities to realize untethered soft robots with programmable morphology and/or properties, repeatable actuation, and advanced multi-functionalities. This review presents the recent progress of soft robots based on two-way and multiple-way thermo-responsive SMPs. All the building blocks important for the design of such robots, i.e., the base materials, manufacturing processes, working mechanisms, and modeling and simulation tools, are covered. Moreover, examples of real-world applications of soft robots and related actuators, challenges, and future directions are discussed.
1. Introduction
Nowadays, soft matter is increasingly being used in robotic technology thanks to its great flexibility, light weight, and inexpensive mass production [1]. In fact, robots based on soft materials (widely known as soft robots) are able to withstand large deformations, perform complex motions, conform to arbitrary geometries, and sustain impacts without damage, and thus they are particularly suited to those applications where a safe interaction with people, fragile objects, and the environment is needed [2]. Accordingly, there has been a boost of research activities dedicated to the design and fabrication of more and more advanced soft robots for several sectors; e.g., automotive [3], aerospace [4,5], wearable [6], medical [7,8,9,10,11], and renewable energy [12] sectors.
When interacting with dynamic environments, soft robots able to tune and adapt their morphology, properties, and/or functionalities by “evolving” in a programmable spatial and temporal sequence, become essential. Moreover, greater adaptability can be achieved in soft robots having a reversible response, in order to be retrieved once the task is completed. From now on, the term “programmable soft robots” will be used to denote such an advanced class of soft robots. A simple example is given by applications that require continuous contact with people (e.g., hands-on assistive devices, exoskeletons, and haptics), where soft robots have to dynamically and actively apply the right force during the interaction, and reversibly return to the initial state once the interaction is completed.
A variety of actuation mechanisms have been explored to generate the desired motion/force under applied external stimuli in programmable soft robots; see, e.g., [13,14]. Generally, such actuation mechanisms are chosen depending on the performances needed (in terms of, e.g., actuation strain/force, response time, fatigue resistance, stiffness), application size scale, operating environment (e.g., in solution, air), stand-alone or tethered power sources, and additional required functionalities (e.g., biocompatibility, biodegradability, self-healing properties).
Common actuation approaches to programmable soft robotics rely on pneumatic actuators [15,16], mechanisms promoting important structural changes (e.g., multi-stability, buckling) [17,18] or inhomogeneous deformations (e.g., multilayer systems) [19,20], architected materials (e.g., auxetics) [21], folding/cutting theories (e.g., origami, kirigami) [22,23], bio-inspired and bio-mimetics architectures [19,24,25], reinforced systems [26], and granular jamming [27]. Generally, such robots are constructed from materials as polymers, hydrogels, and elastomers [28].
From the reviewed literature, two major considerations can be focused on. First, several actuation mechanisms enabling programmable morphology, properties, and/or functionalities of robots have been studied and realized. Second, such actuation mechanisms are often irreversible or enabled through an external intervention, as physical tethers, onboard electronics, or batteries. The latter aspect limits the development and utilization of programmable soft robots, especially in remote applications, since physical tethers or onboard parts may occupy space, may be heavy and difficult to miniaturize, and may complicate the design process [29].
Therefore, new advances are needed to generate untethered, programmable soft robots that exhibit repeatable actuation and multi-functionalities.
To that end, stimuli-responsive soft materials offer a valid solution, since they are able to respond autonomously to an external stimulus (e.g., temperature, magnetic field, humidity) by significant or articulated shape/property/function variations [30,31]. Some contributions to the development of untethered, programmable soft robots that exhibit repeatable actuation and multi-functionalities exist and involve: (i) shape changing soft materials, in which shape-shifting is encoded in the original material structure and allows simple (intrinsically-reversible) shape variations (e.g., [32]); (ii) shape memory soft materials, in which shape-shifting is not encoded in the original material structure, but programming of complex shape variations is allowed on demand (e.g., [31,33]). In the latter case, shape variations are typically not reversible; however, different solutions offering a powerful combination of reversible and programmable shape variations (e.g., [31,33] and references therein) have recently attracted wide attention. Among these solutions, those based on shape memory polymers (SMPs) are promising to expand the range of application of programmable soft robots. SMPs are materials able to “remember” one or more temporary shapes from a permanent shape. According to the number of remembered shapes, SMPs can be classified into three main categories: (i) one-way (or dual) SMPs that have one permanent shape and one temporary shape; (ii) multiple-way (or multi(n)) SMPs that have one permanent shape and (n − 1) temporary shapes; (iii) two-way SMPs that are capable of a reversible transition between to temporary shapes. It is clear that multiple-way and two-way SMPs have great potentiality for the development of untethered robotic systems with programmable and reversible responses. Furthermore, SMPs display several additional advantageous properties that may be exploited to increase the functionalities of soft robots, such as low cost and density, high deformability, easy processability, synthetic flexibility, biocompatibility/biodegradability, and tailorable properties.
Motivated by the discussed framework, the present paper aims to give an overview about the current state-of-the-art on multiple-way and two-way SMPs and their application to programmable soft robotics. The attention will be dedicated to thermo-responsive SMPs, which are the most used and can be remotely actuated. Particularly, thermo-responsive SMPs activated through both direct and indirect heating will be discussed. The review will cover all the building blocks important for the design and fabrication of these robots, i.e., the base materials, manufacturing processes, working mechanisms, and modeling and simulation tools (Figure 1). Examples of real-world applications of soft robots and related actuators from the literature will be described and discussed, together with current challenges and future advancements.
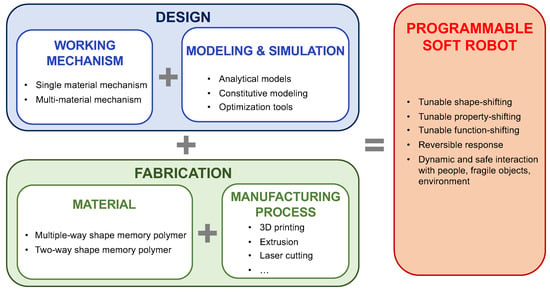
Figure 1.
Programmable soft robots: fundamental building blocks, discussed in the present work, for their design and fabrication.
The paper is organized as follows. Section 2 will present the types of materials featuring the multiple-way and two-way shape memory effect. Then, Section 3 will discuss main approaches for the manufacturing of soft robots based on these materials, with a special focus on 3D printing techniques. Section 4 will present several real-world soft robotic examples from the literature, discussed in terms of working mechanisms, while Section 5 will describe the theoretical and numerical approaches for the modeling of these materials and for the design of such robots. Conclusions will be presented in Section 6.
2. Materials
The present section reviews multiple-way and two-way thermo-responsive SMPs. For the purpose of comparison, one-way SMPs are also recalled. The description covers macroscopic material features, macromolecular architecture, and experimental characterization. For a comprehensive review on SMPs, the reader is referred to [34,35,36,37,38,39,40,41,42,43,44,45,46,47].
2.1. One-Way SMPs
One-way (or dual) thermo-responsive SMPs display the capability of recovering a “permanent" shape (i.e., the shape provided through conventional processing) from a “temporary” shape (i.e., the shape provided through a process named “programming”) when heated; such a capability is known as one-way shape memory effect (SME).
The one-way SME is correlated to a transition temperature (e.g., the glass transition, melting, crystallization, or clearing temperature, depending on the polymer type) and results from a combination of an applied thermo-mechanical history (i.e., the shape memory cycle) with polymer macromolecular architecture.
The shape memory cycle is illustrated in the first row of Figure 2 for a SMP featuring the one-way SME and having a transition temperature denoted as . The material is first formed into a permanent shape through conventional processing. Then, the material is subjected to a cycle, called “programming”, in order to be “fixed” in a temporary shape. The programming step consists of: (i) heating the material up to a temperature , which results in an increase of the mobility of polymer molecular chains; (ii) deforming the material, which induces an orientation of polymer molecular chains and a macromolecular conformation variation, accompanied by a change in entropy, leaving the polymer in a high-energy unstable state; (iii) cooling the material down to , limiting molecular mobility, trapping the high-energy state, and fixing the temporary shape; and (iv) removing the applied load. Typically, temperatures and are 15–40 °C, respectively, above and below the transition temperature (determined by using differential scanning calorimetry). Finally, heating the material back to restores the mobility of the chain segments and allows the recovery of the permanent shape from the temporary shape. As it can be observed from the figure, both fixation of the temporary shape and recovery of the permanent shape are determined by . Moreover, the one-way SME is a non-reversible feature: after the permanent shape is recovered, the SMP cannot reverse to its temporary shape through cooling, but a new programming step is needed to re-fix the temporary shape. The shape memory cycle can be indefinitely repeated and is limited only by the possible degradation of the material [44,48].
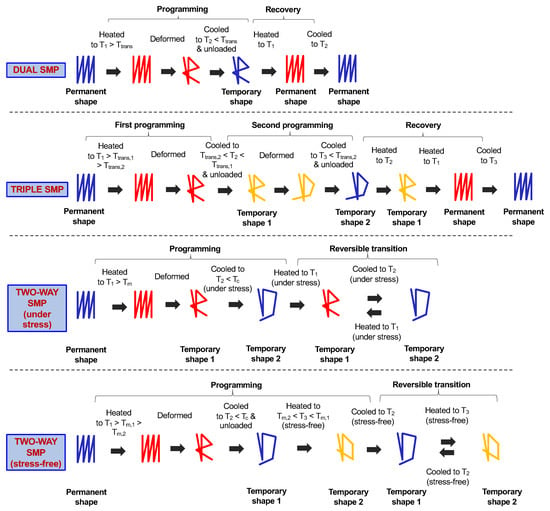
Figure 2.
Shape memory cycle in dual, triple, and two-way SMPs. For two-way SMPs, the shape memory behavior under stressed and stress-free conditions is represented.
Polymer macromolecular architecture consists of a cross-linking structure (net-points) and reversible switching structures (thermal switches). Net-points determine the permanent shape and can be formed by, e.g., molecular entanglement, a crystalline phase, chemical cross-linking, an interpenetrated network, or a cyclodextrin polymer’s inclusion (see [34,38,44,46] and references therein). Thermal switches are responsible for the temporary shape fixation and permanent shape recovery that are determined by the transition temperature, , since chain mobility is trapped (fixing) and liberated (recovery) by cooling below and heating above , respectively. Several reversible switching structures have been employed, such as crystallization/melting transition, vitrification/glass transition, liquid crystal anisotropic/isotropic transition, reversible molecule cross-linking reactions, and supramolecular association/disassociation (see [34,38,46] and references therein). According to the nature of both reversible thermal transition and cross-linking, one-way SMPs can be divided into chemically and physically cross-linked polymers (see [46] and references therein).
Several polymers exhibit the one-way SME with different performances, as discussed in Section 2.4. In general, the type of SMP is chosen according to the temperature range in which the application under investigation operates [49].
2.2. Multiple-Way SMPs
Multiple-way (or multi(n)) thermo-responsive SMPs display the capability of recovering a “permanent” shape (i.e., the shape provided through conventional processing) from two or more “temporary” shapes (i.e., the shapes provided through a process named “programming”) when heated; such a capability is known as multiple-way SME.
Similarly to the one-way SME, the multiple-way SME results from an appropriate combination of the polymeric macromolecular architecture with an applied thermo-mechanical history (i.e., the shape memory cycle).
Two strategies can be adopted to design multiple-way thermo-responsive SMPs: (i) incorporating two or more well-separated transition temperatures into the system (e.g., glass, melting, or clearing crystalline transitions); (ii) introducing a broad (either glass or melting) transition temperature range.
In the case of strategy (i), the SMP may feature a multiple-way SME after a multi-step programming process, which allows one to fix multiple temporary shapes at a temperature below the respective transition temperatures. To clarify the concept, the shape memory cycle is illustrated in the second row of Figure 2 for a triple SMP having two well-separated transition temperatures, denoted as and , such that . The material is first formed into a permanent shape through conventional processing. Then, the material is “fixed” in a first temporary shape and in a second temporary shape by applying two separate and consecutive programming cycles. The two programming steps are similar to those described for the one-way SMP in Section 2.1 and consist of: (i) heating the material up to a temperature ; (ii) deforming the material; (iii) cooling the material down to ; (iv) removing the applied load; (v) deforming the material; (vi) cooling the material down to ; (vii) removing the applied load. Typically, temperature is 15–40 °C above ; is 10–40 °C below and 10–40 °C above ; and is 15–40 °C below [50]. Finally, the permanent shape is recovered, sequentially passing through the second temporary shape and the first temporary shape by heating the material back to . As it can be observed from the figure, both fixation of the temporary shapes and recovery of the permanent shape are determined by the two transition temperatures, and . Moreover, similarly to the one-way SME, the multiple-way SME is a non-reversible feature: after the permanent shape is recovered, the SMP cannot reverse to its temporary shapes through cooling, but a new programming step is needed. However, differently from one-way SMPs, multiple-way SMPs are able to sequentially remember different shapes. Strategy (i) has been largely employed by using either glass or melting transitions, e.g., in [51,52,53,54,55,56,57,58,59,60,61,62,63,64],and nematic-isotropic transformations of nematic network; e.g., in [65,66,67,68,69,70,71,72]. Li et al. [50] proposed triple and quadruple SMPs by designing and synthesizing a series of linear poly(lactic acid)-based copolymers containing a smectic liquid crystal in the main-chain, having two distinguished glass transition temperatures and one liquid crystalline clearing transition temperature. It is worth highlighting that multi-step programming is not a prerequisite for achieving the multiple-way SME and one-step programming has been also applied (see [38,73,74] and references therein). Recently, Zhou et al. [75] proposed an approach consisting of programming different shapes at different stages of an isothermal crystallization process and in heating the SMP to recover the permanent shape sequentially. The approach has been applied to semi-crystalline elastomers to achieve triple SMPs. Alternative methods for creating multiple, well-separated switching transitions in one system consist of laminating two SMPs which have well-separated transition temperatures [76,77] or of developing hybrid SMPs with multiple thermal transitions [78,79,80,81]. In general, when adopting strategy (i), it should be taken into account that well-separated thermal transitions are required to achieve outstanding multiple-way SME. Moreover, the failure strain of these polymers should be high enough to allow for the fixation of multiple different temporary shapes.
In case of strategy (ii), the broad glass/melting transition may be considered a consecutive distribution of a certain number of glass/melting transitions, and the recovery process of the permanent shape from the different temporary shapes is triggered at various temperatures, corresponding to the temperatures at which the material is deformed (often called “deformation temperatures”) [38,44]. In such a case, the SME is also known as temperature-memory effect (TME). Such an approach has been largely employed to achieve multiple-way SMPs with a broad glass transition [82,83,84,85,86,87,88,89,90,91,92] and a broad melting transition [93,94,95] as the switching transition. Mirtschin et al. [96] studied how programming parameters such as the strain rate and temperature holding time at the deformation temperature allow one to gain precise control of the TME in semi-crystalline polyurethanes and to design the TME under stress-free recovery conditions. Some approaches use SMP-based composites or fillers to tune polymer behavior [82,97]. Di Orio et al. [98] created a linear glass transition temperature gradient within one SMP leading to a glass transition distribution throughout the polymer and a recovery in the linear gradient direction. Such an approach (also known as “macroscale spatio-design”), consisting of endowing a material with spatially-distributed transition temperatures, has attracted wide attention (see [47,91,99,100,101] and references therein). In general, strategy (ii) does not require modification in the chemistry of the system; however, it is difficult to fabricate a SMP with the capability of more than four or five shape transitions. In order to achieve quintuple SME, Li et al. [102] incorporated another additional melting transition into a SMP already possessing a broad glass transition.
2.3. Two-Way SMPs
Two-way thermo-responsive SMPs display the capability of a reversible shape effect between two different configurations on the application of an on-off stimulus (i.e., a cooling-heating cycle). Depending of the polymer type, other on-off stimuli may be employed. They may be of the same type (such as different light wavelengths) or of different types (such as light-cooling or electric current-cooling). Such a capability is known as two-way SME and can be either induced by a constant applied stress or under stress-free conditions.
Similarly to the one-way and multiple-way SME, the two-way SME results from an appropriate combination of polymer macromolecular architecture with an applied thermo-mechanical history (i.e., the shape memory cycle).
In particular, the two-way SME under constantly applied stress is a feature shown by two classes of SMPs: (i) semi-crystalline networks (i.e., semi-crystalline crosslinked polymers); (ii) liquid crystalline elastomers (LCEs).
In order to achieve the two-way SME in semi-crystalline networks, i.e., class (i), the simultaneous presence of a crystallizable phase and chemical crosslinks is a strict requirement. The two-way SME under constant tensile stress is based on the elongation of the polymer network, caused by an entropy elasticity effect in the rubbery region and the crystallization upon cooling below the crystallization temperature, and on the contraction of the polymer network, caused by the melting of the temporary-oriented crystalline domain upon heating above the melting temperature. The elongation is also defined as “crystallization-induced elongation” (CIE), while the contraction as “melting-induced contraction” (MIC). The shape memory cycle is illustrated in the third row of Figure 2 for a two-way SMP having a crystallization and a melting temperature, respectively, denoted as and . The material is first formed in a permanent shape through conventional processing. Then, the material is heated up to a temperature and deformed with an external stress to induce a preorientation of the chain segments and to obtain the first reversible temporary shape. Subsequently, the material is cooled down to a temperature under constant applied stress to induce the CIE and to obtain the second reversible temporary shape. Such an elongational process during cooling is composed of a first elongation, which is associated with the chains’ reorientation to satisfy the entropic elasticity constraints as a consequence of the elastic behavior of rubber, and of a second elongation, which is caused by crystallite formation under stress, possibly accompanied by the orientation of the newly formed crystallites [103]. The second elongation is ascribed to a structural evolution process, where crystallite formation, by tending to relax the stress, promotes a further stretching, in order to satisfy the constant stress condition [103,104]. Typically, temperatures and are 15–40 °C, respectively, above and below . Subsequent heating back to determines crystallite melting and a MIC of the material back to the first reversible temporary shape. The complete or almost complete recovery of the first reversible temporary shape generally depends on material and testing conditions [105]. The reversible transition from the first temporary shape and the second temporary shape is then made possible through thermal cycling under constant stress. Similarly to the one-way SME, the two-way SME is governed by the transition temperatures (in such a case, the crystallization and melting temperatures) and is associated to entropic changes of the network. Contributions to semi-crystalline networks can be found; e.g., in [105,106,107,108,109,110,111,112,113]. The approach was even extended to triple SMPs in [114,115,116,117], where a reversible SME was shown over two transition temperatures, with a reversible switching between three shapes under an applied stress. In general, semi-crystalline networks are easy to synthesize and their transition temperatures can be tuned.
LCEs, i.e., class (ii), are shape-changing materials [30,118], that are often grouped into two-way SMPs since they may exhibit the two-way SME. The two-way SME of LCEs results from the combination of the arrangement of mesogenic units in the polymer network and the elastic properties of the network itself. Liquid crystalline domains called poly-domains are usually disorderly oriented with respect to each other, while liquid crystalline domains called mono-domains can be aligned in a particular direction. Some of the physical methods of inducing mono-domains can be employed for achieving the two-way SME; e.g., by applying an external stress. Similarly to semi-crystalline networks, the formation of anisotropic mono-domains aligned in the stress direction undergoes an elongation upon cooling below the clearing temperature and a contraction upon heating above the clearing temperature. While in LCEs phase transitions are directly responsible for shape changes due to the realignment of molecular groups throughout the material, in SMPs phase transitions cause the material to be fixed in or recover a programmed shape. Contributions to LCEs can be found, e.g., in [65,119,120,121,122,123,124,125]. Such an effect has been extended to achieve a two-way triple SME in [126]. Although two-way shape memory LCEs have attractive properties (especially high strain change), their synthesis as well the tailoring of their high transition temperatures may be not trivial.
As anticipated above, the two-way SME does not necessarily require the presence of an applied external stress, but, for polymers with a specific structure and thermo-mechanical history (i.e., the shape memory cycle), it may be based on a provided internal stress. Such an effect, often referred to as reversible bidirectional SME, leads to the possibility of achieving a self-standing reversible actuation [44].
The two-way SME under stress-free conditions is a feature shown by the following classes of SMPs: (i) chemically cross-linked semi-crystalline polymer networks with one broad melting temperature or two melting temperatures; (ii) semi-crystalline polymer networks prepared via a two-stage cross-linking method; (iii) thermoplastic semi-crystalline polymers with one broad melting temperature or two melting temperatures.
According to Wang et al. [46], the polymers belonging to these classes generally contain three phases: (1) a chemically cross-linked phase or a phase within a transition with the highest transition temperature, holding the permanent shape; (2) a semi-crystalline or elastic amorphous phase, determining the shifting-geometry and supplying a stretching tensile force when compressed due to the contraction of the sample; (3) a semi-crystalline or liquid crystalline phase, causing actuation through its melting and crystallization temperatures.
Chemically cross-linked semi-crystalline polymer networks with one broad melting temperature or two melting temperatures, i.e., class (i), require a programming procedure and a molecular mechanism similar to those shown for the two-way SMPs under stress condition. Specifically, the shape memory cycle is illustrated in the fourth row of Figure 2 for a two-way SMP having two melting temperatures, denoted as and , such that . The material is formed in a permanent shape through conventional processing. Then, a programming step, similar to those described for one-way and two-way SMPs, is applied and consists of: (i) heating the material up to a temperature ; (ii) deforming the material with an external stress to induce a preorientation of the chain segments; (iii) cooling the material down to a temperature to introduce a skeleton of geometry-determining domains to the network and to fix a first reversible temporary shape, associated to crystallite formation [44]; (iv) removing the applied load; (v) heating the material up to under stress-free conditions. Such heating causes partial melting and permits it to achieve a partially recovered shape; i.e., a second reversible temporary shape. Subsequent cooling back to permits it to recover the first reversible temporary shape due to the crystallization of the polymer chains along the direction of the internal tensile force produced by the unmelted crystalline phase. The reversible passage from the first temporary shape and the second temporary shape is made possible through thermal cycling between and and can be repeated hundreds of times [127]. Typically, is 15–40 °C above , is 15–40 °C below , and can be varied depending on polymer type in order to tune the actuation mechanism [128]. If the material is heated back to , the material is restored to its original permanent shape and reprogrammed to other shapes. Similarly to the two-way SME under stress conditions, the stress-free two-way SME is governed by the transition temperatures and is associated to entropic changes of the network. Contributions to this class can be found, e.g., in [128,129,130,131,132,133,134,135], and show the possibility of achieving complex reversible shape changes (e.g., elongation/contraction, bending/unbending, coiling/uncoiling), and of tuning the actuation temperature.
The two-stage cross-linking method has been used to fabricate stress-free two-way SMPs, i.e., class (ii); e.g., in [136,137,138]. In this case, an interpenetrating network is obtained as a combination of at least two polymeric networks, where a molecular interlacing exists in the matrix. Particularly, a crystalline phase (responsible for the reversible shape shrinkage at high temperature) and an elastomeric component (providing the stretching force for shape extension during the cooling process) are present. By heating the system to the transition temperature of the crystalline network, the crystalline phase leads to the shrinkage of the system and the elastomer component is compressed. By cooling the system to the switching temperature of the crystalline network, crystallization takes place in the force direction due to the elastic recovery of the elastomer component. These SMPs have low transition temperatures and do not lose the two-way SME at high temperatures. From a practical point of view, the two-stage cross-linking method does not require applying a constant tensile stress and the programming process. However, the temporary shapes are fixed and cannot be erased upon heating. Moreover, at present, such a class of SMPs has achieved simple reversible shape changes of elongation and contraction. This method has been also extended to LCEs and their composites in [139,140]. Recently, two-way SMPs containing dynamic covalent bonds have been prepared by using a method similar to the two-stage cross-linking method (see [46,141] and references therein). SMPs cross-linked by dynamic covalent bonds are advantageous due to their reprocessibility, good mechanical properties, and good recoverability [46].
For several years, chemically cross-linked polymer networks have been considered to be a necessary condition for the two-way SME in order to prevent the flowing of the polymer above . However, some thermoplastic polymers, i.e., class (iii), have been shown to feature the two-way SME under stress-free condition [142,143,144,145,146]. Thermoplastic polymers may be reprocessed and reused, thereby avoiding the synthesis of a new polymer. However, the reversible shape change of this class of SMPs is not as good as chemically cross-linked networks.
It is worth recalling that an alternative approach for developing two-way SMPs, or shape-changing materials in general, consists of composites, hybrids, or laminates. Two-way shape memory composites/laminates usually have two layered polymeric networks made of both SMPs, or both non-SMPs, or a layer of a SMP and a non-SMP [147,148,149,150,151,152,153]. In this case, heating creates unbalanced mechanical stresses arising from different thermal or mechanical properties or from the SME (if SMPs are used). This strategy has also allowed for the development of laminated polymers with double SMP layers exhibiting two-way SME also under stress-free condition [154,155,156]. The main disadvantages of such an approach are related to its preparation that may be sophisticated, and the limited reversible strain change (generally lower that 10%).
2.4. Experimental Testing
Appropriate characterization methods on both macroscopic and molecular/morphological levels of SMPs are needed for the design of soft robotic systems.
The macroscopic behavior of SMPs is generally evaluated through cyclic thermo-mechanical tests and depends on the thermo-mechanical loading conditions, such as the strain/heating/cooling rate, deformation and fixation temperatures, temperature-controlled condition, strain-holding condition, and cyclic loading, in addition to the polymer macromolecular architecture. Tensile tests performed with standard testing machines equipped with a thermo-chamber are the most-often used; however, other methods for the characterization of SME have been applied, such as bending, torsion, compression, or three-point flexural tests. Tests under cyclic thermo-mechanical loading are important for characterizing the actuation behavior and material degradation. Thermal properties are generally investigated by using differential scanning calorimetry and dynamic mechanical thermal analysis. In general, the tests for the characterization of the SME must be chosen and tailored to the specific SMP category and the complexity of the shape change under investigation. For a detailed review on thermo-mechanical characterizationand on morphology investigation of SMPs, the reader is referred to [44,45,157,158,159].
The results of experimental testing are generally presented in stress-temperature-strain diagrams. Apart from standard mechanical metrics, two parameters can be used to describe shape memory performances: (i) the shape fixity ratio, which quantifies the ability of the SMP to maintain an imposed mechanical deformation after the load is removed; (ii) the shape recovery ratio, which quantifies the ability of the SMP to recover the permanent shape. Other quantities, as the recovery rate or the recovery temperature range, can be also obtained.
Several works have investigated one-way SMPs, including cyclic thermo-mechanical tests consisting of a programming module under strain or stress control and a recovery module under stress-free or constant-strain condition. Efforts to improve one-way SMP properties have led to materials that may: (i) be strained up to about 800% before failure; (ii) have elastic-energy densities between 10 and 2000 MJ/m3 for strains approaching 200%; (iii) exert stresses between 0.1 and 10 MPa; (iv) have response times greater than 10 s; (v) high shape fixity and recovery ratios [3]. It is also important to highlight that thermo-responsive SMPs may exhibit high variations in the elastic modulus over the operational temperature range (being softer above the transition temperature and harder below the transition temperature) [3,33]. Several fillers, such as carbon nanotubes (CNTs), carbon black, polypyrrole, and nickel powders, or additives, such as plasticizer molecules, have been used to increase thermal and electrical conductivity or functionalities, mechanical strength, and recovery stresses, and to tune shape memory behavior (see [3,160,161,162] and references therein).
Compared to one-way SMPs, certain multiple-way SMPs (e.g., physically-crosslinked thermoplastic polymers) may exhibit lower shape fixity and shape recovery ratios, due to long-range molecular chain slippage and damage of physical crosslinks integrity, especially under high strain [92]. Moreover, the recovery behavior of these SMPs is susceptible to stress relaxation and creep. Accordingly, some studies have been proposed to design SMPs with multiple-SMEs reaching strains of about 1000% with high shape fixity and shape recovery. Additional functionalities, such as self-healing properties [163,164], moisture-sensitive SME [165], and biodegradability [166], have been included in multiple-way SMPs.
Several studies have been dedicated to the characterization of two-way SMPs under tensile stress, while few studies are available on the compressive stress condition [47]. In fact, much attention has been devoted to the synthesis and thermo-mechanical characterization of semi-crystalline networks exhibiting the two-way SME under tensile stress [105,106,149,167]. Particularly, the two-way SME was shown to be tailored by the applied stress, the cooling/heating rate, and the crosslink density, leading to materials capable of two-way reversible strain variations between 10% and 100% under the application of moderate stresses (typically, between hundreds of kPa and a few MPa) [103]. Moreover, recovery effects were shown to be sharp and fast, since they are triggered by melting instead of being activated by glassy-rubbery transition. The thermal expansion coefficient of the material was also shown to play an important role during the two-way process, especially under low levels of applied stress [105]. Studies on LCEs showed that the material may: (i) be strained up to 400% before failure; (ii) have elastic-energy densities between 3 and 56 kJ/m3; (iii) exert stresses between 0.01 and 0.12 MPa; (iv) have an elastic modulus varying between 0.1 and 5 MPa; (v) response times greater than 10 s [33]. Additional functionalities, such as biodegradability [168] or improved performances [169], have been included.
Experimental studies concerning the two-way SME under stress-free condition, in terms of mechanical performances, generated internal stresses, and the influence of both crystallinity degree and cross-linking density on the reversible absolute strain change, are still limited. Generally, recoverable actuation strains between 10% and 20% are achieved.
Finally, it is worth mentioning that thermally-induced SMPs may be directly triggered by heating with hot gas or water, but indirect heating has been also used (see [3,33,46] and references therein). For example, SMPs with functional fillers may be triggered by light, electricity, magnetic fields, microwaves, or ultrasound, but they are still intrinsically triggered by heat, since different forms of energy are converted into heat through the fillers (see [33,46,47,170,171,172] and references therein). The molecular mechanisms and the programming process are equal to those described for direct heating-triggered SMPs in previous sections. Indirect heating has many advantages, such as local heating and remote control. Many studies have been also devoted to the achievement of a complex, well-controlled, shape recovering, and spatially-controllable multiple-way SME by exploiting selective (direct/indirect) heating of predeformed SMPs or homogeneous (direct/indirect) heating of predeformed structurally inhomogeneous SMPs (see [38,46] and references therein). Obviously, other types of SMPs that are not activated by temperature changes exist (e.g., light-induced or chemo-responsive SMPs), but will be not discussed in the present manuscript (for details, see [3,33,46] and references therein).
3. Manufacturing
The SMPs discussed in Section 2 and related soft robots are generally manufactured through standard fabrication techniques, such as shape extrusion, injection molding, laser cutting, or soft lithography [34,173,174]. Recently, alternative methods, such as dual-curing [175] and electrospinning [176,177], have been employed to obtain more complex structures. Such techniques may require manual intervention, post-processing, and lengthy iterations for assembly, thereby limiting the realization of complex robotic systems.
To avoid costly and time-consuming aspects of current fabrication techniques, researchers have explored alternative approaches for the efficient and effective manufacturing of soft robots, such as 3D printing [13,178]. The advantage in using 3D printing lies in the possibility to realize soft systems with geometrically complex structures in a single-step, without the need for external joints, adhesives, or fasteners. In addition, soft robots can be produced with high accuracy (of the order of sub-millimeters).
In the last few years, considerable advances in soft robotic technology have been made thanks to 4D printing, which allows one to realize structures with arbitrarily complex or customized architectures, capable of evolving their shape, properties, or functionalities along time (denoting the 4th dimension) under the application of proper stimuli [178,179,180,181,182,183,184,185,186,187,188,189]. 4D printing is particularly advantageous to save space for storage and transportation purposes and enlarges the range of applications to those areas in which a dynamical configurational change is required [190], as in the case of soft robotics.
One of the most important ingredients of 4D printing is the stimuli-responsive material [191,192]. Several printing techniques have been developed for the manufacturing of SMP-based robots, including those based on material extrusion (e.g., fused deposition modeling, direct inkjet writing), material jetting (e.g., PolyJet), and VAT photopolymerization (e.g., digital light projection, stereolithography, projection micro-stereolithography) [33,183,188].
In 2014 Tibbits [193] first published a work reporting one-way SMPs 3D printed by using Stratasys’s Connex machine offering multi-material PolyJet printing. After 2014, several works on one-way SMPs with increasing functionalities appeared. As an example, a one-way SMP was printed and structured in [194], by exploiting digital light projection technology and using a photocurable polycaprolactone (PCL). Recently, Invernizzi et al. [195] printed a SMP featuring both the one-way SME and self-healing properties, via digital light projection technology.
More recently, some contributions on 3D printed multiple-way and two-way SMPs were published.
Chen et al. [196] proposed a blending strategy to prepare tunable SMP blends featuring quadruple SME with the feasibility of 3D printing. The monofilament was then applied to a commercial fused deposition modeling 3D printer. Yu et al. [197] used the material under the name Gray 60 in the multi-material Polyjet 3D printer (Stratasys, Connex Object) material library, having a broad glass transition and exhibiting the multiple-way SME. More recently, Inverardi et al. [198] used stereolitography to print multiple-way SMP structures. The effect was possible thanks to the broad glass transition of a commercial photopolymer, known under the name Clear FLGPCL02 and provided by Formlabs company.
Yuan et al. [199] showed the potentialities of 3D printed LCEs, compared to standard fabrication techniques. Recently, voxelated LCEs, capable of actuating reversibly and exhibiting large work capacities, have been produced in thick-film geometries (about 1 mm thick) via 3D printing [200,201,202,203,204].
As discussed in previous sections, the multiple-way and two-way SME can be achieved in composite structures. Accordingly, Ge et al. [205] first realized composites featuring the SME by using a multi-material Polyjet 3D printer (Stratasys, Connex Object). Following this idea, the first example of 3D printed multiple-way SMPs was provided by Wu et al. [206], who fabricated layered composite structures with SMPs having different glass transition temperatures, by using a multi-material Polyjet 3D printer. In particular, the work focused on the commercial material under the name TangoBlack plus and on digital materials known as DM8530 and DM9895. More recently, Ge et al. [207] used a multi-material system based on projection microstereolithography to create composite structures based on photo-curable methacrylate based copolymer networks. The advantages of this technique are the high resolution achievable (1 μm), quick processing time, and automated material exchange. Similarly, Mao et al. [208] developed SMP-based composite structures exhibiting the two-way SME by combining layers of SMPs and hydrogels. Again the multi-material Polyjet 3D printer (Stratasys, Connex Object) was used, with the commercial materials under the names Grey60 and Tangoblack. The idea of realizing composite structures featuring a multiple-way SME was extended to fused deposition modeling 3D printing [209]. Sun et al. [209] created tri-layer, functionally-graded composites made of polylactic acid (PLA) plasticized with different amounts of poly(ethylene glycol) (PEG) across the gradient, to achieve multi-shape memory and localized actuation properties.
In order to avoid the need of the programming step required by most of the approaches discussed above, some authors proposed generating an internal stress in the SMP to be used to recover the permanent shape [201,208,210,211,212]. To generate the internal stress, Ding et al. [211] imparted an eigenstrain during the printing process (the so-called “printing strain”) in SMP/elastomer bilayer structures and named the approach “direct 4D printing”. The multi-material Polyjet 3D printer (Stratasys, Connex Object), and commercial materials known as TangoBlackPlus or TangoPlus, as the elastomer and VeroClear as the SMP, were used. Such an approach allows one to print simple geometries (e.g., two-dimensional flat sheets), thereby reducing the quantity of support material during printing that can transform to a complex geometry (e.g., a three-dimensional object) without the need of post-printing SMP programming. Such a concept was later extended to polyurethane-based SMP structures in [213] and to polylactic acid polymeric structures in [214], printed via fused deposition modeling. Printing parameters, such as filament plying angle, component porosity, thickness, and transition temperatures, were used to control the shrinkage in [214]. Zhang et al. [215] exploited heat-shrinkable properties of polylactic acid (PLA) SMPs to activate shape changing without a shape programming step. In fact, heating the polymer above its transition temperature can release the internal strain energy that is imparted in the polymer during the extrusion-based 3D printing process. Mao et al. [208] used both SMPs and hydrogels responding, respectively, to thermal and aqueous stimuli, to switch between two stable configurations. Hydrogel swelling force was used to induce internal stress in the SMP. Moreover, a layer of hydrogel between the standard SMP and the elastomer bilayer allowed the structure to shift from one-way actuation to two-way actuation. A multi-material Polyjet 3D printer (Stratasys, Connex Object) and commercial materials known as Grey60 and Tangoblack were used. The frontal polymerization process was employed by Zhao et al. [216,217], who exploited the change in the intensity of photo-polymerization to create spatially-varying material parameters in single-material structures.
4. Working Mechanisms and Applications
Two basic working mechanisms are generally adopted for realizing programmable soft robots based on multiple-way and two-way SMPs, and consist of using: (i) one single material and (ii) multiple materials. Such working mechanisms exhibit similar shape memory behaviors; however, the macroscale structure of the robot and the localization of the applied thermal stimulus can be designed to introduce specific behaviors and to achieve complex motions, including linear stretching/contraction, circular expansion, walking, swimming, and folding. In the following, both mechanisms are reviewed and several real-world examples of soft robots and related actuators are presented and discussed. As is noted, common macroscale structures range from simple geometries (e.g., beams or strips) to complex geometries based on multi-stability/buckling concepts, reinforced/layered systems, folding/cutting theories, and metamaterial design. A short discussion is dedicated to the realization of multi-functional soft robotic systems.
4.1. Single-Material Mechanism
Soft robots based on one single SMP receive their properties from those featured by the constituent material itself, from their macroscale structure, and from the localization of the thermal stimulus. In general, the realized soft robots are able to perform tasks such as linear stretching/contraction, coiling, twisting, and folding. Such robots have drawn great interest due to their simple manufacturing process that does not require, e.g., post-processing or the use of multi-material 3D printers.
While several examples, such as grippers and drug delivery systems, employ one-way SMPs (see [13,178,218,219] and references therein), applications based on the multiple-way SME are still limited. Among these, Bodaghi et al. [220] combined polyurethane-based SMPs, hot-cold programming, and fused deposition modeling 3D printing technology to engineer dual and triple SMP self-bending grippers and self-shrinking/tightening staples. Yu et al. [197] used the material under the commercial name Gray 60 in the multi-material Polyjet 3D printer (Stratasys, Connex Object) to realize triple SME in trusses or box-shaped structures, capable of linear stretching/contraction. Pandini et al. [221] printed, through stereolitography, auxetic structures capable of hierarchical motion as a consequence of the broad glass transition region of the employed commercial polymer (known under the name Clear FLGPCL02). Auxetic structures were able to perform autonomous sequential in-plane and out-of-plane motions, as shown in Figure 3. All these structures [197,221] can be potentially used to increment the motion capabilities of soft robotics systems.
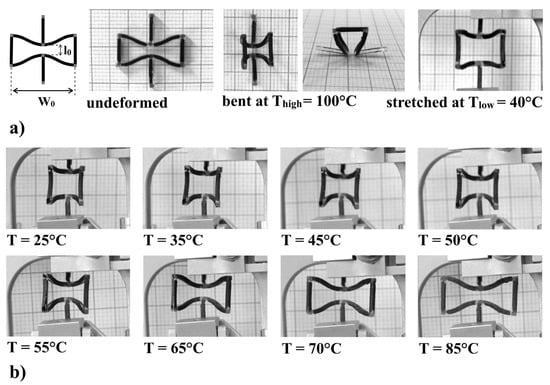
Figure 3.
Temperature-memory effect (TME) exploited for achieving hierarchical motion of a 3D printed auxetic cell. The cell is subjected to: (a) a two-step programming consisting of an early out-of-plane bending at T = 100 °C, and a subsequent stretching at T = 40 °C; (b) shape recovery. Reprinted from [221], copyright 2020, with permission from Elsevier.
To date, limited examples of soft actuators and robots based on two-way SMPs are available. Behl et al. [127] exploited the two-way SME of cross-linked copolymer networks to design self-programmable reversible window shades. Chemically cross-linked poly(ethylene-co-vinyl acetate) two-way SMPs were processed into precursor fibers through twist insertion to manufacture artificial muscles in [222,223]. Two-way SMP particles that are able to switch shape reversibly in response to temperature were utilized as drug carriers in [224]. Free-standing copolymer networks with two types of crystallizable domains were used in [128] to fabricate grippers that reversibly catch and release a penny and reversible fixator devices that collapse upon heating and expand when cooled. Ge and Zao [225] demonstrated a strategy that allows one to realize thermal phase transition-based polymer actuators exhibiting autonomous, self-sustained motion with no need for temperature switching. In particular, Ge and Zao used the crosslinked semi-crystalline random copolymer poly(ethyleneco-vinyl acetate) (EVA) proposed in [127,128], which displays the TME. Ge and Zao verified that, when a sufficiently thick specimen is in contact with a hot substrate surface, a temperature gradient, formed due to heat diffusion along the thickness direction, leads to a superficial melting-induced contractile force that pushes the specimen up, and once cooled in the air, yields a crystallization-induced extensional force that flattens the specimen on the substrate surface to reactivate the motion cycle. Such continuous motion is thus driven by thermal energy and without on/off temperature switching. Actuation with over a thousand cycles of motion was achieved and demonstrated in arch-shaped actuators capable of rotating a wheel and of walking. Farhan et al. [226] realized a manikin equipped with a twisted SMP actuator arm able to non-continuously rotate between three different arrow positions when exposed to a linear change in temperature under stress-free conditions. The SMP was synthesized from cross-linked blends of poly(ε-caprolactone) (PCL) and poly(ethylene-co-vinyl acetate) (PEVA), where the two phase-segregated regions had distinct melting and crystallization temperatures, and different crystallization kinetics. Thermally-responsive liquid crystal networks were used to manufacture a gripper mimicking the self-peeling mechanism of gecko toe pads in [227], while microscale LCE actuators were realized in [228,229]. López-Valdeolivas et al. [203] reported the manufacturing of complex reversible shape-morphing LCE-based structures, such as auxetics and spiral-like devices, through ink printing. Ahn et al. [230] developed a technique to pattern liquid crystal molecules in a LCE. As a result, the patterned LCE had different active deformation modes when subjected to various external stimuli, and thus was able to perform different functions. de Haan et al. [231] described the fabrication, characterization, and modeling of liquid crystalline polymer network films with a multiple patterned 3D nematic director profile, exhibiting complex mechanical actuation under change of temperature or pH. Three-dimensional features were programmed into flat sheets of LCEs by introducing topological defects in [232]. Using this approach, it was possible to align and crosslink individual groups of mesogens in arbitrarily complex patterns, with demonstrations that include an initially flat heated sheet able to lift a load 147 times its own weight with a stroke of about 3000%.
Other application fields of two-way SMPs, such as microfluidic pumps [233], surfaces to modulate optical properties in optical devices [234], biomedical devices [138,235], and selective filtration membranes [236], are available (see [47] and references therein).
By exploiting the approaches that avoid the need of the programming step, discussed in Section 3, self-folding cone and doubly curved shell structures [213], self-folding origami [214,217], an instability-driven pop-up [214], an sequential shape-shifter [214], grippers [216], tetrahedron/box light-emitting diode devices folded by triangular sheets [216], and self-folding lattices [215,237] were realized.
Besides using direct heating, indirect heating was used by Fang et al. [238], who proposed to use both the crosslinked semi-crystalline random copolymer poly(ethyleneco-vinyl acetate), introduced in [127,128] and possessing the TME, and aniline black as near-infrared light triggered photothermal filler. In this way, Fang et al. were able to realize light-triggered releasing devices and grippers in aqueous media. Liu et al. [239] developed self-folding thin sheets using unfocused light. The sheets were made of optically transparent, prestrained polystyrene that shrank in-plane if heated uniformly. Black inks patterned on the polymer sheet provided localized absorption of light to heat the polymer and to cause sheet folding into a three-dimensional object. Yang et al. [240] prepared light-sensitive structures by dispersing CNTs into LCEs with exchangeable links (xLCEs). Photothermal effects induced fast exchange reaction in xLCEs, and as a result, dynamic 3D structures were fabricated by irradiating a stretched film under stress for a few seconds. Different alignment modes were written/programmed in one film, as shown in Figure 4. Light-manipulated processes could be carried out at a broad temperature range, even at extremely low temperatures (e.g., −130 °C in liquid nitrogen vapor). The geometry information could be selectively or completely erased by light and the dynamic 3D structures could be reshaped or reconfigured. The materials also enabled photo-healing of microcracks and recycling. Photo-induced sequential shape-shifting was also achieved by Liu et al. [241], who reported a simple method, using a desktop printer, to pattern inks of different light absorptivity as hinges on homogeneously prestrained polymer (e.g., polystyrene) sheets. Light was absorbed by the inks and thus heated the prestrained polymer across the sheet thickness, which caused the relief of strain to induce folding. This approach enables sequential sheet folding with respect to time and space by controlling light wavelength and ink color. Yang et al. [161] used fused filament fabrication to 3D print light-triggered thermo-responsive SMP structures using polyurethane and carbon black, where the carbon black helps to absorb radiation from light sources. Recently, in [242], a crystalline SMP with thermo- and photo-reversible bonds have been used to create programmable single-component origami-based cranes, capable of wing flapping motions, and elephants, showing curling and uncurling actions.

Figure 4.
Reversible actuation of CNT-xLCE dynamic 3D structures: (A) film, (B) triangle, (C) chair, (D) “Hercules” (18.5 mg) lifts four balls (72.6 mg), (E) tripod, (F) six-petal flower. Reproduced with permission from [240]. Copyright 2016, American Chemical Society.
Peng et al. [243] showed that a three-dimensional porous CNT sponge can be used as a built-in integral conductive network to provide internal, homogeneous, Joule heating for SMPs, thereby significantly improving the mechanical and thermal behavior of SMPs. As a result, a fast response and large exerting forces (with a maximum flexural stress of 14.6 MPa) were demonstrated during shape recovery.
4.2. Multi-Material Mechanism
Soft robots made of multiple materials, such as composites, hybrids, or laminates, receive their properties from the interaction between the constituent materials, from their macroscale structure, and from the localization of the thermal stimulus. In fact, different types of SMPs are generally combined together or with inactive/active materials, and direct/indirect heating creates unbalanced mechanical stresses determined by the thermal or mechanical properties or the relative positions of the base materials in the macroscale structure, which drive the shape change of the structure itself. Soft robots based on multiple materials have drawn great interest due to the possibility of achieving very complex motions, such as walking, rolling, and swimming. However, they require multi-material fabrication techniques or post-processing.
Common designs belonging to this class are, e.g., fiber-reinforced composites, layered structures/metamaterials, multi-stable structures, and origami-based composites (see [3,33,183,244] and references therein). Origami theory is especially suited to simplify the design space of soft robots through hinge-based actuation, since compliant, energy-dense actuators are placed at creases, where deformations are localized, whereas stiffer structural elements work as planar facets [245].
Shape-changing sequences can be realized in composite structures containing spatially-distributed SMPs [246,247]. As an example, Yu et al. [246] used the 3D printing technique of thermally-triggered epoxy-based UV curable SMPs to realize self-locking or self-closing devices. By properly specifying material properties in different sections, Yu et al. demonstrated that the deformed SMP component can successfully return back to the permanent shape in a predefined sequence, thereby exhibiting a multiple-way SME.
Two-way shape memory laminates were prepared by combining a programmed polyurethane-based SMP film with an un-elongated elastic polymer film in [149]. Two-way shape memory behavior, i.e., bending upon heating and reverse bending upon cooling, was observed. Peng et al. [243] studied the construction of a double-layer composite structure for bidirectional actuation, in which the shape change is dominated by the temperature-dependent exerting force from the top and bottom layer, alternately. An inchworm-type robot was demonstrated. Belmonte et al. [248] developed free-standing SMP actuators by using laminating “thiol-epoxy”-based glassy thermoset and stretched liquid-crystalline network films. The actuators were capable of complex motions, such as S-type bending. Kotikian et al. [29] firstly created untethered, soft robots that can reversibly shape-morph and propel itself in response to temperature changes, via multi-material 3D printing. Specifically, LCE hinges, interconnecting structural polymeric tiles, were printed to produce active structures that exhibit large, repeatable, and programmable deformations. Among the design structures, a self-twisting origami polyhedron with three stable configurations and a rollbot that assembles into a pentagonal prism and self-rolls were realized.
Yuan et al. [249] proposed a thermo-mechanically triggered two--stage pattern switching approach, where an amorphous polymer and a flexible elastomer were used. Periodic structures, such as square meshes, re--entrant honeycombs, and tetrachiral lattices, were designed to explore the influence of material layout within the structure and a smart window which can react to the ambient temperature by self--opening was realized.
Zhao et al. [250] combined structural design and multi-material 3D printing to design soft periodic lattice metamaterials containing two distinct deformation modes, controlled by zig-zagged topological defects and thermal activation of the responsive materials, respectively. By regulating the deformation mode with ambient temperature, the effective Poisson’s ratio of the lattice was intentionally switched between negative values and positive values.
Chen et al. [251] combined multi-stability, SME, and multi-material 3D printing to design bistable Von Mises truss actuators. Each actuator was used as unit actuator for the fabrication of a more complex multi-stable actuator based on hierarchical principles. Particularly, a deployable space frame structure and a structure with varying Gaussian curvature was realized. Later, Chen et al. [252] combined these actuators with 3D printed shape memory strips, which respond to different temperatures, to create time-sequenced linear actuators and deployable structures. In particular, an untethered, soft swimming robot with preprogrammed, directional propulsion without a battery or onboard electronics was designed. Locomotion of the robot was achieved by using SMP actuators that harnessed the bistable elements, triggered by surrounding temperature changes. As a proof of concept, Chen et al. showed the ability to program a vessel, which could autonomously deliver a cargo and navigate back to the deployment point. Commercial SMPs, named VeroWhitePlus and FLX9895, were used.
By exploiting the approaches that avoid the need of the programming step, discussed in Section 3, self-folding layered actuators [211], bending strips carrying load of 25–50 g [208], and self-folding periodic macro-structures, strips, and origami [208] were realized.
4.3. Multi-Functional Mechanisms
Recently, the concept of shape-shifting has been extended to the concept of function- or property-shifting, such as tissue maturation, degradability, self-healing, color shifting, optics/conductivity properties (see [188] and references therein). The inclusion of additional functionalities is very promising for the development of autonomous soft robots.
The contributions combining multiple-way and two-way SMPs with the listed function or property shifting features are still limited in the current literature. As an example, for biomedical and pharmaceutical application, SMPs need to be biocompatible with non-toxic degradation products which require switching temperatures in the physiological range [253]. The possibility to print simple actuators for soft robotics with good mechanical properties, one-way SME, and self-healing capabilities has been shown in [195] (see Figure 5).

Figure 5.
SME of a polycaprolactone dimethacrylate (PCLDMA)-2-ureido-4[1H]-pyrimidinone motifs (UPyMA) repaired sample. The sample was (a) cut, (b) repaired after thermal treatment, (c) deformed, and (d–f) heated up to 70 °C recover the permanent shape. Reprinted from [195], copyright 2018, with permission from Elsevier.
Thanks to the advantage of realizing customized and personalized bio-material-based structures, 4D bioprinting also shows great potential for future biomedical applications [188].
5. Modeling and Simulation
Soft robotics systems require a throughout design to achieve the desired change in shape, properties, or functionalities and to optimize the performances in terms of, e.g., deformations, forces, material distribution, geometry, and response times. In this framework, modeling and simulation are fundamental to support the design and avoid costly and time-consuming experiments. Moreover, with the advent of 3D printing techniques, a numerical tool is particularly needed to predict the targeted evolution in time and space of the printed robots.
However, the prediction of the kinematics of these systems is not straightforward, because the majority of soft robots cannot be adequately described by linear models, since they involve many degrees of freedom, material and geometric nonlinearities, shape memory behavior, and need to satisfy a diverse set of boundary conditions. It is therefore particularly needed to formulate reliable modeling and simulation tools for the control of such systems in real-world applications.
Generally, main design approaches consist of: (i) analytical models, (ii) numerical simulations based on constitutive models, and (iii) topology optimization methods.
The first approach involve the formulation of analytical relationships. Common approaches are, for examples, those based on classical beam theory for layered structures [212,217,254,255,256] and origami theory [208,257].
The second approach consists of the constitutive modeling of SMPs and in their implementation into simulation software. Through constitutive modeling, several SMEs can be understood and predicted, such as isothermal and non-isothermal stress-strain responses, shape memory and rate-dependent behavior, and the effect of loading rate on material behavior [258]. Macroscopic, mesoscopic, and microscopic models; molecular dynamic simulations; and quantum-chemical calculations have been proposed for SMPs in both one and three dimensions and under both small and large deformation. For a detailed review, the reader is referred to [36,259,260]. In particular, macroscopic models appear to be a powerful tool for engineering applications, thanks to their easy numerical implementation and fast computations. Currently, macroscopic models for SMPs are mainly based on two approaches: thermoviscoelastic and phase transition approaches. The choice of the approach to use is related to the type of polymer and to the amount of details needed to accurately describe material behavior, in relation to the application under investigation.
The thermoviscoelastic approach introduces rheological models, consisting of springs, dashpots, and frictional elements, to describe the underlying mechanisms of the SME, based on the temperature-dependence of the molecular mobility and of the relaxation time.
Early thermoviscoelastic models were developed for one-way SMPs under small strain framework. Particularly, rheological models with temperature-dependent viscosity and modulus parameters were first developed for SMPs with one glassy transition temperature [261,262,263] and consisted in a parallel combination of the Prandl and Maxwell models. Morshedian et al. [264] first developed a thermoviscoelastic model for SMPs with one melting transition temperature. The Arrhenius equation [265] was first used to describe the increase in the viscosity by decreasing the temperature in glassy SMPs, while Buckley et al. [266] used the Williams-Landel-Ferry (WLF) equation [267] to describe the temperature dependence of the retardation time in rubbery SMPs. Sun et al. [268] extended the thermoviscoelastic modeling approach to qualitatively illustrate the underlying physics in thermo-responsive SMPs exhibiting the TME. Yu et al. [269] improved the work by Sun et al. [268] by proposing a quantitative analysis for the TME. They employed the one-dimensional standard linear solid model under small strains, proposed by Qi et al. [270], to illustrate the multiple relaxation processes of the polymer chains. The mechanical elements consist of an equilibrium branch and several non-equilibrium branches placed in parallel. The equilibrium branch is a linear spring to represent the equilibrium behavior, and the non-equilibrium branches are Maxwell elements where an elastic spring and a dashpot are placed in series to represent the viscoelastic response. Among the non-equilibrium branches, one represents the relaxation behavior of the glassy mode, while the remaining are used to represent the relaxation modes of polymer chains in the rubbery state. As the temperature is increased, for a given temperature, different numbers of branches (or relaxation modes) become shape memory active or inactive, leading to the observed multiple SME. Above the transition temperature, the WLF equation was used, while, below such temperature, the Arrhenius equation was adopted. Such a model was used in [271,272], while extensions to finite strain can be found in [273,274]. Xiao et al. [275] applied a three-dimensional finite strain, nonlinear viscoelastic model to describe the shape memory behaviors of Nafion, which has a broad glass transition region. Compared to Yu et al. [269], who assumed an even distribution of relaxation times, the authors developed a method to obtain the parameters of the relaxation spectrum from the master curve of the relaxation modulus. The model was applied to program several switchable pattern transformations in Nafion-based membranes using finite element simulations. Viscoelastic approaches have been applied to describe the rate-dependent behavior of the stretch-induced polydomain-monodomain transition of LCEs, e.g., in [276].
The thermoviscoelastic approach has been applied to soft robotics and actuators, e.g., focusing on direct 4D printing [211], single-material structures [215],and composite structures [208,252].
The phase transition approach assumes the materials as composed of two phases to reproduce the overall macroscopic behavior of SMPs. During the phase transition a material fraction is in one state, while the remainder is in the other state. Internal variables and constraints are used to describe the transition between the two phases.
While several contributions are available to model the behavior of one-way SMPs (see [260] and references therein), little attention has been dedicated to the constitutive modeling of the two-way SME. In fact, few works considering the two-way SME under stress conditions in semi-crystalline crosslinked polymers are available [103,104,167,277,278]. Westbrook et al. [104] presented a one-dimensional finite-strain model based on the concept of phase evolution and validated on experimental curves related to semi-crystalline thermosets made of covalently crosslinked poly-(cyclooctene). Dolynchuk et al. [167,277] proposed a small-strain approach based on the Gaylord theory of the stress-induced crystallization of crosslinked polymers and validated on covalently crosslinked high-density polyethylene. The paper by Scalet et al. [103] proposes a one-dimensional phenomenological model in the finite-strain framework, based on a phase transition approach. The model is simple, easy to implement, and based on parameters with a physical interpretation. The model is validated on experiments on semi-crystalline networks based on poly(ε-caprolactone) and demonstrates model capability in describing material features such as the effect of the crosslink density on SME, the dependence of microstructural evolution on applied load and heating/cooling rate, and the presence of thermal strains. Contributions to model the two-way SME in LCEs are currently limited. Generally, phase field modeling framework or thermo-mechanical theories are developed, e.g., [279,280].
To the author’s knowledge, no works are currently available to model the stress-free two-way SME.
The phase transition approach has been applied to soft robotics and actuators, e.g., focusing on to the approaches that avoid the need of the programming step (see Section 3) [212,213] and to single-material structures [219].
The third approach consists of a design methodology based on a topology optimization approach and has been recently applied to 4D printed structures made of SMPs capable of programmable shape-shifting. Maute et al. [281] proposed a level set topology optimization approach to determine the spatial arrangement of one-way SMPs within a passive matrix needed to achieve a target shape. A similar approach based on classical origami designs was demonstrated in [282] for self-folding composite structures. Kwok et al. [283] employed shape optimization to determine the optimal layout of cuts to design 4D printed active origami and kirigami structures. Fuchi et al. [284] used a density-based method, employing a simplified linear elastic model, to optimize the layout of self-folding monolithic LCE actuators. Xue et al. [285] combined the concept of moving morphable components by Guo et al. [286] with a genetic algorithm for the topology optimization of post-buckled three-dimensional kirigami structures. Even if each of these approaches greatly reduces the number of design variables, only a subspace of all possible designs is explored. Recently, in [287], a new multi-material density-based topology optimization formulation has been used to determine materials’ placement in structures undergoing large deformation and realized through direct 4D printing. The formulation employs a hyperelastic thermo-mechanical model combined with an higher-order extended finite element method formulation. The shape of the structure is defined by a level set method.
Finally, it worth recalling that a recent approach based on machine-learning has been proposed in [288] for the design of active composite structures. An evolutionary algorithm was used in conjunction with the finite element method and the approach was validated on simple beam geometries, capable of achieving target shape shifting responses.
6. Conclusions
The present paper has reviewed the current progress on soft robots based on multiple-way and two-way SMPs. Attention has been dedicated to the constituent materials, manufacturing techniques, design strategies, applications, and modeling/simulations tools. According to the reviewed papers, the following concluding considerations can be made:
- Materials: (i) Several routes for the synthesis of multiple-way and two-way SMPs are available from the literature, and they differ in terms of preparation method, reprocessibility, achieved shape memory, and mechanical properties. (ii) SMP properties influence the overall robustness and performance of soft robots. Accordingly, SMPs with tunable transition temperatures, high thermal stability, and good mechanical properties in the operational temperature range are highly desired. For example, soft robots for biomedical applications require a switching transition temperature close to the body temperature, while those used for aerospace applications require high transition temperatures. (iii) Appropriate characterization methods on both macroscopic and molecular/morphological levels should be performed for a comprehensive knowledge of the polymer under investigation. In general, shape memory behavior characterization at the macroscopic level must be chosen and tailored to the specific SMP category and application under investigation. (iv) Two-way SMPs under constant stress or stress-free conditions are very promising for achieving reversible actuation in soft robots and require extensive research to improve actuation strains/forces and their mechanical performances. In particular, material behavior under cyclic loading should be investigated.
- Manufacturing: (i) Most of SMP-based components are fabricated through conventional techniques rather than through 3D printing, due to the lack in the variety of SMPs that are usable in 3D printing and the limited applicability of existing 3D printing methods to new SMPs. In fact, polyjet printing and extrusion printing are the most used 3D printing techniques for SMP-based soft robotics: polyjet printing allows for the use of materials with tunable mechanical properties, but has, e.g., high equipment costs, several resin properties’ requirements, and limited material choices; extrusion-based printing is versatile, but has, e.g., slow printing speed and relatively low resolution. Extensive research should be dedicated to the development of two-way and multiple-way SMPs for 3D printing and to the analysis of suitable 3D printing methods. (ii) Composite structures present several advantages to enhance the actuation complexity. However, some 3D printing techniques (e.g., stereolithography) cannot enable multi-material printing. Therefore, modifications to current techniques should be investigated. (iii) Novel inks should be studied to enable 3D printed multi-functional SMPs.
- Working mechanisms and applications: (i) Few examples of real-world programmable soft robots, based on both single-material and multi-material working mechanisms, have been proposed in the literature to be used, mainly, for biomedical (e.g., drug delivery systems) and aerospace (e.g., deployable or exploration components) applications. Further efforts should be made to increase the range of application fields. As an example, two-way SMP-based actuators are promising for dynamic building facades and energy savings [289,290]. However, extensive research should focus on material properties, e.g., extension rate, transparency, recovery stress, operational temperatures, and long-term stability. (ii) Several examples of components (e.g., in the form of trusses, periodic structures, compliant mechanisms), capable of programmable motion, have been proposed in the literature. All these components can be potentially integrated into more complex soft robotics systems to achieve advanced capabilities. (iii) Both shape-change speed and response time are key factors for actuation and depend on materials properties, geometrical design, and actuation stimulus. More efforts should be done to improve these two features. (iv) Complex and controllable movements are preferred in advanced robotics applications. Localized heating provides a simple and efficient method to this purpose, and should be investigated in two-way and multiple-way SMPs. (v) More studies should be dedicated to the combination of two or more stimuli into one single polymer to achieve the two-way or multiple-way SME. In this way, SMPs may adapt better to the overall environmental conditions. Moreover, function or property-shifting features, in addition to shape-shifting, should be investigated in order to increase the autonomy of soft robots. To this end, integrated design and fabrication strategies should be developed, as proposed, e.g., by Wehner et al. [291]. (vi) The application potential for two-way and multiple-way SMPs appears unlimited. However, real examples are still limited due to the lack of standards, especially related to 3D printed SMPs, and of manufacturing techniques that allow the realization of complex components.
- Modeling and simulation: (i) Theoretical models and design methodologies are still limited for 4D printed components and are needed to accurately predict and optimize programmable soft robots. (ii) Constitutive models for multiple-way and two-way SMPs are fundamental for the simulation analysis of parts. More efforts should be done in this regard for both viscoelastic and phase transition approaches, especially in the three-dimensional finite strain framework and for two-way LCEs and two-way SMPs under stress-free conditions.
It can be concluded that the realization of soft robots requires interdisciplinary research and technological advances in various fields, including 3D printing, chemistry, material science, as well as novel design and modeling tools.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Wang, L.; Nurzaman, S.; Iida, F. Soft-Material Robotics; Foundations and Trends in Robotics; Now Publishers Inc.: Boston, MA, USA; Delft, The Netherlands, 2017; Volume 5. [Google Scholar]
- Laschi, C.; Mazzolai, B.; Cianchetti, M. Soft robotics: Technologies and systems pushing the boundaries of robot abilities. Sci. Robot. 2016, 1, eaah3690. [Google Scholar] [CrossRef]
- Hines, L.; Petersen, K.; Lum, G.; Sitti, M. Soft Actuators for Small-Scale Robotics. Adv. Mater. 2017, 29, 1–43. [Google Scholar] [CrossRef] [PubMed]
- Bio-inspiration for future space systems. In Acta Futura—European Space Agency; Barker, D., Ed.; European Space Technology Center (ESTEC): Noordwijk, The Netherlands, 2013; Number 6. [Google Scholar]
- Gong, X.; Yang, K.; Xie, J.; Wang, Y.; Kulkarni, P.; Hobbs, A.; Mazzeo, A. Rotary Actuators Based on Pneumatically Driven Elastomeric Structures. Adv. Mater. 2016, 28, 7533–7538. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.L. Chapter Six - Soft Wearable Robotics Technologies for Body Motion Sensing. In Human Modelling for Bio-Inspired Robotics; Ueda, J., Kurita, Y., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 161–184. [Google Scholar]
- Dehghani, H.; Pourghodrat, A.; Terry, B.; Nelson, C.; Oleynikov, D.; Dasgupta, P. Semi-autonomous locomotion for diagnostic endoscopy device. J. Med. Devices 2015, 9, 030931. [Google Scholar] [CrossRef]
- Cianchetti, M.; Laschi, C.; Menciassi, A.; Dario, P. Biomedical applications of soft robotics. Nat. Rev. Mater. 2018, 3, 143–153. [Google Scholar] [CrossRef]
- Verma, M.; Ainla, A.; Yang, D.; Harburg, D.; Whitesides, G. A soft tube-climbing robot. Soft Robot. 2018, 5, 133–137. [Google Scholar] [CrossRef]
- Manfredi, L.; Capoccia, E.; Ciuti, G.; Cuschieri, A. A Soft Pneumatic Inchworm Double balloon (SPID) for colonoscopy. Sci. Rep. 2019, 9, 11109. [Google Scholar] [CrossRef]
- Runciman, M.; Darzi, A.; Mylonas, G. Soft Robotics in Minimally Invasive Surgery. Soft Robot. 2019, 6, 423–443. [Google Scholar] [CrossRef]
- Svetozarevic, B.; Nagy, Z.; Hofer, J.; Jacob, D.; Begle, M.; Chatzi, E.; Schlueter, A. SoRo-Track: A two-axis soft robotic platform for solar tracking and building-integrated photovoltaic applications. In Proceedings of the 2016 IEEE International Conference on Robotics and Automation (ICRA), Stockholm, Sweden, 16–21 May 2016; pp. 4945–4950. [Google Scholar]
- Zolfagharian, A.; Kouzani, A.Z.; Khoo, S.Y.; Moghadam, A.A.A.; Gibson, I.; Kaynak, A. Evolution of 3D printed soft actuators. Sens. Actuators 2016, 250, 258–272. [Google Scholar] [CrossRef]
- Boyraz, P.; Runge, G.; Raatz, A. An Overview of Novel Actuators for Soft Robotics. Actuators 2018, 7, 48. [Google Scholar] [CrossRef]
- Schaffner, M.; Faber, J.; Pianegonda, L.; Rühs, P.; Coulter, F.; Studart, A. 3D printing of robotic soft actuators with programmable bioinspired architectures. Nat. Commun. 2018, 9, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Wang, T.; Ge, L.; Gu, G. Programmable design of soft pneu-net actuators with oblique chambers can generate coupled bending and twisting motions. Sens. Actuators Phys. 2018, 271, 131–138. [Google Scholar] [CrossRef]
- Overvelde, J.; Kloek, T.; D’haena, J.; Bertoldi, K. Amplifying the response of soft actuators by harnessing snap-through instabilities. Proc. Natl. Acad. Sci. USA 2015, 112, 10863–10868. [Google Scholar] [CrossRef]
- Janbaz, S.; Bobbert, F.; Mirzaali, M.; Zadpoor, A. Ultra-programmable buckling-driven soft cellular mechanisms. Mater. Horizons 2019, 6, 1138–1147. [Google Scholar] [CrossRef]
- Gladman, A.; Matsumoto, E.A.; Nuzzo, R.; Mahadevan, L.; Lewis, J. Biomimetic 4D printing. Nat. Mater. 2016, 15, 413–418. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Boatti, E.; Bertoldi, K.; Kramer-Bottiglio, R. Stimuli-induced bi-directional hydrogel unimorph actuators. Extrem. Mech. Lett. 2018, 21, 35–43. [Google Scholar] [CrossRef]
- Florijn, B.; Coulais, C.; van Hecke, M. Programmable Mechanical Metamaterials. Phys. Rev. Lett. 2014, 113, 175503. [Google Scholar] [CrossRef]
- Gillman, A.; Wilson, G.; Fuchi, K.; Hartl, D.; Pankonien, A.; Buskohl, P. Design of Soft Origami Mechanisms with Targeted Symmetries. Actuators 2019, 8, 3. [Google Scholar] [CrossRef]
- Rafsanjani, A.; Zhang, Y.; Liu, B.; Rubinstein, S.; Bertoldi, K. Kirigami skins make a simple soft actuator crawl. Sci. Robot. 2018, 3, eaar7555. [Google Scholar] [CrossRef]
- Li, S.; Bai, H.; Shepherd, R.; Zhao, H. Bio-inspired Design and Additive Manufacturing of Soft Materials, Machines, Robots, and Haptic Interfaces. Angew. Chem. Int. Ed. 2019, 58, 11182. [Google Scholar] [CrossRef]
- Yoon, C. Advances in biomimetic stimuli responsive soft grippers. Nano Converg. 2019, 6, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Maziz, A.; Concas, A.; Khaldi, A.; Stålhand, J.; Persson, N.K.; Jager, E. Knitting and weaving artificial muscles. Sci. Adv. 2017, 3, e1600327. [Google Scholar] [CrossRef] [PubMed]
- Jiang, Y.; Chen, D.; Liu, C.; Li, J. Chain-Like Granular Jamming: A Novel Stiffness-Programmable Mechanism for Soft Robotics. Soft Robot. 2019, 6, 118–132. [Google Scholar] [CrossRef] [PubMed]
- Majidi, C. Soft-Matter Engineering for Soft Robotics. Adv. Mater. Technol. 2019, 4, 1800477. [Google Scholar] [CrossRef]
- Kotikian, A.; McMahan, C.; Davidson, E.C.; Muhammad, J.M.; Weeks, R.D.; Daraio, C.; Lewis, J.A. Untethered soft robotic matter with passive control of shape morphing and propulsion. Sci. Robot. 2019, 4, eaax7044. [Google Scholar] [CrossRef]
- Zhou, J.; Sheiko, S. Reversible shape-shifting in polymeric materials. J. Polym. Sci. Part Polym. Phys. 2016, 54, 1365–1380. [Google Scholar] [CrossRef]
- Kang, D.; An, S.; Yarin, A.; Anand, S. Programmable soft robotics based on nanotextured thermo-responsive actuators. Nanoscale 2019, 11, 2065–2070. [Google Scholar] [CrossRef]
- Han, J.; Jiang, W.; Niu, D.; Li, Y.; Zhang, Y.; Lei, B.; Liu, H.; Shi, Y.; Chen, B.; Yin, L.; et al. Untethered Soft Actuators by Liquid-Vapor Phase Transition: Remote and Programmable Actuation. Adv. Intell. Syst. 2019, 1, 1900109. [Google Scholar] [CrossRef]
- Carrico, J.; Tyler, T.; Leang, K. A comprehensive review of select smart polymeric and gel actuators for soft mechatronics and robotics applications: Fundamentals, freeform fabrication, and motion control. Int. J. Smart Nano Mater. 2017, 8, 144–213. [Google Scholar] [CrossRef]
- Lendlein, A. (Ed.) Shape-Memory Polymers; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Leng, J.; Lan, X.; Liu, Y.; Du, S. Shape-memory polymers and their composites: Stimulus methods and applications. Prog. Mater. Sci. 2011, 56, 1077–1135. [Google Scholar] [CrossRef]
- Hu, J.; Zhu, Y.; Huang, H.; Lu, J. Recent advances in shape memory polymers: Structure, mechanism, functionality, modeling and applications. Prog. Polym. Sci. 2012, 37, 1720–1763. [Google Scholar] [CrossRef]
- Huang, W.; Yang, B.; Fu, Y. Polyurethane Shape Memory Polymers; CRC Press Taylor & Francis Group: Bosa Raton, FL, USA, 2012. [Google Scholar]
- Meng, H.; Mohamadian, H.; Stubblefield, M.; Jerro, D.; Ibekwe, S.; Pang, S.S.; Li, G. Various shape memory effects of stimuli-responsive shape memory polymers. Smart Mater. Struct. 2013, 22, 093001. [Google Scholar] [CrossRef]
- Hager, M.; Bode, S.; Weber, C.; Schubert, U. Shape memory polymers: Past, present and future developments. Prog. Polym. Sci. 2015, 49, 3–33. [Google Scholar] [CrossRef]
- White, T.; Broer, D. Programmable and adaptive mechanics with liquid crystal polymer networks and elastomers. Nat. Mater. 2015, 14, 1087. [Google Scholar] [CrossRef]
- Pilate, F.; Toncheva, A.; Dubois, P.; Raquez, J.M. Shape-memory polymers for multiple applications in thematerials world. Eur. Polym. J. 2016, 80, 268–294. [Google Scholar] [CrossRef]
- Sun, Q.P.; Matsui, R.; Takeda, K.; Pieczyska, E. Advances in Shape Memory Materials—In Commemoration of The Retirement of Professor Hisaaki Tobushi; Springer International Publishing AG: Cham, Switzerland, 2017. [Google Scholar]
- Ula, S.; Traugutt, N.; Volpe, R.; Patel, R.; Yu, K.; Yakacki, C. Liquid crystal elastomers: An introduction and review of emerging technologies. Liq. Cryst. Rev. 2018, 6, 78–107. [Google Scholar] [CrossRef]
- Lendlein, A.; Gould, O. Reprogrammable recovery and actuation behaviour of shape-memory polymers. Nat. Rev. Mater. 2019, 4, 116–133. [Google Scholar] [CrossRef]
- Mazurek-Budzyńska, M.; Razzaq, M.; Behl, M.; Lendlein, A. Shape-Memory Polymers. In Functional Polymers. Polymers and Polymeric Composites: A Reference Series; Mazumder, M., Sheardown, H., Al-Ahmed, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2019. [Google Scholar]
- Wang, K.; Jia, Y.G.; Zhao, C.; Zhu, X. Multiple and two-way reversible shape memory polymers: Design strategies and applications. Prog. Mater. Sci. 2019, 105, 100572. [Google Scholar] [CrossRef]
- Zare, M.; Prabhakaran, M.P.; Parvin, N.; Ramakrishna, S. Thermally-induced two-way shape memory polymers: Mechanisms, structures, and applications. Chem. Eng. J. 2019, 374, 706–720. [Google Scholar] [CrossRef]
- Kim, K.; Lee, S.; Xu, M. Polyurethanes having shape memory effects. Polymer 1996, 37, 5781–5793. [Google Scholar] [CrossRef]
- Hayashi, S. Properties and Applications of Polyurethane-series Shape Memory Polymer. Int. Prog. Urethanes 1993, 6, 90–115. [Google Scholar]
- Li, M.Q.; Song, F.; Chen, L.; Wang, X.L.; Wang, Y.Z. Flexible material based on poly(lactic acid) and liquid crystal with multishape memory effects. ACS Sustain. Chem. Eng. 2016, 4, 3820–3829. [Google Scholar] [CrossRef]
- Bellin, I.; Kelch, S.; Langer, R.; Lendlein, A. Polymeric triple-shape materials. Proc. Natl. Acad. Sci. USA 2006, 103, 18043–18047. [Google Scholar] [CrossRef] [PubMed]
- Weiss, R.; Izzo, E.; Mandelbaum, S. New Design of Shape Memory Polymers: Mixtures of an Elastomeric Ionomer and Low Molar Mass Fatty Acids and Their Salts. Macromolecules 2008, 41, 2978–2980. [Google Scholar] [CrossRef]
- Behl, M.; Lendlein, A. Triple-shape polymers. J. Mater. Chem. 2010, 20, 3335–3345. [Google Scholar] [CrossRef]
- Pretsch, T. Triple-shape properties of a thermoresponsive poly(ester urethane). Smart Mater. Struct. 2010, 19, 015006. [Google Scholar] [CrossRef]
- Cuevas, J.; Rubio, R.; German, L.; Laza, J.; Vilas, J.; Rodriguez, M.; Leon, L. Triple-shape memory effect of covalently crosslinked polyalkenamer based semicrystalline polymer blends. Soft Matter 2012, 8, 4928–4935. [Google Scholar] [CrossRef]
- Niu, Y.; Zhang, P.; Zhang, J.; Xiao, L.; Yang, K.; Wang, Y. Poly(p-dioxanone)–poly(ethylene glycol) network: Synthesis, characterization, and its shape memory effect. Polym. Chem. 2012, 3, 2508–2516. [Google Scholar] [CrossRef]
- Chen, H.; Liu, Y.; Gong, T.; Wang, L.; Zhao, K.; Zhou, S. Use of intermolecular hydrogen bonding to synthesize triple-shape memory supermolecular composites. RSC Adv. 2013, 3, 7048–7056. [Google Scholar] [CrossRef]
- Wang, L.; Yang, X.; Chen, H.; Gong, T.; Li, W.; Yang, G.; Zhou, S. Design of triple-shape memory polyurethane with photo-cross-linking of cinnamon groups. ACS Appl. Mater. Interfaces 2013, 5, 10520–10528. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, M.; Wang, X.; Zhao, X.; Wang, Z.; Dang, Z.; Ma, L.; Hu, G.; Chen, F. Triple shape memory effects of cross-linked polyethylene/polypropylene blends with cocontinuous architecture. ACS Appl. Mater. Interfaces 2013, 5, 5550–5556. [Google Scholar] [CrossRef] [PubMed]
- Chatani, S.; Wang, C.; Podgórski, M.; Bowman, C. Triple shape memory materials incorporating two distinct polymer networks formed by selective Thiol-Michael addition reactions. Macromolecules 2014, 47, 4949–4954. [Google Scholar] [CrossRef]
- Xiao, L.; Wei, M.; Zhan, M.; Zhang, J.; Xie, H.; Deng, X.; Yang, K.; Wang, Y. Novel triple-shape PCU/PPDO interpenetrating polymer networks constructed by self-complementary quadruple hydrogen bonding and covalent bonding. Polym. Chem. 2014, 5, 2231–2241. [Google Scholar] [CrossRef]
- Xie, H.; Cheng, C.Y.; Du, L.; Fan, C.J.; Deng, X.Y.; Yang, K.K.; Wang, Y. A facile strategy to construct PDLLA-PTMEG network with triple-shape effect via photo-cross-linking of anthracene groups. Macromolecules 2016, 49, 3845–3855. [Google Scholar] [CrossRef]
- Zhuo, S.; Zhang, G.; Feng, X.; Jiang, H.; Shi, J.; Liu, H.; Li, H. Multiple shape memory polymers for self-deployable device. RSC Adv. 2016, 6, 50581–50586. [Google Scholar] [CrossRef]
- Zhou, J.; Cao, H.; Chang, R.; Shan, G.; Bao, Y.; Pan, P. Stereocomplexed and homochiral polyurethane elastomers with tunable crystallizability and multishape memory effects. ACS Macro Lett. 2018, 7, 233–238. [Google Scholar] [CrossRef]
- Qin, H.; Mather, P. Combined one-way and two-way shape memory in a glass-forming nematic network. Macromolecules 2009, 42, 273–280. [Google Scholar] [CrossRef]
- Ahn, S.K.; Deshmukh, P.; Kasi, R. Shape memory behavior of side-chain liquid crystalline polymer networks triggered by dual transition temperatures. Macromolecules 2010, 43, 7330–7340. [Google Scholar] [CrossRef]
- Ahn, S.K.; Kasi, R. Exploiting microphase-separated morphologies of side-chain liquid crystalline polymer networks for triple shape memory properties. Adv. Funct. Mater. 2011, 21, 4543–4549. [Google Scholar] [CrossRef]
- Ahn, S.K.; Deshmukh, P.; Gopinadhan, M.; Kasi, R. Side-chain liquid crystalline polymer networks: Exploiting nanoscale smectic polymorphism to design shape-memory polymers. ACS Nano 2011, 5, 3085–3095. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, H.; Ge, Z.; Chen, S.; Zhuo, H.; Liu, J. Insights into liquid-crystalline shape memory polyurethane composites based on an amorphous reversible phase and hexadecyloxybenzoic acid. J. Mater. Chem. 2014, 2, 1041–1049. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, H.; Zhuo, H.; Chen, S.; Yang, H.; Ge, Z.; Liu, J. Development of liquid-crystalline shape-memory polyurethane composites based on polyurethane with semi-crystalline reversible phase and hexadecyloxybenzoic acid for self-healing applications. J. Mater. Chem. 2014, 2, 4203–4212. [Google Scholar] [CrossRef]
- Wen, Z.; Zhang, T.; Hui, Y.; Wang, W.; Yang, K.; Zhou, Q.; Wang, Y. Elaborate fabrication of well-defined side-chain liquid crystalline polyurethane networks with triple shape memory capacity. J. Mater. Chem. 2015, 3, 13435–13444. [Google Scholar] [CrossRef]
- Fu, S.; Zhang, H.; Zhao, Y. Optically and thermally activated shape memory supramolecular liquid crystalline polymers. J. Mater. Chem. 2016, 4, 4946–4953. [Google Scholar] [CrossRef]
- Zotzmann, J.; Behl, M.; Feng, Y.; Lendlein, A. Copolymer Networks Based on Poly(ω-pentadecalactone) and Poly(ε-caprolactone)Segments as a Versatile Triple—Shape Polymer System. Adv. Funct. Mater. 2010, 20, 3583–3594. [Google Scholar] [CrossRef]
- Chen, S.; Yuan, H.; Chen, S.; Yang, H.; Ge, Z.; Zhuo, H.; Liu, J. Development of supramolecular liquid-crystalline polyurethane complexes exhibiting triple-shape functionality using a one-step programming process. J. Mater. Chem. 2014, 2, 10169–10181. [Google Scholar] [CrossRef]
- Zhou, J.; Li, Q.; Turner, S.; Ashby, V.; Sheiko, S. Isothermal programming of triple shape memory. Polymer 2015, 72, 464–470. [Google Scholar] [CrossRef]
- Xie, T.; Xiao, X.; Cheng, Y. Revealing triple-shape memory effect by polymer bilayers. Macromol. Rapid Commun. 2009, 30, 1823–1837. [Google Scholar] [CrossRef]
- Bae, C.; Park, J.; Kim, E.; Kang, Y.; Kim, B. Organic–inorganic nanocomposite bilayers with triple shape memory effect. J. Mater. Chem. 2011, 21, 11288–11295. [Google Scholar] [CrossRef]
- Luo, X.; Mather, P. Triple-Shape Polymeric Composites (TSPCs). Adv. Funct. Mater. 2010, 202, 649–656. [Google Scholar] [CrossRef]
- Li, G.; King, A.; Xu, T.; Huang, X. Behavior of Thermoset Shape Memory Polymer-Based Syntactic Foam Sealant Trained by Hybrid Two-Stage Programming. J. Mater. Civ. Eng. 2013, 25, 393–402. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, J.; Chen, M.; Yang, M.; Tang, L.; Dang, Z.; Chen, F.; Huang, M.; Dong, X. Dually actuated triple shape memory polymers of cross-linked polycyclooctene-carbon nanotube/polyethylene nanocomposites. ACS Appl. Mater. Interfaces 2014, 6, 20051–20059. [Google Scholar] [CrossRef] [PubMed]
- Mo, F.; Ban, J.; Pan, L.; Shi, B.; Lu, S. Liquid crystalline polyurethane composites based on supramolecular structure with reversible bidirectional shape memory and multi-shape memory effects. New J. Chem. 2019, 43, 103–110. [Google Scholar] [CrossRef]
- Miaudet, P.; Derre, A.; Maugey, M.; Zakri, C.; Piccione, P.; Inoubli, R.; Poulin, P. Shape and temperature memory of nanocomposites with broadened glass transition. Science 2007, 318, 1294–1296. [Google Scholar] [CrossRef] [PubMed]
- Xie, T. Tunable polymer multi-shape memory effect. Nature 2010, 464, 267–270. [Google Scholar] [CrossRef] [PubMed]
- Xie, T.; Page, A.; Eastman, S. Strain-Based Temperature Memory Effect for Nafion and Its Molecular Origins. Adv. Funct. Mater. 2011, 21, 2057–2066. [Google Scholar] [CrossRef]
- Li, J.; Liu, T.; Pan, Y.; Xia, S.; Zhang, Z.; Ding, X.; Peng, Y. A Versatile Polymer Co-Network with Broadened Glass Transition Showing Adjustable Multiple Shape Memory Effect. Macromol. Chem. Phys. 2012, 213, 2246–2252. [Google Scholar] [CrossRef]
- Shao, Y.; Lavigueur, C.; Zhu, X. Multishape memory effect of norbornene-based copolymers with cholic acid pendant groups. Macromolecules 2012, 45, 1924–1930. [Google Scholar] [CrossRef]
- Ware, T.; Hearon, K.; Lonnecker, A.; Wooley, K.; Maitland, D.; Voit, W. Triple-shape memory polymers based on self-complementary hydrogen bonding. Macromolecules 2012, 45, 1062–1069. [Google Scholar] [CrossRef]
- Samuel, C.; Barrau, S.; Lefebvre, J.M.; Raquez, J.M.; Dubois, P. Designing multiple-shape memory polymers with miscible polymer blends: Evidence and origins of a triple-shape memory effect for miscible PLLA/PMMA blends. Macromolecules 2014, 47, 6791–6803. [Google Scholar] [CrossRef]
- Wang, K.; Jia, Y.G.; Zhu, X. Biocompound-based multiple shape memory polymers reinforced by photo-cross-linking. ACS Biomater. Sci. Eng. 2015, 1, 855–863. [Google Scholar] [CrossRef]
- Zhang, Q.; Wei, H.; Liu, Y.; Leng, J.; Du, S. Triple-shape memory effects of bismaleimide based thermosetting polymer networks prepared via heterogeneous crosslinking structures. RSC Adv. 2016, 6, 10233–10241. [Google Scholar] [CrossRef]
- Zheng, N.; Hou, J.; Xu, Y.; Fang, Z.; Zou, W.; Zhao, Q.; Xie, T. Catalyst-free thermoset polyurethane with permanent shape reconfigurability and highly tunable triple shape memory performance. ACS Macro Lett. 2017, 6, 326–330. [Google Scholar] [CrossRef]
- Li, X.; Pan, Y.; Zheng, Z.; Ding, X. A facile and general approach to recoverable high-strain multishape shape memory polymers. Macromol. Rapid Commun. 2018, 39, e1700613. [Google Scholar] [CrossRef] [PubMed]
- Kratz, K.; Madbouly, S.; Wagermaier, W.; Lendlein, A. Temperature—Memory Polymer Networks with Crystallizable Controlling Units. Adv. Mater. 2011, 23, 4058–4062. [Google Scholar] [CrossRef] [PubMed]
- Dolog, R.; Weiss, R. Shape memory behavior of a polyethylene-based carboxylate ionomer. Macromolecules 2013, 46, 7845–7852. [Google Scholar] [CrossRef]
- Yang, X.; Wang, L.; Wang, W.; Chen, H.; Yang, G.; Zhou, S. Triple shape memory effect of star-shaped polyurethane. ACS Appl. Mater. Interfaces 2014, 6, 6545–6554. [Google Scholar] [CrossRef]
- Mirtschin, N.; Pretsch, T. Designing temperature-memory effects in semicrystalline polyurethane. RSC Adv. 2015, 5, 46307–46315. [Google Scholar] [CrossRef]
- Qi, X.; Guo, Y.; Wei, Y.; Dong, P.; Fu, Q. Multishape and temperature memory effects by strong physical confinement in poly(propylene carbonate)/graphene oxide nanocomposites. J. Phys. Chem. 2016, 120, 11064–11073. [Google Scholar] [CrossRef]
- DiOrio, A.; Luo, X.; Lee, K.; Mather, P. A functionally graded shape memory polymer. Soft Matter 2011, 7, 68–74. [Google Scholar] [CrossRef]
- Huang, W.; Yang, B.; An, L.; Li, C.; Chan, Y. Water-driven programmable polyurethane shape memory polymer: Demonstration and mechanism. Appl. Phys. Lett. 2005, 86, 114105. [Google Scholar] [CrossRef]
- Luo, Y.; Guo, Y.; Gao, X.; Li, B.; Xie, T. A general approach towards thermoplastic multishape-memory polymers via sequence structure design. Adv. Mater. 2013, 25, 743–748. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Gao, X.; Luo, Y. Multi-shape memory polymers achieved by the spatio-assembly of 3D printable thermoplastic building blocks. Soft Matter 2016, 12, 3226–3233. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Liu, T.; Xia, S.; Pan, Y.; Zheng, Z.; Ding, X.; Peng, Y. A versatile approach to achieve quintuple-shape memory effect by semi-interpenetrating polymer networks containing broadened glass transition and crystalline segments. J. Mater. Chem. 2011, 21, 12213–12217. [Google Scholar] [CrossRef]
- Scalet, G.; Pandini, S.; Messori, M.; Toselli, M.; Auricchio, F. A one-dimensional phenomenological model for the two-way shape-memory effect in semi-crystalline networks. Polymer 2018, 158, 130–148. [Google Scholar] [CrossRef]
- Westbrook, K.; Parakh, V.; Chung, T.; Mather, P.; Wan, L.; Dunn, M.; Qi, H. Constitutive modeling of shape memory effects in semicrystalline polymers with stretch induced crystallization. J. Eng. Mater. Technol. 2010, 132, 041010. [Google Scholar] [CrossRef]
- Pandini, S.; Baldi, F.; Paderni, K.; Messori, M.; Toselli, M.; Pilati, F.; Gianoncelli, A.; Brisotto, M.; Bontempi, E.; Ricco, T. One-way and two-way shape memory behaviour of semi-crystalline networks based on sol-gel cross-linked poly(ε-caprolactone). Polymer 2013, 54, 4253–4265. [Google Scholar] [CrossRef]
- Chung, T.; Romo-Uribe, A.; Mather, P. Two-way reversible shape memory in a semicrystalline network. Macromolecules 2008, 41, 184–192. [Google Scholar] [CrossRef]
- Hong, S.; Woong-Ryeol, Y.; Youk, J. Two-way shape memory behavior of shape memory polyurethanes with a bias load. Smart Mater. Struct. 2010, 19, 035022. [Google Scholar] [CrossRef]
- Li, J.; Rodgers, W.; Xie, T. Semi-crystalline two-way shape memory elastomer. Polymer 2011, 52, 5320–5325. [Google Scholar] [CrossRef]
- Raquez, J.; Vanderstappen, S.; Meyer, F.; Verge, P.; Alexandre, M.; Thomassin, J.; Jerome, C.; Dubois, P. Design of cross-linked semicrystalline poly(ε-caprolactone)-based networks with one-way and two-way shape-memory properties through Diels-Alder reactions. Chemistry 2011, 17, 10135–10143. [Google Scholar] [CrossRef] [PubMed]
- Bothe, M.; Pretsch, T. Two-way shape changes of a shape-memory poly(ester urethane). Macromol. Chem. Phys. 2012, 213, 2378–2385. [Google Scholar] [CrossRef]
- Baker, R.; Henderson, J.; Mather, P. Shape memory poly(ε-caprolactone)-copoly(ethylene glycol) foams with body temperature triggering and two-way actuation. J. Mater. Chem. 2013, 1, 4916–4920. [Google Scholar] [CrossRef]
- Huang, M.; Dong, X.; Wang, L.; Zhao, J.; Liu, G.; Wang, D. Two-way shape memory property and its structural origin of cross-linked poly(ε-caprolactone). RSC Adv. 2014, 4, 55483–55494. [Google Scholar] [CrossRef]
- Kolesov, I.; Dolynchuk, O.; Jehnichen, D.; Reuter, U.; Stamm, M.; Radusch, H. Changes of crystal structure and morphology during two-way shape-memory cycles in cross-linked linear and short-chain branched polyethylenes. Macromolecules 2015, 48, 4438–4450. [Google Scholar] [CrossRef]
- Zotzmann, J.; Behl, M.; Hofmann, D.; Lendlein, A. Reversible triple-shape effect of polymer networks containing polypentadecalactone- and poly(ε-caprolactone)-segments. Adv. Mater. 2010, 22, 3424–3429. [Google Scholar] [CrossRef]
- Han, J.L.; Lai, S.M.; Chiu, Y. Two-way multi-shape memory properties of peroxide crosslinked ethylene vinyl-acetate copolymer (EVA)/polycaprolactone (PCL) blends. Polym. Adv. Technol. 2018, 29, 2010–2024. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, X.; Wang, Q.; Wang, T. A tough shape memory polymer with triple shape memory and two-way shape memory properties. J. Mater. Chem. 2014, 2, 4771–4778. [Google Scholar] [CrossRef]
- Kolesov, I. Shape-memory behavior of cross-linked semi-crystalline polymers and their blends. Express Polym. Lett. 2015, 9, 255–276. [Google Scholar] [CrossRef]
- Lendlein, A. Progress in actively moving polymers. J. Mater. Chem. 2010, 20, 3332–3334. [Google Scholar] [CrossRef]
- Finkelmann, H.; Kock, H.J.; Rehage, G. Investigations on liquid crystalline poly-siloxanes 3. Liquid crystalline elastomers—A new type of liquid crystalline material. Die Makromol. Chemie/Rapid Commun. 1981, 2, 317–322. [Google Scholar] [CrossRef]
- Thomsen, D.; Keller, P.; Naciri, J.; Pink, R.; Jeon, H.; Shenoy, D.; Ratna, B. Liquid crystal elastomers with mechanical properties of a muscle. Macromolecules 2001, 34, 5868–5875. [Google Scholar] [CrossRef]
- Burke, K.; Mather, P. Soft shape memory in main-chain liquid crystalline elastomers. J. Mater. Chem. 2010, 20, 3449–3457. [Google Scholar] [CrossRef]
- Burke, K.; Rousseau, I.; Mather, P. Reversible actuation in main-chain liquid crystalline elastomers with varying crosslink densities. Polymer 2014, 55, 5897–5907. [Google Scholar] [CrossRef]
- Pei, Z.; Yang, Y.; Chen, Q.; Terentjev, E.; Wei, Y.; Ji, Y. Mouldable liquid-crystalline elastomer actuators with exchangeable covalent bonds. Nat. Mater. 2014, 13, 36. [Google Scholar] [CrossRef] [PubMed]
- Torbati, A.; Mather, P. A hydrogel-forming liquid crystalline elastomer exhibiting soft shape memory. J. Polym. Sci. Part Polym. Phys. 2016, 54, 38–52. [Google Scholar] [CrossRef]
- Wang, Y.; Huang, X.; Zhang, J.; Bi, M.; Zhang, J.; Niu, H.; Li, C.; Yu, H.; Wang, B.; Jiang, H. Two-step crosslinked liquid-crystalline elastomer with reversible two-way shape memory characteristics. Mol. Cryst. Liq. Cryst. 2017, 650, 13–22. [Google Scholar] [CrossRef]
- Wen, Z.; McBride, M.; Zhang, X.; Han, X.; Martinez, A.; Shao, R.; Zhu, C.; Visvanathan, R.; Clark, N.; Wang, Y.; et al. Reconfigurable LC elastomers: Using a thermally programmable monodomain to access two-way free-standing multiple shape memory polymers. Macromolecules 2018, 51, 5812–5819. [Google Scholar] [CrossRef]
- Behl, M.; Kratz, K.; Noechel, U.; Sauter, T.; Lendlein, A. Temperature-memory polymer actuators. Proc. Natl. Acad. Sci. USA 2013, 110, 12555–12559. [Google Scholar] [CrossRef]
- Behl, M.; Kratz, K.; Zotzmann, J.; Nöchel, U.; Lendlein, A. Reversible bidirectional shape-memory polymers. Adv. Mater. 2013, 25, 4466–4469. [Google Scholar] [CrossRef]
- Zhou, J.; Turner, S.; Brosnan, S.; Li, Q.; Carrillo, J.M.; Nykypanchuk, D.; Gang, O.; Ashby, V.; Dobrynin, A.; Sheiko, S. Shapeshifting: Reversible shape memory in semicrystalline elastomers. Macromolecules 2014, 47, 1768–1776. [Google Scholar] [CrossRef]
- Saatchi, M.; Behl, M.; Nöchel, U.; Lendlein, A. Copolymer Networks From Oligo(ε-caprolactone) and n-Butyl Acrylate Enable a Reversible Bidirectional Shape-Memory Effect at Human Body Temperature. Macromol. Rapid Commun. 2015, 36, 880–884. [Google Scholar] [CrossRef] [PubMed]
- Li, Q.; Zhou, J.; Vatankhah-Varnoosfaderani, M.; Nykypanchuk, D.; Gang, O.; Sheiko, S. Advancing reversible shape memory by tuning the polymer network architecture. Macromolecules 2016, 49, 1383–1391. [Google Scholar] [CrossRef]
- Qian, C.; Dong, Y.; Zhu, Y.; Fu, Y. Two-way shape memory behavior of semicrystalline elastomer under stress-free condition. Smart Mater. Struct. 2016, 25, 085023. [Google Scholar] [CrossRef]
- Dolynchuk, O.; Kolesov, I.; Jehnichen, D.; Reuter, U.; Radusch, H.J.; Sommer, J.U. Reversible shape-memory effect in cross-linked linear poly(ε-caprolactone) under stress and stress-free conditions. Macromolecules 2017, 50, 3841–3854. [Google Scholar] [CrossRef]
- Wang, K.; Jia, Y.G.; Zhu, X. Two-way reversible shape memory polymers made of crosslinked cocrystallizable random copolymers with tunable actuation temperatures. Macromolecules 2017, 50, 8570–8579. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, W.; Zhu, S. Reversible shape memory polymer from semicrystalline poly(ethylene-co-vinyl acetate) with dynamic covalent polymer networks. Macromolecules 2018, 51, 8956–8963. [Google Scholar] [CrossRef]
- Wu, Y.; Hu, J.; Han, J.; Zhu, Y.; Huang, H.; Li, J.; Tang, B. Two-way shape memory polymer with “switch–spring” composition by interpenetrating polymer network. J. Mater. Chem. 2014, 2, 18816–18822. [Google Scholar] [CrossRef]
- Meng, Y.; Jiang, J.; Anthamatten, M. Shape actuation via internal stress-induced crystallization of dual-cure networks. ACS Macro Lett. 2015, 4, 115–118. [Google Scholar] [CrossRef]
- Fan, L.; Rong, M.; Zhang, M.; Chen, X. A facile approach toward scalable fabrication of reversible shape-memory polymers with bonded elastomer microphases as internal stress provider. Macromol. Rapid Commun. 2017, 38, 1700124. [Google Scholar] [CrossRef]
- Wang, M.; Sayed, S.; Guo, L.; Lin, B.; Zhang, X.; Sun, Y.; Yang, H. Multi-stimuli responsive carbon nanotube incorporated polysiloxane azobenzene liquid crystalline elastomer composites. Macromolecules 2016, 49, 663–671. [Google Scholar] [CrossRef]
- Wang, L.; Liu, W.; Guo, L.X.; Lin, B.P.; Zhang, X.Q.; Sun, Y.; Yang, H. A room-temperature two-stage thiol–ene photoaddition approach towards monodomain liquid crystalline elastomers. Polym. Chem. 2017, 8, 1364–1370. [Google Scholar] [CrossRef]
- Hanzon, D.; Traugutt, N.; McBride, M.; Bowman, C.; Yakacki, C.; Yu, K. Adaptable liquid crystal elastomers with transesterification-based bond exchange reactions. Soft Matter 2018, 14, 951–960. [Google Scholar] [CrossRef]
- Bothe, M.; Pretsch, T. Bidirectional actuation of a thermoplastic polyurethane elastomer. J. Mater. Chem. 2013, 1, 14491–14497. [Google Scholar] [CrossRef]
- Biswas, A.; Aswal, V.; Sastry, P.; Rana, D.; Maiti, P. Reversible bidirectional shape memory effect in polyurethanes through molecular flipping. Macromolecules 2016, 4889–4897. [Google Scholar] [CrossRef]
- Lu, L.; Li, G. One-way multishape-memory effect and tunable two-way shape memory effect of ionomer poly(ethylene-co-methacrylic acid). ACS Appl. Mater. Interfaces 2016, 8, 14812–14823. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, W.; Zhu, S. Polyolefin thermoplastics for multiple shape and reversible shape memory. ACS Appl. Mater. Interfaces 2017, 9, 4882–4889. [Google Scholar] [CrossRef]
- Yan, W.; Rudolph, T.; Noechel, U.; Gould, O.; Behl, M.; Kratz, K.; Lendlein, A. Reversible actuation of thermoplastic multiblock copolymers with overlapping thermal transitions of crystalline and glassy domains. Macromolecules 2018, 51, 4624–4632. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Zhuo, H.; Zhu, Y. Two-way shape memory effect in polymer laminates. Mater. Lett. 2008, 62, 4088–4090. [Google Scholar] [CrossRef]
- Tobushi, H.; Hayashi, S.; Sugimoto, Y.; Date, K. Two-way bending properties of shape memory composite with SMA and SMP. Materials 2009, 2, 1180–1192. [Google Scholar] [CrossRef]
- Chen, S.; Hu, J.; Zhuo, H. Properties and mechanism of two-way shape memory polyurethane composites. Compos. Sci. Technol. 2010, 70, 1437–1443. [Google Scholar] [CrossRef]
- Tamagawa, H. Thermo-responsive two-way shape changeable polymeric laminate. Mater. Lett. 2010, 64, 749–751. [Google Scholar] [CrossRef]
- Ghosh, P.; Rao, A.; Srinivasa, A. Design of multi-state and smart-bias components using shape memory alloy and shape memory polymer composites. Mater. Des. 2013, 44, 164–171. [Google Scholar] [CrossRef]
- Lama, G.; Cerruti, P.; Lavorgna, M.; Carfagna, C.; Ambrogi, V.; Gentile, G. Controlled actuation of a carbon nanotube/epoxy shape-memory liquid crystalline elastomer. J. Phys. Chem. 2016, 120, 24417–24426. [Google Scholar] [CrossRef]
- Belmonte, A.; Lama, G.; Gentile, G.; Fernandez-Francos, X.; De la Flor, S.; Cerruti, P.; Ambrogi, V. Synthesis and characterization of liquid-crystalline networks: Toward autonomous shape-memory actuation. J. Phys. Chem. 2017, 121, 22403–22414. [Google Scholar] [CrossRef]
- Kang, T.H.; Lee, J.M.; Yu, W.R.; Youk, J.; Ryu, H. Two-way actuation behavior of shape memory polymer/elastomer core/shell composites. Smart Mater. Struct. 2012, 21, 035028. [Google Scholar] [CrossRef]
- Imai, S.; Sakurai, K. An actuator of two-way behavior by using two kinds of shape memory polymers with different Tgs. Precis. Eng. 2013, 37, 572–579. [Google Scholar] [CrossRef]
- Taya, M.; Liang, Y.; Namli, O.; Tamagawa, H.; Howie, T. Design of two-way reversible bending actuator based on a shape memory alloy/shape memory polymer composite. Smart Mater. Struct. 2013, 22, 105003. [Google Scholar] [CrossRef]
- Wagermaier, W.; Kratz, K.; Heuchel, M.; Lendlein, A. Characterization methods for shape memory polymers. In Shape-Memory Polymers. Advances in Polymer Science; Lendlein, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 226. [Google Scholar]
- Lei, M.; Yu, K.; Lu, H.; Qi, H. Influence of structural relaxation on thermomechanical and shape memory performances of amorphous polymers. Polymer 2017, 109, 216–228. [Google Scholar] [CrossRef]
- Pieczyska, E.; Staszczak, M.; Kowalczyk-Gajewska, K.; Maj, M.; Golasiński, K.; Golba, S.; Tobushi, H.; Hayashi, S. Experimental and numerical investigation of yielding phenomena in a shape memory polymer subjected to cyclic tension at various strain rates. Polym. Test. 2017, 60, 333–342. [Google Scholar] [CrossRef]
- Baiardo, M.; Frisoni, G.; Scandola, M.; Rimelen, M.; Lips, D.; Ruffieux, K.; Wintermantel, E. Thermal and mechanical properties of plasticized poly (L-lactic acid). J. Appl. Polym. Sci. 2003, 90, 1731–1738. [Google Scholar] [CrossRef]
- Yang, H.; Leow, W.; Wang, T.; Wang, J.; Yu, J.; He, K.; Qi, D.; Wan, C.; Chen, X. 3D Printed Photoresponsive Devices Based on Shape Memory Composites. Adv. Mater. 2017, 29, 1701627. [Google Scholar] [CrossRef] [PubMed]
- Su, J.W.; Gao, W.; Trinh, K.; Kenderes, S.M.; Tekin Pulatsu, E.; Zhang, C.; Whittington, A.; Lin, M.; Lin, J. 4D printing of polyurethane paint-based composites. Int. J. Smart Nano Mater. 2019, 10, 237–248. [Google Scholar] [CrossRef]
- Chen, S.; Mo, F.; Yang, Y.; Stadler, F.; Chen, S.; Yang, H.; Ge, Z. Development of zwitterionic polyurethanes with multi-shape memory effects and self-healing properties. J. Mater. Chem. 2015, 3, 2924–2933. [Google Scholar] [CrossRef]
- Deng, X.; Xie, H.; Du, L.; Fan, C.; Cheng, C.; Yang, K.; Wang, Y.Z. Polyurethane networks based on disulfide bonds: From tunable multi-shape memory effects to simultaneous self-healing. Sci. China Mater. 2019, 62, 437–447. [Google Scholar] [CrossRef]
- Chen, S.; Mo, F.; Stadler, F.; Chen, S.; Ge, Z.; Zhuo, H. Development of zwitterionic copolymers with multi-shape memory effects and moisture-sensitive shape memory effects. J. Mater. Chem. 2015, 3, 6645–6655. [Google Scholar] [CrossRef]
- Molavi, F.K.; Ghasemi, I.; Messori, M.; Esfandeh, M. Design and Characterization of Novel Potentially Biodegradable Triple-Shape Memory Polymers Based on Immiscible Poly(L-lactide)/Poly(ε-caprolactone) Blends. J. Polym. Environ. 2019, 27, 632–642. [Google Scholar] [CrossRef]
- Dolynchuk, O.; Kolesov, I.; Radusch, H.J. Thermodynamic description and modeling of two-way shape-memory effect in crosslinked semicrystalline polymers. Polym. Adv. Technol. 2014, 25, 1307–1314. [Google Scholar] [CrossRef]
- Xu, M.; Cong, Y.; Zhang, B. Synthesis and characterisation of biodegradable liquid crystal elastomer with the property of shape recovery. Liq. Cryst. 2017, 44, 1701–1708. [Google Scholar] [CrossRef]
- Marotta, A.; Lama, G.; Ambrogi, V.; Cerruti, P.; Giamberini, M.; Gentile, G. Shape memory behavior of liquid-crystalline elastomer/graphene oxide nanocomposites. Compos. Sci. Technol. 2018, 159, 251–258. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y.; Leng, J. Recent developments in shape memory polymer nanocomposites: Actuation methods and mechanisms. Coord. Chem. Rev. 2016, 320, 38–52. [Google Scholar] [CrossRef]
- Yao, Y.; Zhou, T.; Wang, J.; Li, Z.; Lu, H.; Liu, Y.; Leng, J. ‘Two way’ shape memory composites based on electroactive polymer and thermoplastic membrane. Compos. A Appl. Sci. Manuf. 2016, 90, 502–509. [Google Scholar] [CrossRef]
- Sachyani Keneth, E.; Scalet, G.; Layani, M.; Tibi, G.; Degani, A.; Auricchio, F.; Magdassi, S. Pre-programmed Tri-layer Electro-Thermal Actuators Composed of Shape Memory Polymer and Carbon Nanotubes. Soft Robot. 2019. [Google Scholar] [CrossRef] [PubMed]
- Ohm, C.; Brehmer, M.; Zentel, R. Liquid crystalline elastomers as actuators and sensors. Adv. Mater. 2010, 22, 3366–3387. [Google Scholar] [CrossRef] [PubMed]
- Brömmel, F.; Kramer, D.; Finkelmann, H. Preparation of liquid crystalline elastomers. In Liquid Crystal Elastomers: Materials and Applications; De Jeu, F., Ed.; Springer: Berlin, Germany, 2012; pp. 1–48. [Google Scholar]
- Belmonte, A.; Fernández-Francos, X.; Serra, A.; De la Flor, S. Phenomenological characterization of sequential dual-curing of off-stoichiometric “thiol-epoxy” systems: Towards applicability. Mater. Des. 2017, 113, 116–127. [Google Scholar] [CrossRef]
- Krause, S.; Dersch, R.; Wendorff, J.; Finkelmann, H. Photocrosslinkable liquid crystal main-chain polymers: Thin films and electrospinning. Macromol. Rapid Commun. 2007, 28, 2062–2068. [Google Scholar] [CrossRef]
- Lu, Y.; Xiao, X.; Fu, J.; Huan, C.; Shuai, Q.; Yongjun, Z.; Yanqing, Z.; Gang, X. Novel smart textile with phase change materials encapsulated core-sheath structure fabricated by coaxial electrospinning. Chem. Eng. J. 2019, 355, 532–539. [Google Scholar] [CrossRef]
- Gonzalez-Henriquez, C.M.; Sarabia-Vallejos, M.A.; Rodriguez-Hernandez, J. Polymers for additive manufacturing and 4D-printing: Materials, methodologies, and biomedical applications. Prog. Polym. Sci. 2019, 94, 57–116. [Google Scholar] [CrossRef]
- Tibbits, S. Design to self-assembly. Archit. Des. 2012, 82, 68–73. [Google Scholar] [CrossRef]
- Choi, J.; Kwon, O.; Jo, W.; Lee, H.; Moon, M.W. 4D Printing Technology: A Review. Print. Addit. Manuf. 2015, 2, 159–167. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, W.; Kang, S.; Wu, X.; Lu, H.; Fu, J.; Cui, H. From 3D to 4D printing: Approaches and typical applications. J. Mech. Sci. Technol. 2015, 29, 4281–4288. [Google Scholar] [CrossRef]
- Khare, V.; Sonkaria, S.; Lee, G.Y.; Ahn, S.H.; Chu, W.S. From 3D to 4D printing—Design, material and fabrication for multi-functional multi-materials. Int. J. Precis. Eng. Manuf. Technol. 2017, 4, 291–299. [Google Scholar] [CrossRef]
- Lee, A.Y.; An, J.; Chua, C.K. Two-Way 4D Printing: A Review on the Reversibility of 3D-Printed Shape Memory Materials. Engineering 2017, 3, 663–674. [Google Scholar] [CrossRef]
- Miao, S.; Castro, N.; Nowicki, M.; Xia, L.; Cui, H.; Zhou, X.; Zhu, W.; Lee, S.j.; Sarkar, K.; Vozzi, G. 4D printing of polymeric materials for tissue and organ regeneration. Mater. Today 2017, 20, 577–591. [Google Scholar] [CrossRef]
- Momeni, F.; Hassani, S.M.; Liu, X.; Ni, J. A review of 4D printing. Mater. Des. 2017, 122, 42–79. [Google Scholar] [CrossRef]
- Pei, E.; Loh, G. Technological considerations for 4D printing: An overview. Prog. Addit. Manuf. 2014, 3, 95–107. [Google Scholar] [CrossRef]
- Wu, J.J.; Huang, L.M.; Zhao, Q.; Xie, T. 4D Printing: History and Recent Progress. Chin. J. Polym. Sci. 2018, 36, 563–575. [Google Scholar] [CrossRef]
- Kuang, X.; Roach, D.J.; Wu, J.; Hamel, C.M.; Ding, Z.; Wang, T.; Dunn, M.L.; Qi, H.J. Advances in 4D Printing: Materials and Applications. Adv. Funct. Mater. 2019, 29, 1805290. [Google Scholar] [CrossRef]
- Zolfagharian, A.; Kaynak, A.; Kouzani, A. Closed-loop 4D-printed soft robots. Mater. Des. 2020, 188, 108411. [Google Scholar] [CrossRef]
- Raviv, D.; Zhao, W.; McKnelly, C.; Papadopoulou, A.; Kadambi, A.; Shi, B.; Hirsch, S.; Dikovsky, D.; Zyracki, M.; Olguin, C. Active printed materials for complex self-evolving deformations. Sci. Rep. 2015, 4, 7422. [Google Scholar] [CrossRef]
- Khoo, Z.; Teoh, J.; Liu, Y.; Chua, C.; Yang, S.; An, J.; Leong, K.; Yeong, W. 3D printing of smart materials: A review on recent progresses in 4D printing. Virtual Phys. Prototyp. 2015, 10, 103–122. [Google Scholar] [CrossRef]
- Shin, D.G.; Kim, T.H.; Kim, D.E. Review of 4D printing materials and their properties. Int. J. Precis. Eng. Manuf. Technol. 2017, 4, 349–357. [Google Scholar] [CrossRef]
- Tibbits, S. 4D printing: Multi-material shape change. Archit. Des. 2014, 84, 116–121. [Google Scholar] [CrossRef]
- Zarek, M.; Layani, M.; Cooperstein, I.; Sachyani, E.; Cohn, D.; Magdassi, S. 3D printing of shape memory polymers for flexible electronic devices. Adv. Mater. 2016, 28, 4449–4454. [Google Scholar] [CrossRef]
- Invernizzi, M.; Turri, S.; Levi, M.; Suriano, R. 4D printed thermally activated self-healing and shape memory polycaprolactone-based polymers. Eur. Polym. J. 2018, 101, 169–176. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Q.; Feng, J. 3D printing of tunable shape memory polymer blends. J. Mater. Chem. 2017, 5, 8361–8365. [Google Scholar] [CrossRef]
- Yu, K.; Dunn, M.; Qi, H. Digital manufacture of shape changing components. Extrem. Mech. Lett. 2015, 4, 9–17. [Google Scholar] [CrossRef]
- Inverardi, N.; Pandini, S.; Bignotti, F.; Scalet, G.; Marconi, S.; Auricchio, F. Sequential Motion of 4D Printed Photopolymers with Broad Glass Transition. Macromol. Mater. Eng. 2019, 305, 1900370. [Google Scholar] [CrossRef]
- Yuan, C.; Roach, D.; Dunn, C.; Mu, Q.; Kuang, X.; Yakacki, C.; Wang, T.; Yu, K.; Qi, H. 3D printed reversible shape changing soft actuators assisted by liquid crystal elastomers. Soft Matter 2017, 13, 5558. [Google Scholar] [CrossRef]
- Ambulo, C.; Burroughs, J.; Boothby, J.; Kim, H.; Shankar, M.; Ware, T. Four-dimensional printing of liquid crystal elastomers. ACS Appl. Mater. Interfaces 2017, 9, 37332–37339. [Google Scholar] [CrossRef]
- Boothby, J.; Ware, T. Dual-responsive, shape-switching bilayers enabled by liquid crystal elastomers. Soft Matter 2017, 13, 4349. [Google Scholar] [CrossRef] [PubMed]
- Kotikian, A.; Truby, R.; Boley, J.; White, T.; Lewis, J. 3D printing of liquid crystal elastomeric actuators with spatially programed nematic order. Adv. Mater. 2018, 30, 1706164. [Google Scholar] [CrossRef] [PubMed]
- López-Valdeolivas, M.; Liu, D.; Broer, D.; Sánchez-Somolinos, C. 4D Printed Actuators with Soft-Robotic Functions. Macromol. Rapid Commun. 2018, 39, 1700710. [Google Scholar] [CrossRef]
- Saed, M.; Ambulo, C.; Kim, H.; De, R.; Raval, V.; Searles, K.; Siddiqui, D.; Cue, J.; Stefan, M.; Shankar, M.; et al. Molecularly-engineered, 4D-printed liquid crystal elastomer actuators. Adv. Funct. Mater. 2019, 29, 1806412. [Google Scholar] [CrossRef]
- Ge, Q.; Qi, H.; Dunn, M. Active materials by four-dimension printing. Appl. Phys. Lett. 2013, 103, 131901. [Google Scholar] [CrossRef]
- Wu, J.; Yuan, C.; Ding, Z.; Isakov, M.; Mao, Y.; Wang, T.; Dunn, M.; Qi, H. Multi-shape active composites by 3D printing of digital shape memory polymers. Sci. Rep. 2016, 6, 24224. [Google Scholar] [CrossRef]
- Ge, Q.; Sakhaei, A.; Lee, H.; Dunn, C.; Fang, N.; Dunn, M. Multi-material 4D printing with tailorable shape memory polymers. Sci. Rep. 2016, 6, 1–11. [Google Scholar] [CrossRef]
- Mao, Y.; Ding, Z.; Yuan, C.; Ai, S.; Isakov, M.; Wu, J.; Dunn, M.; Qi, H. 3D printed reversible shape changing components with stimuli responsive materials. Sci. Rep. 2016, 6, 24761. [Google Scholar] [CrossRef]
- Sun, Y.; Wan, Y.; Nam, R.; Chu, M.; Naguib, H. 4D-printed hybrids with localized shape memory behaviour: Implementation in a functionally graded structure. Sci. Rep. 2019, 9, 18754. [Google Scholar] [CrossRef]
- Naficy, S.; Gately, R.; Gorkin III, R.; Xin, H.; Spinks, G. 4D printing of reversible shape morphing hydrogel structures. Macromol. Mater. Eng. 2016, 302, 1600212. [Google Scholar] [CrossRef]
- Ding, Z.; Yuan, C.; Peng, X.; Wang, T.; Qi, H.; Dunn, M. Direct 4D Printing Via Active Composite Materials. Sci. Adv. 2017, 3, e1602890. [Google Scholar] [CrossRef] [PubMed]
- Yuan, C.; Ding, Z.; Wang, T.; Dunn, M.; Qi, H. Shape forming by thermal expansion mismatch and shape memory locking in polymer/elastomer laminates. Smart Mater. Struct. 2017, 26, 105027. [Google Scholar] [CrossRef]
- Hu, G.; Damanpack, A.; Bodaghi, M.; Liao, W. Increasing dimension of structures by 4D printing shape memory polymers via fused deposition modeling. Smart Mater. Struct. 2017, 26, 125023. [Google Scholar] [CrossRef]
- van Manen, T.; Janbaz, S.; Zadpoor, A. Programming 2D/3D shape-shifting with hobbyist 3D printers. Mater. Horizons 2017, 4, 1064. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yan, D.; Zhang, K.; Hu, G. Pattern Transformation of Heat-Shrinkable Polymer by Three-Dimensional (3D) Printing Technique. Sci. Rep. 2015, 5, 8936. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, J.; Mu, X.; Chen, H.; Qi, H.; Fang, D. Desolvation Induced Origami of Photocurable Polymers by Digit Light Processing. Macromol. Rapid Commun. 2017, 38, 1600625. [Google Scholar] [CrossRef]
- Zhao, Z.; Wu, J.; Mu, X.; Chen, H.; Qi, H.; Fang, D. Origami by Frontal Photopolymerization. Sci. Adv. 2017, 3, e1602326. [Google Scholar] [CrossRef]
- Zarek, M.; Layani, M.; Eliazar, S.; Mansour, N.; Cooperstein, I.; Shukrun, E.; Szlar, A.; Cohn, D.; Magdassi, S. 4D printing shape memory polymers for dynamic jewellery and fashionwear. Virtual Phys. Prototyp. 2016, 11, 263. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Liao, W. Adaptive metamaterials by functionally graded 4D printing. Mater. Des. 2017, 135, 26–36. [Google Scholar] [CrossRef]
- Bodaghi, M.; Damanpack, A.; Liao, W. Triple shape memory polymers by 4D printing. Smart Mater. Struct. 2016, 27, 065010. [Google Scholar] [CrossRef]
- Pandini, S.; Inverardi, N.; Scalet, G.; Battini, D.; Bignotti, F.; Marconi, S.; Auricchio, F. Shape memory response and hierarchical motion capabilities of 4D printed auxetic structures. Mech. Res. Commun. 2020, 103, 103463. [Google Scholar] [CrossRef]
- Fan, J.; Li, G. High performance and tunable artificial muscle based on two-way shape memory polymer. RSC Adv. 2017, 7, 1127–1136. [Google Scholar] [CrossRef]
- Yang, Q.; Fan, J.; Li, G. Artificial muscles made of chiral two-way shape memory polymer fibers. Appl. Phys. Lett. 2016, 109, 183701. [Google Scholar] [CrossRef]
- Gong, T.; Zhao, K.; Wang, W.; Chen, H.; Wang, L.; Zhou, S. Thermally activated reversible shape switch of polymer particles. J. Mater. Chem. 2014, 2, 6855–6866. [Google Scholar] [CrossRef]
- Ge, F.; Zhao, Y. A new function for thermal phase transition-based polymer actuators: autonomous motion on a surface of constant temperature. Chem. Sci. 2017, 8, 6307–6312. [Google Scholar] [CrossRef]
- Farhan, M.; Rudolph, T.; Nochel, U.; Yan, W.; Kratz, K.; Lendlein, A. Noncontinuously Responding Polymeric Actuators. ACS Appl. Mater. Interfaces 2017, 9, 33559–33564. [Google Scholar] [CrossRef]
- Shahsavan, H.; Salili, S.; Jakli, A.; Zhao, B. Thermally active liquid crystal network gripper mimicking the self-peeling of gecko toe pads. Adv. Mater. 2017, 29, 1604021. [Google Scholar] [CrossRef]
- Buguin, A.; Li, M.H.; Silberzan, P.; Ladoux, B.; Keller, P. Micro-actuators: When artificial muscles made of nematic liquid crystal elastomers meet soft lithography. J. Am. Chem. Soc. 2006, 128, 1088. [Google Scholar] [CrossRef]
- Yang, H.; Buguin, A.; Taulemesse, J.M.; Kaneko, K.; Méry, S.; Bergeret, A.; Keller, P. Micron-Sized Main-Chain Liquid Crystalline Elastomer Actuators with Ultralarge Amplitude Contractions. J. Am. Chem. Soc. 2009, 131, 15000. [Google Scholar] [CrossRef]
- Ahn, C.; Liang, X.; Cai, S. Inhomogeneous stretch induced patterning of molecular orientation in liquid crystal elastomers. Extrem. Mech. Lett. 2015, 5, 30. [Google Scholar] [CrossRef]
- de Haan, L.; Gimenez-Pinto, V.; Konya, A.; Nguyen, T.S.; Verjans, J.; Sánchez-Somolinos, C.; Selinger, J.; Selinger, R.D.; Broer, J.; Schenning, A. Accordion-like Actuators of Multiple 3D Patterned Liquid Crystal Polymer Films. Adv. Funct. Mater. 2014, 24, 1251. [Google Scholar] [CrossRef]
- Ware, T.; McConney, M.; Wie, J.; Tondigliaand, V.; White, T. Voxelated liquid crystal elastomers. Science 2015, 347, 982–984. [Google Scholar] [CrossRef] [PubMed]
- Robertson, J.; Rodriguez, R.; Holmes Jr, L.; Mather, P.; Wetzel, E. Thermally driven microfluidic pumping via reversible shape memory polymers. Smart Mater. Struct. 2016, 25, 085043. [Google Scholar] [CrossRef]
- Tippets, C.; Li, Q.; Fu, Y.; Donev, E.; Zhou, J.; Turner, S.; Jackson, A.M.; Ashby, V.; Sheiko, S.; Lopez, R. Dynamic optical gratings accessed by reversible shape memory. ACS Appl. Mater. Interfaces 2015, 7, 14288–14293. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Liu, X.; Tok, A.; Lipik, V. Body temperature-responsive two-way and moisture-responsive one-way shape memory behaviors of poly(ethylene glycol)-based networks. Polym. Chem. 2017, 8, 3833–3840. [Google Scholar] [CrossRef]
- Ahn, J.S.; Yu, W.R.; Youk, J.; Ryu, H. In situ temperature tunable pores of shape memory polyurethane membranes. Smart Mater. Struct. 2011, 20, 105024. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, K.; Hu, G. Smart three-dimensional lightweight structure triggered from a thin composite sheet via 3D printing technique. Sci. Rep. 2016, 6, 22431. [Google Scholar] [CrossRef]
- Fang, L.; Fang, T.; Liu, X.; Chen, S.; Lu, C.; Xu, Z. Near-infrared light triggered soft actuators in aqueous media pre-pared from shape-memory polymer composites. Macromol. Mater. Eng. 2016, 301, 1111–1120. [Google Scholar] [CrossRef]
- Liu, Y.; Boyles, J.; Genzer, J.; Dickey, M. Self-folding of polymer sheets using local light absorption. Soft Matter 2012, 8, 1764. [Google Scholar] [CrossRef]
- Yang, Y.; Pei, Z.; Li, Z.; Wei, Y.; Ji, Y. Making and Remaking Dynamic 3D Structures by Shining Light on Flat Liquid Crystalline Vitrimer Films without a Mold. J. Am. Chem. Soc. 2016, 138, 2118–2121. [Google Scholar] [CrossRef]
- Liu, Y.; Shaw, B.; Dickey, M.; Genzer, J. Sequential self-folding of polymer sheets. Sci. Adv. 2017, 3, e1602417. [Google Scholar] [CrossRef] [PubMed]
- Jin, B.; Song, H.; Jiang, R.; Song, J.; Zhao, Q.; Xie, T. Programming a crystalline shape memory polymer network with thermo- and photo-reversible bonds toward a single-component soft robot. Sci. Adv. 2018, 4, eaao3865. [Google Scholar] [CrossRef]
- Peng, Q.; Wei, H.; Qin, Y.; Lin, Z.; Zhao, X.; Xu, F.; Leng, J.; He, K.; Cao, A.; Li, Y. Shape-memory polymer nanocomposites with a 3D conductive network for bidirectional actuation and locomotion application. Nanoscale 2016, 8, 18042–18049. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Wu, J.; Paulino, G.; Qi, H. Programmable Deployment of Tensegrity Structures by Stimulus-Responsive Polymers. Sci. Rep. 2017, 7, 3511. [Google Scholar] [CrossRef] [PubMed]
- Ge, Q.; Dunn, C.; Qi, H.; Dunn, M. Active origami by 4D printing. Smart Mater. Struct. 2014, 23, 094007. [Google Scholar] [CrossRef]
- Yu, K.; Ritchie, A.; Mao, Y.; Dunn, M.; Qi, H. Controlled sequential shape changing components by 3D printing of shape memory polymer multimaterials. Procedia IUTAM 2015, 12, 193–203. [Google Scholar] [CrossRef]
- Mao, Y.; Yu, K.; Isakov, M.; Wu, J.T.; Dunn, M.; Qi, H. Sequential self-folding structures by 3D printed digital shape memory polymers. Sci. Rep. 2015, 5, 13616. [Google Scholar] [CrossRef]
- Belmonte, A.; Lama, G.; Cerruti, P.; Ambrogi, V. Motion control in free-standing shape-memory actuators. Smart Mater. Struct. 2018, 27, 075013. [Google Scholar] [CrossRef]
- Yuan, C.; Mu, X.; Dunn, C.; Haidar, J.; Wang, T.; Qi, H. Thermomechanically triggered two-stage pattern switching of 2D lattices for adaptive structures. Adv. Funct. Mater. 2018, 28, 1705727. [Google Scholar] [CrossRef]
- Zhao, Z.; Yuan, C.; Lei, M.; Yang, L.; Zhang, Q.; Chen, H.; Qi, H.; Fang, D. Three-dimensionally printed mechanical metamaterials with thermally tunable auxetic behavior. Phys. Rev. Appl. 2019, 11, 044074. [Google Scholar] [CrossRef]
- Chen, T.; Mueller, J.; Shea, K. Integrated design and simulation of tunable, multi-state structures fabricated monolithically with multi-material 3D printing. Sci. Rep. 2017, 7, 45671. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.; Bilal, O.; Shea, K.; Daraio, C. Harnessing bistability for directional propulsion of soft, untethered robots. Proc. Natl. Acad. Sci. USA 2018, 115, 5698–5702. [Google Scholar] [CrossRef] [PubMed]
- Balk, M.; Behl, M.; Wischke, C.; Zotzmann, J.; Lendlein, A. Recent advances in degradable lactide-based shape-memory polymers. Adv. Drug Deliv. Rev. 2016, 107, 136–152. [Google Scholar] [CrossRef] [PubMed]
- Timoshenko, S. Analysis of bi-metal thermostats. JOSA 1925, 11, 233–255. [Google Scholar] [CrossRef]
- Cui, Y.; Wang, C.; Sim, K.; Chen, J.; Li, Y.; Xing, Y.; Yu, C.; Song, J. A simple analytical thermo-mechanical model for liquid crystal elastomer bilayer structures. AIP Adv. 2018, 8, 025215. [Google Scholar] [CrossRef]
- Ding, Z.; Weeger, O.; Qi, H.J.; Dunn, M. 4D rods: 3D structures via programmable 1D composite rods. Mater. Des. 2018, 137, 256–265. [Google Scholar] [CrossRef]
- Peraza Hernandez, E.; Hartl, D.; Lagoudas, D. Active Origami Modeling, Design, and Applications; Springer International Publishing: Cham, Switzerland, 2019. [Google Scholar]
- Bodaghi, M.; Noroozi, R.; Zolfagharian, A.; Fotouhi, M.; Norouzi, S. 4D printing self-morphing structures. Materials 2019, 12, 1353. [Google Scholar] [CrossRef]
- Nguyen, T. Modeling Shape-Memory Behavior of Polymers. Polym. Rev. 2013, 53, 130–152. [Google Scholar] [CrossRef]
- Xin, X.; Liu, L.; Liu, Y.; Leng, J. Mechanical Models, Structures, and Applications of Shape-Memory Polymers and Their Composites. Acta Mech. Solida Sin. 2019, 32, 535–565. [Google Scholar] [CrossRef]
- Tobushi, H.; Hashimoto, T.; Hayashi, S.; Yamada, E. Thermomechanical constitutive modeling in shape memory polymer of polyurethane series. J. Intell. Mater. Syst. Struct. 1997, 8, 711–718. [Google Scholar] [CrossRef]
- Pieczyska, E.; Staszczak, M.; Maj, M.; Kowalczyk-Gajewska, K.; Golasiński, K.; Cristea, M.; Tobushi, H.; Hayashi, S. Investigation of thermomechanical couplings, strain localization and shape memory properties in a shape memory polymer subjected to loading at various strain rates. Smart Mater. Struct. 2016, 25, 085002. [Google Scholar] [CrossRef]
- Tobushi, H.; Okamura, K.; Hayashi, S.; Ito, N. Thermomechanical constitutive model of shape memory polymer. Mech. Mater. 2001, 33, 545–554. [Google Scholar] [CrossRef]
- Morshedian, J.; Khonakdar, H.; Rasouli, S. Modeling of shape memory induction and recovery in heat-shrinkable polymers. Macromol. Theory Simulations 2005, 14, 428–434. [Google Scholar] [CrossRef]
- Di Marzio, E.; Yang, A. Configurational entropy approach to the kinetics of glasses. J. Res. Natl. Inst. Stand. Technol. 1997, 102, 135–157. [Google Scholar] [CrossRef]
- Buckley, C.; Prisacariu, C.; Caraculacu, A. Novel triol-crosslinked polyurethanes and their thermorheological characterization as shape-memory materials. Polymer 2007, 48, 1388–1396. [Google Scholar] [CrossRef]
- Williams, M.; Landel, R.; Ferry, J. Temperature dependence of relaxation mechanisms in amorphous polymers and other glass-forming liquids. Phys. Rev. 1955, 98, 1549. [Google Scholar] [CrossRef]
- Sun, L.; Huang, W. Mechanisms of the multi-shape memory effect and temperature memory effect in shape memory polymers. Soft Matter 2010, 6, 4403–4406. [Google Scholar] [CrossRef]
- Yu, K.; Xie, T.; Leng, J.; Ding, Y.; Qi, H. Mechanisms of multi-shape memory effects and associated energy release in shape memory polymers. Soft Matter 2012, 8, 5687–5695. [Google Scholar] [CrossRef]
- Qi, H.; Dunn, M. Thermomechanical Behavior and Modeling Approaches. In Shape-Memory Polymers and Multifunctional Composites; Leng, J., Du, S., Eds.; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Yu, K.; Ge, Q.; Qi, H. Reduced time as a unified parameter determining fixity and free recovery of shape memory polymers. Nat. Commun. 2013, 5, 1–9. [Google Scholar] [CrossRef]
- Yu, K.; Qi, H. Temperature memory effect in amorphous shape memory polymers. Soft Matter 2014, 10, 9423–9432. [Google Scholar] [CrossRef]
- Westbrook, K.; Kao, P.; Castro, F.; Ding, Y.; Qi, H. A 3D finite deformation constitutive model for amorphous shape memory polymers: A multi-branch modeling approach for nonequilibrium relaxation processes. Mech. Mater. 2011, 43, 853–869. [Google Scholar] [CrossRef]
- Diani, J.; Gilormini, P.; Frédy, C.; Rousseau, I. Predicting thermal shape memory of crosslinked polymer networks from linear viscoelasticity. Int. J. Solids Struct. 2012, 49, 793–799. [Google Scholar] [CrossRef]
- Xiao, R.; Guo, J.; Nguyen, T. Modeling the multiple shape memory effect and temperature memory effect in amorphous polymers. RSC Adv. 2015, 5, 416–423. [Google Scholar] [CrossRef]
- Azoug, A.; Vasconcellos, V.; Dooling, J.; Saed, M.; Yakacki, C.; Nguyen, T. Viscoelasticity of the polydomain-monodomain transition in main-chain liquid crystal elastomers. Polymer 2016, 98, 165–171. [Google Scholar] [CrossRef]
- Dolynchuk, O.; Kolesov, I.; Androsch, R.; Radusch, H.J. Kinetics and dynamics of two-way shape-memory behavior of crosslinked linear high-density and short-chain branched polyethylenes with regard to crystal orientation. Polymer 2015, 79, 146–158. [Google Scholar] [CrossRef]
- Westbrook, K.; Mather, P.T.; Parakh, V.; Dunn, M.; Ge, Q.; Lee, B.; Qi, H. Two-way reversible shape memory effects in a free-standing polymer composite. Smart Mater. Struct. 2011, 20, 1–9. [Google Scholar] [CrossRef]
- Oates, W.; Wang, H. A new approach to modeling liquid crystal elastomers using phase field methods. Model. Simul. Mater. Sci. Eng. 2009, 17, 064004. [Google Scholar] [CrossRef][Green Version]
- Jin, L.; Zeng, Z.; Huo, Y. Thermomechanical modeling of the thermo-order–mechanical coupling behaviors in liquid crystal elastomers. J. Mech. Phys. Solids 2010, 58, 1907–1927. [Google Scholar] [CrossRef]
- Maute, K.; Tkachuk, A.; Wu, J.; Qi, J.; Ding, Z.; Dunn, M. Level Set Topology Optimization of Printed Active Composites. ASME J. Mech. Des. 2015, 137, 111402. [Google Scholar] [CrossRef]
- Tolley, M.; Felton, S.; Miyashita, S.; Aukes, D.; Rus, D.; Wood, R. Self-Folding Origami: Shape Memory Composites Activated by Uniform Heating. Smart Mater. Struct. 2014, 23, 94006. [Google Scholar] [CrossRef]
- Kwok, T.H.; Wang, C.; Deng, D.; Zhang, Y.; Chen, Y. Four-Dimensional Printing for Freeform Surfaces: Design Optimization of Origami and Kirigami Structures. ASME J. Mech. Des. 2015, 137, 111413. [Google Scholar] [CrossRef]
- Fuchi, K.; Ware, T.H.; Buskohl, P.R.; Reich, G.W.; Vaia, R.A.; White, T.J.; Joo, J.J. Topology Optimization for the Design of Folding Liquid Crystal Elastomer Actuators. Soft Matter 2015, 11, 7288–7295. [Google Scholar] [CrossRef] [PubMed]
- Xue, R.; Li, R.; Du, Z.; Zhang, W.; Zhu, Y.; Sun, Z.; Guo, X. Kirigami Pattern Design of Mechanically Driven Formation of Complex 3D Structures Through Topology Optimization. Extrem. Mech. Lett. 2017, 15, 139–144. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, W.; Zhong, W. Doing Topology Optimization Explicitly and Geometrically a New Moving Morphable Components Based Framework. ASME J. Appl. Mech. 2014, 81, 081009. [Google Scholar] [CrossRef]
- Geiss, M.; Boddeti, N.; Weeger, O.; Maute, K.; Dunn, M. Combined Level-Set-XFEM- Density Topology Optimization of Four-Dimensional Printed Structures Undergoing Large Deformation. ASME J. Mech. Des. 2019, 141, 051405. [Google Scholar] [CrossRef]
- Hamel, C.; Roach, D.; Long, K.; Demoly, F.; Dunn, M.; Qi, H. Machine-learning based design of active composite structures for 4D printing. Smart Mater. Struct. 2019, 28, 065005. [Google Scholar] [CrossRef]
- Clifford, D.; Zupan, R.; Brigham, J.; Beblow, R.; Whittock, M.; Davis, N. Application of the dynamic characteristics of shape-memory polymers to climate adaptive building facades. In Proceedings of the 12th Conference of Advanced Building Skins, Bern, Switzerland, 2–3 October 2017; pp. 171–178. [Google Scholar]
- Li, J.; Duan, Q.; Zhang, E.; Wang, J. Applications of Shape Memory Polymers in Kinetic Buildings. Adv. Mater. Sci. Eng. 2018, 2018, 7453698. [Google Scholar] [CrossRef]
- Wehner, M.; Truby, R.; Fitzgerald, D.; Mosadegh, B.; Whitesides, G.; Lewis, J.; Wood, R. An integrated design and fabrication strategy for entirely soft, autonomous robots. Nature 2016, 536, 451–455. [Google Scholar] [CrossRef]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).