Abstract
This paper presents a comparative analysis of electric field (E-field) mitigation in inductive power transfer (IPT) systems. It focuses on how distributed capacitor placement interacts with coil topology to influence E-field emissions. The study compares traditional sequential-winding coils and the alternating voltage phase coil (AVPC), which employs a sequential inversion winding (SIW) structure to enforce a 180° phase voltage opposition between adjacent turns. While capacitor segmentation is a known method for E-field reduction, this work is the first to systematically evaluate its effects across both conventional and phase-inverted coils. The findings reveal that capacitor placement serves as a topology-dependent design parameter. Finite Element Method (FEM) simulations and experimental validation show that while capacitor placement has a moderate influence on traditional coils due to in-phase voltage relationships, AVPC coils are highly sensitive to segmentation patterns. When capacitors align with the SIW phase structure, destructive interference significantly reduces E-field emissions. Improper capacitor placement disrupts phase cancellation and negates this benefit. This study resolves a critical design gap by establishing that distributed compensation acts as a tuning mechanism in conventional coils but becomes a primary constraint in phase-inverted topologies. The results demonstrate that precise capacitor placement aligned with the coil topology significantly enhances E-field mitigation up to 60% in AVPC coils, greatly outperforming traditional coil configurations and providing actionable guidance for high-power wireless charging applications.
1. Introduction
Inductive Power Transfer (IPT) technology presents a compelling solution for wireless electric vehicle (EV) charging, providing automated and contactless energy transfer []. However, scaling IPT systems to high-power applications introduces significant challenges associated with electromagnetic interference (EMI), electromagnetic field (EMF) emissions [], and compliance with electromagnetic compatibility (EMC) standards []. In particular, strong electric field (E-field) emissions from IPT coils pose safety risks and may adversely affect nearby electronic equipment, necessitating stringent management of coil-induced electric fields []. To comprehensively address these challenges, relevant international standards clearly distinguish several categories of emissions and exposure risks, including general electromagnetic emission standards [], specialized protection standards for telecommunication systems and sensitive electronic equipment [], targeted safety guidelines for implantable medical devices and life-critical systems [,], and stringent human exposure limits governed by ICNIRP guidelines and IEEE standards [,]. Although historically, magnetic fields have been the primary concern in lower-voltage IPT systems, electric fields significantly increase at higher voltages and frequencies, posing critical risks for EMC compliance and safety considerations. Thus, specific research into E-field mitigation strategies remains essential, particularly for high-power wireless EV charging applications.
Traditional IPT coil configurations commonly employ uniformly distributed compensation capacitors to segment coil inductances, aiming to evenly distribute coil voltages and partially reduce E-field emissions []. While this approach has been widely adopted [], recent advancements in distributed compensation strategies have explored non-uniform capacitor arrangements to optimize voltage gradients. For instance, staggered capacitor placement has been shown to reduce peak E-fields compared to uniform segmentation [], and adaptive capacitor networks have been proposed for dynamic load conditions []. However, these methods remain constrained by the inherent in-phase voltage relationships of sequential windings, limiting the potential for destructive interference. Innovations in winding structure configurations have introduced novel geometries to address these limitations. Bifilar and spiral-layered windings have been investigated to reduce inter-turn capacitance [,], while optimized litz wire arrangements aim to minimize proximity effects. A significant development is the Alternating Voltage Phase Coil (AVPC), which employs Sequential Inversion Winding (SIW) to enforce 180° phase shifts between adjacent turns []. This topology leverages destructive interference for E-field suppression. However, the practical realization of AVPC’s benefits critically depends on precise capacitor alignment with the SIW phase pattern; improper placement may inadvertently enhance E-field intensity due to unintended constructive interference.
Electric field analysis in IPT systems has undergone a significant transformation [], evolving from early quasi-static approximations to advanced computational and experimental methodologies. Modern studies leverage full-wave Finite Element Method (FEM) simulations to resolve near-field electromagnetic interactions with high spatial and temporal accuracy []. These tools effectively model complex conditions, including coil misalignment, ferrite tilting [], shielding effects, and dynamic loading. Optimization frameworks ranging from parametric sweeps to machine learning-driven techniques, such as genetic algorithms, are increasingly employed to minimize peak E-field intensities while maintaining efficient power transfer. Complementing these simulations, experimental efforts now provide high-fidelity validation []. Frequency-specific near-field scanning at IPT-relevant operating frequencies (e.g., 85 kHz) enables direct comparison between measured and simulated E-field distributions. High-resolution spatial mapping further reveals field leakage paths [,], localized hot spots, and potential violations of regulatory limits such as the EU’s 87 V/m exposure threshold []. Despite these advances, most existing studies focus on single-coil topologies, lacking direct comparisons between sequential-wound and phase-inverted architectures. This work addresses that gap, delivering unified simulation and measurement-based insights into how coil topology and capacitor placement jointly affect E-field behavior in high-power wireless EV charging systems.
This paper presents a rigorous comparative analysis of electric field mitigation in inductive power transfer systems, focusing on the role of distributed capacitor placement in traditional and phase-inverted coil topologies. Using full-wave FEM simulations and experimental validation, the study evaluates traditional sequential-winding coils and AVPC designs that implement SIW to achieve 180° phase opposition between adjacent turns. Results show that capacitor placement has minimal influence on traditional coils due to their inherently in-phase voltage profiles.
In contrast, AVPC coils exhibit strong sensitivity to capacitor positioning. When capacitors are properly aligned with the SIW phase pattern, destructive interference substantially reduces E-field emissions. However, misalignment disrupts phase cancellation and can degrade performance below that of conventional configurations. These findings demonstrate that while capacitor placement serves as a secondary tuning parameter in traditional systems, it becomes a critical design constraint in phase-inverted architectures. To the best of our knowledge, this study is the first to systematically introduce and experimentally validate the AVPC coil topology, explicitly leveraging sequential phase inversion combined with strategic capacitor alignment as active design parameters for suppressing electric field emissions. Unlike prior influential studies, such as Christ et al. [], which primarily focus on exposure assessment methodologies, safety standards, and biological dosimetry, our approach provides a structural, hardware-level solution validated through comprehensive full-wave FEM simulations and experimental measurements. This fills a critical research gap, significantly reducing peak E-field amplitudes and improving electromagnetic compatibility for practical high-power WPT applications. To clarify the system context, Figure 1 illustrates a typical wireless EV charging architecture based on inductive power transfer, where the proposed transmitter coil topologies and distributed compensation strategies are applied.
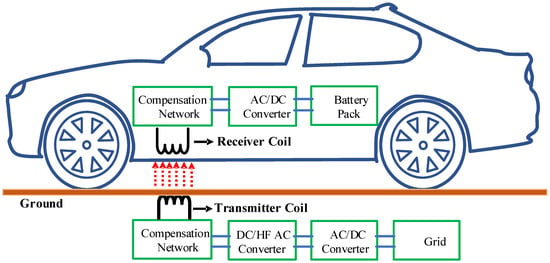
Figure 1.
General wireless power transfer Charging System for EVs.
The paper is structured as follows: Section 2 presents a comparative analysis of traditional and AVPC coil winding techniques. Section 3 discusses E-field behavior through the lens of recent analytical models and provides a detailed design comparison based on voltage distribution and phase relationships. Section 4 details comprehensive FEM-based analyses illustrating the impact of capacitor placements in both traditional and SIW coils. Experimental validation, including setup descriptions and correlation of results with simulations, is presented in Section 5, alongside a critical discussion on measurement accuracy and practical considerations. Section 6 summarizes the primary findings, underscores their practical implications, and proposes directions for future research.
2. Comparative Analysis of Coil Winding
In the context of wireless electric vehicle charging applications, this section compares different coil topologies for the transmitter side of inductive power transfer systems. Traditional IPT coils, as depicted in Figure 2a, are characterized by sequential, uniform turn arrangements (L1→L2→L3→L4→L5→L6). While simple and widely adopted, this straightforward winding inherently results in identical phases along adjacent coil turns. Conversely, SIW, as shown in Figure 2b,c, employs a novel interleaved winding structure: current first traverses odd-numbered turns (L1→L3→L5), then reverses through even-numbered turns (L6→L4→L2) []. This unique configuration inherently produces alternating phase relationships between adjacent coil segments, fundamentally distinguishing SIW coils from traditional winding approaches. This innovative coil topology offers distinct structural advantages and is a promising advancement in wireless power transfer coil designs.
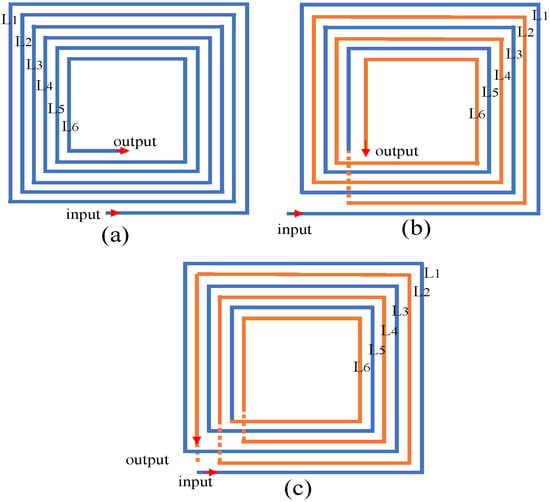
Figure 2.
Structure of the coil prototype. (a) Traditional coil winding, (b) sequential inversion winding coil 1, and (c) sequential inversion winding coil 2. The red arrows indicate the current input and output terminals for each coil configuration.
In each coil structure shown in Figure 2, the input refers to the terminal where current enters the coil, and the output denotes the exit point of current flow.
3. E-Field Behavior and Design Comparison
The coil winding configuration significantly impacts electric field emissions, primarily through its influence on voltage distribution and inter-turn phase relationships. To evaluate and quantify these effects, a detailed comparative analysis was conducted between the traditional sequential coil and the proposed Alternating Voltage Phase Coil, implemented via Sequence Inversion Winding.
The traditional sequential coil, represented by its equivalent circuit in Figure 3b, energizes adjacent coil segments uniformly and sequentially, producing in-phase voltage relationships across all turns. This behavior arises from the symmetric winding geometry and strong magnetic coupling between turns, which induce nearly identical time-varying voltages across each turn. Let Vn denote the voltage across the n-th coil turns. Under in-phase excitation, adjacent voltages satisfy , where V0 is the voltage amplitude per turn and is the angular frequency at the operating frequency . As a result, the total voltage across the coil accumulates linearly:
Figure 3.
(a) Optimized coil design. (b) Equivalent circuit models of a traditional sequential coil. (c) Equivalent circuit models of sequential inversion winding coil.
Here, Vtotal represents the cumulative voltage from the coil’s input to output terminals. This additive voltage behavior amplifies the voltage gradient across the coil and directly contributes to elevated electric field emissions. Such a field buildup exacerbates electromagnetic interference and complicates compliance with EMC regulations. In contrast, the AVPC configuration, physically implemented as shown in Figure 2c and abstracted in the SPICE equivalent circuit of Figure 3c, strategically alternates voltage phases across adjacent segments. The induced voltage in each turn is governed by:
where is the self-inductance of the i-th turn, the current, and is the mutual inductance between turns i and k. The negative sign in the mutual term () is not identical, arising from the opposing flux linkage due to interleaved winding geometry, inherently enforcing a 180° phase inversion mechanism that distinguishes AVPC from traditional topologies. Consequently, adjacent voltages in AVCP satisfy:
This explicit 180° phase relationship ensures destructive interference in the spatial electric field. Mathematically, the phasor sum for adjacent turns cancels:
This expression indicates that the phasor sum of adjacent turn voltages cancels mathematically due to their phase opposition. However, this cancellation does not imply a zero electric field in space. Instead, it reflects a reduction in the local voltage gradient, the principal driver of E-field intensity. In practice, spatial separation, parasitic capacitance, and non-ideal coupling prevent perfect cancellation. As a result, the electric field is not eliminated but significantly attenuated, as confirmed by both FEM simulations and experimental measurements. This destructive voltage interference enabled by the interleaved coil structure and mutual inductive coupling reduces net spatial E-field emissions when the phase-inversion pattern is preserved, as confirmed by detailed SPICE waveform simulations. SPICE simulations further isolate local voltage deviations using the normalized voltage, defined as:
This formulation subtracts the average voltage across all turns, eliminating the common-mode component and highlighting inter-turn voltage differentials. In traditional windings, reflects uniform voltage distribution, whereas in AVPC coils confirms the dominant 180° phase opposition introduced by the sequential inversion strategy. SPICE simulations further validate this behavior, emphasizing AVPC’s role in E-field mitigation.
3.1. Capacitor Placement Impact on Coil Performance
Using the coil dimensions and design parameters from Table 1, ANSYS FEM simulations were conducted to extract the self-inductances and inter-turn coupling coefficients. These extracted electromagnetic parameters were then used to construct equivalent multi-inductor SPICE models. By inserting tuning capacitors at different turn positions in these circuit models, we simulated the coil’s node voltages and phase relationships under various segmentation schemes. This modelling approach ensures that the waveform results reflect the coil’s physical electromagnetic behavior, linking capacitor placement directly to the observed voltage distribution and E-field emission in the system. Theoutcomes of this analysis, illustrating how the choice of capacitor locations influences waveform symmetry and, in turn, the coil’s radiated electric field.

Table 1.
Coil parameters for 22 turns.
Figure 4 illustrates example capacitor placements for both coil topologies. In Figure 4a, capacitors are placed at turns 1, 5, 10, and 15 of a traditional winding coil, representing a typical segmentation strategy used to smooth voltage distribution. In Figure 4b, capacitor placement is shown for the sequential inversion winding coil configuration, with capacitors located at turns 1, 6, 12, and 18. Although only one configuration is shown for each topology, both capacitor arrangements (1, 5, 10, and 15 and 1, 6, 12, and 18) were applied to both the traditional and AVPC coils during simulation and experimental testing. These diagrams serve to visually convey the segmentation approach implemented in the SPICE, FEM, and experimental analyses, supporting the waveform analyses presented in Figure 5, Figure 6, Figure 7 and Figure 8. This representation simplifies the visual comparison by displaying only one illustrative example per topology, while the full results are based on all tested combinations. This figure addresses the physical configuration aspect of the simulation models and clarifies the placement strategy referenced in the subsequent waveform analysis.
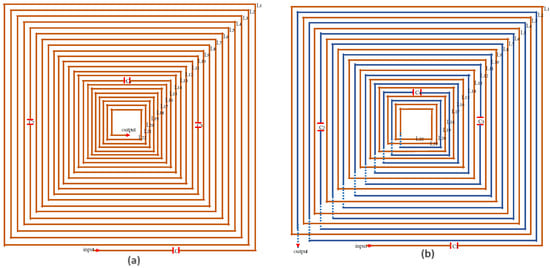
Figure 4.
Capacitor placement examples for both coil topologies. (a) Traditional winding coil with capacitors placed at turns 1, 5, 10, and 15. (b) Alternating Voltage Phase Coil (AVPC) with capacitors placed at turns 1, 6, 12, and 18. Both capacitor configurations were applied to each coil topology during simulations, and in the experiment, only one representative example is shown per topology for illustration. These configurations correspond to the cases analyzed in Figure 5 and Figure 6.
3.2. Traditional Coil Distributed Capacitor Configuration
To study the impact of distributed compensation on the traditional coil topology, capacitors were positioned at specific coil turns, particularly at segments (1, 5, 10, and 15), and alternatively at (1, 6, 12, and 18), within a 22-turn winding (Figure A1). These positions were chosen to assess whether varying capacitor placements influence local voltage waveform characteristics or inter-turn relationships. SPICE simulations (Figure 5a,b) clearly illustrate that, regardless of capacitor placement strategy, adjacent coil turns voltages remain constructively additive, as indicated by the consistent direction of voltage differences shown by the arrows. Although traditional coil winding typically results in voltages between adjacent turns being predominantly in-phase and constructively additive, minor localized phase inversions are occasionally observed (e.g., between turns V5–V6, V11–V12, and V17–V18 in Figure 5a, and turns V9–V10 and V17–V18 in Figure 5b). These isolated inversions can be attributed to local impedance discontinuities introduced by discrete capacitor placements and segmentation effects. Importantly, such localized phenomena are limited in scope and do not indicate systematic destructive interference. Therefore, the overall voltage distribution and E-field emissions in traditional coils remain largely driven by constructive addition, with minor local deviations due to practical capacitor placements.
Specifically, the simulation results show that the voltage difference arrows between adjacent coil turns maintain the same polarity across the coil length, indicating constructive addition rather than cancellation of voltages. Consequently, this confirms that the moderate reductions in E-field intensity observed in traditional coils result solely from voltage gradient smoothing rather than from destructive interference. Importantly, comparing the two capacitor placement scenarios depicted in Figure 5a,b reveals negligible differences in their voltage distribution characteristics. Thus, the simulation conclusively demonstrates that capacitor placement has minimal impact on inter-turn phase relationships in sequential winding structures, and E-field mitigation arises predominantly from local smoothing of voltage distributions.
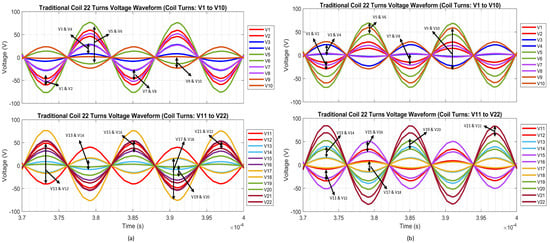
Figure 5.
Traditional winding coil of 22 turns with capacitor placement in each turn. (a) Capacitor placed at turns of winding (1, 5, 10, and 15). (b) Capacitor placed at turns of winding (1, 6, 12, and 18).
3.3. Capacitor Placement in the SIW Coil
Figure 6b shows the simulated voltage waveforms for each coil segment when the capacitors are placed at segments 1, 6, 12, and 18, representing an example of improper segmentation in the SIW configuration. These waveforms reveal clear deviations from the ideal behavior. Notably, the voltage peak magnitudes are non-uniform across the coil, with some segments reaching higher voltages than others, indicating an unbalanced voltage distribution. The waveforms also lack symmetry; the positive and negative peaks for a given segment are not equal in magnitude, suggesting that the oscillations are not centered around zero as cleanly as in the optimal design.
In the ideal SIW coil with proper capacitor placement (Figure 6a), adjacent segments largely exhibit consistent near-180° anti-phase relationships. However, localized in-phase behavior, such as that observed between turns V13–V14 and V21–V22 was noticed even under proper segmentation. These deviations may be attributed to the inherent complexity of phase behavior in segmented coils, where even slight shifts in segment impedance or coupling interactions within the circuit model can produce localized phase mismatches. While the overall SIW structure enforces near-consistent 180° opposition across the majority of turns, such localized deviations are consistent with the sensitivity of the winding to segmentation precision. Therefore, while these minor mismatches may reduce the ideal cancellation slightly, they do not negate the effectiveness of the SIW strategy in suppressing E-field emissions. Future work will focus on refined segmentation tuning or enhanced modeling of distributed parasitics to further improve uniformity.
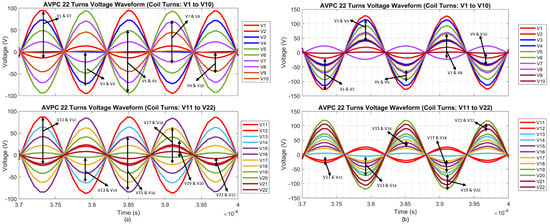
Figure 6.
Coil voltage waveforms of sequential inversion winding coil. (a) Capacitor placed at turns (1, 5, 10, and 15). (b) Capacitor placed at turns (1, 6, 12, and 18).
In contrast, improper capacitor placement (Figure 6b) shows that the phase shift between most adjacent coil segments deviates significantly from the ideal 180° opposition. This widespread phase misalignment clearly indicates improper segmentation. As seen, most segment pairs no longer achieve the expected anti-phase voltage pattern. The loss of systematic phase inversion is evident in both waveform asymmetry and spatial E-field distribution, as shown in the Section 4.2. Such substantial deviations from ideal behavior compromise the intended destructive interference mechanism, thereby significantly increasing E-field emissions. Consequently, with improper segmentation, the coil segments are no longer in strict phase opposition, resulting in a net time-varying electric potential along the coil, producing additional displacement current (∂D/∂t). This increased displacement current directly elevates electric field emissions, particularly in near-field regions above the coil surface, highlighting the critical sensitivity of SIW coil performance to precise capacitor placement.
4. Electric Field Distribution and FEM-Based Analysis
To validate the waveform-based predictions regarding electric field suppression, full-field 3D simulations were performed using FEM for both the traditional and SIW coil configurations. The E-field intensity distributions were computed across the air gap and the surrounding environment under resonant operating conditions. For the FEM simulation, the 22 turns of coil are selected, and the parameters of the coil are shown in Table 1.
4.1. Effect of Capacitor Placement in Traditional Winding Coil
To evaluate the influence of distributed compensation on electric field mitigation in traditional sequential-wound coils, FEM simulations were conducted for two capacitor placement configurations: (i) capacitors at turns 1, 5, 10, and 15, and (ii) capacitors at turns 1, 6, 12, and 18 (Figure 7). These placements were selected to examine whether the position of capacitive segmentation affects E-field suppression performance. The simulated E-field distributions in Figure 7 reveal that capacitive segmentation reduces peak E-field intensity by dividing the coil into multiple inductive-capacitive resonant sections. Each segment supports a reduced portion of the total coil voltage, lowering the local electric field intensity according to . This segmentation also raises the effective self-resonant frequency of each segment suppressing high-frequency transients without degrading magnetic coupling.
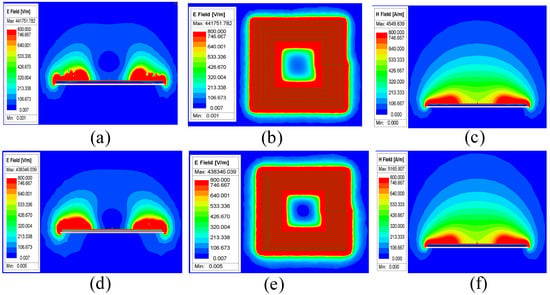
Figure 7.
Traditional winding coil with the distributed compensation topology. (a–c) Capacitor placed at the turn of the winding 1, 5, 10, and 15. (d–f) Capacitor placed at turns of winding 1, 6, 12, and 18.
Importantly, both capacitor placement configurations produce nearly identical E-field distributions. This insensitivity to capacitor location results from the inherently in-phase voltage phasing between adjacent turns in traditional sequential windings. Mutual inductive coupling further reinforces this voltage synchronization, maintaining a consistent E-field profile regardless of capacitor arrangement. These results confirm that in traditional coils, electric field suppression arises primarily from segmentation itself rather than from the specific placement of compensation capacitors. To support this, the corresponding H-field distributions for both configurations are presented in Figure 7c–f. These results reveal minimal variation in magnetic field intensity and distribution, reinforcing that distributed compensation has a negligible effect on H-field behavior in traditional coils. These observations confirm that electric field suppression is the dominant benefit of capacitor segmentation, while magnetic field emissions remain largely unaffected. The observed magnetic field stability is further supported by the flux-guiding role of the PC40 ferrite core beneath the coil, which concentrates the magnetic field vertically and minimizes lateral leakage, thereby contributing to consistent H-field profiles across configurations. This flux guidance is enabled by the high permeability (µr = 2300) and low losses of PC40 ferrite at 85 kHz, which confines the magnetic field within the core area [].
4.2. Effect of Capacitor Placement in Sequential Inversion Winding Coils
Building upon the phase-based mitigation capabilities of sequential inversion winding topologies, this section examines how capacitor placement influences the electric field distribution when inter-turn voltages are intentionally out of phase. Unlike traditional coils, where adjacent turns are energized in-phase, the SIW architecture relies on enforced voltage inversion between neighboring segments to achieve field cancellation. To assess the sensitivity of this cancellation mechanism to capacitor alignment, two distributed compensation schemes were evaluated using FEM simulations, one preserving the intended phase alternation (capacitors at turns 1, 5, 10, and 15) and another disrupting it (capacitors at turns 1, 6, 12, and 18), as shown in Figure 8.
The E-field results in Figure 8 reveal a stark contrast between these two configurations. With capacitors placed symmetrically (1, 5, 10, and 15), the E-field magnitude is significantly reduced across both the coil surface and the surrounding air space. This behavior reflects the proper preservation of the SIW anti-phase voltage pattern, wherein adjacent turns are nearly 180° out of phase. Such conditions facilitate destructive interference between inter-turn voltages, suppressing the net electric field and enhancing overall electromagnetic compatibility.
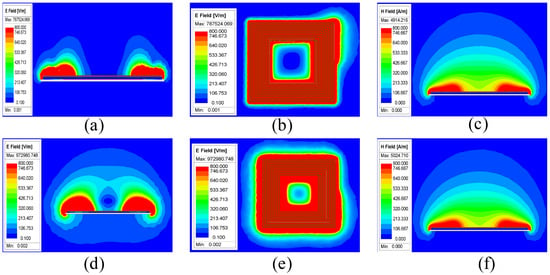
Figure 8.
Sequential Inversion winding coil with the distributed compensation topology. (a–c) Capacitor placed at the turn of the winding 1, 5, 10, and 15. (d–f) Capacitor placed at turns of winding 1, 6, 12, and 18.
In contrast, the configuration with capacitors at (1, 6, 12, and 18) disrupts this phase alternation. The FEM results show increased E-field magnitudes and spatial asymmetry, especially along the lateral coil boundaries. These distortions confirm that improper capacitor positioning leads to phase imbalance, diminishing the SIW’s ability to support uniform voltage inversion and thereby allowing residual fields to propagate. Unlike traditional coils, SIW topologies are inherently phase-sensitive. Their E-field performance is not only governed by segmentation but also by precise capacitor alignment. These findings underscore the importance of preserving phase opposition when implementing distributed compensation in SIW coils, as incorrect placement not only weakens the cancellation mechanism but also exacerbates E-field leakage. For completeness, the magnetic field distributions corresponding to both capacitor placements are shown in Figure 8c–f. As with the traditional winding coils, the SIW topology shows minimal variation in H-field intensity regardless of capacitor alignment. This supports our assertion that the electromagnetic improvements observed in SIW configurations are driven primarily by electric field cancellation, not changes in magnetic field strength.
4.3. Comparative E-Field Performance of Traditional and SIW Coils Under Distributed Compensation
To quantitatively evaluate the electric field mitigation performance of distributed compensation in traditional and Sequential Inversion Winding coils, spatial E-field magnitudes were extracted from FEM simulations at 50 mm above the coil surface (Z = 50 mm plane). Measurements were taken across multiple (X, Y) coordinates, as shown in Figure 9, for four configurations: traditional coils with capacitors at turns (1, 5, 10, and 15) and (1, 6, 12, and 18), and SIW coils with the same capacitor placements.
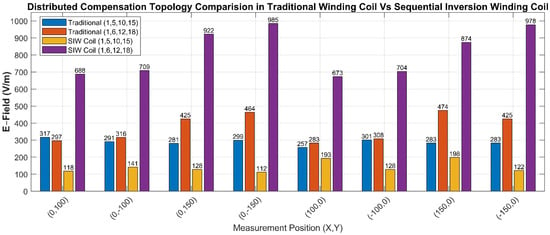
Figure 9.
Distributed Compensation Topology Comparison: Traditional vs. SIW Coils. Measured peak E-field values at 50 mm above the coil for capacitor placements at turns (1, 5, 10, and 15) and (1, 6, 12, and 18) at different positions.
To ensure accuracy and numerical robustness, each capacitor configuration was simulated five times using independent FEM solver runs under identical boundary conditions. This approach accounted for any solver-related numerical artifacts or meshing inconsistencies. The resulting peak E-field values were averaged, and the standard deviation across the three trials was computed. For all configurations, the standard deviation remained below 3%, i.e., σ < 3%, indicating consistent and reproducible electromagnetic field behavior across simulations.
The results indicate that traditional coils exhibit minimal variation in E-field regardless of capacitor placement, while SIW coils demonstrate a strong dependence on alignment. When capacitors are optimally positioned in phase with the SIW pattern (1, 5, 10, and 15), peak E-field levels are reduced below 210 V/m across all measured locations. However, misaligned placement (1, 6, 12, and 18) disrupts the intended 180° phase inversion, resulting in amplified E-fields exceeding 900 V/m at several points. These findings show that in SIW-based systems, effective E-field suppression is governed not only by capacitor segmentation but also by precise synchronization with the coil’s voltage phase distribution.
5. Experimental Setup
To experimentally validate the E-field mitigation performance of distributed compensation, physical prototypes of traditional and Sequential Inversion Winding coils were constructed as detailed in Table 1. The SIW coil enforced a 180°voltage phase shift through interleaved turns, while the traditional coil employed a sequential winding configuration. As part of the coil platform construction, an aluminum shielding plate (2 mm thickness) was installed directly beneath the coil to suppress downward E-field leakage and emulate realistic grounding effects. A ferrite core (material: PC40, dimensions: 460 mm × 460 mm × 2.5 mm) was positioned between the coil and shielding plate to enhance magnetic coupling and direct flux upward. This stacked configuration replicates a typical IPT transmitter pad used in EV charging systems as depicted in Figure 10. The two capacitor placement schemes previously analyzed in Section 4 were implemented for both coil types.

Figure 10.
E-field measurement setup using NF-5035 probe with LCC-compensated coil at 85 kHz.
The measurement setup (Figure 10) utilized an LCC compensation network operating at 85 kHz, with passive elements (LP and Cp1-Cp4) configured and E-field measurements were obtained using an NF-5035 near-field electric field probe positioned 50mm above the coil surface. Spatial measurements were taken at four coordinates, (X, Y) = (0, ±150 mm), (±150 mm, 0). While exact sensor placement was subject to minor positioning deviations due to practical constraints, it corresponded to the FEM-predicted E-field (Section 4.3). Each configuration was tested over three independent trials to account for environmental variability, including ambient EMI and conductive surroundings. E-field values were averaged, with standard deviation occasionally exceeding ±10%, reflecting real-world influences on measurement fidelity. Prior to assembly, individual capacitor values were measured and confirmed to lie within a ±3% tolerance range. System resonance at 85 kHz was verified after placement, confirming proper compensation despite small component-level variations.
Figure 11 shows the spatial E-field readings for each coil design. The tests were conducted under realistic lab conditions to capture environmental variability. Variations in measured E-field values were observed, influenced by nearby metallic objects and ambient electromagnetic interference factors relevant to real-world EV charging scenarios and the public EMF exposure limit of 87 V/m at 85 kHz (per EU Directive) []. Among all configurations, the SIW coil with capacitors placed at turns 1, 5, 10, and 15 showed the lowest variability in E-field intensity, suggesting enhanced resilience to environmental disturbances and better electromagnetic stability in uncontrolled settings.

Figure 11.
Measurement of the E-field comparison across the distributed compensation coils.
5.1. Experimental Correlation with Simulation Results
The electric field simulation results presented in Figure 9 were validated through detailed experimental measurements, as summarized in Figure 12. These experimental data illustrate measured E-field intensities across various spatial points for each coil configuration, allowing direct comparison with the corresponding FEM-predicted distributions. The SIW coils, particularly with capacitors placed at turns 1, 5, 10, and 15, consistently exhibited significantly lower E-field levels compared to traditional coil configurations. Specifically, the SIW coil with optimal capacitor placement maintained measured E-field strengths below 200 V/m across all test points. Conversely, the misaligned SIW coil configuration (turns 1, 6, 12, and 18) resulted in substantially higher measured fields, surpassing 1000 V/m at some spatial positions, consistent with simulation predictions. Traditional coil configurations displayed intermediate E-field strengths, with minimal dependence on capacitor placement. It is important to emphasize that the E-field measurements presented here were taken at a vertical height of 50 mm above the coil surface, representing a deliberately selected worst-case proximity for near-field characterization. These values reflect localized pointwise magnitudes and are not intended for direct comparison with ICNIRP biological exposure limits. Specifically, ICNIRP (2010) recommends internal electric field averaging over 2 × 2 × 2 mm3 tissue volumes to assess electrostimulation thresholds []. For external fields, spatial averaging procedures are left to the relevant standardization bodies. For formal compliance, standards like IEEE C95.1 [] require specific averaging protocols beyond our scope. As such, our pointwise values likely represent a conservative overestimate of actual exposure.
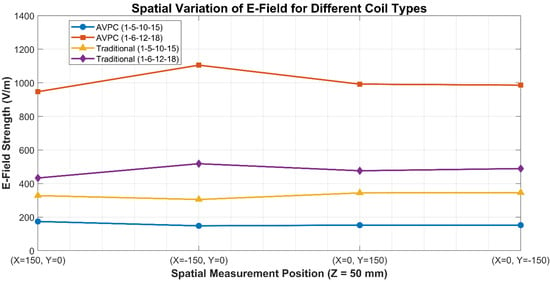
Figure 12.
Impact of segment capacitor placement on E-field emission levels in SIW coil and Traditional IPT coils.
Moreover, in practical EV charging scenarios, physical shielding and typical user distances (>0.5 m) significantly reduce exposure levels. For example, Cirimele et al. [] showed that ICNIRP magnetic field limits may be exceeded only at distances below 75 cm from rear-mounted IPT systems. Similarly, Zhao et al. [] confirmed compliance for various power levels up to 150 kW when user separation exceeds 0.5–1.7 m. While our measurements focus on electric fields, both studies affirm that worst-case peaks decline rapidly with distance. Furthermore, the observed steep lateral E-field gradients (e.g., 148–1100 V/m variation in Figure 12) are characteristic of resonant near-field WPT operation and align with spatial behavior reported in prior magnetic field studies [,]. These gradients are critical when identifying local maxima for emission control. Although not varied experimentally, the E-field magnitude is expected to scale approximately as E ∝ √P with respect to power, consistent with resonant system behavior []. This relationship supports the broader scalability of our findings to higher-power applications.
These measurement results closely correlate with FEM simulations, reinforcing the validity and accuracy of the numerical models employed. Although slight variations between experimental and simulation results occurred due to practical environmental influences such as nearby metallic structures and ambient electromagnetic interference, these measurements nonetheless support the effectiveness of phase-synchronized distributed compensation. Although the measured E-field levels for the optimal SIW configuration remain well below the IEC 61980-3 defined worst-case exposure thresholds [], underscoring the practical viability and EMC compliance benefits of employing precisely aligned capacitor placements within SIW-based wireless power transfer systems.
It is also worth addressing the small deviations observed across spatial measurement points in Figure 12, which ideally should be symmetric. While the coil geometries are symmetric in design, perfect experimental symmetry is difficult to maintain due to slight probe misalignments (±5 mm), environmental factors (e.g., nearby reflective surfaces, metallic structures), and manufacturing tolerances in winding and capacitor positioning. Notably, the AVPC (1-5-10-15) configuration showed the most uniform profile among all cases, indicating not only its E-field reduction capability but also enhanced spatial consistency. This consistency further strengthens its suitability for minimizing emissions in real-world applications. While suppression of E-field components may affect the local wave impedance, FEM simulations confirm that the H-field remains well-confined by the ferrite structure and does not exceed typical safety thresholds. This demonstrates that the AVPC topology offers dual benefits, effective reduction of capacitive emissions while maintaining stable magnetic field behavior within safe limits. It should also be noted that while this study focuses on electric field emission behavior, additional evaluation would be necessary in safety-critical environments, especially for users with implantable medical devices. Interference with such devices may occur at field levels below general ICNIRP thresholds, particularly in the low-frequency range around 85 kHz. Although not directly evaluated here, this is an important consideration for real-world deployment. Notably, the AVPC configuration (capacitors at turns 1, 5, 10, and 15) consistently maintained E-field levels below 220 V/m at all measurement points, reducing the potential for EMI with implantable medical devices even under close-range, unshielded conditions. While our work does not simulate specific implantable device models, these findings provide valuable preliminary guidance for emission-aware design, particularly in ensuring spatial E-field suppression near the coil surface.
5.2. Error Analysis and E-Field Contribution by Coil Type
To complement Figure 13, it is important to emphasize that accurate E-field measurements in a laboratory environment are inherently subject to variations due to uncontrollable environmental factors. These include surrounding conductive materials, ambient EMI sources, and slight probe positioning discrepancies. In our setup, the NF-5035 probe was mounted on a non-conductive arm to eliminate hand/body interference, and the sensor height was referenced to the approximate center of the internal E-field sensing element, located just beneath the front screen of the probe body (not the outer casing), to improve spatial accuracy. As a result, pointwise agreement between experimental and simulated E-field values may not be exact. Although a separate calibration in a uniform reference field was not performed, the use of consistent positioning and repeatable environmental conditions across all coil configurations supports the relative accuracy of the data.
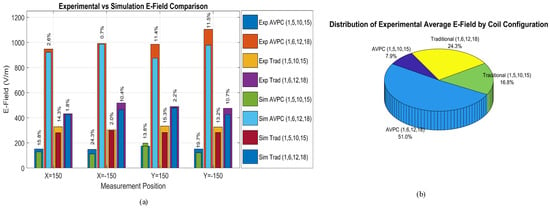
Figure 13.
Experimental Analysis of E-Field Performance. (a) Percent error between FEM simulation and experimental E-field values for each coil configuration. (b) Distribution of average experimental E-field contribution by coil type and capacitor placement.
Despite these limitations, the overall emission profile remains a reliable performance indicator. Across all tested positions, the SIW coil with capacitor segmentation at (1, 5, 10, and 15) consistently exhibited in Figure 13a, the lowest E-field magnitudes in both simulation and experimental domains. This trend reaffirms the coil’s superior electromagnetic behavior, demonstrating not only effective E-field suppression but also robustness to real-world disturbances. By comparison, traditional coils and improper compensation schemes showed higher emission levels and greater susceptibility to measurement variability.
Figure 13b presents the distribution of average experimental E-field contributions by configuration. The SIW (1,5,10,15) configuration accounted for only 7.9% of the total E-field exposure, confirming its superior suppression capability. Conversely, the SIW (1,6,12,18) case contributed over half (51%) of the total E-field, reinforcing the critical importance of phase-aligned capacitor placement and correlating with disrupted cancellation in FEM results (Figure 8c,d). These results collectively validate the SIW coil’s effectiveness in suppressing radiated emissions through phase-coherent compensation, establishing capacitor placement as a primary design constraint in phase-inverted topologies, a fundamental shift from its role as a secondary tuning parameter in traditional coils. These findings also reinforce the importance of localized peak suppression in near-field IPT systems, where steep spatial gradients can lead to concentrated emission zones.
As shown in Section 5.1, the electric field magnitude can vary by nearly an order of magnitude across a small area, highlighting the practical significance of topology-based mitigation. While this study was conducted at a fixed power level (5 A input current), the general relationship E ∝ √P, well established in resonant WPT systems [], suggests that electric field magnitudes will scale with increasing power. This implies that the spatial emission patterns observed here may intensify under higher-power operation unless actively mitigated through coil design and phase-controlled compensation.
6. Limitations of the Study
Although comprehensive FEM simulations and experimental validations were conducted, certain limitations should be considered. FEM models inherently involve simplified assumptions, including idealized material properties, boundary conditions, and meshing approximations, potentially leading to minor deviations from practical coil performance. Experimental validation, while rigorous, was performed in normal laboratory conditions, where slight inaccuracies in probe positioning and the presence of ambient electromagnetic interference or reflections could introduce measurement variability.
Additionally, actual operational environments for wireless EV charging might significantly differ from the experimental setup due to varying ambient temperatures, humidity, and infrastructure interactions. Coil manufacturing tolerances, specifically slight deviations in winding precision and capacitor placements, may also affect the phase alignment and thus compromise the optimal performance of the Sequential Inversion Winding coil configuration. Further practical studies, incorporating broader environmental and operational conditions, are recommended to comprehensively address these limitations.
7. Conclusions
This study presented a rigorous analysis of electric field emissions in inductive power transfer systems, comparing traditional coil configurations with Alternating Voltage Phase Coil designs using Sequential Inversion Winding. Through comprehensive FEM simulations and experimental validation, the research demonstrated that while distributed capacitor segmentation moderately reduces E-field emissions in traditional coils, capacitor placement exhibits minimal influence due to inherently in-phase voltages. Conversely, the AVPC configuration, with strategically aligned capacitors creating a deliberate 180-degree phase shift, achieved substantial E-field mitigation through destructive interference, validated consistently by experimental results and FEM predictions. The study further highlighted the sensitivity of AVPC coils to capacitor placement, noting that improper alignment can significantly increase E-field emissions due to disrupted phase cancellation. These findings emphasize the necessity of precise capacitor placement in AVPC coil designs to meet electromagnetic compatibility standards, thereby advancing practical solutions for safe and efficient high-power wireless EV charging. Future research will focus on extensive in-field validations under diverse operational and environmental conditions, ensuring broader practical feasibility and fostering industry-wide adoption.
Author Contributions
The authors confirm contribution to the article as follows: conceptualization, resources, funding acquisition, writing—original draft preparation, writing—review and editing: Z.S. and J.X.; methodology and data curation: Z.S.; software: Z.S. and T.L.; validation: Z.L. (Zhe Li); formal analysis: Z.L. (Zhe Liu) and S.L. (Sizhao Lu); investigation and project administration: Z.L. (Zhe Li); supervision: S.L. (Siqi Li). All authors have read and agreed to the final version of the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grant 52467023 and in part by Yunnan Fundamental Research Project under Grant 202301AT070429 and 202501CF070119, and in part by the Major Science and Technology Projects in Yunnan Province under Grant 202402AF080001.
Data Availability Statement
All data included in this study are available upon request by contacting the corresponding author.
Conflicts of Interest
The authors declare that they have no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| WPT | Wireless Power Transfer |
| SIW | Sequential Inversion Winding Coil |
| AVPC | Alternating Voltage Phase Coil |
| E-Field | Electric Field |
| EMI | Electromagnetic Interference |
| EV | Electric Vehicle |
| IPT | Inductive Wireless Power Transfer |
| EMC | Electromagnetic Compatibility |
Appendix A
Figure A1 presents a heatmap visualization of the mutual coupling coefficients between all pairs of turns in the 22-turn coil system. This symmetric matrix (Kij = Kji) quantitatively represents electromagnetic coupling strength, where diagonal elements (yellow) denote self-coupling (K = 1) and off-diagonal elements display inter-turn coupling. The color gradient transitioning from blue (weak coupling, K ≈ 0) to yellow (strong coupling, K ≈ 1) reveals a clear physical pattern: coupling strength decays monotonically with increasing separation between turns. Adjacent turns exhibit the strongest coupling (e.g., K1,2 = 0.65, K2,3 = 0.69), while distant turns show minimal interaction (e.g., K1,22 = 0.06, K1,22 = 0.06). These coefficients, calculated as
where Mij is mutual inductance and Li and Lj are self-inductances, provide essential data for electromagnetic modeling. The visualization enables rapid identification of dominant energy-transfer pathways, validates coil symmetry, and confirms the expected inverse relationship between coupling strength and turn separation distance critical for resonance tuning and efficiency optimization in wireless power transfer systems.
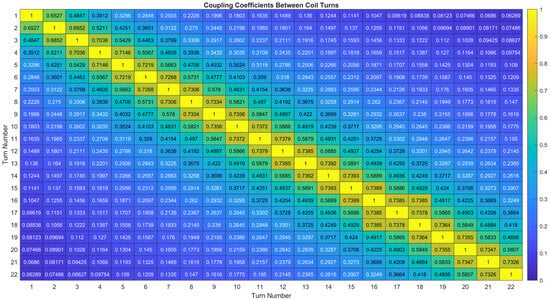
Figure A1.
Coupling coefficient matrix for the 22-turn coil system.
References
- Li, S.; Li, W.; Deng, J.; Nguyen, T.D.; Mi, C.C. A Double-Sided LCC Compensation Network and Its Tuning Method for Wireless Power Transfer. IEEE Trans. Veh. Technol. 2015, 64, 2261–2273. [Google Scholar] [CrossRef]
- Simonazzi, M.; Sandrolini, L. Conducted Emission Analysis of a Near-Field Wireless Power Transfer System. In Proceedings of the 2021 IEEE 15th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Florence, Italy, 14 July 2021; pp. 1–6. [Google Scholar]
- Triviño-Cabrera, A.; Aguado, J.A. (Eds.) Emerging Capabilities and Applications of Wireless Power Transfer; Advances in Wireless Technologies and Telecommunication; IGI Global: Hershey, PA, USA, 2019; ISBN 978-1-5225-5870-5. [Google Scholar]
- Elymany, M.M.; Mohamed, A.A.S.; Shaier, A.A.; Enany, M.A.; Metwally, H.; Selem, S.I. Safety Assessment of Electromagnetic Fields of Different Transmitters and Receivers for EVs Static Charging. Sci. Rep. 2025, 15, 15193. [Google Scholar] [CrossRef] [PubMed]
- TÜV SÜD Canada Inc. EMC/EMI Test Report for Vega 3000G & Vega 3050G Multimedia Class A Equipment* *(Report No. TUV-C3224-7169002108R1); TÜV SÜD Canada Inc.: Gormley, ON, Canada, 2017. [Google Scholar]
- Compatibilità Elettromagnetica (CEM). Parte 6-4, Norme Generiche-Emissione per Gli Ambienti Industriali = Electromagnetic Compatibility (EMC). Part 6-4, Generic Standards--Emission Standard for Industrial Environments; Norma Italiana CEI: Milano, Italy, 2019; ISBN 978-2-8322-5371-7. [Google Scholar]
- ISO 14708-1–5; Implants for Surgery—Active Implantable Medical Devices. ISO: Geneva, Switzerland, 2008–2020.
- Association for the Advancement of Medical Instrumentation. Active Implantable Medical Devices: Electromagnetic Compatibility—EMC Test Protocols for Implantable Cardiac Pacemakers and Implantable Cardioverter Defibrillators; Association for the Advancement of Medical Instrumentation: Arlington, VA, USA, 2000; ISBN 978-1-57020-151-6. [Google Scholar]
- International Commission on Non-Ionizing Radiation Protection (ICNIRP). Guidelines for limiting exposure to time-varying electric and magnetic fields (1 Hz to 100 kHz). Health Physics 2010, 99, 818–836. [Google Scholar] [CrossRef] [PubMed]
- C95.1-2019; IEEE Standard for Safety Levels with Respect to Human Exposure to Electric, Magnetic, and Electromagnetic Fields, 0 Hz to 300 GHz. IEEE: Piscataway, NJ, USA, 2019. [CrossRef]
- Shafiq, Z.; Xia, J.; Min, Q.; Li, S.; Lu, S. Study of the Induced Electric Field Effect on Inductive Power Transfer System. In Proceedings of the 2021 IEEE PELS Workshop on Emerging Technologies: Wireless Power Transfer (WoW), San Diego, CA, USA, 1–4 June 2021; 2021; pp. 1–5. [Google Scholar]
- Li, T.; Li, S.; Liu, Z.; Lu, S.; Qiao, Y.; Xia, J.; Li, Z. Design and Optimization of a Perfectly Symmetric Planar Spiral Receiving Coil with Low E-Field Exposure for Large-Space WPT. IEEE J. Emerg. Sel. Topics Power Electron. 2024. [Google Scholar] [CrossRef]
- Wang, Q.; Saket, M.A.; Troy, A.; Ordonez, M. A Self-Compensated Planar Coil for Resonant Wireless Power Transfer Systems. IEEE Trans. Power Electron. 2021, 36, 674–682. [Google Scholar] [CrossRef]
- Narusue, Y.; Kawahara, Y. Distributed Reactance Compensation for Printed Spiral Coils in Wireless Power Transfer. In Proceedings of the 2017 IEEE Wireless Power Transfer Conference (WPTC), Taipei, Taiwan, 10–12 May 2017; pp. 1–4. [Google Scholar]
- Wang, S.; Lee, C. Generalized Cancellation of Inductor Winding Capacitance Inventors. US7548137B2, 16 September 2017. [Google Scholar]
- Thompson, D.; Romankiw, L.; Krongelb, S. Integrated Multi-Turn Thin Film Recording Head. IEEE Trans. Magn. 1979, 15, 1640. [Google Scholar] [CrossRef]
- Shafiq, Z.; Li, T.; Xia, J.; Li, S.; Yang, X.; Zhao, Y. Addressing EMI and EMF Challenges in EV Wireless Charging with the Alternating Voltage Phase Coil. Actuators 2024, 13, 324. [Google Scholar] [CrossRef]
- Li, T.; Li, S.; Liu, Z.; Fang, Y.; Xiao, Z.; Shafiq, Z.; Lu, S. Enhancing V2G Applications: Analysis and Optimization of a CC/CV Bidirectional IPT System With Wide Range ZVS. IEEE Trans. Transp. Electrif. 2024, 10, 10182–10196. [Google Scholar] [CrossRef]
- Li, T.; Yuan, Y.; Xiao, Z.; Fang, Y.; Yu, X.; Li, S. Large Space Wireless Power Transfer System That Meets Human Electromagnetic Safety Limits. In Proceedings of the 2023 IEEE Wireless Power Technology Conference and Expo (WPTCE), San Diego, CA, USA, 4–8 June 2023; pp. 1–6. [Google Scholar]
- Sagar, A.; Kashyap, A.; Nasab, M.A.; Padmanaban, S.; Bertoluzzo, M.; Kumar, A.; Blaabjerg, F. A Comprehensive Review of the Recent Development of Wireless Power Transfer Technologies for Electric Vehicle Charging Systems. IEEE Access 2023, 11, 83703–83751. [Google Scholar] [CrossRef]
- Onreabroy, W.; Piemsomboon, S.; Traikunwaranon, S.; Wilaiprajuabsang, N.; Kaewpradap, A. Enhancing Wireless Power Transfer Efficiency Through Innovative Metamaterial Configurations for Electric Vehicles. WEVJ 2025, 16, 48. [Google Scholar] [CrossRef]
- National Academy of Engineering. Frontiers of Engineering: Reports on Leading-Edge Engineering from the 2017 Symposium; National Academies Press: Washington, DC, USA, 2018; p. 24906. ISBN 978-0-309-46601-1. [Google Scholar]
- Baikova, E.N.; Melicio, R.; Valtchev, S.S. Study of Electric Field Emissions in Wireless Energy Transfer. In IFIP Advances in Information and Communication Technology, Proceedings of the 11th IFIP WG 5.5/SOCOLNET Advanced Doctoral Conference on Computing, Electrical and Industrial Systems, DoCEIS 2020, Costa de Caparica, Portugal, 1–3 July 2020; Springer International Publishing: Cham, Switzerland, 2020; pp. 233–245. ISBN 978-3-030-45123-3. [Google Scholar]
- Christ, A.; Douglas, M.; Nadakuduti, J.; Kuster, N. Assessing Human Exposure to Electromagnetic Fields From Wireless Power Transmission Systems. Proc. IEEE 2013, 101, 1482–1493. [Google Scholar] [CrossRef]
- TDK Corporation. Ferrite—MnZn Material Characteristics. EPCOS AG, TDK Electronics AG. 2021. Available online: Https://Product.Tdk.Com (accessed on 29 June 2025).
- Cirimele, V.; Freschi, F.; Giaccone, L.; Pichon, L.; Repetto, M. Human Exposure Assessment in Dynamic Inductive Power Transfer for Automotive Applications. IEEE Trans. Magn. 2017, 53, 5000304. [Google Scholar] [CrossRef]
- Zhao, J.; Wu, Z.-J.; Li, N.-L.; Yang, T. Study on Safe Distance between Human Body and Wireless Charging System of Electric Vehicles with Different Power and Frequencies. Electr. Eng. 2020, 102, 2281–2293. [Google Scholar] [CrossRef]
- Ding, P.-P.; Bernard, L.; Pichon, L.; Razek, A. Evaluation of Electromagnetic Fields in Human Body Exposed to Wireless Inductive Charging System. IEEE Trans. Magn. 2014, 50, 1037–1040. [Google Scholar] [CrossRef]
- Park, S. Evaluation of Electromagnetic Exposure During 85 kHz Wireless Power Transfer for Electric Vehicles. IEEE Trans. Magn. 2018, 54, 5100208. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).