Observer-Based Adaptive Cruise Control with Input Saturation and Disturbance Attenuation: An LMI Approach

Abstract

This paper addresses the observer-based controller design for adaptive cruise control (ACC) systems using a linear matrix inequality (LMI) framework, considering both input saturation and disturbance attenuation performance. To formulate the controller design problem as LMIs, the nonlinear input saturation is represented as a convex combination of linear state feedback controllers. Unlike conventional approaches that only reformulate input saturation, this work further incorporates the estimated state and the decay rate of a Lyapunov function to establish an invariant level set condition, leading to a novel LMI-based design criterion. The proposed method incorporates level set conditions to handle input constraints and employs an ${\mathcal{H}}_{\infty }$ criterion to ensure disturbance attenuation. Since the resulting design conditions are non-convex due to bilinear matrix terms, a two-step approach is applied to derive the controller design conditions in the form of LMIs. Finally, simulation results are presented to demonstrate the effectiveness of the proposed method.

1. Introduction

Extensive research on autonomous driving technologies has accelerated the commercialization of advanced driver assistance systems (ADASs) aimed at enhancing vehicle safety and driving convenience [1,2,3]. An ADAS includes technologies ranging from passive features like emergency braking and driver monitoring to active functions such as adaptive cruise control (ACC) and lane keeping. Among them, ACC is considered a key component toward full self-driving and has been widely studied over the past decades [1,2,3,4,5,6]. Early ACC systems relied on full-state feedback using direct measurements of distance, relative velocity, and acceleration [4,7]. However, the high cost and noise sensitivity of required sensors remain major barriers to practical deployment.

Accordingly, observer-based control structures have become essential in ACC systems, where only a subset of measurable state variables is available for feedback control [8]. It is well known that the observer and controller can be designed simultaneously owing to the separation principle. Therefore, numerous studies have proposed LMI-based observer-controller design methods derived from Lyapunov stability criteria [9,10,11,12,13,14,15,16]. Along this line, ref. [10] proposed two independent event-triggered control strategies for the sensor-to-observer and controller-to-actuator channels, respectively, to address the input-to-state stabilization problem to external disturbances. Very recently, continuous-time observer designs have been extended to sampled-data systems composed of digital sensors. For example, ref. [13] proposed a sampled-data observer design for systems with nonlinear output functions, which was further extended in [14] to guarantee the same state estimation performance as previously designed continuous-time observer.

While observer-based control has been widely studied, few works address both input constraints and disturbance attenuation [9,17,18], which are critical for real-world applications. Incorporating actuator limits often leads to bilinear matrix inequality (BMI) conditions, making controller synthesis challenging. Although a two-step iterative linear matrix (ILMI)-based method was proposed in [19] to handle input constraints, the joint treatment of input saturation and disturbance attenuation remains unexplored.

As previously mentioned, it is widely recognized that actuator limitations must be explicitly considered during controller design [20,21,22,23]. To ensure reliable control performance in real vehicles, actuator limitations such as maximum output must be explicitly considered. Generally, two main approaches have been proposed to address such limitations: one directly restricts the norm of the control input [19,24], while the other allows the saturation on the input [21,23,25,26,27,28]. The norm-constrained approach has advantages in terms of design simplicity, but it tends to result in conservative conditions. In contrast, explicitly accounting for input saturation reflects the physical actuator limits more accurately and thus, results in less conservative controller designs. Owing to these benefits, input saturation-based control design has attracted significant attention in recent years [25]. Among various approaches, the authors in [26,27,28] represented the actuator saturation as a convex combination of state feedback controllers, which enables linear matrix inequality (LMI)-based controller design. However, when input saturation is incorporated into an observer-based control structure, the design conditions are typically formulated as BMIs, which cannot be efficiently solved using standard LMI solvers.

In addition to input constraints, maintaining passenger comfort under external disturbances is important. Especially, in the ACC system, acceleration or deceleration of the lead vehicle act as external disturbance. To address disturbance attenuation, $H_{\infty }$ control theory is commonly employed, and extensive research has been conducted on LMI-based $H_{\infty }$ controller design [29,30,31]. However, most existing works did not explicitly account for input saturation in the performance objectives. As a result, few studies simultaneously consider both the disturbance attenuation requirement and actuator saturation constraints, which are essential in practical vehicle control.

Inspired by the analysis above, this paper presents an LMI approach to the design of an observer-based controller for ACC systems under input saturation and external disturbances. The main contributions of this paper are as follows:

• LMI-based observer-based controller design conditions are proposed for ACC systems under input saturation.
• A level set condition is derived to ensure input constraint in the presence of external disturbances and state estimation errors.
• To incorporate input saturation into the LMI formulation, the saturated control input is represented as a convex combination of multiple linear state-feedback controllers outputs.

Notations: For a matrix M, $\mathrm{sym}\left\{M\right\}=M+M^T$. For a vector x, $\parallel x\parallel$ denotes the standard Euclidean norm. ${\mathcal{I}}_x$ with an integer x denotes the integer set $\{1,2,\dots ,x\}$. $\mathrm{col}\{·\}$ denotes a column vector, i.e., $\mathrm{col}\{x_1,\dots ,x_n\}={[x_1^T\cdots x_n^T]}^T$. $\mathrm{diag}\{·\}$ denotes a block diagonal matrix.

2. Problem Formulation

2.1. ACC System Configuration

In this subsection, the structure of the ACC system, composed of a leader and an ego vehicle, is described. It is well known that the longitudinal dynamics of each vehicle is represented by the following linear model [32]:

$$\begin{array}{cc}\hfill {\dot{p}}_i\left(t\right)& =v_i\left(t\right)\hfill \\ \hfill {\dot{v}}_i\left(t\right)& =a_i\left(t\right)\hfill \\ \hfill {\dot{a}}_i\left(t\right)& =-{\displaystyle \frac{1}{{\tau }_i}}{a}_i\left(t\right)+{\displaystyle \frac{1}{{\tau }_i}}{u}_i\left(t\right),\hfill \end{array}$$

(1)

where $p_i\left(t\right)$, $v_i\left(t\right)$, and $a_i\left(t\right)$ are the position $\left[\mathrm{m}\right]$, velocity $[\mathrm{m}/\mathrm{s}]$, and acceleration $[\mathrm{m}/{\mathrm{s}}^2]$ of the ith vehicle, respectively; ${\tau }_i$ denotes the time constant that characterizes the acceleration response of the ith vehicle; $u_i\left(t\right)$ is the control input $[\mathrm{m}/{\mathrm{s}}^2]$, which is the desired acceleration of the ego vehicle that is physically realized through engine or brake forces by a well-designed external controller. Finally, $i=0$ and $i=1$ correspond to the leader and ego vehicles, respectively.

Based on the constant time headway (CTH) policy [33], which accounts for both headway time and standstill distance, the desired inter-vehicle distance, $d_T\left(t\right)$, and the actual distance between the two vehicles, $d\left(t\right)$, are defined as follows:

$$\begin{array}{cc}\hfill d_T\left(t\right)& =d_s+\lambda v_1\left(t\right),\hfill \\ \hfill d\left(t\right)& =p_0\left(t\right)-p_1\left(t\right),\hfill \end{array}$$

(2)

where $d_T\left(t\right)$ is the desired inter-vehicle distance $\left[\mathrm{m}\right]$; $d_s$ is the standstill distance $\left[\mathrm{m}\right]$; and $\lambda$ is the headway time $\left[\mathrm{s}\right]$.

Now, we define the distance tracking error $\overline{d}\left(t\right)$ and the velocity tracking error $\overline{v}\left(t\right)$ as follows:

$$\begin{array}{cc}\hfill \overline{d}\left(t\right)& =d_T\left(t\right)-d\left(t\right),\hfill \\ \hfill \overline{v}\left(t\right)& =v_0\left(t\right)-v_1\left(t\right).\hfill \end{array}$$

(3)

Substituting the vehicle dynamics (1) into the definitions in (2) and (3), we obtain the following dynamics of the ACC system:

$$\begin{array}{cc}\hfill \dot{\overline{d}}\left(t\right)& =\lambda a_1\left(t\right)-\overline{v}\left(t\right),\hfill \\ \hfill \dot{\overline{v}}\left(t\right)& =a_0\left(t\right)-a_1\left(t\right),\hfill \\ \hfill {\dot{a}}_1\left(t\right)& =-{\displaystyle \frac{1}{{\tau }_1}}{a}_1\left(t\right)+{\displaystyle \frac{1}{{\tau }_1}}{u}_1\left(t\right).\hfill \end{array}$$

Before proceeding to next, we introduce the following notations used throughout this paper: $n_x=3$, $n_u=1$, $n_y=1$, and $n_a=1$ denote the dimensions of the state, input, output, and acceleration vectors, respectively; and the state vector is defined as $x\left(t\right)=\mathrm{col}\{\overline{d}\left(t\right),\overline{v}\left(t\right),a_1\left(t\right)\}$.

Then, by summarizing the above, we can derive the following linear state-space model:

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)& =Ax\left(t\right)+B\mu \mathrm{sat}\left\{u\left(t\right)\right\}+D{a}_0\left(t\right)\hfill \\ \hfill y\left(t\right)& =Cx\left(t\right),\hfill \end{array}$$

(4)

where $y\left(t\right)\in {\mathbb{R}}^{n_y}$ is the system output; $u\left(t\right)=u_1\left(t\right)\in {\mathbb{R}}^{n_u}$ is the control input to the ego vehicle; $\mathrm{sat}\left\{u\left(t\right)\right\}=\mathrm{col}\{\mathrm{sat}\left\{u_1\left(t\right)\right\}, \mathrm{sat}\left\{u_2\left(t\right)\right\},\dots ,\mathrm{sat}\left\{u_{n_u}\left(t\right)\right\}\}\in {\mathbb{R}}^{n_u}$ denotes the saturated control input vector, in which each element is computed by $\mathrm{sat}\left\{u_i\left(t\right)\right\}=\mathrm{sign}\left\{u_i\left(t\right)\right\}min\{1,|u_i\left(t\right)\left|\right\}$; $\mu >0$ denotes the saturation level; $a_0\left(t\right)\in {\mathbb{R}}^{n_a}$ is the acceleration of the leader vehicle; and the system matrices are defined as

$$\begin{array}{cc}\hfill A& =\left[\begin{array}{ccc}0& -1& \lambda \\ 0& 0& -1\\ 0& 0& -{\displaystyle \frac{1}{{\tau }_1}}\end{array}\right],B=\left[\begin{array}{c}0\\ 0\\ {\displaystyle \frac{1}{{\tau }_1}}\end{array}\right],\hfill \\ \hfill C& =\left[\begin{array}{ccc}1& 0& 0\end{array}\right],D=\left[\begin{array}{c}0\\ 1\\ 0\end{array}\right].\hfill \end{array}$$

Remark 1.

In this study, the distance tracking error is selected as the system output, since it can be readily obtained using either a radar sensor or an RGB camera. Although the relative velocity is also measurable, we assume that the ACC system considered in this paper relies solely on an RGB camera, which makes it difficult to accurately measure it.

With the system model established above, we now consider an observer dynamics which is given by

$$\begin{array}{cc}\hfill \dot{\widehat{x}}\left(t\right)=& A\widehat{x}\left(t\right)+B\mu \mathrm{sat}\left\{u\left(t\right)\right\}+L\left\{y\left(t\right)-\widehat{y}\left(t\right)\right\}\hfill \\ \hfill \widehat{y}\left(t\right)=& C\widehat{x}\left(t\right),\hfill \end{array}$$

(5)

where $\widehat{x}\left(t\right)\in {\mathbb{R}}^{n_x}$ denotes the estimated state vector; $\widehat{y}\left(t\right)\in {\mathbb{R}}^{n_y}$ is the estimated output; and $L\in {\mathbb{R}}^{n_x\times n_y}$ is the observer gain matrix to be designed.

Then, defining the state estimation error as

$$\begin{array}{c}\hfill e\left(t\right)=x\left(t\right)-\widehat{x}\left(t\right),\end{array}$$

we have the following error dynamics from (4) and (5):

$$\begin{array}{cc}\hfill \dot{e}\left(t\right)=& \dot{x}\left(t\right)-\dot{\widehat{x}}\left(t\right)\hfill \\ \hfill =& Ax\left(t\right)+B\mu \mathrm{sat}\left\{u\left(t\right)\right\}+D{a}_0\left(t\right)\hfill \\ \hfill & -\left\{A\widehat{x}\left(t\right)+B\mu \mathrm{sat}\left\{u\right(t)\}+L\left(y\left(t\right)-\widehat{y}\left(t\right)\right)\right\}\hfill \\ \hfill =& (A-LC)e\left(t\right)+D{a}_0\left(t\right).\hfill \end{array}$$

(6)

Finally, the control input is determined by the following state feedback law:

$$\begin{array}{c}\hfill u\left(t\right)=K\widehat{x}\left(t\right),\end{array}$$

(7)

where $K\in {\mathbb{R}}^{n_u\times n_x}$ is the gain matrix to be designed.

2.2. Preliminaries

First, we define the following level sets:

$$\begin{array}{cc}\hfill ϵ(P,z(t\left)\right)& =\left\{z\left(t\right)\right|z^T\left(t\right)Pz\left(t\right)\le 1\},\hfill \\ \hfill \mathcal{L}(K,\widehat{x}\left(t\right))& =\left\{\widehat{x}\left(t\right)\right|\parallel K\widehat{x}\left(t\right)\parallel \le 1\}.\hfill \end{array}$$

The saturation function introduced in the previous subsection is a nonlinear mapping, which complicates the derivation of stability conditions in the form of LMIs. To address this issue, a convex summation representation of the saturation function has been developed in [27,28]. While previous works have focused on full-state feedback controllers, this paper extends the framework by incorporating the estimated state vector into the feedback loop.

The following lemma provides a convex summation representation of $\mathrm{sat}\left\{u\left(t\right)\right\}=\mathrm{sat}\left\{K\widehat{x}\left(t\right)\right\}$.

Lemma 1

([34]). For a given matrix $K\in {\mathbb{R}}^{n_u\times n_x}$ if $\widehat{x}\left(t\right)\in \mathcal{L}(H,\widehat{x}\left(t\right))$, then there exist a matrix $H\in {\mathbb{R}}^{{\check{n}}_u\times n_x}$ with ${\check{n}}_u=n_u\times 2^{n_u-1}$ and scalar variables ${\eta }_i$ such that the following equation holds:

$$\begin{array}{c}\hfill \mathrm{sat}\left\{K\widehat{x}\left(t\right)\right\}=\sum _{i=1}^{2^{n_u}}{\eta }_i\left\{E_{i}K\widehat{x}\left(t\right)+F_{i}H\widehat{x}\left(t\right)\right\},\end{array}$$

(8)

where ${\sum }_{i=1}^{2^{n_u}}{\eta }_i=1$, $0\le {\eta }_i\le 1$; $E_i\in {\mathbb{R}}^{n_u\times n_u}$ is a diagonal matrix whose diagonal elements are either 0 or 1, and all off-diagonal entries are 0; and $F_i\in {\mathbb{R}}^{n_u\times {\check{n}}_u}$ is defined as

$$\begin{array}{c}\hfill F_i=e_{f\left(i\right)}\otimes F_i^{-},\end{array}$$

with $F_i^{-}=I_{n_u}-E_i$ and $e_{f\left(i\right)}\in {\mathbb{R}}^{1\times 2^{n_u-1}}$ is a row vector whose $f\left(i\right)$-th element is 1 and all other elements are zero. The function $f\left(i\right)$ is defined recursively as

$$\begin{array}{c}\hfill f\left(i\right)=\left\{\begin{array}{cc}f(i-1)+1,\hfill & \mathit{if}{E}_i+E_j\ne I_{n_u},\forall j\in {\mathcal{I}}_i,\hfill \\ f\left(j\right),\hfill & \mathit{if}{E}_i+E_j=I_{n_u},\exists j\in {\mathcal{I}}_i,\hfill \\ f\left(0\right)=0.\hfill \end{array}\right.\end{array}$$

Remark 2.

For the ACC system considered in this paper, the number of control inputs is $n_u=1$. In this case, $2^{n_u}=2$ and ${\check{n}}_u=n_u\times 2^{n_u-1}=1$; therefore, $E_1=\left[1\right]$, $E_2=\left[0\right]$; $F_1=\left[0\right]$, $F_2=\left[1\right]$. In addition, from Lemma 1, the existence of certain scalar variables ${\eta }_i$ is guaranteed, and since $n_u=1$, there are $2^{n_u}=2$ such scalars. However, it is not necessary to explicitly specify the values of ${\eta }_i$. Due to the convex combination property, ${\eta }_i$ is not explicitly considered in the controller design condition. A more detailed analysis can be found in [27,28] and in the following section.

For notational simplicity, we define the following shorthand expressions: $E_{\eta }={\sum }_{i=1}^{2^{n_u}}{\eta }_i{E}_i$ and $F_{\eta }={\sum }_{i=1}^{2^{n_u}}{\eta }_i{F}_i.$ From Lemma 1, the saturation in the controller can be reformulated as shown in (8). Therefore, by substituting (8) into the dynamics (4), the system dynamics becomes

$$\begin{array}{cc}\hfill \dot{x}\left(t\right)=& Ax\left(t\right)+\mu B\left(E_{\eta }K+F_{\eta }H\right)\widehat{x}\left(t\right)+D{a}_0\left(t\right)\hfill \\ \hfill =& \left\{A+\mu B(E_{\eta }K+F_{\eta }H)\right\}x\left(t\right)\hfill \\ \hfill & -\mu B(E_{\eta }K+F_{\eta }H)e\left(t\right)+D{a}_0\left(t\right).\hfill \end{array}$$

(9)

By defining the augmented state vector as $z\left(t\right)=\mathrm{col}\left\{x\right(t),e(t\left)\right\}$, and using the error dynamics in (6) together with (9), the augmented system dynamics can be expressed as the following state space equation:

$$\begin{array}{c}\hfill \dot{z}\left(t\right)=A_{z}z\left(t\right)+D_z{a}_0\left(t\right),\end{array}$$

(10)

where

$$\begin{array}{cc}\hfill A_z& =\left[\begin{array}{cc}A+\mu B(E_{\eta }K+F_{\eta }H)& -\mu B(E_{\eta }K+F_{\eta }H)\\ \mathbf{0}& A-LC\end{array}\right];\hfill \\ \hfill D_z& =\left[\begin{array}{c}D\\ D\end{array}\right].\hfill \end{array}$$

Finally, we define the following main control objective, which is to stabilize the ACC system under input saturation using an observer-based state feedback controller.

Problem 1.

Find gain matrices $K\in {\mathbb{R}}^{n_u\times n_x}$, $H\in {\mathbb{R}}^{{\check{n}}_u\times n_x}$, and $L\in {\mathbb{R}}^{n_x\times n_y}$ such that the following conditions are satisfied:

1. 

When $a_0\left(t\right)=0$, the equilibrium of the augmented system (10) is asymptotically stable.

2. 

If $\parallel a_0{\left(t\right)\parallel }^2\le a_{max}^2$ for all $t\ge 0$, then $ϵ(P,z\left(t\right))\subset \mathcal{L}(H,\widehat{x}\left(t\right))$.

3. 

For $z\left(0\right)=0$ and $a_0\left(t\right)\ne 0$, the following disturbance attenuation performance is satisfied:

$$\begin{array}{c}\hfill {\int }_0^{\infty }{e}^{2\alpha t}{z}^T\left(t\right)Qz\left(t\right)dt\le {\gamma }^2{\int }_0^{\infty }{e}^{2\alpha t}{a}_0^T\left(t\right)a_0\left(t\right)dt,\end{array}$$

where $\alpha >0$ is a prescribed scalar; $Q\in {\mathbb{R}}^{2n_x\times 2n_x}\succ 0$ is a diagonal matrix that specifies the relative importance of the state components; and $\gamma >0$ is a prescribed scalar denoting disturbance attenuation level.

3. Main Results

3.1. Observer-Based Control Under Input Saturation

In this subsection, we derive a matrix inequality condition for the augmented system (10) that guarantees the controller design objectives presented in Problem 1. The following theorem provides a sufficient condition for solving the controller synthesis problem stated in Problem 1.

Theorem 1.

For given scalars $\mu >0$, $\gamma >0$, $\alpha \ge {\gamma }^2{a}_{\max }^2/2$, and $a_{\max }>0$, and an initial condition $z\left(0\right)$, the augmented system (10) satisfies the design criteria described in Problem 1 if there exist a positive definite matrix $P\in {\mathbb{R}}^{2n_x\times 2n_x}$, a symmetric matrix $X\in {\mathbb{R}}^{{\check{n}}_u\times {\check{n}}_u}$, and matrices $K\in {\mathbb{R}}^{n_u\times n_x}$, $H\in {\mathbb{R}}^{{\check{n}}_u\times n_x}$, and $L\in {\mathbb{R}}^{n_x\times n_y}$ such that the following matrix inequalities hold for $i\in {\mathcal{I}}_{2^{n_u}}$:

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\psi }_{11,i}& \ast & \ast \\ {\psi }_{21,i}& {\psi }_{22,i}& \ast \\ D^T{P}_1+D^T{P}_2& D^T{P}_2+D^T{P}_3& -{\gamma }^2{I}_{n_a}\end{array}\right]& \prec 0,\hfill \end{array}$$

(11)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}P& \ast \\ z^T\left(0\right)P& 1\end{array}\right]& ⪰0,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{P}_1& \ast & \ast \\ P_2& P_3& \ast \\ H& -H& X\end{array}\right]& ⪰0,\hfill \end{array}$$

(13)

$$\begin{array}{cc}\hfill X& ⪯I_{{\check{n}}_u},\hfill \end{array}$$

(14)

where $P_1\in {\mathbb{R}}^{n_x\times n_x}$ and $P_3\in {\mathbb{R}}^{n_x\times n_x}$ are symmetric matrices; $P_2\in {\mathbb{R}}^{n_x\times n_x}$ is a matrix;

$$\begin{array}{cc}\hfill P& =\left[\begin{array}{cc}{P}_1& \ast \\ P_2& P_3\end{array}\right];\hfill \\ \hfill {\psi }_{11,i}& =\mathrm{sym}\left\{P_1(A+\mu B{G}_i)\right\}+2\alpha P_1+Q_1;\hfill \\ \hfill {\psi }_{21,i}& =P_2(A+\mu B{G}_i)+{(A-LC)}^T{P}_2-\mu {\left(P_{1}B{G}_i\right)}^T;\hfill \\ \hfill {\psi }_{22,i}& =\mathrm{sym}\{P_3(A-LC)-\mu P_{2}B{G}_i\}+2\alpha P_3+Q_2;\hfill \\ \hfill G_i& =E_{i}K+F_{i}H.\hfill \end{array}$$

Proof. 

Please refer to Appendix A.  □

Remark 3.

Theorem 1 provides sufficient conditions for designing an observer-based controller that satisfies all the objectives defined in Problem 1. However, the decision variables appear in bilinear and multiplicative forms within the matrix inequalities. Consequently, the problem is not easy to be solved using standard convex optimization software such as CVX [35] or YALMIP [36]. Motivated by the result in [19], we propose a two-step approach for solving matrix inequalities in Theorem 1 using convex optimization software.

3.2. LMI-Based State Feedback Controller Design

As the first step of the proposed approach, we consider the case where full-state feedback is available. This is equivalent to assuming $e\left(t\right)=x\left(t\right)-\widehat{x}\left(t\right)=0$, i.e., the estimation error has perfectly converged. Under this assumption, the state equation in (9) reduces to:

$$\begin{array}{c}\hfill \dot{x}\left(t\right)=\left\{A+\mu B(E_{\eta }K+F_{\eta }H)\right\}x\left(t\right)+D{a}_0\left(t\right).\end{array}$$

(15)

The design objective of the first step is to achieve the following problem:

Problem 2.

Find matrices $K\in {\mathbb{R}}^{n_u\times n_x}$ and $H\in {\mathbb{R}}^{{\check{n}}_u\times n_x}$ such that the following conditions are satisfied:

1. 

When $a_0\left(t\right)=0$, the equilibrium of the closed-loop system (15) is asymptotically stable.

2. 

If $\parallel a_0{\left(t\right)\parallel }^2\le a_{max}^2$ for all $t\ge 0$, then $ϵ(P,x(t\left)\right)\subset \mathcal{L}(H,x(t\left)\right)$.

3. 

For $x\left(0\right)=0$ and $a_0\left(t\right)\ne 0$, the following disturbance attenuation performance is satisfied:

$$\begin{array}{c}\hfill {\int }_0^{\infty }{e}^{2\alpha t}{x}^T\left(t\right)Q_{1}x\left(t\right)dt\le {\gamma }^2{\int }_0^{\infty }{e}^{2\alpha t}{a}_0^T\left(t\right)a_0\left(t\right)dt.\end{array}$$

The following theorem gives an LMI-based sufficient condition for Problem 2:

Theorem 2.

For given scalars $\mu >0$, $\gamma >0$, $\alpha \ge {\gamma }^2{a}_{max}^2/2$, and $a_{max}>0$, and an initial condition $x\left(0\right)$, the closed-loop system (15) satisfies the design criteria described in Problem 2 if there exist a positive definite matrix ${\overline{P}}_1\in {\mathbb{R}}^{n_x\times n_x}$, a symmetric matrix $X\in {\mathbb{R}}^{{\check{n}}_u\times {\check{n}}_u}$, and matrices $\overline{K}\in {\mathbb{R}}^{n_u\times n_x}$ and $\overline{H}\in {\mathbb{R}}^{{\check{n}}_u\times n_x}$ such that (14) and the following matrix inequalities hold for $i\in {\mathcal{I}}_{2^{n_u}}$:

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\theta }_i& \ast & \ast \\ D^T& -{\gamma }^{2}I& \ast \\ {\overline{P}}_1& \mathbf{0}& -Q_1^{-1}\end{array}\right]& \prec 0,\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\overline{P}}_1& \ast \\ x^T\left(0\right)& 1\end{array}\right]& ⪰0,\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill \left[\begin{array}{cc}{\overline{P}}_1& \ast \\ \overline{H}& X\end{array}\right]& ⪰0,\hfill \end{array}$$

(18)

where ${\theta }_i=\mathrm{sym}\{A{\overline{P}}_1+\mu B(E_i\overline{K}+F_i\overline{H})\}+2\alpha {\overline{P}}_1$. Then, the control gain matrices can be obtained by

$$\begin{array}{c}\hfill K=\overline{K}{\overline{P}}_1^{-1}\mathit{and}H=\overline{H}{\overline{P}}_1^{-1}.\end{array}$$

Proof. 

Please refer to Appendix B.  □

Remark 4.

The LMI conditions in Theorem 2 are the first step of the proposed two-step approach, derived from the BMI formulation in Theorem 1 to compute the controller gain matrices. Consequently, the scalar parameters (γ, μ) and the matrix (Q) defined in Theorem 1 are utilized in Theorem 2 with exactly the same values and physical meanings. Although the gain matrices obtained from Theorem 2 can be substituted into the matrix inequalities in Theorem 1, the resulting condition remains non-convex due to the bilinear terms involving $P_2$ in (11). The introduction of the non-zero off-diagonal block $P_2$ creates coupling terms between the Lyapunov matrix variables and the controller and observer gains (e.g., products such as $P_{2}B{G}_i$ and $P_2^T(A-LC)$). While standard change-of-variable techniques can linearize terms involving diagonal blocks, they cannot simultaneously linearize the cross-terms involving $P_2$ without introducing non-convexity. Consequently, the inequality contains products of two unknown variables, rendering it a BMI, and it prevents the matrix inequality from being expressed as an LMI. To resolve this problem, we assume $P_2=0$ in the subsequent subsection.

3.3. LMI-Based Observer-Based Controller Design

By letting $P_2=0$, we derive the following sufficient LMI condition for solving Problem 1 from Theorem 1:

Corollary 1.

For given scalars $\mu >0$, $\gamma >0$, $\alpha \ge {\gamma }^2{a}_{max}^2/2$, $a_{max}>0$, and $i\in {\mathcal{I}}_{2^{n_u}}$, an initial condition $z\left(0\right)$, and the control gain matrices, K and H, designed from Theorem 2, the augmented system (10) satisfies the design conditions in Problem 1 if there exist symmetric positive definite matrices $P_1,P_3\in {\mathbb{R}}^{n_x\times n_x}$, a symmetric matrix $X\in {\mathbb{R}}^{{\check{n}}_u\times {\check{n}}_u}$, a matrix $\overline{L}\in {\mathbb{R}}^{n_x\times n_y}$ such that the following LMIs hold:

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\varphi }_{11,i}& \ast & \ast \\ {\varphi }_{21,i}& {\varphi }_{22,i}& \ast \\ D^T{P}_1& D^T{P}_3& -{\gamma }^{2}I\end{array}\right]& \prec 0,\hfill \end{array}$$

(19)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{P}_1& \ast & \ast \\ \mathbf{0}& P_3& \ast \\ x^T\left(0\right)P_1& e^T\left(0\right)P_3& 1\end{array}\right]& ⪰0,\hfill \end{array}$$

(20)

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{P}_1& \ast & \ast \\ \mathbf{0}& P_3& \ast \\ H& -H& X\end{array}\right]& ⪰0,\hfill \end{array}$$

(21)

$$\begin{array}{cc}\hfill X& ⪯I_{{\check{n}}_u},\hfill \end{array}$$

(22)

where $P=\mathrm{diag}(P_1,P_3)$, ${\varphi }_{11,i}=\mathrm{sym}\left\{P_1\left(A+\mu B(E_{i}K+F_{i}H)\right)\right\}+2\alpha P_1+Q_1$, ${\varphi }_{21,i}=-\mu {\left(P_{1}B(E_{i}K+F_{i}H)\right)}^T$, ${\varphi }_{22,i}=\mathrm{sym}\{P_{3}A-\overline{L}C\}+2\alpha P_3+Q_2$. The observer gain matrix can be obtained by $L=P_3^{-1}\overline{L}$.

Proof. 

The LMIs (19)–(22) follow directly from Theorem 1 by substituting $P_2=0$ and $\overline{L}=P_{3}L$.  □

Remark 5.

γ determines the ${\mathcal{H}}_{\infty }$ disturbance attenuation level; smaller γ improves performance but makes the LMI more conservative. The parameter α represents the decay rate of the Lyapunov function; larger α ensures faster convergence but also increases conservatism. Moreover, these parameters are coupled by the condition $\alpha \ge {\gamma }^2{a}_{max}^2/2$. When the LMIs in Corollary 1 become infeasible, feasibility can be recovered by enlarging γ, reducing $a_{max}$, recomputing α accordingly, and then resolving the LMIs in Theorem 2 and Corollary 1.

In addition, selecting an excessively large α may lead to unnecessary conservatism in LMI conditions without providing meaningful improvement in control performance. For this reason, in this paper, α is chosen at its lower bound in the simulations so that the required disturbance attenuation is satisfied while maintaining LMI feasible.

Remark 6.

The following LMI conditions can be further considered to explicitly bound the eigenvalues of the system matrices [37]:

$$\begin{array}{cc}\hfill \mathrm{sym}\{A{\overline{P}}_1+\mu B\overline{K}\}+2{\rho }_c{\overline{P}}_1& \succ 0,\hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill \mathrm{sym}\{P_{3}A-\overline{L}C\}+2{\rho }_o{P}_3& \succ 0,\hfill \end{array}$$

(24)

where ${\rho }_c>0$ and ${\rho }_o>0$ are the predefined lower bounds of eigenvalues, i.e., $0>{\lambda }_i>-{\rho }_o,{\rho }_c$ with eigenvalue ${\lambda }_i$.

4. Simulation Examples

This section presents simulation results to validate the effectiveness of the proposed observer-based control design for ACC systems under input saturation.

4.1. Example 1: Validation of Observer-Based ACC Controller

This example verifies the proposed observer-based controller under input saturation and external disturbance. The vehicle parameters are set to $\lambda =3$, $d_s=2$, and ${\tau }_i=0.3$, implying a 2$\mathrm{m}$ gap at standstill and a 3-s spacing during steady-state cruising. The leader vehicle starts at $p_0\left(0\right)=100\mathrm{m}$ with a constant velocity $v_0\left(0\right)=25\mathrm{m}/\mathrm{s}$.

The controller is designed using the two-step procedure proposed in Section 3. First, the gain matrices K and H are computed by solving the LMI conditions in Theorem 2, with additional constraints in (23) to limit eigenvalues. The following design parameters are chosen: $Q_1=0.0001I_3$, $a_{max}=6\mathrm{m}/{\mathrm{s}}^2$, $\gamma =0.08$, $\alpha ={\gamma }^2{a}_{max}^2/2$, $\mu =10\mathrm{m}/{\mathrm{s}}^2$, and ${\rho }_c=100$. The initial states are $x\left(0\right)=\mathrm{col}\{-1,2,2\}$ and $\widehat{x}\left(0\right)=error\left\{0,0,0\right\}$, respectively, resulting in the initial estimation error $e\left(0\right)=x\left(0\right)-\widehat{x}\left(0\right)=x\left(0\right)$. Under these settings, solving the LMIs (16)–(18) and (23) yields:

$$\begin{array}{cc}\hfill K& =\left[\begin{array}{ccc}-0.6074& 0.5443& -1.3590\end{array}\right],\hfill \\ \hfill H& =\left[\begin{array}{ccc}-0.0327& 0.0414& -0.0290\end{array}\right].\hfill \end{array}$$

In the second step, the observer gain L is computed using the LMI conditions in Corollary 1 along with the eigenvalue bounding constraint in (24). The previously used parameters are retained, with additional design settings $Q_2=0.0001I_3$ and ${\rho }_o=100$. Solving the resulting LMIs yields the following observer gain matrix:

$$\begin{array}{cc}\hfill L& ={\left[\begin{array}{ccc}15.4550& -126.9230& 6.4491\end{array}\right]}^T.\hfill \end{array}$$

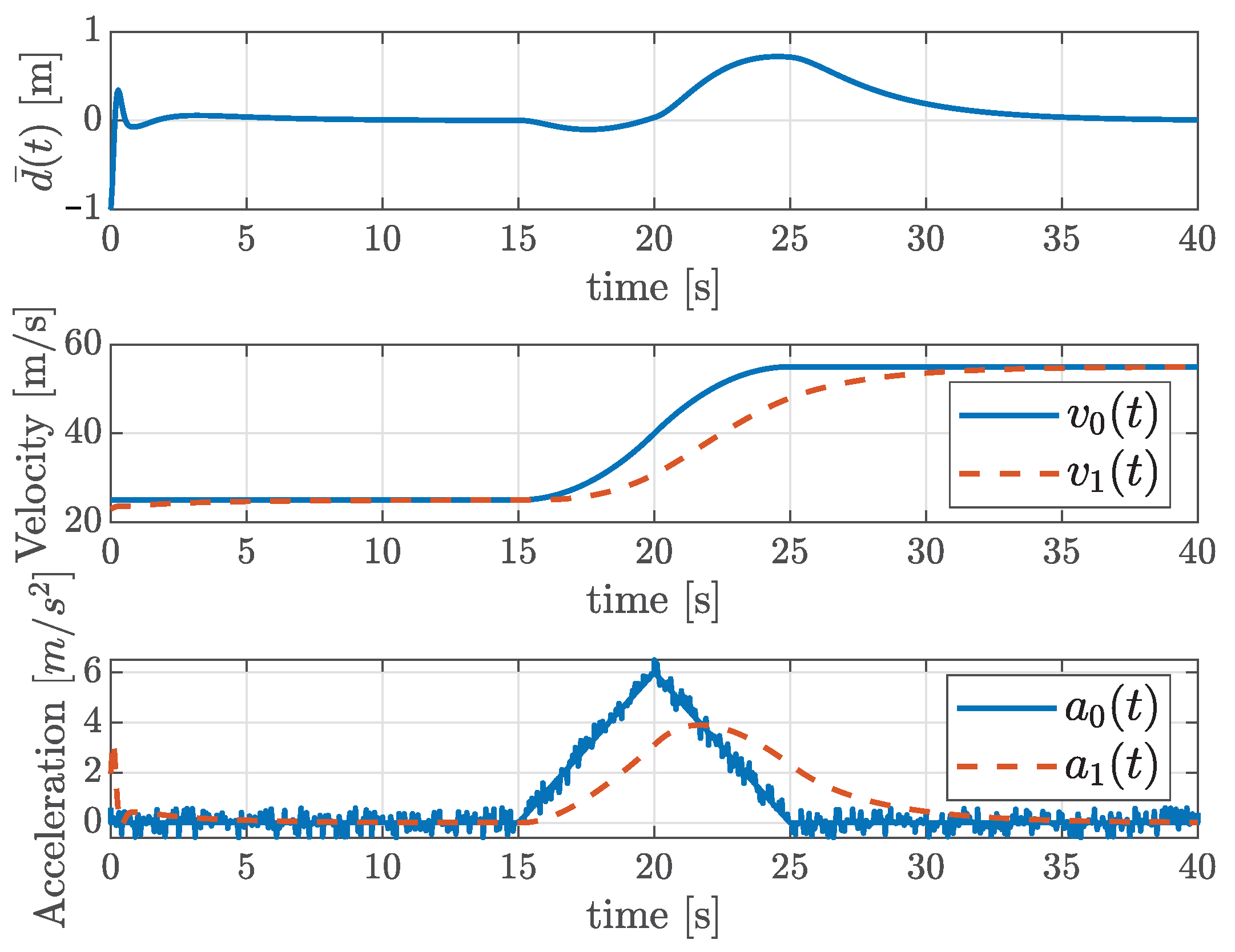
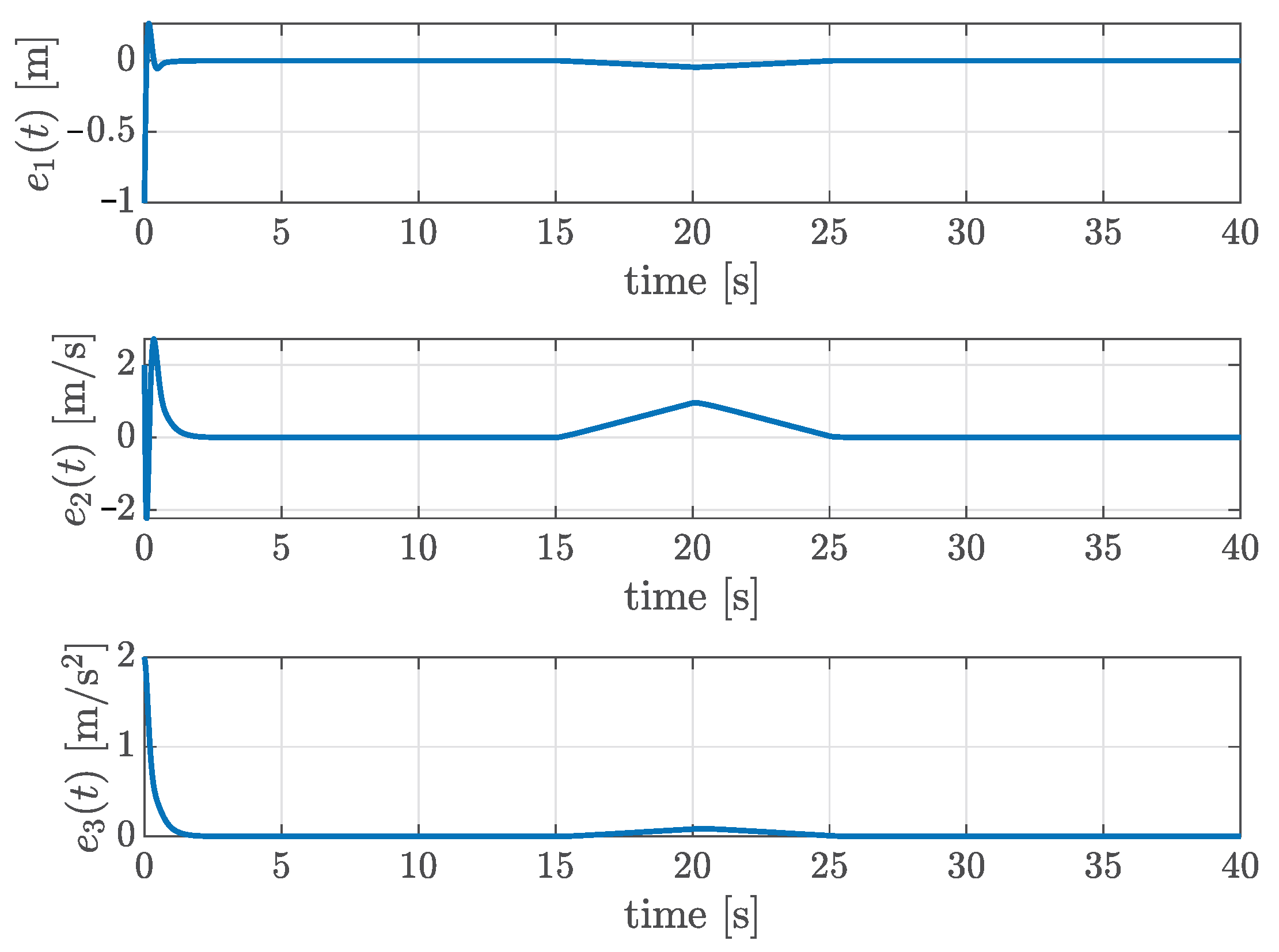
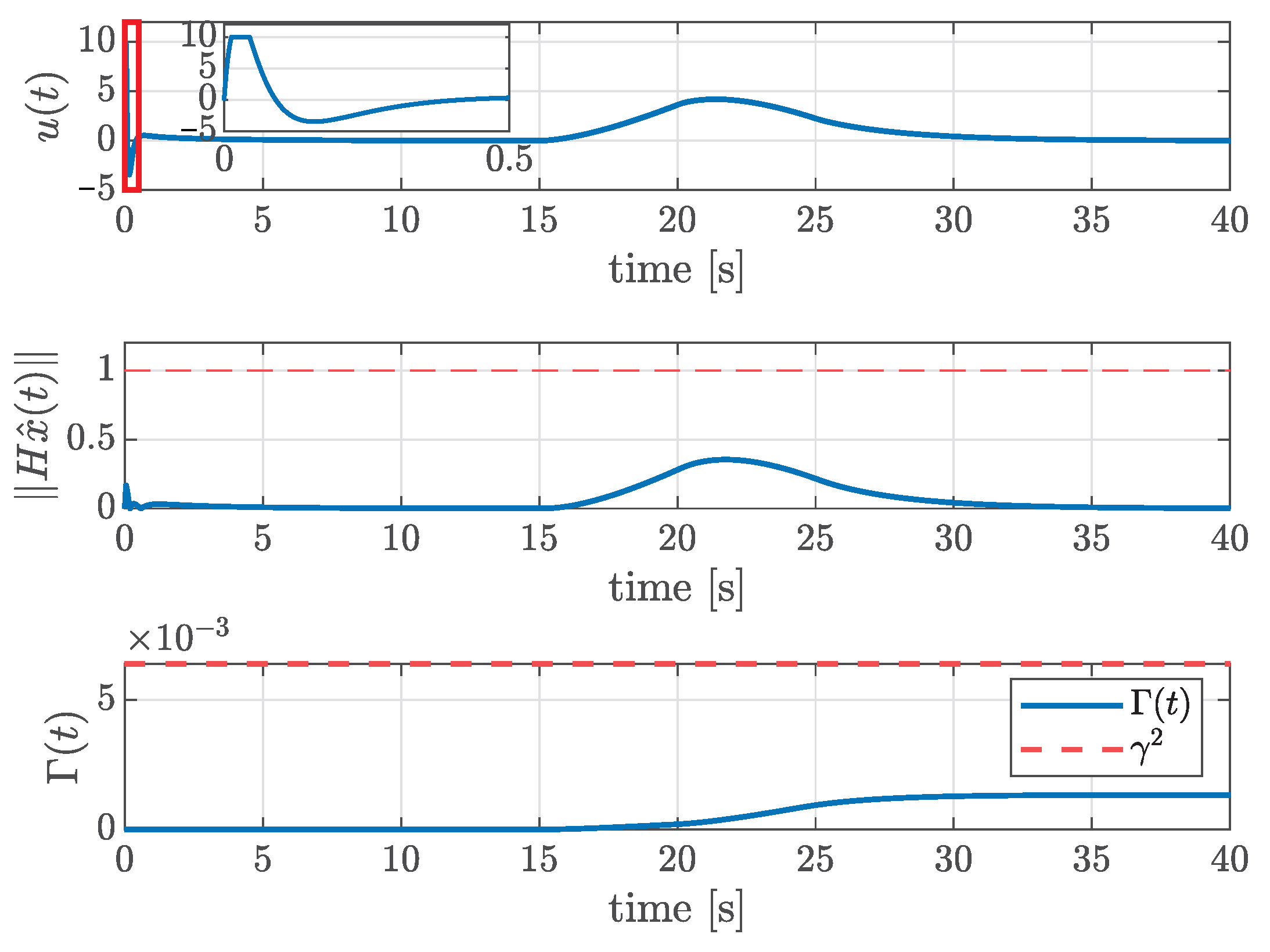
Figure 1 shows the time response of the ACC system. In the simulation, the leader vehicle accelerates as shown in the plot for the time response of the acceleration. To more closely emulate real-world vehicle-operation conditions, a random noise term of $5\times (-1+2\times \mathrm{rand}(\left)\right)$ was added to the acceleration of the lead vehicle. The state estimation errors are presented in Figure 2. From the figures, we can see that all state variables and all estimation errors converge to zero when $a_0\left(t\right)=0$, verifying the first condition in Problem 1. Figure 3 illustrates the control input $\mu \mathrm{sat}\left\{u\right(t\left)\right\}$. The input is initially saturated due to a large distance error, but the proposed method ensures $\parallel H\widehat{x}\left(t\right)\parallel \le 1$. Finally, under the zero initial condition, the disturbance attenuation performance is evaluated using the following performance index: $\Gamma \left(t\right)={\int }_0^t{e}^{2\alpha s}{z}^T\left(s\right)Qz\left(s\right)ds/{\int }_0^t{e}^{2\alpha s}{a}_0^T\left(s\right)a_0\left(s\right)ds$. The maximum value of $\Gamma \left(t\right)$ was measured as $0.0013$, which is lower than the prescribed upper bound ${\gamma }^2=0.{08}^2=0.0064$, verifying that the third design condition in Problem 1 is satisfied.

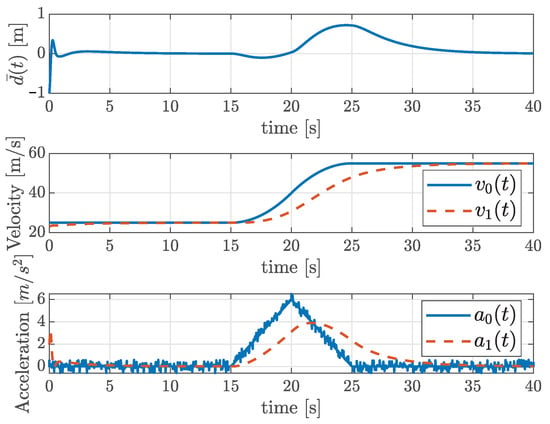
Figure 1. Time responses of the tracking error $\overline{d}\left(t\right)$, velocities of leader and ego vehicles $v_0\left(t\right)$, $v_1\left(t\right)$, and ego vehicle acceleration $a_1\left(t\right)$.

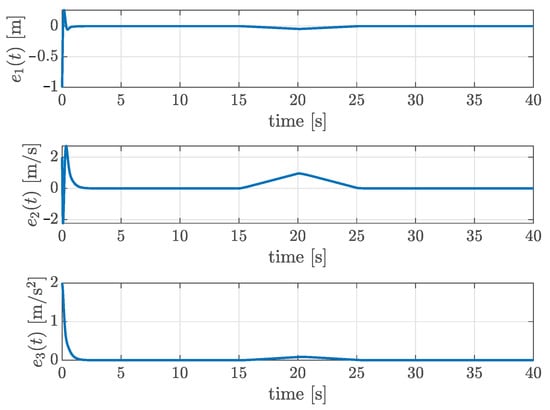
Figure 2. Time responses of the estimation errors $e_i\left(t\right)=x_i\left(t\right)-{\widehat{x}}_i\left(t\right)$.

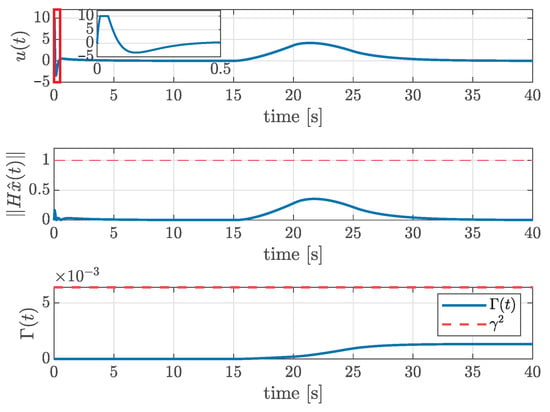
Figure 3. Time responses of $\mathrm{sat}\left\{u\right(t\left)\right\}$, norm $\parallel H\widehat{x}\left(t\right)\parallel$ with its upper bound, and $\Gamma \left(t\right)$.

4.2. Example 2: Comparison of Full-State Feedback Controllers

To validate the effectiveness of the proposed full-state feedback controller design, this example compares its disturbance attenuation performance with two baseline controllers. The first baseline ensures only asymptotic stability without addressing disturbance attenuation, while the second considers the ${\mathcal{H}}_{\infty }$ disturbance attenuation performance. To reflect the physical limitations of the vehicle, both baseline controllers are designed to satisfy the input constraint $\parallel Kx\left(t\right)\parallel \le 1$ instead of input saturation.

As in the previous example, all parameters are the same as in Example 1 except for ${\rho }_c=500$. Then, we obtained the following gain matrices:

$$\begin{array}{cc}\hfill K_{\mathrm{Theorem}2}& =\left[\begin{array}{ccc}-4.4846& 4.0046& -11.6275\end{array}\right],\hfill \\ \hfill H_{\mathrm{Theorem}2}& =\left[\begin{array}{ccc}-0.0357& 0.0427& -0.0294\end{array}\right],\hfill \\ \hfill K_{\mathrm{Asymptotic}}& =\left[\begin{array}{ccc}-0.1224& 0.0781& -0.1536\end{array}\right],\hfill \\ \hfill K_{\mathcal{H}\infty }& =\left[\begin{array}{ccc}-0.0398& 0.0513& -0.0314\end{array}\right].\hfill \end{array}$$

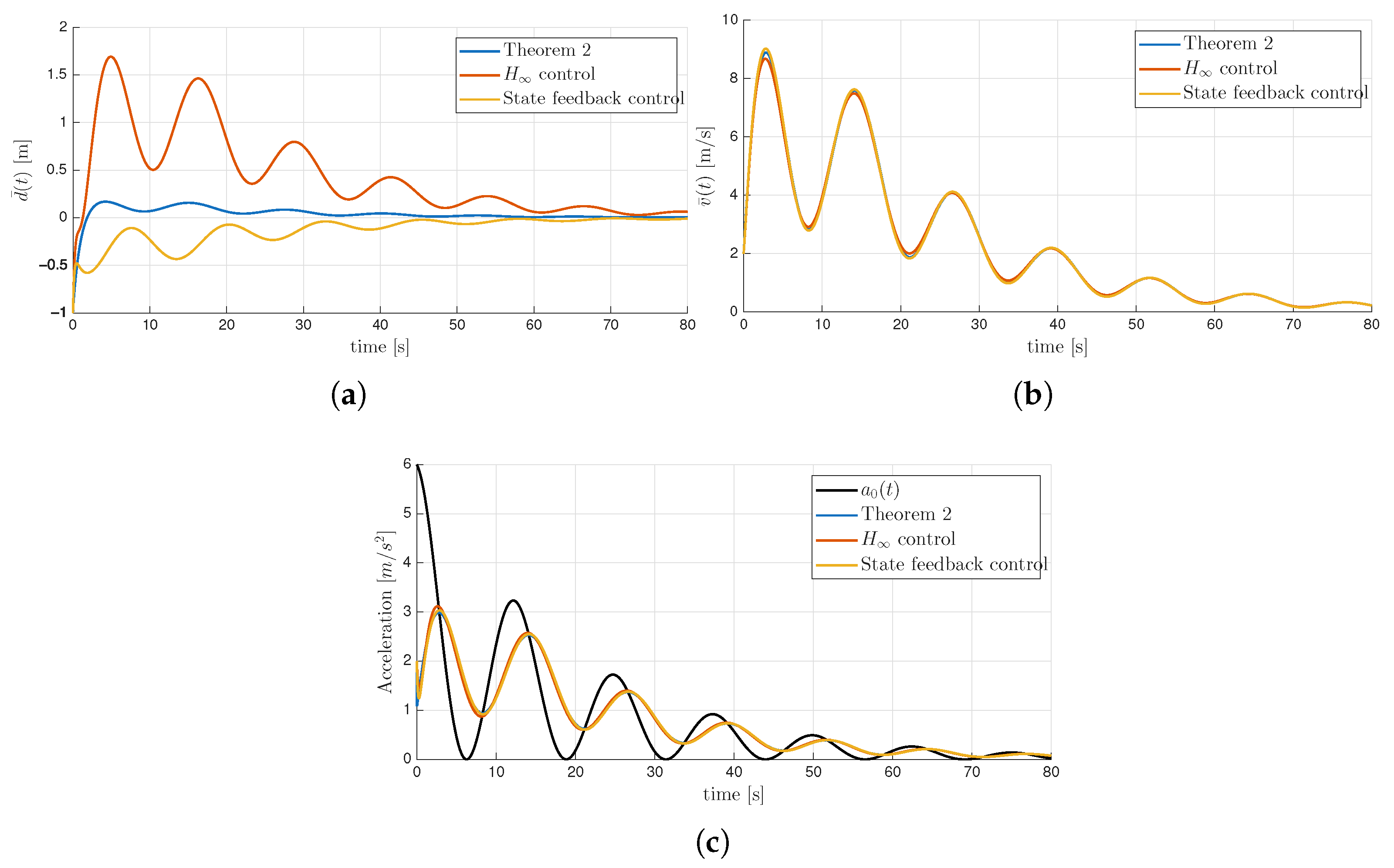
The controller designed from Theorem 2 allows input saturation, resulting in a larger gain K than the baseline controllers. According to the high-gain control principle, we can expect that faster convergence and improved disturbance attenuation performance would be obtained. To compare the disturbance attenuation performance, $a_0\left(t\right)$ was defined as follows: $a_0\left(t\right)=0.5a_{max}\times (1+cos\left(0.5t\right))\times e^{-0.05t}$. Figure 4 illustrates the state responses from each control methods. As can be observed, the proposed method achieves superior disturbance attenuation performance by explicitly allowing input saturation. The baseline controller designed with $H_{\infty }$ conditions shows improved performance compared to the baseline controller that only ensures asymptotic stability; however, due to the absence of saturation consideration, its performance is degraded compared to the proposed method. Finally, the RMS values of position and velocity tracking errors were quantitatively compared and summarized in Table 1.

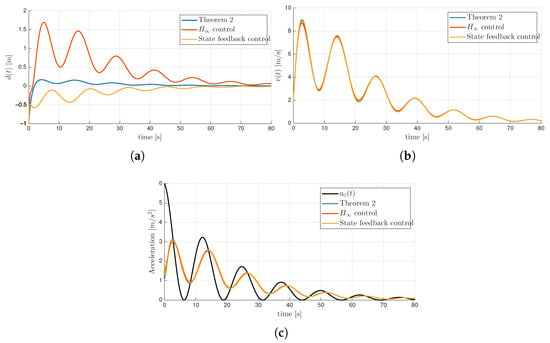
Figure 4. Time responses of (a) the distance tracking error $\overline{d}\left(t\right)$, (b) the velocity tracking error $\overline{v}\left(t\right)$, and (c) the acceleration.

Table 1. RMS value of the distance and velocity tracking errors for each controller.

Controller	$\overline{\mathit{d}}$ [m]	$\overline{\mathit{v}}$ [m/s]
Theorem 2	0.1012	3.2491
Conventional $H_{\infty }$ control	0.6086	3.3561
State feedback control	0.2045	3.2086

5. Conclusions

This paper presented an observer-based controller design for ACC systems under input saturation and disturbances. Unlike previous approaches that handled saturation only for state feedback control systems, the proposed method incorporates the estimated state and decay rate of the Lyapunov function while guaranteeing the invariant level set condition. This enables a systematic two-step observer-based controller design that ensures both constraint satisfaction and disturbance attenuation. Simulation results confirmed that the proposed controller provides superior tracking accuracy and robustness compared with conventional designs.

It should be noted, however, that the observer dynamics may be affected by sensor noise, modeling errors, and unmodeled nonlinearities in vehicle behavior, which were not explicitly addressed in this work. Moreover, since ACC systems are implemented digitally, a discrete-time realization or conversion strategy is essential for practical deployment, but was beyond the scope of this study. These aspects will be considered in future research toward the real-world implementation of constrained ACC systems.

Appendix A.1. Asymptotic Stability Without Disturbance

Consider the following Lyapunov function candidate:

$$\begin{array}{c}\hfill V\left(z\left(t\right)\right)=z^T\left(t\right)Pz\left(t\right),\end{array}$$

(A1)

and define

$$\begin{array}{c}\hfill J\left(t\right)=2\alpha V\left(z\left(t\right)\right)+z^T\left(t\right)Qz\left(t\right)-{\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right),\end{array}$$

where $\alpha$ is a scalar satisfying $\alpha \ge {\gamma }^2{a}_{max}^2/2$; $\gamma >0$ and $a_{max}>0$ are given positive scalars; and $Q=\mathrm{diag}\{Q_1,Q_2\}$; and $Q_1\in {\mathbb{R}}^{n_x\times n_x}$ and $Q_2\in {\mathbb{R}}^{n_x\times n_x}$ are given diagonal matrices with positive elements.

Differentiating (A1) along (10) and adding $J\left(t\right)$ gives:

$$\begin{array}{cc}\hfill & \dot{V}\left(z\left(t\right)\right)+J\left(t\right)\hfill \\ \hfill =& 2z^T\left(t\right)P\left(A_{z}z\left(t\right)+D_z{a}_0\left(t\right)\right)\hfill \\ \hfill & +2\alpha z^T\left(t\right)Pz\left(t\right)+z^T\left(t\right)Qz\left(t\right)-{\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right)\hfill \\ \hfill =& {\left[\begin{array}{c}z\left(t\right)\\ a_0\left(t\right)\end{array}\right]}^T\left[\begin{array}{cc}\mathrm{sym}\left\{P{A}_z\right\}+2\alpha P+Q& \ast \\ D_z^{T}P& -{\gamma }^{2}I\end{array}\right]\left[\begin{array}{c}z\left(t\right)\\ a_0\left(t\right)\end{array}\right].\hfill \end{array}$$

Thus, the following matrix inequality

$$\begin{array}{c}\hfill \left[\begin{array}{cc}\mathrm{sym}\left\{P{A}_z\right\}+2\alpha P+Q& \ast \\ D_z^{T}P& -{\gamma }^{2}I\end{array}\right]\prec 0\end{array}$$

(A2)

ensures $\dot{V}\left(z\left(t\right)\right)+J\left(t\right)\le 0$.

Expanding the terms in (A2) using the definitions of P, $A_z$, $D_z$, and Q leads to

$$\begin{array}{cc}\hfill \mathrm{sym}\left\{P{A}_z\right\}=& \mathrm{sym}\left\{\sum _{i=1}^{2^{n_u}}{\eta }_i\left[\begin{array}{cc}{P}_1& \ast \\ P_2& P_3\end{array}\right]\left[\begin{array}{cc}A+\mu B{G}_i& -\mu B{G}_i\\ \mathbf{0}& A-LC\end{array}\right]\right\}\hfill \\ \hfill =& \mathrm{sym}\left\{\sum _{i=1}^{2^{n_u}}{\eta }_i\left[\begin{array}{cc}{P}_{1}A& P_2^T(A-LC)\\ P_{2}A& P_3(A-LC)\end{array}\right]\right.\left.+\mu \left[\begin{array}{cc}{P}_{1}B{G}_i& -P_{1}B{G}_i\\ P_{2}B{G}_i& -P_{2}B{G}_i\end{array}\right]\right\},\hfill \end{array}$$

(A3)

$$\begin{array}{cc}\hfill 2\alpha P+Q=& \left[\begin{array}{cc}2\alpha P_1+Q_1& \ast \\ 2\alpha P_2& 2\alpha P_3+Q_2\end{array}\right],\hfill \end{array}$$

(A4)

$$\begin{array}{cc}\hfill D_z^{T}P=& \left[\begin{array}{cc}{D}^T{P}_1+D^T{P}_2& D^T{P}_2+D^T{P}_3\end{array}\right].\hfill \end{array}$$

(A5)

Substituting (A3)–(A5) into (A2) leads to the matrix inequality (11). Since $V\left(z\right(t\left)\right)\ge 0$, it is clear that $2\alpha V\left(z\left(t\right)\right)+z^{T}Qz\ge 0$. Therefore, $\dot{V}\left(z\left(t\right)\right)+2\alpha V\left(z\left(t\right)\right)+z^T\left(t\right)Qz\left(t\right)-{\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right)\le 0$ becomes $\dot{V}\left(z\left(t\right)\right)\le {\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right)$. Hence, the equilibrium of (10) is asymptotically stable when $a_0\left(t\right)=0$, satisfying the first condition in Problem 1.

Appendix A.2. Invariant Level Set

Next, to guarantee that the level set $ϵ(P,z(t\left)\right)$ is satisfied, we introduce the following inequality:

$$\begin{array}{c}\hfill z^T\left(0\right)Pz\left(0\right)\le 1,\end{array}$$

which implies that, for some initial condition, $V\left(z\right(0\left)\right)\le 1$. By applying the Schur complement, we obtain the matrix inequality (12).

Given $V\left(z\right(0\left)\right)\le 1$, we now show that $V\left(z\right(t\left)\right)\le V\left(z\right(0\left)\right)$ and thus $V\left(z\right(t\left)\right)\le 1$. As already established, the following inequality holds:

$$\begin{array}{cc}\hfill \dot{V}\left(z\left(t\right)\right)+2\alpha V\left(z\left(t\right)\right)\le & -z^T\left(t\right)Qz\left(t\right)+{\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right)\hfill \\ \hfill \le & {\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right)\le {\gamma }^2{a}_{\max }^2.\hfill \end{array}$$

Multiplying both sides by $e^{2\alpha t}$ yields

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{dt}}\left(e^{2\alpha t}V\left(z\left(t\right)\right)\right)\le e^{2\alpha t}{\gamma }^2{a}_{\max }^2.\end{array}$$

Integrating this from $t=0$ to an arbitrary $t\ge 0$ gives

$$\begin{array}{cc}\hfill & e^{2\alpha t}V\left(z\left(t\right)\right)-V\left(z\left(0\right)\right)\le {\displaystyle \frac{{\gamma }^2{a}_{\max }^2}{2\alpha }}\left(e^{2\alpha t}-1\right)\hfill \\ \hfill \iff & V\left(z\left(t\right)\right)\le e^{-2\alpha t}V\left(z\left(0\right)\right)+{\displaystyle \frac{{\gamma }^2{a}_{\max }^2}{2\alpha }}\left(1-e^{-2\alpha t}\right).\hfill \end{array}$$

Now, assume that the right-hand side of the above inequality satisfies the following:

$$\begin{array}{cc}\hfill & e^{-2\alpha t}V\left(z\left(0\right)\right)+{\displaystyle \frac{{\gamma }^2{a}_{\max }^2}{2\alpha }}(1-e^{-2\alpha t})\le V\left(z\left(0\right)\right)\hfill \\ \hfill \iff & {\displaystyle \frac{{\gamma }^2{a}_{\max }^2}{2\alpha }}(1-e^{-2\alpha t})\le V\left(z\left(0\right)\right)(1-e^{-2\alpha t})\hfill \\ \hfill \iff & {\displaystyle \frac{{\gamma }^2{a}_{\max }^2}{2\alpha }}\le V\left(z\left(0\right)\right)\le 1.\hfill \end{array}$$

Therefore, if $\alpha \ge {\gamma }^2{a}_{\max }^2/2$, it follows that $V\left(z\right(t\left)\right)\le V\left(z\right(0\left)\right)\le 1$, which implies $z\left(t\right)\in ϵ(P,z(t\left)\right)$.

We now show that $\widehat{x}\left(t\right)\in \mathcal{L}(H,\widehat{x}\left(t\right))$ if $z\left(t\right)\in ϵ(P,z(t\left)\right)$. To this end, we rewrite $H\widehat{x}\left(t\right)$ as

$$\begin{array}{c}\hfill H\widehat{x}\left(t\right)=H\left\{x\left(t\right)-e\left(t\right)\right\}=\left[\begin{array}{cc}H& -H\end{array}\right]z\left(t\right)=\tilde{H}z\left(t\right),\end{array}$$

where $\tilde{H}=\left[\begin{array}{cc}H& -H\end{array}\right]$.

Then, the objective is achieved if

$$\begin{array}{c}\hfill z^T\left(t\right)Pz\left(t\right)\le 1\Rightarrow z^T\left(t\right){\tilde{H}}^T\tilde{H}z\left(t\right)\le 1.\end{array}$$

Since $z^T\left(t\right)Pz\left(t\right)\le 1$ is already satisfied, this implication holds if

$$\begin{array}{c}\hfill z^T\left(t\right){\tilde{H}}^T\tilde{H}z\left(t\right)\le z^T\left(t\right)Pz\left(t\right)\iff P-{\tilde{H}}^T\tilde{H}⪰0,\end{array}$$

which can be conservative in practice. To reduce conservatism, we introduce a slack variable $X=X^T\in {\mathbb{R}}^{{\check{n}}_u\times {\check{n}}_u}$ such that $P-{\tilde{H}}^T{X}^{-1}\tilde{H}⪰0$.

By the Schur complement, the above condition is equivalent to:

$$\begin{array}{c}\hfill \left[\begin{array}{cc}P& \ast \\ \tilde{H}& X\end{array}\right]⪰0,\end{array}$$

which corresponds to (13).

Furthermore, to ensure ${\tilde{H}}^T{X}^{-1}\tilde{H}⪰{\tilde{H}}^T\tilde{H}$, it suffices to impose: $X^{-1}⪰I_{{\check{n}}_u},$ which is guaranteed by (14).

Therefore, if the matrix inequalities (13) and (14) hold, it follows that

$$\begin{array}{c}\hfill P⪰{\tilde{H}}^T{X}^{-1}\tilde{H}⪰{\tilde{H}}^T\tilde{H},\end{array}$$

ensuring that $z\left(t\right)\in ϵ(P,z\left(t\right))\subset \mathcal{L}(H,\widehat{x}\left(t\right))$. Thus, the second objective in Problem 1 is satisfied.

Appendix A.3. Disturbance Attenuation

We now revisit the following inequality derived previously:

$$\begin{array}{cc}\hfill & {\displaystyle \frac{d}{dt}}\left\{e^{2\alpha t}V\left(z\left(t\right)\right)\right\}\hfill \\ \hfill +& e^{2\alpha t}\left\{z^T\left(t\right)Qz\left(t\right)-{\gamma }^2{a}_0^T\left(t\right)a_0\left(t\right)\right\}\le 0.\hfill \end{array}$$

Integrating both sides over the interval $[0,t]$ gives

$$\begin{array}{cc}\hfill & e^{2\alpha t}V\left(z\left(t\right)\right)-V\left(z\left(0\right)\right)\hfill \\ \hfill +& {\int }_0^t{e}^{2\alpha s}{z}^T\left(s\right)Qz\left(s\right)ds-{\gamma }^2{\int }_0^t{e}^{2\alpha s}{a}_0^T\left(s\right)a_0\left(s\right)ds\le 0.\hfill \end{array}$$

Assume $z\left(0\right)=0$ and take the limit as $t\to \infty$. Since $V\left(z\right(t\left)\right)\ge 0$ for all t, it follows that

$$\begin{array}{c}\hfill {\int }_0^{\infty }{e}^{2\alpha s}{z}^T\left(s\right)Qz\left(s\right)ds\le {\gamma }^2{\int }_0^{\infty }{e}^{2\alpha s}{a}_0^T\left(s\right)a_0\left(s\right)ds,\end{array}$$

(A6)

which establishes the desired attenuation performance:

$$\begin{array}{c}\hfill \Gamma (\infty )={\displaystyle \frac{{\int }_0^{\infty }{e}^{2\alpha s}{z}^T\left(s\right)Qz\left(s\right)ds}{{\int }_0^{\infty }{e}^{2\alpha s}{a}_0^T\left(s\right)a_0\left(s\right)ds}}\le {\gamma }^2.\end{array}$$

(A7)

This confirms that the third objective in Problem 1 is satisfied.