Cloud-Assisted Nonlinear Model Predictive Control with Deep Reinforcement Learning for Autonomous Vehicle Path Tracking

Abstract

Model Predictive Control (MPC) stands out as a prominent method for achieving optimal control in autonomous driving applications. However, the effectiveness of MPC approaches critically depends on the availability of accurate dynamic models and often necessitates substantial computational overhead for real-time optimization procedures at every iteration. Recently, the research community has been increasingly drawn to the concept of cloud-assisted MPC, which harnesses the capabilities of powerful cloud computing to provide users with on-demand computational resources and data storage services. Within these cloud-assisted MPC frameworks, control signals are merged with a cloud-based MPC, which leverages the substantial processing power of cloud infrastructure to determine optimal control actions using detailed nonlinear models for greater accuracy. Simultaneously, a local MPC runs on simplified linear models constrained by limited on-device computing resources, delivering prompt control responses at the cost of reduced model accuracy. To achieve an effective trade-off between rapid response and model fidelity, this work presents a new model-free deep reinforcement learning structure designed to merge cloud and local MPC outputs. Tests conducted on path-following scenarios show that the introduced method achieves superior control performance compared to existing reinforcement learning baselines and conventional rule-based fusion strategies.

1. Introduction

Autonomous vehicles (AVs) have attracted dramatic research attention in the past decades [1]. The deployment of advanced control systems in autonomous vehicles (AV) can improve road safety by significantly mitigating traffic incidents and associated casualties, while also ensuring a more comfortable ride experience [2]. In a typical hierarchical autonomous driving framework, one key component in achieving safe and comfortable driving is the path tracking module [3], which directly impacts vehicle movement. Specifically, with the objective of accurately and smoothly following the path planned by the upper-level path planner, the path tracking module generates control demands for lower-level actuators in real-time under constrained computation and communication conditions [4].

Several control methods are utilized to design path tracking controllers [5,6], including state feedback controllers, sliding mode control, proportional integral derivative (PID) control, robust control [7], linear quadratic regulator (LQR) control [8] and model predictive control (MPC), etc. The prominence of MPC in recent path tracking research (as shown in [9], Figure 1) is largely attributable to its proficiency in managing the optimization of nonlinear, constrained Multi-Input Multi-Output systems. This specific capability makes it exceptionally applicable to the demands of real-world autonomous vehicle path tracking [10]. However, due to complex vehicle dynamics and limited computing power onboard, solving a constrained MPC with a high-fidelity nonlinear vehicle dynamics model in real-time is always unavailable for onboard deployment [11]. Additionally, state estimation under data loss and noise uncertainty presents significant challenges for vehicle control systems [12].

Figure 1. Illustration of the proposed cloud-assisted MPC framework embedded with DRL-based control fusion policy.

Recently, with the advancement of cloud computing, new opportunities have opened for autonomous driving. Due to the benefits offered by cloud computing in providing seemingly limitless computing capabilities and data storage services, increasing research attention is being directed towards cloud-assisted control systems [13,14], including cloud-assisted MPC design. For example, a dual control framework is proposed in [15,16]. This framework involves solving constrained linear-quadratic MPC problems in the cloud for computing control inputs, supplemented by a local backup controller. However, they lack consideration of critical issues such as plant–model mismatch, connectivity, latency, and feasibility, which are crucial to ensure safety in autonomous driving tasks [17].

Taking into account the existing challenges of communication delays, disturbances, and plant–model mismatch in cloud-assisted MPC, in our previous work [18], we present an innovative cloud-assisted MPC framework to manage system constraints in complex nonlinear systems, as shown in Figure 1, in which a cloud computational node hosts a high-fidelity nonlinear MPC, while a simplified linear MPC version is executed locally. In this way, the computational burden on the local controller can be significantly reduced without compromising optimization due to cloud MPC. The key component of integrating cloud MPC and local MPC is the control fusion module, whose objective is to select appropriate control to minimize future cumulative costs, contributing to enhanced control performance. As a result, our approach successfully achieves improved control performance, offering a well-balanced solution that capitalizes on the strengths of both nonlinear MPC and linear MPC within a cloud-assisted framework. A key limitation of the rule-based switching approach is its requirement for prior closed-loop system knowledge and worst-case cost analysis. Such comprehensive information is often impractical to obtain for complex autonomous vehicle systems affected by dynamic disturbances.

To address the problem mentioned above of the control fusion module in our proposed cloud-assisted MPC framework, in this paper, we exploit the model-free deep reinforcement learning (DRL) technique [19,20] to learn the optimal control fusion policy. The DRL-based fusion strategy empowers the system to acquire optimal control signal fusion techniques through dynamic interactions with the environment, facilitating adaptive adjustments to varying conditions. In contrast to rule-based policies, DRL operates without prior knowledge of closed-loop dynamics and circumvents the need to precisely evaluate how disturbances propagate through complex nonlinear systems. Moreover, our framework achieves a harmonious equilibrium between control precision and effort by incorporating both factors into a multi-objective reward function, thus achieving better path-tracking control performance. The main contributions of this paper are summarized as follows.

1.

A DRL-driven model-free cloud-assisted MPC framework is extended based on our previous work [18]. DRL enables the learning of control fusion strategies, thereby bypassing the requirement for exact future cost estimation under disturbances, a crucial capability for complex dynamic environments.

2.

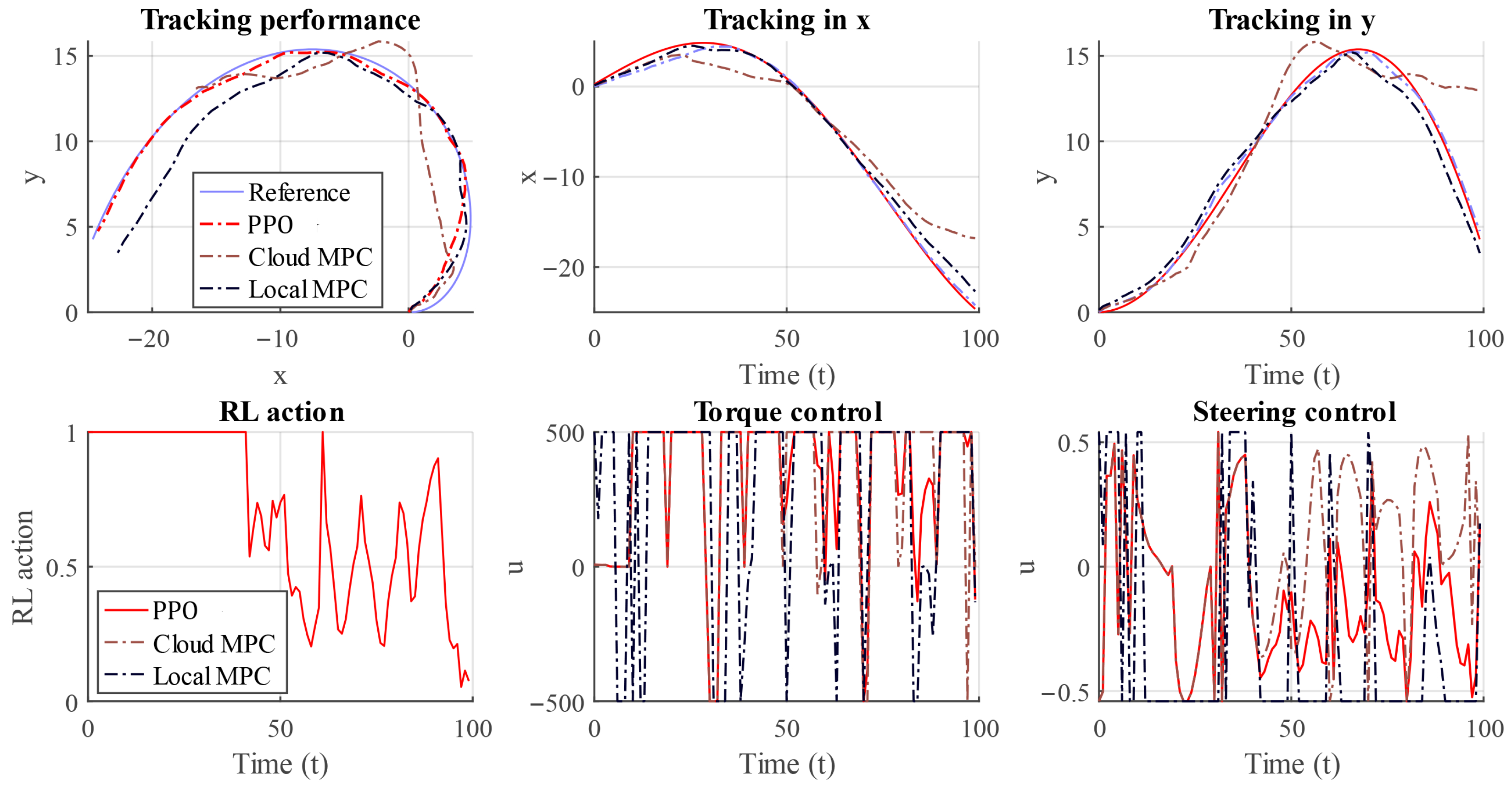
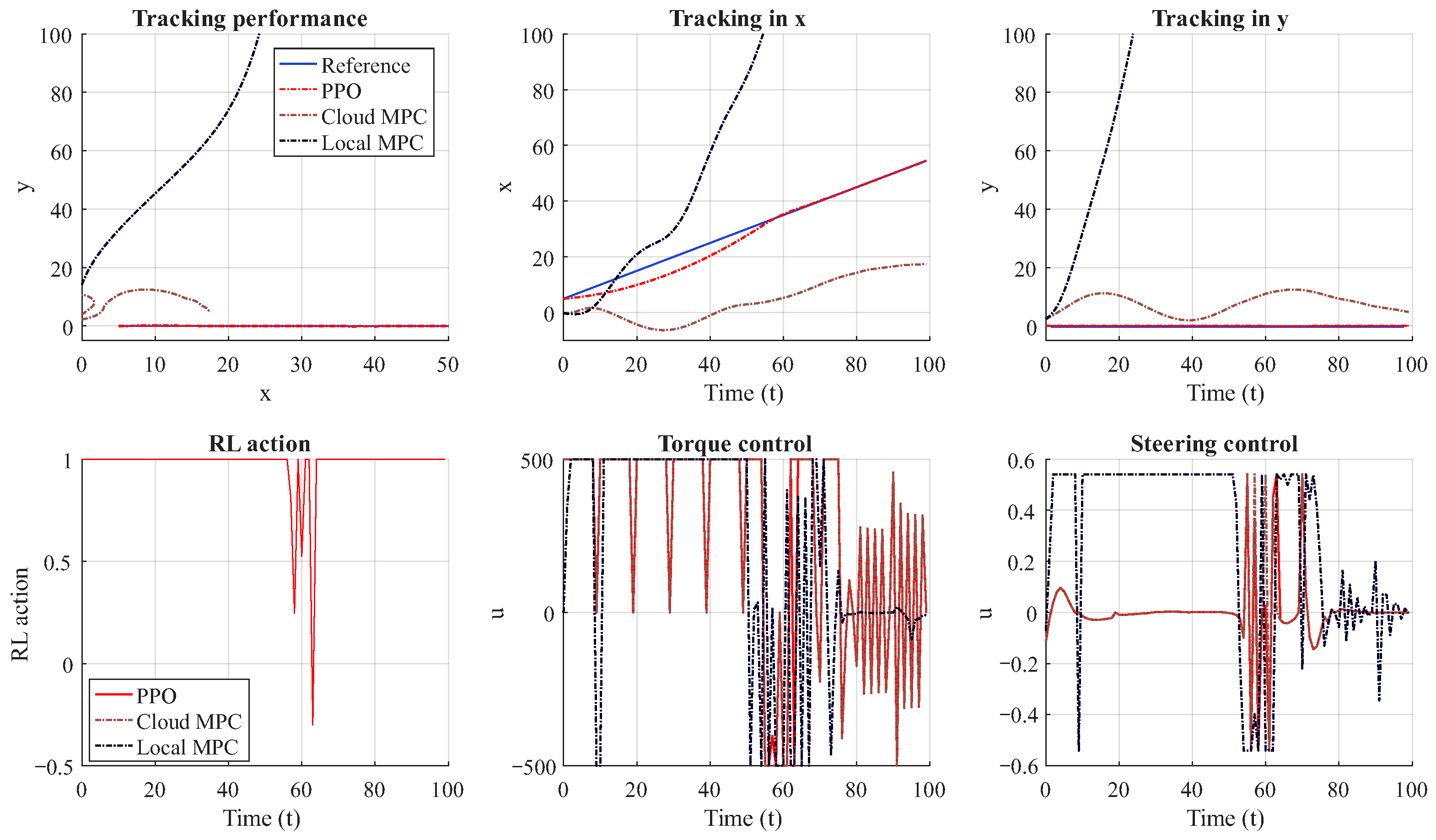
The DRL-cloud-assisted MPC is validated in the AV path-tracking task. In cloud MPC, a high-fidelity nonlinear vehicle dynamics model is applied that considers the angle of tire slip and axle load transfer, which is commonly neglected in existing MPC-based path tracking research due to the limited computing power on board [9]. The results demonstrate superior performance compared to both cloud-only and local-only baselines, as well as the rule-based method.

3.

The developed cloud-assisted MPC with classical DRL algorithms are well benchmarked and the codes are open-sourced (Codes: https://gitee.com/majortom123/mpc, accessed on 1 January 2025), which is expected to be a valuable resource for future research in the domain of cloud-assisted MPC with DRL and beyond.

The remainder of the paper is organized as follows: Section 2 formulates the AV path tracking problem and illustrates the cloud-assisted MPC framework. The DRL-based control fusion policy is presented in Section 3. Experiments, results, and discussions are presented in Section 4. Finally, we conclude the paper and discuss future works in Section 5.

2. Methodology

In this section, we first introduce the nonlinear vehicle dynamics model for the AV path-tracking task. Then, the cloud-assisted MPC framework is introduced.

2.1. Vehicle Dynamics and Path Tracking Problem

We consider a single-track nonlinear vehicle dynamics model with consideration of tire slip characteristics [9,21] to represent the actual vehicle dynamics system. The dynamic behavior of the vehicle’s center of gravity and its wheels is governed by the following equations.

$$\begin{array}{cc}\dot{p_x}\hfill & =v_{x}cos\psi -v_{y}sin\psi \hfill \end{array}$$

(1a)

$$\begin{array}{cc}{\dot{v}}_x\hfill & =v_{y}r+{\displaystyle \frac{2}{m}}\sum _{i=f,r}{F}_{x,i}-gsin{\sigma }_g-{\displaystyle \frac{1}{m}}{F}_a\hfill \end{array}$$

(1b)

$$\begin{array}{cc}\dot{p_y}\hfill & =v_{x}sin\psi +v_{y}cos\psi \hfill \end{array}$$

(1c)

$$\begin{array}{cc}{\dot{v}}_y\hfill & =-v_{x}r+{\displaystyle \frac{2}{m}}\sum _{i=f,r}{F}_{y,i}\hfill \end{array}$$

(1d)

$$\begin{array}{cc}\dot{\psi }\hfill & =r\hfill \end{array}$$

(1e)

$$\begin{array}{cc}\dot{r}\hfill & ={\displaystyle \frac{1}{I}}\left(2L_{xf}{F}_{y,f}-2L_{xr}{F}_{y,r}\right),\hfill \end{array}$$

(1f)

where the state variables are: the CG positions $p_x$ (longitudinal) and $p_y$ (lateral); the global heading angle $\psi$; the body frame velocities $v_x$ (longitudinal) and $v_y$ (lateral); and the yaw rate r. The forces include the aerodynamic drag $F_a$ and the tire forces $F_x$, $F_y$. The parameters are: vehicle mass m, yaw inertia I, and the distances from the CG to the front and rear axles, $L_{xf}$ and $L_{xr}$, respectively.

The vehicle frame tire forces $F_{x,i}$ and $F_{y,i}$ from Equations (1b) and (1d) are obtained via a transformation from the wheel frame:

$$\begin{array}{cc}{F}_{x,i}\hfill & ={\overline{F}}_{x,i}cos{\beta }_i-{\overline{F}}_{y,i}sin{\beta }_i\hfill \end{array}$$

(2a)

$$\begin{array}{cc}{F}_{y,i}\hfill & ={\overline{F}}_{x,i}sin{\beta }_i+{\overline{F}}_{y,i}cos{\beta }_i\hfill \end{array}$$

(2b)

In this model, ${\beta }_i$ is the wheel/road angle, and the index i (f or r) specifies the front or rear wheel. The longitudinal and lateral forces in the wheel frame, ${\overline{F}}_{x,i}$ and ${\overline{F}}_{y,i}$, are determined as follows:

$$\begin{array}{cc}{\overline{F}}_{x,i}\hfill & ={\displaystyle \frac{T_i}{2R}}\hfill \end{array}$$

(3a)

$$\begin{array}{cc}{\overline{F}}_{y,i}\hfill & =C_i{\mu }_i{F}_{z,i}{\alpha }_i\hfill \end{array}$$

(3b)

The parameters in these equations are: axle torque $T_i$, effective tire radius R, tire cornering stiffness $C_i$, road friction coefficient ${\mu }_i$, and slip angle ${\alpha }_i$ [22]. Accurate estimation of road friction coefficient is crucial for vehicle stability control, and recent learning-based frameworks have shown promising results in this domain [23]. The vertical force $F_{z,i}$ in (3b) is approximated by a static load transfer model. The vertical load $F_{z,i}$ in Equation (3b) is given by a static load transfer model:

$$\begin{array}{c}{F}_{z,i}={\displaystyle \frac{L_{x,i}mg}{2\left(L_{x,f}+L_{x,r}\right)}}.\hfill \end{array}$$

(4)

Define state vector $x={[p_x,v_x,p_y,v_y,\psi ,r]}^T$ and the control input $u={[T_f,{\beta }_f]}^T$. With a sampling time of 0.05 s, the above nonlinear vehicle dynamics system can be discretized and written into the state-space form as

$$x_{t+1}=A{x}_t+B{u}_t+f\left(x_t,u_t\right)+w_t,$$

(5)

where $w_t={[w_x,w_{v_x},w_y,w_{v_y},w_{\psi },w_r]}^T\in W$ represents the uncertainties in system dynamics. Here, an assumption is given that the input of the disturbance $w_t$ is bounded, taking values from a known set $W\subset {\mathbb{R}}^p$, with its supremum norm characterized by ${sup}_{w\in W}\left|w\right|=\omega$.

The MPC strategy operates by solving an online optimization problem at each time step to determine the optimal control sequence $U_t=\{u_t,u_{t+1},\dots u_{t+N-1}\}$ and the resulting state sequence $X_t=\{x_{t+1},x_{t+2},\dots x_{t+N}\}$ across a prediction horizon of length N:

$$\begin{array}{cc}\underset{X_t,U_t}{min}\hfill & J=\sum _{k=0}^{N-1}\varphi \left(x_{t+k},u_{t+k}\right)\hfill \end{array}$$

(6a)

$$\begin{array}{cc}\mathrm{s}.\mathrm{t}.\hfill & x_t={\widehat{x}}_t\hfill \end{array}$$

(6b)

$$\begin{array}{cc}\hfill & x_{t+k}=A{x}_{t+k-1}+B{u}_{t+k-1}\hfill \end{array}$$

$$\begin{array}{cc}\hfill & +f\left(x_{t+k-1},u_{t+k-1}\right)+w_{t+k-1},1\le k\le N\hfill \end{array}$$

(6c)

$$\begin{array}{cc}\hfill & x_{min}\le x_{t+k}\le x_{max},1\le k\le N\hfill \end{array}$$

(6d)

$$\begin{array}{cc}\hfill & u_{min}\le u_{t+k}\le u_{max},0\le k\le N-1\hfill \end{array}$$

(6e)

$$\begin{array}{cc}\hfill & {\Delta }_{min}\le u_{t+k}-u_{t+k-1}\le {\Delta }_{max}\hfill \end{array}$$

(6f)

$$\begin{array}{cc}\hfill & 0\le k\le N-1\hfill \end{array}$$

(6g)

where t is the current time instant, $\varphi \left(x_t,u_t\right)$ is the cost to be minimized. The constraints limit changes in states and control inputs within certain limits.

This paper addresses autonomous vehicle trajectory tracking, specifically for the trajectory shaped by

$$\begin{array}{c}{y}_r=4sin\left({\displaystyle \frac{2\pi }{100}}{x}_r\right)\hfill \end{array}$$

(7)

where $x_r$ and $y_r$ are longitudinal and lateral reference positions, respectively. Therefore, the objective in (6a) is rewritten as:

$$\begin{array}{c}J\left(X_t,U_t\right)=\sum _{k=1}^p{\parallel x_{t+k}\left(3\right)-4sin\left({\displaystyle \frac{2\pi }{100}}{x}_{t+k}\left(1\right)\right)\parallel }_{Q_t}^2+\sum _{k=0}^{p-1}\left({∥u_{t+k}-u_{t+k}^r∥}_{Q_u}^2\right).\hfill \end{array}$$

(8)

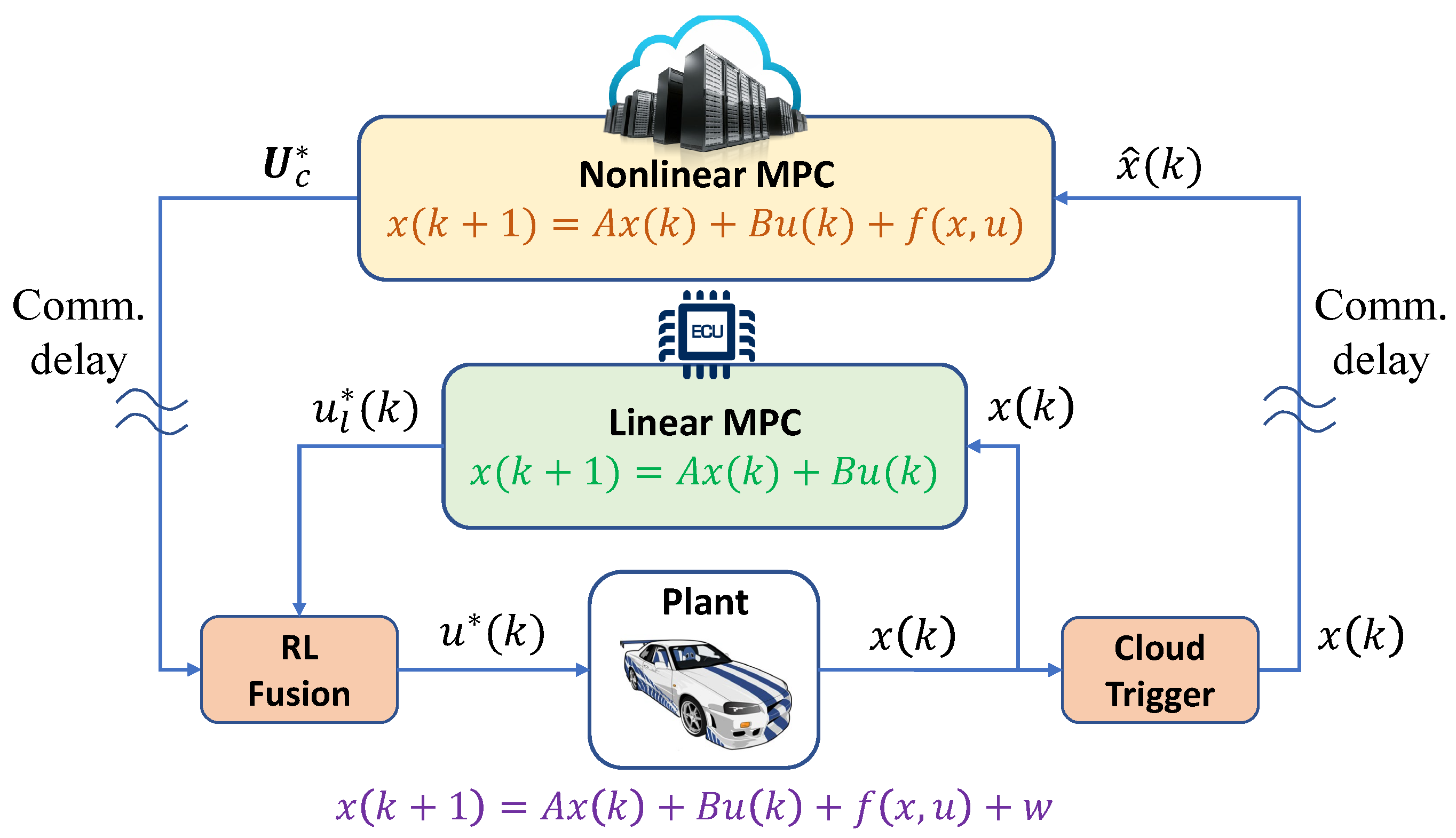
2.2. Cloud-Assisted MPC Framework

As shown in Figure 1, there are two different MPC problems to be solved on the cloud and local sides separately. Based on the framework, the cloud MPC leverages a high-fidelity nonlinear model over an extended prediction horizon, computing a solution only upon receiving a new control task. In parallel, the local MPC utilizes a simplified linear model with a receding horizon, executing an optimization at every sampling instant throughout the task duration. Accordingly, the cloud is tasked with solving the following nonlinear optimization problem:

$$\begin{array}{cc}min\hfill & J=\sum _{\tau =0}^{N-1}\varphi \left({\widehat{x}}_{\tau },u_{\tau }\right)\hfill \end{array}$$

(9a)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.{\widehat{x}}_{t+1}=A{\widehat{x}}_t+B{u}_t+f\left({\widehat{x}}_t,u_t\right)\hfill \end{array}$$

(9b)

$$\begin{array}{cc}\hfill & \left({\left\{{\widehat{x}}_{\tau }\right\}}_{\tau =1}^N,{\left\{u_{\tau }\right\}}_{\tau =0}^{N-1}\right)\in {\Xi }^c\hfill \end{array}$$

(9c)

where $\widehat{x}$ represents predicted states in the cloud MPC. The model used here is a high-fidelity model including the nonlinear term $f\left({\widehat{x}}_t,u_t\right)$. ${\Xi }^c$ is constraints with the same form as in (6d)–(6f).

Given the constrained computational capabilities onboard, the local MPC employs a linear dynamic model for its operations, so the MPC problem is:

$$\begin{array}{cc}min\hfill & J_t=\sum _{\tau =t}^{N-1}\varphi \left({\overline{x}}_{\tau \mid t},u_{\tau \mid t}\right)\hfill \end{array}$$

(10a)

$$\begin{array}{c}\mathrm{s}.\mathrm{t}.{\overline{x}}_{t\mid t}=x_t\hfill \end{array}$$

(10b)

$$\begin{array}{cc}\hfill & {\overline{x}}_{\tau +1\mid t}=A{\overline{x}}_{\tau \mid t}+B{u}_{\tau \mid t}\hfill \end{array}$$

(10c)

$$\begin{array}{cc}\hfill & \left({\left\{{\overline{x}}_{\tau \mid t}\right\}}_{\tau =1}^N,{\left\{u_{\tau \mid t}\right\}}_{\tau =0}^{N-1}\right)\in {\Xi }_t^l.\hfill \end{array}$$

(10d)

where $\overline{x}$ represents predicted states in the local MPC. The symbolic expression ${(·)}_{\tau \mid t}$ in the expressions above signifies a forecast of the variable ${(·)}_{\tau }$ that is computed based on information available at time t.

In terms of cloud triggers, we assume that, the local system can initiate a request to the cloud for solving the nonlinear MPC problem when a control task is assigned. This process inevitably incurs a “request–response delay”, which consists of communication uplink–downlink delay and cloud computation time. To tackle this problem, a “prediction-ahead-of-time” approach is adopted, which ensures that the cloud can predict the state with the maximum delay time $\Delta t$ ahead. For example, if the request is sent to the cloud at $t=k-\Delta t$, the cloud will predict the vehicle state $\Delta t$ time ahead, $\widehat{x}((k-\Delta t)+\Delta t)=\widehat{x}\left(k\right)$ by assuming state remaining constant over the time interval $\Delta t$ or by running forward simulation based on system model (5). The predicted state $\widehat{x}$ then serves as the initial condition for the cloud MPC, which subsequently computes the optimal control sequence. Because the local side can receive the cloud control law within the maximum delay time $\Delta t$, the cloud control law can be exactly started at time instant $t=(k-\Delta t)+\Delta t=k$, thereby ensuring that no stale control commands are applied.

However, due to prediction inaccuracy, an initial state uncertainty for cloud MPC is inevitable. In addition, during the implementation process, the model mismatch and environmental disturbances may also lead to model prediction errors. To address these problems, the robust constraint enforcement technique is used to ensure the states can be constrained even with uncertainty. Because of the limited space and the main focus of control fusion design in this paper, we recommend interested readers to read our previous work [18].

A key innovation of our cloud-assisted nonlinear MPC strategy is a novel integration mechanism that seamlessly merges cloud and local control actions to achieve enhanced performance. In our previous research, we used a rule-based policy to realize the control switching. A main limitation of the proposed switching strategy is its inherent reliance on worst-case bounds, which means it does not guarantee optimality in minimizing the cumulative cost. Achieving optimality would demand an exact evaluation of disturbance effects through the nonlinear system (5), presenting a formidable challenge for complex dynamical systems. Therefore, in this paper, we want to deploy DRL technique to automatically learn an optimal switch policy. The details of DRL-based control fusion design are introduced in Section 3.

3. DRL-Based Control Fusion Design

In this section, we will first introduce the basic knowledge of DRL. Then, the DRL-based control fusion module for cloud-assisted MPC will be developed as shown in Algorithm 1.

Algorithm 1 DRL-based Cloud-Assisted MPC.

Require: M, T, $dt$, $\gamma$, N

Ensure: $\theta$

1: Initialize $\theta$, $\mathcal{D}\leftarrow \varnothing$

2: for $j=0$ to $M-1$ do

3:     Initialize $s_t$, Z, U, $k\leftarrow 0$

4:     while $t\le T$ do

5:         Select fusion action based on current state

6:         $a_t\sim {\pi }_{\theta }\left(s_t\right)$

7:         Environment Simulation

8:         $k\leftarrow 0$

9:         $(Z,U)\leftarrow \mathrm{Solve}\mathrm{cloud}\mathrm{optimal}\mathrm{control}\mathrm{problem}\left(9\mathrm{a}\right)$

10:         $u\leftarrow \mathrm{Solve}\mathrm{local}\mathrm{MPC}\mathrm{problem}\left(10\mathrm{a}\right)\mathrm{to}\mathrm{obtain}{\widehat{u}}_t$ Local control

11:         Fuse control input from the dual controller

12:         $u_t=a\ast {\widehat{u}}_t+(1-a)\ast \overline{U}\left(k\right)$

13:         $k\leftarrow k+1$

14:         Apply control and simulate system dynamics

15:         $x_{t+1}\leftarrow \mathrm{Simulate}\mathrm{system}\mathrm{dynamics}\left(5\right)\mathrm{using}{u}_t$

16:         Calculate reward

17:         $r_t\leftarrow \mathrm{Equation}\left(12\right)$

18:         Observe next state and store experience

19:         $s_{t+1}\leftarrow (x_{t+1},Z\left(k\right))$

20:         Store $(s_t,a_t,r_t,s_{t+1})$ in $\mathcal{D}$

21:         Update policy parameters

22:         Sample N experiences from $\mathcal{D}$ and update $\theta$

23:         Move to next time step

24:         $s_t\leftarrow s_{t+1}$

25:         $t\leftarrow t+dt$

26:     end while

27: end for

3.1. Preliminary of DRL

In an RL setting, an agent sequentially observes states $s_t\in \mathcal{S}\subseteq {\mathcal{R}}^n$, and performs actions $a_t\in \mathcal{A}\subseteq {\mathcal{R}}^m$ at each timestep t, guided by a policy $\pi \left(a_t\right|s_t)$. The simulation environment advances to a subsequent state $s_{t+1}$ according to the transition dynamics $p(·|s_t,a_t)$, concurrently yielding an immediate reward $r_t=r(s_t,a_t,s_{t+1})$. The learning objective is to obtain an optimal policy ${\pi }^{\ast }:\mathcal{S}\to \mathcal{A}$ that maps states to actions such that the cumulative discounted return $R_t={\sum }_{k=0}^T{\gamma }^k{r}_{t+k}$ is maximized, where $r_{t+k}$ denotes the reward at future step $t+k$, while $\gamma \in (0,1]$ and T correspond to the discount factor and episode horizon, respectively.

We define the state–action value function $Q^{\pi }(s_t,a_t)=\mathbb{E}\left(R_t\right|s_t,a_t)$ as the expected total return when starting in state $s_t$, executing action $a_t$, and thereafter following policy $\pi$. The optimal Q-function, given by $Q^{\ast }(s_t,a_t)={max}_{\pi }{Q}^{\pi }(s_t,a_t)$, directly induces the optimal greedy policy ${\pi }^{\ast }\left(a_t\right|s_t)$. Similarly, the state value function $V^{\pi }\left(s_t\right)=\mathbb{E}\left(R_t\right|s_t)$ captures the expected return from state $s_t$ when consistently adhering to policy $\pi$.

Building upon these foundations, we highlight several key RL algorithms tailored for continuous action spaces: Deep Deterministic Policy Gradient (DDPG) is designed for continuous control, utilizing an actor–critic framework where a deterministic actor network maps states directly to actions, and a critic network is used to evaluate the quality (Q-value) of those state–action pairs [24]. Twin Delayed Deep Deterministic (TD3) improves upon DDPG by introducing twin Q-networks to reduce overestimation bias and stabilize policy learning [25]. Soft Actor–Critic (SAC) adds an entropy term to the reward function, encouraging the policy toward diverse actions and enhancing the robustness of the learned policy [26]. Trust Region Policy Optimization (TRPO) aims to monotonically improve policy updates through a constrained optimization framework, ensuring robust policy improvement with theoretical guarantees of performance [27]. In contrast, Proximal Policy Optimization (PPO) offers a practical approach to policy optimization in discrete spaces by employing a clipped surrogate objective, ensuring stable and efficient learning [28]. These algorithms play a crucial role in advancing reinforcement learning by improving both efficiency and stability, and they will be evaluated within the proposed cloud-assisted MPC framework.

3.2. DRL-Based Cloud-Assisted MPC

In this paper, we formulate the problem of DRL-based cloud-assisted MPC for path planning in autonomous vehicles as a Partially Observable Markov Decision Process $\mathcal{M}$ (POMDP) and solve with model-free RL algorithms [19], represented by the tuple $\mathcal{M}=(\mathcal{A},\mathcal{S},\mathcal{R},\mathcal{T},\gamma )$:

1.

Action space $\mathcal{A}$: The action generated by the DRL represents the fusion strategy for the DRL-based cloud-assisted MPC, ranging continuously from 0 to 1. This strategy integrates the control signals from both the cloud and local controllers. When $\mathbf{a}=\mathbf{1}$, the system solely utilizes the cloud MPC, analogous to a cloud-only approach. Conversely, when it comes to $\mathbf{a}=\mathbf{0}$, it employs only the local controller, aligning with the local-only MPC strategy.

2.

State space $\mathcal{S}$: The state space is designed to represent the simulation environment to learn a fusion policy and is defined as follows:

$$\mathcal{S}=\{{\mathit{p}}_{\mathit{x}},{\mathit{p}}_{\mathit{y}},{\mathit{v}}_{\mathit{x}},{\mathit{v}}_{\mathit{y}},\mathit{\psi },\mathit{r}\}.$$

(11)

3.

Reward function $\mathcal{R}$: The design of the reward function plays a critical role in guiding RL agents toward target behaviors. The specific form of the reward function is given in Equation (8), where the term $\mathit{r}({\widehat{\mathit{x}}}_{\mathit{t}},{\mathit{u}}_{\mathit{t}})$ is defined as:

$$\begin{array}{c}\mathit{r}({\widehat{\mathit{x}}}_{\mathit{t}},{\mathit{u}}_{\mathit{t}})={\left|\left|({\widehat{\mathit{x}}}_{\mathit{t}}\left(\mathbf{3}\right)-{\mathit{x}}_{\mathit{t}}^{\mathit{r}}\left(\mathbf{3}\right)\right|\right|}_{{\mathit{Q}}_{\mathit{t}}}^{\mathbf{2}}+\left|\right|{\mathit{u}}_{\mathit{t}}-{\mathit{u}}_{\mathit{t}}^{\mathit{r}}{\left|\right|}_{{\mathit{Q}}_{\mathit{u}}}^{\mathbf{2}},\hfill \end{array}$$

(12)

where ${\widehat{\mathit{x}}}_{\mathit{t}}$ denotes the actual system state (or its current state estimate in the absence of direct measurement), ${\mathit{x}}_{\mathit{t}}^{\mathit{r}}$ represents the reference trajectory and ${\mathit{x}}_{\mathit{t}}^{\mathit{r}}\left(\mathbf{3}\right)=\mathbf{4}sin\left({\displaystyle \frac{\mathbf{2}\mathbf{\pi }}{\mathbf{100}}}{\mathit{x}}_{\mathit{t}}^{\mathit{r}}\left(\mathbf{1}\right)\right)$, and ${\mathit{u}}_{\mathit{t}}$ represents the real-time control action, synthesized as ${\mathit{u}}_{\mathit{t}}=\mathit{a}\ast {\widehat{\mathit{u}}}_{\mathit{t}}+(\mathbf{1}-\mathit{a})\ast {\overline{\mathit{u}}}_{\mathit{t}}$, an affine combination of cloud control and local control.

4.

Transition probabilities $\mathcal{T}$: As a model-free RL approach, our framework operates without an explicit model of the transition dynamics $\mathcal{T}\left({\mathit{s}}^{\prime }\right|\mathit{s},\mathit{a})$, which characterizes the robot’s environmental interactions.

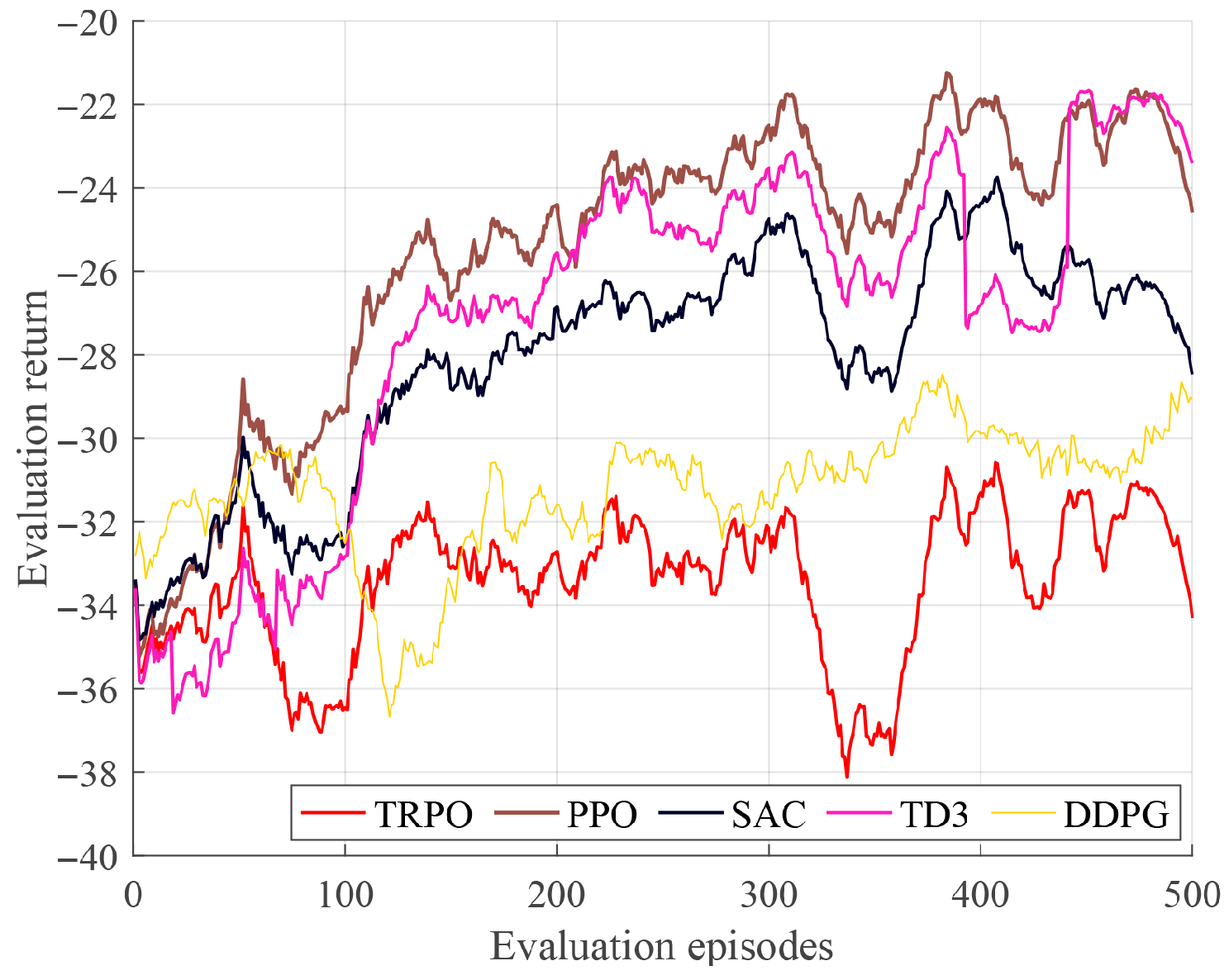
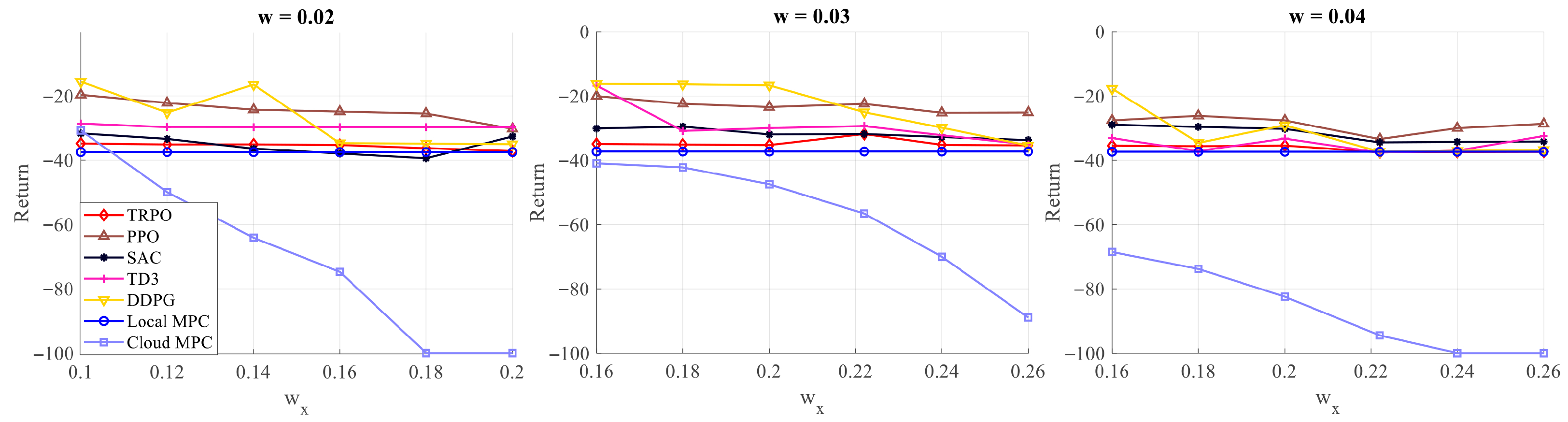
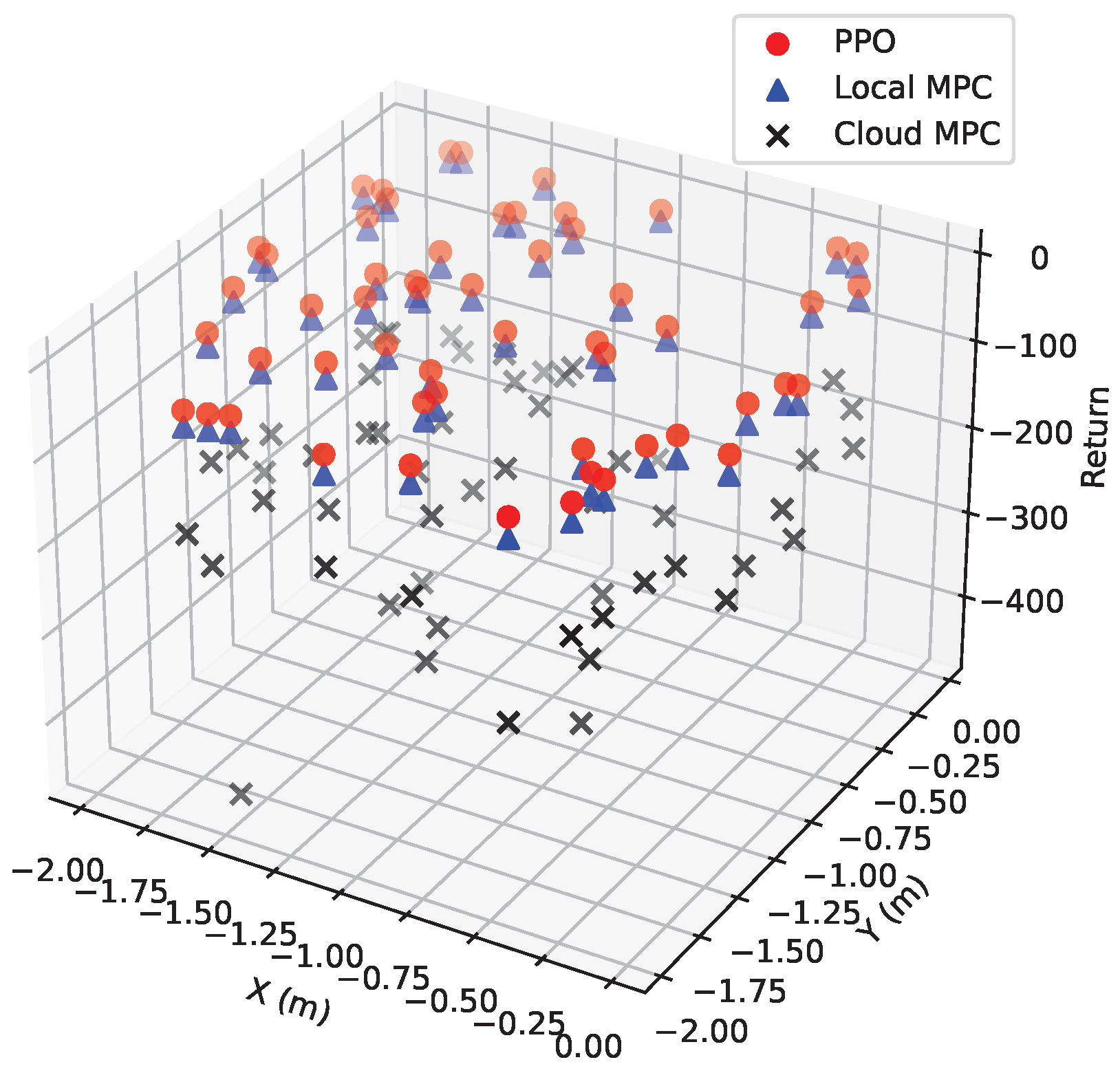
4. Simulation Results

This section presents extensive numerical tests to assess the effectiveness of the proposed framework against multiple baseline methods. The key simulation parameters of the vehicle dyanmics are shown in Table 1. The communication delay is set as 2 steps and the prediction horizon is 5 steps. The readers are referred to our open-sourced code (https://gitee.com/majortom123/mpc, accessed on 1 January 2025) for additional details about the simulation setup. The RL network architecture processes the input state through an initial fully-connected layer comprising 128 units, succeeded by two additional FC layers, each with 128 neurons. For the LSTM variant, the final FC layer is substituted by an LSTM layer containing 128 hidden units. The output layer produces two Q-values, representing the two possible control decisions: to trigger or not to trigger the control intervention. Following the DDQN algorithm, the target network parameters are synchronized with the online network every $N_0=1000$ training steps.

Table 1. The vehicle simulation parameters of MPC.

Parameter	$m\left[\mathrm{kg}\right]$	$L_{\mathit{xf}}\left[\mathrm{m}\right]$	$L_{\mathit{xr}}\left[\mathrm{m}\right]$	$I[\mathrm{kg}·{\mathrm{m}}^2]$	$R\left[\mathrm{m}\right]$	$C_i$ [-]	${\mu }_i$ [-]
Values	1500	1.2	1.4	4192	0.2159	−4.5837	1

The off-policy reinforcement learning models undergo training for 50,000 environmental steps, equivalent to approximately 500 episodes. Each episode spans a duration of T = 20 s with a sampling interval of $dt$ = 200 ms, resulting in an episode horizon of $T_e=100$ decision steps. In contrast, on-policy methods such as PPO typically demand extended training periods while offering enhanced stability [29]; accordingly, these algorithms are trained for 1000 episodes to ensure adequate convergence. The Markov decision process parameters include a discount factor $\gamma =0.99$ and a mini-batch size $N=64$. Additional hyperparameters comprise a learning rate $\eta =1\times {10}^{-4}$ and an experience replay buffer capacity of 5000 transitions. For the DDQN implementation, an $ϵ$-greedy exploration strategy is employed, with $ϵ$ undergoing linear decay from 1.0 to 0.01 throughout the initial 5000 training steps. The reference trajectory we use follows (7). All experiments were conducted on an Ubuntu 20.04 system equipped with two NVIDIA GeForce RTX 2080 Ti GPUs (NVIDIA Corporation, Santa Clara, CA, USA, 12 GB each), an AMD 9820X (Advanced Micro Devices, Santa Clara, CA, USA) processor, and 64 GB of RAM. The implementation is based on PyTorch v2.1.1. Training typically requires approximately 2 h to complete.

We first evaluate some classical RL algorithms to see which algorithm works best for the considered vehicle tracking problem, including TRPO [27], PPO [28], SAC [26], TD3 [25], and DDPG [24]. The evaluation curves of those RL algorithms under nominal disturbances ($w=0.02,w_x=0.1$) are illusrated in Figure 2, which shows that TD3 and PPO are two best-performing models. We further evaluate the performance of different RL models under various disturbance levels. As shown in Figure 3, PPO stands out as the best model that consistently outperforms other models. It is worth noting that all RL models can work better than either local MPC or cloud MPC alone.

Figure 2. Evaluation curves during training with different RL benchmarks for path tracking.

Figure 3. Performance comparison between local, cloud MPC controllers and five classical RL benchmarks.

Since PPO works best, it is chosen as the RL algorithm for further comparisons. A detailed comparison between PPO and local/cloud MPC under different initial conditions is shown in Figure 4. It can be seen that PPO consistently perform better for a wide range of initial conditions.

Figure 4. Performance comparison between local, cloud MPC controllers and PPO under different initial conditions.

In addition, the control and trajectories of different strategies are shown in Figure 5. It can be seen that the RL intelligently fuses local and cloud control to generate smooth tracking performance, demonstrating its capability of learning the hybrid control strategy for improved performance. To further evaluate the generalizability of our method, the same experimental procedure is applied to a straight-line reference trajectory $y=0$. The results shown in Figure 6 consistently demonstrate the effectiveness of our approach across different reference paths.

Figure 5. Tracking Performance under Sinusoidal Reference Path. The first row shows the vehicle trajectories on the X-Y plane. The trajectories tracked by the Local MPC, Cloud MPC, and the PPO-based DRL fusion controller are shown for comparison with reference trajectory (7) under $w=0.11$ and $w_x=0$. The fusion controller achieves the smoothest and most accurate tracking. The second row presents the corresponding control inputs over time. The subplots illustrate the control signals generated by each controller, showing how the DRL agent intelligently blends the local and cloud commands to produce a stable and effective control input, avoiding the oscillations seen in the Local MPC or the latency-induced jumps in the Cloud MPC.

Figure 6. Tracking Performance under Straight-Line Reference Path. The first row shows the vehicle trajectories on the X-Y plane. The trajectories tracked by the Local MPC, Cloud MPC, and the PPO-based DRL fusion controller are shown for comparison with reference trajectory $y=0$ under $w=0.11$ and $w_x=0$. The fusion controller demonstrates minimal lateral deviation and superior stabilization. The second row presents the corresponding control inputs over time. The subplots show the control effort of each strategy. The DRL fusion policy effectively balances the rapid response of the Local MPC and the optimality of the Cloud MPC, resulting in a controlled, smooth input that rejects disturbances and maintains precise path following.

5. Conclusions & Future Work

In this paper, we proposed a novel cloud-assisted framework with advanced reinforcement learning (RL) techniques. A multi-objective reward function was proposed to balance control performance and control efforts. In comparison to existing approach, the proposed algorithm does not require any knowledge of the closed-loop dynamics (i.e., model-free) and delivers superior performance. The proposed approach was comprehensively validated on the path planning problem for autonomous driving. The RL-based approach outperformed both the cloud-only and local-only MPC baselines, as well as the rule-based approach.

In subsequent research, we plan to extend this work by incorporating dynamic computational constraints and associated costs into the deep-RL-eMPC architecture for autonomous path tracking. We also intend to validate the framework using high-fidelity simulation platforms, including professional tools such as CARLA, under more realistic and complex driving scenarios. Finally, the theoretical guarantees of the proposed method, particularly regarding stability and convergence, will be rigorously evaluated through hardware-in-the-loop experiments.