Reliability Analysis on Structural System of Reinforced Concrete Underground Silo Based on LHS-RSM

Abstract

The RC underground silo, a novel grain storage structure, is a cylindrical shell surrounded by rock, soil, and groundwater. It leverages the low-temperature underground setting to preserve grain quality. However, the complex underground geotechnical environment may negatively affect the silo’s reliability, and limited information is available about the reliability of the reinforced concrete underground silo. The current research developed a structural system reliability analysis method based on LHS, the RSM, and EEVET, namely the LHS-RSM, for structural reliability analysis. Performance functions were established and controlled by concrete strength and component deformation on the components of the RC underground silos. The limit state function of the whole RC underground silo system was developed based on the EEVET. Combined with the PDS method in the FE program ANSYS 15.0, the random FE analysis of the RC underground silo based on the LHS-RSM was achieved, and the failure probabilities and corresponding reliability indices were evaluated for both individual components and the overall structural system. The research results show that when the silo is treated as a series system, its failure probability exceeds the values calculated for any single failure mode. Therefore, if only the component failure modes are considered, the reliability of RC underground silos will be overestimated, which proves the necessity of conducting a system reliability analysis on RC underground silos. Under the action of underground soil and groundwater, the calculated reliability index of the structural system of the RC underground silo is 3.40, indicating that the entire series structural system meets the requirements of current design codes. The reliability of this novel underground grain storage structure is satisfactory. The findings offer valuable insights for designing and constructing RC underground silos.

1. Introduction

Ensuring stable grain supplies underpins both public health and national security; it stabilizes society and supports sustained economic expansion. To this end, China has established a comprehensive grain reserve system coupled with an active strategic storage policy that shields the country from supply shocks [1], guaranteeing food for non-rural residents and cushioning the impact of large-scale natural disasters or sudden emergencies [2,3]. At present, grain in China is mainly stored in aboveground granaries or RC silos. High ambient temperatures can drive internal granary temperatures to levels that cause spoilage and insect infestation [4]. To overcome the deterioration and pest problems associated with high temperatures in aboveground granaries, underground storage technologies have attracted increasing attention in recent years. Storing grain underground is a time-honored technique that exploits the space beneath soil and rock masses [5,6,7]. The virtually constant low temperature of the underground environment allows grain to be kept at low ambient temperatures, effectively preserving its quality [8]. Most existing underground granaries, however, are protected by surrounding rock, are strongly constrained by local geology, offer limited storage volume, and fail to make full use of the underground space [6]. The RC underground silo is a novel subterranean grain storage structure. The silo wall is a cylindrical shell, and the silo bottom is a conical shell. This configuration provides excellent mechanical performance together with the advantages of a low-temperature environment, energy conservation, and environmental protection. In addition, RC underground silos offer good concealment, fire resistance, a small surface footprint, and environmental benefits and can avoid becoming a target of attack in war, all of which are of strategic importance. The cylindrical shell wall acts like a bridge, distributing soil and water pressures uniformly through the structure and thereby reducing stress concentrations and making full use of material strength [9]. This largely overcomes the traditional limitation that underground granaries must rely on special topography and simultaneously eliminates the strong influence of the ambient temperature that plagues aboveground granaries [10].

Because RC underground silos are embedded in a complex geotechnical and groundwater environment, large uncertainties arise during investigation, design, construction, and operation [11]. An allowable stress (deterministic) design only accounts for the nominal magnitude of each parameter. Structural safety has a direct bearing on human life and property; conducting a reliability study of RC underground silos can prevent the enormous economic waste and loss that would follow an unexpected safety failure. At present, no design code exists for RC underground silos, so reliability-based design procedures for these structures are urgently needed. Although evaluating individual components provides a basis for structural safety, it risks undervaluing the likelihood of overall system failure. Consequently, the reliability of an engineering project should ultimately be evaluated at the structural–system level.

RC silos, as critical infrastructure, have attracted extensive mechanical performance studies. To date, however, most experimental and numerical work has focused on aboveground RC silos. Blight [12] reported long-term strain measurements on four RC silos and showed how the dead load is shared between the steel and the concrete over the service life. Abdel-Fattah et al. [13,14] employed numerical simulations to analyze the internal forces generated within granular materials while filling concrete silos under various support conditions. Balkaya et al. [15] calculated internal forces in the wall of a single RC silo under grain loading and extended it to investigate the behavior of silo groups. Lapko [16] embedded pressure cells in a model concrete silo filled with white mustard seed and recorded the horizontal pressures generated during eccentric discharge from a bottom outlet, clarifying the dynamic characteristics of the eccentric pressure changes. Kermiche et al. [17] strengthened an existing wheat-filled RC silo by wrapping the exterior with a carbon-fiber-reinforced polymer and subsequently studied the mechanical response of the retrofitted shell. Jayachandran [18] designed a farm-size flat-bottom silo for rough rice in which a bamboo reinforcement replaced steel, developed an FE model of the RC silo, and simulated the grain-filling process. Matiašková et al. [19] examined the behavior of RC silos exposed to fire, analyzed the failure mechanism of the cylindrical wall under the thermal gradients that arise during heating and cooling, and discussed the strengthening required to restore structural safety. Gurfinkel [20] presented a simple design procedure for partially post-tensioned circular concrete silos subjected to combined bending and tension that can be used for both new designs and existing structures. Bywalski & Kamiński [21] described a collapse of the RC roof slab of a cylindrical silo, identified the causes, and explained the failure mechanism. Maraveas [22] surveyed failures of RC silos used in agriculture; reviewed their design, repair, and strengthening; and evaluated the influence of different retrofit strategies on structural performance. Kawecki et al. [23] carried out a nonlinear stability analysis of an RC silo wall using a plastic damage material model with an assumed initial imperfection and investigated the buckling of the wall under post-tensioning forces.

Several researchers have explored RC underground grain silos. Chen et al. [24] used computational fluid dynamics to analyze the temperature field and geometric effects in an RC underground silo. Xiong et al. [25] combined cylindrical shell models and FE analysis to assess the load-bearing capacity of underground silo walls and analyzed the distribution of vertical bending moments and circumferential forces. The field monitoring of lateral earth pressures by Xiong et al. [26] led to the calculation of Rankine pressures and the derivation of earth pressure design formulas. Chen et al. [11] applied a Monte Carlo stochastic FE method to evaluate the reliability of RC underground silos and the sensitivity of performance functions to input parameters. Liu et al. [27,28] conducted reduced-scale uplift tests to measure displacements and analyze forces like buoyancy and friction. Chen et al. [29] derived closed-form solutions for deformations and internal forces using cylindrical shell bending theory. Jin et al. [30] combined stress monitoring with numerical simulations to study the mechanical behavior of silo walls. Chuai et al. [31] tested full-scale steel plate/RC composite walls to compare the mechanical performance of vertical joints in precast underground silos. Zhang et al. [32,33,34] investigated the waterproofing efficiency and mechanical response of plastic concrete silo walls under combined bending and water pressure through experiments and numerical modeling. While most prior studies focus on the mechanical performance of individual components, research on the reliability of RC underground grain silos remains limited, with no reports addressing system-level reliability.

Owing to the scarcity of studies on the system-level reliability of RC underground silos, this paper applies the LHS-RSM framework to address this research gap. Firstly, a structural system reliability method that combines LHS, the RSM, and EEVET was developed; the LHS-RSM framework was used for a reliability analysis of the entire silo. Then, limit state functions were established for the strength-controlled and deformation-controlled failure of the critical components of the RC underground silo. An additional limit state function for the system was then derived with EEVET. Finally, through the LHS-RSM procedure with the PDS module in ANSYS, stochastic FE analyses were performed. The procedure yields the failure probabilities and reliability indices for each component as well as for the silo treated as a serial structural system.

2. LHS-RSM for Structural Reliability Analysis

2.1. Failure Probability of Structure

Structural reliability is measured by the survival probability P_r and the failure probability P_f. When the performance of the structure is governed by n random parameters, collected in the vector $x= {(x_1,x_2,\cdots ,x_n)}^{\mathrm{T}}$, x denotes any random quantity such as the material strength, applied actions, or connection conditions. The performance function can be defined as [35]

$$Z=G(\mathit{x})=G\left(x_1,x_2,\cdots ,x_n\right)$$

(1)

If the performance function solely involves two random variables—the structural resistance R and load effect S—its most elementary form can be written as follows:

$$Z=G(R,S)=R-S$$

(2)

The random variables entering the performance function are continuous, and Z possesses the probability density function f_z(z) and cumulative distribution function F_z(z). The survival and failure probabilities of the structure can be calculated as

$$P_{\mathrm{r}}=P(Z>0)={\displaystyle {\int }_0^{\infty }{f}_Z(z)\mathrm{d}z}=1-F_Z(0)$$

(3)

$$P_{\mathrm{f}}=P(Z\le 0)={\displaystyle {\int }_{-\infty }^0{f}_Z(z)\mathrm{d}z}=F_Z(0)$$

(4)

The joint probability density function of n-dimensional basic random variables $\mathit{x}={(x_1,\hspace{0.33em}{x}_2,\hspace{0.33em}\cdots ,\hspace{0.33em}{x}_n)}^{\mathrm{T}}$ is $f_X(\mathit{x})$ and the joint cumulative distribution function is $F_X(\mathit{x})$, the failure probability of the structure can be expressed as

$$P_{\mathrm{f}}={\int }_{Z\le 0}{f}_X(\mathit{x})\mathrm{d}x={\displaystyle \int \cdots }{\int }_{Z\le 0}{f}_X\left(x_1,x_2,\cdots ,x_n\right)\mathrm{d}{x}_1\mathrm{d}{x}_2\cdots \mathrm{d}{x}_n$$

(5)

If the random variables are mutually independent and the marginal probability density function of each variable x_i is denoted by $f_{X_i}(x_i)$, the failure probability of the structure can be rewritten as

$$P_{\mathrm{f}}={\displaystyle \int \cdots }{\int }_{Z\le 0}{f}_{X_1}(x_1)f_{X_2}(x_2)\cdots f_{X_n}(x_n)\mathrm{d}{x}_1\mathrm{d}{x}_2\cdots \mathrm{d}{x}_n$$

(6)

2.2. LHS-RSM

In structural reliability simulations, the RSM replaces an implicit or computationally expensive true limit state surface with an inexpensive, tractable surrogate [36]. Let the parameters—or design points—be an n-dimensional vector, i.e., the independent variables of the target function. Even if the target function lacks an explicit expression or is only implicitly defined, supplying sample points $x^{(j)}$ allows the corresponding response values $y^{(j)}=y(x^{(j)})$ to be obtained experimentally (numerically). After a sufficient number of samples, undetermined coefficient techniques are used to construct an approximate function of the true performance function [37]:

$$\tilde{G}(\mathit{x})=G(\mathit{x})$$

(7)

where $\tilde{G}(\mathit{x})$ is the approximate RSF of the original objective function.

Because the exact input–output relationship of the target function is unknown, the mathematical form of $\tilde{G}(\mathit{x})$ has to be prescribed beforehand. A reasonable function form can make the approximation more accurate. The selection of the form of the RSF is mostly linear, quadratic without cross terms, and fully quadratic. The forms of each RSF are expressed as follows:

Linear form

$$\tilde{G}(\mathit{x})={\alpha }_0+{\displaystyle \sum _{j=1}^n{\alpha }_j{x}_j}$$

(8)

Quadratic form without cross terms

$$\tilde{G}(\mathit{x})={\alpha }_0+{\displaystyle \sum _{j=1}^n{\alpha }_j{x}_j}+{\displaystyle \sum _{j=1}^n{\alpha }_{jj}{x}_j^2}$$

(9)

Quadratic form with cross terms

$$\tilde{G}(\mathit{x})={\alpha }_0+{\displaystyle \sum _{j=1}^n{\alpha }_j{x}_j}+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=i}^n{\alpha }_{ij}{x}_i{x}_j}}$$

(10)

where ${\alpha }_0$ is the constant term coefficient, ${\alpha }_j$ is the coefficient of the first-order term, and ${\alpha }_{ij}$ is the coefficient of the second-order term.

Equations (8)–(10) can be unified and rewritten as follows:

$$\tilde{G}(\mathit{x})={\displaystyle \sum _{i=1}^{k-1}{\beta }_i{x}_i}$$

(11)

where ${\beta }_i$ is the constant term coefficient.

To determine ${\beta }_i$, m($m\ge k$) experiments are required, with each experiment obtaining response values $G^{(i)}(\mathit{x})(i=0,1,\cdots ,m-1)$ corresponding to sample points through different values. After m experiments, the obtained data can be expressed as

$$\left.\begin{array}{cccc}{x}_0^{(0)}& x_1^{(0)}& \cdots & x_{k-1}^{(0)}\\ x_0^{(1)}& x_1^{(1)}& \cdots & x_{k-1}^{(1)}\\ ⋮& ⋮& & ⋮\\ x_0^{(m-1)}& x_1^{(m-1)}& \cdots & x_{k-1}^{(m-1)}\end{array}\hspace{0.33em}\hspace{0.33em}\right|\hspace{0.33em}\begin{array}{c}{G}^{(0)}(\mathit{x})\\ G^{(1)}(\mathit{x})\\ ⋮\\ G^{(m-1)}(\mathit{x})\end{array}$$

(12)

Substitute the above m sample points $x^{(j)}(j=0,1,\cdots ,m-1)$ into Equation (11) to obtain the RSF values:

$$\left\{\begin{array}{l}\hspace{0.33em}{\tilde{G}}^{(0)}(\mathit{x})={\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(0)}}\\ \hspace{0.33em}{\tilde{G}}^{(1)}(\mathit{x})={\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(1)}}\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⋮\\ {\tilde{G}}^{(m-1)}(\mathit{x})={\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(m-1)}}\end{array}\right.$$

(13)

Since the RSF $\tilde{G}(\mathit{x})$ is an approximation of the performance function $G(\mathit{x})$, the result calculated from Equation (13) is usually not equal to the response value obtained from the experiments, and there is an error between the two functions, which can be expressed as follows:

$$\left\{\begin{array}{l}\hspace{0.33em}{\epsilon }^{(0)}={\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(0)}}-G^{(0)}(\mathit{x})\\ \hspace{0.33em}{\epsilon }^{(1)}={\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(1)}}-G^{(1)}(\mathit{x})\\ \hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}⋮\\ {\epsilon }^{(m-1)}={\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(m-1)}}-G^{(m-1)}(\mathit{x})\end{array}\right.$$

(14)

In Equation (14), the error can be minimized by minimizing ${\displaystyle \sum _{j=0}^{m-1}{\left({\epsilon }^{(j)}\right)}^2}$, which simultaneously determines the coefficient ${\beta }_i(i=0,1,\cdots ,m-1)$. Using the least squares method, the sum of squared errors is minimized to find the RSF that is closest to all sampling points:

$$S(\beta )={\displaystyle \sum _{j=0}^{m-1}{\left({\epsilon }^{(j)}\right)}^2}={\displaystyle \sum _{j=0}^{m-1}{\left({\displaystyle \sum _{i=0}^{k-1}{\beta }_i{x}_i^{(j)}-G^{(j)}(\mathit{x})}\right)}^2\to \min }$$

(15)

To determine the RSF, a series of experimental points for X must first be designed, and a corresponding series of performance function values for the structure must be calculated point by point. The experimental design involves planning experiments through systematic data collection. One of the ideal characteristics of the RSF experimental design is its ability to estimate model parameters with fewer experiments.

LHS is currently the most effective experimental design method [38]. Thanks to its random orthogonal strategy, LHS yields an accurate surrogate response surface with only a handful of points; the sample size need only exceed the minimum required to identify the unknown coefficients and can be chosen freely for any problem.

For the design variable $x={(x_1,\cdots ,x_n)}^{\mathrm{T}}$, take m sample points. Then, following the principle of equal probability, divide the domain of each factor into m different intervals. Arbitrarily select a value x from each interval to obtain n sets of data ${\widehat{x}}_i={(x_i^1,\cdots ,x_i^m)}^{\mathrm{T}}(i=1,\cdots ,n)$. By arbitrarily combining the elements in these arrays, m sample points can be obtained.

LHS first fixes the sample size then slices the cumulative distribution of every variable into equal-probability segments on the [0, 1] axis. A single value is picked from each segment, and the collection of these interval representatives is finally combined to re-approximate the original probability. The ordinal matrix R of the LHS is generated randomly, inevitably introducing some statistical correlation among its columns, which may affect the simulation results. One method to reduce the statistical correlation utilizes the Spearman rank correlation coefficient of the ordinal matrix R [38]. The inter-column dependence in the ordinal matrix R is quantified by the Spearman rank correlation matrix, whose entries ρᵢⱼ provide the rank correlation between columns i and j:

$${\rho }_{ij\mathrm{S}}=1-{\displaystyle \frac{6}{N\left(N^2-1\right)}}{\displaystyle \sum _{k=1}^N{\left(r_{ki}-r_{kj}\right)}^2}$$

(16)

3. Reliability Analysis Method for Structural System

3.1. Failure Probability of Structural System

Structural assemblies with two or more components are usually classified as a series, parallel, or hybrid. A series chain collapses as soon as any link fails, whereas a parallel arrangement survives until every member has failed. The structural system consists of n components; the stress on member i is S_i, and its resistance is R_i. The distribution functions are $F_{S_i}(x)$ and $F_{R_i}(y)$; S_i and R_i are independent of each other. According to reliability theory, the survival probability P_r can be expressed as

$$P_{{\mathrm{r}}_i}=P\left\{G_i=R_i-S_i>0\right\}={\displaystyle {\int }_0^{\infty }{\displaystyle {\int }_x^{\infty }\mathrm{d}{F}_{R_i}(y)\mathrm{d}{F}_{S_i}(x)}}$$

(17)

Then, the failure probability P_f can be expressed as

$$P_{{\mathrm{f}}_i}=P\left\{G_i=R_i-S_i\le 0\right\}=1-P_{{\mathrm{r}}_i}$$

(18)

where $P_{{\mathrm{r}}_i}$ is the survival probability of component i, $P_{{\mathrm{f}}_i}$ is the failure probability of component i, and $P\left\{\bullet \right\}$ is the probability of events occurring.

The failure probability of series and parallel structural systems can be calculated as follows:

$$P_{\mathrm{f}}(n)=P\left(G_1(n)\cup G_2(n)\cup \cdots \cup G_m(n)\le 0\right)=P\left({\displaystyle \underset{i=1}{\overset{m}{\cup }}{G}_i(n)\le 0}\right)$$

(19)

$$P_{\mathrm{f}}(n)=P\left(G_1(n)\cap G_2(n)\cap \cdots \cap G_m(n)\le 0\right)=P\left({\displaystyle \underset{i=1}{\overset{m}{\cap }}{G}_i(n)\le 0}\right)$$

(20)

where $G_i(n)$ is the event of component i failure, n is a vector quantity including basic random variables, and $G(\bullet )$ is the performance function of component i.

3.2. Equivalent Extreme Value Event Theory for Structural System Reliability

The EEVET can be applied to the reliability analysis of structural systems [39]. If X and Y are correlated random variables, and W_min is the minimum value of X and Y, then

$$P\left\{(X>a)\cap (Y>a)\right\}=P\left\{W_{\min }>a\right\}$$

(21)

The probability of a random event $(X>a)\cup (Y>a)$ can be calculated as

$$\begin{array}{ll}P\left\{(X>a)\cup (Y>a)\right\}& ={\displaystyle \underset{x>a}{\iint }{p}_{XY}(x,y)}\mathrm{d}x\mathrm{d}y+{\displaystyle \underset{y>a,x<a}{\iint }{p}_{XY}(x,y)}\mathrm{d}x\mathrm{d}y\\ & ={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left({\displaystyle \underset{a}{\overset{\infty }{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y+{\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{-\infty }{\overset{\infty }{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y\end{array}$$

(22)

Because

$$W_{\max }=\max (X,Y)=\left\{\begin{array}{l}Y\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}X\le Y\\ X\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}X>Y\end{array}\right.$$

(23)

Therefore

$$\begin{array}{ll}P\left\{W_{\max }>a\right\}& ={\displaystyle \underset{a}{\overset{\infty }{\int }}{p}_{W_{\max }}(z)\mathrm{d}z}=P\left\{\max (X,Y)>a\right\}\\ & ={\displaystyle \underset{x<y,y>a}{\iint }{p}_{XY}(x,y)}\mathrm{d}x\mathrm{d}y+{\displaystyle \underset{x>y,x>a}{\iint }{p}_{XY}(x,y)}\mathrm{d}x\mathrm{d}y\\ & ={\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{-\infty }{\overset{a}{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y+{\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{a}{\overset{y}{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y\\ & +{\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{-\infty }{\overset{a}{\int }}{p}_{XY}(x,y)\mathrm{d}y}\right)}\mathrm{d}x+{\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{a}{\overset{x}{\int }}{p}_{XY}(x,y)\mathrm{d}y}\right)}\mathrm{d}x\end{array}$$

(24)

Swapping the integration sequence of x and y in the remaining pair of integrals yields the probability of EEVE, $(X>a)\cup (Y>a)$, which can be calculated as follows:

$$\begin{array}{ll}P\left\{W_{\max }>a\right\}& ={\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{-\infty }{\overset{a}{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y+{\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{a}{\overset{y}{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y\\ & +{\displaystyle \underset{-\infty }{\overset{a}{\int }}\left({\displaystyle \underset{a}{\overset{\infty }{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y+{\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{y}{\overset{\infty }{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y\\ & ={\displaystyle \underset{a}{\overset{\infty }{\int }}\left({\displaystyle \underset{-\infty }{\overset{a}{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y+{\displaystyle \underset{-\infty }{\overset{\infty }{\int }}\left({\displaystyle \underset{a}{\overset{\infty }{\int }}{p}_{XY}(x,y)\mathrm{d}x}\right)}\mathrm{d}y\end{array}$$

(25)

where W_max is the EEVE of $(X>a)\cup (Y>a)$.

According to the EEVET, when there are n random events, W_min is the EEVE of $(X_1>a)\cap (X_2>a)\cap \cdots \cap (X_n>a)$, and W_max is the EEVE of $(X_1>a)\cup (X_2>a)\cup \cdots \cup (X_n>a)$.

Applying the EEVET delivers the system failure probability. For series structural systems,

$$P_{\mathrm{f}}=P\left\{\underset{i=1,m}{\min }\left\{G_i(n)\right\}\le 0\right\}$$

(26)

For a parallel system, the failure probability can be formulated as follows:

$$P_{\mathrm{f}}=P\left\{\underset{i=1,m}{\max }\left\{G_i(n)\right\}\le 0\right\}$$

(27)

Consequently, the system performance function is obtained. For series structural systems,

$$Z=\underset{i=1,m}{\min }\left\{G_i(n)\right\}$$

(28)

For a parallel structure system, the performance function takes the form

$$Z=\underset{i=1,m}{\max }\left\{G_i(n)\right\}$$

(29)

Although Equations (16) and (17) are complex, the reliability of structural systems can be efficiently calculated because each structural system has only one performance function.

4. Structural System Reliability of Underground Silo

4.1. Engineering Background

The present study investigates the structural system reliability of an RC underground grain silo through the proposed LHS-RSM structural system reliability analysis method. The silos are arranged 2 × 1; each silo provides 3500 t of wheat storage. The silo top is located 1.5 m underground, with the maximum depth of the structure reaching 19.96 m. The silo wall, an RC cylindrical shell, has an internal diameter of 25 m, stands 8.76 m high, and is 0.30 m thick. The middle cylinder, likewise a cylindrical shell, features an internal diameter of 0.8 m, a height of 18.36 m, and a wall thickness of 0.18 m. The silo bottom is constructed as an inverted RC conical shell that is 0.40 m thick and with a 35° slope. The silo top is designed as a beam–slab RC system with a 5% slope for drainage purposes, and the slab thickness is 0.15 m. Radial primary beams are 400 × 1300 mm, radial secondary beams are 250 × 600 mm, circumferential primary beams (adjacent to the wall) are 250 × 700 mm, and circumferential secondary beams (adjacent to the shaft) are 250 × 600 mm. The concrete grade is C40, and the reinforcements are HRB400E. The RC underground silo is shown in Figure 1, and the silo top is drawn in Figure 2.

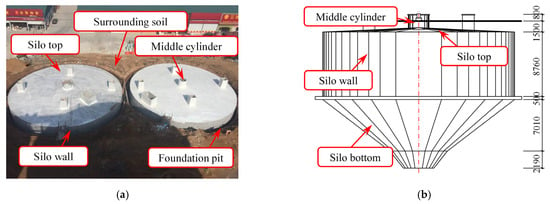
Figure 1. RC underground silo: (a) general view and (b) front view.

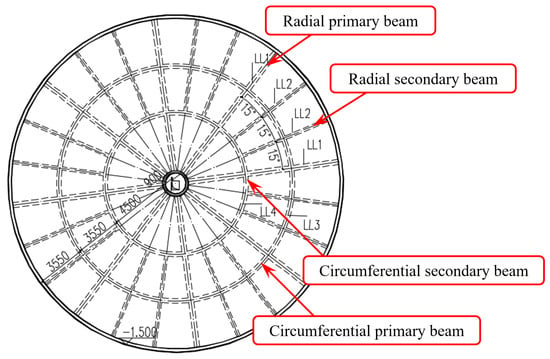
Figure 2. Silo top of RC underground silo.

The mechanical properties of the soil are listed in Table 1. The RC underground silo wall is a cylindrical shell structure. Because of the arching effect, the deformation of the silo wall is small. So, the earth pressure is the static earth pressure. The coefficient of the static earth pressure is $K_i=1-\sin {\phi }_i$. The result of lateral pressure is shown in Figure 3.

Table 1. Mechanical properties of each soil layer.

Soil Layer	Soil Type	Average Thickness (m)	Accumulated Depth (m)	Moisture Content (%)	Specific Gravity (kN/m3)	Void Ratio	Internal Friction Angle (°)
1	Silty sand	1.23	1.23	21.4	20	0.540	28
2	Silty clay	1.76	2.99	22.6	20.4	0.835	13.3
3	Silt	1.85	4.84	22.1	20.8	0.682	24.1
4	Silty sand	5.56	10.40	21.4	20	0.540	28
5	Silt	1.30	11.70	24.4	21.3	0.688	25.5
6	Silty sand	6.58	18.28	21.4	20	0.540	28
7	Silt	1.29	19.57	23.7	20.6	0.678	26
8	Silty sand	6.88	26.45	21.4	20	0.540	28

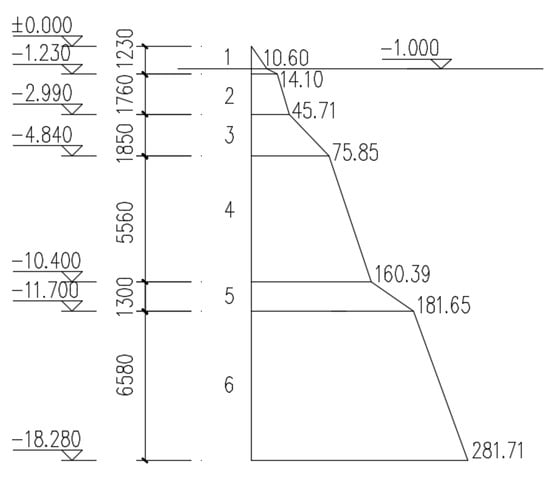
Figure 3. Overall distribution of soil and water lateral pressure on the silo.

4.2. Finite Element Modeling

Based on the actual RC underground silo project, an overall FE model of the underground grain silo was constructed using ANSYS. A bottom-up modeling approach was adopted for its establishment. The ANSYS Solid185 element was selected for meshing the silo structure, while the Link8 element was used for the reinforcement. An element size of 0.3 m was adopted for the mesh, and hexahedral elements were generated via a sweeping method. To maintain computational efficiency, the present study adopts a linear elastic model for both the concrete and steel. This simplification inevitably precludes capturing phenomena such as concrete cracking, steel yielding, and the associated redistribution of internal forces that would occur in highly stressed regions. In the model of the silo structure, the elastic modulus of the concrete was set to 3.25 × 10¹⁰ Pa, and that of the reinforcement was set to 2.06 × 10¹¹ Pa. The FE model was established with a holistic approach. The model was split at the reinforcement locations, and the stiffness assigned to the lines where the reinforcement was located represented the steel embedded in the concrete. The FE model is shown in Figure 4.

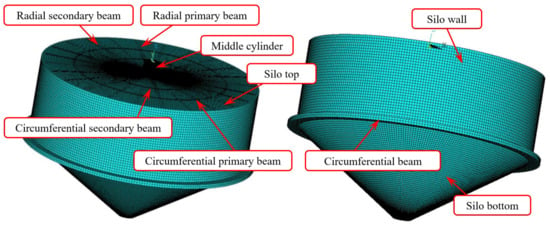
Figure 4. FE model of RC underground silo.

The reinforcement was modeled as embedded in the concrete, without considering the bond–slip between them. At the upper surface of the circumferential beam connecting the silo wall and silo bottom, the degrees of freedom in all directions were constrained. The complete FE model was loaded with gravity, the surcharge of backfill on the top, pore water pressure, and the lateral earth pressure. The existing research indicated that the soil subgrade reaction on the silo bottom can be ignored [40]. Thus, only groundwater buoyancy is added to the silo bottom.

4.3. Performance Function and Random Variables

Regarding the ultimate limit state check for the bearing capacity, the concrete in the RC underground silo is evaluated by functions represented by the Hsich–Ting–Chen strength criterion, which can be expressed as follows [41]:

$$g(X)={\sigma }_c-\left({\displaystyle \frac{A{J}_2}{{\sigma }_c}}+B\sqrt{J_2}+C{\sigma }_1+D{I}_1\right)$$

(30)

where ${\sigma }_1$ is the first principal stress; $I_1$ is the first stress tensor invariant; $J_2$ is the second deviatoric stress tensor invariant; and ${\sigma }_c$ is the compressive strength of concrete. A, B, C, and D are four basic parameters of the concrete material: A = 2.0108, B = 0.9714, C = 9.1412, and D = 0.2312 [41].

Each component of the RC underground silo is checked for bearing capacity failure through the performance function:

$$\begin{array}{ll}{z}_i& =g\left({\sigma }_c,{\sigma }_1,{\sigma }_2,{\sigma }_3\right)\\ & ={\sigma }_c-2.0108{\displaystyle \frac{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2}{6{\sigma }_c}}\\ & -0.9714\sqrt{{({\sigma }_1-{\sigma }_2)}^2+{({\sigma }_2-{\sigma }_3)}^2+{({\sigma }_3-{\sigma }_1)}^2}\\ & -9.1412{\sigma }_1-0.2312({\sigma }_1+{\sigma }_2+{\sigma }_3)\end{array}$$

(31)

where ${\sigma }_1,\hspace{0.33em}{\sigma }_2,\hspace{0.33em}{\sigma }_3$ are the first, second, and third principal stress; $i=1,2,3$ are the concrete strength limit states of the wall, top, and bottom, respectively.

Excessive deformation of the silo wall may breach the serviceability limit. In the existing literature [42], a displacement limit of 20 mm was specified for a 32 m diameter, 45.8 m high aboveground RC silo. The most unfavorable condition for the aboveground RC silo is when it is full, and the silo wall is in a state of circumferential tension. Because the underground silo is smaller in diameter and height and its wall is in circumferential compression when empty, a radial displacement limit of 12 mm was adopted. Thus, the performance function of the structural deformation of the silo wall can be expressed as follows:

$$z_4=g({\zeta }_{\lim },{\zeta }_{\max })={\zeta }_{\lim }-{\zeta }_{\max }$$

(32)

where ${\zeta }_{\max }$ is the maximum radial displacement. ${\zeta }_{\lim }$ is the limit value of radial displacement.

The RC underground silo top is a flexural member. Per the prevailing design code [43], the top deflection is limited; hence, the corresponding serviceability function becomes

$$z_5=g({\omega }_{\lim },{\omega }_{\max })={\omega }_{\lim }-{\omega }_{\max }$$

(33)

where ${\omega }_{\max }$ is the maximum deflection of the top. ${\omega }_{\lim }$ is the corresponding limit value. According to the current design codes [43], the limit value for the deflection of the silo top structure can be taken as l₀/300, where l₀ is the span of the beam.

Few studies have been conducted on the deformation failure of a conical shell. The current design code [44] indicated that the circumferential stiffness of a conical shell is high; hence, it is not necessary to perform a calculation on the deformation of a conical shell.

According to the EEVET, treating each component’s individual failure mode as a series system yields the following system performance function:

$$Z=\min \left\{Z_1,Z_2,Z_3,Z_4,Z_5\right\}$$

(34)

where Z is the system performance function of the RC underground silo.

From Equations (31)–(34), it can be seen that the silo wall deformations, silo top deflections, and concrete stresses in the performance functions of components and structural systems need to be obtained through an FE analysis. That is, Equations (31)–(34) are implicit functions, and the proposed LHS-RSM in this research applies to situations where the performance functions are implicit.

For the reliability assessment of the underground silo system, geometric sizes, material properties, and soil characteristics are all modeled as random variables. Variable statistical characteristics of material properties and soil that effect the reliability of underground silo are listed in Table 2 and Table 3 [45].

Table 2. Variable statistical characteristics of material properties.

Random Variable	Distribution	Mean Value	Variable Coefficient
Thickness of silo top H1	Normal	0.150 m	0.06
Thickness of silo wall H2	Normal	0.300 m	0.06
Thickness of silo bottom H3	Normal	0.400 m	0.06
Radius of silo DN	Normal	12.5 m	0.05
Elastic modulus of concrete M	Normal	3.25 × 1010 Pa	0.05
Compressive strength of concrete FC	Normal	19.1 × 106 Pa	0.15
Density of concrete DEN	Normal	2500 kg/m3	0.03

Table 3. Statistical characteristics of random variables in soil.

Random Variable	Distribution	Mean Value	Variable Coefficient
Unit weight of first-layer soil R1	Gumbel	20.00 kN/m3	0.03
Unit weight of second-layer soil R2	Gumbel	20.40 kN/m3	0.04
Unit weight of third-layer soil R3	Gumbel	20.80 kN/m3	0.03
Unit weight of fourth layer soil R4	Gumbel	20.00 kN/m3	0.03
Unit weight of fifth-layer soil R5	Gumbel	21.30 kN/m3	0.02
Internal friction angle of first-layer soil D1	Normal	28.00°	0.1
Internal friction angle of second-layer soil D2	Normal	13.30°	0.12
Internal friction angle of third-layer soil D3	Normal	24.10°	0.11
Internal friction angle of fourth-layer soil D4	Normal	28.00°	0.1
Internal friction angle of fifth-layer soil D5	Normal	25.50°	0.09

4.4. Reliability Analysis Flowchart

Figure 5 outlines the system reliability analysis procedure for the RC underground silo subjected to soil and groundwater actions.

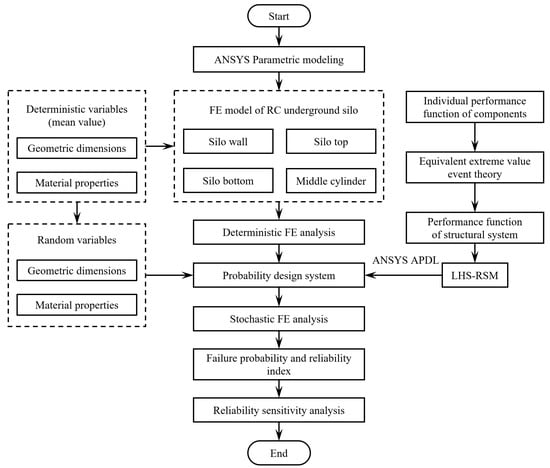
Figure 5. Structural system reliability analysis flowchart of RC underground silo.

5. Results and Discussions

Figure 6 illustrates the stress distribution. The silo demonstrates robust mechanical properties. The von Mises stress is relatively low on the walls, top, and bottom of the silo. However, stress concentrations are evident at the junction of the wall and beam, as well as at the connection between the top and beam. A maximum von Mises stress of 13.4 MPa occurs at the bottom of the mid-span section of the radial primary beam. This high tensile stress arises due to the combined effects of the self-weight and the soil load above.

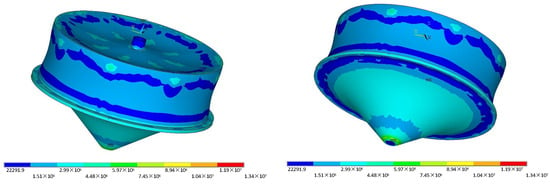
Figure 6. The von Mises stress of the RC underground silo (Pa).

Figure 7 presents the vertical displacement contour of the silo. Influenced by the self-weight and the overlying soil load, the maximum vertical displacement appears at the mid-span cross-section of the radial primary beam, reaching a maximum value of 4.27 mm. This displacement primarily results from the deflection of the silo top under these loads.

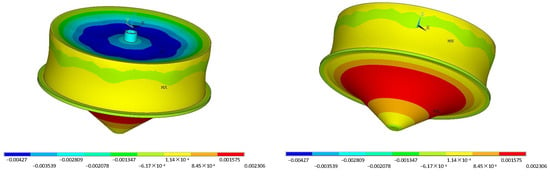
Figure 7. Vertical displacement of RC underground silo (m).

After the deterministic FE analysis, a stochastic FE analysis is required to obtain the approximate RSF of the performance function for the RC underground silo structural system. Through the parametric modeling and FE analysis in ANSYS, a reliability analysis data file was created; an approximate RSF was then fitted to 500 LHS runs, which can be expressed as follows:

$$\begin{array}{ll}Z& =1.0150\times {10}^{-2}+2.7440\times {10}^{-4}{H}_3+ 1.2726\times {10}^{-3}M-6.6385\times {10}^{-4}{M}^2+ 1.1312\times {10}^{-4}{R}_1^2\\ & -1.1669\times {10}^{-4}{D}_1^2-1.6465\times {10}^{-4}{H}_2{R}_1-3.4608\times {10}^{-4}{H}_{3}M-2.0049\times {10}^{-4}{H}_3{R}_4\\ & +3.3574\times {10}^{-4}{D}_{N}M+1.8100\times {10}^{-4}{D}_N{R}_4+2.7305\times {10}^{-4}{D}_N{D}_1-1.8411\times {10}^{-4}{D}_{EN}M\\ & -3.0405\times {10}^{-4}M{D}_3-1.6631\times {10}^{-4}{R}_2{D}_1-1.5993\times {10}^{-4}{R}_3{D}_3-1.9818\times {10}^{-4}{R}_4{D}_1\\ & -2.4354\times {10}^{-4}{D}_1{D}_3+1.3991\times {10}^{-4}M{F}_C-1.8296\times {10}^{-4}M{R}_1-2.7181\times {10}^{-4}M{R}_4\\ & -3.9417\times {10}^{-4}M{D}_1\end{array}$$

(35)

The RSF of Z (FC, M) is shown in Figure 8.

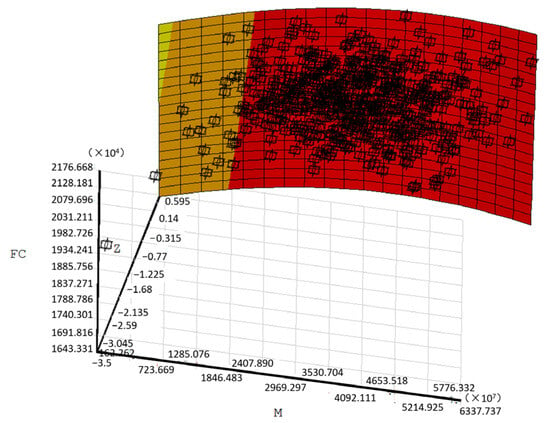
Figure 8. RSF of Z (FC, M) of RC underground silo.

Through 500 rounds of the random FE analysis based on LHS, the RSF of the structural system was fitted. Subsequently, the Monte Carlo method was employed to sample the random variables of the RSF, with a total of 10⁷ samples taken. The distribution of the sampling values, the sampling distribution histogram, and the cumulative distribution curve at a confidence level of 95% for the RSF are presented in Figure 9, Figure 10 and Figure 11.

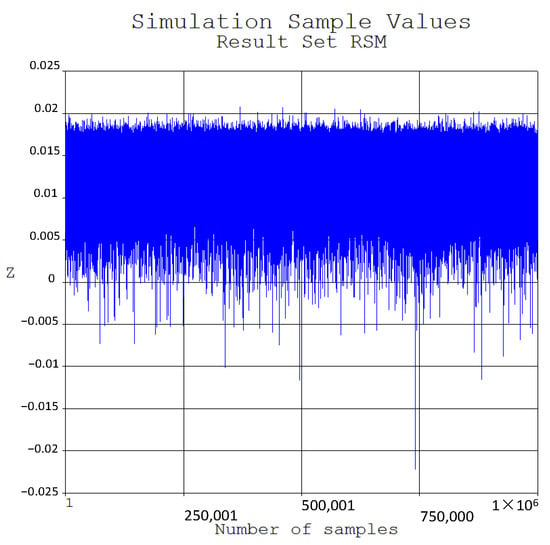
Figure 9. Distribution of sampling values of RSF.

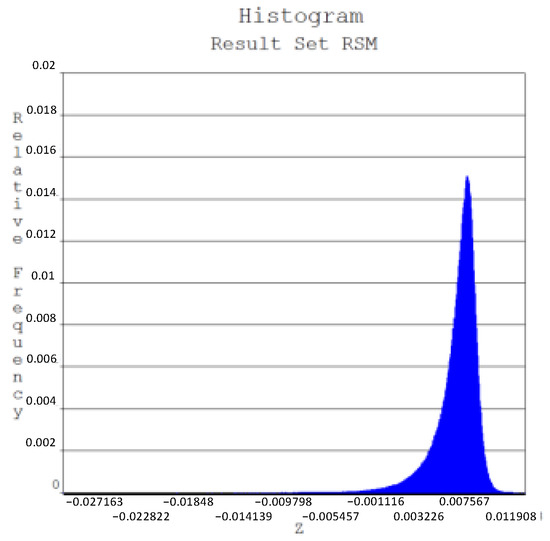
Figure 10. Sampling distribution histogram of RSF.

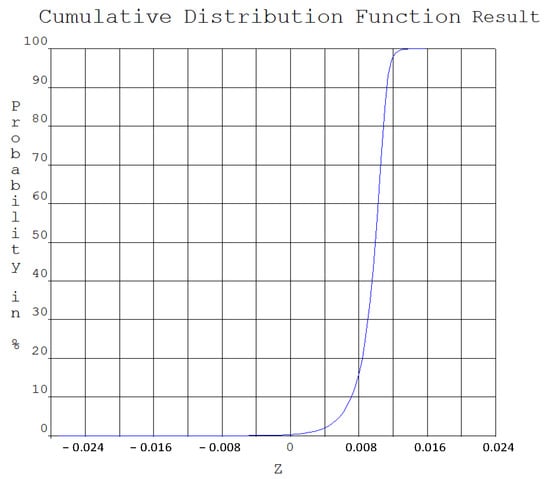
Figure 11. Cumulative distribution curve of RSF at a confidence level of 95%.

It can be observed from Figure 9, Figure 10 and Figure 11 that the RSF sample output history curve of the RC underground silo structural system exhibits good randomness, with a good convergence of the confidence interval curve and high confidence, indicating that the sample size of 10⁷ times meets the reliability requirements. After the Monte Carlo sampling with a sample size of 10⁷ times, the failure probabilities of the performance functions Z₁–Z₅ for each component under different failure modes are 1.984 × 10⁻⁵, 1.396 × 10⁻⁴, 3.174 × 10⁻⁵, 4.000 × 10⁻⁴, and 3.500 × 10⁻⁴, respectively, and their corresponding reliability indexes are 4.11, 3.63, 4.00, 3.35, and 3.39. Whereas the failure probability calculation result for the structural system is 3.365 × 10⁻⁴, and the corresponding reliability index is 3.40.

The reliability index of individual components under a single failure mode and the reliability index of the structural system of the RC underground silo can both meet the requirements of the current design code (reliability index β ≥ 3.2) [46]. The failure probability of the structural system is higher than that of individual components in a single failure mode. Therefore, if a reliability analysis is conducted at the component level, the failure probability of the structure will be underestimated, and the calculation results will be biased towards danger, which is similar to the reliability calculation results of structural systems in the existing research [47,48,49,50].

Due to the complex rock and soil mass and groundwater environment in which the underground silo body is located, factors such as the environment, structure, and materials all have an impact on the structural failure of the silo, and the degree of influence of each factor on reliability remains to be determined. Based on the PDS in ANSYS, an approximate RSF of the underground silo structural system was fitted using the RSM within it. The Monte Carlo method was applied to the RSF with 10⁷ samples to obtain the failure probability results. The post-processing function of the PDS was used to derive the calculation results of the sensitivity of the failure probability to each random parameter, as shown in Figure 12.

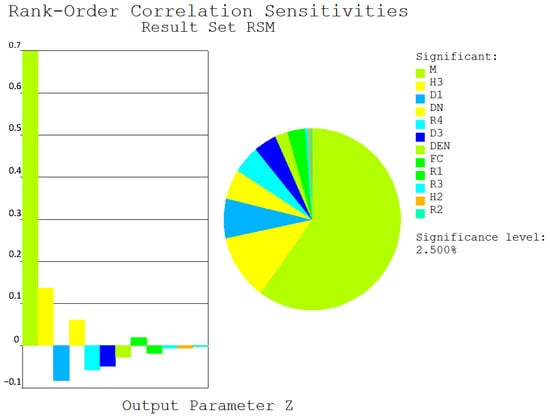
Figure 12. Reliability sensitivity of RC underground silo structural system.

It can be observed that the random variable with the greatest impact on the failure probability of the underground silo structural system is the elastic modulus of the concrete M. In addition, the thickness of the silo bottom H₃ and the internal friction angle of the first-layer soil D₁ also have a significant impact on the failure probability. Furthermore, the sensitivity of 11 random parameters, including the radius of silo D_N, concrete density D_EN, compressive strength of the concrete F_C, thickness of the silo wall H₂, unit weight of the first-layer soil R₁, unit weight of the second-layer soil R₂, internal friction angle of the third-layer soil D₃, unit weight of the third-layer soil R₃, and unit weight of the fourth-layer soil R₄, is greater than 2.5%, indicating a significant impact on the failure probability of the underground silo structural system.

6. Conclusions

The current research develops the LHS-RSM for structural system reliability analysis and implements the method in the PDS within ANSYS. The reliability of individual components of RC underground silos under a single failure mode, as well as the reliability of the structural system, was studied, and the impact of different random variables on reliability was investigated. The following conclusions can be drawn:

(1)

In the FE analysis of RC underground silo structures, the locations of maximum stress and deformation in the structural system are both at the bottom of the mid-span section of the radial primary beam. The maximum von Mises stress and beam deflection are 13.4 MPa and 4.27 mm, respectively.

(2)

The reliability results of individual components of the RC underground silo under a single failure mode, as well as the reliability results of the structural system, can meet the requirements of the current design code. Therefore, this novel type of underground grain silo structure has high safety and applicability.

(3)

System failure probability exceeds any individual component’s value and is not merely their sum; component-level assessment therefore underestimates the overall risk. The reliability analysis of the structure should be based on the structural system level, rather than the component level.

(4)

Random variable with the greatest impact on the failure probability of the underground silo structural system is the elastic modulus of concrete. In addition, the sensitivity of 11 random parameters is greater than 2.5%, indicating a significant impact on the failure probability of the underground silo structural system.

Overall, the current research presents a detailed study of a structural system reliability analysis for an RC underground silo based on the LHS-RSM. The results are expected to provide beneficial references for the structural design and construction of RC underground silos. Since the present study adopts a linear elastic constitutive model, our future work will integrate the LHS-RSM with a stochastic damage model of concrete to develop a nonlinear stochastic FE analysis for RC underground silos. This will enable a more accurate analysis of structural system reliability and will achieve structural system reliability assessments considering the reliability under concrete cracking control conditions.