Impact of Reinforcement Corrosion on Progressive Collapse Behavior of Multi-Story RC Frames
Abstract
1. Introduction
2. Deterioration Modeling Due to Rebar Corrosion Effects
- (1)
- Reduction in the cross–sectional area of the corroded rebar;
- (2)
- Degradation of the mechanical properties of the corroded rebar;
- (3)
- Deterioration of the concrete due to cracking and spalling caused by the expansion of corrosion products;
- (4)
- Reduction in the bond behavior between the corroded rebar and the surrounding concrete.
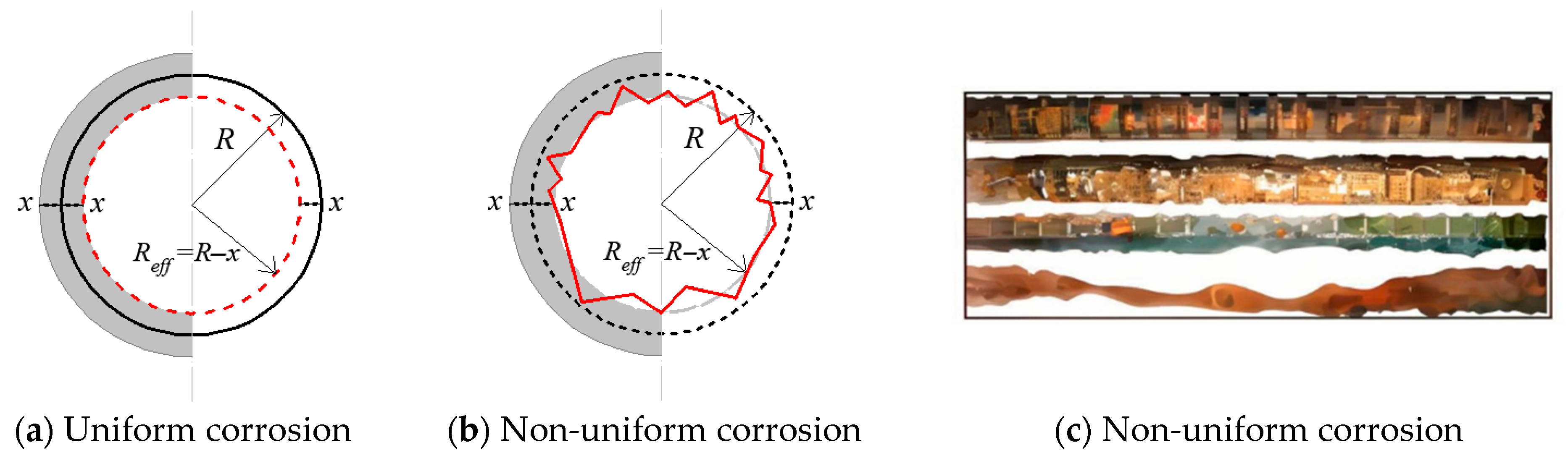
2.1. Corrosion-Induced Reduction in Rebar Cross-Sectional Area
2.2. Corrosion-Induced Deterioration of Rebar Mechanical Properties
2.3. Corrosion-Induced Deterioration of Steel Ductility in Reinforcing Bars
2.4. Influence of Corrosion on Concrete Properties
3. Approaches for Progressive Collapse Analysis
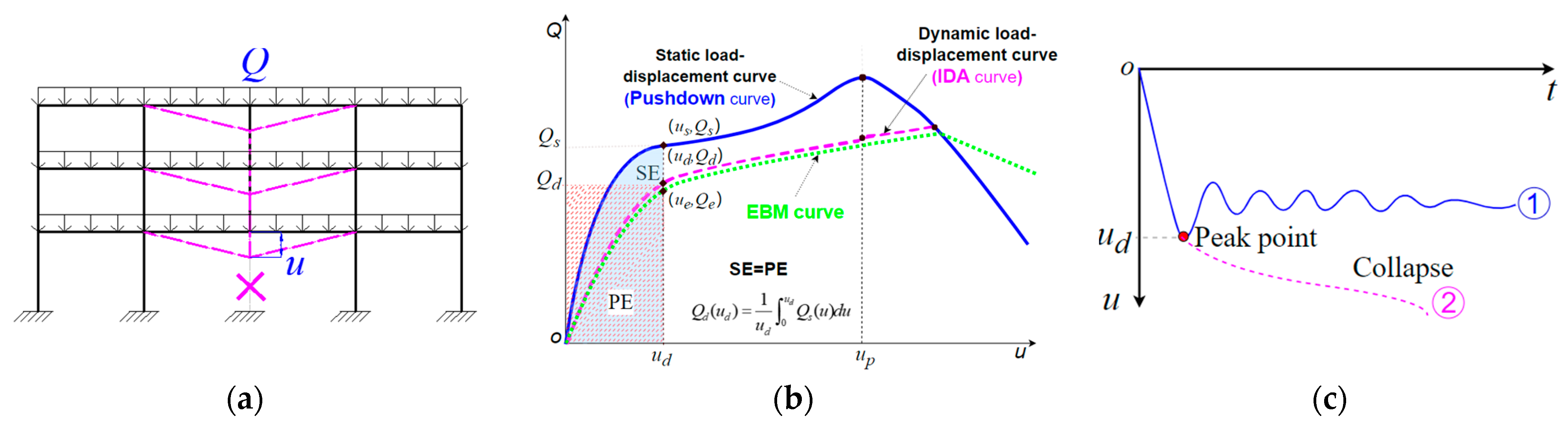
3.1. Alternate Load Path Method
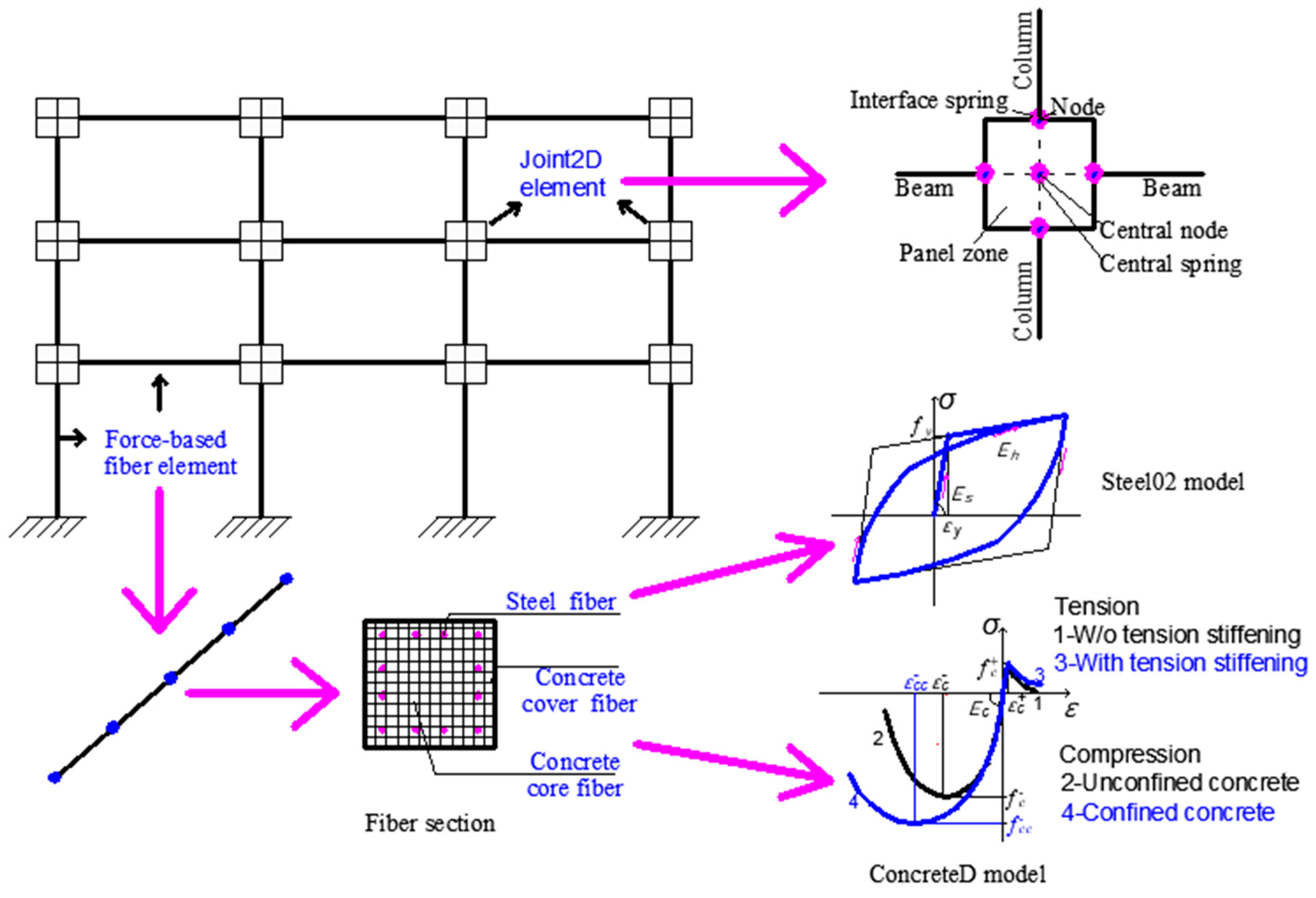
3.2. Numerical Modeling Techniques
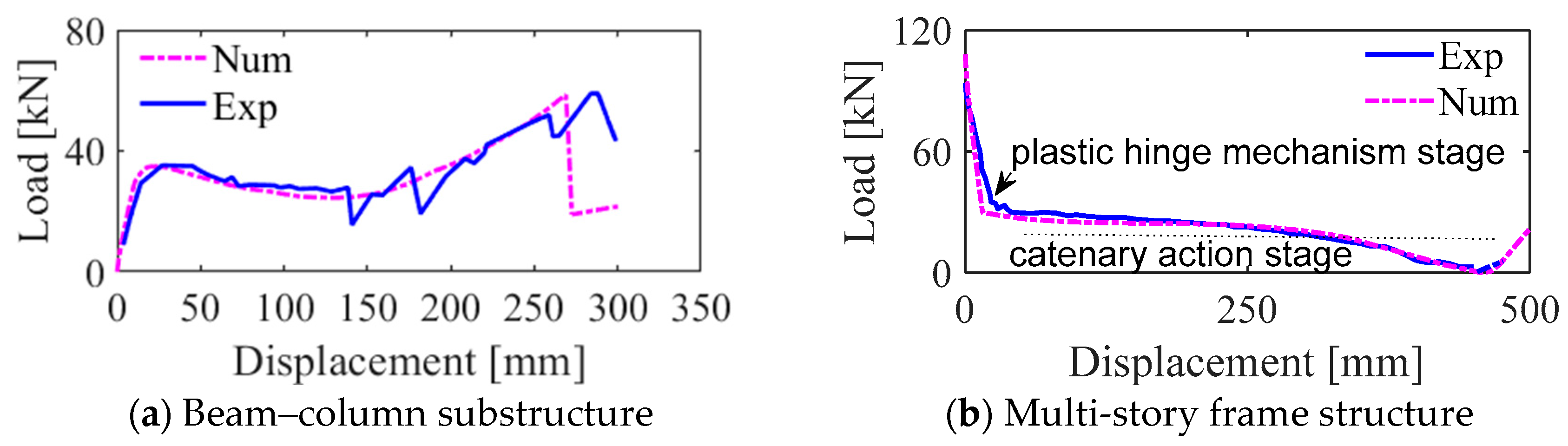
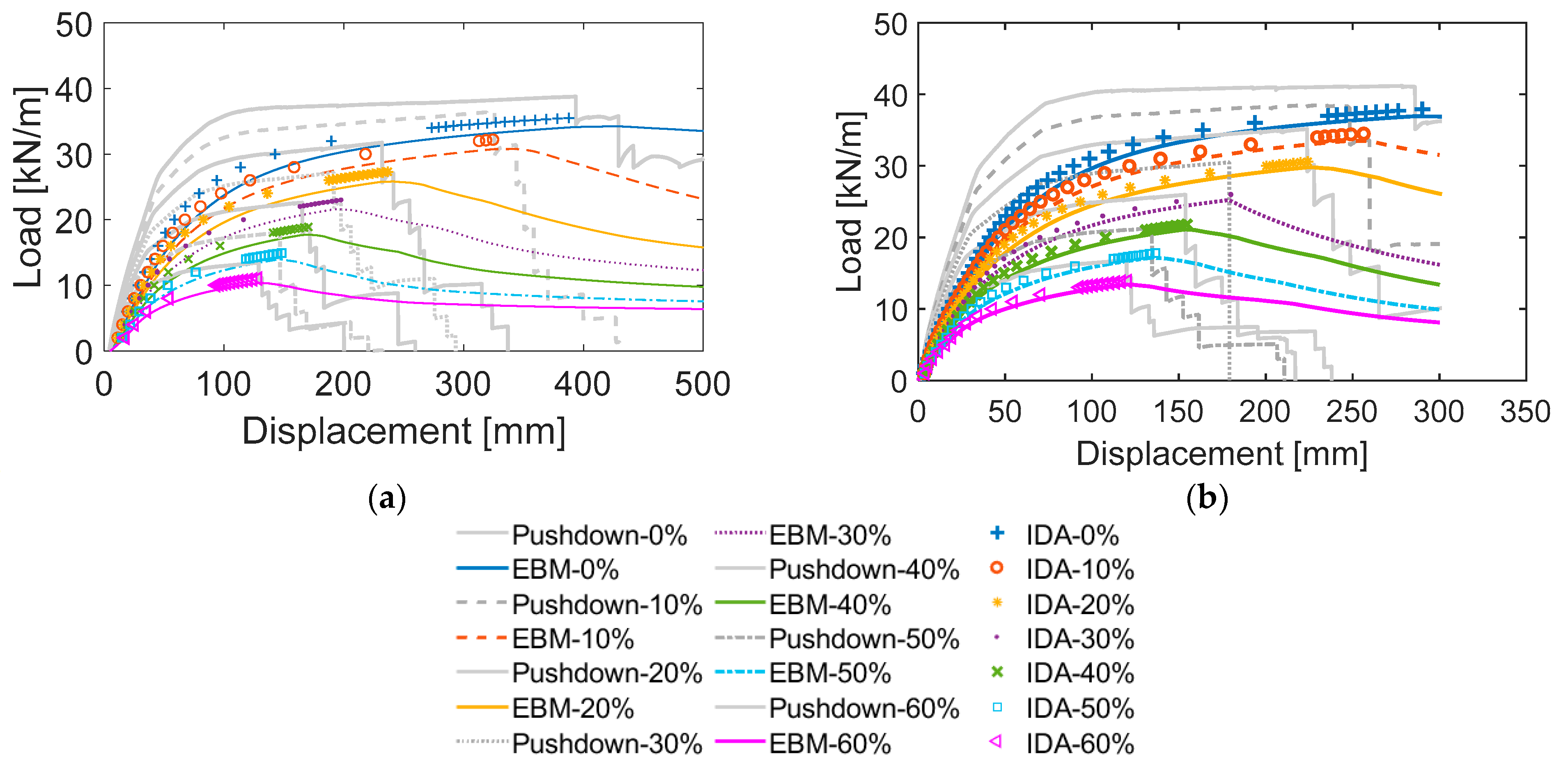
3.3. Validation of Numerical Modeling Strategies
4. Case Study: Structural Description and Results
4.1. Description of the RC Frame Structure
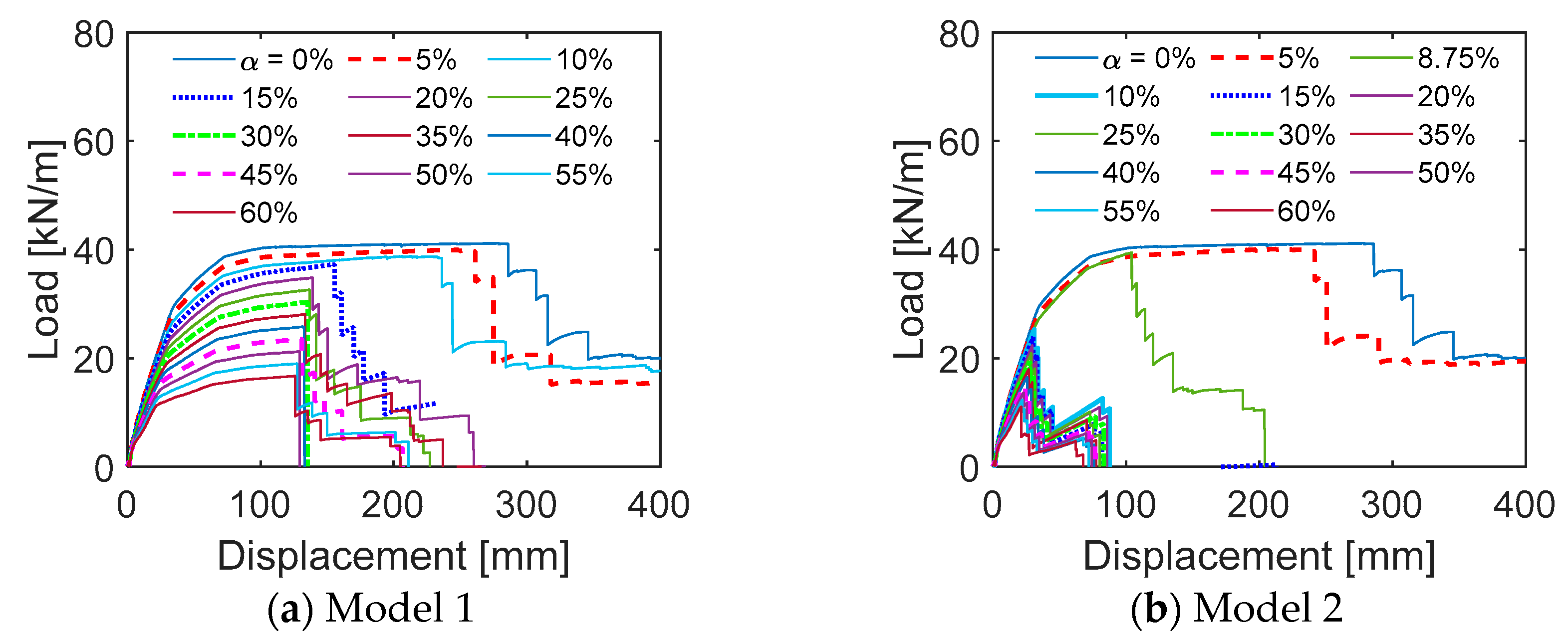
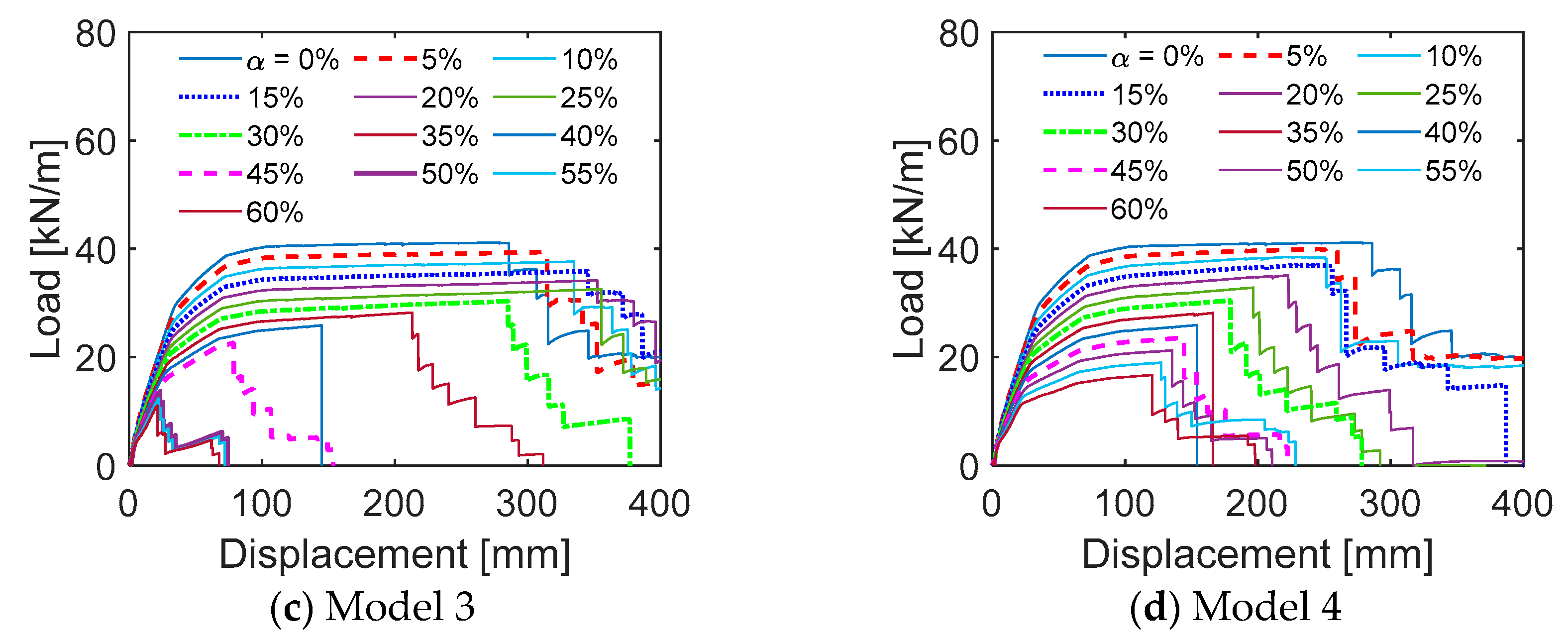
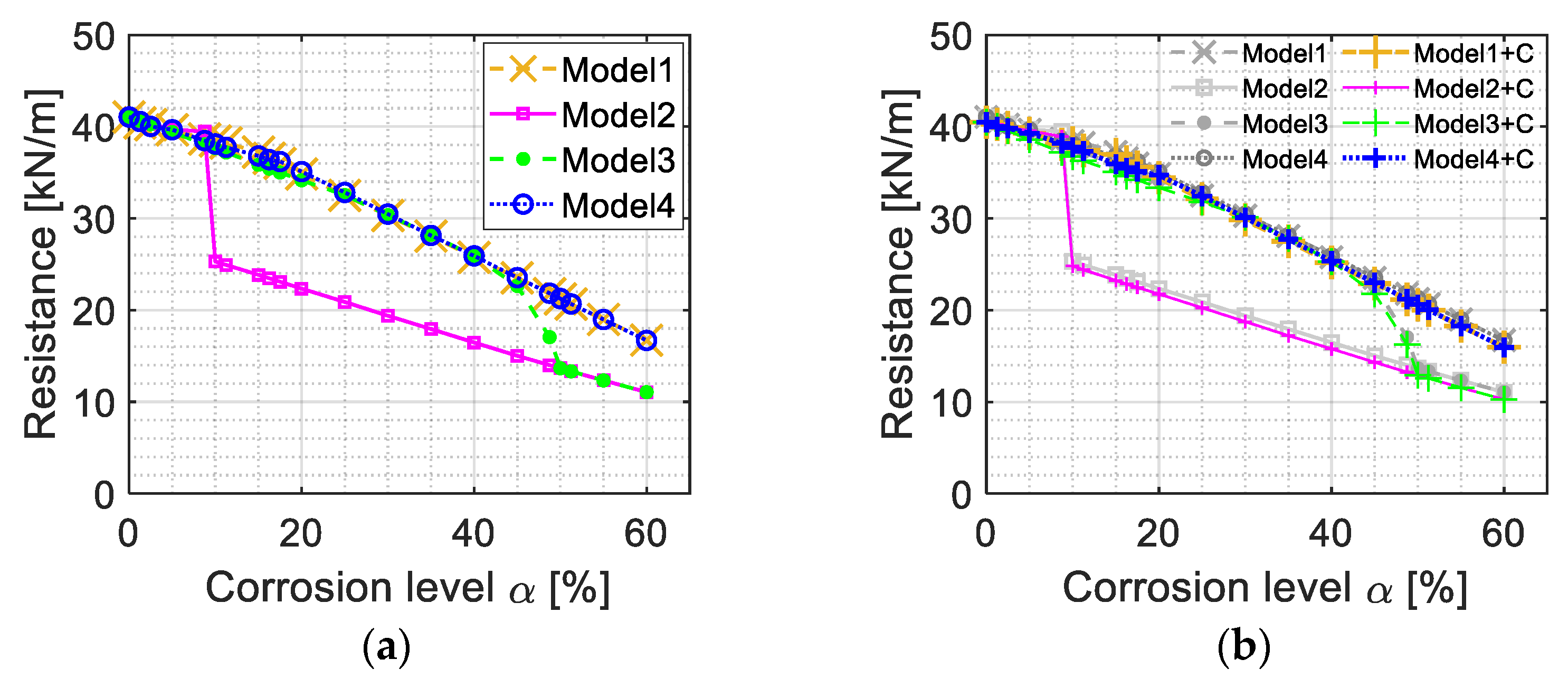
4.2. Influence of Different Material Deterioration: Reinforceing Steel and Concrete
4.2.1. Deterioration of Properties Regarding Corroded Reinforcing Steel
4.2.2. Deterioration of Concrete Properties
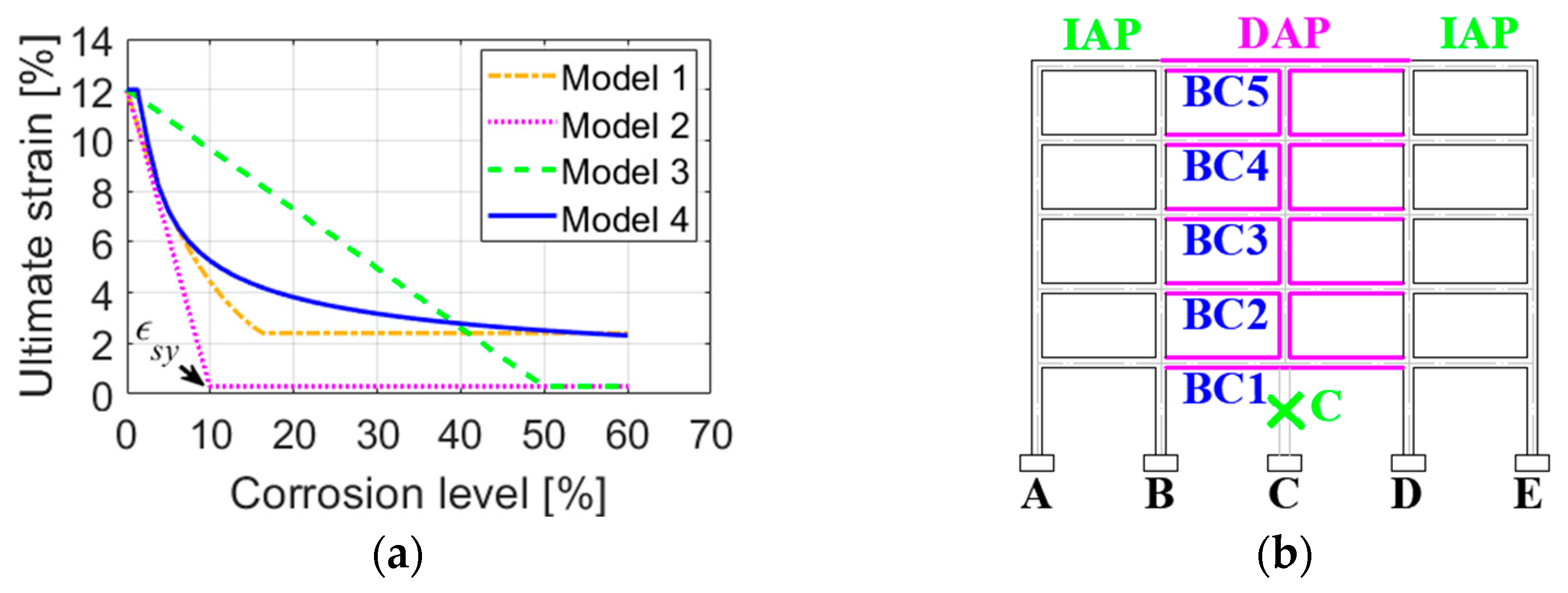
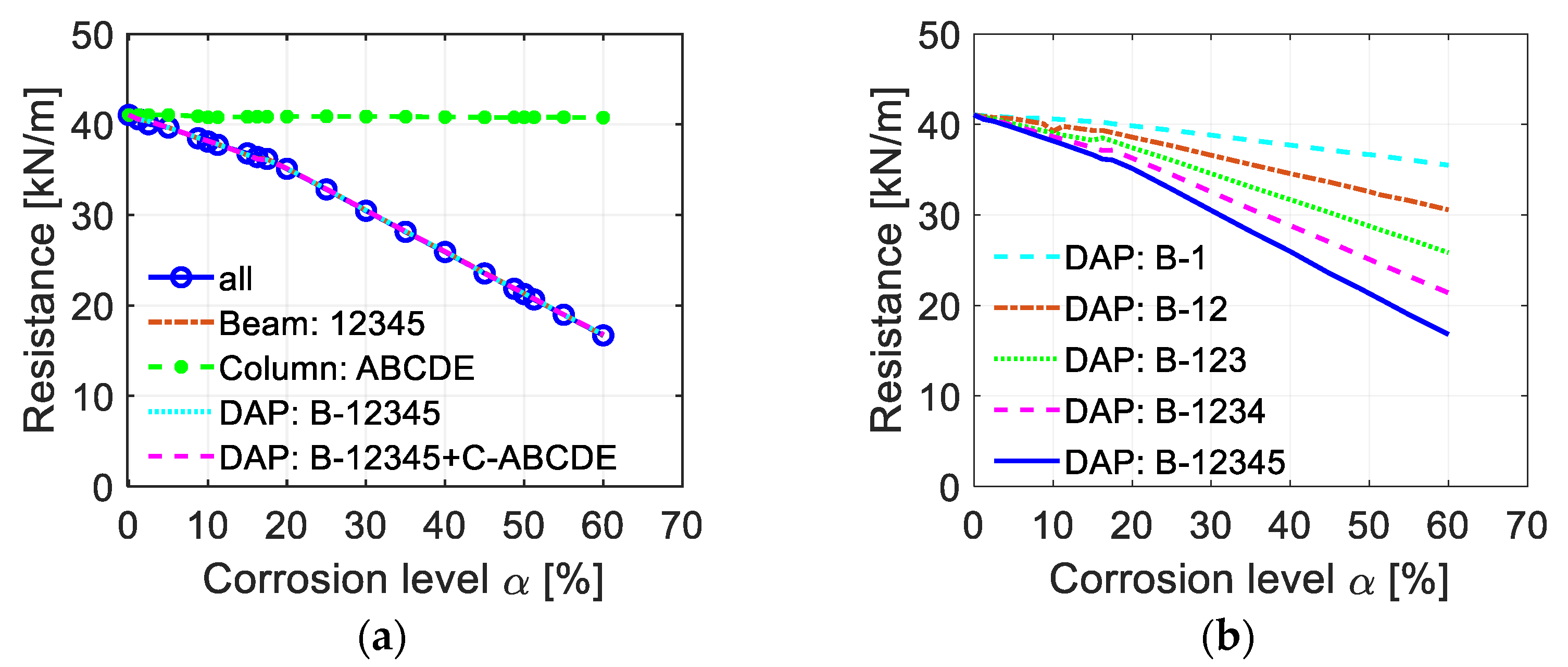
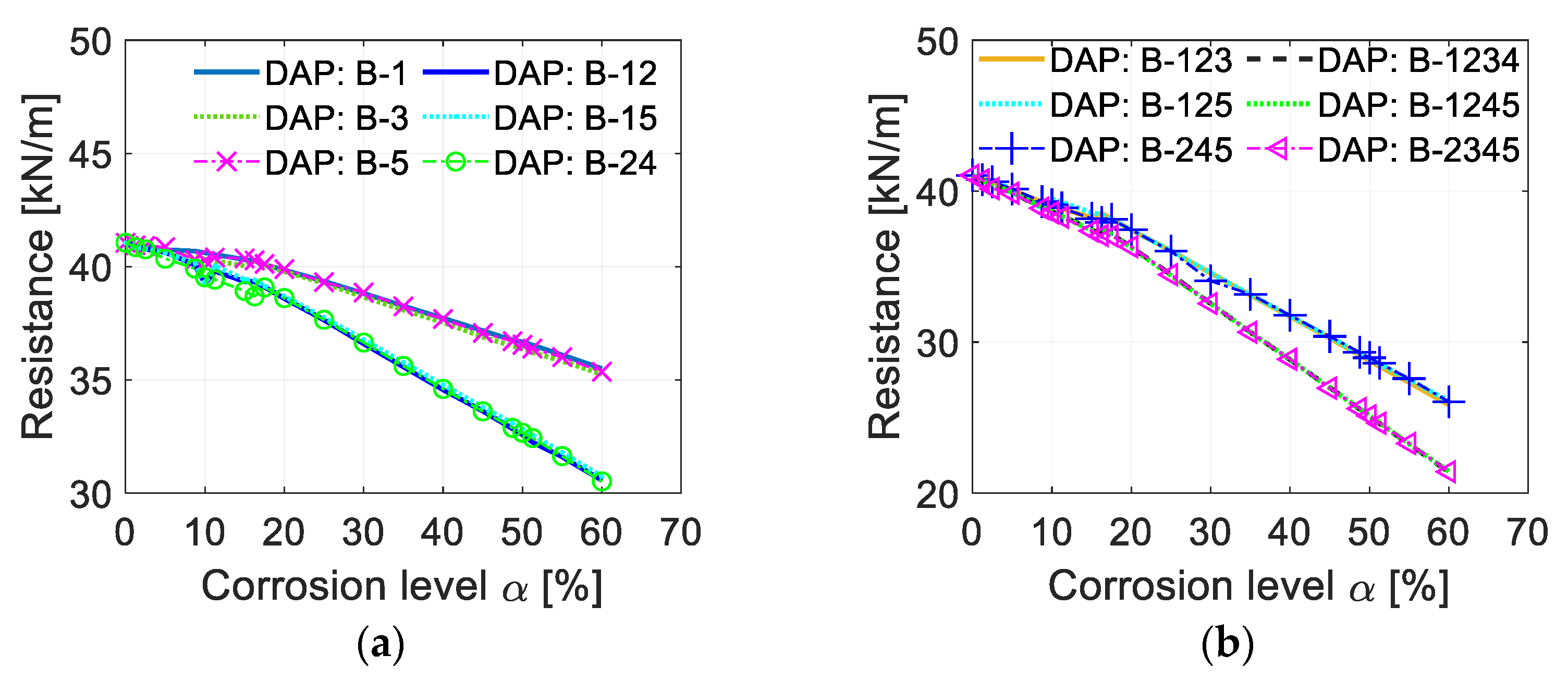
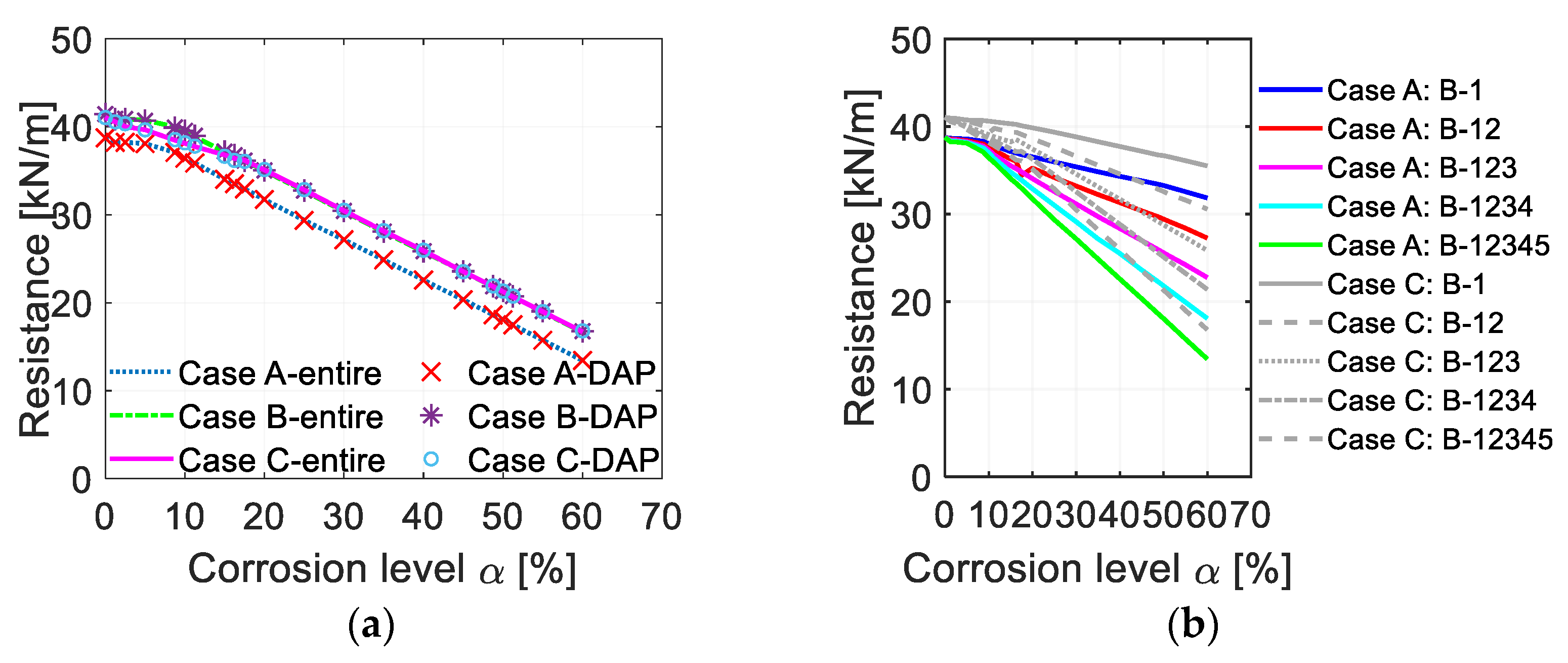
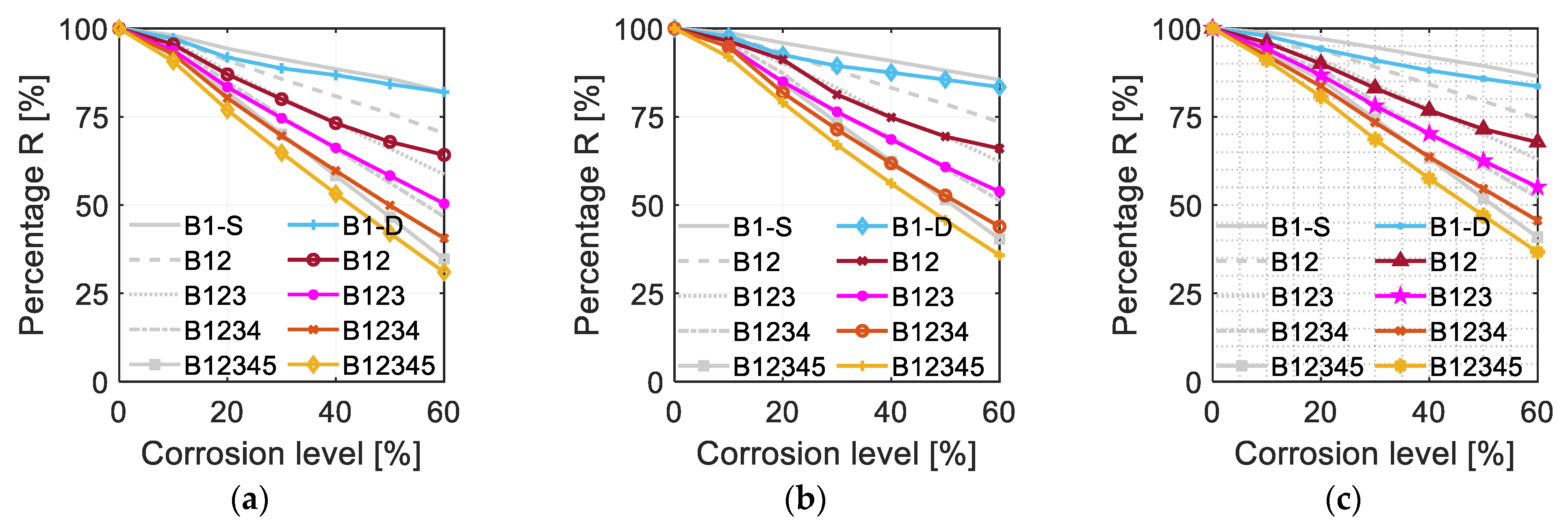
4.3. Influence of Different Corrosion Locations
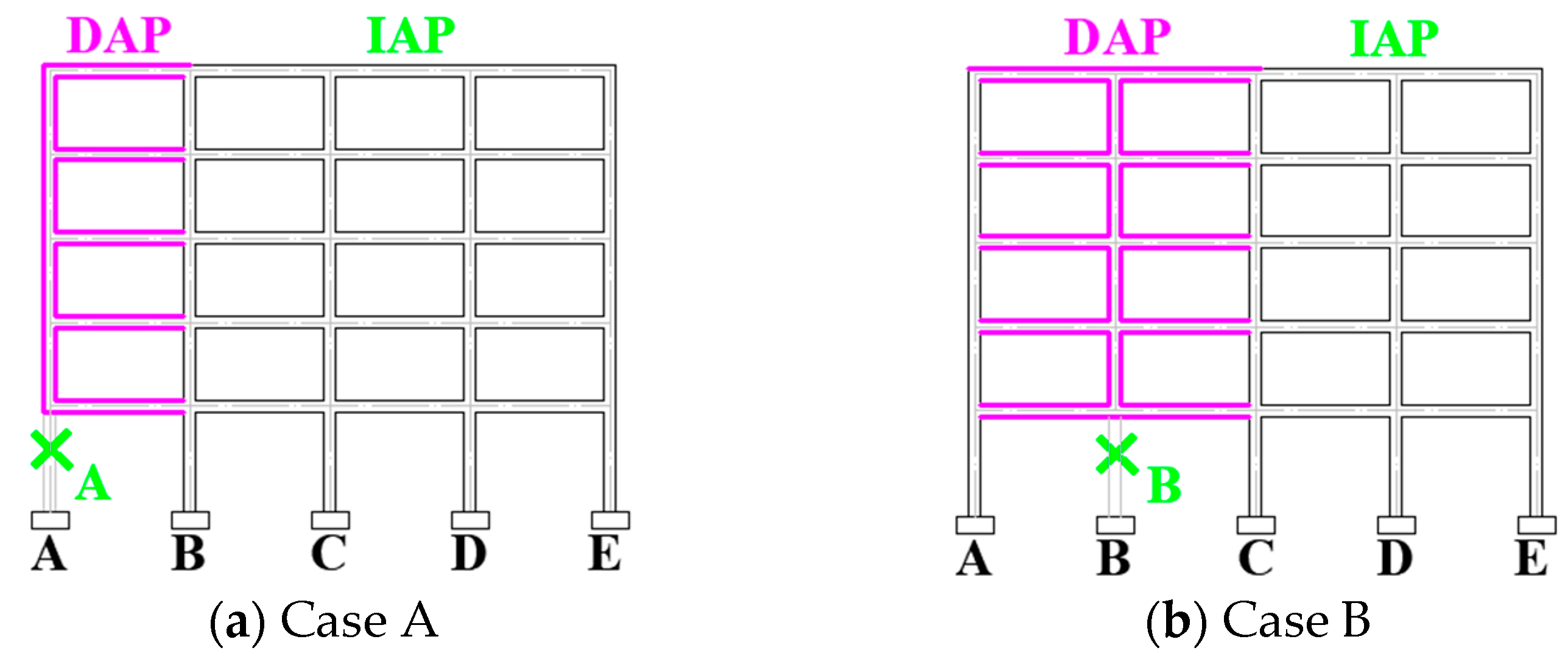
4.3.1. Corrosion in DAP and/or IAP
4.3.2. Corrosion in Different Floors in DAP
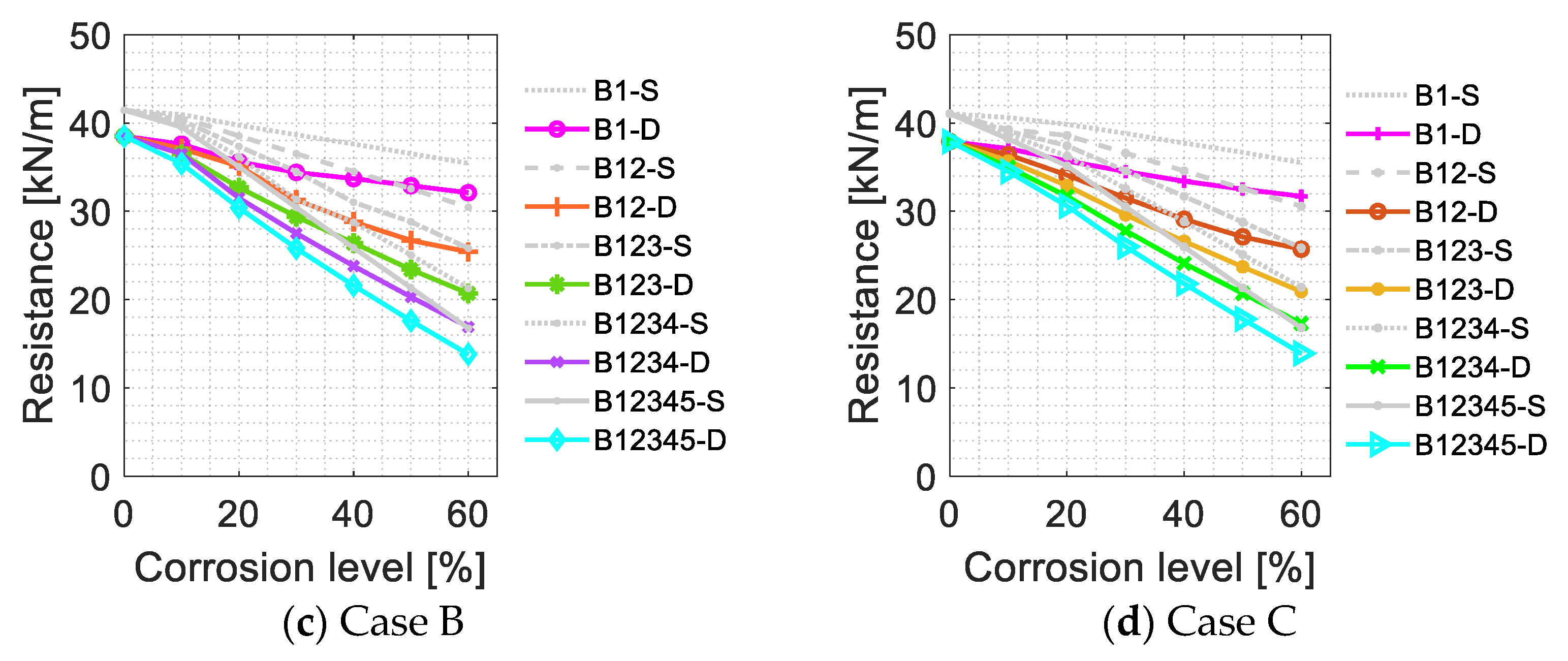
4.4. Influence of Different Column Removal Scenarios
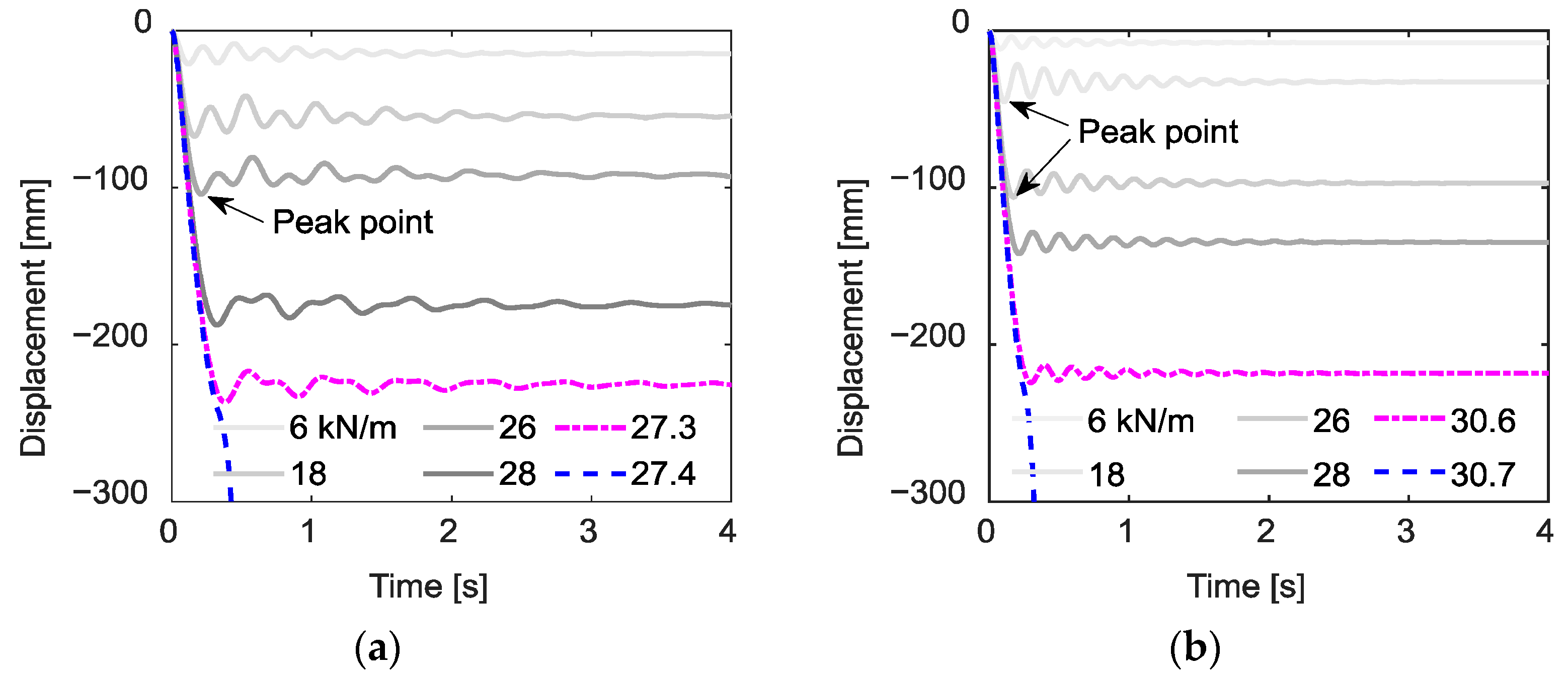
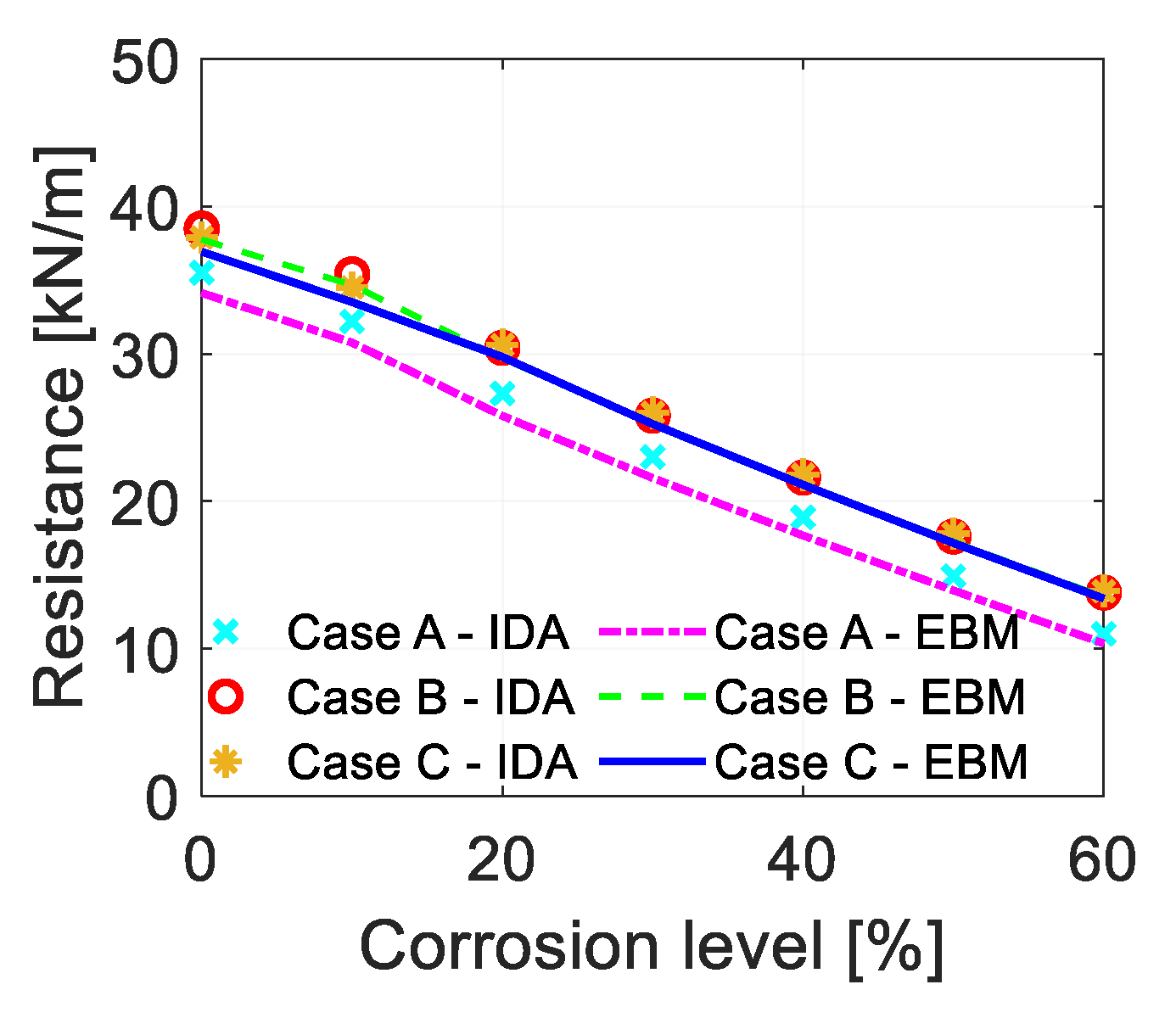
4.5. Influence of Dynamic Effects
4.5.1. Nonlinear Dynamic Analysis
4.5.2. Efficient Approaches for Dynamic Analysis
5. Conclusions
- (1)
- Reinforcement corrosion is identified as the primary factor contributing to the degradation of progressive collapse performance with increasing corrosion levels. In contrast, the effects of concrete deterioration on structural robustness are relatively minor. Furthermore, different deterioration models—particularly those related to the reduction in steel ultimate strain—may lead to variations in both structural response and failure modes.
- (2)
- The structural performance under all three column removal scenarios is predominantly governed by reinforcement corrosion in the beams located within the directly affected part (DAP). Corrosion in other regions of the structure has a minimal influence on overall collapse resistance. Additionally, an increase in the number of corroded floors within the DAP leads to a significantly greater reduction in progressive collapse capacity.
- (3)
- Progressive collapse resistances obtained from dynamic analyses are notably lower than those derived from static analyses, and they exhibit a slightly faster rate of degradation as corrosion levels increase. This highlights the importance of considering dynamic effects in the assessment of deteriorated structures.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| BC | Beam end | JCSS | Joint committee on structural safety |
| DAP | Directly affected part | NTHA | Nonlinear time–history analysis |
| EBM | Energy-based method | PE | Potential energy |
| IAP | Indirectly affected part | RC | Reinforced concrete |
| IDA | Incremental dynamic analysis | SE | Strain energy |
References
- Makoond, N.; Setiawan, A.; Buitrago, M.; Adam, J.M. Arresting failure propagation in buildings through collapse isolation. Nature 2024, 629, 592–596. [Google Scholar] [CrossRef]
- Zeng, Y.; Shen, Y.; Noori, M.; Wu, G. Experimental study on the progressive collapse resistance of emulative precast concrete beam-column subassemblies with various anchorage details. J. Build. Eng. 2024, 88, 109242. [Google Scholar] [CrossRef]
- Gerasimidis, S.; Ellingwood, B. Twenty years of advances in disproportionate collapse research and best practices since 9/11/2001. J. Struct. Eng. 2023, 149, 2022002. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, J.; Xiang, M. PDEM-based reliability assessment of RC frames against progressive collapse considering initial local failure. J. Build. Eng. 2023, 76, 107198. [Google Scholar] [CrossRef]
- Yi, F.; Yi, W.J.; Sun, J.M.; Zhou, Y.; Zhang, W.X.; He, Q.F. Experimental study on progressive collapse behavior of frame structures triggered by impact column removal. Eng. Struct. 2024, 321, 119022. [Google Scholar] [CrossRef]
- Parisi, F.; Scalvenzi, M.; Brunesi, E. Performance limit states for progressive collapse analysis of reinforced concrete framed buildings. Struct. Concr. 2019, 20, 68–84. [Google Scholar] [CrossRef]
- Tsai, M.H.; Lin, B.H. Investigation of progressive collapse resistance and inelastic response for an earthquake-resistant RC building subjected to column failure. Eng. Struct. 2008, 30, 3619–3628. [Google Scholar] [CrossRef]
- Weng, Y.-H.; Fu, F.; Qian, K. Punching shear resistance of corroded slab–column connections subjected to eccentric load. J. Struct. Eng. 2023, 149, 04022219. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, J.; Zeng, H.; Zeng, D. Whole-process analytical model on progressive collapse response of reinforced concrete structures under middle column loss. Eng. Struct. 2024, 302, 117375. [Google Scholar] [CrossRef]
- Yi, F.; Yi, W.J.; Sun, J.M.; Ni, J.; He, Q.F.; Zhou, Y. On the progressive collapse performance of RC frame structures under impact column removal. Eng. Struct. 2024, 307, 117926. [Google Scholar] [CrossRef]
- Zeng, Y.; Caspeele, R.; Matthys, S.; Taerwe, L. Compressive membrane action in FRP strengthened RC members. Constr. Build. Mater. 2016, 126, 442–452. [Google Scholar] [CrossRef]
- Parisi, F.; Scalvenzi, M. Progressive collapse assessment of gravity-load designed European RC buildings under multi-column loss scenarios. Eng. Struct. 2020, 209, 110001. [Google Scholar] [CrossRef]
- Zhang, Z.; Xi, Z.; Qin, W. Experiments and a tension-bending catenary model for the progressive collapse resistance of concrete beam-column structures. J. Build. Eng. 2023, 67, 105971. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, W.; Wang, J.; Xi, Z.; Fan, X. Theoretical and numerical insights into shear performance of steel- and SFCB-reinforced concrete beam-column structures in progressive collapse-resisting design. Structures 2025, 71, 108181. [Google Scholar] [CrossRef]
- Zhang, R.; Hu, S.; Guo, T. Performance and recentering demands of partially self-centering BRBFs in the life-cycle span. Eng. Struct. 2025, 334, 120205. [Google Scholar] [CrossRef]
- Zhang, R.; Wang, W.; Alam, M.S. Deep learning-aided optimization framework for hybrid braced structures to support life-cycle cost-based design. Eng. Struct. 2025, 327, 119603. [Google Scholar] [CrossRef]
- Izzuddin, B.A. Rational robustness design of multistory building structures. J. Struct. Eng. 2022, 148, 04021279. [Google Scholar] [CrossRef]
- Ding, L.; Van Coile, R.; Botte, W.; Caspeele, R. Quantification of model uncertainties of the energy-based method for dynamic column removal scenarios. Eng. Struct. 2021, 237, 112057. [Google Scholar] [CrossRef]
- Ding, L.; Van Coile, R.; Botte, W.; Caspeele, R. Performance assessment of an energy–based approximation method for the dynamic capacity of RC frames subjected to sudden column removal scenarios. Appl. Sci. 2021, 11, 7492. [Google Scholar] [CrossRef]
- Brunesi, E.; Nascimbene, R.; Parisi, F.; Augenti, N. Progressive collapse fragility of reinforced concrete framed structures through incremental dynamic analysis. Eng. Struct. 2015, 104, 65–79. [Google Scholar] [CrossRef]
- Yu, X.; Chen, J.; Chen, J.; Qian, K.; Dai, K.; Ding, L.; Caspeele, R. Effects of reinforcement corrosion on the static and dynamic progressive collapse behavior of RC subassemblies. J. Build. Eng. under review.
- Ding, L.; Botte, W.; Van Coile, R.; Caspeele, R. Evaluation of the energy-based method for dynamic analysis under a sudden column removal scenario. In Proceedings of the fib Symposium 2020: Concrete Structures for Resilient Society, Shanghai, China, 22–24 November 2020. [Google Scholar]
- Izzuddin, B.A.; Vlassis, A.G.; Elghazouli, A.Y.; Nethercot, D.A. Progressive collapse of multi-storey buildings due to sudden column loss—Part I: Simplified assessment framework. Eng. Struct. 2008, 30, 1308–1318. [Google Scholar] [CrossRef]
- Ding, L.; Botte, W.; Van Coile, R.; Caspeele, R. Robustness-evaluation of a stochastic dynamic system and the instant equivalent extreme-value event. Beton- Und Stahlbetonbau 2018, 113, 33–37. [Google Scholar] [CrossRef]
- Ding, L.; Yu, X.; Qian, K.; Ren, X.; Chen, J.; Caspeele, R. A unified regression model for the force-based dynamic increase factor in relation to progressive collapse analyses of frame structures. Eng. Struct. 2025; under review. [Google Scholar]
- Ding, L.; Chen, J.; Caspeele, R. Determination of dynamic collapse limit states using the energy-based method for multi-story RC frames subjected to column removal scenarios. Eng. Struct. 2024, 311, 118170. [Google Scholar] [CrossRef]
- Ding, L.; Droogné, D.; Botte, W.; Van Coile, R.; Caspeele, R. Structural reliability calculations considering concrete tensile membrane action using the probability density evolution method. In Proceedings of the 13th International Conference on Applications of Statistics and Probability in Civil Engineering (ICASP 13), Seoul, Republic of Korea, 26–30 May 2019; pp. 1–7. [Google Scholar]
- Feng, D.C.; Xie, S.C.; Li, Y.; Jin, L. Time-dependent reliability-based redundancy assessment of deteriorated RC structures against progressive collapse considering corrosion effect. Struct. Saf. 2021, 89, 102061. [Google Scholar] [CrossRef]
- Qian, K.; Weng, Y.H.; Liang, S.L.; Fu, F. Punching shear behavior and corrosion resistance of composite slab-column connections reinforced by BFRP and steel rebar. Eng. Struct. 2024, 304, 117589. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Time-variant redundancy and failure times of deteriorating concrete structures considering multiple limit states. Struct. Infrastruct. Eng. 2017, 13, 94–106. [Google Scholar] [CrossRef]
- Biondini, F.; Frangopol, D.M. Life-cycle performance of deteriorating structural systems under uncertainty: Review. J. Struct. Eng. 2016, 142, F4016001. [Google Scholar] [CrossRef]
- Botte, W.; Vereecken, E.; Taerwe, L.; Caspeele, R. Assessment of posttensioned concrete beams from the 1940s: Large-scale load testing, numerical analysis and Bayesian assessment of prestressing losses. Struct. Concr. 2021, 22, 1500–1522. [Google Scholar] [CrossRef]
- Botte, W.; Caspeele, R.; Taerwe, L. Membrane behavior in RC slabs subjected to simulated reinforcement corrosion. Eng. Struct. 2016, 123, 45–58. [Google Scholar] [CrossRef]
- Yu, X.H.; Qian, K.; Lu, D.G.; Li, B. Progressive collapse behavior of aging reinforced concrete structures considering corrosion effects. J. Perform. Constr. Facil. 2017, 31, 04017009. [Google Scholar] [CrossRef]
- Du, Y.G.; Clark, L.A.; Chan, A.H.C. Effect of corrosion on ductility of reinforcing bars. Mag. Concr. Res. 2005, 57, 407–419. [Google Scholar] [CrossRef]
- Qian, K.; Li, J.; Huang, T.; Weng, Y.; Deng, X. Punching shear strength of corroded reinforced concrete slab-column connections. J. Build. Eng. 2022, 45, 103489. [Google Scholar] [CrossRef]
- Bao, C.; Long, H.; Ma, X.; Alshaikh, I.M.H.; Mekhlafi, G.A.; Peng, L.; Wang, H. Experimental study on progressive collapse resistance of corroded RC continuous deep flexural members. Eng. Fail. Anal. 2025, 175, 109543. [Google Scholar] [CrossRef]
- Bao, C.; Wang, H.; Long, H.; Alshaikh, I.M.H.; Gaboby, Z.A.; Ma, X. Study on progressive collapse mechanism of RC frame structures corroded by chloride. Case Stud. Constr. Mater. 2025, 22, e04472. [Google Scholar] [CrossRef]
- Ding, L.C.; Peng, Y.B.; Chen, J.B. Progressive collapse behavior of RC frames subjected to reinforcement corrosion. In Proceedings of the Life-Cycle of Structures and Infrastructure Systems—Proceedings of the 8th International Symposium on Life-Cycle Civil Engineering, IALCCE 2023, Milan, Italy, 2–6 July 2023; pp. 3777–3792. [Google Scholar]
- Ding, L. Quantitative Assessment of Reinforced Concrete Buildings Subjected to Column Removal Scenarios Taking into Account Dynamic Response Behaviour. Ph.D. Thesis, Ghent University, Ghent, Belgium, 2021. [Google Scholar]
- Cavaco, E.S.; Neves, L.A.C.; Casas, J.R. On the robustness to corrosion in the life cycle assessment of an existing reinforced concrete bridge. Struct. Infrastruct. Eng. 2018, 14, 137–150. [Google Scholar] [CrossRef]
- Yu, B.; Ning, C.L.; Li, B. Probabilistic durability assessment of concrete structures in marine environments: Reliability and sensitivity analysis. China Ocean Eng. 2017, 31, 63–73. [Google Scholar] [CrossRef]
- Biondini, F.; Vergani, M. Deteriorating beam finite element for nonlinear analysis of concrete structures under corrosion. Struct. Infrastruct. Eng. 2014, 11, 519–532. [Google Scholar] [CrossRef]
- Yu, X.-H.; Dai, K.-Y.; Li, Y.-S. Variability in corrosion damage models and its effect on seismic collapse fragility of aging reinforced concrete frames. Constr. Build. Mater. 2021, 295, 123654. [Google Scholar] [CrossRef]
- Almusallam, A.A. Effect of degree of corrosion on the properties of reinforcing steel bars. Constr. Build. Mater. 2001, 15, 361–368. [Google Scholar] [CrossRef]
- Du, Y.G.; Clark, L.A.; Chan, A.H.C. Residual capacity of corroded reinforcing bars. Mag. Concr. Res. 2005, 57, 135–147. [Google Scholar] [CrossRef]
- Apostolopoulos, C.A.; Papadakis, V.G. Consequences of steel corrosion on the ductility properties of reinforcement bar. Constr. Build. Mater. 2008, 22, 2316–2324. [Google Scholar] [CrossRef]
- Cairns, J.; Plizzari, G.A.; Du, Y.G.; Law, D.W.; Franzoni, C. Mechanical properties of corrosion-damaged reinforcement. Aci Mater. J. 2005, 102, 256–264. [Google Scholar]
- Zhu, W.; François, R. Effect of corrosion pattern on the ductility of tensile reinforcement extracted from a 26-year-old corroded beam. Adv. Concr. Constr. 2013, 1, 121. [Google Scholar] [CrossRef]
- Yu, L.; François, R.; Dang, V.H.; L’Hostis, V.; Gagné, R. Structural performance of RC beams damaged by natural corrosion under sustained loading in a chloride environment. Eng. Struct. 2015, 96, 30–40. [Google Scholar] [CrossRef]
- Coronelli, D.; Gambarova, P. Structural assessment of corroded reinforced concrete beams: Modeling guidelines. J. Struct. Eng. 2004, 130, 1214–1224. [Google Scholar] [CrossRef]
- Castel, A.; François, R.; Arliguie, G. Mechanical behaviour of corroded reinforced concrete beams—Part 2: Bond and notch effects. Mater. Struct. 2000, 33, 545–551. [Google Scholar] [CrossRef]
- Cairns, J.; Millard, S. Reinforcement corrosion and its effect on residual strength of concrete structures. In Proceedings of the 8th International Conference on Structural Faults and Repair, London, UK, 1 January 1999. [Google Scholar]
- Vereecken, E.; Botte, W.; Lombaert, G.; Caspeele, R. A Bayesian inference approach for the updating of spatially distributed corrosion model parameters based on heterogeneous measurement data. Struct. Infrastruct. Eng. 2020, 18, 30–46. [Google Scholar] [CrossRef]
- Ding, L.; Chen, J. Physically-based collapse failure criteria in progressive collapse analyses of random-parameter multi-story RC structures subjected to column removal scenarios. Eng. Struct. 2025, 325, 119379. [Google Scholar] [CrossRef]
- Liu, M.; Pirmoz, A. Energy-based pulldown analysis for assessing the progressive collapse potential of steel frame buildings. Eng. Struct. 2016, 123, 372–378. [Google Scholar] [CrossRef]
- Zeng, Y.; Botte, W.; Caspeele, R. Reliability analysis of FRP strengthened RC beams considering compressive membrane action. Constr. Build. Mater. 2018, 169, 473–488. [Google Scholar] [CrossRef]
- Gan, Y.; Chen, J.; Li, Y.; Xu, Z. Prediction of progressive collapse resistance of RC frames using deep and cross network model. Structures 2023, 51, 800–813. [Google Scholar] [CrossRef]
- Ding, L.; Chen, J.; Caspeele, R. Dynamic sensitive failure mode in the progressive collapse of RC structures subjected to column removal scenarios. Eng. Struct. 2025, 323, 119301. [Google Scholar] [CrossRef]
- Peng, Y.; Ding, L.; Liu, J.; Chen, J. Probabilistic analysis of seismic mitigation of base-isolated structure with sliding hydromagnetic bearings based on finite element simulations. Earthq. Eng. Resil. 2023, 2, 194–210. [Google Scholar] [CrossRef]
- Vamvatsikos, D.; Cornell, C.A. Incremental dynamic analysis. Earthq. Eng. Struct. Dyn. 2002, 31, 491–514. [Google Scholar] [CrossRef]
- Peng, Y.B.; Ding, L.C.; Chen, J.B.; Liu, J.T.; Villaverde, R. Shaking table test of seismic isolated structures with sliding hydromagnetic bearings. J. Struct. Eng. 2020, 146, 04020174. [Google Scholar] [CrossRef]
- Ding, L.; Botte, W.; Van Coile, R.; Caspeele, R. Model uncertainty quantification for column removal scenario calculations using the energy-based method. In Proceedings of the 13th fib International PhD-Symposium In Civil Engineering, Paris, France, 26–28 August 2020. [Google Scholar]
- Ding, L.; Van Coile, R.; Botte, W.; Caspeele, R. Structural reliability of RC frames under sudden column removal scenarios considering static and dynamic methods. In Proceedings of the IABSE Congress: Structural Engineering for Future Societal Needs, Ghent, Belgium, 22–24 September 2021. [Google Scholar]
- Lin, K.; Wu, Z.; Zhu, Y.; Zheng, J.; Li, Y.; Lu, X. Progressive collapse design optimization of RC frame structures using high-performance computing. Structures 2023, 50, 823–834. [Google Scholar] [CrossRef]
- Ding, L.; Van Coile, R.; Botte, W.; Caspeele, R. Reliability-based robustness quantification of RC structures subjected to dynamic effects following sudden column removal scenarios. In Proceedings of the 13th International Conference on Structural Safety and Reliability (ICOSSAR 2021), Shanghai, China, 21–25 June 2021. [Google Scholar]
- Huang, M.; Huang, H.; Hao, R.; Chen, Z.; Li, M.; Deng, W. Studies on secondary progressive collapse-resistance mechanisms of reinforced concrete subassemblages. Struct. Concr. 2021, 22, 2138–2154. [Google Scholar] [CrossRef]
- Baker, J.W.; Schubert, M.; Faber, M.H. On the assessment of robustness. Struct. Saf. 2008, 30, 253–267. [Google Scholar] [CrossRef]
- Ding, L.C.; Chen, J.B. Determination of dynamic progressive collapse resistances for deteriorating multi-story RC frames subjected to column removal scenarios via the energy-based method. In Proceedings of the 14th International Conference on Application of Statistics and Probability in Civil Engineering (ICASP14), Dublin, Ireland, 9–13 July 2023. [Google Scholar]
- Mazzoni, S.; McKenna, F.; Scott, M.H.; Fenves, G.L. OpenSees Command Language Manual; Pacific Earthquake Engineering Research (PEER) Center: Berkeley, CA, USA, 2006; Volume 264. [Google Scholar]
- Feng, D.; Wang, Z.; Wu, G. Progressive collapse performance analysis of precast reinforced concrete structures. Struct. Des. Tall Spec. Build. 2019, 28, e1588. [Google Scholar] [CrossRef]
- Feng, D.C.; Ren, X.D. Implicit gradient-enhanced force-based Timoshenko fiber element formulation for reinforced concrete structures. Int. J. Numer. Methods Eng. 2021, 122, 325–347. [Google Scholar] [CrossRef]
- Ceresa, P.; Petrini, L.; Pinho, R. Flexure-shear fiber beam-column elements for modeling frame structures under seismic loading—State of the art. J. Earthq. Eng. 2007, 11, 46–88. [Google Scholar] [CrossRef]
- Vecchio, F.J.; Collins, M.P. The modified compression-field theory for reinforced-concrete elements subjected to shear. J Am Concr. I 1986, 83, 219–231. [Google Scholar]
- Lowes, L.N.; Altoontash, A. Modeling reinforced-concrete beam-column joints subjected to cyclic loading. J. Struct. Eng. 2003, 129, 1686–1697. [Google Scholar] [CrossRef]
- Mander, J.B.; Priestley, M.J.N.; Park, R. Theoretical stress-strain model for confined concrete. J. Struct. Eng. 1988, 114, 1804–1826. [Google Scholar] [CrossRef]
- Stevens, N.J.; Uzumeri, S.M.; Will, G.T. Constitutive model for reinforced concrete finite element analysis. Struct. J. 1991, 88, 49–59. [Google Scholar]
- Esmaeiltabar, P.; Vaseghi, J.; Khosravi, H. Nonlinear macro modeling of slender reinforced concrete shear walls. Struct. Concr. 2019, 20, 899–910. [Google Scholar] [CrossRef]
- Qian, K.; Li, B.; Ma, J.X. Load-carrying mechanism to resist progressive collapse of RC buildings. J. Struct. Eng. 2014, 141, 04014107. [Google Scholar] [CrossRef]
- Yi, W.J.; He, Q.F.; Xiao, Y.; Kunnath, S.K. Experimental study on progressive collapse-resistant behavior of reinforced concrete frame structures. ACI Struct. J. 2008, 105, 433–439. [Google Scholar] [CrossRef] [PubMed]
- EN 1991-1-1; Eurocode 1: Actions on Structures-Part 1-1: General Actions-Densities, Self-Weight, Imposed Loads for Buildings. European Committee for Standardization Brussels (CEN): Brussels, Belgium, 2002.
- EN 1992-1-1; Eurocode 2: Design of Concrete Structures—Part 1-1: General Rules and Rules for Buildings. European Committee for Standardization Brussels (CEN): Brussels, Belgium, 2004.
- fib. fib Model Code for Concrete Structures 2010; fib: Lausanne, Switzerland, 2013. [Google Scholar]
- JCSS. Probabilistic Model Code; Joint Committee on Structural Safety: Copenhagen, Denmark, 2001. [Google Scholar]
- Ting, S.; Nowak, A.S. Effect of reinforcing steel area loss on flexural behavior of reinforced concrete beams. Struct. J. 1991, 88, 309–314. [Google Scholar]
- Droogné, D.; Botte, W.; Caspeele, R. A multilevel calculation scheme for risk-based robustness quantification of reinforced concrete frames. Eng. Struct. 2018, 160, 56–70. [Google Scholar] [CrossRef]
- Liang, C.F.; Xiao, J.Z.; Wang, Y.F.; Wang, C.H.; Mei, S.Q. Relationship between internal viscous damping and stiffness of concrete material and structure. Struct. Concr. 2021, 22, 1410–1428. [Google Scholar] [CrossRef]
- Ding, L.; Chen, J. Investigation of dynamic sensitive danger zone for RC structures against progressive collapse by the phase plane method. Eng. Mech. 2024, 1–11. Available online: https://engineeringmechanics.cn/article/doi/10.6052/j.issn.1000-4750.2023.08.0607 (accessed on 1 July 2025).
- Ding, L.; Chen, J.; Peng, Y.; Caspeele, R. Physically-based dynamic collapse criterion for RC frame structures against progressive collapse and its evaluation considering uncertainties. In Proceedings of the 9th International Symposium on Reliability Engineering and Risk Management (ISRERM 2024), Hefei, China, 18–21 October 2024. [Google Scholar]
- Ding, L.; Chen, J.; Caspeele, R. Concept of dynamic sensitive failure mode during progressive collapse of RC building structures. In Proceedings of the 4th International Conference on Vulnerability and Risk Analysis and Management (ICVRAM2024) & 8th International Symposium on Uncertainty Modelling and Analysis (ISUMA2024), Shanghai, China, 25–27 April 2024. [Google Scholar]
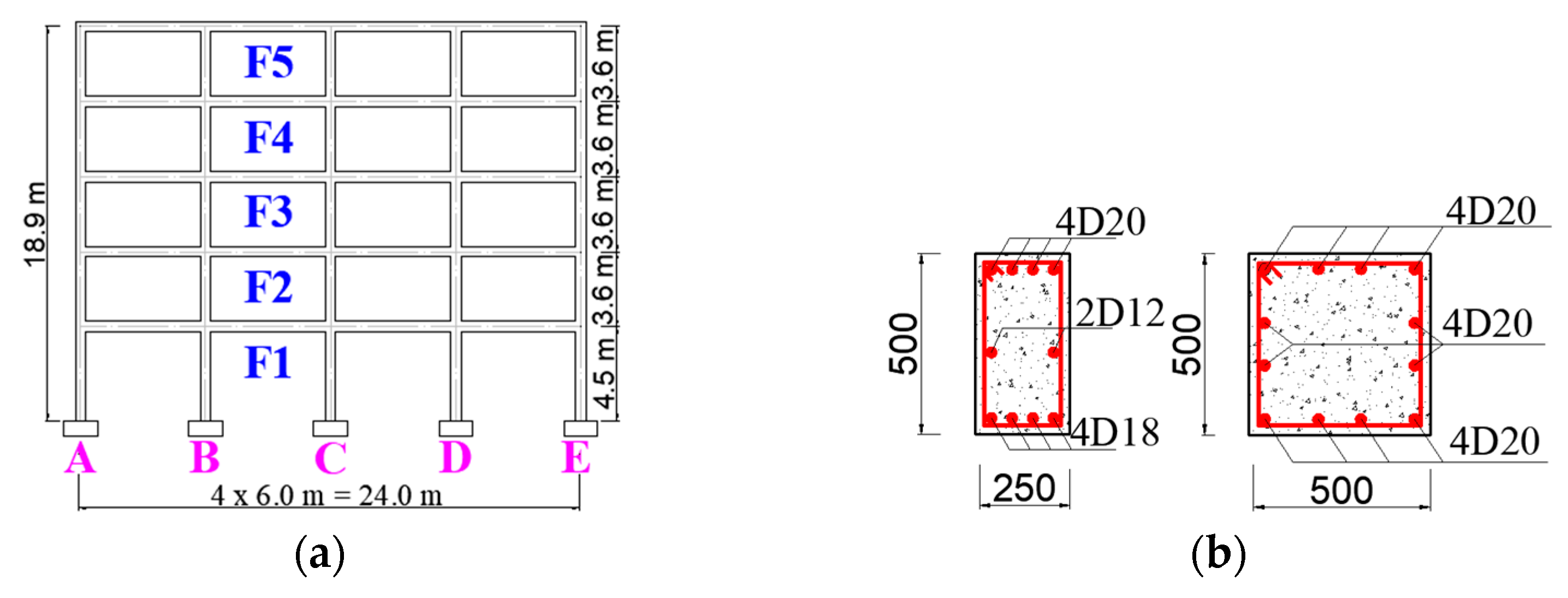

| Material | Parameter | Unit | Mean Value |
|---|---|---|---|
| Concrete | MPa | 28 | |
| % | 0.21 | ||
| MPa | 2.2 | ||
| GPa | 30.3 | ||
| Steel | MPa | 560 | |
| MPa | 655 | ||
| % | 12 | ||
| GPa | 205 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, L.; Dai, X.; Gan, Y.; Zeng, Y. Impact of Reinforcement Corrosion on Progressive Collapse Behavior of Multi-Story RC Frames. Buildings 2025, 15, 2534. https://doi.org/10.3390/buildings15142534
Ding L, Dai X, Gan Y, Zeng Y. Impact of Reinforcement Corrosion on Progressive Collapse Behavior of Multi-Story RC Frames. Buildings. 2025; 15(14):2534. https://doi.org/10.3390/buildings15142534
Chicago/Turabian StyleDing, Luchuan, Xiaodi Dai, Yiping Gan, and Yihua Zeng. 2025. "Impact of Reinforcement Corrosion on Progressive Collapse Behavior of Multi-Story RC Frames" Buildings 15, no. 14: 2534. https://doi.org/10.3390/buildings15142534
APA StyleDing, L., Dai, X., Gan, Y., & Zeng, Y. (2025). Impact of Reinforcement Corrosion on Progressive Collapse Behavior of Multi-Story RC Frames. Buildings, 15(14), 2534. https://doi.org/10.3390/buildings15142534









