Uncertainty Analysis and Risk Assessment for Variable Settlement Properties of Building Foundation Soils
Abstract
1. Introduction
2. Field Experiment and Data Characteristics
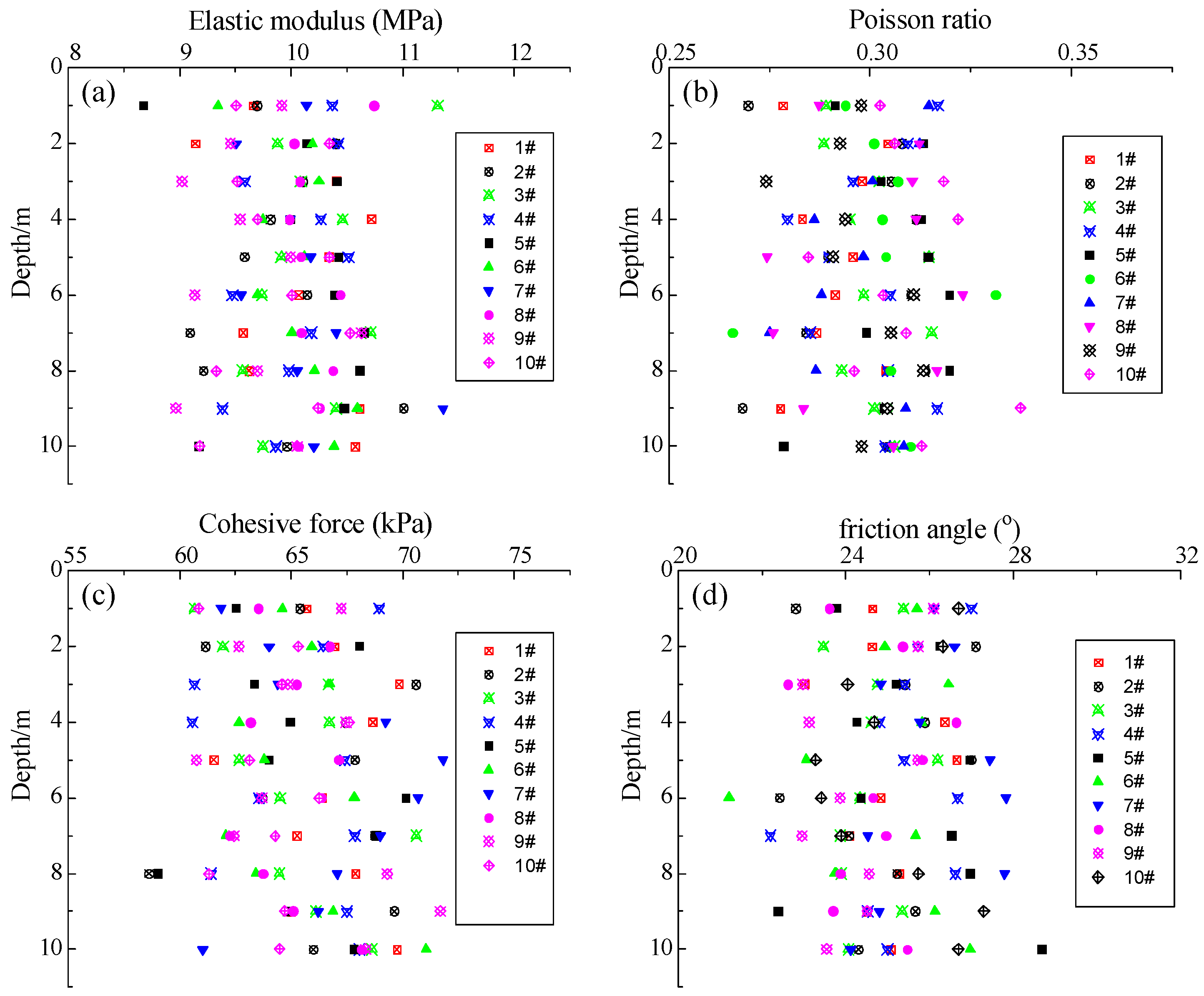
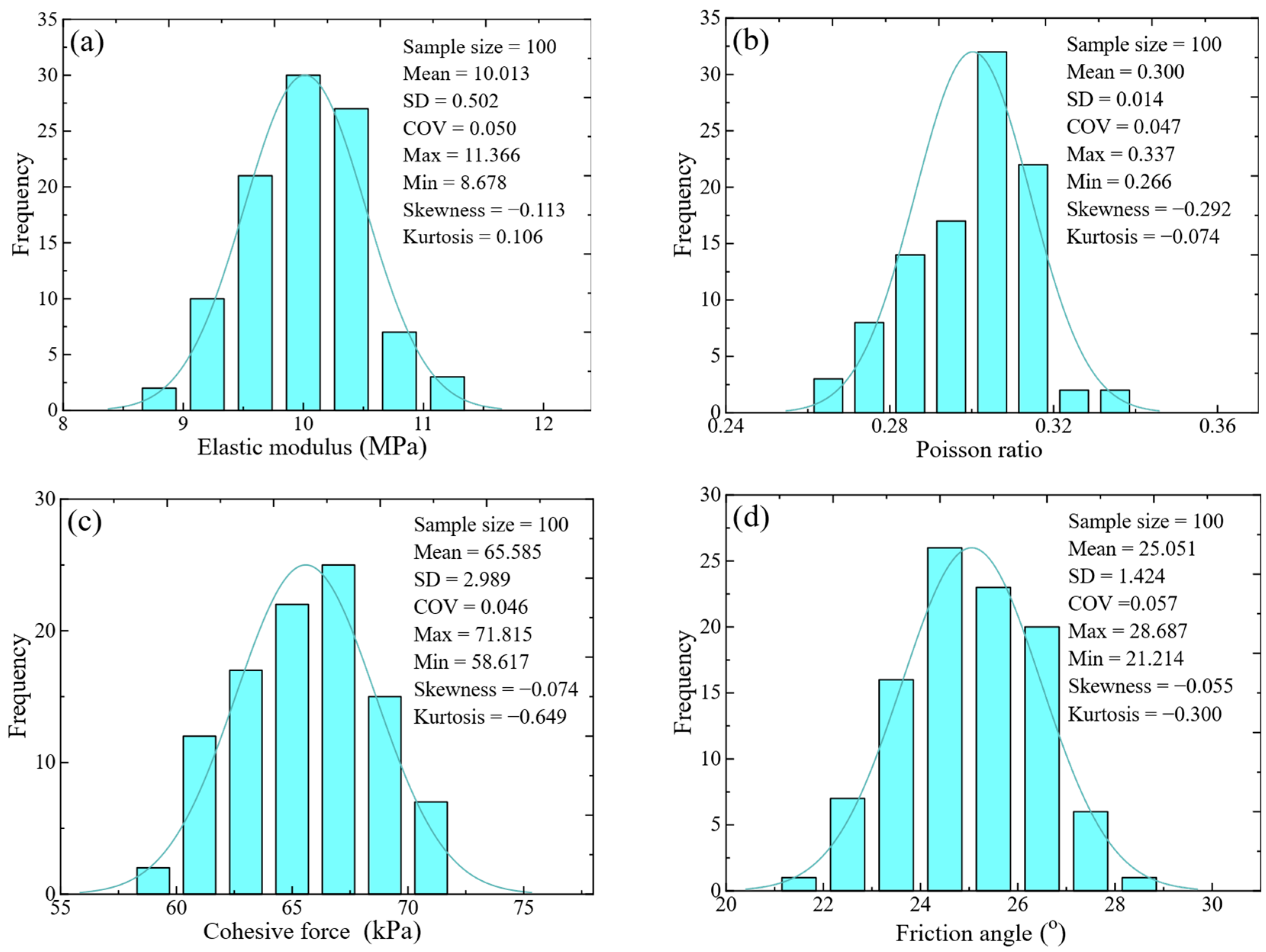
2.1. Test Procedure and Statistical Characteristics
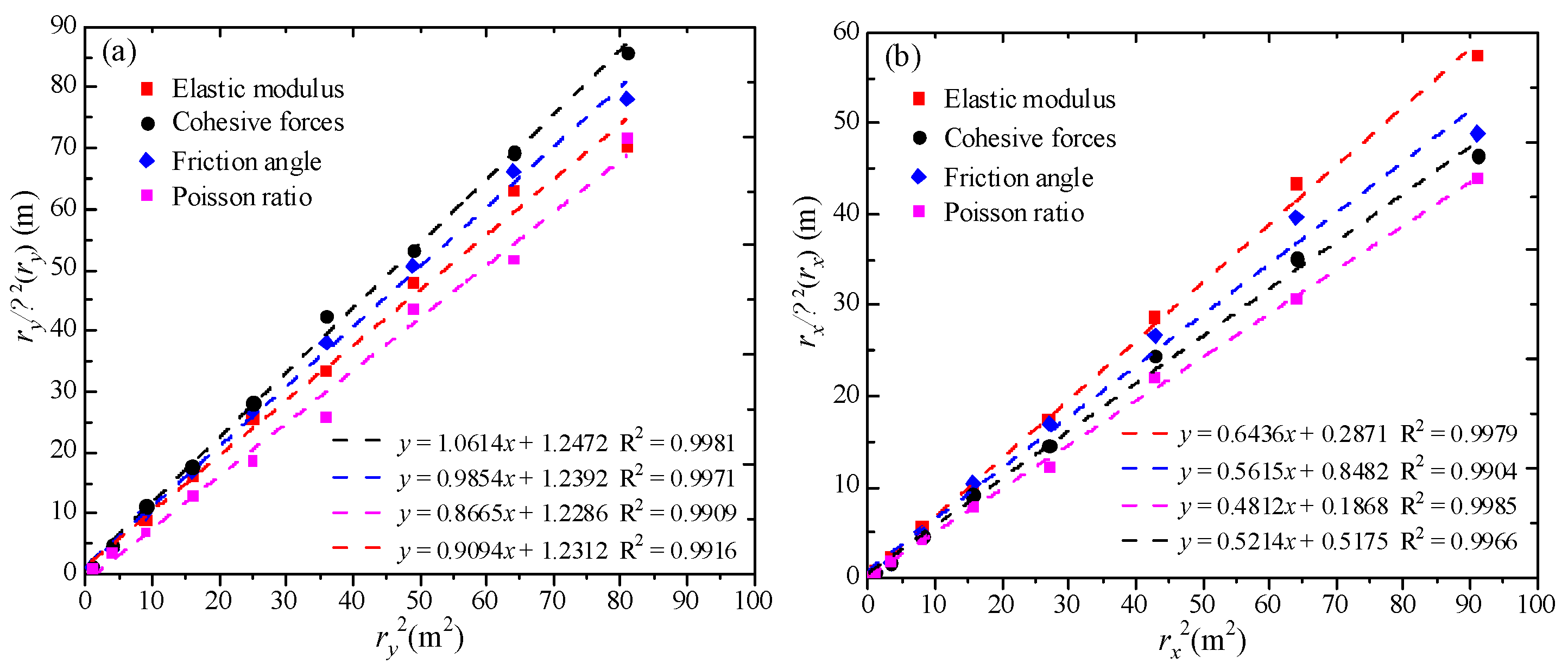
2.2. Spatial Variability Characterization
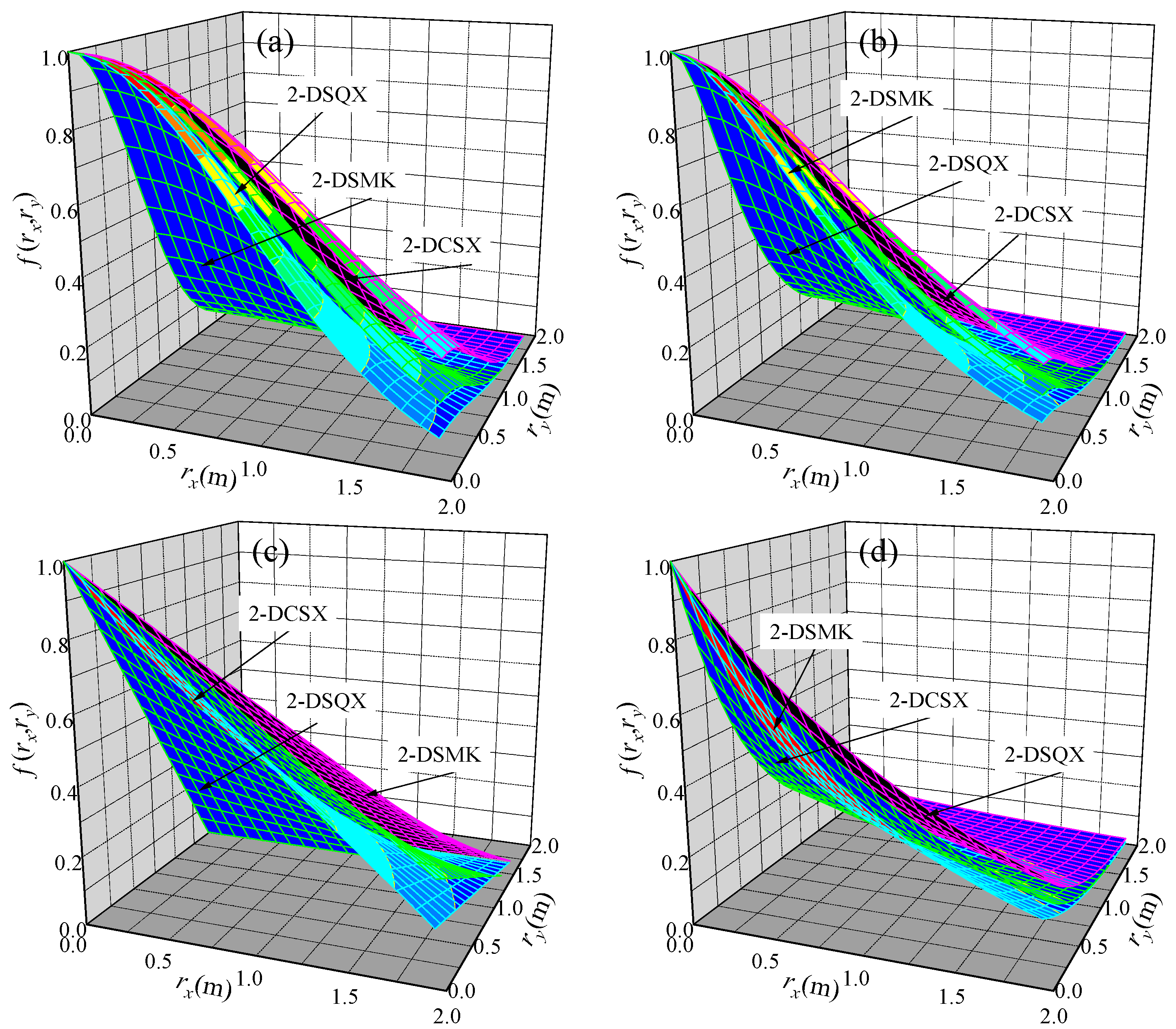
2.3. Cross-Correlation Characterization
3. Uncertainty Analysis of Building Foundation Soils
3.1. Mathematical Equations and Elastoplastic Method
3.2. Uncertainty Analysis Method of Settlement
3.3. Workflow of Proposed Framework
- (1)
- Standard testing procedures to evaluate the soil properties through field and laboratory methods, including sampling, penetration tests, and triaxial compression tests. Statistical analysis processes the measured data to determine the central trends, variability ranges, and spatial correlation patterns.
- (2)
- Quantifying the soil variability using spatial random fields involves analyzing how the soil properties change across locations. This method treats the soil characteristics as continuous random variables, capturing their spatial patterns and correlations.
- (3)
- Copula methods quantify the statistical dependence in the soil properties by modeling their joint distributions without assuming linear relationships. They capture complex correlations between different soil parameters, such as the EM, PR, CF, and FA, using flexible multivariate frameworks.
- (4)
- The variable stiffness elastoplastic method for soil deformation considers how the soil stiffness changes under loading. It combines elastic and plastic behaviors, adjusting the stiffness based on stress levels to better simulate real-world soil responses. Through the incremental stress–strain relationship and considering the load step, the deformation characteristics are calculated by self-programming.
- (5)
- Stochastic finite element analysis for soils involves modeling the spatial variability through random field generation, discretizing it into finite elements, and performing Monte Carlo simulations to compute probabilistic structural responses. This method efficiently quantifies the uncertainty in geotechnical behavior under varying conditions.
4. Risk Assessment of Variable Settlement Properties
4.1. Distribution Fitting Test
4.2. Failure Probability
5. Results and Analyses
5.1. Validation of Uncertainty Stability Analysis Model
5.2. Stability Indicators at Different Locations
5.3. Impact of Spatial Variation on Building Settlement
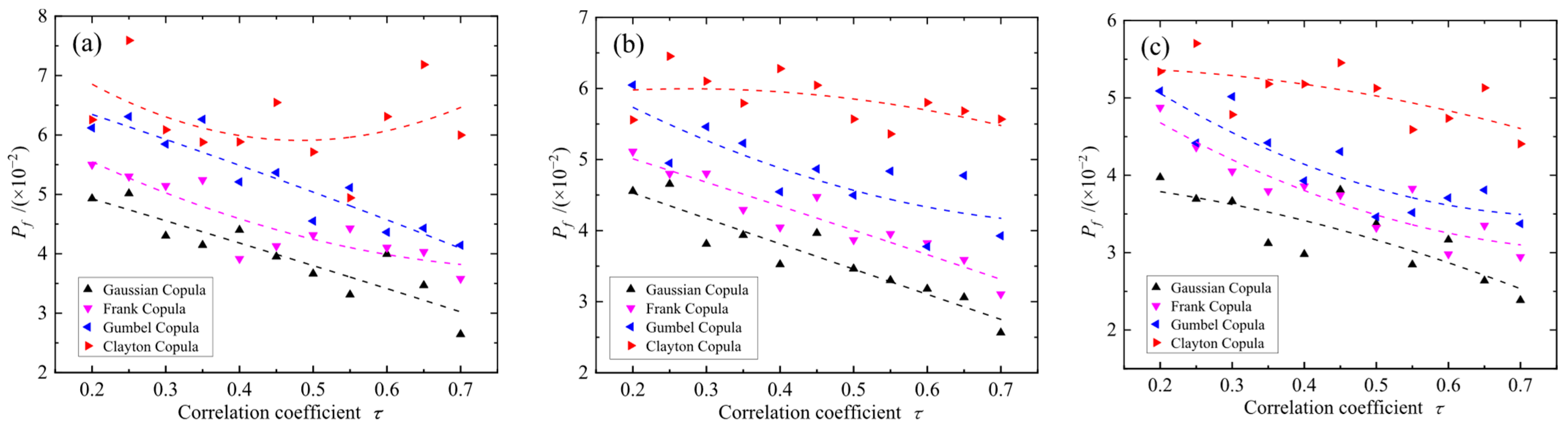
5.4. Impact of Cross-Correlation on Building Settlement
6. Conclusions
- (1)
- The four different mechanical parameters can be regressed to linear equations. The linear fitting degrees are all greater than 0.99. The horizontal fluctuation scale is significantly larger than the vertical scale. This phenomenon primarily results from stratified deposition processes during soil formation, where sedimentation creates more continuous horizontal layers compared to vertical profiles. Different soil parameters have different correlation structures. The most significant difference lies in the rate at which the function graphs change.
- (2)
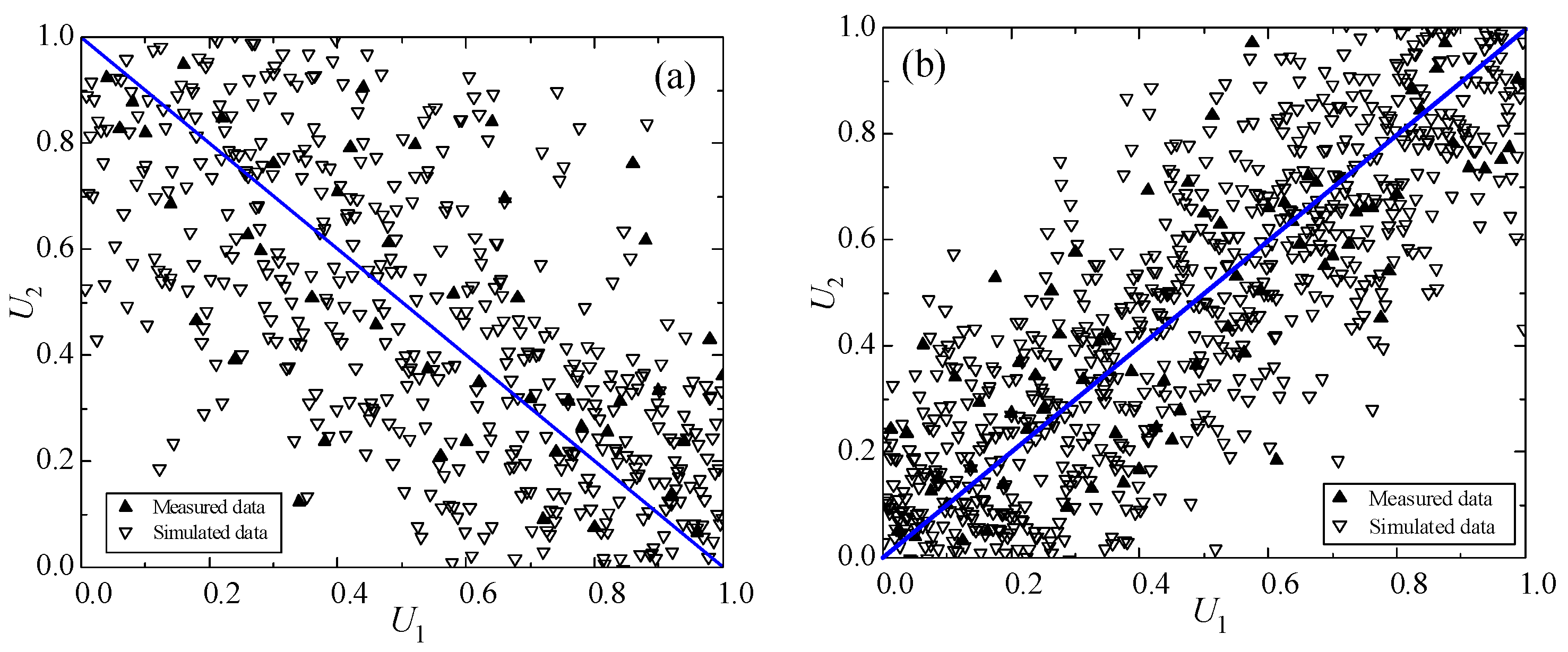
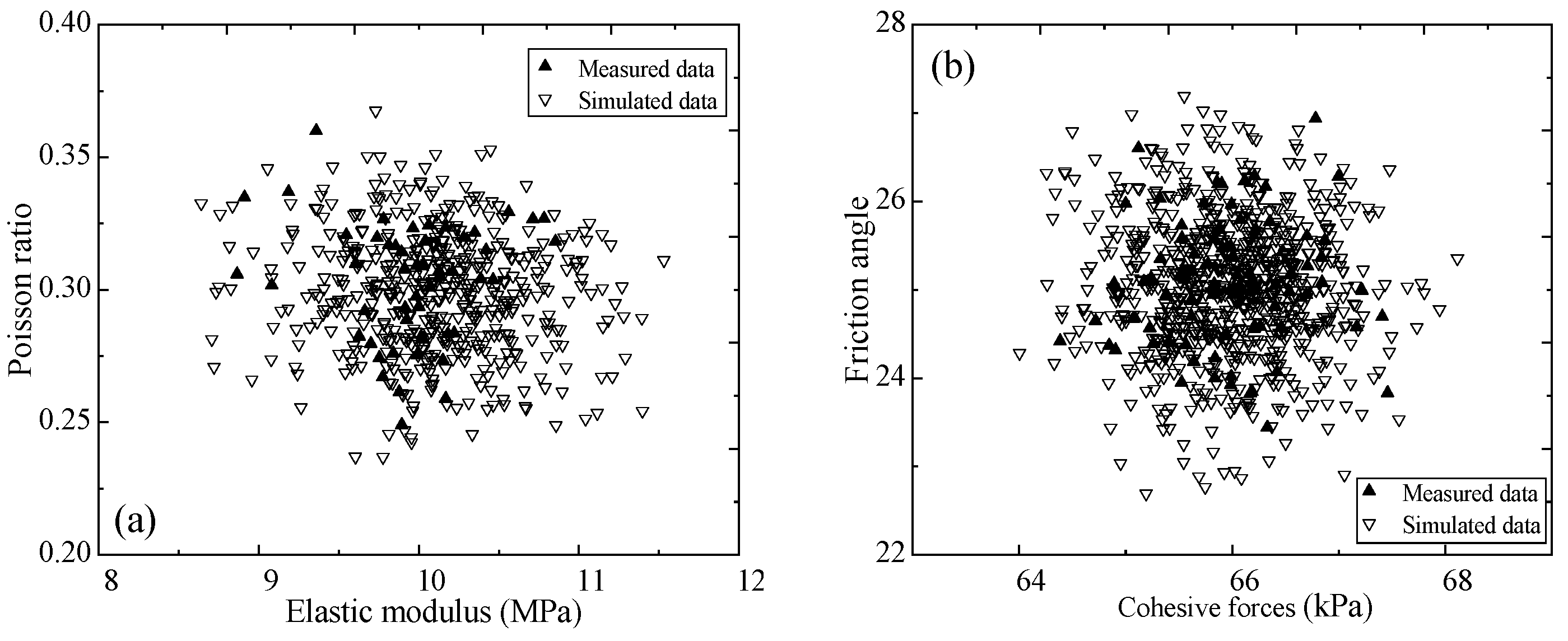
- Copula theory provides a powerful framework for modeling complex dependence structures among soil parameters, overcoming the limitations of traditional correlation coefficients. The EM has a negative correlation with the PR, while the CF has a positively correlation with the FA. The discrete characteristics of the simulated data have similar discrete characteristics to those of the original data. The statistics of the simulated data and test data are basically the same. The bootstrap approach circumvents parametric assumptions by harnessing empirical data to improve the reliability in variable land subsidence analyses.
- (3)
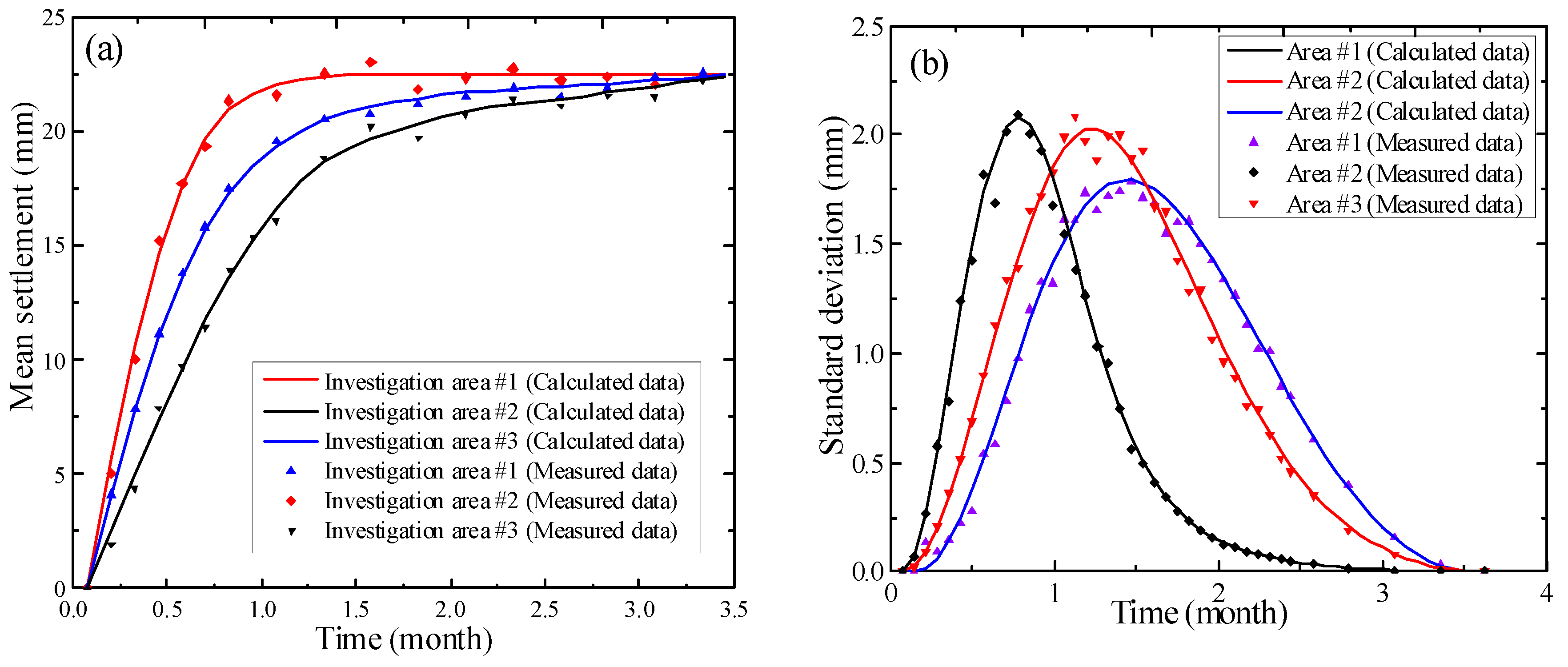
- The test results of the mean settlement are basically the same as the simulation results. The stability analysis method for uncertain geotechnical properties for variable land subsidence processes in this paper is scientific and reasonable. The variable land subsidence follows a normal distribution with a significance level of 0.1. The influence of the variability parameter on the variable land subsidence processes is greater than that of the correlation structure.
- (4)
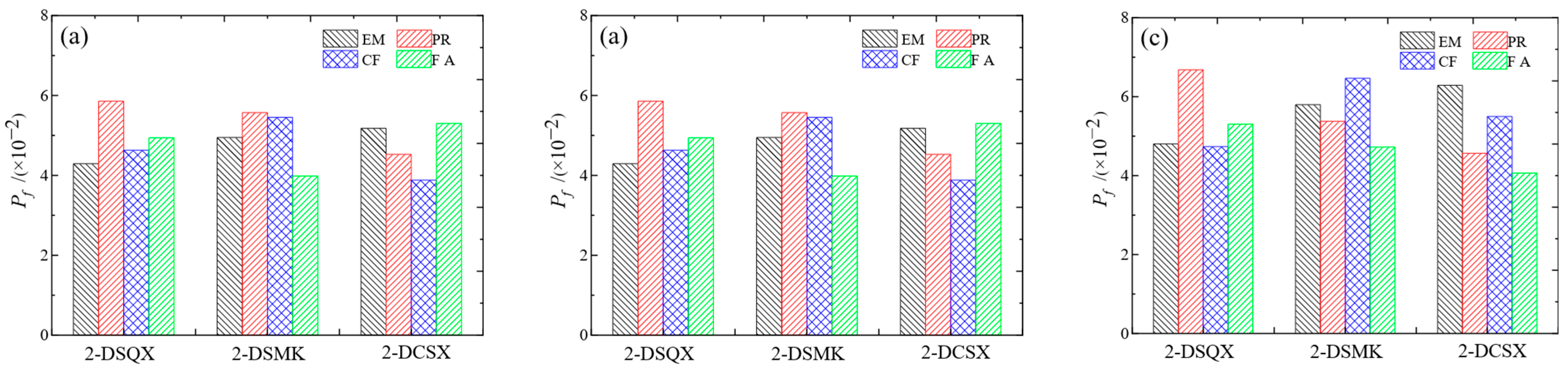
- The failure probabilities of variable stratum settlement for different cross-correlations of geotechnical properties under copula conditions are different. When using the Clayton Copula to characterize the cross-correlation of the geotechnical properties, the failure probability is higher. When using the Gaussian Copula to characterize the cross-correlation of the geotechnical properties, the failure probability is smaller. It can be seen that different cross-correlation structures have different influences on the failure probability of variable stratum settlement.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- El Shinawi, A.; Kuriqi, A.; Zelenakova, M.; Vranayova, Z.; Abd-Elaty, I. Land subsidence and environmental threats in coastal aquifers under sea level rise and over-pumping stress. J. Hydrol. 2022, 608, 127607. [Google Scholar] [CrossRef]
- Ghorbani, Z.; Khosravi, A.; Maghsoudi, Y.; Mojtahedi, F.F.; Javadnia, E.; Nazari, A. Use of InSAR data for measuring land subsidence induced by groundwater withdrawal and climate change in Ardabil Plain, Iran. Sci. Rep. 2022, 12, 13998. [Google Scholar] [CrossRef]
- Moradi, A.; Emadodin, S.; Beitollahi, A.; Abdolazimi, H.; Ghods, B. Assessments of land subsidence in Tehran metropolitan, Iran, using Sentinel-1A InSAR. Environ. Earth Sci. 2023, 82, 569. [Google Scholar] [CrossRef]
- Wu, J.; Shi, B.; Gu, K.; Liu, S.; Wei, G. Evaluation of land subsidence potential by linking subsurface deformation to microstructure characteristics in Suzhou, China. Bull. Eng. Geol. Environ. 2021, 80, 2587–2600. [Google Scholar] [CrossRef]
- Huang, Q.; Gou, Y.; Xue, L.; Yuan, Y.; Yang, B.; Peng, J. Model test study on the mechanical response of metro tunnel to land subsidence. Tunn. Undergr. Space Technol. 2023, 140, 105333. [Google Scholar] [CrossRef]
- Gao, F.; Zhao, T.; Zhu, X.; Zheng, L.; Wang, W.; Zheng, X. Land subsidence characteristics and numerical analysis of the impact on major infrastructure in Ningbo, China. Sustainability 2022, 15, 543. [Google Scholar] [CrossRef]
- Deng, S.; Yang, H.; Chen, X.; Wei, X. Probabilistic analysis of land subsidence due to pumping by Biot poroelasticity and random field theory. J. Eng. Appl. Sci. 2022, 69, 18. [Google Scholar] [CrossRef]
- Intui, S.; Inazumi, S.; Soralump, S. Evaluation of land subsidence during groundwater recovery. Appl. Sci. 2022, 12, 7904. [Google Scholar] [CrossRef]
- Khan, J.; Ren, X.; Hussain, M.A.; Jan, M.Q. Monitoring land subsidence using PS-InSAR technique in Rawalpindi and islamabad, Pakistan. Remote Sens. 2022, 14, 3722. [Google Scholar] [CrossRef]
- Zevgolis, I.E.; Theocharis, A.I.; Koukouzas, N.C. Spatial Variability in Geotechnical Properties Within Heterogeneous Lignite Mine Spoils. Geosciences 2025, 15, 97. [Google Scholar] [CrossRef]
- Nguyen, T.S.; Ngamcharoen, K.; Likitlersuang, S. Statistical characterisation of the geotechnical properties of Bangkok subsoil. Geotech. Geol. Eng. 2023, 41, 2043–2063. [Google Scholar] [CrossRef]
- Nasir, A.; Butt, F.; Ahmad, F. Enhanced mechanical and axial resilience of recycled plastic aggregate concrete reinforced with silica fume and fibers. Innov. Infrastruct. Solut. 2025, 10, 1–17. [Google Scholar] [CrossRef]
- Kalantari, A.R.; Johari, A.; Zandpour, M.; Kalantari, M. Effect of spatial variability of soil properties and geostatistical conditional simulation on reliability characteristics and critical slip surfaces of soil slopes. Transp. Geotech. 2023, 39, 100933. [Google Scholar] [CrossRef]
- Zhao, T.; Wang, Y.; Xu, L. Efficient CPT locations for characterizing spatial variability of soil properties within a multilayer vertical cross-section using information entropy and Bayesian compressive sensing. Comput. Geotech. 2021, 137, 104260. [Google Scholar] [CrossRef]
- Alamanis, N.; Dakoulas, P. Effects of spatial variability of soil properties and ground motion characteristics on permanent displacements of slopes. Soil Dyn. Earthq. Eng. 2022, 161, 107386. [Google Scholar] [CrossRef]
- Ghaaowd, I.; Faisal, A.H.M.H.; Rahman, M.H.; Abu-Farsakh, M. Evaluation of site variability effect on the geotechnical data and its application. Geotech. Test. J. 2021, 44, 971–985. [Google Scholar] [CrossRef]
- Guan, Z.; Wang, Y.; Phoon, K.K. Dictionary learning of spatial variability at a specific site using data from other sites. J. Geotech. Geoenviron. Eng. 2024, 150, 04024072. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Li, Z.; Yang, Z.; Qi, X. A coupled probabilistic site characterization method for estimating soil stratification and spatial variability using multiple-source site investigation data. Eng. Geol. 2025, 351, 108024. [Google Scholar] [CrossRef]
- Ma, G.; Rezania, M.; Nezhad, M.M. Stochastic assessment of landslide influence zone by material point method and generalized geotechnical random field theory. Int. J. Geomech. 2022, 22, 04022002. [Google Scholar] [CrossRef]
- Yoshida, I.; Tomizawa, Y.; Otake, Y. Estimation of trend and random components of conditional random field using Gaussian process regression. Comput. Geotech. 2021, 136, 104179. [Google Scholar] [CrossRef]
- Rawat, S.; Saliba, P.; Estephan, P.C.; Ahmad, F.; Zhang, Y. Mechanical performance of Hybrid Fibre Reinforced Magnesium Oxychloride Cement-based composites at ambient and elevated temperature. Buildings 2024, 14, 270. [Google Scholar] [CrossRef]
- Phoon, K.K.; Ching, J.; Shuku, T. Challenges in data-driven site characterization. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2022, 16, 114–126. [Google Scholar] [CrossRef]
- Wang, C.; Wang, K.; Tang, D.; Hu, B.; Kelata, Y. Spatial random fields-based Bayesian method for calibrating geotechnical parameters with ground surface settlements induced by shield tunneling. Acta Geotech. 2022, 17, 1503–1519. [Google Scholar] [CrossRef]
- Choudhuri, K.; Chakraborty, D. Probabilistic analyses of three-dimensional circular footing resting on two-layer c–ϕ soil system considering soil spatial variability. Acta Geotech. 2022, 17, 5739–5758. [Google Scholar] [CrossRef]
- Ahmad, F.; Rawat, S.; Yang, R.C.; Zhang, L.; Zhang, Y.X. Fire resistance and thermal performance of hybrid fibre-reinforced magnesium oxychloride cement-based composites. Constr. Build. Mater. 2025, 472, 140867. [Google Scholar] [CrossRef]
- Gong, W.; Zhao, C.; Juang, C.H.; Zhang, Y.; Tang, H.; Lu, Y. Coupled characterization of stratigraphic and geo-properties uncertainties–a conditional random field approach. Eng. Geol. 2021, 294, 106348. [Google Scholar] [CrossRef]
- Di, H.; Zhou, S.; Yao, X.; Tian, Z. In situ grouting tests for differential settlement treatment of a cut-and-cover metro tunnel in soft soils. Bull. Eng. Geol. Environ. 2021, 80, 6415–6427. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, F.; Liu, F.; Wang, X. Full-scale in situ experimental study on the bearing capacity of energy piles under varying temperature and multiple mechanical load levels. Acta Geotech. 2024, 19, 401–415. [Google Scholar] [CrossRef]
- Zhang, P.; Jin, Y.F.; Yin, Z.Y. Machine learning—Based uncertainty modelling of mechanical properties of soft clays relating to time-dependent behavior and its application. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 1588–1602. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Xiao, C.; Goh, S.H.; Deng, M.X. Metamodel-based reliability analysis in spatially variable soils using convolutional neural networks. J. Geotech. Geoenviron. Eng. 2021, 147, 04021003. [Google Scholar] [CrossRef]
- Shi, C.; Wang, Y. Assessment of reclamation-induced consolidation settlement considering stratigraphic uncertainty and spatial variability of soil properties. Can. Geotech. J. 2022, 59, 1215–1230. [Google Scholar] [CrossRef]
- Alibeikloo, M.; Khabbaz, H.; Fatahi, B. Random field reliability analysis for time-dependent behaviour of soft soils considering spatial variability of elastic visco-plastic parameters. Reliab. Eng. Syst. Saf. 2022, 219, 108254. [Google Scholar] [CrossRef]
- Yang, Z.; Chen, J.; Feng, Y.; Li, X. Probabilistic analysis of offshore single pile composite foundation considering rotated anisotropy spatial variability of multi-layered soils. Comput. Geotech. 2025, 182, 107159. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Y.; Phoon, K.K.; Beer, M. Similarity quantification of soil spatial variability between two cross-sections using auto-correlation functions. Eng. Geol. 2024, 331, 107445. [Google Scholar] [CrossRef]
- Bao, X.; Li, J.; Shen, J.; Chen, X.; Zhang, C.; Cui, H. Comprehensive multivariate joint distribution model for marine soft soil based on the vine copula. Comput. Geotech. 2025, 177, 106814. [Google Scholar] [CrossRef]
- Cao, J.; Wang, T.; Sheng, M.; Huang, Y.; Zhou, G. A Copula method for modeling the intensity characteristic of geotechnical strata of roof based on small sample test data. Geomech. Eng. 2024, 36, 601–618. [Google Scholar]
- Zhou, X.; Lu, D.; Zhang, Y.; Du, X.; Rabczuk, T. An open-source unconstrained stress updating algorithm for the modified Cam-clay model. Comput. Methods Appl. Mech. Eng. 2022, 390, 114356. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, G.F.; Wei, X.; Deng, X. Numerical modelling of multiple excavations in an ultra-deep foundation using an enhanced distinct lattice spring model with modified cam clay model. Tunn. Undergr. Space Technol. 2024, 152, 105875. [Google Scholar] [CrossRef]
- Chi, S.; Feng, W.; Jia, Y.; Zhang, Z. Stochastic finite-element analysis of earth–rockfill dams considering the spatial variability of soil parameters. Int. J. Geomech. 2022, 22, 04022224. [Google Scholar] [CrossRef]
- Chen, X.J.; Fu, Y.; Liu, Y. Random finite element analysis on uplift bearing capacity and failure mechanisms of square plate anchors in spatially variable clay. Eng. Geol. 2022, 304, 106677. [Google Scholar] [CrossRef]
- Ebner, B.; Liebenberg, S.C.; Visagie, I.J.H. A new omnibus test of fit based on a characterization of the uniform distribution. Statistics 2022, 56, 1364–1384. [Google Scholar] [CrossRef]
- Raza, M.U.; Butt, F.; Ahmad, F.; Waqas, R.M. Seismic safety assessment of buildings and perceptions of earthquake risk among communities in Mingora, Swat, Pakistan. Innov. Infrastruct. Solut. 2025, 10, 1–18. [Google Scholar] [CrossRef]
- Zhang, W.; Huang, Z.; Zhang, J.; Zhang, R.; Ma, S. Multifactor uncertainty analysis of construction risk for deep foundation pits. Appl. Sci. 2022, 12, 8122. [Google Scholar] [CrossRef]
- Ahmad, F.; Rawat, S.; Zhang, L.; Fanna, D.J.; Soe, K.; Zhang, Y.X. Effect of Metakaolin and Ground Granulated Blast Furnace Slag on the Performance of Hybrid Fibre-Reinforced Magnesium Oxychloride Cement-Based Composites. Int. J. Civ. Eng. 2025, 23, 853–868. [Google Scholar] [CrossRef]


| № | Particle Sizes and Their Percentages (%) | ||||
|---|---|---|---|---|---|
| <0.002 mm | 0.002 mm~0.005 mm | 0.005 mm~0.05 mm | 0.05 mm~0.075 mm | >0.075 mm | |
| 1# | 7.26 | 39.80 | 32.05 | 13.24 | 4.40 |
| 2# | 8.16 | 41.96 | 32.13 | 14.64 | 3.83 |
| 3# | 7.16 | 39.79 | 31.90 | 13.32 | 4.71 |
| 4# | 7.39 | 39.99 | 32.17 | 15.69 | 3.91 |
| 5# | 8.41 | 40.06 | 33.05 | 13.66 | 4.18 |
| 6# | 9.38 | 41.28 | 32.13 | 12.55 | 4.50 |
| 7# | 8.15 | 40.04 | 31.79 | 11.85 | 4.98 |
| 8# | 9.23 | 39.89 | 32.31 | 13.89 | 4.79 |
| 9# | 8.23 | 42.33 | 33.09 | 14.20 | 3.93 |
| 10# | 8.27 | 40.17 | 31.62 | 13.01 | 4.34 |
| № | Density (g/cm3) | Dry Density (g/cm3) | Moisture Content (%) | Specific Gravity of Solids | Plastic Limits (%) | Liquid Limits (%) |
|---|---|---|---|---|---|---|
| 1# | 1.77 | 1.37 | 29.16 | 2.67 | 20.48 | 41.07 |
| 2# | 1.83 | 1.43 | 27.80 | 2.74 | 19.53 | 41.89 |
| 3# | 1.91 | 1.47 | 29.81 | 2.78 | 19.24 | 38.67 |
| 4# | 1.78 | 1.42 | 25.67 | 2.65 | 20.40 | 39.97 |
| 5# | 1.99 | 1.51 | 31.84 | 2.58 | 19.16 | 38.67 |
| 6# | 1.91 | 1.52 | 26.03 | 2.70 | 19.22 | 40.90 |
| 7# | 1.94 | 1.52 | 28.02 | 2.75 | 19.64 | 40.60 |
| 8# | 1.89 | 1.46 | 29.56 | 2.71 | 19.11 | 39.38 |
| 9# | 1.54 | 1.18 | 30.74 | 2.83 | 20.34 | 39.33 |
| 10# | 1.93 | 1.49 | 29.77 | 2.67 | 19.83 | 39.10 |
| № | Vertical Direction of the Stratum (m) | Horizontal Direction of the Stratum (m) | ||||||
|---|---|---|---|---|---|---|---|---|
| EM | PR | CF | FA | EM | PR | CF | FA | |
| 1# | 1.05 | 1.20 | 0.90 | 0.95 | 1.45 | 1.91 | 1.92 | 1.61 |
| 2# | 1.06 | 1.16 | 0.97 | 1.01 | 1.58 | 1.96 | 1.87 | 1.77 |
| 3# | 1.13 | 1.15 | 0.88 | 1.04 | 1.51 | 2.03 | 1.99 | 1.66 |
| 4# | 1.03 | 1.15 | 0.90 | 1.00 | 1.47 | 2.10 | 2.02 | 1.72 |
| 5# | 1.16 | 1.10 | 0.92 | 1.01 | 1.61 | 2.10 | 1.97 | 1.70 |
| 6# | 1.15 | 1.11 | 0.95 | 1.02 | 1.59 | 1.95 | 2.18 | 1.77 |
| 7# | 1.06 | 1.15 | 1.03 | 1.04 | 1.54 | 2.15 | 1.90 | 1.87 |
| 8# | 1.14 | 1.21 | 0.95 | 1.10 | 1.52 | 2.12 | 1.96 | 1.92 |
| 9# | 1.17 | 1.12 | 0.92 | 1.12 | 1.48 | 2.23 | 1.73 | 1.82 |
| 10# | 1.12 | 1.24 | 0.97 | 1.05 | 1.41 | 2.03 | 1.87 | 1.73 |
| Function Type | Detailed Mathematical Expression | Relationship Between Parameters |
|---|---|---|
| 2-DSQX | ||
| 2-DSMK | ||
| 2-DCSX |
| Copula | C(u1,u2; θ) | D(u1,u2; θ) | Range of θ |
|---|---|---|---|
| Gaussian | [−1, 1] | ||
| Frank | |||
| Gumbel | |||
| Clayton |
| Statistics | Field Experiment Results | Numerical Simulation Results | Comparative Values | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| EM | PR | CF | FA | EM | PR | CF | FA | EM | PR | CF | FA | |
| Sample size | 100 | 100 | 100 | 100 | 1000 | 1000 | 1000 | 1000 | ||||
| Mean (10A MPa) | 10.013 | 0.300 | 65.585 | 25.051 | 9.895 | 0.297 | 64.787 | 25.216 | 0.118 | 0.003 | 0.798 | −0.165 |
| SD (10A MPa) | 0.502 | 0.014 | 2.989 | 1.424 | 0.491 | 0.014 | 2.987 | 1.408 | 0.011 | 0.000 | 0.002 | 0.016 |
| COV | 0.050 | 0.047 | 0.046 | 0.057 | 0.051 | 0.046 | 0.045 | 0.057 | −0.001 | 0.001 | 0.001 | 0.000 |
| Max (10A MPa) | 11.366 | 0.337 | 71.815 | 28.687 | 11.307 | 0.333 | 70.846 | 28.612 | 0.059 | 0.004 | 0.969 | 0.075 |
| Min (10A MPa) | 8.678 | 0.266 | 58.617 | 21.214 | 8.707 | 0.263 | 58.464 | 20.957 | −0.029 | 0.003 | 0.153 | 0.257 |
| Skewness | −0.113 | −0.292 | −0.074 | −0.055 | −0.113 | −0.296 | −0.074 | −0.055 | 0.000 | 0.004 | 0.000 | 0.000 |
| Peakedness | 0.106 | −0.074 | −0.649 | −0.300 | 0.106 | −0.074 | −0.650 | −0.303 | 0.000 | 0.000 | 0.001 | 0.003 |
| № | Group (ti−1, ti] | Absolute Frequency, fi | Frequency, fi/n | Cumulative Frequency |
|---|---|---|---|---|
| 1 | [11.776, 12.930] | 15 | 0.0015 | 0.0650 |
| 2 | (12.930, 14.084] | 121 | 0.0121 | |
| 3 | (14.084, 15.238] | 619 | 0.0619 | |
| 4 | (15.238, 16.392] | 1902 | 0.1902 | 0.2141 |
| 5 | (16.392, 17.546] | 3011 | 0.3011 | 0.489 |
| 6 | (17.546, 18.701] | 2649 | 0.2649 | 0.7693 |
| 7 | (18.701, 19.855] | 1314 | 0.1314 | 0.9313 |
| 8 | (19.855, 21.009] | 316 | 0.0316 | 0.9313 + 0.0687 = 1 |
| 9 | (21.009, 22.163] | 47 | 0.0047 | |
| 10 | (22.163, 23.317] | 6 | 0.0006 |
| № | Group (ti−1, ti] | Absolute Frequency, fi | Frequency, pi | npi | (fi−npi)2/npi |
|---|---|---|---|---|---|
| 1 | (−∞, 15.238] | 755 | 0.0769 | 769.00 | 0.2549 |
| 2 | (15.238, 16.392] | 1902 | 0.1898 | 1898.00 | 0.0084 |
| 3 | (16.392, 17.546] | 3011 | 0.3050 | 3050.00 | 0.4987 |
| 4 | (17.546, 18.701] | 2649 | 0.2658 | 2658.00 | 0.0305 |
| 5 | (18.701, 19.855] | 1314 | 0.1256 | 1256.00 | 2.6783 |
| 6 | (19.855, +∞] | 369 | 0.0376 | 376.00 | 0.1303 |
| Total | 10,000 | 1.0000 | 10,000 | 3.6011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, X.; Wang, T. Uncertainty Analysis and Risk Assessment for Variable Settlement Properties of Building Foundation Soils. Buildings 2025, 15, 2369. https://doi.org/10.3390/buildings15132369
Zhou X, Wang T. Uncertainty Analysis and Risk Assessment for Variable Settlement Properties of Building Foundation Soils. Buildings. 2025; 15(13):2369. https://doi.org/10.3390/buildings15132369
Chicago/Turabian StyleZhou, Xudong, and Tao Wang. 2025. "Uncertainty Analysis and Risk Assessment for Variable Settlement Properties of Building Foundation Soils" Buildings 15, no. 13: 2369. https://doi.org/10.3390/buildings15132369
APA StyleZhou, X., & Wang, T. (2025). Uncertainty Analysis and Risk Assessment for Variable Settlement Properties of Building Foundation Soils. Buildings, 15(13), 2369. https://doi.org/10.3390/buildings15132369






