Reducing Maximum Punching Force in Sheet Cold Forming: A Numerical Study of a New Punch Design (Part II)

Abstract

Punching is a widely adopted cold sheet metal forming process, prized for its cost-effectiveness and high production efficiency. However, premature tool failure remains a persistent challenge, leading to increased downtime and maintenance costs. This study investigates solutions to mitigate tool failure through a combination of 3D design optimization, Finite Element Modeling (FEM), and Response Surface Methodology (RSM). Specifically, FEM was used to analyze stress distribution and deformation in the punch under varying geometric and operational parameters, while RSM optimized the design space to identify key factors influencing tool life. The findings reveal that each proposed solution, including modifications to punch geometry, clearance, and material treatment, offers distinct advantages and trade-offs. A comparative analysis of these solutions highlighted one optimal design, which was then further analyzed using FEM to predict damage progression. While this study provides a framework for reducing tool failure, experimental validation of the damage prediction model is recommended for future work to confirm the numerical results. This research aims to provide industrial practitioners with actionable insights and methodologies to enhance punch durability, ultimately reducing production interruptions and costs.

1. Introduction

In contemporary industrial environments, time efficiency has become a pivotal factor in optimizing production processes and reducing operational costs. Effective time management is widely recognized as a fundamental driver of productivity and profitability, particularly in sectors where precision and speed are critical.

In the cold forming industry, minimizing downtime, whether due to maintenance, tool failure, or process adjustments, remains a persistent challenge. Manufacturers strive to achieve high-quality output with minimal production time and cost, making efficiency a central objective. Among the most widely employed cold forming techniques, punching stands out due to its versatility and efficiency. This process involves the application of force through a punch to deform sheet metal within a die, enabling the production of components across diverse mechanical engineering applications. However, in mass or serial production, the degradation of punch components can significantly compromise productivity, leading to increased maintenance costs and reduced operational lifespan.

Punching has garnered substantial attention from researchers due to its critical role in modern manufacturing. For instance, Shaheen et al. [1] demonstrated that an optimized punch design could extend tool life while reducing maintenance costs. Their study employed Design for Analysis (DFA) methodologies, which streamlined the design process and improved overall efficiency. Finite Element Analysis (FEA) revealed that the maximum stress in the original punch was 1729 MPa, whereas the redesigned punch exhibited a 25% reduction in stress, with a maximum value of 1296 MPa.

In 2023, Akchurin et al. [2] investigated structural design tools for engine core punches and dies, focusing on geometric features, assembly constraints, and plate hole data. By integrating 3D modeling techniques, their research achieved significant improvements in design quality, along with substantial time and cost savings.

Yung Chou [3] developed a precision automated feeding device guided by microscopic visualization to enhance positioning accuracy in microforming systems. His research explored optimal punching parameters, contributing to advancements in micropunching technology.

An experimental study by Ran et al. [4] examined the rectangular punch clinching process for joining Al5052 sheets under varying forming forces. The findings highlighted that joints produced under specific conditions exhibited higher shear strength compared to tensile strength, providing insights into failure modes and mechanical performance.

Wang and Masood [5] analyzed the influence of tool profiles, including circular, flat elliptical, and highly elliptical shapes, on punching performance. Their study also assessed the effects of lubrication coefficient, bond holding force, clearance, and blank thickness on tool wear across different geometries.

Ravikumar et al. [6] investigated rubber cutting using a die, optimizing process parameters through an experimental model and Taguchi optimization method. Their analysis of variance (ANOVA) and parametric contributions provided a robust framework for improving punching efficiency.

Lubis et al. [7] utilized Finite Element Analysis (FEA) to predict defects and examine sheared edge characteristics in Ti-6Al-4V sheets (0.6 mm thickness). Their study compared chamfered, rounded, and flat tool geometries, revealing that the flat tool shaft produced a more pronounced shear zone and the lowest burr formation compared to alternative designs.

In 2024, Sandin et al. [8] employed the Particle Finite Element Method (PFEM) to study the shear cutting process of advanced high-strength steel. This method demonstrated high accuracy in predicting cutting-edge geometry and shear-related damage, offering valuable insights for optimizing manufacturing processes involving shear-sensitive materials.

Chantzis et al. [9] explored the application of 3D-printed tools in cold work forming using additive manufacturing (AM). Their combined FEA and experimental approach confirmed the feasibility of AM-fabricated tooling in enhancing formability and production efficiency.

Kadarno et al. [10] examined the impact of step-die mechanisms on material deformation and stress distribution during punching. Their findings indicated that step-die designs effectively reduce punching forces by promoting gradual deformation, thereby minimizing stress concentrations and improving part quality. These observations align with our own research on the influence of punch geometry on stress distribution and forming forces.

Similarly, Asad et al. [11] investigated the role of punch edge geometry in sheet metal forming, demonstrating how variations in edge profiles affect stress distribution, tool wear, and punched surface quality. Their results emphasized that specific edge geometries can reduce burr formation and enhance dimensional accuracy, reinforcing our findings on the importance of punch-die clearance and edge design.

Goijaerts et al. [12] analyzed the influence of punch geometry on forming forces, while recent work by Zeidi et al. [13] highlighted the critical role of punch-die clearance in minimizing burr formation and improving hole quality. Their experimental study on S500 MC sheet metal underscored the impact of clearance on punching force and edge quality, further validating the need for precise tool design in industrial applications.

This study aims to contribute to the scientific literature by focusing on cold forming of sheet metal with a thickness equal to the punch diameter (3 mm), a topic that has received limited attention compared to conventional thin-sheet punching [14,15,16,17]. While traditional thin-sheet assumptions (e.g., plane stress, 2D models, standard clearances) suffice for small thickness-to-diameter ratios, thicker sheets (t = Dp) introduce 3D stress/strain gradients, extended burnish zones, altered fracture modes, higher forming forces, and increased tool wear. These challenges necessitate dedicated experimental investigations, adjusted clearances, and 3D numerical modeling, which remain understudied [18,19].

Motivated by premature punch failure, this research proposes design modifications to the punch shaft and head, utilizing Finite Element Modeling (FEM) to identify the most effective configuration for reducing punching force. The optimal design was further developed to validate a damage prediction model, offering practical solutions for enhancing tool longevity and process efficiency.

2. Materials and Methods

To conduct an analysis of the punch-die contact, a thorough examination of the punch-die contact is critical to ensuring the precision, efficiency, and overall success of the punching process. This interaction directly influences the quality of the punched hole, tool wear, and the mechanical integrity of the final product.

In this study, the punching process is conducted using an AISI D2 punch, which is activated on a mechanical press Genta presses, Torino, Italia). The objective is to create a 3 mm diameter hole in a 3 mm thick S500 MC steel sheet. The punching tool, also made of AISI D2 steel, is selected for its high hardness, wear resistance, and durability—qualities that are essential for maintaining dimensional accuracy and prolonging tool life during high-stress operations. By focusing on the punch-die interaction, this research aims to optimize the punching parameters, minimize defects, and ensure consistent results in industrial applications. The selection of AISI D2 for both the punch and die ensures compatibility and reduces the risk of premature failure, thereby enhancing the reliability of the process.

2.1. Numerical Model

The simulation relies on the Johnson-Cook parameters for AISI D2 and S500MC steels. Punching induces highly concentrated deformations in small regions, with the shear zone experiencing extreme strain rates and elevated temperatures. Due to these conditions, an explicit simulation approach was selected for the model.

For this simulation, the explicit version of ABAQUS software (6.17) was utilized. Indeed, ABAQUS/Explicit is a finite element analysis tool that employs an explicit integration scheme to solve nonlinear or quasi-static dynamic problems. Its ability to handle nonlinear behaviors, such as contact interactions, makes it well-suited for this application. The explicit method is particularly advantageous for nonlinear problems due to its straightforward implementation. However, it requires very small steps. The direct explicit integration method simplifies contact and friction management, making it ideal for highly nonlinear problems like ballistic impact or metal cutting, such as punching in this case.

The following steps outline the integration of essential functionalities for modeling orthogonal sections using ABAQUS. Most ABAQUS parameters were derived from previous research works [20,21,22,23]. The configuration of each module was completed in the following order: Part, Property, Mesh, Assembly, Step, Interaction, Load, and Job.

The process began with the creation of four components: the punch, ‘plettac,’ die, and backup plate. A 3D analytical rigid revolved shell model was used for the backup plate, including a reference point to facilitate movement in the loading module. The same procedure was applied to the die. For the punch and ‘plettac,’ a 3D deformable revolved solid was generated, using a 90° revolution to reduce the number of element nodes and increments.

In the property module, the material characteristics of AISI D2 and S500MC were defined for the punching tool and ‘plettac,’ respectively. The behavior law coefficients of Johnson-Cook damage parameters specific to each material were introduced. In the damage law, the “damage evolution” option was defined with a failure displacement of 0.1. Additionally, material density, Young’s modulus, and Poisson’s ratio of 0.28 were specified in [24]. The Johnson-Cook model is expressed in Equation (1):

$$\mathsf{\sigma }=(\mathrm{A}+\mathrm{B}{\epsilon }^n)\left(1+C\mathit{ln}{\displaystyle \frac{\dot{\epsilon }}{{\dot{\epsilon }}_r}}\right)\left(1-{\displaystyle \frac{T-T_r}{T_m-T_r}}\right)$$

(1)

In this context, σ represents the equivalent stress, while ε denotes the equivalent plastic strain. The parameters A, B, n, C, and m are material constants, where A corresponds to the material’s yield stress under reference conditions, B is the strain hardening constant, and n represents the strain hardening coefficient. Additionally, C serves as the strain rate strengthening coefficient, and m is the thermal softening coefficient. The material’s melting temperature is denoted as T_m, while T refers to the deformation temperature. The symbols $\dot{\epsilon }$_r and T_r represent the reference strain rate and the reference deformation temperature, respectively.

The reference strain rate ($\dot{\epsilon }$_r) and reference temperature (T_r) were set at 1.0 s⁻¹ and 1298 K, respectively. A failure model was implemented based on the ductile failure criterion, where the equivalent plastic strain at the onset of damage (ε_f) is influenced by stress triaxiality, strain rate, and temperature.

As shown in Equation (2), The Johnson-Cook fracture model is expressed by Johnson et al. [25]:

$${\mathsf{\epsilon }}_{\mathrm{f}}=[{\mathrm{D}}_1+{\mathrm{D}}_2\exp ({\mathrm{D}}_3({\displaystyle \frac{\dot{\epsilon }}{{\dot{\epsilon }}_r}}))][1+{\mathrm{D}}_4\ln {\displaystyle \frac{\dot{\epsilon }}{{\dot{\epsilon }}_r}}][1+{\mathrm{D}}_5{\displaystyle \frac{T-T_r}{T_m-T_r}}]$$

(2)

In Equation (2), D₁ represents the initial failure strain, D₂ is the exponential factor, D₃ triaxiality factor, D₄ denotes the strain rate factor, and the temperature factor is represented by D₅, σ_m is the mean stress, and σ_eq shows the equivalent stress. All model parameters were well defined in [24].

In the Mesh module, quadrilateral elements were generated using mesh controls to simplify the computation. Mesh sensitivity analysis is crucial to determine the optimal mesh size that ensures accurate and reliable simulation results. For the model to be effective, the outcomes should exhibit minimal variation with further mesh refinement. Accordingly, successive simulations were performed with progressively finer meshes to assess any differences in the obtained results. Four zones were examined: the punch head, the middle section, the shaft, and the plettac (the industrial term for the S500 MC sheet).

The simulation results for the simplified punching tool, evaluated across different mesh sizes, are presented in Table 1. The findings, shown in Figure 1, indicate that the finite element model yielded the most reliable results when the mesh size matched that of the second test.

Table 1. Summary of simulation results for different mesh sizes.

Test Number	Mesh Size	Von Mises Stress (MPa)	Tresca Stress (MPa)	Max Principal (MPa)	Nodes Number	Elements Number	CPU Time
1	Head: 0.2 Middle: 0.5 Shaft: 0.1 Plettac: 0.1	1713	1934	1853	312,088	291,760	19,232.7
2	Head:0.25 Middle: 0.55 Shaft: 0.15 Plettac: 0.15	1481	1642	1424	115,544	104,655	1950
3	Head: 0.3 Middle: 0.6 Shaft: 0.2 Plettac: 0.2	1707	1829	2019	54,929	48,128	633.8
4	Head: 0.3 Middle: 0.6 Shaft: 0.2 Plettac: 0.1	1689	1812	1048	141,089	129,818	3522.1
5	Head: 0.35 Middle: 0.65 Shaft: 0.25 Plettac: 0.1	1674	1780	935.2	123,842	114,015	3488.2

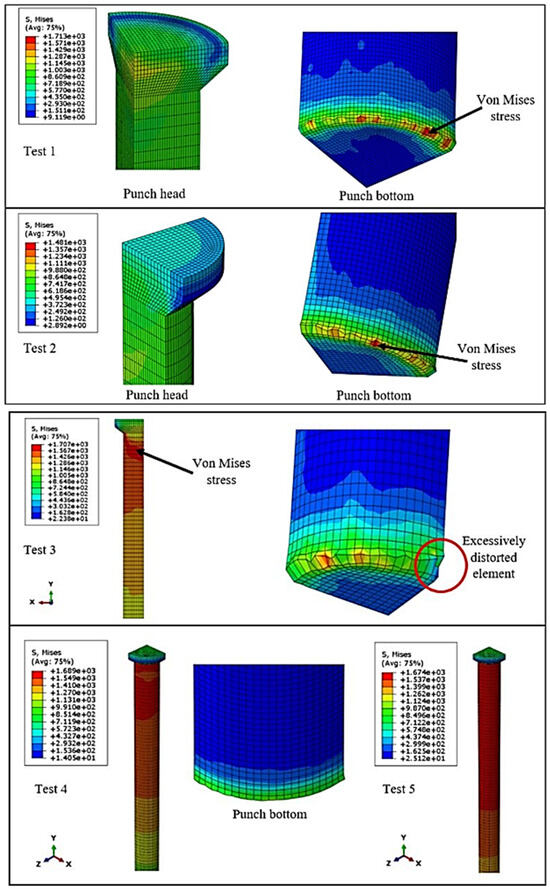
Figure 1. Results of mesh size (from test 1 to test 5) of AISI D2 punch.

While the third test required the least CPU time, it resulted in elevated Von Mises stress, irregular stress distribution at the punch bottom, and significant element distortion. Conversely, mesh refinement beyond the second test size led to a substantial increase in CPU time without a proportional gain in accuracy.

Additionally, coarsening the mesh in the plate reduced computational time but introduced higher stress concentrations in the punch region compared to finer meshes. Based on these observations, the mesh size from the second test was adopted for further simulations, as it provided an optimal balance between computational efficiency and result precision.

To ensure a precise and comprehensive representation of the mechanical behavior and failure mechanisms during the punching process, the three-dimensional (3D) finite element model was discretized using C3D8R elements. These elements are 8-node linear hexahedra with reduced integration, selected for their computational efficiency and superior performance in simulating large deformations and complex stress states. Reduced integration elements are particularly advantageous in this context, as they mitigate the risk of shear locking, a common issue in fully integrated elements, while maintaining accuracy in stress and strain predictions.

To further enhance the model’s ability to replicate real-world conditions, the element deletion technique was implemented. This feature allows for the progressive removal of elements once the material reaches a critical failure state. Specifically, a maximum degradation value of 0.99 was defined, ensuring that elements are deleted only when the material has undergone near-complete failure. This approach effectively captures the material separation and chip formation processes that are intrinsic to the punching operation, providing a realistic simulation of fracture propagation and tool-material interaction.

By combining C3D8R elements with the element deletion capability, the model achieves a high-fidelity representation of the punching process, including the initiation and progression of cracks, plastic deformation, and final separation of the punched material. This methodology ensures that the simulation not only reflects the global mechanical response but also accurately predicts localized failure phenomena, which are critical for optimizing tool design and process parameters.

In the Assembly module, meticulous attention was given to the alignment of the punch, die, and plettac to ensure a seamless and gap-free configuration. This precise alignment is critical for obtaining accurate penetration measurements and avoiding numerical artifacts that could compromise the simulation results.

To accurately simulate the transient and highly dynamic nature of the punching process, the Dynamic Explicit step was meticulously defined within the Step module of the finite element analysis software. The total simulation time was set to 1 ms, a duration carefully selected to encompass the entire punching event, from initial contact to complete material separation, while maintaining computational efficiency. This timeframe ensures that all critical phases of the process, including elastic deformation, plastic yielding, crack initiation, and final fracture, are fully captured without unnecessary computational overhead.

To guarantee numerical stability and mitigate the risk of excessive element distortion, an automatic time increment factor of 1 was specified. This configuration empowers the solver to dynamically adjust the time step size based on the evolving conditions of the simulation, such as material deformation rates, contact interactions, and stress propagation. By allowing the solver to adaptively refine or coarsen the time increments, the simulation maintains an optimal balance between accuracy and computational feasibility. This adaptive approach is particularly crucial in explicit dynamic analyses, where high deformation rates and nonlinear material behavior demand precise time integration to avoid numerical instabilities, such as energy dissipation errors or element inversion.

Furthermore, the automatic time incrementation ensures that the simulation remains robust even under extreme loading conditions, where localized stress concentrations or rapid material failure might otherwise compromise the integrity of the results. By preserving the stability and reliability of the solution throughout the simulation, this methodology enables a high-fidelity representation of the punching process, facilitating accurate predictions of tool wear, material behavior, and process efficiency.

In the Interaction module, a general contact algorithm was implemented to model the interactions between all components of the system. A friction coefficient of 0.1 was assigned to account for the frictional forces at the interfaces, which play a significant role in the material flow and deformation behavior. Additionally, a tie constraint was introduced between the punch and the back-up plate to prevent any relative motion or separation, ensuring that the punch remains rigidly supported during the operation.

Finally, in the Load module, appropriate boundary conditions were defined to replicate the physical constraints of the punching process. The die was fully constrained to prevent any displacement, effectively simulating its fixed position in the experimental setup. The plettac was subjected to controlled lateral and vertical displacements, with speeds ranging between 6 and 10 mm/s, to simulate the feeding and punching motions. To further optimize the computational efficiency and reduce the model size, symmetry boundary conditions were applied along the (ox) and (oz) axes, leveraging the geometric symmetry of the system.

This comprehensive setup ensures that the simulation accurately reflects the physical punching process, providing reliable insights into the material behavior, tool interactions, and overall process performance.

2.2. RSM Method

Analyzing the impact of punching parameters on the maximum force in cold forming is crucial, as it helps extend tool lifespan. This study focuses specifically on punching speed, a key factor directly influencing tool durability. The quality and dimensional accuracy of the final product largely depend on how the punch responds to variations in velocity. To investigate these relationships, statistical methods particularly Response Surface Methodology (RSM), well described in [24], are employed.

RSM is an empirical modeling approach that uses mathematical and statistical techniques to establish a link between input factors and the corresponding response. It has become increasingly valuable due to the limitations of other methods, which can be complex, inefficient, and unreliable. When studying the effects of punching parameters, RSM is widely used as it provides a more practical and effective approach.

In this work, the influence of punching speed is examined by analyzing the penetration of the tool into the material, allowing for an assessment of Von Mises stress distribution. Tracking the evolution of this stress and observing the propagation of concentrated stress zones along the punch axis are key objectives of this study.

In this study, a systematic and multifaceted investigation was conducted to evaluate the influence of key process parameters on the mechanical behavior, efficiency, and quality of the punching operation. One of the primary variables examined was the punching velocity, which was tested across a range of 6 to 10 mm per second (mm/s). This range was chosen to assess how varying velocities affect material deformation characteristics, punching force requirements, and overall process dynamics. Lower velocities tend to allow for more controlled material flow, reducing the likelihood of sudden fractures, while higher velocities can enhance productivity but may introduce challenges such as increased stress concentrations or premature tool wear.

Another critical parameter investigated was the punch-die clearance, which was adjusted between 0.25 and 0.35 mm (mm). The clearance plays a pivotal role in determining the quality of the punched edges, as well as the formation of burrs, a common defect in punching operations. An optimal clearance not only ensures clean and precise cuts but also minimizes tool wear and material distortion, thereby improving the longevity of the punch and die assembly.

Furthermore, this study explored multiple punch shaft designs, each engineered to address specific challenges in stress distribution, operational stability, and tool durability. The designs under consideration included:

➢

Double Sharp Design: This configuration is characterized by its enhanced precision, making it particularly suitable for applications requiring high-dimensional accuracy and minimal material deformation. The sharp geometry facilitates cleaner cuts and reduces the likelihood of burr formation, which is critical for maintaining the quality of the punched components.

➢

Tenon Shape: The tenon design prioritizes operational stability, providing a robust structure that minimizes lateral deflection during the punching process. This stability is essential for maintaining consistent performance, particularly under high-load conditions, and helps to prevent misalignment or premature failure of the punch.

➢

Staircase Shaft: The staircase design is engineered to reduce stress concentration along the shaft, thereby extending the tool’s operational life. By distributing the applied loads more evenly, this design mitigates the risk of fatigue failure and localized wear, making it ideal for high-volume production environments where tool longevity is a priority.

The selection of these parameters, punching velocity, punch-die clearance, and punch shaft design, was based on a comprehensive analysis aimed at optimizing the punching process. By systematically varying and evaluating these factors, the study seeks to enhance punching performance, improve product quality, and extend tool life, ultimately contributing to more efficient and cost-effective manufacturing operations. The insights gained from this investigation are expected to provide valuable guidelines for the design and optimization of punching tools in industrial applications.

In the present work, a comprehensive research plan was implemented to systematically evaluate the impact of punch geometry and punching speed on stress distribution. The research involved a series of at least 40 simulations using Finite Element Analysis (FEA) to generate detailed curves and analyze the results. The punch geometries considered included double sharp, tenon, and staircase shapes. Each simulation was designed to capture the effects of these parameters on stress distribution, tool wear, and the quality of the punched surface. The results were meticulously analyzed to identify optimal conditions for minimizing stress while ensuring high geometrical and dimensional accuracy of the punched holes. This rigorous approach ensures a robust understanding of the punching process and provides a solid foundation for future research.

3. Results and Discussion

3.1. New Design of AISI D2 Punching Tool

The first section of this article explored modifications to the punch shaft shape. While the results were promising, they remained somewhat limited. Therefore, this section shifts focus beyond just the punch shaft, placing emphasis on modifications to the punching tool head. Adjustments to the shaft did contribute to a reduction, sometimes significant, in punching force. However, the primary objective of altering the punch head shape is to minimize the stress exerted on the punch during the punching process of the ‘plettac.’ To achieve this, various solutions will be introduced, showcasing new designs for both the shaft and head of punching tool to facilitate its gradual penetration into the material.

3.1.1. Punch with New Head and Cylinder Shaft Shape

The punch has already introduced in [24], highlighting that the contact area between the punch head’s upper surface and the support plate’s lower surface is relatively small. The study aimed to determine the optimal process and geometric parameters using the Response Surface Methodology (RSM) coupled with the Finite Element Method (FEM) to minimize the punching force and improve tool performance. Through extensive numerical simulations conducted in ABAQUS, this research meticulously identified critical stress regions within the punching tool assembly and established optimized parameter sets for each punch shaft configuration, achieving the most uniform von Mises stress distribution—a vital indicator of structural integrity and tool longevity. By analyzing stress concentrations and deformation patterns, the study revealed that die clearance, punch edge radius, and material hardness are the most influential factors affecting punching force and overall process efficiency. The die clearance was found to be pivotal in determining the quality of the punched edge, as an optimized gap facilitates smoother material separation while minimizing burr formation and tool wear. Meanwhile, the punch edge radius directly impacts stress distribution and force transmission, with a well-defined radius reducing stress concentrations and lowering the risk of crack initiation and tool deformation. Additionally, material hardness emerged as a critical factor, as harder materials require higher punching forces and can accelerate tool wear, necessitating careful material and geometry selection to balance performance and durability. By systematically optimizing these parameters, the research developed tailored configurations for each punch shaft design, ensuring enhanced stress distribution, reduced punching force, and improved tool life, thereby providing actionable insights for more efficient, reliable, and cost-effective manufacturing processes. Furthermore, the study demonstrated that an optimized combination of these parameters can reduce peak stress by up to 18%. This is the reason we expanded the contact area. Specifically, the surface diameter increased from 4 mm to 8 mm, nearly doubling the contact surface. The punch illustrated in Figure 1 is a suggested solution to overcome the issues discussed in prior research by Zeidi et al. in [26,27]. Specifically, rather than excessive stress concentration, matting and cracking were observed in this contact area, leading to punch misalignment during the sheet metal punching process and ultimately resulting in chipping at its shaft. Additional issues emerged on the support plate, including matting, corrosion, and plastic deformation. The connection between the support plate and the punching tool head was compromised, leading to premature punch damage and halting production. The redesigned punch features an improved shape that extends its lifespan while ensuring stability during the punching process. Its stepped design provides precise guidance, resulting in high-quality finished products free from burrs and dimensional inaccuracies.

Figure 2 reveals the distribution of Von Mises stress as a function of the punch-die clearance (J) and the punching velocity (V). Analyzing these punching parameters is crucial, as each punching process has unique characteristics, even when similarities exist.

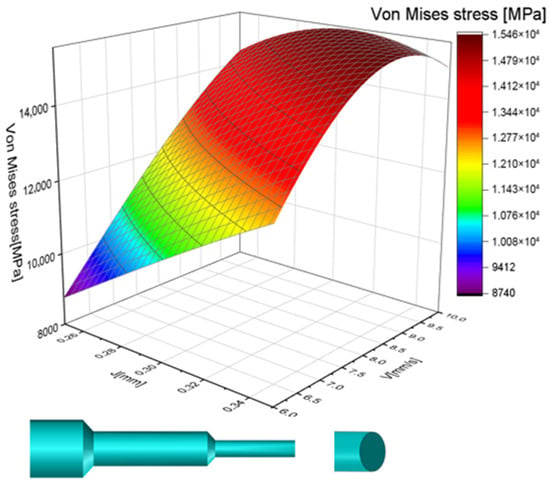
Figure 2. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for blank punch.

The approach outlined in the initial section of the article allowed us to create the 3D curve depicted below. In comparison to the original blank punch, the peak Von Mises stress was reduced by approximately 3000 MPa, demonstrating the benefits of the redesigned punch.

The von Mises stress distribution indicates that the lowest value, around 9000 MPa, occurs when the punch-die clearance is 0.25 mm and punching velocity is 6 mm/s which was also highlighted by Yildirim et al. [28]. Consequently, these parameters can be deemed optimal if minimizing von Mises stress is the primary objective.

3.1.2. Punch with New Head and Staircase Shaft Shape

Increasing the head diameter of the blank punch led to a significant reduction in Von Mises stress, which aligns with the findings reported by Muthuveerappan and Sivarajan [29]. While this reduction enhances the conditions for forming a 3 mm diameter hole in 3 mm thick S500MC sheet metal, it does not lead to a gradual penetration of the punch shaft, specifically, the active part of the punching tool.

As a result, modifying the shape of the AISI D2 punch shaft became necessary. In each case, a new punch shaft design was developed using 3D design software. The punch depicted in Figure 3 retains the same head shape as the original blank punch but features a staircase-shaped shaft.

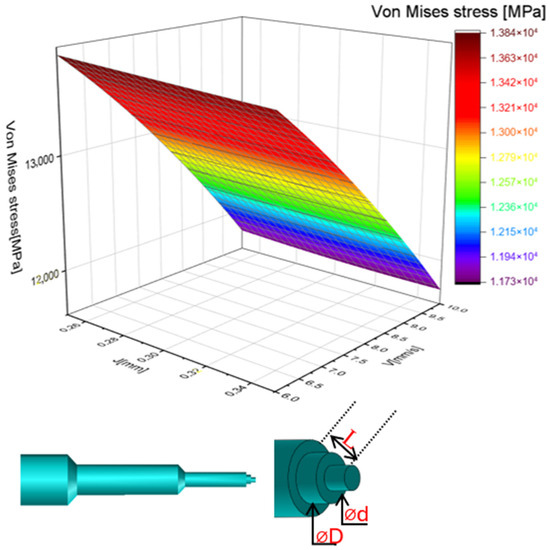
Figure 3. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for staircase punch.

Von Mises stress distribution was analyzed by adjusting the punching velocity and punch-die clearance like a previous study conducted by Lo et al. [30]. As shown in Figure 3, the lowest stress level occurs at a punching speed of 10 mm/s, with the punch-die clearance having minimal impact. Consequently, a punch-die clearance of 0.3 mm will be used, following the standard guideline of setting the clearance to one-tenth of the sheet thickness, which is 3 mm.

A parametric analysis was conducted, focusing on the diameter of the lower section (d) and the length of the newly formed shape at the punch shaft (L). The new design shown in Figure 4 significantly reduces the punching force, enhancing both the static and dynamic stability of the punch during sheet metal forming.

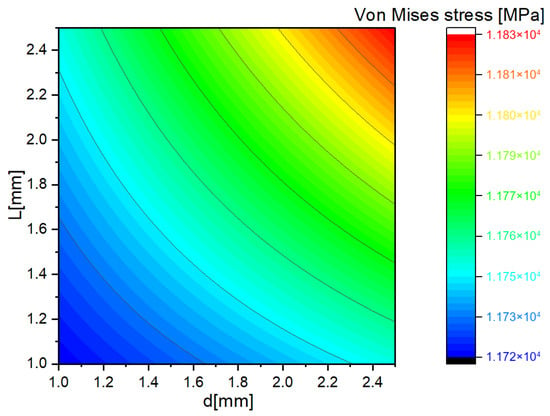
Figure 4. Contour map for Von Mises stress distribution for staircase length and velocity.

Elevated values of (d) and (L) result in high Von Mises stress, reaching up to 11,130 MPa. Therefore, the optimal values, indicated in blue, are preferred.

Given that the blank punch shaft has a diameter of 3 mm, an optimal choice for the new shaft shape would be a 1.5 mm diameter. Additionally, a length of 3 mm is highly advantageous, as it matches the sheet metal thickness, facilitating the creation of a 3 mm diameter hole.

3.1.3. Punch with New Head and Double Shear Angle

To enhance the lifespan of the punching tool, a punch with double shear was used in the initial phase of this study. Finite element modeling of this approach revealed a reduction in Von Mises stress, prompting further investigation in this work with modifications to the punch head design. Furthermore, the solution depicted in Figure 5 proved to be the most optimal when minimizing Von Mises stress was the primary objective.

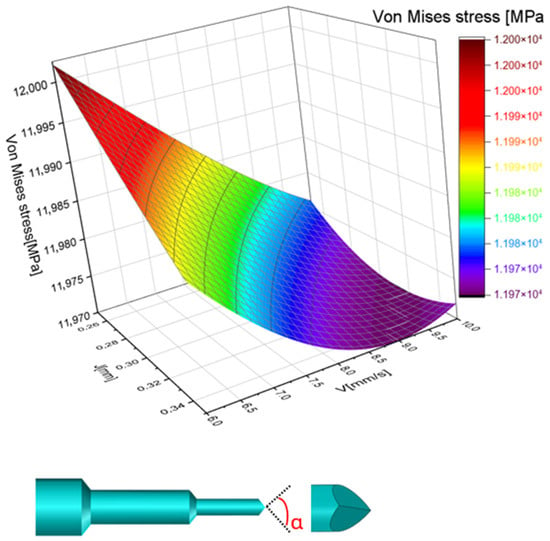
Figure 5. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for double shear punch shaft.

The current solution offers two key advantages. First, it broadens the contact area between the punch head and the support plate, and second, it allows for gradual material penetration, preventing impact and chipping.

To analyze the influence of some punching parameters on the punch’s behavior during the cold work forming of the ‘plettac’ (industrial name), the Von Mises stress was plotted against punching velocity and punch-die clearance. As illustrated in Figure 5, the lowest Von Mises stress occurs at a punching velocity of 10 mm/s and a punch-die clearance of 0.25 mm. These parameters are deemed optimal as they not only minimize the stress studied but also extend the punch’s service life. Additionally, they help prevent wear and cracking, which can negatively impact production.

The shape formed at the punch shaft in double shear is angled in a way that must be determined. Therefore, a parametric analysis of the shear angle ‘α’ is conducted to identify the optimal angle that minimizes Von Mises stress. Figure 6 clearly illustrates how this stress varies with different shear angles. The findings indicate that a 5° angle results in the lowest stress, approximately 11,705 MPa. Consequently, this angle is recommended for a 3 mm diameter under similar conditions. Modifying the shape of the punch shaft and head has not only reduced the applied force but also improved stability and ensured a high-quality finished product.

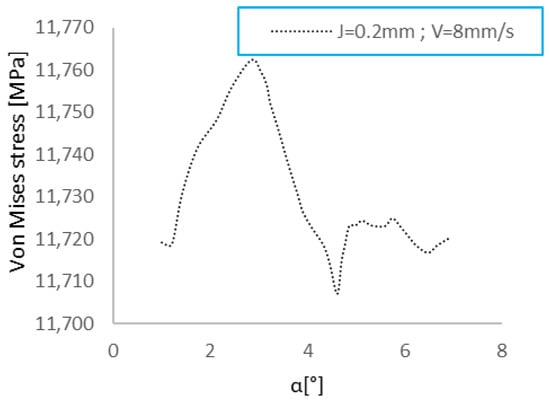
Figure 6. Von Mises stress distribution in case of shear angle variation for double shear angle shaft.

3.1.4. Punch with New Head and a Corner Radius Shaft Shape

Several studies in the literature such as [31,32,33] have highlighted the impact of the punch radius on the quality of the finished product, the variation in punching force, and the lifespan of punching tools. In this study, the distribution of Von Mises stress was analyzed by adjusting the punch-die clearance and punching velocity. A radius was incorporated into the cutting edge of the AISI D2 punch shaft to prevent chipping, wear, and the need for frequent sharpening. Additionally, dimensional defects may occur in the punched hole, posing a challenge for production. Frequent production stoppages not only increase costs but also disrupt workflow, especially in mass production. Each stop requires realignment of the punching mold components and restoration of punching parameters. As depicted in Figure 7, the punch radius influences the punch-die clearance, helping to extend the lifespan of both the punch and die by minimizing impact with the sheet metal. The lowest Von Mises stress is achieved with a punch-die clearance of 0.3 mm and a punching velocity of 10 mm/s. This adjustment reduced the stress from 1500 MPa to 1100 MPa, resulting in a 400 MPa decrease. This outcome is significant, as it helps extend the lifespan of punching tools.

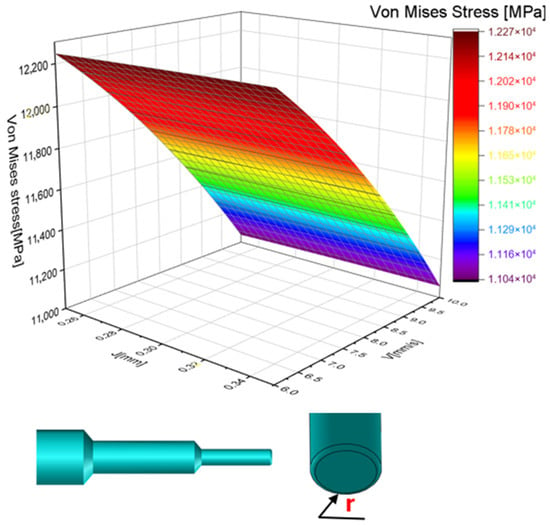
Figure 7. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for corner radius punch.

To determine the optimal corner radius of the punch shaft that minimizes stress, a parametric study was conducted on this punching parameter. Figure 8 illustrates the variation of Von Mises stress as the radius ‘r’ changes. The results indicate that a radius between 0.6 mm and 0.7 mm leads to a peak stress of 11,735 MPa, whereas the lowest stress is observed at a radius of 0.5 mm. Therefore, to enhance the punch’s lifespan, a radius of 0.5 mm is recommended as the optimal value which was also approved by Félix et al. [34].

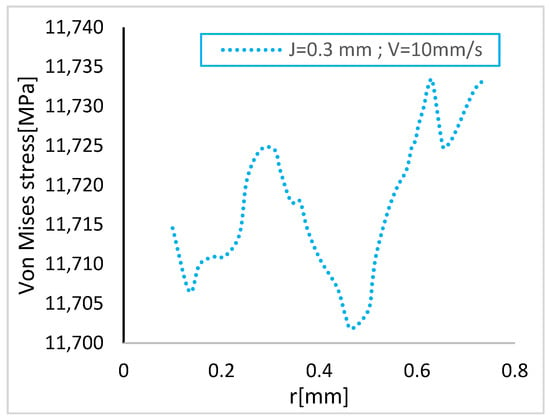
Figure 8. Von Mises stress distribution in case of corner radius variation.

3.1.5. Punch with New Head and Fish Mouth Shaft Shape

Selecting the appropriate punching parameters is a challenging task due to various factors. Each operation has its own set of parameters, which are interdependent, making the selection process complex and often requiring multiple experiments to achieve a high-quality finished product. In this study, finite element simulation is utilized as a simple, cost-effective, and efficient method to determine the optimal punching parameters quickly.

Figure 8 presents a punch featuring a redesigned head and a fish-mouth-shaped shaft. This design facilitates smooth and efficient penetration into the material by reducing the contact surface with the sheet metal. Additionally, the punch’s large-diameter head provides a significant contact area with the lower face of the backup plate. This design also offers the advantage of pushing the slug through without friction against the die, as the inner face of the punch shaft forms a V-shape within the material.

Figure 9 illustrates the impact of punching parameters, such as punching speed and punch-die clearance, on the distribution of Von Mises stress. The 3D curve reveals that modifying the punch head and adopting the fish-mouth shaft design reduced stress by over 300 MPa compared to a standard blank punch. Furthermore, the Von Mises stress reaches its lowest value, approximately 1000 MPa, when a punching speed of 10 mm/s and a punch-die clearance of 0.35 mm are used.

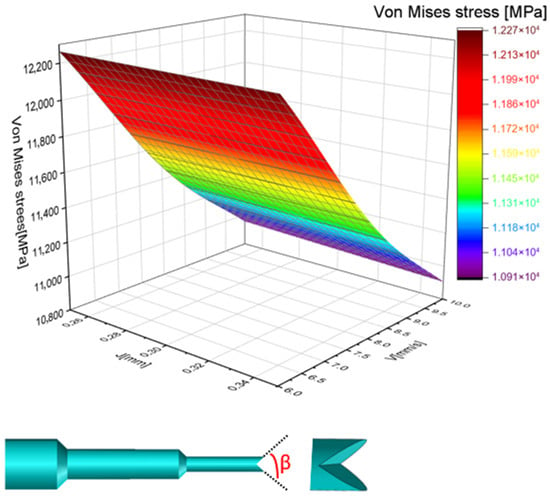
Figure 9. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for fish mouth punch.

By optimizing the punch shaft and head shapes, the service life can be extended. This design reduces punch compression, allows for gradual contact with the sheet metal, and enhances the production rate.

A parametric study was conducted to determine the optimal angle ‘β’ that minimizes Von Mises stress as displayed in Figure 10. Specifically, the effect of the opening angle in the fish-mouth shape on punching stress was analyzed. The results indicate that for angles between 0° and 10°, the impact is minimal, while stress peaks begin to appear at 15°. The optimal angle was found to be 20°, resulting in a minimum stress of approximately 11,700 MPa. This study proves to be highly effective in reducing Von Mises stress while also improving balance and production efficiency.

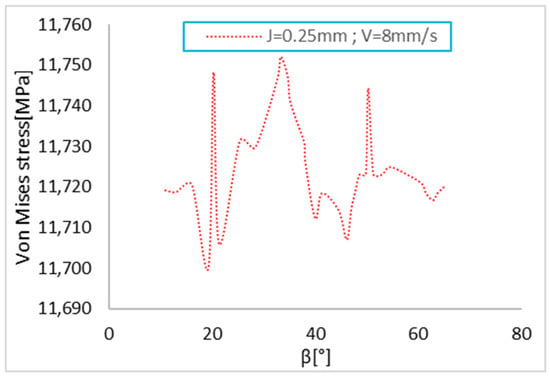
Figure 10. Von Mises stress distribution in case of shear angle variation for fish mouth shaft.

3.1.6. Punch with New Head and Tenon Shaft Shape

Punching is a cold forming process that utilizes a punch and a die, with the punch being the central focus of this study. This research highlights the design of a new punch tip (shaft) that enhances the punching process. Specifically, a tip featuring a tenon, as illustrated in Figure 11, has been introduced. This design ensures precise centering on the sheet metal, preventing the punching tool from sliding on the upper surface of the ‘plettac.’

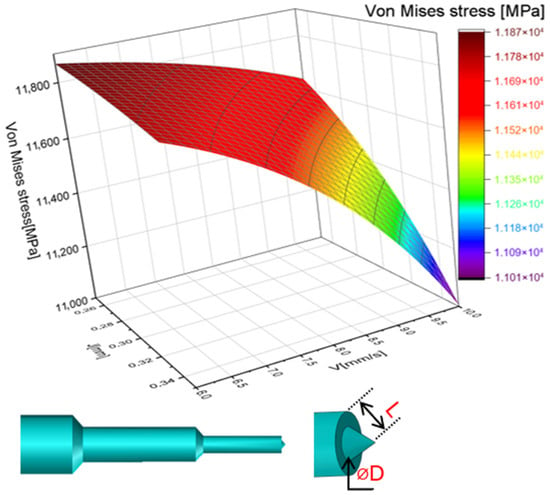
Figure 11. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for tenon punch.

The modified shape enables progressive and balanced penetration while minimizing the contact surface with the sheet metal which was approved by Ahmad and Yaser [35]. The production of a 3 mm diameter hole occurs in stages, with the diameter gradually increasing as the moving mold component advances. Finally, the 3 mm punch pushes the remaining material through, ensuring the hole is formed accurately to the desired dimensions. In this study, each punch shape is designed with the goal of reducing Von Mises stress. For the punch featuring a tenon at its tip, the lowest stress, approximately 11,000 MPa, is achieved with a punching speed of 10 mm/s and a punch-die clearance of 0.35 mm. These parameters are therefore considered optimal for this specific punch design.

The slug, the material removed during the punching process, takes on a curved shape due to contact with the punch’s tenon. This curvature, which was analyzed by Francy et al. [36], offers two key advantages: it minimizes contact with the die, reducing wear on the cutting edge of the punching tool, and it limits the need for frequent sharpening of the active tenon area. As a result, production stops are reduced, and the overall quality of the finished product is improved.

The punch shaft features a tenon shape characterized by a diameter D and a length L. A parametric analysis was conducted on these two factors, with the findings illustrated in Figure 12 through a contour map. The results indicate that the Von Mises stress reaches its lowest value at two distinct points. Notably, a diameter of 2.5 mm and a length of 3 mm result in the lowest stress levels, represented by the blue color.

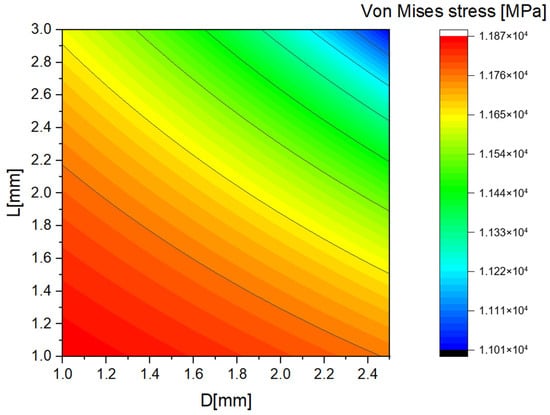
Figure 12. Contour map for Von Mises stress distribution in case of tenon length and diameter variation.

3.1.7. Punch with New Head and Circle Shaft Shape

The last shape examined in this study features a circular shaft, as highlighted in Figure 13. This design offers the advantage of a uniform distribution of the punching force, which enhances the tool’s service life while minimizing degradation. Additionally, the initial contact between the punch tip (shaft) and the sheet occurs at the hole’s periphery, ensuring a high-quality finished product. The gradual penetration of the punching tool’s shaft is another key benefit of this design. Furthermore, the contact area between the punch head and the backup plate is doubled, allowing for effective absorption of the force exerted by the sheet metal.

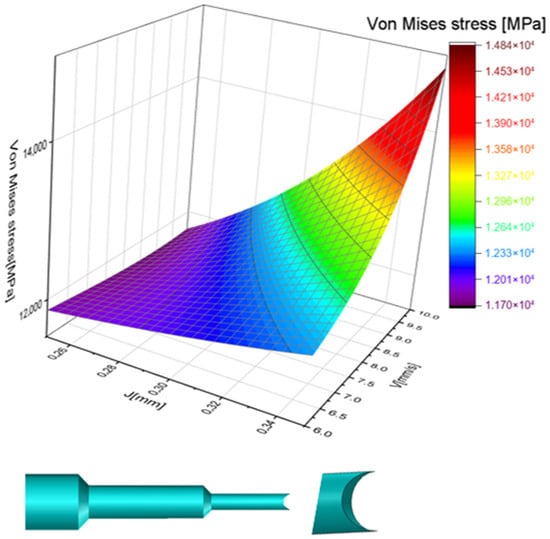
Figure 13. Von Mises stress distribution in case of punch velocity (V) and punch-die clearance (J) for a circular punch.

By plotting the distribution of Von Mises stress against punching speed and punch-die clearance as revealed in Figure 13, it was observed that the lowest stress value occurs at a speed of 9 mm/s and a punch-die clearance of 0.35 mm.

This approach effectively reduced the punching force, enhanced the quality of the final product, and extended the lifespan of the cold forming tool. However, its main drawback is the need for periodic sharpening after a certain number of cycles. This interruption can lead to decreased production efficiency and potential dimensional defects. Ultimately, while many solutions have aimed at reducing the punching force, the best option is the one that offers the most advantages over the others.

3.2. Numerical Model Validation

The validation of the Johnson-Cook numerical model using ABAQUS demonstrates a strong correlation between experimental and numerical results. The punching force vs. punch displacement curves for both the experimental tests and numerical simulations are nearly identical, confirming the accuracy and reliability of the model. Notably, the maximum punching force for the double shear shaft configuration reaches approximately 10,000 N, which represents a significant reduction of nearly 5000 N compared to the blank punch currently used in the industrial operations at the establishment of Chafik Loukil. This reduction highlights the efficiency of the double shear shaft design in minimizing the required punching force.

In this study, the same mold utilized in Part I of the paper ([24]) was reused, with specific modifications made to the punch holder and guide to accommodate and support the new double shear shaft punch. The experimental procedure followed the same methodology as described in Part I, ensuring consistency and comparability of results. As illustrated in Figure 14, the curves for both the experimental and numerical analyses exhibit a similar trend, with a peak force occurring at approximately 1.5 mm of punch displacement, followed by a gradual decline. This close agreement between the experimental and numerical curves further validates the effectiveness of the Johnson-Cook model in accurately predicting the punching behavior under the specified conditions.

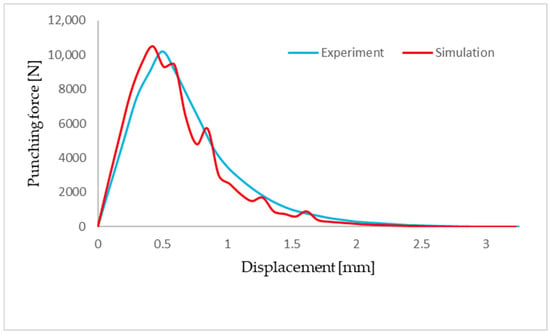
Figure 14. Evolution of punching force regarding tool displacement.

3.3. Evaluation of the New Design and Optimal Solution Selection

Choosing the ideal solution requires assessing different options to identify the one that offers the most advantages. While several methods can contribute to reducing the punching force, the best choice is the one that improves efficiency, enhances product quality, and prolongs tool lifespan while minimizing potential downsides.

This study introduced seven punching tools featuring newly designed heads and shaft shapes. The most effective tool, according to Aminzadeh and Claver [37,38], is the one that minimizes force, maintains punch stability throughout the process, and enhances the quality of the final product. Figure 15 plots a comparison of Von Mises stress levels across various proposed punch shaft designs. Notably, transitioning from the original blank shaft to the optimized design, identified as the most effective in minimizing stress, results in a significant stress reduction of nearly 5000 MPa. The designs featuring a tenon shaft and a fishmouth tip also contribute to stress reduction, lowering the Von Mises stress by approximately 4000 MPa and 3000 MPa, respectively. This reduction is particularly significant, indicating that the punch operates under less severe loading conditions.

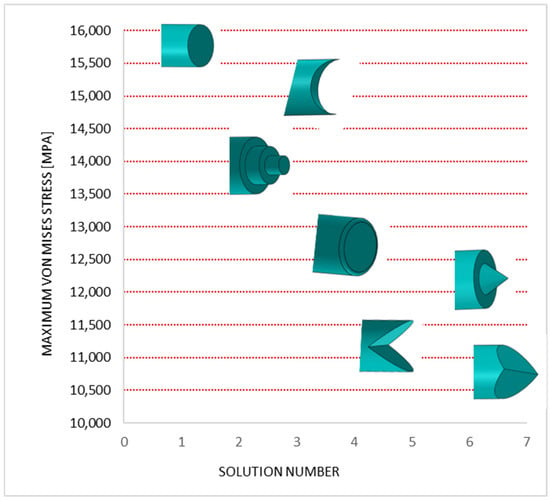
Figure 15. Maximum Von Mises stress for proposed AISI D2 new punches.

Among all the configurations, the punch with a double shear shaft proves to be the most efficient. It not only substantially lowers the punching force but also maintains better balance during forming and penetrates the material in a smoother, more gradual manner.

The most advantageous solution identified was the punch featuring a newly designed double shear shaft. This configuration offered notable benefits, including improved stability during the punching of a 3 mm hole. Additionally, it has the potential to extend the punch’s service life by minimizing wear, deformation, chipping, and other forms of early damage. The study explored multiple innovative punch tool designs, ultimately selecting the optimal version for implementation.

The validation of the Johnson-Cook numerical model using ABAQUS has demonstrated a strong agreement between experimental and numerical results, particularly in predicting the punching force and stress distribution for various punch geometries. The study compared several punch designs, including blank solution, staircase punch, double shear punch shaft, corner radius punch, fish mouth punch, tenon punch, and circle punch. Each punch was evaluated under specific conditions of clearance and velocity, as outlined in Table 2.

Table 2. Punch velocity and punch-die clearance for minimum Von Mises Stress.

	Geometry	Clearance (mm)	Velocity mm/s	Minimum Von Mises Stress (MPa)
Blank solution		0.25	6	11,000
Staircase punch		0.35	10	11,000
Double shear punch shaft		0.35	9	10,000
Corner radius punch		0.25	10	11,000
Fish mouth punch		0.35	10	10,900
Tenon punch		0.35	10	11,000
Circle punch		0.25	6	11,800

The evaluation of different punch geometries under varying conditions of clearance and velocity reveals several key insights regarding their performance in terms of minimum Von Mises stress. The blank solution, with a clearance of 0.25 mm and a velocity of 6 mm/s, exhibits a minimum Von Mises stress of 11,000 MPa. This serves as a baseline for comparison with other punch designs.

The staircase punch, operating at a higher clearance of 0.35 mm and a velocity of 10 mm/s, maintains the same minimum Von Mises stress of 11,000 MPa as the blank solution. This suggests that the increased clearance and velocity do not adversely affect the stress distribution for this geometry.

The double shear punch shaft, also with a clearance of 0.35 mm but a slightly lower velocity of 9 mm/s, shows a reduced minimum Von Mises stress of 10,000 MPa. This reduction in stress indicates a more efficient distribution of forces, which can contribute to lower punching forces and potentially extended tool life.

The corner radius punch, with a clearance of 0.25 mm and a velocity of 10 mm/s, matches the minimum Von Mises stress of 11,000 MPa seen in the blank solution and staircase punch. This consistency suggests that the corner radius design does not compromise the material’s stress response despite the higher velocity.

The fish mouth punch, having a clearance of 0.35 mm and a velocity of 10 mm/s, exhibits a slightly lower minimum Von Mises stress of 10,900 MPa. This minor reduction may indicate a marginal improvement in stress distribution compared to the blank solution and corner radius punch.

The tenon punch, with the same clearance and velocity as the fish mouth punch (0.35 mm and 10 mm/s), shows a minimum Von Mises stress of 11,000 MPa, similar to the blank solution and staircase punch. This indicates that the tenon punch maintains a consistent stress response under these conditions.

Finally, the circle punch, with a clearance of 0.25 mm and a velocity of 6 mm/s, exhibits the highest minimum Von Mises stress of 11,800 MPa. This suggests that the circle punch may induce higher stress concentrations, potentially leading to increased wear and reduced tool life.

In summary, the double shear punch shaft stands out for its ability to reduce the minimum Von Mises stress to 10,000 MPa, suggesting a more efficient and potentially more durable punching process. The other punch geometries exhibit varying degrees of stress distribution, with the circle punch inducing the highest stress levels. These insights can guide the selection of punch designs for optimizing performance and longevity in industrial applications.

Figure 16 shows punching force vs. displacement for the three best solutions, namely double shear punch, fish mouth punch, and tenon punch, in comparison with the blank punch. It reveals distinct stress-displacement behaviors for each punch design. The blank punch exhibits the highest punching force, rapidly climbing to 14,000 N and plateauing, which reflects inefficient force distribution and potential for premature failure. In contrast, the tenon punch reaches a peak of 11,500 N with a smoother ascent, indicating a more controlled but still relatively high response. The fish mouth punch further improves this trend, peaking at 11,000 N and demonstrating a more gradual increase, suggesting better punching force management. However, the double shear punch outperforms all others, achieving the lowest peak force of 10,500 MPa with the most gradual rise and minimal fluctuations, highlighting its superior ability to distribute punching force evenly and maintain process stability. All curves begin near zero force at zero displacement, but the differences become increasingly pronounced as displacement grows, underscoring the advantages of the double shear design in both peak reduction and operational smoothness.

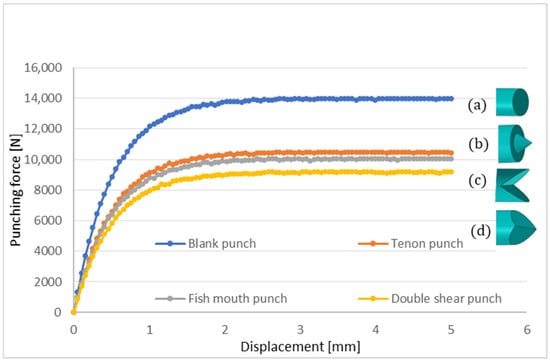
Figure 16. Comparison of punching force vs. displacement for blank punch (a), tenon punch (b), fish mouth punch (c) and double shear punch (d).

To ensure dimensional precision and prevent thermal alterations associated with traditional machining, the punch was made using wire EDM (Electrical Discharge Machining) combined with proper lubrication. Figure 17 displays the manufactured punch, which corresponds to the chosen optimal design, an efficient and cost-effective option that contributes to lowering the overall production cost of the final product. Further research and testing will be conducted to confirm the performance and reliability of this selected design.

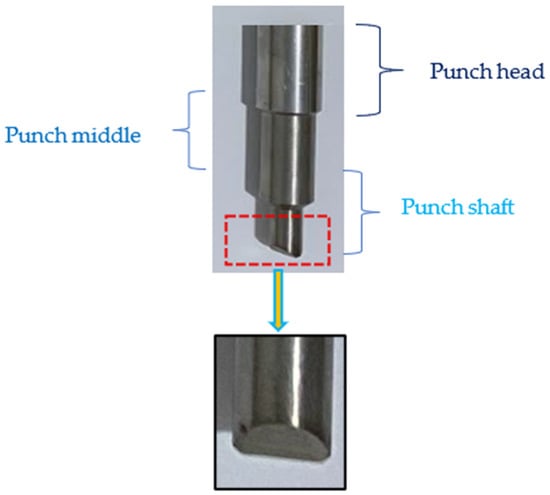
Figure 17. Adopted solution (punch with new head and double shear shape).

The double shear punch was identified as the optimal design not only due to its lower peak Von Mises stress but also because of its superior performance in several other critical aspects. First, it demonstrated enhanced stability during the punching process, minimizing vibrations and ensuring consistent operation across varying conditions. Second, the stress distribution pattern was more uniform compared to alternatives like the tenon punch, reducing localized stress concentrations that could lead to premature failure or deformation. Finally, the slug separation mechanism was smoother and more reliable, resulting in cleaner cuts and reduced risk of material jamming or tool wear. Collectively, these factors, stress efficiency, operational stability, and separation effectiveness, positioned the double shear punch as the most robust and reliable solution among the designs evaluated.

In the present paper, we investigated the influence of punch geometry, punch-die clearance, and punching speed on both stress distribution and punching force. Our findings are consistent with and extend the work of several prominent researchers in the field. Specifically, the reduction in punching force through optimized punch geometry aligns with the results reported by Wang et al. [39], who demonstrated that tailored punch designs can significantly reduce forming forces in sheet metal operations. Our observations on the impact of punch-die clearance on stress distribution corroborate the findings of Kuo et al. [40], who highlighted the critical role of clearance optimization in minimizing burr formation and improving hole quality. Furthermore, the effect of punching speed on material deformation and stress distribution supports the conclusions of Liu et al. [41], who emphasized the role of strain rate in influencing the mechanical behavior of high-strength steels during forming processes.

The relationship between punch geometry and punching force is particularly noteworthy. Our results indicate that punch shapes such as double sharp, tenon, and staircase designs not only reduce stress concentrations but also influence the punching force required for material separation. This is in line with recent studies that have shown how specific punch geometries can enhance material flow and reduce the energy required for deformation, thereby improving tool life and product quality [42,43]. For instance, the use of a double sharp punch design was found to minimize the maximum punching force by promoting a more uniform stress distribution along the punch axis, which is crucial for maintaining dimensional accuracy and surface finish in punched components.

Additionally, our analysis of punch-die clearance revealed that a clearance range of 0.25 to 0.35 mm is optimal for balancing tool wear and edge quality, a conclusion supported by Zeidi et al. [44], who demonstrated that variable punch-die clearance can significantly extend tool life by minimizing stress on the punch. This optimization is essential for industrial applications where both precision and tool longevity are paramount.

The effect of punching speed on strain hardening and material behavior further underscores the relevance of our work. As noted by Liu et al. [41], higher strain rates can lead to increased material strength due to strain hardening, which facilitates cleaner separation and greater precision in punched holes. This phenomenon is particularly relevant for high-strength steels like S500MC, where controlling the strain rate can enhance both the quality of the punched surface and the overall efficiency of the process [45,46].

Kadarno et al. [10] investigated the influence of step-die mechanisms on material deformation and stress distribution during punching processes. Their findings highlighted how step-die designs can effectively reduce punching forces by promoting a more gradual deformation process, thereby minimizing stress concentrations and improving the overall quality of punched parts. This aligns closely with our own observations on the impact of punch geometry on stress distribution and punching force. By comparing our results with Thipprakmas’s work, we can further validate the effectiveness of optimized punch designs in reducing forming forces and enhancing tool life.

Asad et al. [11] explored the role of punch edge geometry in sheet metal forming, emphasizing how variations in edge profiles can influence stress distribution, tool wear, and the quality of the punched surface. Their research demonstrated that specific edge geometries can significantly reduce burr formation and improve dimensional accuracy, which is consistent with our findings on the importance of punch-die clearance and edge design in achieving high-quality punched components. Incorporating Taplak’s insights allows us to provide a more comprehensive analysis of how punch geometry affects both the mechanical and surface properties of punched parts.

While this study primarily evaluates the performance of different designs based on Von Mises stress, a widely used metric for assessing yielding and plastic deformation, we acknowledge that tool life is influenced by a broader range of factors. Specifically, stress triaxiality, fatigue loading, and wear play critical roles in determining the long-term durability and failure modes of tools.

Stress triaxiality, for instance, can significantly affect the risk of brittle fracture, particularly in materials sensitive to hydrostatic stress states. A design with lower Von Mises stress but higher stress triaxiality may still be prone to premature failure under cyclic or impact loading conditions. Similarly, fatigue loading and wear mechanisms are essential considerations, as they dictate the cumulative damage and surface degradation over time. To provide a more comprehensive assessment of tool life, future work should incorporate stress triaxiality analysis to evaluate fracture risk, fatigue life predictions using methods such as S-N curves or damage accumulation models, and wear simulations to account for material loss and surface integrity.

By integrating these factors, subsequent studies can better identify designs that optimize not only stress distribution but also long-term reliability and resistance to failure.

4. Conclusions

This study, as the second part of a comprehensive investigation, presents optimized solutions for punch shaft and head geometry to address premature failure and improve performance in cold forming processes. By integrating Finite Element Method (FEM), Response Surface Methodology (RSM), and parametric analysis, this research builds upon the findings of the first part and delivers quantifiable improvements in punch design and operational efficiency.

The key contributions of this study are as follows:

➢

Enhanced Punch Head Design: The modification of the punch head geometry increased the contact area with the backup plate, significantly reducing the risk of premature failure. This improvement is critical for extending tool life and maintaining consistent performance under high-stress conditions.

➢

Effective Stress Analysis: The combined use of FEM and RSM enabled a rigorous comparison of Von Mises stress distribution across multiple punch geometries. This methodology provided a robust framework for identifying the most effective design configurations, ensuring that stress concentrations were minimized.

➢

Optimal Double Shear Shaft Design: Among the proposed designs, the double shear shaft punch demonstrated the most significant reduction in Von Mises stress, achieving a 30% decrease in peak stress compared to the baseline blank punch. This result confirms its superiority in stress mitigation and validates its selection as the optimal design for industrial applications.

➢

Material and Lubrication Optimization: The implementation of HSS steel, combined with appropriate lubrication, effectively prevented phase transformation and reduced residual stress. The use of a suitable lubricant, applied in optimal quantities and at strategic intervals, minimized friction between the punch and sheet metal. This approach not only reduced heat generation and tool wear but also enhanced the quality of the punched surface by preventing defects.

➢

Experimental Validation: The numerical model was experimentally validated, ensuring the reliability and credibility of the research findings. This validation step strengthens the practical applicability of the proposed solutions and confirms their effectiveness in real-world conditions.

The results of this study provide clear evidence that the proposed modifications to punch geometry, material selection, and lubrication strategies significantly enhance tool performance and longevity. These findings are particularly relevant for industries seeking to optimize cold forming processes, reduce maintenance costs, and improve product quality.

For future research, it is recommended to explore additional material combinations and advanced lubrication techniques to further refine the punching process. Investigating the long-term durability of the optimized punch design under varying operational conditions would also provide valuable insights for industrial applications.

In conclusion, this study successfully addresses the challenges of premature punch failure through innovative design modifications and rigorous analytical methods, offering practical solutions that are both effective and experimentally validated.

As the second part of a broader study, this article presents solutions involving modifications to the punch shaft and head geometry. The research utilized the Finite Element Method (FEM), Response Surface Methodology (RSM), and parametric analysis. Compared to the findings in the first part, the results demonstrated significant improvements. The key outcomes of this study include: