Probing Black Hole Magnetic Fields with QED
Abstract
1. Introduction
2. Model
3. Results
3.1. Polarization-Limiting Radius
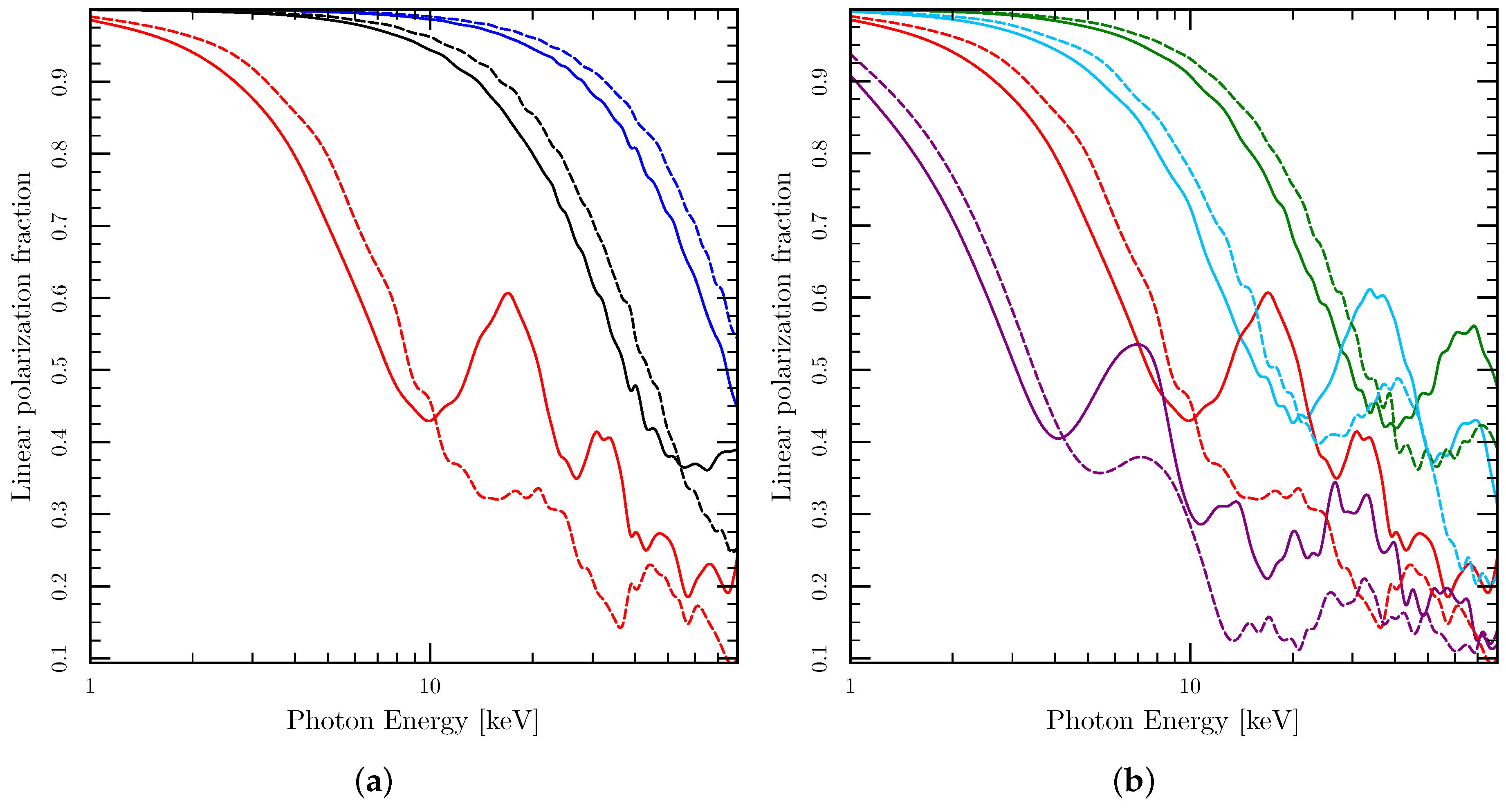
3.2. Edge-on Photons
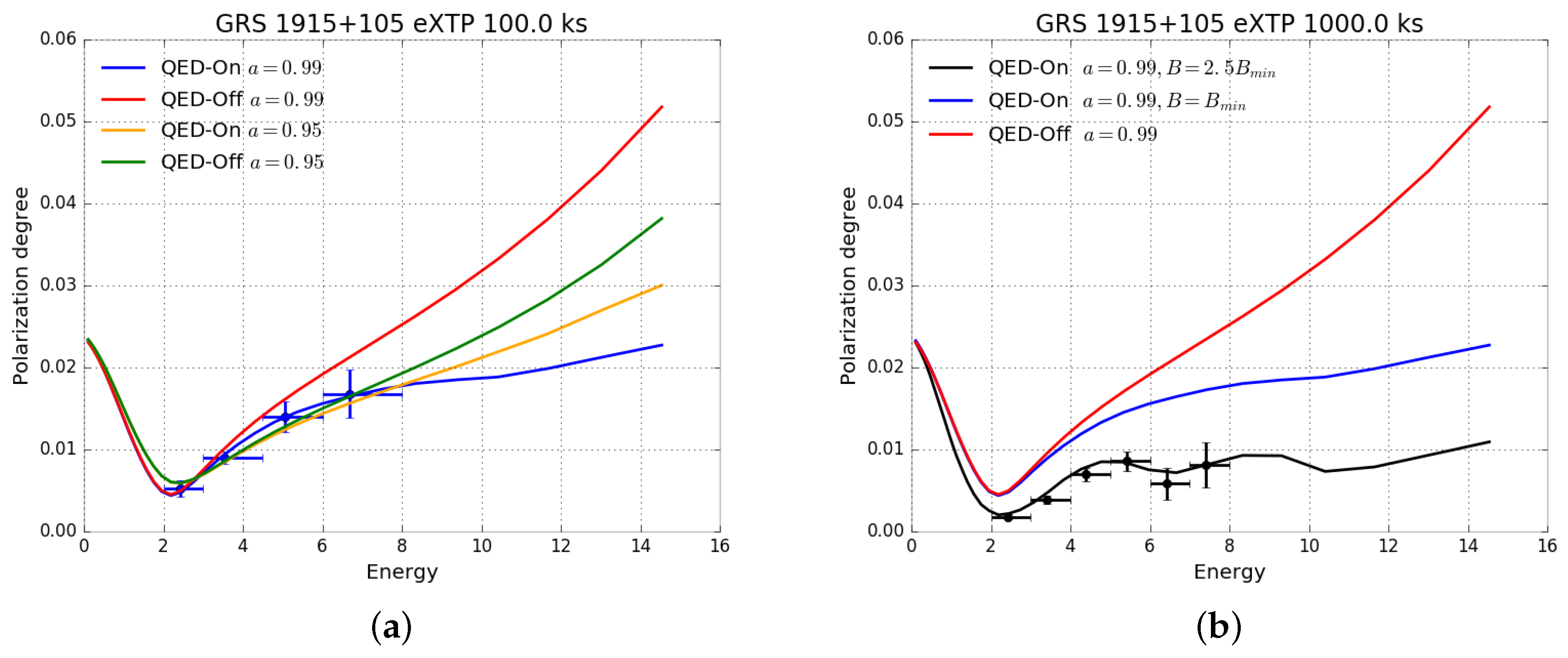
3.3. A Simulation for GRS 1915+105
4. Discussion
5. Materials and Methods
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| QED | quantum electrodynamics |
| ISCO | innermost stable circular orbit |
| PLR | polarization-limiting radius |
| IXPE | Imaging X-ray Polarimetry Explorer |
| eXTP | enhanced X-ray Timing and Polarimetry Mission |
| LAMP | Lightweight Asymmetry and Magnetism Probe |
| REDSox | The sounding Rocket Experiment Demonstration of a Soft X-ray Polarimeter |
References
- Shakura, N.I.; Sunyaev, R.A. Black holes in binary systems. Observational appearance. Astron. Astrophys. 1973, 24, 337–355. [Google Scholar]
- Balbus, S.A.; Hawley, J.F. A powerful local shear instability in weakly magnetized disks. I—Linear analysis. II—Nonlinear evolution. Astron. J. 1991, 376, 214–233. [Google Scholar] [CrossRef]
- Blandford, R.D.; Znajek, R.L. Electromagnetic extraction of energy from Kerr black holes. Mon. Not. R. Astron. Soc. 1977, 179, 433–456. [Google Scholar] [CrossRef]
- Tchekhovskoy, A.; Narayan, R.; McKinney, J.C. Efficient generation of jets from magnetically arrested accretion on a rapidly spinning black hole. Mon. Not. R. Astron. Soc. 2011, 418, L79–L83. [Google Scholar] [CrossRef]
- Miller, J.M.; Raymond, J.; Fabian, A.; Steeghs, D.; Homan, J.; Reynolds, C.; van der Klis, M.; Wijnands, R. The magnetic nature of disk accretion onto black holes. Nature 2006, 441, 953–955. [Google Scholar] [CrossRef] [PubMed]
- Miller, J.M.; Raymond, J.; Reynolds, C.S.; Fabian, A.C.; Kallman, T.R.; Homan, J. The Accretion Disk Wind in the Black Hole GRO J1655-40. Astron. J. 2008, 680, 1359–1377. [Google Scholar] [CrossRef]
- Miller, J.M.; Raymond, J.; Fabian, A.C.; Gallo, E.; Kaastra, J.; Kallman, T.; King, A.L.; Proga, D.; Reynolds, C.S.; Zoghbi, A. The Accretion Disk Wind in the Black Hole GRS 1915+105. Astrophys. J. Lett. 2016, 821, L9. [Google Scholar] [CrossRef]
- Johnson, M.D.; Fish, V.L.; Doeleman, S.S.; Marrone, D.P.; Plambeck, R.L.; Wardle, J.F.C.; Akiyama, K.; Asada, K.; Beaudoin, C.; Blackburn, L.; et al. Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*. Science 2015, 350, 1242–1245. [Google Scholar] [CrossRef] [PubMed]
- Meszaros, P.; Nagel, W. X-ray pulsar models. I-Angle-dependent cyclotron line formation and comptonization. Astron. J. 1985, 298, 147–160. [Google Scholar] [CrossRef]
- Davis, S.W.; Blaes, O.M.; Hirose, S.; Krolik, J.H. The Effects of Magnetic Fields and Inhomogeneities on Accretion Disk Spectra and Polarization. Astron. J. 2009, 703, 569–584. [Google Scholar] [CrossRef]
- Caiazzo, I.; Heyl, J. Vacuum birefringence and the x-ray polarization from black-hole accretion disks. Phys. Rev. D 2018, 97, 083001. [Google Scholar] [CrossRef]
- Mignani, R.P.; Testa, V.; González Caniulef, D.; Taverna, R.; Turolla, R.; Zane, S.; Wu, K. Evidence for vacuum birefringence from the first optical-polarimetry measurement of the isolated neutron star RX J1856.5-3754. Mon. Not. R. Astron. Soc. 2017, 465, 492–500. [Google Scholar] [CrossRef]
- Weisskopf, M.C.; Ramsey, B.; O’Dell, S.L.; Tennant, A.; Elsner, R.; Soffita, P.; Mulieri, F. The Imaging X-ray Polarimetry Explorer (IXPE). Result. Phys. 2016, 6, 1179–1180. [Google Scholar] [CrossRef]
- Zhang, S.N.; Feroci, M.; Santangelo, A.; Dong, Y.W.; Feng, H.; Lu, F.J.; Brandt, S. eXTP: Enhanced X-ray Timing and Polarization mission. In Space Telescopes and Instrumentation 2016: Ultraviolet to Gamma Ray; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 9905, p. 99051Q. [Google Scholar]
- Beilicke, M.; Kislat, F.; Zajczyk, A.; Guo, Q.; Endsley, R.; Stork, M.; Cowsik, R.; Dowkontt, P.; Barthelmy, S.; Hams, T.; et al. Design and Performance of the X-ray Polarimeter X-Calibur. J. Astron. Instrum. 2014, 3, 1440008. [Google Scholar] [CrossRef]
- Chauvin, M.; Florén, H.G.; Friis, M.; Jackson, M.; Kamae, T.; Kataoka, J.; Kawano, T.; Kiss, M.; Mikhalev, V.; Mizuno, T.; et al. The PoGO+ view on Crab off-pulse hard X-ray polarisation. Mon. Not. R. Astron. Soc. 2018, 477, L45–L49. [Google Scholar] [CrossRef]
- She, R.; Feng, H.; Muleri, F.; Soffitta, P.; Xu, R.; Li, H.; Bellazzini, R.; Wang, Z.; Spiga, D.; Minuti, M.; et al. LAMP: A micro-satellite based soft x-ray polarimeter for astrophysics. In UV, X-Ray, and Gamma-Ray Space Instrumentation for Astronomy XIX; International Society for Optics and Photonics: Bellingham, WA, USA, 2015; Volume 9601, p. 96010I. [Google Scholar]
- Gaenther, H.M.; Egan, M.; Heilmann, R.K.; Heine, S.N.T.; Hellickson, T.; Frost, J.; Marshall, H.L.; Schulz, N.S.; Theriault-Shay, A. REDSoX: Monte-Carlo ray-tracing for a soft x-ray spectroscopy polarimeter. In Optics for EUV, X-Ray, and Gamma-Ray Astronomy VIII; International Society for Optics and Photonics: Bellingham, WA, USA, 2017; Volume 10399, p. 1039917. [Google Scholar]
- Novikov, I.D.; Thorne, K.S. Astrophysics of black holes. In Black Holes (Les Astres Occlus); Dewitt, C., Dewitt, B.S., Eds.; Gordon and Breach: Philadelphia, PA, USA, 1973; pp. 343–450. [Google Scholar]
- Riffert, H.; Herold, H. Relativistic Accretion Disk Structure Revisited. Astron. J. 1995, 450, 508. [Google Scholar] [CrossRef]
- Hirose, S.; Krolik, J.H.; Blaes, O. Radiation-Dominated Disks are Thermally Stable. Astron. J. 2009, 691, 16–31. [Google Scholar] [CrossRef]
- Schnittman, J.D.; Krolik, J.H.; Noble, S.C. X-Ray Spectra from Magnetohydrodynamic Simulations of Accreting Black Holes. Astron. J. 2013, 769, 156. [Google Scholar] [CrossRef]
- Kubo, H.; Nagata, R. Determination of dielectric tensor fields in weakly inhomogeneous anisotropic media. II. J. Opt. Soc. Am. 1981, 71, 327–333. [Google Scholar] [CrossRef]
- Kubo, H.; Nagata, R. Vector representation of behavior of polarized light in a weakly inhomogeneous medium with birefringence and dichroism. J. Opt. Soc. Am. 1983, 73, 1719–1724. [Google Scholar] [CrossRef]
- Parfrey, K.; Giannios, D.; Beloborodov, A.M. Black hole jets without large-scale net magnetic flux. Mon. Not. R. Astron. Soc. 2015, 446, L61–L65. [Google Scholar] [CrossRef]
- McClintock, J.E.; Shafee, R.; Narayan, R.; Remillard, R.A.; Davis, S.W.; Li, L.X. The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105. Astron. J. 2006, 652, 518–539. [Google Scholar] [CrossRef]
- Miller, J.M.; Parker, M.L.; Fuerst, F.; Bachetti, M.; Harrison, F.A.; Barret, D.; Boggs, S.E.; Chakrabarty, D.; Christensen, F.E.; Craig, W.W.; et al. NuSTAR Spectroscopy of GRS 1915+105: Disk Reflection, Spin, and Connections to Jets. Astrophys. J. Lett. 2013, 775, L45. [Google Scholar] [CrossRef]
- Mirabel, I.F.; Rodríguez, L.F. A superluminal source in the Galaxy. Nature 1994, 371, 46–48. [Google Scholar] [CrossRef]
- Fender, R.P.; Garrington, S.T.; McKay, D.J.; Muxlow, T.W.B.; Pooley, G.G.; Spencer, R.E.; Stirling, A.M.; Waltman, E.B. MERLIN observations of relativistic ejections from GRS 1915+105. Mon. Not. R. Astron. Soc. 1999, 304, 865–876. [Google Scholar] [CrossRef]
- Schnittman, J.D.; Krolik, J.H. X-ray Polarization from Accreting Black Holes: The Thermal State. Astron. J. 2009, 701, 1175–1187. [Google Scholar] [CrossRef]
- Baldini, L.; Muleri, F.; Soffitta, P.; Omodei, N.; Pesce-Rollins, M.; Sgro, C.; Latronico, L.; Spada, F.; Manfreda, A.; Di Lalla, N. Ximpol: A new X-ray polarimetry observation-simulation and analysis framework. In Proceedings of the 41st COSPAR Scientific Assembly, Istanbul, Turkey, 30 July–7 August 2016; Volume 41. [Google Scholar]

© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Caiazzo, I.; Heyl, J. Probing Black Hole Magnetic Fields with QED. Galaxies 2018, 6, 57. https://doi.org/10.3390/galaxies6020057
Caiazzo I, Heyl J. Probing Black Hole Magnetic Fields with QED. Galaxies. 2018; 6(2):57. https://doi.org/10.3390/galaxies6020057
Chicago/Turabian StyleCaiazzo, Ilaria, and Jeremy Heyl. 2018. "Probing Black Hole Magnetic Fields with QED" Galaxies 6, no. 2: 57. https://doi.org/10.3390/galaxies6020057
APA StyleCaiazzo, I., & Heyl, J. (2018). Probing Black Hole Magnetic Fields with QED. Galaxies, 6(2), 57. https://doi.org/10.3390/galaxies6020057




