Large-Scale Features of the Radio Sky and a Model for Loop I

Abstract

The large-scale radio/microwave sky has been mapped over a range of frequencies from tens of MHz to tens of GHz, in intensity and polarization. The emission is primarily synchrotron radiation from cosmic ray electrons spiralling in the Galactic magnetic field, in addition to free–free radiation from warm ionized gas. Away from the Galactic plane, the radio sky is dominated by very large (tens of degrees) loops, arcs, spurs and filaments, including the well-known North Polar Spur (NPS), which forms part of Loop I with a diameter of ∼${120}^{\circ }$. In polarization data, such features are often more discernible due to their high polarization fractions suggesting ordered magnetic fields, while the polarization angles suggest fields that are parallel to the filament. The exact nature of these features are poorly understood. We give a brief review of these features, focussing on the NPS/Loop I, whose polarization directions can be explained using a simple expanding shell model, placing the centre of the shell at a distance of ∼100–200 pc. However, there is significant evidence for a larger distance in the range ∼500–1000 pc, while larger distances including the Galactic Centre are unlikely. We also briefly discuss other large-scale curiosities in the radio sky such as the microwave haze and anti-correlation of H$\alpha$ filaments and synchrotron polarized intensity.

1. Introduction

The sky has been mapped over a wide range of wavelengths, from radio to microwave, infrared to optical, UV to X-rays and Gamma-rays. There are several full-sky radio and microwave surveys ($\lambda >0.3$ cm or $\nu <100$ GHz) with good signal-to-noise ratio and good fidelity. In particular, they preserve large angular scale ($\theta >1^{\circ }$) information in the maps that is often filtered out either due to the telescope response (e.g., an interferometer) or in the analysis to remove systematic errors in the data. Low frequency surveys (up to ∼10 GHz) are readily made from the ground using large single dish telescopes, while higher frequency surveys can be made from space. The release of the WMAP and Planck data has revolutionized our view of the high frequency sky, providing full-sky multi-frequency data including polarization maps that are not affected by Faraday Rotation.

This article provides a brief overview of large-scale features of the sky at radio and microwave wavelengths (<100 GHz), with a focus on polarization observations and on the large radio loops. For more details and discussion, we refer the interested reader to the two papers [1,2] on which much of the article has been based.

1.1. Emission Mechanisms at Radio Wavelengths

Table 1. Summary of key characteristics of the main emission mechanisms in continuum at radio wavelengths.

Emission Mechanism	Description	Typical Spectrum	Polarization
Synchrotron	Electrons accelerated by magnetic field	Power-law $\beta \approx -2.7$	Up to $75\%$
Free-free	Electrons accelerated by ions	Power-law $\beta =-2.1$	≈0%
AME	Electric dipole radiation from spinning dust grains	Peaked ≈ 30 GHz	≈0%
CMB	Black-body radiation	BB $T_{\mathrm{CMB}}=2.726$ K	≈10%
MDE	Magnetic dipole radiation from dust grains	≈BB in microwave	Up to ≈30%

summarises some of the main emission mechanisms that contribute to the radio/microwave sky. At frequencies below a few GHz, the two main emission mechanisms are synchrotron and free–free radiation. At frequencies above 10 GHz, several additional components become important: a new foreground component termed Anomalous Microwave Emission (AME), the cosmic microwave background (CMB), and at frequencies above ≈70 GHz, thermal dust emission.

Synchrotron radiation is due to relativistic cosmic ray (CR) electrons spiralling in the Galactic magnetic field. The synchrotron intensity at a frequency $\nu$ is given by (e.g., [3])

$$I_{\nu }=const.L{N}_0{B}^{(p+1)/2}{\nu }^{-(p-1)/2},$$

(1)

where $N_0$ is the density of CR electrons, L is the emission depth, B is the magnetic field strength. The p value is the CR electron energy spectral index, of the form $dN/dE=N_0{E}^{-p}$, with typical values for p in the range 2.5–3.0 (e.g., [4]). The radio brightness temperature spectral index ($T_b\propto {\nu }^{\beta }$) is related to p via $\beta =-(p+3)/2$, with typical values in the range $\beta =-2.5$ to $-3.0$.

Free-free radiation on the other hand is a thermal process, produced by free electrons accelerated by ions by Coulombic interactions, and thus is a good tracer of the Warm Ionized Medium (WIM) and HII regions. In the optically thin regime (true at frequencies above ∼1 GHz, except towards dense regions of ionized gas), the spectrum is remarkably stable with a temperature spectral index $\beta =-2.1$ (e.g., [5]). The spectrum is significantly flatter than synchrotron radiation and therefore is more easily separated at higher (>1 GHz) frequencies.

Polarization surveys are of particular interest at radio wavelengths because, unlike free–free radiation, synchrotron radiation is intrinsically highly polarized, with the E-vector pointing perpendicular to the B field. Theoretically, in a regular well-ordered B-field, synchrotron radiation has a polarization fraction of $\mathsf{\Pi }=0.75$, i.e., it can be up to 75% polarized (e.g., [3]). In practice, depolarization by geometric effects (e.g., tangled B-fields and line-of-sight depolarization) reduces this to typical values of tens of per cent at high latitudes and lower at lower latitudes. At low frequencies, Faraday Rotation (FR) rotates the plane of linear polarization. The amount of rotation depends on the line-of-sight integral of the electron density and the line-of-sight component of the B-field, $B_{\left|\right|}$ (in units of Gauss) as

$$\varphi =8.1\times {10}^5{\lambda }^2\int n_e{B}_{\left|\right|}dl\mathrm{radians},$$

(2)

where $\lambda$ is the wavelength in metres, $n_e$ the free electron density in cm${}^{-3}$ and l is the path length from the emitter in parsecs. The rotation is often expressed in terms of the Rotation Measure (RM), in units of rads/m${}^2$, since the effect is proportional to ${\lambda }^2$. Typical values away from the Galactic plane are ∼10–30 rads/m${}^2$ [6] and thus synchrotron radiation becomes “Faraday free” at frequencies above ∼5 GHz.

In intensity, at frequencies above ∼20 GHz synchrotron radiation becomes relatively weak compared to the other components of emission. However, in polarization, synchrotron radiation is thought to be dominant at frequencies below ≈70 GHz, while at high frequencies thermal dust radiation becomes the dominant emitter [7]. The CMB is polarized at the ≈10 % level but is weak in polarization relative to Galactic emission. Free-free is intrinsically unpolarized although sharp edges can induce a polarized component via Thomson scattering. AME, if due to spinning dust grains (the preferred model), is thought to be negligibly polarized with observed upper limits at the ∼1 % level [8]. Magnetic dipole emission (MDE), if significant, could be strongly polarized, but is not thought to be dominant at frequencies of tens of GHz but may be important at frequencies above ∼100 GHz [8,9].

1.2. Radio Surveys

Figure 1 displays images of many of the most important large-scale total-power radio surveys that have been made, covering a frequency range from 10 MHz up to WMAP at 94 GHz (note that Planck maps were not included in this figure). One can see that most of these surveys are not full-sky and many, particularly those at the lowest frequencies, have poor angular resolution or contain significant artifacts.

At low frequencies, the 408 MHz all-sky map [11], with an angular resolution of 51 arcmin, is the best-known. There are several versions of the Haslam map that are available, although the most commonly used is the reprocessed version made by the WMAP team and is available on the LAMBDA website. We recommend the use of the newly reprocessed version of [12], which improves the coordinates and remapping of the original four surveys, improved destriping, and improved source removal. Nevertheless, users of the Haslam map should be aware of the limitations [12,13]. The other full-sky map is the 1.4 GHz map [14,15], although it is not formally published as one map.

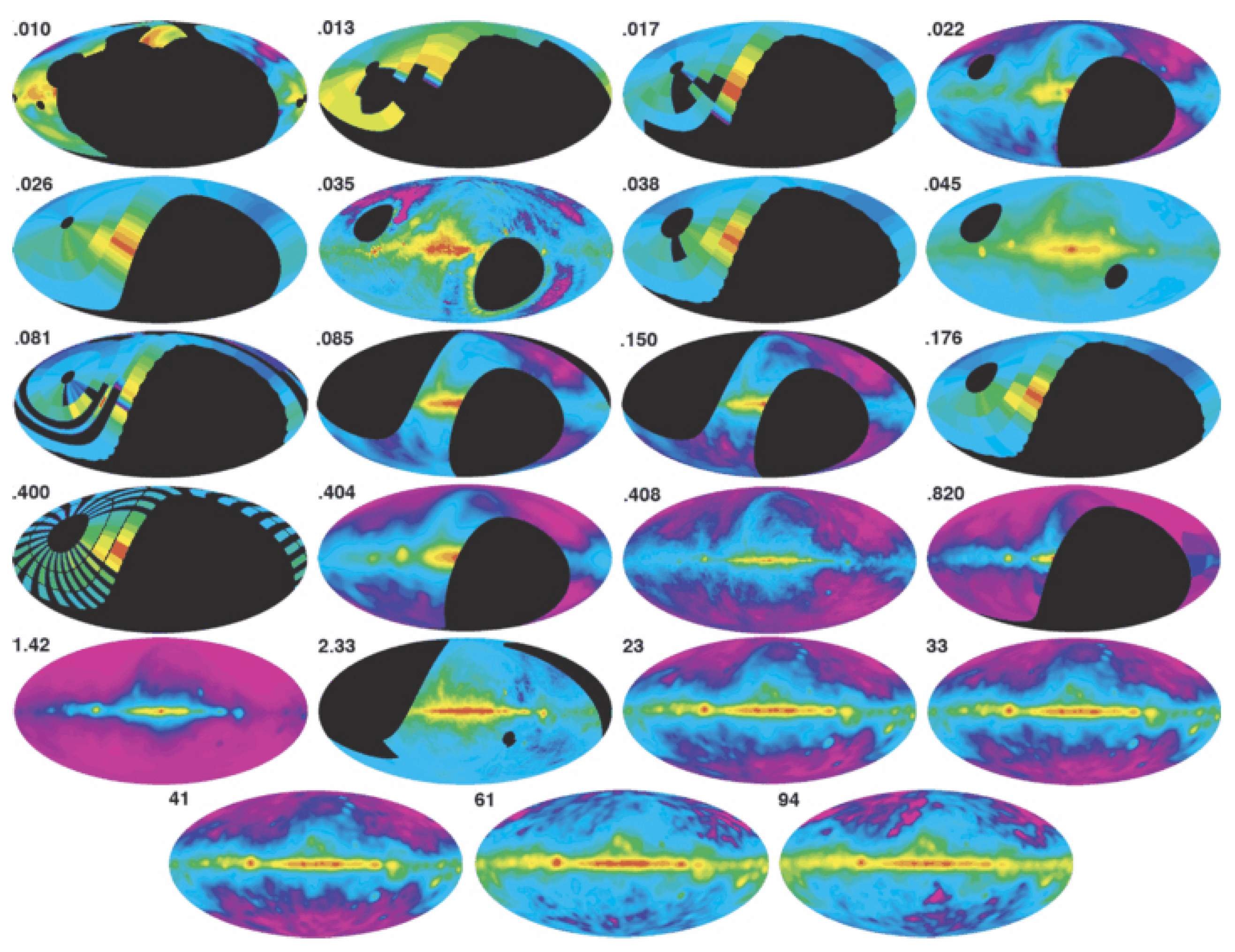
Polarization surveys at radio wavelengths are more scarce. A number of low frequency surveys (≤$2.3$ GHz) are available but are affected by Faraday Rotation. Indeed, there are several ongoing polarization surveys (e.g., GMIMS [16], GALFACTS [17]) that are dedicated to studying the magnetic field/electron distribution using FR.

At higher frequencies (above a few GHz), the WMAP [18] and Planck [19] surveys provide full-sky data with sub-degree angular resolution at frequencies of 23, 28, 33, 41, 44 GHz and beyond. With typical sensitivities of a few $\mathsf{\mu }$K per beam in intensity, these maps allow the detection of the CMB anisotropies as well as diffuse Galactic radiation, although the CMB must be removed to see the faintest diffuse emission at high latitudes. Figure 2 shows how the subtraction of the CMB anisotropies from the Planck 44.1 GHz map reveals faint diffuse Galactic radiation at high latitudes.

The WMAP and Planck maps also contain valuable polarization information. Most importantly, the emission is expected to be almost exclusively due to synchrotron radiation, since other emission mechanisms appear to be weakly or negligibly polarized (except above ≈70 GHz when polarized thermal dust emission becomes important). Figure 3 presents radio polarization maps at 22.8, 33 and 40.7 GHz from WMAP and also the 1.4 GHz polarization map from [20]. Polarized synchrotron emission is clearly detected across large areas of sky over a range of frequencies. At 1.4 GHz, the lack of polarized intensity at low latitudes, and particularly pronounced towards the inner Galaxy for $\left|b\right|<{30}^{\circ }$, is due to Faraday depolarization while at higher latitudes the map looks similar to high frequencies as FR becomes small. A notable exception is the Fan region at $l\sim {140}^{\circ }$, which is a highly polarized region of space that is very close to us and not strongly affected by FR. The WMAP 22.8 GHz map is one of the most important datasets currently available in polarization with a signal-to-noise ratio that is sufficient to detect large-scale synchrotron emission on scales of a few degrees across a significant fraction of the sky while being at a frequency where Faraday effects are negligible, except near the Galactic Centre. At frequencies above 20 GHz, FR is minimal (<$1^{\circ }$) even in the Galactic plane [1], and thus the polarization angles are approximately preserved as a function of frequency.

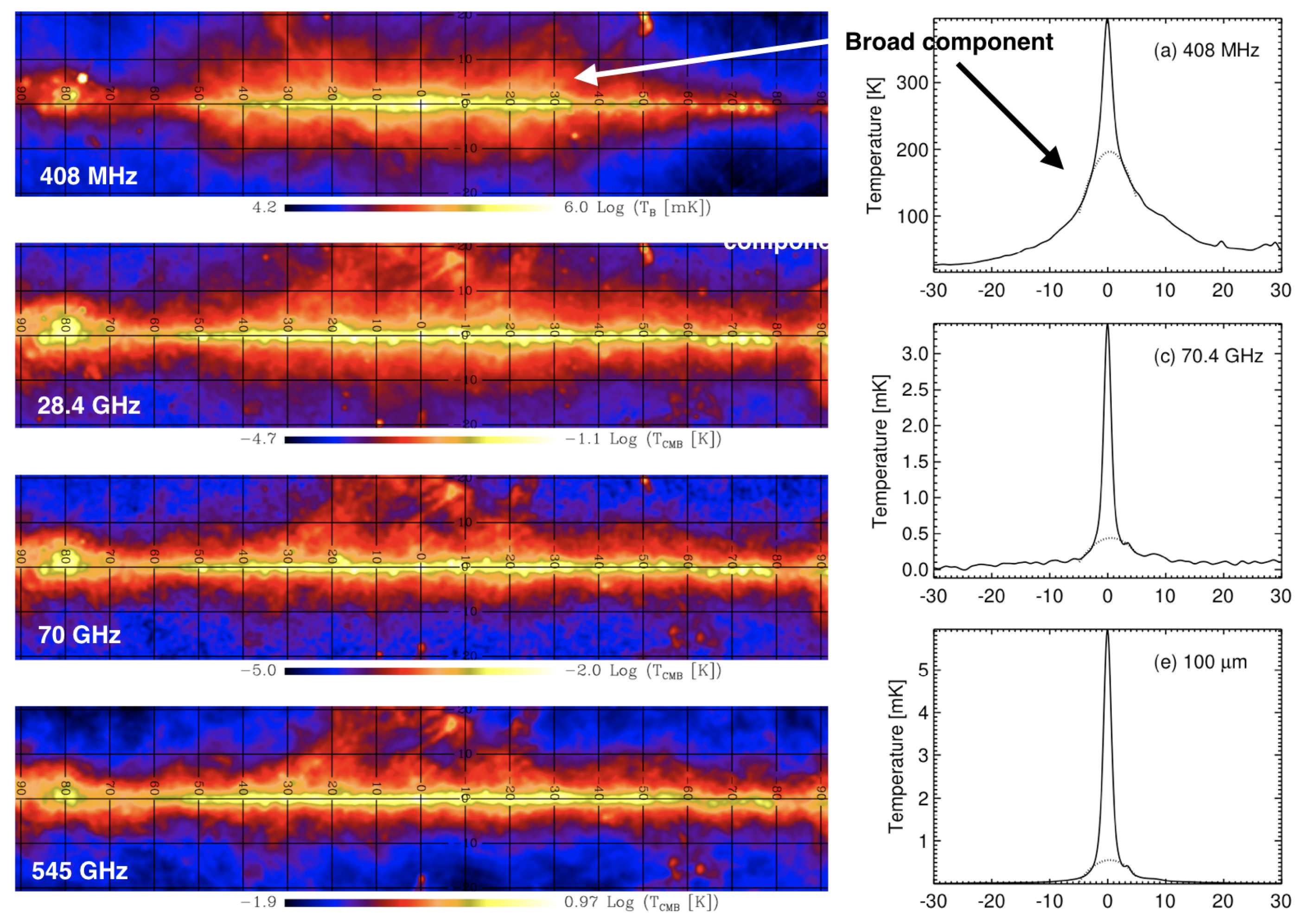
2. Brief Review of Large-Scale Features in the Radio Sky

2.1. Overview

The radio sky is well depicted by the full-sky 408 MHz map [11,12], shown in histogram-equalized form in Figure 4. The band of strong emission from the Galactic disk dominates, particularly in the inner Galaxy within ∼${60}^{\circ }$ of the Galactic Centre. The emission is primarily due to synchrotron radiation from cosmic rays accelerated by shock fronts in supernova remnants (SNRs) and pulsar wind nebulae (PWN). Free-free radiation also contributes, particularly along the Galactic disk, due to high mass OB-type stars ionizing the interstellar gas.

All radio surveys detect compact sources that are unresolved relative to the observation beam size. In single dish surveys, the beam is typically several arcmin or degrees and therefore extragalactic sources are nearly always unresolved (except for the LMC, SMC, Cen-A and M31) as seen by the large number of bright point-like sources in Figure 4. Galactic sources (e.g., SNRs, PWN, HII regions, molecular clouds) are also, in many cases, unresolved. Along the Galactic plane, the large number of Galactic source are integrated both along the line-of-sight and within the relatively large beams of radio telescopes, making it difficult to detect single objects against the truly diffuse radiation, which is emitted by the diffuse interstellar medium around and in between active regions. The exact ratio of these two components depends on the beam size, position in the Galaxy, and to some extent on what is defined as a source (as opposed to diffuse emission). Still, studies of large-scale vs. small-scale emission in the plane suggests that the two components are comparable at radio/microwave frequencies i.e., about half of the emission on large-scales (e.g., [21,22]).

The emission from the Galactic disk can be seen to trace the spiral arms, which enhance the intensity at longitudes that traverse a spiral arm, including $l=\pm {90}^{\circ }$ looking down our own spiral arm. Outside of the spiral arm structure and local features above the Galactic plane, the distribution with Galactic latitude can be approximated by the plane-slab model, which yields a cosecant dependance on the latitude, i.e., $T\propto 1/\sin \left(b\right)$. Interestingly, as shown in Figure 5, the width in latitude of the diffuse emission of low-frequency synchrotron radiation appears to be broader than that of the gas and dust as traced by the stars, free–free radiation and even thermal dust emission [22]. At higher radio frequencies, the synchrotron width appears to be narrow suggesting that there is an older population of CR electrons in the inner plane, perhaps related to previous stages of star formation in the Galactic bar. The Gould Belt system is a ring of star formation, which is most visible near the Solar neighbourhood at up to $b\approx \pm {30}^{\circ }$ above the plane at $l\sim 0^{\circ }$ in Ophiuchus (see Figure 5 at 70.4/545 GHz) and below the plane at $l\sim {180}^{\circ }$ in Orion/Eridanus (see Figure 4).

The most obvious features in the radio sky, besides for the Galactic plane, are the large radio loops, which dominate the high latitude sky. The most famous, the North Polar Spur (NPS), which is part of what is known as Loop I, has been known since the very earliest days of radio astronomy (e.g., [23]). The NPS is a bright ridge of emission emanating perpendicularly from the plane at $l\approx {30}^{\circ }$ with a length of ∼${30}^{\circ }$, before it joins a wider band of emission that loops over (see Figure 4). The first paper to explicitly discuss the NPS was [24] who discussed the fact that this “curious feature” was not then visible at other wavelengths and whose theories were “unsatisfactory”. They also noted the similarity between Loop I and the Cygnus Loop, which is the remnant of a type 2 supernova, and has similar surface brightness and spectral indices. With a thickness ∼10 pc, diameter 40 pc and distance 770 pc, by analogy, this would mean that Loop I is at a distance of ∼50 pc and lying up to 20 pc above the plane.

Further large-scale loops were discovered, known as as Loop II or Cetus arc [25], Loop III [26] and Loop IV [27,28] (Figure 4). A comprehensive study of the four well-known loops (I–IV) is provided by [28]. They found that all of these loops, which are tens of degrees in size, track small circles on the sky, suggesting expanding shells. The shells themselves are not seen at any other wavelength except via radio continuum, but they do have associations with other wavelengths. In particular, there is often a cold border on the outer edge of the shells, as seen in HI (cold gas) and far-IR (dust). In addition, interior to the shell is often filled with soft X-rays indicating hot ($T\sim {10}^6$ K) gas.

In polarization, the structure of the loops and filaments is, to some extent, more visible (Figure 3). The filamentary structures and coherent polarization angles indicates well-ordered B-fields, which is also confirmed by the relatively high polarization fractions of $\mathsf{\Pi }\sim$40–50 %. Vidal et al. [1] identified 11 filaments, five of which are only visible in polarization data, and found $\beta =-3.06\pm 0.02$ with typical variations over the sky of $\Delta \beta \approx 0.2$. In general, the polarization vectors are perpendicular to the filaments meaning that the B-field is parallel to them. The loops and filaments dominate much of the polarized sky, with the Galactic plane being relatively weak due to depolarization resulting in low polarization fractions ($\mathsf{\Pi }\sim 0$–5%). Nevertheless, the polarization angles are nearly always perpendicular to the plane, meaning the B-field is aligned with the plane and spiral arms. A large area of strong polarization is also seen above the plane at $l\sim {140}^{\circ }$, known as the “Fan region”. This is one of the dominant features in the polarized sky yet still little is known; it was originally thought to be of local origin given its high polarization fraction, but recent analyses suggest it could be beyond the Perseus arm and therefore at >2 kpc [29].

To improve the S/N ratio of the WMAP 22.8 GHz polarization map, Planck Collaboration [2] combined the WMAP and Planck maps between 22.8 GHz and 44.1 GHz, assuming a power-law model to the frequency spectrum, to produce the high S/N synchrotron polarized intensity map depicted in Figure 6. In this map, the main loops are clearly discerned and can be seen to extend further than seen before, although not necessarily following the small circle models. Many other loops, spurs and filaments can be discerned, some of which appear to be correlated spatially with each other while others appear to be stand-alone features. There are a number of spurs within the interior of Loop I, some of which were first identified and tabulated by [27], which are much more visible in polarization.

There have been many theories for the origin of these loops and what they really are (see e.g., [30] for a review). The most widely accepted explanation for these large loops are supernova remnants (e.g., [31]). Specifically, given their size and luminosity, they are likely to be the remnants of several successive supernova explosions in the vicinity of the Solar neighbourhood. Their age is probably ∼${10}^5$–${10}^6$ years and thus the emitting electrons are losing energy radiatively resulting in steep spectra ($\beta \le -3$) and will eventually merge into the large-scale diffuse synchrotron background. It is believed that the majority of CR electrons are produced in SNRs, and thus it is reasonable to assume that the distribution of synchrotron radiation as seen on the sky is the sum of all SNRs over the past ∼${10}^6$ years [32]. Inspection of the new maps, particularly in polarization, is supportive of this idea.

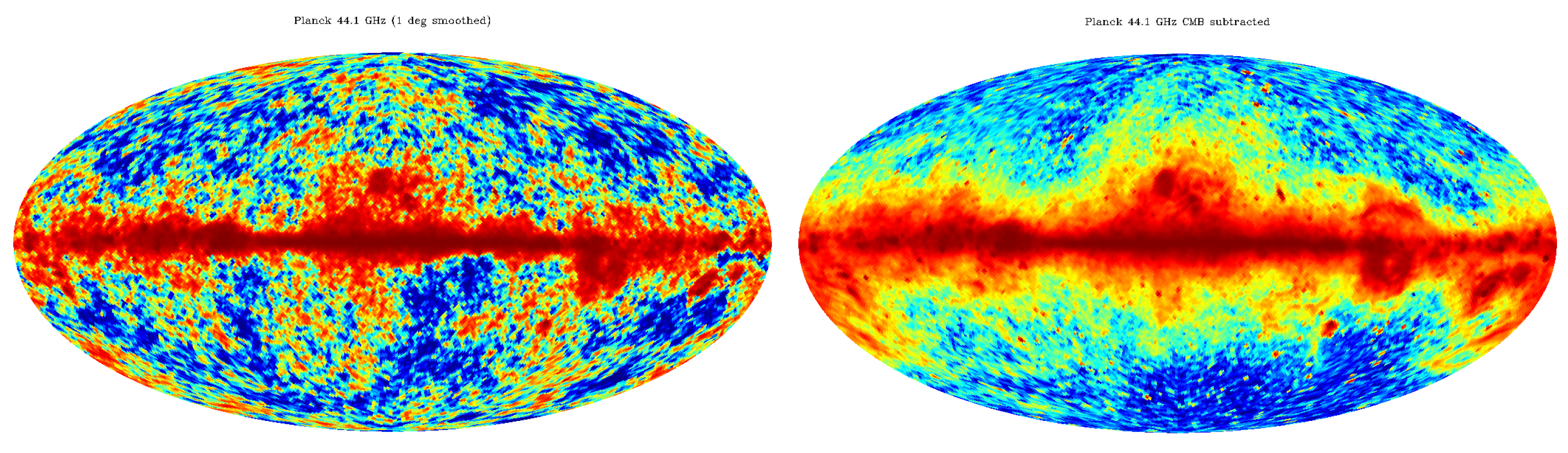
2.2. WMAP/Planck Microwave Haze and Fermi Bubbles

The WMAP/Planck haze is a diffuse structure, approximately centred on the Galactic Centre (GC). The emission was first thought to be due to free–free emission due its unusually flat spectral index but is now believed to be due to a hard component (flat spectrum) of synchrotron radiation, with $\beta \approx -2.5$ [33,34]. The Fermi Bubbles (FB) form a double-lobed feature detected in Fermi data at energies ∼10–500 GeV centred exactly on the GC and reaching up to $b=\pm {55}^{\circ }$ [35,36]. Their $\gamma$-ray spectra are harder than inverse Compton from the Galactic halo or $\pi$ decay from collisions. A number of explanations for the FB have been suggested including dark matter. The most favoured models relate to recent AGN-type activity at the Galactic centre, which is blowing out high energy electrons.

A number of authors have noted a possible connection between the microwave haze and the FB. Morphologically, the two are quite different, with the bubbles having a more well-defined morphology of a bipolar structure with relatively hard edges while the haze is much more diffuse [36]. The FBs are distributed quite symmetrically above and below the plane, while the haze is weaker to the south. Furthermore, in the south, the haze extends to the side and well outside the FB border. Thus, it seems that the structures are not the same, although there may well be a connection to star-formation and AGN activity, perhaps ${10}^5$–${10}^6$ years ago.

Given their location and possibly similar ages, there may be a connection between the FB and the NPS/Loop I. Close inspection of the new microwave polarization data shows that the southern part of FB extends well outside that of Loop I and that there is no trace of any interaction with the bubble in the radio maps. Nevertheless, polarized filaments within Loop I may be associated with FB. Figure 7 shows that one such spur almost exactly traces the outer edge of the FB, both in the north and the south. This is unlikely to be coincidence and suggests that the activity causing the bubbles, must also be responsible for these particular filaments. For example, one possibility could be that the outflow from the GC is sweeping up material and trapping the CR electrons, compressing the magnetic field, and producing synchrotron emission where this builds up the most. Sarkar [37] has shown that the north–south asymmetry can easily be explained by a combination of different circumgalactic medium densities in the north and south in conjunction with projection from our Solar location.

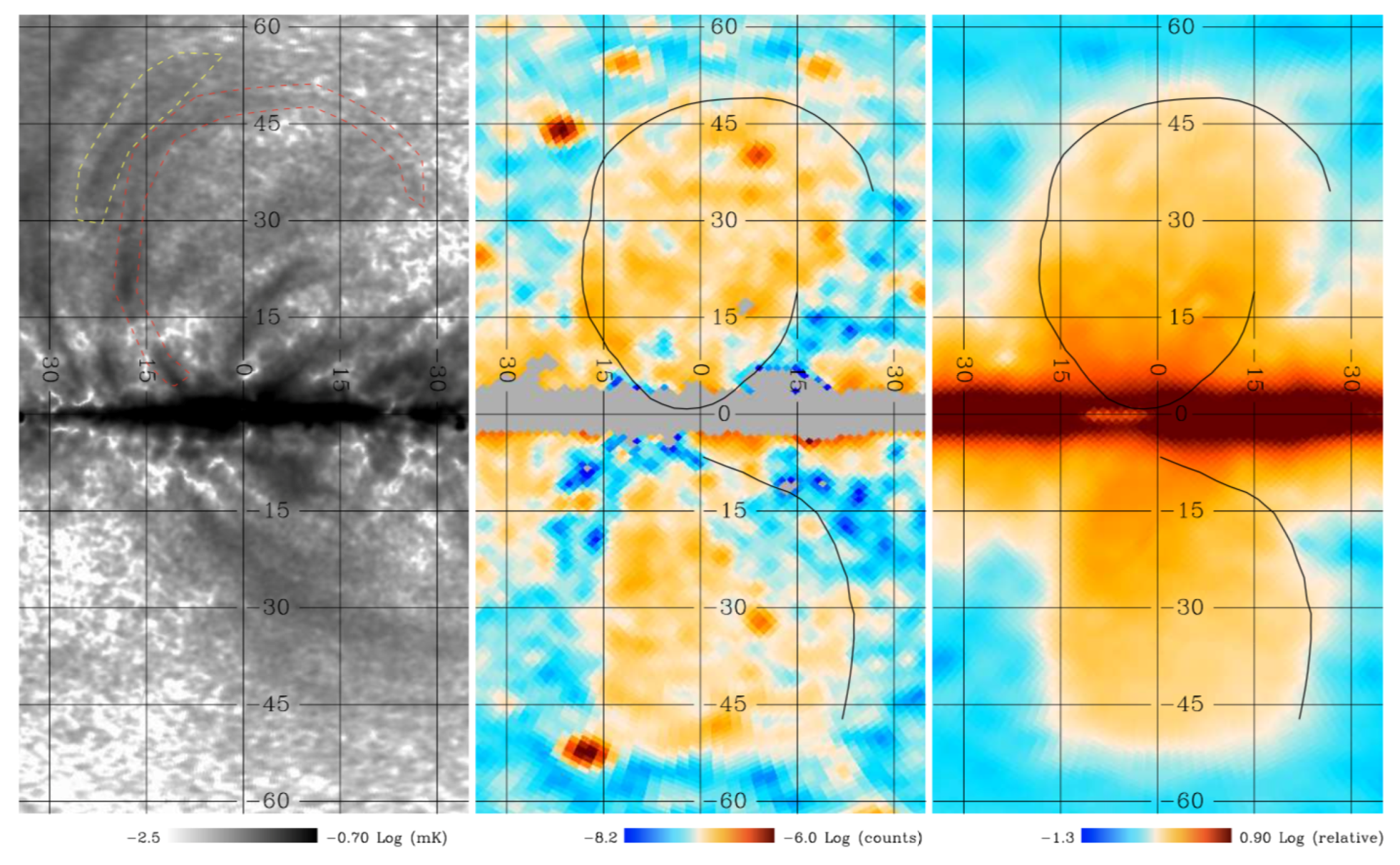
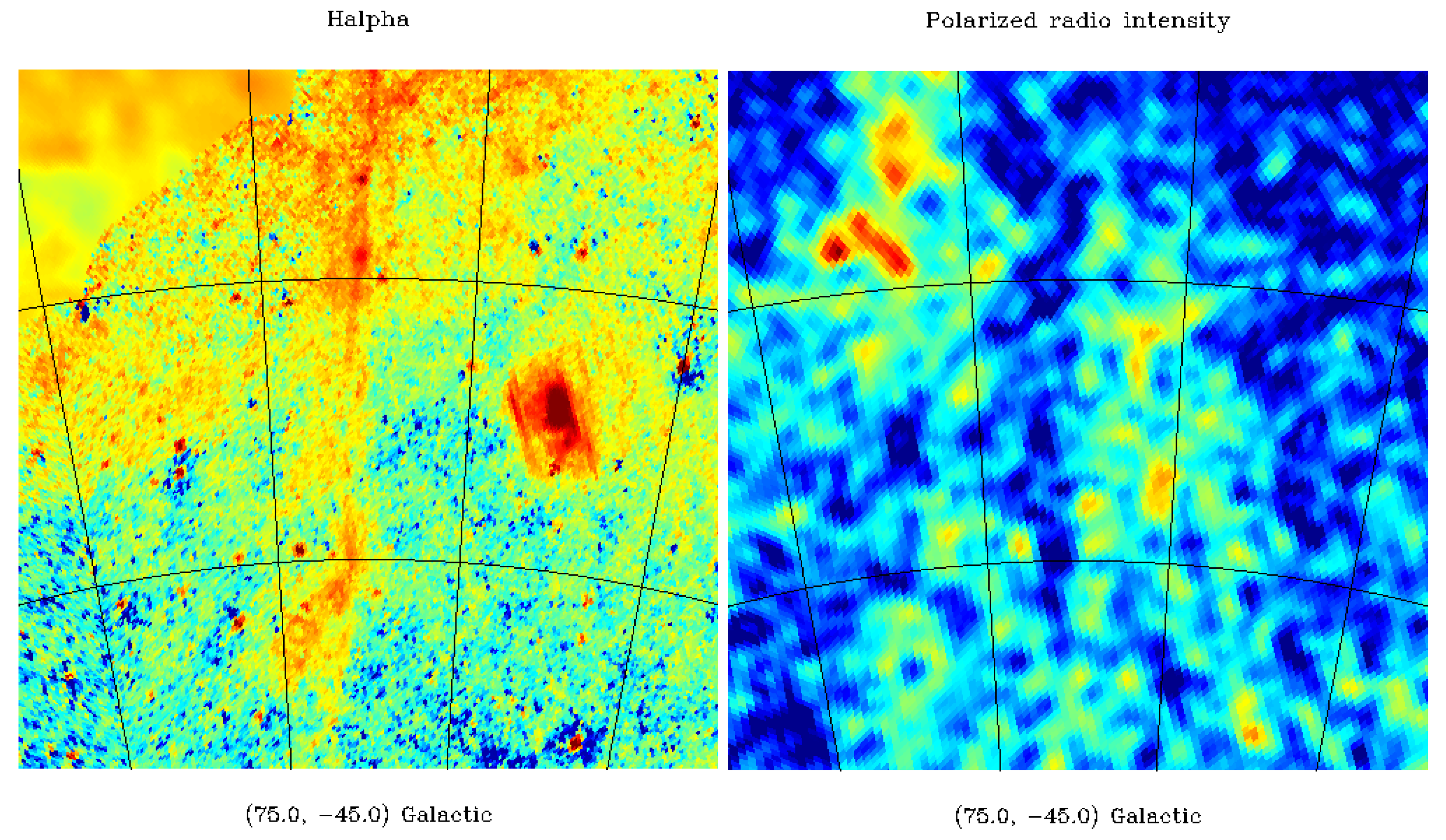
2.3. Anti-Correlation of WIM and Polarized Intensity

At low radio frequencies (below ∼1 GHz), there is a natural tendency for there to be anti-correlation of tracers of warm ionized gas (e.g., H$\alpha$) and polarized radio intensity from synchrotron radiation. This is simply due to the effect of Faraday Rotation, which is proportional to the free electron density along the line-of-sight. However, FR is only significant for frequencies below a few GHz. It is therefore surprising to see an anti-correlation of H$\alpha$ emission with WMAP/Planck polarized intensity maps, particularly at high latitudes [2]. A clear and intriguing example of this is shown in Figure 8. There is a well-defined, very narrow (few arcmin) and long (≈${40}^{\circ }$ in length) filament seen in H$\alpha$, which aligns almost perfectly with a filament of reduced polarized intensity relative to the local background. This feature is also visible in the Faraday depth map of [6]. The features are certainly real and cannot be due to chance correlation, yet the origin is unclear.

As already mentioned, Faraday depolarization is at a level of ≈25 rad/m${}^2$, which corresponds to ${0.}^{\circ }3$ at 22.8 GHz and is therefore negligible. Potential explanations include a strong coherent B-field parallel to the line-of-sight along the filament, or the synchrotron emission is from an ionized region intrinsically weakly polarized from a less-organised field in this region. The H$\alpha$ emission is at negative velocities ($-80<V_{\mathrm{L}SR}<-40$ km/s) suggesting a link with the Perseus arm, which means the background synchrotron emission is coming from a much larger distance (∼2 kpc or more).

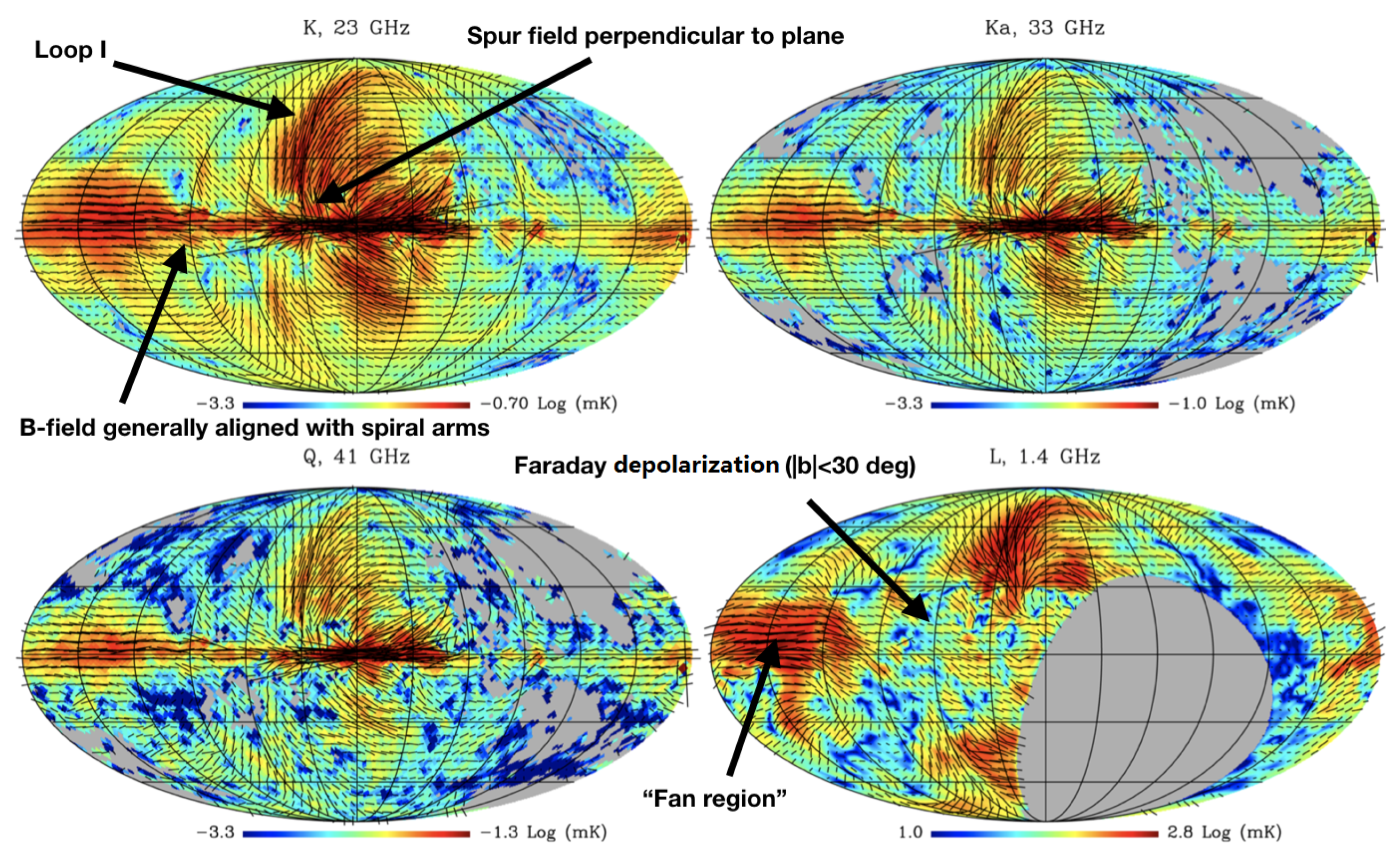
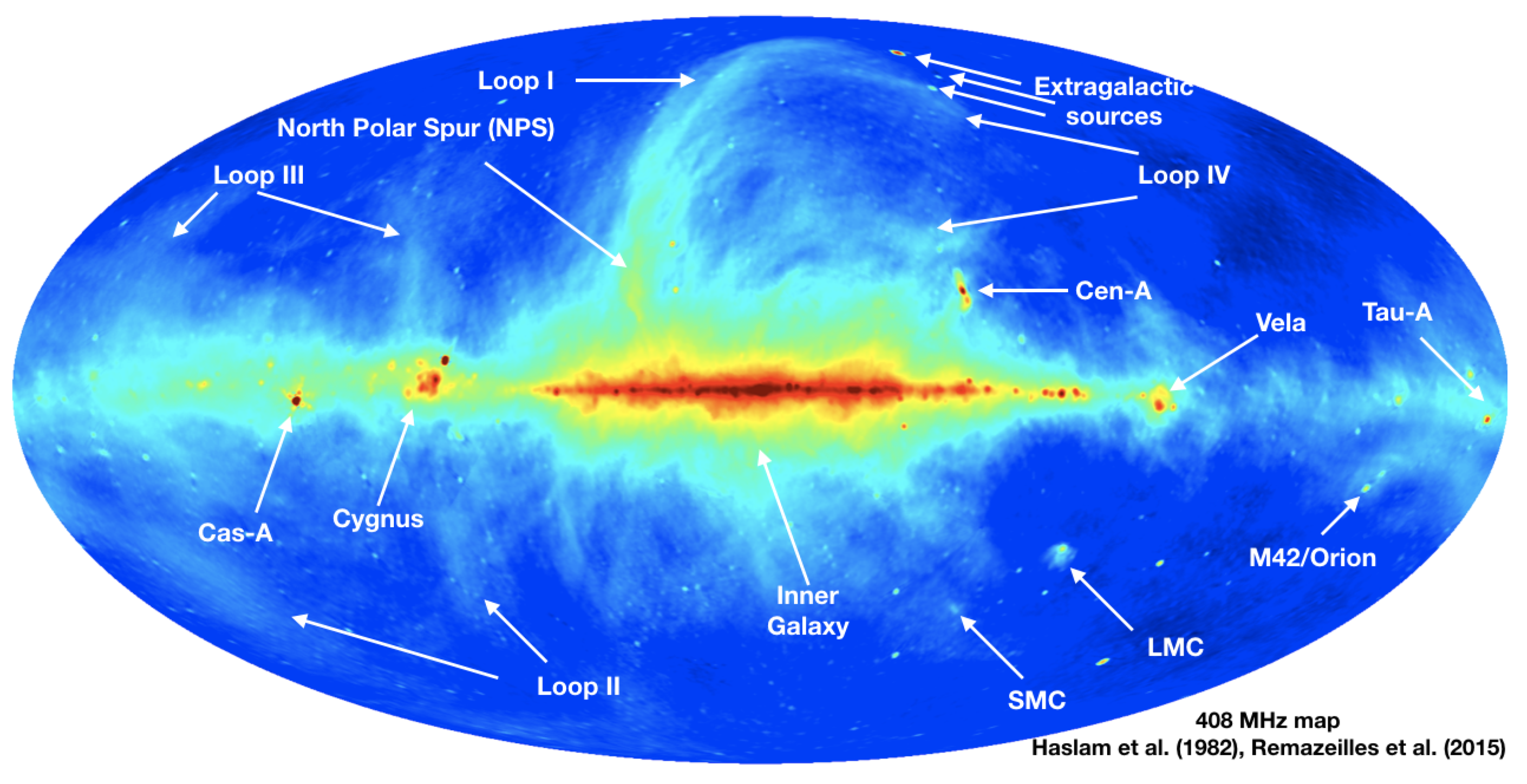
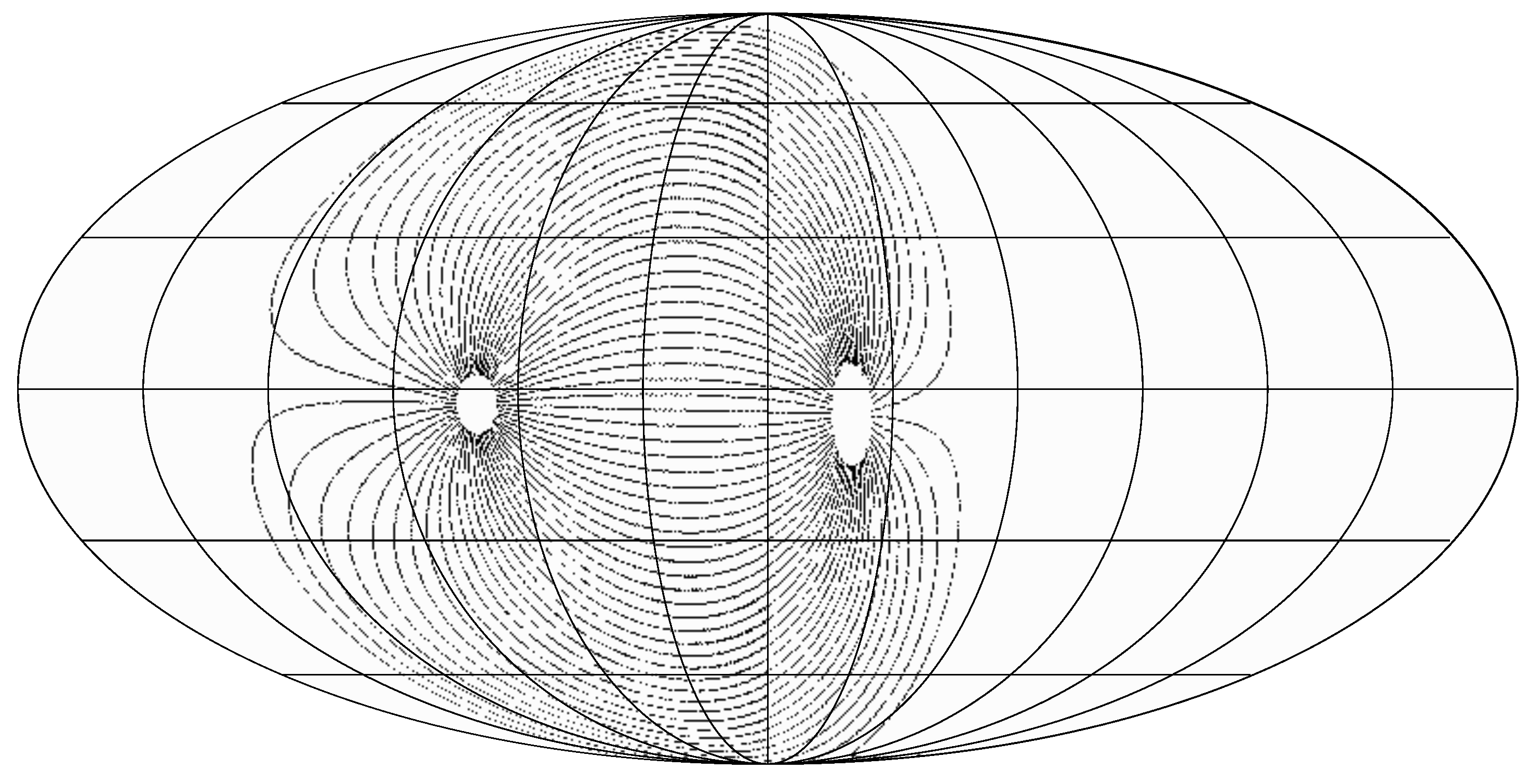
3. Loop I/North Polar Spur

Loop I and the NPS are the most prominent large-scale features of the sky, outside of the Galactic disk (see Figure 3 and Figure 4). Since the other radio loops appear to be similar in nature to Loop I, it seems reasonable that they have a similar origin and it is therefore worth studying in more detail. It should be noted that the outer boundary of the NPS lies several degrees beyond the ridge line of Loop I and therefore could be part of a different structure, potentially at a very different distance. Indeed, many loops away from the loop may be overlapping spatially but at varying distances along the line-of-sight, making them appear to be physically related. Here, we consider a simple model for Loop I and compare it with observations before discussing the distance to Loop I.

3.1. A Simple Explanation for Loop I

There have been many theories to explain the origin of Loop I (see e.g., [28,30]). These include spurs joining across the Galactic plane to form loops, tracers of the helical local Galactic magnetic field, and bubbles or loops in the magnetic field projecting from one side of the Galactic pane due to the instability of the field to CR pressure. Supernova remnants expanding into the Galactic B-field is the preferred model (e.g., [31]), which explains the synchrotron emission, shell morphology, as well as the outer cold border (seen in HI and dust) due to swept up gas and dust. The inevitable compression of the B-field due to the supernova shock wave will act as a source of enhanced synchrotron radiation. Furthermore, this is more easily observable due to limb-brightening resulting in strong emissions from the edge of the expanding shell. A related scenario is that the Loop I cavity is a superbubble, created by stellar winds and consecutive supernovae (e.g., [42]). Either way, the spurs are effectively bundles of B-field lines with enhanced CR density.

From these arguments, Heiles [43] considered a simple model to explain the structure of Loop I and the magnetic field lines and compared the model to starlight absorption data available at the time. He assumed a regular B-field with field lines that are parallel to the Galactic plane near the Solar neighbourhood. A symmetric expanding supershell will bend these lines as the shell expands and compresses the magnetic field. The B-field lines will follow lines of constant longitude on the surface of the expanding sphere. The observed pattern on the sky is not trivial since it depends critically on the viewing angle.

Vidal et al. [1] re-evaluated this model in the light of WMAP polarization data. They considered the same idea as [43] with an expanding supershell of radius 120 pc centred at a distance of 120 pc in the direction of the Sco-Cen supershell at $(l,b)=({320}^{\circ },+5^{\circ })$ i.e., the edge of the shell is at our location. Figure 9 (bottom) compares the data (black) and the model (red). Although the agreement is far from perfect, it is remarkable how well this reproduces the large-scale direction of the projected B-field. The agreement is particularly good in the north where the NPS/Loop I is well defined. In other areas, such as just above the plane at $l\sim {330}^{\circ }$, the agreement is poor. However, this is to be expected since overlapping structures along the line-of-sight can distort the angles, particularly at low latitudes. The lack of emission from the far side of the shell is partly due to the viewing angle but must also be partly due to different ISM densities affecting the compression of the B-field. The 3D mapping of the local ISM by [44] confirms that there is a wall of high density gas towards longitude $l\sim 0^{\circ }$ and the Ophiuchi clouds, located towards the bottom of the NPS [45]; the rest of the gas in the local neighbourhood is a relatively low density cavity. The fact that the near side of Loop I is at (or very close to) our location also explains the near vertical field lines observed in the background outside of Loop I.

It is interesting to note that the comparison with optical starlight observations for stars at a distance $<300$ pc (and even to some degree for <100 pc) still shows a good correlation with the pattern shown in Figure 9 [1], in agreement with a mean distance of ≈100–200 pc.

3.2. Distance to the NPS/Loop I

The distance to the NPS/Loop I has been discussed for decades. There have been two regimes for the distance. Many authors, from the very earliest days to now, believe that Loop I is in very close proximity to the Sun due to its large size (≈${120}^{\circ }$ in diameter) on the sky. Perhaps the most common estimate is a distance of ∼100–200 pc, with 140 pc being a specific value due to the possible connection with the Sco-Cen OB association at that distance. However, some authors have argued for a considerably larger distance. One possibility is that Loop I is ranging from ∼500–1000 pc, therefore still relatively close on Galactic scales, because of absorption of gas in front of the NPS/Loop I in X-rays [46] and via stellar light at a distance of a few hundred pc, placing the NPS/Loop I further out. Some authors (e.g., [37,47,48]) have also argued for a Galactic Centre origin due to its directional proximity to the GC and also the possible link with the Fermi Bubbles, which are almost certainly emanating from the Galactic Centre region. This would place the spur and Loop I at a distance of ≈8 kpc and the linear size of the structure would be of a similar dimension!

The distance to Loop I is therefore still a source of significant debate. Nevertheless, the arguments for a relatively nearby origin (<1 kpc) are strong and most of us believe Loop I, and indeed the other angularly large loops extending to high Galactic latitudes, to be of a local origin. The main arguments for a local distance to Loop I can summarised as follows:

• The centre of Loop I is far (>${30}^{\circ }$) from the Galactic centre.
• The NPS itself traverses the Galactic plane at a longitude $l\approx {20}^{\circ }$.
• If at a large distance, the energy (∼${10}^{55}$ erg) and huge physical size (∼8 kpc) are well above what is expected from supernova remnants.
• Starlight polarized absorption detects NPS beyond 100 pc [49,50]. In addition, a simple magnetic field model only works well for stars at distances $<300$ pc.
• The bright edge of the NPS/Loop I is roughly where dense gas exists and low density in other directions (up to ∼kpc).
• The magnetic field outside of the NPS is consistent with local origin (this could be a coincidence or potentially another pre-existing structure?).
• The southern part of FB extends outside Loop I and no trace of interaction with FB in radio maps.
• Loop I extends through the Galactic plane without any sign of deviation.
• We see lots of other loops/spurs with similar geometry, spectral index (loops I–IV at least) but at very different positions and sizes on the sky.

All these arguments point to a local origin for Loop I. However, there is some evidence that NPS/Loop I lies further than originally thought (∼100–200 pc), possibly up to about 1 kpc. Iwan [45] noted that the wall of dense gas around the Local Cavity should put a “dent” in the spherical structure if at a distance of ≈140 pc. To reconcile the polarization absorption from stars at a distance of ∼100 pc, they suggested a distance of ≈400 pc. Wolleben et al. [20] noted the strong depolarization at 1.4 GHz for $\left|b\right|<{30}^{\circ }$ with the NPS projecting above the dense layer that creates the Faraday horizon. At a near distance, a height of ∼50 pc is much too low for the WIM ($h\sim 1$–2 kpc) to source the FR. Models putting Loop I at the GC seem unlikely. We also note that Sofue [46] argued for a distance beyond 400 pc due to X-ray absorption of the NPS at $b<{10}^{\circ }$ due to the cold clouds in the Aquila rift. However, the Aquila rift is a very large and complicated region containing multiple clouds at a range of distances. Recently, Lallement et al. [51] derived the 3D distribution of dust in the local ISM, which shows that much of the high-latitude dust shells towards the NPS/Loop I is at a distance $<300$ pc. However, they also show that the dust and material in front of the X-ray emission associated with the NPS is at a distance of at 500–800 pc., thus placing the NPS itself at a distance of 800 pc or greater.

In summary, we can be fairly confident that Loop I is within ∼1 kpc of the Sun, but its precise distance and geometry are still sources of significant debate.

4. Discussion and Conclusions

The large-scale radio continuum sky has been mapped over a large range of radio/microwave frequencies and in intensity and polarization. The emission comes primarily from synchrotron radiation from cosmic ray electrons spiralling in the magnetic field with a contribution from free–free radiation from warm ionized gas. The Galactic plane is a strong emitter of both radiations and follows high-mass star formation, which are responsible for supernovae that accelerate electrons to relativistic energies and for UV photons that ionize the gas. However, the radio/microwave sky away from the plane is dominated by large loops and filaments, which are not visible at other wavelengths.

Four large loops (I–IV) have long been known while new polarization data from WMAP/Planck show an even more complex picture of filaments, arcs and spurs. The loops approximately follow small circles on the sky, which suggest expanding shells. However, these are not exact. The high level of polarization suggests well-ordered B-fields and the polarization angles suggest B-fields that are parallel to the ridge lines. The preferred explanation for the loops are expanding supernova remnant shells from successive supernovae activity, which hit dense interstellar gas, trapping the CR electrons and compressing the B-field. This naturally explains the bright synchrotron ridge of emission, as well as the polarization angles. A simple model for Loop I, placing it at a distance of ∼100–200 pc with a similar diameter, can reproduce much of the large-scale geometry of polarization angles. Furthermore, comparison with optical starlight absorption suggests a distance $<300$ pc. We argue for this local distance based on numerous facts. Nevertheless, other arguments suggest a somewhat larger distance of several hundred parsecs, up to ∼kpc, which would increase the dimensions of the loop by a factor of several. We do not find strong evidence for an origin for Loop I at the Galactic Centre.

The radio sky also contains other large-scale curiosities such as the microwave haze that surrounds the GC. Its spectrum is consistent with a hard component of synchrotron radiation, which indicates a harder spectrum of CR electrons and little spectral ageing. It has been suggested that this is the radio counterpart to the Fermi Bubbles, which project from the Galactic Centre. However, their morphology is not the same and the haze is much less symmetric about the plane and therefore they are unlikely to be the same electrons. On the other hand, there is a narrow arc of polarized emission that does trace the outer boundary of the FBs almost exactly, both above and below the plane.

New large-scale radio surveys are becoming available, such as S-PASS at 2.3 GHz, C-BASS at 5 GHz and QUIJOTE at 11–19 GHz. These should provide a more detailed view of the diffuse Galactic radiation. Sensitive measurements covering a wide range of frequencies will allow the spectral index to be measured with good precision. This will be particularly important for cosmological studies of CMB polarization and the pursuit of detecting primordial B-modes, which would be a smoking-gun signature of inflation. Indeed, there are claims that CMB temperature anisotropies are still contaminated by synchrotron radiation from the loops [52,53]. In any case, the strongly polarized foregrounds from large-scale loops and spurs will need to be carefully removed for future sensitive CMB missions [1,54].

More sensitive $\gamma$-ray data will allow a more direct measurement of the CR energy spectrum, which when combined with radio synchrotron maps, should allow a more detailed study of the energetics and origin of the the large high-latitude radio structures in the sky. This will also be important for understanding the large-scale Galactic magnetic field (e.g., [55]), where synchrotron data provide the projected angle of the B-field. However, large local structures must be modelled first.