Parameter Estimation of Weibull Distribution Using Constrained Search Space: An Application to Elevator Maintenance
Abstract
1. Introduction
2. Motivation and Problem Formulation
Proposed Solution
3. Multidimensional Particle Swarm Optimization for 3-p Weibull Distribution
4. Formulation of Constrained Search Space Partitioning (CSSP)
Constrained Search Space Partitioning with Randomness Operator
- 1.
- 2.
- 3.
- 4.
- 5.
- Determine the randomness operator iteration number max iteration, .
- 6.
- 7.
- 8.
- If termination criterion reached, print results.
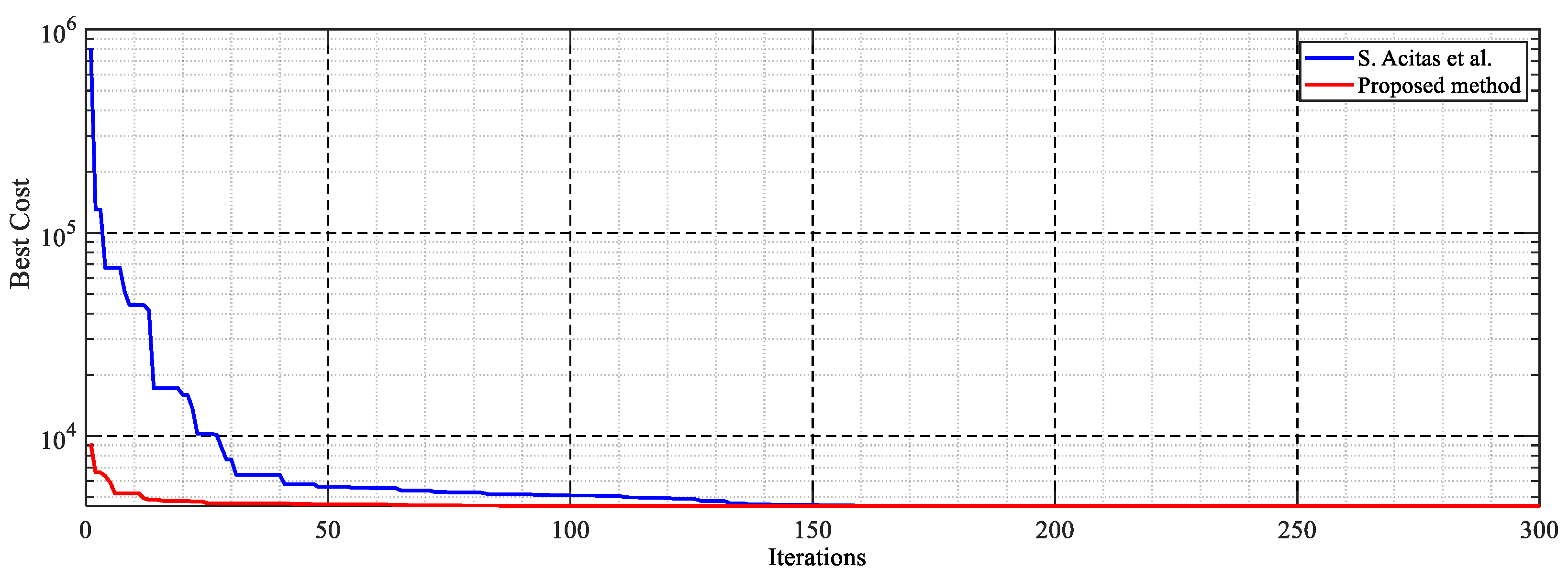
5. Results and Discussion
5.1. Experimental Results
5.2. Parameter Estimation Using CSSP

6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fernandez, J.R.; Cortes, P. A Survey of Elevator Group Control Systems for Vertical Transportation: A Look at Recent Literature. IEEE Control Syst. Mag. 2015, 35, 38–55. [Google Scholar] [CrossRef]
- Yazdi, M. Maintenance strategies and optimization techniques. In Advances in Computational Mathematics for Industrial System Reliability and Maintainability; Springer: Cham, Switzerland, 2024; pp. 43–58. [Google Scholar]
- Eti, M.; Ogaji, S.; Probert, S. Integrating reliability, availability, maintainability and supportability with risk analysis for improved operation of the Afam thermal power-station. Appl. Energy 2007, 84, 202–221. [Google Scholar] [CrossRef]
- Al-Duais, F.S.; Mohamed, A.B.; Jawa, T.M.; Sayed-Ahmed, N. Optimal periods of conducting preventive maintenance to reduce expected downtime and its impact on improving reliability. Comput. Intell. Neurosci. 2022, 2022, 7105526. [Google Scholar] [CrossRef] [PubMed]
- Tao, G.; Liu, Z.; Ji, C.; Yang, G. Establishment and Analysis of Load Spectrum for Bogie Frame of High-Speed Train at 400 km/h Speed Level. Machines 2024, 12, 382. [Google Scholar] [CrossRef]
- Bracke, S. Preventive maintenance planning based on Weibull distribution models: The impact of the random scatter behaviour of the threshold parameter. IFAC-PapersOnLine 2020, 53, 161–166. [Google Scholar] [CrossRef]
- Kovacs, K.; Ansari, F.; Sihn, W. A modified Weibull model for service life prediction and spare parts forecast in heat treatment industry. Procedia Manuf. 2021, 54, 172–177. [Google Scholar] [CrossRef]
- Oke, A.O.; Abafi, J.A.; Adewole, B.Z. Failure data analysis for preventive maintenance scheduling of a bottling company production system. J. Ind. Eng. Manag. Stud. 2021, 8, 32–44. [Google Scholar]
- Wang, W.; Qin, C.; Zhang, J.; Wen, C.; Xu, G. Correlation analysis of three-parameter Weibull distribution parameters with wind energy characteristics in a semi-urban environment. Energy Rep. 2022, 8, 8480–8498. [Google Scholar] [CrossRef]
- Wu, S.; Clements-Croome, D. Optimal maintenance policies under different operational schedules. IEEE Trans. Reliab. 2005, 54, 338–346. [Google Scholar] [CrossRef]
- Duan, C.; Deng, C.; Gong, Q.; Wang, Y. Optimal failure mode-based preventive maintenance scheduling for a complex mechanical device. Int. J. Adv. Manuf. Technol. 2018, 95, 2717–2728. [Google Scholar] [CrossRef]
- Chien, Y.H.; Zhang, Z.G.; Yin, X. On optimal preventive-maintenance policy for generalized Polya process repairable products under free-repair warranty. Eur. J. Oper. Res. 2019, 279, 68–78. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, J.; Wang, S.; Chang, Y.; Jia, M. Fault Prediction and Maintenance of Non-Periodic Incipient Fault for Hydraulic Tube Tester. Asian J. Control 2014, 16, 1670–1678. [Google Scholar] [CrossRef]
- Rivera Torres, P.J.; Serrano Mercado, E.I.; Llanes Santiago, O.; Anido Rifón, L. Modeling preventive maintenance of manufacturing processes with probabilistic Boolean networks with interventions. J. Intell. Manuf. 2018, 29, 1941–1952. [Google Scholar] [CrossRef]
- Duan, C.; Deng, C.; Wang, B. Optimal multi-level condition-based maintenance policy for multi-unit systems under economic dependence. Int. J. Adv. Manuf. Technol. 2017, 91, 4299–4312. [Google Scholar] [CrossRef]
- Yang, L.; Ye, Z.S.; Lee, C.G.; Yang, S.F.; Peng, R. A two-phase preventive maintenance policy considering imperfect repair and postponed replacement. Eur. J. Oper. Res. 2019, 274, 966–977. [Google Scholar] [CrossRef]
- Gouiaa-Mtibaa, A.; Dellagi, S.; Achour, Z.; Erray, W. Integrated Maintenance-Quality policy with rework process under improved imperfect preventive maintenance. Reliab. Eng. Syst. Saf. 2018, 173, 1–11. [Google Scholar] [CrossRef]
- Godoy, D.R.; Álvarez, V.; Mena, R.; Viveros, P.; Kristjanpoller, F. Adopting New Machine Learning Approaches on Cox’s Partial Likelihood Parameter Estimation for Predictive Maintenance Decisions. Machines 2024, 12, 60. [Google Scholar] [CrossRef]
- Huang, X.; Wang, Y.; Mao, Y. Establishment and Solution Test of Wear Prediction Model Based on Particle Swarm Optimization Least Squares Support Vector Machine. Machines 2025, 13, 290. [Google Scholar] [CrossRef]
- Alptekin, B.; Acitas, S.; Senoglu, B.; Aladag, C.H. Statistical determination of significant particle swarm optimization parameters: The case of Weibull distribution. Soft Comput. 2022, 26, 12623–12634. [Google Scholar] [CrossRef]
- Douiri, M.R. Fine-tuning weibull distribution parameters in Morocco’s Tarfaya and Tangier wind farms using two-stage swarm optimization. Wind Eng. 2024, 49, 387–406. [Google Scholar] [CrossRef]
- Lu, Z.; Dong, L.; Zhou, J. Nonlinear least squares estimation for parameters of mixed Weibull distributions by using particle swarm optimization. IEEE Access 2019, 7, 60545–60554. [Google Scholar] [CrossRef]
- Niu, D.; Guo, L.; Bi, X.; Wen, D. Preventive maintenance period decision for elevator parts based on multi-objective optimization method. J. Build. Eng. 2021, 44, 102984. [Google Scholar] [CrossRef]
- Acitas, S.; Aladag, C.H.; Senoglu, B. A new approach for estimating the parameters of Weibull distribution via particle swarm optimization: An application to the strengths of glass fibre data. Reliab. Eng. Syst. Saf. 2019, 183, 116–127. [Google Scholar] [CrossRef]
- Kennedy, J.; Mendes, R. Neighborhood topologies in fully informed and best-of-neighborhood particle swarms. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2006, 36, 515–519. [Google Scholar] [CrossRef]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]



| Symbol | Meaning | Symbol | Meaning |
|---|---|---|---|
| Location parameter (minimum life/failure-free period) | Scale parameter (characteristic lifetime) | ||
| Shape parameter (: early failures, : wear-out) | Random variable (time-to-failure) | ||
| Cumulative distribution function (CDF) | Probability density function (PDF) | ||
| Failure rate function (hazard rate) | L | Likelihood function | |
| Log-likelihood function | n | Sample size (failure observations) | |
| Standardized variable: | Position of particle i at iteration k | ||
| Velocity of particle i at iteration k | Personal best position of particle i | ||
| Global best swarm position | Inertia weight (momentum control) | ||
| Acceleration coefficients | Random numbers | ||
| Number of particles in swarm | Segments per dimension in CSSP | ||
| Stagnation threshold (iterations) | Randomness operator | ||
| Q | Quadrant index matrix | Constrained search space range | |
| Significance level | Upper normal quantile | ||
| MEAN | Mean absolute error | MSE | Mean squared error |
| DEF | Total deficiency (summed MSE) |
| Part Name | Test Duration (Days) | Number of Failure | Failure Rate |
|---|---|---|---|
| Brake | 600 | 109 | 18.167 |
| Traction Wheel | 600 | 112 | 18.667 |
| Rope | 600 | 77 | 12.833 |
| Motor | 600 | 61 | 10.167 |
| Door | 600 | 47 | 7.833 |
| n | Algorithm | Error Type | μ | η | β |
|---|---|---|---|---|---|
| 10 | Proposed method | MEAN | 1.8989 | 2.6265 | 4.0069 |
| MSE | 3.7651 | 3.905 | 5.198 | ||
| DEF | 12.8681 | ||||
| Acitas et al. | MEAN | 2.3393 | 2.4442 | 3.6064 | |
| MSE | 2.04922 | 1.7834 | 10.7942 | ||
| DEF | 14.6269 | ||||
| DE | MEAN | 2.164746 | 2.915415 | 4.327452 | |
| MSE | 3.915704 | 4.0612 | 5.56186 | ||
| DEF | 13.538764 | ||||
| PSO | MEAN | 58.8706 | 44.4998 | 39.991 | |
| MSE | 4639.5832 | 2887.5192 | 2435.5931 | ||
| DEF | 9962.6957 | ||||
| 20 | Proposed method | MEAN | 2.1401 | 2.3544 | 3.0397 |
| MSE | 1.3195 | 1.3544 | 3.8963 | ||
| DEF | 6.5702 | ||||
| Acitas et al. | MEAN | 2.7564 | 1.9267 | 1.3273 | |
| MSE | 1.4991 | 1.1385 | 6.8622 | ||
| DEF | 9.4992 | ||||
| DE | MEAN | 2.418313 | 2.684016 | 3.434861 | |
| MSE | 1.50423 | 1.787808 | 4.246967 | ||
| DEF | 7.539005 | ||||
| PSO | MEAN | 56.4574 | 43.3023 | 38.279 | |
| MSE | 4416.6667 | 2899.3836 | 2529.4298 | ||
| DEF | 9845.4802 | ||||
| 40 | Proposed method | MEAN | 2.15926 | 2.4683 | 2.321 |
| MSE | 1.0846 | 0.7658 | 3.2055 | ||
| DEF | 5.0559 | ||||
| Acitas et al. | MEAN | 2.4119 | 1.6082 | 2.4794 | |
| MSE | 1.1001 | 1.3097 | 4.9838 | ||
| DEF | 7.3937 | ||||
| DE | MEAN | 2.4399638 | 2.838545 | 2.71557 | |
| MSE | 1.258136 | 1.010856 | 3.59016 | ||
| DEF | 5.859152 | ||||
| PSO | MEAN | 58.4164 | 41.0697 | 40.4069 | |
| MSE | 4491.6681 | 2727.8891 | 2498.151 | ||
| DEF | 9717.7067 | ||||
| 60 | Proposed method | MEAN | 2.2205 | 2.3291 | 2.8186 |
| MSE | 0.5595 | 0.367 | 1.1606 | ||
| DEF | 2.0871 | ||||
| Acitas et al. | MEAN | 2.5751 | 1.3057 | 0.9266 | |
| MSE | 1.1606 | 1.1584 | 2.9552 | ||
| DEF | 5.2743 | ||||
| DE | MEAN | 2.5335905 | 2.678465 | 3.297762 | |
| MSE | 0.7726695 | 0.567015 | 1.56681 | ||
| DEF | 2.9064945 | ||||
| PSO | MEAN | 57.5789 | 42.1976 | 38.8488 | |
| MSE | 4437.5001 | 2758.0893 | 2587.6732 | ||
| DEF | 9783.2626 | ||||
| 80 | Proposed method | MEAN | 2.0673 | 2.6265 | 2.2383 |
| MSE | 0.297 | 0.1518 | 0.1105 | ||
| DEF | 0.5593 | ||||
| Acitas et al. | MEAN | 2.5751 | 1.5167 | 0.6511 | |
| MSE | 1.1848 | 1.1226 | 3.4812 | ||
| DEF | 5.7886 | ||||
| DE | MEAN | 2.3670585 | 3.598305 | 2.999322 | |
| MSE | 0.380457 | 0.249711 | 0.182325 | ||
| DEF | 0.812493 | ||||
| PSO | MEAN | 57.9621 | 44.8488 | 37.5116 | |
| MSE | 4522.9166 | 3096.7642 | 2551.0015 | ||
| DEF | 10,170.6824 | ||||
| 100 | Proposed method | MEAN | 2.2013 | 2.3544 | 1.934 |
| MSE | 0.2625 | 0.03797 | 0.0552 | ||
| DEF | 0.3556 | ||||
| Acitas et al. | MEAN | 2.5509 | 1.2778 | 0.4007 | |
| MSE | 0.8341 | 0.7802 | 2.3542 | ||
| DEF | 3.9686 | ||||
| DE | MEAN | 2.5204885 | 3.225528 | 2.59156 | |
| MSE | 0.4675125 | 0.07385165 | 0.14628 | ||
| DEF | 0.68764415 | ||||
| PSO | MEAN | 61.3691 | 43.6046 | 38.8604 | |
| MSE | 4834.3749 | 2824.9614 | 2428.0431 | ||
| DEF | 10,087.37959 |
| n | Algorithm | Error Type | μ | η | β |
|---|---|---|---|---|---|
| 10 | Proposed method | MEAN | 2.373625 | 3.283125 | 4.648004 |
| MSE | 4.555771 | 4.41265 | 5.40592 | ||
| DEF | 14.374341 | ||||
| Acitas et al. | MEAN | 2.830553 | 3.030808 | 4.544064 | |
| MSE | 2.7049704 | 2.443258 | 15.11188 | ||
| DEF | 20.2601084 | ||||
| DE | MEAN | 2.79252234 | 3.7317312 | 5.23621692 | |
| MSE | 5.023848232 | 4.914052 | 6.8967064 | ||
| DEF | 16.83460663 | ||||
| PSO | MEAN | 77.120486 | 53.844758 | 50.828561 | |
| MSE | 5767.001918 | 3667.149384 | 3134.60832 | ||
| DEF | 12,568.75962 | ||||
| 20 | Proposed method | MEAN | 2.675125 | 2.943 | 3.526052 |
| MSE | 1.596595 | 1.530472 | 4.052152 | ||
| DEF | 7.179219 | ||||
| Acitas et al. | MEAN | 3.335244 | 2.389108 | 1.672398 | |
| MSE | 1.978812 | 1.559745 | 9.60708 | ||
| DEF | 13.145637 | ||||
| DE | MEAN | 3.11962377 | 3.43554048 | 4.15618181 | |
| MSE | 1.92992709 | 2.16324768 | 5.26623908 | ||
| DEF | 9.35941385 | ||||
| PSO | MEAN | 73.959194 | 52.395783 | 48.652609 | |
| MSE | 5489.916708 | 3682.217172 | 3255.376153 | ||
| DEF | 12,427.51003 | ||||
| 40 | Proposed method | MEAN | 2.699075 | 3.085375 | 2.69236 |
| MSE | 1.312366 | 0.865354 | 3.33372 | ||
| DEF | 5.51144 | ||||
| Acitas et al. | MEAN | 2.918399 | 1.994168 | 3.124044 | |
| MSE | 1.452132 | 1.794289 | 6.97732 | ||
| DEF | 10.223741 | ||||
| DE | MEAN | 3.147553302 | 3.6333376 | 3.2858397 | |
| MSE | 1.614188488 | 1.22313576 | 4.4517984 | ||
| DEF | 7.289122648 | ||||
| PSO | MEAN | 76.525484 | 49.694337 | 51.3571699 | |
| MSE | 5583.143448 | 3464.419157 | 3215.120337 | ||
| DEF | 12,262.68294 | ||||
| 60 | Proposed method | MEAN | 2.775625 | 2.911375 | 3.269576 |
| MSE | 0.676995 | 0.41471 | 1.207024 | ||
| DEF | 2.298729 | ||||
| Acitas et al. | MEAN | 3.115871 | 1.619068 | 1.167516 | |
| MSE | 1.531992 | 1.587008 | 4.13728 | ||
| DEF | 7.25628 | ||||
| DE | MEAN | 3.268331745 | 3.4284352 | 3.99029202 | |
| MSE | 0.991334969 | 0.68608815 | 1.9428444 | ||
| DEF | 3.620267519 | ||||
| PSO | MEAN | 75.428359 | 51.059096 | 49.3768248 | |
| MSE | 5515.812624 | 3502.773411 | 3330.335408 | ||
| DEF | 12,348.92144 | ||||
| 80 | Proposed method | MEAN | 2.584125 | 3.283125 | 2.596428 |
| MSE | 0.35937 | 0.171534 | 0.11492 | ||
| DEF | 0.645824 | ||||
| Acitas et al. | MEAN | 3.115871 | 1.880708 | 0.820386 | |
| MSE | 1.563936 | 1.537962 | 4.87368 | ||
| DEF | 7.975578 | ||||
| DE | MEAN | 3.053505465 | 4.6058304 | 3.62917962 | |
| MSE | 0.488126331 | 0.30215031 | 0.226083 | ||
| DEF | 1.016359641 | ||||
| PSO | MEAN | 75.930351 | 54.267048 | 47.6772436 | |
| MSE | 5621.985334 | 3932.890534 | 3283.138931 | ||
| DEF | 12,838.0148 | ||||
| 100 | Proposed method | MEAN | 2.751625 | 2.943 | 2.24344 |
| MSE | 0.317625 | 0.0429061 | 0.057408 | ||
| DEF | 0.4179391 | ||||
| Acitas et al. | MEAN | 3.086589 | 1.584472 | 0.504882 | |
| MSE | 1.101012 | 1.068874 | 3.29588 | ||
| DEF | 5.465766 | ||||
| DE | MEAN | 3.251430165 | 4.12867584 | 3.1357876 | |
| MSE | 0.599818538 | 0.089360497 | 0.1813872 | ||
| DEF | 0.870566234 | ||||
| PSO | MEAN | 80.393521 | 52.761566 | 49.3915684 | |
| MSE | 6009.128001 | 3587.700978 | 3124.89147 | ||
| DEF | 12,721.72045 |
| n | Algorithm | Error Type | μ | η | β |
|---|---|---|---|---|---|
| 10 | Proposed method | MEAN | 1.9402 | 2.0013 | 3.4992 |
| MSE | 2.5944 | 2.8249 | 2.7409 | ||
| DEF | 8.1603 | ||||
| Acitas et al. | MEAN | 2.5087 | 2.6498 | 3.8317 | |
| MSE | 2.0601 | 1.944 | 11.7757 | ||
| DEF | 15.7798 | ||||
| DE | MEAN | 2.211828 | 2.221443 | 3.779136 | |
| MSE | 3.735936 | 3.502876 | 3.206853 | ||
| DEF | 10.445665 | ||||
| PSO | MEAN | 60.6616 | 85.5185 | 93.1852 | |
| MSE | 4592.5037 | 4639.991 | 5140.7553 | ||
| DEF | 14,373.2491 | ||||
| 20 | Proposed method | MEAN | 2.0284 | 1.9492 | 4.8341 |
| MSE | 0.7004 | 0.8568 | 2.1958 | ||
| DEF | 3.7531 | ||||
| Acitas et al. | MEAN | 3.0071 | 2.3225 | 2.7476 | |
| MSE | 2.0601 | 1.4826 | 9.4018 | ||
| DEF | 12.9446 | ||||
| DE | MEAN | 2.292092 | 2.222088 | 5.462533 | |
| MSE | 0.868496 | 1.130976 | 2.832582 | ||
| DEF | 4.832054 | ||||
| PSO | MEAN | 58.7866 | 92.2604 | 86.037 | |
| MSE | 4418.5906 | 3820.2226 | 4361.1613 | ||
| DEF | 12.9446 | 12.9446 | |||
| 40 | Proposed method | MEAN | 2.1044 | 1.8785 | 2.4723 |
| MSE | 0.2165 | 0.3375 | 1.7614 | ||
| DEF | 2.3155 | ||||
| Acitas et al. | MEAN | 3.1843 | 2.0031 | 2.4672 | |
| MSE | 1.4287 | 1.317 | 8.3177 | ||
| DEF | 11.0635 | ||||
| DE | MEAN | 2.377972 | 2.160275 | 2.892591 | |
| MSE | 0.27279 | 0.4455 | 1.972768 | ||
| DEF | 2.691058 | ||||
| PSO | MEAN | 59.4133 | 88.2604 | 83.7037 | |
| MSE | 4483.3583 | 4605.1063 | 5182.0896 | ||
| DEF | 14,270.5543 | ||||
| 60 | Proposed method | MEAN | 2.1187 | 1.8264 | 1.6113 |
| MSE | 0.0506 | 0.0571 | 1.2796 | ||
| DEF | 1.3874 | ||||
| Acitas et al. | MEAN | 3.4113 | 1.8257 | 3.271 | |
| MSE | 1.4509 | 1.3188 | 6.8785 | ||
| DEF | 9.6483 | ||||
| DE | MEAN | 2.4174367 | 2.10036 | 1.885221 | |
| MSE | 0.0698786 | 0.0882195 | 1.72746 | ||
| DEF | 1.8855581 | ||||
| PSO | MEAN | 60.1198 | 82.5938 | 86.7407 | |
| MSE | 4686.0569 | 4888.5365 | 5422.4748 | ||
| DEF | 14,997.0683 | ||||
| 80 | Proposed method | MEAN | 2.1107 | 1.7955 | 1.0347 |
| MSE | 0.0092 | 0.0311 | 3.1437 | ||
| DEF | 3.1841 | ||||
| Acitas et al. | MEAN | 3.4501 | 1.7074 | 4.0186 | |
| MSE | 1.5783 | 1.037 | 7.7383 | ||
| DEF | 10.3537 | ||||
| DE | MEAN | 2.4167515 | 2.459835 | 1.386498 | |
| MSE | 0.0117852 | 0.0511595 | 5.187105 | ||
| DEF | 5.2500497 | ||||
| PSO | MEAN | 57.16 | 93.5185 | 93.074 | |
| MSE | 4714.8425 | 5019.3505 | 5596.274 | ||
| DEF | 15,330.46716 | ||||
| 100 | Proposed method | MEAN | 2.0009 | 1.8887 | 0.387 |
| MSE | 0.0276 | 0.0103 | 0.5371 | ||
| DEF | 0.5751 | ||||
| Acitas et al. | MEAN | 3.5941 | 1.873 | 5.0841 | |
| MSE | 1.8607 | 1.4747 | 8.9158 | ||
| DEF | 12.2514 | ||||
| DE | MEAN | 2.2910305 | 2.587519 | 0.51858 | |
| MSE | 0.0491556 | 0.0200335 | 1.423315 | ||
| DEF | 1.4925041 | ||||
| PSO | MEAN | 61.8933 | 96.037 | 87.8148 | |
| MSE | 4837.1814 | 4757.7226 | 5315.5501 | ||
| DEF | 14,910.454 |
| Part Name | Location μ | Scale η | Shape β |
|---|---|---|---|
| Brake | 3.702 | 401.18 | 1.054 |
| Traction Wheel | 3.3701 | 374.461 | 0.7625 |
| Rope | 2.651 | 291.471 | 0.8133 |
| Motor | 2.518 | 316.382 | 0.9167 |
| Car Door | 2.831 | 297.641 | 0.839 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmed, K.; Liu, H.; Ke, L.; Mushtaq, R.T.; Zaman, M.; Akhunzada, A. Parameter Estimation of Weibull Distribution Using Constrained Search Space: An Application to Elevator Maintenance. Machines 2025, 13, 1022. https://doi.org/10.3390/machines13111022
Ahmed K, Liu H, Ke L, Mushtaq RT, Zaman M, Akhunzada A. Parameter Estimation of Weibull Distribution Using Constrained Search Space: An Application to Elevator Maintenance. Machines. 2025; 13(11):1022. https://doi.org/10.3390/machines13111022
Chicago/Turabian StyleAhmed, Khubab, Huaqing Liu, Li Ke, Ray Tahir Mushtaq, Muhammad Zaman, and Adnan Akhunzada. 2025. "Parameter Estimation of Weibull Distribution Using Constrained Search Space: An Application to Elevator Maintenance" Machines 13, no. 11: 1022. https://doi.org/10.3390/machines13111022
APA StyleAhmed, K., Liu, H., Ke, L., Mushtaq, R. T., Zaman, M., & Akhunzada, A. (2025). Parameter Estimation of Weibull Distribution Using Constrained Search Space: An Application to Elevator Maintenance. Machines, 13(11), 1022. https://doi.org/10.3390/machines13111022










