Abstract
If elastic elements are introduced into the mechanical architecture of a robotic manipulator, a free vibration response (Natural Motion) arises that can be exploited to reduce energy consumption in cyclic motions, such as pick-and-place tasks. In this work, this approach is applied to the RR-4R-R manipulator, which is derived from the SCARA robot by replacing the prismatic joint that drives the vertical motion of the end-effector with a four-bar mechanism. This mechanical modification lowers friction and facilitates the introduction of a balancing elastic element. If the elastic element is designed to provide indifferent equilibrium at any position (exact elastic balancing), the actuators need only to overcome the inertial forces; this approach is convenient for slow motions. Conversely, if the elastic element balances gravity exactly only in the median vertical position of the end-effector, Natural Motion around this position arises, and it can be exploited to reduce energy consumption in fast cyclic motions, where inertial forces become prevalent. The threshold of convenience between exact balancing and natural balancing has been evaluated for the RR-4R-R robot by means of a multibody model, assessing different performance indices: the maximum torque of the four-bar actuator, the integral control effort, and the mechanical energy. The simulation campaign was carried out considering different trajectory shapes and the influence of finite stop phases, highlighting the potential benefits of exploiting Natural Motion in robotized manufacturing lines.
1. Introduction
The reduction in energy consumption in robotized manufacturing lines plays a pivotal role in the global challenge of industrial sustainability. Industrial robots must move fast to reduce cycle times, but this results in a high energy demand to overcome the inertial forces acting on the links, since industrial robots are usually much heavier than their payloads. Consequently, improving the energy efficiency of industrial robots has become an essential research area. Some researchers have developed models to accurately estimate the energy consumption of robotized production lines [1,2], while others have designed innovative mechanical architectures that combine high speed with high efficiency [3,4]. Another approach to reducing energy consumption involves optimizing motion planning under given productivity constraints [5].
There are many possible approaches to reducing energy consumption in robotics. Energy-saving methods in robotics can be classified as hardware, software, and mixed methods, as outlined in [6].
Hardware approaches focus on the development of innovative mechanical and electrical solutions. From the mechanical perspective, efficiency improvements can be achieved through innovations in functional or structural design. The synthesis and comparison of mechanical architectures have been extensively discussed in the scientific literature over the past decades [7]. Recent advances in mechanism comparison have focused on balanced mechanisms [8] and parallel architectures [9,10]. Lightweight construction technologies can be employed to reduce the mass of the manipulator’s mechanical structure; however, this introduces flexibility, which must be properly accounted for [11]. From the electrical perspective, regenerative actuators and power storage systems (PSS) can be combined, as proposed in [12].
Conversely, software methods optimize the robot motion independently of the mechanical and electrical architecture. For example, the proper use of spline interpolants defined by a sequence of via-points can significantly reduce the energy required to perform a task under given cycle time constraints [13]. Several methods have also been proposed to synthesize path-constrained trajectories without relying on complex optimization routines [14].
Finally, mixed methods refine hardware and software aspects simultaneously, obtaining the best results. Within the category of mixed methods, a promising approach is based on the exploitation of the robot’s Natural Motion. In the early 1980s, D. Koditschek defined Natural Motion as the concurrent use of dynamic models and appropriate control strategies to align with the internal dynamics of the robot, thereby achieving higher performance with less control effort [15]. In [16], a more specific definition of Natural Motion is proposed: a system response resulting from the conversion of potential elastic energy into kinetic energy. To store potential elastic energy, elastic balancing elements must be added to the robot structure, placed either in series or in parallel with the actuators, thus giving rise to an oscillatory free response. Flexure joints are sometimes employed in robotics to prevent stick-slip phenomena and to improve positioning accuracy [17,18]; in such cases, the same component can serve the dual function of a joint and an elastic element.
In the absence of friction, the oscillatory Natural Motion is undamped and theoretically perpetual. In practice, frictional phenomena are always present in real systems, so the free oscillations caused by nonzero initial conditions decrease over time. Nevertheless, even under real conditions, Natural Motion can be maintained by compensating for the energy dissipation due to friction through the actuators, and the required energy consumption is minimal near resonance. This condition can be profitably exploited when the robot task can be performed with a motion that is similar to the Natural Motion, at least in some phases. To obtain a match between the desired motion and the natural dynamics, the system can be modified through changes in mass and/or stiffness parameters [19,20]. The use of the natural modes of oscillation for efficient performance of complex tasks of a robot with variable parameters and dynamically coupled degrees of freedom is discussed in [21].
In the scientific literature, several approaches have been proposed to exploit the Natural Motion of both serial [22] and parallel robots [23,24], aligning their free vibration response with the task demands. In [22], a compliant actuation concept called series-parallel elastic actuation (SPEA) is proposed. This approach employs multiple dephased, mutilated gears with locking rings and plates, functioning as intermittent mechanisms connected in parallel to the motor; as a result, the motor torque requirements are reduced. In [23], an energy-saving methodology is proposed and experimentally validated on a two-degree-of-freedom Delta-2 robot performing cyclic pick-and-place operations along a predefined trajectory. In [24], a method for determining appropriate spring parameters and the optimal trajectory is introduced and applied to a resonant Delta robot.
Some methods start from predefined trajectories, after which the stiffness of the elastic elements is tuned accordingly. In [25], this approach is applied to the design of highly energy-efficient 2-DOF palletizing robots equipped with variable-stiffness elastic mechanisms that adjust the elasticity of each joint.
Other methods concurrently optimize trajectories and stiffness parameters. For example, a concept for the design and control of energy-saving robots is proposed in [26], based on the use of springs and reaction wheels, through the simultaneous optimization of spring parameters and trajectories with respect to the energy consumption.
Finally, periodic trajectory learning can be used to align the forced response with the system’s resonance. In [27], an adaptive natural oscillator (ANO) is proposed and used to exploit the natural dynamics of a given robotic system. This tool can serve as a pattern generator in robotic applications such as locomotion systems or compliant robotic manipulators performing cyclic tasks.
Predefined trajectory methods are indeed simpler, but they often assume a harmonic response, which is only an approximation of the actual nonlinear free-vibration behavior of the robot. By simultaneously optimizing the trajectory and stiffness parameters, or through the use of trajectory learning techniques, it is possible to achieve greater reductions in energy consumption. However, the application of these methods is challenging for highly nonlinear and dynamically coupled robotic systems.
The first step in the design of a manipulator that exploits Natural Motion is the mechanical conception in terms of joint layout and the placement of elastic elements. A suitable candidate for the Natural Motion approach is the RR-4R-R manipulator, proposed in [28], whose mobility and workspace are very similar to those of the industrially widespread SCARA robot. 4-DOF SCARA robots are particularly suitable for performing tasks that do not require complete 6-DOF mobility but only the so-called Schoenflies motion, characterized by three translations and one rotation about the vertical axis. Consequently, SCARA robots are widely applied in industry, for example, in pick-and-place tasks. The exploitation of the Natural Motion of the RR-4R-R manipulator equipped with a torsional spring for elastic gravity balancing was proposed in [29]. In this paper, the results are extended to consider the influence of finite stop phases, different trajectory types and parameters, and using various performance indices to assess energy efficiency not only under resonance conditions.
2. Mechanical Architecture and Elastic Balancing of the RR-4R-R Robot
The RR-4R-R robot architecture (Figure 1) was proposed in [28]. It is derived from the RRPR SCARA robot by replacing the vertical prismatic joint with a four-bar parallelogram mechanism lying in the vertical plane, which provides the end-effector’s vertical motion. The vector of internal coordinates consists of the four joint angles of the actuators, J1…J4 (θ1…θ4, Figure 1). The vector of the external coordinates consists of the x, y, and z coordinates of the end-effector point E and the end-effector rotation θ about the vertical axis (Figure 1). The kinematics and dynamics of the RR-4R-R architecture are discussed in [28]. The main advantage of this robot compared to the SCARA is the elimination of the prismatic joint, which introduces significantly more friction than revolute joints, even when linear ball bearings are used [30].
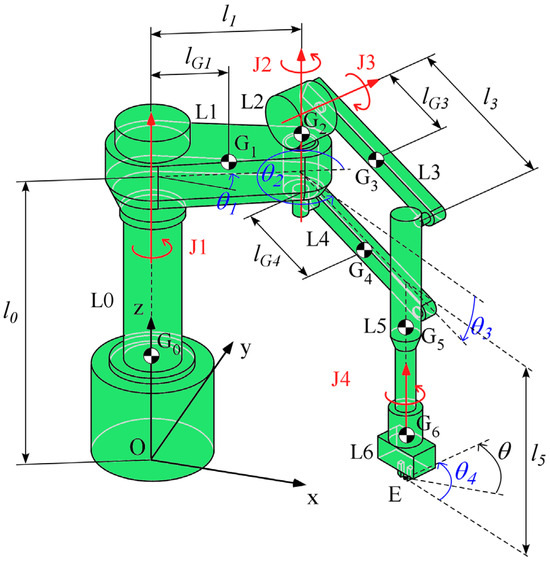
Figure 1.
Scheme of the RR-4R-R robot.
Observing the RR-4R-R architecture, it is evident that the actuators J1, J2, and J4, which drive revolute joints with vertical axes, are not affected by gravitational loads. Conversely, the actuator J3 is subject to gravity, but it can be balanced either by counterweights (mass balancing) or by elastic elements (elastic balancing). Since high-speed motions are necessary to reduce cycle time, mass balancing is excluded to avoid an increase in robot inertia. As for elastic balancing, two possible approaches can be adopted: Exact Balancing (EB) and Natural Balancing (NB). With Exact Balancing, the elastic elements provide indifferent equilibrium at all positions. Consequently, the gravitational force is exactly balanced in any static configuration, and the robot can remain motionless without energy consumption, but no Natural Motion arises. The exact balancing of a four-bar mechanism lying in a vertical plane can be obtained via a zero free-length spring [31]. Conversely, if a linear torsional spring is placed in parallel with actuator J3 in one of the four-bar joints, the robot is balanced only in one vertical position of the end-effector—for example, when links L3 and L4 are horizontal. Consequently, the robot requires power to remain motionless outside the balanced configuration, but Natural Motion arises with a natural period Tn (Natural Balancing). It is evident that EB is preferable for slow motions, close to quasi-static conditions, while NB becomes advantageous when Natural Motion is properly exploited to accomplish the required task. In the remainder of this work, the threshold of convenience between EB and NB is analyzed.
3. Natural Vertical Motion of the Four-Bar Mechanism with Torsional Spring
Figure 2 shows the schematic representation of the vertical four-bar mechanism, composed of the links L2 to L6. Let us consider the free vibration response of the four-bar in the vertical plane, keeping fixed the actuators J1, J2 and J4. Consequently, link L2 can be considered fixed, and links L5 and L6 can be considered as a single rigid body. According to the scheme in Figure 1, actuator J3 is located at the revolute joint R2 and exerts the torque τ3. In the case of Natural Balancing with a linear torsional spring, the most suitable location for the elastic element is at the revolute joint R1 below the actuator J3. Indeed, placing the torsional spring on the same joint as the actuator J3 would be more complex, while placing it on one of the revolute joints R3 or R4 would increase the moving masses of the four-bar, thus slowing down its dynamic response.

Figure 2.
Scheme of the four-bar mechanism.
The total mechanical energy E of the four-bar is the sum of the kinetic energy T, the potential elastic energy Ve, and the potential gravitational energy Vg:
In Equations (1)–(3), mi is the mass of the i-th link; I3 and I4 are the mass moments of inertia of links L3 and L4 with respect to the revolute joints R2 and R1; l3 is the length of links L3 and L4; lG3 and lG4 define the positions of the centers of mass of links L3 and L4 (Figure 2); and kts and θ3n are the stiffness and the neutral position of the linear torsional spring, respectively. In the case of negligible joint friction and in the absence of torque τ3, the dynamic equation of the free vibration response of the four-bar can be obtained by setting the time derivative of the total mechanical energy to zero:
Equation (4) refers to the natural frequency of an undamped system. When elastic elements are implemented, dissipative effects due to the material’s internal damping arise, slightly reducing the frequency of the natural response. However, this damping is typically very small and can be represented by a damping ratio of ζ < 0.05. For such values of ζ, the difference between the damped and undamped natural frequencies is less than 0.3% and can therefore be neglected. Once the robot mass parameters are defined, the equivalent moment of inertia Ieq can be calculated, and the spring stiffness kts can be determined to obtain a natural frequency ωn tuned to the required task. If the right-hand side of the differential Equation (4) is zero, the robot is in static equilibrium with horizontal links L3 and L4 (θ3 = 0), and the natural oscillations of the four-bar are centered around this configuration. This condition is favorable for maximally exploiting the robot’s workspace when the positive and negative mechanical limits of θ3 have the same absolute value. The neutral position of the torsional spring, θ3n, which is negative, can then be obtained by setting the constant term on the right-hand side of (4) to zero.
The differential Equation (4) defines a second-order undamped system, whose free vibration response is harmonic with angular frequency ωn. To exploit this motion for pick-and-place tasks, it is necessary to properly synchronize the vertical harmonic motion with a horizontal displacement of the end-effector. Suppose that the manipulator is statically balanced at θ3 = 0 and z0 = l0 − l5 is the vertical coordinate of the end-effector corresponding to this condition; consequently, the natural vertical oscillations of the end-effector along the vertical direction range from z0 − ht/2 to z0 + ht/2, where ht is the trajectory height (Figure 3). The departure and arrival points of the elementary trajectory shown in Figure 3 are, respectively, Pi = (xi, yi, z0 − ht/2) and Pf = (xf, yf, z0 − ht/2). Both these points lie on the horizontal plane z = z0 − ht/2, which corresponds to the robot’s working plane.

Figure 3.
Parabolic trajectory PiPf, which exploits natural motion.
The trajectory PiPf is expressed by the following laws:
The trajectory PiPf is performed along z with harmonic motion of period Tvert and along the horizontal direction with harmonic motion of period 2Tvert. By applying the trigonometric identity cos(2γ) = cos2(γ) − sin2(γ) to system (5), it is possible to demonstrate that the trajectory PiPf is a parabola lying in the vertical plane containing the points Pi and Pf and is defined by the following equation:
By deriving the motion law (5), it is easy to demonstrate that the end-effector velocity is zero at the initial and final points Pi and Pf. Considering frictionless robot joints, if a PiPf trajectory is imposed on the end-effector under resonance conditions—that is, with the vertical period Tvert equal to the natural period Tn = 2π/ωn—the torque of the actuator J3 to drive the end-effector’s vertical motion is low, but not zero, for the following reasons:
- a harmonic motion of θ3 corresponds to a harmonic motion of z only for small displacements;
- when the robot performs a general 4-DOF motion, there are inertial forces acting on links L3 to L6 that originate from the horizontal motion.
Consequently, the tuning of the parabolic trajectory PiPf with the free vibrational response of the four-bar is only approximated. However, this is compensated for by the torque of actuator J3, which overcomes the inertial forces related to the complex three-dimensional motion. The effectiveness of this approach will be assessed by simulation, as discussed in the following section.
4. Multibody Model
A dynamic model of the robot was implemented by means of the multibody environment Simscape MultibodyTM by MathWorks (Natick, MA, USA). The considered robot dimensions and inertial parameters are collected in Table 1. The mass moments of inertia of the links are calculated considering constant mass distribution along the links, and the joints are considered frictionless.

Table 1.
Geometric and inertial robot parameters.
In the following, two types of reference motion are considered, obtained by composing several parabolic trajectories defined according to Equation (5):
- Trajectory I, with a square projection in the xy plane; it is composed of 4 elementary parabolic motions, P1P2, P2P3, P3P4, and P4P1, performed only in the forward direction along the four positions characterized by the following external coordinates: P1 = [xA + lt, lt, zA, 0], P2 = [xA − lt, lt, zA, 0], P3 = [xA − lt, −lt, zA, 0], and P4 = [xA + lt, −lt, zA, 0]. The horizontal range of each elementary motion is dt = 2lt.
- Trajectory II, with a radial projection in the xy plane; it is composed of 12 elementary parabolic motions with horizontal range dt, performed forward and backward. The forward part of the elementary motion starts at position A, whose external coordinates are xA = l1cos45°+l3cos45°, yA = 0, zA = z0 − ht/2, θA = 0°, and ends at position Bi, whose external coordinates are xBi = xA + dtcosαi, yBi = dtsinαi, zBi = z0 − ht/2, θBi = 0°, with αi = iπ/6, i = 0…11. The backward part of the elementary motion starts at Bi and ends at A.
For both trajectories, the end-effector orientation θ is constantly equal to 0°, so the torque of the actuator J4 is null under the assumption of null joint friction.
In some applications, it is necessary to stop the robot end-effector for a finite time, for example, in pick-and-place operations, to ensure a correct grasp or release. While with EB the robot can remain motionless without power consumption in any position, with NB there is power consumption when the robot remains motionless with θ3 ≠ 0. Therefore, the presence of finite stop phases and their duration affect the threshold of convenience between EB and NB. To consider this effect, finite stop phases with duration Tstop between the elementary motions have been included.
In order to compare EB and NB, different performance indices have been used. The type of balancing (EB or NB) influences only the torque τ3 of the actuator J3, to which the balancing is applied. Therefore, a relevant performance index is the maximum absolute value of this torque (τ3,max).
Another useful index is the Integral Control Effort, which is calculated by the following expression:
where Tmot is the overall motion time and Pi is the mechanical power of the i-th actuator. This formulation considers, for the time integration, only the phases in which the mechanical power is positive or zero. In fact, most modern drivers can brake, exerting negative mechanical power, without electrical power consumption; consequently, this formulation provides a more accurate indication of the power consumption than the classical formulation of the ICE, in which σi is not present. Another considered index is the time integral of the mechanical power, Ep, calculated by considering in the time integration only the phases in which the mechanical power is positive or zero, similarly to ICEp:
where ωi is the angular velocity of the i-th actuator. The exact electrical energy consumption of the robot depends on the technology of the motor drivers and on the friction losses in the joints; therefore, its calculation is possible only after the detailed design phase. However, the combined use of the performance indices τ3,max, ICEp and Ep is adequate to compare the EB and NB approaches in the functional design phase.
5. Simulation Results
Let us compare EB, NB, and the absence of balancing (WB) in the case of trajectory I, with ht = 0.1 m, lt = 0.15 m, Tvert = 0.8 s, and no finite stop phase (Tstop = 0 s). For NB, the resonance condition is imposed by tuning the torsional spring stiffness kts to obtain Tn = Tvert; moreover, the neutral position of the torsional spring θ3n is set to obtain static equilibrium at θ3 = 0. Figure 4 shows the time histories of the torques of the first three actuators (as previously mentioned, τ4 is zero since the end-effector orientation remains constant and joint J4 is frictionless).

Figure 4.
Torques τ1…τ3 for trajectory I, ht = 0.1 m, lt = 0.15 m, Tvert = 0.8 s, and Tstop = 0 s, without balancing (WB), with exact balancing (EB), and with natural balancing (NB) in resonance condition (Tn = Tvert).
It is possible to see that, in the absence of balancing (WB), even though the first and second motors actuate a higher number of links, the maximum magnitudes of the torques τ1 and τ2 (13.3 and 3.8 Nm, respectively) are much smaller than that of τ3 (23 Nm), since actuator J3 is loaded by gravity. Conversely, with EB, the maximum magnitude of τ3 (5.4 Nm) becomes intermediate between those of τ1 and τ2. Finally, with NB in the resonance condition, the maximum magnitude of τ3 is significantly reduced (1.1 Nm).
Figure 5 shows the same comparison as in Figure 4, but in the presence of finite stop phases with a duration Tstop = 0.4 s after each elementary motion. With NB, since during the stop phases gravity balancing is not exact (θ3 ≠ 0), τ3 is not zero to keep the end-effector motionless; conversely, with EB, τ3 is zero during the stop phases. Considering the whole time history, the maximum values of τ3 are similar in the EB and NB cases, but τ3,max is reached with EB during the motion phases and with NB during the stop phases.
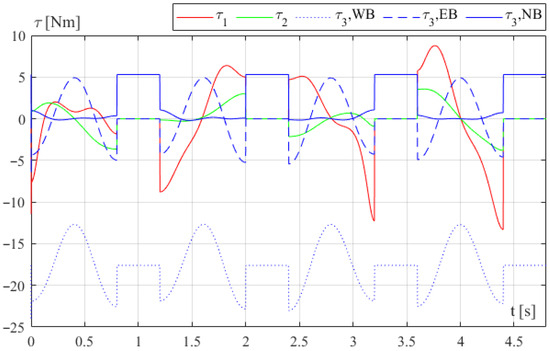
Figure 5.
Torques τ1…τ3 for trajectory I, ht = 0.1 m, lt = 0.15 m, Tvert = 0.8 s, and Tstop = 0.4 s, without balancing (WB), with exact balancing (EB), and with natural balancing (NB) in resonance condition (Tn = Tvert).
Figure 6 and Figure 7 show the same comparisons as Figure 4 and Figure 5, but for the radial trajectory II, with ht = 0.1 m, dt = 0.15 m, and Tvert = 0.8 s. For the NB case, the same spring parameters, kts and θ3n, are imposed to maintain the resonance condition Tn = Tvert. The simulation results in Figure 6 refer to the case without finite stop phases, while in Figure 7, a stop phase with a duration Tstop = 0.4 s is considered after each radial elementary motion with duration 2Tvert.

Figure 6.
Torques τ1…τ3 for trajectory II, ht = 0.1 m, dt = 0.15 m, Tvert = 0.8 s, and Tstop = 0 s, without balancing (WB), with exact balancing (EB), and with natural balancing (NB) in resonance condition (Tn = Tvert).

Figure 7.
Torques τ1…τ3 for trajectory II, ht = 0.1 m, dt = 0.15 m, Tvert = 0.8 s, and Tstop = 0.4 s, without balancing (WB), with exact balancing (EB), and with natural balancing (NB) in the resonance condition (Tn = Tvert).
For trajectory II, the results are qualitatively similar to those of trajectory I in terms of τ3,max for the cases WB, EB, and NB. As for the S trajectory, the values of τ3,max are similar in the EB and NB cases, but τ3,max is reached during the motion phases with EB and during the stop phases with NB.
To obtain a more general comparison of the convenience threshold between NB and EB, it is necessary to consider not only the resonance condition for various reasons. First of all, due to task requirements, sometimes the cycle time must be varied without accordingly tuning the elastic elements. In pick-and-place applications, the magnitude of the payload causes a variation in the vertical natural period Tn. Fortunately, the payload is only a portion of m6, the end-effector mass, so its influence on the equivalent inertia Ieq, and consequently on Tn, is limited (Equation (1)). Even if it is possible to adapt the cycle time according to the exact amount of payload and the corresponding natural period, it is preferable for the robot’s operational flexibility to have a balancing method that is effective not only strictly at resonance. Therefore, the comparison between NB and EB has been extended by performing patterns of simulations with variable Tn and Tvert, both with trajectory I and trajectory II. Moreover, since EB is advantageous with respect to NB in the stop phases, these patterns of simulations have also been performed in the presence of a nonzero Tstop.
The 3D graphs in Figure 8 show the performance indices τ3,max, ICEp and Ep as functions of Tn and Tvert, comparing NB and EB in the case of trajectory I, with the previously considered trajectory parameters and without finite stop phases. The 3D graphs in Figure 9 represent the same comparison but for trajectory II. In these graphs, the performance parameters are expressed in percentage ratios with respect to the same quantities in the absence of balancing (WB case). While the graphs for NB depend on both Tn and Tvert, the graphs for EB are independent of Tn, since natural motion is not present.

Figure 8.
Comparison of Exact Balancing (EB) and Natural Balancing (NB) in terms of maximum absolute values of τ3 (τ3,max), Integral Control Effort (ICEp), and Energy (Ep), for trajectory I, ht = 0.1 m, lt = 0.15 m, Tstop = 0 s; ratios with respect to the absence of balancing (WB).

Figure 9.
Comparison of Exact Balancing (EB) and Natural Balancing (NB) in terms of maximum absolute values of τ3 (τ3,max), Integral Control Effort (ICEp), and Energy (Ep), for trajectory II, ht = 0.1 m, dt = 0.15 m, Tstop = 0 s; ratios with respect to the absence of balancing (WB).
The 3D graphs in Figure 10 and Figure 11 refer to the results for the case of finite stop phases. Their duration, Tstop, is considered proportional to the displacement time, Tdisp, which is equal to Tvert for trajectory I and 2Tvert for trajectory II. Figure 10 and Figure 11 show the results for Tstop = 0.25Tdisp, respectively, for trajectories I and II.

Figure 10.
Comparison of Exact Balancing (EB) and Natural Balancing (NB) in terms of maximum absolute values of τ3 (τ3,max), Integral Control Effort (ICEp), and Energy (Ep), for trajectory I, ht = 0.1 m, lt = 0.15 m, Tstop = 0.25Tdisp; ratios with respect to the absence of balancing (WB).
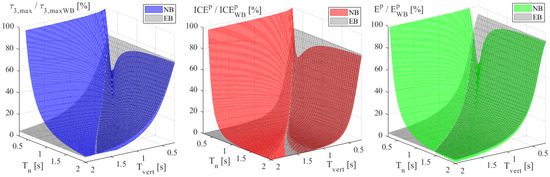
Figure 11.
Comparison of Exact Balancing (EB) and Natural Balancing (NB) in terms of maximum absolute values of τ3 (τ3,max), Integral Control Effort (ICEp), and Energy (Ep), for trajectory II, ht = 0.1 m, dt = 0.15 m, Tstop = 0.25Tdisp; ratios with respect to the absence of balancing (WB).
From the observation of Figure 8, Figure 9, Figure 10 and Figure 11, it is possible to outline the following results:
- For all the cases, the convenience thresholds between NB and EB are represented by the intersections of the NB and EB surfaces.
- As expected, EB is favorable for slow motions, that is, in the regions of the Tn-Tvert plane where Tvert is higher than Tn, tending toward quasi-static conditions, in which it is more important to have exact gravity balancing in all robot positions, while inertial forces are less relevant. Conversely, NB is particularly favorable close to the resonance condition (Tvert = Tn) and, in general, for fast motions, in the regions where Tvert is lower than Tn, and the benefits of the compensation of the inertial forces through natural motion become more significant than exact gravity compensation.
- It is possible to note that the presence of stop phases decreases the region of the Tn-Tvert plane in which NB is preferable in terms of lower τ3,max and ICEp. This occurs because the advantage of NB during the motion phases is partially reduced by its disadvantage during the stop phases. As regards Ep, it is not influenced by the stop phases, since no mechanical power is delivered by the actuators when velocity is zero.
- The convenience threshold between NB and EB is also influenced by the trajectory shape. Trajectory I is characterized by wider horizontal displacements; therefore, the maximum values of the torques τ1 and τ2 are higher, as observed in Figure 5 and Figure 6. This reduces the advantage of NB over EB in terms of ICEp and Ep, since the benefits of natural balancing are related only to the actuator J3, which drives the vertical motion. Conversely, the influence of the trajectory shape on τ3,max is minimal.
In order to analyze the performance indices under the resonance condition, the surfaces in Figure 8, Figure 9, Figure 10 and Figure 11 have been sectioned by vertical planes with Tvert = Tn, obtaining the curves represented in Figure 12 and Figure 13, respectively, referring to trajectories I and II. In Figure 12 and Figure 13, three durations of the stop phases are considered: Tstop = 0s, Tstop = 0.25Tdisp, and Tstop = 0.5Tdisp.

Figure 12.
Comparison of Exact Balancing (EB) and Natural Balancing (NB) in terms of maximum absolute values of τ3 (τ3,max), Integral Control Effort (ICEp), and Energy (Ep), for trajectory I in resonance condition (Tn = Tvert), ht = 0.1 m, lt = 0.15 m, for Tstop = 0 s (left), Tstop = 0.25Tdisp (center), and Tstop = 0.5Tdisp (right); ratios with respect to the absence of balancing (WB).

Figure 13.
Comparison of Exact Balancing (EB) and Natural Balancing (NB) in terms of maximum absolute values of τ3 (τ3,max), Integral Control Effort (ICEp), and Energy (Ep), for trajectory II in resonance condition (Tn = Tvert), ht = 0.1 m, dt = 0.15 m, for Tstop = 0 s (left), Tstop = 0.25Tdisp (center), and Tstop = 0.5Tdisp (right); ratios with respect to the absence of balancing (WB).
- For both trajectories, the advantage of NB in terms of ICEp is maximum when stop phases are absent (for Tvert = 0.25 s: 92.8% for EB and 63.0% for NB for trajectory I; 54.5% for EB and 19.1% for NB for trajectory II). For an intermediate duration of the stop phases (Tstop = 0.25Tdisp), the ICEp values of NB and EB are very similar, independently of Tvert and for both trajectories. When the duration of the stop phases is further increased (Tstop = 0.5Tdisp), EB becomes advantageous over NB (for Tvert = 0.25 s: 86.3% for EB and 120.3% for NB for trajectory I; 38.4% for EB and 68.5% for NB for trajectory II).
- Also for τ3,max, the advantage of NB is maximum in the absence of stop phases (for Tvert = 0.25 s: 75.9% for EB and 39.7% for NB for trajectory I; 57.4% for EB and 29.5% for NB for trajectory II). Once stop phases are introduced, τ3,max becomes very similar for NB and EB, independently of Tvert and for both trajectories. Moreover, it can be noted that, unlike ICEp, τ3,max is not influenced by Tstop, provided that it is nonzero, since the torque values remain constant during the stop phases.
- As already discussed, Ep does not depend on the presence or absence of stop phases, since no mechanical power is delivered when velocity is zero.
6. Conclusions
In this paper, the comparison between Exact Balancing and Natural Balancing for the RR-4R-R manipulator has been discussed, considering the influence of the trajectory shape and the duration of finite stop phases during task execution. A methodology for evaluating the convenience threshold between Exact Balancing and Natural Balancing, given the robot’s geometrical and inertial properties and the required application, has been outlined, based on three performance indices: the maximum torque τ3,max of the third actuator, which drives the vertical motion of the end-effector and can be gravity compensated by the Exact Balancing or Natural Balancing approaches; the Integral Control Effort (ICEp), calculated by considering only the phases in which the mechanical power delivered by the actuators is positive or null; and the mechanical energy (Ep), likewise calculated by considering only the phases in which the mechanical power is not negative.
These performance indices are independent of the specific architecture of actuators and drivers. To accurately estimate the robot’s electrical energy consumption, detailed knowledge of the electrical and electronic components is necessary. In fact, modern motors and drivers can deliver negative mechanical power (during braking phases) without consuming electrical power, or even regenerating a portion of that power. During stop phases, with Exact Balancing, the robot is in static equilibrium; conversely, with Natural Balancing, the third actuator must exert a torque if links L3 and L4 are not horizontal, delivering electrical power even if the mechanical power is null, unless a brake is activated. Nevertheless, the adoption of a motor brake on the third actuator (the remaining three are not loaded by gravity) is critical when the stop phases are short, as often occurs in typical pick-and-place tasks. Moreover, the electrical power required to activate and deactivate the brake is not negligible and must be considered.
For all these reasons, performance indices based solely on mechanical quantities have been applied, suitable for use in the functional design phase. The torque τ3,max provides an indication of motor sizing, which indirectly influences power consumption; in fact, the detailed design of the entire robot, and consequently the inertial properties of the links, also depend on the mass of motor J3. As regards energy consumption, Ep does not detect the electrical power delivered during the stop phases, unlike ICEp. In general, depending on the specific implementation of the actuation system, Ep or ICEp, or a combined use of both indices, can provide an accurate estimation of the robot’s electrical energy consumption.
Simulation results indicate that the application of the RR-4R-R manipulator in pick-and-place tasks characterized by 4-DOF Schoenflies motion, typically performed by SCARA robots, can significantly reduce electrical energy consumption if natural motion is properly exploited, thereby providing a significant contribution to sustainability in industrial manufacturing.
The limitations of the proposed approach are primarily related to the required end-effector trajectory. To fully exploit natural motion, the robot’s movements should be vertically centered with respect to the neutral end-effector position, where gravity is exactly compensated by the elastic element. However, in many pick-and-place and assembly tasks, this condition can be met by properly designing the operational environment and adjusting the neutral angle of the torsional spring.
To the best of the authors’ knowledge, there are currently no robot manufacturers that exploit Natural Motion in commercial products. Hopefully, given the growing emphasis on environmental sustainability, the proposed approach could potentially be considered in the future as a viable solution for reducing emissions associated with robotic production lines.
Author Contributions
Conceptualization, L.B.; methodology, L.B.; software, L.B.; validation, L.B., M.V. and P.F.; formal analysis, L.B.; writing—original draft preparation, L.B.; writing—review and editing, M.V.; supervision, P.F.; project administration, P.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
We thank all the authors for their support. The authors would like to thank all the reviewers who participated in this review.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| NB | Natural Balancing |
| EB | Exact Balancing |
| WB | Without Balancing |
References
- Yao, M.; Zhou, X.; Shao, Z.; Wang, L. A general energy modeling network for serial industrial robots integrating physical mechanism priors. Robot. Comput.-Integr. Manuf. 2024, 89, 102761. [Google Scholar] [CrossRef]
- Xu, C.; Zhang, H.L.; Lin, B. Achieving pollution abatement and carbon reduction synergistically: How can industrial robots play a role? J. Environ. Manag. 2025, 373, 123816. [Google Scholar] [CrossRef]
- Cao, W.-A.; Li, S.; Cheng, P.; Ding, H.; Lai, J. Design and development of a new 4 DOF hybrid robot with Scara motion for high-speed operations in large workspace. Mech. Mach. Theory 2024, 198, 105656. [Google Scholar] [CrossRef]
- Bruzzone, L.E.; Molfino, R.M.; Zoppi, M. An impedance-controlled parallel robot for high-speed assembly of white goods. Ind. Robot. 2005, 32, 226–233. [Google Scholar] [CrossRef]
- Lu, S.; Ding, B.; Li, Y. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv. Mech. Eng. 2020, 12, 1687814020913667. [Google Scholar] [CrossRef]
- Carabin, G.; Wehrle, E.; Vidoni, R. A review on energy-saving optimization methods for robotic and automatic systems. Robotics 2017, 6, 39. [Google Scholar] [CrossRef]
- Joskowicz, L. Mechanism comparison and classification for design. Res. Eng. Des. 1990, 1, 149–166. [Google Scholar] [CrossRef]
- Van der Wijk, V.; Herder, J.L.; Demeulenaere, B. Comparison of various dynamic balancing principles regarding additional mass and additional inertia. ASME J. Mech. Robot. 2009, 1, 041006. [Google Scholar] [CrossRef]
- Wu, H.; Liu, H.; Shan, X.; Yue, W. Comparison Study on the Motion/Force Transmissibility of Four 6-DOF Parallel Mechanisms. Chin. J. Mech. Eng. 2025, 38, 134. [Google Scholar] [CrossRef]
- Du, Z.; Li, J.; Meng, Q.; Ye, P.; Shen, H. Symbolic position analysis for three 6-DOF parallel mechanisms and new insight. Robotica 2024, 42, 1628–1648. [Google Scholar] [CrossRef]
- Boscariol, P.; Gallina, P.; Gasparetto, A.; Giovagnoni, M.; Scalera, L.; Vidoni, R. Evolution of a dynamic model for flexible multibody systems. In Advances in Italian Mechanism Science; Springer: Berlin, Germany, 2017; pp. 533–541. [Google Scholar]
- Inoue, K.; Ogata, K.; Kato, T. An efficient induction motor drive method with a regenerative power storage system driven by an optimal torque. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008. [Google Scholar]
- Boscariol, P.; Richiedei, D. Energy saving in redundant robotic cells: Optimal trajectory planning. In Proceedings of the 4th IFToMM Symposium on Mechanism Design for Robotics, Udine, Italy, 11–13 September 2018. [Google Scholar]
- Trigatti, G.; Boscariol, P.; Scalera, L.; Pillan, D.; Gasparetto, A. A new path-constrained trajectory planning strategy for spray painting robots-rev. 1. Int. J. Adv. Manuf. Technol. 2018, 98, 2287–2296. [Google Scholar] [CrossRef]
- Koditschek, D. Natural motion for robot arms. In Proceedings of the 23rd IEEE Conference on Decision and Control, Las Vegas, NV, USA, 12–14 December 1984. [Google Scholar]
- Scalera, L.; Palomba, I.; Wehrle, E.; Gasparetto, A.; Vidoni, R. Natural motion for energy saving in robotic and mechatronic systems. Appl. Sci. 2019, 9, 3516. [Google Scholar] [CrossRef]
- Bruzzone, L.; Molfino, R.M. A novel parallel robot for current microassembly applications. Assem. Autom. 2006, 26, 299–306. [Google Scholar] [CrossRef]
- Ding, B.; Li, X.; Li, C.; Li, Y.; Chen, S.-C. A survey on the mechanical design for piezo-actuated compliant micro-positioning stages. Rev. Sci. Instrum. 2023, 94, 101502. [Google Scholar] [CrossRef] [PubMed]
- Belotti, R.; Richiedei, D.; Trevisani, A. Optimal design of vibrating systems through partial eigenstructure assignment. J. Mech. Des. Trans. ASME 2016, 138, 071402. [Google Scholar] [CrossRef]
- Wehrle, E.; Palomba, I.; Vidoni, R. In-operation structural modification of planetary gear sets using design optimization methods. Mech. Mach. Sci. 2019, 66, 395–405. [Google Scholar]
- Babitsky, V.; Chitayev, M. Adaptive high-speed resonant robot. Mechatronics 1996, 6, 897–913. [Google Scholar] [CrossRef]
- Mathijssen, G.; Lefeber, D.; Vanderborght, B. Variable recruitment of parallel elastic elements: Series–parallel elastic actuators (SPEA) with dephased mutilated gears. IEEE/ASME Trans. Mechatron. 2015, 20, 594–602. [Google Scholar] [CrossRef]
- Carabin, G.; Palomba, I.; Wehrle, E.; Vidoni, R. Energy expenditure minimization for a Delta-2 robot through a mixed approach. Comput. Methods Appl. Sci. 2020, 53, 383–390. [Google Scholar]
- Barreto, J.P.; Corves, B. Resonant Delta robot for pick-and-place operations. Mech. Mach. Sci. 2019, 73, 2309–2318. [Google Scholar]
- Matsusaka, K.; Uemura, M.; Kawamura, S. Highly energy-efficient palletizing tasks using resonance-based robot motion control. J. Mech. Eng. Autom. 2016, 6, 8–17. [Google Scholar]
- Iwamura, M.; Imafuku, S.; Kawamoto, T.; Schiehlen, W. Design and control of an energy-saving robot using storage elements and reaction wheels. In Multibody Dynamics; Springer: Berlin, Germany, 2016; pp. 277–297. [Google Scholar]
- Khoramshahi, M.; Nasiri, R.; Shushtari, M.; Ijspeert, A.J.; Ahmadabadi, M.N. Adaptive natural oscillator to exploit natural dynamics for energy efficiency. Robot. Auton. Syst. 2017, 97, 51–60. [Google Scholar] [CrossRef]
- Bruzzone, L.; Bozzini, G. A statically balanced SCARA-like industrial manipulator with high energetic efficiency. Meccanica 2011, 46, 771–784. [Google Scholar] [CrossRef]
- Bruzzone, L.; Verotti, M.; Fanghella, P. Natural motion of the RR-4R-R manipulator: Effects of trajectory types and parameters. Mech. Mach. Sci. 2025, 179, 238–245. [Google Scholar]
- Ohta, H.; Ueki, Y. Expressions of friction force of a four-point contact linear ball bearing with two rows under low-speed operation. J. Tribol. 2022, 144, 101502. [Google Scholar] [CrossRef]
- Franchetti, D.; Boschetti, G.; Lenzo, B. Passive gravity balancing with a self-regulating mechanism for variable payload. Machines 2021, 9, 145. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).