Critical Sets and Unavoidable Sets of Strictly Concentric Magic Squares of Odd Order and Their Application to Prime Strictly Concentric Magic Squares of Order 5 †
Abstract
1. Introduction and Preliminaries
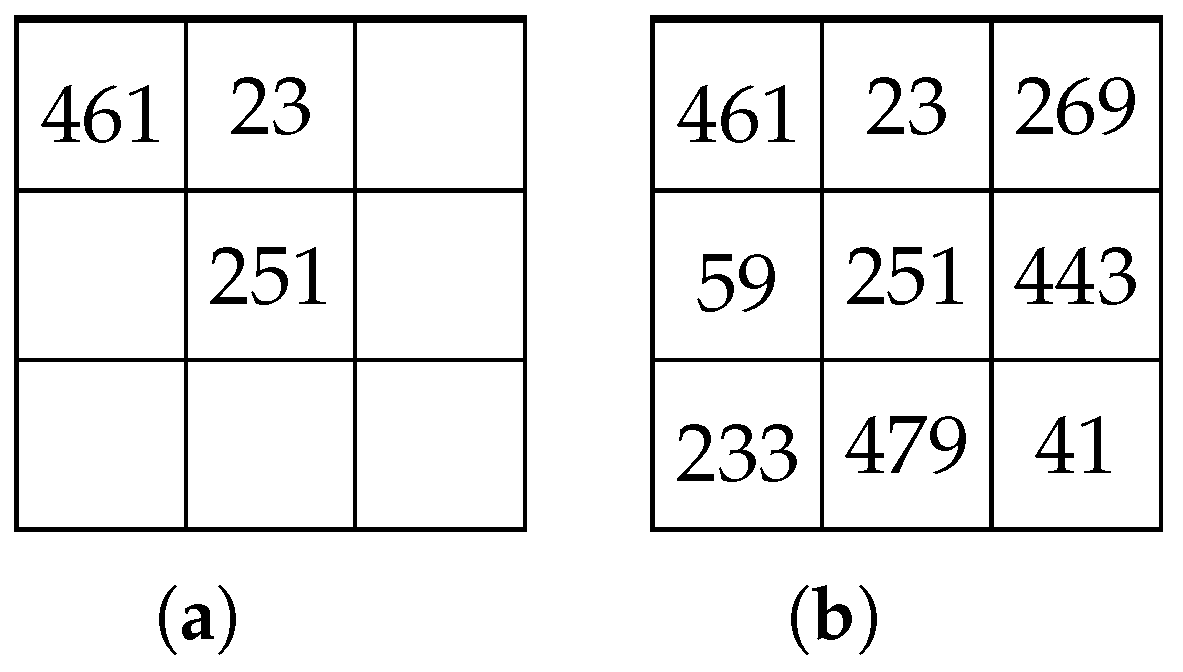
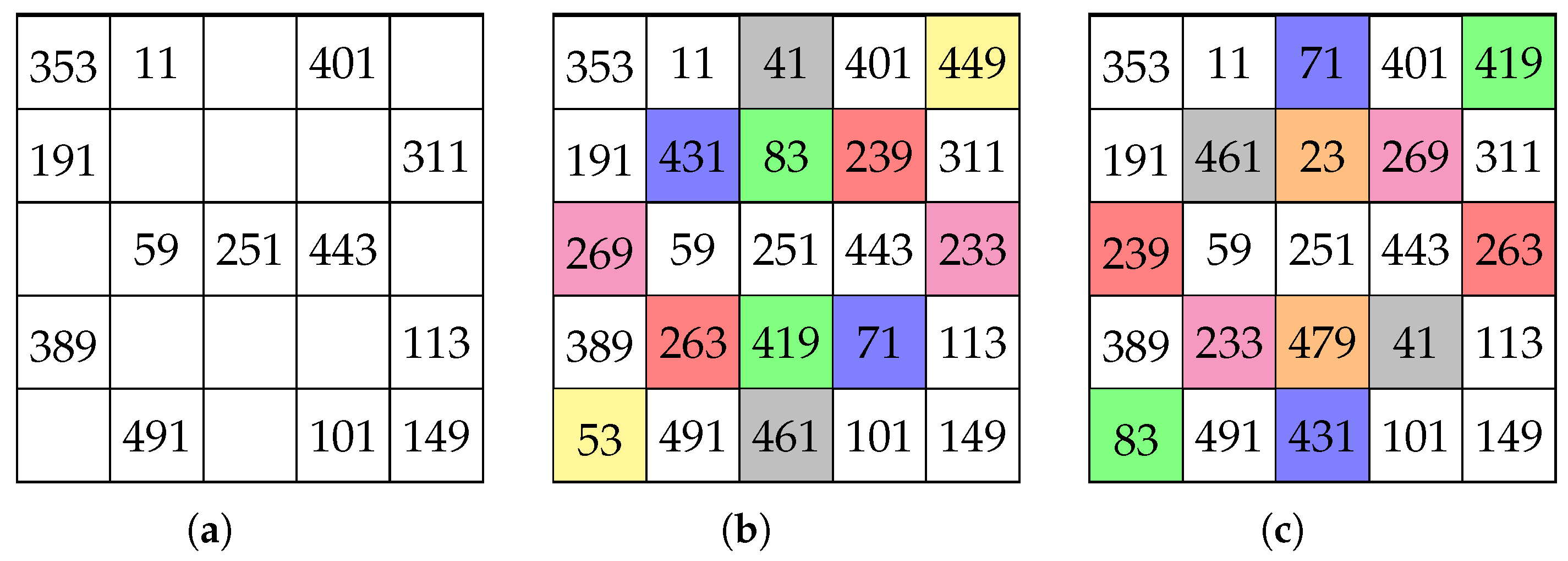
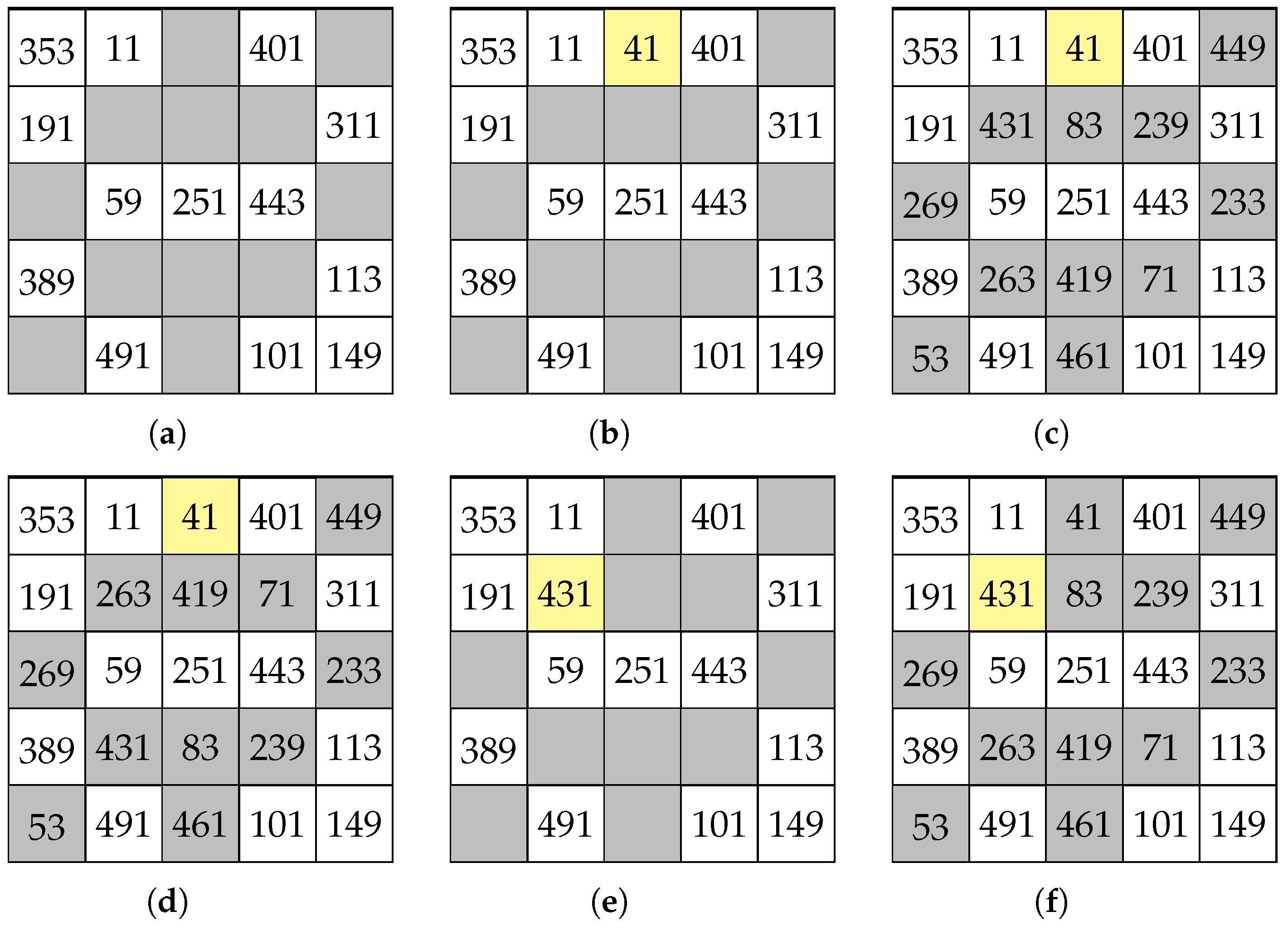
2. Completability of Partial SCMS with Non-Empty Centre Cell
- 1.
- If is a strong partial SCMS, then it is uniquely completable.
- 2.
- If is multiply completable, then it is a weak partial SCMS.
- 3.
- If is a weak partial SCMS, then it is either uniquely completable or multiply completable.
- 4.
- If is uniquely completable, then it is either a strong or a weak partial SCMS.
- 2.
- If a grid is multiply completable, then it cannot be a strong partial SCMS, so it is a weak partial SCMS.
- 3.
- This follows immediately from Lemma 1.
- 4.
- From conditions 1 and 3, both strong and weak partial SCMSs can be uniquely completable.
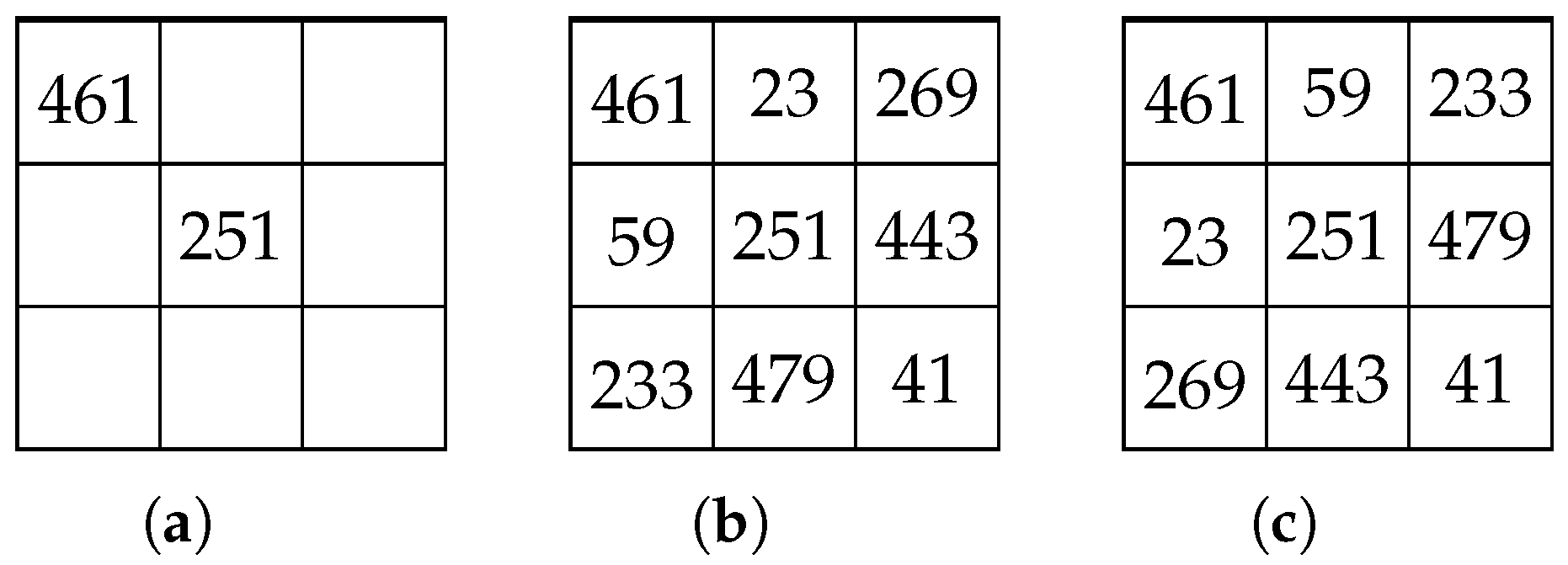
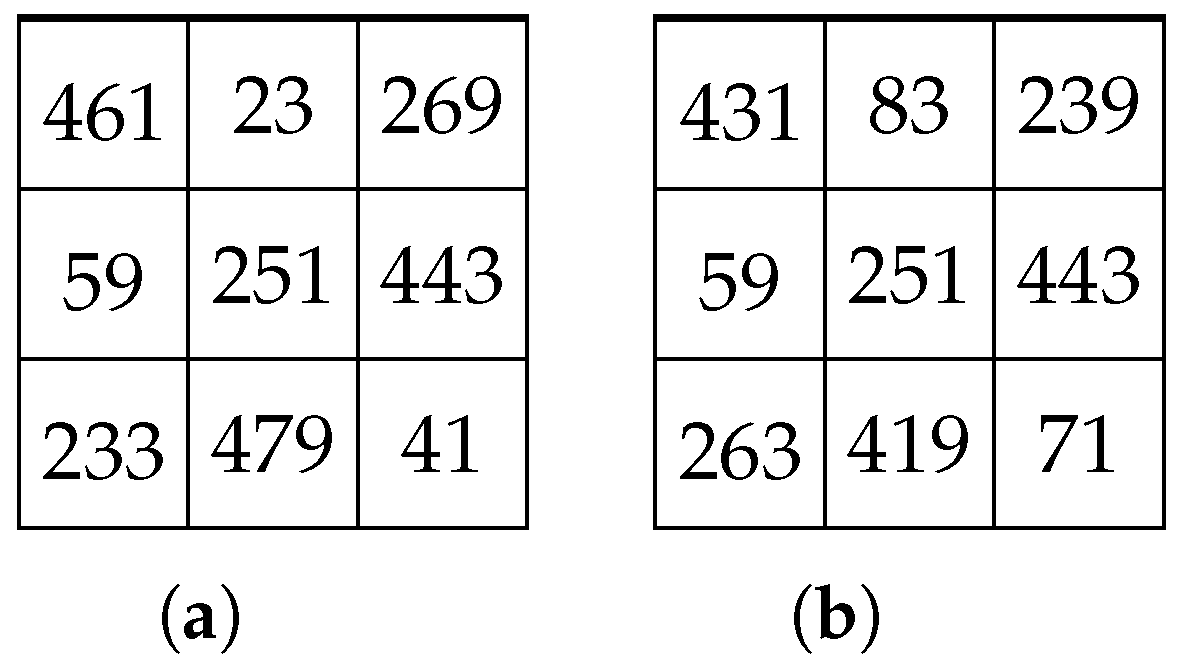
3. Strong Partial SCMSs and Critical Sets of Partial SCMSs
- 1.
- is the only SCMS of order n which has entry in position for all ;
- 2.
- No proper subset of satisfies (1).
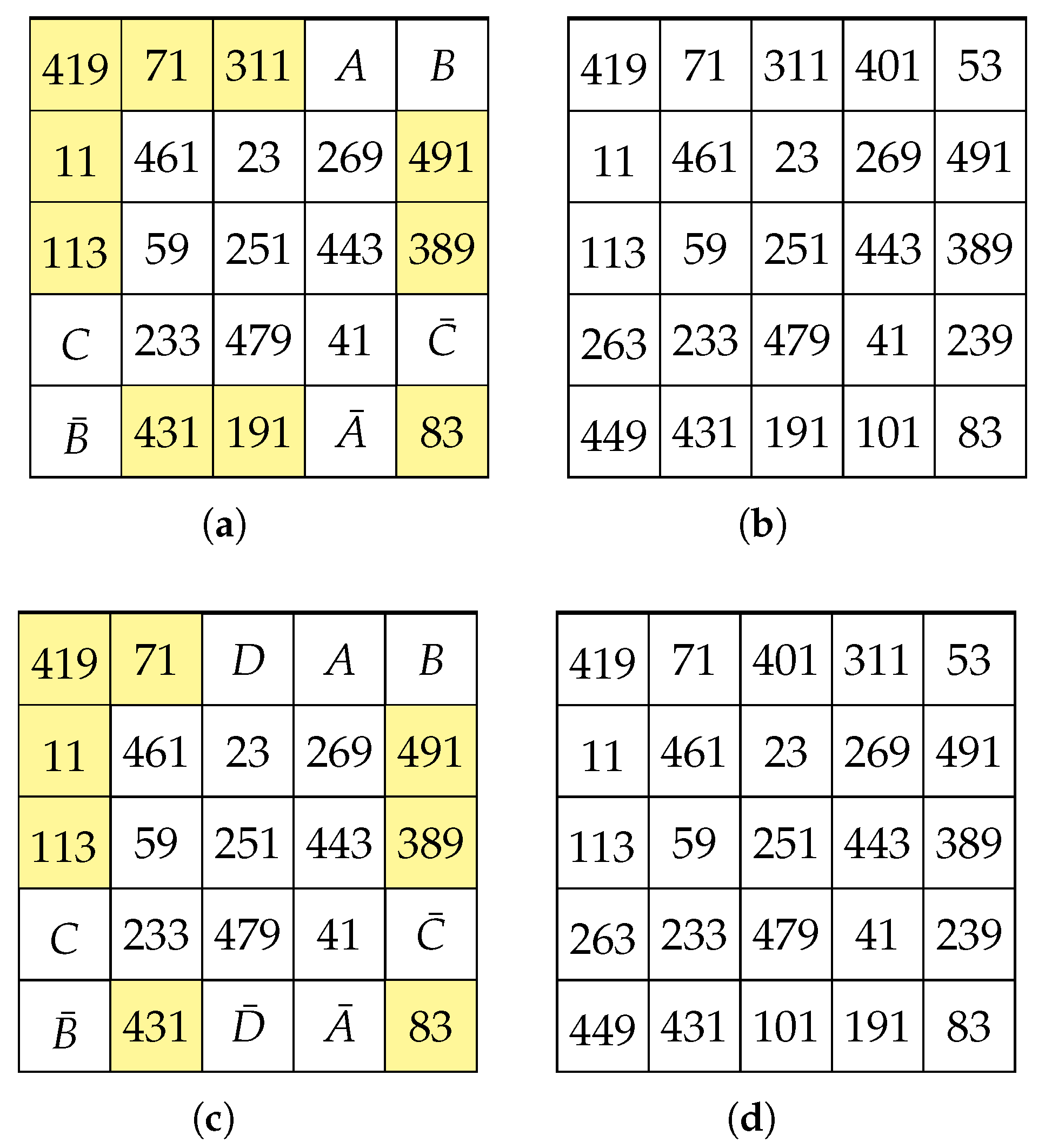
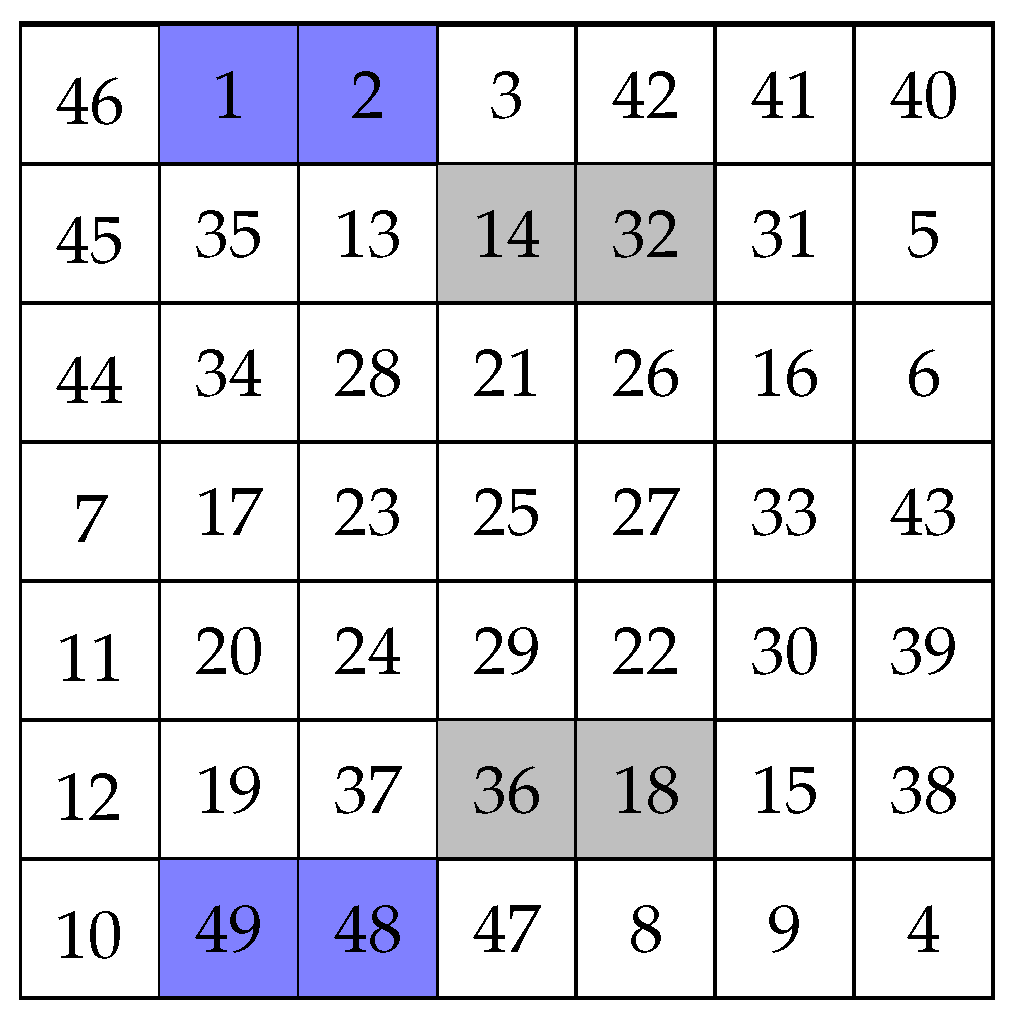
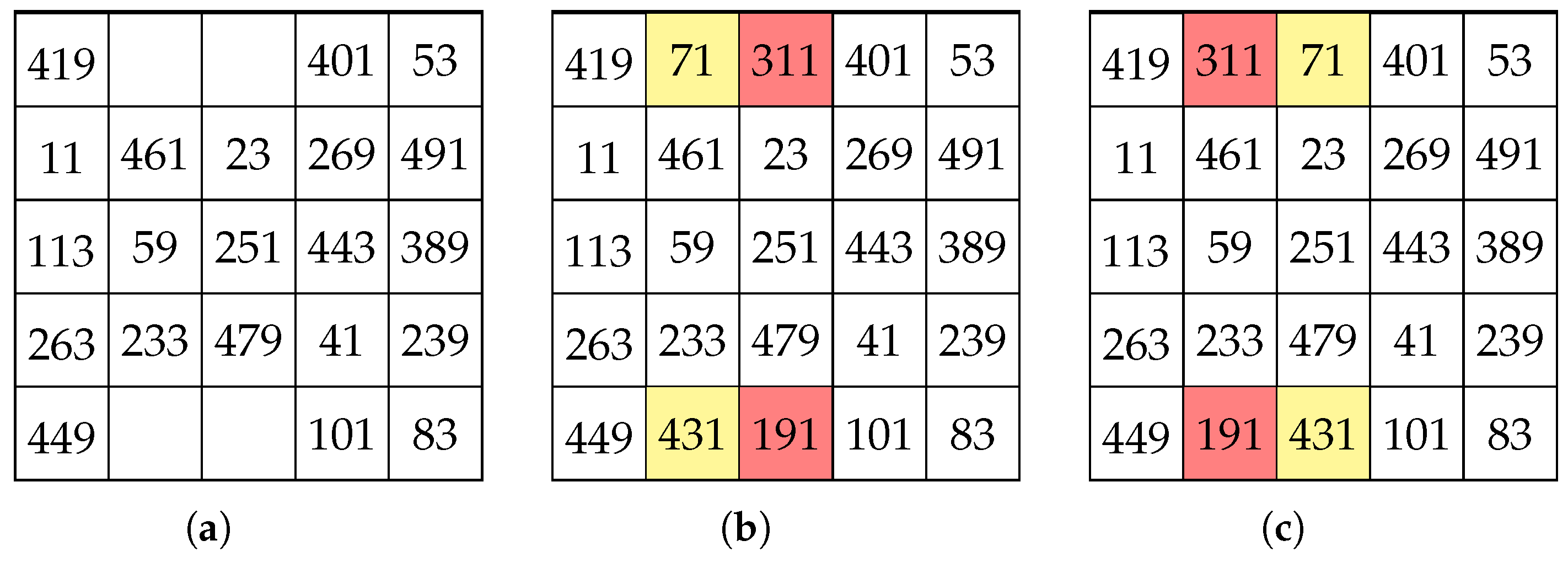
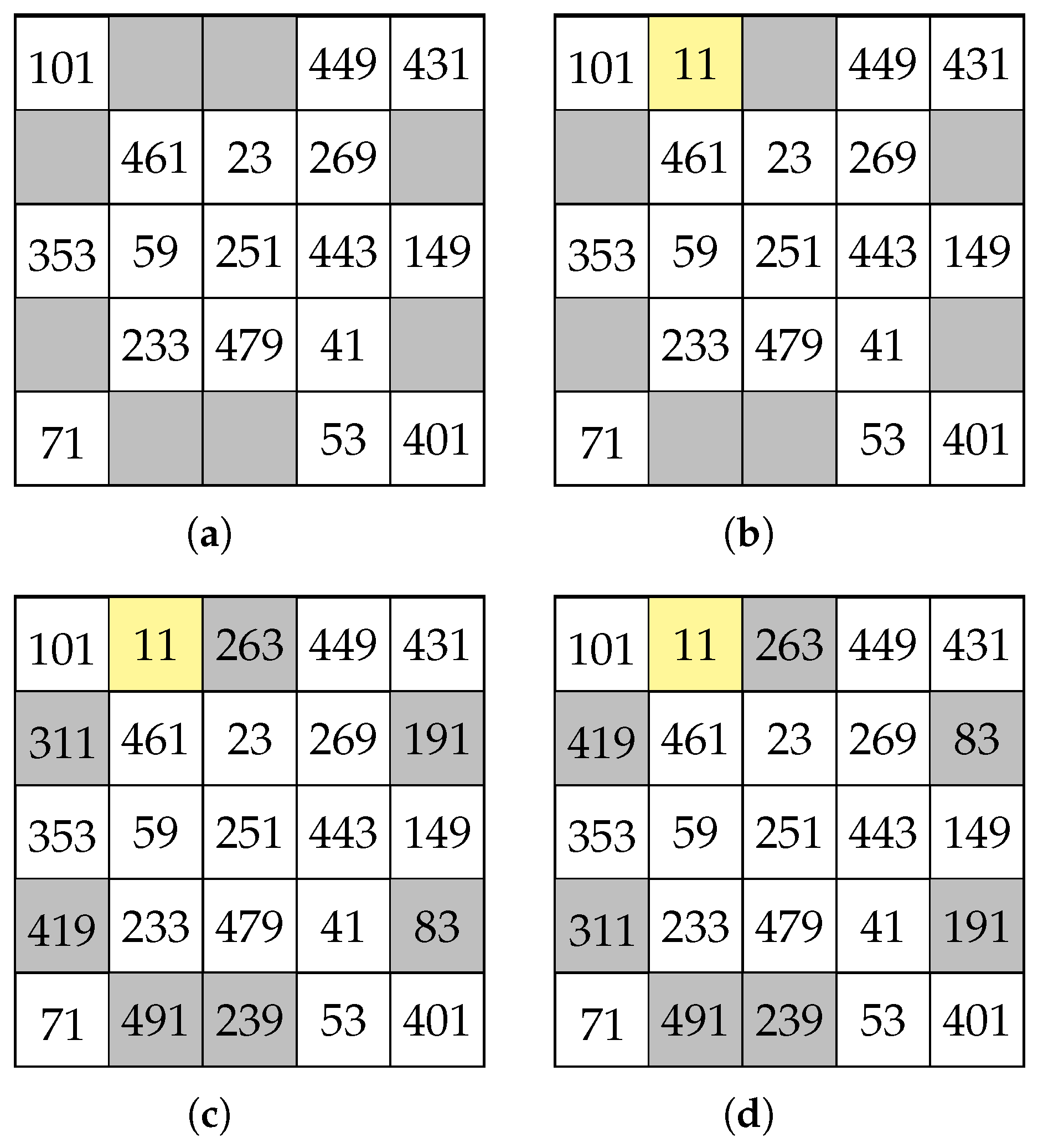
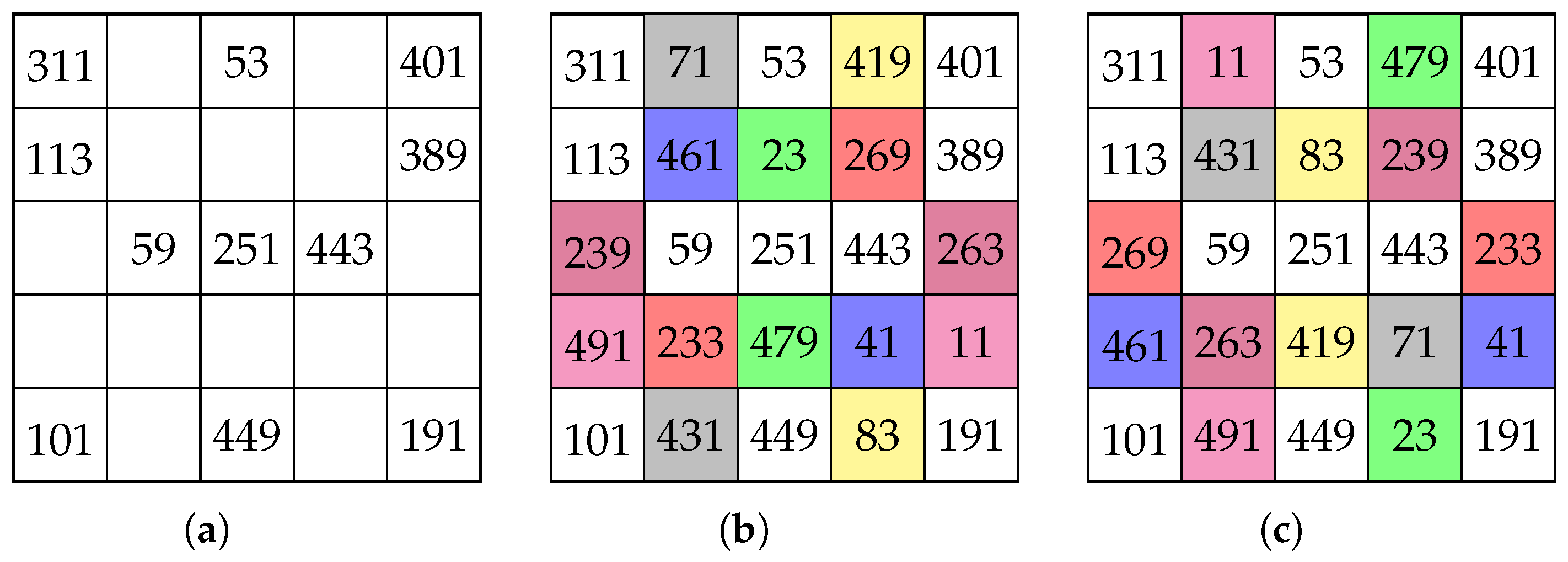
4. Unavoidable Sets of SCMSs
- 1.
- The addition to of any triple , where , produces a partial SCMS, , which is uniquely completable; or
- 2.
- The addition to of any triple where , produces a partial SCMS, , which is either multiply completable to SCMS that are equivalent or possibly, for certain choices of triple , uniquely completable.
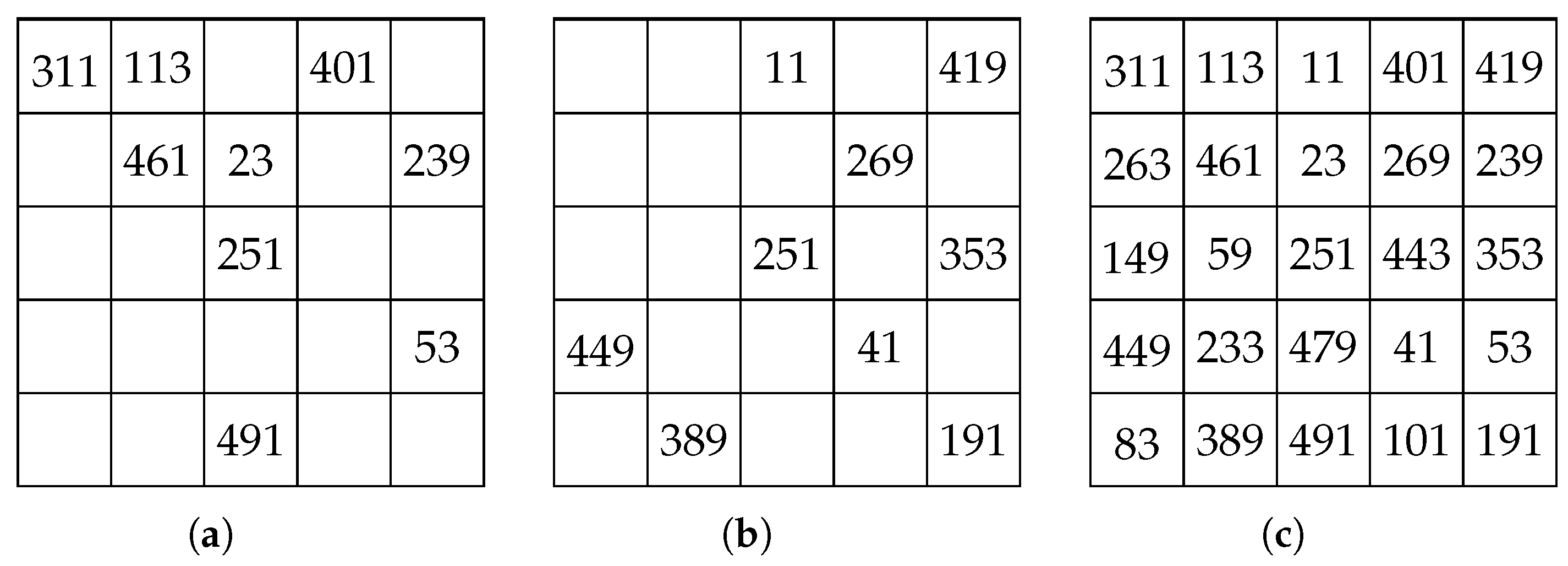
5. Classification of Unavoidable Sets of Order 5
5.1. Proper Unavoidable Sets of Minimum PSCMSs of Order 5
5.2. Improper Unavoidable Sets of Minimum PSCMSs of Order 5
- 1.
- Form 1, the minimum cardinality of the unavoidable set is 4.
- 2.
- Form 2, the minimum cardinality of the unavoidable set is 6.
- 3.
- Form 3, the minimum cardinality of the unavoidable set is 12.
- 4.
- Form 4, the minimum cardinality of the unavoidable set is 8.
- 5.
- Form 5, the minimum cardinality of the unavoidable set is 14.
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| NMS | Normal Magic Square |
| CMS | Concentric Magic Square |
| SCMS | Strictly Concentric Magic Square |
| PSCMS | Prime Strictly Concentric Magic Square |
References
- Johnson, L.; Perkins, S. A discussion of a cryptographical scheme based in F-critical sets of a Latin square. Mathematics 2021, 9, 285. [Google Scholar] [CrossRef]
- Kuhl, J.; Denley, T. Constrained completion of partial latin squares. Discret. Math. 2012, 312, 1251–1256. [Google Scholar] [CrossRef]
- Keedwell, A.D. Defining sets for magic squares. Math. Gaz. 2006, 90, 417–424. [Google Scholar] [CrossRef]
- Williams, D.J.; Jones, S.K.; Roach, P.A.; Perkins, S. Blocking Intercalates In Sudoku Erasure Correcting Codes. IAENG Int. J. Comput. Sci. 2011, 38, 183–191. [Google Scholar]
- McGuire, G.; Tugerman, B.; Civario, G. There Is No 16-Clue Sudoku: Solving the Sudoku Minimum Number of Clues Problem via Hitting Set Enumeration. Exp. Math. 2014, 23, 190–217. [Google Scholar] [CrossRef]
- Skelt, A.L.; Perkins, S.; Roach, P.A. Prime Strictly Concentric Magic Squares of Odd Order. Mathematics 2025, 13, 1261. [Google Scholar] [CrossRef]
- Keedwell, A.D. Two remarks about sudoku squares. Math. Gaz. 2006, 90, 425–430. [Google Scholar] [CrossRef]
- Andrews, W.S. Magic Squares and Cubes, 2nd ed.; Dover: New York, NY, USA, 1960. [Google Scholar]
- Makarova, N. Concentric Magic Squares of Primes. Primes Magic Games. Available online: http://primesmagicgames.altervista.org/wp/forums/topic/concentric-magic-squares-of-primes/ (accessed on 24 January 2025).
- Keedwell, A.D.; Denes, J. Latin Squares and Their Applications; Elsevier: Amsterdam, The Netherlands, 2015. [Google Scholar]
- Cooper, J.; Donovan, D.; Seberry, J. Latin squares and critical sets of minimal size. Australas. J. Comb. 1991, 4, 113–120. [Google Scholar]
- Friedman, E. A058331. The Online Encyclopedia of Integer Sequences. Available online: https://oeis.org/A058331 (accessed on 15 April 2025).
- Adams, P.; Bean, R.; Khodar, A. A Census of Critical Sets in the Latin Squares of Order at Most Six. Ars Comb. 2003, 68, 203–223. [Google Scholar]
- Cutler, J.; Öhman, L. Latin Sqaures with Forbidden Entries. Electron. J. Comb. 2006, 13, R47. [Google Scholar] [CrossRef] [PubMed]
- Andrews, W.S. Magic squares (conclusion). Monist 1905, 15, 555–586. [Google Scholar] [CrossRef]
- Skelt, A.L.; Perkins, S.; Roach, P.A. Strictly Concentric Magic Square Puzzles. Math. Today 2022, 58, 84–86. [Google Scholar]
- Stones, R.J. K-Ples 2-Erasure Codes and Blackburn Partial Latin Squares. IEEE Trans. Inf. Theory 2020, 66, 3704–3713. [Google Scholar] [CrossRef]
- Zolfaghari, B.; Bibak, K. Combinatorial Cryptography and Latin Squares. In Perfect Secrecy in IoT; Springer: Cham, Switzerland, 2022; pp. 37–55. [Google Scholar]
- Singh, M. Latin Squares: Mathematical Significance and Diverse Applications. Res. Rev. J. Stat. Math. Sci. 2023, 9, 24–26. [Google Scholar]
- Rani, N.; Mishra, V. Application of Magic Squares in Cryptography. In Proceedings in Adaptation, Learning and Optimization, Proceedings of the International Conference on Intelligent Vision and Computing (ICIVC 2021), Online, 3–4 October 2021; Sharma, H., Vyas, V.K., Pandey, R.K., Prasad, M., Eds.; Springer: Cham, Switzerland, 2022; Volume 15. [Google Scholar] [CrossRef]
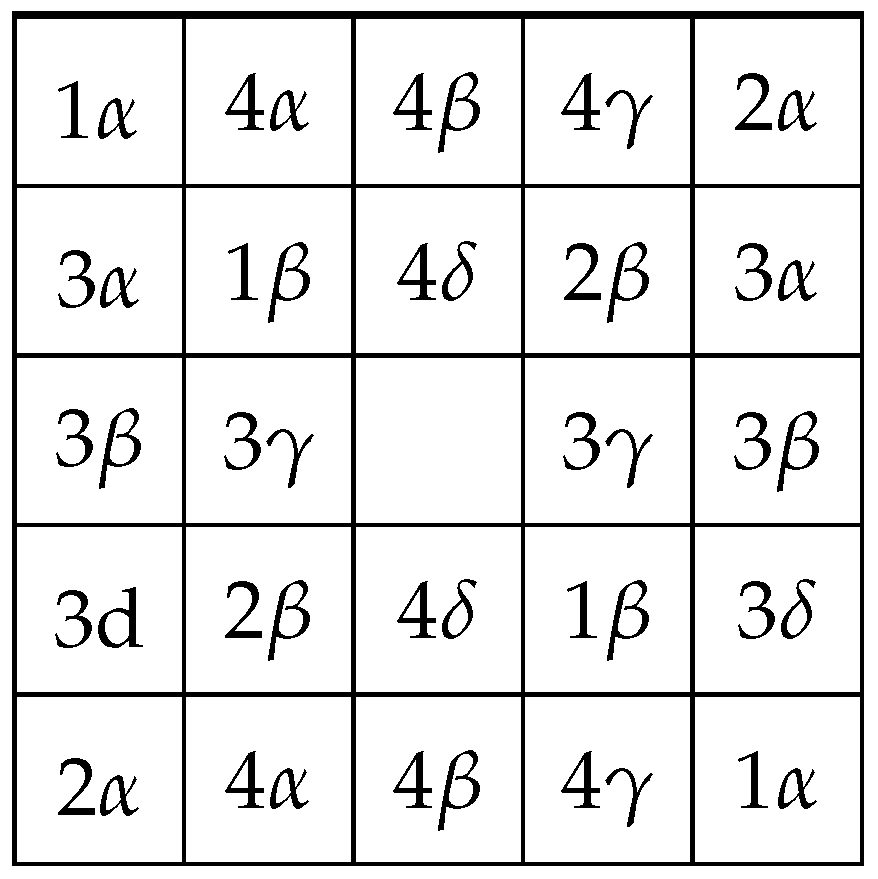






| Permutation | Order |
|---|---|
| Permute the border pairs in columns i, and , | |
| noting that the values remain in their original row | |
| Permute the border pairs in rows i, and , | |
| noting that the values remain in their original column | |
| Permute the value in with the value in | |
| for all | 2 |
| Permute the value in with the value in | |
| for all | 2 |
| Permute the value in with the value in | |
| and the value in with the value in | |
| for all where | 2 |
| Type | List of Primes in the Border of Order 5 |
|---|---|
| 1A | 11, 53, 71, 83, 101, 113, 191, 239, 263, 311, 389, 401, 419, 431, 449, 491 |
| 1B | 11, 53, 83, 101, 113, 149, 191, 239, 263, 311, 353, 389, 401, 419, 449, 491 |
| 1C | 11, 71, 83, 101, 113, 149, 191, 239, 263, 311, 353, 389, 401, 419, 431, 491 |
| 1D | 53, 71, 83, 101, 113, 149, 191, 239, 263, 311, 353, 389, 401, 419, 431, 449 |
| 1E | 11, 53, 71, 83, 101, 113, 149, 239, 263, 353, 389, 401, 419, 431, 449, 491 |
| 1F | 11, 53, 71, 83, 101, 149, 191, 239, 263, 311, 353, 401, 419, 431, 449, 491 |
| 2A | 11, 23, 41, 53, 101, 113, 149, 191, 311, 353, 389, 401, 449, 461, 479, 491 |
| 2B | 11, 23, 41, 53, 101, 113, 149, 233, 269, 353, 389, 401, 449, 461, 479, 491 |
| 2C | 11, 23, 41, 53, 101, 113, 191, 233, 269, 311, 389, 401, 449, 461, 479, 491 |
| 2D | 11, 23, 41, 101, 113, 149, 191, 233, 269, 311, 353, 389, 401, 461, 479, 491 |
| 2E | 11, 23, 41, 53, 101, 149, 191, 233, 269, 311, 353, 401, 449, 461, 479, 491 |
| 2F | 11, 23, 41, 53, 113, 149, 191, 233, 269, 311, 353, 389, 449, 461, 479, 491 |
| 2G | 11, 23, 53, 101, 113, 149, 191, 233, 269, 311, 353, 389, 401, 449, 479, 491 |
| 2H | 11, 41, 53, 101, 113, 149, 191, 233, 269, 311, 353, 389, 401, 449, 461, 491 |
| 2I | 23, 41, 53, 101, 113, 149, 191, 233, 269, 311, 353, 389, 401, 449, 461, 479 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skelt, A.L.; Perkins, S.; Roach, P.A. Critical Sets and Unavoidable Sets of Strictly Concentric Magic Squares of Odd Order and Their Application to Prime Strictly Concentric Magic Squares of Order 5. Axioms 2025, 14, 607. https://doi.org/10.3390/axioms14080607
Skelt AL, Perkins S, Roach PA. Critical Sets and Unavoidable Sets of Strictly Concentric Magic Squares of Odd Order and Their Application to Prime Strictly Concentric Magic Squares of Order 5. Axioms. 2025; 14(8):607. https://doi.org/10.3390/axioms14080607
Chicago/Turabian StyleSkelt, Anna Louise, Stephanie Perkins, and Paul Alun Roach. 2025. "Critical Sets and Unavoidable Sets of Strictly Concentric Magic Squares of Odd Order and Their Application to Prime Strictly Concentric Magic Squares of Order 5" Axioms 14, no. 8: 607. https://doi.org/10.3390/axioms14080607
APA StyleSkelt, A. L., Perkins, S., & Roach, P. A. (2025). Critical Sets and Unavoidable Sets of Strictly Concentric Magic Squares of Odd Order and Their Application to Prime Strictly Concentric Magic Squares of Order 5. Axioms, 14(8), 607. https://doi.org/10.3390/axioms14080607






