Abstract
Efficient truck flow is essential for the efficient operation of a factory and the distribution of its products. This study demonstrated methods to improve truck loading times and overall efficiency at a major sugar manufacturing facility in the Middle East. The objective was to reduce truck waiting times at loading units and increase capacity. The data were collected through questionnaires, observations, and interviews with stakeholders. A simulation software was employed to analyze truck activity at loading stations at the factory. Multi-criteria decision making (MCDM) tools, AHP and TOPSIS, addressed five primary criteria and nine sub-criteria to assist in identifying, evaluating, and ranking feasible solutions. The study suggested different utilization of the various factory loading platforms at different times of the day. The findings from this study emphasize the importance of simulation-based approaches supplemented with decision-making processes to improve efficiency in sugar manufacturing facilities that may have broader applications in the factories of other industries. The study highlights remarkable improvements in operational efficiency, as seen in Alternative 4 substantial 27.9% enhancement, resulting in cost savings and time efficiency. By implementing these findings, factories can enhance their truck flow management system, reduce waiting times, increase capacity utilization, optimize resource allocation, and improve overall efficiency.
Keywords:
MCDM; ranking method; TOPSIS; AHP; simulation; sugar manufacturing; loading unit; facility management MSC:
90B50
1. Introduction
Efficiency plays a crucial role in the competitive world of sugar production [1,2,3,4]. While many studies have focused on improving overall productivity, an area often overlooked is optimizing truck flow and loading time at sugar factories. By streamlining this process, sugar production factories can experience significant improvements in both operational efficiency and profitability. Truck flow within a factory setting refers to the movement and management of trucks during the loading and unloading processes. Indeed, truck flow encompasses every movement from when the truck enters the premises until it leaves after being loaded.
Efficient truck flow is vital for the overall efficiency of a factory. A smooth truck flow can increase factory output by expediting loading, reducing waiting times, and minimizing waiting periods [5]. In contrast, inadequate management can cause delays, increased costs, and customer dissatisfaction due to late deliveries [6]. Loading time is a critical factor in truck operations as it involves loading goods onto trucks. In sugar factories, this involves loading processed sugar onto trucks for distribution to various sale points. Prolonged loading times can lead to a buildup of trucks waiting to be loaded and congestion within the factory’s premises. Such disruption hampers the overall truck flow and leads to potential demurrage charges and decreased factory productivity.
Maximizing the efficiency of truck flows plays a crucial role in enhancing customer satisfaction. Sugar factories can meet customers’ expectations and foster stronger relationships by minimizing loading time and ensuring timely deliveries. While the advantages of improving truck efficiency may appear self-evident, some factories regularly encounter challenges at their loading points due to traffic congestion. Such inefficiencies lead to significant waiting times, ultimately decreasing their ability to pack as many trucks as possible at an optimal cost.
One of the most important contributions of this study is the use of multi-criteria decision-making (MCDM) techniques in decision making when there are conflicting criteria in the loading unit in sugar factories. These methods and the uses of multiple scenarios have not been previously extensively discussed through simulation modeling tools and their integration with the MCDM techniques in making the appropriate decision. Therefore, this provides insight to decision makers into the use of such powerful techniques to improve the overall factory performance.
This study aims to reduce sugar manufacturing waiting times and select optimal strategies using analytic hierarchy process (AHP) and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS), facilitated by a realistic simulation model. By using simulation software, this study analyzed the current state of the manufacturing facility. Then, this study proposed various potential strategies to address the problem. Experts evaluated and assigned weights to different factors that affect traffic congestion utilizing the AHP methodology. Based on these weights, the strategies were ranked using the TOPSIS methodology.
This study was motivated by the pursuit of enhancing operational efficiency and profitability in sugar factories, driven by specific research questions. Firstly, it investigates whether optimizing truck flow and loading time can lead to substantial improvements in operational efficiency and overall profitability within the sugar manufacturing sector. Secondly, it explores how MCDM methods, particularly AHP and TOPSIS, address complex challenges associated with traffic congestion and loading inefficiencies in sugar factories. Thirdly, it evaluates which strategies effectively reduce loading times and analyzes their impact on operational efficiency and customer satisfaction. Lastly, the study examines whether the integration of MCDM techniques offers a viable pathway to enhance operational efficiency across the broader spectrum of the sugar industry.
The remainder of this paper is as follows: Section 2 presents an overview of the current state of sugar manufacturing and discusses previous studies that have utilized MCDM techniques to optimize overall facility performance. Section 3 describes the simulation software used in the study and reviews AHP and TOPSIS methods. Section 4 outlines this study’s quantitative phases and explains the application of the decision-making process. Section 5 presents a comprehensive discussion and shares the study’s findings. Lastly, Section 6 presents the recommendations and conclusions based on the research outcomes.
2. Background and Relevant Literature
The sugar industry faces numerous challenges, including persistent price instability, competition from alternative sweetener manufacturers, and shifting consumer preferences. Fluctuations in supply and demand can result in significant fluctuations in sugar prices that complicate planning for sugar producers. Other sweeteners like high-fructose corn syrup and artificial sweeteners are easier to produce and more cost-effective than sugar, which makes these alternatives appealing to food and beverage manufacturers. In addition, consumers’ growing awareness and concerns regarding the health risks associated with excessive sugar consumption have fostered a robust market of products that contain less sugar or use alternative sweeteners.
The global sugar industry itself remains highly competitive. Thailand, Brazil, and India are currently the largest sugar producers worldwide. These countries enjoy a competitive advantage due to land availability, labor resources, and government subsidies.
2.1. Background
This study analyzes the time required for a major sugar factory in the Middle East to load processed sugar products onto suppliers’ trucks. While other factors may play a role in the factory’s recent and significant financial losses, one obvious problem is its poor record of loading its products onto trucks to be shipped to customers. For example, the factory can occasionally take over 10 h to load a single truck rather than the expected half-hour loading time. The primary cause of this problem is the prolonged waiting period for trucks within the facility’s queue.
Like most large-scale factories, sugar factories must possess efficient organizational processes to meet customer needs. This study focuses on enhancing organization and efficiency related to truck loading times at the factory and subsequent product distribution delays to market. An investigation concluded that the sugar factory under study can accommodate more supplier requests and increase sales by addressing these internal logistical challenges.
The specific issue under examination in this paper arises during the truck-loading phase. The factory has four types of loading units: Retail Shipment Unit (RSU), Finished Product Delivery Unit (FPDU), Direct Loading Unit (DLU), and Bulk Loading Unit (BLU). Figure 1 illustrates the process map of the facility examined in this study.
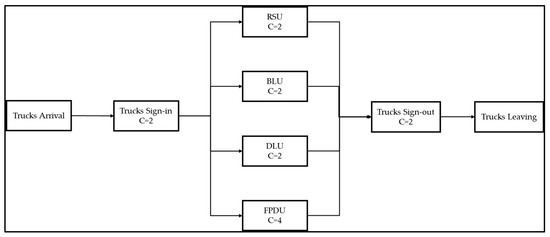
Figure 1.
Facility process map for loading units.
All units can accommodate loading up to two trucks simultaneously except for the FPDU unit, which can load up to four trucks simultaneously. The facility operates 24 h per day with three eight-hour shifts.
Figure 2 provides an overview of a typical 24 h utilization of the loading unit stations. During all shifts, two RSU stations are in use. The RSU units handle smaller packages, typically five-kilogram bags of sugar. One to two BLU stations are typically in use during each shift. The BLU transports sugar directly from the factory into trucks using bulk carriers.
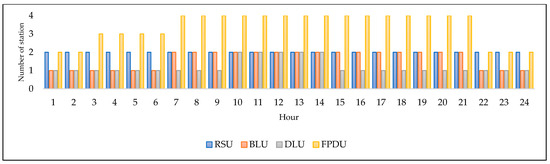
Figure 2.
Facility operation hour shifts.
Similarly, one to two DLU stations are operational throughout all three shifts. The DLU is an automated conveyance that loads 25 kg bags onto trucks. Lastly, between one and four stations use the FPDU for loading large bags, each containing one ton of sugar.
2.2. Relevant Literature
Traffic congestion is common in society and occurs when more vehicles are on a road than it can handle. Numerous studies have addressed this issue and proposed various solutions [7]. Modern simulation tools are often the most essential tool in analyzing traffic movement. Such tools are invaluable in analyzing complex systems and helping to anticipate potential delays [8,9,10,11,12]. Simulation tools create virtual representations of real-world situations, allowing researchers and practitioners to improve their understanding of problematic traffic patterns and review proposed improvements far faster than possible using traditional, time-consuming efforts. For example, some studies have used multi-agent simulations to analyze disorganized traffic flow [13], while others have developed micro-simulation methods for studying congested scenarios on two-way streets [14], A new traffic simulation environment called Traffic3D recently introduced an efficient platform for simultaneously evaluating multiple traffic scenarios [15].
Simulation tools are a valuable resource for decision makers, as they allow for the precise evaluation of different strategies and their impact [16]. Stakeholders can assess alternative scenarios and make well-informed decisions based on reliable data [17]. This capability enables organizations and businesses to implement proactive measures, minimizing delays and optimizing resource allocation. For example, Sajadi et al. [18] identified feasible economic alternatives to reduce waiting times for trucks in factories waiting to load finished goods. Their study utilized system simulation to achieve this objective.
Similarly, Sharifi et al. [19] used simulation techniques to evaluate whether wait times at postal offices could be shortened and customer satisfaction increased. The objective of Gulhane’s study [20], on the other hand, was to improve the administration of hospital waiting lists by employing computer simulations that furthered an understanding of queueing systems. Simulating changes with these systems and making necessary adjustments improved queue management to meet evolving demands. To reduce waiting times, Babashov et al. [21] used a discrete event simulation model to identify bottlenecks in the radiotherapy planning process at the London Regional Cancer Program.
Perez et al. [22] utilized a planning methodology based on simulation to enhance the quality of patient service at walk-in clinics. Walk-in clinics face significant challenges in capacity planning due to uncertainties surrounding patient demand and arrival times. By employing the simulation model developed by Perez et al. [22], clinics have the opportunity to develop protocols that can minimize waiting times for patients by scheduling doctors and medical assistants according to demand fluctuations. To address issues such as overcrowded emergency departments, Monks and Meskarian [23] used simulation modeling because of its flexibility and ability to handle varying demands in a complex system to solve the problem of overcrowded emergency departments, ambulance shortages, canceled elective surgeries, low staff morale, and financial penalties faced by acute hospitals in the UK.
Continuing the exploration of simulation tools and modeling techniques, Viswanadham et al. [24] delved into dynamic modeling techniques for the analysis of supply chain networks using Generalized Stochastic Petri Nets (GSPNs). Their study considered a Poisson-based customer order arrival process and made assumptions about exponential service processes at various points within the supply chain. Their research specifically encompassed both the procurement processes and the intricate delivery logistics operating between different members of the supply chain. In their investigation, they conducted a comparative analysis of two distinct production planning and control policies: the make-to-stock and assemble-to-order systems. This analysis focused on evaluating the overall cost, which included expenses related to inventory carrying and costs arising from delayed deliveries. Furthermore, the authors tackled the decoupling point location problem within supply chains, formulating it as an optimization challenge to minimize total relevant costs, which comprised both inventory carrying costs and delay-related expenses. To address this complex problem effectively, they adopted an integrated modeling approach that combined GSPNs at a higher level with a generalized queuing network at a lower level, allowing them to successfully tackle the decoupling point location problem in supply chain management. Building upon these insights, this section further explores the broader applications of simulation tools in supply chain management.
Numerous modern decision-making tools are available. One of the most frequently used models to discern optimal solutions to complex situations is the multiple criteria decision-making technique. A wide variety of businesses and organizations regularly use MCDM due to its flexibility, allowing decision makers to consider all objective criteria when making decisions. With regard to optimizing sugar production, the insights from recent agricultural studies prove invaluable.
In addition, AHP and TOPSIS are commonly used decision analysis methods to aid in judging complex decision-making scenarios [25,26,27]. Developed independently and based on different principles, AHP and TOPSIS are standalone methodologies that assist in decision making. However, many researchers find that the different approaches are complementary in reaching decisions. Using a hybrid combination model often increases the strength of these models while minimizing their drawbacks. Choosing the optimal strategy to achieve overall objectives for an organization can be challenging. In such cases, the MCDM approach and AHP and TOPSIS methodologies can help determine the best method when faced with conflicting criteria [28,29,30,31,32,33].
Agbejule et al. [34], in a 2021 study, employed the AHP model to select a suitable technology on which to base waste management policies in Accra, Ghana. Other researchers have also utilized the AHP model to address this issue [35] in detail, by assessing four waste technologies in Moscow: incineration, landfill biogas, aerobic composting, and anaerobic digestion [36]. On the other hand, Berdie et al. [37] and Zaidan et al. [38] used a combination of the AHP-TOPSIS models in their studies. Berdie et al. [37] used this model to evaluate three system applications. Similarly, Zaidan et al. [38] employed the combined AHP-TOPSIS technique to assess and choose from a pool of 13 open-source EMR software alternatives [39].
The effectiveness of the AHP-TOPSIS model in software decision making has been established through these studies, and aligns with the findings of Misra and Ray’s research [40]. Furthermore, Bafail and Abdulal [41] also employed the AHP-TOPSIS method to identify the optimal strategy for implementing a recycling strategy. By incorporating this model into their respective research methodologies, these scholars could efficiently evaluate multiple options within various contexts, ranging from system applications to recycling strategies. The utilization of the AHP-TOPSIS technique showcased its versatility as an ideal decision-making tool across diverse fields.
The TOPSIS technique has been extensively employed throughout the academic literature of decision making and evaluating alternatives [42]. Strategies and policies can be ranked using TOPSIS and Fuzzy TOPSIS [43,44]. TOPSIS can also be used to evaluate criteria and weights for determining optimal solutions and rank alternatives [45], selecting optimal solutions, ranking projects [46], and prioritizing and ordering solutions [47]. Lei et al. [48] devised strategies to minimize total passenger waiting time and alleviate congestion in an urban rail transit network that frequently experienced overcrowding during peak hours, resulting in significant passenger backlogs on platforms, especially transfer platforms.
In conclusion, the literature has underscored the significance of optimizing truck flow and loading times within sugar factories, emphasizing their pivotal role in enhancing operational efficiency and competitiveness. This study aims to contribute to this essential area by presenting the integration between AHP-TOPSIS and simulation modeling to address the challenges of traffic congestion and insufficient loading units for sugar manufacturing.
3. Methodology
The Middle Eastern sugar factory study utilized Simio simulation software to examine traffic conditions at their loading unit facility.
Simio, a versatile 3D-modeling software, empowers users to construct dynamic models of various systems, including factories, supply chains, and more. It employs an object-oriented approach that involves combining objects representing the system’s physical components. These objects possess customizable behaviors, responding to system events accordingly. Users can access a Standard Object Library and craft specialized object libraries to tailor models for specific applications. Hierarchical modeling seamlessly integrates within Simio’s framework, granting users flexibility in system representation. Simio distinguishes itself by relying on intelligent objects, which simplifies model assembly through graphical interfaces and ensures an accurate reflection of real-world systems in the models, enhancing user-friendliness and adaptability [49].
Queueing theory is inherently integrated into simulations dealing with systems featuring waiting lines. It serves as an embedded framework within simulations, providing essential guidance on how entities queue, move through queues, and receive service. In essence, queueing theory is seamlessly incorporated into simulations to model and analyze real-world scenarios involving queues effectively. Simulation is a broader modeling technique that can encompass queueing theory when dealing with systems involving queues. Both simulation and queueing theory play crucial roles in understanding and optimizing complex systems in various fields.
Therefore, the simulation assisted in assessing the current situation and developing strategies to reduce waiting times for trucks at the loading units while considering other important criteria. Two MCDM methods, AHP and TOPSIS, assisted in evaluating and ranking these strategies. The AHP was used to calculate the weights of the criteria involved in the study, while TOPSIS assisted in ranking the alternative strategies by identifying the one that best aligned with the factory’s goals.
Simio simulation software was integral in analyzing and addressing traffic flow issues. Questionnaires, direct observations, and interviews conducted with key individuals, such as the facility’s employees, drivers, traffic experts, and management personnel, constituted the data used in the analysis. The interviews and observations revealed that processing time in each loading unit followed a triangular distribution pattern.
Triangular distribution depends on three parameters: the lower limit a, the mode b, and the upper limit c. An exponential distribution is often the foundation for predicting success, failure, or arrival waiting times. Therefore, the trucks’ arrival follows the exponential distribution expressed in Equation (1):
where λ represents the events per unit time and x represents the time.
In business decision analysis, triangular distribution is often the calculation of choice when the only data available are the maximum and minimum values [50]. Equation (2) presents the probability density function for triangle distribution:
This paper developed several strategies to reduce the trucks’ total time in the system to alleviate the logistical traffic issues plaguing the factory. The study considered various criteria, and AHP calculated the weight of each criterion. As a decision-making tool, AHP is a powerful and practical instrument developed by Saaty [51].
The AHP hierarchy enables researchers to break complex problems down into manageable chunks. As a result, it is a preferred method of ranking criteria because it makes it easier to analyze and understand the problem. Making informed decisions is dependent on determining what criteria should be weighted, which is a function of AHP that allows scholars to assign importance to each criterion based on its relative significance. Moreover, quantitative as well as qualitative problems can be addressed using AHP. This flexibility makes it a favored choice among scholars for ranking criteria. One of the strong reasons scholars use the AHP method is due to its ability to measure the consistency of judgments. This is achieved through a metric known as the Consistency Ratio (CR). The CR compares the consistency index of the matrix to the consistency index of a random matrix, indicating how much a person’s preferences deviate from consistency. The steps involved in the AHP methodology were as follows [52]:
Step 1: Hierarchical structures permitted breaking down the problem into goals, criteria, sub-criteria, and alternative forms. Hierarchies imply relationships between elements of one level and those of another.
Step 2: Data collected relating to decision makers and experts following their hierarchical structure served as the basis for pairwise comparisons. To establish the relative importance of different criteria, this study used Saaty’s 1–9 preference scale to assist in developing the pairwise comparison matrix [53]. This AHP methodology ensured a systematic and rigorous decision-making approach, enabling a comprehensive evaluation of various factors.
Step 3: As a result of step 2, a square matrix provided a means to compare different criteria. The diagonal elements of the matrix were set to 1. If an element (i, j) exceeded 1, the criteria in the i-th row were deemed better than those in the j-th column. Conversely, if element (i, j) was less than or equal to 1, the criteria in the j-th column were better than those in the i-th row. Additionally, element (i, j) is not element of matrix. It denotes indices of rows and columns in the matrix.
Step 4: The eigenvalues and normalized right eigenvectors of the comparison matrix provided insight into the relative importance of different criteria. This study referred to the normalized eigenvector elements as weights and ratings, which were determined based on the criteria or sub-criteria and denoted by .
Step 5: The comparisons made using this method were subjective, so assessing the consistency of the matrix of order n was crucial. The AHP allowed for inconsistency through redundancy in its approach. If the consistency index failed to meet the required level, re-evaluating comparisons might have been necessary. Equation (3) expresses the consistency index (CI):
Based on the CI value, the Random Index (RI) is determined from Saaty’s table for CR calculation [54], and Saaty [51] suggests the value of RI should be less than 0.1.
Step 6: To achieve ratings at the local level for each criterion, this study multiplied the weights of the sub-criteria by the rating of each alternative. This process resulted in a global rating by multiplying the local ratings with the weights assigned to each criterion.
In this paper, the TOPSIS method was employed to rank the developed strategies. TOPSIS was introduced in 1981 by Hwang and Yoon [55]. TOPSIS methods provide advantages such as simplicity, rationality, computational efficiency, and measurement of the relative performance of alternatives within a mathematical formulation. The TOPSIS method can be explained in the following steps:
Step 1: Decision matrix determination. A decision matrix, X, can be expressed as follows:
where
represents the alternative strategy i, i = 1, …, m,
denotes decision criteria j, and j = 1, …, n on the basis of which alternative are judged.
represents j-th criteria with respect to i-th alternative strategy.
Step 2: Determination of normalized decision matrix:
Step 3: Determination of the weighted normalized decision matrix: The weighted normalized decision matrix can be determined by multiplying the normalized decision matrix by the weight of decision criteria and is expressed as:
where
is the weight of the j-th criterion.
Step 4: Determination of the positive ideal and negative ideal solutions:
where I is associated with the benefit criteria and I′ is associated with cost criteria.
Step 5: Calculation of the separation measure. The separation of each alternative from the positive ideal solution and from the negative ideal solution are evaluated, respectively as:
Step 6: Calculation of the relative closeness to the positive ideal solution. The relative closeness
of the alternatives to the positive ideal solution is evaluated as follows:
The alternative with the maximum value is the optimal solution.
4. Application and Results
As noted, the issue under investigation arises during the shipping phase of sugar when the trucks load the finished product. Figure 3 illustrates the four loading units involved: RSU, BLU, DLU, and FPDU. At times, congestion and traffic jams occur in truck loading due to the lengthy processing times required by the loading units.
Figure 3.
Similar layout design of the loading units in the sugar facility.
In this study, the data for 365 consecutive days were collected, with this data reflecting the waiting times for each loading unit per hour. The data collection process was meticulous and comprehensive, focusing on gathering detailed information about the movement of trucks within the system, from their entry to the moment of shipment and subsequent exit. In total, an extensive dataset of 61,241 trucks was examined as part of this study. To ensure data quality and reliability, a thorough cleaning process was executed, which involved the removal of outliers and erroneous entries. Notably, any entries with negative time values and exceptionally short total time spent within the system were deemed non-credible and thus eliminated. For instance, a case was identified where a truck purportedly spent only 2 min within the system, an implausible scenario given that the minimum required time for loading such trucks with products is approximately 25 min. After meticulous data cleaning, the analysis revealed valuable insights. Specifically, the average time spent in the system for trucks processed through the Retail Shipment Unit (RSU) was 204 min, encompassing a dataset of 23,957 trucks. In contrast, the Bulk Loading Unit (BLU) exhibited an average system time of 198 min for 5356 served trucks. The Direct Loading Unit (DLU) demonstrated an average system time of 342 min, involving a dataset of 4856 trucks. Lastly, the Finished Product Delivery Unit (FPDU) recorded an average system time of 318 min, encompassing a dataset of 27,072 trucks. These meticulously collected and refined data form the foundation upon which the subsequent analysis and findings of this study are based. Table 1 presents the simulation data.

Table 1.
Simulation input data.
An in-depth analysis of the truck arrival data revealed that the most fitting distribution was the exponential distribution, characterized by a rate parameter (λ) of 8.55 min. In this context, the rate parameter (λ) represents the average rate of truck arrivals per unit of time, with a value of 8.55 min indicating that, on average, a truck arrived at the loading station approximately every 8.55 min. This determination was based on empirical observations and aligned with Equation (1).
All loading units in the system were characterized by a triangular distribution pattern for their processing times. This choice was based on insights gained from interviews with facility experts, who highlighted the influence of human factors on operational dynamics. The triangular distribution was selected for its ability to effectively represent these complexities, as it allowed for the incorporation of minimum, mode, and maximum values for each loading unit’s processing time. As seen in Table 1, the parameters for the triangular distribution were determined through expert interviews, precisely reflecting the specific operational variations at play. For instance, the RSU processing time ranged from 25 to 35 min, while the BLU’s processing time varied between 45 and 70 min. Similarly, the DLU’s processing time ranged from 50 to 70 min, and the FPDU’s processing time spanned from 40 to 55 min. These parameters comprehensively captured the range and intricacies of loading unit operations, accounting for the human-centric factors influencing their performance. By applying Equation (2), these distributions were incorporated into the simulation model, allowing for a more accurate representation of the loading processes within the system. In Table 1, the “Uptime Between Failures” indicated that during an eight-hour shift, the station generally operated smoothly but experienced some disruption towards the end of the shift. Furthermore, the “Time to Repair Failures” mentioned in Table 1 highlighted how quickly these disruptions were addressed and resolved. The dedicated attention ensured that issues were rectified promptly and allowed optimal operational status to resume within a relatively short period. During this verification phase, the model’s precision was assessed by directly comparing it with real-world observations. This practice entailed contrasting the simulation outcomes with empirical data from the actual system. The simulation’s effectiveness was evaluated based on its ability to accurately replicate the actual system’s dynamics, behaviors, and performance metrics. A thorough comparison validated the process further between the simulation outputs and the actual system’s performance. Specifically, this study examined average waiting times at all stations, the number of trucks served by each station, and, in total, through the entire system. Table 2 presents the findings and results of this comparison.

Table 2.
Validation of the simulation model.
Table 2 presents a comprehensive comparison between the real system’s performance and the simulation model’s results, shedding light on the accuracy and effectiveness of the simulation in replicating real-world conditions. The primary metric under scrutiny is the average waiting time in system for trucks, a critical factor directly impacting the efficiency of the loading units within the sugar manufacturing facility. For the Retail Shipment Unit (RSU), the real system data indicate an average waiting time of 204 min, while the simulation model approximates it to be 210 min, resulting in a modest error percentage of 2.94%. Impressively, the number of trucks served in the real system, amounting to 23,957, closely aligns with the simulation’s performance, which served 24,042 trucks, yielding a minimal error percentage of only 0.35%. This close concordance between real system and simulation outcomes for RSU demonstrates the model’s ability to accurately mimic real-world performance. The Bulk Loading Unit (BLU) presents a similar picture, with an average waiting time of 198 min in the real system and 216 min in the simulation. While this shows a slightly higher error percentage of 9.09%, the number of trucks served in both settings closely matches, with an error percentage of merely 0.24%. This indicates that the simulation model adequately captures the essential dynamics of BLU operations. Moving to the Direct Loading Unit (DLU), the real system recorded an average waiting time of 342 min, while the simulation model yielded a lower estimate of 312 min, resulting in an error percentage of 8.77%. Nonetheless, the number of trucks served in both the real system, 4856 trucks, and the simulation, 4860 trucks, is nearly identical, with a negligible error percentage of 0.08%. Despite the discrepancy in waiting times, the simulation showcases a strong ability to replicate the DLU’s overall performance. Lastly, the Finished Product Delivery Unit (FPDU) exhibited an average waiting time of 318 min in the real system, compared to 342 min in the simulation, resulting in a 7.55% error percentage. Similar to the previous units, the number of trucks served in the real system, 27,072 trucks, closely aligns with the simulation’s performance, serving 27,175 trucks, with an error percentage of only 0.38%.
In summary, Table 2 illustrates the simulation model’s commendable accuracy in replicating real-world waiting times and the number of trucks served within the sugar manufacturing facility. While minor discrepancies exist in waiting time estimates, the consistency in the number of trucks served underscores the model’s ability to provide reliable insights into the facility’s operations, making it a valuable tool for decision makers seeking to enhance efficiency and optimize truck flow.
Figure 4 displays the average waiting time for each loading unit, measured in minutes. The FPDU registered an average waiting time of 193 min, followed by the DLU, with an average wait time of 182 min. The RSU had a low average wait time of approximately 98 min. Lastly, BLU registered an average wait time of around 81 min. Figure 5 provides an overview of the current condition of the factory. It shows that the total average waiting time for all trucks within the system was approximately 276 min. Additionally, each station experienced an average waiting time of 140 min for trucks, while their average processing time was 71 min. These findings suggest a significant delay in truck wait times within the system.
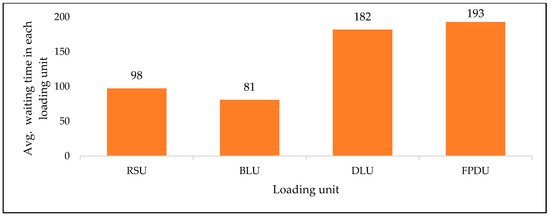
Figure 4.
Average waiting time in each loading unit (minutes).

Figure 5.
The current average waiting time for trucks at the sugar facility.
Finding a suitable solution for the facility to address the challenges was paramount. This solution should align with the facility’s objectives, which included reducing waiting time and increasing capacity to accommodate more trucks. Ultimately, this would lead to increased sales for the manufacturer. One potential approach was to enhance the capacity of one loading unit. However, selecting which loading unit to prioritize involved considering conflicting criteria.
Dealing with conflicting criteria added complexity to the decision-making process. To tackle this challenge effectively, MCDM tools proved useful. To determine the needed criteria, a comprehensive survey was conducted based on previous studies and insights from top management at the facility. All necessary data for these criteria must be readily available to generate viable capacity-enhancing options. As a result of extensive evaluation and analysis, five primary criteria and nine sub-criteria were identified, as seen in Figure 6. These chosen factors played pivotal roles in determining how to increase facility capacity while addressing conflicting considerations. By leveraging MCDM techniques alongside carefully examining essential selection factors within an organization’s context, it became possible to identify feasible solutions and make informed decisions that optimize performance and drive success.
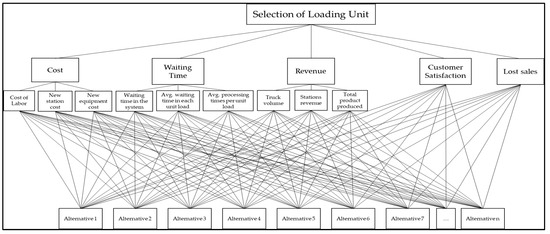
Figure 6.
The hierarchy model of the problem under investigation.
This study incorporated five primary criteria: cost (C1), waiting time (C2), revenue (C3), customer satisfaction (C4), and lost sales (C5) to determine which unit load should be increased. The cost criterion consisted of three sub-criteria: cost of labor (C11) for the new loading unit, new station cost (C12), and new equipment cost (C13). Similarly, the waiting time criterion included three sub-criteria: waiting time in system (C21), the average waiting time at each station (C22), and the average waiting time for processing at each station (C23). The revenue criterion considered truck volume (C31), which means the total number of trucks served, total station revenue (C32), and total production produced by the facility (C33).
Customer satisfaction influenced the average waiting time experienced by customers whose trucks were within the system. Consequently, as customers spent more time waiting, their level of satisfaction decreased. On the other hand, lost sales referred to trucks not loaded due to congestion within the system. A scale from 1 to 9 was utilized to evaluate each criterion mentioned, as presented in Table 3.

Table 3.
Evaluation score used in pairwise matrix.
Table 4 presents the pairwise comparison matrix for the main criteria and sub-criteria. In addition, Table 5 provided the overall weight of each criterion. It is worth noting that all comparison matrices had a consistency ratio below 10%, as recommended by Saaty [51].

Table 4.
The pairwise comparison matrices.

Table 5.
The normalized sub-criteria weightings.
In order to address the issue at hand, this research paper offers several alternative approaches using the TOPSIS method. Table 6 details each of these alternatives. It is worth noting that refers to the current state of affairs in the facility, which includes continuous operation 24 h a day and seven days a week. Three shifts comprise the schedule. The first shift begins at midnight and ends at 8 a.m., followed by the second shift from 8 a.m. to 4 p.m., and the last shift starts at 4 p.m. and ends at midnight. The data presented in Table 7 originate from the simulation model output. Subsequently, these simulation outputs were transformed into input data for the MCDM method, while Table 8 and Table 9 present the TOPSIS weighted normalized matrix and the ideal/negative ideal values, respectively. Finally, Table 10 provides an overview of how each alternative solution ranks based on TOPSIS evaluation criteria.

Table 6.
Alternative solutions.

Table 7.
Summary of the data.

Table 8.
The weighted normalized decision matrix.

Table 9.
TOPSIS ideal and negative ideal values.

Table 10.
The relative closeness of the alternatives to the ideal solution.
5. Discussion
This study employed a hybrid multiple criteria decision-making (MCDM) methodology that combined the analytic hierarchy process (AHP) and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) approaches to evaluate various alternatives for capacity enhancement within a factory setting. The results of the analysis revealed that Alternative 4 emerged as the most viable choice among the options considered. This particular alternative involved the strategic utilization of the factory’s four loading units, with an emphasis on maximizing the capacity of the Dock Loading Unit (DLU) and the Factory Production Dock Unit (FPDU), while allowing the Receiving and Shipping Unit (RSU) and the Bulk Loading Unit (BLU) to operate under regular conditions.
Notably, when we assessed all proposed solutions against the weighted criteria using both the AHP and TOPSIS methodologies, they consistently outperformed the existing system. This underscores the significance of adopting a well-informed and comprehensive approach when contemplating capacity enhancements. Such enhancements must not only aim to increase throughput but also consider their impact on pertinent metrics and criteria, thus ensuring a holistic and sustainable improvement process.
Table 11 presents a detailed comparison of the top five alternatives, along with the selected criteria and their corresponding rankings. These criteria encompass various aspects, such as financial implications, time efficiency, and resource utilization. Each alternative’s performance is evaluated in terms of its impact on these criteria, providing a clear overview of their relative strengths and weaknesses.

Table 11.
Top five alternatives along with the selected criteria comparison.
It is important to note that the improvement percentages were computed by comparing the total time within the system, and all five alternatives demonstrated enhanced performance in terms of reducing this total time. However, in a real-world context, the choice of the optimal solution is not solely based on minimizing waiting time. A holistic perspective encompassing all criteria is crucial, as other factors, such as cost and resource utilization, play a significant role in decision making.
Considering this broader context, Alternative 4 emerges as the best option, as it exhibits a well-rounded performance across various criteria. Nevertheless, it is essential to acknowledge that this study primarily focuses on capacity enhancements, which are relatively straightforward to implement compared to more complex adjustments, such as addressing station failures or altering process times.
Maintaining a delicate equilibrium is imperative, as capacity changes can significantly impact worker utilization rates and overall operational efficiency. While this study presents promising avenues for system enhancement, including potential productivity gains through the scrutiny of processing and failure times, there are still opportunities for future research to delve deeper into these areas. Exploring more complex adjustments and optimizing worker utilization can facilitate substantial advancements in facility performance and efficiency.
Furthermore, the analysis demonstrates that as the arrival rate of products increases, Alternative 4 continues to perform commendably. It exhibits a 27% enhancement compared to the baseline state, albeit accompanied by a minor increase in lost sales. These findings underscore the feasibility and merit of continuous improvement efforts, validating the system’s resilience and growth potential even in the face of increased demand.
Moreover, this study has provided valuable insights into the complex decision-making process surrounding capacity enhancements within a factory setting. By adopting a hybrid MCDM methodology and considering multiple criteria, it has identified Alternative 4 as the most promising choice. However, the path to enhancing facility performance and efficiency is multifaceted, and future research should explore additional dimensions and complexities to further optimize operations in such environments.
While Alternative 20 showcased an impressive reduction in the total time within the system, it is essential to note that the highest percentage of improvement alone does not necessarily make it the recommended choice for implementation. This observation highlights the inherent beauty of employing the AHP and TOPSIS methods in tandem. These methods, by design, consider and weigh multiple criteria simultaneously, ensuring that the chosen alternative aligns with a broader set of objectives beyond just minimizing time. Indeed, decreasing time is a vital factor, but in a holistic decision-making process, it must be considered alongside other crucial factors such as customer satisfaction, cost-effectiveness, resource utilization, and more. The true strength of these methods lies in their ability to facilitate a well-informed, balanced decision that takes into account the multidimensional nature of complex real-world problems. Thus, Alternative 4 emerges as the superior choice, as it offers a well-rounded improvement across the spectrum of criteria, exemplifying the comprehensive nature of the AHP and TOPSIS methodologies in guiding strategic decision making.
The prevalence of Multi-Criteria Decision-Making (MCDM) methods in addressing various quandaries within the realm of the sugar industry is significant. This includes the deployment of simulation models to streamline processes within sugar facilities. For instance, an amalgamation of two MCDM methods—analytic hierarchy process (AHP) and Elimination Et Choix Traduisant la Realité III (ELECTRE III)—was utilized for the optimal site selection of an air quality monitoring station in a sugar factory [56]. Further, an integrated AHP and VIKOR method was implemented for discerning the most suitable material in the sugar industry [57]. In another instance, MCDM methods facilitated the selection of pipe materials within the sugar industry [58].
Moreover, the literature highlights the use of MCDM methods in determining sustainable juice extraction techniques for the non-centrifugal sugar industry [59]. These examples clearly delineate the extensive use and significant benefit derived from MCDM methods within the sugar industry. However, the scope of the current study extends this application to a hypered MCDM technique, aimed at optimizing the flow of trucks within a sugar factory. Our study involved the creation of various scenarios using a simulation model. The integrated MCDM technique was subsequently employed to rank these alternatives. It should be emphasized that the generation of alternative scenarios for loading units within a sugar facility using simulation and the subsequent selection of an optimal one using MCDM techniques is not discussed extensively in the literature. Thus, our study addresses this gap and contributes to the evolving body of knowledge on this subject
6. Conclusions
This paper presents a simulation-based approach to enhancing the flow of truck traffic in sugar manufacturing. Various scenarios were tested and examined based on essential criteria to determine the most feasible one. Sugar industry experts participated in evaluating these criteria using the Analytical Hierarchy Process. AHP calculated the weight of each criterion, and TOPSIS ranked the alternative solutions. This research provides valuable insights for informed decision making within the sugar manufacturing industry through advanced technology and a robust methodology. A hybrid methodology was utilized in this study to offer helpful recommendations for improving their decision-making processes.
In conclusion, the findings and methodologies unveiled in this study hold profound implications for both academic research and practical applications. From an academic perspective, this research showcases the pragmatic and pertinent utilization of advanced simulation tools, such as Simio, in tackling intricate real-world dilemmas within the realms of operations management and industrial engineering. Moreover, the seamless incorporation of Multi-Criteria Decision Making (MCDM) methods, notably AHP and TOPSIS, not only underscores their remarkable adaptability, but also underscores their efficacy in resolving multifaceted challenges pertaining to facility management, logistics, and decision-making processes. These insights present an inspiring avenue for further scholarly inquiry within the realm of decision sciences and management.
On a practical front, the study’s outcomes extend a direct lifeline to sugar manufacturing facilities and industries facing similar logistical challenges. By operationalizing the strategies born from this study, factories stand to amplify their operational efficiency, optimize resource allocation, and elevate their overall throughput. Furthermore, the commitment to ensuring timely deliveries and exceeding customer expectations underscores a direct path to heightened customer satisfaction and more robust client relationships. In a fiercely competitive market landscape, these efficiency enhancements can provide a coveted competitive edge. Remarkably, the methodologies harnessed in this research are not limited to the sugar industry alone. They present a blueprint for broader applicability across industries grappling with analogous logistical hurdles, spanning manufacturing, distribution, and supply chain management. In sum, this study contributes not only to academic knowledge, but also empowers real-world enterprises to thrive in the face of complex operational challenges
Furthermore, this research offers significant practical benefits in the context of sugar manufacturing and beyond. The findings highlight substantial opportunities for process improvement. Alternatives like Alternative 4, which demonstrated a remarkable 27.9% enhancement in performance compared to others, showcase the potential for optimizing operational efficiency, cost reduction, and resource allocation. The practical recommendations derived from simulation and evaluation findings can substantially boost efficiency, productivity, and cost-effectiveness in sugar manufacturing. Moreover, the study suggests expanding the decision-making process by incorporating additional criteria, facilitating even more informed decisions. These versatile methodologies are applicable across industries, providing a pathway to enhanced operational excellence and competitiveness. It is worth noting that the decision-making process can be further extended by containing additional criteria. Therefore, this study suggests including more factors in order to allow manufacturers to make more informed decisions.
However, this study not only offers valuable insights and practical recommendations, but also acknowledges its limitations. The objective of this study was twofold: to minimize waiting times for trucks and to enhance overall operational efficiency while considering various criteria. With the results obtained in this study, it is evident that the percentage of improvement correlates with the reduction in waiting times. This alignment with the main objective of minimizing waiting times underscores the accomplishment of the study’s primary goal. The simulation model and recommendations are constructed based on assumptions and expert judgments collected from industry experts. This introduces a level of subjectivity that may impact the model’s accuracy over time as industry dynamics evolve. Moreover, the study primarily concentrates on enhancing operational efficiency, cost reduction, and resource allocation within the sugar manufacturing domain. While these methodologies exhibit potential for broader application, further empirical validation would be necessary to confirm their effectiveness and adaptability to various industries. In this way, the research goals were realized by providing a comprehensive framework for optimizing truck traffic flow in sugar manufacturing.
Lastly, this research significantly enhances sugar manufacturing by reducing waiting times and improving efficiency. By integrating AHP, TOPSIS, and simulation, it offers a structured framework applicable across industries, fostering informed decision making and competitiveness in today’s business landscape.
Author Contributions
Conceptualization, O.B. and M.A.; methodology, S.I., O.B. and M.A.; software, S.I.; validation, S.I., O.B. and M.A.; investigation, S.I.; data curation, S.I.; writing—original draft preparation, S.I., O.B. and M.A.; writing—review and editing, O.B. and M.A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data supporting the findings of this study are available within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tayyab, M.; Habib, M.S.; Jajja, M.S.S.; Sarkar, B. Economic assessment of a serial production system with random imperfection and shortages: A step towards sustainability. Comput. Ind. Eng. 2022, 171, 108398. [Google Scholar] [CrossRef]
- Mahapatra, A.S.; Mahapatra, M.S.; Sarkar, B.; Majumder, S.K. Benefit of preservation technology with promotion and time-dependent deterioration under fuzzy learning. Expert Syst. Appl. 2022, 201, 117169. [Google Scholar] [CrossRef]
- Khalilpourazari, S.; Mirzazadeh, A.; Weber, G.-W.; Pasandideh, S.H.R. A robust fuzzy approach for constrained multi-product economic production quantity with imperfect items and rework process. Optimization 2019, 69, 63–90. [Google Scholar] [CrossRef]
- Mukherjee, T.; Sangal, I.; Sarkar, B.; Alkadash, T.M. Mathematical estimation for maximum flow of goods within a cross-dock to reduce inventory. Math. Biosci. Eng. 2022, 19, 13710–13731. [Google Scholar] [CrossRef] [PubMed]
- Rajamanickam, G.D.; Ramadurai, G. Simulation of truck congestion in Chennai port. In Proceedings of the 2015 Winter Simulation Conference (WSC), Huntington Beach, CA, USA, 6–9 December 2015; pp. 1904–1915. [Google Scholar] [CrossRef]
- Kanike, U.K. Factors disrupting supply chain management in manufacturing industries. J. Supply Chain Manag. Sci. 2023, 4, 1–24. [Google Scholar]
- Maghableh, G.; Mumani, A. Simulation Based-MCDM Approach for Evaluating Traffic Solutions. Promet-Traffic Transp. 2022, 34, 117–133. [Google Scholar] [CrossRef]
- Lopez, P.A.; Behrisch, M.; Bieker-Walz, L.; Erdmann, J.; Flötteröd, Y.P.; Hilbrich, R.; Lücken, L.; Rummel, J.; Wagner, P.; Wießner, E. Microscopic traffic simulation using sumo. In Proceedings of the 2018 21st International Conference on Intelligent Transportation Systems (ITSC), Maui, HI, USA, 4–7 November 2018; pp. 2575–2582. [Google Scholar]
- Abar, S.; Theodoropoulos, G.K.; Lemarinier, P.; O’hare, G.M. Agent Based Modelling and Simulation tools: A review of the state-of-art software. Comput. Sci. Rev. 2017, 24, 13–33. [Google Scholar] [CrossRef]
- Bock, J.; Krajewski, R.; Moers, T.; Runde, S.; Vater, L.; Eckstein, L. The inD Dataset: A Drone Dataset of Naturalistic Road User Trajectories at German Intersections. In Proceedings of the 2020 IEEE Intelligent Vehicles Symposium (IV), Las Vegas, NV, USA, 19 October–13 November 2020; pp. 1929–1934. [Google Scholar] [CrossRef]
- Melo, S.; Baptista, P. Evaluating the impacts of using cargo cycles on urban logistics: Integrating traffic, environmental and operational boundaries. Eur. Transp. Res. Rev. 2017, 9, 30. [Google Scholar] [CrossRef]
- D’Andrea, E.; Marcelloni, F. Detection of traffic congestion and incidents from GPS trace analysis. Expert Syst. Appl. 2017, 73, 43–56. [Google Scholar] [CrossRef]
- Paruchuri, P.; Pullalarevu, A.R.; Karlapalem, K. Multi agent simulation of unorganized traffic. In Proceedings of the First International Joint Conference on Autonomous Agents and Multiagent Systems: Part 1, Bologna, Italy, 15–19 July 2002; pp. 176–183. [Google Scholar] [CrossRef]
- Caprani, C.C.; Obrien, E.J.; Lipari, A. Long-span bridge traffic loading based on multi-lane traffic micro-simulation. Eng. Struct. 2016, 115, 207–219. [Google Scholar] [CrossRef]
- Garg, D.; Chli, M.; Vogiatzis, G. Traffic3d: A New Traffic Simulation Paradigm. 2019. Available online: https://publications.aston.ac.uk/id/eprint/39573/ (accessed on 11 October 2023).
- Østergård, T.; Jensen, R.L.; Maagaard, S.E. Building simulations supporting decision making in early design—A review. Renew. Sustain. Energy Rev. 2016, 61, 187–201. [Google Scholar] [CrossRef]
- Klein, G.; Crandall, B.W. The role of mental simulation in problem solving and decision making. In Local Applications of the Ecological Approach to Human-Machine Systems; CRC Press: Boca Raton, FL, USA, 2018; pp. 324–358. [Google Scholar]
- Sajadi, S.M.; Ghandehari, M.; Abootalebian, N. Simulation of loading and unloading system to decrease staying and waiting times of arrived-in trucks in Esfahan Steel Company. Int. J. Eng. Syst. Model. Simul. 2015, 7, 256. [Google Scholar] [CrossRef]
- Sharifi, S.; Sajadi, S.M.; Tavakoli, M.M. Simulation process of Isfahan post office using Arena. Int. J. Serv. Oper. Manag. 2014, 17, 50–66. [Google Scholar] [CrossRef]
- Gulhane, K. Enhancing queuing efficiency using discrete event simulation. Int. J. Logist. Syst. Manag. 2020, 36, 531–546. [Google Scholar] [CrossRef]
- Babashov, V.; Aivas, I.; Begen, M.; Cao, J.; Rodrigues, G.; D’souza, D.; Lock, M.; Zaric, G. Reducing Patient Waiting Times for Radiation Therapy and Improving the Treatment Planning Process: A Discrete-event Simulation Model (Radiation Treatment Planning). Clin. Oncol. 2017, 29, 385–391. [Google Scholar] [CrossRef]
- Perez, E.; Anandhan, V.; Novoa, C. A Simulation-Based Planning Methodology for Decreasing Patient Waiting Times in Pure Walk-In Clinics. Int. J. Inf. Syst. Serv. Sect. 2020, 12, 34–54. [Google Scholar] [CrossRef]
- Monks, T.; Meskarian, R. Using simulation to help hospitals reduce emergency department waiting times: Examples and impact. In Proceedings of the 2017 Winter Simulation Conference (WSC), Las Vegas, NV, USA, 3–6 December 2017; pp. 2752–2763. [Google Scholar] [CrossRef]
- Chen, H.; Amodeo, L.; Chu, F.; Labadi, K. Modeling and Performance Evaluation of Supply Chains Using Batch Deterministic and Stochastic Petri Nets. IEEE Trans. Autom. Sci. Eng. 2005, 2, 132–144. [Google Scholar] [CrossRef]
- Τsolaki-Fiaka, S.; Bathrellos, G.D.; Skilodimou, H.D. Multi-Criteria Decision Analysis for an Abandoned Quarry in the Evros Region (NE Greece). Land 2018, 7, 43. [Google Scholar] [CrossRef]
- Rahman, M.A.; Jaumann, L.; Lerche, N.; Renatus, F.; Buchs, A.K.; Gade, R.; Geldermann, J.; Sauter, M. Selection of the Best Inland Waterway Structure: A Multicriteria Decision Analysis Approach. Water Resour. Manag. 2015, 29, 2733–2749. [Google Scholar] [CrossRef]
- Afshari, A.R.; Vatanparast, M.; Ćoćkalo, D. Application of multi criteria decision making to urban planning: A review. J. Eng. Manag. Compet. 2016, 6, 46–53. [Google Scholar] [CrossRef]
- Al-Qudaimi, A.; Kumar, A. Sustainable energy planning decision using the intuitionistic fuzzy analytic hierarchy process: Choosing energy technology in Malaysia: Necessary modifications. Int. J. Sustain. Energy 2016, 37, 436–437. [Google Scholar] [CrossRef]
- Abdullah, L.; Najib, L. Sustainable energy planning decision using the intuitionistic fuzzy analytic hierarchy process: Choosing energy technology in Malaysia. Int. J. Sustain. Energy 2016, 35, 360–377. [Google Scholar] [CrossRef]
- Mir, M.A.; Ghazvinei, P.T.; Sulaiman, N.; Basri, N.; Saheri, S.; Mahmood, N.; Jahan, A.; Begum, R.; Aghamohammadi, N. Application of TOPSIS and VIKOR improved versions in a multi criteria decision analysis to develop an optimized municipal solid waste management model. J. Environ. Manag. 2016, 166, 109–115. [Google Scholar] [CrossRef]
- Jovanovic, S.; Savic, S.; Jovicic, N.; Boskovic, G.; Djordjevic, Z. Using multi-criteria decision making for selection of the optimal strategy for municipal solid waste management. Waste Manag. Res. 2016, 34, 884–895. [Google Scholar] [CrossRef] [PubMed]
- MKharat, M.G.; Raut, R.D.; Kamble, S.S.; Kamble, S.J. The application of Delphi and AHP method in environmentally conscious solid waste treatment and disposal technology selection. Manag. Environ. Qual. An Int. J. 2016, 27, 427–440. [Google Scholar] [CrossRef]
- Kharat, M.G.; Murthy, S.; Kamble, S.J.; Kharat, M.G. Selecting sustainable technologies for municipal solid waste treatment and disposal: An expert based MCDM approach. J. Solid Waste Technol. Manag. 2020, 46, 44–57. [Google Scholar] [CrossRef]
- Agbejule, A.; Shamsuzzoha, A.; Lotchi, K.; Rutledge, K. Application of Multi-Criteria Decision-Making Process to Select Waste-to-Energy Technology in Developing Countries: The Case of Ghana. Sustainability 2021, 13, 12863. [Google Scholar] [CrossRef]
- Farooq, A.; Haputta, P.; Silalertruksa, T.; Gheewala, S.H. A Framework for the Selection of Suitable Waste to Energy Technologies for a Sustainable Municipal Solid Waste Management System. Front. Sustain. 2021, 2, 27. [Google Scholar] [CrossRef]
- Kurbatova, A.; Abu-Qdais, H.A. Using Multi-Criteria Decision Analysis to Select Waste to Energy Technology for a Mega City: The Case of Moscow. Sustainability 2020, 12, 9828. [Google Scholar] [CrossRef]
- Berdie, A.D.; Osaci, M.; Muscalagiu, I.; Barz, C. A combined approach of AHP and TOPSIS methods applied in the field of integrated software systems. IOP Conf. Ser. Mater. Sci. Eng. 2017, 200, 012041. [Google Scholar] [CrossRef]
- Zaidan, A.; Zaidan, B.; Al-Haiqi, A.; Kiah, M.; Hussain, M.; Abdulnabi, M. Evaluation and selection of open-source EMR software packages based on integrated AHP and TOPSIS. J. Biomed. Inform. 2015, 53, 390–404. [Google Scholar] [CrossRef] [PubMed]
- Huiqun, H.; Guang, S. ERP Software Selection Using the Rough Set and TPOSIS Methods Under Fuzzy Environment. Int. J. Adv. Inf. Sci. Serv. Sci. 2012, 4, 111–118. [Google Scholar] [CrossRef]
- Misra, S.K.; Ray, A. Integrated AHP-TOPSIS model for software selection under multi-criteria perspective. In Driving the Economy through Innovation and Entrepreneurship: Emerging Agenda for Technology Management; Springer: New Delhi, India, 2013; pp. 879–890. [Google Scholar]
- Bafail, O.A.; Abdulaal, R.M. New approach for selecting a suitable recycling collection program for recovered paper and pulp recyclables using AHP-TOPSIS techniques. Waste Manag. Res. 2021, 39, 1406–1413. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.-C.; Niu, Z.-W.; Chang, P.-C.; Zhang, B. Assessment approach to stage of lean transformation cycle based on fuzzy nearness degree and TOPSIS. Int. J. Prod. Res. 2017, 55, 7223–7235. [Google Scholar] [CrossRef]
- Prasad, S.; Khanduja, D.; Sharma, S.K. Integration of SWOT analysis with hybrid modified TOPSIS for the lean strategy evaluation. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 1295–1309. [Google Scholar] [CrossRef]
- Vinodh, S.; Mulanjur, G.; Thiagarajan, A. Sustainable concept selection using modified fuzzy TOPSIS: A case study. Int. J. Sustain. Eng. 2013, 6, 109–116. [Google Scholar] [CrossRef]
- Balioti, V.; Tzimopoulos, C.; Evangelides, C. Multi-criteria decision making using TOPSIS method under fuzzy environment. Application in spillway selection. Proceedings 2018, 2, 637. [Google Scholar]
- Vinodh, S.; Swarnakar, V. Lean Six Sigma project selection using hybrid approach based on fuzzy DEMATEL–ANP–TOPSIS. Int. J. Lean Six Sigma 2015, 6, 313–338. [Google Scholar] [CrossRef]
- Yadav, G.; Seth, D.; Desai, T.N. Prioritising solutions for Lean Six Sigma adoption barriers through fuzzy AHP-modified TOPSIS framework. Int. J. Lean Six Sigma 2018, 9, 270–300. [Google Scholar] [CrossRef]
- Lei, Y.; Lu, G.; Zhang, H.; He, B.; Fang, J. Optimizing total passenger waiting time in an urban rail network: A passenger flow guidance strategy based on a multi-agent simulation approach. Simul. Model. Pract. Theory 2022, 117, 102510. [Google Scholar] [CrossRef]
- Sturrock, D.T.; Pegden, C.D. Recent innovations in Simio. In Proceedings of the 2011 Winter Simulation Conference (WSC), Phoenix, AZ, USA, 11–14 December 2011; pp. 52–62. [Google Scholar]
- Stein, W.E.; Keblis, M.F. A new method to simulate the triangular distribution. Math. Comput. Model. 2009, 49, 1143–1147. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy Process: Decision Making in Complex Environments. In Quantitative Assessment in Arms Control: Mathematical Modeling and Simulation in the Analysis of Arms Control Problems; Avenhaus, R., Huber, R.K., Eds.; Springer: Boston, MA, USA, 1984; pp. 285–308. [Google Scholar] [CrossRef]
- Bhushan, N.; Rai, K. Strategic Decision Making. In Strategic Decision Making; Springer: London, UK, 2004. [Google Scholar] [CrossRef]
- Saaty, T.L. The Analytic Hierarchy and Analytic Network Measurement Processes: Applications to Decisions under Risk. Eur. J. Pure Appl. Math. 2008, 1, 122–196. [Google Scholar] [CrossRef]
- Thakkar, J.J. Analytic Hierarchy Process (AHP). In Multi-Criteria Decision Making; Singapore: Singapore, 2021; pp. 33–62. [Google Scholar] [CrossRef]
- Hwang, C.-L.; Yoon, K. Multiple Attribute Decision Making: Methods and Applications: A State-of-the-Art Survey; Springer: Berlin/Heidelberg, Germany, 1981. [Google Scholar]
- Hacıoğlu, H.; Ari, A.; Özkan, A.; Elbir, T.; Tuncel, G.; Yay, O.D.; Gaga, E.O. A New Approach for Site Selection of Air Quality Monitoring Stations: Multi-Criteria Decision-Making. Aerosol Air Qual. Res. 2016, 16, 1390–1402. [Google Scholar] [CrossRef]
- Anojkumar, L.; Ilangkumaran, M.; Vignesh, M. A decision making methodology for material selection in sugar industry using hybrid MCDM techniques. Int. J. Mater. Prod. Technol. 2015, 51, 102. [Google Scholar] [CrossRef]
- Anojkumar, L.; Ilangkumaran, M.; Sasirekha, V. Comparative analysis of MCDM methods for pipe material selection in sugar industry. Expert Syst. Appl. 2014, 41, 2964–2980. [Google Scholar] [CrossRef]
- Beeram, S.; Raj, S.P.; KS, R. Selection of sustainable juice extraction techniques for non-centrifugal sugar industry using multi-criteria decision-making methods. J. Food Process Eng. 2020, 43, e13415. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).