Some New Results for a Class of Multivalued Interpolative Kannan-Type Contractions

Abstract

In this paper, we introduce the notion of multivalued interpolative Kannan-type contractions. We also introduce a more general version of this notion by relaxing the degrees of freedom of the powers arising in the contractive condition. Gaba et al. (2021) recently pointed out a significant error in the paper of Gaba and Karapinar (2019), showing that a particular type of generalized interpolative Kannan-type contraction does not posses a fixed point in general in a complete metric space. Thus, the study of generalized Kannan-type mappings remains an interesting and mathematically challenging area of research. The main aim of this article is to address such existing results for multivalued mappings. We also investigate common fixed points for this type of contractions. Our results extend and unify some existing results in the literature.

1. Introduction

Some well-known fixed point results obtained for multivalued mappings were established by Nadler [1] in 1969. This generalization is based on the idea of the Hausdorff concept—i.e., the distance between two arbitrary sets. The concept of Hausdorff metric space is defined as follows:

Consider a complete metric space (MS) $(\Im ,\eta )$ and the class of all nonempty closed and bounded subsets $CB(\Im )$ of the nonempty set ℑ. Then, construct a map $\mathcal{H}:CB(\Im )\times CB(\Im )\to [0,\infty )$, such that for $S_1,S_2\in CB(\Im )$,

$$\mathcal{H}(S_1,S_2)=max\{\underset{\xi \in S_2}{sup}\mathsf{\Delta }(\xi ,S_1),\underset{\delta \in S_1}{sup}\mathsf{\Delta }(\delta ,S_2)\},$$

where $\mathsf{\Delta }(\delta ,S_2)={inf}_{\xi \in S_2}\eta (\delta ,\xi )$. The pair $\left(CB\right(\Im ),\mathcal{H})$ is known as Pompeiu–Hausdorff metric space, which is induced by $\eta$.

Definition 1

([1]). Suppose $\mathsf{{\rm Y}}:\Im \to CB(\Im )$ is a multivalued map. Then, $\upsilon \in \Im$ is said to be a fixed point of Υ if $\upsilon \in \mathsf{{\rm Y}}\upsilon$ and $Fix\left(\mathsf{{\rm Y}}\right)$ denotes the set of all fixed points of Υ.

Remark 1.

• Suppose $\left(CB\right(\Im ),\mathcal{H})$ is an MS; $\upsilon \in \Im$ is a fixed point of Υ if and only if $\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )=0$.
• We know that the metric function $\eta :\Im \times \Im \to [0,\infty )$ is continuous if $\left\{{\upsilon }_n\right\},\left\{{\xi }_n\right\}$ are two sequences in ℑ with $({\upsilon }_n,{\xi }_n)\to (\upsilon ,\xi )$ for some $\upsilon ,\xi \in \Im$, as $n\to \infty$. Additionally, $\eta ({\upsilon }_n,{\xi }_n)\to \eta (\upsilon ,\xi )$ as $n\to \infty$. This implies that the function Δ is continuous if ${\upsilon }_n\to \upsilon$ as $n\to \infty$. Additionally, as $n\to \infty$, $\mathsf{\Delta }({\upsilon }_n,U)\to \mathsf{\Delta }(\upsilon ,U)$ for any $U\subseteq \Im$.

It is well known that a map satisfying the Banach contraction principle is continuous. In 1968, Kannan [2,3] reported that there are also discontinuous maps which satisfy certain contractive conditions and possess fixed points. Since then, Kannan’s results have been studied and extended in multiple directions (see [4,5,6,7,8]). Recently, Karapinar [9] and Gaba and Karapinar [10] extended Kannan’s theorem via interpolation and produced more general results.

However, in [11], Gaba, Aydi, and Mlaiki pointed out a significant error in the paper published by Gaba and Karapinar [10]. They showed that a $(\rho ,\eta ,\mu )$ interpolative Kannan contraction does not necessarily posses a fixed point in a complete MS. Our current work is also an improvement in that direction where we discuss the existence of a fixed point by assuming that the images of the multivalued mapping under consideration are compact.

For some recent results on interpolative contractions, we refer to the works of Aydi et al. [12,13], Karapinar et al. [14,15], Debnath et al. [16], and Debnath [17], as well as the recent monographs [18,19,20].

Recently, Debnath and Srivastava [21] studied common BPPs for multivalued contractive pairs of mappings. Debnath and Srivastava [22] also proved new extensions of Kannan’s and Reich’s theorems. Another Kannan-type contraction for multivalued asymptotic regular maps was presented by Debnath et al. [23]. Furthermore, a very significant application of fixed points of $F(\psi ,\phi )$-contractions to fractional differential equations was recently provided by Srivastava et al. [24].

Some important results for the present context are listed below:

Lemma 1

([25,26]). Consider an MS $(\Im ,\eta )$ and suppose $S_1,S_2,W\in CB(\Im )$. Then,

(1)

$\mathsf{\Delta }(\mu ,S_2)\le \eta (\mu ,\gamma )$ for any $\gamma \in S_2$ and $\mu \in \Im$;

(2)

$\mathsf{\Delta }(\mu ,S_2)\le \mathcal{H}(S_1,S_2)$ for any $\mu \in S_1$.

Lemma 2

([1]). Suppose that $S_1,S_2\in CB(\Im )$ and $\upsilon \in S_1$. Then, for any $p>0$, there exists $\xi \in S_2$, such that:

$$\eta (\upsilon ,\xi )\le \mathcal{H}(S_1,S_2)+p.$$

However, in every situation there may not be a point $\xi \in S_2$, such that:

$$\eta (\upsilon ,\xi )\le \mathcal{H}(S_1,S_2).$$

If $S_2$ is compact, then such a point ξ exists—i.e., $\eta (\upsilon ,\xi )\le \mathcal{H}(S_1,S_2).$

Lemma 3

([1]). Suppose $\left\{U_n\right\}$ is a sequence in $CB(\Im )$ and for some $U\in CB(\Im )$, ${lim}_{n\to \infty }\mathcal{H}(U_n,U)$ = 0. If ${\upsilon }_n\in U_n$ and for some $\upsilon \in \Im$, ${lim}_{n\to \infty }\eta ({\upsilon }_n,\upsilon )=0$, then $\upsilon \in U$.

In the current paper, our aim is to introduce and establish a multivalued version of Kannan-type contractions via interpolation. The rest of the paper is organised as follows. In Section 2, we introduce multivalued interpolative Kannan-type (MVIK-type, in short) contractions and show that they admit fixed points. We also provide a more general version of this result as a corollary by relaxing the degrees of freedom of the power occurring in the contractive condition. In Section 3, we present a common fixed point theorem for MVIK-type contractions. Section 4 provides our conclusions.

2. MVIK-Type Contractions

First of all, we introduce the definition of MVIK-type contractions and present the corresponding existing result.

Definition 2.

Suppose that $(\Im ,\eta )$ is an MS. A map $\mathsf{{\rm Y}}:\Im \to CB(\Im )$ is called an MVIK-type contraction if there exist $\lambda \in [0,1)$ and $\alpha \in (0,1)$, such that:

$$\mathcal{H}(\mathsf{{\rm Y}}\upsilon ,\mathsf{{\rm Y}}\xi )\le \lambda {\left[\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )\right]}^{\alpha }{\left[\mathsf{\Delta }(\xi ,\mathsf{{\rm Y}}\xi )\right]}^{1-\alpha }$$

(1)

for all $\upsilon ,\xi \in \Im$ with $\upsilon ,\xi \notin Fix\left(\mathsf{{\rm Y}}\right)$.

Theorem 1.

Suppose that $(\Im ,\eta )$ is a complete MS and Υ is an MVIK-type contraction, such that $\mathsf{{\rm Y}}\upsilon$ is compact for each $\upsilon \in \Im$. Then, $Fix\left(\mathsf{{\rm Y}}\right)\ne \varphi .$

Proof. 

Consider ${\upsilon }_0\in \Im$ and choose ${\upsilon }_1\in \mathsf{{\rm Y}}{\upsilon }_0$. Since $\mathsf{{\rm Y}}{\upsilon }_0$ is compact, from Lemma 2 we can select ${\upsilon }_2\in \mathsf{{\rm Y}}{\upsilon }_1$, such that $\eta ({\upsilon }_2,{\upsilon }_1)\le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_1,\mathsf{{\rm Y}}{\upsilon }_0)$. Similarly, we may consider ${\upsilon }_3\in \mathsf{{\rm Y}}{\upsilon }_2$, such that $\eta ({\upsilon }_3,{\upsilon }_2)\le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_2,\mathsf{{\rm Y}}{\upsilon }_1)$ and so on. Continuing in a similar manner, we can create a sequence $\left\{{\upsilon }_n\right\}$ satisfying ${\upsilon }_{n+1}\in \mathsf{{\rm Y}}{\upsilon }_n$, such that $\eta ({\upsilon }_{n+1},{\upsilon }_n)\le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_{n-1})$.

Suppose that ${\upsilon }_n\notin \mathsf{{\rm Y}}{\upsilon }_n$∀$n\ge 0$. Otherwise, we can trivially obtain a fixed point. Thus, $\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)>0$, ∀$n\ge 0$.

Taking $\upsilon ={\upsilon }_{n-1}$ and $\xi ={\upsilon }_n$ in Definition 2, we have:

$$\begin{array}{rr}\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_n)\left(\mathrm{using}\mathrm{Lemma}1\right)\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{1-\alpha }\hfill \\ \hfill \Rightarrow {\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{\alpha }& \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]}^{\alpha }\hfill \\ \hfill \Rightarrow \mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)& \le {\lambda }^{\frac{1}{\alpha }}\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]\le \lambda \left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right].\hfill \end{array}$$

(2)

Therefore, $\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)$ is a non-increasing and non-negative sequence of real numbers; therefore, it converges to some real numbers l. We show that $l=0$.

From Equation (2):

$$\begin{array}{cc}\hfill \mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)& \le \lambda \left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]\le \dots \le {\lambda }^n\left[\mathsf{\Delta }({\upsilon }_0,\mathsf{{\rm Y}}{\upsilon }_0)\right].\hfill \end{array}$$

(3)

Since $\lambda \in [0,1)$, taking the limit in (3) as $n\to \infty$, we have $l=0$.

Next, we verify that $\left\{{\upsilon }_n\right\}$ is a Cauchy sequence.

Taking $\upsilon ={\upsilon }_n$ and $\xi ={\upsilon }_{n-1}$ in Definition 2, we have:

$$\begin{array}{rr}\eta ({\upsilon }_{n+1},{\upsilon }_n)& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_{n-1})\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]}^{1-\alpha }\hfill \\ \hfill & \le \lambda {\left[\eta ({\upsilon }_n,{\upsilon }_{n+1})\right]}^{\alpha }{\left[\eta ({\upsilon }_{n-1},{\upsilon }_n)\right]}^{1-\alpha }\left(\mathrm{using}\mathrm{Lemma}1\right)\hfill \\ \hfill \Rightarrow {\left[\eta ({\upsilon }_n,{\upsilon }_{n+1})\right]}^{1-\alpha }& \le \lambda {\left[\eta ({\upsilon }_{n-1},{\upsilon }_n)\right]}^{1-\alpha }\hfill \\ \hfill \Rightarrow \eta ({\upsilon }_n,{\upsilon }_{n+1})& \le {\lambda }^{\frac{1}{1-\alpha }}\left[\eta ({\upsilon }_{n-1},{\upsilon }_n)\right]\le \lambda \eta ({\upsilon }_{n-1},{\upsilon }_n).\hfill \end{array}$$

(4)

From (4),

$$\eta ({\upsilon }_n,{\upsilon }_{n+1})\le \lambda \eta ({\upsilon }_{n-1},{\upsilon }_n)\le \dots \le {\lambda }^n\eta ({\upsilon }_0,{\upsilon }_1).$$

(5)

For any positive integer k:

$$\begin{array}{rr}\eta ({\upsilon }_n,{\upsilon }_{n+k})& \le \eta ({\upsilon }_n,{\upsilon }_{n+1})+\dots +\eta ({\upsilon }_{n+k-1},{\upsilon }_{n+k})\hfill \\ \hfill & \le {\lambda }^n\eta ({\upsilon }_0,{\upsilon }_1)+\dots +{\lambda }^{n+k-1}\eta ({\upsilon }_0,{\upsilon }_1)\hfill \\ \hfill & =({\lambda }^n+{\lambda }^{n+1}+\dots +{\lambda }^{n+k-1})\eta ({\upsilon }_0,{\upsilon }_1)\hfill \\ \hfill & \le \frac{{\lambda }^n}{1-\lambda }\eta ({\upsilon }_0,{\upsilon }_1).\hfill \end{array}$$

(6)

Letting $n\to \infty$ in (6), we obtain $\eta ({\upsilon }_n,{\upsilon }_{n+k})⟶0$. Therefore, $\left\{{\upsilon }_n\right\}$ is a Cauchy sequence. Since $(\Im ,\eta )$ is complete, ${lim}_{n\to \infty }{\upsilon }_n=\upsilon$ for some $\upsilon \in \Im$.

Next, we show that $\upsilon$ is a fixed point of $\mathsf{{\rm Y}}$. Putting $\upsilon ={\upsilon }_n$ and $\xi =\upsilon$ in (2), we have:

$$\begin{array}{cc}\hfill \mathsf{\Delta }({\upsilon }_{n+1},\mathsf{{\rm Y}}\upsilon )& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_n,\mathsf{{\rm Y}}\upsilon )\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{\alpha }{\left[\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )\right]}^{1-\alpha }.\hfill \end{array}$$

Taking the limit in the above inequality as $n\to \infty$, we find that $\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )=0$ (using $\left(ii\right)$ of Remark 1 and the fact that ${lim}_{n\to \infty }\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)=l=0$). Therefore, $\upsilon \in \mathsf{{\rm Y}}\upsilon$—i.e., $\upsilon$—is a fixed point of $\mathsf{{\rm Y}}$. □

Next, we introduce a more general version of the notion of MVIK-type contraction by relaxing the degrees of freedom of the powers arising in the contractive condition. We call this $(\lambda ,\alpha ,\beta )$-interpolative Kannan-type contraction.

Definition 3.

Suppose that $(\Im ,\eta )$ is an MS and $\mathsf{{\rm Y}}:\Im \to CB(\Im )$ is a multivalued map. Then, Υ is called a $(\lambda ,\alpha ,\beta )$-interpolative Kannan-type contraction if there exist $\lambda \in [0,1)$ and $\alpha ,\beta \in (0,1)$ with $\alpha +\beta <1$, such that:

$$\mathcal{H}(\mathsf{{\rm Y}}\upsilon ,\mathsf{{\rm Y}}\xi )\le \lambda {\left[\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )\right]}^{\alpha }{\left[\mathsf{\Delta }(\xi ,\mathsf{{\rm Y}}\xi )\right]}^{\beta }$$

(7)

for all $\upsilon ,\xi \in \Im$ with $\upsilon ,\notin \mathsf{{\rm Y}}\upsilon$, and $\xi ,\notin \mathsf{{\rm Y}}\xi$.

Remark 2.

In Definition 3, if we admit $\alpha +\beta =1$, we have a direct reference to Definition 2 ($\beta =1-\alpha$). Hence, the condition $\alpha +\beta <1$ allows the parameters $\alpha ,\beta$ to admit various values and still provides the interpolative results.

The corresponding existing result follows as a corollary to Theorem 1.

Corollary 1.

Suppose that $(\Im ,\eta )$ is a complete MS and $\mathsf{{\rm Y}}:\Im \to CB(\Im )$ is a $(\lambda ,\alpha ,\beta )$-interpolative Kannan-type contraction, such that $\mathsf{{\rm Y}}\left(\upsilon \right)$ is compact for each $\upsilon \in \Im$. Then, $Fix\left(\mathsf{{\rm Y}}\right)\ne \varphi$.

Proof. 

Fix ${\upsilon }_0\in \Im$. Applying similar techniques as those in Theorem 1, we construct a sequence $\left\{{\upsilon }_n\right\}$ satisfying:

$$\eta ({\upsilon }_{n+1},{\upsilon }_n)\le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_{n-1}),\mathrm{for}\mathrm{all}n=0,1,2,\dots .$$

Taking $\upsilon ={\upsilon }_{n-1}$ and $\xi ={\upsilon }_n$ in Definition 3, we have:

$$\begin{array}{cc}\hfill \mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_n)\left(\mathrm{using}\mathrm{Lemma}1\right)\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{\beta }\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{1-\alpha },(\sin \mathrm{ce}\beta <1-\alpha )\hfill \\ \hfill \Rightarrow {\left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]}^{\alpha }& \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]}^{\alpha }\hfill \\ \hfill \Rightarrow \left[\mathsf{\Delta }({\upsilon }_n,\mathsf{{\rm Y}}{\upsilon }_n)\right]& \le {\lambda }^{\frac{1}{\alpha }}\left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right]\le \lambda \left[\mathsf{\Delta }({\upsilon }_{n-1},\mathsf{{\rm Y}}{\upsilon }_{n-1})\right].\hfill \end{array}$$

Next, adopting a similar procedure as in the proof of Theorem 1, we can prove that $\left\{{\upsilon }_n\right\}$ is a Cauchy sequence. Furthermore, since $(\Im ,\eta )$ is complete, $\left\{{\upsilon }_n\right\}$ converges to a fixed point of $\mathsf{{\rm Y}}$. □

The example below validates Corollary 1 and consequently Theorem 1.

Example 1.

Consider $\Im =[0,\infty )$ and $\eta (\upsilon ,\xi )=|\upsilon -\xi |$. Then, $(\Im ,\eta )$ is a complete MS.

Construct $\mathsf{{\rm Y}}:\Im \to CB(\Im )$, such that:

$$\mathsf{{\rm Y}}\upsilon =\left\{\begin{array}{cc}\left\{0\right\},\hfill & \mathrm{if}\upsilon \in [0,2)\hfill \\ \{\upsilon ,\upsilon +2\},\hfill & \mathrm{if}\upsilon \ge 2.\hfill \end{array}\right.$$

Let $\upsilon ,\xi \notin Fix\left(\mathsf{{\rm Y}}\right)$. Then, $\upsilon ,\xi \in (0,2)$. Now, $\mathcal{H}(\mathsf{{\rm Y}}\upsilon ,\mathsf{{\rm Y}}\xi )=\mathcal{H}\left(\right\{0\},\{0\left\}\right)=0$.

Thus, Υ is a $(\lambda ,\alpha ,\beta )$-interpolative Kannan-type contraction for any $\lambda \in [0,1)$ and $\alpha ,\beta \in (0,1)$ with $\alpha +\beta <1$. Hence, all the conditions of Corollary 1 and consequently Theorem 1 are satisfied and Υ has infinitely many fixed points.

3. Common Fixed Point Theorem for MVIK-Type Contractions

Throughout this section, we present existing results for common fixed points of MVIK-type contractions.

Theorem 2.

Suppose that $(\Im ,\eta )$ is a complete MS and $\mathsf{{\rm Y}},S:\Im \to CB(\Im )$ are two multivalued maps, such that $\mathsf{{\rm Y}}\upsilon$ and $S\upsilon$ are compact for each $\upsilon \in \Im$. Suppose there exist $\lambda \in [0,1)$ and $\alpha \in (0,1)$, satisfying:

$$\mathcal{H}(\mathsf{{\rm Y}}\upsilon ,S\xi )\le \lambda {\left[\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )\right]}^{\alpha }{\left[\mathsf{\Delta }(\xi ,S\xi )\right]}^{1-\alpha }$$

(8)

for all $\upsilon ,\xi \in \Im$, such that $\upsilon \notin \mathsf{{\rm Y}}\upsilon$ and $\xi \notin S\xi$.

Then, Υ and S have a common fixed point.

Proof. 

Consider ${\upsilon }_0\in \Im$ with ${\upsilon }_0\notin \mathsf{{\rm Y}}{\upsilon }_0$, so that $\mathsf{\Delta }({\upsilon }_0,\mathsf{{\rm Y}}{\upsilon }_0)>0$. Choose ${\upsilon }_1\in \mathsf{{\rm Y}}{\upsilon }_0$. Using Lemma 2, we can select ${\upsilon }_2\in S{\upsilon }_1$, such that:

$$\eta ({\upsilon }_2,{\upsilon }_1)\le \mathcal{H}(S{\upsilon }_1,\mathsf{{\rm Y}}{\upsilon }_0).$$

Similarly, we may choose ${\upsilon }_3\in \mathsf{{\rm Y}}{\upsilon }_2$, such that:

$$\eta ({\upsilon }_3,{\upsilon }_2)\le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_2,S{\upsilon }_1).$$

Continuing in a similar manner, we construct a sequence $\left\{{\upsilon }_n\right\}$, such that ${\upsilon }_{2n+1}\in \mathsf{{\rm Y}}{\upsilon }_{2n}$ and ${\upsilon }_{2n+2}\in S{\upsilon }_{2n+1}$ for all $n=0,1,2,\dots$, satisfying:

$$\eta ({\upsilon }_{2n+2},{\upsilon }_{2n+1})\le \mathcal{H}(S{\upsilon }_{2n+1},\mathsf{{\rm Y}}{\upsilon }_{2n})$$

(9)

and

$$\eta ({\upsilon }_{2n+1},{\upsilon }_{2n})\le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{2n},S{\upsilon }_{2n-1}).$$

(10)

Now,

$$\begin{array}{rr}\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{2n},S{\upsilon }_{2n+1})\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})\right]}^{1-\alpha }\left(\mathrm{using}\left(8\right)\right)\hfill \\ \hfill \Rightarrow {\left[\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})\right]}^{\alpha }& \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]}^{\alpha }\hfill \\ \hfill \Rightarrow \left[\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})\right]& \le {\lambda }^{\frac{1}{\alpha }}\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]\le \lambda \left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right].\hfill \end{array}$$

(11)

Similarly,

$$\begin{array}{rr}\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})& \le \mathcal{H}(S{\upsilon }_{2n-1},\mathsf{{\rm Y}}{\upsilon }_{2n})=\mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{2n},S{\upsilon }_{2n-1})\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_{2n},S{\upsilon }_{2n-1})\right]}^{1-\alpha }\left(\mathrm{using}\left(8\right)\right)\hfill \\ \hfill \Rightarrow {\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]}^{1-\alpha }& \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{2n-1},S{\upsilon }_{2n-1})\right]}^{1-\alpha }\hfill \\ \hfill \Rightarrow \left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]& \le {\lambda }^{\frac{1}{1-\alpha }}\left[\mathsf{\Delta }({\upsilon }_{2n-1},S{\upsilon }_{2n-1})\right]\le \lambda \left[\mathsf{\Delta }({\upsilon }_{2n-1},S{\upsilon }_{2n-1})\right].\hfill \end{array}$$

(12)

Using (11) and (12), we obtain:

$$\begin{array}{cc}\hfill \mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})& \le \lambda \left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]\le {\lambda }^2\left[\mathsf{\Delta }({\upsilon }_{2n-1},S{\upsilon }_{2n-1})\right]\hfill \\ \hfill & \le {\lambda }^3\left[\mathsf{\Delta }({\upsilon }_{2n-2},\mathsf{{\rm Y}}{\upsilon }_{2n-2})\right]\le \dots \le {\lambda }^{2n+1}\left[\mathsf{\Delta }({\upsilon }_0,\mathsf{{\rm Y}}{\upsilon }_0)\right].\hfill \end{array}$$

Taking the limits on both sides of the last inequality, we have:

$$\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})⟶0\mathrm{as}n⟶\infty .$$

(13)

Similarly, we have:

$$\begin{array}{cc}\hfill \mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})& \le \lambda \left[\mathsf{\Delta }({\upsilon }_{2n-1},S{\upsilon }_{2n-1})\right]\le {\lambda }^2\left[\mathsf{\Delta }({\upsilon }_{2n-2},\mathsf{{\rm Y}}{\upsilon }_{2n-2})\right]\hfill \\ \hfill & \le \dots \le {\lambda }^{2n}\left[\mathsf{\Delta }({\upsilon }_0,\mathsf{{\rm Y}}{\upsilon }_0)\right].\hfill \end{array}$$

Again taking the limit, we have:

$$\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})⟶0\mathrm{as}n⟶\infty .$$

(14)

Now,

$$\begin{array}{rr}\eta ({\upsilon }_{2n+1},{\upsilon }_{2n+2})& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{2n},S{\upsilon }_{2n+1})\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})\right]}^{1-\alpha }\left(\mathrm{using}\left(8\right)\right)\hfill \\ \hfill & \le \lambda {\left[\eta ({\upsilon }_{2n},{\upsilon }_{2n+1})\right]}^{\alpha }{\left[\eta ({\upsilon }_{2n+1},{\upsilon }_{2n+2})\right]}^{1-\alpha }\left(\mathrm{using}\mathrm{Lemma}1\right)\hfill \\ \hfill \Rightarrow {\left[\eta ({\upsilon }_{2n+1},{\upsilon }_{2n+2})\right]}^{\alpha }& \le \lambda {\left[\eta ({\upsilon }_{2n},{\upsilon }_{2n+1})\right]}^{\alpha }\hfill \\ \hfill \Rightarrow \eta ({\upsilon }_{2n+1},{\upsilon }_{2n+2})& \le {\lambda }^{\frac{1}{\alpha }}\left[\eta ({\upsilon }_{2n},{\upsilon }_{2n+1})\right]\le \lambda \left[\eta ({\upsilon }_{2n},{\upsilon }_{2n+1})\right].\hfill \end{array}$$

(15)

Similarly,

$$\eta ({\upsilon }_{2n+1},{\upsilon }_{2n})\le \lambda \left[\eta ({\upsilon }_{2n},{\upsilon }_{2n-1})\right].$$

(16)

From (15) and (16), we have:

$$\eta ({\upsilon }_n,{\upsilon }_{n+1})\le \lambda \left[\eta ({\upsilon }_{n-1},{\upsilon }_n)\right].$$

(17)

Now, using similar techniques as those in Theorem 1, we can show that the sequence $\left\{{\upsilon }_n\right\}$ is a Cauchy sequence.

Since $(\Im ,\eta )$ is complete, there exists $\upsilon \in \Im$, such that ${\upsilon }_n⟶\upsilon$, as $n\to \infty$.

Next, we claim that $\upsilon$ is a common fixed point of $\mathsf{{\rm Y}}$ and S. Now,

$$\begin{array}{rr}\mathsf{\Delta }({\upsilon }_{2n+2},\mathsf{{\rm Y}}\upsilon )& \le \mathcal{H}(S{\upsilon }_{2n+1},\mathsf{{\rm Y}}\upsilon )\left(\mathrm{using}\mathrm{Lemma}1\right)\hfill \\ \hfill & =\mathcal{H}(\mathsf{{\rm Y}}\upsilon ,S{\upsilon }_{2n+1})\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )\right]}^{\alpha }{\left[\mathsf{\Delta }({\upsilon }_{2n+1},S{\upsilon }_{2n+1})\right]}^{1-\alpha }\left(\mathrm{using}\left(8\right)\right).\hfill \end{array}$$

(18)

Taking the limit in (18) as $n\to \infty$ and using (13) and $\left(ii\right)$ of Remark 1, we obtain $\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )=0$. Therefore, $\upsilon \in \mathsf{{\rm Y}}\upsilon$.

Additionally, we have:

$$\begin{array}{rr}\mathsf{\Delta }({\upsilon }_{2n+1},S\upsilon )& \le \mathcal{H}(\mathsf{{\rm Y}}{\upsilon }_{2n},S\upsilon )\hfill \\ \hfill & \le \lambda {\left[\mathsf{\Delta }({\upsilon }_{2n},\mathsf{{\rm Y}}{\upsilon }_{2n})\right]}^{\alpha }{\left[\mathsf{\Delta }(\upsilon ,S\upsilon )\right]}^{1-\alpha }.\hfill \end{array}$$

(19)

Taking the limit in (19) and using (14) and $\left(ii\right)$ of Remark 1, we obtain $\mathsf{\Delta }(\upsilon ,S\upsilon )=0$—i.e., $\upsilon \in S\upsilon$.

Hence, $\upsilon$ is a common fixed point of $\mathsf{{\rm Y}}$ and S. □

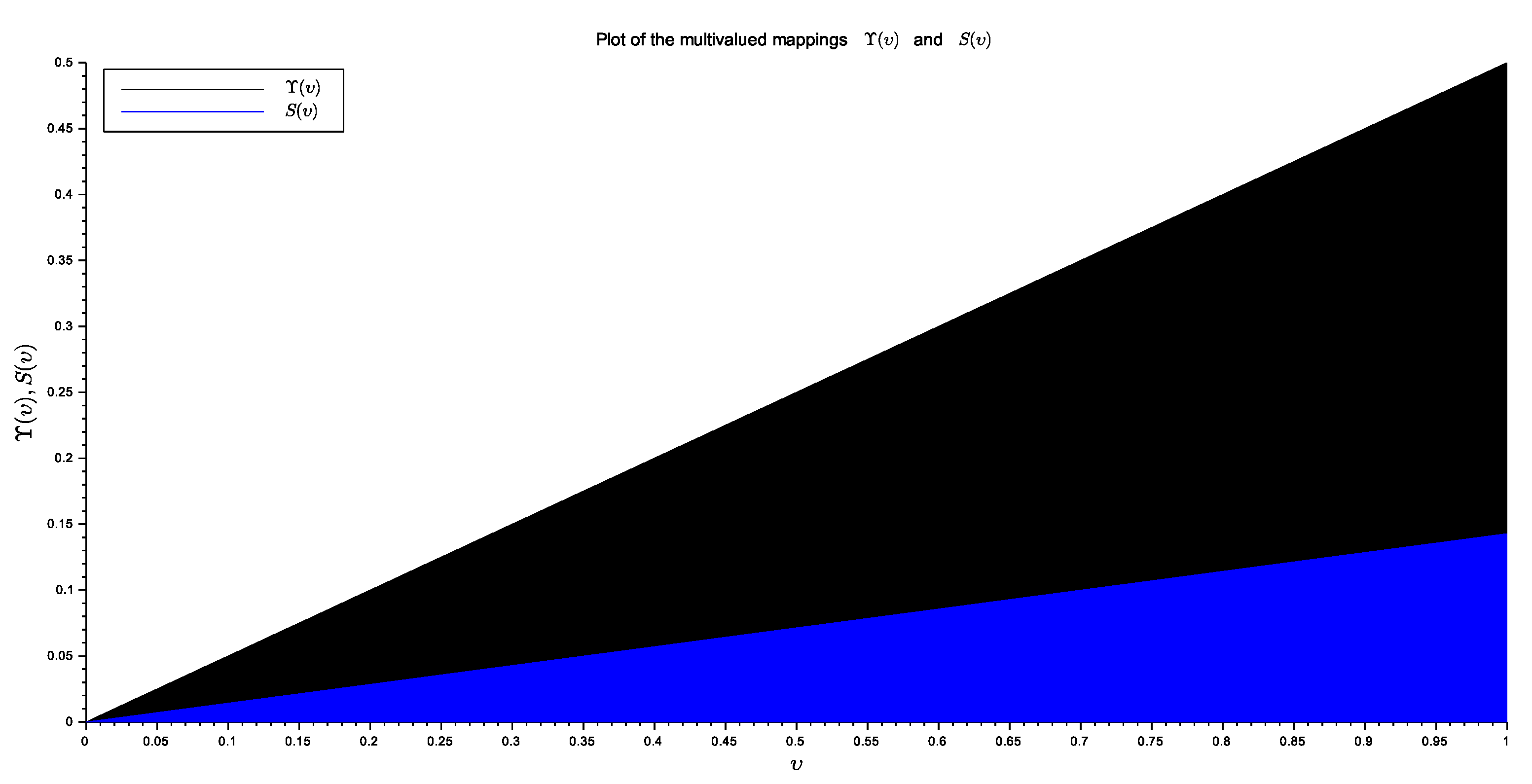
Example 2.

Assume $\Im =[0,1]$ with usual metric $\eta (\upsilon ,\xi )=|\upsilon -\xi |$. Construct $\mathsf{{\rm Y}},S:\Im \to CB(\Im )$, such that:

$$\mathsf{{\rm Y}}\upsilon =\{t\in \Im :0\le t\le \frac{\upsilon }{2}\}$$

and

$$S\upsilon =\{t\in \Im :0\le t\le \frac{\upsilon }{7}\}$$

for all $\upsilon \in \Im$ (see Figure 1).

Figure 1. Combined plot of the multivalued mappings $\mathsf{{\rm Y}}$ and S.

Without a loss of generality, suppose that $\upsilon \ne 0$, $\xi \ne 0$, and $\upsilon <\xi$. Then,

$\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )=|\upsilon -\frac{\upsilon }{2}|$, $\mathsf{\Delta }(\xi ,S\xi )=|\xi -\frac{\xi }{7}|$ and $\mathcal{H}(\mathsf{{\rm Y}}\upsilon ,S\xi )=|\frac{\upsilon }{2}-\frac{\xi }{7}|$.

Therefore, we can check that $|\frac{\upsilon }{2}-\frac{\xi }{7}|\le \lambda |\upsilon -\frac{\upsilon }{2}{|}^{\alpha }{|\xi -\frac{\xi }{7}|}^{1-\alpha }$ is satisfied for $\lambda =\frac{9}{10}$,$\alpha =\frac{1}{2}$ and for all $\upsilon ,\xi \in \Im$, such that $\upsilon \notin \mathsf{{\rm Y}}\upsilon$ and $\xi \notin \mathsf{{\rm Y}}\xi$.

Hence, all the conditions of Theorem 2 are satisfied and hence $0\in \Im$ is a common fixed point of Υ and S.

4. Conclusions and Future Work

In this paper, we introduced MVIK-type contraction and multivalued ($\lambda$, $\alpha$, $\beta$)-interpolative Kannan-type contraction mappings. The existence of fixed point results was investigated for such maps. The existence of common fixed points for MVIK-type contractions was also established. We provided a new and easier technique of proof for common fixed point theorems of multivalued maps. As mentioned earlier, it was observed that all generalized interpolative Kannan-type contractions need not have a fixed point in a complete MS. Hence, we attempted to address this question of existence for certain multivalued mappings. However, we assumed stronger conditions in our hypothesis, such as the compactness of the images of the map under consideration. It would be interesting to investigate, in future work, if this condition can be relaxed and the existence of these mappings can still be proven.

In Definition 2, in place of ${\left[\mathsf{\Delta }(\upsilon ,\mathsf{{\rm Y}}\upsilon )\right]}^{\alpha }$, it may be sufficient to use a real increasing function f, such that $f\left(\mathsf{\Delta }\right(\upsilon ,\mathsf{{\rm Y}}\upsilon \left)\right)$ has suitable properties. In place of ${\left[\mathsf{\Delta }(\xi ,\mathsf{{\rm Y}}\xi )\right]}^{1-\alpha }$, it may be sufficient to assume a real decreasing function g, such that $g\left(\mathsf{\Delta }\right(\xi ,\mathsf{{\rm Y}}\xi \left)\right)$ has suitable properties. Definition 3 and Theorem 2 may also be revised in light of these considerations. All these factors will lead to an important extension of the current results.

Establishing the conditions that imply the uniqueness of a fixed point for multivalued mappings is always of special interest.