The Relationships among Three Kinds of Divisions of Type-1 Fuzzy Numbers

Abstract

The division operation for type-1 fuzzy numbers in its original form is not invertible for the multiplication operation. This is an essential drawback in some applications. To eliminate this drawback several approaches are proposed: the generalized Hukuhara division, generalized division and granular division. In this paper, the expression of granular division is introduced, and the relationships among generalized Hukuhara division, generalized division and granular division are clarified.

1. Introduction

The search for some invertible operations has been an issue for a long time. In 1965, Ref. [1] proposed a difference based on the extension principle, which is an extension of the interval subtraction operation according to the addition and multiplication operations of type-1 fuzzy numbers (T1FNs). This method provides a difference between T1FNs. However, this difference is not the invertible operation of addition for T1FNs. The pioneer work of finding an invertible operation for the addition can be traced to 1967 [2] when Hukuhara proposed the Hukuhara difference (H-difference), which is well known and largely used. However, the existence of H-difference has very restrictive limitations [3]. To overcome this weakness, Stefanini, Bede and Mazandarani introduced a generalized Hukuhara difference (gH-difference) [3], a generalized difference (g-difference) [4,5] and a granular difference (gr-difference) [6].

The division operation of T1FNs has also received much attention. Similarly to the gH-difference, which is defined by Stefanin in [3], the idea is to introduce the generalized division of real intervals and T1FNs by Stefanini [7] (we called the generalized division gH-division in this paper, while Stefanini called it g-division), which gives an inverse operation for the multiplication operation of T1FNs. However, Stefanini also illustrated that the result of the gH-division between two T1FNs is not always a T1FN. Then, Stefanini proposed another division in [7] (we called it g-division, while Stefanini considered it as a generalization of the division of T1FNs). The introduction of this kind of division opens up more fields of applications to interval and fuzzy arithmetic and analysis, such as the concepts of differentiability [3,4,8], the solution of equations [9,10], interval and fuzzy regression analysis [11,12,13], interval and fuzzy integral and differential equations [14,15,16,17], etc.

The horizontal membership function was introduced by Piegat [15], which transforms T1FNs as an algebraic form with a variable that called a relative distance measure (RDM) variable (Please refer to [18] for more details about RDM variable). Through this expression, we could transform the four arithmetic operations of T1FNs into four arithmetic operations of an algebraic expression in order to calculate them easily, which includes the gr-difference and granular division (gr-division). Details on the horizontal membership function and the gr-division are discussed in later sections.

To know which of these three divisions is more practical, we have to consider the relationships among these divisions. Costa et al. in [19] discussed the inclusion isotonic relationship of the gH-division and found that the gH-division was not inclusion isotonic. However, we analyze the relationships among gH-division, g-division and gr-division more clearly in this paper. Furthermore, the following problems are well worth considering in order to help people reasonably select the corresponding division operation in practice. The basic questions posed below are then discussed and conclusions are drawn.

(1)

It has been proved that if the g-division or the gr-division exists between any two T1FNs, then the following question arises: do they get the same results?

(2)

It is also obvious that the g-division is more general than the gH-division and they have the same result if the gH-division exists. Therefore, another question is: does the gH-division have the same relationship with the gr-division or not?

This paper is organized as follows. We first briefly described some related concepts in Section 2. After the statement of these basic problems above, we give an expression of the gr-division between two T1FNs and the complete relationships characterization among gH-division, g-division and gr-division are studied, then we analyze the properties of these approaches, and some examples are illustrated in Section 3. Finally, conclusions and future work are summarized in Section 4.

2. Basic Concepts

We provide some basic terminologies and related definitions which are necessary for the understanding of subsequent results in this section.

Throughout this paper, the set of all real numbers, bounded closed intervals of real numbers and T1FNs on real numbers is denoted by $\mathbb{R}$, $K_c$ and ${\mathcal{F}}_1$, respectively. $cl\left(A\right)$ denotes the closure of set A.

Definition 1.

Let $u\in {\mathcal{F}}_1$. For $\alpha \in (0,1]$, the α-level set of u is defined by ${\left[u\right]}_{\alpha }=\left\{x\right|x\in \mathbb{R},u\left(x\right)\ge \alpha \}$ and for $\alpha =0$ by the closure of the support ${\left[u\right]}_0=cl\left\{x\right|x\in \mathbb{R},u\left(x\right)>\alpha \}$ whose lower and upper endpoints are represented as $u_{\alpha }^{-}$ and $u_{\alpha }^{+}$ with $\alpha \in [0,1]$.

A division of fuzzy numbers and real intervals can be introduced, which is similar to the gH-difference. Let $A=[a^{-},a^{+}]\in K_c$ and $B=[b^{-},b^{+}]\in K_c$ with $b^{+}<0$ or $b^{-}>0$, which means that $0\notin B$. The multiplication $C=AB=[c^{-},c^{+}]$ and the multiplicative “inverse” of A is given by

$$\begin{array}{c}\hfill c^{-}=min\left\{a^{-}{b}^{-},a^{-}{b}^{+},a^{+}{b}^{-},a^{+}{b}^{+}\right\},c^{+}=max\left\{a^{-}{b}^{-},a^{-}{b}^{+},a^{+}{b}^{-},a^{+}{b}^{+}\right\},\end{array}$$

(1)

and

$$\begin{array}{c}\hfill A^{-1}=\left[\frac{1}{a^{+}},\frac{1}{a^{-}}\right].\end{array}$$

(2)

Definition 2

([7]). Let $A,B\in K_c$ with $A=[a^{-},a^{+}]$ and $B=[b^{-},b^{+}]$, then the gH-division ${÷}_{gH}$ is defined as

$$\begin{array}{c}\hfill A{÷}_{gH}B=C⟺\left\{\begin{array}{c}\left(i\right)A=BC,\hfill \\ or\hfill \\ \left(ii\right)B=A{C}^{-1}.\hfill \end{array}\right.\end{array}$$

(3)

We called it $g{H}_i$-division or $g{H}_{ii}$-division if $\left(i\right)$ or $\left(ii\right)$ in (3) holds, respectively.

Remark 1.

We can get the following results for the gH-division from the definition (see [7] for more details).

(1) 

If $0<a^{-}\le a^{+},b^{-}\le b^{+}<0$ and $a^{-}{b}^{-}\ge a^{+}{b}^{+}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{+}}{b^{-}},c^{+}=\frac{a^{-}}{b^{+}},\end{array}$$

(4)

(2) 

If $0<a^{-}\le a^{+},0<b^{-}\le b^{+}$ and $a^{-}{b}^{+}\le a^{+}{b}^{-}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{-}}{b^{-}},c^{+}=\frac{a^{+}}{b^{+}},\end{array}$$

(5)

(3) 

If $a^{-}\le a^{+}<0,b^{-}\le b^{+}<0$ and $a^{+}{b}^{-}\le a^{-}{b}^{+}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{+}}{b^{+}},c^{+}=\frac{a^{-}}{b^{-}},\end{array}$$

(6)

(4) 

If $a^{-}\le a^{+}<0,0<b^{-}\le b^{+}$ and $a^{-}{b}^{-}\le a^{+}{b}^{+}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{-}}{b^{+}},c^{+}=\frac{a^{+}}{b^{-}},\end{array}$$

(7)

(5) 

If $a^{-}\le 0,a^{+}\ge 0,b^{-}\le b^{+}<0$ and

$$\begin{array}{c}\hfill c^{-}=\frac{a^{+}}{b^{-}},c^{+}=\frac{a^{-}}{b^{-}},\end{array}$$

(8)

(6) 

If $a^{-}\le 0,a^{+}\ge 0,0<b^{-}\le b^{+}$ and

$$\begin{array}{c}\hfill c^{-}=\frac{a^{-}}{b^{+}},c^{+}=\frac{a^{+}}{b^{+}},\end{array}$$

(9)

and $\left(i\right)$ in (3) is satisfied which means that $\left(1\right)$–$\left(6\right)$ are $g{H}_i$-divisions.

(7) 

If $0<a^{-}\le a^{+},b^{-}\le b^{+}<0$ and $a^{-}{b}^{-}\le a^{+}{b}^{+}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{-}}{b^{+}},c^{+}=\frac{a^{+}}{b^{-}},\end{array}$$

(10)

(8) 

If $0<a^{-}\le a^{+},0<b^{-}\le b^{+}$ and $a^{-}{b}^{+}\ge a^{+}{b}^{-}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{+}}{b^{+}},c^{+}=\frac{a^{-}}{b^{-}},\end{array}$$

(11)

(9) 

If $a^{-}\le a^{+}<0,b^{-}\le b^{+}<0$ and $a^{+}{b}^{-}\ge a^{-}{b}^{+}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{-}}{b^{-}},c^{+}=\frac{a^{+}}{b^{+}},\end{array}$$

(12)

(10) 

If $a^{-}\le a^{+}<0,0<b^{-}\le b^{+}$ and $a^{-}{b}^{-}\ge a^{+}{b}^{+}$, then

$$\begin{array}{c}\hfill c^{-}=\frac{a^{+}}{b^{-}},c^{+}=\frac{a^{-}}{b^{+}},\end{array}$$

(13)

and $\left(ii\right)$ in (3) is satisfied which means that $\left(7\right)$–$\left(10\right)$ are $g{H}_{ii}$-divisions. In conclusion, we have that

$$\begin{array}{c}\hfill {÷}_{gH}[b^{-},b^{+}]:=\left[min\frac{a^{\pm }}{b^{\pm }},max\frac{b^{\pm }}{b^{\pm }}\right].\end{array}$$

(14)

Definition 3

([7]). Let $a,b\in {\mathcal{F}}_1$ have α-level sets ${\left[a\right]}_{\alpha }=[a_{\alpha }^{-},a_{\alpha }^{+}]$ and ${\left[b\right]}_{\alpha }=[b_{\alpha }^{-},b_{\alpha }^{+}]$ with $0\notin {\left[b\right]}_{\alpha }$, for each $\alpha \in [0,1]$. The gH-division ${÷}_{gH}$ calculates the T1FN $c=a{÷}_{gH},b\in {\mathcal{F}}_1$ is defined by

$$\begin{array}{c}\hfill {\left[a\right]}_{\alpha }{÷}_{gH}{\left[b\right]}_{\alpha }={\left[c\right]}_{\alpha }⟺\left\{\begin{array}{c}\left(i\right){\left[a\right]}_{\alpha }={\left[b\right]}_{\alpha }{\left[c\right]}_{\alpha },\hfill \\ or\hfill \\ \left(ii\right){\left[b\right]}_{\alpha }={\left[a\right]}_{\alpha }{\left[c\right]}_{\alpha }^{-1},\hfill \end{array}\right.\end{array}$$

(15)

where the α-level sets and the multiplicative “inverse” are written as ${\left[c\right]}_{\alpha }=[c_{\alpha }^{-},c_{\alpha }^{+}]$ and ${\left[c\right]}_{\alpha }^{-1}=[1/c_{\alpha }^{+},1/c_{\alpha }^{-}]$.

However, there exist two T1FNs whose gH-division is not a T1FN, for more details, please refer to [7]. If the gH-division ${\left[a\right]}_{\alpha }{÷}_{gH}{\left[b\right]}_{\alpha }$ do not define a proper T1FN, Stefanini [7] proposed a new division named g-division (${÷}_g$) with $\alpha$-level sets that can obtain an approximated division for T1FNs. Similarly to what is done in [5], the convexification is necessary for the new division to always be a T1FN.

Definition 4

([7]). For any $a,b\in {\mathcal{F}}_1$, the g-division with α-level sets is defined as

$$\begin{array}{c}\hfill {\left[a{÷}_{g}b\right]}_{\alpha }=cl\left(conv\bigcup _{\mu \ge \alpha }\left({\left[a\right]}_{\mu }{÷}_{gH}{\left[b\right]}_{\mu }\right)\right).\end{array}$$

(16)

Here, $conv\left(A\right)$ denotes the convex hull of set A. It can be considered that $z=a{÷}_{g}b$ is a generalization of the division of T1FNs because the g-division exists for any $a,b$ with $0\notin {\left[b\right]}_{\mu }$ for all $\mu \in [0,1]$.

Piegat et al. examined a new definition of membership function based on constraint interval arithmetic (CIA) about T1FNs, multidimensional relative distance measure interval arithmetic (RDM-IA) and multidimensional fuzzy arithmetic based on RDM (MD-RDM-F arithmetic), which have been studied as a powerful and effective tool in interval arithmetic and fuzzy mathematics (see [15,20,21,22,23,24]), which overcomes the difficulties found in traditional membership function.

Definition 5

([6,15]). Let $a:[p,q]\to [0,1]$ be a T1FN. The horizontal membership function $a^{gr}:[0,1]\times [0,1]\to [p,q]$ is written as $a^{gr}(\mu ,{\alpha }_a)=a_{\mu }^{-}+(a_{\mu }^{+}-a_{\mu }^{-}){\alpha }_a$ where “gr” represents the granule of information in $x\in [p,q],\mu \in [0,1]$ is the membership degree of x in $a\left(x\right)$ and ${\alpha }_a\in [0,1]$ is called an RDM variable.

Remark 2

([6,25]). $\mathcal{H}\left(a\right)\triangleq a^{gr}(\mu ,{\alpha }_a)$ can be denoted as the horizontal membership function of $a\left(x\right)\in {\mathcal{F}}_1$ and using

$$\begin{array}{cc}\hfill {\mathcal{H}}^{-1}\left(a^{gr}(\mu ,{\alpha }_a)\right)& ={\left[a\right]}_{\mu }=\left[\underset{\beta ⩾\mu }{inf}\underset{{\alpha }_a}{min}{a}^{gr}(\beta ,{\alpha }_a),\underset{\beta ⩾\mu }{sup}\underset{{\alpha }_a}{max}{a}^{gr}(\beta ,{\alpha }_a)\right]\hfill \end{array}$$

(17)

we can obtain the μ-level sets of span of the information granule named vertical membership function of $a\left(x\right)$.

Definition 6

([6]). We say that two T1FNs a and b are equal if and only if for all ${\alpha }_a={\alpha }_b\in [0,1]$, $\mathcal{H}\left(a\right)=\mathcal{H}\left(b\right)$ holds.

Next, we give the definition of four arithmetic operations between T1FNs based on horizontal membership functions.

Definition 7

([6,25]). Let a and b be two T1FNs and $a^{gr}(\mu ,{\alpha }_a)$ and $a^{gr}(\mu ,{\alpha }_a)$ be their horizontal membership functions. Then, the granular division (gr-division) $a{÷}_{gr}b$ is a T1FN, with w such that $\mathcal{H}\left(w\right)\triangleq a^{gr}(\mu ,{\alpha }_a)÷b^{gr}(\mu ,{\alpha }_b)$ with $0\notin b^{gr}(\mu ,{\alpha }_b)$.

Remark 3

([6]). Let $w=a{÷}_{gr}b$. Then, ${\left[w\right]}_{\mu }={\mathcal{H}}^{-1}\left(\frac{a^{gr}(\mu ,{\alpha }_a)}{b^{gr}(\mu ,{\alpha }_b)}\right)$ always presents μ-level sets of w.

3. Main Results

In this section, we give a complete characterization of the relationships among gH-division, g-division and gr-division. Recently, the search for the division operation between T1FNs has received much attention, in order to find the inverse operation of multiplication, such as the study in [26,27,28,29,30,31].

We give the expression of gr-division first. For any $m,n\in {\mathcal{F}}_1$, ${\left[m\right]}_{\beta }=[m_{\beta }^{-},m_{\beta }^{+}]$ and ${\left[n\right]}_{\beta }=[n_{\beta }^{-},n_{\beta }^{+}]$ are their $\alpha$-level sets, $\mathcal{H}(·)$ denotes the horizontal membership function of “·”. According to Definition 5 we have

$$\begin{array}{c}\hfill \mathcal{H}\left(v\right)=\frac{\mathcal{H}\left(m\right)}{\mathcal{H}\left(n\right)}=\frac{m_{\alpha }^{-}+(m_{\alpha }^{+}-m_{\alpha }^{-}){\alpha }_m}{n_{\alpha }^{-}+(n_{\alpha }^{+}-n_{\alpha }^{-}){\alpha }_n}.\end{array}$$

(18)

Because of the monotonicity of numerator and denominator with respect to ${\alpha }_m,{\alpha }_n$ we can get the following extreme values:

$$\begin{array}{cc}\hfill & {\alpha }_m=0,min\{m_{\alpha }^{-}+(m_{\alpha }^{+}-m_{\alpha }^{-}){\alpha }_m\}=m_{\alpha }^{-},\hfill \\ \hfill & {\alpha }_m=1,max\{m_{\alpha }^{-}+(m_{\alpha }^{+}-m_{\alpha }^{-}){\alpha }_m\}=m_{\alpha }^{+},\hfill \\ \hfill & {\alpha }_n=0,min\{n_{\alpha }^{-}+(n_{\alpha }^{+}-n_{\alpha }^{-}){\alpha }_n\}=n_{\alpha }^{-},\hfill \\ \hfill & {\alpha }_n=1,max\{n_{\alpha }^{-}+(n_{\alpha }^{+}-n_{\alpha }^{-}){\alpha }_n\}=n_{\alpha }^{+}.\hfill \end{array}$$

(19)

Moreover, with (17), we can get the expression of the gr-division in the following theorem.

Theorem 1.

For any $m,n\in {\mathcal{F}}_1,m{÷}_{gr},n$ is a T1FN u such that $\mathcal{H}\left(u\right)=\mathcal{H}\left(m\right)/\mathcal{H}\left(n\right)$ and

$$\begin{array}{c}\hfill {\left[u\right]}_{\alpha }={\left[m{÷}_{gr}n\right]}_{\alpha }=[\underset{\beta \ge \alpha }{inf}min\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }},\underset{\beta \ge \alpha }{sup}max\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }}].\end{array}$$

(20)

Proof of Theorem 1. 

The horizontal membership functions of m and n are written as

$$\begin{array}{cc}\hfill & \mathcal{H}\left(m\right)=m_{\alpha }^{-}+(m_{\alpha }^{+}-m_{\alpha }^{-}){\alpha }_m,\hfill \\ \hfill & \mathcal{H}\left(n\right)=n_{\alpha }^{-}+(n_{\alpha }^{+}-n_{\alpha }^{-}){\alpha }_n,\hfill \end{array}$$

(21)

respectively. Then, by (18) we can get the horizontal membership function of $m{÷}_{gr}n$ (which is represented as the T1FN u) as follows:

$$\begin{array}{c}\hfill \mathcal{H}\left(u\right)=\frac{\mathcal{H}\left(m\right)}{\mathcal{H}\left(n\right)}=\frac{m_{\alpha }^{-}+(m_{\alpha }^{+}-m_{\alpha }^{-}){\alpha }_m}{n_{\alpha }^{-}+(n_{\alpha }^{+}-n_{\alpha }^{-}){\alpha }_n}.\end{array}$$

(22)

From (19) and (17), we have

$$\begin{array}{cc}\hfill {\mathcal{H}}^{-1}\left(u^{gr}(\mu ,{\alpha }_u)\right)& ={\left[u\right]}_{\mu }=\left[\underset{\beta \ge \alpha }{inf}min\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }},\underset{\beta \ge \alpha }{sup}max\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }}\right].\hfill \end{array}$$

(23)

□

Next we clarify the relationships among the three divisions. For any $m,n\in {\mathcal{F}}_1$, let ${\left[m{÷}_{gH}n\right]}_{\alpha }={\left[u^{gH}\right]}_{\alpha },{\left[m{÷}_{g}n\right]}_{\alpha }={\left[u^g\right]}_{\alpha }$ and ${\left[m{÷}_{gr}n\right]}_{\alpha }={\left[u^{gr}\right]}_{\alpha }$ denote the gH-division, g-division and gr-division, respectively. The following theorems hold.

Theorem 2.

If there exists $u=m{÷}_{gH},n\in {\mathcal{F}}_1$, then ${\left[u^{gH}\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$ holds. Moreover, if $m=n$ then we have ${\left[u^{gH}\right]}_{\alpha }={\left[u^{gr}\right]}_{\alpha }$.

Proof of Theorem 2. 

Based on (14) and (20) we have

$$\begin{array}{c}\hfill {\left[u^{gH}\right]}_{\alpha }=[min\frac{m_{\alpha }^{\pm }}{n_{\alpha }^{\pm }},max\frac{m_{\alpha }^{\pm }}{n_{\alpha }^{\pm }}]\subseteq [\underset{\beta \ge \alpha }{inf}min\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }},\underset{\beta \ge \alpha }{sup}max\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }}]={[u^{gr}]}_{\alpha },\end{array}$$

(24)

which implies that ${\left[m{÷}_{gH}n\right]}_{\alpha }\subseteq {\left[m{÷}_{gr}n\right]}_{\alpha }$ holds.

If $m=n$, according to Definition 6 and (17), $\mathcal{H}\left(u^{gr}\right)=\mathcal{H}\left(m\right)/\mathcal{H}\left(n\right)=1,{\left[u^{gr}\right]}_{\alpha }=[1,1]$. Since ${\left[u^{gH}\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$ we have ${\left[u^{gH}\right]}_{\alpha }={\left[u^{gr}\right]}_{\alpha }=[1,1]$. □

Theorem 3.

${\left[u^g\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$ holds for all $m,n\in {\mathcal{F}}_1$. Moreover, if $m=n$ then we have ${\left[u^g\right]}_{\alpha }={\left[u^{gr}\right]}_{\alpha }$.

Proof of Theorem 3. 

The relation (20) is equivalent to

$$\begin{array}{c}\hfill {\left[u^{gr}\right]}_{\alpha }=[\underset{\beta \ge \alpha }{inf}min\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }},\underset{\beta \ge \alpha }{sup}max\frac{m_{\beta }^{\pm }}{n_{\beta }^{\pm }}]=cl\left(conv\bigcup _{\beta \ge \alpha }\left({\left[m\right]}_{\beta }{÷}_{gr}{\left[n\right]}_{\beta }\right)\right).\end{array}$$

(25)

According to (16) we have

$$\begin{array}{c}\hfill {\left[u^g\right]}_{\alpha }={\left[m{÷}_{g}n\right]}_{\alpha }=cl\left(conv\bigcup _{\beta \ge \alpha }\left({\left[m\right]}_{\beta }{÷}_{gH}{\left[n\right]}_{\beta }\right)\right).\end{array}$$

(26)

Because of ${\left[m\right]}_{\beta }{÷}_{gH}{\left[n\right]}_{\beta }\subseteq {\left[m\right]}_{\beta }{÷}_{gr}{\left[n\right]}_{\beta }$, we have ${\left[u^g\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$.

If $m=n$ then ${\left[u^{gr}\right]}_{\alpha }=[1,1]$. Since ${\left[u^g\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$ we have ${\left[u^g\right]}_{\alpha }={\left[u^{gr}\right]}_{\alpha }=[1,1]$. □

We illustrate Theorems 2 and 3 with some examples in which the T1FNs are defined in terms of their $\alpha$-level sets.

Example 1.

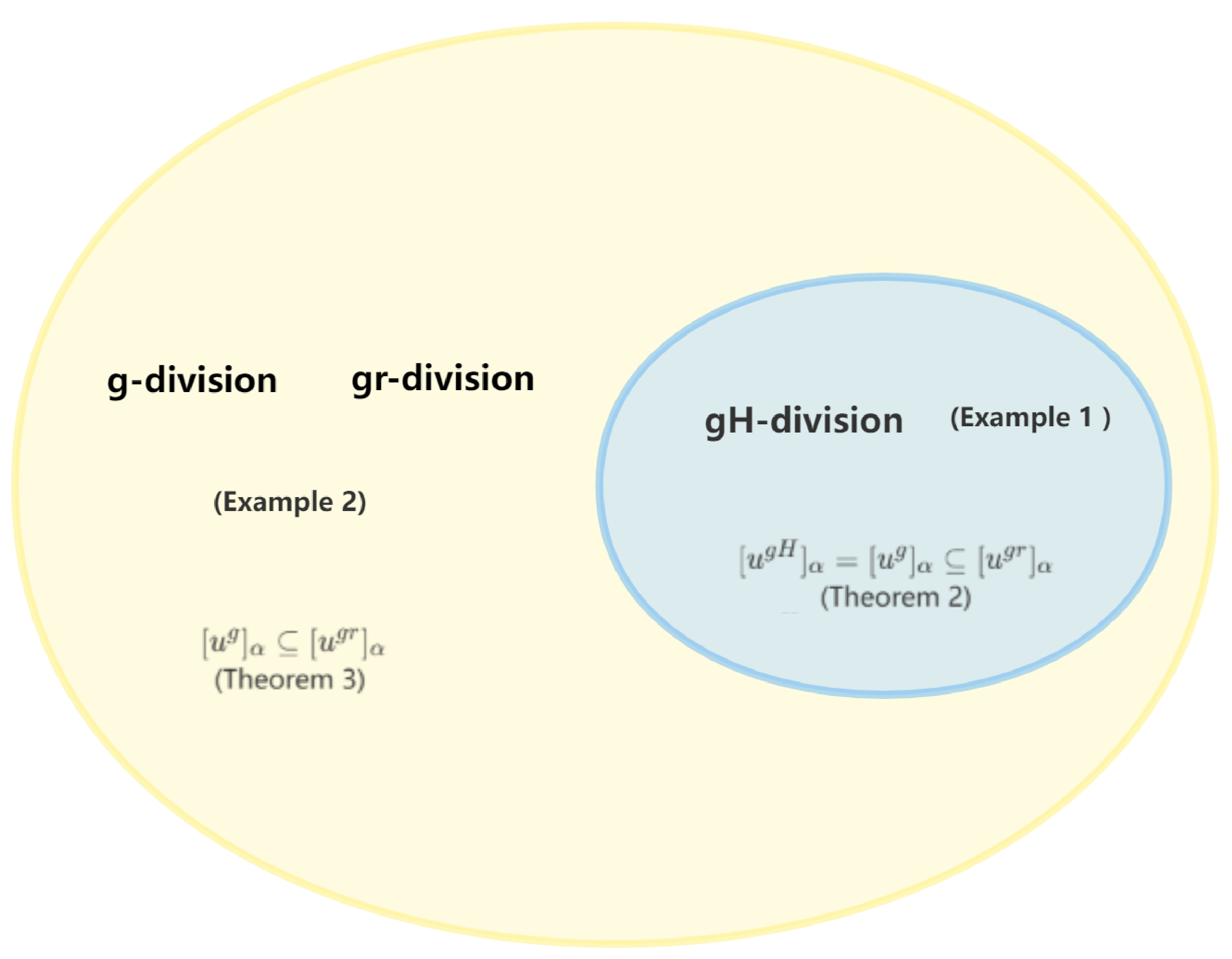
$[1+2\alpha ,7-4\alpha ]{÷}_{gH}[-3+\alpha ,-1-\alpha ]=[(7-4\alpha )/(-3+\alpha ),(1+2\alpha )/(-1-\alpha )]$ [7]. Based on (20) we can get the gr-division:

$$\begin{array}{cc}\hfill {}_{\beta }& =[\underset{\alpha \ge \beta }{inf}\frac{5-3.5\alpha }{-1-\alpha },\underset{\alpha \ge \beta }{sup}\frac{1+0.5\alpha }{-4+2\alpha }]\hfill \\ \hfill & =[\frac{5-3.5\beta }{-1-\beta },\frac{1+0.5\beta }{-4+2\beta }]\hfill \\ \hfill & \supset [\frac{7-4\beta }{-3+\beta },\frac{1+2\beta }{-1-\beta }]={\left[u^{gH}\right]}_{\beta };\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill {}_{\beta }& =cl\left(conv\bigcup _{\alpha \ge \beta }\left({\left[m\right]}_{\alpha }{÷}_{gH}{\left[n\right]}_{\alpha }\right)\right)\hfill \\ \hfill & =cl\left(conv\bigcup _{\alpha \ge \beta }[\frac{7-4\alpha }{-3+\alpha },\frac{1+2\alpha }{-1-\alpha }]\right)\hfill \\ \hfill & =[\frac{7-4\beta }{-3+\beta },\frac{1+2\beta }{-1-\beta }]={\left[u^{gH}\right]}_{\beta }.\hfill \end{array}$$

(28)

Example 2.

$[1+0.5\alpha ,5-3.5\alpha ]{÷}_{gH}[-4+2\alpha ,-1-\alpha ]=[(5-3.5\alpha )/(-4+2\alpha ),(1+0.5\alpha )/(-1-\alpha )]$ exists but the resulting intervals are not the α-level sets of a T1FN. Using (16) and (20) we can get the g-division and the gr-division:

$$\begin{array}{cc}\hfill {}_{\alpha }={\left[m{÷}_{g}n\right]}_{\alpha }& =cl\left(conv\bigcup _{\beta \ge \alpha }\left({\left[m\right]}_{\beta }{÷}_{gH}{\left[n\right]}_{\beta }\right)\right)\hfill \\ \hfill & =cl\left(conv\bigcup _{\beta \ge \alpha }\left[\frac{5-3.5\beta }{-4+2\beta },\frac{1+0.5\beta }{-1-\beta }\right]\right)\hfill \\ \hfill & =\left[\frac{5-3.5\alpha }{-4+2\alpha },-0.75\right];\hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill {}_{\alpha }={\left[m{÷}_{gr}n\right]}_{\alpha }& =cl\left(conv\bigcup _{\beta \ge \alpha }\left({\left[m\right]}_{\beta }{÷}_{gr}{\left[n\right]}_{\beta }\right)\right)\hfill \\ \hfill & =cl\left(conv\bigcup _{\beta \ge \alpha }\left[\frac{5-3.5\beta }{-1-\beta },\frac{1+0.5\beta }{-4+2\beta }\right]\right)\hfill \\ \hfill & =\left[\frac{5-3.5\alpha }{-1-\alpha },\frac{1+0.5\alpha }{-4+2\alpha }\right]\hfill \\ \hfill & \supset \left[\frac{5-3.5\alpha }{-4+2\alpha },-0.75\right]={\left[u^g\right]}_{\alpha }.\hfill \end{array}$$

(30)

In terms of generalization, the gr-division and the g-division are the most generalized but they have different results, and the gH-division has the minimum application range among these three division we talked about.

The relationships among gH-division, g-division and gr-division have been shown in

Table 1. The relationships between $m^{gH},m^g$ and $m^{gr}$.

	gH-Division	g-Division	gr-division
gH-division exists	∖	g-division exists and $m^g=m^{gH}$ (see [7])	gr-division exists and ${\left[m^{gH}\right]}_{\alpha }\subseteq {\left[m^{gr}\right]}_{\alpha }$ (Theorem 2)
g-division exists	gH-division does not necessarily exist (see [7])	∖	gr-division exists and ${\left[m^g\right]}_{\alpha }\subseteq {\left[m^{gr}\right]}_{\alpha }$ (Theorem 3)
gr-division exists	gH-division does not necessarily exist (Example 2)	g-division exists and ${\left[m^g\right]}_{\alpha }\subseteq {\left[m^{gr}\right]}_{\alpha }$ (Theorem 3)	∖

.

As the table shows, resulting from Theorem 2, if there exists $u\in {\mathcal{F}}_1$ such that $m{÷}_{gH}n=u$, then we have ${\left[u^{gH}\right]}_{\alpha }={\left[u^g\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$ such as Example 1. Due to Theorem 3, if the gH-division between m and n does not exist, then we can calculate the g-division and the gr-division, and we have ${\left[u^g\right]}_{\alpha }\subseteq {\left[u^{gr}\right]}_{\alpha }$ as in the case of Example ex:2. We can also see their relationships in Figure 1.

4. Conclusions

As is known to all, the division operation for type-1 fuzzy number in its original form is not invertible for multiplication operation. This is an essential drawback in some applications. Furthermore, there are several approaches proposed: gH-division, g-division and gr-division to eliminate this drawback. However, one should figure out how they relate to each other in order to analyze practical problems, which was the point of this paper.

From the above discussion, the conclusion can be reached that the gr-division exists between any two T1FNs, as well as g-division, but the result of the g-division is contained in that of the gr-division (see Table 1). Costa et al. [19] also discussed the inclusion isotonic relationship of the gH-division and found that the gH-division was not inclusion isotonic. We have pointed out the relations among the gH-division, the g-division and the gr-division in this paper more clearly. In terms of generalization, the gr-division and the g-division are the most generalized, and the gH-division has the minimum application range among these three division types (see Figure 1).

Since different practical problems exist, we can choose a reasonable division according to the above conclusions to deal with specific issues. The division operation of T1FNs present some cues from the theory of fuzzy sets application to fuzzy differential equations and fuzzy regression analysis.

In the future, we will devote ourselves to the four arithmetic operations between fuzzy numbers and use our conclusion to analyze the differentiability and differential equations about fuzzy numbers, which are based on the four arithmetic operations.