Classification of Coal Bursting Liability Based on Support Vector Machine and Imbalanced Sample Set

Abstract

As an inherent property of the accumulation of elastic energy and the sudden instability failure of coal, coal bursting liability (CBL) is the basis of the research on the early warning and prevention of coal burst. To accurately classify the CBL level, the support-vector-machine (SVM) method was introduced in this paper, and the dynamic failure time (DT), elastic energy index (W_ET), impact energy index (K_E) and uniaxial compressive strength (R_C) were selected as the classification indexes. An imbalanced sample set, containing 95 groups of measured data of CBL, was established, and eight SVM classification models were constructed, based on different kernel functions and swarm-intelligence-optimization algorithms. Focusing on the problem of sample imbalance, the classification accuracy, A, F1-score and kappa coefficient were used to comprehensively evaluate the classification performance of SVM models, and the grey-wolf-optimizer SVM (GWO-SVM) model was selected as the best model in this paper, reaching the highest accuracy of 98.9%. The GWO-SVM was applied to identify the CBL level of the 4# coal seam in Xiaozhuang Coal Mine and the 1# coal seam in the Wanfeng Coal Mine. The results of the engineering application are consistent with those from the engineering field, and show that the proposed model is scientific and practical, and can be a new method for CBL classification.

1. Introduction

Coal burst is a kind of dynamic disaster in coal mining, and its harm is mainly manifested in roadway destruction, causing casualties and inducing secondary disasters [1,2,3,4,5]. Figure 1 shows the field damage of coal bursts in Wudong Coal Mine, China [6]. The coal bursting liability (CBL) is an internal cause of coal burst [7,8]. Almost all coal seams of coal-burst mines in China have bursting liability [9], so an accurate evaluation of CBL is the basis of coal-burst risk assessment.

Figure 1. Field damage of coal bursts in Wudong Coal Mine, China.

Scholars have carried out quantitative research on CBL classification from different angles, and the current approaches [10] can be divided into two types, namely the single-index criterion classification method and the multi-index comprehensive classification method. The former type refers to the use of a single index to determine the CBL level, based on the index classification standard, mainly using the energy index [11,12,13], time index [14,15,16], strain index [17,18], stiffness index [19,20,21], and so on. This method is intuitive, but as an inherent property of coal, CBL is affected by many factors. Considering only a single index will cause some errors. Therefore, researchers generally adopt the multi-index comprehensive classification method to classify the CBL, for example, the Chinese national standard Classification and Laboratory Test Method on Bursting Liability of Coal (GB/T 25217.2-2010) comprehensively adopts the dynamic failure time (DT), elastic energy index (W_ET), impact energy index (K_E), and uniaxial compressive strength (R_C), and divides the CBL level into three categories of strong (I), weak (II), and none (III). In the view of the different categories of bursting liability of the four indexes, the standard uses the fuzzy-comprehensive-evaluation method to list the classification results of 73 different combinations, but the remaining eight combinations do not give clear categories.

Looking at this problem, previous researchers have extensively conducted multi-index classification research. Xu et al. [22] established a comprehensive-evaluation model of CBL by introducing the unascertained measure theory. Wang et al. [23] observed a CBL discrimination model based on the theory of information entropy and the method of entropy-weight ideal point. Jia et al. [24] established the mathematical attribute model of CBL classification. Guo [25] constructed a grey prediction model of CBL according to the variable weight thought and grey-correlation analysis. Wang et al. [26] introduced the Mahalanobis distance-discriminant-analysis (DDA) method to establish a DDA model for CBL classification. The above research focuses on the mathematical methods (e.g., the fuzzy-comprehensive-evaluation method, the unascertained-measurement model, attribute mathematics, etc.), taking into account the degree of importance and correlation of evaluation indexes, and achieves some results, but there are also existing problems, such as complex calculation, and a great influence of subjective factors. How to better solve the problem of CBL classification has become a top priority, and will be a feasible answer to developing a scientific, practical, accurate, efficient and intelligent classification method.

As a supervised-machine-learning algorithm for classification problems, the support vector machine (SVM) has been widely used in engineering, and its black box feature can skip the complex mechanisms and conditions of engineering problems. SVM can summarize the commonness of data, and the established classification model has strong applicability. At present, the application of SVM in CBL classification has been rarely reported. In view of this, the SVM method was introduced in this paper to establish eight SVM models, and the comprehensive performance of each model was evaluated using the classification accuracy A, F1-score and kappa coefficient. Finally, the best SVM model was selected and used in the engineering application for CBL classification.

2. Methods

2.1. SVM

SVM is based on the Vapnik–Chervonenkis dimension theory of statistical learning and the principle of structural risk minimization; it has a good generalization ability for unknown samples, which are classified using the optimal hyperplane [27,28]. In this paper, eight SVM models are established in the MATLAB 2018b environment, including Linear SVM (LSVM), Quadratic SVM (QSVM), Cubic SVM (CSVM), Fine Gaussian SVM (FG-SVM), Medium Gaussian SVM (MG-SVM), Coarse Gaussian SVM (CG-SVM), Adaptive Particle Swarm Optimization SVM (APSO-SVM) and Grey Wolf Optimization SVM (GWO-SVM). Among them, APSO-SVM is an adaptive-particle-swarm-optimization algorithm model with compression factor and asynchronous learning factor, and GWO-SVM is a grey-wolf-algorithm-optimization model simulating the group predation of gray wolves.

This paper takes SVM based on the RBF kernel as an example, to introduce its classification principle [29].

Sampling in n-dimensional space, setting dataset E = [(x₁, y₁), …, (x_l, y_l)], decision function f(x) = ω·k(x) + b, where ω is the weight vector, b is the threshold, k(x) is a non-linear mapping function, and the optimization of classification plane-constraints should satisfy the Formula (1):

$$y_i\left({\omega }^T\cdot k\left(x_i\right)+b\right)\ge 1$$

(1)

The optimization problem is converted to Formulas (2) and (3) by introducing a non-negative relaxation variable ${\xi }_i$:

$$\min \frac{1}{2}{\Vert \omega \Vert }^2+c{\displaystyle \sum _{i=1}^n{\xi }_i,c\ge 0}$$

(2)

$$s.t.y_i\left({\omega }^T\cdot k\left(x_i\right)+b\right)\ge 1-{\xi }_i$$

(3)

where c is a penalty factor. When the c value is large, the penalty value for misclassification will increase; otherwise, it will be small. The Lagrange multiplier algorithm is introduced to obtain Formula (4):

$$L\left(\omega ,b,{\alpha }_i\right)=\frac{1}{2}{\Vert \omega \Vert }^2+{\displaystyle \sum _{i=1}^n{\alpha }_i\left(1-y_i\left({\omega }^T\cdot k\left(x_i\right)+b\right)\right)},{\alpha }_i=\left({\alpha }_1,{\alpha }_2,\cdots {\alpha }_n\right)$$

(4)

The partial derivatives of the Lagrange function L with respect to ω and b, respectively, can be obtained by Formulas (5) and (6):

$$\omega ={\displaystyle \sum _{i=1}^m{\alpha }_i{y}_i{x}_i}$$

(5)

$${\displaystyle \sum _{i=1}^m{\alpha }_i{y}_i}=0$$

(6)

Formula (7) can be obtained by substituting the Lagrange multiplier algorithm:

$$L\left(\omega ,b,{\alpha }_i\right)={\displaystyle \sum _{i=1}^n{\alpha }_i}-\frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{}^T{x}_j}}$$

(7)

That is $\underset{\omega ,b}{\min }L\left(\omega ,b,{\alpha }_i\right)={\displaystyle \sum _{i=1}^n{\alpha }_i}-\frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i{x}_j}}$. Where ω is the weight vector, and b is the threshold. Thus, the optimization problem is transformed into a dual problem, namely Formulas (8) and (9):

$$\min \frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{y}_i{y}_j{x}_i{x}_{j}K\left(x_i,x_j\right)}}-{\displaystyle \sum _{i=1}^n{\alpha }_i}$$

(8)

$$s.t.{\displaystyle \sum _{i=1}^n{y}_i{\alpha }_i=0,0\le {\alpha }_i\le c}$$

(9)

where $K\left(x_i,x_j\right)=\left(k\left(x_i\right)\cdot k\left(x_j\right)\right)$, the RBF kernel is Formula (10):

$$K\left(x_i,x_j\right)=\exp {\left(-g\Vert x_i-x_j\Vert \right)}^2$$

(10)

where, g is the kernel function parameter, so the above optimization problem is converted to Formulas (11) and (12):

$$\min \frac{1}{2}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^n{y}_i{y}_j{\alpha }_i{\alpha }_j\exp {\left(-g\Vert x_i-x_j\Vert \right)}^2-{\displaystyle \sum _{i=1}^n{\alpha }_i}}}$$

(11)

$$s.t.{\displaystyle \sum _{i=1}^n{y}_i{\alpha }_i=0,0\le {\alpha }_i\le c}$$

(12)

2.2. Data Processing

(1)

Sample Dataset

In accordance with the standard GB/T 25217.2-2010 and Reference [26], DT, W_ET, K_E and R_C are selected as the classification indexes of CBL, and the bursting-liability grade is divided into three categories of strong (I), weak (II), and none (III). DT is the time from ultimate strength to complete failure of coal samples under the uniaxial-compression-test conditions. W_ET is the ratio of elastic deformation energy to plastic deformation energy of coal specimens unloaded when the stress reaches a certain value under uniaxial compression. K_E is the ratio of deformation energy accumulated before the maximum peak to that dissipated after the maximum peak, in the complete stress–strain curve of a specimen under uniaxial compression. R_C is the maximum load on unit area of the specimen under the condition of infinite-side and axial-pressure for failure. A total of 95 groups of CBL samples in Table 1 are chosen as the training samples and the test samples.

Table 1. Measurement data and classification of coal samples.

No.	Index				Engineering Guidance Level	No.	Index				Engineering Guidance Level
	DT/ms	WET	KE	RC/Mpa			DT/ms	WET	KE	RC/Mpa
1	161	7.1	7.08	25.6	I	49	193	1.14	5.74	12.5	II
2	33	5.2	69	2.84	I	50	6	9.1	1.14	2.1	II
3	4	4.85	112	6.3	I	51	5	6.3	1.9	2.01	II
4	7	4.8	96	5.8	I	52	66	4	1.7	1.8	II
5	7	5.9	67	5.4	I	53	77	5.8	4.6	1.4	II
6	13	6.5	123	5.1	I	54	300	2.76	2.74	11.8	II
7	14	3.4	66	5.67	I	55	351	2.63	1.64	13	II
8	14	4.1	112	3.23	I	56	255	3.4	3.7	11.2	II
9	22	8.2	87	4.3	I	57	212	4.34	0.88	7.31	II
10	224	6.44	6.32	18.6	I	58	363	6.02	1.34	8.61	II
11	34	5.15	6.5	17.4	I	59	140	3.19	3.34	13.3	II
12	267	12.4	0.87	24.8	I	60	249	2.15	1.84	12	II
13	42	14.4	3.63	29	I	61	53	6.62	4.32	9.52	II
14	13	3.67	5.67	29.2	I	62	138	0.968	3.54	10	II
15	45	4.34	5.99	22.6	I	63	82	4.78	10.2	13.9	II
16	316	8.1	1.4	16.7	I	64	340	4.58	1.26	15.8	II
17	68	12.7	6.73	14.6	I	65	275	3.53	3.56	13.1	II
18	346	11.3	6.45	15.2	I	66	306	1.63	2.06	9.93	II
19	45	12.3	12.6	18.8	I	67	55	4.67	4.93	16	II
20	33	10.3	9.84	12.1	I	68	301	3.84	2.47	10.2	II
21	20	9.43	8.72	16.5	I	69	92	4.3	4.53	14.7	II
22	54	19.6	1.29	17.3	I	70	252	3.11	1.93	6.51	II
23	12	3.6	2.3	37.7	I	71	216	2.62	1.81	13.1	II
24	41	11.9	11.8	5.49	I	72	316	3.47	2.27	4.93	II
25	47	9.2	4.13	17.4	I	73	284	3.96	1.84	10.5	II
26	31	17.5	5.42	11.9	I	74	256	3.96	2.31	17	II
27	66	10.4	6.3	28.6	I	75	391	6.29	1.48	9.4	II
28	24	4	2.85	23.9	I	76	288	1.63	2.34	15.4	II
29	42	7.39	5.67	20.5	I	77	239	1.4	2.03	11.1	II
30	45	5.13	4.96	18.5	I	78	119	4.55	2.95	15.3	II
31	46	8.12	10.6	25.9	I	79	58	3.77	2.13	19.8	II
32	40	6.49	7.73	24.3	I	80	156	4.19	3.67	14.4	II
33	34	4.45	12.6	24.4	I	81	375	2.1	1.93	11.4	II
34	19	7.42	13.7	9.72	I	82	137	5.28	4.15	13.8	II
35	43	14.6	11.8	34.1	I	83	258	2.01	2.05	12.5	II
36	167	17.6	15.7	22.6	I	84	185	2.78	3.26	13.2	II
37	69	12.5	35.7	33.9	I	85	464	3.16	1.5	8.9	II
38	30	10.9	14.8	29.3	I	86	213	2.06	2.68	21.4	II
39	32	5.35	5.25	19.2	I	87	287	9.18	4.99	9.53	II
40	44	5.03	5.96	18.4	I	88	90	2.5	2.6	9.51	II
41	33	3.63	2.25	29.4	I	89	260	1.88	1.67	12.9	II
42	15	3.37	5.25	30	I	90	2943	1.1	2.17	2.19	III
43	48	8.06	9.4	10.6	I	91	83	1.2	1.3	1.5	III
44	189	6.05	6.49	18.6	I	92	1414	3.29	2.38	5.26	III
45	461	2.23	1.45	7.3	II	93	760	2.13	1.17	5.92	III
46	409	2.16	1.39	8.16	II	94	520	1.6	1.9	0.4	III
47	306	5.91	2.48	8.86	II	95	725	1.58	1.4	5.36	III
48	102	2.67	2.26	13.3	II

The number of samples with strong (I), weak (II) and none (III) bursting liability in Table 1 is 44, 45 and 6, respectively. Figure 2 shows the proportion of the three categories of CBL samples, which clearly exhibits the imbalance of samples.

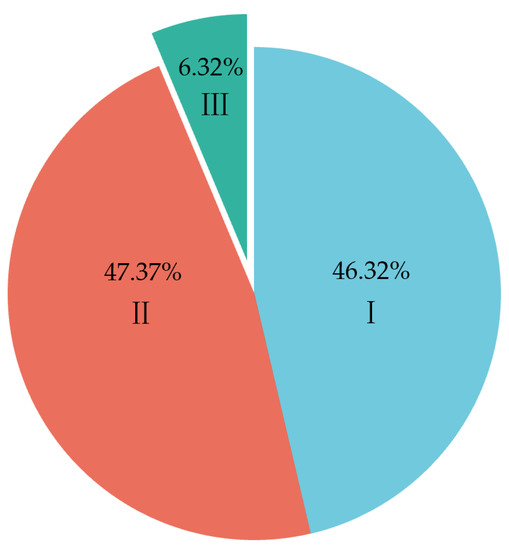
Figure 2. The proportion of three categories of CBL samples: (I) strong; (II) weak; (III) none.

The imbalanced data will have a direct impact on the quality of modeling. Ensuring the rationality of data is an important condition for modeling, and data analysis of sample sets can determine the rationality of data. Table 2 lists the statistical information of each classification index, including minimum, maximum, median, interquartile range (IQR), lower quartile, upper quartile, mean, standard deviation (SD) and standard error (SE). Figure 3 shows the boxplot of the corresponding sample set.

Table 2. Information statistics of CBL classification indexes.

Index	CBL Level	Minimum	Maximum	Median	IQR	Lower Quartile	Upper Quartile	Mean	SD	SE
DT (ms)	I	4	346	40.5	28	21.5	49.5	65.886	82.267	12.402
	II	5	464	249	182	119	301	221.8	120.572	17.974
	III	83	2943	742.5	679.25	571.25	1250.5	1074.167	1011.746	413.044
WET	I	3.37	19.6	7.245	6.015	4.985	11	8.247	4.21	0.635
	II	0.968	9.18	3.47	2.35	2.23	4.58	3.747	1.889	0.282
	III	1.1	3.29	1.59	0.703	1.295	1.998	1.817	0.808	0.33
KE	I	0.87	123	6.905	8.597	5.377	13.975	23.085	34.343	5.177
	II	0.88	10.2	2.27	1.73	1.81	3.54	2.769	1.63	0.243
	III	1.17	2.38	1.65	0.777	1.325	2.103	1.72	0.5	0.204
RC (MPa)	I	2.84	37.7	18.55	13.425	11.575	25	18.442	9.352	1.41
	II	1.4	21.4	11.4	4.4	8.9	13.3	11.075	4.377	0.653
	III	0.4	5.92	3.725	3.663	1.672	5.335	3.438	2.354	0.961

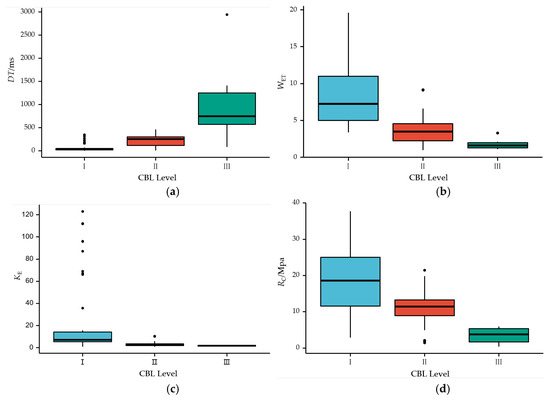
Figure 3. Boxplot of the classification indexes: (a) DT; (b) W_ET; (c) K_E; (d) R_C.

Index correlation analysis is also an important part of data analysis. The correlation information among the classification indexes selected in this paper is shown in Figure 4, in which the correlation curve is fitted, where r is the correlation coefficient and P is the significance level. As can be seen from the figure, the correlation between any two of the four indexes is weak, which indicates that the four indexes are very suitable for the establishment of the classification model.

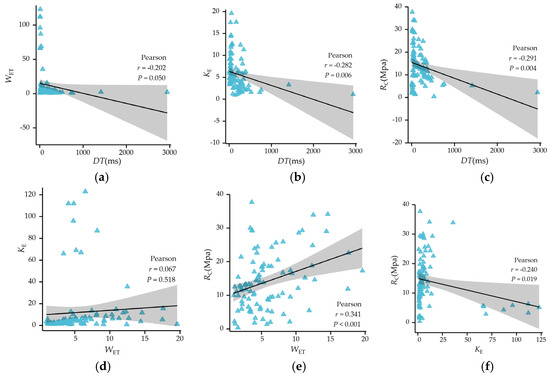
Figure 4. Correlation analysis of classification indexes: (a) DT and W_ET; (b) DT and K_E; (c) DT and R_C; (d) W_ET and K_E; (e) W_ET and R_C; (f) K_E and R_C.

(2)

Data Standardization

Table 1 shows that the dimensions and orders of magnitude of the four classification indexes are different. This can also be roughly seen from the boxplot in Figure 3. The value ranges of the vertical axes of the boxplot of different indexes are significantly different, and the difference is even more obvious under different levels of bursting liability. In order to clearly reflect the dimensional differences among indexes, the data of different indexes are plotted into ridge plots, as shown in Figure 5, so that the variation trend of each group of data and the data comparison between groups can be intuitively seen.

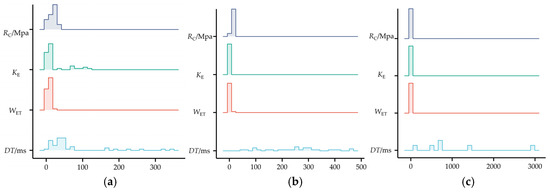
Figure 5. Ridge plots of classification index data. (a) Strong CBL; (b) Weak CBL; (c) None CBL.

Figure 5 shows that the orders of magnitude of the four classification indexes are very different, resulting in a large gap in data distribution. For example, in the sample of strong bursting liability, the data distribution of W_ET, K_E and R_C are concentrated in the area with small values, while the data distribution of DT is relatively scattered. If the original index value is directly used in the classification, the function of the index with the higher value will be highlighted, and the function of the index with the lower value will be relatively weakened. Therefore, it is necessary to standardize the original data. In this paper, the mapminmax function is selected for normalization processing, and the principle is shown in Formula (13):

$${x_{ij}}^{*}=\frac{x_{ij}-\min \left(x_j\right)}{\max \left(x_j\right)-\min \left(x_j\right)}\left(i=1,2,\cdots ,m;j=1,2,\cdots ,n\right)$$

(13)

where, x_ij is the original data of jth index of ith sample; x_ij^* is the processed data, whose value is between 0 and 1, and the data distribution is consistent with that processed before; max(x_j) and min(x_j) are the maximum and minimum value of the original data of index j, respectively.

Table 3 shows the standardized data. Draw the above standardized data into ridge plots, as shown in Figure 6. X₁~X₄ correspond to the standardized data labels of the four indexes respectively. It can be seen that the standardized data reduces the difference of orders of magnitude between indexes, due to dimensional differences, which is most obvious in the samples of weak bursting-liability.

Table 3. Standardized data.

No.	Index				Engineering Guidance Level	No.	Index				Engineering Guidance Level
	X1	X2	X3	X4			X1	X2	X3	X4
1	0.0534	0.3291	0.0508	0.6756	I	49	0.0643	0.0092	0.0399	0.3244	II
2	0.0099	0.2271	0.5578	0.0654	I	50	0.0007	0.4365	0.0022	0.0456	II
3	0.0000	0.2084	0.9099	0.1582	I	51	0.0003	0.2862	0.0084	0.0432	II
4	0.0010	0.2057	0.7789	0.1448	I	52	0.0211	0.1627	0.0068	0.0375	II
5	0.0010	0.2647	0.5415	0.1340	I	53	0.0248	0.2593	0.0305	0.0268	II
6	0.0031	0.2969	1.0000	0.1260	I	54	0.1007	0.0962	0.0153	0.3056	II
7	0.0034	0.1305	0.5333	0.1413	I	55	0.1181	0.0892	0.0063	0.3378	II
8	0.0034	0.1681	0.9099	0.0759	I	56	0.0854	0.1305	0.0232	0.2895	II
9	0.0061	0.3881	0.7052	0.1046	I	57	0.0708	0.1810	0.0001	0.1853	II
10	0.0749	0.2937	0.0446	0.4879	I	58	0.1222	0.2711	0.0038	0.2201	II
11	0.0102	0.2245	0.0461	0.4558	I	59	0.0463	0.1193	0.0202	0.3458	II
12	0.0895	0.6136	0.0000	0.6542	I	60	0.0834	0.0634	0.0079	0.3110	II
13	0.0129	0.7209	0.0226	0.7668	I	61	0.0167	0.3033	0.0282	0.2445	II
14	0.0031	0.1450	0.0393	0.7721	I	62	0.0456	0.0000	0.0219	0.2574	II
15	0.0140	0.1810	0.0419	0.5952	I	63	0.0265	0.2046	0.0764	0.3619	II
16	0.1062	0.3828	0.0043	0.4370	I	64	0.1143	0.1939	0.0032	0.4129	II
17	0.0218	0.6297	0.0480	0.3807	I	65	0.0922	0.1375	0.0220	0.3405	II
18	0.1164	0.5545	0.0457	0.3968	I	66	0.1028	0.0355	0.0097	0.2555	II
19	0.0140	0.6082	0.0960	0.4933	I	67	0.0174	0.1987	0.0332	0.4182	II
20	0.0099	0.5009	0.0734	0.3137	I	68	0.1011	0.1541	0.0131	0.2627	II
21	0.0054	0.4542	0.0643	0.4316	I	69	0.0299	0.1788	0.0300	0.3834	II
22	0.0170	1.0000	0.0034	0.4531	I	70	0.0844	0.1150	0.0087	0.1638	II
23	0.0027	0.1413	0.0117	1.0000	I	71	0.0721	0.0887	0.0077	0.3405	II
24	0.0126	0.5867	0.0895	0.1365	I	72	0.1062	0.1343	0.0115	0.1214	II
25	0.0146	0.4418	0.0267	0.4558	I	73	0.0953	0.1606	0.0079	0.2708	II
26	0.0092	0.8873	0.0373	0.3083	I	74	0.0857	0.1606	0.0118	0.4450	II
27	0.0211	0.5062	0.0445	0.7560	I	75	0.1317	0.2856	0.0050	0.2413	II
28	0.0068	0.1627	0.0162	0.6300	I	76	0.0966	0.0355	0.0120	0.4021	II
29	0.0129	0.3447	0.0393	0.5389	I	77	0.0800	0.0232	0.0095	0.2869	II
30	0.0140	0.2234	0.0335	0.4853	I	78	0.0391	0.1922	0.0170	0.3995	II
31	0.0143	0.3839	0.0797	0.6836	I	79	0.0184	0.1504	0.0103	0.5201	II
32	0.0122	0.2964	0.0562	0.6408	I	80	0.0517	0.1729	0.0229	0.3753	II
33	0.0102	0.1869	0.0960	0.6434	I	81	0.1262	0.0608	0.0087	0.2949	II
34	0.0051	0.3463	0.1051	0.2499	I	82	0.0453	0.2314	0.0269	0.3592	II
35	0.0133	0.7316	0.0895	0.9035	I	83	0.0864	0.0559	0.0097	0.3244	II
36	0.0555	0.8927	0.1214	0.5952	I	84	0.0616	0.0973	0.0196	0.3432	II
37	0.0221	0.6189	0.2852	0.8981	I	85	0.1565	0.1176	0.0052	0.2279	II
38	0.0088	0.5331	0.1141	0.7748	I	86	0.0711	0.0586	0.0148	0.5630	II
39	0.0095	0.2352	0.0359	0.5040	I	87	0.0963	0.4407	0.0337	0.2448	II
40	0.0136	0.2180	0.0417	0.4826	I	88	0.0293	0.0822	0.0142	0.2442	II
41	0.0099	0.1429	0.0113	0.7775	I	89	0.0871	0.0489	0.0066	0.3351	II
42	0.0037	0.1289	0.0359	0.7936	I	90	1.0000	0.0071	0.0106	0.0480	III
43	0.0150	0.3806	0.0698	0.2735	I	91	0.0269	0.0125	0.0035	0.0295	III
44	0.0629	0.2728	0.0460	0.4879	I	92	0.4798	0.1246	0.0124	0.1303	III
45	0.1555	0.0677	0.0047	0.1850	II	93	0.2572	0.0624	0.0025	0.1480	III
46	0.1378	0.0640	0.0043	0.2080	II	94	0.1756	0.0339	0.0084	0.0000	III
47	0.1028	0.2652	0.0132	0.2268	II	95	0.2453	0.0328	0.0043	0.1330	III
48	0.0333	0.0913	0.0114	0.3458	II

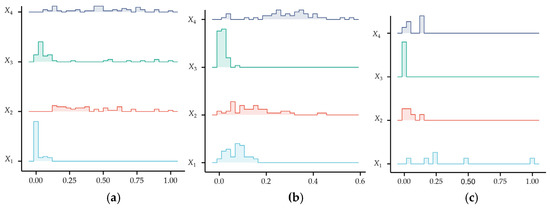
Figure 6. Ridge plots of classification index data after standardization: (a) strong CBL; (b) weak CBL; (c) No CBL.

(3)

Data Segmentation

Currently, there are two ways to divide samples in classification research: one is where there is no need to divide them into the training set and the test set, with small samples, and the other is to divide them according to a fixed proportion. The existing research on CBL classification mainly focuses on small-scale data sets, which is prone to the problem of unreasonable data division, leading to the overfitting of the model on the training set. To solve this problem, this paper adopts a 5-fold cross-validation method to divide the training set and the test set, which can avoid the limitations and particularity of the fixed-division dataset, and this advantage is more obvious in the small-scale dataset. The 5-fold cross-validation divides the data set into five parts in equal proportion, four of which are used as training data, and the remaining one is used as test data. After five operations, each data was tested once, and the average of the results of the five models was used as the final result.

2.3. Parameters Optimization

The penalty factor, c, and the kernel-function parameter, g, are essential parameters for SVM classification, and determine the classification effect of SVM. In this paper, three optimization methods were used to obtain these two parameters, among which the LSVM, QSVM, CSVM, FG-SVM, MG-SVM and CG-SVM models were optimized by a grid-search algorithm, the APSO-SVM model was optimized by the APSO algorithm, and the GWO-SVM model was optimized by the GWO algorithm. The optimization process of the three methods is shown in Figure 7.

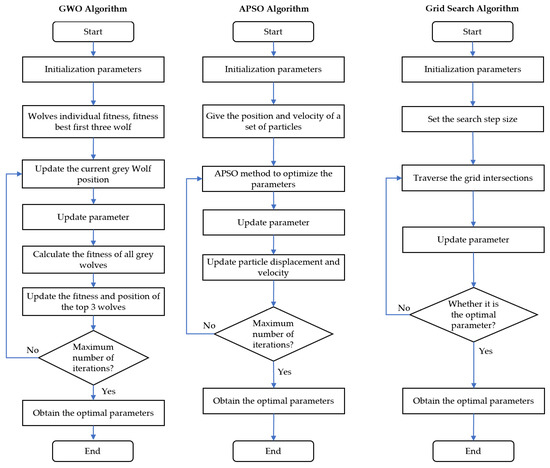
Figure 7. SVM parameter optimization.

2.4. Research Route

In this paper, an imbalanced sample set of CBL, containing 95 groups of measured data, is constructed. The sample set is divided into training set and test set, in accordance with the 5-fold cross-validation. Eight SVM models are used for classification research, and the best SVM model is selected for the engineering application. The research flowchart is shown in Figure 8.

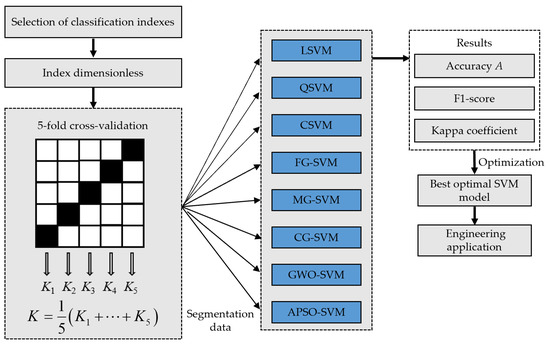
Figure 8. Research flowchart.

3. Results and Discussion

3.1. Classified Results

To better evaluate the performance of the eight classification models, it is necessary to consider not only the overall classification effect of the models, but also the classification effect of the models on different levels of bursting liability. Sorting the classification results of the models built in this paper into a confusion matrix graph, the classification of samples of each category by different models can be obtained, as shown in Figure 9.

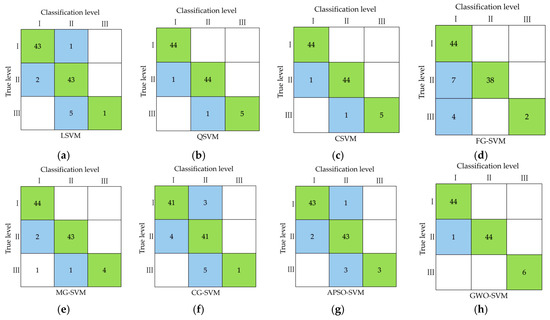
Figure 9. Classification results of eight SVM models: (a) LSVM; (b) QSVM; (c) CSVM; (d) FG-SVM; (e) MG-SVM; (f) CG-SVM; (g) APSO-SVM; (h) GWO-SVM.

3.2. Performance Evaluation

3.2.1. Evaluation Index

For the imbalanced sample dataset established in this paper, the classification accuracy A, F1-score and kappa coefficient are comprehensively selected, to evaluate the performance of the classification models. The three indexes are all positive indexes, that is, the larger the value, the better the performance of the model.

(1)

Classification Accuracy A

The classification accuracy A is the ratio of the number of accurately classified samples (N_accurate) to the total number of samples (N_total) in the modeling process. It represents the overall classification accuracy of the model and is the most commonly used evaluation index in classification problems. Its calculation formula is given as follows:

$$A=\frac{N_{accurate}}{N_{total}}$$

(14)

(2)

F1-Score

As an index used to measure the accuracy of classification models in machine learning, the F1-score is often used to evaluate models based on imbalanced dataset. This index weighs the accuracy rate and recall rate of models.

(3)

Kappa Coefficient

The kappa coefficient is an index adopted to measure whether the classification result of the model is consistent with the actual classification result, and it has certain penalty attribute. When the classification result of the model built based on the imbalanced dataset favors the category with a large number and ignores the category with a small number, the kappa coefficient value of the model is low. This biased evaluation mechanism ensures the rationality of the model performance evaluation.

3.2.2. Evaluation Result

In this paper, eight SVM models are adopted to classify the CBL grade, and three indexes are used to evaluate the classification performance of the models. The results are shown in Table 4 and Figure 10.

Table 4. Evaluation performance of SVM models.

No.	SVM Model	Accuracy (%)	F1-Score	Kappa Coefficient
1	LSVM	91.6	0.804	0.843
2	QSVM	97.9	0.960	0.962
3	CSVM	97.9	0.960	0.962
4	FG-SVM	88.4	0.817	0.786
5	MG-SVM	95.8	0.920	0.923
6	CG-SVM	87.4	0.774	0.765
7	APSO-SVM	93.7	0.878	0.884
8	GWO-SVM	98.9	0.993	0.980

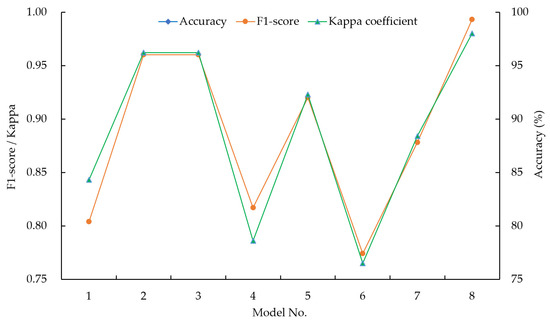
Figure 10. Comparison of model-classification performance.

3.3. Model Analysis and Optimization

(1)

Model Analysis

It can be seen from Table 4 and Figure 10 that the SVM models established in this paper have excellent classification performance, and are suitable for CBL classification under an imbalanced dataset. The following analysis is of the impact of data quality, model selection and data-processing methods on the SVM model performance.

In machine-learning research, the quality of data used for modeling often has a great effect on the classification results. The indexes used in modeling are an essential part of the dataset, and the scientific and reasonable selection of the indexes is the key to subsequent research. The CBL is affected by water, gas, temperature, size effect, loading rate, pore structure of coal and many other factors, which are finally reflected in the forms of strength and energy. The DT and R_C selected in this paper are strength indexes, and W_ET and K_E are energy indexes. These four indexes are more consistent with the nature of CBL, so the dataset established in this paper is of high quality.

Model selection is also a key factor affecting the classification effect. The SVM model constructed in this paper has a high matching degree with the imbalanced sample set, and the SVM model based on the principle of structural risk minimization can avoid the problem of over-learning, enhance the generalization ability, and reduce the requirement of data size and distribution.

The CBL data contains information about energy and strength. In this paper, two kinds of data processing methods, normalization and 5-fold cross-validation, are carried out on the sample data. The 5-fold cross-validation can avoid the limitations and particularities of a fixed-partition dataset, thus improving the generalization ability of the model, and is very suitable for the imbalanced sample set established in this paper.

(2)

Model Optimization

The classification accuracy A, F1-score and kappa coefficient selected in this paper comprehensively consider the overall and local classification effects of the model, and are suitable for the classification of imbalanced sample sets. As can be seen from Table 3, from the overall classification effect, the performance of the GWO-SVM model is the best, with a classification accuracy of 98.9%, higher than that of the other seven SVM models. The F1-score value (0.993) and kappa coefficient value (0.980) of this model are also the largest among all models, indicating that the model has the best classification effect for each level of CBL classification. As can be seen from Figure 10, the classification accuracy of this model in different levels of bursting liability is the largest, so the GWO-SVM model is selected as the optimal SVM model built in this paper.

4. Engineering Application

In order to verify the practicability of the GWO-SVM model, the model was applied to the 4# coal seam of the Xiaozhuang coal mine [30] and the 1# coal seam of Wanfeng coal mine for CBL classification [31].

(1)

4# Coal Seam of Xiaozhuang Coal Mine

The 4# coal seam is the main coal seam, and the coal pillar of the 40214 working face will cause stress concentration. The buried depth of the coal seam is approximately 430~600 m, the average buried depth is 560 m, and the mining depth exceeds the critical depth of coal burst of 380 m. During the mining of the 40203 working surface, strong mine-pressure behaviors appeared several times. The optimized GWO-SVM model was applied to classify the CBL of three groups of samples from the 4# coal seam. In accordance with the GB/T 25217.2-2010, engineering-guidance-level determination results are shown in Table 5; the single index in the table determines the results on the right-hand side of the index value, and the results are shown in Table 5.

Table 5. CBL classification results of 4# Coal Seam.

No.	DT (ms)	Level (DT)	WET	Level (WET)	KE	Level (KE)	RC (MPa)	Level (RC)	Engineering Guidance Level	GWO-SVM
1	208.8	II	7.316	I	1.526	II	13.232	II	II	II
2	172.8	II	14.948	I	1.561	II	18.105	I	II	II
3	201.6	II	6.529	I	1.724	II	20.615	I	II	II

(2)

1# Coal Seam of Wanfeng Coal Mine

The Wanfeng coal mine adopts the underground mining method: the mining level is +430~−10 m, and no coal burst occurred in the mining process. The engineering-guidance level obtained from the single-index discrimination result and the actual situation are consistent with the engineering guidance level. The GWO-SVM model is adopted to classify the bursting liability of the coal seam and compare it with the actual situation. See Table 6 for details.

Table 6. CBL classification results of 1# Coal Seam.

No.	DT (ms)	Level (DT)	WET	Level (WET)	KE	Level (KE)	RC (MPa)	Level (RC)	Engineering Guidance Level	GWO-SVM
1	463	II	1.216	III	1.266	III	4.133	III	II	III

It can be seen from Table 5 and Table 6 that the classification results of the GWO-SVM model selected in this paper are consistent with the actual situation of the mine, and it is an intelligent model that can manage the classification of CBL.

5. Conclusions

The existing CBL classification methods are challenging for giving clear results when identifying specific types of coal, and the calculations are complicated and subject to subjective factors. In view of these deficiencies, DT, W_ET, K_E and R_C were selected as classification indexes, an imbalanced sample set was constructed based on 95 groups of measured data, and eight SVM models were established to carry out intelligent classification and optimization of CBL. The following conclusions were reached:

(1) Differently from the existing data segmentation methods, this paper adopted 5-fold cross-validation to divide the dataset into training set and test set. The classification accuracy of the eight SVM models is above 87.4%, with an average of 94.0%.

(2) Aiming at the problem of sample imbalance at different levels, the classification accuracy A, F1-score and kappa coefficient were comprehensively used to evaluate the performance of the established models, and the best model was selected as the GWO-SVM model, with a classification accuracy of 98.9%, F1-score of 0.993, and kappa coefficient of 0.980. All of these were the highest values in the eight SVM models.

(3) The GWO-SVM model was applied to the working surfaces of the Xiaozhuang Coal Mine and Wanfeng Coal Mine, for CBL classification. The results were consistent with the actual situation on site, indicating that the model has good practicability.