Abstract
Tin phthalocyanine (SnPc) nanoprobes with strong reverse saturable absorption (RSA) are extremely needed for photoacoustic (PA) molecular imaging. The optical properties and dynamics of SnPc nanoprobes by pulse trains were studied. During the propagating of pulse trains in SnPc, the electronic structure of SnPc is simplified to the five-state energy model. The pulse train contains 25 subpulses with space 13 ns, and the widths of subpulses were set as ps, 35 ps, 350 ps, ns, 10 ns, 20 ns, 35 ns and 100 ns, respectively. In this work, we solved two-dimensional paraxial field coupled with rate equations employing the Crank–Nicholson numerical method. The results reveal the unique optical properties and outstanding optical limiting (OL) effects of SnPc nanoprobes, indicating huge application potential as optical limiters, sensors and switches.
1. Introduction
In recent years, with the development of modern laser technology, progress in high-power laser calls have called for effective protection for experimental devices and human eyes [1,2,3,4,5]. Among various types of organic materials, increasing research attention has been paid to phthalocyanines and porphyrins and their derivatives, attributing to their excellent optical limiting (OL) effects and low synthesis costs. Accordingly, they are widely used as optical limiters, optical sensors or switches [6,7,8,9,10,11,12,13].
Phthalocyanines and porphyrins show specific optical characteristics, thanks to their large conjugated -electrons ring structures [14,15]. Therefore, they have typical reverse saturable absorption (RSA) features, namely larger absorption cross sections in excited states than that in ground states [16,17,18,19,20,21]. During the interaction of organic materials with long-duration pulses, two-step two-photon absorption (TPA) primarily occurs, which is a representative RSA process. It is worth noting that symmetric 18 -electrons conjugated ring exist in macrocyclic structures of phthalocyanines (Pcs) [22,23,24], prompting nonlinear optical response along with thermal and chemical stability [25,26,27]. Pcs, therefore, have been devised as nanoprobes to be applied to organic solar cells [28,29,30,31], light-emitting diodes [32,33,34,35] as well as photomedicine therapy, diagnostics and photoacoustic imaging [36,37,38,39,40,41].
Recently, tin phthalocyanine (SnPc) nanoprobes were designed and the nonlinear optical absorption was studied with different laser pulse widths in experimental work [42]. Phthalocyanines interacting with pulse trains in experiments were widely studied [43,44,45,46]. In this work, we investigated the dynamical interaction of pulse train with SnPc. The pulse train was composed of 25 subpulses, spaced 13 ns apart. These pulse train parameters, such as subpulses number and spacing between subpulses, were set according to the experiments in works [47,48,49,50,51]. In our previous work, we also discussed how pulse train parameters take effect on OL properties of materials such as naphthalocyanines and phthalocyanines [52]. There were several works about OL properties of materials versus the pulse-width in one single pulse [53,54,55]. However, subpulse widths modification of pulse trains in OL effects were rarely studied. Especially, there was barely research to study the distinction about OL effects by pulse trains with nanosecond and picosecond subpulse widths in one work. In order to study the nonlinear absorption distinction between picosecond and nanosecond subpulse widths in SnPc nanoprobes, the subpulse widths in this work were set as ps, 35 ps, 350 ps, ns, 10 ns, 20 ns, 35 ns and 100 ns, respectively, in accordance with the experiment [42]. Coupled rate equations of population and paraxial intensity equation were solved by the Crank–Nicholson method with second-order accuracy in time and space [56,57]. Our results displayed the novel finding that each subpulse produces cumulative nonlinear response. When the subpulse width increases, OL effects of SnPc occur earlier and stronger. This work provides new ideas for optical limiters, optical sensors or switches applications by using pulse trains with wider subpulse widths. Furthermore, the proposed pulse width regulation strategy provides a theoretical thread for the design of micro-electro-mechanical systems (MEMS)-integrated micro-optical limiting devices, micro-laser protection coatings or optical switches in phthalocyanines [58,59,60] and MEMS optical modules [61,62,63].
2. Method
The structure of tin phthalocyanine (SnPc) is presented in Figure 1. When interacting with long-duration pulse such as pulse trains [42], the electronic energy structure of SnPc can be simplified to the generalized five-state model (Figure 2). In these cases, together with the incident pulse frequency close to the resonant one-photon absorptions, one-step TPA and nonresonant one-photon absorption can be neglected during the transmission of pulse trains in SnPc. Accordingly, the most preferential channels of population absorption are two-step TPA or .
Figure 1.
Structure of SnPc nanoprobes [42].
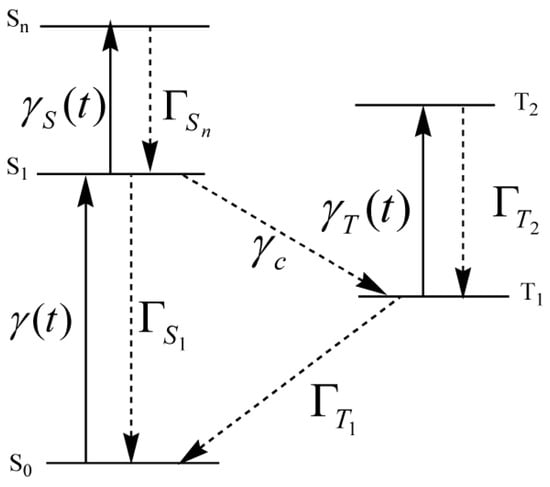
Figure 2.
The diagram of a five-state model consisting of the ground singlet state (), first excited singlet state (), higher excited singlet state (), first excited triplet state (), and higher excited triplet states ().
A pulse train contains a sequence of subpulses marked with serial number n as follows:
where is set as the total subpulses number. Considering the radial distribution of the pulse trains, the intensity of each subpulse with temporal rectangle shape is described as follows [64,65]:
where , , and ns is set as the subpulses spacing. Radial parameter mm is initial beam width. In the light of the experiment [42], the duration of each subpulse is set as ps, 35 ps, 350 ps, ns, 10 ns, 20 ns, 35 ns and 100 ns, respectively, in this work.
The following paraxial equation describes the evolution of each subpulse depending on time t and distance z [64]:
where is set as the concentration and c is the light speed in vacuum. Since refraction index has almost no impact on OL behaviour according to the calculation, here, we set refraction index . Different states are denoted by i, and j. is the absorption cross section of one-photon transition from state i to j. The following set of equations are the rate equations of populations [66],
where and are the decay and pump rates separately. Specifically, , , denote the pump rate of processes , and , respectively, and marks the transition rate of intersystem crossing (ISC) . Pump rate can be calculated by the following expression depending on resonant one-photon absorption cross section [66],
where is the incident frequency of pulse trains, and wave length nm is set based on the experiment [42].
Total energy transmittance is calculated to investigate the OL effects,
where total pulse train energy of integral over instantaneous intensity is calculated by
3. Results and Discussion
Photophysical parameters in Table 1 of SnPc were extracted from the experiment [42]. In addition, we set the relaxation time of state as s [67].

Table 1.
Photophysical parameters of SnPc at nm [42]. , .
In Figure 3, we plotted the energy transmittances of SnPc depending on the incident intensities of pulse trains with different subpulse widths based on Equation (6). One can see clearly that the transmittance evidently decreases when incident intensities increase. SnPc shows obvious OL effects interacting with pulse trains of different subpulse widths. One can also notice that in weak and strong intensity regions, the tendencies of transmittances with different subpulse widths conform to the convergent transmittance as follows:
Regardless of the subpulse widths, the limit values of transmittances are decided on the absorption cross sections of one-photon resonance processes and (Table 1) for weak and strong intensity regions, respectively. Considering the subpulse widths, one can notice that the transmittances reach the limit value at different intensities. When the incident intensity increases to W/m2, the transmittance of pulse train with subpulse width 100 ns reaches the limit value. However, for the pulse train with shorter subpulse width ps, the transmittance reaches the limit value at much stronger intensity W/m2 approximately. Consequently, the pulse train with wider subpulse width reaches the limit value of energy transmittance at lower incident intensity.
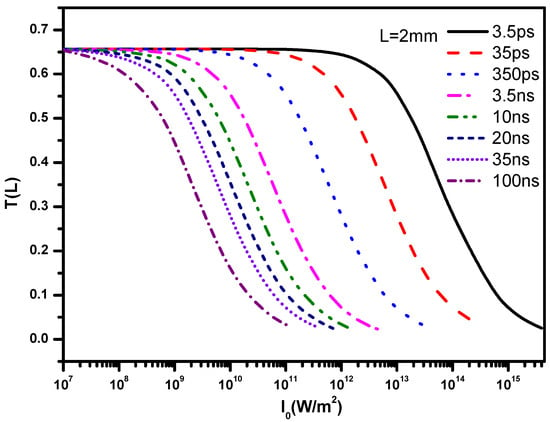
Figure 3.
Energy transmittances (Equation (6)) as a function of the incident peak intensities of pulse trains with different subpulse widths at mm for SnPc.
The dependences of energy transmittances of SnPc on propagation distances L for pulse trains with different subpulse widths at W/m2 were plotted in Figure 4. It shows that SnPc is excellent optical limiting material. When distance increases, the transmittance clearly decreases. For pulse trains with different subpulse widths, the descending speeds of transmittances are different. The wider the subpulse width, the shorter the distance required to reach the limit value of transmittance. For the pulse train with subpulse width 100 ns, the transmittance reaches the limit value at a rather short distance, approximately mm. However, for the pulse train with shorter subpulse width ps, the distance exceeds more than mm. The reason of these trends is that wide subpulse width carrying more energy would promote more intense absorption in the second step in the two-step TPA. Therefore, the transmittance of SnPc will reach the limit value much earlier than the cases with shorter subpulse widths.
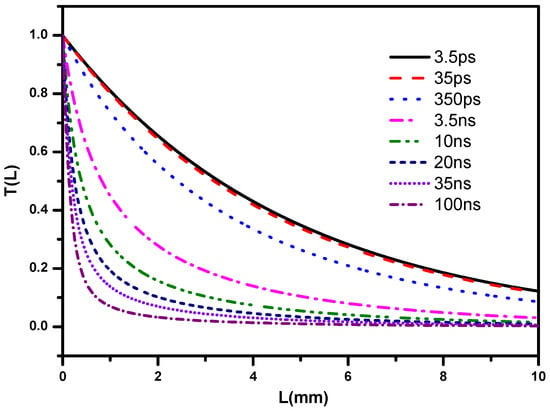
Figure 4.
Energy transmittances (Equation (6)) as a function of the propagation distances L with incident peak intensity W/m2 of pulse trains with different subpulse widths for SnPc.
In Figure 5, we plotted the dynamical populations on states and for pulse trains with subpulse widths ps, ns and 35 ns at W/m2. Since populations are scarcely distributed in states , and , so , and were not drew. One can see clearly that each subpulse produces cumulative nonlinear response. The more subpulses participate in the nonlinear absorption, the more obvious the population inversion. In Figure 5a with short subpulse widths ps, one can see that almost all populations stay still in state and very few populations are in state , which leads to unachievable second step of the two-step TPA. So the OL effect for pulse train with subpulse width ps is weak. When the subpulse width increases to ns in Figure 5b, one can see that approximately 56% of populations were transformed to . For the case with subpulse width 35 ns in Figure 5c, almost all populations are distributed in state . Large populations would be conducive to the second-step absorption of the two-step TPA, which promotes the OL effect greatly.
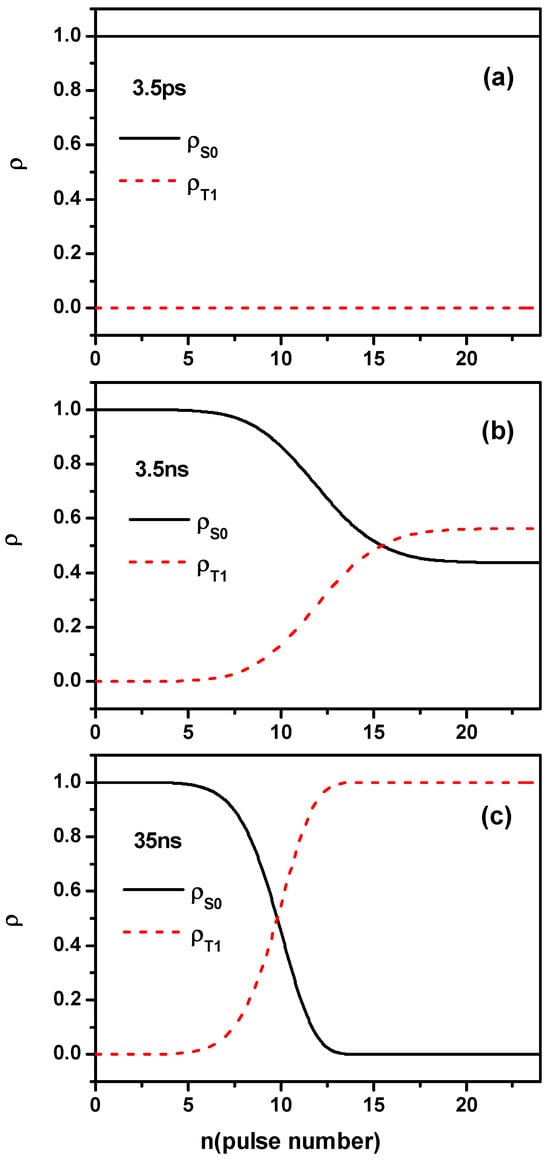
Figure 5.
Population dynamics and at with incident peak intensity W/m2 of pulse trains with different subpulse widths: (a) ps, (b) ns and (c) 35 ns for SnPc.
Figure 6 displayed the populations effective transfer times of the process for pulse trains with subpulse widths ps, ns and 35 ns at W/m2. The values of at the central part with high intensities are quite small, which means that the transfer process is fast and it is beneficial to the whole two-step TPA. at two wings with low intensities are large so the OL effects in these regions are weak. Depending on intensity, is mainly attributed to the absorption cross-section of the one-photon resonance process and intersystem crossing time (Table 1). In addition, all the curves are approximately symmetrical, and the pulse train with subpulse width 35 ns shows the lowest compared to other two cases with shorter subpulse widths. It is interesting to notice that there is a time delay of the minimal value for the case 35 ns compared to other two cases, ps and ns. The reason for this is that a pulse train with subpulse width 35 ns carrying more energy would lead to longer continuous populations accumulation in state .
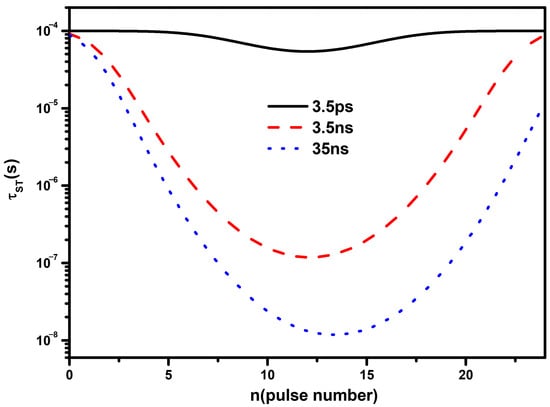
Figure 6.
The populations’ effective transfer times at and with incident peak intensity W/m2 of pulse trains with different subpulse widths ps, ns and 35 ns for SnPc.
In order to show the dynamical absorptions intuitively, in Figure 7, we plotted the two-dimensional output intensities of pulse trains with subpulse widths ps, ns and 35 ns when W/m2. At the short propagation distance mm in Figure 7a–d, one can see there is an obvious deformation of the output intensities when the subpulse width increases to a wider value and the output intensity decreases by one order of magnitude. When the distance increases to cm in Figure 7e–h, the deformation of the output intensities becomes even more obvious and the output intensity decreases by two orders of magnitude from subpulse width ps to 35 ns. The deformation phenomenon is caused by different absorption courses during pulse trains propagation in SnPc. In front parts with weak intensities, there are mainly linear absorption process , while in latter parts with high intensities, a nonlinear strong TPA absorption process dominates due to populations accumulation on state by the populations transferring after front parts. Furthermore, one can notice that the peak values of output intensities occur earlier when the subpulse width increases, which could be seen more clearly in Figure 7a,e. The pulse train with wider subpulse width carrying more energy would promote faster population accumulation on state , and subsequently would be conducive to the two-step TPA, which results in better OL effects.
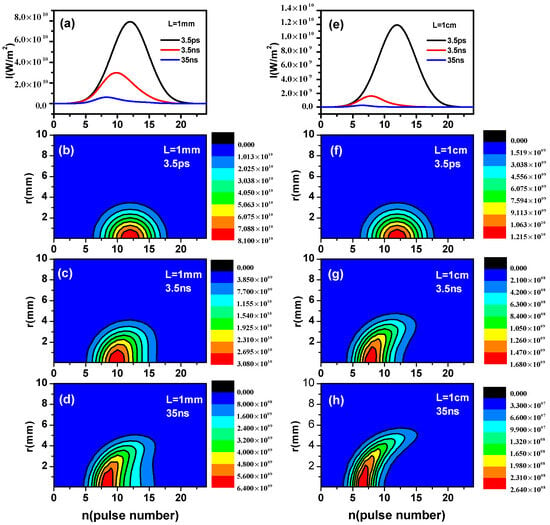
Figure 7.
Two-dimensional maps of the laser intensities after absorbing with incident peak intensity W/m2 of pulse trains with different subpulse widths (b) ps, (c) ns and (d) 35 ns for SnPc at mm and (f) ps, (g) ns and (h) 35 ns for SnPc at cm. Output intensities at with subpulse widths ps, ns and 35 ns at (a) mm and (e) cm.
4. Conclusions
Considering the interactions of pulse trains with SnPc, we explored the dynamical absorption of pulse trains with different subpulse widths. SnPc shows excellent OL behaviour with different pulse trains. Absorption cross-sections and of one-photon resonance processes determine the limit values of transmittances for weak- and high-intensity regions, respectively. The OL effect of SnPc becomes better when the subpulse width increases. With weak intensity or short subpulse width, linear absorption occurs mainly in SnPc. However with high intensity or wide subpulse width, nonlinear TPA occurs due to large and fast population accumulation in state . In practical applications of SnPc as an optical limiter or in another role, changing the pulse duration is an effective method to improve the OL behaviour and optical response characteristics. The findings suppose important prospects which could offer effective methods to strengthen the optical features of organic compounds via employing pulse trains with wider subpulse widths. Furthermore, the pulse width regulation strategy proposed in this work provides a theoretical reference for the design of MEMS-integrated micro-optical limiting devices, micro-laser protection coatings or optical switches in MEMS optical modules, and future research may focus on the compatibility of SnPc nanoprobe fabrication processes with MEMS technologies.
Author Contributions
Conceptualization, Q.M. and Y.X.; data curation, Q.M. and E.S.; funding acquisition, Q.M.; project administration, Y.X.; supervision, Y.X.; visualization, Q.M. and E.S.; writing—original draft, Q.M.; writing—review and editing, Q.M., E.S. and Y.X. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support received from the Youth Expert Program of Taishan Scholar of Shandong Province, China (grant no. tsqn202103072) and Natural Science Foundation of Shandong Province, China (grant no. ZR2022MA085) is gratefully acknowledged.
Data Availability Statement
The data that support the findings of this study are available upon reasonable request from the authors.
Conflicts of Interest
The authors declare no conflics of interest.
References
- Nwaji, N.; Dingiswayo, S.; Mack, J.; Nyokong, T. Photophysical and Enhanced Nonlinear Optical Response in Asymmetric Benzothiazole Substituted Phthalocyanine Covalently Linked to Semiconductor Quantum Dots. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2018, 204, 629–639. [Google Scholar] [CrossRef] [PubMed]
- Pei, H.; Pang, H.; Quan, W.; Fan, W.; Yuan, L.; Zhang, K.; Fang, C. Pulsed optical pumping in electron spin vapor. Measurement 2024, 231, 114619. [Google Scholar] [CrossRef]
- Dong, Y.; Li, W.; Zhang, J.; Luo, W.; Fu, H.; Xing, X.; Hu, P.; Dong, Y.; Tan, J. High-speed PGC demodulation model and method with subnanometer displacement resolution in a fiber-optic micro-probe laser interferometer. Photonics Res. 2024, 12, 921–931. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Song, J.; Liu, X.; Liu, S.; Yang, N.; Wang, L.; Liu, Y.; Zhao, Y.; Zhou, W.; et al. Tumor Cell-Targeting and Tumor Microenvironment–Responsive Nanoplatforms for the Multimodal Imaging-Guided Photodynamic/Photothermal/Chemodynamic Treatment of Cervical Cancer. Int. J. Nanomed. 2024, 19, 5837–5858. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.; Chen, Y.; Xie, B.; Wu, H.; Cheng, L.; Guo, Y.; Cai, C.; Hou, M.; Chen, X. Microdynamic behaviors of Au/Ni-assisted chemical etching in fabricating silicon nanostructures. Appl. Surf. Sci. 2025, 696, 162915. [Google Scholar] [CrossRef]
- Xu, Y.F.; Liu, Z.B.; Zhang, X.L.; Wang, Y.; Tian, J.G.; Huang, Y.; Ma, Y.F.; Zhang, X.Y.; Chen, Y.S. A Graphene Hybrid Material Covalently Functionalized with Porphyrin: Synthesis and Optical Limiting Property. Adv. Mater. 2009, 21, 1275–1279. [Google Scholar] [CrossRef]
- Ren, J.S.; Yang, P.Y.; Wang, A.J.; Zhu, W.H.; Shang, D.H.; Song, Y.L. Synergistic promoted nonlinear optical effects in polyaniline nanohybrids covalently functionalized with tin porphyrin. Colloids Surfaces A Physicochem. Eng. Asp. 2022, 650, 129588. [Google Scholar] [CrossRef]
- Li, D.J.; Li, Q.H.; Gu, Z.G.; Zhang, J. Oriented Assembly of 2D Metal-Pyridylporphyrinic Framework Films for Giant Nonlinear Optical Limiting. Nano Lett. 2021, 21, 10012–10018. [Google Scholar] [CrossRef]
- Dini, D.; Calvete, M.J.F.; Hanack, M. Nonlinear optical materials for the smart filtering of optical radiation. Chem. Rev. 2016, 116, 13043–13233. [Google Scholar] [CrossRef]
- Di Zazzo, L.; Magna, G.; Lucentini, M.; Stefanelli, M.; Paolesse, R.; Di Natale, C. Sensor-Embedded Face Masks for Detection of Volatiles in Breath: A Proof of Concept Study. Chemosensors 2021, 9, 356. [Google Scholar] [CrossRef]
- Thanopulos, I.; Paspalakis, E.; Yannopapas, V. Optical switching of electric charge transfer pathways in porphyrin: A light-controlled nanoscale current router. Nanotechnology 2008, 19, 445202. [Google Scholar] [CrossRef]
- Szyszko, B. Phenanthrene-Embedded Carbaporphyrinoids and Related Systems: From Ligands to Cages and Molecular Switches. Eur. J. Org. Chem. 2022, 30, e202200714. [Google Scholar] [CrossRef]
- Liu, W.; Yang, S.; Li, J.T.; Su, G.R.; Ren, J.C. One molecule, two states: Single molecular switch on metallic electrodes. Eur. J. Org. Chem. 2020, 11, e1511. [Google Scholar] [CrossRef]
- Zhu, H.; Chen, Q.; Roncevic, I.; Christensen, K.E.; Anderson, H.L. Anthracene-Porphyrin Nanoribbons. Angew. Chem. Int. Ed. 2023, 62, e202307035. [Google Scholar] [CrossRef] [PubMed]
- Durantini, J.E.; Rubio, R.; Solis, C.; Macor, L.; Morales, G.M.; Mangione, M.I.; Heredia, D.A.; Durantini, E.N.; Otero, L.; Gervaldo, M. Electrosynthesis of a hyperbranched dendrimeric porphyrin polymer: Optical and electronic characterization as a material for bifunctional electrochromic supercapacitors. Sustain. Energy Fuels 2020, 4, 6125–6140. [Google Scholar] [CrossRef]
- Gavrilyuk, S.; Polyutov, S.; Jha, P.C.; Rinkeviciu, Z.; Ågren, H.; Gel’mukhanov, F. Many-Photon Dynamics of Photobleaching. J. Phys. Chem. A 2007, 111, 11961–11975. [Google Scholar] [CrossRef]
- Eriksson, A.; Bertlisson, K.; Lindgren, M. Simulation of beam propagation with time-dependent nonlinear processes in optical limiting applications. Synth. Met. 2002, 127, 147–150. [Google Scholar] [CrossRef]
- Polyzos, I.; Fakis, G.T.M.; Giannetas, V.; Persephonis, P.; Mikroyannidis, J. Two-photon absorption properties of novel organic materials for three-dimensional optical memories. Chem. Phys. Lett. 2003, 369, 264–268. [Google Scholar] [CrossRef]
- Blau, W.; Byrne, H.; Dennis, W.M.; Dennis, J.M.; Kelly, J.M. Reverse saturable absorption in tetraphenylporphyrins. Opt. Commun. 1985, 56, 25–29. [Google Scholar] [CrossRef]
- Dini, D.; Hanack, M.; Meneghetti, M. Nonlinear Optical Properties of Tetrapyrazinoporphyrazinato Indium Chloride Complexes Due to Excited-State Absorption Processes. J. Phys. Chem. B 2005, 109, 12691–12696. [Google Scholar] [CrossRef] [PubMed]
- De Boni, L.; Rezende, D.C.J.; Mendonca, C.R. Reverse saturable absorption dynamics in indocyanine green. J. Photochem. Photobiol. A Chem. 2007, 190, 41–44. [Google Scholar] [CrossRef]
- Quintiliani, M.; Perez-Moreno, J.; Asselberghs, I.; Vazquez, P.; Clays, K.; Torres, T. Synthesis and Nonlinear Optical Properties of Tetrahedral Octupolar Phthalocyanine-Based Systems. J. Phys. Chem. B 2010, 114, 6309–6315. [Google Scholar] [CrossRef]
- Yagodin, A.V.; Martynov, A.G.; Gorbunova, Y.G.; Tsivadze, A.Y. Synthesis, electronic structure and NH-tautomerism of novel mono- and dibenzoannelated phthalocyanines. Dye. Pigment. 2020, 181, 108564. [Google Scholar] [CrossRef]
- Britton, J.; Martynov, A.G.; Oluwole, D.O.; Gorbunova, Y.G.; Tsivadze, A.Y.; Nyokong, T. Improvement of nonlinear optical properties of phthalocyanine bearing diethyleneglycole chains: Influence of symmetry lowering vs. heavy atom effect. J. Porphyr. Phthalocyanines 2016, 10, 1296–1305. [Google Scholar] [CrossRef]
- Kadish, K.M.; Smith, K.M.; Guilard, R. (Eds.) Handbook of Porphyrin Science; World Scientific Publishing: Singapore, 2010; Volume 3, pp. 1–323. [Google Scholar]
- Lukyanets, E.A.; Nemykin, V.N. The key role of peripheral substituents in the chemistry of phthalocyanines and their analogs. J. Porphyr. Phthalocyanines 2010, 14, 1–40. [Google Scholar] [CrossRef]
- Nemykin, V.N.; Lukyanets, E.A.A. Synthesis of substituted phthalocyanines. Arkivoc 2010, 1, 136–208. [Google Scholar] [CrossRef]
- Ince, M.; Yum, J.-H.; Kim, Y.; Mathew, S.; Grätzel, M.; Torres, T.; Nazeeruddin, M.K. Molecular Engineering of Phthalocyanine Sensitizers for Dye-Sensitized Solar Cells. J. Phys. Chem. C 2014, 118, 17166–17170. [Google Scholar] [CrossRef]
- Singh, V.P.; Singh, R.S.; Parthasarathy, B.; Aguilera, A.; Anthony, J.; Payne, M. Copper-phthalocyanine-based organic solar cells with high open-circuit voltage. Appl. Phys. Lett. 2005, 86, 082106. [Google Scholar] [CrossRef]
- Yuen, A.P.; Jovanovic, S.M.; Hor, A.M.; Klenkler, R.A.; Devenyi, G.A.; Loutfy, R.O.; Preston, J.S. Photovoltaic properties of M-phthalocyanine/fullerene organic solar cells. Sol. Energy 2012, 86, 1683–1688. [Google Scholar] [CrossRef]
- Walter, M.G.; Rudine, A.B.; Wamser, C.C. Porphyrins and phthalocyanines in solar photovoltaic cells. J. Porphyr. Phthalocyanines 2010, 14, 759–792. [Google Scholar] [CrossRef]
- Bae, Y.J.; Lee, N.J.; Kim, T.H.; Cho, H.; Lee, C.; Fleet, L.; Hirohata, A. Growth and characterization of thin Cu-phthalocyanine films on MgO(001) layer for organic light-emitting diodes. Nanoscale Res. Lett. 2012, 7, 650. [Google Scholar] [CrossRef]
- Kao, P.-C.; Chu, S.-Y.; Liu, S.-J.; You, Z.-X.; Chuang, C.-A. Improved Performance of Organic Light-Emitting Diodes Using a Metal-Phthalocyanine Hole-Injection Layer. J. Electrochem. Soc. 2006, 153, H122–H126. [Google Scholar] [CrossRef]
- Wang, Y.-L.; Xu, J.-J.; Lin, Y.-W.; Chen, Q.; Shan, H.-Q.; Yan, Y.; Roy, V.A.L.; Xu, Z.-X. Tetra-methyl substituted copper (II) phthalocyanine as a hole injection enhancer in organic light-emitting diodes. AIP Adv. 2015, 5, 107205. [Google Scholar] [CrossRef]
- Xu, J.; Wang, Y.; Chen, Q.; Lin, Y.; Shan, H.; Roy, V.A.L.; Xu, Z. Enhanced lifetime of organic light-emitting diodes using soluble tetraalkyl-substituted copper phthalocyanines as anode buffer layers. J. Mater. Chem. C 2016, 4, 7377–7382. [Google Scholar] [CrossRef]
- Josefsen, L.B.; Boyle, R.W. Unique diagnostic and therapeutic roles of porphyrins and phthalocyanines in photodynamic therapy, imaging and theranostics. Theranostics 2012, 9, 916–966. [Google Scholar] [CrossRef] [PubMed]
- Taratula, O.; Schumann, C.; Naleway, M.A.; Pang, A.J.; Chon, K.J.; Taratula, O. A multifunctional theranostic platform based on phthalocyanine-loaded dendrimer for image-guided drug delivery and photodynamic therapy. Mol. Pharm. 2013, 10, 3946–3958. [Google Scholar] [CrossRef] [PubMed]
- Attia, A.B.E.; Balasundaram, G.; Driessen, W.; Ntziachristos, V.; Olivo, M. Phthalocyanine photosensitizers as contrast agents for in vivo photoacoustic tumor imaging, Biomed. Opt. Express 2015, 6, 591–598. [Google Scholar] [CrossRef]
- Rizvi, W.; Berisha, N.; Farley, C.; Bhupathiraju, N.V.S.D.K.; Andreou, C.; Khwaja, E.; Fuentes, G.V.; Kircher, M.F.; Gao, R.; Drain, C.M. Phthalocyanine photosensitizers as contrast agents for in vivo photoacoustic tumor imaging. Chemistry 2019, 25, 14517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lovell, J.F. Recent applications of phthalocyanines and naphthalocyanines for imaging and therapy. Wiley Interdiscip. Rev. 2017, 9, e1420. [Google Scholar] [CrossRef]
- Borg, R.E.; Rochford, J. Molecular Photoacoustic Contrast Agents: Design Principles and Applications. Photochem. Photobiol. 2018, 94, 1175–1209. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Y.; Zhang, Z.; Xing, D. Nonlinearly enhanced photoacoustic microscopy by picosecond-laser-pumped excited state absorption of phthalocyanine nanoprobes. Appl. Phys. Lett. 2021, 118, 193701. [Google Scholar] [CrossRef]
- Yang, S.S.; Wei, T.H.; Huang, T.H.; Chang, Y.C. Z-scan study of thermal nonlinearities in silicon naphthalocyanine-toluene solution with the excitations of the picosecond pulse train and nanosecond pulse. Opt. Express 2007, 15, 1718–1731. [Google Scholar] [CrossRef]
- Soboh, R.S.M.; Al-Masoodi, A.H.H.; Erman, F.N.A.; Al-Masoodi, A.H.; Arof, H.; Yasin, M.; Harun, S.W. Zinc phthalocyanine thin film as saturable absorber for Q-switched pulse generation. Opt. Fiber Technol. 2020, 57, 102235. [Google Scholar] [CrossRef]
- Vivas, M.G.; de Boni, L.; Gaffo, L.; Mendonca, C.R. Investigation of ground and excited state photophysical properties of gadolinium phthalocyanine. Dye. Pigment. 2014, 101, 338–343. [Google Scholar] [CrossRef]
- De Boni, L.; Piovesan, E.; Gaffo, L.; Mendonca, C.R. Resonant nonlinear absorption in Zn-phthalocyanines. J. Phys. Chem. A 2008, 112, 6803–6807. [Google Scholar] [CrossRef]
- Gonçalves, P.J.; Bezerra, F.C.; Almeida, L.M.; Alonso, L.; Souza, G.R.L.; Alonso, A.; Zílio, S.C.; Borissevitch, I.E. Borissevitch. Effects of bovine serum albumin (BSA) on the excited-state properties of meso-tetrakis(sulfonatophenyl) porphyrin (TPPS4). Eur. Biophys. J. 2019, 48, 721–729. [Google Scholar] [CrossRef] [PubMed]
- Goncalves, P.J.; Correa, D.S.; Franzen, P.L.; De Boni, L.; Almeida, L.M.; Mendonca, C.R.; Borissevitch, I.E.; Zilio, S.C. Effect of interaction with micelles on the excited-state optical properties of zinc porphyrins and J-aggregates formation. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2013, 112, 309. [Google Scholar] [CrossRef]
- De Paoli, V.M.; De Paoli, S.H.; Borissevitch, I.E.; Tedesco, A.C. Fluorescence lifetime and quantum yield of TMPyPH2 associated with micelles and DNA. J. Alloys Compd. 2002, 344, 27–31. [Google Scholar] [CrossRef]
- Goncalves, P.J.; De Boni, L.; Barbosa Neto, N.M.; Rodrigues, J.J., Jr.; Zilio, S.C.; Borissevitch, I.E. Effect of protonation on the photophysical properties of meso-tetra(sulfonatophenyl) porphyrin. Chem. Phys. Lett. 2005, 407, 236–241. [Google Scholar] [CrossRef]
- Wei, T.H.; Huang, T.H.; Hu, J.K. Electronic energy dissipation in chloro-aluminum phthalocyanine/methanol system following nonlinear interaction with a train of picosecond pulses. J. Chem. Phys. 2002, 116, 2536. [Google Scholar] [CrossRef]
- Miao, Q.; Song, R.; Sun, E.; Xu, Y. How pulse train parameters take effect on nonlinear dynamics of naphthalocyanines and phthalocyanines? Mol. Phys. 2018, 116, 465–470. [Google Scholar] [CrossRef]
- Song, G.; Wu, X.; Zhou, W.; Xiao, J.; Zhang, X.; Wang, Y.; Song, Y. Pulse-width-dependent optical limiting properties of a novel twist-acene compound. Opt. Mater. 2023, 136, 113394. [Google Scholar] [CrossRef]
- Vivien, L.; Riehl, D.; Lançon, P.; Hache, F.; Anglaret, E. Pulse duration and wavelength effects on the optical limiting behavior of carbon nanotube suspensions. Opt. Lett. 2001, 26, 223–225. [Google Scholar] [CrossRef]
- Perumbilavil, S.; Sridharan, K.; Abraham, A.; Janardhanan, H.; Kalarikkal, N.; Philip, R. Nonlinear transmittance and optical power limiting in magnesium ferrite nanoparticles: Effects of laser pulsewidth and particle size. RSC Adv. 2016, 6, 106754–106761. [Google Scholar] [CrossRef]
- Hendow, S.T.; Shakir, S.A. Recursive numerical solution for nonlinear wave propagation in fibers and cylindrically symmetric systems. Appl. Opt. 1986, 25, 1759. [Google Scholar] [CrossRef]
- Press, W.H.; Teukolsky, S.A.; Vetterling, W.T.; Flannery, B.P. Numerical Recipes: The Art of Scientific Computing, 3rd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Miao, Q.; Sun, E.P.; Xu, Y. Optical Dynamics of Picosecond Pulse Trains in Aluminum and Zinc Tetracarboxy-Phthalocyanines. Symmetry 2024, 16, 1337. [Google Scholar] [CrossRef]
- Ridhi, R.; Saini, G.S.S.; Tripathi, S.K. Effect of central metal ions on interaction of Metal Phthalocyanines composites with chemical analytes. Appl. Phys. A—Mater. Sci. Process. 2024, 130, 359. [Google Scholar] [CrossRef]
- Basova, T. Phthalocyanine and Porphyrin Derivatives and Their Hybrid Materials in Optical Sensors Based on the Phenomenon of Surface Plasmon Resonance. Chemosensors 2024, 12, 56. [Google Scholar] [CrossRef]
- Wei, S.; Gao, B.; Wang, J.; You, Z. Vision Gaze-Driven Micro-Electro-Mechanical Systems Light Detection and Ranging Optimization. Research 2025, 8, 0756. [Google Scholar] [CrossRef] [PubMed]
- Gilewski, M. Micro-Electro-Mechanical Systems in Light Stabilization. Sensors 2023, 6, 2916. [Google Scholar] [CrossRef] [PubMed]
- Dong, W.; Sugai, Y.; Wang, Y.J.; Zhang, H.M.; Zhang, X.M.; Sasaki, K. Experimental Study on Enhanced Methane Detection Using an MEMS-Pyroelectric Sensor Integrated with a Wavelet Algorithm. ACS Omega 2024, 9, 9956–19967. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.-P.; Gavrilyuk, S.; Liu, J.-C.; Wang, C.-K.; Ågren, H.; Gel’mukhanov, F. Optical limiting and pulse reshaping of picosecond pulse trains by fullerene C60. J. Electron. Spectrosc. Relat. Phenom 2009, 174, 125–130. [Google Scholar] [CrossRef]
- Gel’mukhanov, F.; Ågren, H. Resonant X-ray Raman scattering. Phys. Rep. 1999, 312, 87–330. [Google Scholar] [CrossRef]
- Gavrilyuk, S.; Liu, J.C.; Kamada, K.; Ågren, H.; Gel’mukhanov, F. Optical limiting for microsecond pulses. J. Chem. Phys. 2009, 130, 054114. [Google Scholar] [CrossRef] [PubMed]
- Goncalves, P.J.; De Boni, L.; Borissevitch, I.E.; Zilio, S.C. Excited State Dynamics of meso-Tetra(sulphonatophenyl) Metalloporphyrins. J. Phys. Chem. A 2008, 112, 6522–6526. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).