Numerical Simulation of Principal Stress Axes Rotation in Clay with an Anisotropic Bounding Surface Model Incorporating a Relocatable Mapping Center
Abstract
1. Introduction
2. Model Formulations
2.1. Bounding Surface
2.2. Hardening Rules
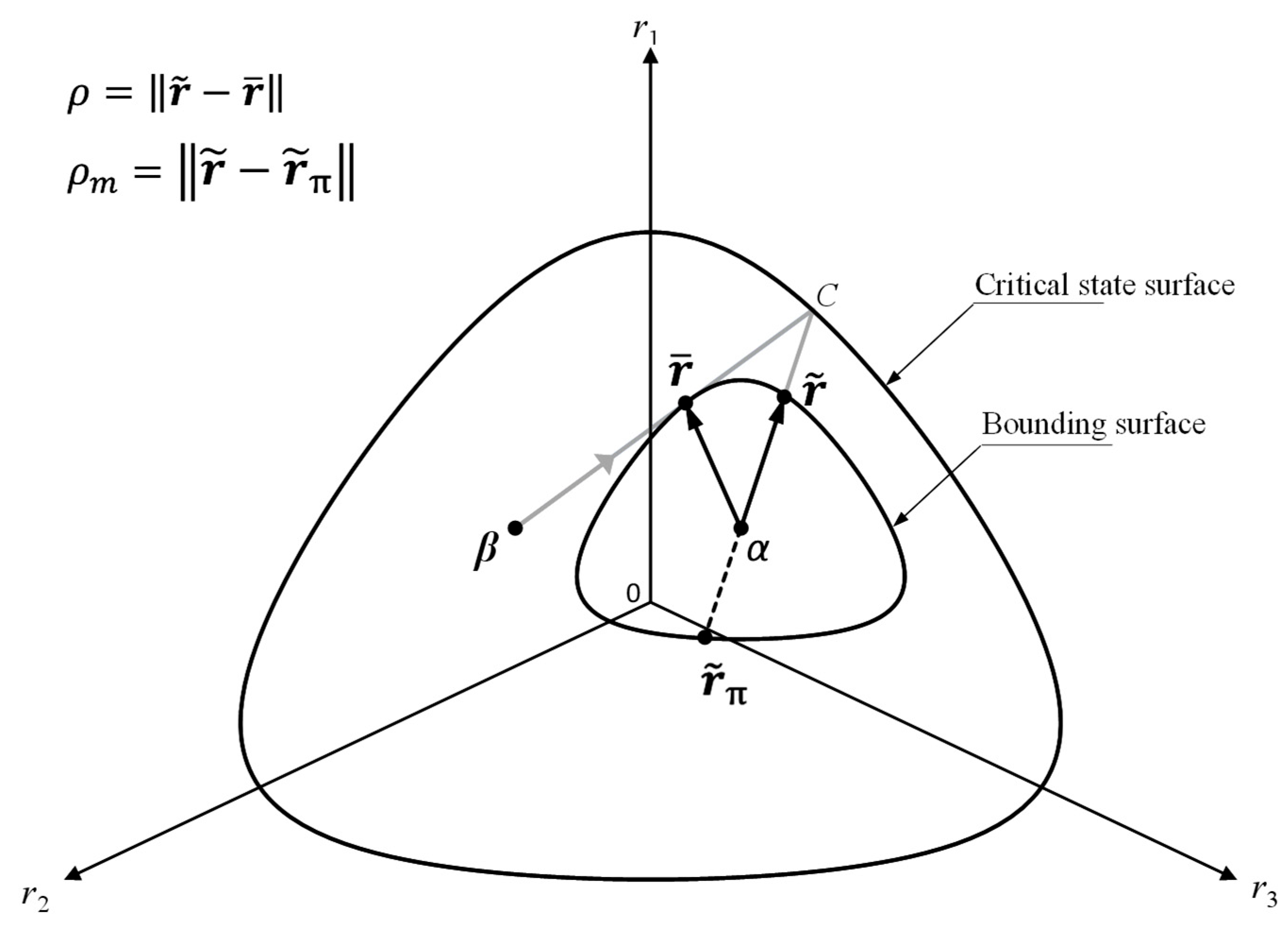
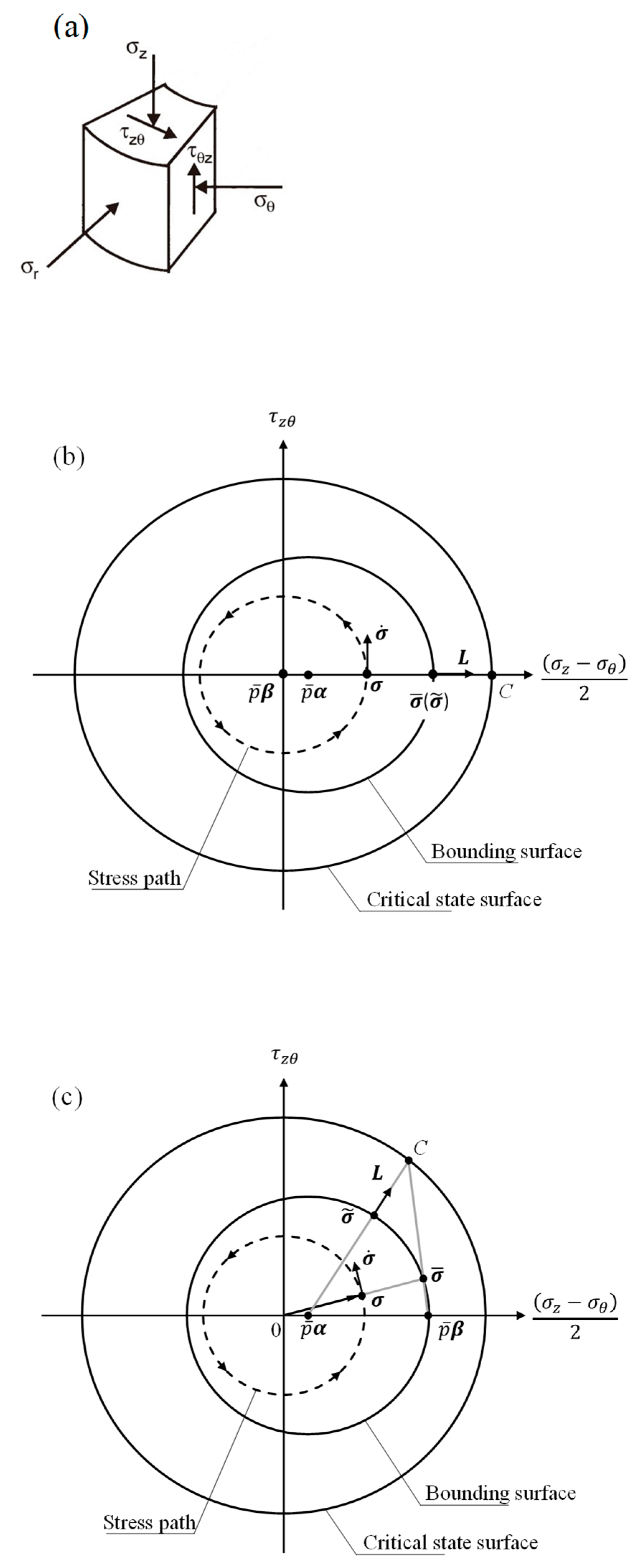
2.3. Mapping Rules
2.3.1. First Step of Mapping in the Meridional Plane
2.3.2. Second Step of Mapping in the Deviatoric Stress Ratio Plane
- (1)
- In Figure 2, draw a straight line from through to locate the point of intersection with the critical state surface, denoted as point C;
- (2)
- Link the back stress ratio and point C to find the point of intersection with the bounding surface, denoted as in Figure 2.
2.4. Loading Direction and Flow Direction
2.5. Plastic Modulus
3. Numerical Simulations
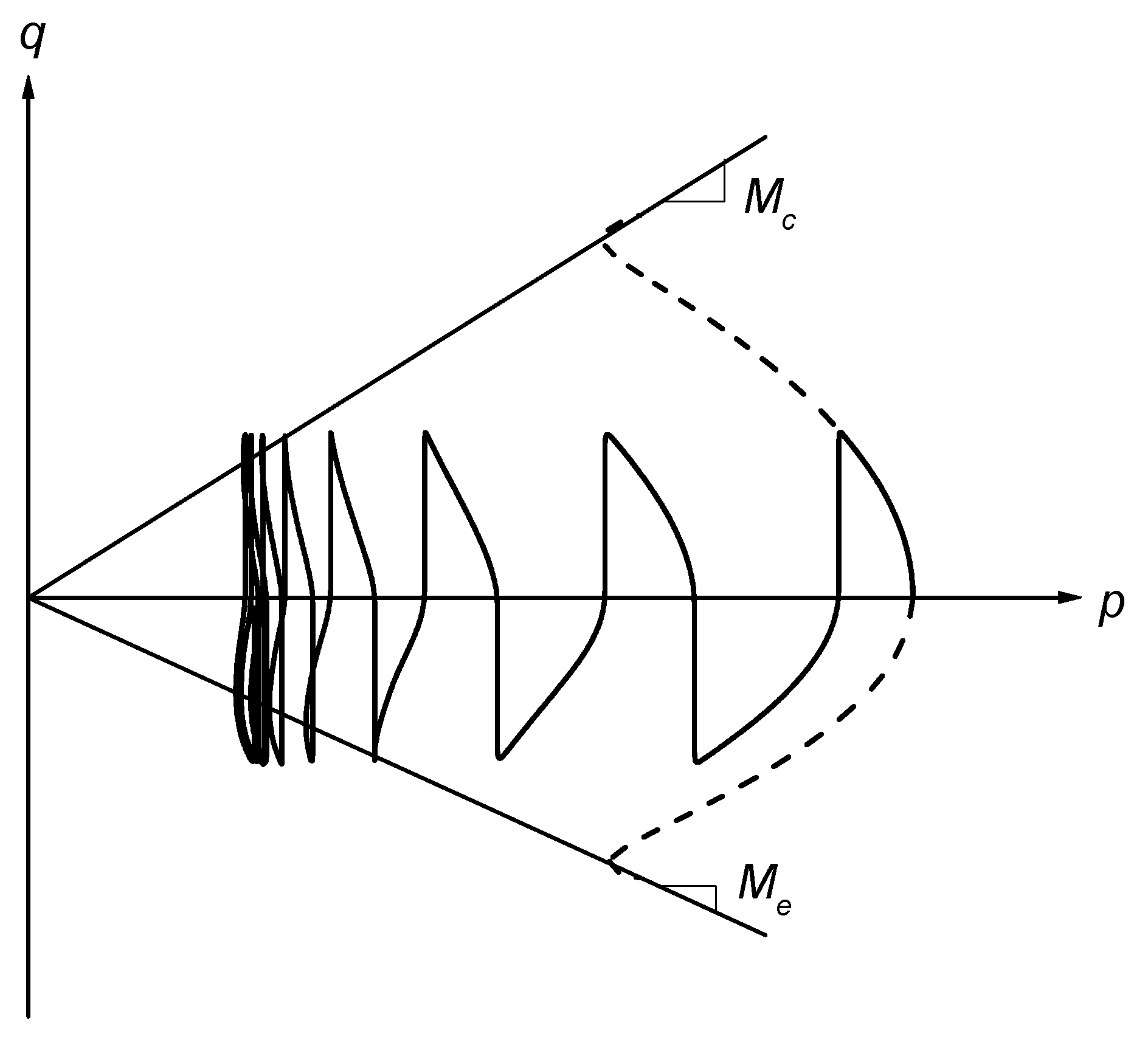
3.1. General Model Performance
3.2. Calibration Methods
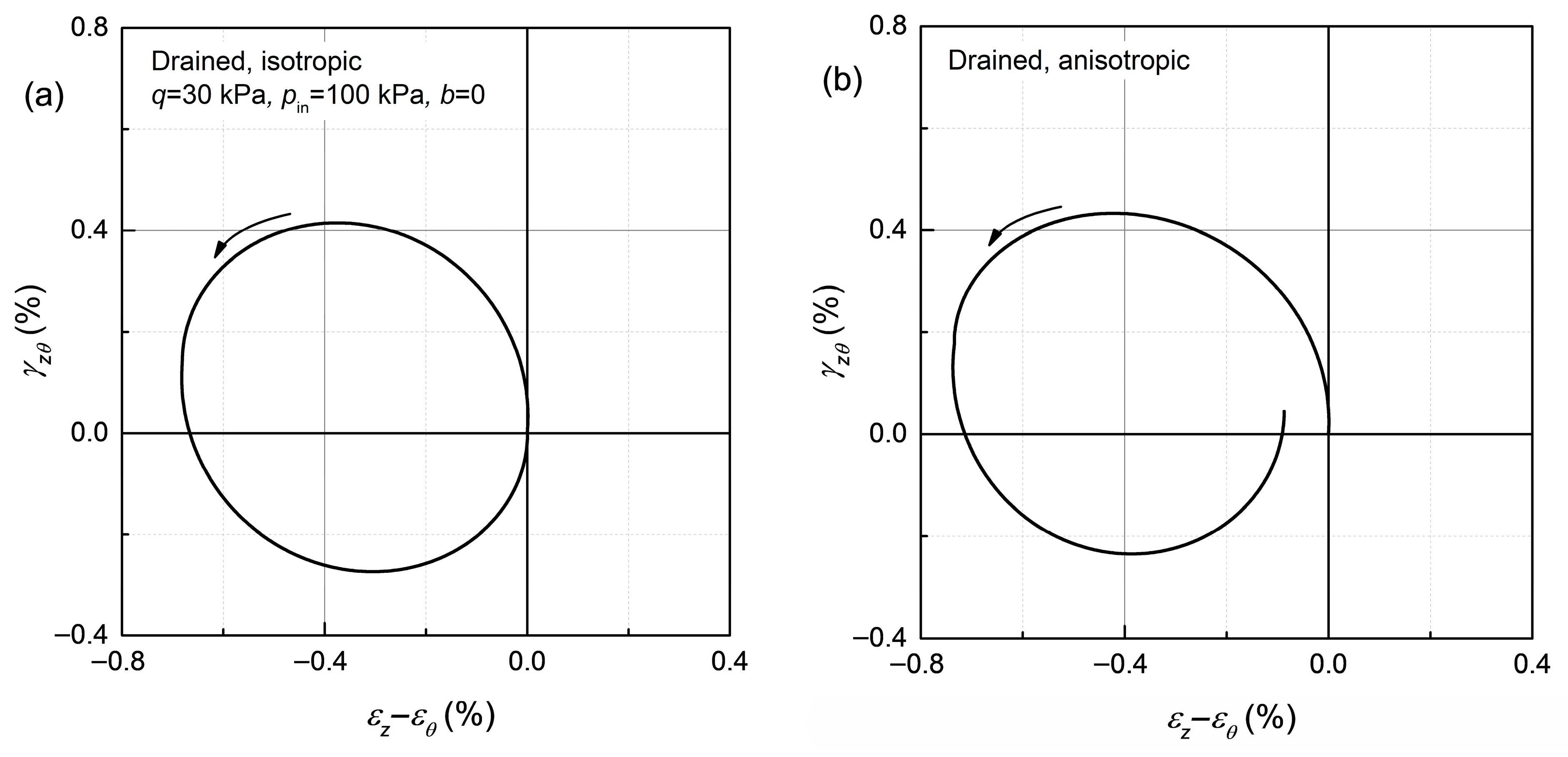
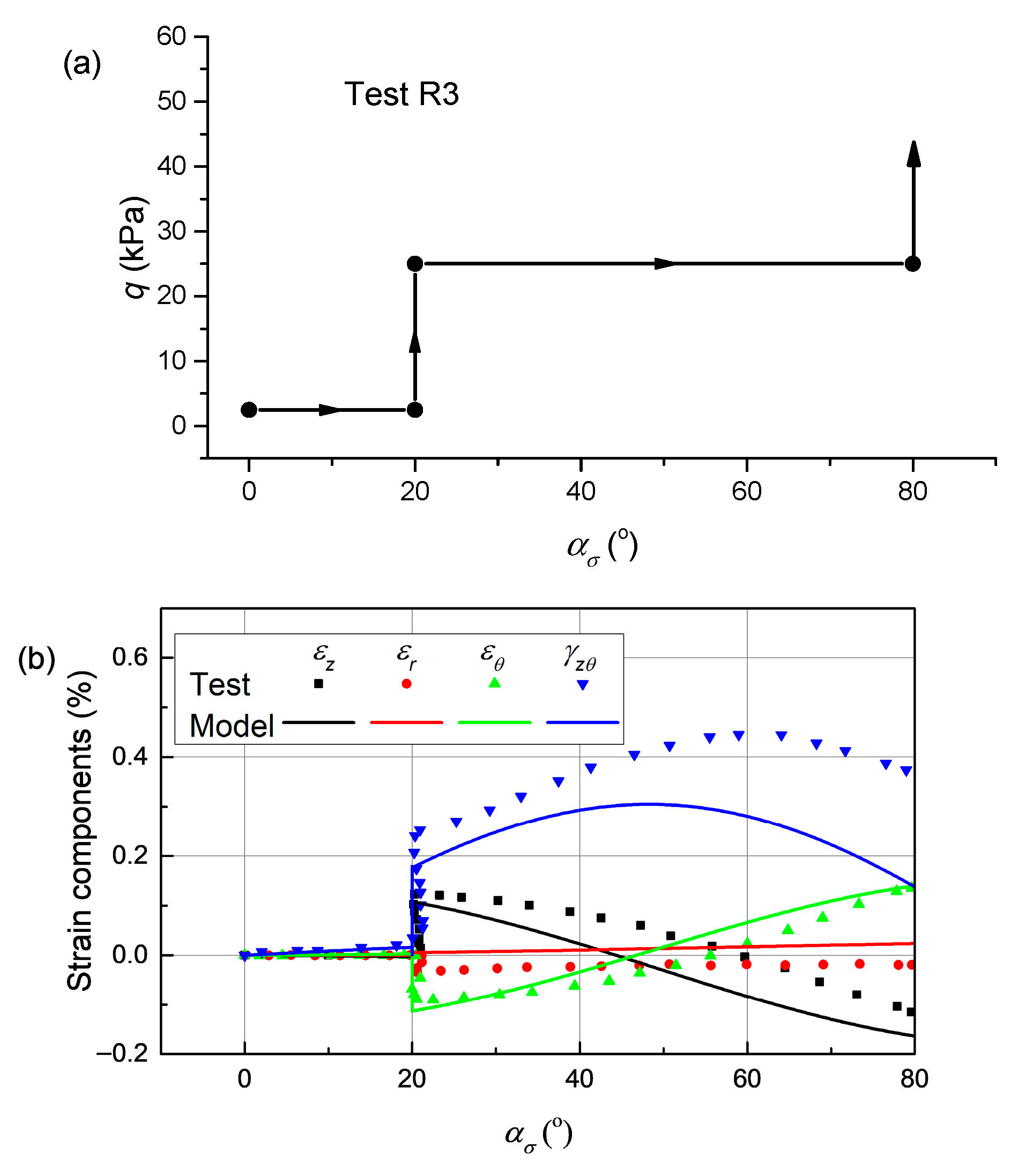
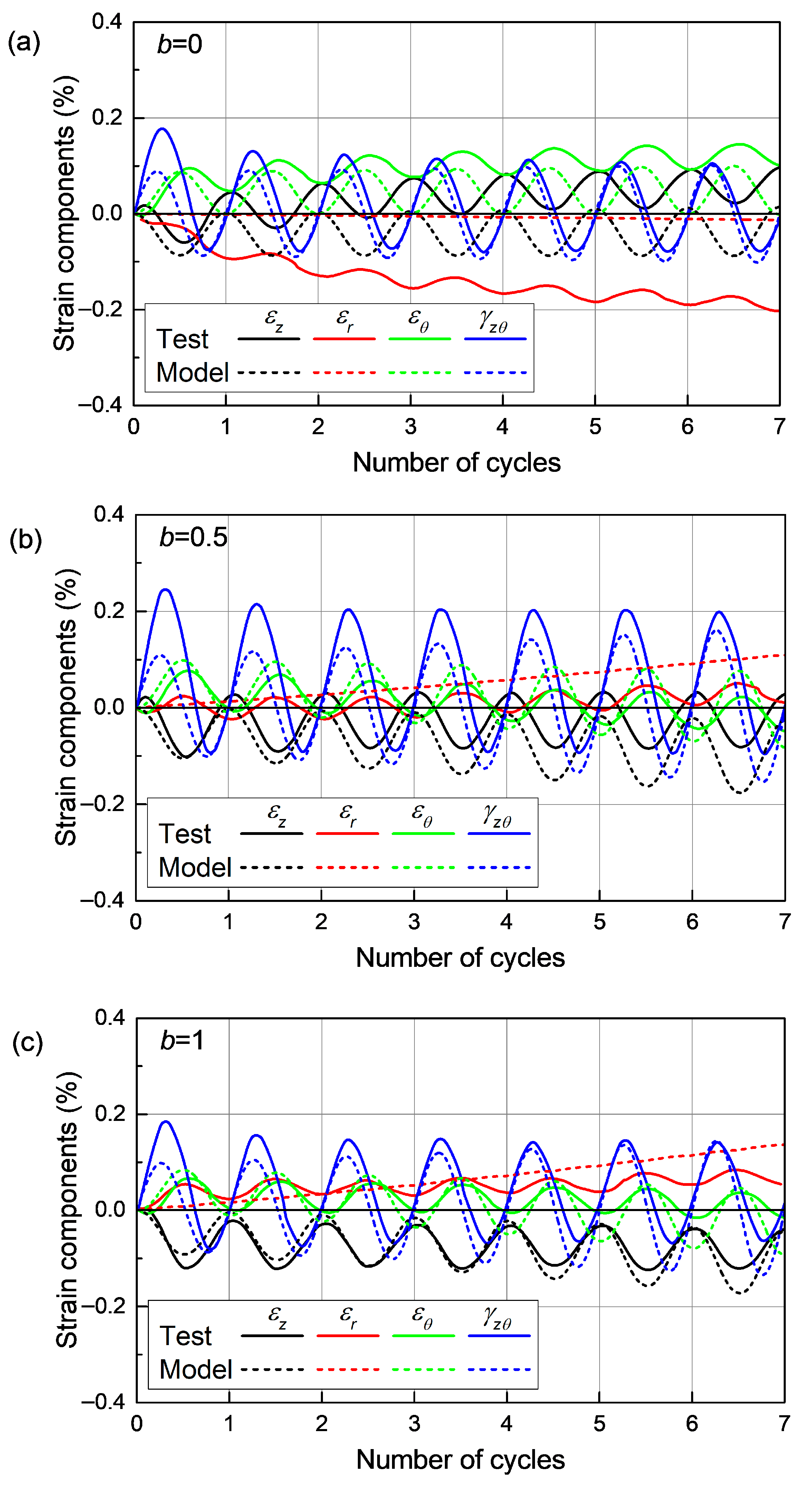
3.3. Model Validation Against Experimental Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arthur, J.; Chua, K.; Dunstan, T. Dense sand weakened by continuous principal stress direction rotation. Geotechnique 1979, 1, 91–96. [Google Scholar] [CrossRef]
- Wong, R.; Arthur, J. Sand sheared by stresses with cyclic variations in direction. Geotechnique 1986, 36, 215–226. [Google Scholar] [CrossRef]
- Hight, D.; Gens, A.; Symes, M. The development of a new hollow cylinder apparatus for investigating the effects of principal stress rotation in soils. Geotechnique 1983, 33, 355–383. [Google Scholar] [CrossRef]
- Ishihara, K.; Towhata, I. Sand response to cyclic rotation of principal stress directions as induced by wave loads. Soils Found. 1983, 23, 11–26. [Google Scholar] [CrossRef] [PubMed]
- Symes, M.; Gens, A.; Hight, D. Undrained anisotropy and principal stress rotation in saturated sand. Geotechnique 1984, 34, 11–27. [Google Scholar] [CrossRef]
- Miura, K.; Miura, S.; Toki, S. Deformation behavior of anisotropic dense sand under principal stress axes rotation. Soils Found. 1986, 26, 36–52. [Google Scholar] [CrossRef]
- Tong, Z.-X.; Zhang, J.-M.; Yu, Y.-L.; Zhang, G. Drained deformation behavior of anisotropic sands during cyclic rotation of principal stress axes. J. Geotech. Geoenviron. Eng. 2010, 136, 1509–1518. [Google Scholar] [CrossRef]
- Yu, H.-S.; Yang, L.-T.; Li, X.; Wanatowski, D. Experimental investigation on the deformation characteristics of granular materials under drained rotational shear. Geomech. Geoengin. 2016, 11, 47–63. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.-S. Numerical investigation of granular material behaviour under rotational shear. Géotechnique 2010, 60, 381–394. [Google Scholar] [CrossRef]
- Tong, Z.; Fu, P.; Dafalias, Y.F.; Yao, Y. Discrete element method analysis of non-coaxial flow under rotational shear. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1519–1540. [Google Scholar] [CrossRef]
- Wu, Q.X.; Yang, Z.X. Undrained Responses of Anisotropic Granular Material under Rotational Shear by DEM. J. Geotech. Geoenviron. Eng. 2022, 148, 04022112. [Google Scholar] [CrossRef]
- Cui, X.; Li, X.; Du, Y.; Bao, Z.; Zhang, X.; Hao, J.; Hu, Y. Macro-micro numerical analysis of granular materials considering principal stress rotation based on DEM simulation of dynamic hollow cylinder test. Constr. Build. Mater. 2024, 412, 134818. [Google Scholar] [CrossRef]
- Akagi, H.; Saitoh, J. Dilatancy characteristics of clayey soil under principal axes rotation. In Proceedings of the International Symposium on Pre-Failure Deformation Characteristics of Geomaterials, Sapporo, Japan, 12–14 September 1994; pp. 311–314. [Google Scholar]
- Zhou, J.; Xu, C. Impact of shear stress on strain and pore water pressure behavior of intact soft clay under principal stress rotation. Geotech. Test. J. 2014, 37, 447–462. [Google Scholar] [CrossRef]
- Qian, J.-G.; Du, Z.-B.; Yin, Z.-Y. Cyclic degradation and non-coaxiality of soft clay subjected to pure rotation of principal stress directions. Acta Geotech. 2017, 13, 943–959. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Cai, Y.; Guo, L. Effect of initial state and intermediate principal stress on noncoaxiality of soft clay–involved cyclic principal stress rotation. Int. J. Geomech. 2018, 18, 04018081. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Guo, L.; Yang, Z. Influence of intermediate principal stress and principal stress direction on drained behavior of natural soft clay. Int. J. Geomech. 2018, 18, 04017128. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, Y.; Li, B.; Guo, L.; Cai, Y.; Mahfouz, A.H. Influence of initial state and intermediate principal stress on undrained behavior of soft clay during pure principal stress rotation. Acta Geotech. 2018, 14, 1379–1401. [Google Scholar] [CrossRef]
- Lei, H.; Yang, X.; Feng, S.; Ma, T. Softening and deformation characteristics of Tianjin soft soil under principal stress rotation induced by traffic loading. Soil Dyn. Earthq. Eng. 2023, 164, 107587. [Google Scholar] [CrossRef]
- Tsutsumi, S.; Hashiguchi, K. General non-proportional loading behavior of soils. Int. J. Plast. 2005, 21, 1941–1969. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, H.-S. A non-coaxial critical state soil model and its application to simple shear simulations. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1369–1390. [Google Scholar] [CrossRef]
- Qian, J.; Yang, J.; Huang, M. Three-dimensional noncoaxial plasticity modeling of shear band formation in geomaterials. J. Eng. Mech. 2008, 134, 322–329. [Google Scholar] [CrossRef]
- Papamichos, E.; Vardoulakis, I. Shear band formation in sand according to non-coaxial plasticity model. Geotechnique 1995, 45, 649–661. [Google Scholar] [CrossRef]
- Lu, N. Elastoplastic Constitutive Modelling of Clay Behaviour Under Principal Stress Rotation. Ph.D. Thesis, University of Nottingham, Nottingham, UK, 2019. [Google Scholar]
- Pande, G.N.; Sharma, K. Multi-laminate model of clays—A numerical evaluation of the influence of rotation of the principal stress axes. Int. J. Numer. Anal. Methods Geomech. 1983, 7, 397–418. [Google Scholar] [CrossRef]
- Neher, H.; Cudny, M.; Wiltafsky, C.; Schweiger, H. Modelling principal stress rotation effects with multilaminate type constitutive models for clay. Numer. Models Geomech. 2002, 42, 41–47. [Google Scholar]
- Dafalias, Y.F. Bounding surface plasticity. I: Mathematical foundation and hypoplasticity. J. Eng. Mech. 1986, 112, 966–987. [Google Scholar] [CrossRef]
- Wang, Z.-L.; Dafalias, Y.F.; Shen, C.-K. Bounding surface hypoplasticity model for sand. J. Eng. Mech. 1990, 116, 983–1001. [Google Scholar] [CrossRef]
- Li, X.; Dafalias, Y. A constitutive framework for anisotropic sand including non-proportional loading. Geotechnique 2004, 54, 41–55. [Google Scholar] [CrossRef]
- Gao, Z.; Zhao, J. A non-coaxial critical-state model for sand accounting for fabric anisotropy and fabric evolution. Int. J. Solids Struct. 2017, 106, 200–212. [Google Scholar] [CrossRef]
- Xue, L.; Yu, J.K.; Pan, J.H.; Wang, R.; Zhang, J.M. Three-dimensional anisotropic plasticity model for sand subjected to principal stress value change and axes rotation. Int. J. Numer. Anal. Methods Geomech. 2020, 45, 353–381. [Google Scholar] [CrossRef]
- Liao, D.; Yang, Z. Hypoplastic modeling of anisotropic sand behavior accounting for rotation of principal stress direction. J. Eng. Mech. 2022, 148, 04022060. [Google Scholar] [CrossRef]
- Liao, D.; Zhou, C.; Yang, Z. A Constitutive Model for Anisotropic Sand Considering Fabric Evolution Under Proportional and Non-Proportional Loadings. Int. J. Numer. Anal. Methods Geomech. 2025, 49, 1575–1596. [Google Scholar] [CrossRef]
- Fu, L.-y.; Zhou, J.; Gong, X.-N. A hypoplastic model simulating the cyclic clay behaviors under principal stress rotation. Soil Dyn. Earthq. Eng. 2025, 199, 109681. [Google Scholar] [CrossRef]
- Gutierrez, M.; Ishihara, K.; Towhata, I. Model for the deformation of sand during rotation of principal stress directions. Soils Found. 1993, 33, 105–117. [Google Scholar] [CrossRef]
- Lashkari, A.; Latifi, M. A non-coaxial constitutive model for sand deformation under rotation of principal stress axes. Int. J. Numer. Anal. Methods Geomech. 2008, 32, 1051–1086. [Google Scholar] [CrossRef]
- Papadimitriou, A.G.; Chaloulos, Y.K.; Dafalias, Y.F. A fabric-based sand plasticity model with reversal surfaces within anisotropic critical state theory. Acta Geotech. 2019, 14, 253–277. [Google Scholar] [CrossRef]
- Wang, R.; Cao, W.; Xue, L.; Zhang, J.-M. An anisotropic plasticity model incorporating fabric evolution for monotonic and cyclic behavior of sand. Acta Geotech. 2021, 16, 43–65. [Google Scholar] [CrossRef]
- Ueda, K.; Iai, S. Noncoaxiality considering inherent anisotropy under various loading paths in a strain space multiple mechanism model for granular materials. Int. J. Numer. Anal. Methods Geomech. 2021, 45, 815–842. [Google Scholar] [CrossRef]
- Yang, Y.; Yu, H.S. A kinematic hardening soil model considering the principal stress rotation. Int. J. Numer. Anal. Methods Geomech. 2013, 37, 2106–2134. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Lu, N.; Li, Y.; Yu, H.-S. Effects of the principal stress rotation in numerical simulations of geotechnical laboratory cyclic tests. Comput. Geotech. 2019, 109, 220–228. [Google Scholar] [CrossRef]
- Petalas, A.L.; Dafalias, Y.F.; Papadimitriou, A.G. SANISAND-FN: An evolving fabric-based sand model accounting for stress principal axes rotation. Int. J. Numer. Anal. Methods Geomech. 2018, 43, 97–123. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Anisotropic critical state theory: Role of fabric. J. Eng. Mech. 2011, 138, 263–275. [Google Scholar] [CrossRef]
- Hu, N.; Zhuang, P.-Z.; Yang, D.-S.; Yu, H.-S. On the evolution law of a contact normal-based fabric tensor for granular materials. Comput. Geotech. 2021, 132, 103857. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, Y.; Li, Y.; Liu, S.; Zhou, P. Numerical simulation of cyclic shear tests considering the fabric change and principal stress rotation effects. Int. J. Numer. Anal. Methods Geomech. 2022, 46, 1409–1432. [Google Scholar] [CrossRef]
- Liu, H.; Nagula, S.; Petter Jostad, H.; Piciullo, L.; Nadim, F. Considerations for using critical state soil mechanics based constitutive models for capturing static liquefaction failure of tailings dams. Comput. Geotech. 2024, 167, 106089. [Google Scholar] [CrossRef]
- Lu, N.; Yang, Y.; Yu, H.-S.; Wang, Z. Modelling the simple shear behaviour of clay considering principal stress rotation. Mech. Res. Commun. 2020, 103, 103474. [Google Scholar] [CrossRef]
- Tian, Y.; Yao, Y.-P. Constitutive modeling of principal stress rotation by considering inherent and induced anisotropy of soils. Acta Geotech. 2018, 13, 1299–1311. [Google Scholar] [CrossRef]
- Du, Z.; Shi, Z.; Qian, J.; Huang, M.; Guo, Y. Constitutive modeling of three-dimensional non-coaxial characteristics of clay. Acta Geotech. 2022, 17, 2157–2172. [Google Scholar] [CrossRef]
- Du, Z.; Qian, J.; Zhang, J.; Liu, Y.; Huang, M. Elastoplastic modeling cyclic behavior of natural soft clay with principal stress rotation under traffic loading. Acta Geotech. 2023, 18, 3643–3660. [Google Scholar] [CrossRef]
- Li, X.S.; Dafalias, Y.F. Noncoaxiality between Two Tensors with Application to Stress Rate Decomposition and Fabric Anisotropy Variable. J. Eng. Mech. 2020, 146, 04020004. [Google Scholar] [CrossRef]
- Dafalias, Y.F. An anisotropic critical state soil plasticity model. Mech. Res. Commun. 1986, 13, 341–347. [Google Scholar] [CrossRef]
- Van Eekelen, H. Isotropic yield surfaces in three dimensions for use in soil mechanics. Int. J. Numer. Anal. Methods Geomech. 1980, 4, 89–101. [Google Scholar] [CrossRef]
- Sheng, D.; Sloan, S.W.; Yu, H.-S. Aspects of finite element implementation of critical state models. Comput. Mech. 2000, 26, 185–196. [Google Scholar] [CrossRef]
- Roscoe, K.H.; Burland, J.B. On the Generalized Stress-Strain Behaviour of Wet Clay. In Engineering Plasticity; Heyman, J., Leckie, F.A., Eds.; Cambridge University Press: Cambridge, UK, 1968; pp. 535–609. [Google Scholar]
- Wheeler, S.J.; Näätänen, A.; Karstunen, M.; Lojander, M. An anisotropic elastoplastic model for soft clays. Can. Geotech. J. 2003, 40, 403–418. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Taiebat, M. Anatomy of rotational hardening in clay plasticity. Géotechnique 2013, 63, 1406–1418. [Google Scholar] [CrossRef]
- Li, T.; Meissner, H. Two-surface plasticity model for cyclic undrained behavior of clays. J. Geotech. Geoenviron. Eng. 2002, 128, 613–626. [Google Scholar] [CrossRef]
- Hu, C.; Liu, H. Implicit and explicit integration schemes in the anisotropic bounding surface plasticity model for cyclic behaviours of saturated clay. Comput. Geotech. 2014, 55, 27–41. [Google Scholar] [CrossRef]
- Seidalinov, G.; Taiebat, M. Bounding surface SANICLAY plasticity model for cyclic clay behavior. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 702–724. [Google Scholar] [CrossRef]
- Dafalias, Y.F.; Manzari, M.T.; Papadimitriou, A.G. SANICLAY: Simple anisotropic clay plasticity model. Int. J. Numer. Anal. Methods Geomech. 2006, 30, 1231–1257. [Google Scholar] [CrossRef]
- Hu, C.; Liu, H.; Huang, W. Anisotropic bounding-surface plasticity model for the cyclic shakedown and degradation of saturated clay. Comput. Geotech. 2012, 44, 34–47. [Google Scholar] [CrossRef]
- Abbo, A.J. Finite Element Algorithms for Elastoplasticity and Consolidation. Ph.D. Thesis, The University of Newcastle, Callaghan, Australia, 1997. [Google Scholar]
- Sloan, S.W.; Abbo, A.J.; Sheng, D. Refined explicit integration of elastoplastic models with automatic error control. Eng. Comput. 2001, 18, 121–194. [Google Scholar] [CrossRef]
- Akagi, H.; Yamamoto, H. Stress-dilatancy relation of undisturbed clay under principal axes rotation. In Proceedings of the Deformation and Progressive Failure in Geomechanics, Nagoya-shi, Japan, 1 October 1997; Volume 216. [Google Scholar]
- Jiang, J.; Ling, H.I.; Kaliakin, V.N. An associative and non-associative anisotropic bounding surface model for clay. J. Appl. Mech. 2012, 79, 031010. [Google Scholar] [CrossRef]
- Ling, H.I.; Yue, D.; Kaliakin, V.N.; Themelis, N.J. Anisotropic elastoplastic bounding surface model for cohesive soils. J. Eng. Mech. 2002, 128, 748–758. [Google Scholar] [CrossRef]
- Liu, Z. Study on Yielding Characteristic and Anisotropic Yield Surface Equation of Soft Clay. Master’s Thesis, Zhejiang University, Hangzhou, China, 2014. (In Chinese). [Google Scholar]
- Xia, Y. Study of Mechanical Behavior of Hangzhou clay Considering Samll Strain Stiffness and Its Engineering Application. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, 2014. (In Chinese). [Google Scholar]






| Constants | Hangzhou Soft Clay | Shanghai Soft Clay | Calibration Remarks | |
|---|---|---|---|---|
| Elasticity | 0.022 | 0.024 | Oedometer or triaxial test | |
| 0.25 | 0.03 | Lateral stress oedometer test | ||
| Critical state | 0.123 | 0.157 | Oedometer or triaxial test | |
| 1.174 | 1.727 | Triaxial compression test | ||
| 0.844 | 1.096 | Triaxial extension test | ||
| Rotational hardening | 100 | 150 | Constant stress ratio test | |
| 1.383 | 1.74 | Theoretically estimated | ||
| Stiffness | 10 | 40 | Trial-and-error | |
| 20 | 40 | Trial-and-error | ||
| Flow rule | 0.7 | 0.85 | Trial-and-error | |
| Hangzhou Soft Clay [10] | |||||
|---|---|---|---|---|---|
| Test | Drainage Condition | ||||
| R1 | Undrained | 150 kPa | stage ①: 2.5 kPa → 25 kPa stage ②: = 25 kPa stage ③: 25 kPa → failure | 0.5 | stage ①: = 0° stage ②: 0° → 80° stage ③: = 80° |
| R3 | stage ①: = 2.5 kPa stage ②: 2.5 kPa → 25 kPa stage ③: = 25 kPa → failure stage ④: 25 kPa → failure | stage ①: 0° → 20° stage ②: = 20° stage ③: 20° → 80° stage ④: = 80° | |||
| Shanghai Soft Clay [11] | |||||
| Test | Drainage Condition | ||||
| 1 | Undrained | 150 kPa | 30 kPa | 0 | 0° → 1260° (7 cycles) |
| 2 | 0.5 | ||||
| 3 | 1 | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, N.; Wang, Z.; Zhang, H. Numerical Simulation of Principal Stress Axes Rotation in Clay with an Anisotropic Bounding Surface Model Incorporating a Relocatable Mapping Center. Symmetry 2025, 17, 1741. https://doi.org/10.3390/sym17101741
Lu N, Wang Z, Zhang H. Numerical Simulation of Principal Stress Axes Rotation in Clay with an Anisotropic Bounding Surface Model Incorporating a Relocatable Mapping Center. Symmetry. 2025; 17(10):1741. https://doi.org/10.3390/sym17101741
Chicago/Turabian StyleLu, Nan, Zhe Wang, and Hanwen Zhang. 2025. "Numerical Simulation of Principal Stress Axes Rotation in Clay with an Anisotropic Bounding Surface Model Incorporating a Relocatable Mapping Center" Symmetry 17, no. 10: 1741. https://doi.org/10.3390/sym17101741
APA StyleLu, N., Wang, Z., & Zhang, H. (2025). Numerical Simulation of Principal Stress Axes Rotation in Clay with an Anisotropic Bounding Surface Model Incorporating a Relocatable Mapping Center. Symmetry, 17(10), 1741. https://doi.org/10.3390/sym17101741





