Symmetry-Constrained Dual-Path Physics-Guided Mamba Network: Balancing Performance and Efficiency in Underwater Image Enhancement

Abstract

The field of underwater image enhancement (UIE) has advanced significantly, yet it continues to grapple with persistent challenges stemming from complex, spatially varying optical degradations such as light absorption, scattering, and color distortion. These factors often impede the efficient deployment of enhancement models. Conventional approaches frequently rely on uniform processing strategies that neither adapt effectively to diverse degradation patterns nor adequately incorporate physical principles, resulting in a trade-off between enhancement quality and computational efficiency. To overcome these limitations, we propose a Dual-Path Physics-Guided Mamba Network (DPPGM), a lightweight framework designed to synergize physical optics modeling with data-driven learning. Extensive experiments on three benchmark datasets (UIEB, LSUI, and U45) demonstrate that DPPGM outperforms 13 state-of-the-art methods, achieving an exceptional balance with only 1.48 M parameters and 25.39 G FLOPs. The key to this performance is a symmetry-constrained architecture: it incorporates a dual-path Mamba module for degradation-aware processing, physics-guided optimization based on the Jaffe–McGlamery model, and compact subspace fusion, ensuring that quality and efficiency are mutually reinforced rather than competing objectives.

1. Introduction

Underwater image enhancement (UIE) aims to restore the visual quality of imagery degraded by the underwater optical environment. Central to this work are two of the most prevalent and challenging degradations: color distortion caused by the wavelength-selective attenuation of light, and haze-like blurring accompanied by significant contrast reduction resulting from light scattering. The effective correction of these issues is critical for reconstructing obscured details, enhancing contrast, and restoring a natural visual appearance [1]. Advances in underwater imaging systems have enabled large-scale and convenient image acquisition, providing a valuable data foundation for marine science and engineering applications [2]. Consequently, the ability to reliably address these core problems has established UIE as a pivotal research direction in marine computer vision, with broad applications spanning marine resource exploration [3], underwater robotic navigation [4], environmental monitoring, and archaeological surveying [5].

Early UIE methods can be broadly categorized into two paradigms: physical model-based and non-physical model-based approaches [6]. Methods grounded in physical models, such as the Underwater Dark Channel Prior (UDCP) [7] and red-channel restoration techniques [8], leverage principles of underwater optics to estimate transmission maps and perform degradation compensation. However, these methods often face challenges in accurately estimating scene-dependent parameters under dynamically changing underwater conditions. Non-physical approaches, including histogram stretching in color spaces [9], multi-scale fusion strategies [5,10], and Retinex-based decomposition models [11,12], operate primarily in the pixel or frequency domains to improve perceptual quality, while these methods demonstrate effectiveness in certain scenarios, they often produce visually inconsistent or physically implausible results—primarily because they fail to account for the underlying optical mechanisms governing underwater image formation. Wang et al. [13] further categorized these methods via experimental review, laying groundwork for later data-driven approaches.

The advent of data-driven methodologies, particularly deep learning, has markedly reshaped the UIE landscape. These methods learn complex degradation-to-clean mappings from large collections of paired underwater images, enabling end-to-end enhancement without explicit physical assumptions. Convolutional Neural Networks (CNNs) have seen widespread application in this field. For instance, the seminal UWCNN framework [14] adopts a multi-branch design to decouple and hierarchically process color and structural information, efficiently learning feature representations tailored for UIE. Despite their success, the local inductive bias of convolution operations limits their ability to capture long-range, spatially variant degradation patterns. Generative Adversarial Networks (GANs) have also gained prominence. Models such as WaterGAN [15] incorporate physical priors into the generator to simulate realistic underwater scenes and employ adversarial learning to improve perceptual authenticity. Nevertheless, GAN-based methods remain prone to training instability and mode collapse, directly leading to the generation of artifacts and inconsistent outputs in practical UIE tasks.

Recent years have witnessed data-driven approaches advancing UIE, though they also bring new challenges. Transformer-based models, such as the architecture proposed by Lu et al. [16], integrate transformer blocks into a ResNet-50 backbone and leverage multiscale feature fusion to capture global contextual information. These methods often incorporate multi-dimensional attention mechanisms to identify regions requiring enhancement and employ multi-color-space inputs (e.g., RGB, HSV, LAB) to improve restoration performance across diverse degradation types. Although effective in handling spatially varying degradations, their high computational demands—stemming from the quadratic complexity of self-attention—and large parameter counts hinder deployment on resource-constrained underwater platforms. Conversely, lightweight models—such as UResNet [17] (with Sobel-filter and squeeze-and-excitation variants) and Zhang et al.’s efficient CNN [18]—prioritize computational economy. The latter; for example, uses a compact CNN and YUV post-processing to enable real-time enhancement. Yet these approaches typically apply uniform processing, lacking distinction between clean and severely degraded regions, which leads to localized over- or under-enhancement. Notably, both types of methods suffer from a fundamental symmetry-breaking issue: transformer-based models over-emphasize performance optimization at the cost of efficiency, while lightweight models prioritize efficiency at the expense of quality. This asymmetry between performance and efficiency violates the symmetry principle in system design, where balanced adaptation to task requirements is essential for robust practical deployment.

To address the aforementioned challenges, this paper proposes a Dual-Path Physics-Guided Mamba Network (DPPGM) for UIE. By integrating physical optics principles with deep learning, DPPGM not only effectively handles spatially heterogeneous degradations but also achieves a balanced trade-off between enhancement performance and computational efficiency—two critical requirements for practical underwater deployment. Central to this approach is the principle of symmetry, which we define as the dynamic equilibrium maintained between data-driven learning and physical constraints throughout the enhancement process.

Diverging from traditional techniques that rely exclusively on either rigid physical models (lacking adaptability to complex degradation variations) or unconstrained data-driven learning (prone to non-physical artifacts), DPPGM effectively combines these two paradigms through symmetric collaboration. The model operates through four key stages: First, a degradation-aware detector extracts shallow features while identifying initial degradation distribution. Second, a dual-path Mamba module processes clean and degraded regions in parallel—this design establishes symmetric functional paths where each region receives processing intensity proportional to its degradation level, avoiding the asymmetry resulting from uniform processing of conventional methods. Third, physics-guided optimization, rooted in the Jaffe–McGlamery underwater optical model, introduces symmetry constraints derived from optical propagation laws, ensuring enhancements align with real-world physics. Finally, a compact subspace fusion mechanism achieves symmetric aggregation of multi-stage features, preventing dominance of any single feature scale and balancing detail preservation with computational efficiency. By unifying degradation-adaptive processing, physical constraints, and efficient feature fusion, DPPGM provides a principled and deployable solution for high-quality underwater image restoration. The main contributions of this work are summarized as follows:

(1)

A Dual-Path Physics-Guided Mamba Network (DPPGM) is tailored for underwater image enhancement, specifically targeting the handling of spatially varying optical degradations while balancing enhancement quality and computational efficiency. Distinguishing itself from conventional methods that use uniform processing or overlook physical–optical integration, this method employs a degradation-aware dual-path Mamba module to separately process clean and degraded regions, leveraging selective sequence modeling to capture long-range degradation dependencies.

(2)

An integrated framework incorporating symmetry-constrained physics-guided optimization and compact subspace fusion. The former, constrained by the Jaffe–McGlamery model, ensures symmetric alignment between enhancements and optical laws, while the latter enables symmetric multi-stage feature integration, preserving critical information without efficiency loss. This synergy bridges physical principles and data-driven learning through symmetric collaboration, delivering balanced gains in quality and efficiency.

(3)

Comprehensive experimental evaluations were conducted on three benchmark UIE datasets—UIEB, LSUI, and U45—to systematically assess the performance of the proposed DPPGM. Quantitative and qualitative results collectively demonstrate that DPPGM achieves accuracy comparable to, or even surpasses, current state-of-the-art (SOTA) techniques. Notably, this competitive performance is attained while maintaining lightweight computational complexity: the model has only 1.48 M trainable parameters and requires 25.39 G FLOPs for inference, far outperforming SOTA methods in terms of efficiency.

The remainder of this paper is structured as follows: Section 2 reviews related work; Section 3 details the proposed DPPGM framework; Section 4 presents experimental settings and results; and Section 5 concludes the study with future directions.

2. Related Work

UIE seeks to alleviate degradation from wavelength-dependent light absorption, scattering, and color distortion—factors that significantly undermine critical applications like marine exploration and underwater robotics. This section reviews key field methodologies, emphasizing their core mechanisms and inherent limitations.

2.1. Traditional Underwater Image Enhancement Methods

Traditional UIE methods are primarily rooted in either physical models of light propagation or empirical image processing techniques, seeking to reverse degradation through analytical or heuristic adjustments. These approaches can be broadly categorized into physical model-based and non-physical model-based methods.

Non-physical model-based methods—Model-free methods—aim to enhance the visual quality of underwater images by directly manipulating pixel values, without relying on explicit physical or mathematical models. Instead, they improve the quality of underwater images by directly processing pixel values. Such methods utilize information such as color space characteristics [19], multi-scale information [20], and retinex decomposition [21]. They enhance underwater images through various means, including pixel dynamic range stretching, image fusion weight maps, and adjustment of illumination and reflectance components. These methods improve the contrast and color performance of underwater images from the perspective of directly optimizing visual effects.

Physical model-based methods for UIE build on the principles of optical imaging to construct physical models, leveraging a diverse range of information to estimate model parameters—including modified dark channel prior (DCP) [22], underwater dark channel prior (UDCP) [7], red channel information [8], minimum information [23], blurriness information [24], general dark channel information [25], and attenuation curve prior [26]; in addition, they integrate key indicators such as scene depth, background light, and transmission map [14] to enhance underwater images by reversing degradation, with practical implementations varying from simplifying restoration to single image dehazing and adopting structure–texture decomposition to utilizing RGB-D images for color correction. Despite their foundational role, these methods have key limitations, where they tend to be computationally expensive or image-type sensitive, while parameter estimation often lacks accuracy—especially in challenging environments where statistical priors fail and optical models error due to irregular scenes. This ultimately results in poor robustness and unreliable outcomes.

2.2. Deep Learning-Based Underwater Image Enhancement Methods

With the rapid advancement of deep learning, data-driven approaches have become dominant in UIE. These methods learn complex degradation patterns from data without relying on explicit physical modeling and can be broadly classified into CNN-based models, generative adversarial network (GAN)-based frameworks, and hybrid architectures incorporating attention or transformer mechanisms.

CNN-based methods primarily learn direct mappings from degraded to enhanced images. Early representative work includes UWCNN, which was trained on synthetic datasets covering various types of water and degradation levels and can be extended to video enhancement [27]. Water-Net, introduced alongside the UIEB benchmark dataset, serves as a baseline for evaluating generalization in real-world scenarios [28]. Subsequent innovations include wavelet-integrated CNNs and gated fusion networks that leverage preprocessed input, such as gamma-corrected and white-balanced images. More recent advances include AirNet, an all-in-one restoration network that handles diverse corruptions through a contrastive-based degraded encoder and degradation-guided restoration module [29], and HCLR-Net, which employs hybrid contrastive learning regularization with local patch perturbations to improve generalization [30]. Zhu et al. [31] also proposed a lightweight optimized U-Net for efficient UIE.

GAN-based frameworks are widely recognized for their ability to generate perceptually realistic enhanced images. Representative methods include WaterGAN, which pioneered the unsupervised synthesis of underwater-like imagery [15], and PUGAN, which introduced a physics-guided framework with dual discriminators and a degradation-aware module [32]. Despite their strengths, these methods often face challenges including training instability, sensitivity to hyperparameters, and high computational demands, which can limit their practicality for real-time underwater applications.

Hybrid architectures aim to integrate the advantages of diverse paradigms to overcome the limitations of single-paradigm methods. A prominent trend involves the incorporation of transformer and attention mechanisms to capture long-range dependencies in degraded underwater images. U-Transformer pioneered this direction by introducing transformer blocks into UIE, employing channel-wise and spatial-wise attention modules trained on the large-scale LSUI dataset [33]. DDformer further advanced efficient global modeling through dimension-decomposed attention and a semi-supervised learning framework [34]. Other notable hybrid models include UnFold (DUN), which combines iterative model-based optimization with deep learning using a color prior guidance block and inter-stage feature transformer [35], as well as cross-wise transformer architectures equipped with feature supplement modules to mitigate information loss across processing stages [36]. Despite their representational capacity, these methods often suffer from high computational overhead due to the quadratic complexity of self-attention, which restricts their applicability in real-time underwater scenarios. Additional limitations include increased model complexity, sensitivity to architectural choices, and challenges in balancing physical constraints with data-driven learning.

Despite these advances, deep learning-based UIE methods continue to face several persistent challenges. The scarcity of high-quality real-world paired data remains a fundamental constraint, prompting increased reliance on unsupervised and semi-supervised learning paradigms. Methods such as UDnet attempt to mitigate this by modeling uncertainty distributions during reference map generation [37], yet issues of generalization persist. GAN-based frameworks, while capable of producing visually compelling results, still suffer from training instability and mode collapse, requiring meticulous hyperparameter tuning and architectural balancing. Furthermore, many approaches are overly dependent on synthetically generated data or insufficiently model the wavelength-dependent attenuation characteristics of water, a shortcoming partially alleviated by Deep WaveNet through receptive field adaptation based on color channel properties [38]. Moreover, prevailing methods frequently overlook the spatially heterogeneous nature of underwater degradation, lack principled integration of optical physics, and prioritize performance gains at the expense of computational efficiency. These collective limitations underscore the urgent need for novel frameworks that harmonize physical plausibility with lightweight, degradation-aware processing, a research gap that motivates the approach proposed in this work.

2.3. State Space Model (SSM)-Based Methods

Based on classical system theory and control engineering [39], State Space Models (SSMs) have recently garnered significant attention in deep learning research due to their ability to model long-range dependencies with linear computational complexity. This scalability advantage positions SSMs as a compelling alternative to transformer-based architectures, particularly in applications requiring efficient processing of long sequences. Among contemporary SSM variants, the Mamba architecture [40] has emerged as a breakthrough by introducing a selection mechanism that enables data-dependent state transitions, achieving state-of-the-art performance in both natural language processing and fundamental vision tasks including image classification and restoration.

Within computer vision, numerous studies have adapted Mamba’s selective state space formulation to harness its sequential modeling capabilities while addressing the unique requirements of visual data. Several approaches employ multiscale strategies that combine selective atrous scanning with hierarchical feature extraction, utilizing SSMs to capture global contextual dependencies at higher resolutions while utilizing convolutional networks for local feature processing at smaller scales [41]. Alternative methodologies integrate cross-scanning mechanisms to expand receptive fields through systematic 1D traversal of spatial dimensions [42], though these methods remain constrained by their fixed scanning patterns and uniform architectural application across all network stages. The recently proposed MambaVision framework [43] introduces a hybrid Mamba-Transformer backbone that incorporates redesigned Mamba components complemented by self-attention blocks, achieving enhanced capability in capturing both local and global visual dependencies.

Notwithstanding these promising developments, in general, vision tasks, the application of state space models to underwater image enhancement remains notably underexplored. Existing Mamba-based restoration techniques [44] primarily utilize conventional architectural designs with 2D selective scanning limited to four spatial directions, failing to incorporate the channel-adaptive processing crucial for addressing wavelength-specific degradation in underwater environments. More critically, these methods lack explicit mechanisms to address fundamental underwater optical challenges such as wavelength-dependent attenuation, spectral distortion, and red-channel deficiency [45]. This oversight significantly limits their effectiveness in real-world underwater scenarios where physical fidelity is paramount. The absence of SSM frameworks that effectively integrate optical constraints with data-driven learning represents a conspicuous gap in the literature, a gap that our proposed dual-path physics-guided Mamba network aims to address through its synergistic combination of selective sequence modeling and physically grounded optimization.

3. Proposed DPPGM Framework

3.1. Overview

Given a degraded underwater image $I\in {\mathbb{R}}^{H\times W\times 3}$, where H and W denote spatial dimensions, the objective is to recover the corresponding clean image $J\in {\mathbb{R}}^{H\times W\times 3}$. This restoration task is formulated as the following minimization problem:

$$arg\underset{\theta }{min}\mathcal{L}(f_{\theta }\left(I\right),J)$$

(1)

where $f_{\theta }$ represents the enhancement model parameterized by $\theta$, and $\mathcal{L}$ enotes a loss function quantifying the discrepancy between the enhanced image $f_{\theta }\left(I\right)$ and ground truth J. The goal is to produce outputs that are both visually superior and physically consistent.

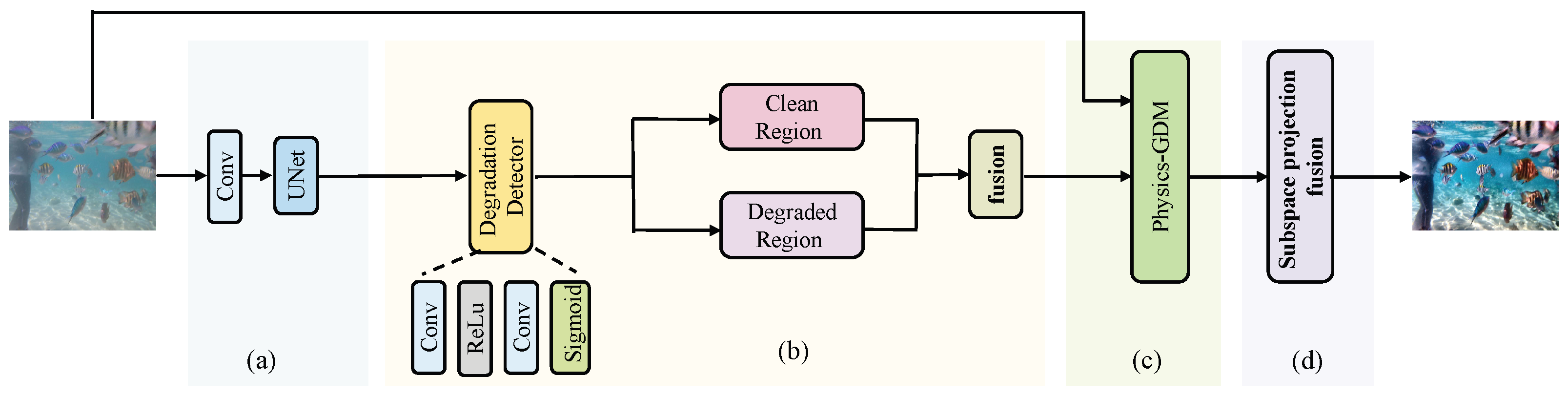
The proposed Dual-Path Physics-Guided Mamba Network (DPPGM) is designed to integrate adaptive degradation-aware processing with physically grounded constraints. This framework combines data-driven learning with physics-based optimization, leveraging their complementary strengths: the former captures complex and spatially variant degradation patterns, while the latter ensures strict fidelity to established underwater optical principles. As illustrated in Figure 1, the DPPGM comprises four core components: (a) Shallow Feature Extractor: Uses a CNN for initial low-level feature extraction and a UNet for multiscale processing, building foundational representations for enhancement. (b) Dual-Path Mamba Module: Employs a lightweight degradation detector to guide separate processing of clean and degraded regions through Mamba blocks, enabling adaptive handling of spatially varying degradation. (c) Physics-Guided Gradient Descent Module: Integrates physical constraints derived from the Jaffe–McGlamery model to refine intermediate results toward physically plausible outputs. (d) Subspace Projection Fusion: Combines low-rank subspace projection for compact cross-stage feature integration (reducing redundancy while preserving critical information) and Mamba-based refinement to enhance feature consistency.

3.2. Shallow Feature Extractor

As the foundational feature extraction component of the DPPGM framework, this module employs convolutional operations to transform the raw underwater input into an initial set of low-level features. These features are subsequently processed by a UNet-based encoder–decoder architecture to capture multi-scale representations.

The extraction process consists of two primary steps. First, a convolutional layer $3\times 3$ projects the 3-channel RGB input into a 40-channel feature space, enhancing representational capacity while retaining local spatial structures. This expanded feature map then serves as input to a UNet structure, through a series of strided convolutions (for downsampling), transposed convolutions (for upsampling), and skip connections, the UNet effectively captures multi-scale information: the encoder pathway condenses spatial resolution to encode high-level semantics, while the decoder progressively reconstructs spatial details by integrating upsampled features with skip-connected encoder outputs. This design enables the module to represent both fine-grained textures and larger structural patterns, forming a critical foundation for subsequent enhancement stages.

Although the UNet excels at capturing local spatial correlations through its convolutional inductive bias, it remains limited in modeling long-range dependencies and adapting to spatially varying degradation patterns. These limitations are explicitly addressed in the subsequent Dual-Path Mamba Module, which incorporates selective state-space modeling to efficiently capture global context and dynamically focus on degraded regions. This combination ensures that the framework benefits from the robust local feature learning of the UNet while extending its capability to handle complex, non-uniform underwater degradation in a computationally efficient manner.

3.3. Dual-Path Mamba Module

As the adaptive core of the DPPGM, the Dual-Path Mamba Module provides a differentiated solution for addressing the spatially heterogeneous degradation specific to underwater images, including uneven turbidity gradients, localized backscattering hotspots, and wavelength-dependent light attenuation disparities. Unlike conventional uniform feature processing paradigms, this module fully leverages Mamba’s SSM capability to efficiently capture long-range cross-pixel degradation correlations with linear computational complexity. Simultaneously, a novel region-aware mechanism enables dynamic allocation of computational resources—prioritizing processing for severely degraded regions while preserving original details in clean regions, thereby achieving an optimal balance between restoration performance and computational efficiency. This design follows a symmetry principle by establishing a “degradation level-processing intensity” mapping between clean and degraded regions, avoiding symmetry-breaking from uniform processing.

The module takes feature maps from the shallow feature extractor (dimensions $B\times C\times H\times W$, where C = 40) as input. As illustrated in the Dual-Path Mamba Module (Figure 1b, it processes features through three core stages—degradation mask generation, dual-path feature processing, and adaptive fusion—to produce degradation-adaptive feature maps for subsequent physics-guided refinement.

First, a lightweight degradation detector generates a pixel-level degradation mask $\mathcal{M}$ through a compact convolutional structure:

$$\mathcal{M}=\sigma \left({\mathrm{Conv}}_{3\times 3}^2\left(\mathrm{ReLU}\left({\mathrm{Conv}}_{3\times 3}^1\left(x\right)\right)\right)\right)$$

(2)

where the first convolution compresses channels from 40 to 5 ($C/8$), and the second produces a single-channel output. Physically, ${\mathcal{M}}_{b,i,j}\approx 0$ corresponds to clean regions with preserved textures, ${\mathcal{M}}_{b,i,j}\approx 1$ indicates severely degraded regions, and intermediate values represent transition zones.

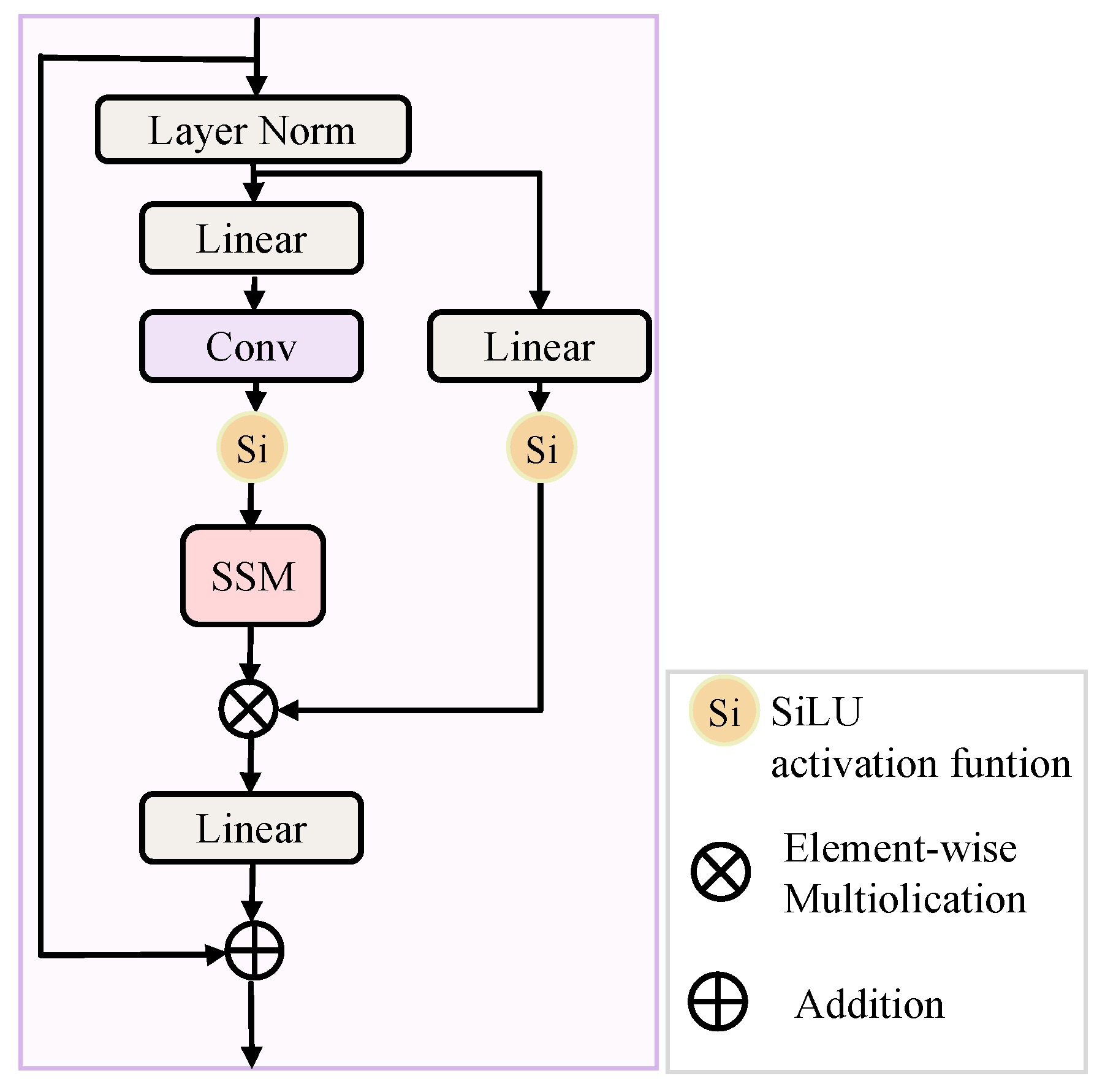
Within the overall architecture, two parallel Mamba base units—designated as the Clean Region path and the Degraded Region path, as shown in Figure 1b—operate concurrently under the guidance of the degradation mask $\mathcal{M}$. It is noteworthy that both units share an identical architectural design, as depicted in Figure 2.

The Clean Region unit specializes in preserving and refining features in less-corrupted areas, while the Degraded Region unit focuses on reconstructing and enhancing severely degraded regions. Both follow a consistent processing pipeline: initial feature normalization via Layer Norm, followed by a sequence comprising linear projection, convolutional operations, and SSM. Between these stages, SiLU activation functions introduce nonlinearity, while element-wise multiplication and addition operations facilitate the integration of intermediate features.

The selective state space mechanism implements Mamba’s core formulation:

$$\begin{array}{ccc}\hfill h_t& =\overline{A}\odot h_{t-1}+\overline{B}\odot x_t{y}_t\hfill & \hfill =C\odot h_t\end{array}$$

(3)

with data-dependent parameterization:

$${\mathrm{\Delta }}_t=\mathrm{softplus}\left(W_{\mathrm{\Delta }}{x}_t\right),B_t=W_B{x}_t,C_t=W_C{x}_t$$

(4)

and discrete-time transformation:

$$\begin{array}{cc}\hfill \overline{A}& =exp\left(\mathrm{\Delta }A\right)\hfill \\ \hfill \overline{B}& ={\left(\mathrm{\Delta }A\right)}^{-1}(exp\left(\mathrm{\Delta }A\right)-I)\mathrm{\Delta }B\hfill \end{array}$$

(5)

For computational efficiency, we employ parallel scan algorithms that maintain $O\left(L\right)$ sequential complexity while enabling $O\left(logL\right)$ parallel depth. The selection of G = 4 and $\mathrm{d\_state}$ = 16 reflects a standard trade-off in lightweight model design, aiming for sufficient modeling capacity without excessive complexity. This configuration is consistent with effective practices established in related state-space literature.

The two Mamba units achieve functional specialization through mask-weighted gradient modulation: the clean-unit’s learning is weighted by $1-\mathcal{M}$, focusing on noise suppression and detail preservation; the degradation-unit’s learning is weighted by $\mathcal{M}$, specializing in turbidity modeling and backscatter suppression.

Finally, pixel-level adaptive fusion integrates the outputs:

$${\mathbf{X}}_{\mathrm{b}}={\mathbf{F}}_{\mathrm{clean}}\odot (1-\mathcal{M})+{\mathbf{F}}_{\mathrm{deg}}\odot \mathcal{M}$$

(6)

This strategy ensures natural preservation in clean regions, effective restoration in degraded areas, and seamless transitions in boundary zones.

3.4. Physics-Guided Gradient Descent Module

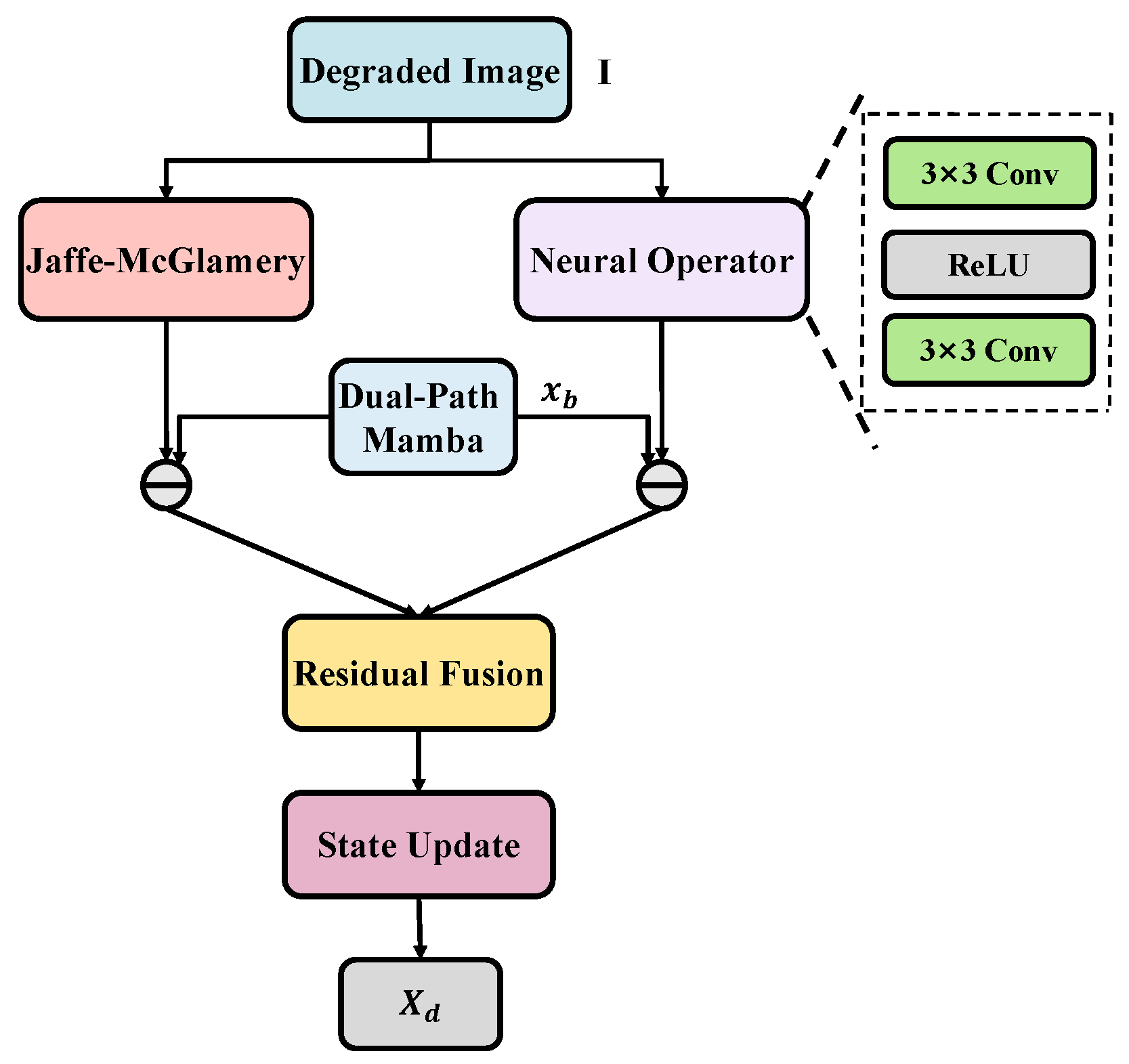
The Physics-Guided Gradient Descent Module (PhysicsGDM) establishes a bidirectional integration framework that synergizes data-driven enhancement with underwater optical physics. As illustrated in Figure 3, this module merges a physics-informed formulation with learned feature representations to ensure both physical plausibility and adaptive enhancement performance.

The core of PhysicsGDM is built upon a Jaffe–McGlamery-inspired optical model that explicitly incorporates depth-dependent light propagation, effectively capturing wavelength-specific attenuation and backscattering effects inherent in underwater environments. The scene radiance (restored optical signal) is computed as follows:

$$\mathcal{J}\left(x\right)={\displaystyle \frac{I-B_c·(1-e^{-c·d\left(x\right)})}{e^{-c·d\left(x\right)}+ϵ}}$$

(7)

where $e^{-c·d\left(x\right)}$ denotes transmittance (governed by the learnable attenuation coefficient c), $d\left(x\right)$ is the depth map derived from wavelength-specific attenuation properties:

$$d\left(x\right)=1-{\left(R\left(x\right)-0.5B\left(x\right)\right)}_{+}$$

(8)

and $B_c$ (background light) is estimated via dark channel prior and spatial pooling:

$$B_c=\underset{\mathrm{\Omega }}{\max }\left(\underset{c\in \{R,G,B\}}{\min }{I}^c\left(x\right)\right)$$

(9)

All physical parameters are constrained to positive values, ensuring consistency with optical principles while enabling adaptive adjustment to varying water conditions.

The module employs a dual-branch architecture that integrates physical modeling with data-driven learning through convolutional operators $\varphi \left(·\right)$ and ${\varphi }^{†}\left(·\right)$. A physics-based residual $\mathcal{J}\left(x_t\right)-y$ quantifies deviations from the optical model, while a neural residual $\varphi \left(x_t\right)-y$ captures data-driven enhancement errors. These residuals are adaptively fused via a learned weighting factor $\gamma =\sigma \left(\lambda \right)$, where $\sigma$ denotes the sigmoid function and $\lambda$ is a trainable step size parameter:

$$\mathrm{combined\_res}=\gamma ·(\mathcal{J}\left(x_t\right)-y)+(1-\gamma )·(\varphi \left(x_t\right)-y)$$

The enhanced image is iteratively refined through physics-informed gradient descent:

$$x_{t+1}=x_t-\eta ·{\varphi }^{†}\left(\mathrm{combined\_res}\right)$$

(10)

where $\eta$ denotes the learning rate.

This design preserves the well-posed inverse problem structure of underwater image enhancement by incorporating explicit depth-dependent scattering modeling, adaptively tuned physical parameters, and a stable fusion mechanism. The integration of these physical constraints serves to regularize the solution space, anchoring it to optically plausible outcomes. This regularization not only contributes to stable training convergence but also enhances the model’s generalization capability by reducing over-reliance on patterns specific to the training data, thereby supporting robust performance across diverse turbidity conditions through a balance between physics-derived plausibility and data-driven adaptability.

3.5. Subspace Projection Fusion

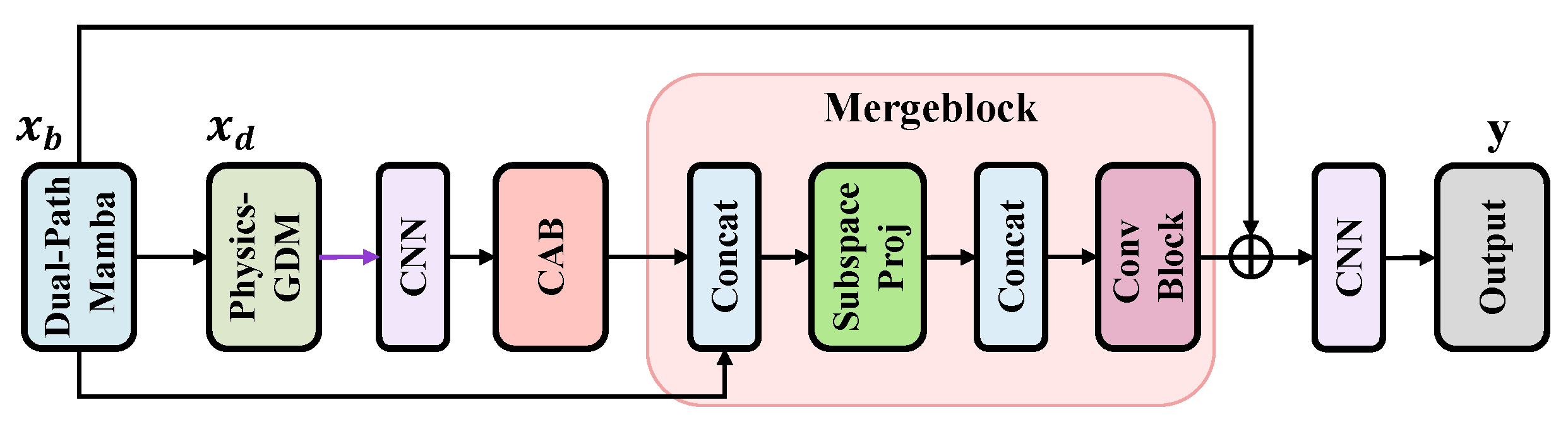
This module is designed for the efficient integration of multi-stage features, with a primary input stream originating from the Dual-Path Mamba Module. As illustrated in Figure 4, it employs low-rank subspace projection to compactly combine features while preserving critical information, particularly from the Mamba-enhanced pathway.

Implemented within the MergeBlock class, the fusion process integrates two feature sources: the current-stage features $x_{\mathrm{d}}$ and cross-stage features $x_{\mathrm{b}}$ (which include outputs from the Dual-Path Mamba Module). The computational workflow proceeds as follows:

Feature Concatenation: The current-stage features $x_{\mathrm{d}}$ are processed by a CNN and a CAB (Convolution-based Attention Block). Then, the cross-stage features $x_{\mathrm{b}}$ are concatenated with the output of the processed $x_{\mathrm{d}}$ along the channel dimension:

$$\mathrm{z}=\mathrm{cat}(x_{\mathrm{b}},\mathrm{CNN}\left(\mathrm{CAB}\left(x_{\mathrm{d}}\right)\right))$$

(11)

Low-Rank Subspace Projection: The concatenated features are projected into a low-dimensional subspace to reduce redundancy while retaining essential structural and semantic information. A convolutional subnetwork $\psi$($·$) generates a projection matrix $V_t$:

$$V_t=\psi \left(\mathrm{z}\right)·\mathrm{N}$$

(12)

where N is a normalization term ensuring orthogonality. The transpose projection matrix is obtained through dimension permutation:

$$V=V_t^{\top }$$

(13)

Orthogonal Reconstruction: Matrix inversion stabilizes the projection operation:

$$M={\left(V_t·V\right)}^{-1}$$

(14)

The bridge features b are then reconstructed in the low-rank subspace:

$${\mathrm{b}}_{\mathrm{proj}}=V·{\left(\mathrm{M}·V_t·{\mathrm{b}}^T\right)}^T$$

(15)

Feature Re-integration: The projected bridge features $b_{p}roj$ are merged with the original features I via concatenation, followed by a $3\times 3$ convolutional layer $C_{3\times 3}$ and residual connection:

$$\mathrm{y}=C_{3\times 3}\left(\mathrm{cat}(I,b_{proj})\right)+I$$

(16)

This design effectively integrates Mamba-enhanced features through a compact low-rank representation, reducing computational complexity while preserving critical information from the multi-stage processing pipeline. The subspace fusion mechanism ensures efficient feature recombination while maintaining enhancement performance across diverse underwater conditions.

4. Experiments

4.1. Dataset Description

To comprehensively evaluate the performance of the proposed DPPGM framework, experiments are conducted on two categories of test datasets: (1) full-reference datasets containing paired degraded and clear images, and (2) no-reference datasets without ground truth references.

4.1.1. Full-Reference Datasets

UIEB (Underwater Image Enhancement Benchmark): This benchmark includes 890 paired underwater images (e.g., coral reefs, marine fauna) and adopts a standard split: 800 pairs for training and 90 for testing. The model was trained and evaluated on this fixed partition under supervised learning, ensuring fair comparison with consistent data distribution. (Dataset available at: https://www.kaggle.com/datasets/larjeck/uieb-dataset-raw, accessed on 20 October 2024).

LSUI (Large-Scale Underwater Image): Focused on challenging underwater conditions, these dataset contains 4279 paired images. We used a fixed random split (3879 training / 400 test pairs) and followed the same supervised learning protocol as UIEB for model training and evaluation. (Dataset available at: https://github.com/LintaoPeng/U-shape_Transformer_for_Underwater_Image_Enhancement, accessed on 20 October 2024).

4.1.2. No-Reference Dataset

U45: These dataset comprises 45 underwater images exhibiting complex degradation patterns, including high turbidity and non-uniform illumination, without corresponding reference images. It serves as a challenging testbed to evaluate the generalization capability and practical applicability of enhancement methods in real-world scenarios. Since U45 lacks ground truth, it was only used for testing: after the model was fully trained on UIEB and LSUI’s training sets, its generalization was validated on U45’s 45 images. (Dataset available at: https://github.com/qianday/U45, accessed on 23 September 2025).

Challenging60 (C60): This subset of the UIEB benchmark contains 60 particularly difficult images characterized by extreme turbidity, dense suspended particles, and severe visibility degradation. It represents some of the most challenging conditions encountered in practical underwater imaging. Following the standard evaluation protocol, we used C60 exclusively as a test set to rigorously assess the model’s robustness and generalization capability under near-zero visibility scenarios that are distinct from the training data distribution.(Dataset available at: https://github.com/qianday/Challenging60, accessed on 23 September 2025).

To ensure a fair and reproducible comparison, the performance of all competing methods was obtained by either using officially released pre-trained models or by our strict re-implementation following the training details and data splitting strategies described in their respective original publications.

4.2. Experimental Details

Experimental Setting: All experiments are implemented using PyTorch 2.1.1 and conducted on a Linux workstation equipped with an NVIDIA GeForce RTX 4090 GPU. The manufacturer of this GPU is NVIDIA Corporation, and the GPU was procured in Yantai, Shandong Province, China. During training, multiple data augmentation techniques are applied to enhance diversity, including random flipping, rotation, transposition, mixing, and cropping. The model is trained with a batch size of 4 for both UIEB and LSUI datasets using the AdamW optimizer (${\beta }_1=0.9$, ${\beta }_2=0.999$) with an initial learning rate of $3\times {10}^{-4}$. A CosineAnnealingLR scheduler is adopted to dynamically adjust the learning rate within the range of $1\times {10}^{-6}$ to $2\times {10}^{-4}$, incorporating periodic warm-up phases to mitigate the risk of convergence to local minima. The model was trained for a total of 300 epochs.

Evaluation Metrics: For full-reference evaluation on UIEB and LSUI datasets, we employ the following metrics: A comprehensive set of metrics is employed to evaluate enhancement performance across different aspects. For full-reference assessment on UIEB and LSUI, we utilize: Peak Signal-to-Noise Ratio (PSNR) for pixel-level fidelity, Structural Similarity Index (SSIM) for structural consistency, and Learned Perceptual Image Patch Similarity (LPIPS) for deep feature-based perceptual quality. Underwater-specific metrics include the Underwater Color Image Quality Evaluation (UCIQE) for color restoration and the Underwater Image Quality Measure (UIQM) for integrated colorfulness, sharpness, and contrast performance. For the no-reference U45 and Challenging60 dataset, evaluation incorporates Total Variation (TV) for noise and smoothness assessment, Blind/Referenceless Image Spatial Quality Evaluator (BRISQUE) for naturalness estimation, and Natural Image Quality Evaluator (NIQE) for no-reference perceptual quality. UCIQE and UIQM are also reported to maintain consistency with full-reference benchmarks.

4.3. Comparison with State-of-the-Art Methods

4.3.1. Quantitative Results

In this section, we present a comprehensive evaluation of the proposed DPPGM framework across three benchmark datasets—UIEB, LSUI, and U45—and compare its performance against 13 state-of-the-art underwater image enhancement methods: WaterNet [28], UWCNN [14], AirNet [29], PUIE-Net [46], DeepWaveNet [38], PUGAN [32], U-Transformer [33], DDFormer [34], HCLR-Net [30], Unfold [35], HUPE [47], UVZ [36], and UDNet [37]. The comparison encompasses both objective metric-based assessments and qualitative visual analyses to thoroughly demonstrate the effectiveness and superiority of our approach.

Comprehensive quantitative evaluations across three benchmark datasets demonstrate the superior performance of DPPGM compared to state-of-the-art methods. As detailed in

Table 1. Quantitative comparison on UIEB test set in terms of PSNR, SSIM, LPIPS, UIQM, and UCIQE. The top two scores are marked in red and blue.

Method	PSNR↑	SSIM↑	LPIPS↓	UCIQE↑	UIQM↑
WaterNet [28]	22.861	0.873	0.114	0.435	3.040
UWCNN [14]	13.443	0.656	0.273	0.338	2.598
AirNet [29]	16.582	0.639	0.227	0.377	2.624
PUIE-Net [46]	22.735	0.908	0.173	0.398	3.243
DeepWaveNet [38]	22.960	0.905	0.082	0.463	2.731
PUGAN [32]	22.480	0.816	0.149	0.429	3.100
U-Transformer [33]	20.954	0.785	0.174	0.389	3.238
DDFormer [34]	23.909	0.904	0.087	0.442	3.235
HCLR-Net [30]	18.097	0.822	0.134	0.430	2.530
Unfold [35]	23.396	0.903	0.091	0.428	3.163
HUPE [47]	22.548	0.906	0.088	0.410	4.201
UVZ [36]	24.985	0.910	0.094	0.358	0.087
UDNet [37]	23.831	0.912	0.081	0.412	3.896
DPPGM (Ours)	24.165	0.921	0.093	0.431	4.053

, on the UIEB dataset, DPPGM achieves the highest SSIM value of 0.921, surpassing the second-best method, UVZ (0.910), by a clear margin, while the absolute improvement in SSIM (0.011) may appear modest, it represents a consistent and meaningful enhancement observed across multiple test samples. This performance advantage is especially pronounced in complex underwater scenes containing fine details such as coral branches and fish fins, where DPPGM effectively preserves subtle structural information that is often compromised or oversmoothed by other methods. In terms of UIQM, which holistically evaluates color, sharpness, and contrast, DPPGM attains a score of 4.053, ranking among the top performers and underscoring its balanced enhancement capability. Furthermore, DPPGM maintains strong pixel-level fidelity with a PSNR of 24.16, remaining competitive with leading approaches such as UVZ and DDFormer.

On the LSUI dataset, which focuses on low-light underwater conditions, DPPGM demonstrates consistent performance advantages as shown in

Table 2. Quantitative comparison on LSUI test set in terms of PSNR, SSIM, LPIPS, UIQM and UCIQE. The top two scores are marked in red and blue.

Method	PSNR↑	SSIM↑	LPIPS↓	UCIQE↑	UIQM↑
WaterNet [28]	22.439	0.851	0.154	0.429	3.200
UWCNN [14]	16.857	0.718	0.275	0.358	2.960
AirNet [29]	17.810	0.700	0.247	0.382	2.721
PUIE-Net [46]	21.307	0.876	0.106	0.409	3.160
DeepWaveNet [38]	20.750	0.835	0.155	0.464	2.876
PUGAN [32]	21.039	0.839	0.144	0.449	3.117
U-Transformer [33]	14.671	0.635	0.306	0.350	2.361
DDFormer [34]	24.900	0.883	0.105	0.443	3.090
HCLR-Net [30]	21.411	0.855	0.121	0.443	3.071
Unfold [35]	21.197	0.835	0.166	0.415	3.118
HUPE [47]	25.467	0.899	0.162	0.462	3.143
UVZ [36]	26.590	0.887	0.103	0.425	3.180
UDNet [37]	26.982	0.908	0.127	0.448	3.236
DPPGM (Ours)	28.269	0.931	0.0957	0.429	3.399

. It achieves a leading SSIM of 0.931, representing a 0.032 point improvement over the second-best method HUPE (0.899)—a margin that substantially exceeds typical variations in underwater image enhancement benchmarks. Similarly, DPPGM attains a PSNR of 28.269, surpassing UVZ by 1.679 and HUPE by 2.802, differences that are considered substantial in visual quality assessment. The method also excels perceptually, achieving an LPIPS score of 0.0957. The consistent and substantial improvements across multiple independent metrics provide strong evidence of statistical significance.

For the no-reference U45 dataset, DPPGM again delivers outstanding results to

Table 3. Quantitative comparison on U45 test set in terms of TV, BRISQUE, NIQE, UCIQE, and UIQM. The top two scores are marked in red and blue.

Method	TV↓	BRISQUE↓	NIQE↓	UCIQE↑	UIQM↑
WaterNet [28]	31.428	9.676	8.495	0.416	3.391
UWCNN [14]	17.765	11.323	5.920	0.355	3.006
AirNet [29]	16.958	20.513	5.996	0.375	2.378
PUIE-Net [46]	29.610	8.228	5.704	0.388	3.416
DeepWaveNet [38]	38.261	7.875	6.348	0.467	3.087
PUGAN [32]	32.824	10.376	6.467	0.446	3.374
U-Transformer [33]	30.508	8.291	5.375	0.329	2.542
DDFormer [34]	35.887	37.052	7.516	0.428	3.057
HCLR-Net [30]	35.976	7.267	6.087	0.437	3.359
Unfold [35]	35.851	6.619	6.096	0.430	3.340
HUPE [47]	30.871	6.546	6.417	0.447	3.120
UVZ [36]	36.885	6.543	6.115	0.401	3.088
UDNet [37]	53.189	31.385	5.898	0.473	3.396
DPPGM (Ours)	29.138	9.249	4.203	0.413	3.594

. It achieves the lowest NIQE score of 4.203, reflecting superior naturalness and perceptual quality in the absence of ground truth. With a UIQM value of 3.594, it ranks first among all compared methods, demonstrating comprehensive strength in color enhancement, sharpness improvement, and contrast adjustment. Moreover, DPPGM attains a TV value of 29.138, illustrating its ability to effectively suppress noise while preserving critical structural details, further validating its generalization capability in real-world underwater scenarios.

The evaluation is extended to the Challenging60 dataset to assess performance under more severe degradation conditions. As shown in

Table 4. Quantitative comparison on C60 test set in terms of TV, BRISQUE, NIQE, UCIQE, and UIQM. The top two scores are marked in red and blue.

Method	TV↓	BRISQUE↓	NIQE↓	UCIQE↑	UIQM↑
WaterNet [28]	34.183	9.789	8.964	0.434	3.048
UWCNN [14]	19.648	10.654	6.528	0.332	3.150
AirNet [29]	20.753	18.288	6.028	0.400	2.907
PUIE-Net [46]	32.772	11.639	6.793	0.478	3.178
DeepWaveNet [38]	40.210	8.567	5.273	0.335	2.813
PUGAN [32]	38.345	26.380	7.419	0.054	3.080
U-Transformer [33]	35.186	7.663	6.210	0.478	2.736
DDFormer [34]	38.284	36.851	6.820	0.445	3.144
HCLR-Net [30]	39.810	10.583	6.567	0.478	3.239
Unfold [35]	39.533	7.792	6.571	0.408	3.173
HUPE [47]	33.375	11.930	4.997	0.475	3.117
UVZ [36]	38.634	8.497	5.843	0.307	3.084
UDNet [37]	40.315	42.860	4.893	0.338	3.122
DPPGM (Ours)	33.589	8.626	5.847	0.476	3.626

, DPPGM achieves a leading UIQM score of 3.626, demonstrating a substantial advantage in overall perceptual quality. The method also attains competitive scores in noise reduction (TV: 33.589) and naturalness preservation (NIQE: 5.847). The consistent superiority of DPPGM on this challenging benchmark, which contains turbidities distinct from the training data, underscores its strong generalization capability and practical utility in diverse underwater environments.

4.3.2. Qualitative Visual Analysis

To provide a concise yet comprehensive visual comparison, we select seven representative models from the thirteen state-of-the-art methods considered in this study. The selection criteria encompass overall performance across datasets, architectural diversity, and methodological representativeness, ensuring coverage of various technical paradigms—including physics-based, CNN-based, transformer-based, and lightweight approaches.

As supported by quantitative metrics, the visual results produced by our DPPGM consistently demonstrate superior performance across the UIEB, LSUI, and U45 datasets, with enhancements tailored to the specific characteristics of each scenario.

As illustrated in Figure 5, DPPGM demonstrates exceptional performance on the UIEB dataset, particularly in preserving fine structural details and maintaining natural color fidelity across diverse marine scenes. In images featuring fish and complex aquatic vegetation, our method successfully retains delicate patterns including skin textures and fin contours, while effectively avoiding the over-saturation or excessive smoothing commonly observed in other approaches. Comparative analyses reveal that while DeepWaveNet tends to over-enhance colors and DDFormer often oversmooths subtle elements, DPPGM achieves a balanced and visually coherent reconstruction that closely aligns with natural underwater appearance. The consistent outperformance against models like UVZ and DDFormer underscores the effectiveness of our core innovation: the symmetry-constrained dual-path cooperative design. Unlike the sequential processing in these methods, our framework enables deeper synergy between physical principles and data-driven learning, leading to more balanced and robust enhancement.

Figure 6 showcases DPPGM’s remarkable capability in enhancing poorly illuminated seabed environments from the LSUI low-light dataset. The visual results demonstrate effective restoration of topographic details including rock formations and coral branches without introducing unnatural artifacts or excessive noise. In contrast to PUIE-Net and WaterNet, which frequently fail to maintain structural consistency in dark regions, and UVZ, which may produce inconsistent local contrasts, DPPGM leverages its physics-informed design to ensure harmonized brightness adjustment and detail recovery.

The performance on the challenging no-reference U45 dataset, depicted in Figure 7, further confirms DPPGM’s robustness in handling complex coral reef imagery with significant color casts and spatial degradation. Our method achieves accurate color correction—effectively recovering the natural hues of coral communities—while preserving crucial textural sharpness and edge information. Comparative visual assessments show that UDNet tends to oversmooth detailed regions and PUGAN occasionally introduces color shifts, whereas DPPGM’s dual-path architecture enables adaptive handling of spatially varying degradation, producing enhancements that are both visually appealing and physically plausible.

The generalization capability of DPPGM is further validated on the UIEB-Challenging60 dataset, as shown in Figure 8. In scenes characterized by extreme turbidity and dense suspended particles, our method demonstrates exceptional haze penetration and contrast recovery capabilities, while compared methods like DeepWaveNet and DDFormer struggle with persistent haze or loss of detail in such demanding conditions, DPPGM effectively restores visibility while preserving the integrity of delicate structures like coral polyps and fish scales. The physics-guided pathway proves particularly beneficial in these scenarios, providing constraints that prevent the introduction of non-physical artifacts while recovering plausible scene radiance. This performance on genuinely challenging, real-world imagery underscores the practical viability of our approach for deployment in unpredictable underwater environments.

These qualitative outcomes align closely with the quantitative results, confirming that DPPGM effectively translates its architectural advantages into perceptually superior underwater image enhancement across a variety of challenging conditions.

4.4. Model Complexity

To provide a comprehensive evaluation of the trade-off between efficiency and performance—a key challenge related to symmetry in UIE—we conduct extensive comparisons with 13 state-of-the-art underwater image enhancement methods. As summarized in

Table 5. Comprehensive model complexity and performance comparison. The top two scores are marked in red and blue.

Method	Params (M)↓	FLOPs (G)↓	UIEB		LSUI		U45
			PSNR↑	SSIM↑	PSNR↑	SSIM↑	UCIQE↑	UIQM↑
WaterNet [28]	24.81	193.7	22.861	0.873	22.439	0.851	0.416	3.391
UWCNN [14]	0.04	5.23	13.443	0.656	16.857	0.718	0.355	3.006
AirNet [29]	5.767	301.274	16.582	0.639	17.810	0.700	0.375	2.378
PUIE-Net [46]	1.410	30.09	22.735	0.908	21.307	0.876	0.388	3.416
DeepWaveNet [38]	0.279	18.148	22.960	0.905	20.750	0.835	0.467	3.087
PUGAN [32]	95.660	72.05	22.480	0.816	21.039	0.839	0.446	3.374
U-Transformer [33]	65.600	66.2	20.954	0.785	14.671	0.635	0.329	2.542
DDFormer [34]	7.581	4.467	23.909	0.904	24.900	0.883	0.428	3.057
HCLR-Net [30]	4.871	401.966	18.097	0.822	21.411	0.855	0.437	3.359
Unfold [35]	4.187	112.785	23.396	0.903	21.197	0.835	0.430	3.340
HUPE [47]	10.21	2.4	22.548	0.906	25.467	0.899	0.447	3.120
UVZ [36]	5.388	124.879	24.985	0.910	26.590	0.887	0.401	3.088
UDNet [37]	1.402	7.537	23.831	0.912	26.982	0.908	0.473	3.396
DPPGM (Ours)	1.48	25.39	24.16	0.921	28.269	0.931	0.413	3.594

, the evaluation encompasses both computational complexity (parameters and FLOPs) and enhancement performance across three benchmark datasets. Metric selection is tailored to each dataset’s characteristics: full-reference metrics (PSNR and SSIM) are employed for UIEB and LSUI, while no-reference metrics (UCIQE and UIQM) are adopted for U45, ensuring a holistic assessment of restoration quality and perceptual effectiveness.

As shown in Table 5, DPPGM achieves a superior trade-off between computational efficiency and enhancement performance—effectively restoring the symmetry broken by most methods that prioritize one metric over the other. With only 1.48 M parameters and 25.39 G FLOPs, it maintains a lightweight architecture compared to most competitors: it is significantly more parameter-efficient than heavyweight models like WaterNet (24.81 M), PUGAN (95.66 M), and U-Transformer (65.60 M), while also outperforming methods with comparable complexity (e.g., PUIE-Net: 1.410 M, DDFormer: 7.581 M) in all performance metrics.

In terms of computational cost (FLOPs), DPPGM (25.39 G) is more efficient than resource-intensive methods such as AirNet (301.27 G) and HCLR-Net (401.96 G), and even rivals lightweight designs like UWCNN (5.23 G) and DDFormer (4.47 G) despite delivering substantially better results. Performance-wise, DPPGM leads across critical metrics: it achieves the highest SSIM (0.921) on UIEB and sets new state-of-the-art results on LSUI with PSNR (28.269) and SSIM (0.931). On the challenging U45 dataset, its UIQM score (3.594) outperforms all compared methods, demonstrating robust generalization to real-world underwater scenes. Notably, while methods like UVZ and UDNet show strong performance on specific datasets, they either incur higher computational costs (UVZ: 124.88 G FLOPs) or lag in cross-dataset consistency compared to DPPGM. This balance of efficiency and performance confirms that DPPGM avoids the common pitfall of excessive complexity in high-performance models, upholding the symmetry principle of balanced system design and making it suitable for practical deployment in resource-constrained underwater imaging systems.

4.5. Ablation Study

To quantify the contribution of each core component in DPPGM, we conduct ablation experiments by systematically removing three critical modules—dual-path structure (DPS), Mamba-based physics-guided degradation model (PGDM), and subspace projection fusion (SPF)—and evaluating performance changes. We use Peak Signal-to-Noise Ratio (PSNR, pixel-level fidelity) for UIEB and LSUI, and Underwater Image Quality Measure (UIQM, no-reference quality) for U45, with results summarized in

Table 6. Ablation study of key components.

Case	Components			Performance
	DPS	PGDM	SPF	PSNR↑ on UIEB	PSNR↑ on LSUI	UIQM↑ on U45
1	✓	✓	✓	24.17	28.27	3.59
2	✓	✓	–	23.88	28.09	3.32
3	✓	–	✓	23.98	28.11	3.35
4	–	✓	✓	23.65	27.73	3.24
5	✓	–	–	23.47	27.54	3.21
6	✓ *	–	–	23.21	27.19	3.13

Note: Case 6: DPS ^* denotes the variant where the degradation-aware mask is replaced with uniform weighting (all values = 0.5). ↑ denotes that higher values indicate better performance; The top two scores are marked in red and blue.

.

The results confirm each module’s indispensability and their synergistic effects: Case 1 (the full model integrating DPS, PGDM, and SPF) achieves the best performance across all metrics (UIEB PSNR: 24.17, LSUI PSNR: 28.27, U45 UIQM: 3.59), fully validating the framework’s efficacy. Removing SPF (Case 2) leads to consistent performance degradation, with UIEB PSNR decreasing by 0.29, LSUI PSNR by 0.18, and U45 UIQM by 0.27—this reflects SPF’s key role in aggregating fine-grained features to preserve underwater scene structural details. Disabling PGDM (Case 3) results in a 0.19 drop in UIEB PSNR, a 0.16 decline in LSUI PSNR, and a 0.24 reduction in U45 UIQM, confirming that PGDM’s embedded physical constraints effectively align enhancement results with real-world optical principles. The most significant performance loss occurs when excluding DPS (Case 4): UIEB PSNR decreases by 0.52, LSUI PSNR by 0.54, and U45 UIQM by 0.35, highlighting DPS’s critical value in addressing spatially heterogeneous degradation through separate processing of low-frequency global context and high-frequency local details. Retaining only DPS while removing PGDM and SPF (Case 5) leads to further performance drops, with UIEB PSNR reaching 23.47, LSUI PSNR 27.54, and U45 UIQM 3.21—this underscores that PGDM and SPF are necessary to balance pixel-level fidelity and physical plausibility, as DPS alone enables basic adaptive handling of heterogeneous degradation but lacks PGDM’s physical constraints and SPF’s efficient fusion, severely undermining the model’s ability to balance fidelity and plausibility. In Case 6, we replaced the learned degradation-aware mask with uniform weighting. The resulting performance drop (UIEB PSNR: 23.21, LSUI PSNR: 27.19, U45 UIQM: 3.13) compared to Case 5 confirms that the mask’s region-separation ability is crucial to the DPS module’s effectiveness.

Collectively, these findings demonstrate that all three core components are indispensable for DPPGM’s optimal performance.

5. Conclusions

This paper has proposed the Dual-Path Physics-Guided Mamba Network (DPPGM), a novel framework for underwater image enhancement that effectively addresses the challenges of complex degradation patterns and computational efficiency—with symmetry constraints as a core design logic. By integrating degradation-aware processing with physics-guided optimization and compact feature fusion, our method achieves an exceptional balance between enhancement quality and operational efficiency. Comprehensive experiments demonstrate that DPPGM outperforms state-of-the-art methods across multiple benchmarks, exhibiting superior performance in both objective assessments and subjective visual quality. The framework successfully mitigates typical underwater degradations while maintaining minimal computational requirements. Future work will explore the model’s deployment potential on embedded platforms, investigate its robustness to variations in physical parameter estimation under more dynamic underwater conditions, and further refine the symmetry-driven architecture.