Abstract
Fluid flow through a sphere has practical applications in numerous areas of technology, for instance, mineralogy, food engineering, and oilfield drilling. The goal of this paper is to look at how quadratic thermal radiation and activation energy affect the dissipative flow of hybrid nanofluids around a sphere with the heat source parameter. bvp4c (a MATLAB in-built function) is used to solve a system of nonlinear ordinary differential equations, which is the transformed version of the system of governing equations. Using multiple linear regression, the effects of relevant parameters on the mass transfer rate, the Nusselt number, and the skin friction coefficient are investigated. The key findings of this study are that increasing the radiation parameter improves the fluid temperature and increasing the activation energy parameter improves the fluid concentration. When the Eckert number and the parameter of the heat source are increased, the convective heat transmission is reduced. It appears that the magnetic field parameter reduces the shear stress near the surface. It is discovered that increasing the volume percentage of nanoparticles increases the skin friction coefficient and increasing the Schmidt number increases the mass transfer rate. Furthermore, the current results are validated against previously published data.
1. Introduction
The energy required to transform reactants into products, expressed as an absolute minimum, is referred to as activation energy (AE). There are several applications for this idea in the fields of water and oil emulsions, as well as in oil reservoir engineering. An activation energy-dependent nonlinear radiative flow of Maxwell fluid was modelled computationally by Mustafa et al. [1], and the Deborah number was stressed as a useful tool to reduce the velocity of the fluid. Khan et al. [2] considered the Arrhenius action energy term and elucidated the magnetohydrodynamic (MHD) Cross fluid flow by assuming an elongating surface. They observed the reduction in the mass transfer rate with the rise in activation energy. Kumar et al. [3] and Hayat et al. [4] examined the entropy generation optimization on distinct nanofluid flows using various geometries with activation energy. Cross fluid flow through a stable plate with activation energy and pressure gradient was modelled by Mustafa et al. [5]. They discovered that lowering the reaction rate parameter reduced the fluid concentration. Patil et al. [6] analyzed the impact of the roughness of the boundary surface and diffusion of liquid gases, such as liquid oxygen and hydrogen, on mixed convection nanofluid flow past a sphere. Ullah et al. [7] used NDsolve procedures to numerically resolve the mathematical model of non-Darcy nanofluid flow with the same parameter. It was shown that increasing the Forchheimer number decreased the fluid temperature. Ramaiah et al. [8] and Rashid et al. [9] used different stretching surfaces with activation energy to elucidate various Maxwell fluid flows. Increasing the heat source parameter led to a higher fluid temperature, whereas increasing the chemical reaction parameter resulted in a lower fluid concentration. By assuming the same geometries and the same parameter (activation energy), Haq et al. [10] and Islam et al. [11] discussed various nanofluid flows and observed that the stratification parameter reduced the concentration profiles. In a mixed convective flow of Casson fluid, Abdelmalek et al. [12] performed entropy generation optimization and stability analyses. It was discovered that the Stefan blowing parameter was well known for lowering fluid velocity. Li et al. [13] assumed a Riga plate and elaborated the characteristics of the heat transfer of a viscous fluid with the CC (Cattaneo–Christov) model using the HAM (Homotopy Analysis Method). Different nanofluid flows in various geometries were researched by several researchers [14,15,16,17,18,19] to see what effect the activation energy parameter had. As a result of their research, they discovered that increasing the thermophoresis parameter raised the fluid temperature, whereas increasing the Dufour number lowered the mass flux.
The magnetic field is used in various applications such as laser welding and other operations, such as flow stabilization, the external magnetic field in the fluid flow plays a vital role. MHD fluid has further applications in the industrial sector, including that of a lubricant, since it precludes lubricant viscosity from changing unexpectedly with the temperature. In Soundalgekar’s [20] explanation of the incompressible fluid flow amongst two plates accompanied by an external magnetic field, the Laplace transform operations were utilized. It was found that the strength of the magnetic field had a direct correlation with the reduction in the velocity of the fluid. Oreper and Szekely [21] emphasized that the magnetic field parameter was useful to modify the velocity field when buoyancy forces were considered in a fluid flow. Andersson [22] observed that the impact of the magnetic field was same as that of viscoelasticity on the flow field in the examination of viscoelastic fluid flow by an elongating sheet. Patil et al. [23] carried out a numerical investigation of a double diffusive mixed convection flow over a permeable vertical surface with surface mass transfer in the presence of convective boundary conditions. Sadaf and Nadeem [24] discovered that the rise in the magnetic field minimized the pressure gradient in their analysis on the cilia-induced flow in a bending channel. The RKF (Runge–Kutta–Fehlberg) method was utilized by Gholinia et al. [25] in order to solve the mathematical model of the mixed convective flow of a nanofluid that was modelled using a circular cylinder at the stagnation point. In comparison with the silver-based nanofluid, the temperature of the copper-based nanofluid was seen to be significantly higher. Deo et al. [26] examined the flow of a micropolar fluid within a porous cylindrical tube while an external magnetic field was present. They found that the amount of microrotation decreased as the magnetic field parameter increased. Later, several researchers [27,28,29] assumed porous media and discussed the impact of the magnetic field on various flows under different boundary conditions. Alharbi [26] graphically explained the impact of several parameters, including the magnetic parameter, using the finite element method on the hybrid nanofluid flow by a vertical plate. They found that the Prandtl number lessened the fluid temperature. Recently, various researchers [30,31,32,33,34,35,36] examined the effect that various types of magnetic field characteristics had on a variety of fluid flows over a variety of geometries. Finally, it is worth mentioning here that nanofluid/hybrid nanofluid flows with different geometries under the effect of different physical parameters were extensively examined by different researchers [37,38,39,40,41].
Metal nanoparticles (NPs), in particular, plasmonic metal NPs including silver, gold, and copper, have the highest thermal conductivities. These NPs possess local surface plasmon resonance (LSPR) [42,43], which offers a very large heat transfer surface. In addition to the NP size and composition, the morphology of the NPs has a significant impact on LSPR [41,42,43] and thus thermal conductivity. Therefore, in addition to the composition of the NPs suspended in a nanofluid, their morphology should be taken in consideration.
The previous literature led us to the conclusion that no work has been performed on the topic of hybrid nanofluid flow over a sphere with activation energy and quadratic thermal radiation. As a result, the purpose of this paper is to theoretically study the quadratic convective flow of a hybrid nanofluid (Water + Cu + SiO2) across a sphere with Arrhenius activation energy and quadratic thermal radiation. The results are presented in a graphical format using bvp4c (MATLAB in-built function). In order to determine the influence that the parameters have on the heat transfer rate, the mass transfer rate, and the skin friction coefficient, a statistical method known as multiple linear regression is utilized.
2. Formulation
This work is intended to scrutinize the impact of quadratic thermal radiation and Arrhenius activation energy on hybrid nanofluid (Water + Cu + SiO2) flow through a convectively heated sphere with viscous dissipation and quadratic thermal convection parameters. The current flow pattern of a fluid over a sphere is depicted in Figure 1. Table 1 presents the thermo-physical property values of the base fluid and the nanomaterials utilized in the production of the present hybrid nanofluid. It is assumed that is the coordinate measured along the surface of the sphere starting from the lower stagnation point and is the coordinate measured in the direction normal to the surface of the sphere. Surface temperature and free stream temperature are denoted by and , respectively. The heat flux and mass flux of the sphere are indicated by and , respectively. is the radius of the sphere; is the radial distance between the symmetrical axis and the sphere’s surface, and is the acceleration due to gravity. is the uniform magnetic field strength applied in the direction perpendicular to the surface. Fluid flow is considered near the stagnation point only. In addition to this, it is presumed that the induced magnetic field is not taken into account.
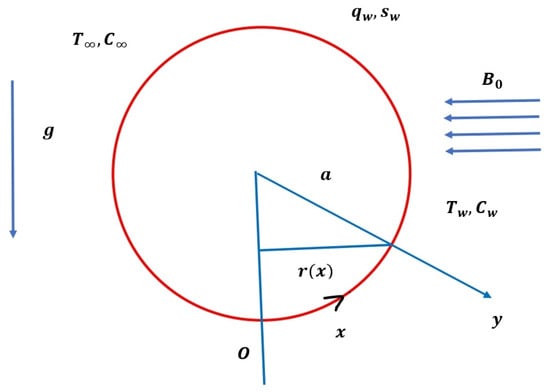
Figure 1.
Flow diagram.
In light of these presumptions, the governing equations and boundary conditions for this problem can be expressed as follows (Alam et al. [44], Al-Kouz et al. [45], and Irfan et al. [46]):

Table 1.
The values of base fluid and nanomaterial thermophysical properties (Jayadevamurthy et al. [47]).
Table 1.
The values of base fluid and nanomaterial thermophysical properties (Jayadevamurthy et al. [47]).
| S. No. | ||||
|---|---|---|---|---|
| 1 | 997.1 | 8933 | 2200 | |
| 2 | 4179 | 385 | 745 | |
| 3 | 0.613 | 400 | 1.4 | |
| 4 | 0.05 | 0.000975 |
Here:
With the aid of Taylor’s series expansion about and by truncating the series after the second-order term, we obtain:
Using (7), (6) becomes:
With this, Equation (3) becomes:
The variables for transformations proposed by Alam et al. [36] are:
Note that .
As a result of (9), Equation (1) is trivially satisfied, and Equations (2), (4), and (8) can be redrafted as follows:
The corresponding boundary conditions (5) for the present problem thus turn into:
where ‘ (prime) indicates the derivative wr.t .
It can be seen that near the lower stagnation point of the sphere, i.e., when , Equations (10)–(12) and the conditions in (13) can be redrafted as:
where: and
Engineering Parameters of Concern
The friction factor is defined as:
where .
By using (9), the term in (18) can be redrafted as:
The following formulas are used to calculate heat and mass transmission rates:
where (wall heat flux) and (wall mass flux).
The formulas in (19) are reworked with the help of (9) as:
3. Validation of Current Results
Validation is carried out by comparing our results to those that were previously published. A satisfactory compromise is reached (See Table 2).

Table 2.
Comparison of current findings to previous results under specific circumstances such as .
4. Discussion of the Outcomes
Equations (10)–(12) together with the conditions in (13) are solved with the help of bvp4c, a Matlab in-built function. The numerical solutions start at the lower stagnation point of the sphere, i.e., , with the initial profile as given by Equations (14)–(16) along with the boundary conditions in (17) and proceed around the sphere up to point . The results are explained for two different types of nanofluids: mono nanofluid and hybrid (binary) nanofluid ( + + ). In this study, we assume the range of parameters as
The effect of the magnetic field on the velocity profile is displayed in Figure 2a. It is established that there is a negative correlation between the increase in the magnetic field parameter and the velocity. A magnetic field has an effect on fluid motion. Fluid particles form a chain when an attracting field is applied and flow in that direction. Particles create a barrier that prevents liquids from flowing freely when they come into contact with one another. The fluid velocity decreases as the viscosity increases. As a result, an increase in the magnetic field causes a reduction in the velocity profile. The increase in the volume percentage of nanoparticles causes an increase in the fluid viscosity, which in turn impedes the flow of the fluid. As a result, the decrease in velocity is accompanied by an increase in (volume fraction of nanoparticles) (Figure 2b). It can be clearly seen from Figure 2c that an increase in (buoyancy parameter) results in an increase in the velocity of the fluid. Generally, when the buoyancy parameter rises, there is a rise in the concentration gradient. The greater the difference in concentration, the quicker the rate of diffusion. As a result, particles move more quickly, therefore, the fluid velocity increases. Figure 3a shows that an increase in the Biot number causes an increase in the amount of heat that is transferred to the fluid via the convection process. Because of this, the temperature of the fluid increases (Figure 3a). When thermal radiation is incident continuously on a fluid, depending on the type of fluid, the total or a portion of radiation is absorbed by the fluid, increasing the energy of the fluid particles. As a result, the collisions between the particles increase, and the fluid temperature increases (Figure 3b). As shown in Figure 3c, increasing the heat source causes a rise in the fluid temperature due to the absorbing of more heat energy from the source. It appears that the fluid concentration decreases as the reaction rate parameter increases (Figure 4a). When (Schmidt number) rises, momentum diffusivity surpasses mass diffusivity by a wide margin, indicating that the fluid moves quickly and its concentration drops (Figure 4b). Figure 4c elucidates the impression of activation energy on the concentration profile. A rise in the activation energy of a fluid, in most cases, results in the reduction in its threshold energy, which in turn expresses the average kinetic energy. From the above condition, we can conclude that the average kinetic energy is lower. Hence, diffusion is lower, which leads to the high concentration of the fluid.
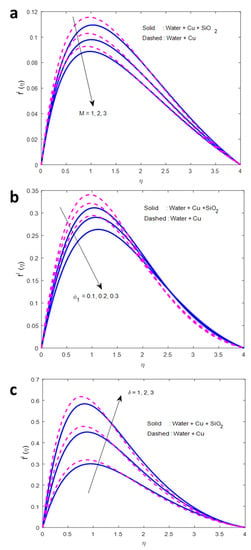
Figure 2.
Effects of (a) , (b) , and (c) on fluid velocity.
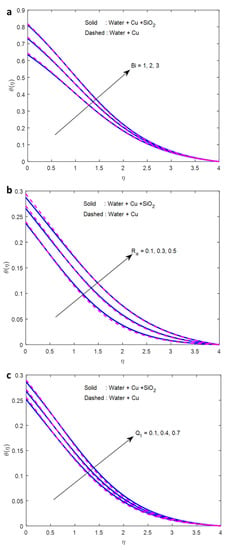
Figure 3.
Effects of (a) , (b) , and (c) on fluid temperature.
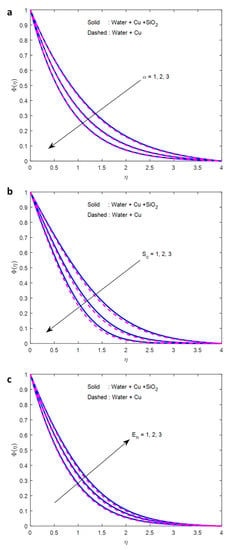
Figure 4.
Effects of (a) , (b) , and (c) on fluid concentration.
Multiple linear regression is a statistical technique for estimating the correlation amongst at least two independent variables and one dependent variable.
The formula for multiple linear regression is:
where —dependent variable; —independent variable; —-intercept; and —regression coefficient of for .
While obtaining the values of ’s, if the -value is less than 0.05, then the relation between and is significant.
In this study, we use of the following models to determine the link between the engineering parameters of importance, such as the rate of heat transfer, and the factors, which include the radiation parameter:
With the assistance of 25 different sets of values for each equation, we can obtain the following findings:
According to Equation (23), has a detrimental effect on the friction factor, but and have a positive influence on the same. Equation (24) exhibits the fact that the radiation parameter, the Eckert number, the heat source, and the nanoparticle volume fraction parameters have a detrimental effect on the Nusselt number. The relationship between the Sherwood number and can be seen in Equation (25). Moreover, the activation energy parameter has a detrimental effect on the rate of mass transfer.
5. Conclusions
In this study, the impact of the quadratic radiative flow of a dissipative hybrid nanofluid (Water + + ) via a sphere with activation energy is investigated. The outcomes are obtained using the bvp4c method. For the purpose of determining the influence that relevant parameters have on engineering parameters such as the heat transfer rate, a multiple linear regression analysis is performed. The primary findings of this work are presented as follows:
- The magnetic field parameter can be used to influence the fluid flow;
- A bigger buoyancy ratio parameter escalates the fluid velocity;
- An increase in the Biot number leads to the rise in the fluid temperature;
- As the Eckert number improves, the Nusselt number decreases;
- The concentration of the fluid enriches with the raise in the activation energy;
- The increase in the Sherwood number is caused by a rise in both ;
- The radiation parameter and the heat source parameter have a negative influence on the Nusselt number;
- The friction factor increases when the volume percentage of nanoparticles gets larger, and the buoyancy ratio parameter also increases;
- In the future, this work may serve as a good reference case for extension to more complicated situations, involving unsteady flows, non-uniform flows, and/or non-spherical bodies.
Author Contributions
A.V.: Conceptualization, Investigation, Writing—original draft, Writing—review & editing. N.M.: Coordination, Formal analysis, Writing—review & editing, proofreading. H.M.: Conceptualization, Writing—review & editing. M.A.-s.: Methodology, Investigation, S.S.: Resources, Writing—original draft, Writing—review & editing. M.J.B.: Validation, Data curation, Writing—review & editing. C.S.K.R.: Modelling, Software, Simulation. R.Z.H.: Resources, Writing—review & editing. W.A.-K.: Methodology, Writing—review & proofreading, corrections. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data sharing is not applicable to this article as no datasets were generated or analysed during the current study.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Radius of the sphere | |
| Local thermal Grashoff number | |
| Fitted rate constant | |
| Thermal conductivity (W·m−1·K−1) | |
| Acceleration due to gravity | |
| Dimensionless velocity | |
| Molecular diffusivity (m2·s−1) | |
| Dimensional temperature of fluid (K) | |
| Convective heat transfer coefficient | |
| Dimensionless temperature of fluid | |
| Heat capacity | |
| Dimensional concentration of fluid (mol·m−3) | |
| Velocity components in directions (m·s−1) | |
| Eckert number | |
| Schmidt number | |
| Mean absorption coefficient | |
| Activation energy parameter | |
| Volumetric rate of heat source parameter | |
| Magnetic field parameter | |
| Heat source parameter | |
| Boltzmann constant—8.314 J·mol−1·K | |
| Dimensional activation energy parameter | |
| Local diffusion Grashoff number | |
| Prandtl number | |
| Chemical reaction rate | |
| Biot number | |
| Dimensional reaction rate parameter | |
| Greek Letters | |
| Dynamic viscosity of fluid (kg·m−1·s−1) | |
| Stefan–Boltzmann constant | |
| Buoyancy ratio parameter | |
| Dimensionless coordinate | |
| Nonlinear thermal convection parameter | |
| Kinematic viscosity (m2·s−1) | |
| Volumetric coefficient of thermal expansion | |
| Reaction rate constant | |
| Stream function | |
| Density of fluid (kg·m−3) | |
| Similarity variable | |
| Volumetric coefficient of diffusion expansion | |
| Nonlinear thermal convection parameter | |
| Nonlinear diffusion convection parameter | |
| Electrical conductivity | |
| Dimensionless nonlinear convection parameter related to species concentration parameter | |
| Dimensionless concentration of fluid | |
| Temperature ratio parameter | |
| Subscripts | |
| Fluid | |
| Nanofluid | |
| Hybrid nanofluid |
References
- Mustafa, M.; Mushtaq, A.; Hayat, T.; Alsaedi, A. Numerical study of MHD viscoelastic fluid flow with binary chemical reaction and Arrhenius activation energy. Int. J. Chem. React. Eng. 2017, 15, 20160131. [Google Scholar] [CrossRef]
- Khan, M.I.; Hayat, T.; Khan, M.I.; Alsaedi, A. Activation energy impact in nonlinear radiative stagnation point flow of Cross nanofluid. Int. Commun. Heat Mass Transf. 2018, 91, 216–224. [Google Scholar] [CrossRef]
- Kumar, A.; Tripathi, R.; Singh, R. Entropy generation and regression analysis on stagnation point flow of Casson nanofluid with Arrhenius activation energy. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 1–18. [Google Scholar] [CrossRef]
- Hayat, T.; Khan, S.A.; Khan, M.I.; Alsaedi, A. Theoretical investigation of Ree–Eyring nanofluid flow with entropy optimization and Arrhenius activation energy between two rotating disks. Comput. Methods Programs Biomed. 2019, 177, 57–68. [Google Scholar] [CrossRef] [PubMed]
- Mustafa, M.; Sultan, A.; Rahi, M. Pressure-driven flow of Cross fluid along a stationary plate subject to binary chemical reaction and Arrhenius activation energy. Arab. J. Sci. Eng. 2019, 44, 5647–5655. [Google Scholar] [CrossRef]
- Patil, P.M.; Shashikant, A.; Hiremath, P.S.; Roy, S. Study of liquid oxygen and hydrogen diffusive flow past a sphere with rough surface. Int. J. Hydrog. Energy 2019, 44, 26624–26636. [Google Scholar] [CrossRef]
- Ullah, M.Z.; Alshomrani, A.S.; Alghamdi, M. Significance of Arrhenius activation energy in Darcy–Forchheimer 3D rotating flow of nanofluid with radiative heat transfer. Phys. A Stat. Mech. Its Appl. 2020, 550, 124024. [Google Scholar] [CrossRef]
- Ramaiah K, D.; Kotha, G.; Thangavelu, K. MHD rotating flow of a Maxwell fluid with Arrhenius activation energy and non-Fourier heat flux model. Heat Transf. 2020, 49, 2209–2227. [Google Scholar] [CrossRef]
- Rashid, M.; Alsaedi, A.; Hayat, T.; Ahmed, B. Magnetohydrodynamic flow of Maxwell nanofluid with binary chemical reaction and Arrhenius activation energy. Appl. Nanosci. 2020, 10, 2951–2963. [Google Scholar] [CrossRef]
- Haq, F.; Kadry, S.; Chu, Y.M.; Khan, M.; Khan, M.I. Modeling and theoretical analysis of gyrotactic microorganisms in radiated nanomaterial Williamson fluid with activation energy. J. Mater. Res. Technol. 2020, 9, 10468–10477. [Google Scholar] [CrossRef]
- Islam, S.; Jawad, M.; Gokul, K.C.; Zubair, M.; Alrabaiah, H.; Shah, Z.; Khan, W.; Saeed, A. Entropy optimization in MHD nanofluid flow over a curved exponentially stretching surface with binary chemical reaction and Arrhenius activation energy. J. Phys. Commun. 2020, 4, 075021. [Google Scholar] [CrossRef]
- Abdelmalek, Z.; Mahanthesh, B.; Basir, M.F.M.; Imtiaz, M.; Mackolil, J.; Khan, N.S.; Nabwey, H.A.; Tlili, I. Mixed radiated magneto Casson fluid flow with Arrhenius activation energy and Newtonian heating effects: Flow and sensitivity analysis. Alex. Eng. J. 2020, 59, 3991–4011. [Google Scholar] [CrossRef]
- Li, Y.X.; Shah, F.; Khan, M.I.; Chinram, R.; Elmasry, Y.; Sun, T.C. Dynamics of Cattaneo-Christov Double Diffusion (CCDD) and arrhenius activation law on mixed convective flow towards a stretched Riga device. Chaos Solitons Fractals 2021, 148, 111010. [Google Scholar] [CrossRef]
- Saeed, A.; Gul, T. Bioconvection Casson nanofluid flow together with Darcy-Forchheimer due to a rotating disk with thermal radiation and Arrhenius activation energy. SN Appl. Sci. 2021, 3, 1–19. [Google Scholar] [CrossRef]
- Shaheen, N.; Alshehri, H.M.; Ramzan, M.; Shah, Z.; Kumam, P. Soret and Dufour effects on a Casson nanofluid flow past a deformable cylinder with variable characteristics and Arrhenius activation energy. Sci. Rep. 2021, 11, 1–19. [Google Scholar] [CrossRef]
- Revathi, G.; Sajja, V.S.; Raju, C.S.K.; Babu, M.J. Numerical simulation for Arrhenius activation energy on the nanofluid dissipative flow by a curved stretching sheet. Eur. Phys. J. Spec. Top. 2021, 230, 1283–1292. [Google Scholar] [CrossRef]
- Sadham Hussain, I.; Prakash, D.; Kumar, S.; Muthtamilselvan, M. Bioconvection of nanofluid flow in a thin moving needle in the presence of activation energy with surface temperature boundary conditions. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2021, 53969. [Google Scholar] [CrossRef]
- Patil, P.M.; Kulkarni, M. Influence of activation energy and applied magnetic field on triple-diffusive quadratic mixed convective nanoliquid flow about a slender cylinder. Eur. Phys. J. Plus 2022, 137, 1–14. [Google Scholar] [CrossRef]
- Murshid, N.; Mulki, H.; Abu-Samha, M.; Owhaib, W.; Raju, S.S.K.; Raju, C.S.K.; JayachandraBabu, M.; Homod, R.Z.; Al-Kouz, W. Entropy Generation and Statistical Analysis of MHD Hybrid Nanofluid Unsteady Squeezing Flow between Two Parallel Rotating Plates with Activation Energy. Nanomaterials 2022, 12, 2381. [Google Scholar] [CrossRef]
- Soundalgekar, V.M. On the flow of an electrically conducting, incompressible fluid near an accelerated plate in the presence of a parallel plate, under transverse magnetic field. Proc. Indian Acad. Sci.-Sect. A 1967, 65, 179–187. [Google Scholar] [CrossRef]
- Oreper, G.M.; Szekely, J. The effect of an externally imposed magnetic field on buoyancy driven flow in a rectangular cavity. J. Cryst. Growth 1983, 64, 505–515. [Google Scholar] [CrossRef]
- Andersson, H.I. MHD flow of a viscoelastic fluid past a stretching surface. Acta Mech. 1992, 95, 227–230. [Google Scholar] [CrossRef]
- Patil, P.M.; Momoniat, E.; Roy, S. Influence of convective boundary condition on double diffusive mixed convection from a permeable vertical surface. Int. J. Heat Mass Transf. 2014, 70, 313–321. [Google Scholar] [CrossRef]
- Sadaf, H.; Nadeem, S. Fluid flow analysis of cilia beating in a curved channel in the presence of magnetic field and heat transfer. Can. J. Phys. 2020, 98, 191–197. [Google Scholar] [CrossRef]
- Gholinia, M.; Gholinia, S.; Hosseinzadeh, K.; Ganji, D.D. Investigation on ethylene glycol nano fluid flow over a vertical permeable circular cylinder under effect of magnetic field. Results Phys. 2018, 9, 1525–1533. [Google Scholar] [CrossRef]
- Deo, S.; Maurya, D.K.; Filippov, A.N. Influence of magnetic field on micropolar fluid flow in a cylindrical tube enclosing an impermeable core coated with porous layer. Colloid J. 2020, 82, 649–660. [Google Scholar]
- Raju, A.; Ojjela, O. Numerical investigation of induced magnetic field and variable mass diffusivity on double stratified Jeffrey fluid flow with heat and mass flux boundary conditions. Heat Transf. 2021, 50, 1073–1094. [Google Scholar] [CrossRef]
- Biswas, N.; Datta, A.; Manna, N.K.; Mandal, D.K.; Gorla, R.S.R. Thermo-bioconvection of oxytactic microorganisms in porous media in the presence of magnetic field. Int. J. Numer. Methods Heat Fluid Flow 2020, 31, 1638–1661. [Google Scholar] [CrossRef]
- Hosseinzadeh, K.; Roghani, S.; Mogharrebi, A.R.; Asadi, A.; Ganji, D.D. Optimization of hybrid nanoparticles with mixture fluid flow in an octagonal porous medium by effect of radiation and magnetic field. J. Therm. Anal. Calorim. 2021, 143, 1413–1424. [Google Scholar] [CrossRef]
- Suganya, S.; Muthtamilselvan, M.; Al-Amri, F.; Abdalla, B. An exact solution for unsteady free convection flow of chemically reacting Al2O3−SIO2/water hybrid nanofluid. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 3749–3763. [Google Scholar] [CrossRef]
- Muthtamilselvan, M.; Suganya, S.; Al-Mdallal, Q.M. Stagnation-point flow of the Williamson nanofluid containing gyrotactic micro-organisms. Proc. Natl. Acad. Sci. India Sect. A Phys. Sci. 2021, 91, 633–648. [Google Scholar] [CrossRef]
- Patil, P.M.; Shankar, H.F.; Hiremath, P.S.; Momoniat, E. Nonlinear mixed convective nanofluid flow about a rough sphere with the diffusion of liquid hydrogen. Alex. Eng. J. 2021, 60, 1043–1053. [Google Scholar] [CrossRef]
- Alharbi, S.O. Impact of hybrid nanoparticles on transport mechanism in magnetohydrodynamic fluid flow exposed to induced magnetic field. Ain Shams Eng. J. 2021, 12, 995–1000. [Google Scholar] [CrossRef]
- Sabir, Z.; Imran, A.; Umar, M.; Zeb, M.; Shoaib, M.; Raja, M.A.Z. A numerical approach for 2-D Sutterby fluid-flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts. Therm. Sci. 2021, 25, 1975–1987. [Google Scholar] [CrossRef]
- Suganya, S.; Muthtamilselvan, M.; Abdalla, B. Effects of radiation and chemical reaction on Cu–Al2O3/water hybrid flow past a melting surface in the existence of cross magnetic field. Ric. Di Mat. 2021, 1–29. [Google Scholar]
- Alam, M.K.; Bibi, K.; Khan, A.; Noeiaghdam, S. Dufour and Soret Effect on Viscous Fluid Flow between Squeezing Plates under the Influence of Variable Magnetic Field. Mathematics 2021, 9, 2404. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Aissa, A.; Koulali, A.; Jamshed, W.; Moria, H.; Nisar, K.S.; Mourad, A.; Abdel-Aty, A.-H.; Khashan, M.M.; Yahia, I.S. MHD darcy-forchheimer nanofluid flow and entropy optimization in an odd-shaped enclosure filled with a (MWCNT-Fe3O4/water) using galerkin finite element analysis. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Mukhtar, T.; Jamshed, W.; Aziz, A.; Al-Kouz, W. Computational Investigation of Heat Transfer in a Flow Subjected to Magnetohydrodynamic of Maxwell Nanofluid over a Stretched Flat Sheet with Thermal Radiation. Numer. Methods Partial. Differ. Equ. 2020. early view. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/num.22643 (accessed on 1 August 2022).
- Mourad, A.; Aissa, A.; Mebarek-Oudina, F.; Al-Kouz, W.; Sahnoun, M. Natural convection of nanoliquid from elliptic cylinder in wavy enclosure under the effect of uniform magnetic field: Numerical investigation. Eur. Phys. J. Plus 2021, 136, 1–18. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Bendrer, B.A.I.; Aissa, A.; Almuhtady, A.; Jamshed, W.; Nisar, K.S.; Mourad, A.; Alsheri, N.A.; Zakarya, M. Galerkin finite element analysis of magneto two-phase nanofluid flowing in double wavy enclosure comprehending an adiabatic rotating cylinder. Sci. Rep. 2021, 11, 1–15. [Google Scholar] [CrossRef]
- Rashidi, M.M.; Nazari, M.A.; Mahariq, I.; Assad, M.E.H.; Ali, M.E.; Almuzaiqer, R.; Nuhait, A.; Murshid, N. Thermophysical properties of hybrid nanofluids and the proposed models: An updated comprehensive study. Nanomaterials 2021, 11, 3084. [Google Scholar] [CrossRef]
- Murshid, N.; Keogh, D.; Kitaev, V. Optimized synthetic protocols for preparation of versatile plasmonic platform based on silver nanoparticles with pentagonal symmetries. Part. Part. Syst. Charact. 2014, 31, 178–189. [Google Scholar] [CrossRef]
- Cathcart, N.; Murshid, N.; Campbell, P.; Kitaev, V. Selective Plasmonic Sensing and Highly Ordered Metallodielectrics via Encapsulation of Plasmonic Metal Nanoparticles with Metal Oxides. ACS Appl. Nano Mater. 2018, 1, 6514–6524. [Google Scholar] [CrossRef]
- Alam, M.M.; Alim, M.A.; Chowdhury, M.M. Viscous dissipation effects on MHD natural convection flow over a sphere in the presence of heat generation. Nonlinear Anal. Model. Control 2007, 12, 447–459. [Google Scholar] [CrossRef]
- Al-Kouz, W.; Mahanthesh, B.; Alqarni, M.S.; Thriveni, K. A study of quadratic thermal radiation and quadratic convection on viscoelastic material flow with two different heat source modulations. Int. Commun. Heat Mass Transf. 2021, 126, 105364. [Google Scholar] [CrossRef]
- Irfan, M.; Khan, M.; Khan, W.A.; Ahmad, L. Influence of binary chemical reaction with Arrhenius activation energy in MHD nonlinear radiative flow of unsteady Carreau nanofluid: Dual solutions. Appl. Phys. A 2019, 125, 179. [Google Scholar] [CrossRef]
- Jayadevamurthy, P.G.R.; Rangaswamy, N.K.; Prasannakumara, B.C.; Nisar, K.S. Emphasis on Unsteady Dynamics of Bioconvective Hybrid Nanofluid Flow over an Upward–Downward Moving Rotating Disk. Numer. Methods Partial. Differ. Equ. 2020. early view. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1002/num.22680 (accessed on 19 September 2021).
- Alkasasbeh, H.T. Numerical solution of micropolar Casson fluid behaviour on steady MHD natural convective flow about a solid sphere. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 50, 55–66. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).