Abstract
Binary mixtures of surfactants build a binary mixed micelle in which the ratio of surfactants usually differs from the initial ratio of surfactants in their binary mixture. The thermodynamic stabilization of the binary mixed micellar pseudophase about the hypothetical ideal state (intermolecular interactions between the different particles and the conformational states of the particles are identical to those of monocomponent states) is described by the molar excess Gibbs free energy (gE). The dependence of gE on the molar fraction of surfactant i (xi) from the binary mixed micelle can be described by a symmetric function (symmetry is described to the line parallel to the y-axis and passes through xi = 0.5) or by an asymmetric function. Theoretical analysis (canonical partition function, conformational analysis) examines how the presence of different polar functional groups, some of which are sterically shielded from the steroid skeleton of bile salts (surfactant), affect the symmetry of the function gE of the binary mixed micelle of the cholic acid anion (bile salts) and classic cationic surfactant (hydrophobic tail and polar head). Suppose the steroid skeleton of the bile salt contains non-sterically shielded polar groups (or the temperature is relatively high). In that case, gE is a symmetric function. At the same time, if the steroid skeleton also contains sterically shielded polar groups, then the gE function is asymmetric.
1. Introduction
Surfactants are molecules or ions with a hydrophobic and a polar segment in their structure (Figure 1). In an aqueous solution, surfactants are embedded in the water–air interface, where their hydrophobic segment is oriented towards the air. In an aqueous solution, with an increase in the surfactant’s concentration, the number of surfactant particles in the boundary surface increases, and at a specific concentration—the critical micellar concentration (characteristic value for a given surfactant at a constant temperature)—the boundary surface becomes saturated with surfactant particles. Meanwhile, in the bulk of the aqueous solution, surfactant self-association occurs over their hydrophobic molecular surfaces—micelles’ formation [1]. Suppose two types of surfactants are present in the aqueous solution. In that case, an aqueous solution of a binary mixture of surfactants exists. At a specific characteristic total concentration of a given binary mixture (with a certain mole fraction of surfactant in the mixture)—the critical micellar concentration of a binary mixture of surfactants—binary mixed micelles are formed [2]. Usually, the mole fraction of surfactant i in a binary mixed micelle differs from the mole fraction of the same surfactant in the starting surfactant mixture [3]. The change in the molar Gibbs free energy of the formation of a binary mixed micelle () according to the phase separation model is represented as the sum of the changes in the molar Gibbs free energy of two processes. The process () of forming the monocomponent micellar pseudophases from the monomer particles of surfactants ( and ). Furthermore, the process () of forming a binary mixed micellar pseudophase from the monocomponent micellar pseudophases [4,5,6]:
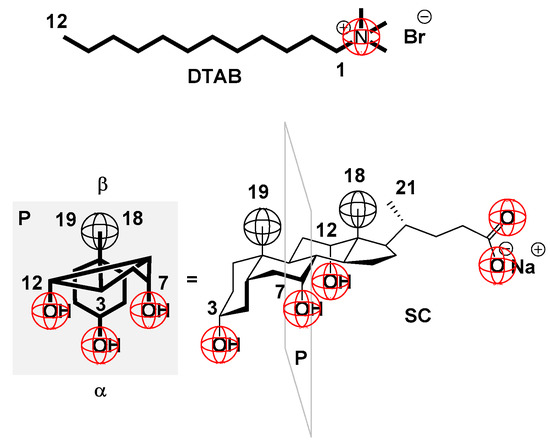
Figure 1.
Classical surfactant: hydrophobic conformationally flexible “tail” and polar “head” (example: (DTAB)) and representative of bile salts (sodium 5β-cholate (SC)): possessing a conformationally rigid steroid skeleton with a concave surface (where C7 and C12 axial OH groups and C3 pseudo-axial OH group)—α side of the steroid skeleton and with a convex surface (C19 and C18 angular methyl groups)—β side of the steroid skeleton; the side chain of the steroid skeleton contains a carboxylate group which, in aqueous solution, has an α orientation; by projecting all the C and O atoms of the cholic acid anion into the plane P, it can be seen that in the case of bile salts, unlike classic surfactants, the surfactant particle has two surfaces: α—polar surface and β—hydrophobic surface.
In Equation (1), and are the mole fractions of surfactants i and j in the binary mixed micellar pseudophase, represents the molar Gibbs free energy of mixing monocomponent micellar pseudophases at constant temperature and pressure. The term corresponds to the molar ideal Gibbs free energy of mixing—it originates exclusively from the entropic contribution due to the random mixing (at the “atomic” level) of different surfactant particles [2,6]. With ideal mixing, only the distribution of particles changes in space. In the mixture, the particles’ conformations remain identical to the conformations in the monocomponent state, i.e., with ideal mixing, the particles are considered rigid systems [7]. There is no enthalpy contribution to changes in the Gibbs free energy . It follows from the previous statement that the energies of intermolecular interactions between the identical surfactant particles in the monocomponent micellar pseudophases are equal to the energies of intermolecular interactions between the different surfactant particles in a mixed micellar pseudophase [2,7,8,9]. The term represents the molar excess Gibbs free energy that occurs due to deviations from the ideal mixture: different intermolecular interactions compared to the monocomponent states, deviation from random mixing, and changes in particle conformations [2,10,11]. The real (not ideal) binary-mixed micellar pseudophase in the case of is thermodynamically more stable than the hypothetical ideal binary-mixed micellar pseudophase (with the same molar fractions of surfactants)—synergistic interactions between the different types of surfactants of the binary mixed micelle. The real binary mixed micellar pseudophase in the case of is thermodynamically destabilized concerning the ideal binary mixed micellar pseudophase—antagonistic interactions between the structurally different particles of the mixed micelle [6,9]. Suppose, at a certain mole fraction ( and ) of surfactants, the of the binary mixed micellar pseudophase has a sufficiently small (negative) value. In that case, the critical micellar concentration of the binary mixture of surfactants, which corresponds to the given composition of the binary mixed micelle ( and ), can have a smaller value even than the critical micellar concentration of the more hydrophobic surfactant (from the given mixture) [2,9]. It follows that a smaller amount from the binary mixture of surfactants is needed than the amount of monocomponent surfactants to achieve the same surface effect. Therefore, is an important parameter (thermodynamic function) in describing binary mixed micelles. The function most often corresponds to the first-order Margules function of the molar fractions of surfactants from a binary mixed micelle [8,9,12,13,14,15,16,17,18]:
where corresponds to the interaction coefficient between surfactants i and j. Function (2) is a symmetric function (U-shaped or inverse U-shaped) about the line parallel to the y-axis and passes through (parabolic symmetry concerning composition). Therefore, the binary mixtures of surfactants whose mixed micelles for have the Function (2) are designated symmetric surfactant mixtures [19]. Equation (2) can be obtained analytically—regular solution theory (RST)—if there is no excess molar entropy (random mixing of rigid surfactant particles), i.e., ( = molar excess enthalpy) [7]. However, in the experiments where the Margules function of the first order is obtained for the , the RST condition is usually not imposed () [6,10,19]. Analytically, it can be shown that Function (2) can also be obtained with the condition during the random mixing of particles if, in the binary mixed micellar pseudophase, the surfactants occupy conformational states that differ from the conformational states of the monocomponent micellar pseudophases [10,11]. The molar excess Gibbs free energies cannot be described with a symmetric Function (2)—asymmetric mixtures—for certain binary mixtures of surfactants. However, a second-order Margules function is used (subregular model), which can be given in the form [20,21]:
where and are the interaction coefficients in the limit cases, i.e., when the mole fraction of one of the building surfactants of the binary mixed micellar pseudophase tends to zero (or unity) [22]:
Bile acid anions are amphiphilic particles—surfactants that have a different distribution of hydrophobic and hydrophilic molecular segments compared to classic surfactants with a hydrophobic tail and a polar head (Figure 1). Bile acid salts are steroid derivatives with a hydrophobic and less hydrophobic (hydrophilic) molecular surface. In the case of 5β derivatives, the steroid skeleton’s concave surface (α side) is hydrophilic (the presence of OH groups). In contrast, the convex surface (β side) is a hydrophobic molecular surface. Suppose the OH groups of the steroid skeleton have an α axial spatial orientation (or α pseudo-axial orientation). In that case, the hydrophobic and hydrophilic surface separation is most pronounced (cholic acid (SC); Figure 1). If the orientation of the OH group moves towards the convex surface of the steroid skeleton (equatorial orientation), then the hydrophobicity of the α side of the steroid skeleton increases (the hydrophilicity of the α side decreases). In contrast, the hydrophobicity of the β side of the steroid skeleton decreases, i.e., the difference in hydrophobicity between the concave and the convex molecular surfaces decreases [23]. The specific molecular geometry and distribution of the hydrophobic and hydrophilic surface result in the bile acid salts forming structurally different micelles compared to classic surfactants [24,25]. Bile acid salts build relatively small micelles (2–15 structural units) of ellipsoidal or cylindrical shape; due to the stiffness of the steroid skeleton, the hydration of the hydrophobic surfaces of the steroid skeleton is relatively high. In comparison, classic surfactants build relatively large spherical micelles (with several hundred building units) with a low degree of hydrophobic hydration [26,27,28,29].
The goal is to show analytically how certain structural elements of a surfactant (surfactants with multiple functional groups and having different steric environments, for example, SC) from a binary-mixed micellar pseudophase affect the shape of the function (symmetric or asymmetric concerning ). In a binary mixture of surfactants, one surfactant is the anion of bile acid (for example, the anion of cholic acid, SC), i.e., a surfactant with a conformationally rigid steroid skeleton and with two types of polar groups: hydroxyl and carboxylate groups. In contrast, the second component of the binary mixture of surfactants is a classic surfactant with a conformationally flexible hydrocarbon segment and a rigid polar head. In the first approximation, in the case of a conformationally rigid surfactant, it is assumed that both polar groups are not sterically shielded. In the second approximation, the real state is assumed when some of the steroid skeleton’s OH groups are sterically shielded in the anion of cholic acid. The carboxylate group of the SC’s side chain is not sterically shielded (Figure 1).
2. Methods
An analytical procedure was applied based on a canonical ensemble of 2D (dimensions) or 1D quasi-crystalline binary-mixed micellar pseudophase of constant volume and located in a thermo-reservoir ( = const.). For canonical microstates, the Helmholtz free energy () was defined by the partition function ():
where represents Boltzmann’s constant. The canonical partition function has the form:
where represents the energy of the mth microstate from the canonical ensemble; the summation in Equation (6) refers to each microstate from the canonical ensemble, i.e., to the sum of microstates of the same and different energies [30]. It is easier to manipulate canonical partition function, that determines Helmholtz free energy, than the isobaric partition function that defines Gibbs free energy; in micellar pseudophases , so that [7].
To determine the steric shielding of the functional groups of the steroid skeleton, the Newman projection of the 4-atom segment was applied. Suppose the terminal atoms of the observed segment of the steroid skeleton in Newman’s projection formula were mutually in a synclinal or synperiplanar position. In that case, the functional group (one of the terminal atoms of the observed segment) would be sterically shielded [23,24,31].
3. Results and Discussion
Suppose we observe a binary mixed micelle of classic cationic and anionic surfactants, then, in the 2D lattice (quasi-crystalline representation of the pseudo micellar phase [7]) in every possible spatial direction between the different surfactants of the first neighbors in terms of the energy size (intensity), there are identical intermolecular interactions (Figure 2).
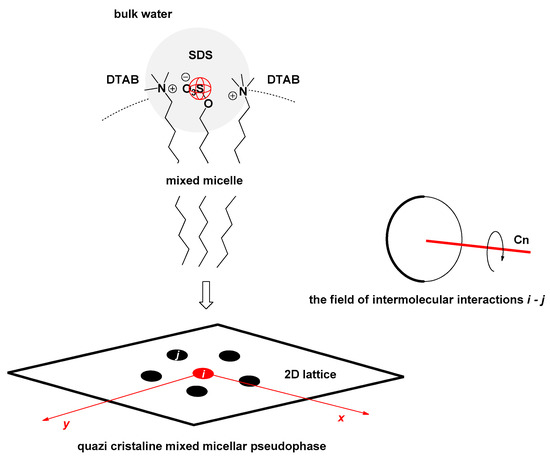
Figure 2.
Micelle section: binary mixed micelle is formed by classic surfactants, cationic surfactant dodecyl trimethylammonium bromide (DTAB = j), and anionic surfactant sodium dodecyl sulfate (SDS = i); in the 2D representation of the micellar pseudophase (2D lattice), whether SDS or DTAB is chosen as the central particle, there are identical intermolecular interactions between the first neighbors of the different types of surfactants in each spatial direction—the field of intermolecular interactions of the first neighbors i−j is characterized by the symmetry axis Cn where n = ∞.
In binary mixed micelles of classic surfactants and bile acid salts, the steroid skeleton of bile acid anions occupies a position where its convex surface (hydrophobic surface) faces the hydrophobic core of the micelle formed by the hydrocarbon chains of the classic surfactant. Its concave surface (hydrophilic surface) faces an aqueous solution [32]. This spatial orientation of bile acid anions (for example, SC, Figure 3) allows the particles of classic surfactants (for example, DTAB, Figure 3) to simultaneously form intermolecular interactions both with the carboxylate function and with the OH groups of the bile acid anions, especially if the OH groups are axial (because then the spatial orientation of the OH group is parallel to the spatial orientation of the classic surfactant with an elongated conformation of the hydrocarbon chain, Figure 3). However, the formation of intermolecular interactions between steroid OH groups and the classic surfactant is also influenced by the steric environment of the OH group, i.e., their sternal shielding.
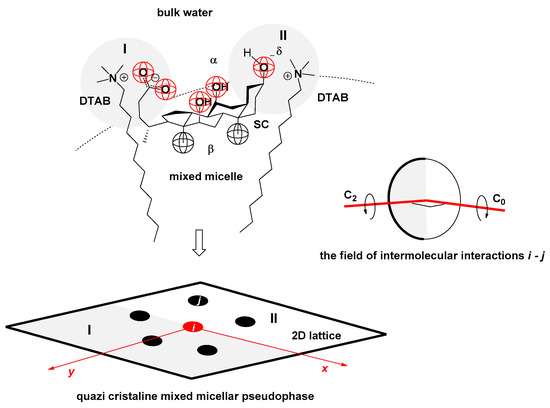
Figure 3.
A binary mixed micelle is formed by the classic (cationic) surfactant dodecyl trimethylammonium bromide (DTAB = j) and the anion of cholic acid (SC = i); in the 2D representation of the micellar pseudophase (2D lattice) in the vicinity of the SC (SC as the central particle), there are two particular regions of intermolecular interactions: the first (I) in the vicinity of the carboxylate function and the second (II) in the vicinity of the C3 α pseudo-axial OH group—the field of intermolecular interactions of the first neighbors i−j is characterized by the axis of symmetry of the second order C2.
Depending on the position of the OH groups, they are more or less sterically shielded in the steroid skeleton of SC (this also applies to bile acid salts in general). The OH group from the C7 carbon has a cis position about the D ring of the steroid skeleton (the reference element is the C2 symmetry axis of the largest longitudinal subgraph, Figure 4) [23,24]. Therefore, around this OH group, there is a reduced spatial angle at which the functional group of another particle can approach to establish intermolecular interactions (H-bonds or interactions via the dipole of the -O-H bond). In addition, the cis position of the C7 OH group with the D ring (SC) results in Newman’s projection formula of the C7–C8 bond of the steroid skeleton that the C7 α axial OH group is in the mutual synclinal (sc) positions with the C9 and C14 methine groups (Figure 5). The synclinal position means that if the functional group of a particle approaches the C7 α axial OH group, then steric repulsive interactions occur that reduce the synergistic interaction between the observed OH group and a particular functional group. The degree of shielding of the spatial angle around the C7 OH group by the D ring of the steroid skeleton does not depend on temperature, i.e., it is a permanent character. In contrast, the repulsive interaction (energy) between the sc groups and the C7 α OH group (with the functional group of some other particle with which it builds intermolecular interaction) depends on the temperature. Similar steric interactions exist with the C12 α axial OH group (Appendix A).
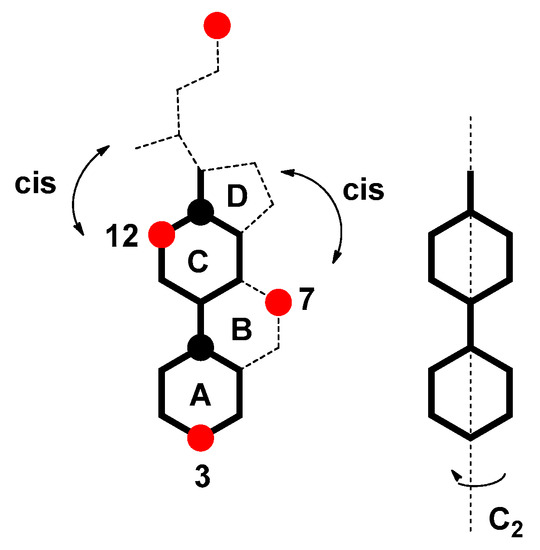
Figure 4.
Molecular graph of the SC steroid skeleton: the largest longitudinal subgraph of the steroid skeleton is given with a separate graph, where the second order symmetry axis (C2) is indicated; the C7 OH group and the D ring of the steroid skeleton are in the cis mutual position similar to the C12 OH group and the side chain of the steroid skeleton are also in the mutual cis position (the reference element to which the cis-trans stereochemistry is determined is C2); red circle = OH group; black circle = angular methyl group.
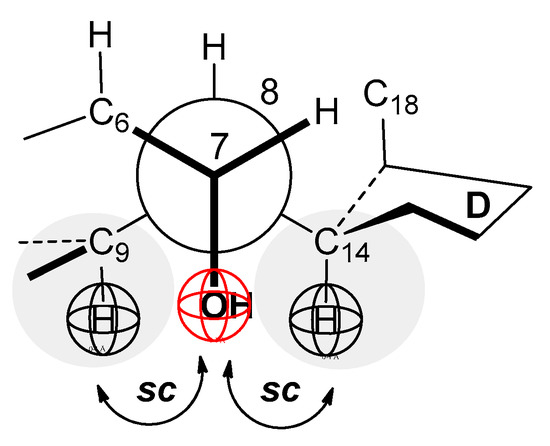
Figure 5.
Newman’s projection of the C7–C8 bond of the SC steroid skeleton (sc = synclinal); repulsive interactions between mutually synclinal groups: the C9, C14 methine groups, and the C7 α axial OH group.
In the 2D lattice as a model for the binary mixed micellar pseudophase, if, for example, the anion of cholic acid (Figure 1 and Figure 3) is considered as a central particle (SC), then in the first part of the 2D lattice between the first neighbors SC-DTAB (DTAB—classic surfactant) there will be an intermolecular interaction (the interaction between the quaternary ammonia group (cation, DTAB) and the carboxylate group (anion, SC)) that will differ from the intermolecular interactions of the first neighbors in the second part of the 2D lattice (interactions between the quaternary ammonia group (cation) and OH groups (dipoles, SC)). Therefore, the symmetry in the spatial distribution of the energy of intermolecular interactions in the 2D lattice of classic surfactants (Figure 2) is no longer present (Figure 3). However, with cholic acid anions (and bile salts with similar geometry), DTAB surfactants can simultaneously form intermolecular interactions with the carboxylate group and with the pseudo-axial C3 OH group, which is not sterically shielded [23,24,33]. Therefore, the 2D lattice of SC-DTAB intermolecular interactions can be viewed as two separate 2D lattices, one in which there are only intermolecular interactions of DTAB and the carboxylate group of SC and the other with intermolecular interactions between DTAB and the C3 OH group of SC (Figure 6).
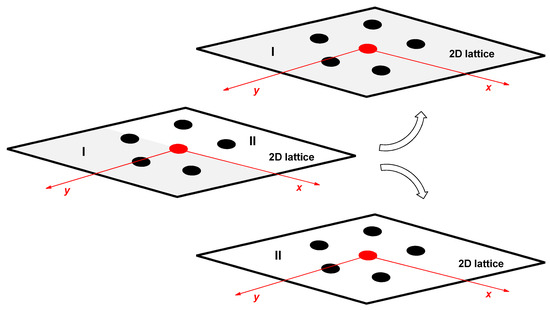
Figure 6.
2D lattice: the intermolecular interaction between DTAB and SC (non-symmetrical distribution of the intensity of intermolecular interactions in 2D space) is divided into two 2D lattices by the symmetrical distribution of intermolecular interaction energies (one 2D lattice refers to the intermolecular interactions between the cationic head of DTAB surfactant and the carboxylate group of SC, while the second 2D lattice on the intermolecular interactions between the cationic head DTAB and the C3 OH group (dipole) SC).
3.1. The First Approximation
It is assumed that, due to the steric shielding of the C7 OH and C12 OH groups (shielding with fragments of SC steroid skeleton (Figure 4 and Figure 5)) as well as due to mutual interactions of SC particles (Figure 7), these OH groups do not interact with DTAB particles, but only with the C3 α pseudo-axial OH group and the C24 carboxylate group. Therefore, in general, the first approximation refers to binary mixtures with a classic surfactant and a surfactant with a rigid structure containing different sterically unscreened polar functional groups that build intermolecular interactions with the classic surfactant with different energy content.
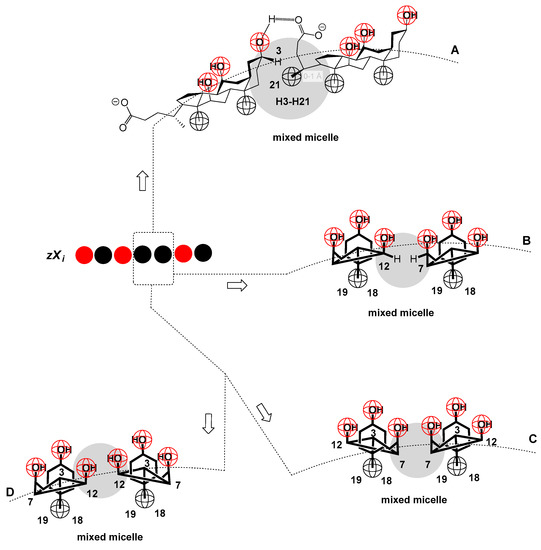
Figure 7.
In the 1D lattice, one microstate (i.e., one permutation with repetition, zXi) is represented, in which two SC particles are next to each other, and mutual interactions can be realized in several ways: mutual interaction via the C3 α pseudo-axial OH group (one SC particle) and carboxylate functions of the second SC particle—where in this dimer one carboxylate and one C3 OH group remain free (A); interactions via the lateral C7 and C12 sides of the steroid skeletons, with each SC particle, the C3 OH group and the carboxylate function remain free (C–D).
A 2D (or 1D) lattice representing a binary mixed micellar pseudophase of a classicsurfactant (DTAB = j) and cholic acid anion (SC = i) contains a total of surfactant particles . In both lattices (I-lattice and II-lattice, Figure 3 and Figure 6), the number of intermolecular interactions (first neighbor type) between different surfactant particles is:
where represents the coordination number of the real lattice; meanwhile, represents the Guggenheim parameter [7]. In microstates (permutation with repetition of DTAB and SC particles), the size corresponds to the number of intermolecular interactions between cationic heads of DTAB surfactants and anionic groups (carboxylate functions) of SC surfactants; also, corresponds to the number of intermolecular interactions between cationic heads of DTAB surfactants and dipoles of C3 OH groups SC particle (Figure 8):
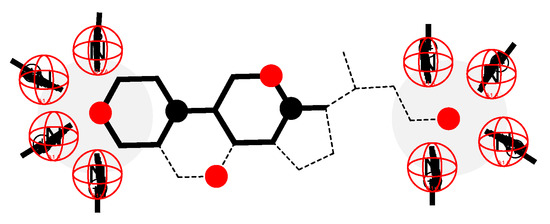
Figure 8.
Molecular graph of SC and 2D projections of DTAB into the plane of the molecular graph of the steroid skeleton: C3 OH group and C24 carboxylate function of SC approximately have identical coordination numbers.
According to the approximation (8a), both lattices (with SC central particle) have identical coordination numbers:
Suppose in a hypothetical 2D lattice, instead of the SC particle the central particle is DTAB. Around the cationic head of the DTAB particle, there are carboxylate groups SC (I-lattice) or C3 OH groups SC (II-lattice). The approximation is also taken that both lattices have identical coordination numbers and which are equal to the coordination number of the real lattice:
From the approximations, i.e., the Equations (8b) and (8c), it follows:
The geometry of the 2D lattice—the absence of crystal defects—is defined by Equation (8d), from which it follows that the number of DTAB particles around a selected DTAB particle is equal to the number of SC particles around a selected SC particle (Figure 9).
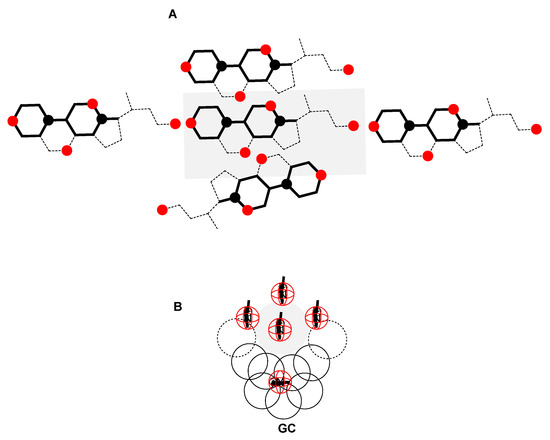
Figure 9.
In the global (not separated according to the functional groups) 2D lattice, approximately SC (A) and DTAB (B) have identical coordination numbers; since in the binary mixed micelle DTAB is a conformationally flexible surfactant in the hydrophobic segment, it follows that in addition to DTAB in all antiperiplanar conformation (elongated conformation) DTAB is also present in a more or less globular conformation (GC), whose projection in the 2D plane occupies a larger area than the projections of DTAB in an elongated conformation.
Value of the Guggenheim parameter ( i.e., ) changes depending on the binary mixture configuration (microstate), i.e., permutation with repetition (Figure 10). Bearing in mind Equation (8d), i.e., approximation (8d), it is sufficient to observe two one-dimensional (1D) lattices (whose microstates are permutations with repeating SC and DTAB particles): the first one in which i−j intermolecular interactions are between the cationic heads of DTAB and the carboxylate groups of SC (I-lattice) and the other in which i−j intermolecular interactions are between the cationic heads of DTAB and the C3 OH group of SC particles (II-lattice). Both 1D lattices have identical microstates (repetitive permutations). Such two 1D lattices, in terms of the intensity of intermolecular interactions of the first neighbors, have identical properties as 2D lattices I and II with SC and (or) DTAB central particles. However, they have a distortion in the coordination number; of course, both 1D lattices have identical coordination numbers.
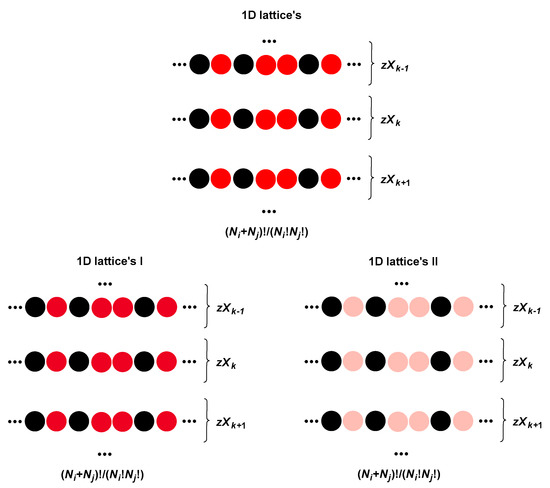
Figure 10.
Microstates of a 1D lattice (permutations with repetition), each microstate is characterized by the parameter (several microstates can have the same value for , i.e., microstates can degenerate by ) since two types of intermolecular interaction can simultaneously exist between the different types of particles (first neighbor type) cation–anion and cation–dipole; therefore, the global 1D lattice is viewed as two 1D lattices, one with cation–anion (1D I-lattice) and the other with cation–dipole (1D II-lattice) interactions; both lattices (I and II) have identical parameter with the global 1D lattice.
In the 1D I-lattice and II-lattice, the number of intermolecular interactions between the identical particles (taking into account Equation (7)) is:
Suppose the energy of particle i in the lattice is (i.e., ). In that case, the energy along each spatial direction where there is a first neighbor (i.e., energy per coordination number) is , while the energy of one i−i intermolecular interaction is:
The same applies to the energy of one j−j intermolecular interaction ( = energy of one j particle in the lattice):
In some k-th microstate of a 1D lattice (a permutation with repetition of elements and ) characterized by the parameter, the total energy of all intermolecular interactions between the identical particles of the first neighbor (it is identical for both lattices) is:
The exchange reaction between the lattice of i particle (monocomponent state) and the lattice of j particle (monocomponent state) is:
The energy change during reaction (15) is:
where corresponds to the energy of a (single) first neighbor intermolecular interaction between the different types of particles, and represents the Hildebrand exchange parameter [34]. The energy value of intermolecular interaction i−j can be —attractive interaction or —repulsive interaction. However, if the mutual exchange parameter is , it means: and —synergistic interactions between the different particles. If the mutual exchange parameter is , then there are antagonistic interactions between the different types of particles: and or . Therefore, for the synergistic interactions (i.e., exothermicity of reaction (16)), it is not a sufficient condition that there are attractive interactions between the different types of particles (), but the relation must be fulfilled. The energy of (one) i−j intermolecular interaction from Equation (16) is:
The energy (17) differs between 1D I-lattice and 1D II-lattice. The total energy of intermolecular interactions i−j in the k-th microstate of a 1D lattice (I or II) defined by the parameter (according to Equations (7) and (17)) is:
i.e., (18) applied to 1D lattice I and II:
The total energy of the 1D I-lattice in some k-th microstate is the sum of the total energy of intermolecular interactions (of the first neighbor type) between identical (13), (14), and different types of particles (19):
The same is true for the II-lattice:
The total energy of the k-th microstate of the global 1D lattice is the sum of the energies of the 1D lattice I and 1D lattice II, where care should be taken that the energy of intermolecular interactions between the identical particles is taken into account only once since both and contain this energy (Figure 11):
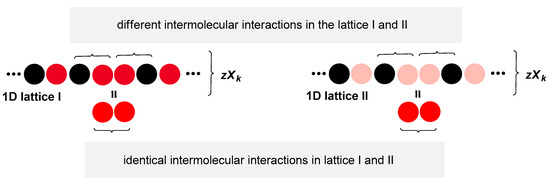
Figure 11.
Since 1D lattice I and 1D lattice II between the identical particles have intermolecular interactions with the identical energy content when calculating the total energy of the global 1D lattice this energy should only be taken into account once.
The canonical partition function for the global 1D lattice at some constant temperature is:
In expression (24), the sum of exponential energy functions is taken, i.e., each microstate has a single exponential term of energy (the energy of a given microstate), while the number of microstates is:
Over the set whose elements are permutations with the repetition of two objects, i and j, by number and , Guggenheim’s Equation (27) obtains the mean value for the parameter that gives the number of mutual contacts (of the first neighbor type) between different objects. Therefore, the mean value of the parameter from Equation (7) is [7]:
where and are the mole fractions of i and j particles (surfactants) in the global 1D lattice as a model for a crystalline binary mixed micellar pseudophase. Since the parameter is identical for both 1D lattices (I and II), the canonical partition function is:
Furthermore, if at each of (26) microstates, the parameter is characterized by the mean value of the given parameter (27), it follows:
The Helmholtz free energy of the global 1D lattice of i and j particles according to Equations (5) and (29) is:
Using the Sterling expression () [30] in this Equation (30), we obtain:
Let us consider that the global 1D lattice (binary mixed micellar pseudophase of i and j surfactants) is formed by mixing (at the atomic level) the monocomponent 1D lattices (monocomponent micellar pseudophases) of i and j surfactants (Figure 12). The Helmholtz free energy of the mixing is:
where and are the Helmholtz free energies of the monocomponent states of the i and j particles; meanwhile, and are the canonical partition functions of the monocomponent states. The monocomponent states are characterized by only one microstate, therefore and are:
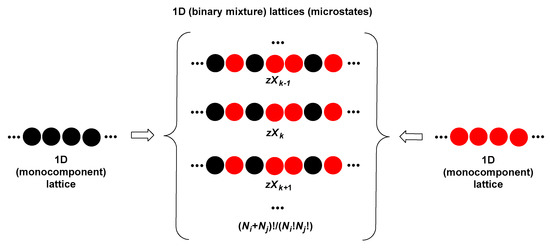
Figure 12.
The formation of a binary mixture, which exists in several microstates, from monocomponent states (characterized by a single microstate).
Based on Equations (31)–(34), the Helmholtz free energy of mixing is:
Alternatively, if 1 mol of the binary mixture is observed ( denotes Avogadro’s number):
where represents the molar Helmholtz free energy of mixing; corresponds to the molar Gibbs free energy of mixing; meanwhile, is the universal gas constant. Taking into account Guggenheim’s Equation (27), is:
The first term in Equation (37) corresponds to the ideal Helmholtz free energy of mixing when obtaining an ideal binary mixture:
and which originates from the entropic contribution [6,7,35,36]. Since the enthalpy change is zero for an ideal binary mixture, the second term in Equation (37), according to expression (1), corresponds to the molar excess Gibbs free energy, i.e., in RST to the molar excess enthalpy [7,8,9]. Namely, according to RST, in a binary mixture, different particles are randomly mixed, i.e., every microstate from the set of all microstates is equally likely—a permutation with repeating elements and (Figure 12). In addition, the approximation is taken that the conformations of surfactants in the binary micellar pseudophase are identical to those in the monocomponent state. Therefore, the molar excess entropy () is 0:
Therefore, Equation (37) in the theory of regular solutions is:
In Rubingh, in the theory of binary mixed micelles (RST), instead of the Hildebrand exchange coefficient (), they used the interaction coefficient [8,9,37]:
where are interaction molar energies of the first neighbors. Multiplying Equation (16) by Avogadro’s number () gives:
If the expression (42b) is introduced into the equation that defines the interaction coefficient (41), then the connection between the exchange coefficient () and the interaction coefficient () is obtained:
By introducing the interaction coefficient (), the equation that defines the molar excess Gibbs free energy (39) is:
The Gibbs Function (44) is a first-order Margules function with parameter , and which is symmetric concerning about the line parallel to the y-axis and passes through . Therefore, in a binary mixture of surfactants (particles), one component is a classicsurfactant, while the other component is a conformationally rigid particle with two different polar groups (functional groups) which are not sterically shielded (Figure 1). Then, each functional group in the overall interaction coefficient has its (individual) contribution originating from the interaction coefficient of the observed functional group and the classic surfactant (as if the second functional group on a conformationally rigid particle with two polar groups is not even present). Of course, in the experiments where the critical micellar concentration of the binary mixture of surfactants is determined (and from which the Function (44) is obtained), the overall interaction coefficient is obtained () [6,8,9,10,11].
3.2. The Second Approximation
If it is taken into account that in the intermolecular interactions between SC (or some other bile acid salt) and DTAB (or some other classic surfactant) in addition to the C24 carboxylate group and the C3 pseudo-axial OH group of the steroid skeleton, the axial C7 and C12 OH groups (sterically shielded OH groups) can also participate, then the intermolecular interactions between these OH groups—which are sterically shielded—and the cationic heads of DTAB surfactants can be viewed as belonging to a particular 1D lattice (the first one, I). The second 1D lattice consists of the sterically unprotected polar groups of the SC steroid skeleton. As the C24 carboxylate group is located on the C17 side chain of the steroid skeleton, in interaction with the cationic head of the DTAB surfactant, it can be considered that parts of the steroid skeleton do not sterically screen this carboxylate group (some carbons from the side chain may contribute to the steric shielding of the C12 α axial OH group). Similarly, the C3 α pseudo-axial OH group is not sterically shielded (there are no Newman projection formulas of the corresponding bonds from the steroid skeleton in which this OH group would be synclinal with some fragments of the steroid skeleton, Figure 13). Therefore, the C3 OH group and C24 carboxylate group–the groups that are not sterically shielded—in intermolecular interactions with cationic polar heads of DTAB surfactant form another (second, II) hypothetical 1D lattice.
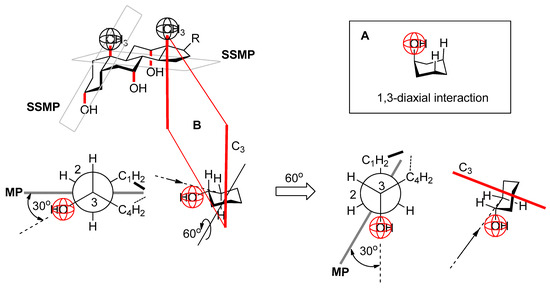
Figure 13.
A: the axially oriented substituent (OH group) in the cyclohexane ring in the chair conformation is in a 1,3-diaxial interaction with the axial hydrogens (repulsive steric strain equivalent to van der Waals strain); B: equatorially oriented substituent (cyclohexane in chair conformation) has no 1,3-diaxial steric strain (no synclinal or synperiplanar interactions in the Newman projection of the C3–C2 bond) by rotating the cyclohexane ring by 60° degrees (counter-clockwise) about the axis that is normal to the C3 symmetry axis of cyclohexane (in the chair conformation without a substituent), the A ring of the steroid skeleton is obtained which is cis connected to the B ring, whereby the equatorial OH group (in the isolated ring of cyclohexane) is parallel to the axial OH groups—pseudo-axial C3 OH group without steric strain unlike true axial OH groups (MP = mean plane of cyclohexane; SSMP = steroid skeleton mean plane).
So, if we consider the molar excess Gibbs free energy of the binary mixed micellar pseudophase (as a hypothetical crystalline mixed 1D lattice), then this Gibbs free energy is the sum of the Gibbs energy of the hypothetical 1D lattice (I) and the Gibbs free energy of the hypothetical 1D lattice (II):
where the linear combination coefficient is: and has the role of a stoichiometric coefficient; the parameter shows a static dependence on the degree of shielding of a functional group in the steroid skeleton (it always exists, i.e., it does not depend on temperature as long as the conformation of the steroid skeleton is rigid); and the parameter shows a dynamic dependence on steric shielding (it depends on temperature).
Let first. When forming one mole of a 1D crystalline binary mixed lattice, in the Gibbs free energy of intermolecular interactions of the first neighbor type (excess Gibbs free energy originates from intermolecular interactions and which do not exist in monocomponent states [2]), the Gibbs free energy of intermolecular interactions from the lattice (II) contributes with stoichiometric coefficient . However, due to the steric shielding of C7(12) OH groups, if intermolecular interactions are formed between the cationic heads of classic surfactants and the C24 carboxylate group and C3 α pseudo-axial OH group of SC particles, this does not mean that the common 1D lattice will simultaneously form intermolecular interactions between the cationic heads of classic surfactants and the sterically screened OH groups of SC. Therefore, for 1 mol of hypothetical 1D lattice (II) comes a smaller amount of hypothetical 1D lattice (I):
The C7(12) OH groups of SC are not only sterically screened with parts of the steroid skeleton but also with neighboring SC particles in repeating permutations (when another SC particle is adjacent to the observed SC particle from the C7 or C12 lateral side of the steroid skeleton, Figure 7). The higher the mole fraction () of the classic surfactant (j), the higher the probability for intermolecular interactions of the first neighbor type with the sterically screened groups of particle i, i.e., SC, so it is valid:
With the increase in in a 1D crystalline binary mixed lattice (i.e., in permutations with repetition), the number of intermolecular interactions decreases, in which, next to some selected particle i, is also a particle i (neighboring particle).
The dynamic parameter considers that the formation of intermolecular interaction has the character of a chemical reaction (15), i.e., that there is a specific energy barrier that the particles that form the intermolecular interaction must possess. The greater the steric shielding, the greater the repulsive interactions, i.e., the higher the energy barrier to the formation of intermolecular interaction. At a specific temperature value T, the number of particles j (DTAB)—which form intermolecular interactions with the sterically screened functional groups of particle i (SC)—with an energy content equal to the energy barrier () is determined by the Boltzmann distribution:
where represents the total number of particle j; meanwhile, is the molecular partition function [30].
Taking into account the equation for the molar excess Gibbs free energy (44) as well as expressions (46) and (47), Equation (45) is:
Figure 14 presents the functions (49) for the value and the values and ; the more significant the term with (i.e., ) is, the more the Function (49) deviates from the symmetrical first-order Margules function, which means that sterically shielded functional groups are more likely to form intermolecular interactions with surfactants of a classical structure. Applying the two-fluid theory [38,39] to the binary-mixed micellar pseudophase for the molar excess Gibbs free energy always yields the second-order Margules Function (2). Therefore, the influence of sterically shielded and non-sterically shielded polar groups of surfactant i on the formation of intermolecular interactions with classic surfactant j cannot be distinguished. If the temperature of the system, i.e., the thermal energy of surfactant j (surfactant of a classic structure) is large enough, then the following applies:
which means that , so the Function (49) is:
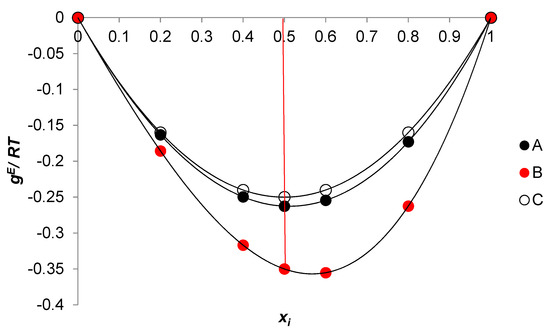
Figure 14.
Dependence of the excess molar Gibbs free energy on the surfactant mole fraction in the binary-mixed micellar pseudophase; A: ; B: ; C: .
If during the formation of the transition state, when the intermolecular interaction with the sterically shielded functional group is formed, is high and the temperature is low, then the Function (48) tends to zero (particle j does not have sufficient thermal energy to form an intermolecular interaction with the sterically shielded functional group of particle i), i.e., . It follows that the Function (49) turns into the first-order Margules function:
In the case of SC and DTAB, a symmetric Function (52) is obtained experimentally for the molar excess Gibbs free energy, which means that in the binary-mixed micellar pseudophase, the intermolecular interactions occur between the cationic head of DTAB and the sterically unprotected groups of SC (C3 α axial OH group and C24 carboxylate group) [11]. On the contrary, in the binary mixed micelle of sodium deoxycholate (bile acid anion, unlike SC, which has no C7 OH group) and sodium decyl sulfate, the dependence of on is an asymmetric function. This is probably a consequence of the sulfate groups of sodium decyl sulfate forming hydrogen bonds with the C12 OH group (sterically protected group) of the anion of deoxycholic acid [40]. During the formation of a hydrogen bond, a sufficient amount of energy is probably released to reduce the energy barrier in the transition state of H-bond formation (i.e., the structure of the transition state tends to the structure of a classic surfactant, which means that the classic surfactant is far from the synclinal methine groups of the steroid skeleton—Hammond’s postulate [41]). So that the limit value (50) can be fulfilled even at lower temperature values, i.e., the molar excess Gibbs free energy is described by the asymmetric Function (51).
The molar excess Gibbs free energy of the binary-mixed micellar pseudophase according to the asymmetric Function (49) or (51) originates from the principle of the theory of regular solutions (random mixing of two types of particles, whose conformations do not change compared to the monocomponent states) which would mean that the molar excess entropy equal to zero (), i.e.,: . However, the condition is rarely fulfilled [10,11], but the existence of excess entropy does not disturb the form of the Function (49) or (50); it only modifies the parameters of the Function (49) or (51) with the condition . Namely, the phenomenon of enthalpy–entropy compensation applies to the formation of the binary mixed micelles: ( = compensation temperature; = coefficient that can be assumed to be ) [42]. Therefore, based on the Function (49) and , and with the condition , the molar excess entropy is (Appendix B):
where is the enthalpy share parameter (Appendix B). Considering the molar excess entropy Function (53) and the molar excess enthalpy function (49), the excess molar Gibbs free energy is (with application [43]):
where . Function (54) at a constant temperature and pressure is an asymmetric function similar to that in (49).
The excess chemical potential (partial molar excess Gibbs free energy [43]) based on the Function (49) is (Appendix C):
The excess chemical potential is related to the coefficient of activity: . Therefore, the activity coefficients of surfactants i and j in the binary-mixed micellar pseudophase are:
In the limiting case, the hypothetical state of an infinitely dilute micellar pseudophase, when the mole fraction of surfactant i (SC, i.e., surfactant with a rigid conformation and with sterically shielded as well as sterically unshielded polar groups) tends to zero [44], then the ln of the activity coefficient of surfactants i is:
From the above expression, it follows that with a large amount of a classic surfactant (hypothetical micelle contains only one i particle, while the other particles are j), both types of polar groups (sterically shielded and sterically not shielded) of surfactant i participate in the intermolecular interactions with a classic surfactant. At the other extreme, when the micellar mole fraction of the classic surfactant tends to zero, then the ln of the activity coefficient of the classic surfactant is:
In this case, the intermolecular interactions are possible only between the classic surfactant and the sterically unshielded polar group of surfactant i.
4. Conclusions
Suppose the molar excess Gibbs free energy originates from the intermolecular interactions of sterically unshielded functional groups of surfactants with a steroid skeleton and classic surfactants. In that case, each sterically unshielded functional group has an individual interaction coefficient (it depends on the structure, i.e., a classic surfactant’s polar heads). The total interaction coefficient is obtained experimentally, where the molar excess Gibbs free energy function is the first-order Margules function. At low temperatures and with significant repulsive steric interactions, intermolecular interactions with the sterically screened functional groups can be ignored, so for , a symmetric function is obtained. If the sterically screened functional groups also participate in the intermolecular interactions, then there is a deviation from the symmetrical function. Conformational analysis and analysis of microstates in a 1D or 2D lattice (canonical ensemble) are general. The applied steroid skeleton is a good example of the sterically shielded polar functional groups. So, the conclusions are valid for every binary system of surfactants in which one component has a rigid conformation with several functional groups, and where some functional groups are sterically screened with parts of the rigid conformation (i.e., with parts of the observed surfactant molecule’s structure). At the same time, the second component is a surfactant with a conformationally flexible hydrophobic segment and one polar head that is not sterically shielded.
Funding
This research received no external funding.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
The side chain from the C17 carbon of the steroid skeleton in the molecular graph (Figure 4) is cis with the C12 α axial OH group, which sterically allows the C24 carboxylate function (from the SC side chain) to form a hydrogen bond with the C12 OH group (Figure A1). In contrast to the D ring, which represents a permanent steric shielding of the spatial angle in the vicinity of the C7 OH group of SC, the C17 side chain with the carboxylate group represents a steric shielding of the C12 OH’s spatial angle (SC) with a variable character, since by shifting the equilibrium towards the form where the side chain is not H-bonded connection decreases the steric shielding of the C12 OH group. However, the C12 OH group, in the same way as the C7 OH group (SC), is in a synclinal position with two methine groups (C17 and C14) that create steric strain if the C12 OH group participates in intermolecular interactions (Figure A1).
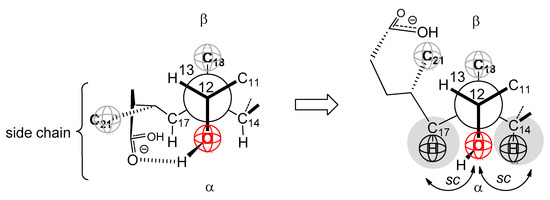
Figure A1.
Newman’s projection formula of the C12–C13 bond of the SC steroid skeleton.
Appendix B
If there are synergistic interactions between structurally different particles of a binary mixed micelle, then the excess enthalpy (based on Function (49)) is:
This enthalpy (A1, heat at P = const.) during the formation of a binary mixed micelle goes to the thermo-reservoir (thermal energy that leaves the system, i.e., the mixed micelles, to the environment, i.e., the thermo-reservoir). However, part of this enthalpy (A1):
returns to the binary mixed micelle (system) and is spent on repulsive interactions when surfactants occupy the globular conformational states (conformational states that do not exist in monocomponent micelles) ().
Appendix C
Based on the expressions (A4) and (A5), the excess chemical potential of component i is (A3):
The above partial derivative (A7) is solved similarly to derivative (A3):
References
- Kumar, H.; Kaur, G. Scrutinizing Self-Assembly, Surface Activity and Aggregation Behavior of Mixtures of Imidazolium Based Ionic Liquids and Surfactants. A Comprehensive Review. Front. Chem. 2021, 9, 667941. [Google Scholar] [CrossRef] [PubMed]
- Nagarajan, R. Molecular theory for mixed micelles. Langmuir 1985, 1, 331–341. [Google Scholar] [CrossRef]
- Kamrath, R.F.; Franses, E.I. Mass-action model of mixed micellization. J. Phys. Chem. 1984, 88, 1642–1648. [Google Scholar] [CrossRef]
- Shiloach, A.; Blankschtein, D. Prediction of critical micelle concentration and synergism of binary surfactans mixtures containing zwitterionic surfactants. Langmuir 1997, 13, 3968–3981. [Google Scholar] [CrossRef]
- Shiloach, A.; Blankschtein, D. Predicting micellar solution properties of binary surfactants mixtures. Langmuir 1998, 14, 1618–1636. [Google Scholar] [CrossRef]
- Poša, M. Mixed micelles of binary surfactant mixtures: Tween 40—Na-3,12-dioxo-5β-cholanoate; Tween 80—Na-3,12-dioxo-5β-cholanoate and their thermodynamic description-characterization. Chem. Eng. Res. Des. 2014, 92, 1826–1839. [Google Scholar] [CrossRef]
- Guggenheim, E.A. Mixtures; The Clarendon Press: Oxford, UK, 1952; pp. 23–46. [Google Scholar]
- Holland, P.M.; Rubingh, D.N. Nonideal multicomponent mixed micelle model. J. Phys. Chem. 1983, 87, 1984–1990. [Google Scholar] [CrossRef]
- Holland, P.M. Nonideal mixed micellar solutions. Adv. Colloid Interface Sci. 1986, 26, 111–129. [Google Scholar] [CrossRef]
- Poša, M. Conformationally rigid and flexible surfactant binary (pseudoternary) mixed micelle with mutual synergistic interaction. J. Mol. Liq. 2021, 334, 116158. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A.; Popović, K.; Kumar, D. Thermodynamics of trimethyltetradecylammonium bromide—sodium deoxycholate binary mixed micelle formation in aqueous solution: Regular Solution Theory with mutual compensation of excess configurational and excess conformational entropy. J. Mol. Liq. 2022, 360, 119473. [Google Scholar] [CrossRef]
- Bagheri, A.; Jafari-Chashmi, P. Study of aggregation behavior between N-lauryl sarcosine sodium and Dodecyltrimethylammonium bromide in aqueous solution, using conductometric and spectrophotometric techniques. J. Mol. Liq. 2019, 282, 466–473. [Google Scholar] [CrossRef]
- Bagheri, A.; Khalili, P. Synergism between and cationic surfactants in a concentration range of mixed monolayers at an air–water interface. RSC Adv. 2017, 7, 18151–18161. [Google Scholar] [CrossRef]
- Szymczyk, K.; Janczuk, B. The properties of a binary mixture of surfactants in water at the water/air interface. Langmuir 2007, 23, 4972–4981. [Google Scholar] [CrossRef] [PubMed]
- Azum, N.; Rub, M.A.; Asiri, A.M. Bile salt–bile salt interaction in mixed monolayer and mixed micelle formation. J. Chem. Thermodyn. 2019, 128, 406–414. [Google Scholar] [CrossRef]
- Rub, M.A.; Azum, N.; Khan, F.; Asiri, A.M. Aggregation of sodium salt of ibuprofen and sodium taurocholate mixture in different media: A tensiometry and fluorometry study. J. Chem. Thermodyn. 2018, 121, 199–210. [Google Scholar] [CrossRef]
- Ren, Z.H.; Huang, J.; Zheng, Y.C.; Lai, L.; Mei, P.; Yu, X.R.; Chang, Y.L. Micellization and interaction for ternary mixtures of amino sulfonate surfactant and octylphenol polyoxyethylene ethers in aqueous solution: 2 blending with surfactant with a longer or shorter hydrophilic chain. J. Mol. Liq. 2018, 272, 380–386. [Google Scholar] [CrossRef]
- Maeda, H. Phenomenological approaches in the thermodynamics of mixed micelles with electric charge. Adv. Colloid Interf. Sci. 2010, 156, 70–82. [Google Scholar] [CrossRef]
- Hoffmann, H.; Pössnecker, G. The mixing behavior of surfactants. Langmuir 1994, 10, 381–389. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A. Micellisation of the binary mixture of surfactants Triton X100 and Brij S10 in a water solution at T = (278.15–318.15) K: The excess Gibbs free energy of the binary mixed micelles formation and its interpretation by the first order and the second order Margules function. J. Chem. Thermodyn. 2019, 138, 167–178. [Google Scholar] [CrossRef]
- Schulz, E.P.; Durand, G.A. Equation oriented mixed micellization modeling based on asymmetric Margules-type formulations. Comput. Chem. Eng. 2016, 87, 145–153. [Google Scholar] [CrossRef]
- Ganguly, J. Thermodynamic modelling of solid solutions. EMU Notes Mineral. 2001, 3, 37–69. [Google Scholar]
- Poša, M. Heuman indices of hydrophobicity in bile acids and compared with new developed and conventional molecular descriptors. Biochimie 2014, 97, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Poša, M.; Sebenji, A. Determination of the number average aggregation numbers of bile salt micelles with a special emphasis on their oxo derivatives—the effect of the steroid skeleton. BBA-Gen. Subj. 2014, 1840, 1072–1082. [Google Scholar] [CrossRef] [PubMed]
- Small, D.M. The physical chemistry of cholanic acids. In The Bile Acids: Chemistry, Physiology and Metabolism; Nair, P.P., Kritchevsky, D., Eds.; Plenum Press: New York, NY, USA, 1971; Volume 3, pp. 249–332. [Google Scholar]
- Pártai, L.B.; Jedlovszky, P.; Sega, M. Molecular aggregates in aqueous solutions of bile acid salts. Molecular dynamics simulation study. J. Phys. Chem. B 2007, 111, 9886–9896. [Google Scholar] [CrossRef]
- Pártai, L.B.; Sega, M.; Jedlovszky, P. Morphology of bile salts micelles as studied by computer simulation methods. Langmuir 2007, 23, 12322–12328. [Google Scholar] [CrossRef] [PubMed]
- Haustein, M.; Schiller, P.; Wahab, M.; Mogel, H.J. Computer simulations of the formation of bile salt micelles and bile salt/DPPC mixed micelles in aqueous solutions. J. Solution Chem. 2014, 43, 1755–1770. [Google Scholar] [CrossRef]
- Jójárt, B.; Poša, M.; Fisher, B.; Szöri, M.; Farkaš, Z.; Viskolcz, B. Mixed micelles of sodium cholate and sodium dodecylsulphate 1:1 binary mixture at different temperatures—experimental and theoretical investigations. PLoS ONE 2014, 9, e102114. [Google Scholar] [CrossRef]
- Nash, L.K. Elements of Statistical Thermodynamics, 2nd ed.; Dover Publications: Mineola, NY, USA, 2006. [Google Scholar]
- Kagan, H. Le stéréochimie Organique; Presses Univ. De France: Paris, France, 1975. [Google Scholar]
- Poša, M.; Popović, K.; Ćirin, D.; Farkaš Agatić, Z. Binary mixed micelles of Triton X-100 and selected bile salts: Thermodynamic stabilization and pKa values of micellar bile acids. J. Chem. Thermodyn. 2016, 103, 333–341. [Google Scholar] [CrossRef]
- Poša, M. Hydrophobicity and self-association of bile acids with a special emphasis on oxo derivatives of 5-β-cholanic acid. Curr. Org. Chem. 2012, 16, 1876–1904. [Google Scholar] [CrossRef]
- Hildebrand, J.H. Solubility. XII. Regular Solutions. J. Am. Chem. Soc. 1929, 51, 66–80. [Google Scholar] [CrossRef]
- Sandler, S.I. Chemical, Biochemical, and Engineering Thermodynamics, 4th ed.; John Wiley & Sons: Singapore, 2006. [Google Scholar]
- Daily, J.W. Statistical Thermodynamics an Engineering Approach; Cambridge University Press: Cambridge, UK, 2019. [Google Scholar]
- Rubingh, D.N. Mixed Micelle Solutions. In Solution Chemistry of Surfactants; Mittal, K.L., Ed.; Springer: New York, NY, USA, 1979; Volume 1, pp. 337–354. [Google Scholar]
- Brandani, V.; Prausnitz, J.M. Two-fluid theory and thermodynamic properties of liquid mixtures: General theory. Proc. Natl. Acad. Sci. USA 1982, 79, 4506–4509. [Google Scholar] [CrossRef] [PubMed]
- Renon, H.; Prausnitz, J.M. Local compositions in thermodynamic excess functions for liquid mixtures. AlChE J. 1968, 14, 135–144. [Google Scholar] [CrossRef]
- Poša, M.; Pilipović, A.; Tepavčević, V.; Obradović, S. Micellisation in water solutions of binary mixture of surfactants Na-deoxycholate—Na-decyl-sulphate and Na-hyodeoxycholate—Na-decyl-sulphate: Rational development (selection) of the thermodynamic model for describing GE. J. Chem. Eng. Data 2018, 63, 691–701. [Google Scholar] [CrossRef]
- McMurry, J. Organic Chemistry, 6th ed.; Brooks/Cole-Thomson Learning: Belmont, CA, USA, 2004; pp. 192–195. [Google Scholar]
- Straikov, B.E.; Norden, B. Enthalpy-entropy compensation: A phantom or something useful? J. Phys. Chem. B 2007, 111, 14431–14435. [Google Scholar] [CrossRef] [PubMed]
- Alberty, R.A. Use of Legendre Transforms in Chemical Thermodynamics. Pure Appl. Chem. 2001, 73, 1349–1380. [Google Scholar] [CrossRef]
- Lozar, J. Thermodynamique des Solutions et des Mélanges; Elipses: Paris, France, 2013; pp. 100–116. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).