Abstract
In this article, we take into account the -dimensional stochastic Chiral nonlinear Schrödinger equation (2D-SCNLSE) in the Itô sense by multiplicative noise. We acquired trigonometric, rational and hyperbolic stochastic exact solutions, using three vital methods, namely Riccati–Bernoulli sub-ODE, He’s variational and sine–cosine methods. These solutions may be applicable in various applications in applied science. The proposed methods are direct, efficient and powerful. Moreover, we investigate the effect of multiplicative noise on the solution for 2D-SCNLSE by introducing some graphs to illustrate the behavior of the obtained solutions.
Keywords:
Chiral nonlinear Schrödinger equation; Riccati–Bernoulli sub-ODE method; variational principles; sine–cosine method; soliton solutions; multiplicative noise; physical applications MSC:
60H15; 60H10; 3 15; 35Q51
1. Introduction
Mathematical models of different phenomena in various areas of the physical sciences, including nonlinear optics, biology, economy, fluid mechanics and plasma physics, can be interpreted by nonlinear systems of nonlinear partial differential equations (NPDEs) [1,2,3,4,5,6,7,8,9]. Exact solutions of the NPDEs are crucial for the analysis of natural phenomena in a wide variety of physical sciences. Accordingly, a lot of methods have been proposed to get exact solutions for NPDEs; for instance, the -expansion method [10,11], sine–cosine method [12,13], the homotopy perturbation method [14], Hirota’s method [15], inverse scattering method [16], Petrov–Kudrin–Xiong method [17,18], perturbation method [19], the variational iteration method [20,21], Riccati–Bernoulli sub-ODE method [22,23], the tanh-sech method [24], the Jacobi elliptic function method [25], the -expansion method [26].
The nonlinear Schrödinger equation (NLSE), which exhibits solitary type solutions, becomes the main representative way for describing wave behaviors in a nonlinear large number of applications, such as optics, quantum mechanics, biophysics, deep water, plasma physics, electro magnetic wave propagation, and others [27,28,29]. There are various solutions for the NLSE, such as general breather (GB), Akhmediev breather (AB), Ma soliton (MS) and rogue wave (RW) solutions. One of the important types of solutions is the Kuznetsov–Ma (KM) soliton, which shows that an unusual pulsating dynamics has attracted particular attention in plasma physics in the context of understanding nonlinear coherent phenomena [30].
Furthermore, the stochastic perturbations that occur in the physical setting, occur from various unknown reasons. These reasons may give rise to some statistical features and significant phenomena in applied science. Thus stochastic differential equations that are more accurate mathematical models of real-world situations are created [31]. Moreover, stochastic nonlinear equations are important in various areas, including nonlinear optics, biology, economy, and plasma physics [32,33].
In this paper, we consider the 2D-SCNLSE, which is given in the following form [34]
where is a complex function, * represents the complex conjugate, a is the second-order dispersion coefficient, and are the self-steepening coefficients, is the noise strength and is the time derivative of the Brownian motion . This noise may be used as an attempt to describe the impact of neglected terms on the modulating of the NLS equation. Stochastic Schrödinger equations have been used in quantum optics to explain the system state conditioned by measurement outcomes. Additionally, the noise term in Equation (1) can describe inhomogeneity in the medium where the wave propagates the source of the noise.
At this point, it is convenient to provide a definition of Brownian motion (also called one-dimensional Wiener process) is a stochastic process with the following properties: (i) (ii) has continuous trajectories, (iii) the process has stationary, independent increments, and (iv) for the stochastic variable has the normal distribution . The multiplicative noise in Equation (1) describes a process where the phase of the excitation is disturbed. In this paper, we consider the Brownian motion as a constant in space. The stochastic integral is called Itô, if we evaluate this integral at the left end—see [31,35] for more details.
Various methods have been investigated to look for the solutions of the 2D-SCNLSE with (without stochastic term); this includes the extended direct algebraic and extended trial equation method [36], the -expansion method and the modified simple equation method [37], and the trial solution method [34], while Equation (1) with stochastic term is not studied before.
Our aim in this paper is to get the stochastic exact solutions of the 2D-SCNLSE (1) by using three methods—Riccati–Bernoulli sub-ODE, He’s variational and sine-cosine method. We also consider the effect of the stochastic term on the solutions of this equation. This paper is the first to obtain the different kinds of the exact solutions of the 2D-SCNLSE (1) coercive by multiplicative noise. The fundamental advantages for the proposed three methods over the most of other methods is that they give many new exact solutions along with additional free parameters. These methods are straightforward, direct, simple and powerful. Indeed these methods give different types of soliton wave solutions, which describe different phenomena in chiral nature. Since our approach is new, namely studying the stochastic equations in the Itô sense by multiplicative noise, we plan to consider the 2D-SCNLSE (1) with other interesting methods in the future work.
This article is arranged as follows: In Section 2, we obtain the solitary wave solution by applying three different methods and therefore the stochastic exact solutions of the 2D-SCNLSE. In Section 3, we give physical interpretation for the 2D-SCNLSE. In Section 4, we illustrate the influence for multiplicative noise on the solution to the 2D-SCNLSE (1). In Section 5, we give the conclusions of this paper.
2. The Exact Solutions of the 2D-CNLSE
In this section, to get the solitary wave solution of the the 2D-SCNLSE (1), we utilize the wave transformation
are nonzero constants for , u is a real function whereas is the noise strength. Substituting Equation (2) into Equation (1) and using
to obtain for imaginary part
and for real part
From Equation (4) we obtain the velocity profile of the soliton
Dividing Equation (5) by to get
where
In the following subsections we apply three methods—Riccati–Bernoulli sub-ODE method, He’s variational principle and sine–cosine method to obtain the solitary wave solutions of Equation (7). After that we get the solutions of the 2D-SCNLSE (1) with stochastic term.
2.1. Riccati–Bernoulli Sub-ODE Method
Here, we take the following Riccati–Bernoulli equation [2,22]:
where are constants.
From Equation (9), we obtain
utilizing Equation (9), gives
Substituting (10) into (7), we have
Putting each coefficient of with zero, yields system of algebraic equations. Solving these equations, gives
and
where we used Equation (8).
Now, let us deduce the stochastic solution of the Equation (1). There are many cases depending on
First case: If then the solution of Equation (9) is
or
In this case, we can use Equation (2) with Equations (14) and (15), respectively to get the stochastic solution of the Equation (1) as
Or
2.2. He’s Variational Principle Method
Based on the He’s variational principle [20,38,39], one establish the following trial-functional:
According to Ref. [40], the solution for constant R of Equation (7) is
Superseding Equation (23) into Equation (22) gives
Making J stationary with R results in
From this equation, we have
Hence
where and are defined in Equation (8).
2.3. Sine–Cosine Method
We apply the sine–cosine method to solve Equation (7) and consequently the stochastic solution of the 2D-CNLSE (1). According to [12,13], let the solution u of Equation (7) take the form
where
Substituting Equation (26) into Equation (7) we have
rewriting the above equation
Balancing the term of in Equation (28), we get
Substituting Equation (29) into Equation (28)
Equating each coefficient of and to zero, we obtain
and
By solving these equations we get
Then the solitary wave solution of Equation (7) takes the form
therefore, we can use Equation (2) with Equation (34) to get the stochastic exact solution of the 2D-CNLSE (1) as
or
where A and B are defined in (33).
3. Physical Interpretation
The 2D-CNLS equation has been constructed by a 1-D reduction of the structure that defines the fractional quantum Hall effect. The exact solutions of the 2D-CNLSE (1) were obtained in the explicit form with the aid of the Riccati–Bernoulli sub-ODE, He’s variational approach and sine–cosine methods. Distinct types of traveling wave solutions are revealed—for example, solitary wave, dark solitons, bright solitons and periodic solitary wave solutions. The behavior of solutions for the Equation (1) being solitons, dissipative or periodic and so on, is an indication for the values of the physical parameters in the dispersion and nonlinear coefficients. Indeed the NLSE plays a vital role to describe the full spatiotemporal optical solitons or light bullets in nonlinear optics. Our study shows that the proposed three methods are reliable in handling NPDEs to establish a variety of exact solutions.
Dark and bright solitons propagate in nonlinear dispersive media. Dark soliton depicts the solitary waves with lower intensity than the background while bright soliton depicts the solitary waves whose peak intensity is larger than the background [41]. The all gained solutions in this article depict the wave profiles in various applications in applied science. Specifically, the acquired solutions may be interpreted the spatio-temporal solutions, nuclear physics, telecommunications experiments, space observations, space observations, capillary profiles, chaotic pulses laser and transistor [42,43,44,45,46]. Indeed, the gained solutions are of great importance in the development of quantum mechanics, namely in quantum hall effect, the entire computer industry and nuclear medicine.
The understanding of the effect of a noise on the propagation of waves is a very vital problem. Even the propagation is often depicted by deterministic models, in many circumstances randomness should be considered. It can drastically change the qualitative behavior and result in new properties. Stochastic Schrodinger equations have been utilized in quantum optics to explain the system state conditioned by measurement outcomes. Additionally, the noise term in Equation (1) can depict inhomogeneity in the medium where the wave propagates or the source of the noise. In sequel, we are particularly interested in the effect of a noise acting as a potential on this behavior.
4. The Effect of Multiplicative Noise on the Solutions of the 2D-CNLSE
In this section, we study the effect of multiplicative noise on the solution of the 2D-CNLSE (1). The behavior of the solutions for the 2D-CNLSE (1) being solitons, dissipative or periodic and so on, is an indication for the values of the physical parameters in the dispersion and nonlinear coefficients. We introduce some 2D, 3D and the contour graphs for different values of noise strength. For our purpose, we use Matlab package in the following sense. Fix the parameters . We introduce a variety of simulations for various value of (noise intensity).
We consider the solution (19) in order to illustrate our purpose in a completely unified way. For the noise intensity the profile wave for the 2D-CNLSE (1) fluctuates and its profile is depicted in Figure 1. When the noise intensity increases, the profile wave is destroyed, as shown in Figure 2, Figure 3 and Figure 4. Figure 5 illustrates the 2D graph corresponding to the solution (19) for . The figures highlight the physical nature of the solution by the careful choice of arbitrary parameters satisfying the constraints.
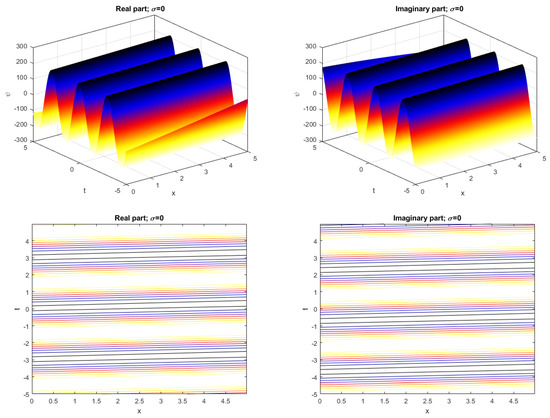
Figure 1.
The 3D graph and the contour of in (19) and .
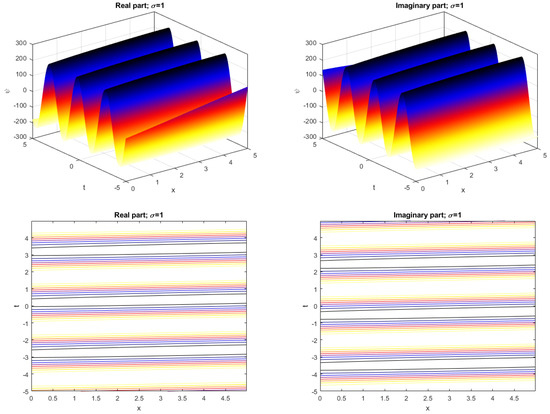
Figure 2.
The 3D graph and the contour of in (19) and .
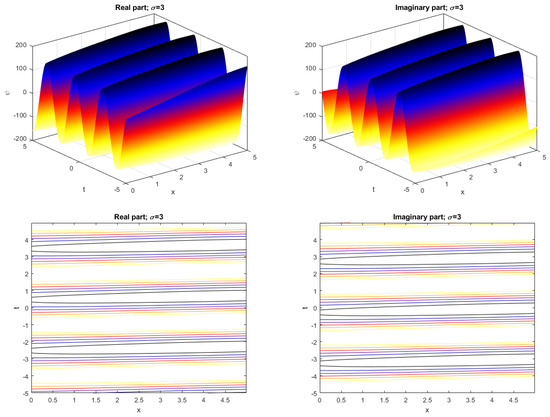
Figure 3.
The 3D graph and the contour of in (19) and .
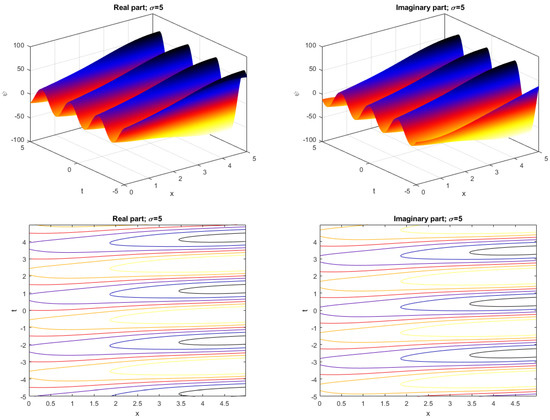
Figure 4.
The 3D graph and the contour for in (19) and .
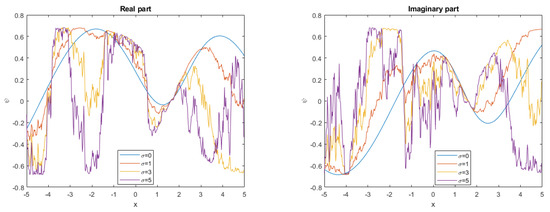
Figure 5.
The 2D graph for in (19).
5. Conclusions
In this study, the powerful Riccati–Bernoulli sub-ODE, He’s variational principle and sine-cosine methods are utilized in searching the presence of soliton solutions in quantum hall effect via the -dimensional stochastic Chiral nonlinear Schrödinger equation. We successfully obtained some dark and bright soliton solutions to this equation. The obtained solutions are essential in interpreting some complicated physical phenomena. Moreover, we considered the influence of multiplicative noise on the solutions for the 2D-CNLSE. Some graphic representations were introduced with the aid of Matlab software 18 to demonstrate the behavior of these solutions. We observed that three proposed methods are simple and powerful mathematical tools that give vital results when applied to various types of nonlinear models.
Author Contributions
S.A.: Data curation, Project administration, Methodology, Writing—original draft. W.W.M.: Data curation, Methodology, Software, Writing—original draft. M.A.A.: Software, Writing—review, Project administration, editing. M.A.E.A.: Data curation, Software, Project administration, Writing—review editing. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
This work is supported by the deanship of scientific research at the University of Ha’il-Kingdom of Saudi Arabia under Badi program No. BA-1923.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Eslami, M. Soliton-like solutions for the coupled Schrödinger’s-Boussinesq equation. Opt. Int. J. Light Electron Opt. 2016, 126, 3987–3991. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Hassan, S.Z.; Inc, M. The coupled nonlinear Schrödinger-type equations. Mod. Phys. Lett. 2020, 34, 2050078. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Mohammed, W.W. The impact of multiplicative noise on the solution of the Chiral nonlinear Schrödinger equation. Phys. Scr. 2020, 95, 085222. [Google Scholar] [CrossRef]
- Malik, H.K.; Srivastava, R.; Kumar, S.; Singh, D. Small amplitude dust acoustic solitary wave in magnetized two ion temperature plasma. J. Taibah Univ. Sci. 2020, 14, 417–422. [Google Scholar] [CrossRef]
- Abdelwahed, H.G. Nonlinearity contributions on critical MKP equation. J. Taibah Univ. Sci. 2020, 14, 777–782. [Google Scholar] [CrossRef]
- Abouelregal, A.E. A novel model of non-local thermoelasticity with time derivatives of higher order. Math. Methods Appl. Sci. 2020, 43, 6746–6760. [Google Scholar] [CrossRef]
- Liu, S.; Zhou, Q.; Biswas, A.; Liu, W. Phase-shift controlling of three solitons in dispersion-decreasing fibers. Nonlinear Dyn. 2019, 98, 395–401. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Abdelrahman, M.A.E.; Inc, M.; Hamza, A.E.; Akinlar, M.A. Soliton solutions for system of ion sound and Langmuir waves. Opt. Quant. Elect. 2020, 52, 460. [Google Scholar] [CrossRef]
- Abouelregal, A.E.; Mohammed, W.W. Effects of nonlocal thermoelasticity on nanoscale beams based on couple stress theory. Math. Methods Appl. Sci. 2020, 1–17. [Google Scholar] [CrossRef]
- Wang, M.L.; Li, X.Z.; Zhang, J.L. The ()-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics. Phys. Lett. A 2008, 372, 417–423. [Google Scholar] [CrossRef]
- Zhang, H. New application of the ()-expansion method. Commun. Nonlinear Sci. Numer. Simul. 2009, 14, 3220–3225. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Exact solutions to the double sinh-Gordon equation by the tanh method and a variable separated ODE. method. Comput. Math. Appl. 2005, 50, 1685–1696. [Google Scholar] [CrossRef]
- Wazwaz, A.M. A sine-cosine method for handling nonlinear wave equations. Math. Comput. Model. 2004, 40, 499–508. [Google Scholar] [CrossRef]
- He, J.H. An approximate solution technique depending on an artificial parameter: A special example. Commun. Nonlinear Sci. Numer. Simul. 1998, 3, 92–97. [Google Scholar] [CrossRef]
- Hirota, R. Exact solution of the Korteweg-de Vries equation for multiple collisions of solitons. Phys. Rev. Lett. 1971, 27, 1192–1194. [Google Scholar] [CrossRef]
- Ieda, J.; Uchiyama, M.; Wadati, M. Inverse scattering method for square matrix nonlinear Schrödinger equation under nonvanishing boundary conditions. J. Math. Phys. 2007, 48, 013507. [Google Scholar] [CrossRef]
- Petrov, E.Y.; Kudrin, A.V. Exact Axisymmetric Solutions of the Maxwell Equations in a Nonlinear Nondispersive Medium. Phys. Rev. Lett. 2010, 104, 190404. [Google Scholar] [CrossRef]
- Xiong, H.; Si, L.; Ding, C.; Lü, X.; Yang, X.; Wu, Y. Solutions of the cylindrical nonlinear Maxwell equations. Phys. Rev. E 2012, 85, 016602. [Google Scholar] [CrossRef]
- Mohammed, W.W. Approximate solution of the Kuramoto-Shivashinsky equation on an unbounded domain. Chin. Ann. Math. Ser. B 2018, 39, 145–162. [Google Scholar] [CrossRef]
- He, J.H. An new approach to nonlinear partial differential equations. Commun. Nonlinear Sci. Numer. Simul. 1997, 2, 230–235. [Google Scholar] [CrossRef]
- Yusufoglu, E. The variational iteration method for studying the Klein-Gordon equation. Appl. Math. Lett. 2008, 21, 669–674. [Google Scholar] [CrossRef]
- Yang, X.F.; Deng, Z.C.; Wei, Y. A Riccati-Bernoulli sub-ODE method for nonlinear partial differential equations and its application. Adv. Diff. Equ. 2015, 1, 117–133. [Google Scholar] [CrossRef]
- Abdelrahman, M.A.E.; Sohaly, M.A. Solitary waves for the nonlinear Schrödinger problem with the probability distribution function in stochastic input case. Eur. Phys. J. Plus 2017, 132, 339. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The tanh method: Exact solutions of the Sine–Gordon and Sinh–Gordon equations. Appl. Math. Comput. 2005, 167, 1196–1210. [Google Scholar] [CrossRef]
- Yan, Z.L. Abunbant families of Jacobi elliptic function solutions of the-dimensional integrable Davey-Stewartson-type equation via a new method. Chaos Solitons Fractals 2003, 18, 299–309. [Google Scholar] [CrossRef]
- Khan, K.; Akbar, M.A. The exp(-(ξ))-expansion method for finding travelling wave solutions of Vakhnenko-Parkes equation. Int. J. Dyn. Syst. Differ. Equ. 2014, 5, 72–83. [Google Scholar] [CrossRef]
- Triki, H.; Bensalem, C.; Biswas, A.; Khan, S.; Zhou, Q.; Adesanya, S.; Moshokoa, S.P.; Belic, M. Self-similar optical solitons with continuous-wave background in a quadratic-cubic non-centrosymmetric waveguide. Opt. Commun. 2019, 437, 392–398. [Google Scholar] [CrossRef]
- Biswas, A. Conservation laws for optical solitons with anti-cubic and generalized anti-cubic nonlinearities. Optik 2019, 176, 198–201. [Google Scholar] [CrossRef]
- Wazwaz, A.M. The integrable time-dependent sine-Gordon with multiple optical kink solutions. Optik 2019, 182, 605–610. [Google Scholar] [CrossRef]
- Xiong, H.; Gan, J.; Wu, Y. Kuznetsov-Ma Soliton Dynamics Based on the Mechanical Effect of Light. Phys. Rev. Lett. 2017, 201, 153901. [Google Scholar] [CrossRef]
- Prévôt, C.; Röckner, M. A Concise Course on Stochastic Partial Differential Equations; Springer: Berlin/Heidelberg, Germany, 2007. [Google Scholar]
- Shi, Y.; Pana, M.; Peng, D. Replicator dynamics and evolutionary game of social tolerance: The role of neutral agents. Econ. Lett. 2017, 159, 10–14. [Google Scholar] [CrossRef]
- Mohammed, W.W. Modulation Equation for the Stochastic Swift—Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics 2019, 7, 1217. [Google Scholar] [CrossRef]
- Eslami, M. Trial solution technique to chiral nonlinear Schrödinger’s equation in (1+2)-dimensions. Nonlinear Dyn. 2016, 85, 813–816. [Google Scholar] [CrossRef]
- ⌀Ksendal, B. Stochastic Differential Equations: An Introduction with Applications, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Raza, N.; Javid, A. Optical dark and dark-singular soliton solutions of (1 + 2)-dimensional chiral nonlinear Schrodinger’s equation. Waves Random Complex Media 2019, 29, 496. [Google Scholar] [CrossRef]
- Javid, A.; Raza, N. Chiral solitons of the (1+2)-dimensional nonlinear Schrodinger’s equation. Mod. Phys. Lett. 2019, 33, 1950401. [Google Scholar] [CrossRef]
- He, J.H. Variational principles for some nonlinear partial dikerential equations with variable coencients. Chaos Solitons Fractals 2004, 19, 847–851. [Google Scholar] [CrossRef]
- He, J.H. Some asymptotic methods for strongly nonlinear equations. Int. J. Mod. Phys. B 2006, 20, 1141–1199. [Google Scholar] [CrossRef]
- Ye, Y.H.; Mo, L.F. He’s variational method for the Benjamin–Bona–Mahony equation and the Kawahara equation. Comput. Math. Appl. 2009, 58, 2420–2422. [Google Scholar] [CrossRef]
- Scott, A.C. Encyclopedia of Nonlinear Science; Routledge: New York, NY, USA, 2005. [Google Scholar]
- Taylor, J.R. Optical Solitons: Theory and Experiment; Cambridge University Press: Cambridge, UK, 1992. [Google Scholar]
- Bailung, H.; Sharma, S.K.; Nakamura, Y. Observation of Peregrine Solitons in a Multicomponent Plasma with Negative Ions. Phys. Rev. Lett. 2011, 107, 255005. [Google Scholar] [CrossRef]
- Kibler, B.; Fatome, J.; Finot, C.; Millot, G.; Dias, F.; Genty, G.; Akhmediev, N.; Dudley, J.M. The Peregrine soliton in nonlinear fibre optics. Nat. Phys. 2010, 6, 790–795. [Google Scholar] [CrossRef]
- Chabchoub, A.; Hoffmann, N.P.; Akhmediev, N. Rogue wave observation in a water wave tank. Phys. Rev. Lett. 2011, 106, 204502. [Google Scholar] [CrossRef] [PubMed]
- Pathak, P.; Sharma, S.K.; Akamura, Y.N.; Bailung, H. Observation of ion acoustic multi-Peregrine solitons in multicomponent plasma with negative ions. Phys. Lett. A 2017, 381, 4011–4018. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).