Thermal Viscous Dissipative Couette-Poiseuille Flow in a Porous Medium Saturated Channel
Abstract
:1. Introduction
2. Problem Formulation and Analytical Solution
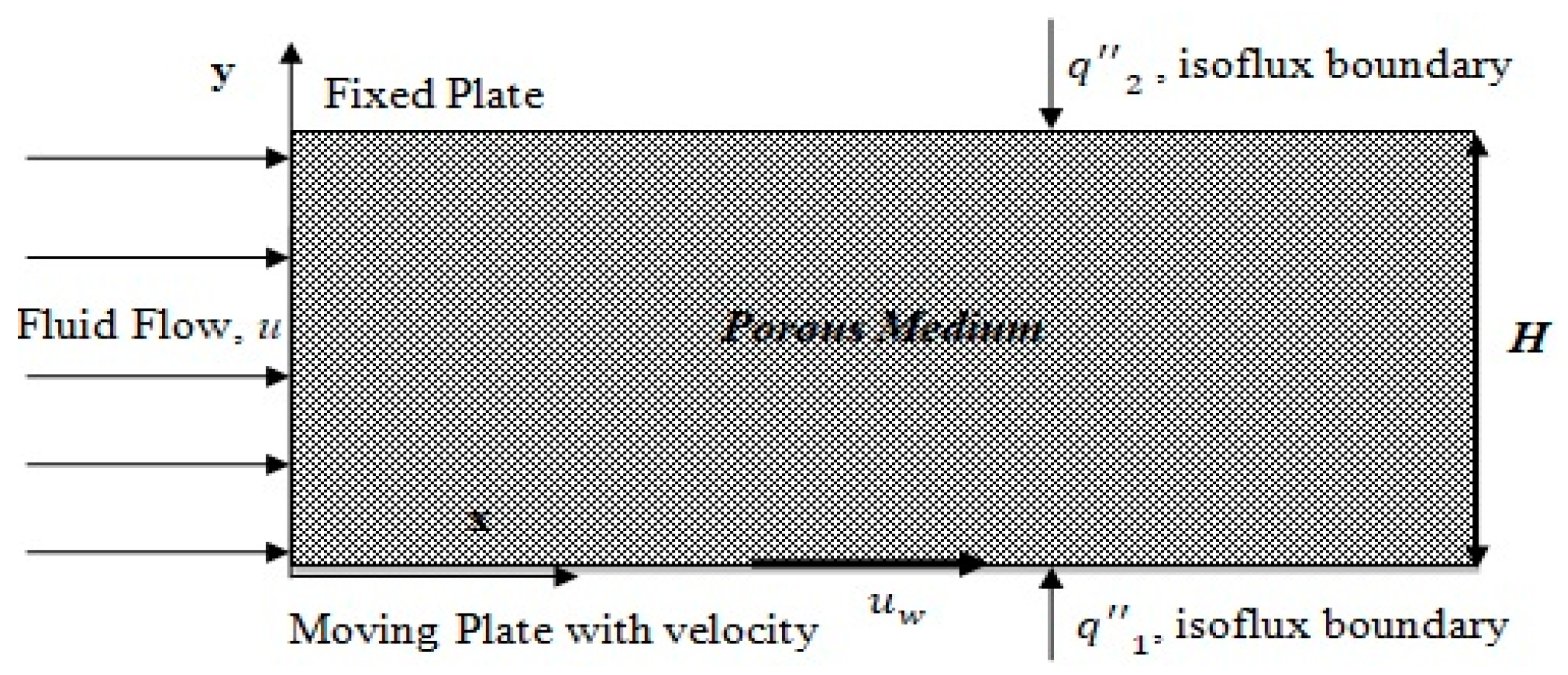
2.1. Governing Equation
2.2. Nusselt Number
2.3. Nusselt Number Verification
3. Results and Discussion
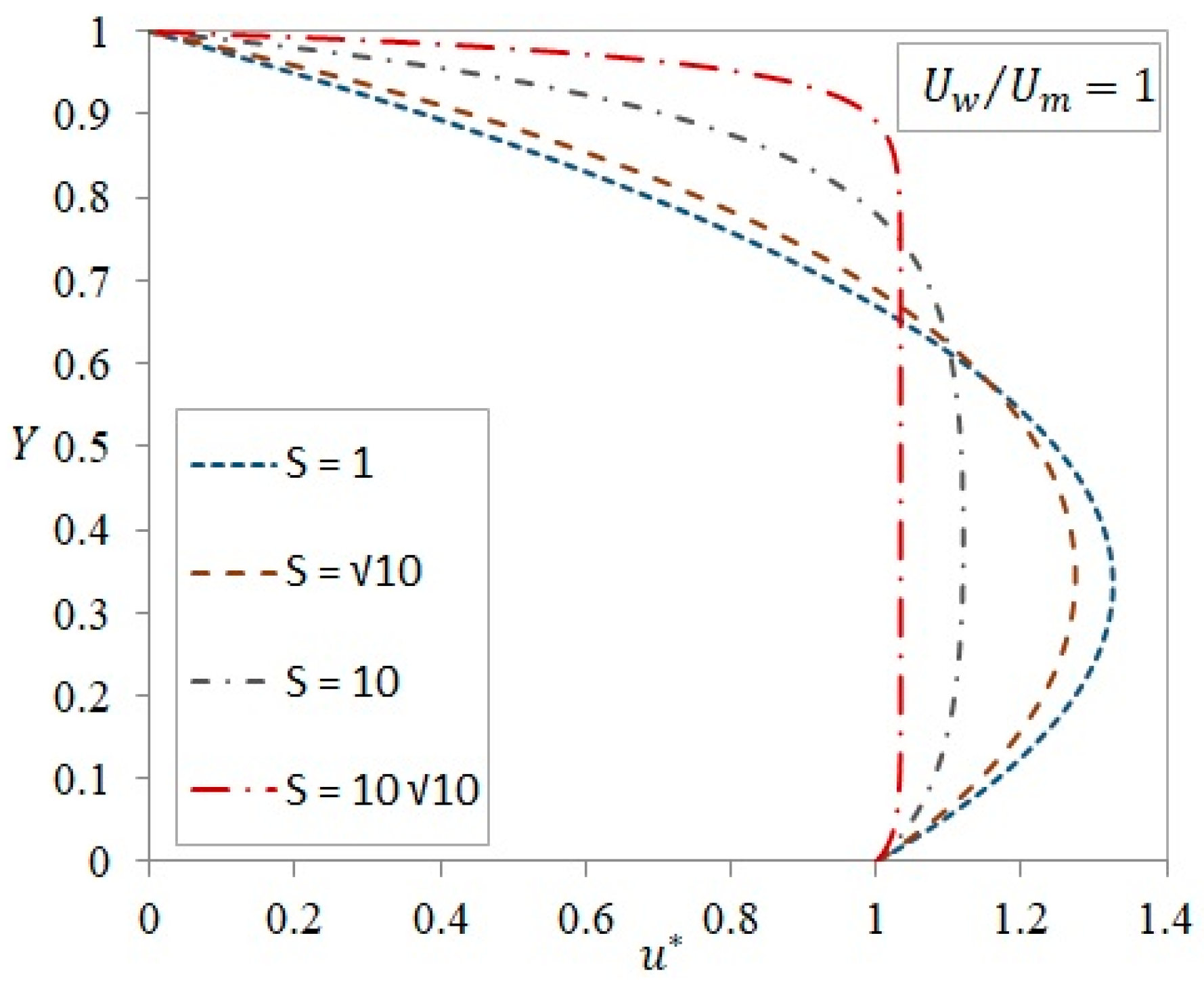
3.1. Velocity Profile
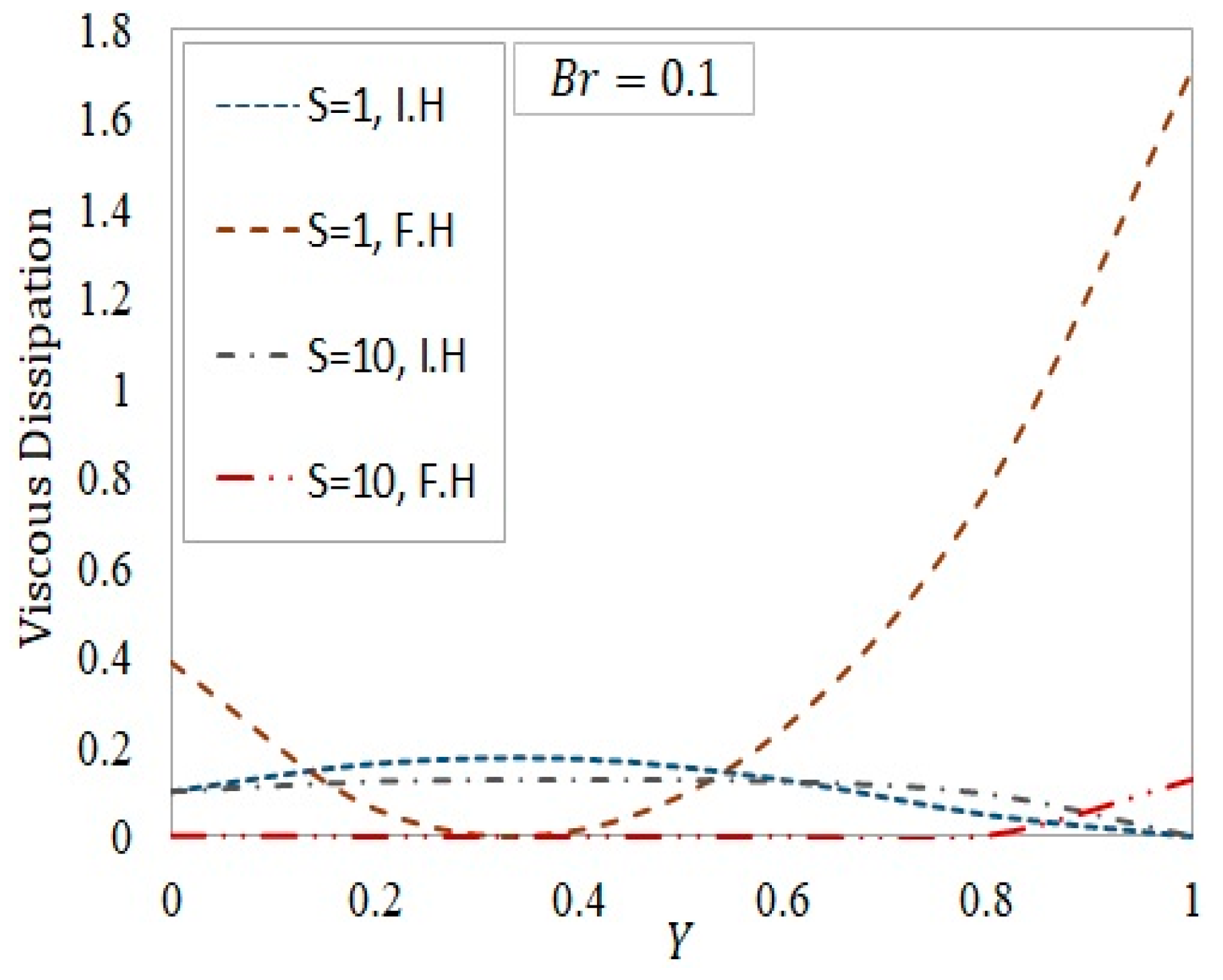
3.2. Temperature Distribution
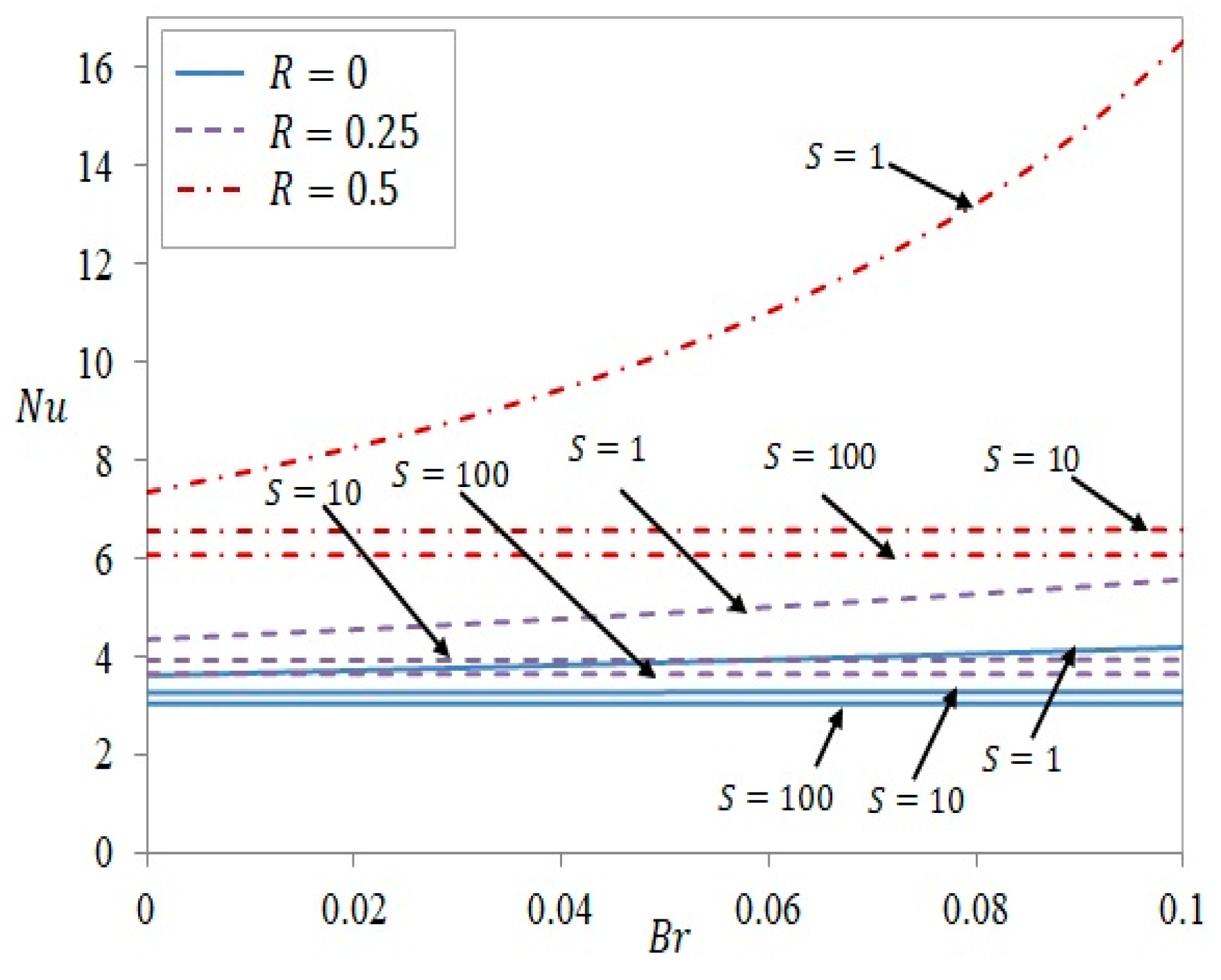
3.3. Nusselt Number Variation
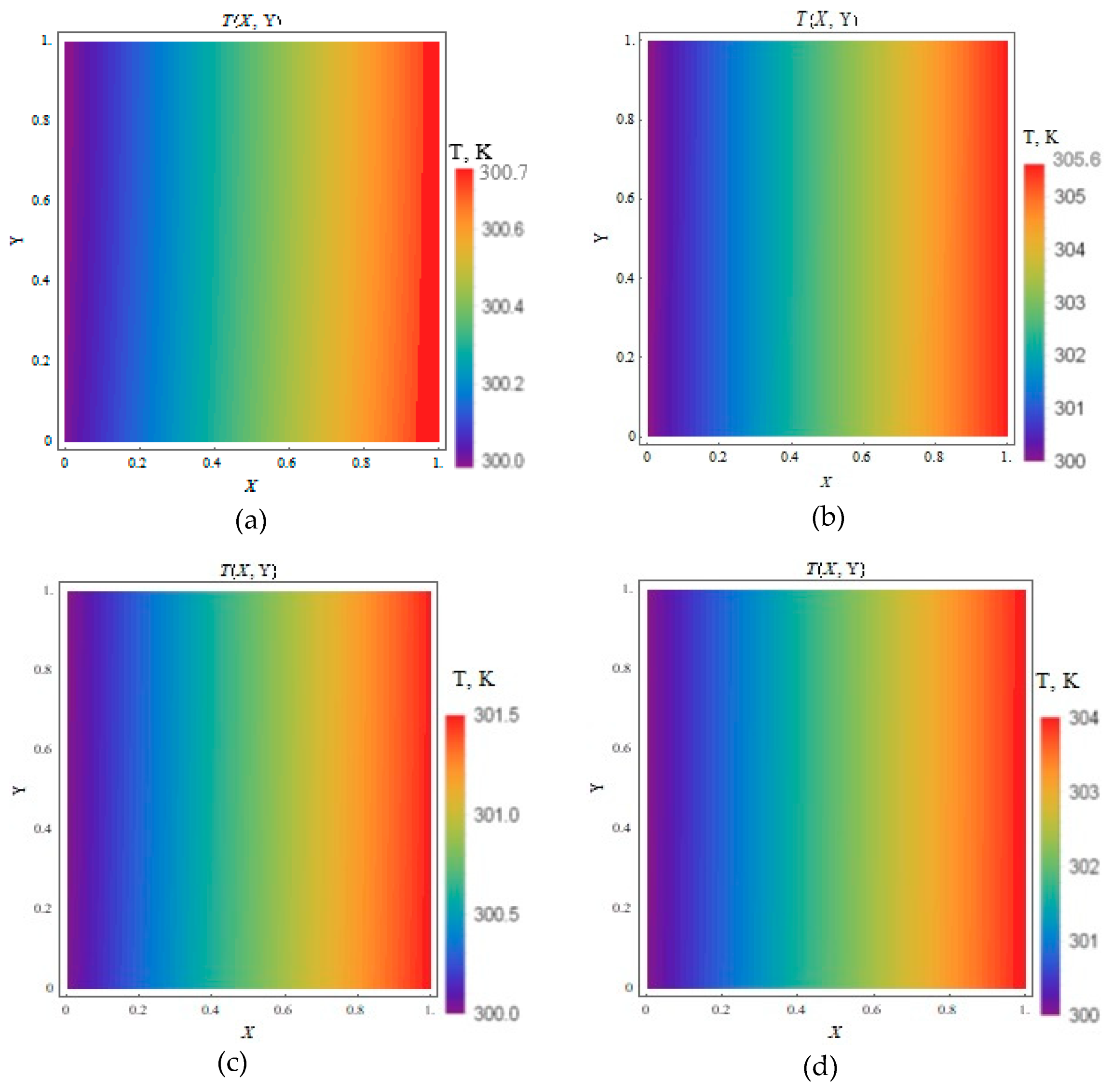
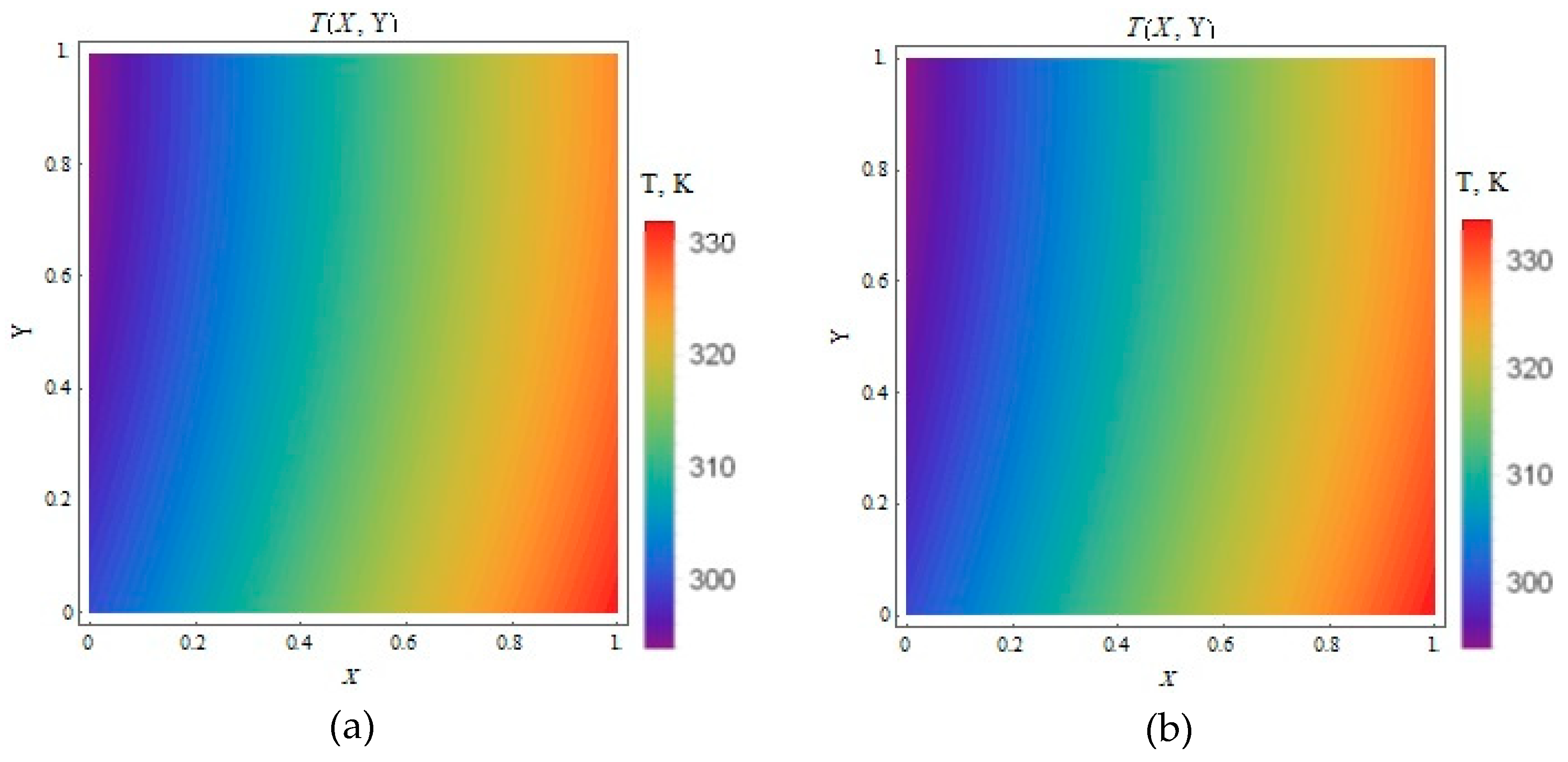
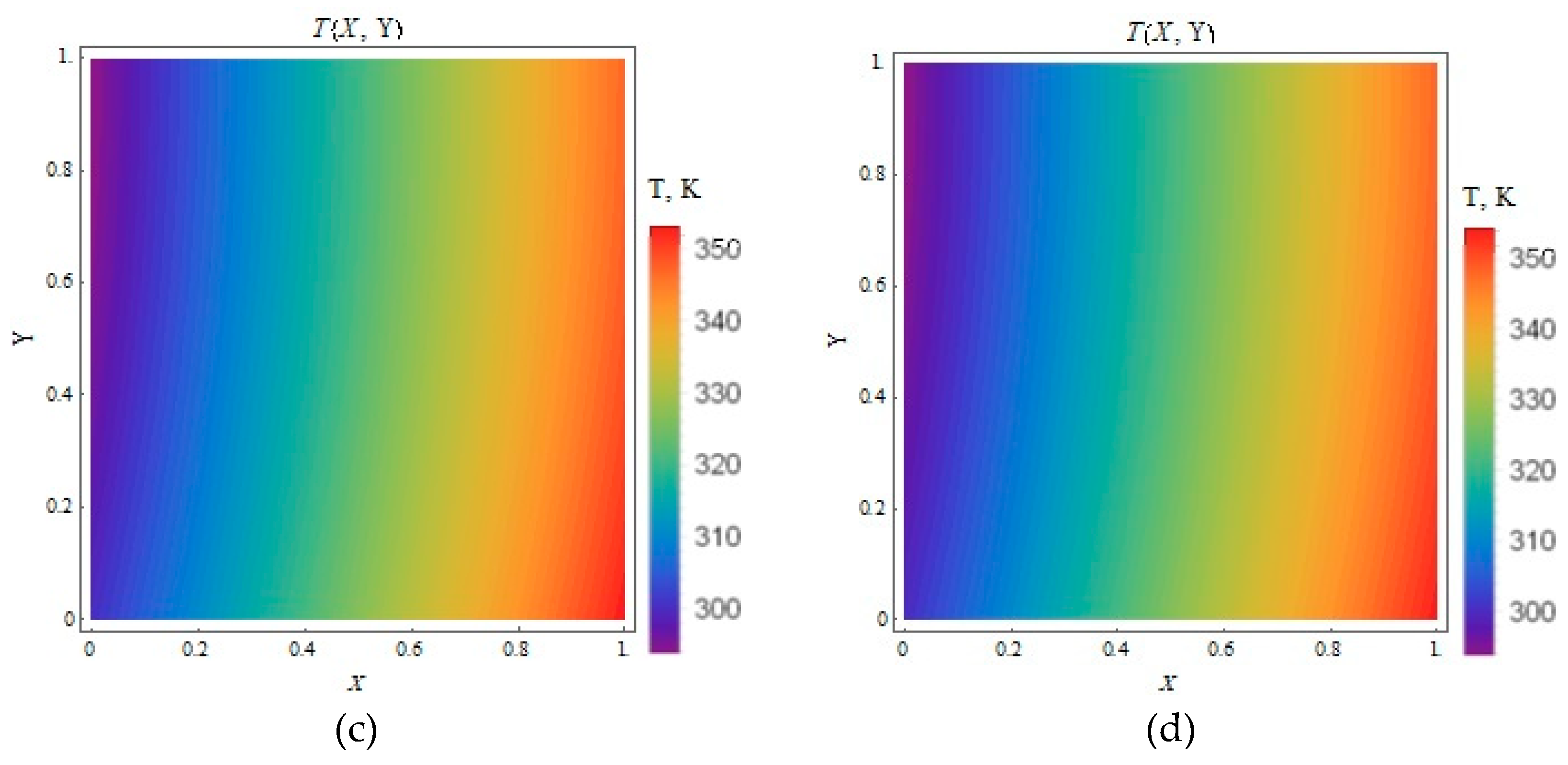
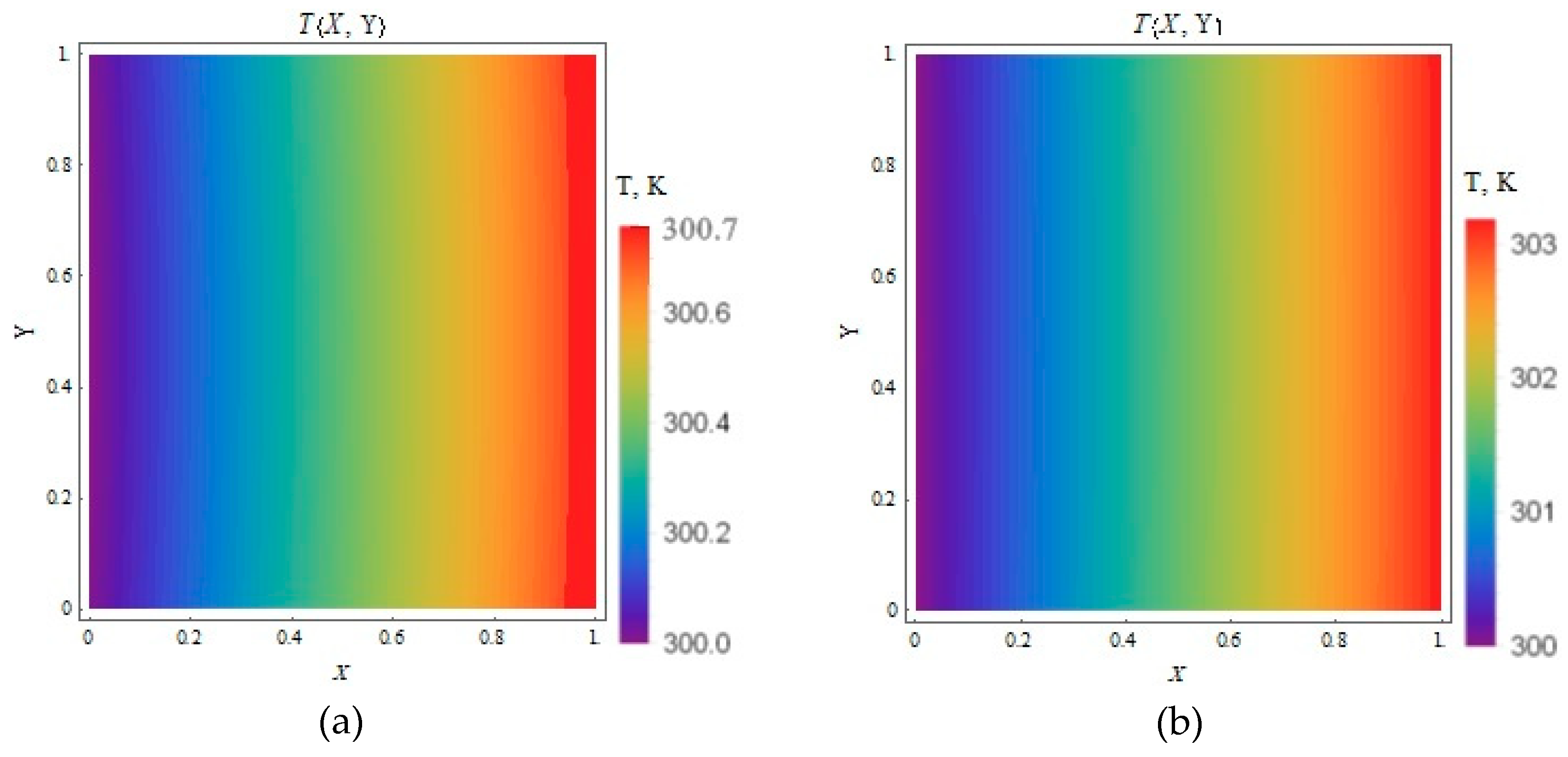
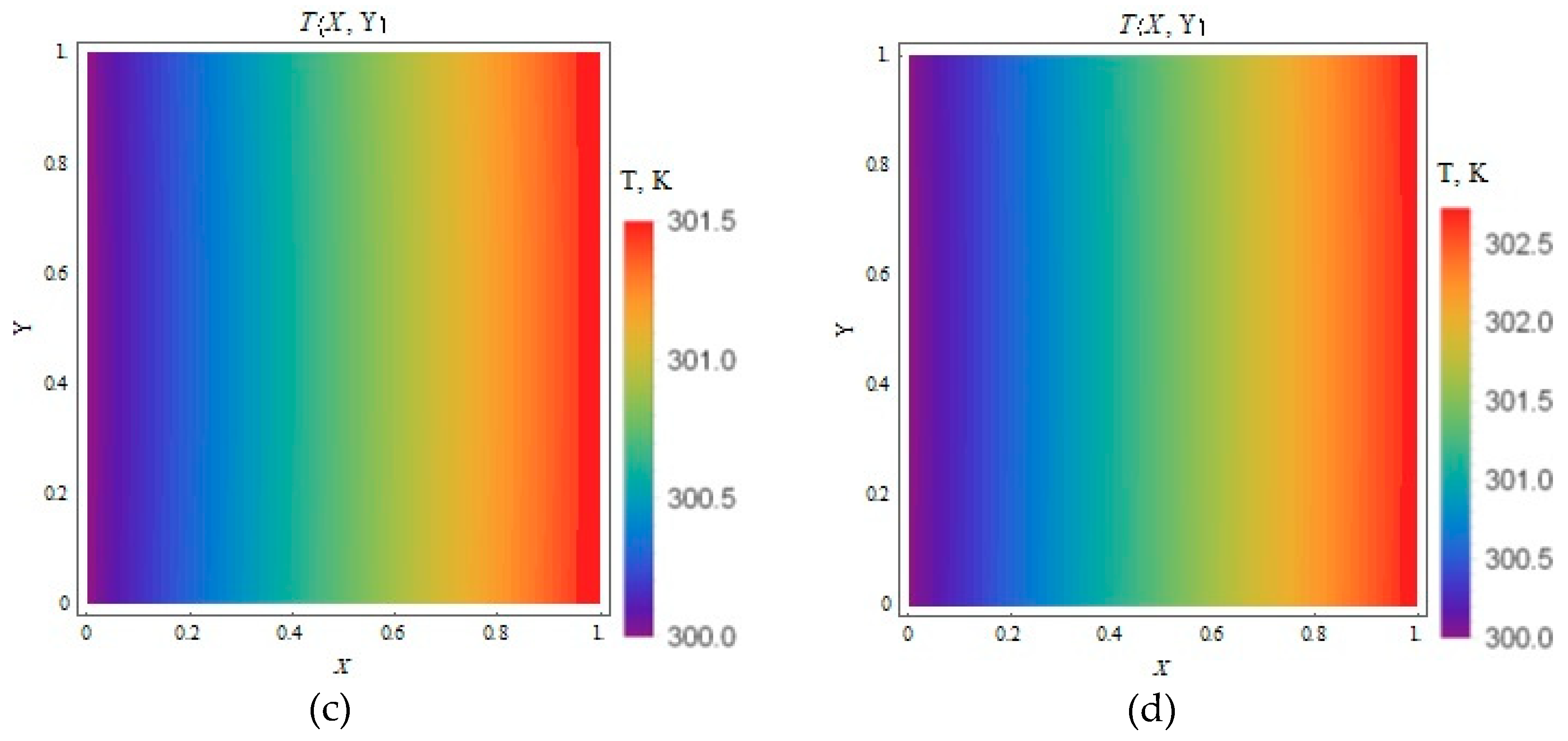
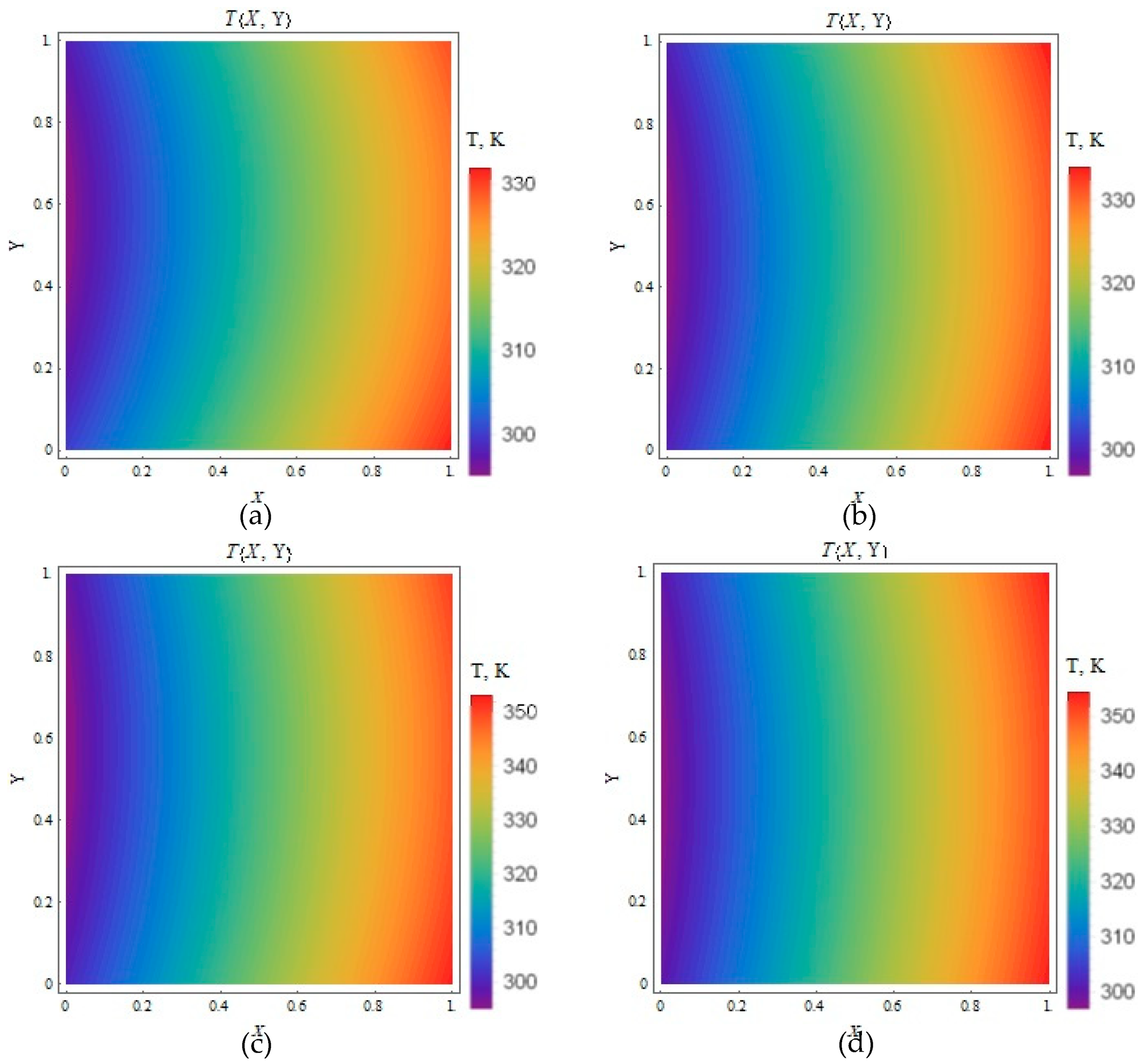
3.4. Temperature Contour Plots
3.4.1. (Heat Flux Applied to the Moving Plate Only)
3.4.2. (Equal Heat Flux Applied to Both Plates)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Constant, defined in Equation (13) | |
| Brinkman number | |
| Coefficients in Equation (16), listed in Appendix A | |
| Specific heat of fluid, J/kg·K | |
| Darcy number, | |
| Height of the channel, m | |
| Permeability of the porous medium, m2 | |
| Thermal conductivity, W/m·K | |
| Effective thermal conductivity of porous medium, W/m·K | |
| Length of the channel, m | |
| Ratio of effective viscosity to viscosity, defined as, | |
| Nusselt number, defined as, | |
| Heat flux, W/m2 | |
| Reynolds number, defined as | |
| The fraction of heat flux applied to fixed wall, defined as, | |
| Porous medium shape factor, defined as, | |
| Fluid temperature, K | |
| Mean temperature, K | |
| Wall temperature at lower plate, K | |
| Fluid velocity, m/s | |
| Moving wall velocity, m/s | |
| um | Mean velocity, m/s |
| Dimensionless mean velocity | |
| Dimensionless velocity, defined as, | |
| Dimensionless wall velocity, defined as, | |
| Dimensionless velocity, defined as, | |
| Axial coordinate of the channel, m | |
| Dimensionless length, | |
| Dimensionless transverse distance, defined as, | |
| Vertical coordinate, m | |
| Pressure gradient, N/m3 | |
| Density of the fluid, kg/m3 | |
| Viscosity of the fluid, N·s/m2 | |
| Effective viscosity of the porous medium, N·s/m2 | |
| Dimensionless temperature, | |
| Dimensionless temperature, | |
| Dimensionless temperature, |
Appendix A: List of coefficients
References
- Davaa, G.; Shigechi, T.; Momoki, S. Effect of viscous dissipation on fully developed heat transfer of non-newtonian fluids in plane laminar poiseuille-couette flow. Int. Commun. Heat Mass Transf. 2004, 31, 663–672. [Google Scholar] [CrossRef]
- Shah, R.K.; London, A.L. Laminar flow forced convention in ducts; Advances in heat transfer, Supplement 1; Academic press: New York, NY, USA, 1978. [Google Scholar] [CrossRef]
- Aydin, O.; Avci, M. Viscous-dissipation effects on the heat transfer in a Poiseuille flow. Appl. Energy 2006, 83, 495–512. [Google Scholar] [CrossRef]
- Lin, S.H. Heat transfer to plane non-Newtonian Couette flow. Int. J. Heat Mass Transf. 1979, 22, 1117–1123. [Google Scholar] [CrossRef]
- Aydin, O.; Avci, M. Laminar forced convection with viscous dissipation in a Couette-Poiseuille flow between parallel plates. Appl. Energy 2006, 83, 856–867. [Google Scholar] [CrossRef]
- Sheela-Francisca, J.; Tso, C.P.; Rilling, D. Heat Transfer with Viscous Dissipation in Couette-Poiseuille Flow under Asymmetric Wall Heat Fluxes. Open J. Fluid Dyn. 2012, 2, 111–119. [Google Scholar] [CrossRef]
- Chan, Y.H.; Chen, G.M.; Tso, C.P. Effect of Asymmetric Boundary Conditions on Couette–Poiseuille Flow of Power-Law Fluid. J. Thermophys. Heat Transf. 2015, 29, 496–503. [Google Scholar] [CrossRef]
- Hashemabadi, S.H.; Etemad, S.G.; Thibault, J. Forced convection heat transfer of Couette-Poiseuille flow of nonlinear viscoelastic fluids between parallel plates. Int. J. Heat Mass Transf. 2004, 47, 3985–3991. [Google Scholar] [CrossRef]
- Aydin, O.; Avci, M. Analytical Investigation of Heat Transfer in Couette–Poiseuille Flow Through Porous Medium. J. Thermophys. Heat Transf. 2011, 25, 468–472. [Google Scholar] [CrossRef]
- Al-Hadhrami, A.K.; Elliott, L.; Ingham, D.B. A new model for viscous dissipation in porous media across a range of permeability values. Transp. Porous Media 2003, 53, 117–122. [Google Scholar] [CrossRef]
- Davaa, G.; Shigechi, T.; Momoki, S. Effect of viscous dissipation on fully developed heat laminar heat transfer of Power-Law non-newtonian fluids in plane Couette-Poiseuille laminar flow. Rep. Fac. Eng. Nagasaki University 2000, 30, 97–104. [Google Scholar]
- Tso, C.P.; Sheela-Francisca, J.; Hung, Y.M. Viscous dissipation effects of power-law fluid flow within parallel plates with constant heat fluxes. J. Nonnewton. Fluid Mech. 2010, 165, 625–630. [Google Scholar] [CrossRef]
- Tan, L.Y.; Chen, G.M. Analysis of entropy generation for a power-law fluid in a microchannel. In Proceedings of the ASME 2013 4th International Conference on Micro/Nanoscale Heat and Mass Transfer, Hong Kong, China, 11–14 December 2013. [Google Scholar]
- Ting, T.W.; Hung, Y.M.; Guo, N. Viscous dissipative forced convection in thermal non-equilibrium nanofluid-saturated porous media embedded in microchannels. Int. Commun. Heat Mass Transf. 2014, 57, 309–318. [Google Scholar] [CrossRef]
- Hwang, G.J.; Chao, C.H. Heat transfer measurement and analysis for sintered porous channels. J. Heat Transfer. 1994, 116, 456–464. [Google Scholar] [CrossRef]

| Nu, Present Study | Nu, Chen et al. [7] | Nu, Aydin et al. [9] | Nu, Davaa et al. [11] | Nu*, Tso et al. [12] | Nu, Tan and Chen [13] | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 5.385 | 5.385 | 5.385 | 5.385 | 5.385 | --- | |
| 0 | 0 | 1 | 7.238 | --- | 7.241 | --- | --- | --- | |
| 0.2 | 0 | 0 | 3.805 | 3.804 | 3.804 | 3.804 | --- | --- | |
| 0.2 | 0 | 1 | 9.992 | 10 | --- | 10 | --- | --- | |
| 0 | 0.5 | 0 | 8.237 | 8.235 | --- | --- | 8.235 | 8.235 | |
| 0.5 | 0.5 | 0 | 3.183 | 3.182 | --- | --- | --- | 3.182 |
| 1 | 0.1129 | 0.4001 |
| 0.1106 | 0.0412 | |
| 10 | 0.1048 | 0.0064 |
| 0.1015 | 0.0016 | |
| 100 | 0.1005 | 0.0005 |
| Fluid | Water |
| Solid | Silicon |
| Porosity, | 0.9 |
| Density of fluid, (kg/m3) | 997 |
| Specific heat of fluid, (J/kg·K) | 4179 |
| Viscosity of fluid, (N·s/m2) | 8.55 × 10-4 |
| Heat flux, (W/m2) | 1 × 104 |
| Moving wall temperature, (K) | 300 |
| Thermal conductivity of fluid, (W/m·K) | 0.613 |
| Thermal conductivity of solid, (W/m·K) | 148 |
| Effective thermal conductivity of porous material, (W/m·K) | 15.3 |
| Fluid | Air |
| Solid | Sintered Bronze Beads |
| Porosity, | 0.37 |
| Permeability, | 0.422 × 10−9 |
| Density of fluid, (kg/m3) | 1.177 |
| Specific heat of fluid, (J/kg·K) | 1005 |
| Viscosity of fluid, (N·s/m2) | 1.846 × 10−5 |
| Heat flux, (W/m2) | 0.8 × 104 |
| Moving wall temperature, (K) | 300 |
| Thermal conductivity of fluid, (W/m·K) | 26.14 × 10−3 |
| Thermal conductivity of solid, (W/m·K) | 10.287 |
| Effective thermal conductivity of porous material, (W/m·K) | 6.5 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.M.; B., M.F.; Lim, B.K.; Tso, C.P. Thermal Viscous Dissipative Couette-Poiseuille Flow in a Porous Medium Saturated Channel. Symmetry 2019, 11, 869. https://doi.org/10.3390/sym11070869
Chen GM, B. MF, Lim BK, Tso CP. Thermal Viscous Dissipative Couette-Poiseuille Flow in a Porous Medium Saturated Channel. Symmetry. 2019; 11(7):869. https://doi.org/10.3390/sym11070869
Chicago/Turabian StyleChen, G. M., M. Farrukh B., B. K. Lim, and C. P. Tso. 2019. "Thermal Viscous Dissipative Couette-Poiseuille Flow in a Porous Medium Saturated Channel" Symmetry 11, no. 7: 869. https://doi.org/10.3390/sym11070869
APA StyleChen, G. M., B., M. F., Lim, B. K., & Tso, C. P. (2019). Thermal Viscous Dissipative Couette-Poiseuille Flow in a Porous Medium Saturated Channel. Symmetry, 11(7), 869. https://doi.org/10.3390/sym11070869







