Abstract
In this study, we present an analytical study on blood flow analysis through with a tapered porous channel. The blood flow was driven by the peristaltic pumping. Thermal radiation effects were also taken into account. The convective and slip boundary conditions were also applied in this formulation. These conditions are very helpful to carry out the behavior of particle movement which may be utilized for cardiac surgery. The tapered porous channel had an unvarying wave speed with dissimilar amplitudes and phase. The non-dimensional analysis was utilized for some approximations such as the proposed mathematical modelling equations were modified by using a lubrication approach and the analytical solutions for stream function, nanoparticle temperature and volumetric concentration profiles were obtained. The impacts of various emerging parameters on the thermal characteristics and nanoparticles concentration were analyzed with the help of computational results. The trapping phenomenon was also examined for relevant parameters. It was also observed that the geometric parameters, like amplitudes, non-uniform parameters and phase difference, play an important role in controlling the nanofluids transport phenomena. The outcomes of the present model may be applicable in the smart nanofluid peristaltic pump which may be utilized in hemodialysis.
1. Introduction
Peristaltic motion [1,2,3,4,5,6] is a fundamental physiological mechanism which has many applications in bio-mechanical and engineering sciences where transport phenomena at micro/macro level occur. This mechanism is also applicable in transporting the nanofluids without any contaminations. The nanofluid term was first invented by Choi and Eastman [7] with reference to a conventional heat transfer liquid retention distribution of a nanosized particle. The behavior of nanoliquid in thermal conductivity enhancement has been observed by Masuda et al. [8] and experimental results of nanoparticle into pure fluid may conduct to reduce in heat transfer. The closed form model for convective transport in nanofluids studying the thermophoresis and Brownian diffusion has been studied by Buongiorno and Hu [9] and Buongiorno [10].
In the peristaltic pumping models, nanoliquid was introduced by Akbar and Nadeem [11]. They investigated endoscopic influences on the peristaltic motion of a nanofluid. Akbar [12] further presented the peristaltic transport of a Sisko nanoliquid in an asymmetric channel. It was noticed that enhances in the Sisko nanoliquid parameter axial pressure rise in the peristaltic pumping region. The effect of nanoliquid features on peristaltic heat transfer in a two-dimensional axisymmetric channel was discussed by Tripathi and Beg [13]. They examined that the nanoliquids incline to suppress backflow equated with Newtonian fluids. Akbar et al. [14] discussed the magnetohydrodynamic (MHD) peristaltic motion of a Carreau nanoliquid in an asymmetric channel. Furthermore, Beg and Tripathi [15] introduced the double diffusion process in peristaltic pumping. They discussed the salute and nanoparticle concentrations in their analysis. The effects of nanoparticle geometry on peristaltic motion has been analyzed by Akbar et al. [16]. MHD peristaltic pumping with viscoelastic nanofluids have been studied by Reddy and Makinde [17]. The velocity and slip influences on peristaltic pumping of nanoliquids have been examined by the Akbar et al. [18]. Heat and mass transfer analysis on peristaltic pumping through the rectangular duct was presented by Nadeem et al. [19]. Peristaltic transport of Prandtl nanofluid through the rectangular duct was studied by Ellahi et al. [20] and with magnetic field [21]. Hyperbolic tangent nanofluid with peristaltic pumping was implemented by Kothandapani and Prakash [22] in the presence of a radiation parameter and inclined magnetic field. Peristaltic pumping by eccentric cylinders has been discussed by the Nadeem et al. [23]. In similar directions, many more investigations [24,25,26,27,28,29,30,31,32,33,34,35,36,37] on peristaltic pumping, nanofluids and non-Newtonian nanofluids with various physical constraints and various flow geometries had been described in the literature.
The analysis of fluid flow through porous channels or tubes had gained attention recently because of its several applications in biomedical engineering and many other engineering areas like the flow of blood oxygenators, gall bladder with stones, in small blood vessels, the design of filters, in transpiration cooling boundary layer control, the flow of blood in the capillaries, the dialysis of blood in artificial kidney, gaseous diffusion in the spreading of fatty cholesterol and artery-clogging blood clots in the lumen of a coronary artery [38,39,40,41,42,43,44,45,46,47]. The steady laminar incompressible free convective flow of a nanofluid over a permeable upward facing horizontal plate located in a porous medium in an existence of thermal convective boundary condition was considered numerically by Uddin et al. [48]. Chamkha et al. [49] studied the mixed convection boundary layer flow in the existence of laminar and isothermal vertical porous medium. The onset of convection in a horizontal layer of a porous medium by a nanofluid was analytically studied by Kuznetsov and Nield [50]. Akbar [51] investigated the double-diffusive peristaltic transport of Jeffrey nanoliquids in a porous region in the presence of natural convective. Double-diffusive natural convective peristaltic flow of a Jeffrey nanofluid in a porous channel has been analyzed by Nadeem et al. [52] and investigated the peristaltic flow of nanofluid eccentric tubes which comprises a porous medium. Two-phase flow driven by the peristaltic pumping through porous medium was studied by Bhatti et al. [53]. Perturbation solutions have been obtained and it is observed that chemical reaction and Soret numbers oppose the particle concentration. The applications of porosity can be deeply studied by using nanofluid model in [54,55].
Moreover, the no-slip condition is inadequate when a fluid revealing macroscopic wall slip is considered and that, in general, is governed by the relation between the slip velocity and grip. The slip condition plays significant role in shear skin, spurt and hysteresis belongings. The nanofluids that exhibit boundary slip have vital technological purposes such as in shining valves of the artificial heart and internal holes. The proposed mathematical geometry is very similar to the blood vessel models. The blood vessels can be classified into three types: the largest vessels, small vessels and intermediate blood vessels. The largest vessels are identified in the aorta and vena cava and also experience very little heat transfer with the tissue. In addition, there are also more blood vessels that fall into this category. The smallest vessels are noticed in place of arterioles, capillaries and venules which basically experience ideal heat transfer with the blood departure at tissue temperature. The intermediate blood vessels fall in a relatively narrow band with uniformly distributed temperature. These classifications are dependent on the amplitude of vessels and width of channel. Hence, the main purpose of this paper is to study a theoretical analysis of peristaltic transport of a Newtonian nanofluid with slip through a porous medium in the tapered wavy channel subject to convective boundary conditions. The long wavelength and low Reynolds number assumptions are considered. The exact solutions are found in the form of axial velocity from which temperature and volumetric concentration are deduced. Computational results are illustrated and discussed in detail.
2. Mathematical Formulation
Consider an incompressible viscous nanofluid filling the porous space in the tapered wavy channel. The heat transfer between the blood network and living tissues which passes through the channel depends on the geometry of the blood vessel and it is important to understand the behavior of the blood flow and the neighboring tissue nature. Let and be, correspondingly, the lower and upper blood vessel boundaries of the channel. The sinusoidal waves propagating along the wavy walls of the tapered channel are demonstrated in Figure 1 and mathematically shown as:
here , , , , , , , are the width of the channel at the inlet, amplitudes of lower wavy wall, amplitude of upper wavy wall, dimensional non–uniform parameter, wave length, phase speed of the wave and phase difference varies in the range , which corresponds to tapered symmetric channel i.e., together walls move towards inward or outward concurrently.
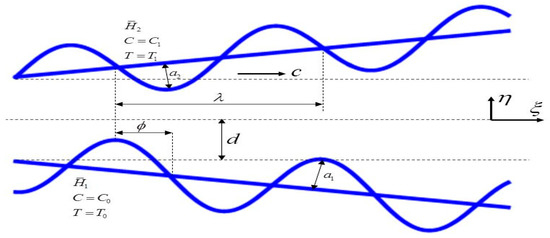
Figure 1.
Geometry for peristaltic pumping of nanofluids through a tapered microchannel.
For an incompressible viscous nanofluid the balance of mass, momentum, nanoparticle temperature and volumetric concentration are presented as [56,57,58,59]:
in which , are the components of axial velocity along and directions correspondingly, , , , , , , , , , , , and are the dimensional time, material time derivative, dimensional pressure, density of the fluid, density of the particle, nanoparticle temperature, thermal conductivity, permeability of porous medium, Brownian diffusion coefficient, themophoretic diffusion coefficient, mean temperature, nanoparticle volumetric volume fraction and the ratio of the effective heat capacity of nanoparticle material and heat capacity of the fluid with being the density. Additionally, and are the temperature and nanoparticle volume fraction at the lower and upper walls.
3. Convective Boundary Conditions
The convective boundary conditions [60,61] are utilized using Newton’s cooling law as:
where , , , , and are the permeability of the porous walls (Darcy number), slip coefficient at the surface of the porous walls, the heat transfer coefficients, mass transfer coefficients respectively, the thermal conductivity and the mass conductivity.
4. Non-Dimensional Analysis
In order to depict the nanoliquid flow in the following non-dimensional measures are introduced in Equations (1)–(8). are the velocity components in direction of , is the stream function, is the dimensionless time, and represent the dimensionless form of the lower and upper channel, and is the Reynolds number, is the dimensionless pressure, is the amplitude of lower wavy wall, is the amplitude of upper wavy wall, is the dimensionless non-uniform parameter, is the wave number, is the Schmidt number, is the Permeability parameter, is the dimensionless nanoparticle temperature, is the nanoparticle volumetric concentration or dimensionless rescaled nanoparticle volume fraction, is the Prandtl number, is the Brownian motion parameter is the thermophoresis parameter, is the Eckert number, is the Brinkman number, and is the thermal radiation parameter and also, applying the long wavelength and low Reynolds number approximations, we attain:
Equation (10) shows that p is not dependent on x. Reducing the pressure gradient term from Equations (9) and (10), it yields:
Additionally, it is noticed that the continuity equation is routinely fulfilled.
where is the velocity slip parameter, is the heat transfer Biot number and is the mass transfer Biot number.
5. Analytical Solution
The solution of the Equation (13) subject to the conditions in Equation (14) is obtained as:
The integration of Equation (12) with respect to , we obtain
Solving Equations (11) and (12) and substituting in Equation (16) subject to boundary conditions of Equations (14), the dimensionless nanoparticle temperature field is attained as
and the nanoparticle volumetric concentration is obtained as:
The coefficient of nanoparticle heat transfer at the lower wall is specified by
The above mentioned constants are elaborated in the Appendix A.
6. Computational Results and Discussion
In general, exact solutions for temperature, nanoparticle volumetric concentrations and coefficient of nanoparticle temperature depend on the value of First of all, can be influenced by hiring for and from Equation (16). It ought to be noticed that observing the value of analytically from Equation (16) in terms of the other parameters set is a very difficult task and it may be impossible. Nevertheless, with the help of MATHEMATICA/MATLAB software, the numerical solutions are still available. The numerical value of plays an important role in plotting the graphs for variation of the streamlines, nanoparticle temperature distribution, nanoparticle volumetric concentration and coefficient of nanoparticle temperature.
To analyze the results, instantaneous volume rate is considered as varying exponentially with the relation (Kikuchi [62])
where is the mean flow rate or flow constant, A is the blood flow constant. Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 were plotted to examine the stream function , nanoparticle temperature , nanoparticle concentration and heat transfer coefficient . Additionally, it is noticed that the flow rate for the non-positive and positive flow rate or may be according to or . It was detected through an experiment performed by Kikuchi [62] that the flow rate decreases exponentially with time however mean flow rate does not depend on the structural details of the channel.
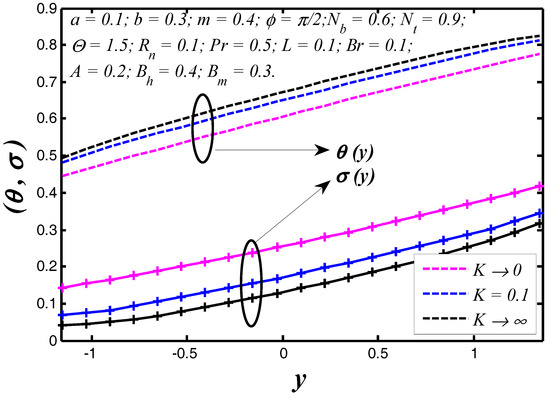
Figure 2.
Nanoparticle temperature and concentration profiles for .
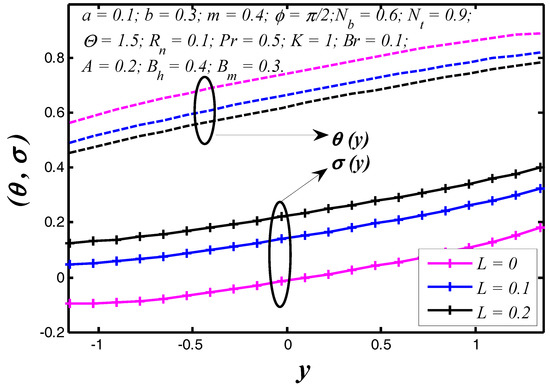
Figure 3.
Nanoparticle temperature and concentration profiles for .
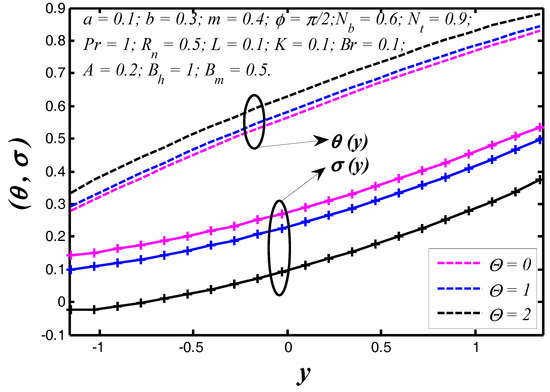
Figure 4.
Nanoparticle temperature and concentration profiles for .
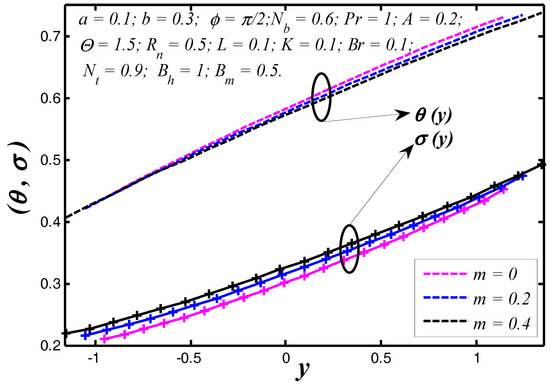
Figure 5.
Nanoparticle temperature and concentration profiles for .
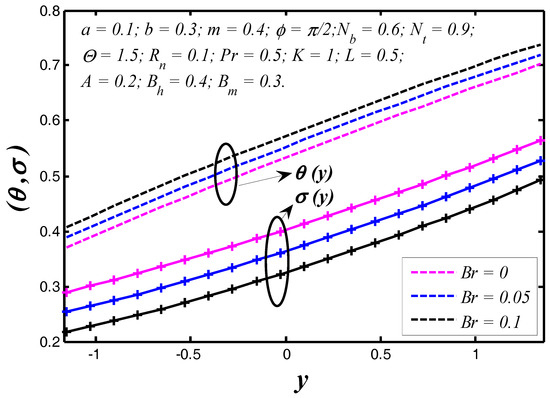
Figure 6.
Nanoparticle temperature and concentration profiles for .
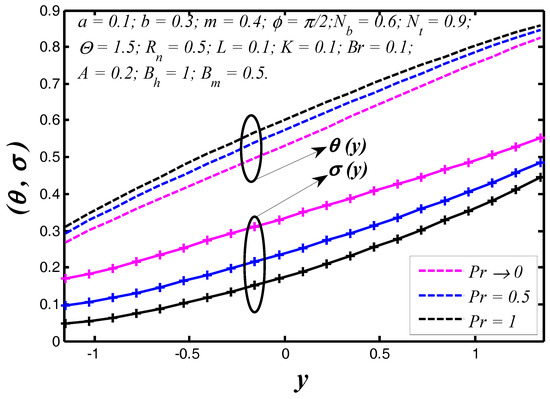
Figure 7.
Nanoparticle temperature and concentration profiles for .
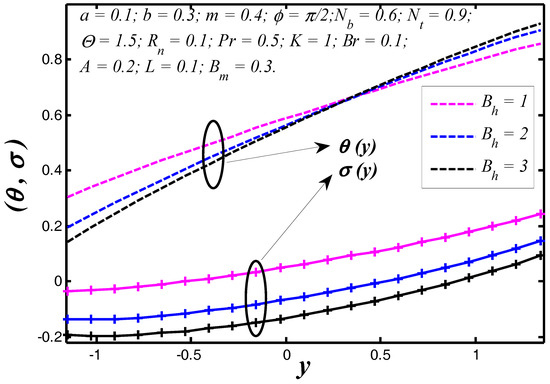
Figure 8.
Nanoparticle temperature and concentration profiles for .
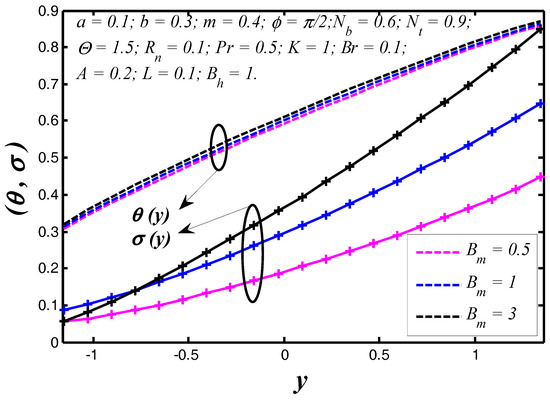
Figure 9.
Nanoparticle temperature and concentration profiles for .
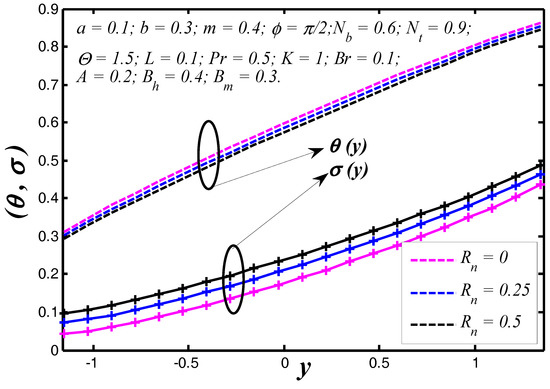
Figure 10.
Nanoparticle temperature and concentration profiles for .
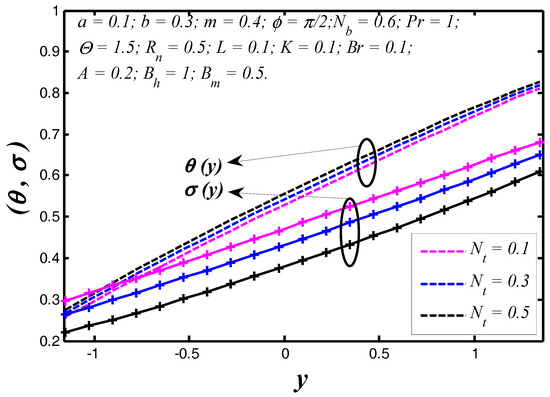
Figure 11.
Nanoparticle temperature and concentration profiles for .
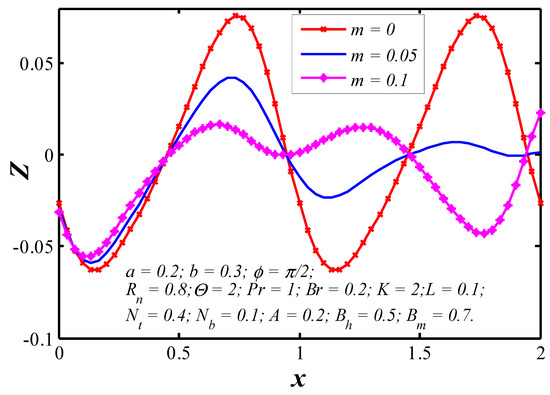
Figure 12.
Nanoparticle heat transfer coefficient profiles for various values of .
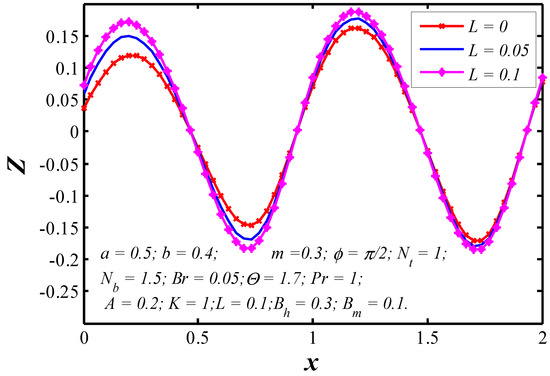
Figure 13.
Nanoparticle heat transfer coefficient profiles for various values of .
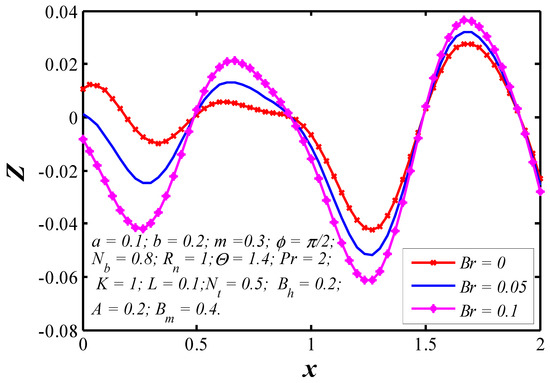
Figure 14.
Nanoparticle heat transfer coefficient profiles for various values of .
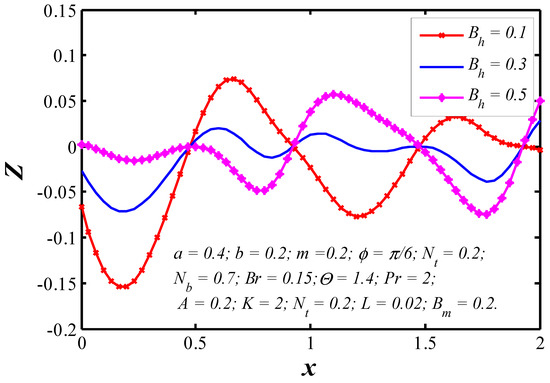
Figure 15.
Nanoparticle heat transfer coefficient profiles for various values of .
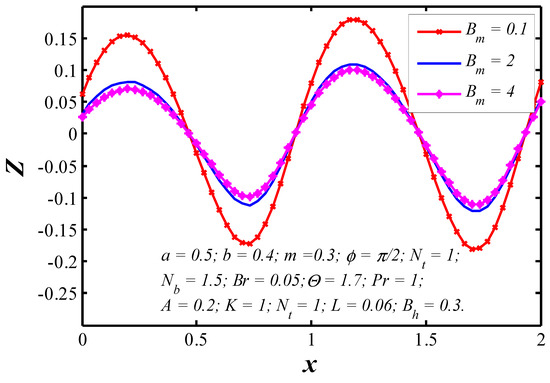
Figure 16.
Nanoparticle heat transfer coefficient profiles for various values of .
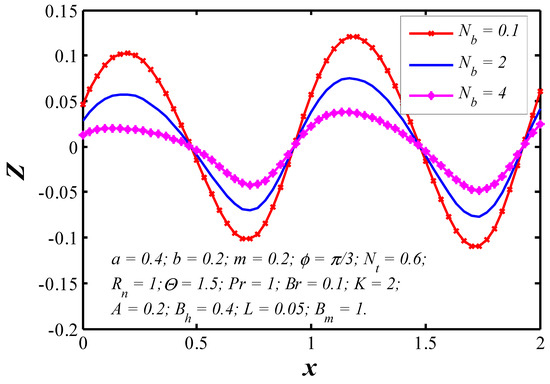
Figure 17.
Nanoparticle heat transfer coefficient profiles for various values of .
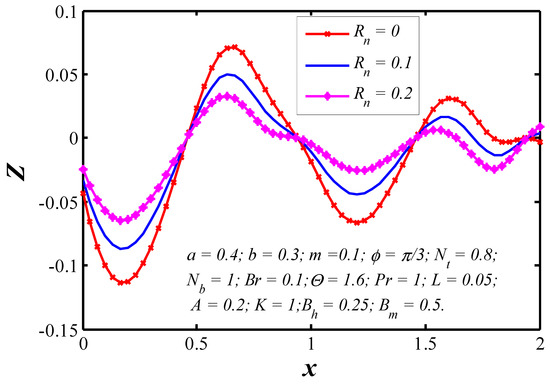
Figure 18.
Nanoparticle heat transfer coefficient profiles for various values of .
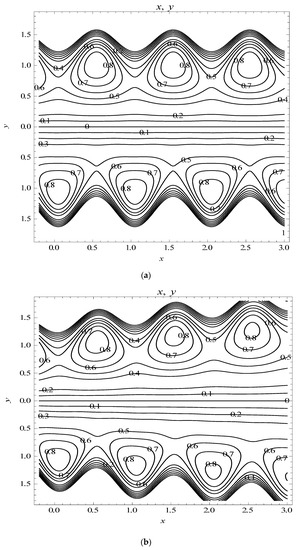
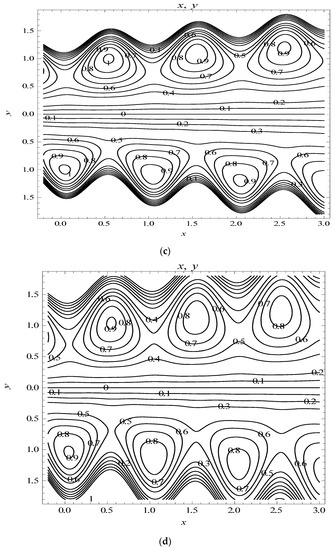
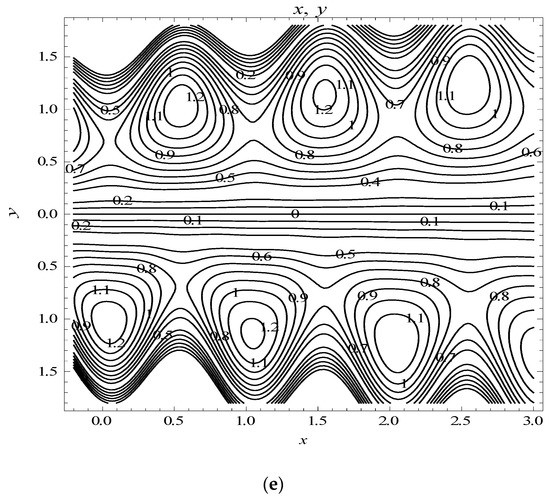
Figure 19.
Streamlines when , , , , , (a) , , , , (b) , , , , (c) , , , , (d) , , , , (e) , , , .
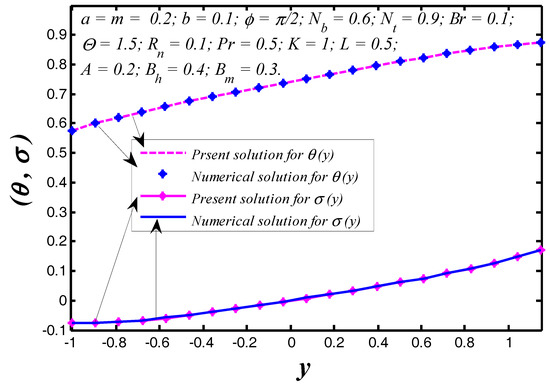
Figure 20.
Comparison between numerical and present solutions for temperature and nanoparticle volume fraction profiles.
6.1. Thermal and Concentration Profiles
Effects of permeability parameter slip parameter mean flow rate , non-uniform parameter Brinkman number Prandtl number heat transfer Biot number mass transfer Biot number thermal radiation and thermophoresis parameter on temperature profile are analyzed through Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, Figure 9, Figure 10 and Figure 11. In accordance with physical laws, the energy fluency requires to destroy cancer cells greatly depends on the number of nanoparticles temperature within the cell. Additionally, the role of this study is to improve correlations and estimation methods for calculating magnitudes of upper and lower tapered wavy wall boundaries of heat transfer in and around the individual blood vessels. The analysis did not consider vessel size and any experimental values because flow oscillations due to the heartbeat are not present in these small vessels. The aim of this study is to improve correlations and estimation methods for scheming magnitudes and upper and lower limits of heat and mass transfer in and around individual blood vessels.
The nanoparticle temperature and concentration profiles resulted in the vessel exit are shown in Figure 2 for three different permeability parameter values such as . It is noticed, theoretically, the absence of a permeability parameter shows very few heat exchanges in the blood vessel, but the particles movement is raised in the blood vessel. In Figure 3, we noticed the effects of slip parameter on the nanoparticle temperature and concentration profiles for fixed values of other parameters. Three different slip parameters are used in the nanoparticle temperature and concentration distribution such as and . It is important to note with the enhancement in the velocity slip parameter, the nanoparticle temperature and concentration at any point in the flow medium enhances, but the behavior of temperature profile decreases and at the same time nanoparticle concentration increases when the velocity slip parameter rises. The effects of flow constant on nanoparticle temperature and concentration profiles are shown in Figure 4. It is noticed that presence of a flow constant increases the nanoparticle temperature and also enhances uniformly in the boundaries of the channel. However, the nanoparticle concentration shows the revised behavior in nature of temperature distribution. From Figure 5, which elucidates the effect of the non-uniform parameter on the nanoparticle temperature and concentration profiles, it is exposed that when the non-uniform parameter increases, the nanoparticle temperature of blood flow consistently reduces with the flow medium. The nanoparticle displacement increases with increasing of the non-uniform parameter. These physical changes play crucial roles in the treatment of thermotherapy. In Figure 6, the causes of Brinkman number on nanoparticle temperature and concentration are captured. It is noticed that the temperature of the fluid increases with the increase of Brinkman number. It is well known about nanofluids that when the nanoparticle temperature rises, the distance between molecules increases due to cohesive force decreases. Therefore, viscosity of nanofluids decreases when the nanoparticle temperature increases. On the flip side, absence of Brinkman number shows the maximum displacement of the particles. The effect of the Prandtl number on nanoparticle temperature and concentration are depicted in Figure 7. It is observed that with an increase in , the temperature of the fluid increases. It indicates that nanofluids can have significantly better heat transfer characteristics than the base fluids. Additionally, it is noticed that the nanoparticle concentration decreases with increasing the Prandtl number. This indicates that enhances in Prandtl number is accompanied by an enrichment of the heat transfer rate at the tapered wavy wall of the blood vessel. The fundamental physics behind this can be depicted as follows. When the blood achieves a higher Prandtl number, its thermal conductivity is dropped down and so its heat conduction capacity is reduced. Simultaneously, the heat transfer rate at the vessel wall is enhanced. We noticed from Figure 8 that the temperature enhances with rise of heat transfer Biot number at the upper portion of the channel, but the influence is reversed at the lower portion of the channel. Further, it can be noted that the temperature at the upper wall is maximum and it reduces slowly towards the lower wall. The small value of heat transfer Biot number shows the conduction nature, while high values of heat transfer Biot number indicates that the convection is the main heat transfer mechanism. Any rate of nanoparticle concentration reduces with increase of the heat transfer Biot number. Figure 9 reveals that the nanoparticle temperature and concentration enhance as mass transfer Biot number increases. Figure 10 illuminates the influence of the thermal radiation on nanoparticle temperature and concentration distribution. This figure highlights that thermal radiation enhances during blood flow in the channel, thereby the nanoparticle temperature of the tapered asymmetric wavy channel is reduced by increase of thermal radiation. Additionally, the converse situation occurred in the nanoparticle concentration profile. It shows that the external radiation dilutes the temperature, and at the same time movement of the particle increases. This concept may be very useful in the treatment of heart transfer mechanism. Figure 11 illuminates a very significant influence of the thermophoresis parameter on the nanoparticle temperature and concentration profiles. It is well known that the strength of thermophoresis rises due to temperature gradient enhancement, which increases the blood flow in the channel. At the same time, the nanoparticle concentration of the particle displacement reduces with increases of the thermophoresis parameter.
6.2. Nanoparticle Heat Transfer Coefficient
The effects of various parameters on the nanoparticle heat transfer coefficient at the upper wall are represented in Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18. The nanoparticle heat transfer coefficients for a viscous nanofluid in the tapered wavy channel depends on many physical quantities related to the fluid or the geometry of the system through which the fluid is flowing. It is observed that the heat transfer coefficient is in oscillatory behavior which may be due to contraction and equation of walls. The absolute value of heat transfer coefficient increases with the increase of and while it decreases with increasing and .
6.3. Trapping
In this subsection, the streamlines for the tapered asymmetry channels are shown in Figure 19. The effects of the non-uniform parameter on trapping are presented in Figure 19a,b. One can observe that the size of the trapped bolus increases with an increase in . The effect of slip parameter L on trapping can be seen in Figure 19b,c. It is observed that by increasing the value of velocity slip parameter L, the circulation of trapped bolus increases, at the same time size of the bolus is reduced. To see the effects of permeability parameter on trapping, Figure 19c,d was illustrated. It is noted that an increase in the permeability parameter increases the size of channel, but the size of the trapped bolus decreases. The streamline patterns in the wave frame for viscous nanofluid for different values of Blood flow rate parameter are shown in Figure 19d,e. It is observed that for small values of only one trapped bolus is formed. It is also observed that the bolus near the upper and lower wavy walls increase eventually with the tapered micro channel.
6.4. Validation
The results of present mathematical model obtained by direct analytical approach were authenticated with the numerical solutions computed by MATLAB through BVP4c command. A validation was completed in Figure 20 and it is portrayed for nanoparticle temperature and concentration distribution at fixed values of pertinent parameters. Additionally, it is noticed that the analytical solution for the entire values of the tapered wavy channel width has a good correlation with the numerical solution computed by the MATLAB. The proposed mathematical formulation has very good correlation in axial velocity with Mishra and Rao [63] in the absence of and .
7. Conclusions
The analytical and numerical solutions of Equations (9)–(12) were estimated for stream function, nanoparticle temperature and concentration distribution. The expressions for nanoparticle temperature, volumetric fraction, heat transfer coefficient profile and stream function were discussed graphically. The following observations were noticed.
- Nanoparticle heat transfer between the tapered walls strongly depends on Brinkman number because the tissue presents the chief resistance to heat flow.
- Thermal radiation contains the potential to contribute a significant change in the nanoparticle temperature distribution.
- With increasing the radiation parameter, the nanoparticle temperature and heat transfer coefficient enhance.
- The nanoparticle temperature reduces with enhancing the Prandtl number, however, reverse behavior is noticed for nanoparticle concentration.
- Heat transfer coefficient depends on the flow, thermal and geometrical nature of flow regime.
- The trapping phenomenon also alters with changing the magnitude of slip and permeability parameters.
- The findings of the present models can be utilized to engineer smart peristaltic pumps which can be applicable for transporting drugs and delivery of nanoparticles.
Author Contributions
Conceptualization, D.T.; Investigation, J.P.; Methodology, A.K.T.; Visualization, R.E.; Writing—review and editing, S.M.S.
Funding
This research received no external funding.
Acknowledgments
R. Ellahi thanks Sadiq M. Sait, the Director Office of Research Chair Professors, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia, to honor him with the Chair Professor at KFUPM.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Symbol | description | Unit |
| Dimensional amplitude of the lower and upper walls | m | |
| Wave speed | m/s | |
| Nanoparticle volumetric volume fraction | Kg/m3 | |
| Nanoparticle concentration at the lower and upper walls | Kg/m3 | |
| Brownian diffusion coefficient | m/s | |
| Themophoretic diffusion coefficient | m2/s | |
| Dimensionless half width of the channel | m | |
| Heat transfer coefficient | W/m2K (or) kg/s3K | |
| Mass transfer coefficient | m/s | |
| Permeable of porous medium | H/m | |
| Permeability of the porous wavy wall | Darcy (or) m2 | |
| Thermal conductivity of wavy wall | W/mK | |
| Mass conductivity of wavy wall | W/mK | |
| Dimensional non-uniform parameter | m | |
| Dimensional pressures | Pa (or) N/m2 (or) kg/ms2 | |
| Uni-directional thermal radiative flux | kg/s3 (or) W/m2 | |
| Dimensional time | s | |
| Nanoparticle temperature | K | |
| Mean temperature | K | |
| Temperature at the lower and upper walls | K | |
| Velocity components in the wave frame | m/s | |
| Rectangular coordinates | m | |
| Density of the fluid | Kg/m3 | |
| Density of the particle | Kg/m3 | |
| Dynamic Viscosity | kg/m.s | |
| Thermal conductivity of the fluid | m2/s | |
| Wave length | m |
Dimensionless parameters:
| Slip coefficient at the surface of the porous walls | |
| Blood flow constant | |
| Dimensionless amplitude of the lower and upper walls | |
| Heat transfer Biot number | |
| Mass transfer Biot number | |
| Brinkman number | |
| Eckert number | |
| Dimensionless flow rate | |
| Lower and upper wall boundaries of the micro- asymmetric channel | |
| Dimensionless lower and upper wall shapes in wave frame | |
| Slip parameter | |
| Dimensionless non-uniform parameter | |
| Thermophoresis parameter | |
| Brownian motion parameter | |
| Dimensionless pressure | |
| Prandtl number | |
| R | Reynolds number |
| Thermal radiation | |
| Schmidt number | |
| Dimensionless time | |
| Velocity components in the wave frame | |
| Constant flow rate | |
| Dimensionless rescaled nanoparticle volume fraction | |
| Dimensionless nanoparticle temperature | |
| Stream function | |
| Phase difference | |
| Permeability parameter | |
| Wave number |
Appendix A
The following constants are utilized in the solution of the manuscript.
References
- Burns, J.C.; Parkes, T. Peristaltic motion. J. Fluid Mech. 1967, 29, 731–743. [Google Scholar] [CrossRef]
- Zien, T.F.; Ostrach, S. A long wave approximation to peristaltic motion. J. Biomech. 1970, 3, 63–75. [Google Scholar] [CrossRef]
- Raju, K.K.; Devanathan, R. Peristaltic motion of a non-Newtonian fluid. Rheol. Acta 1972, 11, 170–178. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Asadollahi, A. Peristaltic blood flow of couple stress fluid suspended with nanoparticles under the influence of chemical reaction and activation energy. Symmetry 2019, 11, 276. [Google Scholar] [CrossRef]
- Zeeshan, A.; Ijaz, N.; Abbas, T.; Ellahi, R. The sustainable characteristic of Bio-bi-phase flow of peristaltic transport of MHD Jeffery fluid in human body. Sustainability 2018, 10, 2671. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A.; Vafai, K. Modelling study on heated couple stress fluid peristaltically conveying gold nanoparticles through coaxial tubes: A remedy for gland tumors and arthritis. J. Mol. Liq. 2018, 268, 149–155. [Google Scholar] [CrossRef]
- Choi, S.U.S.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles. In Proceedings of Enhancing Thermal Conductivity of Fluids with Nanoparticles, San Francisco, CA, USA; American Society of Mechanical Engineers, FED: New York, NY, USA, 1995; Volume 231, pp. 99–105. Available online: https://www.osti.gov/biblio/196525-enhancing-thermal-conductivity-fluids-nanoparticles (accessed on 21 June 2019).
- Masuda, H.; Ebata, A.; Teramae, K.; Hishinuma, N. Alteration of thermal conductivity and viscosity of liquids by dispersing ultra-fine particles. Netsu Bussei. 1993, 7, 227–233. [Google Scholar] [CrossRef]
- Buongiorno, J.; Hu, W. Nanofluid Coolants for Advanced Nuclear Power Plants. In Proceedings of the nternational Congress on Advances in Nuclear Power Plants (ICAPP’05), Seoul, Korea, 15–19 May 2005. [Google Scholar]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2005, 128, 240–250. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S. Endoscopic effects on the peristaltic flow of a nanofluid. Commun. Theor. Phys. 2011, 56, 761–768. [Google Scholar] [CrossRef]
- Akbar, N.S. Peristaltic Sisko nanofluid in an asymmetric channel. Appl. Nanosci. 2014, 4, 663–673. [Google Scholar] [CrossRef]
- Tripathi, D.; Beg, O.A. A study on peristaltic flow of nanofluids: Application in drug delivery systems. Int. J. Heat Mass Transf. 2014, 70, 61–70. [Google Scholar] [CrossRef]
- Akbar, N.S.; Nadeem, S.; Khan, Z.H. Numerical simulation of peristaltic flow of a Carreau nanofluid in an asymmetric channel. Alexandria Eng. J. 2013, 53, 191–197. [Google Scholar] [CrossRef]
- Bég, O.A.; Tripathi, D. Mathematica simulation of peristaltic pumping with double-diffusive convection in nanofluids: A bio-nano-engineering model. Proc. Inst. Mech. Eng. Part N J Nanoeng. Nanosyst. 2012, 225, 99–114. [Google Scholar] [CrossRef]
- Akbar, N.S.; Tripathi, D.; Bég, A.O. Modeling nanoparticle geometry effects on peristaltic pumping of medical magnetohydrodynamic nanofluids with heat transfer. J. Mechan. Med. Bio. 2016, 16, 1650088. [Google Scholar] [CrossRef]
- Reddy, M.G.; Makinde, O.D. Magnetohydrodynamic peristaltic transport of Jeffrey nanofluid in an asymmetric channel. J. Mol. Liq. 2016, 223, 1242–1248. [Google Scholar] [CrossRef]
- Akbar, N.S.; Huda, A.B.; Tripathi, D. Thermally developing MHD peristaltic transport of nanofluids with velocity and thermal slip effects. Eur. Phys. J. Plus. 2016, 131, 332. [Google Scholar] [CrossRef]
- Nadeem, S.; Riaz, A.; Ellahi, R.; Akbar, N.S.; Zeeshan, A. Heat and mass transfer analysis of peristaltic flow of nanofluid in a vertical rectangular duct by using the optimized series solution and genetic algorithm. J. Comput. Theor. Nanosci. 2014, 11, 1133–1149. [Google Scholar] [CrossRef]
- Ellahi, R.; Riaz, A.; Nadeem, S. A theoretical study of Prandtl nanofluid in a rectangular duct through peristaltic transport. Appl. Nanosci. 2014, 4, 753–760. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Riaz, A.; Sheikholeslami, M. Effects of magnetohydrodynamics on peristaltic flow of Jeffrey fluid in a rectangular duct through a porous medium. J. Por. Med. 2014, 17, 143–157. [Google Scholar] [CrossRef]
- Kothandapani, M.; Prakash, J. Influence of heat source, thermal radiation and inclined magnetic field on peristaltic flow of a hyperbolic tangent nanofluid in a tapered asymmetric channel. IEEE Trans. NanoBiosci. 2015, 14, 385–392. [Google Scholar] [CrossRef]
- Nadeem, S.; Riaz, A.; Ellahi, R.; Akbar, N.S. Effects of heat and mass transfer on peristaltic flow of a nanofluid between eccentric cylinders. Appl. Nanosci. 2014, 4, 393–404. [Google Scholar] [CrossRef]
- Prakash, J.; Sharma, A.; Tripathi, D. Thermal radiation effects on electroosmosis modulated peristaltic transport of ionic nanoliquids in biomicrofluidics channel. J. Mol. Liq. 2018, 249, 843–855. [Google Scholar] [CrossRef]
- Tripathi, D.; Shashi, B.; Bég, O.A.; Akbar, N.S. Transient peristaltic diffusion of nanofluids: A model of micropumps in medical engineering. J. Hydrodyn. 2018, 30, 1001–1011. [Google Scholar] [CrossRef]
- Tripathi, D.; Sharma, A.; Bég, O.A. Joule heating and buoyancy effects in electro-osmotic peristaltic transport of aqueous nanofluids through a microchannel with complex wave propagation. Adv. Powder Technol. 2018, 29, 639–653. [Google Scholar] [CrossRef]
- Prakash, J.; Siva, E.P.; Tripathi, D.; Kuharat, S.; Bég, O.A. Peristaltic pumping of magnetic nanofluids with thermal radiation and temperature-dependent viscosity effects: Modelling a solar magneto-biomimetic nanopump. Renew. Energ. 2019, 133, 1308–1326. [Google Scholar] [CrossRef]
- Prakash, J.; Tripathi, D. Electroosmotic flow of Williamson ionic nanoliquids in a tapered microfluidic channel in presence of thermal radiation and peristalsis. J. Mol. Liq. 2018, 256, 352–371. [Google Scholar] [CrossRef]
- Prakash, J.; Jhorar, R.; Tripathi, D.; Azese, M.N. Electroosmotic flow of pseudoplastic nanoliquids via peristaltic pumping. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 61. [Google Scholar] [CrossRef]
- Mosayebidorcheh, S.; Hatami, M. Analytical investigation of peristaltic nanofluid flow and heat transfer in an asymmetric wavy wall channel (Part I: Straight channel). Int. J. Heat Mass Transf. 2018, 126, 790–799. [Google Scholar] [CrossRef]
- Abbasi, F.M.; Gul, M.; Shehzad, S.A. Hall effects on peristalsis of boron nitride-ethylene glycol nanofluid with temperature dependent thermal conductivity. Physica E Low Dimens. Syst Nanostruct. 2018, 99, 275–284. [Google Scholar] [CrossRef]
- Ranjit, N.K.; Shit, G.C.; Tripathi, D. Joule heating and zeta potential effects on peristaltic blood flow through porous micro vessels altered by electrohydrodynamic. Microvasc. Res. 2018, 117, 74–89. [Google Scholar] [CrossRef]
- Sadiq, M.A. MHD stagnation point flow of nanofluid on a plate with anisotropic slip. Symmetry 2019, 11, 132. [Google Scholar] [CrossRef]
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1457. [Google Scholar] [CrossRef]
- Zeeshan, A.; Shehzad, N.; Abbas, A.; Ellahi, R. Effects of radiative electro-magnetohydrodynamics diminishing internal energy of pressure-driven flow of titanium dioxide-water nanofluid due to entropy generation. Entropy 2019, 21, 236. [Google Scholar] [CrossRef]
- Hussain, F.; Ellahi, R.; Zeeshan, A. Mathematical models of electro magnetohydrodynamic multiphase flows synthesis with nanosized hafnium particles. Appl. Sci. 2018, 8, 275. [Google Scholar] [CrossRef]
- Ellahi, R.; Zeeshan, A.; Hussain, F.; Abbas, T. Study of shiny film coating on multi-fluid flows of a rotating disk suspended with nano-sized silver and gold particles: A comparative analysis. Coatings 2018, 8, 422. [Google Scholar] [CrossRef]
- Harvey, R.W.; Metge, D.W.; Kinner, N.; Mayberry, N. Physiological considerations in applying laboratory-determined buoyant densities to predictions of bacterial and protozoan transport in groundwater, Results of in-situ and laboratory tests. Enviorn. Sci. Technol. 1997, 31, 289–295. [Google Scholar] [CrossRef]
- Mishra, M.; Rao, A.R. Peristaltic transport in a channel with a porous peripheral layer: Model of a flow in gastrointestinal tract. J. Biomech. 2005, 38, 779–789. [Google Scholar] [CrossRef]
- Mekheimer, K.S. Nonlinear peristaltic transport through a porous medium in an inclined planar channel. J. Por. Med. 2003, 6, 13. [Google Scholar] [CrossRef]
- Siddiqui, A.M.; Ansari, A.R. A note on the swimming problem of a singly flagellated microorganism in a fluid flowing through a porous medium. J. Porous Med. 2005, 8, 551–556. [Google Scholar] [CrossRef]
- Wernert, V.; Schäf, O.; Ghobarkar, H.; Denoyel, R. Adsorption properties of zeolites for artificial kidney applications. Microporous Mesoporous Mat. 2005, 83, 101–113. [Google Scholar] [CrossRef]
- Jafari, A.; Zamankhan, P.; Mousavi, S.M.; Kolari, P. Numerical investigation of blood flow part II: In capillaries. Commun. Nonlinear Sci. Numeri. Simulat. 2009, 14, 1396–1402. [Google Scholar] [CrossRef]
- Goerke, A.R.; Leung, J.; Wickramasinghe, S.R. Mass and momentum transfer in blood oxygenators. Che. Eng. Sci. 2002, 57, 2035–2046. [Google Scholar] [CrossRef]
- Mneina, S.S.; Martens, G.O. Linear phase matched filter design with causal real symmetric impulse response. AEU Int. J. Electron. Commun. 2009, 63, 83–91. [Google Scholar] [CrossRef]
- Andoh, Y.H.; Lips, B. Prediction of porous walls thermal protection by effusion or transpiration cooling. An analytical approach. Appl. Thermal. Eng. 2003, 23, 1947–1958. [Google Scholar] [CrossRef]
- Runstedtler, A. On themodified Stefan–Maxwell equation for isothermal multi component gaseous diffusion. Chemical Eng. Sci. 2006, 61, 5021–5029. [Google Scholar] [CrossRef]
- Uddin, M.J.; Khan, W.A.; Ismail, A.I.M. Free convection boundary layer flow from a heated upward facing horizontal flat plate embedded in a porous medium filled by a nanofluid with convective boundary condition. Transp. Porous Med. 2012, 92, 867–881. [Google Scholar] [CrossRef]
- Chamkha, A.J.; Abbasbandy, S.; Rashad, A.M.; Vajravelu, K. Radiation effects on mixed convection over a wedge embedded in a porous medium filled with a nanofluid. Transp. Porous Med. 2011, 91, 261–279. [Google Scholar] [CrossRef]
- Kuznetsov, A.V.; Nield, D.A. Effect of local thermal non-equilibrium on the onset of convection in a porous medium layer saturated by a nanofluid. Transp. Porous Med. 2010, 83, 425–436. [Google Scholar] [CrossRef]
- Akbar, N.S. Double-diffusive natural convective peristaltic flow of a Jeffrey nanofluid in a porous channel. Heat Trans. Res. 2014, 45, 293–307. [Google Scholar] [CrossRef]
- Nadeem, S.; Riaz, A.; Ellahi, R.; Akbar, N.S. Mathematical model for the peristaltic flow of nanofluid through eccentric tubes comprising porous medium. Appl. Nanosci. 2014, 4, 733–743. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Zeeshan, A.; Ellahi, R.; Shit, G.C. Mathematical modeling of heat and mass transfer effects on MHD peristaltic propulsion of two-phase flow through a Darcy-Brinkman-Forchheimer porous medium. Adv. Powder Technol. 2018, 29, 1189–1197. [Google Scholar] [CrossRef]
- Alamri, S.Z.; Ellahi, R.; Shehzad, N.; Zeeshan, A. Convective radiative plane Poiseuille flow of nanofluid through porous medium with slip: An application of Stefan blowing. J. Mol. Liq. 2019, 273, 292–304. [Google Scholar] [CrossRef]
- Shehzad, N.; Zeeshan, A.; Ellahi, R.; Rashidid, S. Modelling study on internal energy loss due to entropy generation for non-Darcy Poiseuille flow of silver-water nanofluid: An application of purification. Entropy 2018, 20, 851. [Google Scholar] [CrossRef]
- Kothandapani, M.; Prakash, J. The peristaltic transport of Carreau nanofluids under effect of a magnetic field in a tapered asymmetric channel: Application of the cancer therapy. J. Mech. Med. Bio. 2015, 15, 1550030. [Google Scholar] [CrossRef]
- Hayat, T.; Abbasi, F.M.; Al-Yami, M.; Monaquel, S. Slip and Joule heating effects in mixed convection peristaltic transport of nanofluid with Soret and Dufour effects. J. Mol. Liq. 2014, 194, 93–99. [Google Scholar] [CrossRef]
- Kothandapani, M.; Prakash, J. Effects of thermal radiation parameter and magnetic field on the peristaltic motion of Williamson nanofluids in a tapered asymmetric channel. Int. J. Heat Mass Transf. 2015, 51, 234–245. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Ahmad, B.; Chen, B. Simultaneous effects of convective conditions and nanoparticles on peristaltic motion. J. Mol. Liq. 2014, 193, 74–82. [Google Scholar] [CrossRef]
- Makinde, O.D. Thermal stability of a reactive viscous flow through a porous-saturated channel with convective boundary conditions. Appl. Therm. Eng. 2009, 29, 1773–1777. [Google Scholar] [CrossRef]
- Parti, M. Mass transfer Biot numbers. Periodica Polytechnica Mech. Eng. 1994, 38, 109–122. [Google Scholar]
- Kikuchi, Y. Effect of leukocytes and platelets on blood flow through a parallel array of microchannels: Micro-and Macroflow relation and rheological measures of leukocytes and platelate acivities. Microvasc. Res. 1995, 50, 288–300. [Google Scholar] [CrossRef]
- Mishra, M.; Rao, A.R. Peristaltic transport of a Newtonian fluid in an asymmetric channel. Z. Angew. Math. Phys. 2003, 54, 532–550. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).