Abstract
The updated flood guidelines in Sweden have led to higher design discharges for many existing dams. While the primary function of a spillway chute is to convey floodwater, roughness appurtenances are proposed for installation along the chute. The aim is to dissipate an extra portion of the flow’s energy before release into the tailwater. One straight and three labyrinth roughness configurations are designed and manufactured. Their effectiveness is assessed through model tests. The roughness leads to an increase in water depth and induces an undulating streamwise water-surface profile. Due to their lateral interaction with the flow, the labyrinth shapes exhibit less distinct contours of surface unevenness than the straight one. With an increasing water depth, the free surface becomes gradually smeared out. For all the shapes, the roughness effect on the surface flow almost disappears if the water depth exceeds 6.5–7.0 times the roughness height. Compared to the smooth chute, the straight elements augment the energy loss by a factor of 1.9–3.8; the labyrinth configurations outperform the straight ones by 16–35% more energy dissipation. The differences among the triangular, trapezoidal, and rectangular shapes are, however, minor. Introducing chute roughness is a complementary measure. If the chute is sufficiently long, an adequate number of roughness rows could replace the function of a stilling basin.
1. Introduction
The incorporation of roughness elements in waterways is an effective approach to modifying flow patterns and enhancing energy dissipation. One of their most common applications is in hydraulic jumps, where they help achieve comparable or improved performance within a shorter basin length [,,], a practice dating back to the 1950s []. Hassanpour et al. [] investigated lozenge-shaped roughness elements in a stilling basin with lateral expansion and found that this configuration reduces the required tailwater depth for hydraulic jump formation. Another widely studied roughness form is bed corrugation, tested in various configurations [,]. Model studies by Izadjoo and Shafai-Bejestan [] demonstrated that compared with a smooth bed, trapezoidal corrugations decrease the conjugate tailwater depth by about 20% and the jump length by 50%. Similarly, Abbaspour et al. [] examined sinusoidal corrugations with different steepness ratios, showing that the bed shear stress is approximately ten times higher than on a smooth surface, leading to greater energy dissipation. In numerical simulations by Ghaderi et al. [], three roughness geometries—triangular, square, and semi-oval—were analyzed, indicating that roughness elements reduce the relative maximum velocity in submerged hydraulic jumps, with the triangular shape being the most effective in shortening jump length. Evcimen [,] further investigated prismatically shaped roughness elements, extending the understanding of their hydraulic behavior.
In the construction of low-head dams, gabions are often employed to form stepped chutes that promote effective energy dissipation [,,,]. With the advancement of roller-compacted concrete (RCC) technology, stepped spillways have become a common type of flood-release structure in large dams. To reduce unit discharge, the chute width can be substantially increased—sometimes extending nearly the entire dam length. The steps act as distinct roughness elements that modify pressure distributions, enhance air entrainment, and improve energy dissipation while reducing cavitation risk. The effects of baffles and sills on stepped chutes have been widely examined [,,,], showing that baffle-edged chutes dissipate more energy than sill-edged ones, and that shifting baffles or sills away from sharp edges leads to reduced energy dissipation. Moreover, parameters such as step chamfering, cavity blockage, step-face inclination, and step planform significantly influence flow patterns and turbulence structures, thereby affecting energy dissipation efficiency [,,,,,,,]. The stepped concept has also been adapted for embankment dams with mild downstream slopes [,,]. Depending on the unit flow and water head, cellular concrete blocks are sometimes employed. Precast wedge-shaped blocks provide step-overlay protection, combining efficient energy dissipation with high stability under high-velocity flow conditions.
Each of these topics has been the focus of extensive research, and the related literature is virtually innumerable. The introduction of a roughened bed can eliminate the need for a costly stilling basin or significantly reduce its length, resulting in a more efficient and streamlined design. More generally, a stepped spillway can be regarded as a form of baffled chute, although the geometry of its steps may vary. One of the most widely adopted designs is the Bureau of Reclamation type IX chute spillway, which incorporates impact baffle blocks []. The Maple River spillway, for instance, includes twelve rows of baffle blocks, while similar configurations are found in numerous low-head dams across the United States []. In contrast, the Yeoman Hey spillway in the United Kingdom features staggered rows of block baffles extending along the entire chute (Figure 1a). Each row comprises five or six baffles, contributing to substantial energy dissipation [].

Figure 1.
Examples of roughened spillway chutes: (a) Yeoman Hey spillway, looking downstream (© Paul Anderson); (b) Siah-Bishel stepped spillway chute on bedrock (Courtesy Anton J. Schleiss).
Robles et al. [] investigated the use of staggered rows of vertical pipes in a diverging chute spillway to dissipate energy and reduce flow velocities to acceptable levels. These vertical risers additionally serve to supply air to offset aerators. In experiments conducted by Nugroho et al. [], multiple rows of cubical blocks were installed on a 45° overflow apron immediately downstream of the spillway threshold. The blocks were evenly spaced along the chute, with variations in both lateral and streamwise spacing. Their results indicate that optimal energy dissipation occurs when the flow depth equals the block height, and that the presence of a baffled chute leads to a shorter hydraulic jump length. For stilling basins preceded by a roughened chute, Stojnic et al. [] examined the influence of steps on the flow, revealing that due to reductions in terminal energy, the design principles for such basins differ significantly from those applied to smooth chutes (Figure 1b).
The chute is a critical component of a spillway and can be constructed directly on high-quality bedrock. In such cases, the natural roughness of the rock affects floodwater flow and may reduce the required size of an energy dissipator, if one is present [,,]. However, the deliberate incorporation of artificial roughness—whether on bedrock or on a concrete-lined chute bed—is less common than its use in energy dissipators.
In Sweden, updated flood criteria require many existing spillways to accommodate design discharges higher than those for which they were originally constructed. Statistics show that revised design floods are typically 20–50% greater than previous values []. Managing this additional flow energy poses a significant challenge. Expanding an energy dissipator is often costly, and construction difficulties further limit modifications in existing structures.
Many Swedish spillways feature long chutes whose primary function is to simply convey water. Their slopes are usually gentle, below 3.5–7%. Introducing roughness along the chute bed could help dissipate a portion of the energy before the water re-enters the river, providing a potential alternative to enlarging energy dissipators. However, studies of roughened chutes remain limited, an observation echoed by Tullis and Bradshaw []. With the successful application of straight roughness beams in a Swedish spillway [], to explore more effective roughness shapes is the motivation of this study. Several configurations—both straight and cranked—have been designed as roughness appurtenances for chute energy dissipation. Laboratory experiments were conducted to evaluate the performance of these configurations. The effect of the roughened chutes on energy losses was assessed in comparison with a smooth chute. Additionally, head losses along the chute were compared with those of the preceding energy dissipator. This study aims to provide guidance for the design of roughened chutes in low-head spillways.
2. Configuration of Roughness Elements
As part of a spillway upgrade, eight rows of roughness elements were installed in the existing chute to promote more uniform flow distribution across the cross-section and enhance energy dissipation []. The spillway comprises seven gated openings, with a chute ~63 m long and a 3.8% slope. The roughness elements are straight concrete beams, each 0.5 m wide and 0.4 m high. Figure 2 illustrates the baffled chute and the flow pattern during a low flood. With the inclusion of these elements, the terminal energy at the new design flood—~40% higher than the previous one—remains at a comparable level. With certain simplifications, the model in this study is partially derived from this prototype spillway. Froude similarity is used, and the model scale is approximately 1:18.

Figure 2.
Chute spillway after upgrade: (a) straight roughness ribs on the chute bottom (© Eniro); (b) chute flow pattern at low discharges [].
Referring to this installation with straight ribs, three labyrinth roughness configurations were developed (Figure 3). The design follows these principles:
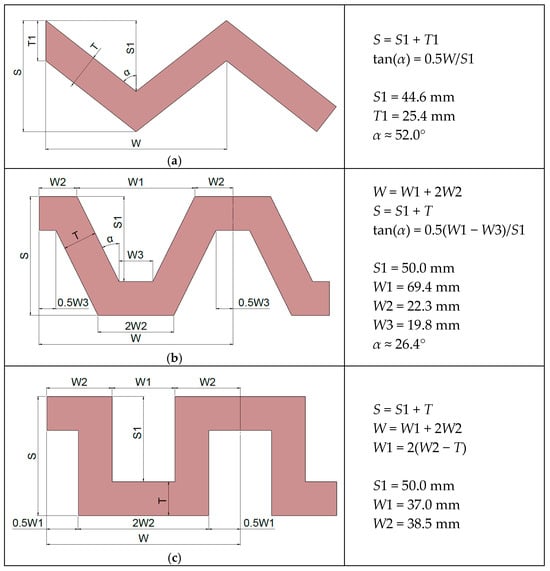
Figure 3.
Geometrical definitions of roughness elements in cranked forms: (a) triangle; (b) trapezoid; and (c) rectangle. The width W refers to one roughness unit in a row.
- ○
- Each configuration has a rectangular cross-section with width T = 20 mm and height D = 21 mm, corresponding to the dimensions of the available wood product.
- ○
- Regardless of the roughness type, each unit is symmetrical along its streamwise axis and maintains consistent dimensions in both streamwise (S) and spanwise (W) directions. The adopted unit size is S = 70 mm and W = 114 mm, with the spanwise dimension chosen to fit ten units across the chute width.
- ○
- The triangular units with an angle of α ≈ 52.0°.
- ○
- The trapezoidal units with an angle of α ≈ 26.4°. The edge facing up- and downstream is 2.0 × W2 = 44.6 mm.
- ○
- The rectangular units. Their edge facing up- and downstream is 2.0 × W2 = 77.0 mm.
The chosen wood is aspen, relatively dense to resist water. To ensure uniformity and high quality, all elements were manufactured using a waterjet cutting machine (Figure 4). Quality control measurements confirmed that geometric deviations for each unit remained below 0.3–0.5 mm.

Figure 4.
The roughness elements were precisely fabricated using waterjet cutting: (a) waterjet cutting machine; (b) a row of triangular, trapezoidal, and rectangular elements made of aspen.
3. Experimental Setup
Figure 5 and Figure 6 show the layout of the experimental rig. The spillway model, with a width of B = 114 cm, is placed at the lower end of the flume, measuring 11.0 m long, 2.0 m wide, and 2.0 m high. The overflow crest length is L = B = 114 cm. Water is supplied to the model through a Ø250 mm inlet pipe. A flow barrier is installed near the downstream end of the inlet to suppress turbulence. In the middle of the flume, a straight channel with a streamlined entrance, matching the crest width, is also provided.
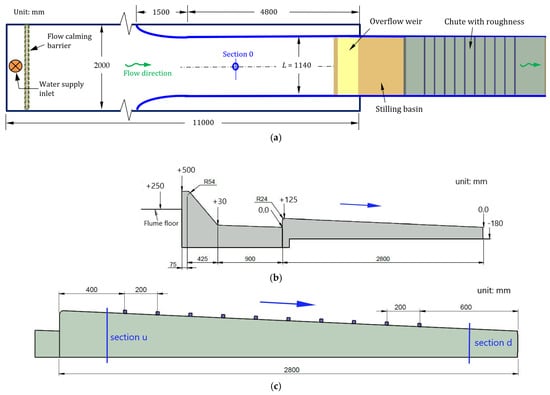
Figure 5.
Experimental setup: (a) layout of the spillway model, plan view; (b) longitudinal profile of the model from the overflow crest to the chute exit; (c) longitudinal profile of the chute with roughness elements. The downstream end of the chute serves as reference point, with its elevation set at 0.0. The units are in mm.

Figure 6.
Spillway model: (a) view from upstream and above; (b) tests with the straight elements (H = 18.6 cm). The overflow crest has the same size as the chute (114 cm).
The model is constructed from water-resistant plywood with a fairly smooth surface (with micro-evenness) and has a total length of 420 cm, including a 280 cm chute section. Its dark surface is coated with light gray paint to enhance visibility for photography and observation. The chute’s downstream end is set at elevation +0.0 cm, while the spillway crest is at +50 cm. The flume bed is positioned H0 = 25.0 cm below the crest, featuring a 90° upper corner and a 5.4 cm radius at the lower corner. A 90.0 cm long stilling basin precedes the chute. With its upper end at +12.5 cm, the chute itself has a 4.5% slope. In this study, the use of this gentle slope is mainly based on the Swedish conditions. Steeper chutes are not discussed. Figure 7 shows the chute layout with each of the configurations.

Figure 7.
Layout of roughness elements in the chute (10 rows): (a) straight ribs; (b) triangular; (c) trapezoidal; and (d) rectangular. The arrow indicates the flow direction.
For each roughness type, ten rows of roughness elements were installed along the chute, with the first row positioned 40.0 cm from the upper end and the last row 60.0 cm from the lower end (measured at the row centerlines). Each row consists of 10 units (width 10 × W) for the cranked shapes, covering the entire chute width. The centerline spacing between consecutive rows is 20.0 cm (10 × T). The elements were painted in different colors to aid identification.
In the inlet pipe of the rig, a calibrated magnetic flow meter measures the flow rate (accuracy better than 0.2%). The water level measured 3.0 m upstream of the crest, labeled as section 0 (Figure 5a), is used to calculate the water head (H) and specific energy (E0). At this section, the flume bed elevation is Z0 = 0.25 m. Point gauges are employed for estimating cross-sectionally averaged water depths (h) within the chute. A standard laboratory setup is used, featuring a plastic tube from a measurement point on the floor leading to a panel with an 8 cm measurement tube, in which a point gauge is placed, with an accuracy of better than 0.2 mm. Along the chute, two key sections are defined: an upstream section (u), located 29 cm from its upper end, and a downstream section (d), located 29 cm from its lower end (see Figure 5c). Water depths at these sections are labeled as hu (upstream) and hd (downstream), calculated as the average of measurement results taken at 12 points across the chute. At each point of either cross-section, repeated measurements are made to minimize errors, and its water depth represents a time-averaged value. Key flow parameters include flow rate, flume water level, and flow velocity and depth within the chute. Flow patterns are documented using photographs and video recordings. Because the chute contains ten discrete rows of macro-roughness elements, the flow along the 2.8 m chute does not reach a classical fully developed state in which velocity and shear-stress distributions become invariant in the streamwise direction.
4. Results and Discussions
Owing to the accurate construction of the model, the flow remains uniform across the cross-section from upstream to downstream. Energy losses in a smooth chute are examined first, followed by those in the straight and cranked types. For each chute type, several flow rates are tested, namely, H ≈ 7.5, 10.0, 12.5, 15.0, and 18.6 cm. Preceded by the basic flow features, observations and analyses are presented below.
4.1. Basic Flow Parameters
Froude and Reynolds numbers are defined as F = and R = , where V = cross-sectional average of flow velocity, Rh = hydraulic radius, g = gravitational acceleration, ρ = density of water, and μ = dynamic viscosity of water. Within the examined flow range, their values in the upstream flume are F = 0.03–0.07 and R = (1.9–6.9) × 104.
The free-surface flow (Q) over an overflow weir is expressed as
where C = discharge coefficient. Figure 8 plots its H-Q relationship. Within the examined H range, Q = 35–140 L/s, and C = 1.47–1.55.
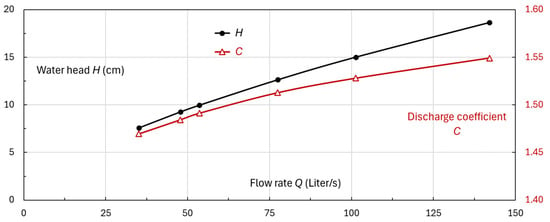
Figure 8.
The H-Q relationship of the weir in the rig.
For the smooth chute, the streamwise variations of water depth h at the locations where roughness elements are to be installed are shown in Figure 9. In the absence of roughness, the chute’s water surface is relatively smooth and undisturbed, exhibiting only minor perturbations even at high water heads (e.g., H = 15.0 and 18.6 cm). Within the examined H interval, the average flow velocity (V) is Vu = 1.0–1.4 m/s at section u and Vd = 1.5–2.1 m/s at section d. The corresponding R range is 3.0 × 104–1.1 × 105. If R > 105, then the viscous effect is negligible []. Obviously, the results are somewhat affected by the viscous force.
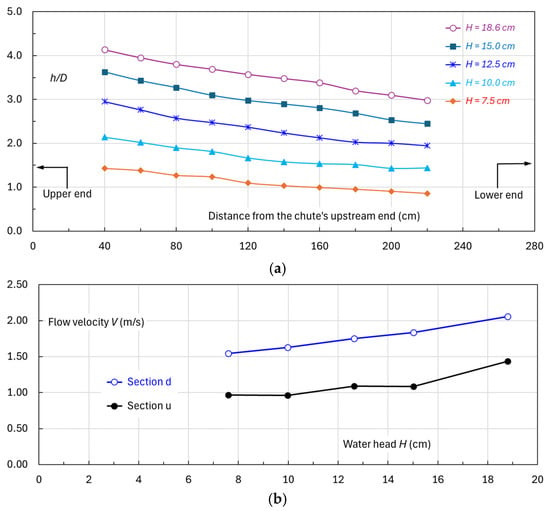
Figure 9.
Flow parameters of the smooth chute: (a) along-chute water depth h; (b) flow velocity V at cross-sections u and d.
4.2. Flow Patterns with Roughness Elements
The roughness protrusions significantly alter the local flow structure, with the magnitude of these changes depending on the flow rate. To quantify their effects, water depths at the roughness elements are compared with those in a smooth chute. Figure 10 shows the water depth h at the 1st and 10th rows for the triangular elements, while Figure 11 presents the streamwise h-profiles for the trapezoidal shapes. Due to surface fluctuations, the profiles represent averaged measurements. The other cranked elements exhibit similar h variations. The plots do not mirror the slightly smaller water depths between adjacent rows. These results can be compared with those in Figure 9. Clearly, the presence of roughness, regardless of shape, leads to a substantial increase in water depth.
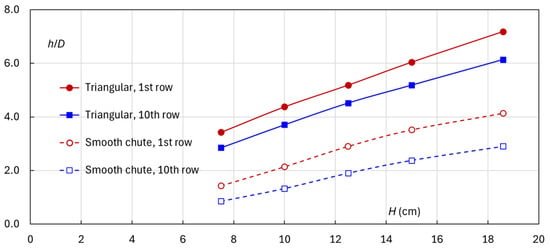
Figure 10.
Chute roughened by the triangular elements—averaged water depths at the 1st and 10th rows as compared to the smooth chute flows (measured at the roughness centerlines).
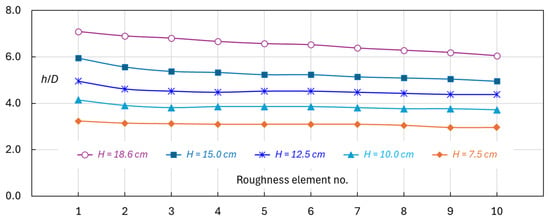
Figure 11.
Chute roughened by the trapezoidal elements—along-chute water depths at each row (measured at the element centerlines).
All the labyrinth elements exhibit similar results of water depth. With a 4.5% chute slope, the flow accelerates and the water depth decreases progressively downstream. The roughness clearly leads to a substantial increase in water depth—by a factor of 2.5 to 3.0 at low flows (H ≤ 12.5 m) and 1.7 to 2.1 at high flows (H > 12.5 m). Unlike flows in the smooth chute, the streamwise water surface exhibits noticeable fluctuations, typically varying within 0.5–1.0 cm along the row centerline, depending on flow rate and roughness type. Figure 12 and Figure 13 show the flow patterns at H ≈ 7.5 and 15.0 cm, respectively.

Figure 12.
Chute flow patterns at H ≈ 7.5 cm: (a) straight; (b) triangular; (c) trapezoidal; and (d) rectangular.

Figure 13.
Chute flow patterns at H ≈ 15.0 cm: (a) straight; (b) triangular; (c) trapezoidal; and (d) rectangular.
For the straight layout, the free-surface perturbations in the streamwise direction are readily noticeable at low water heads (e.g., H < 10.0–12.5 cm). Across each row, a solitary ripple with a distinct crest and steep flanks appears. The flow is essentially two-dimensional, with negligible lateral variation. As the flow rate or chute water depth increases, these solitary ripples gradually become smeared.
All three labyrinth (cranked) configurations exhibit similar behavior, with little distinction between them. At low flow rates (e.g., H < 10.0 cm), a solitary hump forms across each element row. Each hump features a somewhat diffused crest with a leading and trailing edge, most pronounced for the rectangular shape. Owing to the streamwise element dimension (S) being larger than that of the straight type, the crest is observed to be flatter and longer in the flow direction. The cranked shapes also promote lateral flow diffusion in the cross-section. At higher flow rates, the humps blur, and water-surface fluctuations become less pronounced.
The roughness elements are oriented vertically and have a rectangular crest in cross-section. At low heads, the flow over these elements resembles that over a labyrinth weir or spillway, differing mainly in scale []. Each unit within a row exhibits overflow characterized by an interference region—where nappes collide—and submergence. Within the examined flow range, the water surfaces over both straight and cranked shapes are never as smooth as in the smooth chute. However, when the chute water depth satisfies h/D > 6.5–7.0, the influence of the elements on the surface flow becomes negligible.
4.3. Energy Losses
When a bluff protuberance is introduced in the chute, it disrupts the smooth flow, generating flow separation, recirculation zones, and a pressure drop. This disturbance alters the flow structures and enhances turbulent mixing. As a result, additional head losses occur due to increased friction and flow resistance. At the 0, u, and d sections, the specific energies—denoted as E0, Eu, and Ed—are used as proxies to quantify energy losses within the waterway. The definitions of these variables are listed in Table 1.

Table 1.
Definition of specific energy at three measurement cross-sections.
Figure 14 illustrates the difference in specific energy, E0 − Eu, between sections 0 and u, representing the total energy loss from the reservoir to the start of the chute. The stilling basin accounts for the majority of this loss. This energy difference increases slightly with increasing head H. For a given flow rate, Eu remains essentially constant, as confirmed by measurements at 12 positions across the chute in repeated tests. The energy loss along this portion of the waterway is independent of the roughened chute. However, small measurement errors lead to some discrepancy in the results.
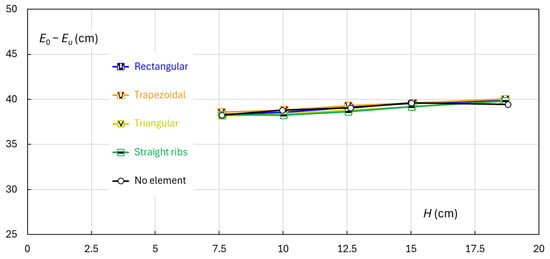
Figure 14.
Change of E0 − Eu as a function of H.
The energy loss caused by the roughened chute itself is Eu − Ed, and the energy dissipation efficiency is defined as
Figure 15 compares the variations of Eu − Ed with H and χ with H/H0. In the smooth chute, head loss is dominated by the surface friction of the plywood, which serves as a reference for evaluating the roughness appurtenances. For each roughness configuration, energy loss gradually decreases with increasing water head. This indicates that at shallow flow depths, the roughness intrusions affect the entire flow depth, resulting in high dissipation efficiency.
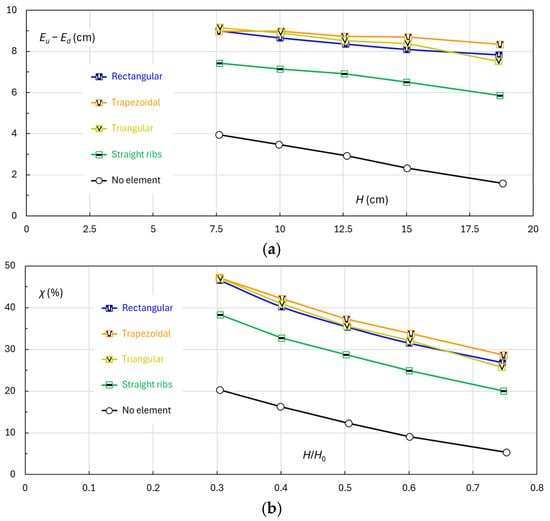
Figure 15.
Energy losses along the chute due to the straight and cranked roughness configurations: (a) change of Eu − Ed with H; (b) change of χ with H/H0.
Compared to the smooth chute, the straight ribs exhibit significantly higher energy dissipation efficiency. Although the energy loss decreases with increasing H, the difference relative to the smooth chute becomes more pronounced. For instance, the dissipation efficiency differs by a factor of 38.3%/20.2% = 1.9 at H/H0 = 0.30 and of 20.0%/5.3% = 3.8 at H/H0 = 0.75.
Relative to the straight elements, all labyrinth (cranked) shapes demonstrate even more effective energy dissipation. The trapezoidal shape yields slightly higher efficiency than the other two, although differences among the three cranked types are minor. On average, their efficiency enhancement ranges from 16% to 35% across the examined flow range.
4.4. Discussion
This study is conducted using fixed element sizes and row spacings. The element dimensions, T = 20 mm and D = 21 mm, correspond to an approximate prototype size of 0.4–0.5 m. The row spacing (10 × T = 20.0 cm) is based on, and scaled from, the prototype chute [], with slight modification. This spacing determines how each roughness row interacts with the flow from its upstream row, which in turn influences the energy dissipation between rows. For a given flow, it may be possible to identify an “optimum” spacing that maximizes dissipation efficiency; however, achieving this across a range of flows is unlikely. No tests were conducted in this regard. The highest head tested is H = 18.6 cm, and beyond roughly H = 20.0 cm, sweeping-out of the stilling basin would occur.
The performance of the labyrinth elements can be further evaluated from two perspectives. The first concerns the energy dissipated along the chute compared with that dissipated in the stilling basin. The second relates to the influence of the staggered arrangement of the elements.
Normalized by E0, the following parameters are defined:
For the three cranked configurations, Figure 16 plots the variations of η1 and η2 with H/H0. The η1 curve primarily represents the energy dissipated in the stilling basin. The results highlight the contrast between the dissipation efficiencies of the basin and the roughened chute. The stilling basin usually serves as the major source of energy dissipation, while the chute plays a complementary role. However, if the chute is sufficiently long and more roughness elements are installed, the energy dissipated along the chute can become comparable to that of the stilling basin. Considering the ten cranked elements (of any given type) as one group and repeating this group downstream, the additional group dissipates even more energy than the first one, as the water depth gradually decreases and the flow velocity increases along the chute. Assuming that each added group dissipates the same amount of energy as the first, achieving the same overall energy dissipation as the stilling basin would require four to five groups depending on water head. In other words, in the absence of a stilling basin, a sufficient number of roughness rows could produce an equivalent dissipation effect.
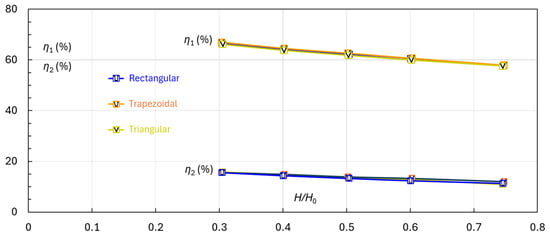
Figure 16.
The stilling basin versus the three cranked elements—energy dissipation rates η1 and η2. Since the differences in energy dissipation among the cranked elements are small, the data for both η1 and η2 tend to collapse onto a single curve.
In the preceding tests, the labyrinth elements of each type are arranged so that all rows are identical, without any lateral offset. Traditionally, isolated blocks or piers in a baffled apron (so-called impact dissipator) are arranged in a staggered configuration to enhance flow performance [,,]. Accordingly, supplementary tests are carried out to examine the influence of a staggered arrangement of the rectangular elements, in which all even rows are shifted by half the element width (0.5 × W) relative to the odd rows (Figure 17a). The corresponding flow pattern at H = 7.5 cm is shown in Figure 17b.

Figure 17.
Energy dissipation of staggered formation: (a) staggered rectangular elements; (b) flow pattern at H = 7.5 cm. The numbers on the wall refer to row numbering from up- to downstream.
Without any lateral offset, the streamwise spacing between the crests of adjacent rows remains constant, and the flow pattern is identical in cross-section over each row. The tests indicate that introducing a 0.5 × W offset modifies the flow pattern. As shown in Figure 17b, the water surface along the right sidewall exhibits streamwise undulations, with a local dip (or depression) between two neighboring rows. However, the dip from odd to even rows (e.g., from row 1 to 2) extends farther than that from even to odd rows (e.g., from row 2 to 3). This streamwise pattern is repeated at each element unit in cross-section and is readily visible under low-flow conditions. As the discharge increases, the surface undulations gradually smooth out.
The corresponding χ-values are presented in Figure 18. Despite the modification in flow structure, the staggered arrangement results in negligible changes in energy loss, even at low flow rates.
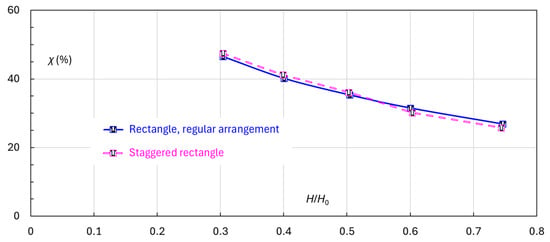
Figure 18.
Energy dissipation of the rectangular elements—staggered formation relative to the regular arrangement.
5. Conclusions and Comments
Introducing roughness appurtenances in a chute is an effective method to reduce the terminal energy at its end and mitigate the erosion potential in the tailwater. This study is based on a prototype spillway with eight straight beams, which have functioned satisfactorily since installation. To enhance energy dissipation, one straight and three labyrinth (cranked) configurations—triangular, trapezoidal, and rectangular—were designed and manufactured with precision. The experiments aim to compare the efficiency of these roughness layouts at varying flow rates. The following conclusions can be drawn.
Compared to the chute without elements, the presence of roughness elements leads to a substantial increase in water depth, by a factor of 1.7–3.0 depending on the water head. At low flows, the flow over the periodic bed roughness of any type generates strong streamwise water-surface waviness. As the flow rate increases, these surface fluctuations gradually smooth out. When the chute water depth reaches 6.5–7.0 times the roughness height, the influence of the elements on the surface water nearly disappears, and the water surface becomes relatively smooth. This behavior is observed for both straight and cranked elements.
Compared to the smooth chute, the straight ribs profoundly augment energy dissipation efficiency, by a factor of 1.9–3.8 depending on water head. Within the examined flow range, the labyrinth configurations dissipate 16–35% more energy than the straight beams. However, the differences among the triangular, trapezoidal, and rectangular shapes are small. A staggered formation does not heighten the energy dissipation either. Introducing roughness on the chute is considered a complementary measure. However, if the chute is sufficiently long, an adequate number of roughness rows could replace the function of a stilling basin.
Roughness elements contribute to enhanced air entrainment in the flow. In a prototype, turbulence intensity is considerably higher than in the corresponding model, resulting in stronger air entrainment and higher actual energy dissipation efficiency. Roughness elements can also compensate for asymmetrical spillway or discharge conditions by redistributing the flow across the chute.
The use of roughness elements is recommended for spillway chutes with gentle slopes, typically less than 5–6%, and a water head preferably below 12–15 m. Higher heads may be acceptable if an energy dissipator is installed upstream of the chute. Compared to a smooth chute, a roughened chute produces a greater flow depth, requiring higher sidewalls. In prototype applications, the width and height of individual roughness elements generally range from 0.4 to 0.5 m, with row spacing approximately ten times the element width.
This study is limited to gentle chute slopes. Their use in steeper chutes might be practicable, as long as resulting splash and spray are contained or the discharge safety is ensured. Any proposed design should be validated through hydraulic model studies, considering factors such as chute slope, roughness dimensions, water-head range, sidewall height, and other relevant parameters. Drainage holes or slots should be incorporated to facilitate dewatering and prevent ice formation during winter.
Author Contributions
Concept, funding acquisition, model design, resource, experiments, formal analysis, manuscript, and revision, J.Y. Participation in experiments, quality control, check of results, manuscript review, and revision, S.L. and U.F. Rig operation, experiments with measurements, and manuscript review, A.H. All authors have read and agreed to the published version of the manuscript.
Funding
As part of research project “Engineering measures for energy dissipation improvements in existing spillway chutes” (contract no. VKU32030), the study is funded by the Swedish Centre for Sustainable Hydropower (SVC). As industry in-kind, Vattenfall R&D covers costs for the test facility and model construction. The SVC has been established by the Swedish Energy Agency, Energiforsk, and Svenska Kraftnät together with the Royal Institute of Technology, Luleå University of Technology, Chalmers University of Technology, and Uppsala University. Participating companies and industry associations are AFRY, Andritz Hydro, Boliden, Fortum Generation, Holmen Energi, Jämtkraft, Karlstads Energi, LKAB, Mälarenergi, Norconsult, Rainpower, Skellefteå Kraft, Sollefteåforsens, Statkraft Sverige, Sweco Energuide, Sweco Infrastructure, Tekniska verken i Linköping, Uniper, Vattenfall R&D, Vattenfall Vattenkraft, Voith Hydro, WSP Sverige, and Zinkgruvan.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Acknowledgments
The tests were conducted at Vattenfall’s Hydraulic Laboratory in Älvkarleby. James Yang expresses his gratitude to Anders Sjödin for resource coordination, to Erik Skepparkrans for CAD work and construction supervision, to John Eriksson and Meho Delic for model construction, to Magnus Lagerkvist and Dennis Ek for waterjet cutting, and to Patrik Lidberg and Mikael Östlund for instrumentation. The project administration by Carolina Homberg of the Swedish Centre for Sustainable Hydropower (SVC) and Anders Ansell of KTH Royal Institute of Technology is also acknowledged.
Conflicts of Interest
Authors James Yang and Anna Helgesson are employed by the company Vattenfall AB. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest. This study receives funding from the Swedish Centre for Sustainable Hydropower (SVC). The funder is not involved in the design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.
Notation
The following symbols are used in this paper:
| B | Chute width (1140 mm) |
| C | Discharge coefficient of overflow weir |
| D | Cross-sectional height of roughness elements (21 mm) |
| E0, Eu, Ed | Specific energy at three designated cross-sections |
| F | Froude number |
| g | Gravitational acceleration |
| H | Water head of overflow crest |
| h, hu, hd | Cross-sectionally averaged water depth |
| L | Weir crest length (1140 mm) |
| Q | Flow rate in the rig |
| R | Reynolds number |
| Rh | Hydraulic radius |
| S, S1, S2 | Element size in the along-chute direction |
| T | Cross-sectional width of roughness elements (20 mm) |
| T1 | Element size in the along-chute direction |
| V, V0, Vu, Vd | Cross-sectionally averaged velocity |
| W | Width of one roughness unit in a row (114 mm) |
| W1, W2, W3 | Element size in the cross-chute direction |
| Z0, Zu, Zd | Rig bed elevation at three measurement cross-sections |
| α | Element arm angle |
| χ | Chute energy dissipation rate (normalized by Eu) |
| η1, η2 | Stilling basin and chute energy dissipation rate (normalized by E0) |
| ρ | Density of water |
| μ | Dynamic viscosity of water |
| Subscripts 0, u, d | Cross-sections upstream of the crest, at the chute entrance, and at the chute exit |
References
- Chow, V.T. Open Channel Hydraulics; McGraw Hill Book Company: New York, NY, USA, 1959. [Google Scholar]
- Leutheusser, H.J.; Schiller, E.J. Hydraulic jump in a rough channel. Water Power Dam Constr. 1975, 27, 186–191. [Google Scholar]
- Hughes, W.C.; Flack, J.E. Hydraulic jump properties over a rough bed. J. Hydraul. Eng. 1984, 110, 1755–1771. [Google Scholar] [CrossRef]
- Peterka, A.J. Hydraulic Design of Stilling Basins and Energy Dissipators; Engineering Monograph 25; Bureau of Reclamation: Denver, CO, USA, 1958. [Google Scholar]
- Hassanpour, N.; Hosseinzadeh, D.A.; Farsadizadeh, D.; Gualtieri, C. An experimental study of hydraulic jump in a gradually expanding rectangular stilling basin with roughened bed. Water 2017, 9, 945. [Google Scholar] [CrossRef]
- Ead, S.A.; Rajaratnam, N. Hydraulic jumps on corrugated beds. J. Hydraul. Eng. 2002, 128, 656–663. [Google Scholar] [CrossRef]
- Akib, S.; Ahmed, A.A.; Imran, H.M.; Mahidin, M.F.; Ahmed, H.S.; Rahman, S. Properties of hydraulic jump over apparent corrugated beds. Dam Eng. 2015, 25, 65–77. [Google Scholar]
- Izadjoo, F.; Shafai-Bejestan, M. Corrugated bed hydraulic jump stilling basin. Appl. Sci. 2007, 7, 1164–1169. [Google Scholar] [CrossRef]
- Abbaspour, A.; Dalir, A.H.; Farsadizadeh, D.; Sadraddini, A.A. Effect of sinusoidal corrugated bed on hydraulic jump characteristics. J. Hydro-Environ. Res. 2009, 3, 109–117. [Google Scholar] [CrossRef]
- Ghaderi, A.; Dasineh, M.; Aristodemo, F.; Ghahramanzadeh, A. Free and submerged hydraulic jumps over different macroroughnesses. J. Hydroinformatics 2020, 22, 1554–1572. [Google Scholar] [CrossRef]
- Evcimen, T.U. Effect of Prismatic Roughness Elements on Hydraulic Jump. Master’s Thesis, Middle East Technical University, Ankara, Turkey, 2005. [Google Scholar]
- Evcimen, T.U. Effect of Prismatic Roughness on Hydraulic Jump in Trapezoidal Channels. Ph.D. Thesis, Middle East Technical University, Ankara, Turkey, 2012. [Google Scholar]
- Stephenson, D. Gabion energy dissipators. In Proceedings of the 13th International Congress on Large Dams, New Dehli, India, 29 October–2 November 1979. [Google Scholar]
- Leutheusser, H.J.; Chisholm, W.O. Baffled chute spillways for gabion-lined channels. In Proceedings of the IAHR International Symposium on River Engineering & Its Interaction with Hydrological and Hydraulic Research, Belgrade, Serbia, 26–28 May 1980. [Google Scholar]
- Peyras, L.; Royet, P.; Degoutte, G. Flow and energy dissipation over stepped gabion wiers. J. Hydraul. Eng. 1992, 118, 707–717. [Google Scholar] [CrossRef]
- Maynord, S.T. Gabion-mattress channel protection design. J. Hydraul. Eng. 1995, 121, 519–522. [Google Scholar] [CrossRef]
- Sorensen, R.M. Stepped spillway hydraulic model investigation. J. Hydraul. Eng. 1985, 111, 1461–1472. [Google Scholar] [CrossRef]
- Chanson, H. The Hydraulics of Stepped Chutes and Spillways; Balkema: Lisse, The Netherlands, 2001. [Google Scholar]
- Boes, R.M.; Hager, W.H. Hydraulic design of stepped spillways. J. Hydraul. Eng. 2003, 129, 671–679. [Google Scholar] [CrossRef]
- Zare, H.K.; Doering, J.C. Energy dissipation and flow characteristics of baffles and sills on stepped spillways. J. Hydraul. Res. 2012, 50, 192–199. [Google Scholar] [CrossRef]
- Chinnarasri, C.; Wongwises, S. Flow regimes and energy loss on chutes with upward inclined steps. Can. J. Civ. Eng. 2004, 31, 870–879. [Google Scholar] [CrossRef]
- Bai, Z.L.; Wang, Y.; Zhang, J.M. Pressure distributions of stepped spillways with different horizontal face angles. Proc. Inst. Civ. Eng.-Water Manag. 2017, 171, 299–310. [Google Scholar] [CrossRef]
- Bai, Z.L.; Zhang, J.M. Comparison of different turbulence models for numerical simulation of pressure distribution in V-shaped stepped spillway. Math. Probl. Eng. 2017, 2017, 3537026. [Google Scholar] [CrossRef]
- Li, S.C.; Zhang, J.M. Numerical investigation on the hydraulic properties of the skimming flow over pooled stepped spillway. Water 2018, 10, 1478. [Google Scholar] [CrossRef]
- Li, S.C.; Li, Q.L.; Yang, J. CFD modelling of a stepped spillway with various step layouts. Math. Probl. Eng. 2019, 2019, 6215739. [Google Scholar] [CrossRef]
- Li, S.C.; Yang, J.; Li, Q.L. Numerical modelling of air-water flows over a stepped spillway with chamfers and cavity blockages. KSCE J. Civ. Eng. 2020, 24, 99–109. [Google Scholar] [CrossRef]
- Li, S.C.; Yang, J. Effects of inclination angles on stepped chute flows. Appl. Sci. 2020, 10, 6202. [Google Scholar] [CrossRef]
- Ma, X.; Zhang, J.; Hu, Y. Analysis of energy dissipation of interval-pooled stepped spillways. Entropy 2022, 24, 85. [Google Scholar] [CrossRef]
- Felder, S.; Fromm, C.; Chanson, H. Air Entrainment and Energy Dissipation on a 8.9° Slope Stepped Spillway with Flat and Pooled Steps; Report CH86/12; University of Queensland: Brisbane, Australia, 2012. [Google Scholar]
- Felder, S. Air-Water Flow Properties on Stepped Spillways for Embankment Dams: Aeration, Energy Dissipation and Turbulence on Uniform, Non-Uniform and Pooled Stepped Chutes. Ph.D. Thesis, University of Queensland, Brisbane, Australia, 2013. [Google Scholar]
- Felder, S.; Chanson, H. Aeration, flow instabilities, and residual energy on pooled stepped spillways of embankment dams. J. Irrig. Drain. Eng. 2013, 139, 880–887. [Google Scholar] [CrossRef]
- Bureau of Reclamation. Design of Small Dams, 3rd ed.; Bureau of Reclamation: Denver, CO, USA, 1987. [Google Scholar]
- Tullis, B.P.; Bradshaw, R.D. Impact dissipators. In Energy Dissipation in Hydraulic Structures; Chanson, H., Ed.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Rennison, R.W. Civil Engineering Heritage, Northern England; Thomas Telford: London, UK, 1996. [Google Scholar]
- Robles, I.; Palacio, A.; Rodriguez, A. Analysis of the design of energy-dissipating structure in spillways. In Dam Protection Against Overtopping and Accidental Leakage; Toledo, M.Á., Morán, R., Oñate, E., Eds.; Taylor and Francis Group: London, UK, 2015. [Google Scholar]
- Nugroho, J.; Soekarno, I.; Soeharno, A.W.H. Experimental study of energy dissipation at baffled chute spillway. J. Tek. Sipil 2019, 26, 33–38. [Google Scholar] [CrossRef]
- Stojnic, I.; Pfister, M.; Matos, J.; De Cesare, G.; Schleiss, A.J. Hydraulic design of classical stilling basins downstream of stepped chutes. Int. J. Hydropower Dams 2020, 27, 46–54. [Google Scholar]
- Hager, W.H. Energy Dissipaters and Hydraulic Jump; Kluwer Academic: Dordrecht, The Netherlands, 1992. [Google Scholar]
- Yang, J.; Andreasson, P.; Teng, P.H.; Xie, Q.C. The past and present of discharge capacity modelling for spillways—A Swedish perspective. Fluids 2019, 4, 10. [Google Scholar] [CrossRef]
- Yang, J.; Andreasson, P. Rebuilding of a chute spillway for effective energy dissipation. Int. J. Hydropower Dams 2023, 30, 56–61. [Google Scholar]
- Söderström, A.; Cederborg, D.; Broström, A.; Ligier, P.-L. Methods for Hydraulic Modelling of Flows in Dry River Courses for Environmental Adaptation of Hydropower; Report 2020:702; Energiforsk AB: Stockholm, Sweden, 2020. [Google Scholar]
- Chanson, H. The Hydraulics of Open Channel Flow: An Introduction, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Crookston, B.M. Labyrinth Weirs; All Graduate Theses and Dissertations, 802; Utah State University: Logan, UT, USA, 2010. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).