Abstract
A classical approach to flood frequency modeling is based on the choice of the probability distribution to best describe the analyzed series of annual or seasonal maximum flows. In the paper, we discuss the two main problems, the uncertainty and instability of the upper quantile estimates, which serve as the design values. Ways to mitigate the above-mentioned problems are proposed and illustrated by seasonal maximum flows at the Proszówki gauging station on the Raba River. The inverse Gaussian and generalized exponential distributions, which are not commonly used for flood frequency modeling, were found to be suitable for Polish data of seasonal peak flows. At the same time, the heavy tailed distributions, which are currently recommended for extreme hydrological phenomena modeling, were found to be inappropriate. Applying the classical approach of selecting the best fitted model to the peak flows data, significant shifts in the upper quantile estimates were often observed when a new observation was added to the data series. The method of aggregation, proposed by the authors, mitigates this problem. Elimination of distributions that are poorly fitted to the data series increases the stability of the upper quantile estimates over time.
1. Introduction
The main goal of flood frequency analysis (FFA) is to assess the size of the probable flood peak flows. As the true probability distribution function (PDF), which describes the analyzed series of annual or seasonal maximum flows, is not known, the flood frequency analysis refers to a hypothetical distribution whose parameters are estimated based on the observation series. Due to many practical applications, interest has been focused on the upper quantile estimates. For example, their values are necessary when most hydraulic structures are dimensioned and when the limits of flood zones are determined. The most commonly used design value is the 1% quantile estimate and it represents the probable maximum flow that is exceeded on average once in a hundred years. The 1% quantile is equivalent to the 0.99th quantile in the notation of probability of non-exceedance.
Research on FFA has been conducted for almost a century [1,2], resulting in numerous PDFs proposed for describing the maximum flow series. According to the World Meteorological Organization (WMO) in 1989, the Gumbel and log-normal distributions were the most widely used, followed by log-Pearson 3 and Pearson 3 distributions [3]. Nowadays, heavy-tailed distributions are recommended such as the generalized extreme values distribution (GEV), generalized log-logistic (GLL), or log-Pearson 3 (LP3) [4,5,6]. However, the heavy-tailed form of hydrological variables is not sufficiently supported in Polish conditions [7,8] and soft-tailed distributions appear to be more adequate [9]. In general, the selection of the appropriate distribution function for peak discharges modeling is to some extent subjective and driven by the regional regime of the rivers or the particular country’s regulations (e.g., [4,10,11]). Therefore, one cannot point out one model that would be the best or even better than the others to be generally used for the estimation of flood quantiles.
For annual and seasonal maximum flow models, the unbounded distributions with non-negative skewness are usually used. In this paper, two-parameter distributions with the scale and shape parameters and lower bounded at zero were investigated, instead of their three-parameter equivalents, since two parameters are more reliable to estimate from short hydrological data series, which are usually available [3,12]. Note that two-parameter distributions are commonly used for academic and practical applications when dealing with short measurement series and when there is no regional information. The list of probability density functions analyzed here is presented in Table 1. The domain of the shape parameter is given, while the scale parameter and random variable

Table 1.
Probability density functions used in the paper.
The distributions of gamma (Ga), Weibull (We), log-normal (LN), log-logistic (LL), and log-Gumbel (LG) are commonly used in FFA, while the inverse Gaussian (IG) and generalized exponential (GE) distributions are not in standard practice. The inverse Gaussian has alternative names such as the Wald distribution and, in Poland, the convective diffusion distribution [13] and has revealed a good fit to the numerous annual maximum flow series for Polish lowland rivers [9]. The generalized exponential distribution developed by Gupta and Kundu [14] has been compared to gamma, Weibull, Pareto, and log-normal distributions [15,16,17], since all of them have a positive skewness. In Poland, Brzeziński presented the possibility of using GE distribution in order to describe the random properties of maximum flows [18], while Markiewicz introduced GE to flood frequency analysis of annual Polish data [19]. In the last paper, the GE distribution has been an alternative to IG distribution and has proven to be promising in modeling the annual peak flows for Polish rivers.
To select the theoretical distribution for the observed data series, the method of the moment ratio diagram (MRD) is used in many fields [20,21]. When two-parameter distributions are considered, the skewness coefficient is usually plotted against the variation coefficient both for the candidate PDFs and for the data series, and their relative locations are compared [22]. The MRD based on the L-moment ratios is superior to the conventional MRD, since the results from the L-moment MRD are more compatible with the results obtained from the goodness-of-fit statistics than in the case of conventional MRD [5,23,24].
The scope of this study refers to the seasonal maximum flows. In Poland and countries with similar hydrological regimes, two general hydrological seasons are considered: the summer season, which in Poland goes from May 1 to October 31, and the winter season from November 1 to April 30. The floods occurring in each season have different origins: rainfalls in summer and thaws in winter. However, nowadays, when global climate changes are observed, the genesis of floods in particular seasons is not as clear and other factors are becoming more important such as land cover, retention, or air circulation, which differs in summer and winter [25,26,27]. At present, very few snowmelt floods are observed [28] and we can at most say that there are floods from the mixture of rain and snowmelt. The snowmelt as a factor causing floods is of little relevance for some regions like the northern United Kingdom, western France, or northern Iberia [28,29]. The seasonal approach is beneficial in analyzing the impact of climatic change on the high water regime due to the greater vulnerability of seasonal flood generation processes on climate drivers [30,31]. The comparison of annual and seasonal approaches for modeling the peak flow series of Polish data has been investigated in theoretical and real aspects [32,33].
The seasonal maximum flows are genetically homogeneous [34,35]. If they are independent, the product model of seasonal distributions can be used [35,36]. Although the issue of the independence of seasonal peak flows can be disputed [37], for the Polish hydrological regime, the assumption of the independence of summer and winter maximum flows is reasonable [32,33,38]. Otherwise, the bivariate distributions or copula functions ought to be used [38,39].
The aim of the study was to evaluate the accuracy and stability of the estimates of seasonal maximum flows and give suggestions for their improvement. A particular purpose was the assessment of the applicability of two distributions, which has not been used for the modeling of seasonal maximum flows thus far, and these are the generalized exponential (GE) and the inverse Gaussian (IG) distributions. The second particular goal of this study was a popularization of the aggregation method, which was developed by the authors in [40], but has not been investigated within the context of flood frequency analysis as yet. Here, the influence of the number and type of competitive distributions on the aggregation of seasonal flood quantile estimates was analyzed. The novelty of this research consists of attracting the attention of researchers to the problem of changing design estimates along with the lengthening observational series. To the best our knowledge, this issue has not been addressed in theoretical studies, however, its scrutinized analysis is necessary for engineering, planning, and water-economic applications. As we are going to show here, the aggregation method provides design values that are more stable than in the case of choosing one as the best model.
2. Case Study
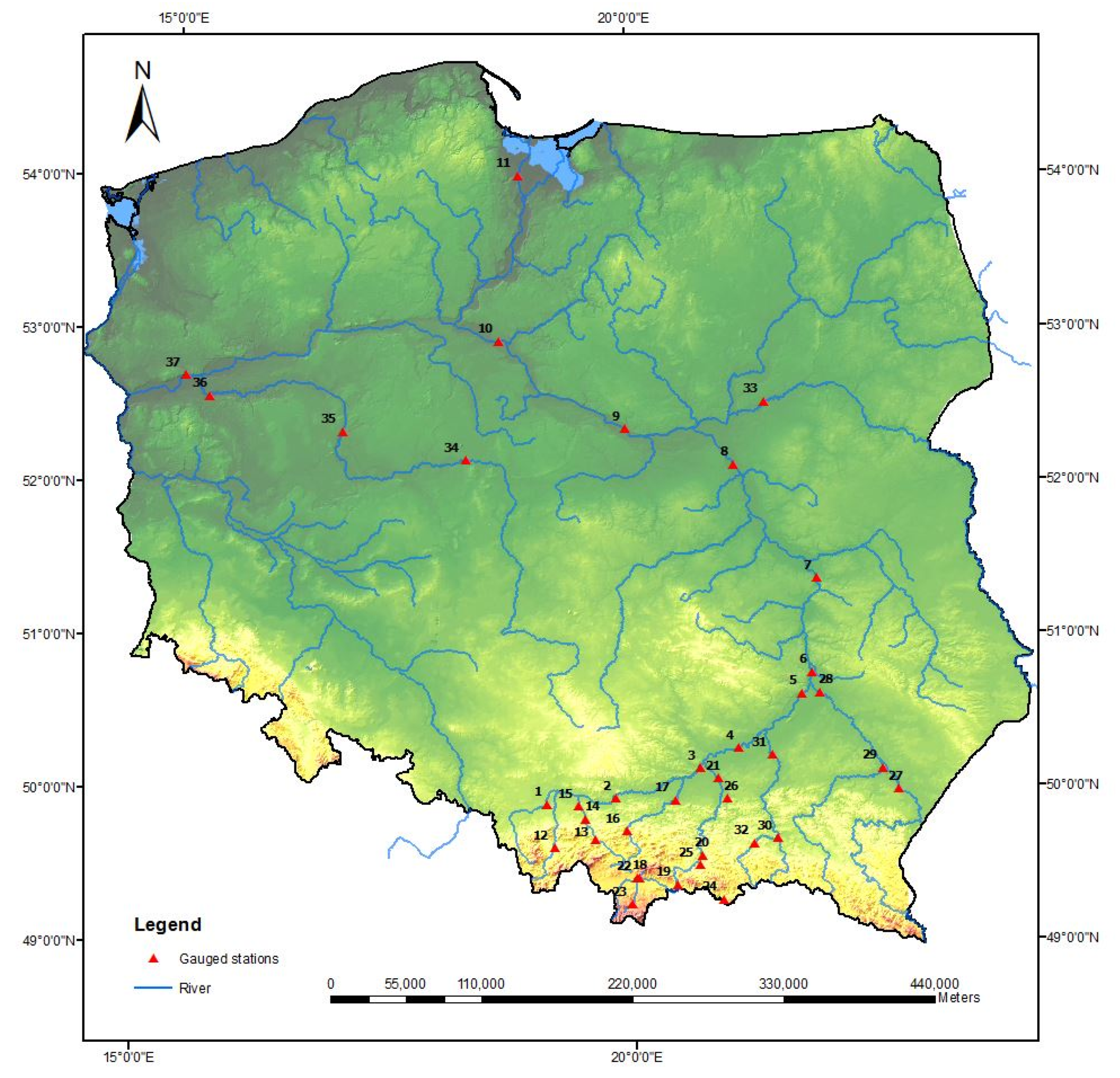
In this paper, the data of seasonal maximum flows from 37 gauging stations at Polish Rivers were investigated. The stations are listed in Appendix A (Table A1), along with the observation periods and the mean value of both the summer and winter maximum flows, while the location of all stations is illustrated in Figure 1. The studies mainly focused on the catchment of the Vistula Basin, which is characterized by high flood potential in its southern part. Here, the dominance of summer floods caused by intensive, long-lasting rainfall is observed. Gauging stations in the central part of the country represent mainly a snowmelt or mixed snowmelt-rainfall flood regime.
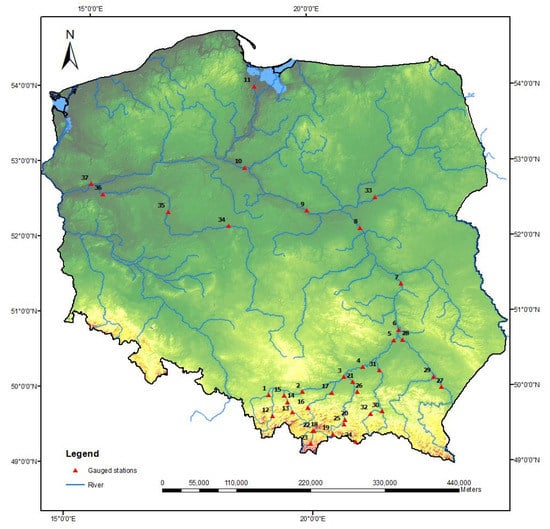
Figure 1.
The location of 37 gauging stations at Polish rivers that were analyzed in this paper.
The studies presented in the paper are illustrated for the Proszówki gauging station on the Raba River (no. 17, Figure 1). The data series of seasonal peak flows from the period 1951–2016 was considered. A choice of this hydrological station was caused by the main reason to reflect the difficulties hydrologists come across in their work. Proszówki Station is the closing station of the Raba River catchment. The reduction of flood peaks at Proszówki is due to the Dobczyce Reservoir (put in use in 1986) situated about 30 km upstream. The reservoir, which has total storage capacity of 127 million m³ and a flood storage capacity of about 30 million m³, is a multi-purpose reservoir for flood protection, hydropower generation, and drinking water supply. In the face of a lack of information about water management for the reservoir and the awareness of the importance of naturalization of the flow, we decided to apply the simplified method for the reconstruction of the seasonal flood peak flows based on regression analysis with the reservoir upstream station, Stróża, for the common observation period before 1986, the coefficients of determination being equal to 82.36% for winter and 74.25% for summer, respectively. It was obvious that this simplified procedure introduced additional uncertainty to the data series. However, there are other sources of uncertainty one cannot avoid (e.g., uncertainties of flow measurements, upper parts of rating curves, and in data processing and control). Despite the continuous development of measurement methods, the assessment of high waters is still not perfect. Moreover, we cannot quantify or eliminate uncertainty from historical data, when the measurement methods were much less precise than today. All of these uncertainties, together with different criteria of the best model selection, makes the problem of design quantile assessment equivocal, what is shown in the next sections.
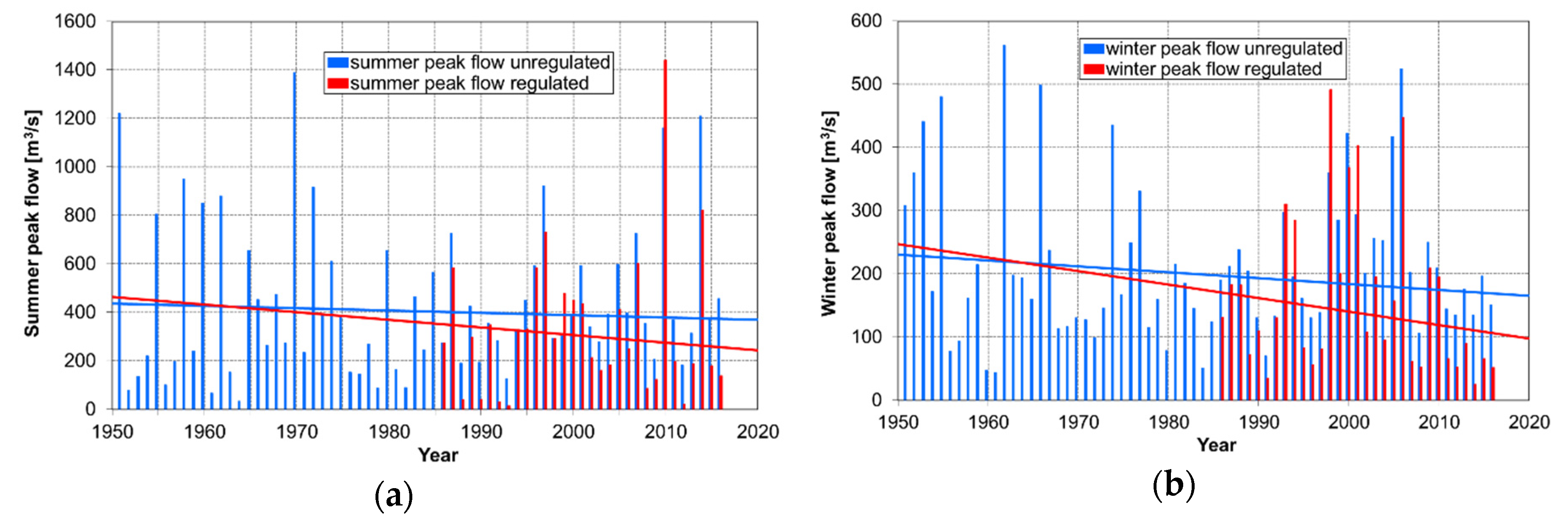
The bar charts of regulated (observed) and unregulated (reconstructed) maximum seasonal flow series are presented in Figure 2. Then, flood frequency analysis was performed with unregulated flood data (blue columns in Figure 2). The applied procedure diminished the decreasing trends in the average value of the maximum seasonal flows caused by the reduction in the culmination of flood waves by the reservoir (red and blue lines in Figure 2).
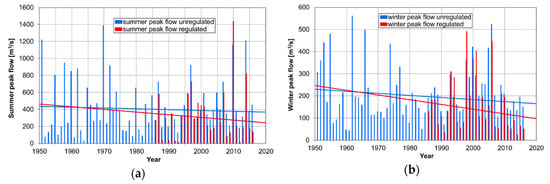
Figure 2.
Regulated (red color) and unregulated (blue color) peak flows at the Proszówki gauging station along with the trends in their average values for the (a) summer season; (b) winter season.
The mean of unregulated flow maxima in 1951–2016 for summer peak flows was 433 (m3/s), and for winter peak flows it was 213 (m3/s), while the variation coefficient Cv was 0.718 and 0.569, respectively.
3. Materials and Methods
3.1. Model Selection Procedures
To determine which of the alternative models was the best for modeling the maximum flow series of each season, the following procedures of model selection were used in this paper:
- 1.
- The AIC criterion (Akaike information criterion) is based on the likelihood function of distribution maximized with respect to the parameter values, also taking into account the number of distribution parameters . The selection statistic is defined by Equation (1) for the i-th distribution of the probability density function from among m alternative distributions and for [41]:where is the sample size and denotes the parameters of the i-th distribution, which can be determined by any estimation method. In this paper, three methods were used: the method of conventional moments (MOM) [42]; the linear moments method (LMM) [43]; and the maximum likelihood method (MLM) [44].
- 2.
- The QK (Quesenberry–Kent) procedure is based on the density function modified to the form given by Equation (2), which is invariant under a scale transformation of the data [45]:where is the probability density function of i-th distribution with its scale parameter equal to one, and the unknown shape parameter that is estimated by the MLM method. To facilitate the analysis of the results and to compare the positive numbers with each other, the original selection statistic is preceded by a minus sign and a minimum value from all models is determined as the solution, instead of the maximum value.
- 3.
- The KS (Kolmogorov–Smirnov) goodness of fit test is based on the Kolmogorov–Smirnov statistics defined by Equation (3) [46,47]:where denotes the theoretical probability of the j-th element of the ordered sample with its empirical probability , expressed here by the Weibull formula (i.e., . The parameters of distribution can be estimated using three methods. The advantage of the Kolmogorov–Smirnov statistics is the independence of probability distribution from the CDF that is tested [48].
- 4.
- The R (range) procedure has two variants. The first variant, R1, is based on the distance between the estimate of the 1% quantile from the maximum likelihood method and its value from the method of moments, and it is calculated using Equation (4) [49]:
Another variant of range statistic is , proposed by the authors [19], and is based on the distance between the 1% quantile estimate from the maximum likelihood method and its value from the linear moments method. The statistic is defined by Equation (5):
Regarding the decision rules of model selection procedures 1–4, the probability distribution with the smallest value of the selection statistic was the closest to the true population distribution among all competing models, while the model with the highest value of the selection statistic was the least fitting. The efficiency of the above model selection procedures has been studied in the literature for various configurations of distributions [19,49,50,51].
3.2. Models Aggregation
In the classical approach, to estimate the probable maximum flow that serves as a hydrological design value, the commonly used methods are based on the choice of the best probability distribution from among candidate distributions . Meanwhile, the aggregation method proposed by the authors uses all of the information contained in these distributions by aggregating quantiles of individual distributions in the form of the weighted average. The formula of the aggregated (average) quantile is expressed by Equation (6) [40]:
The weights are based on the value of the criterion according to Equation (7):
where is the difference between the AIC value for the i-th model and the lowest value of AIC among all distribution candidates, which in fact means the best fitted distribution to the data series, according to the AIC criterion. For the set of PDFs with the same number of parameters, Equation (7) reduces to Equation (8), and then the likelihood function is used instead of the AIC value:
Note that the weights can be interpreted (based on the Bayes theorem with equal a priori probabilities for all models) as the a posteriori probabilities of the adequacy of the i-th model. Hence, the aggregated quantile represents the expected value of quantiles conditioned by the set of models used for estimation as the candidate models.
4. Results
4.1. Models for Seasonal Maximum Flows of Polish Data
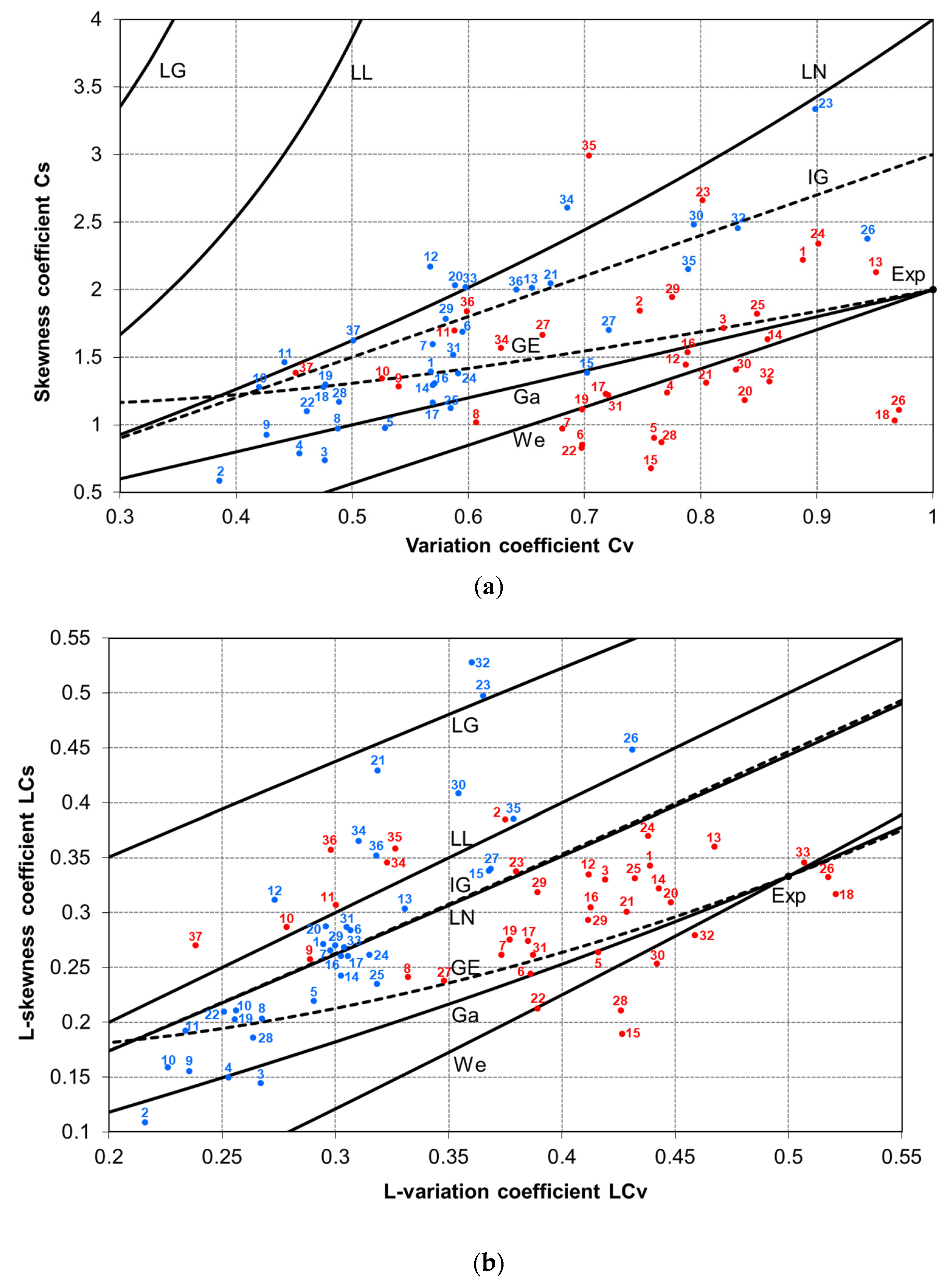
For making the initial selection of appropriate distributions for Polish data of seasonal peak flows, both conventional and linear moment ratio diagrams MRD were plotted in Figure 3. For two-parameter distributions, both the relation of conventional skewness coefficient Cs versus variation coefficient Cv (Figure 3a) and the relation of linear skewness coefficient LCs versus linear variation coefficient LCv (Figure 3b) were plotted as the curves, while the above relations for the data series were plotted as the point. Point number 17 (red and blue) in Figure 3 represents Proszówki Station on the Raba River, which will serve here for the case study.
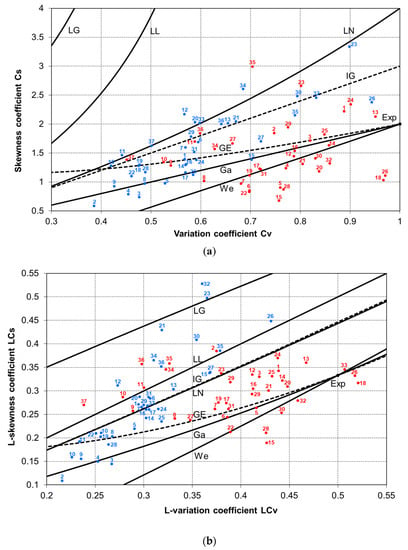
Figure 3.
Skewness coefficient versus variation coefficient for two-parameter distributions and Polish data of summer (red color) and winter (blue color) peak flows for 37 gauging stations: (a) conventional moment ratio diagrams of Cs vs. Cv; (b) linear moment ratio diagrams of LCs vs. LCv. Key to the distributions: Ga—gamma, We—Weibull, GE—generalized exponential, IG—inverse Gaussian, LN—log-normal, LL—log-logistic, LG—log-Gumbel, Exp—exponential.
When a point representing a gauging station is near a line that corresponds to a distribution, it means that this distribution may be the best fit for the peak flow series from the station. In an ideal situation, when the data follow a given distribution, an exact match would be achieved for an infinite sample. Since the data series are of limited length, the above graphs can only provide an approximation and should be established by procedures of model selection. The analysis of this issue is provided in Section 4.2.2.
In Figure 3, there is a range of the values for Cv-Cs and LCv-LCs, respectively, which was achieved by a large group of Polish measurement series and not covered by two-parameter distributions usually used in FFA, marked by solid lines. The dotted lines illustrate inverse Gaussian and generalized exponential distributions, which appear to fit well within the scope of Polish data of seasonal peak flows. This is particularly evident for winter peak flows in Figure 3a and summer peak flows in Figure 3b, where about half of the stations are out of range to match the commonly used probability distributions.
4.2. Distribution Identification and Its Parameter Estimation: Comparative Study
4.2.1. Estimation of Quantiles of the Maximum Flow Distribution
For seasonal maximum flows at Proszówki Station, seven hypothetical distributions were successively assumed (see Table 1). For each of the PDFs, two goodness of fit tests, and the Kołmogorov–Smirnov tests [47], were performed and both of them determined that all seven PDFs were acceptable under the null hypothesis. The estimates of the 1% quantile calculated with three methods are shown in Table 2 along with the standard deviation of the estimates for the individual methods.

Table 2.
Estimates of the 1% quantile of seasonal maximum flows (m3/s) from the period 1951–2016 at the Proszówki gauging station and assuming selected two-parameter distributions along with the standard deviation of estimates.
For both seasons, the bolded number represents the smallest value among all considered models, which is yielded by the Weibull distribution along with the MLM for the summer season and with LMM for the winter one. The underlined number represents the greatest value and, for both seasons, it comes from the log-Gumbel distribution along with the MLM estimation method, and it stands out with a huge value in comparison with other models. The heavy-tailed distributions, represented by the LL and LG, were included in our studies, although their poor fit to the Polish data (see Figure 3) may result in the overestimation of , especially in the case of the LG distribution and the MLM. The MLM’s estimators of quantiles are unbiased only if a parent (true) distribution is used for the estimation and the sample is large (asymptotic). Moreover, the MLM concentrates on the main mass of probability (i.e., far from the upper quantiles). In contrast, the MOM or LMM generally produces less biased estimators of upper quantiles [52,53,54]. Please also note that the MOM, and to a lesser extent the LMM, is more robust to the misspecification of the applied statistical models, and the values of the estimators of the upper quantiles are similar, regardless of the model applied (see the values of the standard deviation in the last column).
Regarding the variability of the quantile estimates for a given distribution depending on the choice of the estimation method, the Ga, We, GE distributions remain the least sensitive to the choice of estimation method, while the LG is the most sensitive.
4.2.2. Uncertainty of Distribution Selection
To determine which of the alternative models is the best for modeling the maximum flow series of each season, four procedures of model selection were used (Section 3.1) and the results are presented in Table 3.

Table 3.
The results of the model selection procedures for the two-parameter distributions being fitted to the seasonal maximum flows in 1951–2016 at the Proszówki gauging station.
For each model selection procedure and estimation method, the best fitting distribution is marked in bold, while the PDFs fitting at the second and third place are marked in italics and underlined fonts, respectively. For instance, for the summer peak flows, according to the AIC criterion and using the MOM estimation method, the distribution best fitting the data was GE, followed by Ga and We, which is identical to the results of the AIC criterion and the LMM and MLM estimation methods, and also coincides with the results of the R1 procedure. The GE distribution also turns out to be the best fit to the data among all competitive PDFs, after which the LN and LL are placed. The GE distribution also turns out to be the best fit to the data among all competitive PDFs, when QK procedure or KS test along with MOM method of estimation are applied. In both cases, the second and third place are occupied by Ga and LN distributions, respectively. For the KS test with the LMM estimation method, the best distribution was IG, followed by GE and LN, while with the MLM estimation method, surprisingly, the best was the LL distribution, followed by LN and GE, respectively. Finally, according to the R2 selection procedure, first place was taken by the Ga distribution, followed by We and GE.
In the case of the winter maximum flows, there was a very similar layout of the best fitted distributions (i.e., the first place) as was in the case of the summer maximum flows. The GE distribution was the best according to the AIC criterion, regardless of the estimation method and according to the QK and R1 procedures. The IG and LL distributions occupied first place when the KS test was applied, together with the LMM and MLM estimation methods, respectively. Except for the case of the R1 procedure, in all variants of the model selection procedure with an estimation method, the LN distribution was in second place.
Summarizing summer season, the GE distribution ranked first in six out of nine possible variants of the model selection procedure with the estimation method, while the Ga, IG, and LL distributions had one win each. For the winter season, the GE distribution was best in five out of nine possible variants, IG ranked first in two variants, while We and LL had one each.
It is worth noting that for the Proszówki gauging station, the results of the distribution fitting to the data from the model selection procedures coincided with the results from the LCv-LCs diagram (Figure 3b). In general, the GE, Ga, LN, and IG distributions were the best fit for the summer peak flow series (red point 17), while the GE, IG, LN, and LL were right for the winter peaks (blue point 17).
The analysis conducted for Proszówki and several other gauging stations from the Vistula and Oder Basins presented in Figure 1 showed that both the GE and IG distributions can be recommended for modeling the seasonal maximum flows in Poland. Compared with the distributions popular in flood frequency modeling, the IG and GE distributions occupied leading positions. Nevertheless, the choice of one model that best fits the data is ambiguous and depends on the selection of the estimation method and the model selection procedure. This problem is typical for samples usually available in hydrology. Meanwhile, at practical applications, for example, the design of hydraulic structures, one value for the maximum flow estimate is desirable with the least uncertainty. The solution may be the method of quantile aggregation proposed by the authors [19,40] and discussed in the next section.
4.3. Aggregation of Quantiles
4.3.1. Instability of High Quantile Estimates with Increasing Length of Data Series
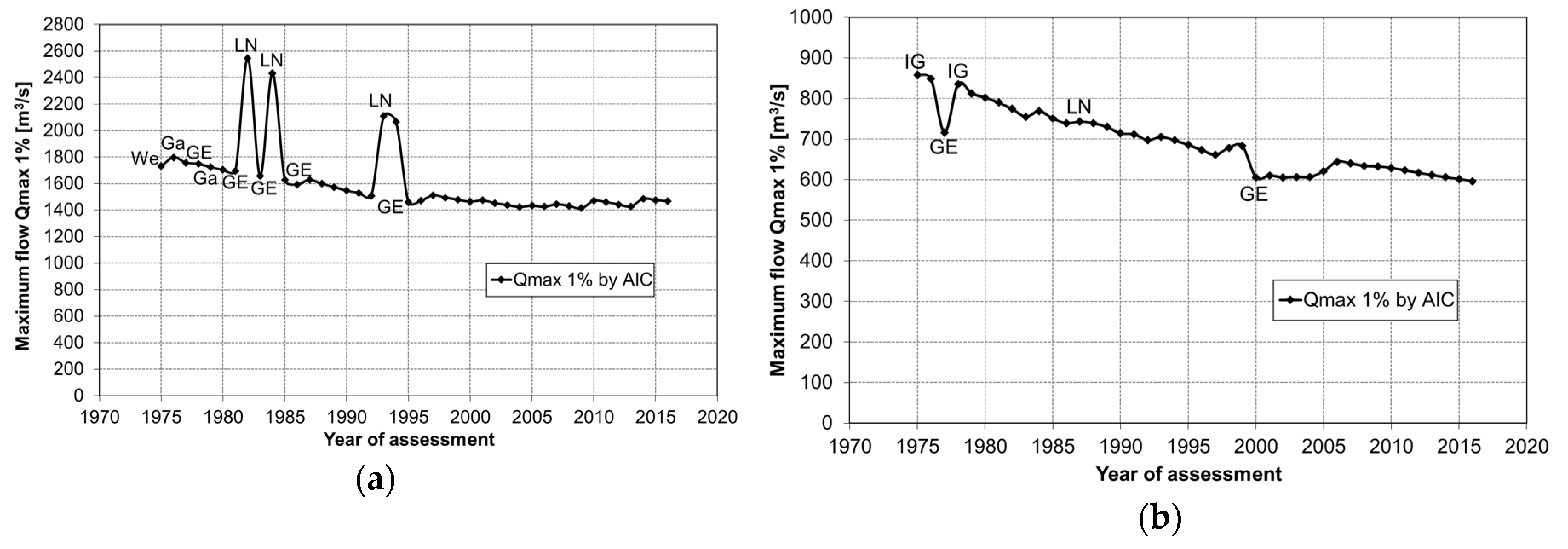
In the classical approach to estimating quantiles of maximum flow distributions, apart from the uncertainty resulting from the choice of the best distribution, there is a problem of the instability of estimations when lengthening the measurement series. As the length of the observation series increases, the repetition of the procedure (choice of distribution, estimation method, and model selection procedure) can lead to a change in the type of the best distribution, and at least to a change in the values of the parameter estimates of the current distribution. Due to the small size of the series and hence the strong dependence of the result on the successive incoming elements, these changes are periodic and chaotic and can cause significant changes in the design quantile during the multistage procedure of designing. This phenomenon (more or less accentuated) has been observed for almost all investigated seasonal peak flow series, as illustrated by the example of seasonal maximum flows from the period 1951–2016 for the Proszówki gauging station on the Raba River (Figure 4).
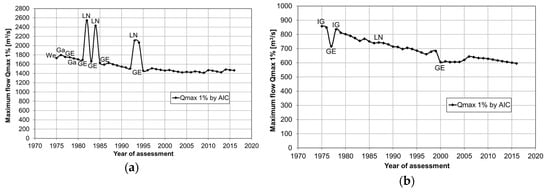
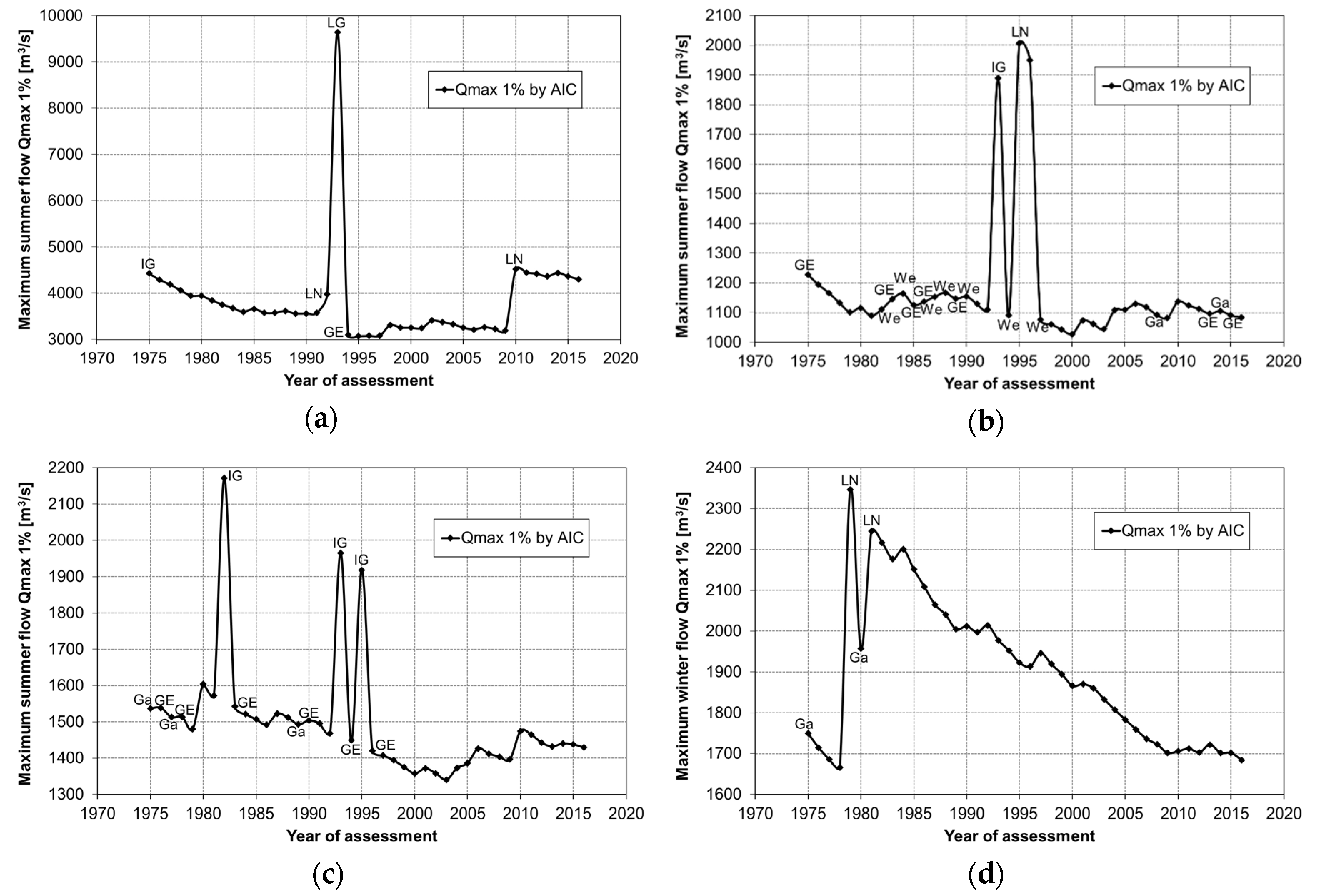
Figure 4.
Estimates of the 1% quantile of maximum flows at Proszówki Station along with the best matching distributions for: (a) summer season; (b) winter season. Distributions: Ga—gamma, We—Weibull, GE—generalized exponential, IG—inverse Gaussian, LN—log-normal.
Starting from the 25-year series of seasonal peak flows (i.e., the measurements from 1951 to 1975), the best fitted distribution was chosen from among seven candidate distributions (see Table 1) and the quantile corresponding to the best fitted distribution was assigned. This procedure has been repeated for data series extended for a successive year, up to the complete 66-year series. The MLM method was applied to estimate the distribution parameters and the AIC criterion was used to choose the best fit distribution.
For the series of maximum summer flows (Figure 4a), a significant difference in the estimates of 1% quantile was observed in the years 1982, 1984, and 1993–1994. Then, the type of the best fitted distribution changed from GE to LN, resulting in a significant increase in design value. The changes of other types of distribution did not cause such large changes in the estimates. It is worth noting that the peaks in the estimation curve are related to those of the smallest value of the observations, especially the peaks in 1982 and 1993 (see Figure 4a). For the series of maximum winter flows (Figure 4b), the greatest decreases were observed in 1977 and 2000. These were due to the change in the distribution type from IG or LN into GE. Moreover, in 2005–2006, there was a two-step increase in the 1% quantile estimates. Since 2000, the GE was the best fit distribution among the seven competing models, the jump was due to a change in the parameters of the current (GE) distribution with the addition of observations from 2005 and 2006. Interestingly, the largest shifts in the estimation curve (i.e., in 1977 and 2000) were downhill and were associated with those of the highest observation values (see Figure 4b).
The above results of the best matching distributions for the summer and winter maximum flows are consistent with the LCv-LCs graph (Figure 2b) for the red and blue points of number 17, respectively. Moreover, the variability of the seasonal 1% quantile estimates (Figure 4) broadly overlapped with the earlier studies [55] and with the latest studies [28]. In general, the summer peak flows were identified as stationary, while the winter peak flows were decreasing.
The jumps in the 1% quantile estimates occurred at various scales in all of the investigated data series. Some examples are given in Figure 5.
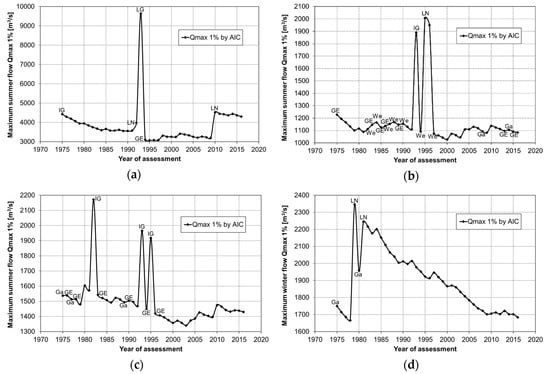
Figure 5.
Estimates of the 1% quantile of maximum flows along with the best matching distributions by the Akaike information criterion (AIC) for the stations: (a) Jagodniki [3]*; (b) Koszyce Wielkie [26]; (c) Mielec [31]; (d) Wyszków [33]. Distributions: Ga—gamma, We—Weibull, GE—generalized exponential, IG—inverse Gaussian, LN—log-normal, LG—log-Gumbel. * The number of the station in Table A1.
Significant differences in the estimates of hydrological design values in subsequent years are a big problem for designers of hydrotechnical structures and engineers. As hydrological design investments last several years, the projects require multiple revisions, resulting in high financial costs. To minimize the effect of unstable design values, the method of aggregation (see Section 3.2) can be used to assess the quantile of the peak flows.
4.3.2. Case Study of Model Aggregation
Characteristic values of the aggregation method calculated for seasonal maximum flows at the Proszówki gauging station on the Raba River from the period 1951–2016 are shown in Table 4 for seven candidate distributions.

Table 4.
Data for the aggregation of the 1% quantile for individual candidate distributions of seasonal maximum flows from 1951–2016 at Proszówki Station.
For the summer season, the lowest AIC value corresponding to the GE distribution represents the best fit of this distribution to the data series from all candidate distributions. This results in the largest share (i.e., the highest weight) of the quantile of GE distribution in the aggregated quantile and is equal to 0.352. The second distribution in order was Ga with a slightly smaller weight equal to 0.31. Hence, a contribution of both the GE and Ga distributions to the aggregated quantile was similarly high. Significantly smaller weights had the quantiles of We, LN, and LL distributions, which are 0.125, 0.112, and 0.082, respectively. The other two PDFs (i.e., IG and LG) yielded a much smaller contribution to the aggregated quantile, especially LG, since its weight is of the order of zero (it is 7E-06 exactly).
Regardless of the matching criterion, the distribution matches were less pronounced when the observation series was shorter. For instance, for the 40-element series from the period 1951–1990, the weights of candidate distributions are in sequence: Ga—0.219, We—0.154, GE—0.230, IG—0.126, LN—0.195, LL—0.073, and LG—0.003. Thus, the leaders have lower weights and the least fit distributions have higher weights, compared to the whole observation period.
For the winter season, the GE distribution was clearly dominant as the best fit to the data and the next was LN. The smallest weights corresponded to the We and LG distributions and the latter had an exact weight equal to 14E-05.
Due to the above considerations, the question arises as to how the poorly matched distributions affect the value of an aggregate quantile. Is it more sensible to take into account the poorly matching distributions, or to use selection and reject the distribution (or distributions) with the weakest fit and not include them in the calculation of the aggregate quantile? The analysis of the above issue is presented in the next subsection.
4.3.3. Impact of Competitive Distributions on Aggregated Quantiles
For the analyzed station, the 1% quantile estimates obtained from the classical method of selecting the best fitted distribution (using the MLM estimation method and AIC for the selection of the best matched distribution) were compared with the estimates from the aggregation method with several variants of the distribution sets. The results are illustrated in Figure 6.
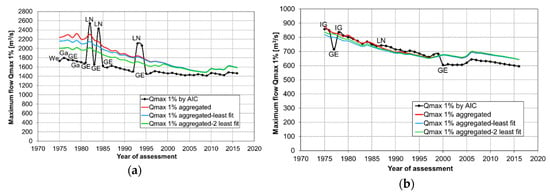
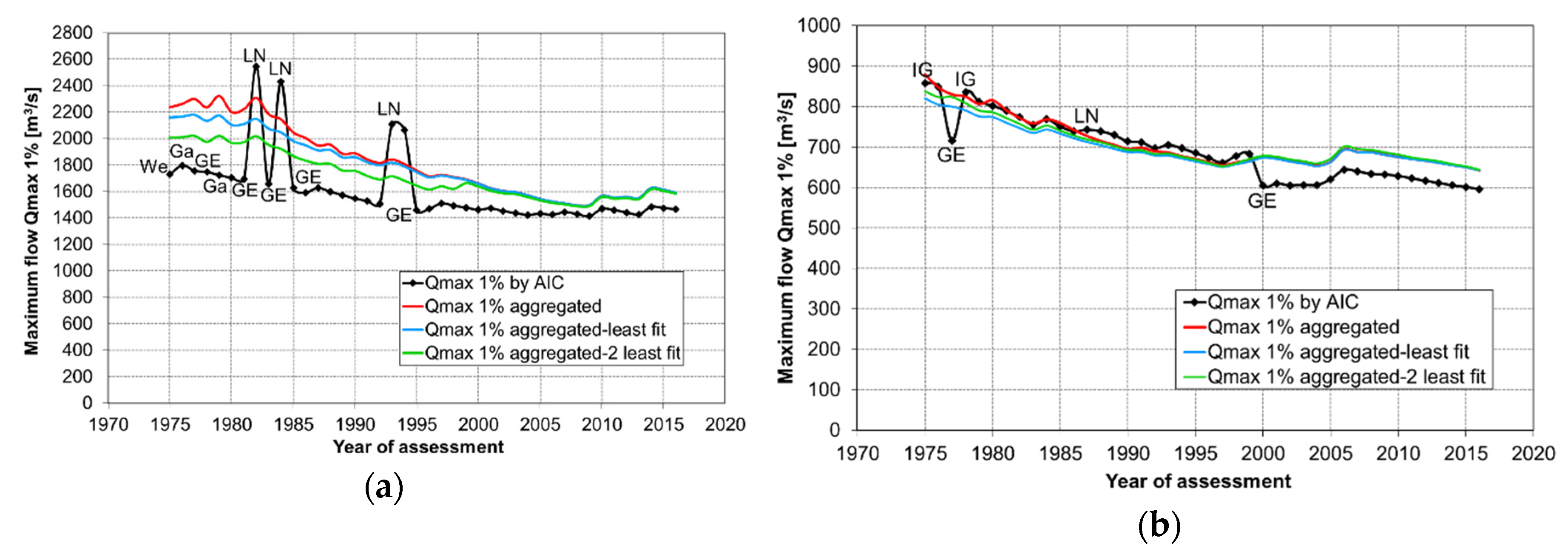
Figure 6.
The estimates of the 1% quantile of (a) summer and (b) winter peak flows for the Proszówki gauging station on the Raba River obtained by the method of selecting the best fit distribution and by the aggregation method with variants of the candidate distributions.
In comparison with the classical approach to flood quantile estimation (black line with dots in Figure 6), the original variant of the aggregation method (i.e., when all alternative distributions are taken into account (red line)) significantly reduced the variability of the 1% quantile estimate when extending the observation series for subsequent years. For both the summer and winter seasons, the jumps at the quantile estimates were smoothed out. When the least fitted distribution (i.e., the one with the lowest weight) was removed from the group of candidate distributions, then the estimate value of the 1% quantile decreased for a given observation length (blue line). This was due to the fact that for each length of the measurement series of the maximum flows for both seasons, the distribution of the least fit was the LG distribution, which provided much higher estimates of the design values than the other alternative distributions (see Table 1). After the removal of the second worst-fit distribution (green line), the estimates of still decreased in the case of the summer season, while they slightly increased in the winter season. In the case of the maximum summer flows, the second least fit distribution is the LL until 1998 and since 1999 it is the IG distribution. Meanwhile, in the case of the maximum winter flows, the second weakest matching distribution was We. It is worth noting that the 1% quantile estimates were almost identical for all three variants of aggregation method (i.e., for all three groups of candidate distributions, for the summer peak flow series of more than 49 elements, that is, for the series ending in 1999 or later (Figure 6a). In this case, for the long observation series, the least-fitting distributions (i.e., LG and IG) had very small weights of zero order, so their removal from the set of alternative distributions did not significantly affect the estimation value of . A similar effect was observed for the same period (from 1999) of the winter peak flows, but only for two variants of aggregation, when all seven candidate distributions were considered and when the least fit PDF was excluded from aggregation (Figure 6b). Excluding two least fit distributions caused a slight increase of .
5. Conclusions
In this paper, the classical and alternative approaches to the estimation of the upper quantiles of the probability distribution of maximum seasonal flows were presented for the Proszówki gauging station on the Raba River. Despite the multiplicity of probability distributions that have been proposed for flood frequency modeling, the analysis of Polish data of seasonal maximum flows from 37 gauging stations shows that new models are still desirable. The classical approach based on the selection of the best fitting distribution among candidate distributions reveals that the inverse Gaussian and generalized exponential distributions, which are not commonly applied in standard flood frequency modeling, occupy leading positions in the fit to the seasonal peak flows of Polish rivers. At the same time, the heavy tailed distributions turned out to not be suitable for the description of seasonal maximum flows for Polish rivers, in particular the log-Gumbel distribution (i.e., two-parameter equivalent of the GEV distribution). Generally, the choice of the best model and consequently the estimation of the hydrological design value (e.g., 1% quantile) strongly depends on the estimation method and the model selection procedure, which is characteristic of hydrological sample sizes. As a consequence, the development of flood frequency analysis methods by improving statistical techniques using new probability distributions, estimation methods, and model selection procedures, increases the uncertainty of flood quantile estimates.
When the ML method and model selection procedure based on AIC criterion were used for year to year successive evaluation of design quantiles, then their sudden upward or downward jumps can occur. This is not explainable by the changes of the flood generating processes themselves, but results only from the properties of the procedure applied. Our long-term research and experience in the field of FFA and design quantile assessment confirm the occurrence of sudden changes in the design quantiles in most of the analyzed cases. In the meantime, both researchers and practitioners like hydrological designers desire one specific design value with the least uncertainty. The solution may be a method of the aggregation of models, providing quantile estimates, and thus design values that are much more stable by extending the data series than the classical statistical methods used in FFA. The problem yet to be solved is the objective selection of models for aggregation. As was shown, the poorly suited models (with low weights) may significantly affect the quantile values while used in aggregation, especially in the range where the classical FFA shows high variability of quantile estimates. It is difficult to impose a strict limit on the weights as a selection criterion. In practice, hydrologists can support their decisions through the analysis of neighboring stations on the same river or in all region to narrow or enlarge the list of potential best distributions or to justify their use. However, it should be stressed that by aggregating the models, we take advantage of the wider information provided by several best fitted models.
The application of the method has utility in many areas, especially in the natural sciences, when performing experiments of the passive type (i.e., not being able to control all of the parameters of the experiment or the experiment cannot be repeated under the same, fixed conditions.
Author Contributions
I.M. and E.B. designed the studies; I.M. and K.K. created new software; I.M. and E.B. drafted the paper. All authors analyzed the results and reviewed the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
The research was partially funded by the Ministry of Science and Higher Education of Poland within the statutory activities No. 3841/E-41/S/2019 and by the COST Action CA17109 “Understanding and modeling compound climate and weather events”.
Acknowledgments
The authors thank the four anonymous reviewers for their careful reading and detailed remarks that helped to significantly improve the first version of this manuscript. The research was partially funded by the Ministry of Science and Higher Education of Poland within the statutory activities No. 3841/E-41/S/2019 and by the COST Action CA17109 “Understanding and modeling compound climate and weather events”. The authors thank the Institute of Meteorology and Water Management–National Research Institute (IMGW-PIB) in Warsaw, Poland, for sharing the data. Contact: Databases and Expertise Office, email: ekspertyzy@imgw.pl, phone: +48 22 56 94 366.
Conflicts of Interest
The authors declare no conflicts of interest.
Appendix A

Table A1.
Basic characteristics of the seasonal peak flows of 37 gauging stations at Polish rivers analyzed in paper.
Table A1.
Basic characteristics of the seasonal peak flows of 37 gauging stations at Polish rivers analyzed in paper.
| No | Gauging Station | River | Observation Period | Mean of Summer Peak Flows (m3/s) | Mean of Winter Peak Flows (m3/s) |
|---|---|---|---|---|---|
| 1 | Jawiszowice | Wisła | 1951–2016 | 153 | 68 |
| 2 | Tyniec | 1951–1990 | 642 | 378 | |
| 3 | Jagodniki | 1921–2016 | 990 | 621 | |
| 4 | Szczucin | 1921–2016 | 1700 | 1018 | |
| 5 | Sandomierz | 1921–2016 | 2010 | 1443 | |
| 6 | Zawichost | 1951–2016 | 2727 | 2074 | |
| 7 | Puławy | 1951–2016 | 2432 | 1960 | |
| 8 | Warszawa | 1921–2016 | 2225 | 2302 | |
| 9 | Kępa | 1921–2016 | 2545 | 3305 | |
| 10 | Toruń | 1921–2016 | 2532 | 3334 | |
| 11 | Tczew | 1921–2016 | 2400 | 3383 | |
| 12 | Żywiec | Sola | 1956–2016 | 330 | 160 |
| 13 | Sucha | Skawa | 1951–2016 | 148 | 66 |
| 14 | Wadowice | 1951–2016 | 253 | 117 | |
| 15 | Rudze | Wieprzówka | 1961–2016 | 61 | 22 |
| 16 | Stróża | Raba | 1956–2016 | 202 | 93 |
| 17 | Proszówki | 1951–2016 | 433 | 213 | |
| 18 | Kowaniec | Dunajec | 1951–2016 | 240 | 87 |
| 19 | Krościenko | 1951–2016 | 427 | 161 | |
| 20 | Nowy Sącz | 1946–2016 | 887 | 366 | |
| 21 | Żabno | 1956–2016 | 1010 | 444 | |
| 22 | Nowy Targ | Czarny Dunajec | 1961–2016 | 160 | 56 |
| 23 | Zakopane | Biały Dunajec | 1961–2016 | 40 | 9 |
| 24 | Muszyna | Poprad | 1951–2016 | 214 | 120 |
| 25 | Stary Sącz | 1951–2016 | 278 | 171 | |
| 26 | Koszyce Wlk. | Biała | 1951–2016 | 240 | 121 |
| 27 | Jarosław | San | 1951–2016 | 469 | 465 |
| 28 | Radomyśl | 1951–2016 | 435 | 657 | |
| 29 | Tryńcza | Wisłok | 1951–2016 | 158 | 178 |
| 30 | Żółków | Wisłoka | 1951–2016 | 152 | 99 |
| 31 | Mielec | 1951–2016 | 419 | 331 | |
| 32 | Klęczany | Ropa | 1951–2016 | 129 | 55 |
| 33 | Wyszków | Bug | 1921–2016 | 272 | 587 |
| 34 | Konin | Warta | 1921–1991 | 122 | 238 |
| 35 | Poznań | 1822–2016 | 156 | 404 | |
| 36 | Skwierzyna | 1921–2016 | 184 | 362 | |
| 37 | Gorzów | 1921–2016 | 276 | 494 |
References
- Gumbel, E.J. The return period of flood flows. Ann. Math. Stat. 1941, 12, 163–190. [Google Scholar] [CrossRef]
- Moran, P.A.P. The statistical treatment of flood flows. Trans. Am. Geophys. Union 1957, 38, 519–523. [Google Scholar] [CrossRef]
- Cunnane, C. Operational Hydrology Report No. 33: Statistical Distributions for Flood Frequency Analysis; World Meteorological Organization: Geneva, Switzerland, 1989; ISBN 9789263107183. [Google Scholar]
- FEH. Flood Estimation Handbook 3: Statistical Procedures for Flood Frequency Estimation; Institute of Hydrology: Wallingford, UK, 1999; ISBN 9781906698003. [Google Scholar]
- Rao, A.R.; Hamed, K.H. Flood Frequency Analysis; CRC Press: Boca Raton, FL, USA, 2000; ISBN 9780849300837. [Google Scholar]
- Griffis, V.W.; Stedinger, J.R. Evolution of flood frequency analysis with Bulletin 17. J. Hydrol. Eng. 2007, 12, 283–297. [Google Scholar] [CrossRef]
- Rowiński, P.M.; Strupczewski, W.G.; Singh, V.P. A note on the applicability of log-Gumbel and log-logistic probability distributions in hydrological analyses: I. Known pdf. Hydrol. Sci. J. 2002, 47, 107–122. [Google Scholar] [CrossRef]
- Węglarczyk, S.; Strupczewski, W.G.; Singh, V.P. A note on the applicability of log-Gumbel and log-logistic probability distributions in hydrological analyses: II. Assumed pdf. Hydrol. Sci. J. 2002, 47, 123–137. [Google Scholar] [CrossRef][Green Version]
- Strupczewski, W.G.; Kochanek, K.; Markiewicz, I.; Bogdanowicz, E.; Weglarczyk, S.; Singh, V.P. On the tails of distributions of annual peak flow. Hydrol. Res. 2011, 42, 171–192. [Google Scholar] [CrossRef]
- Salinas, J.L.; Castellarin, A.; Viglione, A.; Kohnová, S.; Kjeldsen, T.R. Regional parent flood frequency distributions in Europe—Part 1: Is the GEV model suitable as a pan-European parent? Hydrol. Earth Syst. Sci. 2014, 18, 4381–4389. [Google Scholar] [CrossRef]
- Rizwan, M.; Guo, S.; Xiong, F.; Yin, J. Evaluation of various probability distributions for deriving design flood featuring right-tail events in Pakistan. Water 2018, 10, 1603. [Google Scholar] [CrossRef]
- Kuczera, G. Robust flood frequency models. Water Resour. Res. 1982, 18, 315–324. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Węglarczyk, S. Impulse response of linear diffusion analogy model as a flood frequency probability density function. Hydrol. Sci. J. 2001, 46, 761–780. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Generalized exponential distributions. Aust. N. Z. J. Stat. 1999, 41, 173–188. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Discriminating between gamma and generalized exponential distributions. J. Stat. Comput. Sim. 2004, 74, 107–121. [Google Scholar] [CrossRef]
- Gupta, R.D.; Kundu, D. Discriminating between the Weibull and the GE distributions. Comput. Stat. Data Anal. 2003, 43, 179–196. [Google Scholar] [CrossRef]
- Kundu, D.; Gupta, R.D.; Manglick, A. Discriminating between the log-normal and generalized exponential distribution. J. Stat. Plan. Infer. 2005, 127, 213–227. [Google Scholar] [CrossRef]
- Brzeziński, J. Zastosowanie uogólnionego rozkładu wykładniczego w analizie sezonowych przepływów maksymalnych rocznych [Application of generalized exponential distribution in seasonal maximum annual flow analysis]. In Hydrologia w Inżynierii i Gospodarce Wodnej, Tom 1; Więzik, B., Ed.; Polska Akademia Nauk, Komitet Inżynierii Środowiska: Warsaw, Poland, 2010; Volume 68, pp. 71–82. ISBN 9788389293930. [Google Scholar]
- Markiewicz, I.; Strupczewski, W.G.; Bogdanowicz, E.; Kochanek, K. Generalized exponential distribution in flood frequency analysis for Polish rivers. PLoS ONE 2015, 10, e0143965. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C.; Chebana, F. Review of criteria for the selection of probability distributions for wind speed data and introduction of the moment and L-moment ratio diagram methods, with a case study. Energy Convers. Manag. 2016, 124, 247–265. [Google Scholar] [CrossRef]
- Rahman, A.S.; Rahman, A.; Zaman, M.; Haddad, K.; Ahsan, A.; Imteaz, M.A. A study on selection of probability distributions for at-site flood frequency analysis in Australia. Nat. Hazards 2013, 69, 1803–1813. [Google Scholar] [CrossRef]
- Ouarda, T.B.M.J.; Charron, C. Changes in the distribution of hydro-climatic extremes in a non-stationary framework. Sci. Rep. 2019, 9, 8104. [Google Scholar] [CrossRef]
- Hosking, J.R.M. L-moments: Analysis and estimation of distributions using linear combination of order statistics. J. R. Stat. Soc. B 1990, 52, 105–124. [Google Scholar] [CrossRef]
- El Adlouni, S.; Ouarda, T.B.M.J.; Bobée, B. Orthogonal projection L-moment estimators for three-parameter distributions. Adv. Appl. Stat. 2007, 7, 193–209. [Google Scholar]
- Hall, J.; Blöschl, G. Spatial patterns and characteristics of flood seasonality in Europe. Hydrol. Earth Syst. Sci. 2018, 22, 3883–3901. [Google Scholar] [CrossRef]
- Parajka, J.; Kohnová, S.; Merz, R.; Szolgay, J.; Hlavčová, K.; Blöschl, G. Comparative analysis of the seasonality of hydrological characteristics in Slovakia and Austria. Hydrol. Sci. J. 2009, 54, 456–470. [Google Scholar] [CrossRef]
- Hasson, S.; Lucarini, V.; Pascale, S.; Böhner, J. Seasonality of the hydrological cycle in major South and Southeast Asian river basins as simulated by PCMDI/CMIP3 experiments. Earth Syst. Dyn. 2014, 5, 67–87. [Google Scholar] [CrossRef]
- Blösch, G.; Hall, J.; Viglione, A.; Perdigăo, R.A.P.; Parajka, J.; Merz, B.; Lun, D.; Arheimer, B.; Aronica, G.T.; Bilibashi, A.; et al. Changing climate both increases and decreases European river floods. Nature 2019, 573, 108–111. [Google Scholar] [CrossRef] [PubMed]
- Blösch, G.; Hall, J.; Parajka, J.; Perdigao, R.A.P.; Merz, B.; Arheimer, B.; Kjeldsen, T. Changing climate shifts timing of European floods. Science 2017, 357, 588–590. [Google Scholar] [CrossRef] [PubMed]
- Wilson, D.; Hisdal, H.; Lawrence, D. Has streamflow changed in the Nordic countries? Recent trends and comparisons to hydrological projection. J. Hydrol. 2010, 394, 334–346. [Google Scholar] [CrossRef]
- Stramska, M.; Kowalewska-Kalkowska, H.; Swirgon, M. Seasonal variability in the Baltic Sea level. Oceanologia 2013, 55, 787–807. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kochanek, K.; Bogdanowicz, E.; Markiewicz, I. On seasonal approach to flood frequency modelling. Part I: Two-component distribution revisited. Hydrol. Process. 2012, 26, 705–716. [Google Scholar] [CrossRef]
- Kochanek, K.; Strupczewski, W.G.; Bogdanowicz, E. On seasonal approach to flood frequency modelling. Part II: Flood frequency analysis of Polish rivers. Hydrol. Process. 2012, 26, 717–730. [Google Scholar] [CrossRef]
- Strupczewski, W. Częstość wielkich wód [Frequency of peak waters]. Przegląd Geofiz. X (XVIII) 1965, 1, 83–93. [Google Scholar]
- Ozga-Zielinska, M.; Brzezinski, J.; Ozga-Zielinski, B. Guidelines for Flood Frequency Analysis. In Long Measurement Series of River Discharge; WMO HOMS Component I81.3.01; Institute of Meteorology and Water Management: Warsaw, Poland, 2005. [Google Scholar]
- Ozga-Zielińska, M.; Brzeziński, J.; Ozga-Zieliński, B. Zasady obliczania największych przepływów rocznych o określonym prawdopodobieństwie przewyższenia przy projektowaniu obiektów budownictwa hydrotechnicznego. Długie ciągi pomiarowe przepływów. [Guidelines for the determining the annual maximum flows with a certain probability of exceedance in the design of hydrotechnical structures. Long data series of flows]. In Materiały Badawcze, Seria: Hydrologia i Oceanologia; IMGW: Warszawa, Poland, 1999; p. 27. [Google Scholar]
- Węglarczyk, S. Metoda alternatywy zdarzeń identyfikacji rozkładu prawdopodobieństwa przepływów maksymalnych w roku—Analiza krytyczna [The method of alternative events identifying the probability distribution of maximum flows in a year—Critical analysis]. Gospod. Wodna 2007, 5, 185–190. [Google Scholar]
- Debele, S.E.; Bogdanowicz, E.; Strupczewski, W.G. The impact of seasonal flood peak dependence on annual maxima design quantiles. Hydrol. Sci. J. 2017, 62, 1603–1617. [Google Scholar] [CrossRef]
- Salvadori, G.; De Michele, C. Frequency analysis via copulas: Theoretical aspects and applications to hydrological events. Water Resour. Res. 2004, 40, 1–17. [Google Scholar] [CrossRef]
- Bogdanowicz, E. Podejście wielomodelowe w zagadnieniach estymacji kwantyli rozkładu wartości maksymalnych [Multimodel approach to estimation of extreme value distribution quantiles]. In Hydrologia w Inżynierii i Gospodarce Wodnej, Tom 1; Więzik, B., Ed.; Polska Akademia Nauk, Komitet Inżynierii Środowiska: Warsaw, Poland, 2010; Volume 68, pp. 57–70. ISBN 9788389293930. (In Polish) [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics, Vol. 1. Distribution Theory; Charles Griffin and Company Limited: London, UK, 1969. [Google Scholar]
- Hosking, J.R.M.; Wallis, J.R. Regional Frequency Analysis. An Approach Based on L-Moment; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kendall, M.G.; Stuart, A. The Advanced Theory of Statistics. Vol. 2. Inference and Relationship; Charles Griffin and Company Limited: London, UK, 1973. [Google Scholar]
- Quesenberry, C.P.; Kent, J. Selecting among probability distributions used in reliability. Technometrics 1982, 24, 59–65. [Google Scholar] [CrossRef]
- Kolmogorov, A. Sulla determinazione empirica di una legge di distribuzione [On the empirical determination of a distribution law]. G. Inst. Ital. Attuari 1933, 4, 83–91. [Google Scholar]
- Kaczmarek, Z. Statistical Methods in Hydrology and Meteorology; Published for the Geological Survey, US Department of the Interior and the National Science Foundation, Washington, DC, by the Foreign Scientific Publications Department of the National Centre for Scientific, Technical and Economic Information; Foreign Scientific Publications Department of the National Center for Scientific, Technical and Economic Information: Warsaw, Poland, 1977. [Google Scholar]
- Chakravarti, I.M.; Laha, R.G.; Roy, J. Handbook of Methods of Applied Statistics, Vol. 1; John Wiley and Sons: New York, NY, USA, 1967. [Google Scholar]
- Mitosek, H.T.; Strupczewski, W.G.; Singh, V.P. Three procedures for selection of annual flood peak distribution. J. Hydrol. 2006, 323, 57–73. [Google Scholar] [CrossRef]
- Kim, J.S.; Yum, B.J. Selection between Weibull and lognormal distributions: A comparative simulation study. Comput. Stat. Data Anal. 2008, 53, 477–485. [Google Scholar] [CrossRef]
- Dey, A.K.; Kundu, D. Discriminating among the log-normal, Weibull, and generalized exponential Distributions. IEEE Trans. Reliab. 2009, 58, 416–424. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Kochanek, K.; Singh, V.P.; Weglarczyk, S. Are Parsimonious Flood Frequency Models More Reliable than the True Ones? I. Accuracy of Quantiles and Moments Estimation (AQME)—Method of Assessment. Acta Geophys. Pol. 2005, 53, 419–436. [Google Scholar]
- Kochanek, K.; Strupczewski, W.G.; Singh, V.P.; Weglarczyk, S. Are Parsimonious Flood Frequency Models More Reliable than the True Ones? II. Comparative assessment of the perfor-mance of simple models versus the parent distribution. Acta Geophys. Pol. 2005, 53, 437–457. [Google Scholar]
- Strupczewski, W.G.; Kochanek, K.; Weglarczyk, S.; Singh, V.P. On robustness of large quantile estimates to largest elements of the observation series. Hydrol. Process. 2007, 21, 1328–1344. [Google Scholar] [CrossRef]
- Strupczewski, W.G.; Singh, V.P.; Mitosek, H.T. Non-stationary approach to at-site flood frequency modelling. III. Flood analysis of Polish rivers. J. Hydrol. 2001, 248, 152–167. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).