Abstract
Natural rivers have many branching junctions. The flow in branching junctions is complex, owing to significant changes associated with flow dynamics and sediment transport that result in erosion and deposition problems. A branching channel of the Tigris River in Missan, Iraq, was selected for investigation of the scouring and deposition zones. A two-dimensional (2D) numerical model was used to simulate the hydro-morphodynamics in the branching channel, where hypothetical vanes as control structures were included at the junction to control the scouring and deposition zones. The simulation results suggest the most effective location, dimension, and angle of the introduced vanes. For the studied junction, controlling morphological features was achieved by introducing a single vane with an inclination angle of 90° on the flow direction of the Tigris River. The most effective location of the introduced vane was the location that caused considerable enhancement in the flow depth and velocity distribution.
1. Introduction
A branching channel or bifurcation is defined as a node where the water flow is divided from a single channel into multiple channels [1]. Branching channels can exist in many forms, such as braided rivers, alluvial fans, and deltas. These forms result from the hydro-morphodynamic processes of the river [1,2]. Man-made branching channels are widely used in irrigation networks, municipal water supplies, and hydropower projects [3]. Studying the flow behaviour in the branching channel and the location of the flow diversion is essential for water management [4] and for morphological management downstream of the diversion [5]. Early studies focused on hydrodynamic features with rigid boundaries, which meant that the experiments did not include sediment transport and movable beds [6,7], but still received attention for their explanations using different parameters and geometric forms [8,9,10,11]. The main hydrodynamic features are the separation zones, stagnation point, and contraction region. Separation zones occur in areas of water recirculation and low flow velocity [8,12]. As a result of the recirculation and low velocities, deposition areas appear in these zones [13,14]. These zones cause loss in the capacity of the branching channel and consequently reduce the inflow discharge passing through it. This will affect irrigation networks and threatens municipal water supplies and operation of power plants [10]. In branching channels, two main separation zones result from the flow, and these zones are shown in Figure 1.
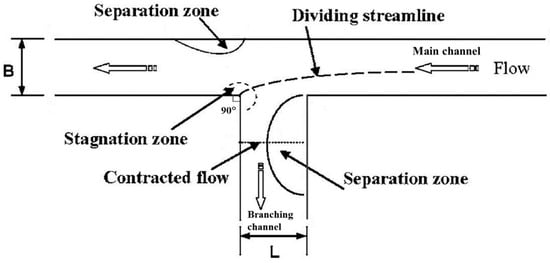
Figure 1.
Characteristics of flow dynamics at a branching channel (Ramamurthy et al. [8]).
Separation zone (1) is developed in the branching channel when the flow in the main channel is discharged toward the branching channel. The size and location of the zone (1) are mainly dependent on the discharge ratio and branching angle. An increase in discharge ratio leads to a decrease in the size of the zone (1) [15]. However, an increase in branching angle from 45° to 90° leads to movement of the separation zone downstream in the branch channel. The smallest separation zone occurred when the branching angle was 30° [16]. Separation zone (2) is formed near the right bank in the main channel and downstream of the branching junction as shown in Figure 1. Zone (2) may not form all the time; it usually forms when the discharge in the branching channel takes the major portion of the discharge from the main channel. This flow condition causes the streamlines to curve towards the branching channel where the separation zone expands [8,14,17].
Another hydrodynamic feature found at the corner downstream of the junction is a stagnation point in which the highest pressure and flow depth are found [8]. The flow contraction zone is formed, owing to the flow separation zone at the beginning of the branching channel. This zone is usually associated with high velocity due to the flow contracted by the separation zone (1). Ramamurthy et al. [18] found a linear relationship between the contraction area and the discharge ratio (the area increases with the increase in discharge ratio). Lama et al. [19] found that the contraction flow width at the bottom of the zone is wider than at the surface.
Two important aspects can be summarised from the morpho-dynamic features, and erosion and deposition zones resulted from the nonuniform sediment movements in the diversion channel. In an early experiment, Bulle [20] recognised sedimentation problems at the branching channel and found that diversion angle, the roundness of the edge of the upstream corner of the diversion, and width ratio between the main and branching channels influence the branching channel behaviour according to the distributions of water and sediment discharge. This had been confirmed by other experimental studies [21,22]. Barkdoll et al. [13] and Herrero et al. [23] observed a scour hole in the main and diversion channel beds at the downstream junction when the diversion angle was 90°. This scour hole was produced by secondary vortexes created in the junction region. These vortexes played a major role in changing the bed morphology in the main and diversion channels. Alomari et al. [16] designated that the branching angle should be decreased as much as possible to decrease the scour depth. They conducted experiments with different diversion angles (30°, 45°, 60°, 75°, and 90°) and observed that the minimum scour depth was associated with a diversion angle of 30°.
Studies on controlling morphological features at the junction region used submerged vanes. These studies tried to manage the movement of sediment accumulation at the branching channel section. Submerged vanes are considered one of the most common ways used to control sediment transport at a branching channel [24,25,26,27]. These submerged vanes are installed in front of the branching channel in the form of rows which created a scour trench [28] to reduce bed load transport from the main channel to the branching channel. The scour trench traps the sediment from the main channel and redirects it downstream of the main channel [29,30]. The size, angle, and number of submerged vanes are considered the most effective parameters in controlling bed sediment movement [31]. Numerous arrangement schemes of vane rows have been investigated to evaluate their performance in preventing bed sediment transport from entering the branching channel and forming the deposition zone. Barkdoll et al. [13] investigated two schemes of submerged vane arrangement and found that these vanes could reduce approximately 40% of the branching sediment discharge when the discharge ratio (the percentage of the branching channel discharge relative to the main channel discharge) is >20%. Another different vane arrangement has been tested in different boundary conditions, such as parallel, regular, and zigzag, installed in different numbers of rows with different angles. Table 1 summarises the several studies that have been conducted experimentally and the practical applications in different sites.

Table 1.
Summary of the studies that used submerged vanes for controlling sediment dynamics at branching channels.
The studies related to the practical application for controlling the sediment that enters the branching channel are those of Wang et al. [30], Nakata and Ogden [32], and Michell et al. [25]. Some limitations and conditions were found in practical cases. For example, Wang et al. [30] found that the vanes are an effective way for controlling sediment at the branching channel when the flow is small enough, and the velocity at the branching channel is <20% of the main upstream flow velocity. While the other researchers (Nakata and Ogden [32] and Michell et al. [25]) combined submerged vanes with other structures such as a skimming or barrier wall to develop a more effective method for controlling sediment movement.
However, we can conclude that the effectiveness of using submerged vanes was limited by flow conditions in which the effective approach had a discharge ratio of up to 20–30%. In some cases, submerged vanes may adversely affect the navigation of the main channel, especially given that these vanes produce a nonuniform velocity distribution near their location [13]. In addition, submerged vanes are potentially costly because of their number. The limitations of using submerged vanes to control and manage hydro-morphodynamics display the importance of investigating different types of obstacles and approaches. However, in the present study, unsubmerged obstacles, such as vanes, are proposed as control structures to manage the hydro-morphodynamic features in branching channels. In general, the obstacle is used to navigate both flow and bed variations. The hydraulic performance of the obstacle mainly depends on its location, dimensions, and morphological conditions [37,38,39]. For this reason, no specific criteria have been established for designing the obstacle in a channel system. Physical or numerical simulation is needed to optimise the design of the obstacle. However, the use of physical models has some limitations, such as high cost, steady flow, and scale effect. On the other hand, numerical models are low-cost and can be used efficiently for unsteady mobile bed conditions.
Thus, a real branching channel was considered as a case study, in which most of the hydro-morphodynamic features were presented (branching channel in the Tigris River, Iraq). In this site, efforts are made almost annually to remove the sediment accumulation at the separation zone by using a sediment dredging boat. Therefore, studies are needed to find an appropriate method for the management of branching channel systems, especially in urban areas. The significance of this study can be attributed to the simulation of various configurations for controlling deposition and scour zones using vanes and the recommendation of the best solution that provides minimum deposition and scouring zones, while enhancing channel flow dynamics.
2. Materials and Methods
2.1. Study Area and Data Acquisition
The Tigris branching channel located in the Missan governorate at the southern part of Al-Iraq was chosen as a case study (Figure 2). The flow in the southern reach of the Tigris River has a significant number of diversion channels, and this branching is considered one of the important junctions in the southern part of the Tigris River system because it is located in the second biggest city in Iraq (Basra city) and many towns depend on its water for municipal and agriculture activities.
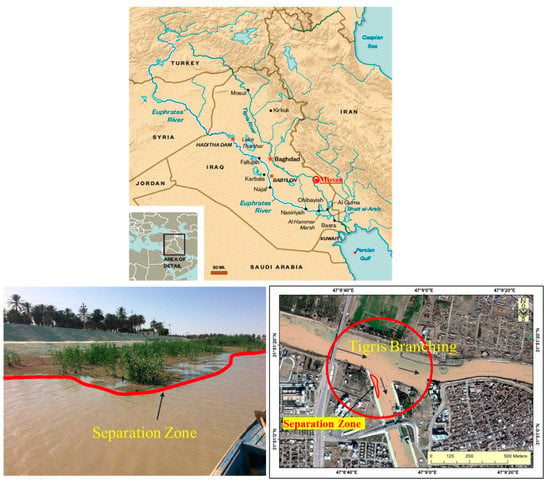
Figure 2.
Tigris branching channel.
Hydro-morphodynamic data of the Tigris branching channel were collected from May to July 2017. Field work included measurements of discharge, velocity, transection geometry (achieved by using the SonTek River Surveyor M9 device), and water levels at various locations in the cross-sections of the main and diversion channels. Bathymetric surveys were conducted using the Garmin echoMap 50s device. For the M9 device, the space between the cross-section was less than 25 m, while for using the echoMap 50s device, the space between the points was around 0.3 m. The slope of the Tigris River at the junction site was measured and found to be 4 cm/km, as it is located in a flat area. The width of the main river is approximately 200 m, while the width of the branching channel is approximately 120 m. The diversion of the branching channel is placed at an angle of 50° from the flow direction of the main Tigris River.
Figure 3 shows the digital elevation map resulting from the measurements of the dense of points at the junction. In addition, Figure 3 represents the velocity distributions along the cross-sections of the inflow discharge of each reach in the Tigris branching junction. The velocity distributions in the cross-sections are as follow: (a) of Q1 with discharge 247 m3/s, (b) of Q2 with discharge 127 m3/s, and (c) of Q3 with discharge 121 m3/s.
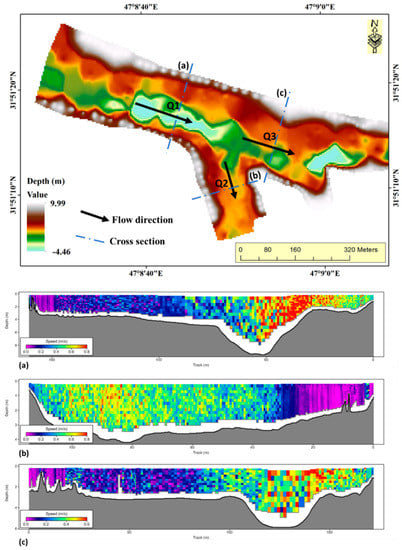
Figure 3.
Observed bathymetry survey, with velocity distribution at each reach of the Tigris branching junction, (a) with discharge 247 m3/s, (b) with discharge 127 m3/s, and (c) with discharge 121 m3/s
Samples from the riverbed were collected using a van Veen grab sampler to specify the soil type, size, and gradation. The samples of bed material were obtained from 14 points to cover the study area of the branching channel. Two methods are used in the laboratory to determine the characteristics of the particles. First is sieve analysis, which is used to determine the particle size distribution of materials with a diameter of >2 mm. The second method is hydrometer analysis, which is used to determine the particles of soil smaller than sieve no. 200 (0.075 mm). However, in this study, hydrometer analysis was used because most of the particles passed through the sieve. The results from the particle size distribution curves for the Tigris branching channel showed that the average median particle dimeter (d50) was approximately 0.055 mm.
However, the dataset that was measured on 11 May 2017 and included discharge, velocity, water level, cross-section geometry, and bathymetry survey was used to build and calibrate the model, while the dataset measured on 20 July 2017 was used to validate the model. Table 2 shows the summary of the field data.

Table 2.
Summary of the field data.
2.2. Critical Velocity of the Sediment Inception Motion
The critical shear velocity () of the bed material in this study was determined using Shield’s diagram. The dimensionless shear stress () expressed in Equation (1) was obtained from the diagram. Critical shear velocity was calculated from Equation (2).
: Critical shear stress of the bed material
: Specific weight of the bed material
: Specific weight of water
: Water density
: Median particle diameter.
By using Shield’s diagram and applying Equations (1) and (2), we obtained a value of 0.013 m/s for the critical shear velocity of the bed material, with a median d50 of 0.055 mm.
For movable bed and sediment transport, knowledge of the threshold point of the sediment particles to be in motion is essential, and most existing studies represent the threshold point of sediment particles in terms of critical mean velocity, . Many methods can be used for estimating critical mean velocity, of which the Simons and Şentürk method, which is shown in Equation (3), is one of the most common [16,40].
: Sediment density.
This equation is frequently adopted to compute the critical mean velocity, and the values range from 0.26 to 0.32 m/s, with low and high water depths (y). Critical velocity is a function of water depth (y), in which the median particle diameter (d50) is known, and the other variables are kept constant for the selected branching of the Tigris River.
2.3. Solver Background, Structure, Characteristics, and Application Procedure
In this study, the solver Mflow_02 was used as a tool to simulate unsteady flow in a selected branching channel of the Tigris River, Iraq. The original version of Mflow_02 was based on the program developed by Tomitokoro et al. [41] and subjected to improvements. The version made by iRIC [42] includes additional functions such as a moving boundary model and riverbed variation calculation. This enables the program to calculate 2D plane unsteady flow and riverbed variation by using unstructured meshes of the finite element method in the orthogonal coordinate system (Cartesian coordinate system). The later development enables the model to reproduce the exact structural shape of a complicated landform, particularly in distributaries and confluences. For this reason, the Mflow_02 solver was used to simulate the hydro-morphodynamics of the selected branching channel of the Tigris River in the Missan governorate of Iraq, including the proposed engineering solutions for controlling the scouring and deposition zones. Two main models are embedded in the Mflow_02 solver, namely the flow field and riverbed variation models. These models have many submodels which can help achieve a wide range of calculations.
2.3.1. Flow Field Model
The characteristics of the flow field model are as follows:
- A Galerkin finite element submodel (a type of weighted residual method) is used to discretize continuity and momentum equations.
- Open boundary conditions (upstream and downstream boundaries, etc.) enable the setting up of various conditions, such as time series of flow discharge, time series of water level, and water level discharge.
- The friction of the river bed can be set by using the Manning roughness coefficient. This coefficient can be represented in the model as a polygon for the entire area or for each element (cell), thus providing spatial distribution of roughness.
- Three submodels are available for computing the turbulence field (flows with large and small eddies). These are the zero equation submodel, simple k-ε, and direct input of kinematic eddy viscosity. In this study, the zero equation submodel was selected because of its stability in calculating large and small eddies. The kinematic eddy viscosity, υ, is expressed by using the von Kàrmàn coefficient with (0.40).: Bottom friction velocity.This formula is called the zero equation submodel for turbulence statistics without a transport equation. In flow fields where the water depth and roughness change gradually in the cross-sections of the branching channel, the kinematic eddy viscosity in horizontal and vertical directions is assumed to be in the same order.
- Other effects, such as the effect of wind on the water surface and of vegetation on flow, are available in this solver but were disregarded in this study.
2.3.2. Riverbed Variation Model
The characteristics of riverbed variation are as follows:
- The riverbed variation associated with the flow field model is calculated. This model can calculate the flow field only or together with riverbed variation.
- The riverbed material can be selected from uniform and mixed grain diameters. If a mixed grain diameter is selected, then a variation in grain distribution can be assumed for deep directions and multiple layers.
- Three methods for calculating the total bed load of depth-averaged flow velocity are available in the Mflow_02 solver, and these are the Meyer-Peter and Müller formula [43], Ashida and Michiue formula [44] and Engrlund–Hansen formula [45]. In this study, the Meyer-Peter and Müller formula was adopted for computing the total bed load.: Gravel density: Critical tractive force (calculated by the Iwagaki formula, [46]): Calculated by Kishi and Kuroki in the formula below [47].: Vertical average flow velocity in the flow direction.The total sediment discharge set by the Meyer-Peter and Müller formula is converted to the normal direction (n) and tangential direction (s) of the streamline, in consideration of the effect of secondary flow and riverbed slope, which is caused by streamline curvature of depth-averaged flow velocity [48].: (s) direction component of sediment discharge near the riverbed: (n) direction component of sediment discharge near the riverbed: Absolute value of velocity near the riverbed: (s) direction component of flow velocity near the riverbed: (n) direction component of flow velocity near the riverbed: Static friction factor: Kinetic friction factor: Height of the riverbed.
- The scour limit of the riverbed, secondary flow coefficient, and morphological factor can be set accordingly.
Figure 4 shows additional details on the solver’s application.
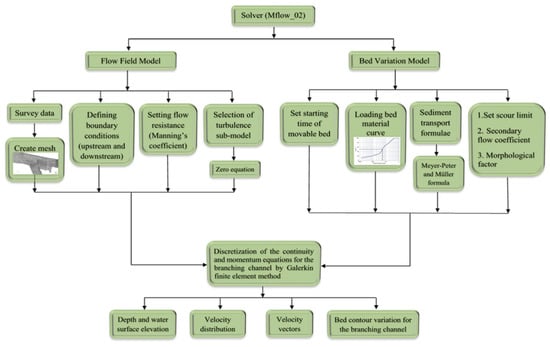
Figure 4.
Flowchart summarizing solver procedures.
2.4. Model Implementation and Boundary Conditions
The Mflow_02 model was used to assess morphological changes in the Tigris branching channel. The initial input data were imported from a bathymetry survey for the branching of the Tigris River. A fine unstructured grid consisting of 4511 nodes was created by drawing many lines until good performance was achieved (Figure 5). A finer grid resolution provides more accurate results, but it needs a small time step (Δt). Time step has a direct relationship with the dimension of the grid () and velocity (), which can be expressed as . In the current model, different time steps were attempted until the hydrodynamic simulation operated smoothly with a time step of 0.04 s. The second input data involved the curves of the grain size distribution of the bed material, in which the average median particles of the Tigris branching channel was approximately 0.055 mm (Figure 6).
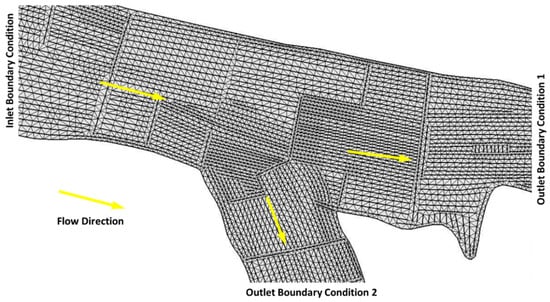
Figure 5.
Unstructured grid of the Tigris branching channel.
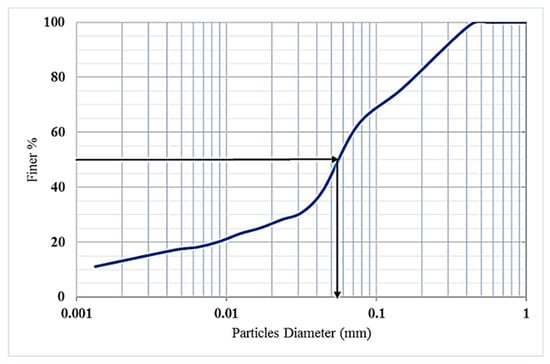
Figure 6.
Particles size distribution of the Tigris branching channel, (d50 = 0.055 mm).
The third input data contained the flow rate at the upstream and the water level at the downstream. A flow rate of 247 m3/s was set in the inlet boundary condition upstream of the Tigris branching channel. Water levels of 7.205 and 7.2 m above mean sea level were set in outlet boundary conditions 1 and 2, respectively, located downstream of the main and branching channels. Among the turbulence models, a zero-equation model was adopted, and a movable bed computation with a starting time of 800 s was set up to provide stability to the flow field mode operation first and then to the sediment transport and bed deformation. For sediment transport computation, Mflow_02 uses the Ashida and Michiue [44], Meyer-Peter and Müller [43], and Engelund–Hansen [45] equations to compute the total bed load transport. In this study, the Meyer-Peter and Müller equation was selected to compute sediment transport because the equation provides reasonable results for simulated bed elevations. The accuracy of the simulated bed elevations was demonstrated in the calibration and validation results of both models. Other settings related to riverbed morphology and sediment transport were as follows: the scour limit of the riverbed in which the selected branching channel has no limit for scouring was set in the model, the secondary flow coefficient was set to 7 (based on the Engelund model [45]), and the morphological factor (the ratio of bed deformation to flow) was set to 1. The above-mentioned setting was considered for a real simulation, in which an increase in one of the values leads to an increase in the bed deformation of the branching channel.
2.5. Unsubmerged Vanes as Control Structures
Many types of obstacles have been used in riverine systems to manage and control the training of the rivers. Spur dykes, vanes, groynes, and weirs are among the obstacles used by the US Army Corps of Engineers [38]. In this study, vanes were used as obstacles to assess the hydro-morphodynamics of the branching channel. This type of structure was introduced in the model by creating a polygon that was excluded throughout the mesh computing and regarded by the model as a nonerodible material [42]. The impact of the following four configurations on the flow in a branching of the Tigris River was clearly shown in the computations of riverbed variation and velocity distribution with the development, appearance, and movement of the sandbar.
- Two vanes 30 m long and an inclination angle of 15° from the axis perpendicular to the flow of the main river
- Two vanes 30 m long perpendicular to the direction of the flow of the main river
- A single vane 50 m long with an inclination angle of 30° from the axis perpendicular to the flow of the main river
- A single vane 50 m long perpendicular to the direction of the flow of the main river.
2.6. Statistical Indices
Four statistical indices were used to assess the accuracy of the prediction of the Mflow_02 model, and these were mean absolute deviation (MAD), mean square error (MSE), root mean square error (RMSE), and mean absolute percentage error (MAPE). The criterion for using these methods is to determine the accuracy of the simulation, in which a low statistical value between measured and predicted values indicates high accuracy of simulation performance. These methods can be described by the following equations.
: Amount of data used
M: Measured value
S: Simulated value.
3. Results and Discussion
3.1. Model Calibration
The model was calibrated with Manning’s roughness, in which the adopted value was calculated as n = 0.03 based on field measurements [49], node number, time step, and turbulence model until good agreement was found between the model predictions and measured data on depth-averaged velocity, water surface elevation, and bed elevation. Figure 7, Figure 8, and Figure 9 displayed the simulation results of the velocity magnitude, water surface elevation, and depth, respectively. The results of velocity magnitude for running the model for 24 h (simulation time of the model calibration) and average values of the simulated velocities along the cross-sections at different times (1, 6, 12, 18, and 24 h) are shown in Figure 7. The results of the calibration flow velocities at different times confirmed the stability of the software and the extent to which the velocity changed during the 24 h duration.
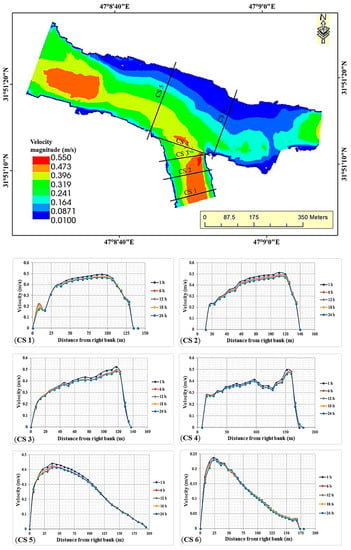
Figure 7.
Simulation results for velocity magnitude at the Tigris branching junction and profiles of average flow velocity in m/s within 24 h at cross-sections CS 1, CS 2, CS 3, CS 4, CS 5, and CS 6.
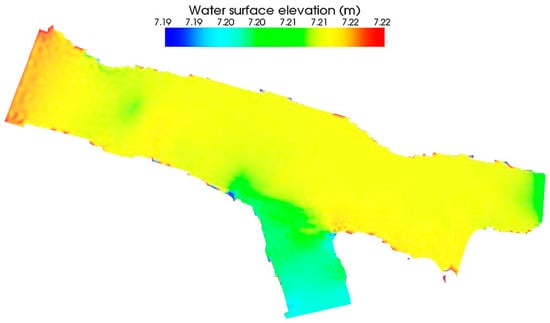
Figure 8.
Simulation of water surface elevation of the Tigris branching junction.
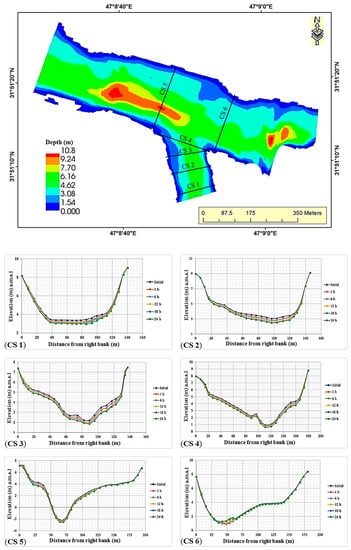
Figure 9.
Depth simulation of the Tigris branching junction and profiles of simulated bed elevation (m) within 24 h at cross-sections CS 1, CS 2, CS 3, CS 4, CS 5, and CS 6.
Four statistical indices were used to assess the accuracies of the measured and predicted average flow velocities of the model calibration. These indices are MAD in Equation (10), MSE in Equation (11), RMSE in Equation (12), and MAPE in Equation (13). The assessment results of these statistical indices are shown in Table 3. The error values differ because they depend on the concept behind each statistical index. A maximum error of approximately 9.5% was associated with MAPE. In general, MAPE provides values higher than those of other methods because it represents the difference between the measured and predicted values as a percentage of the measured values. In addition, a graphical comparison between measured and simulated average velocity along the cross-sections was plotted to evaluate the performance of the model calibration predictions (Figure 10a). The solid line in Figure 10 represents the line of perfect agreement, while the two hidden lines represent bounds of 25% deviation from the line of the perfect agreement. However, the measured and simulated average velocities are observed to match well.

Table 3.
Statistical indices for measured and simulated average velocities.
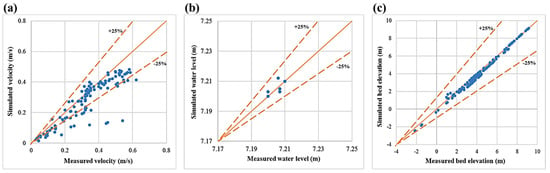
Figure 10.
Comparison between measured and simulated data used in the model calibration (a) averaged velocity; (b) water level; (c) bed elevation.
The simulation of water surface elevation is shown in Figure 8. The simulated and measured water surface elevations at different locations were found with minimum errors because the boundary condition at the outlets is time-varying elevation. Figure 10b shows the measured values versus simulated values. The values of MAD, MSE, RMSE, and MAPE between the measured and simulated results were 0.002 m, 1 × 10−5 m, 0.003 m, and 0.035%, respectively.
To ensure the accuracy of the morpho-dynamic simulation, calibrations were performed by comparing the simulated and measured bed elevations. Figure 9 shows the depth simulation with the locations of six cross-sections at the branching of the Tigris River. These sections were used to demonstrate the differences between the measured and simulated bed elevations. The calibrations were based on the model output obtained after running the model continuously for 24 h. The comparisons showed good agreement between the simulated and measured bed elevations (Figure 10c), thus confirming the accuracy of the model output.
3.2. Model Validation
The model was validated using the recorded data of the Tigris branching channel at the Missan site for a period of one week, in order to improve and display the accuracy of the simulation for the selected case study. Comparisons were performed between the simulated and measured water levels, average depths, average velocities, and bed elevations. The discharge of the Tigris branching channel at Missan is fully controlled by many regulators upstream of the site. This is the main reason why the inflow discharge at this site does not change much on a daily or weekly basis. Table 4 shows the data of the discharges in the upstream location and water levels downstream of the main and branching channel. The model’s running time was approximately three days for seven days’ worth of data, with 4511 nodes and time steps of 0.04 s.

Table 4.
Discharge and water level of the Tigris branching channel used for model validation.
To demonstrate the accuracy of model prediction, the simulation results on the third day (with a discharge of 119.3 m3/s) were compared with measured data for water level, average flow depth, average velocity, and bed elevation, and the results were shown in Table 5 and Table 6, and Figure 11, respectively. The model output showed that the simulation of water levels was highly accurate according to the values of the four statistical indices (Table 5). The values of MAD, MSE, RMSE, and MAPE were 0.002 m, 8 × 10−6 m, 0.003 m, and 0.038%, respectively; the simulated average flow depth was within the observed range, and the values of the statistical indices were 0.407 m, 0.181 m, 0.426 m, and 18.33% respectively. On top of that, a graphical comparison in Figure 12 shows the accuracy of the model validation and the errors of the simulated values from the measured values.

Table 5.
Comparisons of water level and average flow depth.

Table 6.
Comparisons between measured and simulated average flow velocity.
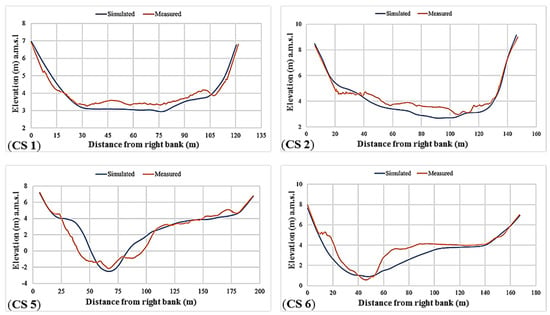
Figure 11.
Comparison of measured and simulated bed elevations at CS 1, CS 2, CS 5, and CS 6.
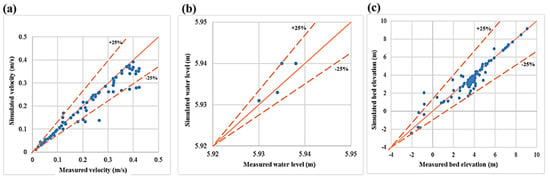
Figure 12.
Comparison between measured and simulated data used in the model validation (a) averaged velocity; (b) water level; (c) bed elevation.
The simulated average velocities were in agreement with the measured average velocities, as shown in Table 6 and Figure 12a. The simulated velocities were lower than the measured velocities, and the values of the statistical indices were 0.042 m, 0.002 m, 0.04 m, and 16.38%. The errors refer to the uncertainties in both measured and predicted values. Papanicolaou et al. [50] reported that the typical acceptable errors in depth and velocity predictions are in the range of 25% to 35%. Pinto et al. [51] suggested accepting the underprediction in velocity because it results in fewer errors. Thus, the range of errors mentioned above is acceptable when compared with other simulated results [37,52].
With regard to the morphological validation, Mflow_02 showed the model’s ability to simulate morphological changes such as scouring, deposition, and movement of sediment transport, leading to changes in the cross-sections. The simulated and measured cross-sections are shown in Figure 11.
The results of the simulated bed elevations were found to be in agreement, particularly in cross-sections 1 and 2, and lesser degrees of agreement were observed for cross-sections 5 and 6. The errors between the measured and simulated bed elevations were within the range of 25% as shown in Figure 12c. The errors could be attributed to the spatial locations of the collected data and to the complex river reach geometry. Papanicolaou et al. [53] related the sources of errors to computational errors from the numerical schemes used to solve the governing equations and to the truncation errors from the discretisation. In addition, data collection could be another source of error. For example, the eddy viscosity models used in solving the governing hydrodynamic equations for turbulent flows had some degree of empiricism in their formulations.
3.3. Model Simulation of Tigris Branching Junction with Vanes
The suggested vane arrangements in Section 2.5 were evaluated by introducing unsubmerged vanes as control structures to enhance the hydraulic efficiency of the Tigris branching junction. Eight model iterations with vanes were compared with data from the model without using the vanes. The time for running each model was approximately three days. The effects of the vanes on the flow in the Tigris branching junction include variation of the riverbed, changes in the pattern of velocity distribution, and movement of a sandbar. Simulations of the Tigris branching channel bathymetry with and without vanes for two different seasons with low and high discharges were conducted. The results of the simulations were observed and marked as hydro-morphodynamic changes in the flow depth, deposition zone, scouring zone, and velocities with the corresponding vectors. The details and evaluations of these models can be summarised for the following four configurations.
3.3.1. First Configuration: Two Vanes of Length 30 m Each
Two vanes of length 30 m each were placed at the junction, one at the beginning of the separation zone and the other in front of the scouring zone, almost at the centre of the junction, as shown in Figure 13b. The angle of the obstacle was adjusted to be around 15°, as recommended by Odgaard and Spoljaric [28] and Barkdoll et al. [13]. They reported that the scour depth increased with an increase in the obstacle angle, which is why the vane was installed at an angle of 15°. Each model was run for seven days, with a low discharge of 120 m3/s (dry season) and high discharge of 247 m3/s (wet season); the greatest change in the hydro-morphodynamic features was associated with the high-flow season. Model outputs of this configuration were compared with the outputs of other configurations (Figure 13 and Figure 14). The results of the simulation with and without obstacles show that the velocity at the upstream location of the junction is always higher than the velocity downstream. The low velocity zones that were recognised at the branching channel of the Tigris River were also observed in other experimental studies [8,16] and denoted as flow separation zones. The first low-velocity zone appears in the main river opposite to the branching channel entrance downstream of the junction. This zone is formed owing to the movement of the streamlines from the main river towards the branching channel. The streamlines attempt to align and transfer to a uniform flow state in the main river after passing the junction. The second low-velocity zone is formed upstream near the right bank of the branching channel. This zone is formed owing to flow contraction at the beginning of the branching channel. For bed topography, two sediment deposition areas are formed with low-velocity zones; the larger of the two areas is located on the right side of the upstream branching channel and considered as one of the most important features that affect the inflow discharge pass through the branching junction. The erosion zone (scour hole) was found on the left side of the flow downstream of the branching channel [23]. This zone was associated with a region of high velocity and vortexes. Vanes were installed to manage the flow at the diversion channel through redirecting the inflow discharge toward the flow separation zone, which consequently led to increased velocity in this area and the deposition zone diminishing over time. The process of deposition zone removal occurs when the velocity of the flow is greater than the critical velocity of the deposition particles. The critical mean velocity was determined based on the Simons and Şentürk equation, and the values for the studied branching channel ranged from 0.26 to 0.32 m/s. The results of this configuration show that there are noticeable changes in the flow depth, velocity distribution with the vectors, and shape of the attached bar at the deposition zone. The flow depths increase at the locations of the vanes, wherein the velocities increased marginally, especially in front of the vane, while the minimum velocity was observed behind the vane (Figure 14b). Furthermore, the simulation results show the existence of a small point bar, which indicates that the velocity and sediment transport distributions in the branching channel section are not uniform. The existing deposition zone area was found to be 3261 m2, and when the vanes were used, this area reduced to 1422 m2; as a percentage, this reduction is approximately 56% compared with the case where no vanes are used (Figure 13a).
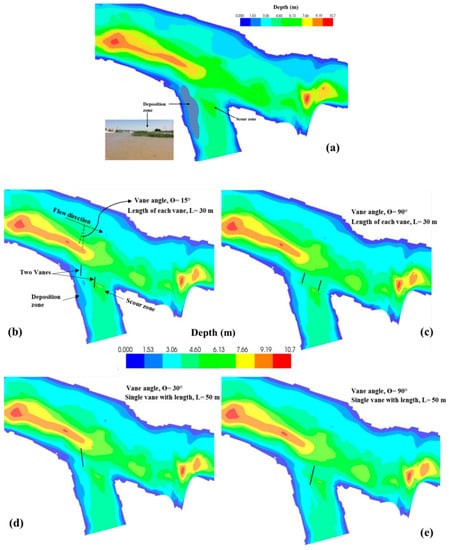
Figure 13.
Simulated flow depth for the study site (a) without vanes structure; (b) First configuration; (c) Second configuration; (d) Third configuration; (e) Fourth configuration.
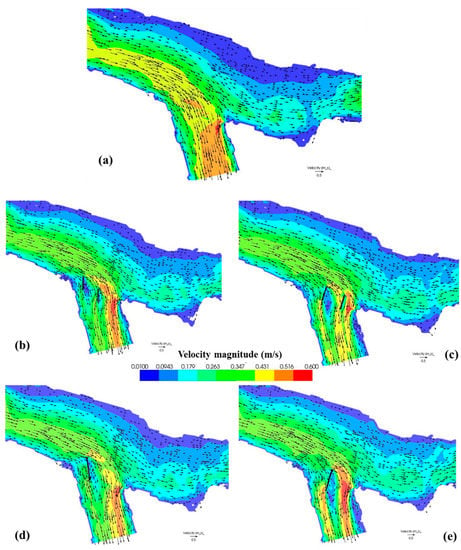
Figure 14.
Simulated velocity distribution with its vectors for the study site (a) without vanes structure; (b) First configuration; (c) Second configuration; (d) Third configuration; (e) Fourth configuration.
3.3.2. Second Configuration: Two Vanes of Length 30 m Each and Perpendicular to the Direction of Flow in the Main River
In the second configuration, the simulations were conducted using two vanes of length 30 m each, which were placed at 90° to the flow direction in the main part of the Tigris (Figure 13c). One vane is placed near the flow separation zone to redirect the flow toward this zone and to increase the velocity. The second vane is placed next to the scour zone to reduce the flow velocity. The simulation results show that the flow depths and velocities in the separation zone (deposition zone) increased, and the area of the deposition zone reduced to 913 m2, which is approximately 72% compared with the case of no vane. Flow depths increased in the deposition zone by 1.2 m, and the volume of sediment removed was approximately 2817 m3. This increment occurs owing to the removal of sedimentation when the mean velocity increases and exceeds the critical mean velocity of the sediment (Figure 14c). Increasing velocities lead to increases in bottom friction velocity (), and this value has a direct effect on the calculation of riverbed shear stress (). Increasing the riverbed shear stress leads to strengthening of the amount of sediment eroded from the flow separation zone, which in turn increases the flow depth. The velocity distribution and its vectors after the vanes appear to be equally distributed along the transverse direction of the branching channel after the obstacles, with their values ranging between 0.347 and 0.431 m/s. The results of this configuration were compared with the first configuration, and it is shown that the location and angle of the vane are important factors that affect the morphological changes in the branching channel. However, the results of this configuration provide significant improvements to the hydro-morphodynamics of the branching channel.
3.3.3. Third Configuration: A Single Vane of Length 50 m at an Inclination of 30° from the Axis Perpendicular to the Flow in the Main River
A single vane of length 50 m was placed upstream of the branching channel near the right corner with an angle of approximately 30° (Figure 13d). This vane was installed to maintain the hydro-morphodynamics of the branching channel with focus on increasing inflow discharge and velocity toward the deposition zone. The results of the simulated flow depth and velocity distribution with the associated vectors are shown in Figure 13d and Figure 14d. The remarkable result observed with this configuration is the area of the minimum velocity behind the vane, which could be attributed to the angle of the vane with the direction of the flow. The velocity distribution in this configuration with an angle of 30° displays the best velocity uniformity among all configurations with vane angles in the range of 15° to 90°. The velocity magnitude at the flow separation zone increased from around 0.24 to 0.35 m/s, and the flow depth is also increased slightly. The area of the deposition zone changed naturally and decreased by about 65% when compared with the simulations without the vane (Figure 13a); however, there is still a noticeable narrowing of the attached bar on the right bank of the branching channel (Figure 13d).
3.3.4. Fourth Configuration: A Single Vane of Length 50 m and Perpendicular to the Direction of Flow in the Main River
In this configuration, a single vane of length 50 m was placed at the centre of the branching channel perpendicular to the flow of the main river (Figure 13e). The vane was mounted between the separation and scour zones to increase the velocities toward the separation zone and decrease the velocities at the scouring zone. The simulated flow depth and velocity distribution with the associated vectors are shown in Figure 13e and Figure 14e. This configuration offered a good solution because the deposition zone and maximum scour hole were maintained. The flow depths and distribution of velocities at the deposition area were found to be high compared with those of other configurations, as shown in Figure 13 and Figure 14. The velocity in the flow separation zone exceeded 0.45 m/s, which increased the amount of sediment transport from this area; the flow depth increased from around 1.8 to 3 m. The deposition zone formation was decreased by approximately 82% compared with the simulation case with no vane, in which the area of the deposition zone was reduced from 3261 to 594 m2, and the volume of sediment removed was around 3200 m3.
3.4. Discussion on Recommended Configurations
The comparison between different configurations revealed that the second and fourth configurations provide the best solutions for maintaining morphodynamics at the branching channel through the diminishing of the deposition zone and increase of navigation depth, while the third configuration demonstrated more uniformity in the velocity distribution but less impact on improving the morphology of the branching channel. Also, the comparison of different vane configurations showed that not much change occurred in erosion zone (scour zone), in which this zone was maintained and decreased slightly when compared with the simulation without vanes. The significant observations in these configurations were the reduction in the separation zone and the uniformity of velocity distribution after using the vanes. The summary of the results is shown in Figure 15, in which the velocities at the deposition zone increased from 0.24 to 0.3, 0.39, 0.35, and 0.45 m/s, consequently with area reduction from 3261 to 1422, 913, 1114, and 594 m2, respectively, for the first, second, third, and fourth configurations.
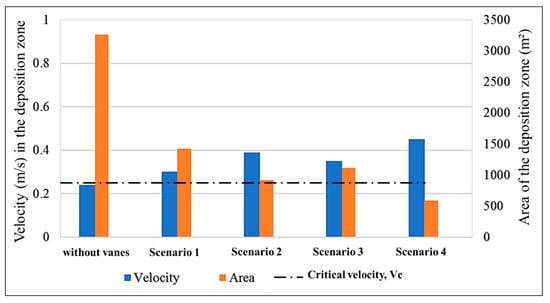
Figure 15.
Impact of using vanes on velocity and reduction area in the deposition zone for the studied configurations.
The results show that the fourth configuration has the best solution for minimising the deposition zone and increasing channel navigation, in which the velocities doubled in this zone and led to increasing bed sediment transport. This solution worked when used to remove the deposition zone in the branching channel located in the Tigris river at Missan governorate. The branching channel had an angle of 50°, median particle diameter d50 of 0.055 mm, and discharge ratio of 52% (at wet season). Furthermore, simulation results during the dry season showed a good production in managing and reduction of the deposition zone. The average velocity in the deposition zone increased from 0.14 to 0.3 m/s and led to enhancing the sediment transport. As a result, the flow depth increased by approximately 0.5 m at many locations along the deposition zone. Figure 16 shows the simulation results during the dry season with and without vanes (fourth configuration) on the flow depth, and velocity distribution with its vectors.
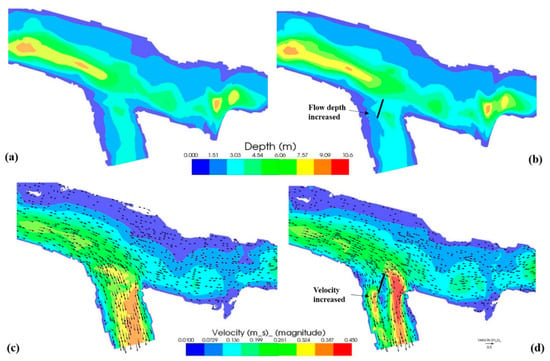
Figure 16.
Simulation of flow depth and velocity distribution with its vectors during low flow conditions. (a) Simulated flow depth without vane; (b) Simulated flow depth with vane; (c) Simulated velocity distribution with its vectors without vane; (d) Simulated velocity distribution with its vectors with vane.
However, when comparing the results of this research work with others listed in Table 1, in which submerged vanes were used for managing hydro-morpho dynamics, the results of Allahyonesi et al. [33], AbdelHaleem et al. [34], and Moghadam and Keshavarzi [35] ranged between 40 and 75%, while five studies performed by Nakata and Ogden [32] gave more than 75% due to a sediment-barrier wall with sets of submerged vanes to enhance its performance. The limitations associated with submerged vanes are restriction of navigation and production of nonuniform velocity distribution. Therefore, this research work adopted unsubmerged vanes and the best solution consisted of introducing a single unsubmerged vane.
4. Conclusions
The control of flow in a branching open channel is complex, and this can be attributed to the formulation of different hydro-morphodynamic features at its location. A 2D numerical model was used to simulate the hydro-morphodynamics of the branching channel with an angle of 50° in the Tigris River, Missan, Iraq. The numerical model was calibrated and validated using field data. Vanes were proposed to control the attached bar at the deposition zone and the scour hole at the erosion zone that usually exist in the benching channel. Furthermore, the Mflow_02 model was applied to simulate the morphological changes for different configurations with and without vanes. The results show that introducing a single obstacle at an angle of 90° on the flow direction of the main river (fourth configuration) was a successful solution compared with other configurations in terms of reducing the deposition and scouring zones. Future studies may apply the proposed mitigation procedure in other study areas to validate the performance of introducing a single vane. Furthermore, other shapes of a single vane can be tested in the selected study areas. In summary, this study addressed the applicability of using a 2D numerical model in a complex riverine system for predicting and managing hydro-morphodynamic changes with and without vanes as training structures in a dynamic branching channel.
Author Contributions
B.Y. and H.L.A. conceptualization the overall idea of this research. T.A.M. and H.L.A. designed overall the methodology; Y.S. provided the software with training; H.L.A. carried out the computer simulations; H.L.A. wrote the paper; M.S.A.R. and B.M.R. review and editing the paper.
Funding
This research received no external funding and the APC was funded by Universiti Putra Malaysia.
Acknowledgments
I would like to express my sincere appreciation and deepest gratitude to my friends that helping me to collect the data and those are Ali Mutar Fanos, PhD-GIS and Geomatics Engineering, Abdulzahra Alhello, University of Basrah Department of Environmental Chemistry, and engineer Falih Hareja for his hospitality and great arrangement to achieve the data collection at Missan Governorate. I also would extend my thanks to General Director Samira Abed and my colleagues Ali Aboalasal, Suray Hameed, and Kareem Audah in Center for the Restoration of the Iraqi Marshlands and Wetlands (CRIMW).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kleinhans, M.G.; Ferguson, R.I.; Lane, S.N.; Hardy, R.J. Splitting rivers at their seams: Bifurcations and avulsion. Earth Surf. Process. Landf. 2013, 38, 47–61. [Google Scholar] [CrossRef]
- Redolfi, M.; Zolezzi, G.; Tubino, M. Free instability of channel bifurcations and morphodynamic influence. J. Fluid Mech. 2016, 799, 476–504. [Google Scholar] [CrossRef]
- Meselhe, E.A.; Sadid, K.M.; Allison, M.A. Riverside morphological response to pulsed sediment diversions. Geomorphology 2016, 270, 184–202. [Google Scholar] [CrossRef]
- Yousefi, S.; Ghiassi, R.; Yousefi, S. Modelling and analyzing flow diversion in branching channels with symmetric geometry. River Res. Appl. 2011, 27, 805–813. [Google Scholar] [CrossRef]
- Baker, D.W.; Bledsoe, B.P.; Albano, C.M.; Poff, N.L. Downstream effects of diversion dams on sediment and hydraulic conditions of Rocky Mountain streams. River Res. Appl. 2011, 27, 388–401. [Google Scholar] [CrossRef]
- Taylor, E.H. Flow characteristics at rectangular open-channel junctions. Trans. Am. Soc. Civ. Eng. 1944, 109, 893–902. Available online: https://ci.nii.ac.jp/naid/10003774753/ (accessed on 6 September 2019).
- Grace, J.L.; Priest, M.S. Division of Flow in Open Channel Junctions; Engineering Experiment Station, Alabama Polytechnic Institute: Auburn, AL, USA, 1958. [Google Scholar]
- Ramamurthy, A.S.; Qu, J.; Vo, D. Numerical and experimental study of dividing open-channel flows. J. Hydraul. Eng. 2007, 133, 1135–1144. [Google Scholar] [CrossRef]
- Mignot, E.; Zeng, C.; Dominguez, G.; Li, C.W.; Rivière, N.; Bazin, P.H. Impact of topographic obstacles on the discharge distribution in open-channel bifurcations. J. Hydrol. 2013, 494, 10–19. [Google Scholar] [CrossRef]
- Mignot, E.; Doppler, D.; Riviere, N.; Vinkovic, I.; Gence, J.N.; Simoens, S. Analysis of flow separation using a local frame axis: Application to the open-channel bifurcation. J. Hydraul. Eng. 2013, 140, 280–290. [Google Scholar] [CrossRef]
- Seyedian, S.M.; Bajestan, M.S.; Farasati, M. Effect of bank slope on the flow patterns in river intakes. J. Hydrodyn. 2014, 26, 482–492. [Google Scholar] [CrossRef]
- Neary, V.; Sotiropoulos, F.; Odgaard, A. Three-dimensional numerical model of lateral-intake inflows. J. Hydraul. Eng. 1999, 125, 126–140. [Google Scholar] [CrossRef]
- Barkdoll, B.D.; Ettema, R.; Odgaard, A.J. Sediment control at lateral diversions: Limits and enhancements to vane use. J. Hydraul. Eng. 1999, 125, 862–870. [Google Scholar] [CrossRef]
- Shamloo, H.; Pirzadeh, B. Numerical investigation of velocity field in dividing open-channel flow. In Proceedings of the 12th WSEAS International Conference on Applied Mathematics, Cairo, Egypt, 29–31 December 2007; pp. 194–198. [Google Scholar]
- Goudarzizadeh, R.; Hedayat, N.; Jahromi, S.M. Three-dimensional simulation of flow pattern at the lateral intake in straight path, using finite-volume method. World Acad. Sci. Eng. Technol. 2010, 47, 656–661. [Google Scholar]
- Alomari, N.K.; Yusuf, B.; Mohammad, T.A.; Ghazali, A.H. Experimental investigation of scour at a channel junctions of different diversion angles and bed width ratios. CATENA 2018, 166, 10–20. [Google Scholar] [CrossRef]
- Satish, M.; Ramarnurthy, A.; Narasiah, K. Pressure recovery in dividing open channels. J. Hydraul. Eng. 1989, 115, 995–999. [Google Scholar] [CrossRef]
- Ramamurthy, A.; Zhu, W.; Carballada, B. Dividing rectangular closed conduit flows. J. Hydraul. Eng. 1996, 122, 687–691. [Google Scholar] [CrossRef]
- Lama, S.K.; Kuroki, M.; Hasegawa, K. Study of flow bifurcation at the 30° open channel junction when the width ratio of branch channel to main channel is large. Annu. J. Hydraul. Eng. JSCE 2002, 46, 583–588. [Google Scholar] [CrossRef][Green Version]
- Bulle, H. Untersuchungen Über die geschiebeableitung bei der Spaltung von Wasserläufen; Forschungsarbeiten auf dem Gebiete des Ingenieurwesens; VDI-Verl.: Berlin, Germany, 1926; Volume 282, pp. 57–84. (In German) [Google Scholar]
- Rezapour, S.; Moghadam, K.F.; Omid Naceni, S.T. Experimental study of flow and sedimentation at 90° openchannel diversion. In Proceedings of the 33rd IAHR Congress, Vancouver, BC, Canada, 9–14 August 2009; pp. 2979–2986. [Google Scholar]
- Riad, K. Analytical and Experimental Study of Bed Load Distribution at Alluvial Diversions. Ph.D. Thesis, Department of Engineering, Delft University of Technology, Delft, The Netherlands, 1961. [Google Scholar]
- Herrero, A.; Bateman, A.; Medina, V. Water flow and sediment transport in a 90° channel diversion: An experimental study. J. Hydraul. Res. 2015, 53, 253–263. [Google Scholar] [CrossRef]
- Neill, C.R.; Evans, B.J.; Odgaard, A.J.; Wang, Y. Discussion and Closure: Sediment Control at Water Intakes. J. Hydraul. Eng. 1997, 123, 670–671. [Google Scholar] [CrossRef]
- Michell, F.; Ettema, R.; Muste, M. Case study: Sediment control at water intake for large thermal-power station on a small river. J. Hydraul. Eng. 2006, 132, 440–449. [Google Scholar] [CrossRef]
- Odgaard, A.J. River Training and Sediment Management with Submerged Vanes; ASCE Press: Reston, VA, USA, 2009. [Google Scholar]
- Beygipoor, G.; Bajestan, M.S.; Kaskuli, H.A.; Nazari, S. The effects of submerged vane angle on sediment entry to an intake from a 90 degree converged bend. Adv. Environ. Biol. 2013, 7, 2283–2292. [Google Scholar]
- Odgaard, A.J.; Spoljaric, A. Sediment control by submerged vanes. J. Hydraul. Eng. 1986, 112, 1164–1180. [Google Scholar] [CrossRef]
- Ouyang, H.T.; Lai, J.S.; Yu, H.; Lu, C.H. Interaction between submerged vanes for sediment management. J. Hydraul. Res. 2008, 46, 620–627. [Google Scholar] [CrossRef]
- Wang, Y.; Odgaard, A.J.; Melville, B.W.; Jain, S.C. Sediment control at water intakes. J. Hydraul. Eng. 1996, 122, 353–356. [Google Scholar] [CrossRef]
- Odgaard, A.J.; Wang, Y. Sediment management with submerged vanes. I: Theory. J. Hydraul. Eng. 1991, 117, 267–283. [Google Scholar] [CrossRef]
- Nakato, T.; Ogden, F.L. Sediment control at water intakes along sand-bed rivers. J. Hydraul. Eng. 1998, 124, 589–596. [Google Scholar] [CrossRef]
- Allahyonesi, H.; Omid, M.H.; Haghiabi, A.H. A study of the effects of the longitudinal arrangement sediment behavior near intake structures. J. Hydraul. Res. 2008, 46, 814–819. [Google Scholar] [CrossRef]
- Abdel Haleem, F.; Helal, Y.; Ibrahim, S.; Sobeih, M. Sediment control at river intakes using a single row of vanes. Ain Shams J. Civ. Eng. 2008, 2, 395–401. [Google Scholar]
- Moghadam, M.K.; Keshavarzi, A.R. An optimised water intake with the presence of submerged vanes in irrigation canals. Irrig. Drain. 2010, 59, 432–441. [Google Scholar] [CrossRef]
- Mirzaei, S.H.S.; Ayyoubzadeh, S.A.; Firoozfar, A.R. The effect of submerged-vanes on formation location of the saddle point in lateral intake from a straight channel. Am.J. Civ. Eng. Archit. 2014, 2, 26–33. [Google Scholar]
- Karmaker, T.; Dutta, S. Prediction of short-term morphological change in large braided river using 2D numerical model. J. Hydraul. Eng. 2016, 142, 04016039. [Google Scholar] [CrossRef]
- USACE (U.S. Army Corps of Engineers). Upper Mississippi River Restoration Environmental Management Program, Environmental Design Handbook; USACE: Washington, DC, USA, 2012.
- Bhuiyan, F.; Hey, R.D.; Wormleaton, P.R. Bank-attached vanes for bank erosion control and restoration of river meanders. J. Hydraul. Eng. 2010, 136, 583–596. [Google Scholar] [CrossRef]
- Simons, D.B.; Şentürk, F. Sediment Transport Technology: Water and Sediment Dynamics; Water Resources Publication: Highlands Ranch, CO, USA, 1992. [Google Scholar]
- Tomidokoro, G.; Araki, M.; Yoshida, H. Three-Dimensional Analysis of Open Channel Flows. Annu. J. Hydraul. Eng. 1985, 29, 727–732. [Google Scholar]
- iRIC. Mflow_02 Solver Manual Produced by Mineyuki Gamou. 10 July 2014. Available online: http://i-ric.org/en/software/?c=19 (accessed on 6 September 2019).
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Delft, The Netherlands, 7 June 1948; Volume 2, pp. 39–64. [Google Scholar]
- Ashida, K.; Michiue, M. Study on hydraulic resistance and bedload transport rate in alluvial streams. Transcr. Jpn. Soc. Civ. Eng. 1972, 1972, 59–69. [Google Scholar] [CrossRef]
- Engelund, F. Flow and bed topography in channel bends. J. Hydraul. Div. 1974, 100, 1631–1648. [Google Scholar]
- Iwagaki, Y. Hydrodynamical Study on Critical Tractive Force. J. Jpn. Soc. Civ. Eng. 1956, 41, 1–21. [Google Scholar] [CrossRef]
- Kishi, T.; Kuroki, M. Bed Forms and Resistance to Flow in Erodible-Bed Channels (1). Bull. Fac. Eng. Hokkaido Univ. 1973, 67, 1–23. (In Japanese) [Google Scholar]
- Hasegawa, K. Hydraulic Study on Alluvial Meandering Channel Planes and Bedform Topography-Affected Flows. Ph.D. Thesis, Hokkaido University, Sapporo, Japan, 1984. [Google Scholar]
- Ali, A. Three Dimensional Hydro-Morphological Modeling of Tigris River. Ph.D. Thesis, Luleå Tekniska Universitet, Luleå, Sverige, 2016. [Google Scholar]
- Papanicolaou, A.N.; Elhakeem, M.; Dermisis, D.; Young, N. Evaluation of the Missouri River shallow water habitat using a 2D-hydrodynamic model. River Res. Appl. 2011, 27, 157–167. [Google Scholar] [CrossRef]
- Pinto, L.; Fortunato, A.; Freire, P. Sensitivity analysis of non-cohesive sediment transport formulae. Cont. Shelf Res. 2006, 26, 1826–1839. [Google Scholar] [CrossRef]
- Papanicolaou, A.N.; Elhakeem, M.; Wardman, B. Calibration and verification of a 2D-hydrodynamic model for simulating flow around bendway weir structures. J. Hydraul. Eng. 2010, 75–89. [Google Scholar] [CrossRef]
- Papanicolaou, A.T.N.; Elhakeem, M.; Krallis, G.; Prakash, S.; Edinger, J. Sediment transport modeling review—Current and future developments. J. Hydraul. Eng. 2008, 134, 1–14. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).