Abstract
Wherever the flow of water in a gravity pipeline is regulated by a pressure control valve, hydraulic energy in the form of water pressure can instead be converted into useful mechanical and electrical energy via a turbine. Two classes of potential turbine sites exist—those with (class 1, “buffered”) and those without (class 2, “non-buffered”) a storage tank that decouples inflow from outflow, allowing the inflow regime to be modified to better suit turbine operation. A new method and Excel tool (freely downloadable, at no cost) were developed for determining the optimal hydraulic parameters of a turbine at class 1 sites that maximize annual energy generation. The method assumes a single microturbine with a narrow operating range and determines the optimal design flow rate based on the characteristic site curve and a historical time series of outflow data from the tank, simulating tank operation with a numerical model as it creates a new inflow regime. While no direct alternative methods could be found in the scientific literature or on the internet, three hypothetically applicable methods were gleaned from the German guidelines (published by the German Technical and Scientific Association for Gas and Water (DVGW)) and used as a basis of comparison. The tool and alternative methods were tested for nine sites in Germany.
1. Introduction
1.1. Advantages and Characteristics of Potential Drinking Water Hydropower Facilities
Hydropower is among the renewable energy sources with the best life-cycle energy balance—the ratio between the energy output (e.g., electricity) and the energy input required to manufacture, install, operate and dispose of the infrastructure and equipment needed for energy generation [1,2]. Drinking water hydropower has further advantages compared to much larger hydropower facilities at dams, weirs and run-of-river schemes, including high water quality (enabling long lifetime and low-maintenance operation), minimal to no environmental impact (due to a previously existing, closed system) and relatively good economic viability [2,3,4]. Thanks to technological progress, capitalizing on drinking water hydropower potential is increasingly becoming economically viable even at the bottom of the capacity spectrum, below 10 kW of available hydraulic power [4,5,6,7,8,9]. Practical methods and easy-to-use design tools play an important role in facilitating the implementation of such projects.
A gravity pipeline is the central element of most drinking water hydropower schemes, connecting a higher-elevation water source to lower-elevation water storage tanks and water users. With respect to hydropower development, there are two relevant types of gravity pipelines: those with and those without pressure control at points downstream, such as transfer stations or outlets into storage tanks. Gravity pipelines with pressure control valves can be thought of as possessing “surplus” potential energy, which can be “harvested” by using a turbine rather than “wasted” by using a pressure control valve, which “throttles” the flow of water (see Appendix A.1 for more background on gravity pipelines and the hydraulic explanation for surplus energy).
There are two main classes of eligible turbine sites for drinking water hydropower (as illustrated by Figure 1), in which the flow rate is either
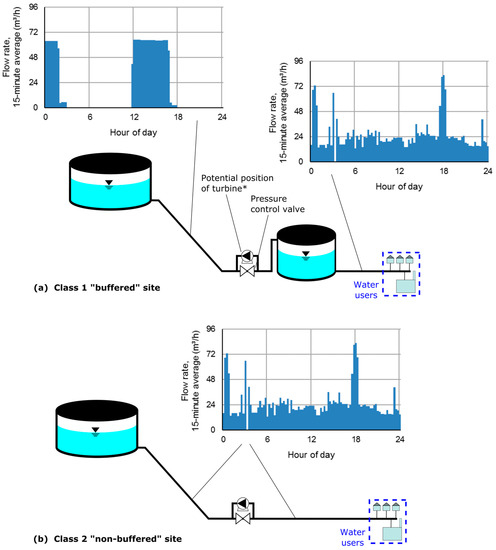
Figure 1.
Key difference between class 1 (“buffered”) and class 2 (“non-buffered”) sites, based on data from 27 April 2017 from the class 1 site “Voigtsgrün” in Saxony, Germany (the isolated, very high peaks occurring between 00:00 and 04:00 and at 18:00 are due to a beer brewery). *This illustration only intends to show the turbine in parallel to the control valve; the turbine does not need to be located above the control valve and is typically located at nearly the same elevation.
- decoupled from uncontrolled downstream water use through a storage tank (“buffered”), or
- determined by uncontrolled water use in the downstream supply zone(s) (“non-buffered”).
Table 1 summarizes the most relevant consequences for drinking water hydropower development that follow from the presence or absence of pressure control and a storage tank. As sites without pre-existing pressure control are not promising for hydropower development, they will not be further considered in this paper.

Table 1.
Matrix of consequences for drinking water hydropower development, depending on the type of gravity pipeline and site.
1.2. Available Literature and Comparison of Class 1 vs. Class 2 Sites
Common examples of class 2 sites include transfer nodes between pressure zones or a gravity-fed water treatment plant between a gravity source and destination supply tank (e.g., [2,5,8,10,11,12]). They are most often located within the water “distribution” section of the water supply chain [13]. In contrast to class 1 sites, class 2 sites offer no flexibility in the choice of flow rate, such that a turbine must be designed to efficiently operate over a broad spectrum of flow rates and corresponding available pressure heads. As the pressure may fluctuate both downstream and upstream of the turbine installation site, class 2 sites generally require more information and a more complex, customized design process. Based on a review of the scientific literature, the authors perceive a dominant focus on class 2 sites, with many researchers devising design algorithms and control solutions using microturbines and pumps-as-turbines (PATs) [7,8,9,13,14,15,16,17,18,19,20,21,22].
Class 1 sites are generally intermediate (such as break-pressure tanks (BPTs)) or terminal storage tanks with pressure control valves [6], typically located within the water “transmission” section of the water supply chain [13]. In the authors’ experience and estimation, class 1 sites are common and represent a relatively cost-effective opportunity for renewable energy generation. They offer the water supplier flexibility (positively correlated with storage volume) in determining the rate, duration and timing of tank filling (and thus turbine operation), as this must not necessarily occur simultaneously with the downstream use in the supply zone (see Figure 1). Assuming that the inflow rate is not restricted (e.g., by the naturally occurring, seasonally varying flow from a mountain spring), the inflow regime can often be freely adjusted to maximize energy generation through a turbine, regardless of how it was managed in the past [12].
While comparatively less common, there are also studies that focus on class 1 sites. Several authors present case studies of sites at the bottom of dams [7], spring-fed pipelines [23] and storage tanks in general [24,25]. Others focus on BPTs, both isolated [6] and in series along a long-range pipeline [26,27]. However, many if not all of these authors effectively treat class 1 sites as if they were class 2 sites, assuming that the inflow regime remains unchanged and attempting to design turbines to fit this inflow regime, rather than adjusting it to allow the choice of a single, optimized turbine. Thus, they do not use the fundamental technical advantage that separates class 1 from class 2 sites [12,28]. For more background on class 1 vs. class 2 sites, see Appendix A.3.
1.3. Filling a Gap in Currently Available Design Methods for Class 1 Sites
Several other authors present methods that might be useful for class 1 sites, but the effort required to successfully adapt the methods and restrictions imposed by technical understanding and software availability for the authors’ intended user group (practitioners at water supply companies and non-research water professionals) speak against pursuing this further. For instance, since the authors set out to create a tool that is free to use and based on a common tool (i.e., Microsoft Excel, which in the authors’ experience is standard practice at most water supply companies), and software such as MATLAB is non-standard and requires specialized knowledge, possible adaptation of such algorithms was not considered. Furthermore, while some authors provide the basic underlying equations, the software or code in which the algorithms are implemented is not made accessible to the reader and therefore cannot be easily tested or used.
The 2016 guidelines published by the German Technical and Scientific Association for Gas and Water (DVGW) [12] identify the flexibility advantage provided by class 1 “buffered” sites, and imply that with additional data analysis a turbine can be “ideally tuned” to “balance the demands of storage management and energy generation”. However, they offer no specific instructions or examples for how to translate this information into actual design parameters (flow rate and pressure drop). This is precisely the gap that the authors intend to fill with the method and accompanying Excel tool presented here. As the authors of this paper have encountered many class 1 sites and experienced an unfulfilled need for a design solution, they decided to develop their own solution. While designing turbine systems for class 2 sites represents the greater technical challenge, a practical design method for class 1 sites appears to be low-hanging fruit that has yet to be sufficiently plucked.
Given a recently resurging interest in drinking water hydropower in Germany [29,30,31,32] and elsewhere [6,7,19], the authors intend to facilitate the installation of such facilities by making it easier for small and medium water suppliers to estimate their hydropower potential and perform the basic design (determination of turbine parameters) themselves. The tool is implemented in Microsoft Excel for Windows (Office 2010 or newer), available free of cost for download at the authors’ university website [33] and intended to be easily useable by practicing engineers or water professionals. If successful, it should both save time and reduce users’ inhibitions about approaching this non-standard topic. To the authors’ knowledge, it is the only such tool freely available on the internet.
This paper will explain the methodology behind the Excel tool, along with three other methods covered in DVGW guidelines that serve as a useful basis of comparison. These four methods will be applied to nine sites in Germany, and the results will be used to show the method in practice as well as providing a sense of the technical and economic potential that is available at class 1 drinking water hydropower sites.
2. Materials and Methods
2.1. Design Premise
The intention of this method and related Excel tool is to facilitate the implementation of microturbines in water supply systems. This is accomplished by automating the calculations required to determine the pressure head and flow rate for a hypothetical turbine that will (to the fullest extent possible with the given data) lead to the maximum electrical energy generation (kWh/annum, or kWh/a) at a given class 1 site. A basic economic analysis is also performed to provide an estimate of the project’s viability.
While the Excel tool includes four calculation options to accommodate all anticipated variations on data availability for a given site (see Appendix B.1 and Appendix B.2 for a more detailed explanation), optimization of the turbine design parameters is only possible using option 1 or 2 (both slight variants on the same method), which take historical flow data into account. The primary advantage of options 1 and 2 is that there is no need to be biased by the typical inflow regime of past operations. The analysis of historical data thus allows the determination of turbine parameters from “first principles”, rather than by analogy from the previous inflow rate, which may have been selected for reasons unknown to the current responsible engineer or site operator. Critically, this assumes that historic water use patterns are a reliable proxy for future water use. This paper will present the main design algorithm for calculation options 1 and 2 in its recommended form. The tool provides some additional options for the user to customize the design solution (e.g., regarding the bypass flow rate and multipliers for the outflow rate (Qout) to reflect anticipated future changes), which are further described in Appendix B.3 and Appendix B.4 and the tool itself.
This method was inspired by Haakh [28], who provided a foundational and mathematically thorough treatment of turbine and pump operation in the context of water supply systems. The authors expect that the Excel tool and this article will provide a somewhat simplified, more user-friendly approach to solving a sub-set of the design challenges laid out there, with a focus on class 1 “buffered” sites. The following sections describe the essential tasks performed by the tool.
2.2. Determining the Characteristic Site Curve
Also known as the “system” curve, this describes the relationship between the exerted pressure and flow rate in the inflow pipeline as observed from a downstream reference point within the pipeline. It can also be thought of as the pressure “available” as a function of the chosen flow rate. Typically, this reference point is taken just upstream of the pressure control valve, to capture the hydraulic conditions relevant for a potential turbine. The available pressure head is equal to the maximum pressure head (hmax, at flow rate = 0) minus the head loss up to the point of interest (hloss) and the pressure head just downstream of the control valve (hdownstream), which is necessary for the water to reach the storage tank. Since head loss increases proportionally to the square of flow rate, the curve can be well approximated (Equation (1)) with a downward-facing parabola with its vertex centered on the positive y-axis (flow rate = 0), crossing the positive x-axis at the maximum possible flow rate (pressure exerted on reference point upstream of valve = 0), at which the pressure control valve is completely open and offers no hydraulic resistance (see Figure 8 in Section 3.1 for an example). This is predicated on a simplifying assumption that assumes a constant coefficient of major pipe friction loss (defined in the U.S. as “lambda”, λ), which is known to be flow rate-dependent (e.g., as captured in Moody’s diagram), but is valid for conditions commonly encountered at water supply sites. The resulting second-order polynomial equation takes the following form:
where Kloss is the head loss coefficient, which integrates the major head loss due to pipe friction and minor head loss(es) due to sources of local resistance (e.g., pipe bends, partially opened valves upstream). hloss as defined in Figure A1 (Appendix A.1) is the central term in Equation (1), the product of Kloss with the square of the flow rate Q. While hmax, Kloss and hdownstream could be determined analytically, the authors found empirical determination to be both more accurate and less labor-intensive. To empirically determine this parabolic curve, two points must be defined, which requires measuring five field data points:
- Q1_inflow: non-zero inflow rate at control valve, position 1 (e.g., at normal operating flow)
- h1_upstream: pressure head upstream of control valve, position 1 (e.g., at normal operating flow)
- hdownstream: pressure head just downstream of the control valve, which is necessary for the water to reach the (frequently somewhat higher) storage tank (e.g., at normal operating flow)
- Q2_inflow: inflow rate at control valve, position 2 (ideally zero flow; i.e., closed valve, but can also be a second, sufficiently different non-zero flow rate than Q1, if closing the valve is not feasible)
- h2_upstream: pressure head upstream of control valve, position 2 (ideally at zero flow; see above)
These data can usually be easily obtained, for example during a 30-min visit to a site or based on past data already acquired using a supervisory control and data acquisition (SCADA) system. If feasible, long-term measurements as well as further points along the site curve provide a more accurate picture of the real site conditions and reduce uncertainty in the resulting turbine performance. Since Kloss can effectively be considered a constant, it can be determined indirectly by substituting all measured values into Equation (1). Qmax can then be determined simply by setting Equation (1) to zero and solving for Q (Equation (2)).
The reader should note that the timing of the measurement of h1_upstream and h2_upstream will impact the value of hmax, since the pressure measured depends to a small degree on the water level in the upstream tank. Ideally, these measurements should be conducted when the upstream tank is known to be at its typical lowest level, as this will provide a conservative estimate of the pressure that will at a minimum be reliably available to a potential turbine. Furthermore, the flow-dependent head losses between the control valve and storage tank are integrated into the measurement of hdownstream, if performed using a pressure gauge. The change in these losses (and therefore a change in hdownstream) due to a deviation in the turbine flow rate from Q1_inflow (normal operating flow) is likely negligible, but can also be easily measured by changing the flow rate to the potential future turbine flow rate. The value for hdownstream is usually primarily determined either by the height of the pipe outlet above the turbine (as portrayed in Figure 2) or the water level in the downstream tank (as portrayed in Figure A1), in case the pipe outlet is at the bottom of the downstream tank. Figure 2 provides a visual explanation of some of these terms for the typical case as encountered by the authors in Germany.
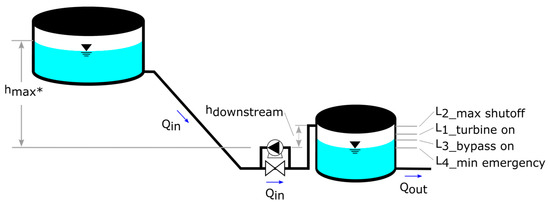
Figure 2.
Visual explanation of some key parameters used in the method, as introduced in Section 2.2 and Section 2.5. * Note that hmax depends on the current water level in the upstream tank, which is why the measurement of h1_upstream and h2_upstream should be conducted when the upstream tank is known to be at its typical lowest level.
2.3. Calculating the Hydraulic Power Available to the Turbine
The hydraulic power carried by the flowing, pressurized water and ultimately available to a turbine can be calculated using Equation (3):
where ρ is the density of water (kg/m3), g is gravitational acceleration (m/s2), Q is the flow rate (m3/s) and havailable is the available pressure head (m). Since ρ and g can be assumed constant (1000 kg/m3 and 9.81 m/s2, respectively), the equation can be simplified (Equations (4a) and (4b)) to allow the input of flow rate in more commonly used units of m3/h or L/min:
Given that havailable is approximated as a second-order polynomial function of Q (Equation (3)), and this function is multiplied with Q and a constant to compute available hydraulic power, the characteristic curve of hydraulic power available to a turbine can therefore be approximated as a third-order polynomial function of Q (Equation (5)), adjusted by the appropriate constant as per Equation (4):
The flow rate at which the maximum possible hydraulic power Pmax occurs can be determined by first taking the derivative of Equation (5) with respect to flow rate Q, resulting in Equation (6):
Since Equation (5) defines a polynomial with a single maximum, setting its derivative P’available to zero leads to Equation (7) for the flow rate corresponding to Pmax:
Substituting QP_max into Equation (5) yields the maximum possible hydraulic power for the given class 1 site. This information becomes relevant upon comparing the results of this method with the method from the 1994 DVGW guidelines [34] (see Section 2.10).
2.4. Consideration of a Bypass Pipeline Parallel to the Turbine
The tool assumes that the turbine is installed in the inflow pipeline to the storage tank and in parallel with a bypass. This ensures at a minimum that the turbine can be easily removed without interrupting supply and can also be used for the compensation of short periods of high water demand via rapid filling of the storage tank. In the event that the bypass flow rate Qbypass is substantially above the turbine design flow rate Qturbine, this can maximize total annual energy generation, by enabling Qturbine to be as low possible, which reduces unnecessary friction losses that would otherwise occur with a higher Qturbine. This relationship between Qbypass and Qturbine should become clearer in the coming sections. The recommended setting is the maximum permissible inflow rate, but this can be freely adjusted by the user.
2.5. Using a Numerical Model to Ensure Supply Reliability Based on Historical Flow Data
The inflow rate Qin must at any point in time be sufficient to meet the demand placed on the storage tank by the water users in the supply zone and cannot endanger the reliability of supply by causing the storage tank to temporarily run below a minimum emergency level (e.g., for fire-fighting reserves). To determine whether this is likely to happen based on a given Qbypass and Qturbine, a simple linear, deterministic, dynamic numerical model was incorporated into the tool. The model takes a historical time series of the outflow rate from the storage tank Qout as input (ideally at a maximum time interval of 15 min) and simulates Qin through the turbine and bypass as well as the resulting storage tank water level Ltank. The initial condition for Ltank is 75% if no water level time series data are provided along with the time series for Qout. The basic governing equation (Equation (8)) for Ltank at a given timestamp t+1 is as follows:
where Ltank @ t+1 reflects the resulting tank water level at timestamp t+1 at the end of the time step T (between timestamps t and t+1), Vin @ T and Vout @ T are the volume of water entering and leaving the tank during the time step T (between timestamps t and t + 1), respectively, and Vtank is the volume of the storage tank at 100% capacity (m3). To clarify, “timestamp” t refers to an instantaneous point in time (e.g., 12:00:00 (noon) on 20 June 2019), whereas “time step” T refers to the duration of time passing between the two timestamps t and t+1 (e.g., the 15 min between 12:00:00 and 12:15:00). Vout and Vin are obtained by multiplying the duration of the time step T ([t + 1] − t) with Qout and Qin, respectively, to yield a water volume. Qout is taken from the historical time series provided by the user, whereas Qin is determined by Equation (9):
where Qbypass is the chosen bypass flow rate, Qturbine is the chosen turbine flow rate, L2_max shutoff is the maximum permissible tank water level (% of full), L1_turbine on is the threshold tank level at which the turbine is operated, L3_bypass on is the threshold tank level at which the bypass pipe is opened, and the turbine pipe is closed. A further value, L4_min emergency, signifies the lowest permissible water level. If Ltank falls short of this, the Qturbine is excluded from the set of feasible solutions. See Figure 2 for a visual representation of these tank levels. For the method to properly function, the following relationships between values must be true (Equations (10a) and (10b)):
where Qmax inflow is the maximum permissible inflow rate into the tank, either legally according to a contract with a long-term water supplier or technically due to pipeline’s natural Qmax (see Appendix A.1 for elaboration) or a limitation on the water source (e.g., a mountain spring). The recommended setting is for Qturbine to be equal to Qmax inflow.
L2_max shutoff > L1_turbine on > L3_bypass on > L4_min emergency
Qmax inflow ≥ Qbypass ≥ Qturbine
Expressed in words, the system is operated such that the tank is normally filled via the turbine at Qturbine. Only in cases of high water withdrawal (Qout) in which the tank level falls very rapidly is the bypass opened (and the turbine pipe closed) to increase the inflow rate to Qbypass and kept open until the maximum permissible water level is exceeded (tank is full). Then normal operation with the turbine resumes. The number of occasions on which the bypass is opened increases as Qturbine decreases.
By defining Qin to exclusively be equal to Qturbine and Qbypass, taking into account the impact on Ltank, the tool thus re-defines the inflow regime in such a way that both supply reliability can be guaranteed, and energy generation can be maximized (see Figure 1). This is the step in the tool’s algorithm at which the key advantage of class 1 “buffered” sites is utilized.
2.6. Calculating Total Annual Hydraulic Energy Capture
The term “capture” refers to the annual average amount of hydraulic energy Ehydraulic that is applied to the turbine wheel, before being converted to the mechanical energy Emechanical of the spinning wheel and shaft, and then further converted to electrical energy Eelectrical through a generator. Ehydraulic is calculated using Equation (11):
where the time step ([t + 1] – t) is measured in units of days (standard for Microsoft Excel). The resulting Qin at each timestamp t (Equation (9)) depends on the outcome of the numerical model described above. This model therefore performs two functions: (1) calculating the energy production for each time step and (2) monitoring whether the water level falls below the minimum permissible level in the storage tank and flagging such solutions as invalid.
2.7. Selection of Microturbines, Global Efficiency Curves and Calculating Total Annual Electric Energy Generation
The tool assumes a single turbine having only a narrow operating range with acceptable efficiency. The turbine’s characteristic resistance curve is assumed constant, since it is fixed by the frequency of the electrical power connection (presumed to be grid electricity at 50 or 60 Hz) and the number of pole pairs in the electrical generator, which pre-determine the rotational speed of the turbine.
To provide the tool user with the calculated electrical energy generation, it is necessary to estimate the total efficiency, which is a product of the efficiency of the turbine (hydraulic to mechanical energy) and efficiency of the generator (mechanical to electrical energy). To make the tool as appealing as possible to practicing engineers, the authors chose to use data from two microturbines that are currently on the market: the in-line axial “AXENT” turbine from Stellba Hydro [35] and pumps-as-turbines (PAT) from KSB [36], companies with whom the authors have worked previously. The total efficiency ηtotal at the hydraulic best efficiency point for turbines of varying capacities was plotted relative to Phydraulic, leading to Figure 3. For each type, AXENT and PAT (two separate models), natural log curves were fitted to the data to generate equations that enabled the estimation of ηtotal based on the input of Phydraulic (Equations (12a) and (12b)). The tool can be updated with new data for other types of turbines from other companies, although this cannot currently be easily done by a normal user.
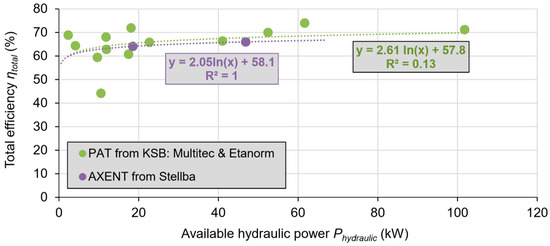
Figure 3.
Global efficiency data for AXENT and pumps-as-turbines (PAT) microturbines, with best-fit natural log curves.
It is important to note that the curves in Figure 3 represent the global efficiency curve of single, optimal values of ηtotal for a hypothetical range of different turbines, not the characteristic efficiency curve of a single turbine over its operating range. Each turbine also has its own flow-dependent efficiency, such that the operating efficiency will vary from the optimal ηtotal in the event that it is operated off of its design flow rate, or if a turbine cannot be manufactured to have its peak efficiency precisely at the chosen Qturbine. For simplicity’s sake, the tool assumes that the turbine is only operated at its optimal ηtotal, at a single operating point. The flow rate must be high enough to enable the use of a microturbine with a practical size and sufficiently high efficiency, as the efficiency of turbines and generators drops rapidly with declining physical dimensions.
The total annual electrical energy generation Eelectrical for a given Qturbine and choice of turbine type is then determined by Equation (13):
2.8. Iteratively Determining the Optimal Turbine Design Parameters
The optimal turbine parameters are defined in the tool as the combination of Q and h that lead to the greatest annual electrical energy generation in kWh/a, based on a numerical simulation of turbine operation with the historical Qout data provided by the user (see above). Generally speaking, a longer historical time series produces more reliable results by accounting for a wider range of realistic supply scenarios, but a very long time series runs the risk of using obsolete data that does not reflect the expected future supply scenarios and therefore producing sub-optimal results. In the authors’ experience, 12 to 24 months is ideal.
To determine the optimal parameters, the possible solution space of values for Qturbine is iteratively run through the numerical model, calculating Eelectrical for each value of Qturbine. This is first done at intervals of 5 m3/h to determine the approximate optimal Qturbine, and then again at intervals of 0.5 m3/h to refine this result. The Qturbine leading to the greatest Eelectrical is declared optimal, and the corresponding hturbine calculated using Equation (1).
2.9. Estimating Economic Viability
Similar to the determination of ηtotal, the estimation of economic viability is based on available cost data for actual microturbines from the companies Stellba and KSB. These costs are based on past implemented projects, recent price quotes and the experience of collaborating engineers, and include the cost of purchase, installation and commissioning. Table 2 shows the cost items and the ranges for the two different types of turbines incorporated into the tool, as well as the total costs including the 19% value-added tax (VAT) for Germany. The peripheral costs for the AXENT turbine are generally lower, because the design elements required to install it are less complex, and it does not require protection against pressure shocks (water “hammer”), contrary to a typical PAT. Figure 4 shows the specific total cost Cspecific data for both types of turbines.

Table 2.
Summary of cost parameters for AXENT turbines and PATs.
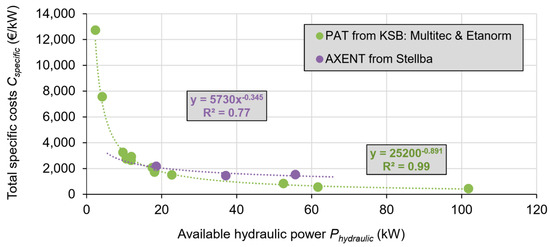
Figure 4.
Specific project costs for AXENT and PATs, with best-fit power law curves.
Equations (14a) and (14b) show the specific cost function for each turbine type. The shape of these curves corresponds approximately to data compiled from turbine projects in Switzerland [1]. The total specific costs Cspecific are calculated by entering Phydraulic into Equations (14a) and (14b), and the total costs Ctotal for a given site and turbine are obtained by multiplying Phydraulic with Cspecific.
The annual benefits Bannual are based on user input on the applicable feed-in tariff or other electricity price at which the generated energy could be sold. In Germany, for example, the legally guaranteed feed-in tariff for turbines below a total capacity of 100 kW commissioned in 2019 is 12.27 ct. €/kWh, for a contract length of 20 years. A site is only eligible for this tariff if the water flows via gravity from its natural source to the turbine. Otherwise, the energy must normally be used on site, replacing electrical energy that would otherwise been purchased from the grid, in Germany at a price of approximately 20 ct. €/kWh. The tool combines the estimated benefits from both of these sources (Equation (15)), which can also complement each other (e.g., if there is a pump set that can be occasionally but not continuously supplied with energy by the turbine, or if the turbine is only able to cover a portion of the energy demand of the pumps).
The payback period for the project is calculated in a simple manner by comparing the initial costs and annual benefits to each other (Equation (16)), assuming the energy generation remains unchanged and without taking into account the time-dependent value of money. Depending on the tool user and decision-maker, the payback period can serve as an indicator of economic viability, if necessary complemented by consideration of Ctotal, as many projects are hindered by insufficient initial funding.
2.10. DVGW 1994 and 2016 Methods as a Basis of Comparison
In order to provide a frame of reference for the new method, it is compared to three methods available in the 1994 and 2016 editions of the DVGW guidelines published on the topic of energy recovery through turbines in the drinking water supply. While these guidelines provide a very useful overview of the technical and operational aspects of implementing a drinking water hydropower project, these methods are not known to generate optimal design solutions for class 1 sites, and therefore only serve as a frame of reference for the new method being introduced here. The methods are compared based on the parameter Eelectrical in units of kWh/a.
The most recent edition of the DVGW guidelines [12] provides guidance in the case of class 2 “non-buffered” sites. They suggest using a frequency distribution of the occurring flow rates to determine the design flow rate of the turbine or multiple turbines. The flow rate (or mean of a range of flow rates; e.g., 52.5 m3/h representing the range from 50 to 55 m3/h) having the greatest energy density (result of Equation (17), applied to each range of flow rates) should be the design turbine flow rate. The resulting Qturbine is then given as input into the Excel tool to calculate Eelectrical assuming the inflow regime is modified as with the tool’s optimization algorithm. In this way, this method is evaluated more generously than if it were applied as intended to class 2 sites, since the flow rates occurring above and below the chosen Qturbine would not contribute to energy generation, being too high or low to be efficiently processed by the turbine (see Section 3.2 and Table 4 for a concrete example).
This method is divided into two sub-methods, one based on the Qin into the tank (approximately representing the “status quo”, if the inflow regime were not modified), and the other based on Qout from the tank. Historical time series are required for both in order to apply Equation (17).
The original edition of the DVGW guidelines [34] make no distinction between class 1 and 2 sites and suggests using the historically most frequently occurring flow rate to select the turbine. However, they imply that the theoretical optimal flow rate is given by Equation (18) (obtained by substituting Equation (2) into Equation (7)), at which the hydraulic power carried by the flowing water is mathematically at its maximum (see also [28,37]).
This method is tested on the basis of the flow rate of maximum hydraulic power. Just as for the 2016 DVGW method, the resulting Qturbine is given as input into the Excel tool to calculate Eelectrical assuming the inflow regime is modified as with the tool’s optimization algorithm. Table 3 offers a concise summary of all methods that are compared in this paper with their corresponding short names.

Table 3.
Summary of turbine design methods from the authors’ perspective.
3. Results
3.1. Case Study of Tool Application: Break Pressure Tank (BPT) Rützengrün, Germany
The best way to understand the methodology implemented in the tool is to follow its use step-by-step for a real-world example and show the data and results as they appear to the user. A blank version of the tool as well as a version with the data for the example site BPT Rützengrün is included in the Supplementary Materials. BPT Rützengrün of the water supply utility ZWAV Plauen is located above the city of Auerbach in the Vogtland region of Saxony and receives its water (via the higher elevation BPT Vogelsgrün) from the long-range water supplier Südsachsen Wasser out of the drinking water reservoir Carlsfeld, located about 180 m above. Figure 5 shows a diagram of this supply system. The BPT serves primarily as a pressure-reducing installation, but also has a small storage tank with a capacity of about 100 m3. Thanks to this storage, BPT Rützengrün is a class 1 site, which permits a degree of flexibility in regulating the inflow and turbine flow rate.
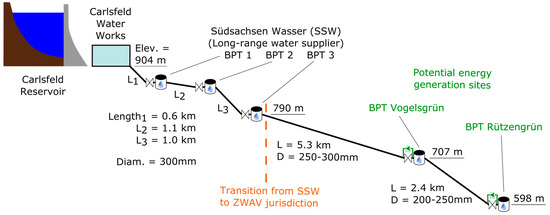
Figure 5.
Diagram of the Carlsfeld supply system, with break pressure tank (BPT) Vogelsgrün and BPT Rützengrün. As illustrated in Figure 1, the potential turbines would be positioned in parallel with the existing pressure control valves.
Figure 6 shows the first input mask, in which the user enters the minimum required information in the form of single values. Depending on the choice of calculation option (in this case option 1 and 2), those cells requiring user input turn orange. To determine the most reliable turbine parameters, the planner must not only supply the data needed to define the site curve, but also provide information about the storage tank, including volume and the feasible tank level thresholds for opening and closing the inflow valve. As per the recommended setting, the bypass flow rate Qbypass is set equal to the maximum permissible inflow rate, in this case 90 m3/h.

Figure 6.
Excerpt of the first data input mask for single values, with values for BPT Rützengrün.
The second input mask (not shown here) is for the time series. For BPT Rützengrün, the input time series of Qout from the tank (to the downstream supply zones) ranged from 29.05.2017 to 15.02.2018 and was processed from so-called delta-event (event-based recording) raw data to have a 15-min time interval. These data are necessary to achieve reliable results. While historical time series for water level and tank inflow rate can be used by the tool to infer the storage tank volume (hence the input fields), they were neither available nor necessary, since the volume was known to be 100 m3. With the information about tank volume and the switching thresholds provided in the first input mask (Figure 6), the tank operation was simulated to determine both acceptable and optimal turbine parameters. This “simulation” consists of a simple numerical model (see Section 2.5), modifying a starting value for the tank level according to the net change in storage volume, as calculated by the difference between the inflow and outflow volumes. The planner must also choose between two types of turbines. In this case, the in-line AXENT turbine was chosen (see Section 2.7 for more details).
Once all necessary input data has been provided, the Visual Basic (VBA) algorithms are run to determine the optimal turbine parameters under the given boundary conditions. The algorithms iteratively progress through all possible design flow rates (see Section 2.5 through Section 2.8), computing and graphically plotting the corresponding performance parameters annual energy generation (Ehydraulic as well as Eelectrical), power (Phydraulic and Pelectrical) and total efficiency ηtotal for the chosen turbine type at the corresponding Phydraulic (for the best possible turbine, not the characteristic curve of a single turbine—see Section 2.7) (Figure 7). The optimal parameters (head and flow rate) are also displayed and added to the site curve diagram (Figure 8).
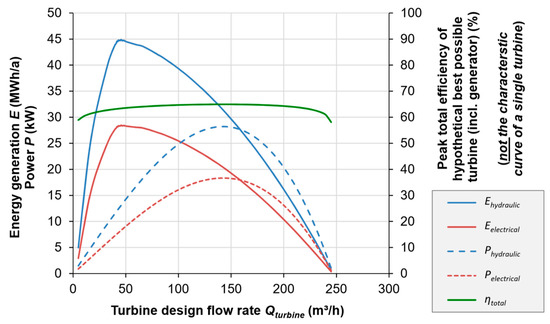
Figure 7.
Calculated performance parameters of hypothetical turbines (at best efficiency point) with iteratively varied design flow rates (here from 5 to 245 m3/h), with values for BPT Rützengrün.
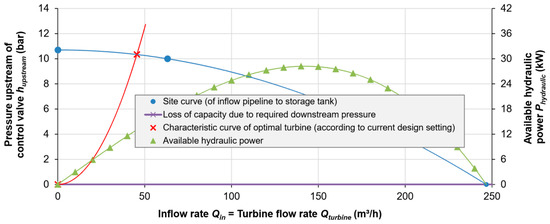
Figure 8.
Site curve of BPT Rützengrün with characteristic curves of the corresponding hydraulic power as well as the (hypothetical) turbine with optimal operating parameters. 1 bar = 10.19 m of head.
After determining the optimal turbine parameters, the annual financial benefits Bannual are determined based on the information provided. In the same step, the total costs for purchase and installation of the turbine Ctotal are calculated on the basis of available values from the authors’ experience, to roughly estimate the simple (non-inflation-adjusted) payback period (see Section 2.9 for more information). In the case of BPT Rützengrün for the input data shown here and using the recommended calculation and bypass options, Eelectrical is estimated at 26,000 kWh/a (Table 4) and the payback period at 10.0 years. According to the water supply company ZWAV Plauen, if the turbine lifetime can be assumed at 20 years, the payback period must be ≤ 10 years (less than half of the device’s lifetime) to be an acceptable investment. A turbine at this site would therefore be borderline economically viable according to this assessment.

Table 4.
Summary of the results for BPT Rützengrün using all four methods described in this article.
3.2. Assessing the Impact of Quality Control for Input Data
This case study also provides an opportunity to show the importance of critically assessing the data used. Figure 9 shows the time series of outflow data for BPT Rützengrün. It is clear upon inspection that the period of available data at sufficient resolution (at 15-min rather than 2-h intervals) and without gaps (which cause errors in the calculation) was not representative of the typical past operation and the expected typical future operation of BPT Rützengrün. While these data were sufficient for determining the optimal turbine parameters using the Excel tool, they estimated a much lower annual flow volume Vannual (144,000 m3/a) than was normal in the past and is expected for future operation (252,000 m3/a), based partially on the multi-year 2-h data. This was corroborated by the ZWAV Plauen staff, who explained that the period captured as 15-min values was unusual due to some maintenance work that was performed on the supply system. To compensate for this, Eelectrical and consequently Bannual were linearly increased by multiplication with the ratio between these flow volumes, a factor of 1.75. This adjustment increases Eelectrical from 26,000 to 45,600 kWh/a and lowers the payback period from 10.0 to 5.7 years (Table 4), making this project much more economically attractive than would have been the case without a careful analysis of the data. This highlights the fact that the acquisition and handling of data is not always straightforward, and ought to be done with a critical eye.
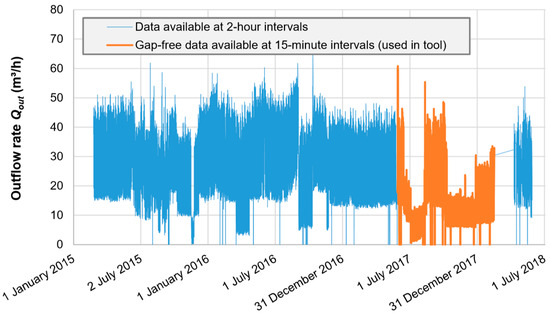
Figure 9.
Outflow data series available for BPT Rützengrün, with the data used in the Excel tool highlighted in orange.
Experience with this site also demonstrated the importance of sufficiently high temporal resolution for the input data. Due to the low storage volume of 100 m3, a time interval greater than 15 min led to an unreliable simulation of the tank levels, since the incremental change in storage volume at times exceeded the tank capacity. In this case, only 2-h values were available for a longer time period (Figure 9). As these occasionally exceeded 50 m3/h, more than 100 m3 would potentially leave the tank in a single time interval. This allows no opportunity for the simulation to react by opening the inflow valve in response to the tank level falling below the switching threshold—the tank would simply be “instantly” emptied. This led the authors to embrace a rule of thumb that 15 min ought to be the maximum time interval between values for Qout, even if not always strictly necessary, such as for sites with more than 1000 m3 of storage. In general, a longer input time series is better than a shorter one, but as mentioned in Section 2.8 and for reasons made clear here, there is a trade-off between having a sufficiently long dataset for capturing the seasonally varying conditions and accidentally capturing conditions that are obsolete or unlikely to be representative of the future. A period of 12 to 24 months should be sufficient in most cases, but should also be checked for anomalies.
Some other authors have used long-term average values in their turbine design methods [15,25]. It is worth noting that average hourly or average daily flow data can be misleading, since the inflow rate might be much higher than the hourly average but occurring only periodically for only short periods of time (e.g., for 5 min at a time, with 15 min in between times of active flow). If this were to persist for 60 min, the hourly average flow rate would be four times lower than the actual flow rate when the inflow valve is opened, since the water volume would have flowed over 15 min rather than 60 min. The authors have encountered this situation multiple times. Designing a turbine based on the average hourly flow rate without planning to adjust the inflow rate can therefore lead to a large error, since the actual flow rate greatly deviates from the inferred flow rate based on average hourly data.
3.3. Comparison of Results Using the Newly Proposed Method with Other Methods
One purpose of this article is to compare the newly introduced method with existing methods for determining turbine parameters. Figure 10 illustrates application of method “a” suggested by the 2016 DVGW guidelines (Table 3), based on selecting the inflow rate (Qout) range with the highest estimated energy generation. In this case, the Qout range from 10 to 15 m3/h is both the most frequent and most promising for highest energy generation. Thus, an average flow rate of 12.5 m3/h emerges as the design flow rate Qturbine. It is worth noting that the frequency of occurrence of a range of flow rates does not imply that this range will have the greatest estimated energy generation, due to the other factors that influence energy generation, such as the efficiency of the expected turbine (which declines rapidly with declining power rating), occasionally high demand that reduces energy generation at lower design flow rates (due to the necessity of bypassing more water around the turbine) and the increase in frictional head losses (with increasing flow rate). For example, the flow rate ranges 25 to 30 m3/h and 30 to 35 m3/h have nearly the same frequency, but the latter range has a substantially greater expected annual energy generation.
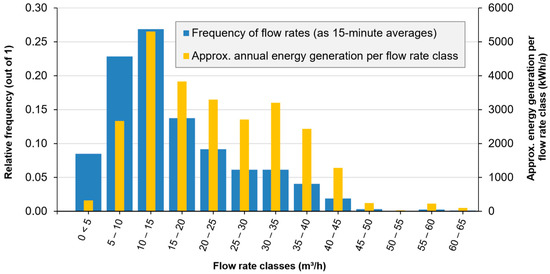
Figure 10.
Frequency distribution of outflow rates and corresponding estimated annual electrical energy generation per flow rate class, at 15-min intervals for BPT Rützengrün.
The 1994 DVGW guidelines suggest that the point of maximum hydraulic power Phydraulic is also the optimal operating point for a turbine (Table 3). This point can be seen on the green curve of Figure 11, corresponding to a Phydraulic of 28.2 kW and occurring at a flow rate of 142 m3/h. A hypothetical turbine suitable for operating at this point would have a pressure drop hturbine of 72.7 m, as can be seen where the fictive characteristic curve (red curve with triangle markers) of such a turbine crosses the characteristic site curve of the inflow pipeline for BPT Rützengrün.
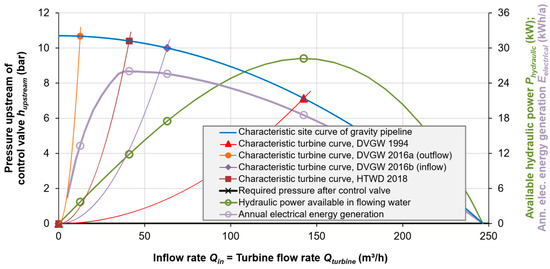
Figure 11.
Site curve of BPT Rützengrün, hypothetical turbine curves for design results of all four methods, and corresponding hydraulic power as well as estimated annual electrical energy generation at each operating point.
Figure 11 also shows the results of the other three methods and their respective hypothetical turbine curves. The green and lavender curves with open circle markers respectively show the Phydraulic and Eelectrical corresponding to each of the turbine operating points. For the 2016 DVGW method “b” (based on inflow rate Qin), no time series was available, so the single data point used to define the characteristic site curve of the inflow pipeline was taken as the most frequent inflow rate with the highest expected annual energy generation. The corresponding numbers are also summarized in Table 4. The results confirm that the 2018 University of Applied Sciences Dresden (HTWD) method yields the greatest energy generation.
It is important to reiterate (see Section 2.10) that the 2016 DVGW guidelines are explicitly intended for class 2 “non-buffered” sites, in which the system operator can “make the best” out of a hydraulic situation over which they can exercise no control. In this case, the emerging design flow rate of 12.5 m3/h is intentionally “improperly” entered into the HTWD Excel tool, which is built for class 1 “buffered” sites, and modifies the inflow regime to optimize the energy generation. In this way, the only permitted values for Qin are Qturbine and Qbypass—no other inflow rates occur. When properly applied to class 2 sites, this method yields a much lower expected energy generation, since water arriving at all flow rates not falling within a narrow range (e.g., 10 to 15 m3/h) would be bypassed around the turbine. The energy generation possible within other flow rate ranges (represented by the orange columns in Figure 10) would be lost. Using the HTWD tool for a class 1 site, these other orange columns can be almost entirely and efficiently captured by modifying the inflow rate, which is made possible by the storage tank that decouples the inflow and outflow to and from the site. This is the fundamental advantage of a class 1 site.
This difference between the improper and proper application of this method is shown in Table 4 (method 3i vs. 3ii), and highlights the great advantage that class 1 sites have over class 2 sites for energy generation using microturbines with narrow acceptable operating ranges (see Section 2.10 for elaboration). BPT Rützengrün as a class 1 site would have an annual electrical energy generation of about 24,000 kWh/a at the turbine flow rate of 12.5 m3/h, while it would have only 9300 kWh/a if it lacked the 100 m3 storage tank and was therefore a class 2 site—a factor of 2.6 less energy generation.
Furthermore, the use of the 2016 DVGW method “b” (based on the most frequent inflow rate with the highest expected annual energy generation) is also an improper application, since the inflow and outflow at class 2 sites are necessarily equal, as there is no storage tank. However, both of these “improper” applications of the 2016 DVGW method serve as useful comparisons, since in the absence of another method, the designer of a turbine system might choose to select a design flow rate corresponding to a known quantity about the system. As such, this flow rate also generally corresponds to the current operating state, providing a comparison with a design approach that would choose a turbine to fit the existing inflow rate. And as is evident from Table 4, using the substantially higher flow rate of 63.1 m3/h yields a total energy generation that is 98.3% of that yielded by the 2018 HTWD method—in this case hardly a significant loss. However, it cannot be assumed that this will hold true in every case, as the analysis of further sites in the following section shows. In cases where it does hold true, this method can be used to confirm this truth, which provides the designer and operator with a greater level of confidence in the ultimate design decision.
3.4. Results for Nine Sites in Germany
The four turbine design methods were applied to a total of nine sites from Saxony, Germany. The sites had a variety of characteristics and data availability and led to a range of results with varying degrees of confidence (Table 5). To highlight the hydraulic differences between the sites, Figure 12 shows the characteristic sites curves of each inflow pipeline—a kind of “finger print” for each site. The current inflow rates range from 24 to 145 m3/h, whereas the newly proposed design flow rates range from 34 to 84 m3/h, with an outlier of 300 m3/h at the newly planned site Rehbocksberg. With the exception of two sites having very small (100 m3) tanks and one site having a very large (10,000 m3) tank, the storage capacity ranged from 1000 to 5000 m3.

Table 5.
Summary of the site characteristics, with selected design results obtained using the 2018 HTWD method.
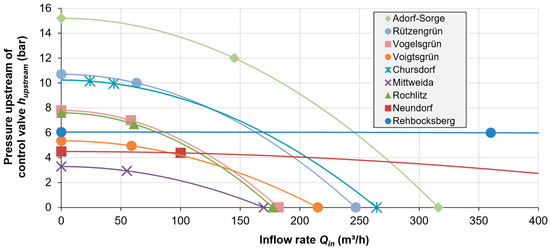
Figure 12.
Overview of the hydraulic characteristic curves for all nine sites analyzed.
For five of the nine sites it was possible to obtain sufficiently detailed data to perform the highest-quality design. In the case of Mittweida, 15-min data existed, but were saved in such a way in the (early generation) SCADA system that made them very time-consuming to retrieve. Thus one-day data were used, which were more easily accessible. For the remaining three sites no time series were available, due to one site not yet existing (the Rehbocksberg storage tank is being newly constructed) and having no SCADA data transmission. The calculation options 3 and 4 in the Excel tool are designed to handle precisely such cases, but the results are to be used with caution.
For Neundorf and Rehbocksberg, the design was based on the operating conditions planned by the respective water utilities, who were confident that they would able to maintain the design turbine flow rates. For Rochlitz, the maximum daily flow volume for any given future year was estimated and used to calculate the corresponding flow rate. This was done by first calculating the average daily flow volume in the month with the greatest flow volume (these data were available), which was 674 m3/d. This number was then multiplied with the ratio (taken from the nearby site Chursdorf) between the maximum daily flow volume in the year and the average daily flow volume in the month with the greatest flow volume, which was 1.34. The resulting “worst-case day” had a flow volume of 900 m3/d, which was assumed to enter the tank over a 24-h period, producing an inflow and turbine design flow rate of 37.5 m3/h.
Table 6 and Table 7 show a comparison of the technical and economic results, respectively, for all nine sites across all four methods. The HTWD method provides the greatest energy generation for every site. Using the 1994 DVGW method, the energy generation is consistently low, on average only about 71% of the optimum, ranging from 63% to 74%. The 2016 DVGW method “a” (based on the most frequent Qout with the highest expected annual energy generation) produced very mixed results, ranging from 53% to 98% of the optimum, with a weighted average of 78%. The 2016 DVGW method “b” (based on Qin) performed consistently better, ranging from 79% to 100% of the optimum and having a weighted average of 91%.

Table 6.
Comparison of the estimated Eelectrical (in kWh/a) achieved by four different turbine design methods, in italics as percentages of the value given by method 1.

Table 7.
Comparison of the estimated annual revenue (in €/a) and simple payback period (in a) for the turbine parameters determined using the four different turbine design methods.
The economic results mirror the technical results. The revenue for all sites was calculated assuming 100% feeding in of the generated electricity, at the 2018 German rate of 12.33 ct. €/kWh, as all sites are eligible for the feed-in tariff under the German Renewable Energy Law. The estimated specific project costs follow a power law and ranged from 1700 €/kWhydraulic for the highest-capacity turbine (30.0 kWelectrical, Rehbocksberg) to 12,000 €/kWhydraulic for the lowest-capacity turbine (2.0 kWelectrical, Mittweida), based on past project experience from other sites with similar conditions. The estimated total project costs therefore ranged from approx. 28,000 € to 37,000 €. For the optimal case using the 2018 HTWD method, the annual revenue ranges from 1110 to 22,200 €/a, with simple payback periods from 24.2 to 1.7 years. Of the nine sites, four have payback periods less than 10 years, making them economically viable according to the standards used by the water utility ZWAV Plauen. For the remaining sites, the project costs would have to be reduced in some way to make the installation of a turbine economically viable, for example by reducing the costs of the turbine or other items (see Table 2), or acquiring financial support through state or federal grant funding for renewable energy projects.
4. Discussion
4.1. Archetypical Sites: Handling in Excel Tool and Practical Considerations
During analysis of the nine sites presented here there were five archetypes that emerged, the closer examination of which may prove useful to the reader.
The first archetype is a typical supply tank site, with moderate storage and a more or less typical water demand pattern, reflecting a mixture of household and commercial or industrial users. Voigtsgrün, Chursdorf, Mittweida, Rochlitz, Neundorf and Rehbocksberg fall into this category.
The second archetype is a site that predominantly serves as a break pressure tank along a long-distance pipeline through mountainous terrain. Rützengrün and Vogelsgrün fall into this category. For these two sites in particular, only very small storage tanks (100 m3) are present, which demands that temporally high-resolution outflow data is available to the Excel tool for determining both acceptable and optimal turbine flow rates. As with these two sites (see Figure 5), these kinds of sites can exist in several stages in series, which can have a simplifying cascade effect, since the downstream BPT regulates the outflow of the upstream BPT.
The third archetype is a site with a very flat characteristic site curve, resulting from very low friction losses within the desired operating range of flow rates. Normally this is a consequence of a particularly large inflow pipeline. The sites Rehbocksberg and Neundorf fall into this category (see Figure 12). In this case, the designer has much greater flexibility, because the flow rate can be made higher without risking unnecessary energy loss to pipe wall friction. For example, while the site operator ZWAV Plauen chose 50 m3/h as the design flow rate for Neundorf, a flow rate of 100 m3/h or even 150 m3/h would subtract very little from the total possible energy generation. Both these sites also have high storage capacities of 5000 and 10,000 m3 (although this is not necessarily a property of this archetype), which makes it unlikely that brief periods of high demand would endanger the security of supply by depleting tank levels. Thus, there is also less urgency for having a high-resolution time series of outflow data to verify that the chosen turbine is suitable.
The fourth archetype is a data-lean site, for which only limited information is available. If storage is large enough compared to the demand and the site can be flexibly operated due to system-level redundance (as with Neundorf and Rehbocksberg, which both have parallel supply systems that can replace or supplement water in case of an outage), the limited data may be sufficient to produce a reliable design using the Excel tool. For cases like Rochlitz, however, more data must be gathered to see how the possible short-term spikes in demand impact the energy generation.
The fifth archetype is a site at which energy generation potential may exist, but no economically viable options are available for using the generated electricity. In the case of Adorf-Sorge, which is the second-most promising site after Rehbocksberg, the electrical power output of the turbine at the optimal operating point would be approximately 21 kW. However, the site is located deep in a forest, and is connected to the electricity grid via a 3-km-long cable, such that the maximum possible feed-in power input would be about 2.3 kW before the cable would be overloaded. This low Pelectrical could not be economically fed into the grid. There is also not sufficient energy demand at the site (no pumps or other substantial energy users), such that there is currently no known practical way to use the energy that could be generated with a turbine. Unfortunately, this removes Adorf-Sorge from the list of potential sites.
4.2. Cases in Which the Excel Tool is Not Needed or Appropriate
Pragmatic readers may ask themselves whether the data acquisition and evaluation required for using the full functionality of the Excel tool is warranted in every case. There are two main cases in which the designer of a turbine site should elect not to use the tool as recommended:
- There is limited data available for the site and time or other constraints make it undesirable to perform new measurements. In this case the site operator can take the shortcut of using the equivalent of the 2016 DVGW method “b”, and simply select a turbine that operates efficiently at the current typical Qin. According to the seven sites analyzed here, this leads on average to 10% less energy generation (and annual revenue), with a risk of up to 20% less energy generation. This is the best known alternative method that removes the need for data-based work.
- The site in question is a class 2 “non-buffered” site, for which this tool is not appropriate. Using the tool for class 2 sites will lead to gross overestimates of the potential energy generation, as shown in Table 4. This is due to the fact that the tool assumes a complete modification of the Qin regime, which is not possible at a class 2 site, for which Qin is necessarily equal to Qout.
4.3. Limitations of the Tool
The main limitation of the Excel tool presented here is its lack of functionality for accommodating class 2 “non-buffered” sites without storage tanks. While the authors suspect that class 2 sites with economically viable energy generation potential are in the minority compared to class 1 sites, the authors already identified several sites for which a practical and technically accessible design method would be needed. Collaborators of the authors in 2013 developed a preliminary Excel tool according to this method (currently available only in German [38]), which systematically tests the historical distribution of flow rates against typical efficiency curves for different types of turbines (e.g., Francis, Pelton, pump-as-turbine) to determine both the optimal turbine type and parameters for a given site. However, the authors are not confident that this tool properly accounts for the hydraulic nature of class 2 sites. Future work could pick up where this preliminary tool left off, and perhaps incorporate its functionality directly into the Excel tool presented here. In the best case, this could also build and improve on the 2016 DVGW methods.
The remaining limitations deal with ways in which the methodology and Excel tool might not lead to optimal solutions for class 1 sites, and could be improved in the future:
- The tool assumes the selection of a single turbine with a narrow acceptable operating range, and considers neither the possibility of turbines with wide operating ranges nor that of multiple turbines, the latter of which might lead to greater energy generation [25,27]. This was decided partly for simplicity’s sake and partly out of the belief that a single turbine generally represents the most economically viable solution for class 1 sites, which is supported by one of the studies cited above [25]. Furthermore, as indicated in Section 1.2, these studies do take into account the fundamental advantage of class 1 sites, which is the ability to modify the inflow regime, instead using multiple turbines to adapt to the wide range of flow rates occurring based on the current site conditions.
- The tool does not have a sophisticated way to support users with sites for which a feed-in tariff is either not available or not applicable (e.g., in Germany, if the water does not flow 100% via natural gradient). There is an option to enter in the total energy use on site and the percentage of which the user expects to be covered by the turbine. In the future it is planned to implement an algorithm that takes as input a time series of electricity use on site (parallel to the Qout time series) and estimates how much of this energy use could be covered by the turbine, such that the user does not need to estimate this herself.
- There is a lack of decision support in accounting for future changes in water use patterns, which other design methods seem to have accounted for [14,39,40]. However, there is a simplified factor which can be adjusted to account for possible increases or decreases in water use. In this way, an expected future water use pattern can be roughly simulated, and a turbine designed that will still be suitable for this future condition.
- The impact of iteratively varying the threshold tank levels (see Figure 6) to activate and deactivate the turbine and bypass has not been sufficiently assessed. Sitzenfrei and Rauch [14] presented an optimization method that is similar in spirit to the one presented by the authors but applied it to a class 2 site. They pursued an optimization approach by varying parameters in a randomized fashion through 1000 simulations (Monte Carlo simulation), selecting the best solution based on the amount of energy generated over 10 years. The parameters varied in this case are the set-point water levels in the supply tank upstream of the turbine: the overflow level, the level for switching from high to low turbine flow, and the minimum level required for fire-fighting. The HTWD method introduced in this paper could be improved by implementing a similar kind of randomized (e.g., Monte Carlo) variation of the four water level thresholds used to determine when water flows through the turbine, bypass or neither. This might increase the robustness of the solution suggested by the tool and also slightly increase the total annual energy generation predicted by the tool.
- As mentioned in Section 3.2, gaps (i.e., time intervals larger than the smallest time interval; e.g., due to missing data) in the input data time series of Qout lead to an error in the calculations performed by the tool. Currently, the burden is on the user to ensure that the time series contains no gaps. In the future, this could be improved through an algorithm that automatically checks for and linearly interpolates to fill these gaps.
- Currently, the data from only two types of turbines from two manufacturers are incorporated into the tool. This merely reflects the authors’ experience and available data until now and is not intended to imply that there are not further options. No funding links or other conflicts of interest exist between the authors and these two turbine manufacturers.
4.4. Relative Potential of Class 1 vs. Class 2 Sites
As mentioned previously, class 2 sites represent a greater technical challenge for the optimization-minded engineer than class 1 sites. Although they have not been able to confirm it, the authors suspect that class 1 sites exist in greater numbers and possess greater potential for energy generation than class 2 sites, due to their generally higher pressure heads. In particular, class 1 sites seem most relevant for small and medium-sized water suppliers with low population densities and relatively low water distribution flow rates, since their class 2 sites are unlikely to provide economically viable energy generation. It may be the case for the largest water suppliers that class 1 sites were long ago tapped for their hydropower potential, leaving predominantly class 2 sites that remain to be developed. As the largest water suppliers also tend to be more innovative, this may explain the apparently greater scientific attention given to class 2 sites (Appendix A.4). If the authors’ suspicions are accurate, it would be useful to better understand the relative potential for drinking water hydropower at class 1 vs. class 2 sites, as this could provide an incentive for greater focus on supporting the design and development of class 1 sites for small and medium-sized water suppliers, which tend to make up the vast majority in the total count of a given country’s water suppliers. The German water suppliers featured in this study are medium-sized.
5. Conclusions
This paper presented a novel method and accompanying Excel tool for determining the optimal parameters of a microturbine for water supply sites having a storage tank that decouples the inflow and outflow patterns, the so-called class 1 “buffered” sites. The method determines the optimal turbine flow rate based on key site characteristics and a historical time series of outflow data from the tank, simulating tank operation with a numerical model as it creates a new inflow regime. The main criterion for a viable solution is that the tank water level does not fall below a user-specified minimum. The Excel tool is not currently suitable for analyzing class 2 “non-buffered” sites without a storage tank but could conceivably be expanded to include this functionality.
The method was inspired by Haakh [28], who provided a foundational treatment of turbine and pump operation in the context of water supply systems. It fills a gap in the known methods for designing microturbines for water supply sites, which recognize the design advantages of class 1 sites, but provide no practical instructions on how to determine the optimal flow rate and corresponding pressure drop. The tool is intended to be widely accessible by being implemented in the commonly used software Microsoft Excel and is offered free of cost for download and use by any interested parties [33]. A blank version of the tool as well as a version with the data for the example site BPT Rützengrün (see Section 3.1) is included in the supplementary material.
The 2018 HTWD method presented here is compared with three other methods from two different generations of DVGW guidelines from 1994 and 2016. All four methods were used to analyze a total of nine sites located in Saxony, Germany, and the results were compared in terms of the annual energy generation. The HTWD design method estimates the greatest energy generation for each site, whereas the other three methods lead to an average of 70% to 91% of the HTWD results. If an alternative method had to be chosen, the 2016 DVGW method “b” (based on the most frequent range of inflow rates with the highest expected annual energy generation) provided the second-best results overall, ranging from 79% to 100% (with an average of 91%) of the energy generation predicted using the HTWD method (see Section 3.3 and Section 3.4 for details).
Of the nine sites analyzed, four are very likely economically viable (estimated payback periods of 1.7 to 6.9 years), while four are borderline viable (payback in 10.3 to 12.7 years) and could be made viable with sufficient reduction in project costs to the operator, for example through grant funding. The remaining site (Mittweida) is very unlikely economically viable, with an estimated payback period of 24.2 years. Other factors prevent the second-most promising site (Adorf-Sorge) from being economically viable, since there is no known practical way to transport the generated electricity off site or use it on site. While a turbine has not yet been implemented at any of these nine sites, at the time of submission, the site Rehbocksberg is the furthest along in the planning, and should be installed before the end of 2019, the site Rützengrün is in an advanced planning stage and the site Chursdorf is in an early planning stage. The experience gained from analyzing all nine sites led to the description of five archetypical sites (see Section 4.1 for details), which the reader can use as points of reference when analyzing sites under his or her supervision.
Supplementary Materials
The following are available online at https://www.mdpi.com/2073-4441/11/7/1403/s1, Two appendices, and two Excel files—one containing no data (File “MicroturbineTool_HTWD_v35_blank.xlsb”) and one containing data from the example site in this paper, BPT Rützengrün (File “MicroturbineTool_HTWD_v35_BPT-Ruetzengruen.xlsb”).
Author Contributions
T.J.V. devised the design method and Excel tool presented in this paper, performed the analysis of the nine sites, and wrote the paper. T.G. initiated the research efforts into microturbines in the water supply in 2013, acquired the funding that enabled the work to be performed and edited the final manuscript.
Funding
The authors are grateful to the German Federal Ministry of Education and Research (BMBF) for supporting the project “Energy Efficiency in the Water Supply” (grant number 03FH018I3). Preparation of the final paper was supported by the AquaNES project (grant number 689450), which received funding from the European Union’s Horizon 2020 Research and Innovation Program.
Acknowledgments
The authors are grateful to the communal water suppliers ZWA Hainichen, ZWAV Plauen and RZV Glauchau for providing data, insights from their practical experience and support during site visits. Julia Wetzel made important contributions to the development of the tool’s methodology as part of her bachelor thesis work.
Conflicts of Interest
The authors declare no conflict of interest. No funding was received from the turbine manufacturers Stellba and KSB.
Appendix A. Practical Considerations for Deploying Hydropower in Water Supply Systems
Appendix A.1. Origin of Surplus Energy in Gravity-Based Water Supply Systems and Hydraulic Aspects of Their Operation
Gravity pipelines connect higher-elevation water reservoirs to lower-elevation points of water storage and water users, and are a ubiquitous feature of water supply systems. The higher-elevation reservoirs can have natural (e.g., river dams) or artificial (e.g., elevated storage tank) origins. In all gravity pipelines, the difference in potential energy (elevation head) between the upstream inlet and downstream outlet or reference point within the pipeline is fully converted into three components:
- kinetic energy of the flowing water (velocity head),
- pressure energy between the water molecules (pressure head) and
- heat (and some sound) due to pipe wall (major) and local (minor) frictional resistance (head “loss”) in reaction to the flowing water.
With respect to hydropower development, there are two relevant types of gravity pipelines: those with and those without pressure control at points downstream, such as transfer stations or outlets into storage tanks. In a gravity pipeline without pressure control, head loss is at a minimum, velocity head is at a maximum and pressure head fluctuates between zero and small negative or positive values along the length of the pipeline depending on the pipeline’s exact downslope path (inevitably equaling zero at the outlet), such that the maximum possible flow rate is established [41]. The only remaining energy at the pipeline outlet is the velocity head of the flowing water. In a gravity pipeline with pressure control, head loss can be intentionally increased, increasing the pressure head upstream of the turbine and reducing the velocity head until the desired flow rate is established, normally using a pressure control valve at the downstream outlet (a local resistance). In cases with raw water in excess (e.g., a mountain spring during the rainy season), pressure control could also be achieved with an open basin, into which a gravity pipeline (without a pressure control valve) flows, reducing the relative pressure back to zero, and allowing excess water to spill over into natural watercourses. However, this becomes more the territory of “small” rather than “micro” hydropower, specifically a “run-of-river” scheme, which very well might precede a water supply scheme, but is not really “drinking water hydropower”. These kinds of schemes are covered by many papers and by manuals (e.g., [2,42,43]).
Like a pressure control valve, a hydropower turbine also represents a local resistance. Introducing a hydropower turbine into a gravity pipeline without pressure control would therefore reduce the flow rate, which is generally undesirable for an existing water supply scheme. In a gravity pipeline with pressure control, however, a turbine can functionally replace the pressure control valve, causing no change in the flow rate. And whereas a pressure control valve converts potential energy (as elevation head) into useless head loss, a turbine converts potential energy into useful mechanical energy, and often via a generator into electrical energy. Gravity pipelines with pressure control valves can thus be thought of as possessing “surplus” potential energy, which can be “harvested” by using a turbine rather than “wasted” by using a pressure control valve, which “throttles” the flow of water.
The simplest theoretically possible gravity-fed water supply pipeline would supply water at the required flow rate without the need for any flow regulation. This would require the precise selection of the pipeline’s total frictional resistance (a function of its length, diameter and inner surface material roughness), such that the maximum unregulated flow rate is equivalent to the required supply flow rate. In practice, however, a majority of existing gravity-fed supply pipelines would permit a far higher flow rate than usually required, if operated without any flow regulation. This means that these pipelines possess surplus hydraulic capacity. This arises in two main ways:
- Intentionally, because the designer anticipates periods during which nearly the maximum flow rate will be required (e.g., evenings in a dry summer period) or expects the total demand of the supply zone to increase due to population growth and/or increase in commercial or industrial activity, or
- Unintentionally, because the pipeline was chosen with a very generous factor of safety [14], or because demand in the supply zone is decreasing, due to declining population, increasing water use efficiency and/or cessation of commercial and industrial water use.
Both cases are common in Germany, where numerous water supply organizations have been able to construct hydropower facilities at their gravity-based systems for many decades [44,45,46]. Cases are also well documented in Austria [3,47], Switzerland [2] and England [48]. Regardless of the reason, in both cases flow regulation is generally employed in the form of pressure control to restrict the flow rate to the level required for supply. Pressure control is normally accomplished using a manually or remotely operated valve. While specially designed pressure-reducing valves exist, they are expensive, such that other fittings like gate or butterfly valves are frequently used, although they may not be designed for this purpose. In cases with very large altitude differences (e.g., above 200 m), pressure control can be achieved through break-pressure tanks (BPTs) over several elevation stages, to reduce the risk of pipe bursts. Here, passive pressure control can also be employed, for example using an energy-dissipating baffle wall or an in-pipe fixed-diameter orifice plate [6].
Both active and passive pressure control converts energy in the form of hydraulic pressure to energy in the form of heat, and to a lesser extent sound and vibration (at the point of resistance). It is precisely this energy that can instead be converted into useful mechanical work or electrical energy by operating a hydropower facility. In this way, the hydropower unit serves two purposes at the same time, by reducing excess pressure and simultaneously converting it to useful energy. Figure A1 illustrates the hydraulic nature of a typical potential turbine site with a pressure control valve. The turbine can be installed in a bypass pipe in parallel with the existing pressure control device or at the inflow to an existing BPT, without endangering the primary goal of supplying water [6]. Models of axial in-pipe turbines are also available, which do not necessarily require a bypass for normal operation, as they provide the same hydraulic resistance whether they are electrically connected or not, and thus pose no danger of pressure shocks (water hammer) in the case of a power outage or sudden mechanical failure.
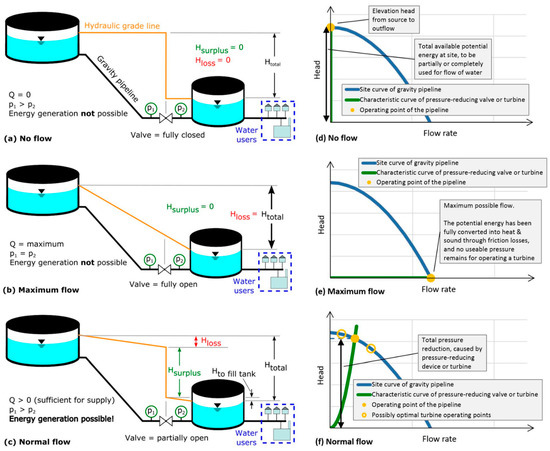
Figure A1.
The basic hydraulics of a drinking water hydropower system prior to the installation of a turbine, illustrated under three conditions (no flow, maximum flow, normal flow) using the hydraulic grade line and process diagram (a–c) as well as a diagram of head vs. flow rate (d–f).
Appendix A.2. Favorable Site Characteristics for Hydropower
To maximize energy generation and economic viability (defined by initial investment, annual revenue and payback period) for both classes of sites, the following characteristics are most favorable [49]:
- Nearly constant flow rate, either due to a site being class 1, or because the water use profile in the downstream supply zones do not fluctuate very much in the case of class 2 sites
- Nearly constant pressure conditions
- Existing infrastructure that can be used with only minor modifications to the piping and without any civil construction works (e.g., an easily accessible and enclosed building, control valves and pipe systems with generous amounts of space)
- Local energy needs, such that the energy generated can most economically be used, by replacing the need to purchase energy from the grid (typically the most expensive source)
- Conditions that meet the requirements for receiving a feed-in tariff (e.g., in Germany this is a purely natural gradient, without any pumping upstream of the turbine site)
Appendix A.3. Further Characteristics of and Implications for Turbines at Class 1 and Class 2 Sites
Appendix A.3.1. Class 1 “Buffered” Sites
Class 1 sites are generally intermediate (such as break-pressure tanks (BPTs)) or terminal storage tanks with pressure control valves [6], typically located within the water “transmission” section of the water supply chain [13]. In the authors’ experience and estimation, class 1 sites represent a relatively cost-effective opportunity for renewable energy generation. They offer the water supplier flexibility (positively correlated with storage volume) in determining the rate, duration and timing of tank filling (and thus turbine operation), as this must not necessarily occur simultaneously with the downstream use in the supply zone. Assuming that the inflow rate is not restricted (e.g., by the naturally occurring flow from a mountain spring), the inflow regime can often be freely adjusted to maximize energy generation through a turbine, regardless of how it was managed in the past [12].
Pressure control at such sites is generally accomplished using a fixed resistance (e.g., orifice plate) or a simple valve (e.g., butterfly or gate), which is opened to a pre-determined set-point to reduce the inflow rate to the desired level. Since the higher-elevation water reservoir is normally a fixed point, and substantial withdrawals seldom occur en route to the storage tank (which would increase the flow rate along stretches of the pipeline, thus increasing head loss), the pressure available to a turbine generally remains constant as long as the flow rate is held constant.
This enables the selection of inexpensive turbines such as pumps-as-turbines (PATs) [36] or axial in-line turbines (such as the “AXENT” from Germany [35] or “PAM PERGA” from Spain and Germany [29]), which have a narrow effective operational spectrum and are best suited for a fixed operating point [2,42]. These also offer the greatest flexibility for installation, not normally requiring a significant structural change to the storage tank building and only minor changes to the piping. If the tank is located below the turbine installation site and the elevation head is sufficiently high, then a traditional Pelton impulse turbine can also be an option, since this reduces the pressure in the pipeline to atmospheric pressure [2,43,50]. While a so-called “counter pressure” Pelton turbine was developed by the Swiss companies Blue Water Power and Häny [51] to address precisely this limitation, it is only suitable for high-potential sites due to its very high cost, on the order of 50 times more expensive than a PAT of comparable capacity [52].
Appendix A.3.2. Class 2 “Non-Buffered” Sites
Common examples of class 2 sites include transfer nodes between pressure zones or gravity-fed water treatment plants in between gravity source and destination supply tanks (e.g., [2,5,8,11,12]). They are most often located within the water “distribution” section of the water supply chain [8]. In contrast to class 1 sites, class 2 sites offer no flexibility in the choice of flow rate, such that a turbine must be designed or chosen to efficiently operate over a broad spectrum of flow rates and corresponding available pressure heads.
Pressure control is practiced to both keep the pressure within an acceptable range for water users, to prevent pipe bursts through very high pressure, and to reduce water leakage through moderately high pressure that is not needed for maintaining satisfactory supply, for example through “pressure management” at certain times of the day (e.g., night) or in certain locations (e.g., low-elevation pressure zones). These sites are generally outfitted either with specially designed pressure-reducing valves (PRVs) or simpler gate or butterfly valves. The specially designed PRVs have an automatically adjusting variable resistance that mechanically responds to changes in pressure on both its upstream and downstream sides, to maintain a constant downstream pressure independent of flow rate. The simpler valves have a fixed characteristic curve relating their head loss coefficient to the degree of opening, and are generally opened to pre-determined set points to reduce flow rate, for example at class 1 sites or class 2 sites with a relatively constant flow rate.
At sites with sufficiently high hydropower potential (e.g., >100 kW at nearly constant operation), the best option is often a classic custom-made Francis turbine, which possesses a guide vane apparatus to flexibly react and adjust to the changing flow rates as determined by downstream water use, enabling a high efficiency over a broad operating range [2,43]. For sites with more modest hydropower potential, many scientists have devised control system designs that enable the use of inexpensive PATs to flexibly react to changing hydraulic conditions while still fulfilling the pressure control goals [7,50,53,54], in some cases accepting slightly higher leakage as a trade-off for achieving energy generation [55,56].
Appendix A.4. Review of Scientific Literature on Turbine Design Methods for Class 1 and Class 2 Sites
The potential for hydropower development in water supply schemes has been assessed by numerous scientists and engineers worldwide, and in some cases practical guidelines for implementation including design methods have been developed. However, based on a review of the scientific literature, there seems to be a dominant focus on class 2 sites, as the authors try to show in the following text.
For clarification, the term “turbine design” in this paper refers to the determination of the turbine parameters (flow rate and pressure drop across the turbine). The physical design and construction of the turbine (e.g., impeller and housing) should be carried out by a competent turbine manufacturer or research lab.
Appendix A.4.1. Studies Focusing on Class 2 Sites
Santolin et al. [57] present a method for determining the parameters of a run-of-river turbine (a variant of class 2 sites), optimizing for energy generation and economic performance. This method is similar in spirit to the method presented here for class 1 sites in water supply systems, but does not seem easily transferable.
Colombo and Kleiner [40] conduct a theoretical analysis of a turbine meant to replace a PRV for a reservoir-fed water supply system. However, this is for a class 2 site, and they also seem to make the error of associating a higher momentary power production (in kW) with a more desirable outcome, which is not necessarily true, as it often does not lead to the greatest total annual energy generation, as we show in our paper.
Carravetta et al. [13] propose a “variable operating strategy”, a method for designing PAT systems to replace PRVs at class 2 sites within water distribution networks, which involves PAT in series-parallel combinations and/or with electrical rotational speed control (e.g., variable-frequency drives) to flexibly adapt to the wide range of head-flow combinations that occur. They stipulate that this complex approach is not intended for water transmission networks (i.e., class 1 sites), where there is less variability in flow conditions.
McNabola et al. [5] and Corcoran et al. [10,11] assess the potential of both class 1 and class 2 sites in Ireland and the UK, but on a conceptual and technically approximate level. They provide rough estimates of potential energy generation, without any clear guidelines on how to design a turbine for a specific site.
De Marchis et al. [53] present a hydrodynamic numerical simulation based on the “Method of Characteristics” to determine optimal parameters for PAT to be installed at class 2 sites within a water distribution network. They apply this to one of the 17 supply networks in the city of Palermo, Italy.
Sitzenfrei and Rauch [14] present a method using EPANET2 and MATLAB for determining turbine parameters at a non-conventional class 2 site in an alpine supply zone in Austria. Due to a surplus supply of natural spring water, a turbine is proposed at an outflow from the distribution network into a nearby watercourse, which serves to simultaneously generate useful energy while also flushing parts of the pipe network through increased flow rates. The amount of water released through the turbine is the surplus that remains between the amount provided naturally by the higher-elevation spring (which varies seasonally as well as daily) and the amount demanded by water users (which varies seasonally, daily and hourly).
Power et al. [15] assess the use of PAT and other turbines for four wastewater treatment plant outflows in Ireland, which are functionally equivalent to class 2 sites in drinking water supply systems. They use an optimization algorithm in Microsoft Excel, but rely on daily average flow data “to examine turbine selection, design optimization, and economic viability”.
Lima et al. [16] present a mathematical model with the software MATLAB and use the “Particle Swarm Optimization” algorithm to determine optimal parameters for turbines to replace PRVs at 2 class 2 sites with PRVs in Brazil. They also simultaneously determine the optimal sizes of the existing pipe network to optimize energy production through PAT at the former PRV sites.
Several papers mentioned here [13,14,15,16] and others not elaborated on [7,8,17,18,19,20,21,22] present methods that might be useful for class 1 sites, but the effort required to successfully adapt the methods and restrictions imposed by technical understanding and software availability for the authors’ intended user group speak against pursuing this further. For instance, since the authors set out to create a tool that is free to use and based on a common tool (i.e., Microsoft Excel), and MATLAB is a non-standard software requiring specialized knowledge, possible adaptation of such algorithms [14,16] was not considered. Furthermore, while some authors provide the basic underlying equations, the software in which the algorithms are implemented is not made accessible to the reader.
Some German-language technical guidelines provide more concrete advice. The most recent 2016 edition of the German guidelines published by the German Technical and Scientific Association for Gas and Water (DVGW) [12] provides easy-to-follow guidance in the case of class 2 sites. They suggest using a frequency distribution of the occurring flow rates to determine the design flow rate of the turbine or multiple turbines. The flow rate (or group of flow rates; e.g., between 50 and 55 m3/h) having the greatest energy density (product of total flow volume and hydraulic power) should be the design turbine flow rate.
The original 1994 edition of the DVGW guidelines [34] make no distinction between class 1 and 2 sites, and suggests using the historically most frequently occurring flow rate to select the turbine (explained in Section 2.10 above). However, they imply that the theoretical optimal flow rate is 0.577 × Qmax (with Qmax defined as the greatest possible flow rate, with no pressure reduction in the pipeline), at which the hydraulic power contained in the flowing water is mathematically at its maximum [37].
Appendix A.4.2. Studies Focusing on Class 1 Sites
While comparatively less common, there are also studies that focus on class 1 sites.
Ramos et al. [7] describe an approach to design turbines for replacing PRVs at class 2 sites using the pipe network simulation tool EPANET and genetic algorithms, but also include a case study of a class 1 site in Portugal at the base of a reservoir. However, no details are provided regarding the design of the PAT proposed for this class 1 site.
Kucukali [26] analyzes a long-range water transmission pipeline with a total of 12 class 1 sites with BPTs but does not provide a concrete method regarding the ideal parameter selection of the turbines for each of the sites, presumably because the discharge remains largely constant. Since the pipeline terminates in a storage tank, however, it is conceivable that the possibility of adjusting this flow rate is neglected, which might sacrifice a possible increase in energy generation.
McNabola et al. [6] assess the potential of 10 class 1 BPT sites in Ireland, but provide only a rough estimate of the energy yield, and provide no design method for determining the optimal parameters of a turbine that would maximize the total annual energy generation.
Kougias et al. [27] present a case study with class 1 sites from northern Greece, where they have a long-range spring-fed water supply and transmission system with three BPTs (over a total of 200 vertical meters) along the route from the spring to the city 22 km further downstream. They use a so-called “Harmony Search Algorithm” (HSA) in the commercially licensed software MATLAB to determine the optimal number and dimensions of turbines for energy generation.
However, the authors prefer not to use MATLAB (as previously stated) and the HSA is not explained in detail in the paper, making it difficult to assess its usefulness. Furthermore, the flow conditions are stated to be rather constant, which makes it seem unlikely that optimization is even necessary. While not explicitly stated, this also implies the existence of a buffering storage tank at the end of the transmission pipeline, such that further optimization of energy generation might be possible as with [26].
Vilanova and Balestieri [23] present a case study in Brazil of a spring-fed supply and transmission system terminating at a water treatment plant, presumably a class 1 site with a storage tank. However, they do not provide any method for determining the optimal turbine parameters. As with other sites, the authors suspect that the inflow rate is taken as a given, rather than being seen as a parameter than can be modified to increase overall energy generation.
Novara [24] presents one simplified case study of using a PAT at a class 1 site in Italy, but provides no information about determining turbine parameters, and seems to use a very rough approximation to calculate the energy generation.
Monteiro et al. [25] introduce a method for assessing energy generation and determining the optimal number and parameters of turbines at class 1 sites, which they apply to one of three identified sites in Portugal. However, they seem to effectively treat class 1 sites as if they were class 2 sites, assuming that the inflow regime remains unchanged and attempting to design turbines to fit the inflow regime, rather than adjusting the inflow regime to allow the choice of a single, optimized turbine. Thus, they do not use the fundamental technical advantage that separates class 1 from class 2 sites.
Appendix B. User Guidelines for the Excel Tool
The following information is pertinent to users of the Excel tool, but is less relevant for judging the scientific merit of the method and results described in the article’s body.
Appendix B.1. Description of the Tool
The user is only required to obtain the necessary input data and verify their accuracy, and the tool performs the calculations. The quality of the hypothetical turbine parameters depends on the amount and quality of information provided. Generally, providing more information leads to solutions that are both more reliable and more accurate.
The Excel tool has five worksheets (tabs) that are relevant for a general user:
- Rough estimate: This sheet estimates the energy generation and economic costs and benefits based on four single input values, making the very optimistic simplifying assumption of a constant flow profile. This allows the user to determine whether it is worthwhile to continue on to the more time-intensive steps of a detailed analysis (the subsequent three sheets).
- Single values: This sheet is for entering between 7 and 14 single values, used for generating the hydraulic site curve, calculating the economic benefits and (optionally) ensuring that the storage tank does not fall below the minimum permissible fill level due to a reduction in the flow rate (which provides the apparent “benefit” of increased energy generation).
- Time series: This sheet is for entering time series (of the past six months to three years), used to iteratively simulate possible turbine parameters with historic data, to determine which parameters provide the greatest energy generation while still providing the daily flow volume required and (optionally) without causing unacceptable reductions in the storage tank level. Up to six time series can be entered, but generally only two are required.x
- Turbine design: This sheet automatically determines the optimal turbine parameters based on the calculation options chosen regarding (a) level of detail and (b) choice of bypass flow. The user may then fine-tune certain design aspects before generating the technical and economic results.
- Results: This sheet contains the results saved using a button on the previous sheet “Turbine design”, providing an overview of the results obtained using various design approaches.
There are further sheets contained within the tool that perform calculations in the background, but also that display the site curve and hydraulic power curve for the current site, and display the results of the automated optimization algorithm graphically and as numbers.
Appendix B.2. Data Requirements and Corresponding Quality Criteria for Solutions
There are four main calculation options incorporated into the tool. These options are:
- Detailed calculation with time series interval ≤15 min and consideration of storage tank levels using a historical time series of tank levels (to determine the storage capacity by inference)
- (recommended) Detailed calculation with time series interval ≤15 min and consideration of storage tank levels using known or estimated useable storage tank capacity
- Rough calculation with time series interval between 15 min and 1 d and only time series of storage tank outflow
- Rough calculation with partially estimated single values (no time series)
The data requirements for each of these options are summarized in Table A1 below.

Table A1.
Data requirements depending on desired quality of results (and corresponding calculation option): “X” = required and “(X)” = optional.
Table A1.
Data requirements depending on desired quality of results (and corresponding calculation option): “X” = required and “(X)” = optional.
| Data Type | Unit | (1) Detailed Calc., Tank Level Check via Time Series | (2) Detailed Calc., Tank Level Check via Storage Volume | (3) Rough Calc., Only Outflow Time Series | (4) Rough Calc., Estimated Single Values |
|---|---|---|---|---|---|
| Single values (sheet 2) | |||||
| Inflow rate (Qin) at control valve, position 1 (e.g., at normal flow) | m3/h | X | X | X | X |
| Upstream pressure (h1_upstream) at control valve, position 1 | m; bar | X | X | X | X |
| Qin at control valve, position 2 (e.g., at zero flow) | m3/h | X | X | X | X |
| h2_upstream at control valve, position 2 | m; bar | X | X | X | X |
| hdownstream at control valve (worst case) | m; bar | X | X | X | X |
| Eligible for feed-in tariff? (yes/no) | --- | X | X | X | X |
| Max. permissible Qin (e.g., by contract), Qmax inflow | m3/h | X | X | (X) | |
| Min. tank level (Ltank) in normal operation, L1_turbine on | % | X | X | ||
| Max. permissible tank level, L2_max shutoff | % | X | X | ||
| Threshold for opening bypass, L3_bypass on | % | X | X | ||
| Min. tank level in an emergency, L4_min emergency | % | X | X | ||
| Useable storage volume, Vtank | m3 | X | |||
| Electricity price on site | €/kWh | X | X | X | X |
| Feed-in tariff (if relevant) | €/kWh | (X) | (X) | (X) | (X) |
| Time series (sheet 3)—for the previous six months to three years | |||||
| Timestamp for data time series (in format TT.MM.YYYY HH:mm:ss) | --- | X | X | X | |
| Qout, from storage tank | m3/h | X | X | X | |
| Storage tank level, Ltank | % | X | |||
| Qin, to storage tank | m3/h | X | (X) | ||
| Timestamp for Qin | --- | (X) | (X) | ||
| Energy usage on site | kWh | (X) | (X) | ||
In general, the more data that are provided at a higher temporal resolution, the more reliable the resulting turbine parameters will be and the greater the chance of reaching the optimal energy generation. Thus calculation option 2 is recommended, with option 1 as an alternative offering a possible increase in accuracy (this was discovered after the numbering was set). These require more time and effort due to greater data requirements. If data or time are scarce, a compromise can be made on the solution quality, and a simpler calculation option 3 or 4 can be chosen. The four different options are compared on various quality criteria below (Table A2), using the rough estimate (from sheet 1 of the tool) as a benchmark.

Table A2.
Quality criteria for solutions provided by the Excel tool, depending on the chosen calculation option, where 1 = lowest and 5 = highest.
Table A2.
Quality criteria for solutions provided by the Excel tool, depending on the chosen calculation option, where 1 = lowest and 5 = highest.
| Calculation Option | Rough Estimate (Sheet 1) | (1) Detailed Calc., Tank Level Check via Time Series | (2) Detailed Calc., Tank Level Check via Storage Volume | (3) Rough Calc., Only Outflow Time Series | (4) Rough Calc., Estimated Single Values | |
|---|---|---|---|---|---|---|
| Quality Criteria for Solution | ||||||
| Time needed for gathering and quality-checking data (per site) | 30 min. to 2 h | 8 to 24 h | 8 to 24 h | 4 to 16 h | 2 to 4 h | |
| Confidence that tank level does not fall below min. permissible level | 1 | 5 | 4 | 2 | 1 | |
| Accuracy in estimating energy generation | 1 | 5 | 5 | 3 | 2 | |
| Robustness against high variation in tank outflow | 1 | 5 | 5 | 3 | 1 | |
| Main advantages | Quick feedback | Best all-around solution | Faster, sometimes reliable | Small step up from rough estimate | ||
| Main disadvantages | Not reliable | Takes most time and effort | Tank levels uncertain; energy generation estimates based on daily flow volumes | |||
Calculation options 3 and 4 have the disadvantage that they do not account for tank levels. In order to yield reliable solutions, these options require that a turbine flow rate lies above the current typical flow rate for a given site. This assumes that the “typical” inflow rate chosen is high enough to compensate for possible short-term spikes in user demand (and outflow rate). At some sites, the inflow rate is automatically increased (above and beyond the “normal” inflow rate) in response to such events. If this behavior is known to the tool user, this higher emergency inflow rate can be chosen. If it is unknown, then a turbine could be chosen that leads to the tank level occasionally falling below the minimum permissible limit—a nonviable solution. This risk can be greatly reduced or entirely avoided by choosing calculation option 1 or 2. However, if the typical inflow rate is known to be historically constant, and the problem of low water levels has never come up, then option 3 or 4 can be acceptable, time-saving alternatives to options 1 and 2.
The primary advantage of options 1 and 2 is that there is no need to be biased by the typical inflow rate of past operations. The analysis of historical data thus allows the determination of turbine parameters from “first principles”, rather than by analogy from the previous inflow rate, which may have been selected for reasons unknown to the current responsible engineer or site operator.
Appendix B.3. Choice of Bypass Flow
Since calculation options 1 and 2 may lead to the suggestion of flow rates that are lower than the current typical inflow rate, a bypass with varying flow rates is also included (as previously mentioned), as it is possible that the periodic re-routing of water around the turbine can lead to greater energy generation by selecting a relatively low turbine design flow rate. There are three options for determining the bypass flow, each with its own advantages and disadvantages:
- Smallest possible bypass flow (minor reduction in energy generation, but smaller difference between turbine and bypass flow, which is preferable to some water supply system operators),
- (recommended) Maximum permissible bypass flow (based on the user input, implies larger difference between turbine and bypass flow, but maximum energy generation and greater supply reliability) and
- Choose the turbine flow such that in a typical situation no bypass is required (moderate reduction in energy generation, but greatest supply reliability and possibly lowest investment costs, as there is no need for electronically automated bypass valve regulation).
Appendix B.4. Assumptions/Limitations/Remarks
The following assumptions are implicit in the tool’s algorithms:
- Historic water use patterns are a reliable proxy for the future. While the tool allows for some adjustment factors to account for possible future changes in both quantity and variation of user water demand, these do not aid in predicting major future trends. Therefore, it behooves the water supplier to have sufficient safeguards in place to enable manual interventions in the case that storage tank levels unexpectedly fall below permissible levels.
- Insofar as it is not already the case, the inflow rate can be kept constant during the operation of a turbine. This assumes that there are no restrictions on the inflow side, such as any put in place by the third-party operator of the reservoir or long-range supply pipeline.
The following limitations are relevant for using the tool:
- If time series are used, as recommended, having any gaps (for example, a 120-min gap in a series with otherwise 15-min intervals) leads to a false result and must be avoided by quality-checking the data.
- Only one time interval is currently possible for all data types (e.g., 15 min for both outflow and storage tank level, with the exception of the inflow rate, which has the option of a different time interval).
The following remarks may be helpful for users or potential users of the tool:
- The diameter of the pipeline plays an essential role in the availability of excess energy for hydropower generation. However, the exact diameter is not normally essential information regarding the selection of a turbine. The most reliable basis for turbine selection is the actual characteristic hydraulic site curve, derived from measurements at the storage tank flow. The turbine can normally be flexibly integrated into most pipeline systems with suitably tapered reducer and expander joints. The pipelines leading to the sites described here ranged in diameter from 150 mm at the smallest to 600 mm at the largest (for a supply main from a long-distance regional water supplier), while the pipelines in the immediate run-up to the tank typically ranged from 150 mm to 350 mm.
- When measuring pressure at field sites, one should be aware that manometers sometimes exhibit drift after years of use, such that the manometer should be separated from the water pressure and exposed to atmospheric pressure (for example, using an aeration valve) to obtain a reliable reference value corresponding to a relative pressure of 0 bar. This value can then simply be deducted from the value read when the manometer is again fully exposed to water pressure.
- Some supervisory control and data acquisition (SCADA) systems provide an option to convert the time interval of the collected data from e.g., delta-event (random, event-based time interval) to a fixed 15-min interval. If this is a feasible and reliable option, this should be used. Alternatively, the authors have developed a further Excel tool solely for the purpose of converting such delta-event time series into time series with a fixed, regular time interval. This tool can be made freely available upon request.
The maximum total annual energy generation (kWh/a) is typically achieved not at the point of maximum hydraulic power, but at the minimum feasible flow rate, limited by two factors:
- The flow rate must at any point in time be sufficient to meet the demand placed on the storage tank by the water users in the supply zone, and cannot endanger the reliability of supply (e.g., by causing the storage tank to temporarily run empty). The bypass can, for example, be set at a higher flow rate than the turbine flow rate, in order to enable rapid filling in periods of high water withdrawal from the tank.
- The flow rate must be high enough to enable the use of a microturbine with a practical size and sufficiently high efficiency, as the efficiency of turbines and generators drops rapidly with declining physical dimensions, and the turbine should fit into the existing infrastructure without making large structural changes in the piping network.
Exceptions to this typical case are possible, and accounted for by the Excel tool. For example, it is possible for the pipeline to have such a low friction loss-coefficient as to not exhibit a substantial drop in pressure with increasing flow rate over the conceivable operating range. The design flow rate could be made as high or low as desired, as there would be no penalty for increasing the flow rate. In this (rare) case, the site curve would resemble a horizontal line over the conceivable operating range of flow rates. As more sites are analyzed, further instances of exceptions to the typical case may be discovered.
References
- Hintermann, M. Electricity from Drinking Water Systems: Inventory and Feasibility Study of Drinking Water Hydropower Facilities in Switzerland (In German & French Only); Projektleitung DIANE Klein-Wasserkraftwerke; Bundesamt für Energiewirtschaft: Bern, Switzerland, 1994; p. 65. Available online: http://www.infrawatt.ch/sites/default/files/1994_DIANE_4df_Elektrizit%C3%A4t%20aus%20Trinkwasser-Systemen.pdf (accessed on 1 April 2019).
- EnergieSchweiz und SVGW. Energy in the Water Supply: Guidebook for Optimizing Energy Costs and Operation (In German Only); Bundesamt für Energie und SVGW: Zurich, Switzerland, 2004. [Google Scholar]
- Aste, C.M.; Moritz, G. TrinkHYDRO-Kärnten: Assessment of the Potential for Drinking Water Power Plants in Kärnten (In German Only); Technical report nr. B-EBK 9-036; ELWOG: Klagenfurt, Austria, 2009. [Google Scholar]
- Laghari, J.A.; Mokhlis, H.; Bakar, A.H.A.; Mohammad, H. A comprehensive overview of new designs in the hydraulic, electrical equipments and controllers of mini hydropower plants making it cost effective technology. Renew. Sustain. Energy Rev. 2012, 20, 279–293. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Corcoran, L.; Power, C.; Williams, A.P.; Harris, I.; Gallagher, J.; Styles, D. Energy recovery in the water industry using micro-hydropower: An opportunity to improve sustainability. Water Policy 2013, 1–16. [Google Scholar] [CrossRef]
- McNabola, A.; Coughlan, P.; Williams, A.P. Energy recovery in the water industry: An assessment of the potential of micro-hydropower. Water Environ. J. 2013, 1–11. [Google Scholar] [CrossRef]
- Ramos, H.M.; Mello, M.; De, P.K. Clean power in water supply systems as a sustainable solution: From planning to practical implementation. Water Sci. Technol. Water Supply 2010, 10, 39–49. [Google Scholar] [CrossRef]
- Carravetta, A.; Fecarotta, O.; Ramos, H.M. A new low-cost installation scheme of PATs for pico-hydropower to recover energy in residential areas. Renew. Energy 2018, 2. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; Sánchez-Romero, F.J.; López-Jiménez, P.A.; Ramos, H.M. PATs selection towards sustainability in irrigation networks: Simulated annealing as a water management tool. Renew. Energy 2017. [Google Scholar] [CrossRef]
- Corcoran, L.; McNabola, A.; Coughlan, P. Energy Recovery Potential of the Dublin Region Water Supply Network. In Proceedings of the World Congress on Water, Climate and Energy, Dublin, Ireland, 13–18 May 2012. [Google Scholar]
- Corcoran, L.; Coughlan, P.; McNabola, A. Energy recovery potential using micro hydropower in water supply networks in the UK and Ireland. Water Sci. Technol. Water Supply 2013, 13, 552–560. [Google Scholar] [CrossRef]
- DVGW. Energy Recovery through Hydropower Facilities in the Water Supply (In German Only); Technical Guidelines, Worksheet W 613 (A); DVGW: Bonn, Germany, 2016. [Google Scholar]
- Carravetta, A.; Del Giudice, G.; Fecarotta, O.; Ramos, H.M. Energy Production in Water Distribution Networks: A PAT Design Strategy. Water Resour. Manag. 2012, 26, 3947–3959. [Google Scholar] [CrossRef]
- Sitzenfrei, R.; von Leon, J.; Rauch, W. Design and Optimization of Small Hydropower Systems in Water Distribution Networks Based on 10-Years Simulation with Epanet2. Procedia Eng. 2014, 89, 533–539. [Google Scholar] [CrossRef][Green Version]
- Power, C.; Coughlan, P.; McNabola, A. Microhydropower Energy Recovery at Wastewater-Treatment Plants: Turbine Selection and Optimization. J. Energy Eng. 2016. [Google Scholar] [CrossRef]
- Lima, G.M.; Brentan, B.M.; Luvizotto, E. Optimal design of water supply networks using an energy recovery approach. Renew. Energy 2017. [Google Scholar] [CrossRef]
- Samora, I.; Manso, P.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Feasibility Assessment of Micro-Hydropower for Energy Recovery in the Water Supply Network of the City of Fribourg; Sustainable Hydraulics in the Era of Global, Change; Erpicum, S., Dewals, B., Archambeau, P., Pirotton, M., Eds.; Taylor & Francis Group: London, UK, 2016; pp. 961–965. ISBN 978-1-138-02977-4. [Google Scholar]
- Samora, I.; Franca, M.J.; Schleiss, A.J.; Ramos, H.M. Simulated Annealing in Optimization of Energy Production in a Water Supply Network. Water Resour. Manag. 2016, 230, 1533–1547. [Google Scholar] [CrossRef]
- Carravetta, A.; del Guidice, G.; Fecarotta, O.; Ramos, H.M. PAT Design Strategy for Energy Recovery in Water Distribution Networks by Electrical Regulation. Energies 2013, 6, 411–424. [Google Scholar] [CrossRef]
- Fecarotta, O.; Ramos, H.M.; Derakhshan, S.; Del Giudice, G.; Carravetta, A. Fine Tuning a PAT Hydropower Plant in a Water Supply Network to Improve System Effectiveness. J. Water Resour. Plan. Manag. 2018, 144. [Google Scholar] [CrossRef]
- Novara, D.; McNabola, A. The Development of a Decision Support Software for the Design of Micro-Hydropower Schemes Utilizing a Pump as Turbine. Proceedings 2018, 2, 678. [Google Scholar] [CrossRef]
- Pérez-Sánchez, M.; López-Jiménez, P.A.; Ramos, H.M. PATs Operating in Water Networks under Unsteady Flow Conditions: Control Valve Manoeuvre and Overspeed Effect. Water 2018, 10, 29. [Google Scholar] [CrossRef]
- Vilanova, M.R.N.; Balestieri, J.A.P. Hydropower recovery in water supply systems: Models and case study. Energy Convers. Manag. 2014, 84, 414–426. [Google Scholar] [CrossRef]
- Novara, D. Energy Harvesting from Municipal Water Management Systems: From Storage and Distribution to Wastewater Treatment. Extended Abstract (Not Peer-Reviewed). 2016. Available online: https://fenix.tecnico.ulisboa.pt/downloadFile/281870113703554/Extended%20Abstract%20-%20Daniele%20Novara.pdf (accessed on 9 January 2019).
- Monteiro, L.; Delgado, J.; Covas, D.C. Improved Assessment of Energy Recovery Potential in Water Supply Systems with High Demand Variation. Water 2018, 10, 773. [Google Scholar] [CrossRef]
- Kucukali, S. Water supply lines as a source of small hydropower in Turkey: A Case study in Edremit. In Proceedings of the World Renewable Energy Congress 2011, Hydropower Applications, Linköping, Sweden, 8–13 May 2011; pp. 1400–1407. Available online: http://www.ep.liu.se/ecp/057/vol6/004/ecp57vol6_004.pdf (accessed on 5 March 2019).
- Kougias, I.; Patsialis, T.; Zafirakou, A.; Theodossiou, N. Exploring the potential of energy recovery using micro hydropower systems in water supply systems. Water Util. J. 2014, 7, 25–33. [Google Scholar]
- Haakh, F. Hydraulic Aspects of the Economic Viability of Pumps, Turbines and Pipelines in the Water Supply (In German Only), 1st ed.; HUSS-MEDIEN GmbH: Berlin/Oldenbourg, Germany; Industrieverlag: München, Germany, 2009; pp. 111–174. ISBN 978-3410211389. [Google Scholar]
- Kracht, S. Out of water comes electricity—Microturbine “PAM PERGA” in water supply network (in German only). Energie|Wasser-Praxis 2018, 10, 78–81. [Google Scholar]
- Wieprecht, S.; Kramer, M. Investigations into the Use of Microturbines in Drinking Water Supply and Distribution Networks; Technical report nr. 09/2012; Funded under DVGW Project W8/01/10; DVGW: Bonn, Germany, 2012. [Google Scholar]
- Plath, M.; Wichmann, K.; Ludwig, G. Handbook for Energy Efficiency and Energy Savings in the Water Supply (In German Only); DVGW & DBU: Bonn/Osnabrück, Germany, 2010. [Google Scholar]
- Parra, S.; Krönlein, F.; Krause, S.; Günthert, F.W. Energy generation in the water distribution network through intelligent pressure management (in German only). Energie|Wasser-Praxis 2015, 12, 99–103. [Google Scholar]
- Voltz, T.; Grischek, T. Energy management in the water supply: Excel Toolbox. Available online: https://www.htw-dresden.de/energy-in-water (accessed on 4 July 2019).
- DVGW. Energy Recovery through Hydropower Facilities in the Water Supply (In German Only); Technical guidelines, Worksheet W 613; DVGW: Eschborn, Germany, 1994. [Google Scholar]
- Stellba Hydro: Axent. Available online: http://www.stellba-hydro.com/axent/ (accessed on 13 December 2018).
- KSB. Application-Oriented Planning Documents for Pumps as Turbines. Available online: https://www.ksb.com/blob/52858/13564c16a6b15b3c28b1d544ae52d0e4/pat-en-data.pdf (accessed on 5 May 2019).
- Mikus, K. Energy savings and recovery in drinking water supply (in German only). In Mechanical and Electrical Installations in Water Works, 1st ed.; Ebel, O.-G., Ed.; DVGW & Oldenbourg Industrieverlag: München, Germany, 1995; Volume 3, pp. 93–98. ISBN 3-486-26339-0. [Google Scholar]
- Bahner, P.; Voltz, T.; Grischek, T. Bemessung von Pumpen als Turbinen. Available online: https://www2.htw-dresden.de/~wasser5/ (accessed on 5 July 2019).
- Corcoran, L.; McNabola, A.; Coughlan, P. Predicting and quantifying the effect of variations in long-term water demand on micro-hydropower energy recovery in water supply networks. Urban Water J. 2016. [Google Scholar] [CrossRef]
- Colombo, A.; Kleiner, Y. Energy recovery in water distribution systems using microturbines. In Proceedings of the Probabilistic Methodologies in Water and Wastewater Engineering, Toronto, ON, Canada, 23–27 September 2011; pp. 1–9. [Google Scholar]
- Brown, L. Understanding Gravity-Flow Pipelines. Livestock Watering Factsheet. January 2006. British Columbia Ministry of Agriculture and Lands, Order No. 590.304–5. Available online: https://www.itacanet.org/doc-archive-eng/water/gravity_flow_pipelines.pdf (accessed on 12 December 2018).
- Chapallaz, J.-M.; Eichenberger, P.; Fischer, G. Manual on Pumps Used as Turbines, MHPG Series, Harnessing Water Power on a Small Scale, 11, GATE, GTZ, Eschborn. 1992. Available online: Skat.ch/book/manual-on-pumps-used-as-turbines-volume-11/ (accessed on 16 March 2019).
- Chapallaz, J.-M.; Mombelli, H.-P.; Renaud, A. Small Hydropower Plants: Water Turbines (In German Only); Impulsprogramm PACER; Bundesamt für Konjunkturfragen: Bern, Switzerland, 1995; ISBN 3-905232-54-5. [Google Scholar]
- Jesinger, G. Possibilities and limits of energy recovery in water supply facilities (in German only). In Proceedings of the 11th Technical Water Seminar, Report Nr. 73, Munich, Germany, 22 October 1986; Bischofsberger, W., Ed.; TU Munich: Munich, Germany, 1987; pp. 185–210. [Google Scholar]
- Heinzmann, K. Experiences with pressure-relieving turbines—Munich water works (in German only). In Proceedings of the 11th Technical Water Seminar, Report Nr. 73, Munich, Germany, 22 October 1986; Bischofsberger, W., Ed.; TU Munich: Munich, Germany, 1987; pp. 211–228. [Google Scholar]
- Mikus, K. Experiences with pressure-relieving turbines—Stuttgart technical works (in German only). In Proceedings of the 11th Technical Water Seminar, Report Nr. 73, Munich, Germany, 22 October 1986; Bischofsberger, W., Ed.; TU Munich: Munich, Germany, 1987; pp. 237–252. [Google Scholar]
- Schatz, J. Experiences with pressure-relieving turbines—Long-range water supply of Mühlveirtel/Austria (in German only). In Proceedings of the 11th Technical Water Seminar, Report Nr. 73, Munich, Germany, 22 October 1986; Bischofsberger, W., Ed.; TU Munich: Munich, Germany, 1987; pp. 229–236. [Google Scholar]
- Williams, A.A.; Smith, N.P.A.; Bird, C.; Howard, M. Pumps as Turbines and the Induction Motors as Generators for Energy Recovery in Water Supply Systems. Water Environ. J. 1998, 12, 175–178. [Google Scholar] [CrossRef]
- Voltz, T.J.; Bahner, P.; Grischek, T. Energy efficiency of pumps and small turbines—Case studies (in German only). In Proceedings of the 2nd Saxon Drinking Water Conference, Dresden, Germany, 5 September 2013; Grischek, T., Ed.; DVGW: Dresden, Germany, 2013; pp. 99–112. [Google Scholar]
- Gaius-obaseki, T. Hydropower opportunities in the water industry. Int. J. Environ. Sci. 2010, 1, 392–402. [Google Scholar]
- Baumann, R.; Juric, T. The counter pressure Pelton turbine as a solution for energy generation in drinking water systems (in German only). Wasserwirtschaft 2010, 7–8, 15–18. [Google Scholar]
- Bahner, P. Deployment of Microturbines in Drinking Water Supply Networks of the FWV Elbaue-Ostharz GmbH (In German only). Diploma Thesis, Faculty of Civil Engineering, University of Applied Sciences (HTW), Dresden, Germany, 2013. [Google Scholar]
- De Marchis, M.; Fontanazza, C.M.; Freni, G.; Messineo, A.; Milici, B.; Napoli, E.; Notaro, V.; Puleo, V.; Scopa, A. Energy recovery in water distribution networks. Implementation of pumps as turbine in a dynamic numerical model. Procedia Eng. 2014, 70, 439–448. [Google Scholar] [CrossRef]
- Fecarotta, O.; McNabola, A. Optimal Location of Pump as Turbines (PATs) in Water Distribution Networks to Recover Energy and Reduce Leakage. Water Resour. Manag. 2017, 31, 5043–5059. [Google Scholar] [CrossRef]
- Giugni, M.; Fontana, N.; Ranucci, A. Optimal Location of PRVs and Turbines in Water Distribution Systems. J. Water Resour. Plan. Manag. 2014, 140. [Google Scholar] [CrossRef]
- Lima, G.M.; Luvizotto, E.; Brentan, B.M. Selection and location of pumps as turbines substituting pressure reducing valves. Renew. Energy 2017. [Google Scholar] [CrossRef]
- Santolin, A.; Cavazinni, G.; Pavesia, G.; Ardizzon, G.; Rossetti, A. Techno-economical method for the capacity sizing of a small hydropower plant. Energy Convers. Manag. 2011, 52, 2533–2541. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).