Applying a New Force–Velocity Synchronizing Algorithm to Derive Drag Coefficients of Rigid Vegetation in Oscillatory Flows
Abstract
1. Introduction
2. Materials and Methods
2.1. The Direct Measuring Method for CD Derivation
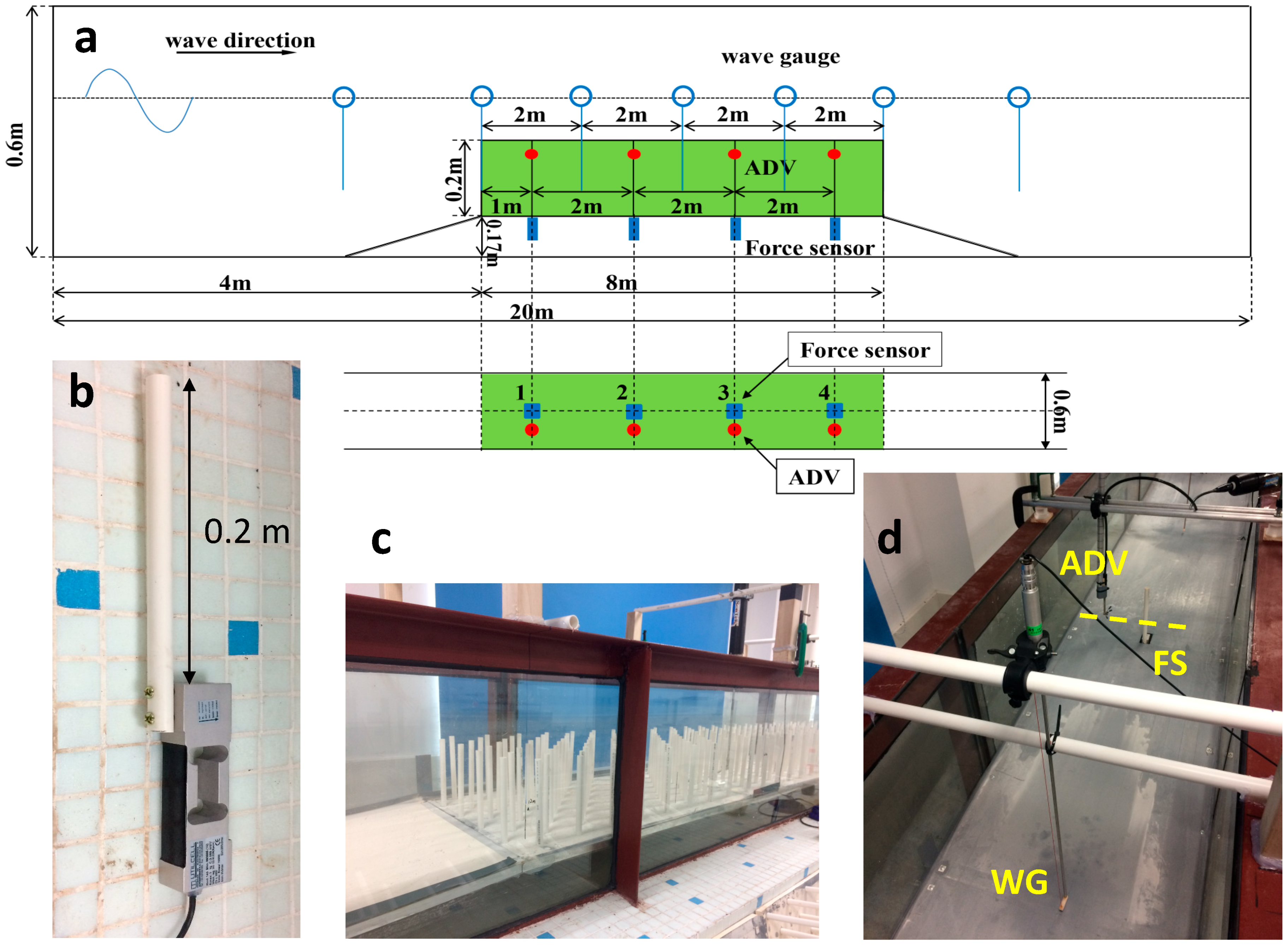
2.2. Synchronized Force–Velocity Measuring System
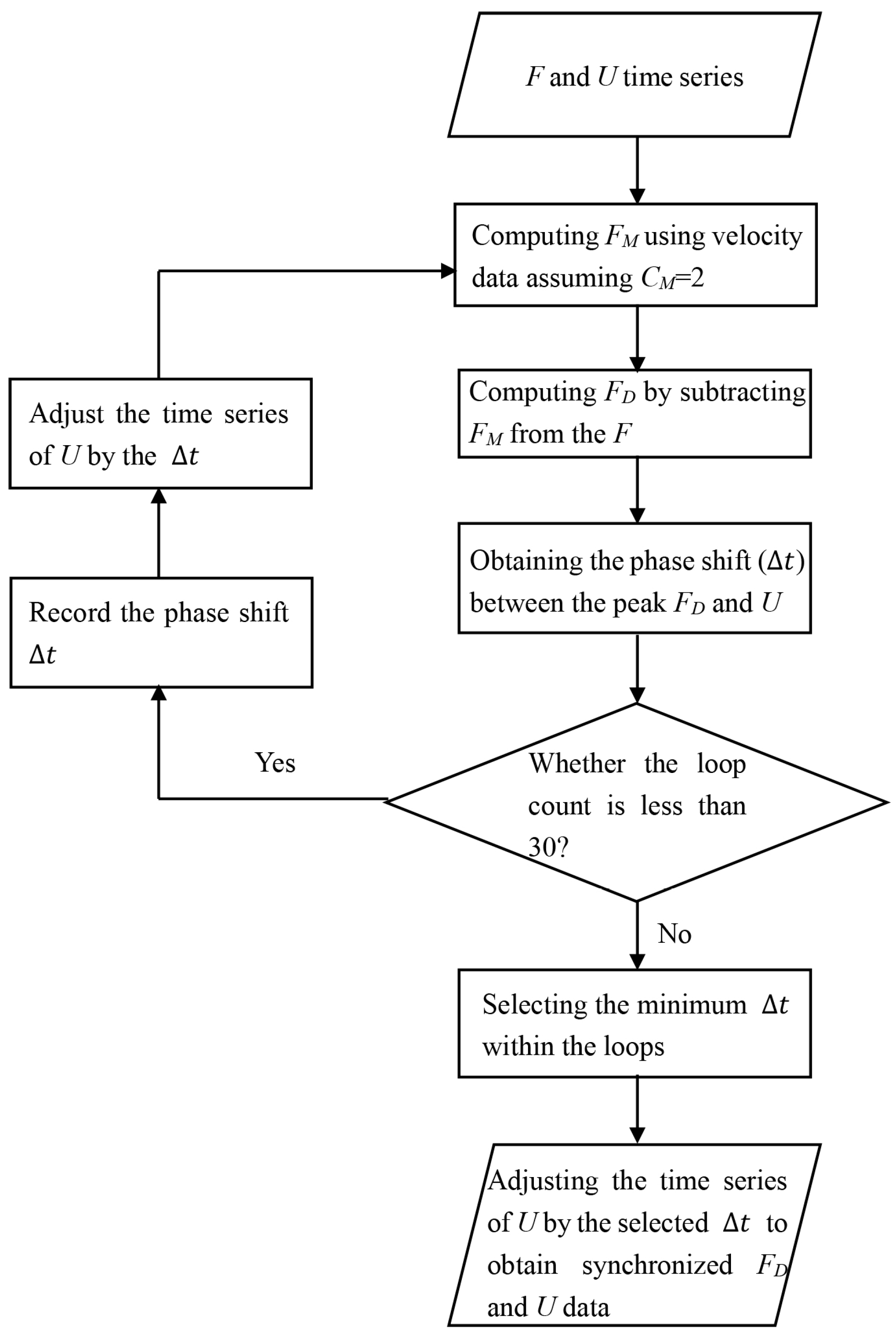
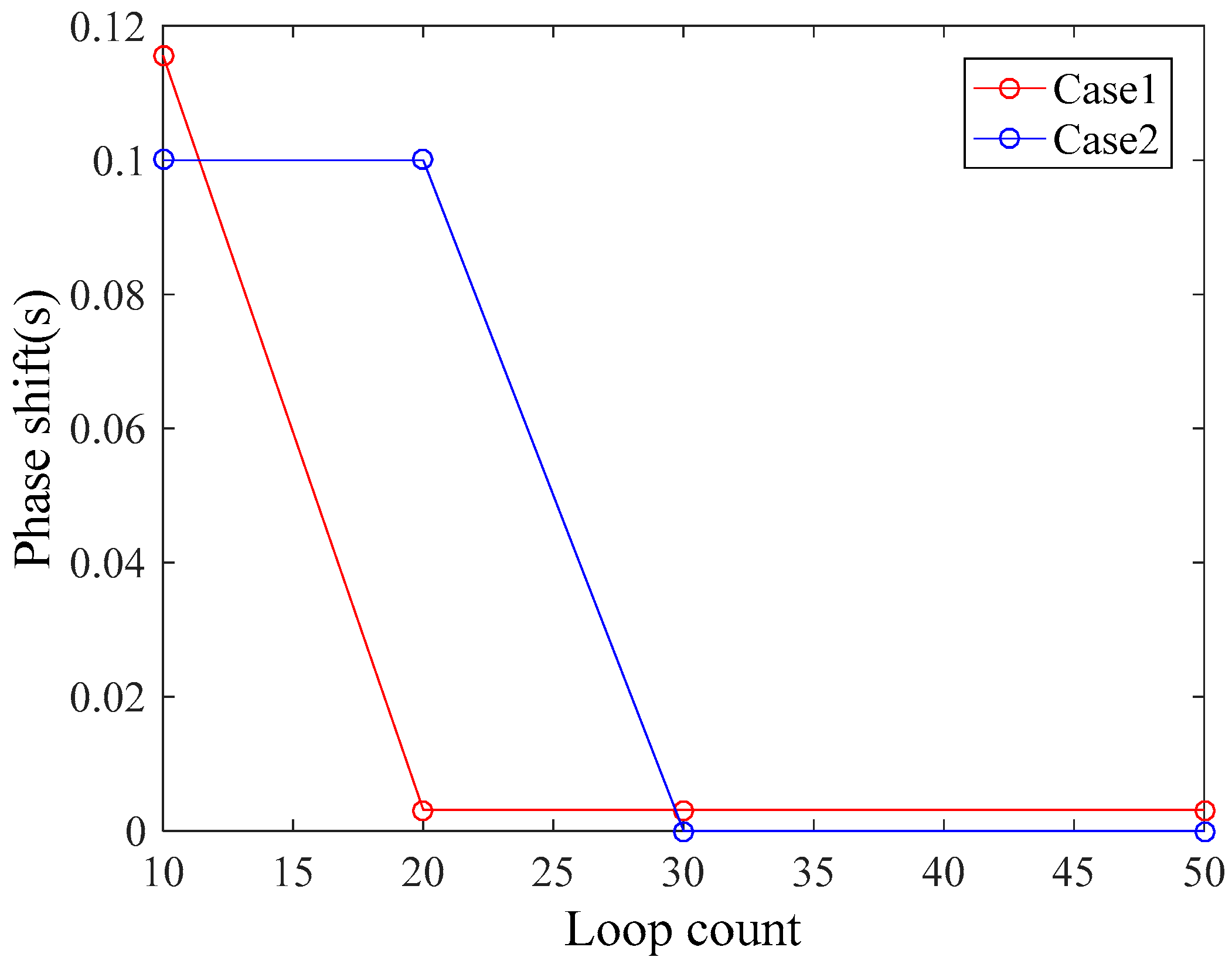
2.3. Automatic Alignment Algorithm
3. Results
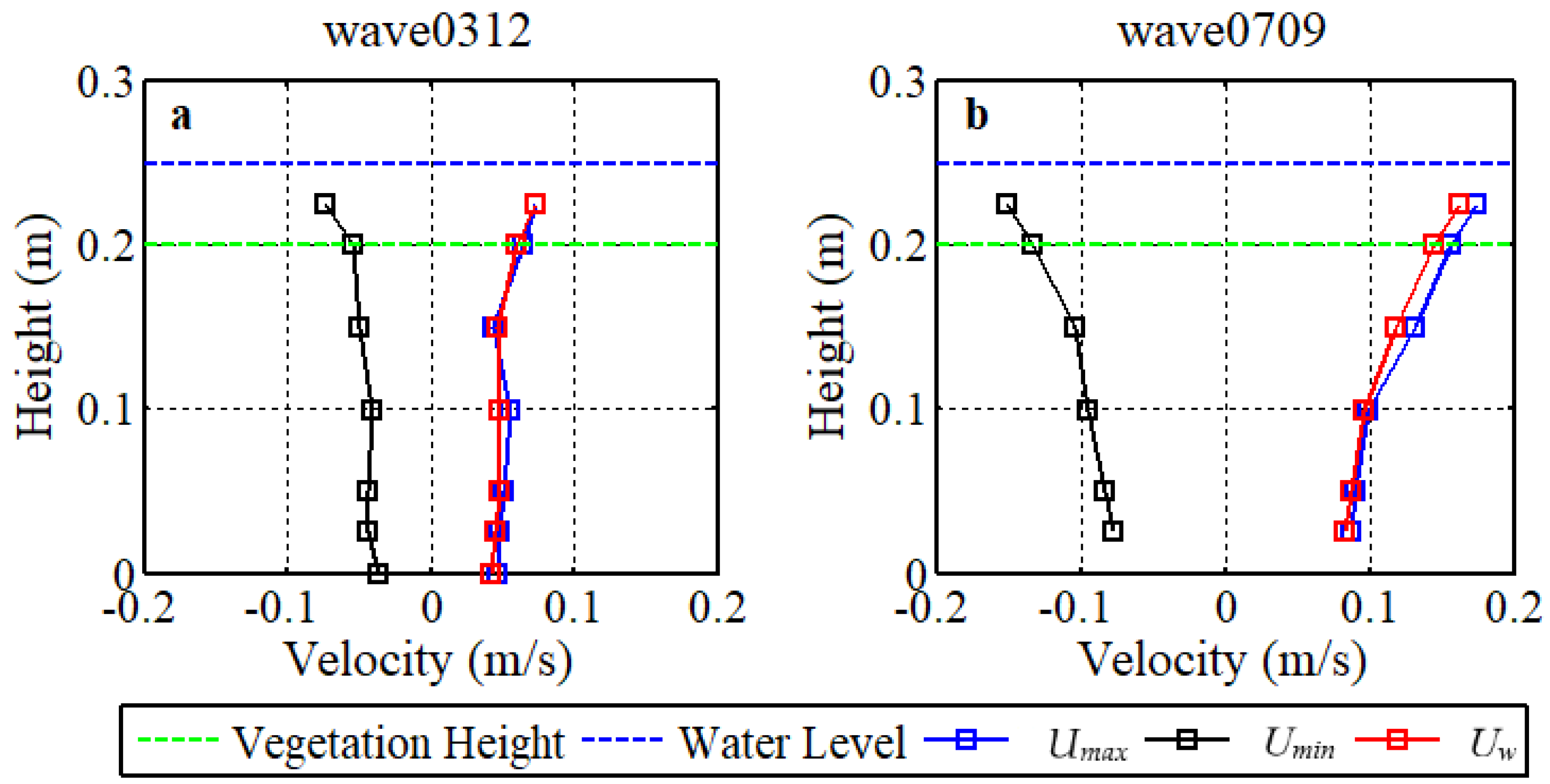
3.1. Velocity Profiles in the Vegetation Canopy
3.2. Wave Height and Wave Orbital Velocity in the Mimicked Vegetation Canopy
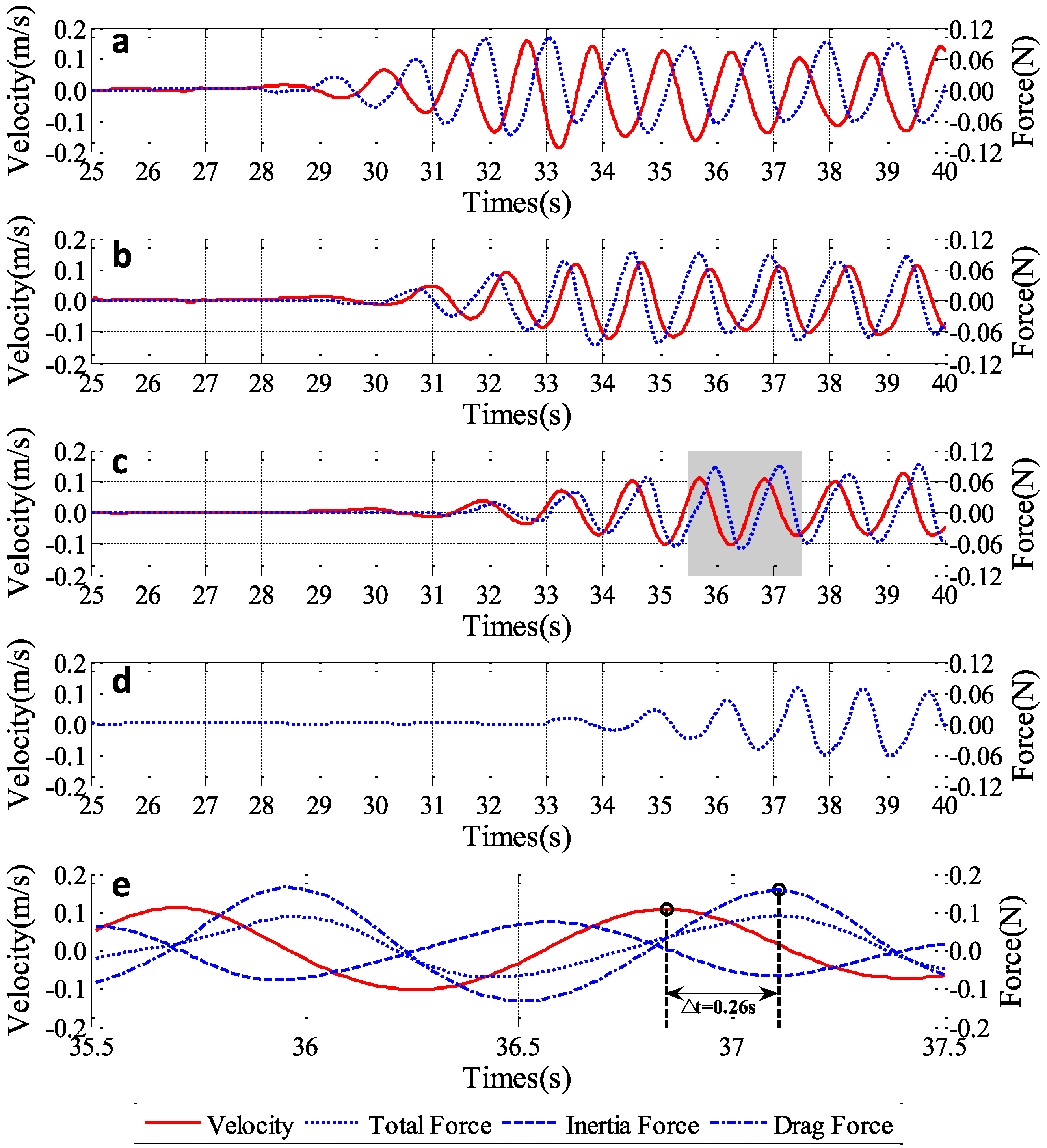
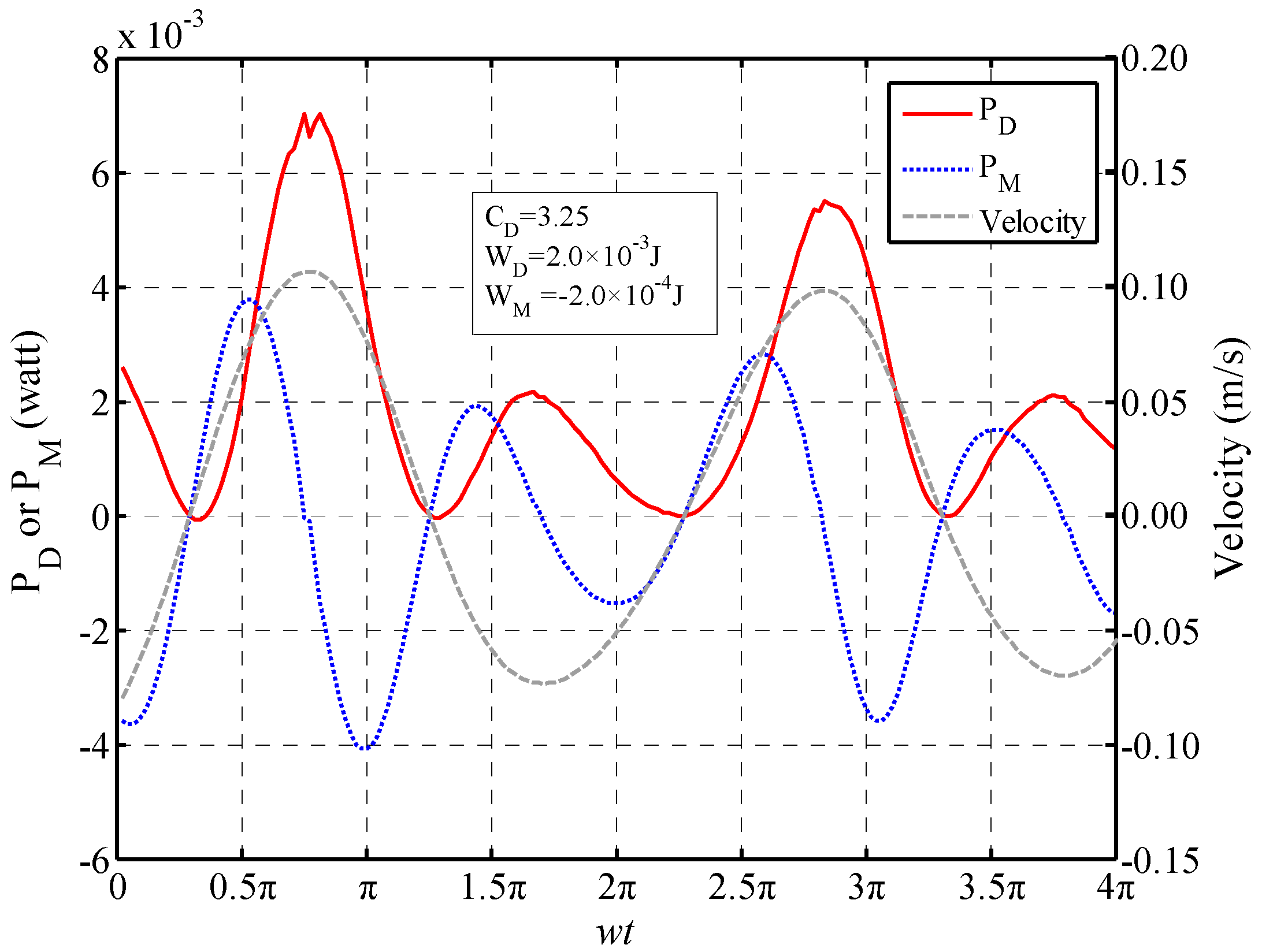
3.3. Data Alignment and Time-Varying CD
3.4. Deriving Period-Averaged CD
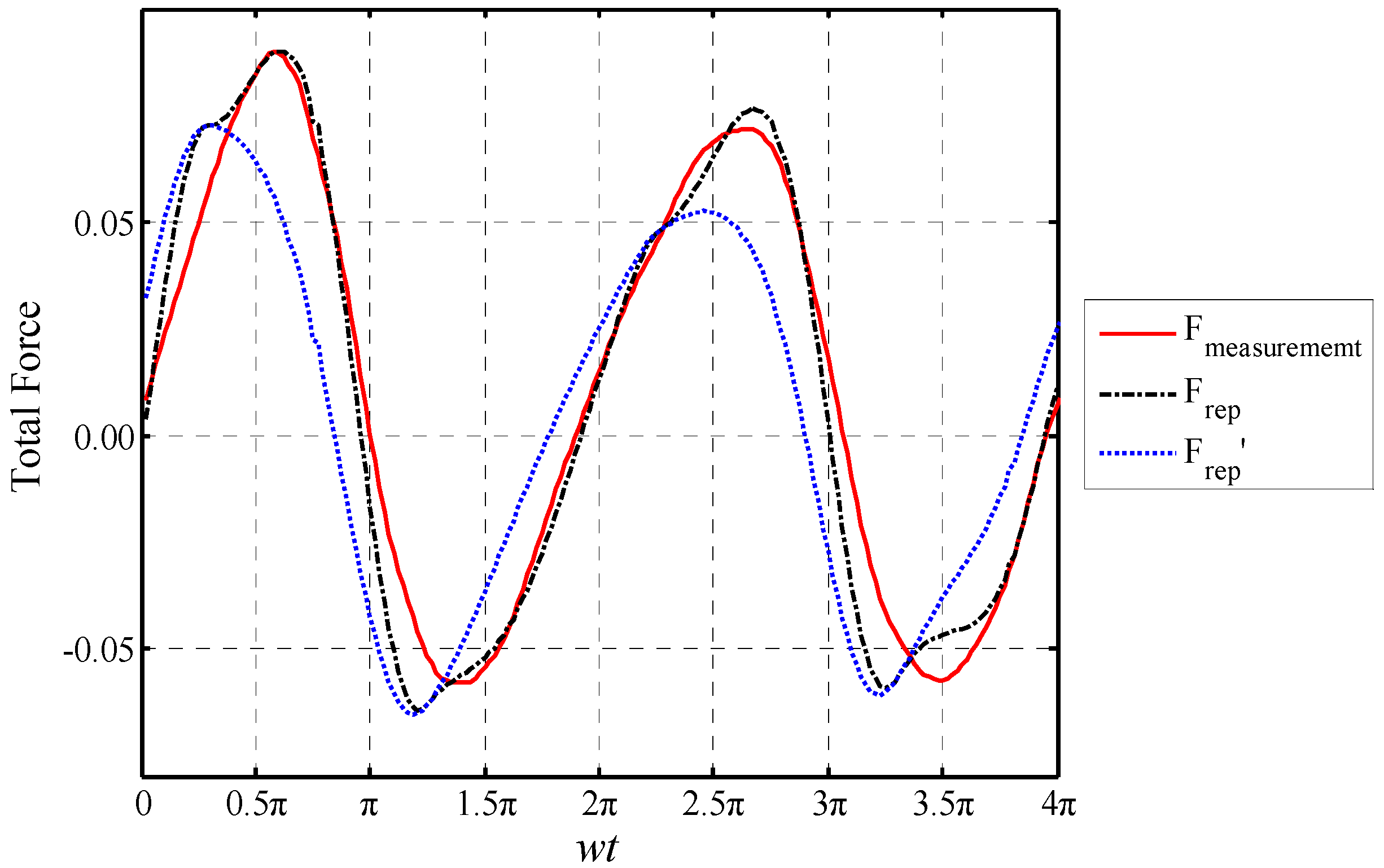
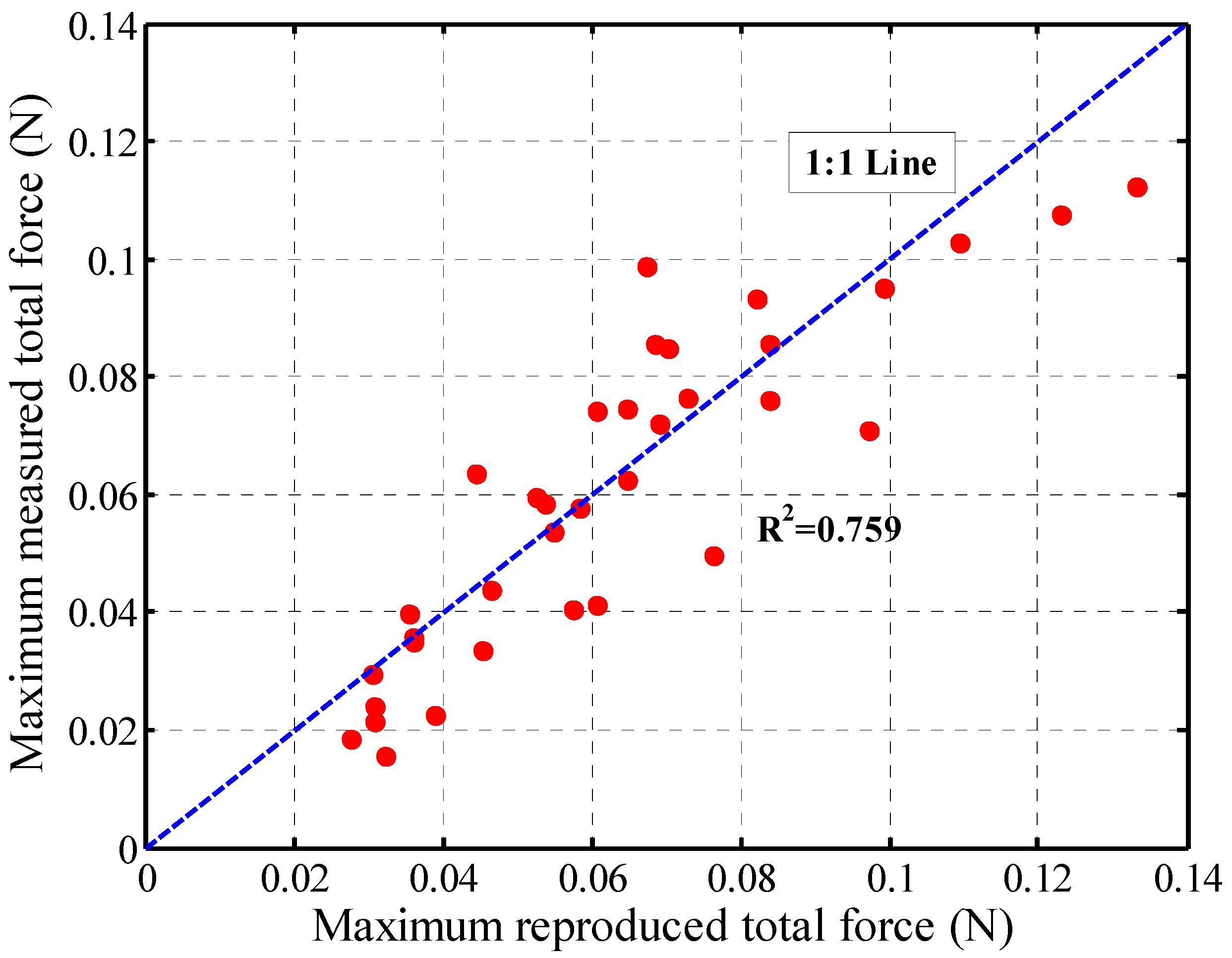
3.5. Assessing the Derived CD by Reproducing Acting Force
4. Discussion
4.1. Advantages of the Current Measuring System and Alignment Algorithm
4.2. Current Limitations and Future Applications
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. MATLAB Code for Force and Velocity Data Realignment
References
- Bouma, T.J.; van Belzen, J.; Balke, T.; Zhu, Z.; Airoldi, L.; Blight, A.J.; Davies, A.J.; Galvan, C.; Hawkins, S.J.; Hoggart, S.P.G.; et al. Identifying knowledge gaps hampering application of intertidal habitats in coastal protection: Opportunities & steps to take. Coast. Eng. 2014, 87, 147–157. [Google Scholar] [CrossRef]
- Balke, T.; Friess, D.A. Geomorphic knowledge for mangrove restoration: A pan-tropical categorization. Earth Surf. Process. Landf. 2016, 41, 231–239. [Google Scholar] [CrossRef]
- Barbier, E.B. Valuing the storm protection service of estuarine and coastal ecosystems. Ecosyst. Serv. 2015, 11, 32–38. [Google Scholar] [CrossRef]
- Temmerman, S.; Meire, P.; Bouma, T.J.; Herman, P.M.J.; Ysebaert, T.; De Vriend, H.J. Ecosystem-based coastal defence in the face of global change. Nature 2013, 504, 79–83. [Google Scholar] [CrossRef] [PubMed]
- Horstman, E.M.; Dohmen-Janssen, C.M.; Narra, P.M.F.; van den, B.; Siemerink, M.; Hulscher, S.J. Wave attenuation in mangroves: A quantitative approach to field observations. Coast. Eng. 2014, 94, 47–62. [Google Scholar] [CrossRef]
- Zhang, X.; Chua, V.P.; Cheong, H.-F. Hydrodynamics in mangrove prop roots and their physical properties. J. Hydro-Environ. Res. 2015, 9, 281–294. [Google Scholar] [CrossRef]
- Zhang, X.; Chua, V.P.; Cheong, H.-F. Geometrical and material properties of Sonneratia alba mangrove roots. Trees-Struct. Funct. 2014, 29, 285–297. [Google Scholar] [CrossRef]
- Mazda, Y.; Wolanski, E.; King, B.; Sase, A.; Ohtsuka, D.; Magi, M. Drag force due to vegetation in mangrove swamps. Mangroves Salt Marshes 1997, 1, 193–199. [Google Scholar] [CrossRef]
- Alongi, D.M. Mangrove forests: Resilience, protection from tsunamis, and responses to global climate change. Estuar. Coast. Shelf Sci. 2008, 76, 1–13. [Google Scholar] [CrossRef]
- Möller, I.; Kudella, M.; Rupprecht, F.; Spencer, T.; Paul, M.; van Wesenbeeck, B.K.; Wolters, G.; Jensen, K.; Bouma, T.J.; Miranda-Lange, M.; Schimmels, S. Wave attenuation over coastal salt marshes under storm surge conditions. Nat. Geosci. 2014, 7, 727–731. [Google Scholar] [CrossRef]
- Arkema, K.K.; Guannel, G.; Verutes, G.; Wood, S.A.; Guerry, A.; Ruckelshaus, M.; Kareiva, P.; Lacayo, M.; Silver, J.M. Coastal habitats shield people and property from sea-level rise and storms. Nat. Clim. Chang. 2013, 3, 913–918. [Google Scholar] [CrossRef]
- Zhu, Z.; Van, B.; Hong, T.; Kunihiro, T.; Ysebaert, T.; Herman, P.M.J.; Bouma, T.J. Sprouting as a gardening strategy to obtain superior supplementary food: Evidence from a seed-caching marine worm. Ecology 2016, 97, 3278–3284. [Google Scholar] [CrossRef] [PubMed]
- Young, I.R.; Zieger, S.; Babanin, A.V. Global Trends in Wind Speed and Wave Height. Science 2011, 332, 451–455. [Google Scholar] [CrossRef] [PubMed]
- Cheng, Y.; Ezer, T.; Hamlington, B.D. Sea Level Acceleration in the China Seas. Water 2016, 8, 293. [Google Scholar] [CrossRef]
- Lin-Ye, J.; Garcia-Leon, M.; Gracia, V.; Isabel Ortego, M.; Stanica, A.; Sanchez-Arcilla, A. Multivariate Hybrid Modelling of Future Wave-Storms at the Northwestern Black Sea. Water 2018, 10, 221. [Google Scholar] [CrossRef]
- Wolf, J.; Lowe, J.; Howard, T. Climate downscaling: Local mean sea level, surge and wave modelling. In Broad Scale Coastal Simulation: New Techniques to Understand and Manage Shorelines in the Third Millennium; Springer: Dordrecht, The Netherlands, 2015; pp. 79–102. ISBN 978-94-007-5258-0. [Google Scholar]
- Wolf, J.; Brown, J.M.; Bolaños, R.; Hedges, T.S. Waves in Coastal and Estuarine Waters. In Treatise on Estuarine and Coastal Science; Wolanski, E., McLusky, D., Eds.; Academic Press: Waltham, MA, USA, 2011; pp. 171–212. ISBN 978-0-08-087885-0. [Google Scholar]
- Van Loon-Steensma, J.M.; Slim, P.A.; Decuyper, M.; Hu, Z. Salt-marsh erosion and restoration in relation to flood protection on the Wadden Sea barrier island Terschelling. J. Coast. Conserv. 2014, 18, 1–16. [Google Scholar] [CrossRef]
- Hu, Z.; Van Belzen, J.; Van Der Wal, D.; Balke, T.; Wang, Z.B.; Stive, M.; Bouma, T.J. Windows of opportunity for salt marsh vegetation establishment on bare tidal flats: The importance of temporal and spatial variability in hydrodynamic forcing. J. Geophys. Res. Biogeosci. 2015, 120, 1450–1469. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, H.; Zhao, K.; Tang, J.; Qin, H. Evolution of wave and tide over vegetation region in nearshore waters. Ocean Dyn. 2017, 67, 973–988. [Google Scholar] [CrossRef]
- Dalrymple, R.; Kirby, J.; Hwang, P. Wave Diffraction Due to Areas of Energy Dissipation. J. Waterw. Port Coast. Ocean Eng. 1984, 110, 67–79. [Google Scholar] [CrossRef]
- Koch, D.L.; Ladd, A.J.C. Moderate Reynolds number flows through periodic and random arrays of aligned cylinders. J. Fluid Mech. 1997, 349, 31–66. [Google Scholar] [CrossRef]
- Morison, J.R.; O’Brien, M.P.; Johnson, J.W.; Schaaf, S.A. The Force Exerted by Surface Waves on Piles. J. Pet. Technol. 1950, 2, 149–154. [Google Scholar] [CrossRef]
- Nepf, H.M. Flow over and through Biota. In Treatise on Estuarine and Coastal Science; Wolanski, E., McLusky, D., Eds.; Academic Press: Waltham, MA, USA, 2011; pp. 267–288. ISBN 978-0-08-087885-0. [Google Scholar]
- Augustin, L.N.; Irish, J.L.; Lynett, P. Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast. Eng. 2009, 56, 332–340. [Google Scholar] [CrossRef]
- Tang, J.; Shen, S.; Wang, H. Numerical model for coastal wave propagation through mild slope zone in the presence of rigid vegetation. Coast. Eng. 2015, 97, 53–59. [Google Scholar] [CrossRef]
- Cao, H.; Feng, W.; Hu, Z.; Suzuki, T.; Stive, M.J.F. Numerical modeling of vegetation-induced dissipation using an extended mild-slope equation. Ocean Eng. 2015, 110, 258–269. [Google Scholar] [CrossRef]
- van Loon-Steensma, J.M.; Hu, Z.; Slim, P.A. Modelled Impact of Vegetation Heterogeneity and Salt-Marsh Zonation on Wave Damping. J. Coast. Res. 2016, 32, 241–252. [Google Scholar] [CrossRef]
- Peruzzo, P.; De Serio, F.; Defina, A.; Mossa, M. Wave Height Attenuation and Flow Resistance Due to Emergent or Near-Emergent Vegetation. Water 2018, 10, 402. [Google Scholar] [CrossRef]
- Tang, J.; Causon, D.; Mingham, C.; Qian, L. Numerical study of vegetation damping effects on solitary wave run-up using the nonlinear shallow water equations. Coast. Eng. 2013, 75, 21–28. [Google Scholar] [CrossRef]
- Kobayashi, N.; Raichle, A.W.; Asano, T. Wave attenuation by vegetation. J. Waterw. Port Coast. Ocean Eng.-ASCE 1993, 119, 30–48. [Google Scholar] [CrossRef]
- Méndez, F.J.; Losada, I.J.; Losada, M.A. Hydrodynamics induced by wind waves in a vegetation field. J. Geophys. Res. Oceans 1999, 104, 18383–18396. [Google Scholar] [CrossRef]
- Ozeren, Y.; Wren, D.G.; Wu, W. Experimental investigation of wave attenuation through model and live vegetation. J. Waterw. Port Coast. Ocean Eng. 2014, 140. [Google Scholar] [CrossRef]
- Anderson, M.E.; Smith, J.M. Wave attenuation by flexible, idealized salt marsh vegetation. Coast. Eng. 2014, 83, 82–92. [Google Scholar] [CrossRef]
- Losada, I.J.; Maza, M.; Lara, J.L. A new formulation for vegetation-induced damping under combined waves and currents. Coast. Eng. 2016, 107, 1–13. [Google Scholar] [CrossRef]
- Infantes, E.; Orfila, A.; Bouma, T.J.; Simarro, G.; Terrados, J. Posidonia oceanica and Cymodocea nodosa seedling tolerance to wave exposure. Limnol. Oceanogr. 2011, 56, 2223–2232. [Google Scholar] [CrossRef]
- Hu, Z.; Suzuki, T.; Zitman, T.; Uijttewaal, W.; Stive, M. Laboratory study on wave dissipation by vegetation in combined current-wave flow. Coast. Eng. 2014, 88, 131–142. [Google Scholar] [CrossRef]
- Maza, M.; Adler, K.; Ramos, D.; Garcia, A.M.; Nepf, H. Velocity and Drag Evolution From the Leading Edge of a Model Mangrove Forest. J. Geophys. Res. Oceans 2017, 122, 9144–9159. [Google Scholar] [CrossRef]
- Dean, R.; Dalrymple, R. Water Wave Mechanics for Engineers and Scientists; Advanced Series on Ocean Engineering; World Scientific: Tokyo, Japan, 1991. [Google Scholar]
- Strom, K.B.; Papanicolaou, A.N. ADV measurements around a cluster microform in a shallow mountain stream. J. Hydraul. Eng.-ASCE 2007, 133, 1379–1389. [Google Scholar] [CrossRef]
- Persoons, T.; O’Donovan, T.S. High Dynamic Velocity Range Particle Image Velocimetry Using Multiple Pulse Separation Imaging. Sensors 2011, 11, 1–18. [Google Scholar] [CrossRef] [PubMed]
- Martino, R.; Paterson, A.; Piva, M. Double-average mean flow and local turbulence intensity profiles from PIV measurements for an open channel flow with rigid vegetation. Environ. Fluid Mech. 2012, 12, 45–62. [Google Scholar] [CrossRef]
- You, Z.; Chen, Y. The Use of Tactile Sensors and PIV Analysis for Understanding the Bearing Mechanism of Pile Groups. Sensors 2018, 18, 476. [Google Scholar] [CrossRef] [PubMed]


| Direction | Known Weights (g) | 1st Reading a (g) | 2nd Reading b (g) | 3rd Reading c (g) | Mean Reading (g) | Absolute Error (g) | Relative Error |
|---|---|---|---|---|---|---|---|
| + | 5 g | 5.10 | 5.00 | 5.00 | 5.03 | 0.03 | 0.60% |
| 10 g | 10.10 | 10.10 | 10.00 | 10.07 | 0.07 | 0.70% | |
| 20 g | 20.10 | 20.00 | 20.00 | 20.03 | 0.03 | 0.15% | |
| 50 g | 49.90 | 49.90 | 49.90 | 49.90 | 0.10 | 0.02% | |
| − | 5 g | −5.00 | −5.00 | −5.10 | −5.03 | −0.03 | −0.60% |
| 10 g | −10.00 | −10.10 | −10.10 | −10.07 | −0.07 | −0.70% | |
| 20 g | −20.00 | −20.00 | −20.00 | −20.00 | 0 | 0% | |
| 50 g | −50.0 | −49.9 | −49.9 | −49.93 | 0.07 | 0.14% |
| Test Number | Wave Height (m) | Wave Period (s) | CD at Location 1 | CD at Location 2 | CD at Location 3 | Space-Mean CD | Standard Deviation |
|---|---|---|---|---|---|---|---|
| 1 | 0.03 | 0.6 | 5.41 | 10.02 | 10.14 | 8.52 | 7.28 |
| 2 | 0.03 | 0.9 | 3.19 | 4.88 | 7.09 | 5.05 | 3.82 |
| 3 | 0.03 | 1.2 | 3.60 | 2.79 | 5.25 | 3.88 | 1.56 |
| 4 | 0.05 | 0.6 | 7.61 | 5.83 | 5.96 | 6.46 | 0.98 |
| 5 | 0.05 | 0.9 | 3.82 | 2.36 | 3.62 | 3.27 | 0.62 |
| 6 | 0.05 | 1.2 | 2.84 | 3.03 | 3.97 | 3.28 | 0.37 |
| 7 | 0.07 | 0.6 | 3.43 | 3.01 | 7.04 | 4.49 | 4.90 |
| 8 | 0.07 | 0.9 | 1.97 | 1.83 | 2.94 | 2.25 | 0.37 |
| 9 | 0.07 | 1.2 | 1.77 | 2.77 | 3.51 | 2.68 | 0.76 |
| 10 | 0.09 | 0.6 | 3.02 | 5.76 | 6.10 | 4.96 | 2.86 |
| 11 | 0.09 | 0.9 | 1.26 | 1.79 | 2.64 | 1.89 | 0.49 |
| 12 | 0.09 | 1.2 | 1.44 | 2.54 | 3.00 | 2.33 | 0.64 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yao, P.; Chen, H.; Huang, B.; Tan, C.; Hu, Z.; Ren, L.; Yang, Q. Applying a New Force–Velocity Synchronizing Algorithm to Derive Drag Coefficients of Rigid Vegetation in Oscillatory Flows. Water 2018, 10, 906. https://doi.org/10.3390/w10070906
Yao P, Chen H, Huang B, Tan C, Hu Z, Ren L, Yang Q. Applying a New Force–Velocity Synchronizing Algorithm to Derive Drag Coefficients of Rigid Vegetation in Oscillatory Flows. Water. 2018; 10(7):906. https://doi.org/10.3390/w10070906
Chicago/Turabian StyleYao, Peng, Hui Chen, Bensheng Huang, Chao Tan, Zhan Hu, Lei Ren, and Qingshu Yang. 2018. "Applying a New Force–Velocity Synchronizing Algorithm to Derive Drag Coefficients of Rigid Vegetation in Oscillatory Flows" Water 10, no. 7: 906. https://doi.org/10.3390/w10070906
APA StyleYao, P., Chen, H., Huang, B., Tan, C., Hu, Z., Ren, L., & Yang, Q. (2018). Applying a New Force–Velocity Synchronizing Algorithm to Derive Drag Coefficients of Rigid Vegetation in Oscillatory Flows. Water, 10(7), 906. https://doi.org/10.3390/w10070906




