Design Issues for Low Power Integrated Thermal Flow Sensors with Ultra-Wide Dynamic Range and Low Insertion Loss

Abstract

Flow sensors are the key elements in most systems for monitoring and controlling fluid flows. With the introduction of MEMS thermal flow sensors, unprecedented performances, such as ultra wide measurement ranges, low power consumptions and extreme miniaturization, have been achieved, although several critical issues have still to be solved. In this work, a systematic approach to the design of integrated thermal flow sensors, with specification of resolution, dynamic range, power consumption and pressure insertion loss is proposed. All the critical components of the sensors, namely thermal microstructure, package and read-out interface are examined, showing their impact on the sensor performance and indicating effective optimization strategies. The proposed design procedures are supported by experiments performed using a recently developed test chip, including several different sensing structures and a flexible electronic interface.

1. Introduction

An accurate measurement of gas flow is required in many applications, including industrial processes control, internal combustion engines optimization, monitoring of gas distribution lines, control of ventilation and air-conditioning systems and monitoring of patient breathing. The introduction of MEMS (Micro-Electro-Mechanical Systems) technology allowed the fabrication of miniaturized flow sensors with unprecedented performance in terms of spatial resolution, response times, sensitivities, measurement range and power consumption. Integrated flow sensors have been largely investigated in last decades and literature reviews can be found in [1,2,3,4,5,6]. The wide majority of the proposed devices are based on a thermal principle. This is mainly due to their suitability to be integrated on silicon chips using standard microelectronic processes, making them ideal candidates for the fabrication of integrated smart sensors. According to the operating principle, thermal flow sensors can be divided into three main categories, namely hot-wire sensors, calorimetric sensors and time-of-flight sensors. Hot-wire sensors are based on the heat loss of a heater exposed to the fluid and the output signal is the heater temperature (constant power anemometry) or the heater power needed to stabilize the heater temperature (constant temperature anemometry). Calorimetric sensors measures the difference between the downstream and upstream heat fluxes stemming from one or more heaters exposed to the flow. Time-of-flight sensors measure the time that elapses between a heat pulse applied to the heater and the pulse detection by a downstream temperature probe. Sensors based on a combination of multiple principles for extending the operating range have been proposed [7,8].

Calorimetric sensors are the sensors of choice when superior performance in terms of resolution, linearity and offset are required. These properties, partly due to their differential structure, are fundamental in applications involving the measure and control of very low flow rates. This is the case, for example, of gas distribution lines in semiconductor manufacturing equipments [9], fuel/air mixing system in car engines [10] and propellant feed system in thrusters on board satellites [11,12]. Recently, very sensitive integrated flow sensors have been proposed for the development of a directional wind sensor, with robustness, power consumption and miniaturization characteristics suitable for application in wireless sensor networks [13].

Although differential temperature flow sensors have been widely investigated [1,2,3,4,5,6], very few works have been devoted to find the impact of the sensor structure and dimensions on the key figures of merit of the devices [14,15,16,17,18,19,20]. Fluid dynamic simulations provide useful indications on particular aspects of the sensor operation, but are unable to embrace the whole transduction process, involving different physical domains that altogether contribute to the sensor performance. Studies based only on thermal and fluid-dynamic simulations generally lack a framework capable of organizing the simulated results into simple and general design formulas. As a result, the constraints and drawbacks that limit the effectiveness of the various design parameters are often overlooked, together with the connections to real figures of merit, such as resolution, dynamic range and power consumption. In fact, tailoring a flow sensor for a real application is a process that should necessarily involve several different parameters, including: (i) noise and offset from either the sensor or the amplifier; (ii) pressure drop (head loss) introduced by the insertion of the sensor in the fluidic system; (iii) correlation between the sensor characteristics and the readout interface specifications (i.e., power consumption).

In this work, a systematic approach for the design of integrated calorimetric flow sensors, taking into account all the critical components of the devices, namely thermal microstructure, package and read-out interface, is proposed. Some design strategies for the device optimization are analytically extrapolated starting from a simplified model of the sensors and are experimentally verified by means of a recently developed test chip, including several different sensing structures and a flexible electronic interface [21].

2. Design Parameters and Optimization

2.1. Description of the Sensor Structure and Main Performance Parameters

The general structure of the flow sensors analyzed in this work is shown in Figure 1(a). Two temperature sensors (thermopiles) are placed on cantilevers suspended over a cavity etched into the substrate in order to provide thermal insulation. The thermopiles are composed of N_T thermocouples with the hot and cold junctions placed on the cantilever tip and the substrate, respectively. A variable number of heaters are placed in the space between the thermopiles. The heaters are deposited over thermally insulating membranes (rectangular), anchored to the cavity edges through a series of arms. The particular shape of the suspending arms is dictated by the properties of the wet anisotropic etch used to open the cavity. The considerations made in this paper can be easily extended to different sensor layouts. The basic operating principle of the sensor is simple: as the flow progressively increases, heat transfer in the downwind direction increases as well, producing a temperature difference that is sensed by the thermopiles. The typical configuration includes a single heater whereas multi-heater structures can be used to perform particular functions [17,22,23,24] or simply extend the effective heater area with no adverse consequences on the etching time required to release the suspending membranes.

Figure 1. (a) Schematic view of a thermal flow sensor, based on a calorimeter type configuration with the main dimensions indicated; (b) Representation of the flow channel.

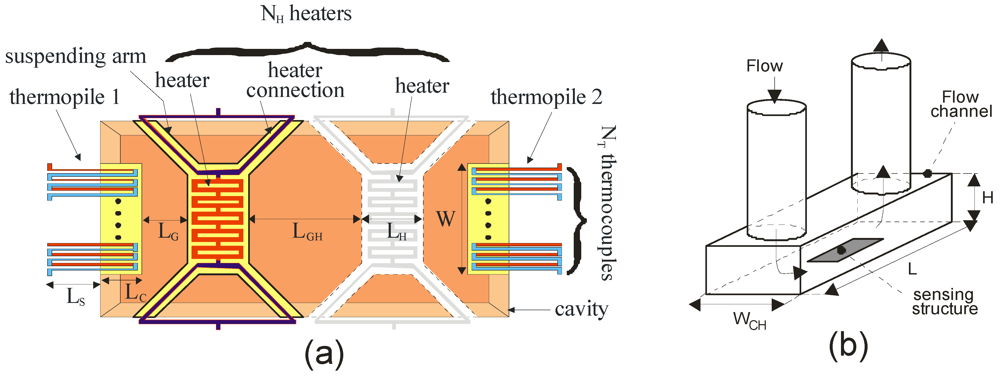
Figure 1. (a) Schematic view of a thermal flow sensor, based on a calorimeter type configuration with the main dimensions indicated; (b) Representation of the flow channel.

Possible alternatives to the structure shown in Figure 1(a) are often used. A simple modification is the replacement of the thermopiles with resistive temperature detectors (RTD) [14,17,24], with the drawback of an additional offset term derived from resistor mismatch. Another variant that adds robustness to the device, but requires front-to-back alignment equipments and significantly longer etching times, is the placement of all sensor elements on a single closed membrane [25]. The devices are placed into channels where they are directly exposed to the flow. The shape of the flow channels is shown in Figure 1(b) with the most relevant dimensions indicated.

Several phenomena, regarding the fluid-dynamic, thermal and electrical domains, are involved in the operating principle of a flow sensor. In order to simplify the analysis, it is useful to introduce a block diagram such as Figure 2(a), representing the successive conversions of the original quantity (flow rate) resulting in the output voltage. The amplifier (A), used to read the output voltage, is also included, since it contributes to the overall device accuracy. Fluid-dynamic and thermal mechanisms are confined to block “h”, which converts the volumetric flow rate Q into a temperature difference ΔT_S using the heating power P_H (total power delivered to the heaters).

Figure 2. (a) Signal flow path representation of the transduction mechanism, with the main non-idealities indicated; (b) Effect of the offset and noise on the sensor detection limit. Q_meas is the flow sensor reading under still fluid conditions.

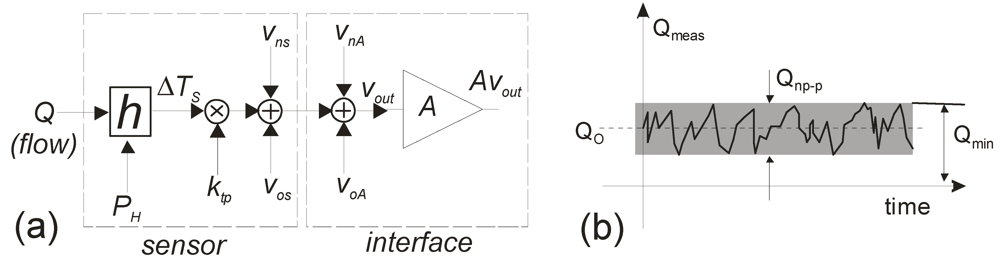
Figure 2. (a) Signal flow path representation of the transduction mechanism, with the main non-idealities indicated; (b) Effect of the offset and noise on the sensor detection limit. Q_meas is the flow sensor reading under still fluid conditions.

The thermopiles, represented by the multiplication of the constant k_tp, convert the temperature difference into the output voltage. Note that ΔT_S is considered free of random phenomena such as offset and noise, which are taken into account with the terms V_nS and V_OS (sensor noise and offset voltage), added to the output voltage. The sensor noise is mainly thermal noise from the thermopile resistance, while the sensor offset is dominated by geometrical asymmetries of the sensor structure, producing a temperature difference even at zero flow rate. Finally, a noise and offset contribution comes also from the amplifier, as represented in the figure.

Several parameters are used to specify the performance of a flow sensor. These parameters are strictly correlated and, generally, it is meaningless to boost a single characteristic (e.g., high sensitivity) without clearly indicating at which cost it has been achieved. Some of the most important performance parameters are listed below.

• (a)Sensitivity, defined as S = dV_out/dQ. The sensitivity depends generally on the input flow rate, although differential calorimeters exhibit a nearly linear behavior at small flow rates, where a constant sensitivity S(0) can be used. The sensitivity alone is not a real figure of merit, but it is a fundamental parameter for the design of the interface and, together with other parameters, contributes to the resolution and detection limit, defined below.
• (b)Resolution, defined as the minimum variation of the input flow that can be detected. The resolution is expressed in terms of the equivalent noise flow rate, Q_np−p = v_np−p/S, where v_np−p is the peak to peak amplitude of the total output noise voltage.
• (c)Offset flow rate, defined as Q_O = v_O/S(0), where v_O is the total offset voltage. The offset flow rate coincides with the reading of the flow sensor when the fluid velocity is zero.
• (d)Detection limit Q_min, defined as the minimum (unsigned) flow value that can be reliably detected by the flow sensor. This parameter is particularly important for leakage sensors, which should be able to determine if very small flow rates are present. Figure 2(b) shows a sketched time diagram of the flow sensor readings in conditions of zero flow. If calibration of the offset is not performed, Q₀ is an unknown quantity and we only have statistical information about it, i.e., we can presume that it falls between –Q_0max and Q_0max, where Q_0max is the maximum offset for that kind of sensor. It is apparent that, in this case, if a reading is within –Q_0max − Q_np−p/2 and Q_0max + Q_np−p/2, it is not possible to determine whether a flow rate is present or Q = 0 and the measurement is simply the result of a possible combination of offset and noise. Therefore, in the case of no offset calibration, the detection limit is Q_min = Q_Omax + Q_np−p/2. Even if an offset calibration procedure is applied, a residual offset will still be present. The detection limit coincides with the theoretical limit Q_np−p/2 only if the residual offset is negligible with respect to noise.
• (e)Bandwidth, B, defined as the frequency range of the flow velocity in which the sensor sensitivity remains over nearly 70% of the value for constant flow. The sensor response time is inversely proportional to the bandwidth. Note that the intrinsic bandwidth, due to the sensor thermal masses and resistances, can be further reduced in the interface to limit the noise and improve resolution.
• (f)Full scale flow rate, Q_max. The response of thermal flow sensors tends to saturate at high flows, for the effect of several concomitant causes. As a result, the sensitivity progressively drops, degrading the resolution. The maximum value Q_max can be conventionally set at the point where the sensitivity drops below a given fraction of the initial S(0) value. Response saturation is mainly due to fluid-dynamics and forced convection mechanisms that can be studied only by means of simulations or experiments. In this work we will provide some indications based on tests performed on different sensor configurations.
• (g)Dynamic range, DR=Q_max/Q_np−p. The DR coincides with the number of distinct flow levels that can be distinguished by the flow sensor. This parameter is particularly important for flow sensors used to measure large flow rates with high resolution. High dynamic range flow sensors are required in flow control units designed to deliver precise fluid flows to reaction chambers (as in semiconductor processing equipments [9]) or ionic thrusters for fine handling of satellite attitude and orbital parameters [11]. The DR of traditional macroscopic flow sensors is typically lower than 10² while it may exceed 10³ in MEMS flow sensors.
• (h)Insertion loss, p_loss, defined as the pressure drop across the sensor flow channel, measured at Q_max.
• (i)Power consumption P_H. This is an extremely important parameter for battery powered applications.

2.2. Lumped Element Model of the Transduction Principle

Analytical solution of the fluid-dynamic and heat transfer equations involved in the operation of thermal flow sensors is feasible only for very simplified cases, that are poorly related to the complex three dimensional structures used in MEMS sensors. In this sub-section, a lumped element model for the whole transduction process will be introduced in order to provide some design indications. The fluid flow and the substrate will be assumed to be at the same temperature of the surrounding environment, indicated with T_A (ambient temperature). The temperature difference of the sensor elements with respect to T_A will be indicated as “overheating”. The model is based on the hypothesis that the relationship between overheating and the heater powers is linear (linearity hypothesis). This approximation derives from considering that: (i) heat transfer is dominated by conduction and forced convection; and that (ii) the fluid parameters are independent of temperature.

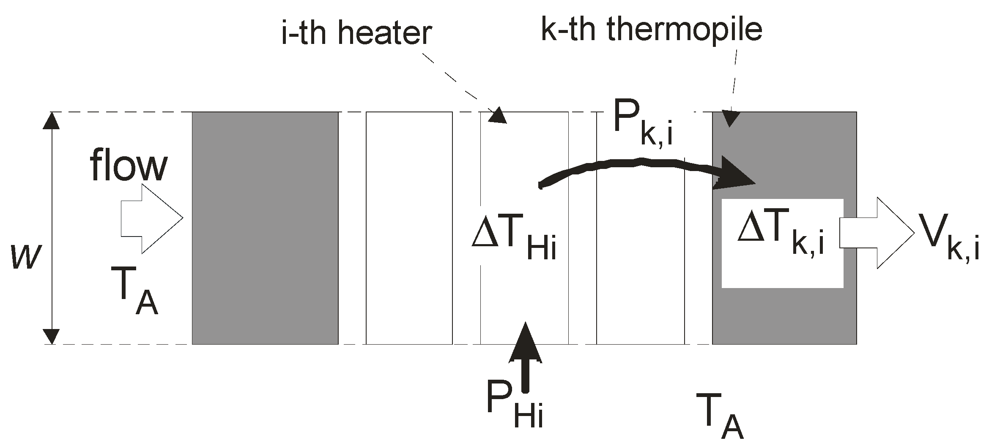
Figure 3. Visual representation of the symbols used to define the lumped element model.

Figure 3. Visual representation of the symbols used to define the lumped element model.

Figure 3 represents the interaction of the i-th heater with the k-th thermopile. The heater receives the power P_Hi while all the other heaters are not powered. The overheating of the heater is given by:

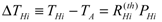   (1)

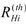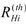where is the total thermal resistance between the heater and the environment. The fraction of the power P_Hi, indicated with P_k,i that reaches hot junctions of the k-th thermopile can be expressed as:

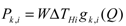   (2)

where g_k,i is a flow dependent coupling coefficient. With Equation (2) we have considered that the linear power density across the device width (W) is constant (2-dimensional approximation). Several geometrical parameters of the sensing structure affect coefficients g_i,k(Q), including the depth of the insulating cavity underneath the sensor elements. The temperature overheating of the thermopile, ΔT_k,i is given by:

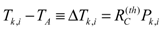   (3)

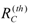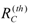where is the thermal resistance between the thermopile hot junctions and the environment. For the structure of Figure 1(a) the thermal resistance is dominated by conduction through solid elements (cantilever), and is then given by:

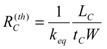   (4)

where t_c is the cantilever thickness and k_eq the effective conductivity that takes into account the cantilever and the thermopile material [20].

Introducing parameters a_k,i, defined as:

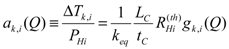   (5)

It is possible to write the transduction law between power P_Hi and voltage V_k,i:

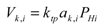   (6)

Using the linearity hypothesis, we can consider that the total thermopile voltage is the superposition of the effects of the N_H heaters. Therefore:

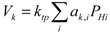   (7)

The output signal is the difference V₂-V₁, resulting in:

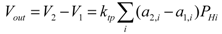   (8)

The sensor sensitivity can be calculated from Equation (8) and written in the following compact form:

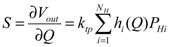   (9)

where the coefficients h_i are defined as follows:

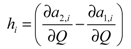   (10)

It is convenient to relate the powers P_Hi of the individual heaters to the total power P_H, through a set of dimensionless parameters x_i, indicated as “power distribution”:

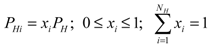   (11)

Thus, Equation (9) becomes:

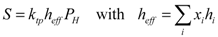   (12)

2.3. Sensor Resolution

In order to calculate the equivalent noise flow it is necessary to estimate the total noise voltage v_np−p. The peak-to-peak noise can be derived from the rms value, considering that, for Gaussian noise, it can be assumed that v_np−p = 4v_nrms. With this choice, the noise voltage exceeds the conventional peak-to-peak value only for 4.6% of the observation time. The sensor noise is essentially thermal noise from the thermopile resistance (R). This contribution is clearly independent of the amplifier noise. With these considerations:

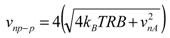   (13)

where v_nA is the amplifier rms input noise voltage, k_B the Boltzmann constant, T the absolute temperature, B the sensor bandwidth, considered coincident with the equivalent noise bandwidth. Note that the thermopile overheating is generally limited to a few Kelvin in this type of sensors, so that we can assume that T coincides with T_A. In order to find the degrees of freedom on the sensor design that actually affect the resolution, it is necessary to obtain an expression for the thermopile resistance.

Figure 4 shows a single thermocouple, formed by conductors A and B. The pitch, by which the thermocouple are lined up over the cantilever, is indicated with W_P = 2(W_S + W_T), where W_S is the minimum spacing between two lines, while W_T is the dimension of a single conductor forming the thermocouple. For the sake of simplicity, we have considered that the two materials A and B have identical sheet resistance R_S, otherwise the mean sheet resistance can be used.

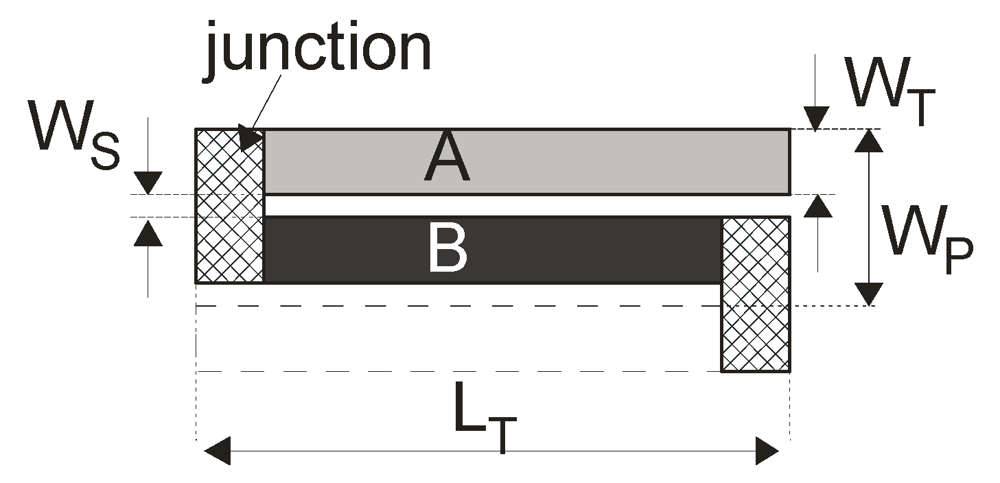
Figure 4. Dimensions used to describe the thermocouple geometry.

Figure 4. Dimensions used to describe the thermocouple geometry.

Considering that the thermopile spans the whole cantilever width, and neglecting the margin at the cantilever borders we get: W_P = W/N_T. The line width W_T is then given by:

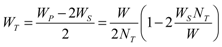   (14)

The total sensor electrical resistance, R, is the sum of the resistances of the two thermopiles. With the above simplifications:

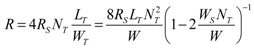   (15)

where R_S is the thermopile layer sheet resistance, equal to the resistivity to thickness ratio. The total thermopile sensitivity (k_tp) is simply given by N_T·s_AB, where s_AB is the Seebeck coefficient of the A-B couple. The spacing W_S should be kept at the minimum value allowed by the technology, W_SMIN, in order to reduce the resistance, so that we assume W_S = W_SMIN. The W_SMIN/W ratio can be expressed in term of the maximum number of thermocouples, N_TMAX , given by:

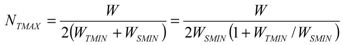   (16)

where W_TMIN is the minimum width of conductors A and B allowed by the technology. Generally, in microelectronic processes, W_TMIN ≥ W_SMIN, so that m = (1 + W_TMIN/W_SMIN) ≥ 2. Using Equation (16) and the above consideration, the following expression can be derived:

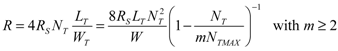   (17)

Substitution of Equation (17) in Equation (13) yields:

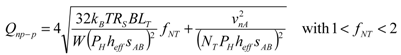   (18)

where f_NT = (1-N_T/mN_TMAX)⁻¹ is a factor that monotonically increases with N_T. Now, let us make a few considerations about the amplifier noise. The fact that the output signal of a flow sensor includes a DC component dictates the use of dynamic techniques, such as chopper stabilization or autozeroing to cancel the amplifier offset and offset drift [26]. These techniques also strongly reduce the low frequency (Flicker) components, so that the amplifier noise consists only of thermal noise. For a given amplifier topology it is possible to express the rms thermal noise as in [27]:

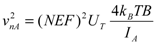   (19)

where U_T is the thermal voltage (nearly 26 mV at 300 K), I_A the total current absorbed by the amplifier and NEF (noise efficiency factor) is a figure of merit associated to the amplifier architecture.

2.4. Offset Flow Rate

Considering the sensor and amplifier contribution to the total offset voltage it is possible to write:

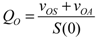   (20)

The second term can be made very small using the mentioned dynamic approaches to cancel the amplifier offset. Such techniques are ineffective with respect to the sensor offset, which constitutes the main contribution. The sensor offset can be calculated using Equation (8) in condition of zero flow

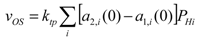   (21)

In practice, the majority of flow sensors exhibit a thermopile and heater arrangement that is symmetric with respect to a plane perpendicular to the flow direction. Therefore, if the heaters are driven with identical power, the v_OS should be nominally zero. Unavoidable random asymmetries due to the fabrication process add errors to the a_k,i(0) terms in Equation (21). Introducing the relative errors e_k,i associated to the quantities a_k,i, it is possible to write the offset in the case of uniform power distribution (x_i = 1/N_H) as:

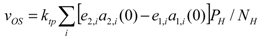   (22)

From the sensitivity expression Equation (12), finally we get:

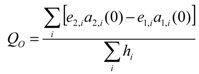   (23)

where the amplifier offset has been neglected. Since the entity of relative errors is a technological parameter, the numerator is larger in sensors where the static coupling coefficients a_k,i(0) are larger. In turn, considering Equation (7), the larger the a_k,i(0) values, the larger the voltages V₁ and V₂, individually produced by the two thermopiles at zero flow (static thermopile voltages). On the other hand, the denominator includes the derivative of the a_i,k parameters with respect to flow. In deriving Equation (7), one finds that the larger the a_i,k derivatives, the larger V₁ and V₂ derivatives with respect to flow. Then, as a general rule, in order to achieve a small offset, the thermopile voltage should exhibit a small static value and a large derivative with respect to flow rate.

2.5. Insertion Loss vs. Sensitivity

The pressure drop across the flow channel sketched in Figure 1(b) can be approximated by the following expression [28]:

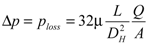   (24)

where a laminar flow regime have been assumed, A is the channel cross sectional area, µ the gas dynamic viscosity and D_H the hydraulic diameter, defined as:

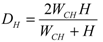   (25)

where W_CH and H are the channel width and height, respectively, as shown in Figure 1(b). Combining Equations (24) and (25) we get:

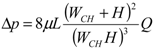   (26)

Equation (26) states that reducing the channel cross section (either reducing W_CH or H, or both) for a given flow rate leads to an increase in pressure drop. Note that reducing the cross section is the most commonly used method to increase the sensitivity of flow sensors. This occurs through the sum of the a_i,k derivatives with respect to flow, included in the parameter h_eff. In turn, these derivatives are proportional to the flow dependent components of g_i,k terms, i.e., to the forced convection contribution to heat transfer from the heaters to the thermopiles. This contribution is proportional to the velocity gradient perpendicular to the sensor element surfaces [2]. Therefore:

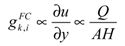   (27)

where y is a coordinate referred to an axis parallel to the channel dimension H (see Figure 1(b)) and is the g_i,k component due to forced convection. Note that the rightmost proportionality relationship in Equation (27) is valid if the shape of the velocity distribution does not change with flow (e.g., remains parabolic for a laminar regime). Considering Equations (5), (10) and (12) we finally get:

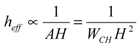   (28)

Equation (28) shows that reducing the channel cross-section, and in particular the channel height, is a very effective way to improve the sensor sensitivity but at the cost of improved pressure drop, as pointed out by Equation (26).

2.6. Design Considerations

The expressions found so far do not allow ab-initio prediction of the sensor performances but should be complemented with experimental data measured on test structures. It is beyond the aim of this work to examine all possible combinations of design constraints, so that this section is limited to a simple example where we will suppose that parameters h_i have been measured on a prototype and that the following parameters are fixed: (i) bandwidth, dictated by the application; (ii) s_AB, R_S, t_C, W_S, W_TMIN, deriving from the fabrication technology; (iii) N_H, dictated by the chosen sensor architecture. As a design constraint we will consider a target resolution indicated with Q*. Note that, if we neglect the amplifier noise term in Equation (18), we get the intrinsic resolution limit of the sensor. At this point the designer needs to impose that:

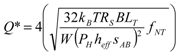   (29)

The following design indications are straightforward:

• (1)The sensor width W should be set at the maximum allowed value, imposed by the fabrication process (etching times) and by the channel width W_CH. Increasing W_CH to make room for a further W increase is ineffective, since h_eff proportionally decreases through Equation (28).
• (2)The power P_H should be set to the maximum value, which can be due either to a power consumption constraint or a reliability issue, the latter deriving from the maximum allowed heater temperature.
• (3)The effect of the thermopile number is rather weak, since it acts only on f_NT, which varies in a narrow interval. From Equation (17) the optimum situation seems to be represented by N_T = 1. Nevertheless, we will discover later that such a choice can adversely affect the amplifier design and should generally be avoided.
• (4)If the above operations are not sufficient to obtain the target resolution, parameter h_eff should be improved. The relevant equations are (5), (10) and (12). Improvement of the heater insulation ( 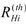) is effective only if the power constraint does not derive from reliability issues, since, in this case, an increase of 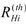with the maximum allowed power applied would simply result in exceeding the maximum heater temperature. Improving the thermopile insulation by increasing L_C produces significant h_eff improvements when L_C < L_S, so that L_T is not proportionally affected. Furthermore, L_C is often limited by the allowed etching times and mechanical robustness. Thermopile insulation can also be improved by reducing the cantilever thickness t_c, as clearly shown by Equation (4). Using the post-processing approach, this parameter is determined by the dielectric thickness deriving from the original process. Thickness reduction can be achieved in the post-processing phase by selective etching steps. The minimum thickness value is fixed by structural issues and by the necessity to maintain a sufficient margin with respect to the thermopile conductors, in order to prevent them from being damaged by the etching process. The last parameter to be taken into account to improve the sensitivity is ∂g_i,k/∂Q. Reducing the channel height (H) is strongly effective as shown by Equation (28). However, the concomitant pressure drop increase, deriving from Equation (26), should be carefully taken into account.
• (5)If the previous steps are successful, then it is necessary to design an amplifier with an input noise just low enough not to significantly change the achieved resolution. To obtain that, the following condition should be met:

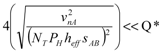   (30)

Equation (19) states that, once an optimum amplifier topology has been chosen, the amplifier noise can be reduced only by increasing the absorbed current and, as a consequence, the amplifier power consumption. The latter, given by I_AV_DD, where V_DD is the amplifier supply voltage, adds to the heater power P_H, increasing the overall power consumption of the system. As anticipated earlier, it is generally convenient to renounce to the marginal advantage of the choice N_T = 1 and adopt an N_T number as close as possible to the maximum value N_TMAX. In this way the noise constraint on the amplifier is relaxed, with proportional advantages in terms of power consumption.

3. Experimental Results and Discussion

3.1. Test Chip Architecture and Technology

In order to find additional information about the design of thermal flow sensors, measurements have been performed on sample structures included in a test chip. An optical micrograph of the latter is shown in Figure 5(a), while an enlargement of three different sensor structures is shown in Figure 5(b). The chip includes also a low noise chopper amplifier, properly designed to introduce negligible noise contributions with respect to the thermopile thermal noise. The amplifier can read the differential voltage (V_out = V₂ − V₁) or the individual thermopile voltages V₁ and V₂. The electronic interface includes also a driver for the sensor heaters. More details on the interface can be found in [21]. The sensing structures share a series of common parameters, shown in Table 1, regarding either the structure and channel dimensions. The differences between the devices are described in next sub-section.

Figure 5. (a) Optical micrograph of the test chip, including the read-out electronics and the flow sensors before the post-processing; (b) Magnification of the sensing structures after post-processing, showing the three different configurations, namely the single heater, the double heater and the triple heater.

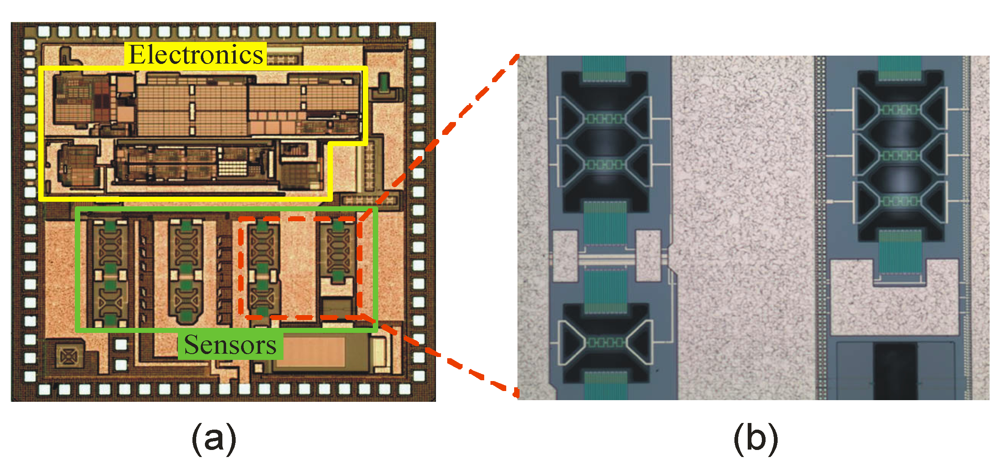
Figure 5. (a) Optical micrograph of the test chip, including the read-out electronics and the flow sensors before the post-processing; (b) Magnification of the sensing structures after post-processing, showing the three different configurations, namely the single heater, the double heater and the triple heater.

Table 1. Parameter values common to all sensing structures. The Seebeck coefficient was measured with a test structure on the chip.

NT	sAB	LC	LS	LH	LGH	W	L	WCH
10	315 µV/K	35 µm	90 µm	46 µm	71 µm	121 µm	2 mm	0.5 mm

Table 1. Parameter values common to all sensing structures. The Seebeck coefficient was measured with a test structure on the chip.

NT	sAB	LC	LS	LH	LGH	W	L	WCH
10	315 µV/K	35 µm	90 µm	46 µm	71 µm	121 µm	2 mm	0.5 mm

The test chip has been designed with the BCD6s (Bipolar, CMOS, DMOS) process of STMicroelectronics. The heaters are polysilicon resistors placed over suspended dielectric membranes while the thermopiles consist of N_T = 10 n + poly/p + poly thermocouples with the hot contacts at the tip of a cantilever beam. Each thermopile has an electrical resistance of 50 kΩ. The thermal insulation of the heaters and the thermopiles from the substrate has been obtained applying a post-processing technique based on front-side bulk micromachining, as schematically shown in Figure 6.

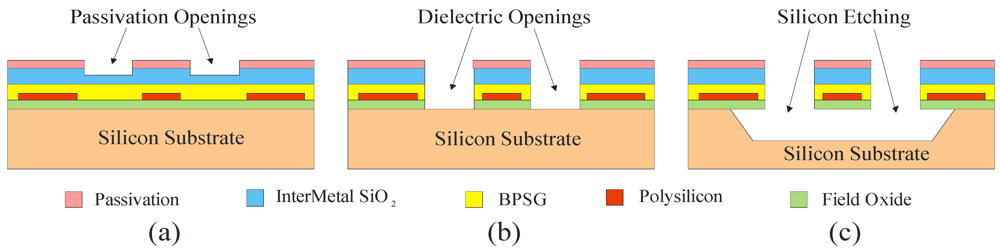
Figure 6. Schematic view of the post-processing: (a) passivation openings performed by the silicon foundry; (b) dielectric openings by reactive ion etching (RIE); (c) silicon anisotropic etching in TMAH solution.

Figure 6. Schematic view of the post-processing: (a) passivation openings performed by the silicon foundry; (b) dielectric openings by reactive ion etching (RIE); (c) silicon anisotropic etching in TMAH solution.

In order to access the bulk silicon in selected areas of the chip, the dielectric layers have been selectively removed from the front-side. In particular, the passivation layer and a part of the inter-metal dielectric layers have been removed directly by the silicon foundry at the end of the chip fabrication (Figure 6(a)). This was obtained exploiting the same etching step used by the foundry to open the passivation layer over the pads [29]. Then, during the post-processing phase, residual dielectric layers have been completely removed by means of a photolithographic step followed by silicon dioxide reactive ion etching (RIE) (Figure 6(b)). A silicon anisotropic etch was then applied through the openings, using an aqueous solution of TMAH with silicic acid and ammonium persulfate [29] (Figure 6(c)). An optical micrograph of the sensing structures after the silicon removal is shown in Figure 5(b). The depth of the cavity was 80 µm for all devices used in this work.

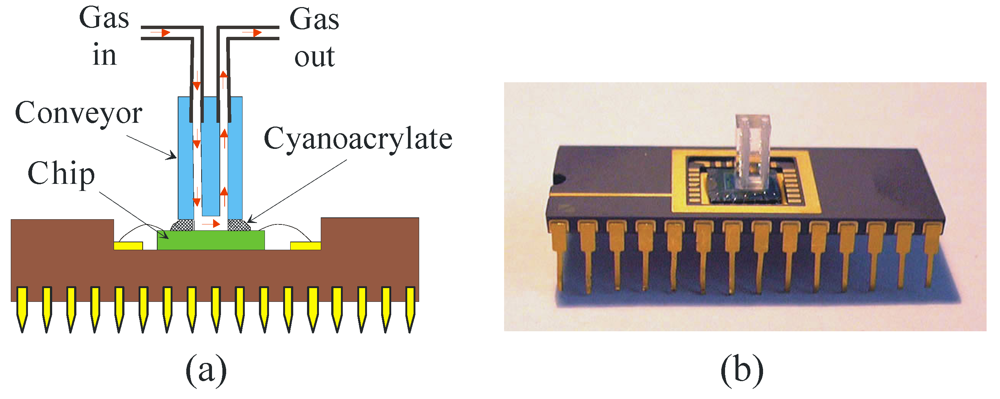
Figure 7. (a) Schematic view and (b) photograph of the assembled device.

Figure 7. (a) Schematic view and (b) photograph of the assembled device.

After post-processing, the chips were glued to ceramic DIP28 cases by means of epoxy resin and wedge bonding was used to connect selected chip pads to the case pins. A recently proposed packaging technique [30] has been used to connect the integrated flow sensor to the gas lines. This technique is based on a purposely built poly-methyl-methacrylate (PMMA) conveyor which is aligned to the chip by means of a guide and is capable to convey multiple flows to different areas of the chip [31]. Trenches with different cross-section dimensions have been milled on the flat face of the conveyor by means of a precision computer controlled milling machine (VHF CAM 100) and cyanocrylate glue has been used to fix the conveyor to the chip surface, as schematically shown in Figure 7(a). In Figure 7(b) a photograph of a device after packaging is shown.

3.3. Measurements

The first set of measurements has been performed on the triple-heater sensor and was devoted to check the validity of the linearity hypothesis. The responses to nitrogen flow have been measured delivering a constant power (1.25 mW) to one heater at a time. The channel height (H) is 0.5 mm. The other dimensions are specified in table 1. The response of the three heaters H₁₋₃ is shown in Figure 8. Clearly, only the case where the central heater (H₂) is activated produces an ideally symmetrical power distribution, resulting in a relatively low offset (30 µV), due only to random asymmetries, while in the other two cases a large systematic offset is present.

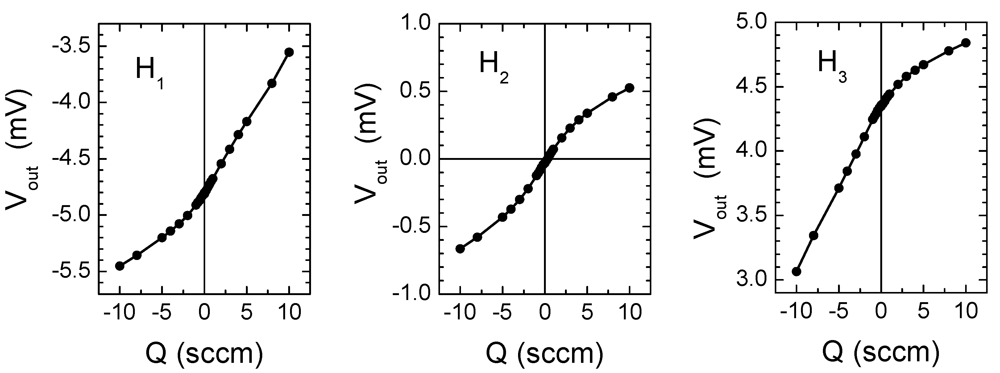
Figure 8. Response to nitrogen flow rate of a triple heater sensor with only one heater powered at a time. The powered heater is indicated in the plots.

Figure 8. Response to nitrogen flow rate of a triple heater sensor with only one heater powered at a time. The powered heater is indicated in the plots.

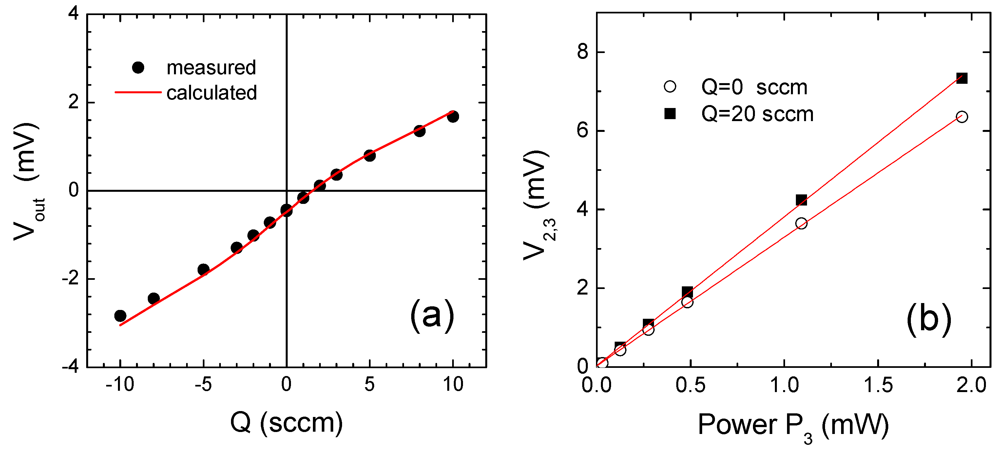
Figure 9. (a) Measured (symbols) and calculated (line) response of the triple heater sensor to a nitrogen flow with all the heaters powered with 1.25 mW; (b) Overheating of the 2nd thermopile with respect to H₃ heater.

Figure 9. (a) Measured (symbols) and calculated (line) response of the triple heater sensor to a nitrogen flow with all the heaters powered with 1.25 mW; (b) Overheating of the 2nd thermopile with respect to H₃ heater.

Figure 9(a), shows the response to nitrogen flows when all the heaters are powered with 1.25 mW. The solid symbols represent the result of an actual measurement, while the line has been obtained by superposition of the three responses shown in Figure 8. A good agreement, confirming the validity of the linearity hypothesis, is visible. To test also the supposed linearity of the sensor element overheating with respect to the heater powers, we have measured the output voltage of the 2nd thermopile (downstream thermopile) as a function of the power delivered to the H₃ (downstream heater). The measurements have been performed with zero flow and 20 sccm and the results are shown in Figure 9(b). In both cases an excellent linearity can be observed.

The second series of experiments, which involved samples with one, two and three heaters was devoted to test the effects of parameters change on the sensor resolution and dynamic range. The resolution is calculated considering the thermal noise of the two thermopiles over a bandwidth of 100 Hz (v_np−p = 1.6 µV) and the sensitivity at zero flow rate, S(0), also reported in Table 2. Numerical derivation of the sensor responses was used to calculate the sensitivity. The full scale flow rate, Q_max, was set at the point the sensitivity dropped below 50% of S(0). The results, all referring to nitrogen flows, are summarized in Table 2, where the parameters that distinguish the various samples are also reported. Note that in the single heater samples (first three lines) metal interconnections (Aluminum) are used to access the heaters through the suspending arms (heater connection column). The other samples in the table use silicided polysilicon (Si-Poly), providing a low enough sheet resistance with much less thermal conductivity than Aluminum. As a result, the heater thermal resistance is nearly 50% higher for the samples using silicided interconnections, with a proportional benefit in terms of h_eff, and, consequently, low power performances.

Table 2. Main parameters and performances of the sensors used in this work. The sensor resolution (Q_np−p) has been estimated considering a 100 Hz bandwidth. All figures refer to nitrogen flows.

Sensor parameters				Sensor performance (PHi = PH/NH = 1.25 mW)
NH	Heater	H	LG	S(0)		ktpheff at Q = 0	VK(0)	Qnp−p	Qmax	DR
	connection	mm	µm	µV/sccm	K/mW	µV/sccm/mW	mV	sccm	sccm
1	Metal	0.5	40	87	30.8	69.6	3.28	1.8 × 10−2	30	1.7 × 103
1	Metal	0.5	60	100	30.8	80	1.88	1.6 × 10−2	21.5	1.3 × 103
1	Metal	0.5	80	96	30.8	76.8	1.14	1.7 × 10−2	20	1.2 × 103
2	Si-poly	0.25	60	940	46.7	376	3.87	1.7 × 10−3	3.6	2.1 × 103
2	Si-poly	0.5	60	313	46.7	125	3.61	5.1 × 10−3	12	2.3 × 103
2	Si-poly	1	60	100	46.7	40	3.73	1.6 × 10−2	42	2.6 × 103
3	Si-poly	0.5	40	278	46.7	74	4.9	5.6 × 10−3	20	3.5 × 103

Table 2. Main parameters and performances of the sensors used in this work. The sensor resolution (Q_np−p) has been estimated considering a 100 Hz bandwidth. All figures refer to nitrogen flows.

Sensor parameters				Sensor performance (PHi = PH/NH = 1.25 mW)
NH	Heater	H	LG	S(0)		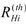ktpheff at Q = 0	VK(0)	Qnp−p	Qmax	DR
	connection	mm	µm	µV/sccm	K/mW	µV/sccm/mW	mV	sccm	sccm
1	Metal	0.5	40	87	30.8	69.6	3.28	1.8 × 10−2	30	1.7 × 103
1	Metal	0.5	60	100	30.8	80	1.88	1.6 × 10−2	21.5	1.3 × 103
1	Metal	0.5	80	96	30.8	76.8	1.14	1.7 × 10−2	20	1.2 × 103
2	Si-poly	0.25	60	940	46.7	376	3.87	1.7 × 10−3	3.6	2.1 × 103
2	Si-poly	0.5	60	313	46.7	125	3.61	5.1 × 10−3	12	2.3 × 103
2	Si-poly	1	60	100	46.7	40	3.73	1.6 × 10−2	42	2.6 × 103
3	Si-poly	0.5	40	278	46.7	74	4.9	5.6 × 10−3	20	3.5 × 103

The experiments performed on single heater structures have been devoted to investigate the role of the heater-thermopile gap, L_G. The test chip includes single heater structures with L_G = 40, 60 and 80 µm. The measured sensor responses are shown in Figure 10. Note that the curves are similar, with a zero flow sensitivity that exhibit variations less than 13%. This experiment suggests that variation of the thermopile-heater gap in this range does not constitute a viable method to improve sensitivity. This result is in contrast with [15,16], where the sensitivity was found to increase with larger thermopile-heater spacing. A possible reason is that in [15,16] all sensor elements were placed on a single membrane, so that the distance between the heater and the thermopile strongly affects the thermal insulation of the thermopile. On the other hand, L_G strongly affects the static thermopile voltage V_K(0) that in Table 2 indicates the average value of V₁(0) and V₂(0). This quantity is significantly higher for the smallest L_G value, proving that the a_k,i(0) parameters are larger. Considering that the sensitivity (and then h_eff) does not change with L_G, a proportionally higher sensor offset should be expected for the smallest L_G value. A higher offset is actually visible in Figure 10 for L_G = 40 µm.

Figure 10. Response to a nitrogen flow of the three single heater structures, differing for the dimension of the thermopile-heater gap L_G, indicated in the figure together with the sensitivity at zero flow.

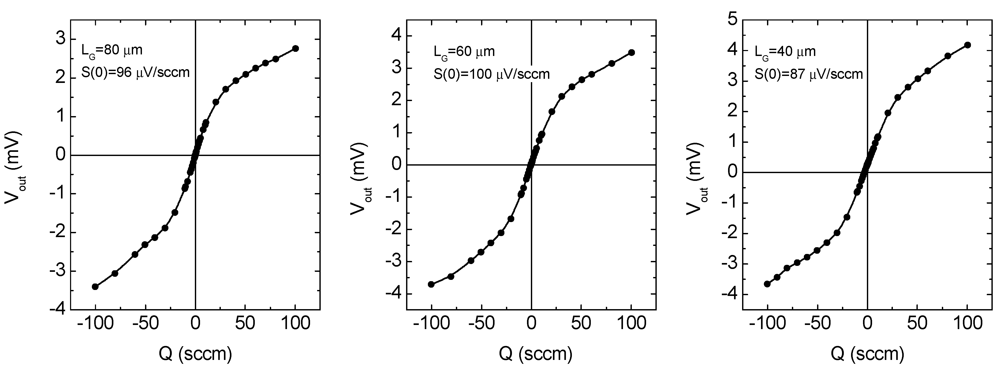
Figure 10. Response to a nitrogen flow of the three single heater structures, differing for the dimension of the thermopile-heater gap L_G, indicated in the figure together with the sensitivity at zero flow.

The last series of experiments was devoted to investigate the effect of channel height, H. The measurements, shown in Figure 11, were performed on double-heater structures, with both the heaters driven with 1.25 mW. These curves clearly show the sensitivity increase that can be obtained by reducing the channel height, as predicted by Equation (28). The sensitivity increase was obtained at the cost of increased pressure drop, which passed from 0.1 kPa at 100 sccm for the 0.5 mm channel to 0.4 kPa for the 0.25 mm channel, at the same conditions. The actual sensitivity gain obtained by halving the channel height is nearly 3, while a factor of 4 was expected from Equation (28). A not fully developed flow regime in the relatively short channel can be a reasonable explanation.

Figure 11. Responses of double heater structures to a nitrogen flow. The structures were packaged with different channel heights, H, indicated in the figure for each curve.

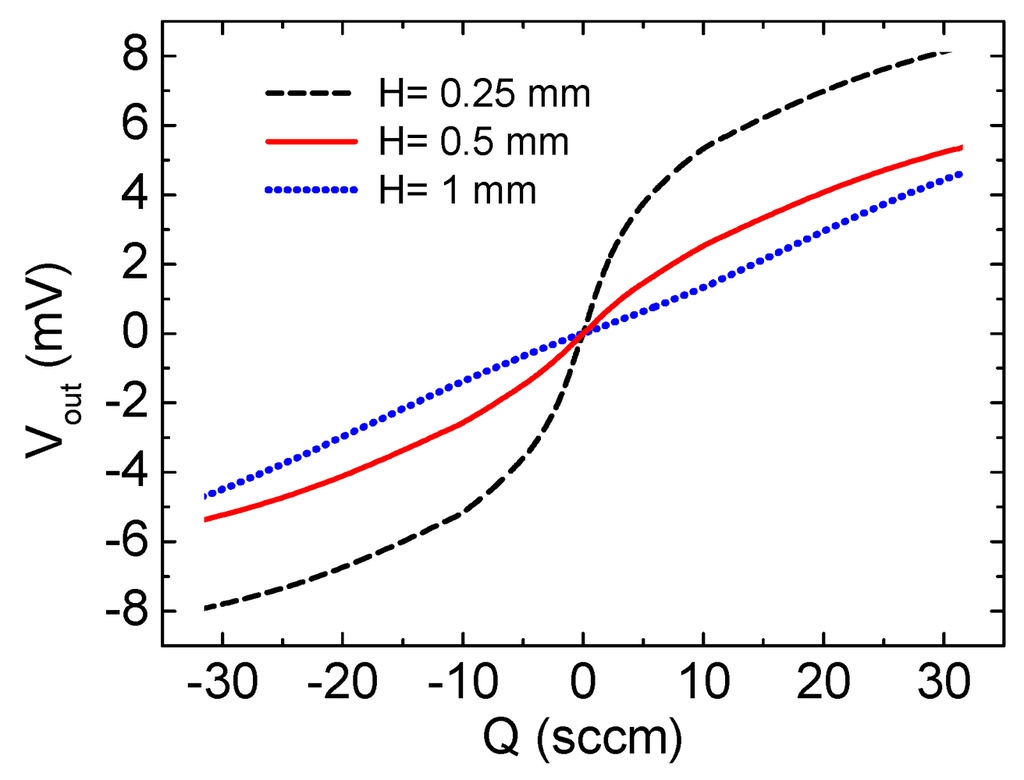
Figure 11. Responses of double heater structures to a nitrogen flow. The structures were packaged with different channel heights, H, indicated in the figure for each curve.

As far as the dynamic range is concerned, all tested sensors feature DR value greater than 10³, which is an excellent result for this kind of sensors. Considering the single heater sensors, the effect of reducing the thermopile-heater gap (L_G) produces an interesting DR improvement, due to higher full scale flow rate. On the contrary, the resolution increase obtained reducing the channel height is accompanied by a range (Q_max) reduction, resulting in a slight deterioration of the DR. Finally, it can be observed that increasing the number of heaters improves the DR at the cost of increased power consumption.

All considerations made in this work on the sensor resolution and DR are based on the hypothesis that the only significant contribution to the overall noise is thermal noise of the thermopile resistance. This hypothesis is confirmed by recording the sensor output signal, properly amplified by the on-chip amplifier (gain = 230). Data digitalization has been performed using a 16 bit acquisition system (Pico Technology Ltd, mod. ADC216) combined with a program for spectral analysis. Figure 12(a) shows the total noise voltage spectral density of the sensor and the amplifier background noise. The latter was measured by substituting the sensor with a short circuit.

Figure 12. (a) Noise voltage spectral density (total sensor noise) referred to the amplifier input, measured on double heater samples with a total heater power (PH) of 2.5 mW, kept in still nitrogen. The heater power distribution on the two heaters was slightly unbalanced to compensate for the sensor offset. The amplifier background noise and ideal thermopile thermal noise are also indicated; (b) Time diagram of the total voltage noise, referred to the amplifier input.

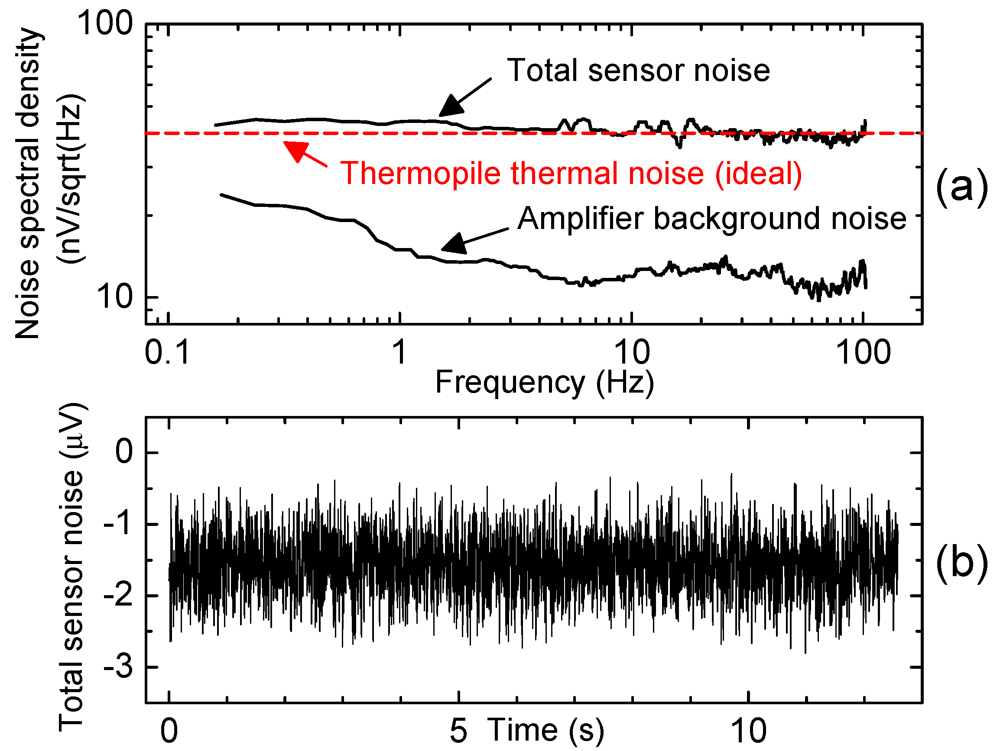
Figure 12. (a) Noise voltage spectral density (total sensor noise) referred to the amplifier input, measured on double heater samples with a total heater power (PH) of 2.5 mW, kept in still nitrogen. The heater power distribution on the two heaters was slightly unbalanced to compensate for the sensor offset. The amplifier background noise and ideal thermopile thermal noise are also indicated; (b) Time diagram of the total voltage noise, referred to the amplifier input.

The sensor is a double heater version, with 0.5 mm channel height, maintained in still nitrogen (zero flow). Both quantities are referred to the amplifier input, as in the scheme of Figure 2(a). A fifth order Butterworth low pass filter is inserted at the amplifier output port, to limit the signal bandwidth and eliminate aliasing phenomena. The actual frequency response of the filter has been experimentally determined and the result has been used to correct the measured spectra shown in Figure 12(a), which can be considered free of filtering effects in the whole displayed frequency interval. DC coupling is used in all measurements; spectra are averaged over 25 independent captures. The ideal thermal noise density (40 nV/sqrt(Hz) of the total thermopile resistance (R = 100 kΩ) is indicated by the dashed line. The results shown in Figure 12(a) prove that the approximation of considering only the thermal noise contribution is appropriate, at least for the sensors used in this work. This was confirmed also by measurement of the rms noise voltage, estimated by data recorded over intervals of 12.6 s, with a 100 Hz signal bandwidth. Figure 12(b) shows a time diagram of the signal measured from a double heater sample kept in still nitrogen. The original sensor offset (around 100 µV) was compensated by balancing the heater power as described in [21]; a residual offset of nearly −1.5 µV can be observed. The estimated rms noise voltage (i.e., the signal standard deviation) was 0.41 µV, in good agreement with the theoretical 0.4 µV value calculated by considering only thermal noise.

4. Conclusions

A detailed lumped element model of integrated thermal flow sensors has been introduced. The main advantage of the model is the separation of the transduction process into distinct phases, which can be independently analyzed in order to find concise expressions to be used for global optimization of the device. A linearity hypothesis, based on reasonable approximations and supported by experimental results, is used to analyze multi-heater sensors, which have been recently proposed as an effective method to cancel the sensor offset [23] and extend the operating range [17,24]. The expressions derived from the proposed schematization include several sensor specifications and may constitute a framework for organizing new data obtained with further experimental investigations or fluid-dynamic simulations. Application to the optimization of the sensor resolution provided guidelines that should contribute to reduce the number of design-fabrication-testing cycles necessary for meeting the target specifications. A limitation of the model is the presence of generic heat exchange terms g_i,k(Q) that, with their derivatives, determine the sensor sensitivity. Indications about the sensitivity dependence on parameters that have a direct effect on the g_ik factors, such as the flow channel height and heater thermopile gap, are extrapolated by the experiments performed on the test chip.