Integrating Remotely Sensed Thermal Observations for Calibration of Process-Based Land-Surface Models: Accuracy, Revisit Windows, and Implications in a Dryland Ecosystem
Highlights
- Linear-corrected MODIS land surface temperature (LST) enables accurate calibration of the dynamic soil–vegetation–atmosphere transfer model for drylands.
- Remote sensing thermal observations enable high model accuracy, with an optimal revisit frequency of 8 days for parameter calibration for drylands.
- Provides a practical pathway for integrating remote sensing with process-based models to advance understanding of dryland ecosystem functioning.
- Guides the design of observation strategies and satellite missions, enhancing the ap-plication of remote sensing for ecohydrological monitoring.
Abstract
1. Introduction
2. Study Site and Data
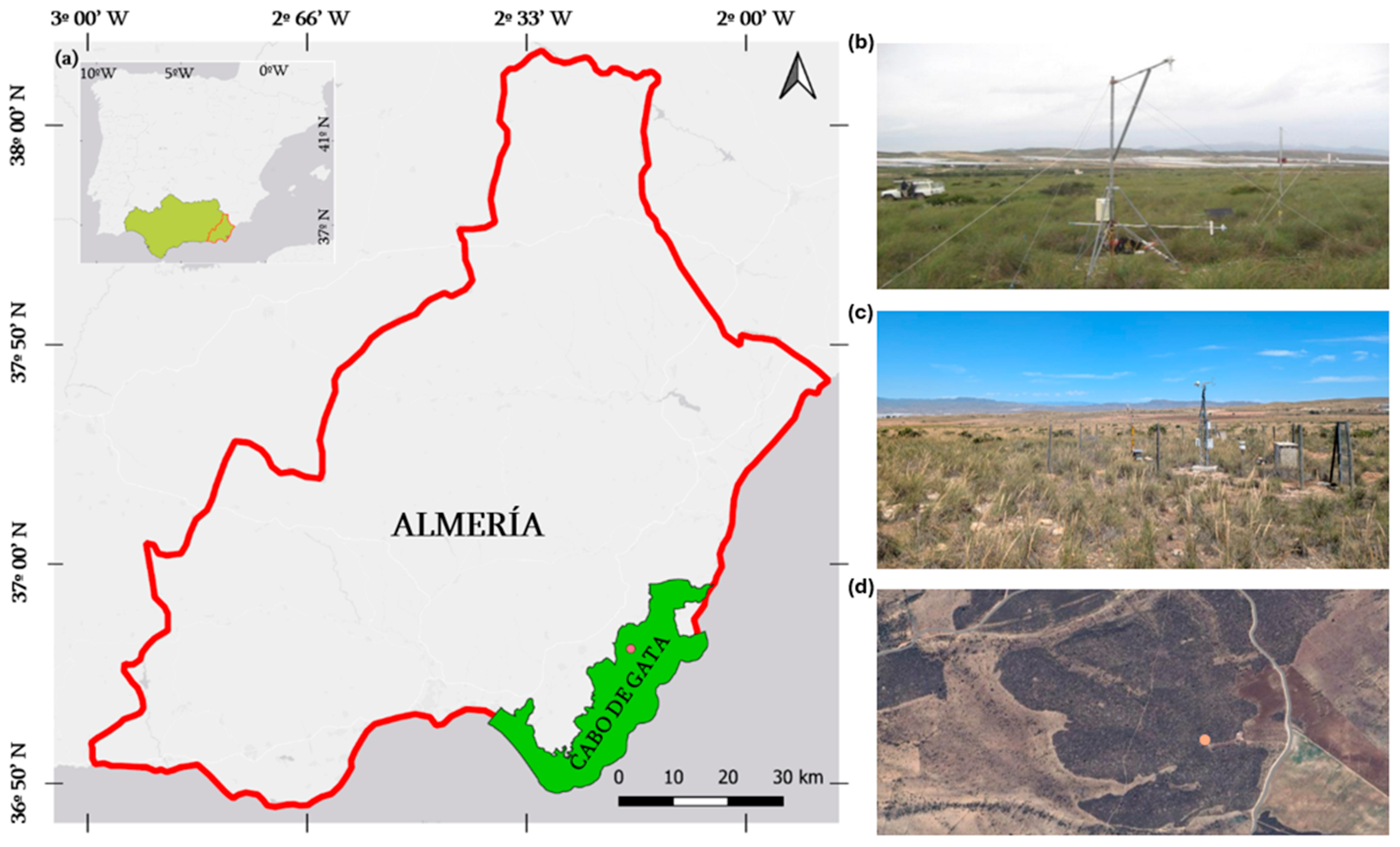
2.1. Study Site
2.2. Field Measurements
2.3. Satellite Data
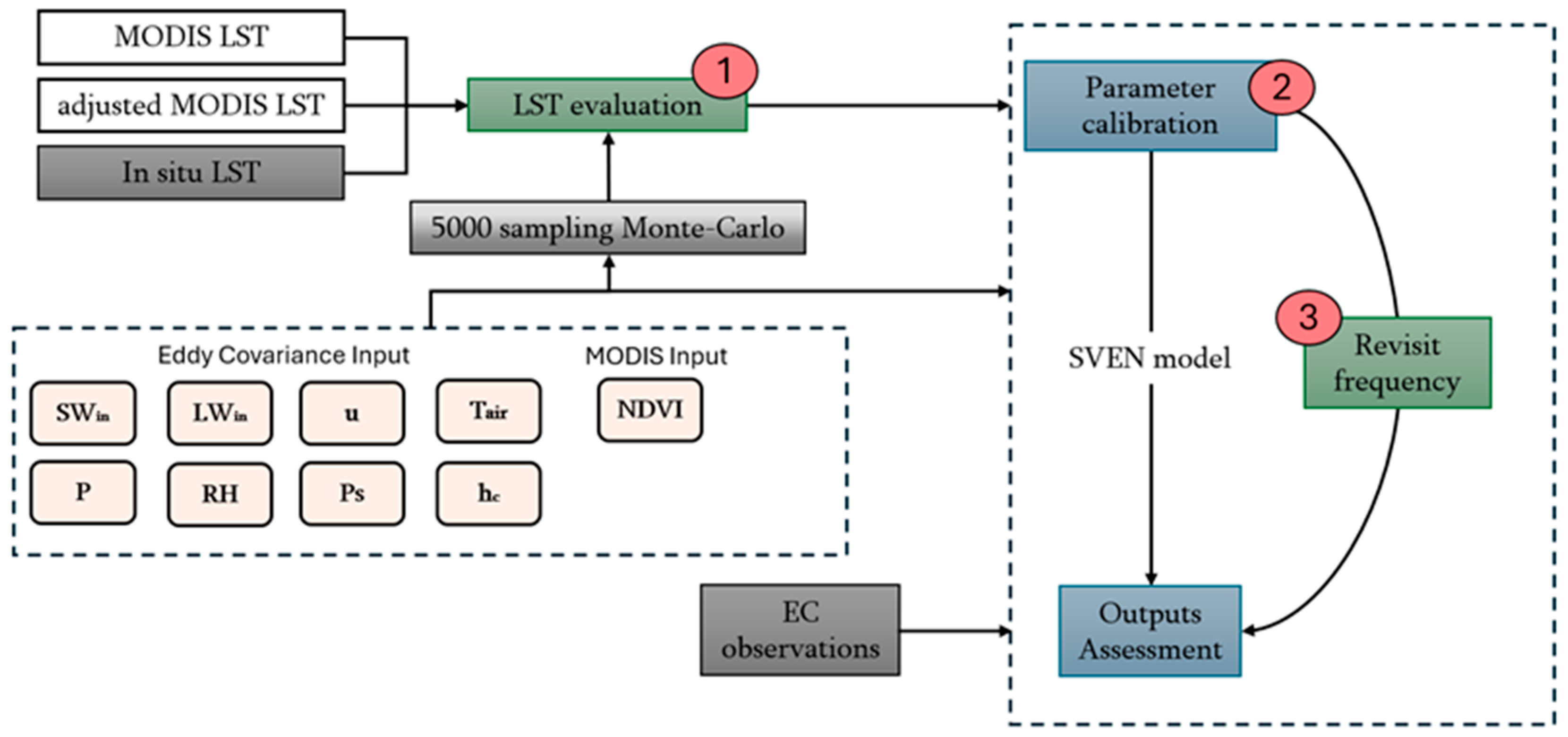
3. Method
3.1. Model Inputs
3.2. Model Parameters and Optimization
3.3. Model Simulation Assessment
4. Results
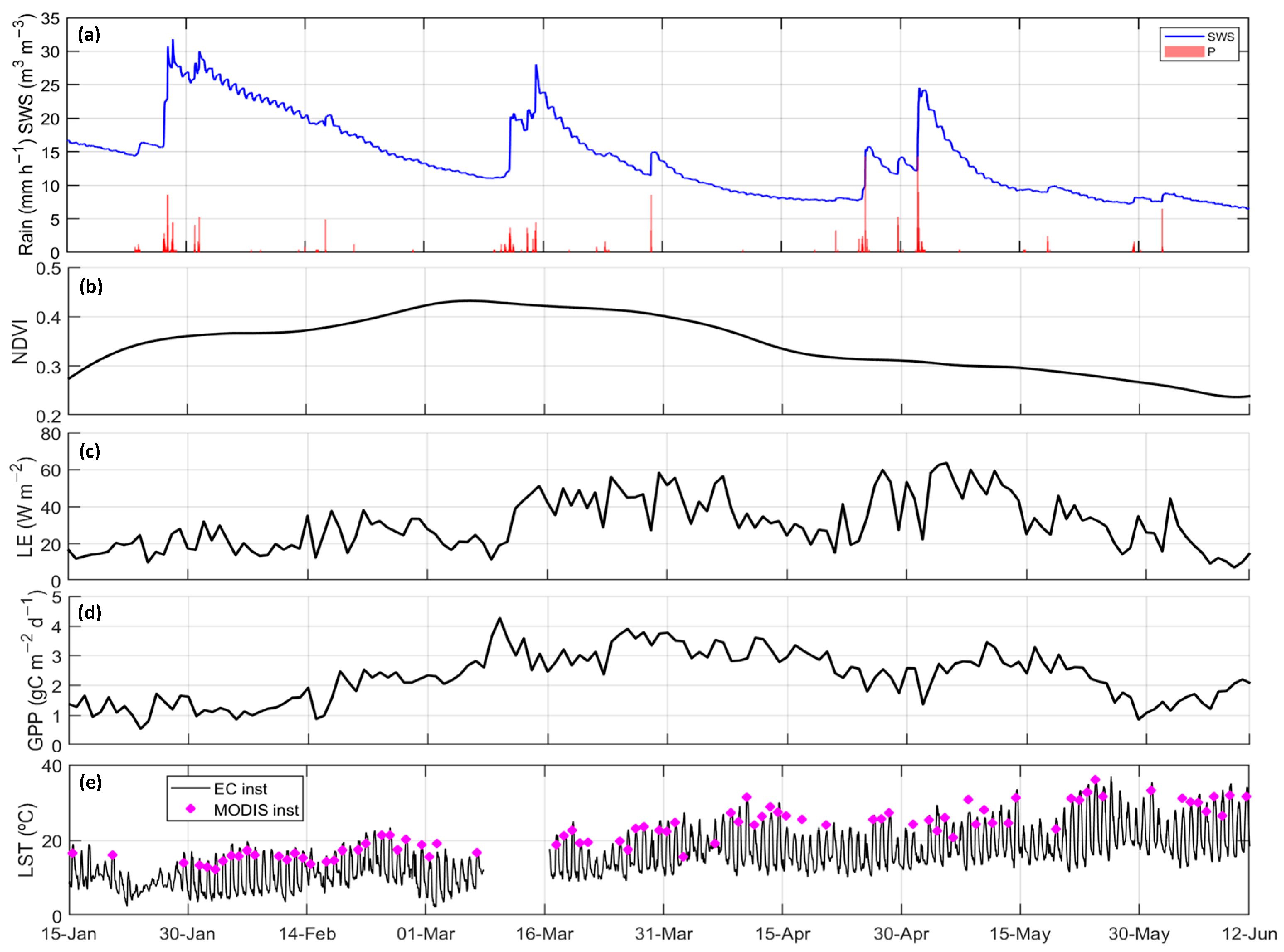
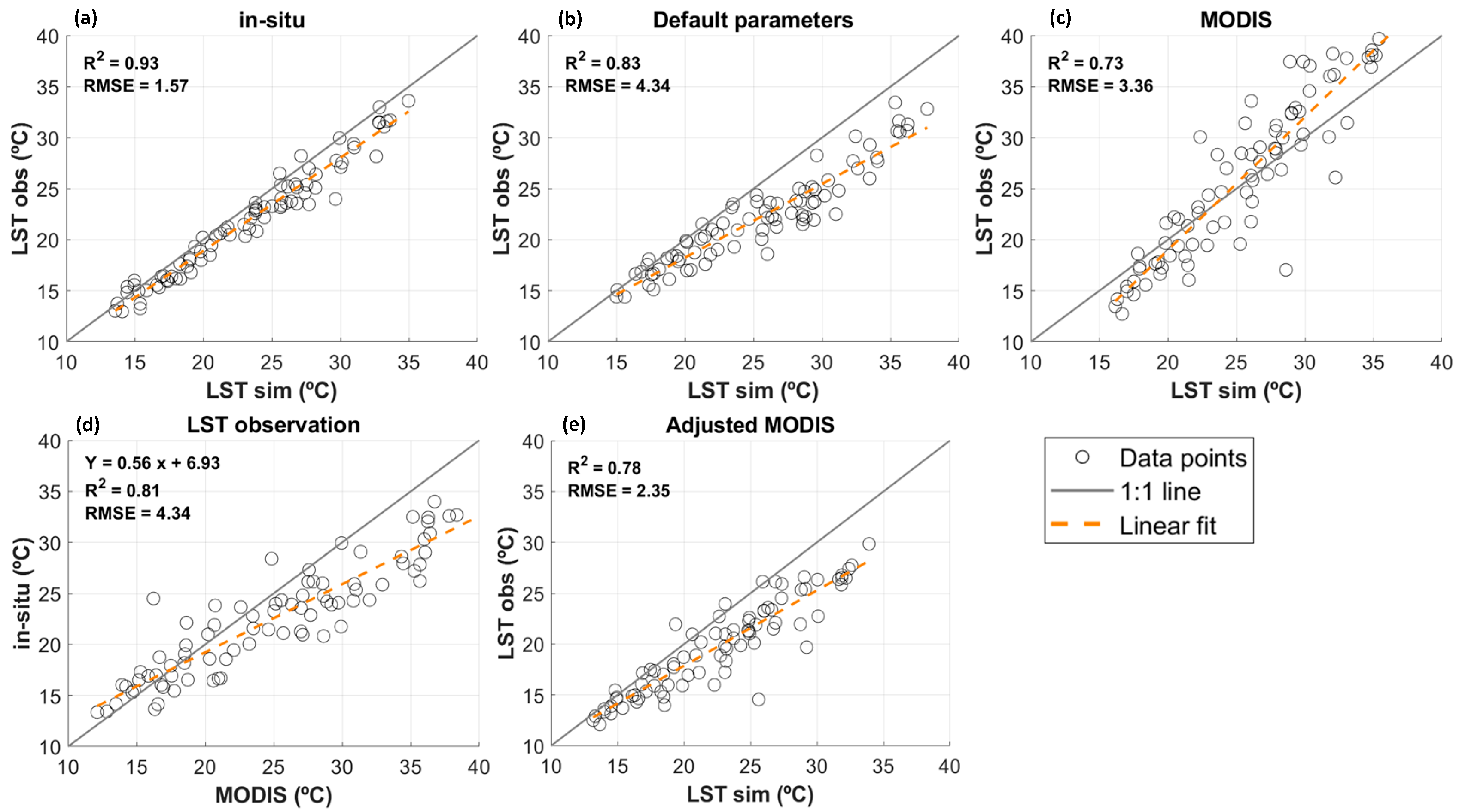
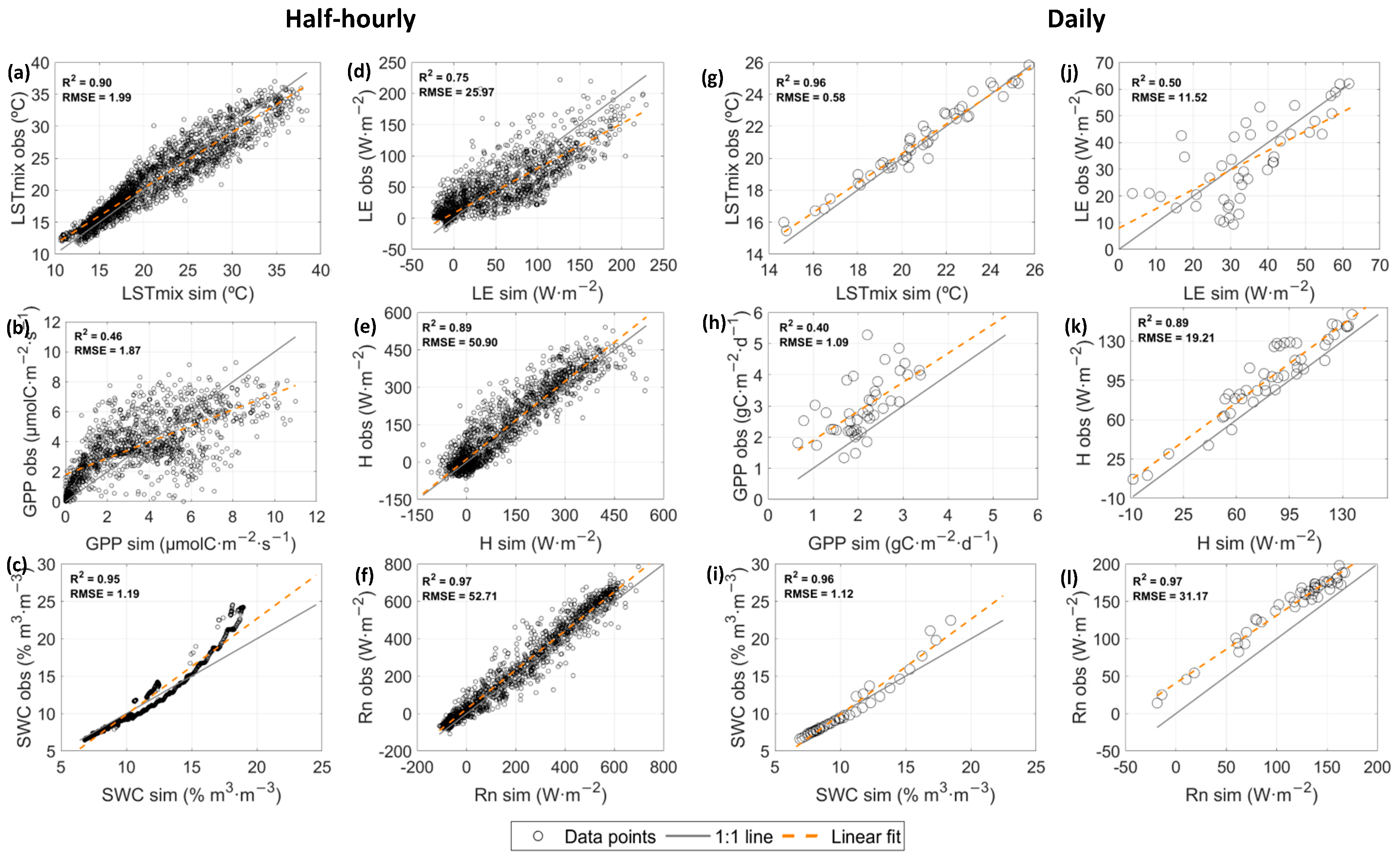
4.1. Accuracy of MODIS LST Data and Flux Simulations
4.2. Validation at the Half-Hourly and Daily Time Scale
4.3. Revisit Satellite Frequency for Parameter Calibration
5. Discussion
5.1. Comparison with Existing Surface Flux Models
5.2. Further Improvements for Surface Flux Simulations
5.3. Remotely Sensed Surface Temperature for Model Optimization
5.4. Scalability Challenges
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Swift, J.; DM, E.M.C. Climate Variability, Ecosystem Stability and the Implications for Range and Livestock Development. Range Ecol. Disequilibrium Overseas Dev. Inst. Lond. 1993, 31–41. [Google Scholar]
- Glenn, E.P.; Huete, A.R.; Nagler, P.L.; Hirschboeck, K.K.; Brown, P. Integrating Remote Sensing and Ground Methods to Estimate Evapotranspiration. Crit. Rev. Plant Sci. 2007, 26, 139–168. [Google Scholar] [CrossRef]
- Giorgi, F.; Lionello, P. Climate Change Projections for the Mediterranean Region. Glob. Planet. Change 2008, 63, 90–104. [Google Scholar] [CrossRef]
- Baldocchi, D. “Breathing” of the Terrestrial Biosphere: Lessons Learned from a Global Network of Carbon Dioxide Flux Measurement Systems. Aust. J. Bot. 2008, 56, 1–26. [Google Scholar] [CrossRef]
- Brogaard, S.; Runnstrom, M.; Seaquist, J. Primary Production of Inner Mongolia, China, between 1982 and 1999 Estimated by a Satellite Data-Driven Light Use Efficiency Model. Glob. Planet. Change 2005, 45, 313–332. [Google Scholar] [CrossRef]
- Beer, C.; Reichstein, M.; Tomelleri, E.; Ciais, P.; Jung, M.; Carvalhais, N.; Rödenbeck, C.; Arain, M.A.; Baldocchi, D.; Bonan, G.B.; et al. Terrestrial Gross Carbon Dioxide Uptake: Global Distribution and Covariation with Climate. Science 2010, 329, 834–838. [Google Scholar] [CrossRef]
- Ito, A.; Inatomi, M. Water-Use Efficiency of the Terrestrial Biosphere: A Model Analysis Focusing on Interactions between the Global Carbon and Water Cycles. J. Hydrometeorol. 2012, 13, 681–694. [Google Scholar] [CrossRef]
- Jung, M.; Reichstein, M.; Margolis, H.A.; Cescatti, A.; Richardson, A.D.; Arain, M.A.; Arneth, A.; Bernhofer, C.; Bonal, D.; Chen, J.; et al. Global Patterns of Land-Atmosphere Fluxes of Carbon Dioxide, Latent Heat, and Sensible Heat Derived from Eddy Covariance, Satellite, and Meteorological Observations. J. Geophys. Res. 2011, 116, G00J07. [Google Scholar] [CrossRef]
- Fisher, J.B.; Melton, F.; Middleton, E.; Hain, C.; Anderson, M.; Allen, R.; McCabe, M.F.; Hook, S.; Baldocchi, D.; Townsend, P.A.; et al. The Future of Evapotranspiration: Global Requirements for Ecosystem Functioning, Carbon and Climate Feedbacks, Agricultural Management, and Water Resources. Water Resour. Res. 2017, 53, 2618–2626. [Google Scholar] [CrossRef]
- Denis, G.; Claverie, A.; Pasco, X.; Darnis, J.-P.; De Maupeou, B.; Lafaye, M.; Morel, E. Towards Disruptions in Earth Observation? New Earth Observation Systems and Markets Evolution: Possible Scenarios and Impacts. Acta Astronaut. 2017, 137, 415–433. [Google Scholar] [CrossRef]
- Anderson, M.; Norman, J.; Kustas, W.; Houborg, R.; Starks, P.; Agam, N. A Thermal-Based Remote Sensing Technique for Routine Mapping of Land-Surface Carbon, Water and Energy Fluxes from Field to Regional Scales. Remote Sens. Environ. 2008, 112, 4227–4241. [Google Scholar] [CrossRef]
- Bhattacharya, B.K.; Mallick, K.; Desai, D.; Bhat, G.S.; Morrison, R.; Clevery, J.R.; Woodgate, W.; Beringer, J.; Cawse-Nicholson, K.; Ma, S.; et al. A Coupled Ground Heat Flux–Surface Energy Balance Model of Evaporation Using Thermal Remote Sensing Observations. Biogeosciences 2022, 19, 5521–5551. [Google Scholar] [CrossRef]
- Mallick, K.; Baldocchi, D.; Jarvis, A.; Hu, T.; Trebs, I.; Sulis, M.; Bhattarai, N.; Bossung, C.; Eid, Y.; Cleverly, J.; et al. Insights Into the Aerodynamic Versus Radiometric Surface Temperature Debate in Thermal-Based Evaporation Modeling. Geophys. Res. Lett. 2022, 49, e2021GL097568. [Google Scholar] [CrossRef]
- Bai, Y.; Bhattarai, N.; Mallick, K.; Zhang, S.; Hu, T.; Zhang, J. Thermally Derived Evapotranspiration from the Surface Temperature Initiated Closure (STIC) Model Improves Cropland GPP Estimates under Dry Conditions. Remote Sens. Environ. 2022, 271, 112901. [Google Scholar] [CrossRef]
- Bayat, B.; Van Der Tol, C.; Verhoef, W. Integrating Satellite Optical and Thermal Infrared Observations for Improving Daily Ecosystem Functioning Estimations during a Drought Episode. Remote Sens. Environ. 2018, 209, 375–394. [Google Scholar] [CrossRef]
- Kustas, W.; Anderson, M. Advances in Thermal Infrared Remote Sensing for Land Surface Modeling. Agric. For. Meteorol. 2009, 149, 2071–2081. [Google Scholar] [CrossRef]
- Ryu, Y.; Baldocchi, D.D.; Kobayashi, H.; Van Ingen, C.; Li, J.; Black, T.A.; Beringer, J.; Van Gorsel, E.; Knohl, A.; Law, B.E.; et al. Integration of MODIS Land and Atmosphere Products with a Coupled-Process Model to Estimate Gross Primary Productivity and Evapotranspiration from 1 Km to Global Scales: GLOBAL GPP AND ET. Glob. Biogeochem. Cycles 2011, 25, 271–284. [Google Scholar] [CrossRef]
- Amthor, J.S.; Chen, J.M.; Clein, J.S.; Frolking, S.E.; Goulden, M.L.; Grant, R.F.; Kimball, J.S.; King, A.W.; McGuire, A.D.; Nikolov, N.T.; et al. Boreal Forest CO2 Exchange and Evapotranspiration Predicted by Nine Ecosystem Process Models: Intermodel Comparisons and Relationships to Field Measurements. J. Geophys. Res. 2001, 106, 33623–33648. [Google Scholar] [CrossRef]
- Reichstein, M.; Falge, E.; Baldocchi, D.; Papale, D.; Aubinet, M.; Berbigier, P.; Bernhofer, C.; Buchmann, N.; Gilmanov, T.; Granier, A.; et al. On the Separation of Net Ecosystem Exchange into Assimilation and Ecosystem Respiration: Review and Improved Algorithm. Glob. Change Biol. 2005, 11, 1424–1439. [Google Scholar] [CrossRef]
- Sitch, S.; Smith, B.; Prentice, I.C.; Arneth, A.; Bondeau, A.; Cramer, W.; Kaplan, J.O.; Levis, S.; Lucht, W.; Sykes, M.T.; et al. Evaluation of Ecosystem Dynamics, Plant Geography and Terrestrial Carbon Cycling in the LPJ Dynamic Global Vegetation Model. Glob. Change Biol. 2003, 9, 161–185. [Google Scholar] [CrossRef]
- Morillas, L.; Leuning, R.; Villagarcía, L.; García, M.; Serrano-Ortiz, P.; Domingo, F. Improving Evapotranspiration Estimates in Mediterranean Drylands: The Role of Soil Evaporation: Evapotranspiration Estimation in Mediterranean Dry Lands. Water Resour. Res. 2013, 49, 6572–6586. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Ibrom, A.; Bauer-Gottwein, P. Temporal Interpolation of Land Surface Fluxes Derived from Remote Sensing—Results with an Unmanned Aerial System. Hydrol. Earth Syst. Sci. 2020, 24, 3643–3661. [Google Scholar] [CrossRef]
- Baldocchi, D.D. Assessing the Eddy Covariance Technique for Evaluating Carbon Dioxide Exchange Rates of Ecosystems: Past, Present and Future. Glob. Change Biol. 2003, 9, 479–492. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Bauer-Gottwein, P.; Jakobsen, J.; Zarco-Tejada, P.J.; Bandini, F.; Paz, V.S.; Ibrom, A. High Spatial Resolution Monitoring Land Surface Energy, Water and CO2 Fluxes from an Unmanned Aerial System. Remote Sens. Environ. 2019, 229, 14–31. [Google Scholar] [CrossRef]
- Kalma, J.D.; McVicar, T.R.; McCabe, M.F. Estimating Land Surface Evaporation: A Review of Methods Using Remotely Sensed Surface Temperature Data. Surv. Geophys. 2008, 29, 421–469. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. A Review of Global Terrestrial Evapotranspiration: Observation, Modeling, Climatology, and Climatic Variability. Rev. Geophys. 2012, 50, 2011RG000373. [Google Scholar] [CrossRef]
- Carlson, T.N.; Gillies, R.R.; Schmugge, T.J. An Interpretation of Methodologies for Indirect Measurement of Soil Water Content. Agric. For. Meteorol. 1995, 77, 191–205. [Google Scholar] [CrossRef]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A Simple Interpretation of the Surface Temperature/Vegetation Index Space for Assessment of Surface Moisture Status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Fisher, J.B.; Tu, K.P.; Baldocchi, D.D. Global Estimates of the Land–Atmosphere Water Flux Based on Monthly AVHRR and ISLSCP-II Data, Validated at 16 FLUXNET Sites. Remote Sens. Environ. 2008, 112, 901–919. [Google Scholar] [CrossRef]
- Mu, Q.; Zhao, M.; Running, S.W. Improvements to a MODIS Global Terrestrial Evapotranspiration Algorithm. Remote Sens. Environ. 2011, 115, 1781–1800. [Google Scholar] [CrossRef]
- Running, S.W.; Nemani, R.R.; Heinsch, F.A.; Zhao, M.; Reeves, M.; Hashimoto, H. A Continuous Satellite-Derived Measure of Global Terrestrial Primary Production. BioScience 2004, 54, 547. [Google Scholar] [CrossRef]
- García, M.; Sandholt, I.; Ceccato, P.; Ridler, M.; Mougin, E.; Kergoat, L.; Morillas, L.; Timouk, F.; Fensholt, R.; Domingo, F. Actual Evapotranspiration in Drylands Derived from In-Situ and Satellite Data: Assessing Biophysical Constraints. Remote Sens. Environ. 2013, 131, 103–118. [Google Scholar] [CrossRef]
- Alfieri, J.G.; Anderson, M.C.; Kustas, W.P.; Cammalleri, C. Effect of the Revisit Interval and Temporal Upscaling Methods on the Accuracy of Remotely Sensed Evapotranspiration Estimates. Hydrol. Earth Syst. Sci. 2017, 21, 83–98. [Google Scholar] [CrossRef]
- Huang, F.; Zhan, W.; Voogt, J.; Hu, L.; Wang, Z.; Quan, J.; Ju, W.; Guo, Z. Temporal Upscaling of Surface Urban Heat Island by Incorporating an Annual Temperature Cycle Model: A Tale of Two Cities. Remote Sens. Environ. 2016, 186, 1–12. [Google Scholar] [CrossRef]
- Sun, X.; Wilcox, B.P.; Zou, C.B. Evapotranspiration Partitioning in Dryland Ecosystems: A Global Meta-Analysis of in Situ Studies. J. Hydrol. 2019, 576, 123–136. [Google Scholar] [CrossRef]
- Wang, S.; Garcia, M.; Ibrom, A.; Jakobsen, J.; Josef Köppl, C.; Mallick, K.; Looms, M.C.; Bauer-Gottwein, P. Mapping Root-Zone Soil Moisture Using a Temperature–Vegetation Triangle Approach with an Unmanned Aerial System: Incorporating Surface Roughness from Structure from Motion. Remote Sens. 2018, 10, 1978. [Google Scholar] [CrossRef]
- McCallum, I.; Wagner, W.; Schmullius, C.; Shvidenko, A.; Obersteiner, M.; Fritz, S.; Nilsson, S. Satellite-Based Terrestrial Production Efficiency Modeling. Carbon. Balance Manag. 2009, 4, 8. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Mallick, K.; Hulley, G.C.; Planells, L.P.; Göttsche, F.M.; Schlerf, M.; Hitzelberger, P.; Didry, Y.; Szantoi, Z.; Alonso, I.; et al. Continental-Scale Evaluation of Three ECOSTRESS Land Surface Temperature Products over Europe and Africa: Temperature-Based Validation and Cross-Satellite Comparison. Remote Sens. Environ. 2022, 282, 113296. [Google Scholar] [CrossRef]
- Valladares, F. Tradeoffs Between Irradiance Capture and Avoidance in Semi-Arid Environments Assessed with a Crown Architecture Model. Ann. Bot. 1999, 83, 459–469. [Google Scholar] [CrossRef]
- Ramírez, D.A.; Bellot, J.; Domingo, F.; Blasco, A. Can Water Responses in Stipa Tenacissima L. during the Summer Season Be Promoted by Non-Rainfall Water Gains in Soil? Plant Soil 2007, 291, 67–79. [Google Scholar] [CrossRef]
- Balaguer, L.; Pugnaire, F.I.; Martínez-Ferri, E.; Armas, C.; Valladares, F.; Manrique, E. Ecophysiological Significance of Chlorophyll Loss and Reduced Photochemical Efficiency under Extreme Aridity in Stipa Tenacissima L. Plant Soil 2002, 240, 343–352. Plant Soil 2002, 240, 343–352. [Google Scholar] [CrossRef]
- Rey, A.; Pegoraro, E.; Oyonarte, C.; Were, A.; Escribano, P.; Raimundo, J. Impact of Land Degradation on Soil Respiration in a Steppe (Stipa Tenacissima L.) Semi-Arid Ecosystem in the SE of Spain. Soil Biol. Biochem. 2011, 43, 393–403. [Google Scholar] [CrossRef]
- Pilegaard, K.; Ibrom, A.; Courtney, M.S.; Hummelshøj, P.; Jensen, N.O. Increasing Net CO2 Uptake by a Danish Beech Forest during the Period from 1996 to 2009. Agric. For. Meteorol. 2011, 151, 934–946. [Google Scholar] [CrossRef]
- Ibrom, A.; Dellwik, E.; Flyvbjerg, H.; Jensen, N.O.; Pilegaard, K. Strong Low-Pass Filtering Effects on Water Vapour Flux Measurements with Closed-Path Eddy Correlation Systems. Agric. For. Meteorol. 2007, 147, 140–156. [Google Scholar] [CrossRef]
- Fratini, G.; Ibrom, A.; Arriga, N.; Burba, G.; Papale, D. Relative Humidity Effects on Water Vapour Fluxes Measured with Closed-Path Eddy-Covariance Systems with Short Sampling Lines. Agric. For. Meteorol. 2012, 165, 53–63. [Google Scholar] [CrossRef]
- Webb, E.K.; Pearman, G.I.; Leuning, R. Correction of Flux Measurements for Density Effects Due to Heat and Water Vapour Transfer. Quart. J. R. Meteoro Soc. 1980, 106, 85–100. [Google Scholar] [CrossRef]
- Kowalski, A.S.; Anthoni, P.M.; Vong, R.J.; Delany, A.C.; Maclean, G.D. Deployment and Evaluation of a System for Ground-Based Measurement of Cloud Liquid Water Turbulent Fluxes. J. Atmos. Ocean. Technol. 1997, 14, 468–479. [Google Scholar] [CrossRef]
- McMillen, R.T. An Eddy Correlation Technique with Extended Applicability to Non-Simple Terrain. Bound. Layer. Meteorol. 1988, 43, 231–245. [Google Scholar] [CrossRef]
- Wilson, K.; Goldstein, A.; Falge, E.; Aubinet, M.; Baldocchi, D.; Berbigier, P.; Bernhofer, C.; Ceulemans, R.; Dolman, H.; Field, C.; et al. Energy Balance Closure at FLUXNET Sites. Agric. For. Meteorol. 2002, 113, 223–243. [Google Scholar] [CrossRef]
- Twine, T.E.; Kustas, W.P.; Norman, J.M.; Cook, D.R.; Houser, P.R.; Meyers, T.P.; Prueger, J.H.; Starks, P.J.; Wesely, M.L. Correcting Eddy-Covariance Flux Underestimates over a Grassland. Agric. For. Meteorol. 2000, 103, 279–300. [Google Scholar] [CrossRef]
- AppEEARS Team. Application for Extracting and Exploring Analysis Ready Samples (AppEEARS). 2020. Available online: https://appeears.earthdatacloud.nasa.gov/ (accessed on 22 May 2024).
- Savitzky, A.; Golay, M.J. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Sanz, E.; Almeida-Ñaulay, A.F.; Díaz-Ambrona, C.G.H.; Mínguez, S.Z.; Tarquis, A.M. Joint Multiscale Dynamics in Soil–Vegetation–Atmosphere Systems: Multifractal Cross-correlation Analysis of Arid and Semiarid Rangelands. Vadose Zone J. 2025, 24, e20374. [Google Scholar] [CrossRef]
- Monteith, J.L. Solar Radiation and Productivity in Tropical Ecosystems. J. Appl. Ecol. 1972, 9, 747. [Google Scholar] [CrossRef]
- Noilhan, J.; Mahfouf, J.-F. The ISBA Land Surface Parameterisation Scheme. Glob. Planet. Change 1996, 13, 145–159. [Google Scholar] [CrossRef]
- Noilhan, J.; Planton, S. A Simple Parameterization of Land Surface Processes for Meteorological Models. Mon. Wea. Rev. 1989, 117, 536–549. [Google Scholar] [CrossRef]
- Kustas, W.P.; Nieto, H.; Morillas, L.; Anderson, M.C.; Alfieri, J.G.; Hipps, L.E.; Villagarcía, L.; Domingo, F.; Garcia, M. Revisiting the Paper “Using Radiometric Surface Temperature for Surface Energy Flux Estimation in Mediterranean Drylands from a Two-Source Perspective.”. Remote Sens. Environ. 2016, 184, 645–653. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Amer J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability Distributions of Soil Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef]
- Zhou, Y.; Wu, X.; Ju, W.; Chen, J.M.; Wang, S.; Wang, H.; Yuan, W.; Andrew Black, T.; Jassal, R.; Ibrom, A.; et al. Global Parameterization and Validation of a Two-leaf Light Use Efficiency Model for Predicting Gross Primary Production across FLUXNET Sites. JGR Biogeosci. 2016, 121, 1045–1072. [Google Scholar] [CrossRef]
- Calvet, J.-C.; Noilhan, J.; Bessemoulin, P. Retrieving the Root-Zone Soil Moisture from Surface Soil Moisture or Temperature Estimates: A Feasibility Study Based on Field Measurements. J. Appl. Meteor. 1998, 37, 371–386. [Google Scholar] [CrossRef]
- Kustas, W.P.; Norman, J.M. Use of Remote Sensing for Evapotranspiration Monitoring over Land Surfaces. Hydrol. Sci. J. 1996, 41, 495–516. [Google Scholar] [CrossRef]
- Bandini, F.; Lopez-Tamayo, A.; Merediz-Alonso, G.; Olesen, D.; Jakobsen, J.; Wang, S.; Garcia, M.; Bauer-Gottwein, P. Unmanned aerial vehicle observations of water surface elevation and bathymetry in the cenotes and lagoons of the Yucatan Peninsula, Mexico. Hydrogeol. J. 2018, 26, 2213–2228. [Google Scholar] [CrossRef]
- Köppl, C.J.; Malureanu, R.; Dam-Hansen, C.; Wang, S.; Jin, H.; Barchiesi, S.; Sandí, J.M.S.; Muñoz-Carpena, R.; Johnson, M.; Durán-Quesada, A.M.; et al. Hyperspectral reflectance measurements from UAS under intermittent clouds: Correcting irradiance measurements for sensor tilt. Remote Sens. Environ. 2021, 267, 112719. [Google Scholar] [CrossRef]
- Choudhury, B.J. Multispectral Satellite Observations for Arid Land Studies. ISPRS J. Photogramm. Remote Sens. 1992, 47, 101–126. [Google Scholar] [CrossRef]
- Hulley, G.C.; Gottsche, F.M.; Rivera, G.; Hook, S.J.; Freepartner, R.J.; Martin, M.A.; Cawse-Nicholson, K.; Johnson, W.R. Validation and Quality Assessment of the ECOSTRESS Level-2 Land Surface Temperature and Emissivity Product. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–23. [Google Scholar] [CrossRef]
- Anderson, M.C.; Zolin, C.A.; Sentelhas, P.C.; Hain, C.R.; Semmens, K.; Tugrul Yilmaz, M.; Gao, F.; Otkin, J.A.; Tetrault, R. The Evaporative Stress Index as an Indicator of Agricultural Drought in Brazil: An Assessment Based on Crop Yield Impacts. Remote Sens. Environ. 2016, 174, 82–99. [Google Scholar] [CrossRef]
- Pateromichelaki, I.M. Modelling of Interactions within the Soil–Vegetation–Atmosphere Continuum in a Coffee Plantation in Costa Rica. Master’s Thesis, Technical University of Denmark, Department of Environmental Engineering, Lyngby, Denmark, 2020. [Google Scholar]
- Fisher, J.B.; Lee, B.; Purdy, A.J.; Halverson, G.H.; Dohlen, M.B.; Cawse-Nicholson, K.; Wang, A.; Anderson, R.G.; Aragon, B.; Arain, M.A.; et al. ECOSTRESS: NASA’s Next Generation Mission to Measure Evapotranspiration From the International Space Station. Water Resour. Res. 2020, 56, e2019WR026058. [Google Scholar] [CrossRef]
| Parameter | Description | Value | Range | Unit | Reference |
|---|---|---|---|---|---|
| The force-restore thermal coefficient for saturated soil | * | [4.00, 10.00] | 10−6·K·m−2·J−1 | [56] | |
| b | The slope of the retention curve for the “force-restore” thermal coefficient | * | [4.61, 6.91] | (-) | [56] |
| n | The shape parameter of the van Genuchen ([58]) soil–water retention relationship | 1.89 | [1.01, 2.50] | (-) | [59] |
| Saturated volumetric soil moisture | 0.410 | [0.360, 0.460] | m3·m−3 | [59] | |
| Residual volumetric soil moisture | 0.065 | [0.034, 0.100] | m3·m−3 | [59] | |
| Saturated hydraulic conductivity | * | [1.00, 2.00] | mm·h−1 | [59] | |
| Maximum light use efficiency | 1.69 | [0, 5.00] | gC·m−2·MJ−1 | [60] | |
| Maximum soil water content | * | [1.00, 2.50] | 10−3 m | [61] | |
| The “force-restore” thermal coefficient for vegetated surface | * | [1.00, 4.00] | 10−6·K·m−2·J−1 | [61] |
| In Situ | Adjusted MODIS | ||||
|---|---|---|---|---|---|
| Parameters | Csat (10−6·K·m−2·J−1) | 9.711 | 9.595 | ||
| b (-) | 5.817 | 5.632 | |||
| SWCmax (m3·m−3) | 1.082 | 2.292 | |||
| Cveg (10−6·K·m−2·J−1) | 2.306 | 2.190 | |||
| Ks (mm·h−1) | 1.949 | 1.016 | |||
| RMSE | NRMSE (%) | RMSE | NRMSE (%) | ||
| Validation | LST (°C) | 2.15 | 8.43 | 1.99 | 7.84 |
| LE (W·m−2) | 26.15 | 10.49 | 28.21 | 11.32 | |
| Rn (W·m−2) | 53.12 | 5.72 | 52.71 | 5.67 | |
| H (W·m−2) | 49.05 | 7.52 | 50.90 | 7.81 | |
| SWC (m3·m−3) | 1.99 | 11.03 | 1.19 | 6.59 | |
| Timescale | Statistics | LST Mix (°C) | LST Soil (°C) | LST Canopy (°C) | LE (W·m−2) | Rn (W·m−2) | H (W·m−2) | GPP (µmolC·s−1·m−2 or gC·d−1·m−2) | SWC (m3·m−3) |
|---|---|---|---|---|---|---|---|---|---|
| Half-hourly | RMSE | 1.99 | 2.63 | 2.10 | 25.97 | 52.71 | 50.9 | 1.87 | 1.19 |
| MAE (%) | 1.59 | 2.09 | 1.65 | 16.54 | 39.56 | 34.42 | 1.46 | 0.77 | |
| bias | 0.23 | 1.12 | 0.01 | −1.37 | 29.81 | 15.19 | −0.18 | −0.05 | |
| R2 | 0.90 | 0.89 | 0.90 | 0.75 | 0.97 | 0.89 | 0.46 | 0.95 | |
| NRMSE (%) | 7.84 | 8.94 | 8.54 | 10.81 | 5.67 | 7.81 | 24.03 | 6.59 | |
| Daily | RMSE | 0.58 | 1.29 | 0.56 | 11.52 | 31.17 | 19.21 | 1.09 | 1.12 |
| MAE (%) | 0.47 | 1.19 | 0.45 | 9.42 | 29.81 | 15.89 | 0.87 | 0.76 | |
| bias | 0.23 | 1.12 | −0.01 | −1.38 | 29.81 | 15.2 | −0.82 | −0.04 | |
| R2 | 0.96 | 0.94 | 0.96 | 0.50 | 0.97 | 0.89 | 0.40 | 0.96 | |
| NRMSE (%) | 5.68 | 12.22 | 5.45 | 21.88 | 16.93 | 13.10 | 37.33 | 6.53 |
| Revisit Frequency | n | Optimized Parameter Values | Simulation Performance (RMSE—∆ vs. 1-Day) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Csat (10−6·K·m−2·J−1) | b (-) | SWCmax (m3·m−3) | Cveg (10−6·K·m−2·J−1) | Ks (mm·h−1) | LST (°C) | LE (W·m−2) | Rn (W·m−2) | H (W·m−2) | SWC (m3·m−3) | ||
| 1 day | 56 | 9.595 | 5.632 | 2.292 | 2.194 | 1.016 | 1.99 | 28.21 | 52.71 | 50.89 | 1.19 |
| 2 days | 28 | 9.004 | 5.586 | 2.308 | 2.383 | 1.016 | 2.10 (+0.11 +5.50%) | 28.16 (−0.05 −0.18%) | 52.97 (+0.26 +0.49%) | 50.22 (−0.67 −1.32%) | 1.20 (+0.01 +0.84%) |
| 4 days | 14 | 9.571 | 6.401 | 2.439 | 2.397 | 1.083 | 2.18 (+0.19 +9.50%) | 28.01 (−0.2 −0.71%) | 52.88 (+0.17 +0.32%) | 50.16 (−0.73 −1.43%) | 1.29 (+0.1 +8.40%) |
| 6 days | 9 | 8.978 | 6.797 | 2.352 | 2.505 | 1.001 | 2.25 (+0.26 +13.10%) | 28.26 (+0.05 +0.18%) | 52.93 (+0.22 +0.42%) | 51.32 (+0.43 +0.84%) | 1.25 (+0.06 +5.04%) |
| 8 days | 7 | 9.514 | 6.604 | 2.490 | 2.403 | 1.173 | 2.20 (+0.21 +10.60%) | 27.77 (−0.44 −1.56%) | 52.93 (+0.22 +0.42%) | 50.15 (−0.74 −1.45%) | 1.32 (+0.13 +10.92%) |
| 16 days | 4 | 9.801 | 4.849 | 2.361 | 3.906 | 1.880 | 3.15 (+1.16 +58.30%) | 27.67 (−0.54 −1.91%) | 60.10 (+7.39 +14.02%) | 81.33 (+30.44 +59.82%) | 1.44 (+0.25 +21.01%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Riba, A.; Garcia, M.; Tarquís, A.M.; Domingo, F.; Antala, M.; Feng, S.; Liu, J.; Johnson, M.S.; Kim, Y.; Wang, S. Integrating Remotely Sensed Thermal Observations for Calibration of Process-Based Land-Surface Models: Accuracy, Revisit Windows, and Implications in a Dryland Ecosystem. Remote Sens. 2025, 17, 3630. https://doi.org/10.3390/rs17213630
Riba A, Garcia M, Tarquís AM, Domingo F, Antala M, Feng S, Liu J, Johnson MS, Kim Y, Wang S. Integrating Remotely Sensed Thermal Observations for Calibration of Process-Based Land-Surface Models: Accuracy, Revisit Windows, and Implications in a Dryland Ecosystem. Remote Sensing. 2025; 17(21):3630. https://doi.org/10.3390/rs17213630
Chicago/Turabian StyleRiba, Arnau, Monica Garcia, Ana M. Tarquís, Francisco Domingo, Michal Antala, Sijia Feng, Jun Liu, Mark S. Johnson, Yeonuk Kim, and Sheng Wang. 2025. "Integrating Remotely Sensed Thermal Observations for Calibration of Process-Based Land-Surface Models: Accuracy, Revisit Windows, and Implications in a Dryland Ecosystem" Remote Sensing 17, no. 21: 3630. https://doi.org/10.3390/rs17213630
APA StyleRiba, A., Garcia, M., Tarquís, A. M., Domingo, F., Antala, M., Feng, S., Liu, J., Johnson, M. S., Kim, Y., & Wang, S. (2025). Integrating Remotely Sensed Thermal Observations for Calibration of Process-Based Land-Surface Models: Accuracy, Revisit Windows, and Implications in a Dryland Ecosystem. Remote Sensing, 17(21), 3630. https://doi.org/10.3390/rs17213630








