Abstract
Permafrost is one of the crucial components of the cryosphere, covering about 25% of the global continental area. The active layer thickness (ALT), as the main site for heat and water exchange between permafrost and the external atmosphere, its changes significantly impact the carbon cycle, hydrological processes, ecosystems, and the safety of engineering structures in cold regions. This study constructs a Stefan CatBoost-ET (SCE) model through machine learning and Blending integration, leveraging multi-source remote sensing data, the Stefan equation, and measured ALT data to focus on the ALT in the Qinghai-Tibet Plateau (QTP). Additionally, the SCE model was verified via ten-fold cross-validation (MAE: 20.713 cm, RMSE: 32.680 cm, R2: 0.873, and MAPE: 0.104), and its inversion of QTP’s ALT data from 1958 to 2022 revealed 1998 as a key turning point with a slow growth rate of 0.25 cm/a before 1998 and a significantly increased rate of 1.26 cm/a afterward. Finally, based on multiple model input factor analysis methods (SHAP, Pearson correlation, and Random Forest Importance), the study analyzed the ranking of key factors influencing ALT changes. Meanwhile, the importance of Stefan equation results in SCE model is verified. The research results of this paper have positive implications for eco-hydrology in the QTP region, and also provide valuable references for simulating the ALT of permafrost.
Keywords:
active layer thickness; ALT; permafrost; machine learning; blending; Qinghai-Tibet Plateau 1. Introduction
Permafrost is defined as soil or rock that remains at or below 0 °C for at least two consecutive years, covering about 25% of the global land surface [1,2,3,4].The permafrost layer is composed of two parts: the active layer that freezes in winter and thaws in the following summer, and the perennially frozen layer that remains in a frozen state throughout the year. Changes of the active layer are one of the most important indicators characterizing the degradation of permafrost. Currently, the World Meteorological Organization has identified the ALT as an essential variable for monitoring the status of permafrost [5]. In recent years, the intensification of global warming has led to rising permafrost temperature, shrinking permafrost area and thickening of active layer [6,7]. These changes have resulted in the frequent occurrence of geological disasters such as surface collapse, subsidence, and retrogressive thaw slumps, which have caused significant losses to infrastructure in permafrost regions worldwide [8,9]. Over the past 50 years, climate change has continuously reduced the extent of permafrost in the Arctic and high-latitude mountainous areas. The continuous increase in the temperature of the permafrost layer has also led to a thickening trend of the ALT [10,11]. The increase of ALT has led to an increase in the activity of soil microorganisms in the permafrost, and a large amount of soil organic carbon has been decomposed and released into the atmosphere, thereby affecting the carbon cycle process of the earth system and accelerating the intensification of global warming [12,13,14]. Therefore, studying the changes of ALT is not only critical for assessing the degree of permafrost degradation, but also has important significance for the research on multiple aspects of the Earth’s ecosystem, such as the carbon cycle, hydrology, climate, and vegetation.
Currently, ALT data are mainly obtained through field investigation such as drilling, trenching, and geophysical physical detection [15,16]. While field investigations yield precise and dependable in situ data, their use is often limited by the harsh environmental conditions in permafrost regions [17]. With the rapid advancement of remote sensing technology in recent years and the establishment of the permafrost monitoring network, researchers can acquire permafrost observation data and a substantial amount of high-resolution remote sensing data through a range of methods. These data are utilized to develop diverse models for simulating and studying the distribution, the mean annual ground temperature of permafrost, as well as the distribution and variations of ALT within a specific area [18,19,20]. The existing models predominantly include empirical models, physical mechanism models, and machine learning models. For example, the Kudryavtsev method and the Stefan method are commonly employed empirical models [21,22,23]. Empirical models are characterized by their simplicity and efficiency, and they can adapt to different environmental conditions, thus being widely used in the field of permafrost research. However, these models often fail to accurately represent the freeze-thaw cycles of permafrost and the processes of heat and water exchange between soil and atmosphere, which may result in potential lagged effect [24]. Physical mechanism models are also commonly for simulating permafrost extent and ALT, and they generally offer a relatively high level of accuracy. Widely applied models include the Community Land Model (CLM) [25] and the Noah Land Surface Model [26]. With the continuous development of artificial intelligence technology in the fields of remote sensing and geosciences, a variety of machine learning algorithms have been extensively utilized in the simulation and prediction of ALT [27,28,29]. Commonly used machine learning algorithms include models such as Support Vector Machines [30], Random Forest [31] and Extreme Gradient Boosting [32]. Machine learning enables the utilization of numerous permafrost-related environmental factors for model building, without being constrained by the input variables and model parameters of physical and empirical models [33]. It offers convenience and flexibility in application, and the simulation accuracy is relatively high. Nevertheless, it lacks an internal mechanism for the freeze-thaw cycle, and the computational process is difficult to interpret. Moreover, it is sensitive to the quantity and quality of the training dataset. Furthermore, in other studies, deep Learning (DL) models have been employed to simulate the distribution of permafrost and the changes of ALT within a specific region. Liu et al. (2022) utilized Random Forest, Convolutional Neural Networks, and Long Short-Term Memory to estimate the interannual variations of ALT and the seasonal thawing depth on the Qinghai-Tibet Plateau, and they directly compared the performance of machine learning and deep learning models [34]. With the continuous evolution of machine learning algorithms, simulating ALT using machine learning methods based on remote sensing data while comprehensively considering various environmental factors has become one of the focal issues in the research fields of permafrost and climate change, and it also represents the future development trend in permafrost research.
Numerous researchers have conducted extensive studies on the simulation and prediction of ALT. However, differences in input data, simulation methods, and other factors, have introduced significant uncertainties. Further research is still required regarding the spatiotemporal variations of ALT and its influencing factors. When applied to large-scale simulations, empirical models often encounter difficulties in obtaining certain parameters, and the calculation process is relatively complex, resulting in significant errors in the outcomes [20,23]. Due to the limitation of the resolution of input remote sensing data and observation data, the simulation accuracy of physical mechanism model is relatively low in some areas lacking permafrost observation. Additionally, the accuracy of physical mechanism models is often limited by the resolution of input remote sensing and observational data, particularly in regions with sparse permafrost observation data, resulting in lower simulation accuracy [35]. Machine learning models, as typical “black boxes,” lack physical mechanism support. Additionally, most machine learning studies employ a single type of model, and variations in input parameters leading to discrepancies. Therefore, different simulation methods, data sources, model parameters and spatio-temporal resolution of data in many studies lead to obvious differences in the spatial distribution and variation of simulated ALT. In addition, the topography of the QTP region is complex and there is a lack of high-resolution meteorological data and suitable models, resulting in the simulation of ALT remaining a controversial topic.
To address the aforementioned issues, this study utilizes multi-source remote sensing data calibrated using meteorological station data from 1958 to 2022. By leveraging the measured ALT data and building upon the Stefan empirical equation, a Stefan-CatBoost-ET ALT (SCE-ALT) model is constructed through the comparison, verification, and integration of multiple machine learning models. Simultaneously, the accuracy of the simulation results of the SCE-ALT model is validated, and a spatiotemporal analysis of the ALT in the QTP region is conducted. Additionally, various factors influencing ALT are explored individually. The SCE-ALT model established based on the Stefan empirical equation in this study capitalizes on the advantages of multiple machine learning models through integration, enhancing the simulation capability of machine learning for ALT. The research results have significant implications for water conservation, climate regulation, and ecological security in the QTP region, and also provide certain references for simulating the active layer thickness of permafrost. Moreover, the research findings contribute to a better under-standing of the permafrost responds.
2. Study Area
The Qinghai-Tibet Plateau (QTP), which constitutes the major part of the Third Pole, is characrized by complex and diverse topography. It is extensively scattered with mountains and predominantly comprises mountainous areas and plateaus. With a rugged terrain, its average elevation exceeds 4000 m. The annual mean temperature in the QTP region ranges between −3.1 °C and 4.4 °C, and the annual average precipitation amounts to between 103 mm and 694 mm [36]. At the same time, the soil in the QTP region is poor and the soil layer is relatively thin, making the ecological environment extremely fragile. [37].
QTP is a typical cryosphere comprising a dynamic system of glaciers, snow accumulations, and permafrost, which collectively form a critical component of the global cryospheric system [8]. As the largest permafrost region in mid-low latitude areas globally, the QTP is covered with approximately 1.06 × 106 km2 of permafrost, accounting for roughly 40% of its total area and representing a unique geological feature shaped by the plateau’s high-altitude and cold-climate conditions [29]. Among them, 40% of the permafrost is classified as especially warm and unstable (with a ground temperature > −0.5 °C), characterized by thin active layers, high ice content, and marginal thermal stability, which render it particularly vulnerable to small-scale temperature fluctuations [38,39]. The relatively warm permafrost is highly susceptible to the influences of climate change and ecosystem perturbations (both natural and anthropogenic factors included) [40,41]. The permafrost degradation trend in the QTP region is accelerating, including rising ground temperatures, thickening active layers, and soil subsidence caused by freeze-thaw cycles. These processes collectively pose significant threats to the stability of the plateau’s ecological and hydrological systems [24].
3. Data and Method
3.1. Data
3.1.1. Remote Sensing Data and Meteorological Data
TerraClimate is a high-precision dataset based on the high-spatial resolution climate normal of the WorldClim dataset, combined with CRU TS4.0 and JRA-55 data, using climate-assisted interpolation technology. TerraClimate is often used in remote areas where ground observation data is extremely scarce. Interpolation algorithms are used to fill the observational data gaps, thus ensuring data integrity and consistency, and improving the availability and accuracy of data on a global scale [42]. The TerraClimate data spans from 1958 to 2023, with a temporal resolution of months and a spatial resolution of about 4 km. This study mainly used the precipitation, temperature max and temperature min data products of the TerraClimate dataset.
ERA5-Land is the fifth generation of global climate and Weather reanalysis datasets from the European Centre For Medium-Range Weather Forecasts (ECMWF). ERA5-Land is obtained by taking atmospheric variable data of ERA5 as input, and then using modified Land surface hydrological models HTESSEL and CY45R1 [43]. ERA5-Land has a higher spatial resolution than ERA5, with a horizontal resolution of up to 0.1° [44]. This study mainly utilized the following data from the ERA5-Land dataset: Total Precipitation, Skin Temperature, Leaf Area Index Vegetation (Low and High), Snow Depth, Surface Net Solar Radiation, and Volumetric Soil Water Layer (100–200 cm).
Soil organic carbon content data were obtained from ISRIC-World Soil Information (https://files.isric.org/soilgrids/latest/data_aggregated/5000m/soc/, accessed on 26 October 2024). This dataset includes the soil organic carbon content of various depth intervals, including 0–5 cm, 5–15 cm, 15–30 cm, 30–60 cm, 60–100 cm, and 100–200 cm, with a spatial resolution of 5 km × 5 km [45].
3.1.2. Active Layer Thickness (ALT) Data and Permafrost Data
This study collected 596 Active Layer thickness (ALT) data. Among them, 40 data were obtained from the publicly available dataset Circumpolar Active Layer Monitoring Network (https://www2.gwu.edu/~calm/data/north.htm, accessed on 14 September 2024) [17]. The rest of the measured data are derived from the previously published literatures [46,47,48,49,50,51,52]. All ALT data used in this study are shown in Figure 1. In addition, this study used the permafrost distribution map developed by Zou et al. (2017) [50] as the basis for distinguishing permafrost and non-permafrost areas on the Tibetan Plateau. This data is based on the Top Temperature of Permafrost (TTOP) model to simulate the distribution of permafrost, which is widely applied due to its high simulation accuracy [50].
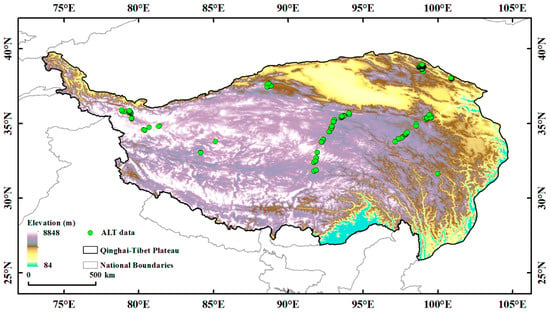
Figure 1.
Geographical sketch map of the study area.
3.1.3. Meteorological Station Data
Based on the “Daily Data set of Basic Meteorological Elements of China National Ground Meteorological Stations (V3.0)” (https://data.cma.cn/, accessed on 12 October 2024), this study utilized the daily observation data of meteorological stations on the QTP from 1958 to 2010 to correct the temperature of the QTP. The measured data of precipitation used the “Daily adjusted Precipitation dataset of Qinghai-Tibet Plateau meteorological stations (1981–2017)” stablished by Wang et al. [53]. This data is used to solve the problem of precipitation deviation in the QTP. Based on the dew point temperature threshold, the daily precipitation pattern division scheme was constructed to correct the daily precipitation observation data of 78 meteorological observation stations in the QTP [53]. In this study, meteorological data of stations in the QTP region were processed as monthly scale data by numerical statistics, and then a correction formula based on remote sensing data was constructed by using the processed data.
3.2. Method
3.2.1. Extra Trees
The model architecture of Extra Trees is similar to that of Random Forest, both of which are composed of multiple decision trees (Figure 2). The feature of Extra Trees model is that when constructing each decision tree, the original training set is directly used for training, which is different from the way that Random Forest model randomly extracts samples from the original data set to generate sub-data sets for training [54]. Extra Trees model introduces additional randomness by selecting a split point for each feature of the sample to divide, which makes the model have stronger randomness, better model efficiency and reduced risk of overfitting ability compared with Random Forest [55].
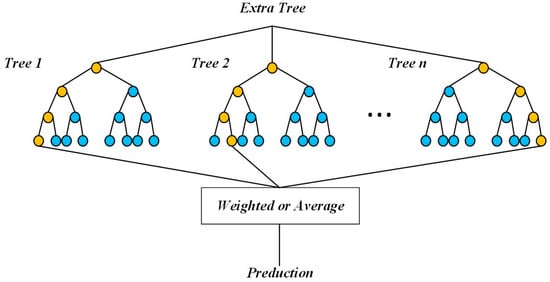
Figure 2.
Structural Diagram of Extra Trees.
3.2.2. CatBoost
CatBoost is a machine learning model derived from Gradient Boosting Decision Tree (GBDT), which employs oblivious trees and builds decision tree by gradient boosting iteration [56]. CatBoost initially establishes the basic model, and adjusts the parameters of the decision tree such as nodes and layers after several iterations to minimize the error (Figure 3). The CatBoost model selects the optimal parameter combination through cross-validation, and optimizes the model by adjusting the parameters. Additionally, the model incorporates adaptive learning rate, process the outliers in the training data, improve the generalization ability of the model, and effectively improve the accuracy of the algorithm [57].
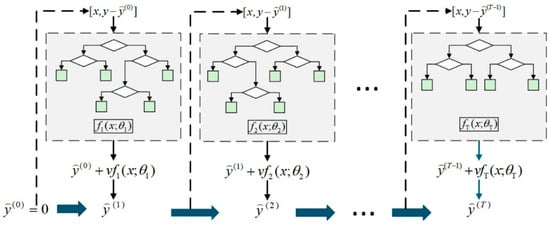
Figure 3.
Structural Diagram of CatBoost.
3.2.3. Blending
Blending is a simple and efficient machine learning model integration strategy, which essentially combines the prediction results of multiple different machine learning models twice to obtain better prediction performance. Blending has two layers of algorithms: Level 1 (multiple Strong Learner) and Level 2 (one Meta Learner). Blending trains multiple machine learning models at Level 1 and is responsible for fitting the relationship between data and features, then combines the output prediction results into a new feature matrix, and finally learns and predicts on the new feature matrix of Meta Learner on level 2 [58].
Compared to the Stacking method, Blending has a simpler process, lower computational complexity, and faster integration. Especially when dealing with small amounts of data, integration results can be quickly verified [59]. In addition, blending can effectively integrate the advantages of different machine learning models, avoid the shortcomings of a single machine learning model, and effectively improve performance indicators such as prediction accuracy and stability of the final model [60].
3.3. Feature Selection
In this study, Land Surface Temperature (LST), Degree Days freezing (DDF), Degree days thawing (DDT), Precipitation, Soil carbon content, Snow Depth and Volumetric soil Water Layer 4 (Soil layer 100–289 cm) were selected and used as model input features to build machine learning models to simulate ALT in the QTP region.
The positive and negative accumulated temperature indices, i.e., DDF and DDF were calculated to represent the accumulation of energy in warm and cold seasons respectively. DDF and DDT reflect the depth and intensity of freeze-thaw processes, and have been widely used to estimate soil freezing depth and ALT, etc. [61]. This study calculated the DDF and DDT using modified LST data. DDF refers to the total cumulative temperature of the air or ground temperature below 0 °C from July to June of the next year. DDT refers to the total cumulative temperature of the air or ground temperature above 0 °C, and the calculate from January to December.
The calculation formulas of DDF and DDT are as follows:
where and represents the daily land surface temperature below and above 0 °C, respectively, through a year.
Solar radiation and precipitation are important factors affecting ALT changes by influencing the heat exchange between the surface, atmosphere, and soil. The occurrence of extreme precipitation events leads to an increase in soil moisture, which significantly enhances the soil’s thermal conductivity, causing an increase in soil temperature and the thawing depth [62]. Additionally, the amount of precipitation can alter the soil moisture content, endowing the soil with different thermal conductivities, thus having an impact on ALT. Snow cover plays a certain role in thermal insulation. It restricts the heat loss from the ground surface in winter and regulates the changes in the surface heat state, which in turn affects the variation of ALT [24]. Snow cover also exerts an important influence on the soil freeze-thaw process and the soil carbon decomposition process. An increase in snow cover can promote the warming of deep soil (≥0.5 m) and soil respiration, while inhibiting the decomposition of surface soil (≤0.2 m), especially in colder climate regions (with an annual average temperature ≤ −10 °C) [63].
Vegetation can reduce radiation absorption and interact with the atmosphere. In summer, it mainly reduces transfer from the atmosphere to the ground, while in winter, it retains heat at the ground surface [23]. The Leaf Area Index quantifies the quantity of leaf area in an ecosystem. It is a key variable in processes such as vegetation photosynthesis, respiration, and precipitation interception, and it is also an important indicator for measuring the growth status of vegetation. Moreover, the growth of vegetation changes the moisture content of both the surface and deep soil layers, which will affect the heat conduction performance of the soil and thus influence the changes in ALT [64,65]. The organic layer in the soil can change the thermal conductivity and water retention of the soil, and reduce the heat transfer from the surface to the underlying soil [66]. In winter, the organic layer can effectively prevent the rapid transfer of low surface temperature to the lower soil layers, providing thermal insulation for the lower soil layers and slowing down the soil freezing process. In summer, it can block the excessive heat brought by solar radiation from being conducted downward, preventing the overheating of the lower soil layers, thereby influencing the changes in ALT [67,68]. Therefore, the regulatory effect of the organic layer will change the melting rate of permafrost, and further affect the regional ecosystem balance, water resource distribution, and geological stability, etc. [69].
3.4. Stefan CatBoost-ET Model
This study is based on multi-source remote sensing data, Stefan equation and ALT measured data. By CatBoost, Random Forest, Extremely randomized trees, Light Gradient Boosting, Gradient Boosting, and Extreme Gradient Boosting and other common machine learning model methods to simulate, and carry out cross-integration for models with higher simulation accuracy, and carry out one-by-one accuracy verification for all integrated models by the ten-fold cross-verification method. Finally, the CatBoost and ET models were used as base models, and the Blending method was applied to fuse the models to construct the Stefan CatBoost-ET ALT (SCE-ALT) Model. Based on the results of the SCE-ALT model, the spatial distribution and change trends of ALT in the QTP were analyzed, and the input features of the model were discussed using the Person, Random Forest Important, and SHAP methods. The specific process is shown in Figure 4.
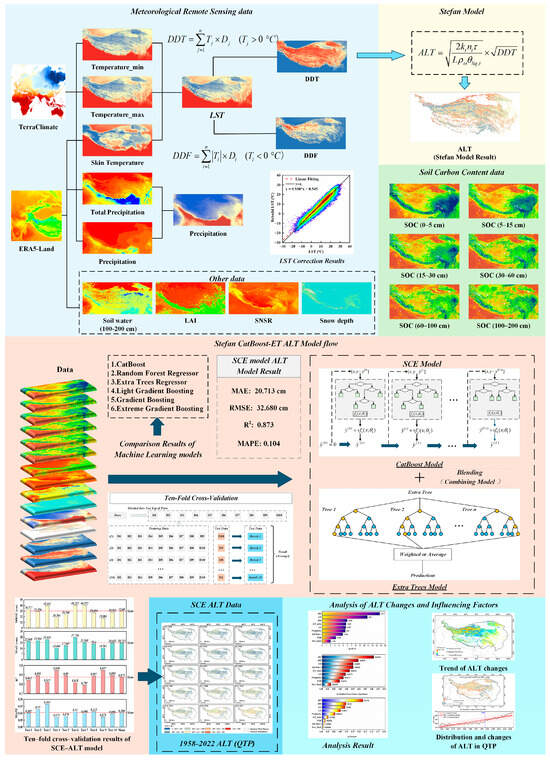
Figure 4.
SCE-ALT Model Flowchart.
3.5. Data Processing
Factors such as climate, snow cover, vegetation, soil temperature, and humidity can all influence the changes in ALT. These influencing factors can be directly obtained through remote sensing or indirectly retrieved. To ensure data consistency, all datasets were spatially harmonized to a 1 km resolution using bilinear resampling. Existing remote sensing data have demonstrated high accuracy in global-scale monitoring and analysis, and can provide important information support for many fields [70]. However, limited by the special geographical environment and climatic conditions in alpine regions, as well as complex topographical features and other factors, the accuracy of remote sensing data in this area is not satisfactory, and it is difficult to meet the requirements of high-precision research and applications [71] Therefore, in this study, relatively easily accessible ground temperature and precipitation data were selected to correct the existing remote sensing data.
In this study, based on the measured LST data, the Temperature (including Temperature Max and Temperature Min) from the TerraClimate dataset, and the Skin Temperature from the ERA5 Land dataset, the LST data in the QTP region were corrected by linear fitting. Specifically, both the ERA5 and TerraClimate datasets were resampled to 1 km resolution using bilinear interpolation before being incorporated into the analysis. The specific formula is as follows:
In this study, according to the measured Precipitation data, and based on the Precipitation data of the TerraClimate dataset and the Total Precipitation data of the ERA5 Land dataset, the Precipitation in the QTP region was corrected by linear fitting. Specifically, both the ERA5 and TerraClimate datasets were resampled to 1 km resolution using bilinear interpolation before being incorporated into the analysis. The specific formula is as follows:
Based on the above formulas, the LST and Precipitation were corrected. The accuracy of the Rebuild data has a relatively obvious improvement compared with the original TerraClimate and ERA5 data (Figure 5). Among them, the MAE of the Rebuild LST data is 1.94 °C, the RMSE is 2.49 °C, and the R2 is 0.938. Compared with the Skin Temperature data of ERA5_Land, the MAE of the Rebuild LST data is reduced by 5.65 °C, the RMSE is reduced by 6.59 °C, and the R2 is increased by 0.155. Compared with the temperature data of TerraClimate, although the increase in R2 is not significant, the errors in MAE and RMSE are reduced (MAE: 2.45 °C, RMSE: 2.58 °C). In terms of precipitation, the accuracy of the Rebuild Precipitation data has been significantly improved. Compared with the ERA5 Land data, the MAE and RMSE are reduced by 368.73 mm and 393.59 mm respectively, and the R2 is increased by 0.13. Compared with the TerraClimate data, the MAE and RMSE are reduced by 24.66 mm and 26.99 mm respectively, and the R2 is increased by 0.03. According to the data reconstruction process and results, it is found that the TerraClimate data have higher accuracy than the ERA5 Land data, especially the precipitation data. In addition, the accuracy of the ERA5 Land Precipitation data in alpine mountainous areas is poor, which is consistent with the results of previous studies [72].
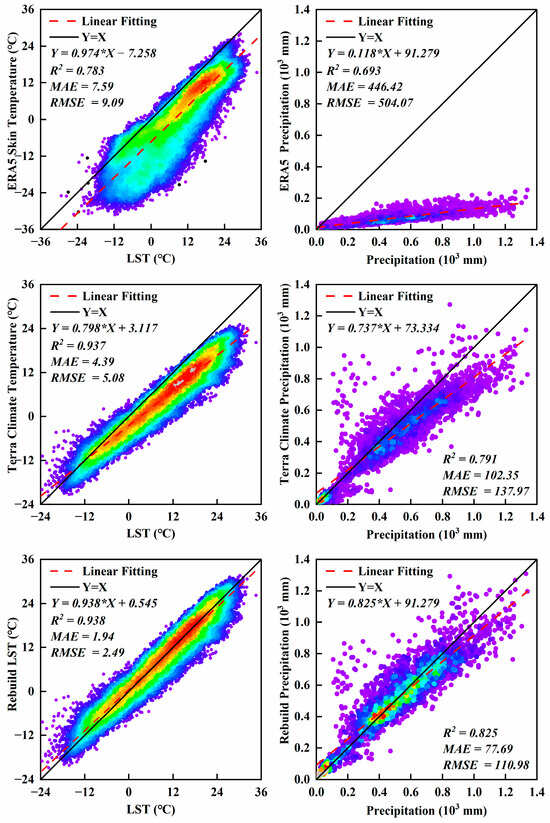
Figure 5.
Validation analysis of LST and Precipitation data results.
Based on the measured data from meteorological stations, the LST and Precipitation in the QTP were corrected, reducing the relative errors of the remote sensing data. This makes the results of the SCE-ALT model constructed in this study more consistent with the real values and enhances the scientific credibility of the research conclusions. The schematic diagrams of some of the corrected products in this study are as follows (Figure 6):
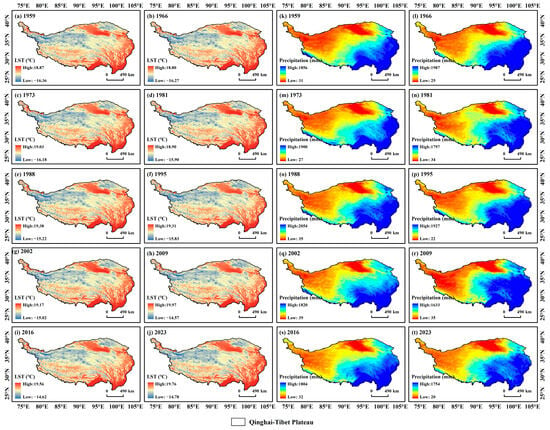
Figure 6.
The Results Display of LST and Precipitation Data.
In this study, the Stefan empirical equation was combined with the machine learning model to improve the simulation accuracy of the SCE-ALT model for the ALT in the QTP. The Stefan formula is relatively simple, mainly using parameters such as the soil thermal conductivity, bulk density, water content, as well as surface temperature or air temperature data. Due to the relatively small number of input parameters, and through continuous research and improvement, this method has been widely used to calculate the ALT. However, since the Stefan formula assumes that all the heat absorbed by the surface is used to melt the ice in the soil, without considering the heat consumption during soil thawing and the heat transfer from the freeze-thaw interface to the lower permafrost layer, there is a certain degree of uncertainty in its calculation results. The specific Stefan equation is as follows:
In the formula, represents the thermal conductivity coefficient of the thawed soil [W/(m·K)], DDT is the degree days thawing (°C·d); is the dry bulk density of the soil (kg/m3); is the soil water content.
Based on the field soil survey data, Li et al. [73] mapped the soil distribution in the QTP. In this study, based on the above-mentioned soil distribution map, the soils in the QTP are classified into five soil types, namely Gelisols, Aridisols, Mollisols, Inceptisols and Entisols, according to the United States Soil Taxonomy. Then, the parameters , and in the Stefan equation are assigned values respectively.
3.6. Model Accuracy Evaluation and Robustness Index
To verify the simulation accuracy of the model for ALT, Coefficient of Determination (R2), Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and Mean Absolute Percentage Error (MAPE) were selected to evaluate the model error. The calculation formula of the evaluation parameters is as follows:
In the formula, and represent the observed and simulated values, and n represents the sample size.
4. Result
4.1. ALT Simulation Results Using Multiple Machine Learning Models
In this study, six common and representative machine learning models were selected to simulate ALT in the QTP region. By analyzing the evaluation parameters of the results of various machine learning models (Table 1), it was found that different models exhibited their respective advantages in simulating the ALT. Among them, the CatBoost model stood out in terms of overall performance. Its R2 value reached 0.83, which was the highest among the six models. Meanwhile, its RMSE was 37.84 cm, the lowest among all the models, indicating that the CatBoost model had a strong fit for the ALT and a relatively small average degree of deviation. The Extra Trees model, however, performed the best in terms of MAE and MAPE. With an MAE of 25.27 cm and a MAPE of 0.13, it showed that this model had clear advantages in measuring the absolute error and relative error between the predicted values and the true values.

Table 1.
Comparison of Multiple Machine Learning Results.
In this study, models A (CatBoost), B (Random Forest) and C (Extra Trees) with the top three accuracy verification results were selected, and the above models were cross-integrated (Figure 7). Through the Blending integration method, models D (A, B, and C), E (A and C), F (B and C), and G (A and C) were constructed based on models A, B, and C. After conducting verification and analysis on the results of models A, B, C, D, E, F, and G, it can be seen that the four integrated models D, E, F, and G have improved in RMSE, MAE, R2, and MAPE compared with the three base models A, B, and C. Among these, model E achieved the highest overall accuracy, followed by model C and model F, while model G showed lower performance. During the integration process, model E has taken advantage of the superior performance of the CatBoost model in terms of R2 and RMSE, and has aggregated the good performance of the Extra Trees model in terms of MAE and MAPE, making model E the best-performing model in a comprehensive sense among many models. These comparison results demonstrate that the integration method can effectively improve the inversion results of the model, making the model results closer to the true values of ALT. At the same time, this study also proves to a certain extent that the number of integrated models is not the only factor determining the model accuracy. Only by integrating appropriate models can the inversion accuracy be significantly improved.
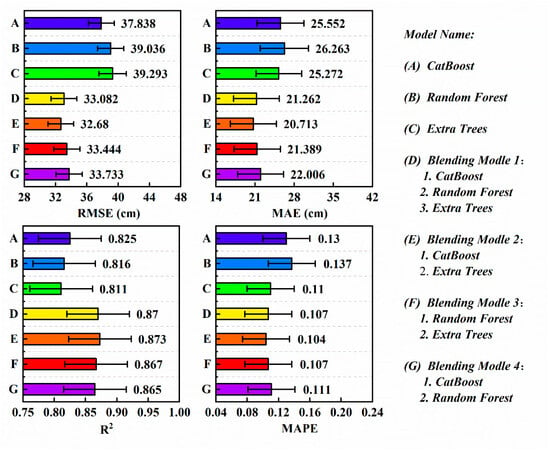
Figure 7.
Comparison of ten-fold cross results of SCE-ALT model.
In this study, to comprehensively evaluate the performance of the SCE model, the results of the SCE model were validated using ten-fold cross-validation. The ten-fold cross-validation method divides the data into ten equal parts on average. In turn, nine of these parts are used as training data, and one part is used as test data to examine the generalization ability of the model on unknown data. For each experiment of the ten-fold cross-validation, the evaluation parameters of the corresponding results will be calculated. Through numerical analysis of the evaluation parameters of the 10 results, the average value is calculated as the final result of the model accuracy. Based on the SCE-ALT model, ten-fold cross-validation was carried out (Figure 8). Finally, the MAE is 20.713 cm, the RMSE is 32.680 cm, the R2 is 0.873, and the MAPE is 0.104. In addition, the standard deviation (std) is used to measure the stability of the model performance. The std of MAE is 4.14 cm, the std of RMSE is 8.86 cm, the std of R2 is 0.05, and the std of MAPE is 0.03. The low standard deviation of the SCE indicates that during multiple cross-validation processes, the performance indicators of the model fluctuate slightly, verifying that the SCE-ALT model has high stability. Based on the above indicators, it can be concluded that the SCE-ALT model not only has high accuracy when inverting the ALT in the QTP, but also performs excellently in terms of stability, and can provide reliable data support and scientific basis for research and applications in related fields.
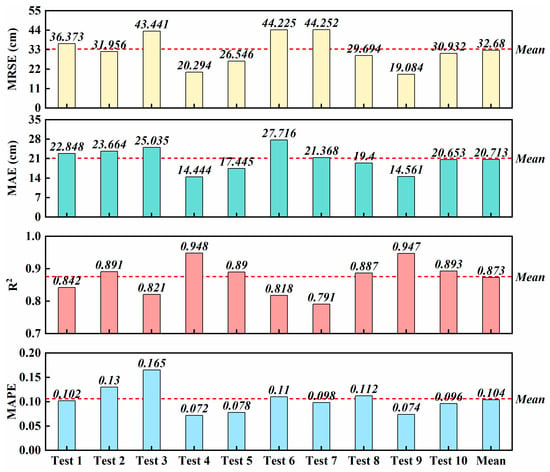
Figure 8.
Ten-fold cross-validation results of SCE-ALT model.
In this study, the input covariates (Precipitation and LST) have uncertainties such as observation errors, and error propagation analysis is further used to describe the cascade influence of variable uncertainties on the prediction results. At the same time, Bootstrap error analysis aims to evaluate the stability and generalization ability of the model under different sample subsets and quantify the distribution characteristics of prediction errors through the resampling technique with placement. Moreover, Bootstrap error analysis uses all ALT data, and the model’s overall optimal results (training dataset and validation dataset) are RMSE of 17.499 cm, MAE of 8.452 cm, R2 of 0.964, and MAPE of 0.048.
Based on the Bootstrap error analysis framework, the evaluation of SCE model shows that the model has good reliability in predicting the ALT (Figure 9): the RMSE is 24.156, the Bootstrap mean value is consistent with the basic value, the standard deviation is 1.971, accounting for 8.16% (<10%) of the mean value, and the 95% confidence interval is [20.224, 28.005]. The R2 is 0.931, and the standard deviation is only 0.0113(<0.05), which shows that the model can explain the stability of data. The MAE is 12.187, and the MAPE is 0.064. The standard deviations of both are less than 10% of the mean, which indicates that the error distribution is concentrated and relatively small. On the whole, the SCE model verifies the controllability of the prediction error and the robustness of the sample through Bootstrap analysis. Additionally, 95% CI were incorporated into the long-term trend analysis of annual ALT predictions. Measured data indicate that the multi-year average ALT from 1995 to 2018 was 220.469 cm, with a corresponding 95% CI of [213.522, 227.142], within which the predictive results of the SCE model fully fall. Further analysis reveals a long-term ALT trend of 0.6 cm/a, suggesting a significant thickening of the active layer thickness during the study period. It is important to note that ALT measurement points are widely distributed across the QTP, and the spatial heterogeneity of ALT at individual sites may explain why the measured thickening result is slightly lower than the SCE model’s prediction for the entire QTP region, reflecting the inherent discrepancy between point-scale observations and regional-scale model predictions. Combined with the uncertainty characteristics of the input covariates, error propagation analysis can be introduced to improve the uncertainty quantification system of the model, further enhance its reliability in ALT inversion of frozen soil, and provide a more comprehensive method support for the quantitative study of frozen soil environmental changes.
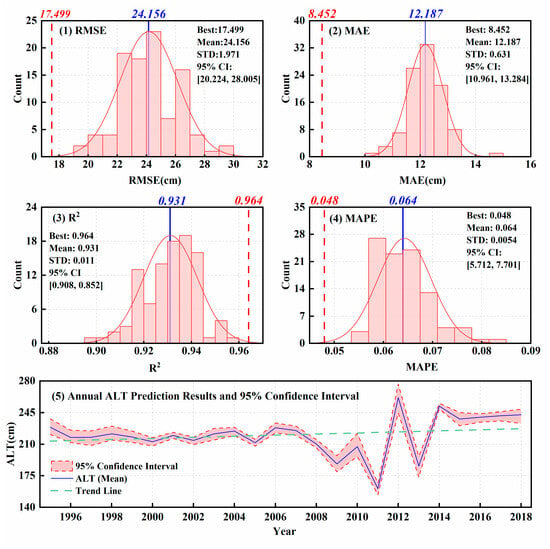
Figure 9.
Error Analysis of the SCE-ALT Model.
This study also simulated the ALT based on Linear Regression method and compared its evaluation accuracy with multiple machine learning methods (Table 2). The results showed that the linear regression method performed poorly in simulation (RMSE: 69.876 cm, MAE: 53.767 cm, R2: 0.429, MAPE: 0.273). The findings indicate that machine learning methods are effective tools for simulating the ALT in the QTP region.

Table 2.
Comparison of ALT simulation results between the linear regression method and the SCE-ALT model.
Additionally, to assess the potential absence of critical predictor variables and the presence of systematic bias, residual plots were employed to validate the model’s capture of key environmental factors. Residual plots of ALT against latitude, longitude, and elevation (Figure 10) were supplemented. The results indicated no discernible trends in residuals with longitudinal or latitudinal variations, nor a significant association with elevation. The linear correlation coefficients between residuals and latitude, longitude, and elevation were all less than 0.04, suggesting that no obvious critical predictor variables were missing in this study and that no significant systematic bias existed.
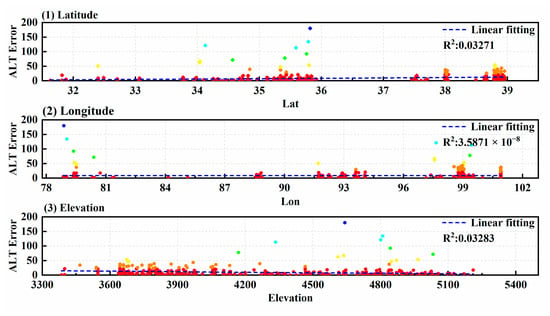
Figure 10.
Residual Plots of the SCE Model Result Against Latitude, Longitude, and Elevation.
Based on the constructed SCE-ALT model, the ALT data in the QTP from 1958 to 2022 were obtained. Figure 11 is a schematic diagram of the SCE-ALT product, which shows in detail the spatial distribution of the ALT in the QTP, providing data support for the subsequent analysis of the change trend of the ALT in the QTP in this study.
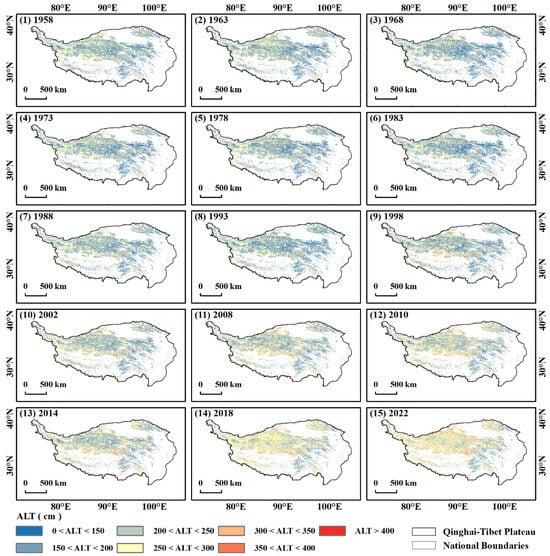
Figure 11.
SCE-ALT model product display diagram.
4.2. Analysis of ALT Changes
In this study, the spatial distribution and temporal trend of ALT in the QTP were analyzed through statistics methods (Figure 12). According to the multi-year average distribution map of the ALT in Figure 10, it can be obtained that the multi-year average of the ALT in the QTP region is 218.67 cm, the highest multi-year average of the ALT reaches 421.53 cm, and the lowest multi-year average of the ALT is 97.12 cm. The ALT shows spatial distribution differences. The ALT in the eastern and southern regions of the QTP is relatively small, while other regions exhibit strong heterogeneity. Among them, the ALT in the inter-mountain high plains is relatively high, followed by the mountainous areas and the zones where glaciers are distributed. According to the change trend chart of the ALT in Figure 10, the ALT in the QTP region generally increased from 1958 to 2022 at a rate of 0.68 cm/a. The sliding T-test was used to detect mutation points (Sliding Windows Size: 3). The year 1998 exhibited the lowest p-value across all measurement points and was thus identified as the primary mutation point, which coincides with a significant shift in the growth trend of the ALT in the QTP. From 1958 to 1998, the ALT in the QTP showed a slow growth trend (0.25 cm/a), whereas from 1998 to 2022, the ALT in the QTP entered a period of rapid growth (1.26 cm/a). Compared with the slow growth period (1958–1998), the thickening rate increased by about 4 times (an increase of 1.01 cm), showing a rapid growth trend.
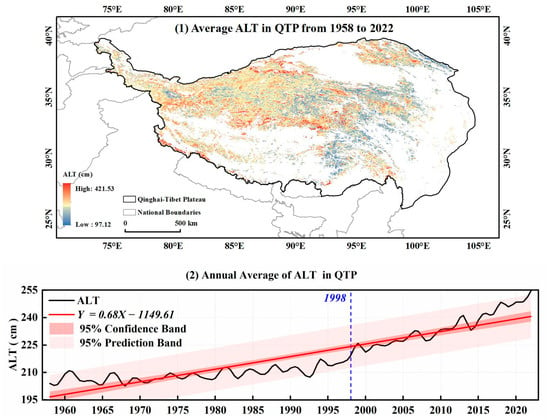
Figure 12.
Distribution and changes of ALT in QTP.
A spatial trend analysis was conducted using multi-year ALT data (Figure 13). In the central and north-western regions of the QTP, the ALT change rate is relatively fast, with a maximum rate of up to 2.61 cm/a. This region is mostly an inland arid area with sparse vegetation. The soil is directly affected by the climate, and temperature changes have a more direct and intense impact on the permafrost, leading to accelerated permafrost thaw. Conversely, the ALT changes more slowly in the eastern and southern regions of the QTP. Influenced by the monsoon climate, these areas receive more precipitation than other parts of the QTP and have better vegetation cover. This reduces the impact of temperature changes on permafrost to some extent. The areas where the ALT is thinning are scattered, mainly distributed in the low-lying areas near the periphery of the plateau. Additionally, from the ALT change trend, it is found that the ALT changes rapidly around glaciers and lakes. It is speculated that the cold-water flow generated by glacier melting can lower the temperature of the surrounding soil, slowing down permafrost thaw. Lakes, through processes such as evaporation and heat exchange, affect the hydro-thermal conditions of the surrounding soil, thereby influencing ALT changes.
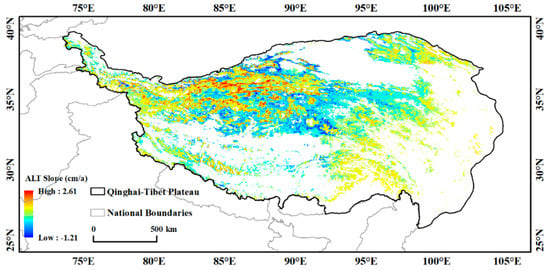
Figure 13.
Trend of ALT changes in QTP.
4.3. Analysis of ALT Influencing Factors
ALT is influenced by different factors such as temperature, precipitation, soil texture, vegetation coverage, and terrain. In the northern hemisphere, the impact of rising temperatures on ALT is stronger [24]. In addition, other factors such as precipitation, snow depth, and solar radiation also have a certain impact on the changes in ALT [74].
Based on the SCE-ALT model, ALT in the QTP was inverted, and the importance and contribution of different factors to permafrost ALT were quantified using SHAP, Person, and Random Forest Importance methods. Among them, the SHAP method is used to measure the contribution of each feature to the model prediction results; Random Forest Importance measures the importance of a feature for model prediction by evaluating its cumulative contribution to reducing node impurities during the process of constructing a decision tree. Person correlation is used to measure the degree of linear correlation between features and target variables. Regarding the feature importance weighting, the SHAP values, Pearson correlation coefficients, and Random Forest Importances were first normalized to [0, 1] using min-max scaling, and then the variables were ranked within each method. Equal weights (1/3 each) were assigned to the ranks of the three methods, and the weighted average was calculated to obtain the composite ranking of each variable. In addition, due to the use of constant quantitative organic carbon content data, it has not been thoroughly explored in the analysis of influencing characteristics.
Analyze the various features that affect ALT using three methods: SHAP, Person, and Random Forest Importance. The three factors with the highest numerical values in the SHAP method results (Figure 14a) are DDT (13.7), LST (10.7), and DDF (5.94). The high SHAP values of DDT and LST indicate that they play a crucial role in model prediction. The top three rankings in Random Forest Importance (Figure 14b) are DDT (8.18), DDF (5.74), and LST (4.993). DDT has the greatest contribution to reducing prediction uncertainty in the Random Forest model, indicating its important role in decision-making in regression. The three variables with the highest values in Person correlation (Figure 14c) are DDT (0.194), LST (0.113), and DDF (0.108), indicating a strong linear relationship between DDT and the target variable. In summary, from the perspective of model contribution, decision tree impurity reduction contribution, and linear correlation degree, the importance of DDT, DDF, and LST features is relatively stable and important, which verifies that temperature is still the most important climate factor affecting ALT changes. By weighted averaging the results of SHAP, Random Forest Importance, and Person methods, the results are shown in Figure 14d. According to the weighted results, the meteorological factors that affect ALT changes are ranked as Temperature, Leaf Area Index, Preparation, etc. Meanwhile, the ranking of ALT_Stefan results is high (No. 4), confirming that the Stefan equation can enhance the simulation accuracy of machine learning models for ALT.
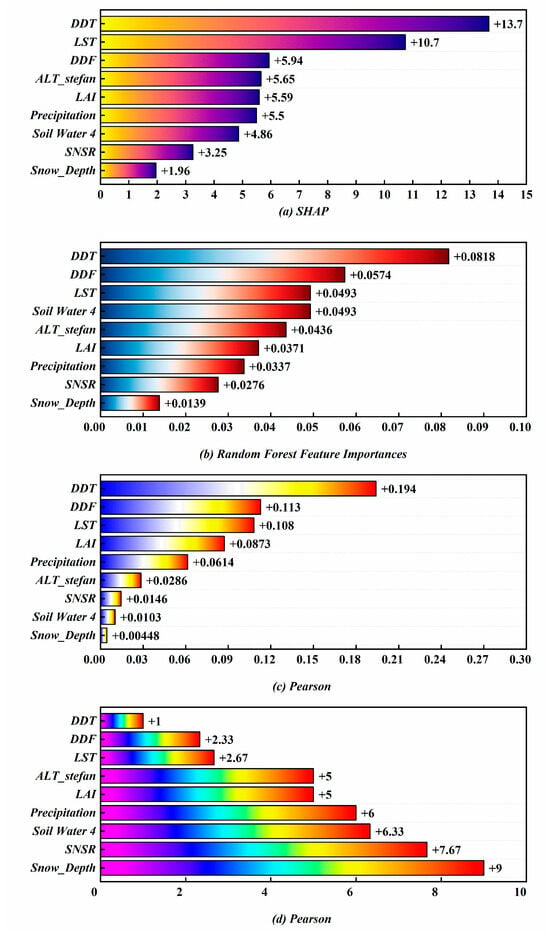
Figure 14.
Analysis of the influence of input features on SCE-ALT Model.
5. Discussion
This study is based on multi-source remote sensing data and utilizes various machine learning algorithms (CatBoost, Random Forest, Extra Trees, Light Gradient Boosting Machine, Gradient Boosting and Extreme Gradient Boosting), and adopts the blending ensemble approach to construct the SCE-ALT model. Through this model, the distribution and changes of ALT in the QTP region from 1958 to 2022 were simulated. Compared with Stefan equation, machine learning methods, and mathematical statistical methods, the SCE-ALT model constructed in this study has significant advantages in simulating ALT, and performs better in key indicators such as RMSE and R2. Compared with the results of Stefan’s equation, the RMSE of the SCE-ALT model decreased by 22.86 cm and the R2 increased by 0.327 cm [19], Compared with the multiple linear regression model (Δ-error: RMSE = 37.196 cm, MAE = 33.054 cm, R2 = 0.444, MAPE = 0.169), the SCE model demonstrates higher simulation capability. Compared to other machine learning methods in research (Table 3), RMSE of the SCE-ALT model decreased by 35.49 cm on average, and R2 increased by 0.376 on average [19,28]; Comparing the use of measured soil data and remote sensing soil data to simulate ALT, the RMSE of the SCE-ALT model increased by 59.32 cm and 37.32 cm, respectively, and the R2 increased by 0.243 and 0.203, respectively [75]; Compared to the Statistical Estimation Model, the RMSE of the SCE-ALT model increased by 6.32 cm, and the R2 increased by 0.353 [76]. The growth rate of ALT during the rapid growth period reached 1.26 cm/a, which is roughly similar to the research results of others (Li et al.: 0.09 cm/a [20]; Zhao et al.: 1.9 cm/a [77]). Due to differences in input data and methods, different studies have slight variations in specific research results, but the overall trend is consistent, further verifying the reliability of simulating ALT data in the QTP region using the results of this study.

Table 3.
Comparison between SCE-ALT model and similar products.
This study used the Sliding T-test (Sliding Window Size: 3) to identify mutation points, determining 1998 as the primary one (lowest p-value, 1958–2022). This year marked a significant inflection point in QTP’s ALT growth trend: ALT increased from 0.25 cm/year (1958–1998) to 1.26 cm/year (1998–2022), with a fourfold thickening rate increase (Δ = 1.01 cm). This aligns with Yang et al.’s findings of rapid post-1997 elevation-dependent warming (EDW+) in QTP [78]. The accelerated rise in ALT after 1998 is linked to the enhanced role of snow cover in temperature regulation. Altitude-related warming driven by snow cover, specific humidity, and soil moisture has emerged as a key driver of ALT dynamics in the QTP, underscoring the feedback mechanisms of climate and hydrology in permafrost response.
However, this study also has certain limitations. During the simulation process, the complex influence of soil factors on ALT was not fully considered. In particular, variations in soil texture can introduce errors into ALT simulation [69]. In future research, soil attribute data from SoilGrids 250 can be utilized to improve the simulation accuracy of ALT through soil property parameters related to permafrost, such as Bulk density, Clay content, Coarse fragments, Sand, and Silt. In addition, the boundary data of the permafrost region used in this study was based on fixed boundary data, and temporal changes in the spatial distribution of permafrost in the QTP were not dynamically simulated. This static boundary assumption may lead to inaccuracies in ALT estimations across the region. Although this study emphasizes natural drivers of ALT, human activities like infrastructure development and grazing in the Qinghai-Tibet Plateau are increasingly altering the permafrost environment. These disturbances can indirectly impact ALT by changing surface energy balance, soil moisture, and vegetation cover. Future research could use World Pop data to correlate population distribution with ALT trends, pinpointing human-impacted hotspots and clarifying ALT’s complex drivers.
With the development of remote sensing technology, advanced techniques such as microwave and InSAR provide new tools and datasets for ALT simulation. Microwave technology, with its strong penetrability, can stably obtain data under complex meteorological conditions, providing data support for ALT simulation; InSAR technology utilizes phase information to accurately capture subtle changes caused by surface variations, providing high-precision data for simulating ALT [75,76]. Microwave and InSAR technologies have great potential in simulating ALT. In future research, more comprehensive methodologies can be employed to enhance the accuracy and expand the applicability of ALT simulations. On one hand, integrating high-resolution terrain, meteorological, and soil datasets with diverse remote sensing information (Optical data, microwave data, and InSAR data) can better capture the spatial heterogeneity of permafrost environments. On the other hand, advanced machine learning techniques, including deep neural networks, ensemble learning algorithms, and spatio-temporal models, can be utilized to dissect the complex correlations between environmental variables and active layer thickness dynamics. By merging data-driven models with physics-based simulations, researchers can achieve more granular and real-time ALT simulations across various geographic regions.
6. Conclusions
This study utilized multi-source remote sensing data, employed CatBoost model and ET model, and construct the SCE-ALT model through blending integration. This model was validated through ten-fold cross validation, with a MAE of 20.713 cm, RMSE of 32.680 cm, R2 of 0.873, and MAPE of 0.104. Compared with similar products, this model demonstrates high superior accuracy and robustness. According to the ALT data simulated by the SCE-ALT model, the ALT in the QTP region exhibited an overall thickening trend from 1958 to 2022. Specifically, the ALT in the QTP region experienced a slow growth trend from 1958 to 1998, and from 1998 to 2022, the ALT has shown accelerated growth trend. Furthermore, three methods including Person, SHAP, and Random Forest Important were applied to analyze the input variables and explore the factors that affect ALT changes. The results show that temperature is the most important factor affecting ALT, followed by LAI, precipitation, etc. Notably, the important factors of Stefan equation for SCE-ALT model were verified through the analysis of influencing factors. The emerging machine learning model combined with traditional physics empirical equation can effectively improve the simulation accuracy of ALT model.
The SCE-ALT model constructed in this study accurately simulates and analyzes the changes in ALT in the QTP region, and deeply explores the climate factors that affect its changes, providing key data support for climate research and permafrost studies. Meanwhile, the simulated ALT dynamics can directly inform regional water resource management by identifying hotspots vulnerable to permafrost thaw and guiding adaptive strategies for water supply systems. In addition, the SCE model can also provide a theoretical basis and methodological framework for simulating ALT in the QTP and even establishing similar models in high mountain areas of Asia.
Author Contributions
Conceptualization, G.W. and D.Y.; methodology, G.W.; validation, G.W. and S.N.; resources, G.W. and D.Y.; data curation, G.W. and D.Y.; writing—original draft preparation, G.W. and S.N.; writing—review and editing, D.Y., S.L., Y.S., W.W., T.Y., X.S. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences (Grant No. XDA2010010306), the National Natural Science Foundation of China (Grant Nos. 41072191, 41330634, and 91125011), the China Geological Survey, the Fundamental Research Funds for Central Universities, and the Central Guidance on Local Science and Technology Development Fund of Hebei Province, China (Grant No. 236Z4201G).
Data Availability Statement
The daily adjusted precipitation dataset of Qinghai—Tibet Plateau meteorological stations (1981–2017) is provided by the National Tibetan Plateau/Third Pole Environment Data Center (https://doi.org/10.11888/Atmos.tpdc.301192); A new map of permafrost distribution on the Tibetan Plateau (2017) is provided by the National Tibetan Plateau/Third Pole Environment Data Center (https://doi.org/10.11888/Geocry.tpdc.270468); The observation data of permafrost active layer depth along the Qinghai-Tibet Highway (2004–2009) is provided by the National Tibetan Plateau/Third Pole Environment Data Center. https://doi.org/10.11888/GlaciologyGeocryology.tpe.249295.db.
Acknowledgments
The authors appreciate all the data provided by each open database. The authors would like to thank the editor and anonymous reviewers for their valuable comments and suggestions on this article. Thanks for datasets is provided by National Tibetan Plateau/Third Pole Environment Data Center (http://data.tpdc.ac.cn, accessed on 12 October 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ALT | Active Layer Thickness |
| QTP | Qinghai-Tibet Plateau |
| LST | Land Surface Temperature |
| DDF | Degree Days Freezing |
| DDT | Degree Days Thawing |
References
- Brown, R.J.E.; Kupsch, W.O. Permafrost terminology. Biul. Peryglac. 1992, 32, 1–176. [Google Scholar]
- French, H.M. The Periglacial Environment; John Wiley & Sons: Hoboken, NJ, USA, 2017. [Google Scholar]
- Guo, D.; Wang, H. CMIP5 permafrost degradation projection: A comparison among different regions. J. Geophys. Res. Atmos. 2016, 121, 4499–4517. [Google Scholar] [CrossRef]
- Heginbottom, J.A. Permafrost mapping: A review. Prog. Phys. Geogr. 2002, 26, 623–642. [Google Scholar] [CrossRef]
- Michaelides, R.J.; Schaefer, K.; Zebker, H.A.; Parsekian, A.; Liu, L.; Chen, J.; Natali, S.; Ludwig, S.; Schaefer, S.R. Inference of the impact of wildfire on permafrost and active layer thickness in a discontinuous permafrost region using the remotely sensed active layer thickness (ReSALT) algorithm. Environ. Res. Lett. 2019, 14, 035007. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change. Climate change 2007: The physical science basis. Agenda 2007, 6, 333. [Google Scholar]
- Yan, D.; Feng, M.; Hu, Z.; Xu, J.; Li, X. Improving Permafrost Mapping in Southern Tibetan Plateau Using Machine Learning and Rock Glacier Inventory. Permafr. Periglac. Process. 2025, 36, 230–244. [Google Scholar] [CrossRef]
- Ran, Y.; Cheng, G.; Dong, Y.; Hjort, J.; Lovecraft, A.L.; Kang, S.; Tan, M.; Li, X. Permafrost degradation increases risk and large future costs of infrastructure on the Third Pole. Commun. Earth Environ. 2022, 3, 238. [Google Scholar] [CrossRef]
- Hjort, J.; Streletskiy, D.; Doré, G.; Wu, Q.; Bjella, K.; Luoto, M. Impacts of permafrost degradation on infrastructure. Nat. Rev. Earth Environ. 2022, 3, 24–38. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T. Recent permafrost warming on the Qinghai-Tibetan Plateau. J. Geophys. Res. Atmos. 2008, 113, D13. [Google Scholar] [CrossRef]
- Zhao, L.; Wu, Q.; Marchenko, S.; Sharkhuu, N. Thermal state of permafrost and active layer in Central Asia during the international polar year. Permafr. Periglac. Process. 2010, 21, 198–207. [Google Scholar] [CrossRef]
- Schuur, E.A.; McGuire, A.D.; Schädel, C.; Grosse, G.; Harden, J.W.; Hayes, D.J.; Hugelius, G.; Koven, C.D.; Kuhry, P.; Lawrence, D.M. Climate change and the permafrost carbon feedback. Nature 2015, 520, 171–179. [Google Scholar] [CrossRef]
- Mu, C.; Li, L.; Wu, X.; Zhang, F.; Jia, L.; Zhao, Q.; Zhang, T. Greenhouse gas released from the deep permafrost in the northern Qinghai-Tibetan Plateau. Sci. Rep. 2018, 8, 4205. [Google Scholar] [CrossRef]
- Miner, K.R.; D’Andrilli, J.; Mackelprang, R.; Edwards, A.; Malaska, M.J.; Waldrop, M.P.; Miller, C.E. Emergent biogeochemical risks from Arctic permafrost degradation. Nat. Clim. Change 2021, 11, 809–819. [Google Scholar] [CrossRef]
- Hinkel, K.; Paetzold, F.; Nelson, F.; Bockheim, J. Patterns of soil temperature and moisture in the active layer and upper permafrost at Barrow, Alaska: 1993–1999. Glob. Planet. Change 2001, 29, 293–309. [Google Scholar] [CrossRef]
- Xiaodong, W.; Tonghua, W. Permafrost degradation has important effects on climate and human society. Chin. J. Nat. 2020, 42, 425–431. [Google Scholar]
- Brown, J.; Hinkel, K.M.; Nelson, F. The circumpolar active layer monitoring (CALM) program: Research designs and initial results. Polar Geogr. 2000, 24, 166–258. [Google Scholar] [CrossRef]
- Park, H.; Kim, Y.; Kimball, J.S. Widespread permafrost vulnerability and soil active layer increases over the high northern latitudes inferred from satellite remote sensing and process model assessments. Remote Sens. Environ. 2016, 175, 349–358. [Google Scholar] [CrossRef]
- Shen, T.; Jiang, P.; Ju, Q.; Yu, Z.; Chen, X.; Lin, H.; Zhang, Y. Changes in permafrost spatial distribution and active layer thickness from 1980 to 2020 on the Tibet Plateau. Sci. Total Environ. 2023, 859, 160381. [Google Scholar] [CrossRef]
- Li, G.; Zhang, M.; Pei, W.; Melnikov, A.; Khristoforov, I.; Li, R.; Yu, F. Changes in permafrost extent and active layer thickness in the Northern Hemisphere from 1969 to 2018. Sci. Total Environ. 2022, 804, 150182. [Google Scholar] [CrossRef]
- Anisimov, O.A.; Shiklomanov, N.I.; Nelson, F.E. Global warming and active-layer thickness: Results from transient general circulation models. Glob. Planet. Change 1997, 15, 61–77. [Google Scholar] [CrossRef]
- Stefan, J. Über die Theorie der Eisbildung, insbesondere über die Eisbildung im Polarmeere. Annalen der Physik 1891, 278, 269–286. [Google Scholar] [CrossRef]
- Wang, K.; Jafarov, E.; Overeem, I. Sensitivity evaluation of the Kudryavtsev permafrost model. Sci. Total Environ. 2020, 720, 137538. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.L.; O’Neill, H.B.; Isaksen, K.; Noetzli, J.; Romanovsky, V.E. The changing thermal state of permafrost. Nat. Rev. Earth Environ. 2022, 3, 10–23. [Google Scholar] [CrossRef]
- Guo, D.; Wang, H. Simulated historical (1901–2010) changes in the permafrost extent and active layer thickness in the Northern Hemisphere. J. Geophys. Res. Atmos. 2017, 122, 12285–12295. [Google Scholar] [CrossRef]
- Chen, H.; Nan, Z.; Zhao, L.; Ding, Y.; Chen, J.; Pang, Q. Noah modelling of the permafrost distribution and characteristics in the West Kunlun area, Qinghai-Tibet Plateau, China. Permafr. Periglac. Process. 2015, 26, 160–174. [Google Scholar] [CrossRef]
- Aalto, J.; Karjalainen, O.; Hjort, J.; Luoto, M. Statistical forecasting of current and future circum-Arctic ground temperatures and active layer thickness. Geophys. Res. Lett. 2018, 45, 4889–4898. [Google Scholar] [CrossRef]
- Ni, J.; Wu, T.; Zhu, X.; Hu, G.; Zou, D.; Wu, X.; Li, R.; Xie, C.; Qiao, Y.; Pang, Q. Simulation of the present and future projection of permafrost on the Qinghai-Tibet Plateau with statistical and machine learning models. J. Geophys. Res. Atmos. 2021, 126, e2020JD033402. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Che, J.; Aalto, J.; Karjalainen, O.; Hjort, J.; Luoto, M.; Jin, H.; Obu, J. New high-resolution estimates of the permafrost thermal state and hydrothermal conditions over the Northern Hemisphere. Earth Syst. Sci. Data 2022, 14, 865–884. [Google Scholar] [CrossRef]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.; Vapnik, V. Support vector regression machines. Adv. Neural Inf. Process. Syst. 1996, 9, 155–161. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Mahanta, K.K.; Pradhan, I.P.; Gupta, S.K.; Shukla, D.P. Assessing Machine Learning and Statistical Methods for Rock Glacier-Based Permafrost Distribution in Northern Kargil Region. Permafr. Periglac. Process. 2024, 35, 262–277. [Google Scholar] [CrossRef]
- Liu, Q.; Niu, J.; Lu, P.; Dong, F.; Zhou, F.; Meng, X.; Xu, W.; Li, S.; Hu, B.X. Interannual and seasonal variations of permafrost thaw depth on the Qinghai-Tibetan plateau: A comparative study using long short-term memory, convolutional neural networks, and random forest. Sci. Total Environ. 2022, 838, 155886. [Google Scholar] [CrossRef] [PubMed]
- Bonnaventure, P.P.; Lamoureux, S.F. The active layer: A conceptual review of monitoring, modelling techniques and changes in a warming climate. Prog. Phys. Geogr. 2013, 37, 352–376. [Google Scholar] [CrossRef]
- Wei, Z.; Du, Z.; Wang, L.; Zhong, W.; Lin, J.; Xu, Q.; Xiao, C. Sedimentary organic carbon storage of thermokarst lakes and ponds across Tibetan permafrost region. Sci. Total Environ. 2022, 831, 154761. [Google Scholar] [CrossRef]
- Wei, R.; Hu, X.; Zhao, S. Changes in the Distribution of Thermokarst Lakes on the Qinghai-Tibet Plateau from 2015 to 2020. Remote Sens. 2025, 17, 1174. [Google Scholar] [CrossRef]
- Wang, S.; Niu, F.; Chen, J.; Dong, Y. Permafrost research in China related to express highway construction. Permafr. Periglac. Process. 2020, 31, 406–416. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Cheng, G.; Nan, Z.; Che, J.; Sheng, Y.; Wu, Q.; Jin, H.; Luo, D.; Tang, Z. Mapping the permafrost stability on the Tibetan Plateau for 2005–2015. Sci. China Earth Sci. 2021, 64, 62–79. [Google Scholar] [CrossRef]
- Yu, Q.; Zhang, Z.; Wang, G.; Guo, L.; Wang, X.; Wang, P.; Bao, Z. Analysis of tower foundation stability along the Qinghai–Tibet Power Transmission Line and impact of the route on the permafrost. Cold Reg. Sci. Technol. 2016, 121, 205–213. [Google Scholar] [CrossRef]
- Ran, Y.; Jorgenson, M.T.; Li, X.; Jin, H.; Wu, T.; Li, R.; Cheng, G. Biophysical permafrost map indicates ecosystem processes dominate permafrost stability in the Northern Hemisphere. Environ. Res. Lett. 2021, 16, 095010. [Google Scholar] [CrossRef]
- Abatzoglou, J.T.; Dobrowski, S.Z.; Parks, S.A.; Hegewisch, K.C. TerraClimate, a high-resolution global dataset of monthly climate and climatic water balance from 1958–2015. Sci. Data 2018, 5, 170191. [Google Scholar] [CrossRef]
- Niu, S.; Sun, M.; Wang, G.; Wang, W.; Yao, X.; Zhang, C. Glacier change and its influencing factors in the northern part of the Kunlun Mountains. Remote Sens. 2023, 15, 3986. [Google Scholar] [CrossRef]
- Wang, G.; Hao, X.; Yao, X.; Wang, J.; Li, H.; Chen, R.; Liu, Z. Simulations of snowmelt runoff in a high-altitude mountainous area based on big data and machine learning models: Taking the Xiying River basin as an example. Remote Sens. 2023, 15, 1118. [Google Scholar] [CrossRef]
- Poggio, L.; De Sousa, L.M.; Batjes, N.H.; Heuvelink, G.B.; Kempen, B.; Ribeiro, E.; Rossiter, D. SoilGrids 2.0: Producing soil information for the globe with quantified spatial uncertainty. Soil 2021, 7, 217–240. [Google Scholar] [CrossRef]
- Guangyue, L.; Lin, Z.; Changwei, X.; Qiangqiang, P.; Erji, D.; Yongping, Q. Variation characteristics and impact factors of the depth of zero annual amplitude of ground temperature in permafrost regions on the Tibetan Plateau. J. Glaciol. Geocryol. 2016, 38, 1189–1200. [Google Scholar]
- Wu, Q.; Dong, X.; Liu, Y.; Jin, H. Responses of permafrost on the Qinghai-Tibet Plateau, China, to climate change and engineering construction. Arct. Antarct. Alp. Res. 2007, 39, 682–687. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wu, T.; Xiao, Y.; Du, E.; Liu, G.; Qiao, Y. Temporal and spatial variations of the active layer along the Qinghai-Tibet Highway in a permafrost region. Chin. Sci. Bull. 2012, 57, 4609–4616. [Google Scholar] [CrossRef]
- Wang, Q.; Jin, H.; Zhang, T.; Cao, B.; Peng, X.; Wang, K.; Xiao, X.; Guo, H.; Mu, C.; Li, L. Hydro-thermal processes and thermal offsets of peat soils in the active layer in an alpine permafrost region, NE Qinghai-Tibet plateau. Glob. Planet. Change 2017, 156, 1–12. [Google Scholar] [CrossRef]
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T. Changes in active layer thickness over the Qinghai-Tibetan Plateau from 1995 to 2007. J. Geophys. Res. Atmos. 2010, 115, D09107. [Google Scholar] [CrossRef]
- Cao, B.; Zhang, T.; Peng, X.; Mu, C.; Wang, Q.; Zheng, L.; Wang, K.; Zhong, X. Thermal characteristics and recent changes of permafrost in the upper reaches of the Heihe River Basin, Western China. J. Geophys. Res. Atmos. 2018, 123, 7935–7949. [Google Scholar] [CrossRef]
- Wang, C.; Zhao, L.; Ma, L.; Hu, G.; Zhang, L.; Zou, D.; Xing, Z.; Xiao, Y.; Zhou, H.; Qiao, Y. Precipitation adjustment by the OTT Parsivel2 in the central Qinghai–Tibet Plateau. Earth Surf. Process. Landf. 2024, 49, 2424–2441. [Google Scholar] [CrossRef]
- Geurts, P.; Ernst, D.; Wehenkel, L. Extremely randomized trees. Mach. Learn. 2006, 63, 3–42. [Google Scholar] [CrossRef]
- Galelli, S.; Castelletti, A. Assessing the predictive capability of randomized tree-based ensembles in streamflow modelling. Hydrol. Earth Syst. Sci. 2013, 17, 2669–2684. [Google Scholar] [CrossRef]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased boosting with categorical features. Adv. Neural Inf. Process. Syst. 2018, 31, 1–11. [Google Scholar]
- Hancock, J.T.; Khoshgoftaar, T.M. CatBoost for big data: An interdisciplinary review. J. Big Data 2020, 7, 94. [Google Scholar] [CrossRef]
- Dietterich, T.G. Ensemble methods in machine learning. In Proceedings of the International Workshop on Multiple Classifier Systems, Cagliari, Italy, 21–23 June 2000; pp. 1–15. [Google Scholar]
- Zhou, Z.-H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2025. [Google Scholar]
- Sill, J.; Takács, G.; Mackey, L.; Lin, D. Feature-weighted linear stacking. arXiv 2009, arXiv:0911.0460. [Google Scholar]
- Peng, X.; Zhang, T.; Cao, B.; Wang, Q.; Wang, K.; Shao, W.; Guo, H. Changes in freezing-thawing index and soil freeze depth over the Heihe River Basin, western China. Arct. Antarct. Alp. Res. 2016, 48, 161–176. [Google Scholar] [CrossRef]
- Biskaborn, B.K.; Smith, S.L.; Noetzli, J.; Matthes, H.; Vieira, G.; Streletskiy, D.A.; Schoeneich, P.; Romanovsky, V.E.; Lewkowicz, A.G.; Abramov, A. Permafrost is warming at a global scale. Nat. Commun. 2019, 10, 264. [Google Scholar] [CrossRef]
- Yi, Y.; Kimball, J.S.; Rawlins, M.A.; Moghaddam, M.; Euskirchen, E.S. The role of snow cover affecting boreal-arctic soil freeze–thaw and carbon dynamics. Biogeosciences 2015, 12, 5811–5829. [Google Scholar] [CrossRef]
- Morse, P.; Wolfe, S.; Kokelj, S.; Gaanderse, A. The occurrence and thermal disequilibrium state of permafrost in forest ecotopes of the Great Slave Region, Northwest Territories, Canada. Permafr. Periglac. Process. 2016, 27, 145–162. [Google Scholar] [CrossRef]
- Fisher, J.P.; Estop-Aragonés, C.; Thierry, A.; Charman, D.J.; Wolfe, S.A.; Hartley, I.P.; Murton, J.B.; Williams, M.; Phoenix, G.K. The influence of vegetation and soil characteristics on active-layer thickness of permafrost soils in boreal forest. Glob. Change Biol. 2016, 22, 3127–3140. [Google Scholar] [CrossRef] [PubMed]
- Fu, Q.; Hou, R.; Li, T.; Wang, M.; Yan, J. The functions of soil water and heat transfer to the environment and associated response mechanisms under different snow cover conditions. Geoderma 2018, 325, 9–17. [Google Scholar] [CrossRef]
- Andersland, O.B.; Ladanyi, B. Frozen Ground Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Zhang, T. Influence of the seasonal snow cover on the ground thermal regime: An overview. Rev. Geophys. 2005, 43, 4. [Google Scholar] [CrossRef]
- Jorgenson, M.T.; Romanovsky, V.; Harden, J.; Shur, Y.; O’Donnell, J.; Schuur, E.A.; Kanevskiy, M.; Marchenko, S. Resilience and vulnerability of permafrost to climate change. Can. J. For. Res. 2010, 40, 1219–1236. [Google Scholar] [CrossRef]
- Wu, B.; Zhang, M.; Zeng, H.; Tian, F.; Potgieter, A.B.; Qin, X.; Yan, N.; Chang, S.; Zhao, Y.; Dong, Q. Challenges and opportunities in remote sensing-based crop monitoring: A review. Natl. Sci. Rev. 2023, 10, nwac290. [Google Scholar] [CrossRef]
- Song, C.; Huang, B.; Ke, L.; Richards, K.S. Remote sensing of alpine lake water environment changes on the Tibetan Plateau and surroundings: A review. ISPRS J. Photogramm. Remote Sens. 2014, 92, 26–37. [Google Scholar] [CrossRef]
- Ferguglia, O.; Palazzi, E.; Arnone, E. Elevation dependent change in ERA5 precipitation and its extremes. Clim. Dyn. 2024, 62, 8137–8153. [Google Scholar] [CrossRef]
- Li, W.; Zhao, L.; Wu, X.; Wang, S.; Sheng, Y.; Ping, C.; Zhao, Y.; Fang, H.; Shi, W. Soil distribution modeling using inductive learning in the eastern part of permafrost regions in Qinghai–Xizang (Tibetan) Plateau. Catena 2015, 126, 98–104. [Google Scholar] [CrossRef]
- Wang, Z.; Kim, Y.; Seo, H.; Um, M.-J.; Mao, J. Permafrost response to vegetation greenness variation in the Arctic tundra through positive feedback in surface air temperature and snow cover. Environ. Res. Lett. 2019, 14, 044024. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, H.; Wang, C.; Tang, Y.; Zhang, B.; Wu, F.; Wang, J.; Zhang, Z. Active layer thickness retrieval over the Qinghai-Tibet Plateau using Sentinel-1 multitemporal InSAR monitored Permafrost subsidence and temporal-spatial multilayer soil moisture data. IEEE Access 2020, 8, 84336–84351. [Google Scholar] [CrossRef]
- Jia, S.; Zhang, T.; Hao, J.; Li, C.; Michaelides, R.; Shao, W.; Wei, S.; Wang, K.; Fan, C. Spatial Variability of Active Layer Thickness along the Qinghai–Tibet Engineering Corridor Resolved Using Ground-Penetrating Radar. Remote Sens. 2022, 14, 5606. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Du, E.; Pang, Q.; Xiao, Y.; Li, R.; Sheng, Y.; Wu, X.; Sun, Z. Changing climate and the permafrost environment on the Qinghai–Tibet (Xizang) plateau. Permafr. Periglac. Process. 2020, 31, 396–405. [Google Scholar] [CrossRef]
- Yang, Y.; You, Q.; Zuo, Z.; Zhang, Y.; Liu, Z.; Kang, S.; Zhai, P. Elevation dependency of temperature trend over the Qinghai-Tibetan Plateau during 1901–2015. Atmos. Res. 2023, 290, 106791. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).