Abstract
Ground filtering is crucial for airborne Light Detection and Ranging (LiDAR) data post-processing. The progressive triangulated irregular network densification (PTD) algorithm and its variants outperform others in accuracy, stability, and robustness, using grid-based seed point selection, TIN construction, and iterative rules for ground point identification. However, these methods still face limitations in removing low points and accurately preserving terrain details, primarily due to their sensitivity to grid size. To overcome this issue, a novel PTD filtering algorithm based on an adaptive grid (AGPTD) was proposed. The main contributions of the proposed method include an outlier removal method using a radius outlier removal algorithm and Kd-tree, a method for establishing an adaptive two-level grid based on point cloud density and terrain slope, and an adaptive selection method for angle and distance thresholds in the iterative densification processing. The performance of the AGPTD algorithm was assessed based on widely used benchmark datasets. Results show that the AGPTD algorithm outperforms the classical PTD algorithm in retaining ground feature points, especially in reducing Type I error and average total error significantly. In comparison with other advanced algorithms developed in recent years, the novel algorithm showed the lowest average Type I error, the minimal average total error, and the greatest average Kappa coefficient, which were 1.11%, 2.28%, and 90.86%, respectively. Additionally, the average accuracy, precision, and recall of AGPTD were 97.69%, 97.52%, and 98.98%, respectively.
1. Introduction
Light Detection and Ranging (LiDAR) is a sophisticated remote sensing technology employed across diverse fields and applications, including digital terrain model (DTM) generation [1,2], forest surveys [3,4], urban planning and road identification [5,6], environmental monitoring [7], point cloud classification [8,9] and three-dimensional reconstruction [10,11,12].
Numerous algorithms have been developed for ground filtering (i.e., separating the point cloud into ground points and non-ground points), which is the core of post-processing for LiDAR data [13,14]. These filtering algorithms can be generally categorized into five groups, including slope-based filtering [15,16], morphological filtering [17,18,19], segmentation-based filtering [20,21,22], Triangulated Irregular Network (TIN)-based filtering [23,24,25,26,27], and deep learning-based filtering [28,29,30,31]. Recently, there has been remarkable advancement in the sophistication and automation of algorithms used to extract bare earth information from airborne LiDAR data [32,33]. Most filtering algorithms perform well in areas with continuous terrain, gentle slopes, and low vegetation coverage. However, it is still a great challenge to effectively filter in regions marked by disconnected terrain, steep slope terrain, and lush vegetation [34].
The classical progressive triangulated irregular network densification (PTD) algorithm proposed by Axelsson [23] has good robustness, effectiveness, and terrain adaptability. The algorithm builds an initial TIN surface using the initial ground seed point derived from the division of the regular grid. Subsequently, those ground points that meet the judgment conditions will be incrementally included in the set of ground points until a TIN surface close to the real ground is constructed. Nevertheless, the classical PTD filtering algorithm exhibits certain limitations in preserving terrain details and eliminating low points (i.e., outliers with lower elevations), owing to its sensitivity to the size of the grid [24,25,26,27,35,36].
To overcome the above-mentioned limitations, Zhang and Lin [24] extended the ground seed point set as much as possible by embedding smoothness-constrained segmentation between the two steps of constructing the initial TIN and the iterative densification of the TIN; Lin and Zhang [25] preserved target discontinuities and filtered out non-target points through three critical stages involving segmentation of the point cloud, analysis of multiple echoes, and iterative judgment; Nie et al. [26] improved the classical PTD algorithm by creating a refined TIN and modifying the original iterative evaluation criterion; Cai et al. [27], combining cloth simulation and PTD, obtained a high-quality initial provisional DTM by cloth simulation, then refined the initial DTM by PTD with adaptive parameter thresholds; Gu et al. [35] introduced a hybrid filtering algorithm that merges the self-adaptive grid technique with point-to-surface comparison to extract bare ground in mining areas with terrain fluctuations; and Chen et al. [36] obtained potential ground seed points through a progressive morphological filtering algorithm to optimize the selection of seed points and computational efficiency.
There are still some limitations of the above-mentioned methods. (1) The algorithms proposed by Zhang and Lin [24] and Lin and Zhang [25] perform poorly in reducing type II error (T.II, i.e., commission error, refers to the percentage of ground points misclassified as non-ground points), and increase the complexity and uncertainty of the algorithm due to more input parameters. Additionally, in the outlier removal process, the scientific quality of the algorithms is somewhat diminished by relying on visual inspection of the visualized elevation histogram and manual selection of elevation thresholds to eliminate the lowest and highest tails. (2) The algorithm introduced by Nie et al. [26] does not require more input parameters, but it still has limitations in reducing type I error (T.I, i.e., omission error, refers to the percentage of non-ground points misclassified as ground points) and eliminating T.I in the subsequent manual filtering. (3) The algorithm proposed by Cai et al. [27] exhibits poor performance in terms of T.II, particularly within regions characterized by low vegetation, discontinuity, ramps and steep slopes. (4) The algorithm proposed by Gu et al. [35] focuses solely on the application of the algorithm to complex terrain areas in mining regions and lacks a quantitative evaluation based on benchmark datasets. (5) The method proposed by Chen et al. [36] also suffers from the efficiency issue mentioned in issue (1) due to the lack of automation for selection of parameters.
The grid size is crucial to the performance of the classical PTD algorithm, particularly in selecting the ground seed points. A larger grid size will lead to a reduced number of extracted ground seed points, leading to over-smoothness in the generated initial TIN and, accordingly, cannot adequately preserve terrain details [37]. Moreover, it may misclassify ground points as non-ground points during the iteration process, i.e., increasing T.I in the filtering result. Contrarily, a smaller grid size will increase the number of ground seed points and introduce more non-ground points, i.e., increasing T.II. As the iteration continues, these misclassified non-ground points may be selected into the ground point set, further amplifying T.II.
To overcome the above-mentioned limitations, this study proposes an adaptive grid-based progressive TIN densification filtering algorithm (named AGPTD), which, by refining primary grids to achieve extraction of initial ground seed points and construction of the initial TIN, aims to maximally preserve terrain details in areas with complex topography. The improvements of the proposed algorithm primarily focus on three aspects. (1) For outlier removal, a radius outlier removal algorithm is first employed to eliminate some extremely high and low elevation points. Subsequently, the K-dimensional tree (Kd-tree) method is used to calculate elevation variance, thereby filtering out certain conspicuous non-ground points, such as extremely high or low elevation points and isolated noise points; this process reduces the likelihood of T.II in subsequent seed point selection. (2) For seed point selection, the appropriate size for each grid is determined by the density of the point cloud and the slope of the terrain. The improved algorithm can better enhance filtering performance when dealing with complex terrain, particularly in regions with disconnected terrain and steep slopes. (3) For iterative densification, firstly, the maximum grid slope generated during the seed point selection process is taken as the maximum terrain slope for the judgment of the mirroring technique. Secondly, a trial-and-error method is employed to adaptively select the most appropriate parameters to achieve optimal filtering performance.
2. Datasets
Eight widely used benchmark datasets supplied by the ISPRS Working Group III/3 were used for the performance evaluation of algorithms. These datasets include both urban and rural areas, and a total of 15 reference samples were meticulously created using a combination of existing knowledge and accessible imagery. Comprehensive description of the aforementioned datasets is accessible in their research documentation at https://www.itc.nl/isprs/wgIII-3/filtertest/report/ (accessed on 30 September 2024). Specifically, disconnected terrain and steep slopes are predominantly found in Samples 11, 23, 31, 52, 53, 61, and 71. Meanwhile, Sample 41 exhibits a clump of low points arising, while Sample 42 demonstrates low (objects) and high points reflecting high-frequency landscape variations.
3. Methodology
The proposed AGPTD algorithm overall contains three steps (Figure 1). The first step involves using a radius outlier removal algorithm and implementing a K-nearest neighbor search with the Kd-tree to eliminate outliers. The second step achieves adaptive grid selection based on the number of point clouds and relative slope in the primary grid. Specifically, additional seed points are selected through two levels of grids, and then they are added to the initial set of ground seed points. The third step uses the initial set of ground seed points to establish the initial TIN model. Based on the established iterative decision rules, each of the remaining unclassified points is evaluated one by one. If a point meets the criteria for a ground point, it is added to the TIN model. This process is reiterated until no new data points meet the decision criteria or the number of iterations reaches the maximum iteration limit.
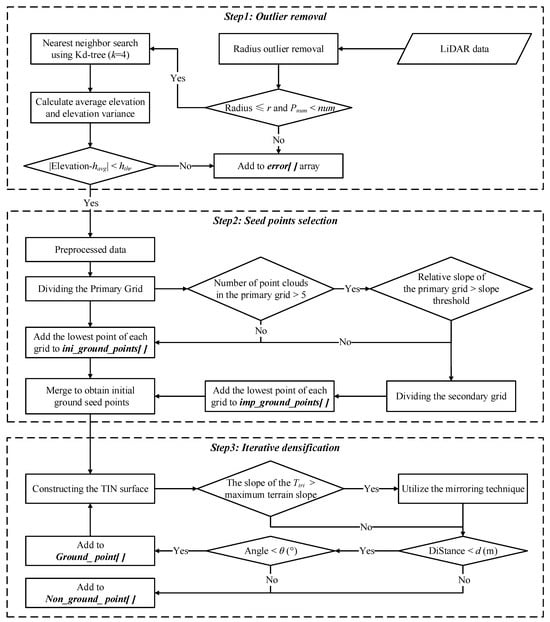
Figure 1.
Flowchart of the proposed AGPTD algorithm. (The error[ ] array contains all the outliers, the ini_ground_points[ ] array stores the seed points extracted from the primary grid, the imp_ground_points[ ] array retains the seed points extracted from the secondary grid, the Ground_point [ ] array holds the ground points, and the Non_ground_point [ ] array stores the non-ground points. r indicates four times the maximum point spacing of the sample. num indicates the minimum number of neighbors, and Pnum represents the number of neighboring points for the point to be judged. havg denotes the average elevation obtained through the calculation involving the point to be judged and its neighboring points. hthr represents the elevation threshold. is the corresponding TIN facet of the point to be judged).
The parameter settings of the samples are shown in Table 1. Here, k denotes the count of neighboring values to be assessed, which is determined after considering factors such as computational efficiency, local features, and the prevention of overfitting. The variable s (m) signifies the size of the primary grid, and its setting is based on the point spacing of the test sites (the recorded point spacing for urban sites is 1–1.5 m, and for rural areas, it is 2–3.5 m) as well as the topographical features, while θ (°) and d (m) refer to the angular and distance thresholds, used in the iterative densification process, respectively (which are automatically selected through trial and error to obtain the optimal values [25,26]).

Table 1.
Parameter settings for samples.
3.1. Outlier Removal
The point cloud data acquired by airborne LiDAR systems inevitably contain massive outliers due to various uncontrollable factors. Such noise points include high outliers, low outliers, and isolated noise points. The presence of these noise points can negatively impact the accuracy of subsequent point cloud data processing. Denoising is an indispensable pre-processing step for ground filtering, which can effectively improve the accuracy of subsequent processing steps. Because elevation extremes, particularly low points, do not accurately represent the actual surface elevation, these low points can be mistakenly chosen as initial ground seed points by the PTD algorithms. Such algorithms typically assume that the lowest elevation point in a local area is a ground point when selecting seed points, thereby increasing the occurrence of T.II.
Here, the radius outlier removal algorithm and Kd-tree are utilized to identify and eliminate outliers of point cloud datasets.
3.1.1. Radius Outlier Removal Algorithm
Step 1: Set parameters. Set the radius r (in this paper, it is set to four times the maximum point spacing of the sample) and the minimum number of neighbors (num) as parameters for the radius outlier removal algorithm.
Step 2: Traverse each point in the point cloud. Within r, search for the neighboring points of the point to be judged and calculate the corresponding number Pnum.
Step 3: Judge and remove outliers. If Pnum < num, the point to be judged is identified as an outlier and removed.
3.1.2. Kd-Tree Outlier Removal Algorithm
Step 1: Ascertain neighboring points. The K-nearest neighbor search of a Kd-tree is utilized to ascertain the neighboring points of each point.
Step 2: Statistically analyze the elevation of each point and all its neighboring points to calculate the corresponding average elevation (havg), elevation variance (hvar), and the elevation difference (hdif) between the point to be judged and hvar.
Step 3: Judge and remove outliers. If hdif > hthr (hthr is obtained by dividing hvar by 20), the point to be judged is identified as an outlier and removed.
3.2. Seed Point Selection
Theoretical outcomes denote that a lower T.II correlates with higher filtering precision. However, considering that automatic filtering may not meet expected precision requirements, manual intervention is often employed to enhance the precision of filtering in subsequent filtering stages [25,26]. Therefore, reducing T.I presents a far greater challenge than reducing T.II, which makes decreasing T.I a higher priority.
To achieve the aforementioned objective of reducing T.I, an adaptive grid method was proposed to obtain the initial ground seed points. This method achieves the division of adaptive grids by analyzing the density of point clouds and their relative slopes within the primary grid, thus preserving terrain details in those areas with disconnected terrain. For grid division, the initial ground seed points extracted by a two-level grid exceed those obtained by the classical algorithm by 50.83–103.45%, with an accuracy rate of over 96.69%. However, a three-level grid introduces unnecessary computational overhead without a significant enhancement in performance. Therefore, taking into account specific application requirements, dataset characteristics, algorithm efficiency, and computational burden, this study ultimately elected to adopt a two-level grid division.
Figure 2 shows the initial ground seed points (blue dots) extracted using the regular grid and adaptive grid and their simulated initial TIN facet effects (the cyan dashed line and the red dashed line, respectively). It can be seen that classical PTD methods often struggle to accurately capture and preserve the terrain features. However, AGPTD can increase the density of initial ground seed points in areas with steep slopes by refining the grid, which results in the simulated initial TIN facet being closer to the actual terrain.
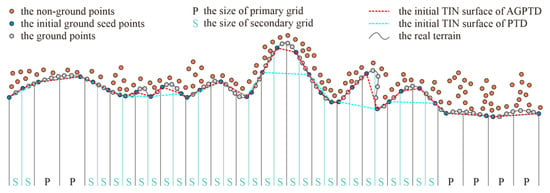
Figure 2.
Ground seed points are extracted by regular grid using the classical PTD algorithm, and adaptive grid using the proposed AGPTD algorithm.
3.2.1. Primary Grid Division
The process of obtaining primary ground seed points from the primary grid includes the following three steps.
Step 1: Divide the study area into regularly distributed grids by setting the dimensions of the primary grid, and then project all points after outlier removal onto the X–Y plane.
Assume that the maximum and minimum values of the x and y coordinates in the original point cloud data are , , , and , respectively. Then, by setting the primary grid size , a planar grid of dimensions m × n can be calculated and determined through Equations (1) and (2). Herein, ‘ceil’ signifies the ceiling function, which rounds a number up to the nearest integer.
Step 2: Establish an indexing mechanism between the points and the grid, allowing for the retrieval of point cloud data contained in each grid by querying its grid number.
Allocate all the point cloud data into the corresponding grids through Equations (3) and (4). Herein, (X, Y) represents the grid number, and (x, y) represents the planar coordinates of the point to be processed.
Step 3: Sequentially retrieve all points within each grid and extract the point with the lowest elevation to add to the set of primary ground seed points.
3.2.2. Secondary Grid Division
In the process of obtaining initial ground seed points, the classical PTD algorithm usually leads to the loss of terrain details due to the use of grids with fixed sizes, particularly in areas with pronounced terrain undulations such as ridges and steep slopes.
To overcome this problem, this paper proposes an adaptive grid method. After dividing the primary grid, the necessity for grid refinement is determined based on the number of point clouds within the grid and the relative slope. Ideally, as shown in Figure 3, the grid is refined in areas with pronounced terrain undulation while remaining unchanged in flatter regions. This method allows for a more accurate initial TIN that closely resembles the true terrain surface while ensuring computational efficiency.
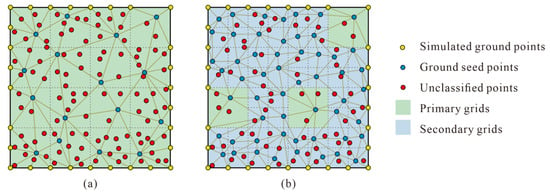
Figure 3.
Construction of the initial TIN using ground seed points extracted by (a) regular grid and (b) adaptive grid. The usage of simulated ground points, which consist of the grid corners of the boundary, originates from Zhao et al. [38].
Assume is the point with the lowest elevation in the primary grid, and represents any other point. The slope values between these points and are calculated in turn using Equation (5). Then, the average slope and the minimum slope value are obtained. The relative slope for this primary grid is the result of subtracting from . The criteria for refinement of the primary grid are set as follows: (1) The number of point clouds in the primary grid ≥ 5; (2) The relative slope in the primary grid exceeds the predetermined slope threshold.
The process of obtaining secondary ground seed points from the secondary grid is as follows.
Step 1: Calculate in the primary grid. If refinement criterion (1) is met, proceed to Step 2. Otherwise, extract the point with the lowest elevation from the grid, add it to the set of secondary ground seed points, and then evaluate the next primary grid.
Step 2: Calculate in the primary grid. If refinement criterion (2) is met, then perform a refinement process on the primary grid. The size of the secondary grid is set to 1/2 of . Otherwise, extract the point with the lowest elevation from the grid, add it to the set of secondary ground seed points, and then evaluate the next primary grid.
Step 3: Calculate the number of point clouds in the secondary grid. If ≥ 1, extract the point with the lowest elevation from the grid and add it to the secondary initial ground seed point set. Otherwise, proceed to the assessment of the next secondary grid.
Step 4: Repeat steps 1 to 3 until all primary grids have been traversed and a set of secondary ground seed points has been obtained.
Step 5: Merge the sets of primary and secondary initial ground seed points, then remove duplicate points to obtain a complete initial ground seed point set.
3.3. Iterative Densification
Iterative densification of the TIN involves judging all unclassified points against critical parameter thresholds. Figure 4 illustrates the detailed judgment process, where in each iteration an unclassified point is considered a ground point if its two principal parameters stay within the respective thresholds. Herein, θ (°) and d (m) refer to the angle and distance thresholds, respectively. is the point to be judged, is the corresponding TIN facet of (Figure 4a).
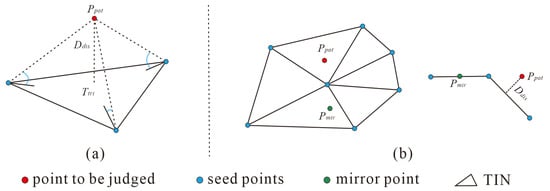
Figure 4.
The schematic diagram of iterative densification. (a) Angle and distance measurements for iterative densification; (b) Mirroring technique.
Step 1: Calculate the two key parameters; one is , the other is . represents the spacing from to , while denotes the intersection angle between and the linkage from to its nearest vertex on .
Step 2: Utilize the mirroring technique to enhance the acquisition of ground points, helping to prevent errors in the identification of and preserve disconnected terrain, particularly in areas with steep slopes (Figure 4b). If the slope of is greater than the maximum terrain slope (the maximum grid slope generated during the seed point selection process), is replaced by the corresponding mirror point and then judgment is performed in Step 3 [23,24,25,26,27]. is the vertex with the highest elevation value in and is the mirror point corresponding to . The formula is shown in Equation (6).
After obtaining the coordinates of the mirror points and the corresponding TIN facets using the mirroring technique, then perform an iteration judgment using the same rules present in step 3.
Step 3: Label as the ground point if both ≤ d and ≤ θ. Otherwise, label the point as a non-ground point, and proceed to evaluate the next point.
Step 4: Judgment occurs on a point-by-point basis. After each iteration, newly identified ground points are integrated into the TIN. This iterative process is repeated until no additional points meeting the judgment criteria can be found or until the number of iterations reaches the upper limit value.
3.4. Evaluation Strategy
In this study, both qualitative and quantitative analyses were conducted to evaluate the filtering performance. Herein, visualization is used for qualitative analysis and four evaluation indicators for quantitative analysis, including T.I, T.II, total error (T.E., i.e., the percentage of points misclassified in all points), and kappa coefficient (kp). To ascertain the ratio of incorrectly classified ground and non-ground points, the three errors are employed. Additionally, the kp value is indicative of the accuracy of the classification. The relevant formulas are presented in Table 2, as documented by Zhao et al. [38].

Table 2.
Calculation of T.I, T.II, T.E., kp, accuracy, precision, and recall; a, b, c, d and e represent correctly classified ground points, misclassified ground points, misclassified non-ground points, correctly classified non-ground points, and the total number of points in the dataset, respectively.
In addition, we introduce three additional indicators: accuracy (i.e., the proportion of correct predictions), precision (i.e., the precision rate of predicted positive cases), and recall (i.e., the recall rate of actual positive cases), to evaluate the results (Table 2).
4. Results
4.1. Outlier Removal
There were anomalous outliers in the point cloud datasets, including high outliers, low outliers, and isolated noise points, due to various uncontrollable factors. Here, the radius outlier removal algorithm and Kd-tree were utilized to identify and eliminate outliers in the point cloud datasets. Table 3 presents the results of the outlier removal process. For the 15 sample datasets analyzed, the precision of outlier removal ranges from 97.14% to 99.97%. Additionally, the proportion of filtered non-ground points relative to actual non-ground points for those samples spans from 34.27% to 97.82%. The count of filtered outliers shows significant variation among those samples, predominantly due to the varying numbers of both low points and extreme high points for each sample. As detailed in the dataset description, Sample 41 exhibits a clump of low points arising from multipath error, while Sample 42 demonstrates low (objects) and high points reflecting high-frequency landscape variations. The outlier results for Samples 41 and 42 highlight the superior proficiency of the proposed algorithm in eliminating both the low points and the extreme high points, with specific examples illustrated in Figure 5.

Table 3.
Statistics of results after implementing outlier removal.
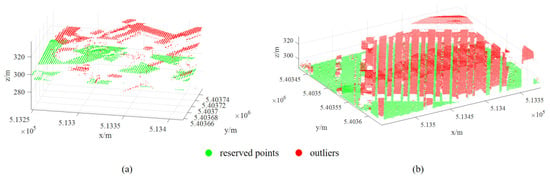
Figure 5.
The results of outlier removal for (a) Sample 41 and (b) Sample 42.
4.2. Seed Point Selection
In the seed point selection stage, a two-level adaptive grid was utilized to conserve terrain details in regions with disconnected terrain, aligning the initial TIN surface more closely with the real ground surface and minimizing T.I as much as possible. Table 4 and Figure 6 display the results of seed point selection utilizing adaptive grids across 15 sample datasets. The initial ground seed points extracted by the AGPTD algorithm surpass those extracted by the classical algorithm by 50.83% to 103.45%. Moreover, the seed points identified by AGPTD for the 15 samples all have a precision exceeding 96.69%, with an average precision of 98.91%. For the nine samples categorized under urban areas, there is an average increase of 73.06% in the number of initial ground seed points. Among these samples, Samples 31, 42, and 41 exhibit the smallest increments of 43.62%, 50.83%, and 63.98%, respectively. These results are associated with low points where the samples contain a higher proportion. Compared to the urban scenario, the results derived from the six samples representing rural areas indicate a relatively smaller average increase of 63.09% in the number of initial ground seed points, especially in those areas with steep slopes and disconnected terrain.

Table 4.
The difference in seed point selection between AGPTD and the classical PTD.
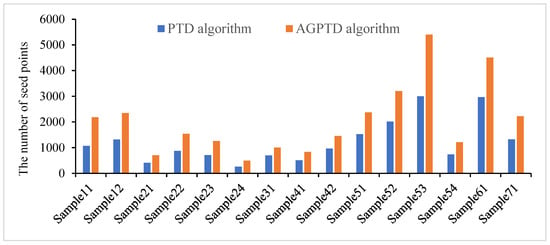
Figure 6.
Number of selected seed points for different sample datasets.
Figure 7 provides a visual representation of seed point selection outcomes for Samples 52 and 53. The results are consistent using the PTD and AGPTD algorithms in flat areas. However, in regions with disconnected terrain, the quantity and distribution of ground seed points extracted using the classical PTD algorithm with a regular grid struggle to capture terrain details. Conversely, deploying the AGPTD algorithm in such areas can preserve the terrain details more effectively, ensuring that the initial TIN facet is not overly smoothed.
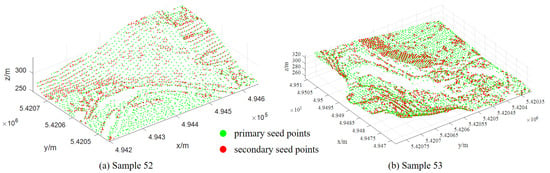
Figure 7.
The results of seed point selection for (a) Sample 52 and (b) Sample 53.
4.3. Filtering Performance
4.3.1. Qualitative Analysis
Figure 8 illustrates the outcome of iterative densification for Sample 52 and Sample 53. After removing outliers, point cloud data were subjected to iterative densification using the regular grids and the adaptive grids, respectively. A comparison of Figure 7 and Figure 8 reveals that the regions where a significant reduction in T.I occurred correspond closely with the initial ground seed points identified by the secondary grid in the AGPTD algorithm. This finding confirms that preserving as many terrain details as possible before the iterative densification process effectively reduces filtering errors, especially for T.I.
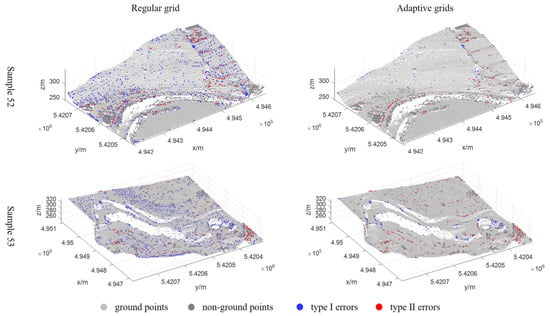
Figure 8.
The results of iterative densification for representative sample sets using the PTD and AGPTD algorithms.
Figure 9 presents the filtering outcomes for 15 sample datasets. The AGPTD algorithm addresses the issues encountered with the classical PTD algorithm in https://www.itc.nl/isprs/wgIII-3/filtertest/report/ (accessed on 30 September 2024), specifically bridges in Sample 21 and gangways in Sample 22, which effectively reduces T.II. Moreover, the AGPTD algorithm rectifies the misclassification of non-ground points as ground points in slope areas of Sample 51 and regions with disconnected terrain in Sample 53, further reducing T.II. Additionally, the AGPTD algorithm overcomes the deficiencies of the classical PTD in processing low points in Sample 31 and unfiltered courtyards in Sample 41, effectively decreasing T.I. These enhancements significantly improve the performance of the AGPTD algorithm, reducing both T.I and T.II, and further demonstrating that the AGPTD algorithm outperforms the classical PTD in preserving ground feature points.

Figure 9.
The filtering results of the 15 sample datasets using (a) PTD and (b) AGPTD. The number in the upper left corner of each picture is the sample number.
4.3.2. Quantitative Analysis
Table 5 displays the accuracy, precision, and recall of the results for 15 samples using the AGPTD algorithm. As indicated in the table, the accuracy ranges from 95.37% to 99.26%, the precision ranges from 94.53% to 99.23%, and the recall ranges from 97.63% to 99.52%.

Table 5.
The accuracy, precision and recall of results of the AGPTD algorithm (%).
Table 6 presents the filtering outcomes and error analysis for 15 sample datasets processed by the classical PTD algorithm and the AGPTD algorithm. The table indicates that, on average, T.I decreases by 4.44% with the AGPTD algorithm compared to the classical PTD algorithm. T.I for Samples 21, 51, 54, and 71 increases marginally, between 0.02% and 0.96%, whereas there is an improvement in the other samples. Additionally, there is an average increase of 1.42% in T.II. The average T.E. decreases by 2.54%, except for Sample 71, which shows a marginal increase of 0.03%, but the others exhibit enhancements. Notably, the kp values for all samples see a substantial increase, with an average improvement of 6.67%. Due to the limitations of the classical algorithm, especially in processing steep slopes and disconnected terrain, samples featuring such landscapes tend to show less pronounced improvements.

Table 6.
The errors of results using the classical PTD algorithm and the AGPTD algorithm (the bolded values represent the best performance for the same error).
5. Discussion
5.1. Comparison with Publicized Improved PTD Algorithm
Figure 10 presents the comparative results of the classical PTD algorithm, five improved PTD algorithms [24,25,26,27,36], and the AGPTD algorithm, based on three metrics: average T.I, average T.II, and average T.E. for the 15 samples. Table 7 presents the comparative results of the AGPTD algorithm against the five other improved PTD algorithms in terms of T.I and T.II of the 15 samples. The AGPTD algorithm exhibited an average T.I, T.II, and T.E. of 1.11%, 8.88%, and 2.28%, respectively. Compared to the other five improved PTD algorithms, AGPTD had the best performance in terms of average T.E, average T.I, and standard deviation of T.I, with values of 2.28%, 1.11%, and 0.65%, respectively. In terms of T.I, the AGPTD algorithm achieved the lowest T.I in 10 out of 15 samples, specifically Samples 11, 12, 21, 22, 23, 24, 41, 42, 52, and 53. These samples encompass complicated terrain including steep slopes, small objects, short vegetation, and disconnected terrain profiles. Cai et al. [27] showed the smallest T.I in the remaining four samples. Regarding T.II, AGPTD has the third smallest average T.II of 8.88%. Nie et al. [26] achieved the lowest T.II in 10 out of the 15 samples, with the lowest average T.II of 2.84%. Although Chen et al. [36] did not achieve the lowest average T.II, they obtained the optimal standard deviation for T.II, which was 3.22%.
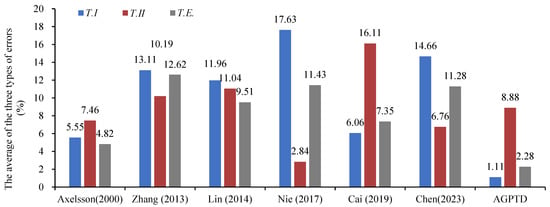
Figure 10.
The average of T.I, T.II, and T.E. for the 15 samples using the classical PTD algorithm, five improved PTD algorithms, and the AGPTD algorithm [23,24,25,26,27,36].

Table 7.
Comparison of the AGPTD algorithm with five improved PTD algorithms in terms of T.I (%) and T.II (%) of 15 samples (the bolded values represent the best performance for the same error).
The AGPTD algorithm shows notable performance in reducing T.I and is relatively weaker in reducing T.II. This is mainly because the more ground seed points that are extracted by the adaptive grid, the greater the risk of increasing T.II. However, the overall average precision of the ground seed points obtained by the AGPTD algorithm is as high as 98.91%, which effectively keeps the risk of T.II at an acceptable level. Furthermore, since T.II is easier to correct manually compared to T.I, the algorithm’s tendency towards T.II may not necessarily be a critical flaw in the filtering strategy [25,26].
5.2. Comparison with Other Filtering Methods
Table 8 and Figure 11 display a comparison of T.E. across 15 samples, as well as the average T.E. (Avg), standard deviation of T.E. (Std), and average kp (Akp) for the AGPTD algorithm versus other filtering algorithms [19,23,24,25,26,27,32,33,34,36,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54]. Figure 11 includes the algorithms listed in Table 8 as well as eight classical algorithms in https://www.itc.nl/isprs/wgIII-3/filtertest/report/ (accessed on 30 September 2024). The results indicate that in predominantly flat terrain, all filtering algorithms achieved fairly satisfactory outcomes. When compared with other optimized PTD algorithms, the AGPTD algorithm recorded the lowest T.E. values for four urban samples. Moreover, the AGPTD algorithm attained the lowest average T.E. at 2.28%, the smallest standard deviation of T.E. at 1.15%, and the highest kp at 90.86%. The results imply that the AGPTD algorithm has better adaptability for samples with a variety of terrain features and exhibits good filtering stability. Chen et al. [47] achieved the smallest T.E. in 5 out of the remaining 11 samples, which are primarily located in rural areas.

Table 8.
Comparison of the T.E. (%) of 15 samples, average T.E. (Avg), standard deviation of T.E. (Std), and average kp (Akp) using the AGPTD algorithm against results produced by other filtering algorithms (the bolded values represent the optimal performance).
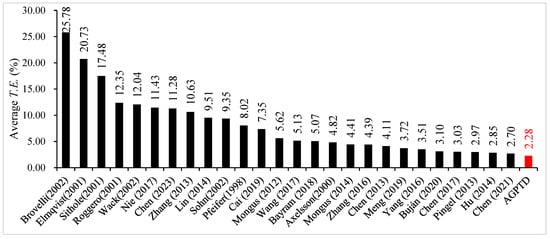
Figure 11.
Average T.E. on 15 samples for 27 filters [19,23,24,25,26,27,32,33,34,36,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54].
Overall, compared to the classical PTD algorithm, the AGPTD algorithm reduces the average T.I and average T.E. by 4.44% and 2.54% respectively, and the kp value increases by an average of 6.67%, at the cost of a 1.42% increase in the average T.II. Meanwhile, the AGPTD algorithm also demonstrates significant advantages over the classical PTD algorithm in preserving terrain details and adapting to complex terrain. Against the other five other improved PTD algorithms, the AGPTD algorithm achieves the smallest average T.I at 1.11%. Compared to the other methods, the AGPTD algorithm has the smallest standard deviation of T.I at 0.65%, the smallest average T.E. at 2.28%, and the highest average kp at 90.86%. The results indicate that the advantages presented by the AGPTD algorithm remain significant.
5.3. Limitations and Prospects
The key advantage of the AGPTD algorithm is its wide applicability, particularly in areas with significant topographical variations such as mountain tops, steep slopes, and disconnected terrain, where it retains terrain details more effectively. At the same time, the AGPTD algorithm also has some limitations: (1) Although PTD and its variants are good at urban areas, their generalization is very poor for terrain variations, particularly mountainous areas or forest-covered areas. The superiority of the AGPTD algorithm cannot be sufficiently demonstrated by the ISPRS dataset alone; (2) The AGPTD algorithm involved many parameters to be set. Therefore, choosing the appropriate grid level and optimal grid size that balances both filtering precision and computational efficiency presents a critical challenge for the AGPTD algorithm; (3) As deep learning has progressed, variants of the PTD algorithm have increasingly leveraged this approach for enhancement, whereas the AGPTD algorithm still relies on traditional algorithms.
Hence, in future research: (1) To enhance the generalization capability of the algorithm, we will aim to utilize a greater number of complex scenarios for the practical application and evaluation of the algorithm; (2) We will conduct more experiments to determine the appropriate number of grid levels and the optimal grid size to ensure the effective implementation of the algorithm; (3) We will attempt to adopt more advanced methods, such as deep learning, to further improve the AGPTD algorithm, thereby enhancing its robustness and efficiency.
6. Conclusions
This study proposed a novel algorithm (named AGPTD) by introducing adaptive grid technology to improve the widely used PTD algorithm. Specifically, the AGPTD algorithm can remove outliers with high precision before seed point selection and the construction of the initial TIN. It significantly increases the number of initial ground seed points through an adaptive grid to preserve terrain features, and it obtains the optimal filtering results through a trial-and-error method. In addition, it overcomes the issues encountered with the classic PTD algorithm, specifically non-filtered bridges and gangways. Furthermore, AGPTD can rectify the misclassification of non-ground as ground points in slope areas and disconnected terrain.
In terms of both qualitative and quantitative assessments, the AGPTD algorithm demonstrates outstanding performance. The proposed novel algorithm demonstrates significant advantages over the classical PTD algorithm in terms of preserving terrain details and adapting to complex terrain. The AGPTD algorithm exhibits superior outcomes in average T.E., average T.I, and the standard deviation of T.I when benchmarked against five others improved PTD algorithms. On the whole, the AGPTD algorithm excels markedly in minimizing T.I while showing somewhat less efficacy in mitigating T.II. Additionally, the average accuracy, precision, and recall of AGPTD are 97.69%, 97.52%, and 98.98%, respectively. The achievement of the lowest average T.E., the smallest standard deviation of T.E., and the highest kp implies that the AGPTD algorithm asserts its strengths in terrain adaptability and filtering stability relative to its counterparts. In the future, we will aim to decrease T.I while also minimizing T.II as much as possible, and to apply our algorithm in a greater variety of practical scenarios.
Author Contributions
Conceptualization, J.Z. (Jinjun Zheng), M.X., T.Z. and J.Z. (Ji Zhou); methodology, J.Z. (Jinjun Zheng), M.X., T.Z. and J.Z. (Ji Zhou); software, M.X. and J.Z. (Jinjun Zheng); validation, M.X., J.Z. (Jinjun Zheng) and J.Z. (Ji Zhou); formal analysis, M.X.; investigation, M.X. and T.Z.; data curation, J.Z. (Jinjun Zheng) and M.X.; writing—original draft preparation, J.Z. (Jinjun Zheng) and M.X.; writing—review and editing, J.Z. (Jinjun Zheng), M.X., T.Z. and J.Z. (Ji Zhou); supervision, J.Z. (Ji Zhou). All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported in part by the National Key Research and Development Program of China (grant number: 2023YFF1303502), and the Science Fund for Distinguished Young Scholars of Sichuan Province (grant number: 2023NSFSC1907).
Data Availability Statement
The data presented in this study are openly available in ISPRSWGII-3 at https://www.itc.nl/isprs/wgIII-3/filtertest/downloadsites/ (accessed on 30 September 2024).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ali, M.E.N.O.; Taha, L.G.E.-D.; Mohamed, M.H.A.; Mandouh, A.A. Generation of Digital Terrain Model from Multispectral LiDar Using Different Ground Filtering Techniques. Egypt. J. Remote Sens. Space Sci. 2021, 24, 181–189. [Google Scholar] [CrossRef]
- Chen, C.; Wu, H.; Yang, Z.; Li, Y. Adaptive Coarse-to-Fine Clustering and Terrain Feature-Aware-Based Method for Reducing LiDAR Terrain Point Clouds. ISPRS J. Photogramm. Remote Sens. 2023, 200, 89–105. [Google Scholar] [CrossRef]
- Shao, J.; Yao, W.; Wan, P.; Luo, L.; Wang, P.; Yang, L.; Lyu, J.; Zhang, W. Efficient Co-Registration of UAV and Ground LiDAR Forest Point Clouds Based on Canopy Shapes. Int. J. Appl. Earth Obs. Geoinf. 2022, 114, 103067. [Google Scholar] [CrossRef]
- Guo, L.; Wu, Y.; Deng, L.; Hou, P.; Zhai, J.; Chen, Y. A Feature-Level Point Cloud Fusion Method for Timber Volume of Forest Stands Estimation. Remote Sens. 2023, 15, 2995. [Google Scholar] [CrossRef]
- Gao, J.; Chen, Y.; Junior, J.; Wang, C.; Li, J. Rapid Extraction of Urban Road Guardrails From Mobile LiDAR Point Clouds. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1572–1577. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Li, J.; Tian, M.; Dai, W.; Zhong, R. Automated Reconstruction of Building LoDs from Airborne LiDAR Point Clouds Using an Improved Morphological Scale Space. Remote Sens. 2017, 9, 14. [Google Scholar] [CrossRef]
- Almeida, D.R.A.; Broadbent, E.N.; Zambrano, A.M.A.; Wilkinson, B.E.; Ferreira, M.E.; Chazdon, R.; Meli, P.; Gorgens, E.B.; Silva, C.A.; Stark, S.C.; et al. Monitoring the Structure of Forest Restoration Plantations with a Drone-Lidar System. Int. J. Appl. Earth Obs. Geoinf. 2019, 79, 192–198. [Google Scholar] [CrossRef]
- Morsy, S.; Shaker, A.; El-Rabbany, A. Classification of Multispectral Airborne LiDAR Data Using Geometric and Radiometric Information. Geomatics 2022, 2, 370–389. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, C.; Tian, S.; Lu, B.; Zhang, L.; Ning, X.; Bai, X. Deep Learning-Based 3D Point Cloud Classification: A Systematic Survey and Outlook. Displays 2023, 79, 102456. [Google Scholar] [CrossRef]
- Pan, Y.; Han, Y.; Wang, L.; Chen, J.; Meng, H.; Wang, G.; Zhang, Z.; Wang, S. 3D Reconstruction of Ground Crops Based on Airborne LiDAR Technology. IFAC-Pap. 2019, 52, 35–40. [Google Scholar] [CrossRef]
- Coiffier, G.; Basselin, J.; Ray, N.; Sokolov, D. Parametric Surface Fitting on Airborne Lidar Point Clouds for Building Reconstruction. Comput.-Aided Des. 2021, 140, 103090. [Google Scholar] [CrossRef]
- Bizjak, M.; Mongus, D.; Žalik, B.; Lukač, N. Novel Half-Spaces Based 3D Building Reconstruction Using Airborne LiDAR Data. Remote Sens. 2023, 15, 1269. [Google Scholar] [CrossRef]
- Qin, N.; Tan, W.; Guan, H.; Wang, L.; Ma, L.; Tao, P.; Fatholahi, S.; Hu, X.; Li, J. Towards Intelligent Ground Filtering of Large-Scale Topographic Point Clouds: A Comprehensive Survey. Int. J. Appl. Earth Obs. Geoinf. 2023, 125, 103566. [Google Scholar] [CrossRef]
- Qi, C.; Wang, X.; Su, D.; Guo, Y.; Yang, F. Comparison and Analysis of Ground Seed Detectors and Interpolation Methods in Airborne LiDAR Filtering. Egypt. J. Remote Sens. Space Sci. 2023, 26, 1009–1019. [Google Scholar] [CrossRef]
- Vosselman, G. Slope Based Filtering of Laser Altimetry Data. Int. Soc. Photogramm. Remote Sens. 2000, 33 Pt B3, 935–942. [Google Scholar]
- Susaki, J. Adaptive Slope Filtering of Airborne LiDAR Data in Urban Areas for Digital Terrain Model (DTM) Generation. Remote Sens. 2012, 4, 1804–1819. [Google Scholar] [CrossRef]
- Chen, Q.; Gong, P.; Baldocchi, D.; Xie, G. Filtering Airborne Laser Scanning Data with Morphological Methods. Photogramm. Eng. Remote Sens. 2007, 73, 175–185. [Google Scholar] [CrossRef]
- Li, Y.; Yong, B.; Van Oosterom, P.; Lemmens, M.; Wu, H.; Ren, L.; Zheng, M.; Zhou, J. Airborne LiDAR Data Filtering Based on Geodesic Transformations of Mathematical Morphology. Remote Sens. 2017, 9, 1104. [Google Scholar] [CrossRef]
- Meng, X.; Lin, Y.; Yan, L.; Gao, X.; Yao, Y.; Wang, C.; Luo, S. Airborne LiDAR Point Cloud Filtering by a Multilevel Adaptive Filter Based on Morphological Reconstruction and Thin Plate Spline Interpolation. Electronics 2019, 8, 1153. [Google Scholar] [CrossRef]
- Filin, S. Surface Clustering from Airborne Laser Scanning Data. Remote Sens. Spat. Inf. Sci. 2002, 34, 119–124. [Google Scholar]
- Ni, H.; Lin, X.; Zhang, J.; Chen, D.; Peethambaran, J. Joint Clusters and Iterative Graph Cuts for ALS Point Cloud Filtering. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 990–1004. [Google Scholar] [CrossRef]
- Liu, H.; Dong, P.; Wu, C.; Wang, P.; Fang, M. Individual Tree Identification Using a New Cluster-Based Approach with Discrete-Return Airborne LiDAR Data. Remote Sens. Environ. 2021, 258, 112382. [Google Scholar] [CrossRef]
- Axelsson, P. DEM Generation from Laser Scanner Data Using Adaptive TIN Models. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2000, 33, 111–118. [Google Scholar]
- Zhang, J.; Lin, X. Filtering Airborne LiDAR Data by Embedding Smoothness-Constrained Segmentation in Progressive TIN Densification. ISPRS J. Photogramm. Remote Sens. 2013, 81, 44–59. [Google Scholar] [CrossRef]
- Lin, X.; Zhang, J. Segmentation-Based Filtering of Airborne LiDAR Point Clouds by Progressive Densification of Terrain Segments. Remote Sens. 2014, 6, 1294–1326. [Google Scholar] [CrossRef]
- Nie, S.; Wang, C.; Dong, P.; Xi, X.; Luo, S.; Qin, H. A Revised Progressive TIN Densification for Filtering Airborne LiDAR Data. Measurement 2017, 104, 70–77. [Google Scholar] [CrossRef]
- Cai, S.; Zhang, W.; Liang, X.; Wan, P.; Qi, J.; Yu, S.; Yan, G.; Shao, J. Filtering Airborne LiDAR Data Through Complementary Cloth Simulation and Progressive TIN Densification Filters. Remote Sens. 2019, 11, 1037. [Google Scholar] [CrossRef]
- Hu, X.; An, X.; Li, L. Easy Synthesis of Highly Fluorescent Carbon Dots from Albumin and Their Photoluminescent Mechanism and Biological Imaging Applications. Mater. Sci. Eng. C 2016, 58, 730–736. [Google Scholar] [CrossRef]
- Jin, S.; Su, Y.; Zhao, X.; Hu, T.; Guo, Q. A Point-Based Fully Convolutional Neural Network for Airborne LiDAR Ground Point Filtering in Forested Environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 3958–3974. [Google Scholar] [CrossRef]
- Nurunnabi, A.; Teferle, F.; Li, J.; Lindenbergh, R.; Hunegnaw, A. An Efficient Deep Learning Approach for Ground Point Filtering in Aerial Laser Scanning Point Clouds. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci.-ISPRS Arch. 2021, 43, 31–38. [Google Scholar] [CrossRef]
- Qin, N.; Tan, W.; Ma, L.; Zhang, D.; Guan, H.; Li, J. Deep Learning for Filtering the Ground from ALS Point Clouds: A Dataset, Evaluations and Issues. ISPRS J. Photogramm. Remote Sens. 2023, 202, 246–261. [Google Scholar] [CrossRef]
- Mongus, D.; Žalik, B. Parameter-Free Ground Filtering of LiDAR Data for Automatic DTM Generation. ISPRS J. Photogramm. Remote Sens. 2012, 67, 1–12. [Google Scholar] [CrossRef]
- Yang, B.; Huang, R.; Dong, Z.; Zang, Y.; Li, J. Two-Step Adaptive Extraction Method for Ground Points and Breaklines from Lidar Point Clouds. ISPRS J. Photogramm. Remote Sens. 2016, 119, 373–389. [Google Scholar] [CrossRef]
- Pingel, T.J.; Clarke, K.C.; McBride, W.A. An Improved Simple Morphological Filter for the Terrain Classification of Airborne LIDAR Data. ISPRS J. Photogramm. Remote Sens. 2013, 77, 21–30. [Google Scholar] [CrossRef]
- Gu, Y.; Zhou, D.; An, Y.; Wang, R.; Wu, K.; Diao, X. Ground Point Extraction Using Self-Adaptive-Grid and Point to Surface Comparison. Measurement 2022, 204, 112057. [Google Scholar] [CrossRef]
- Chen, N.; Wang, N.; He, Y.; Ding, X.; Kong, J. An Improved Progressive Triangular Irregular Network Densification Filtering Algorithm for Airborne LiDAR Data. Front. Earth Sci. 2023, 10, 1015153. [Google Scholar] [CrossRef]
- Dong, Y.; Cui, X.; Zhang, L.; Ai, H. An Improved Progressive TIN Densification Filtering Method Considering the Density and Standard Variance of Point Clouds. ISPRS Int. J. Geo-Inf. 2018, 7, 409. [Google Scholar] [CrossRef]
- Zhao, X.; Guo, Q.; Su, Y.; Xue, B. Improved Progressive TIN Densification Filtering Algorithm for Airborne LiDAR Data in Forested Areas. ISPRS J. Photogramm. Remote Sens. 2016, 117, 79–91. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Li, W.; Dai, H. A Multiresolution Hierarchical Classification Algorithm for Filtering Airborne LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2013, 82, 1–9. [Google Scholar] [CrossRef]
- Hu, H.; Ding, Y.; Zhu, Q.; Wu, B.; Lin, H.; Du, Z.; Zhang, Y.; Zhang, Y. An Adaptive Surface Filter for Airborne Laser Scanning Point Clouds by Means of Regularization and Bending Energy. ISPRS J. Photogramm. Remote Sens. 2014, 92, 98–111. [Google Scholar] [CrossRef]
- Mongus, D.; Zalik, B. Computationally Efficient Method for the Generation of a Digital Terrain Model From Airborne LiDAR Data Using Connected Operators. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 340–351. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An Easy-to-Use Airborne LiDAR Data Filtering Method Based on Cloth Simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Chen, C.; Li, Y.; Zhao, N.; Guo, J.; Liu, G. A Fast and Robust Interpolation Filter for Airborne Lidar Point Clouds. PLoS ONE 2017, 12, e0176954. [Google Scholar] [CrossRef]
- Wang, L.; Xu, Y.; Li, Y. Aerial Lidar Point Cloud Voxelization with Its 3D Ground Filtering Application. Photogramm. Eng. Remote Sens. 2017, 83, 95–107. [Google Scholar] [CrossRef]
- Bayram, E.; Frossard, P.; Vural, E.; Alatan, A. Analysis of Airborne LiDAR Point Clouds With Spectral Graph Filtering. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1284–1288. [Google Scholar] [CrossRef]
- Buján, S.; Cordero, M.; Miranda, D. Hybrid Overlap Filter for LiDAR Point Clouds Using Free Software. Remote Sens. 2020, 12, 1051. [Google Scholar] [CrossRef]
- Chen, C.; Chang, B.; Li, Y.; Shi, B. Filtering Airborne LiDAR Point Clouds Based on a Scale-Irrelevant and Terrain-Adaptive Approach. Measurement 2021, 171, 108756. [Google Scholar] [CrossRef]
- Roggero, M. Airborne Laser Scanning-Clustering in Raw Data. ISPRS Arch. 2001, XXXIV, 227–232. [Google Scholar]
- Kraus, K.; Pfeifer, N. Determination of Terrain Models in Wooded Areas with Airborne Laser Scanner Data. ISPRS J. Photogramm. Remote Sens. 1998, 53, 193–203. [Google Scholar] [CrossRef]
- Wack, R.; Wimmer, A. Digital Terrain Models from Airborne Laser Scanner Data—A Grid Based Approach. ISPRS Arch. 2002, 34, 293–296. [Google Scholar]
- Sithole, G. Filtering of Laser Altimetry Data Using a Slope Adaptive Filter. ISPRS Arch. 2001, XXXIV-3/W4, 22–24. [Google Scholar]
- Brovelli, M.; Cannata, M.; Longoni, U. Managing and Processing LIDAR Data within GRASS; University of Trento: Trento, Italy, 2002. [Google Scholar]
- Elmqvist, M.; Jungert, E.; Lantz, F.; Persson, Å.; Söderman, U. Terrain Modelling and Analysis Using Laser Scanner Data. ISPRS Arch. 2001, 34, 219–226. [Google Scholar]
- Sohn, G.; Dowman, I. Terrain Surface Reconstruction by the Use of Tetrahedron Model with the MDL Criterion. ISPRS Arch. 2002, 34, 336–344. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).