Multitemporal Monitoring of Rocky Walls Using Robotic Total Station Surveying and Persistent Scatterer Interferometry
Abstract
1. Introduction
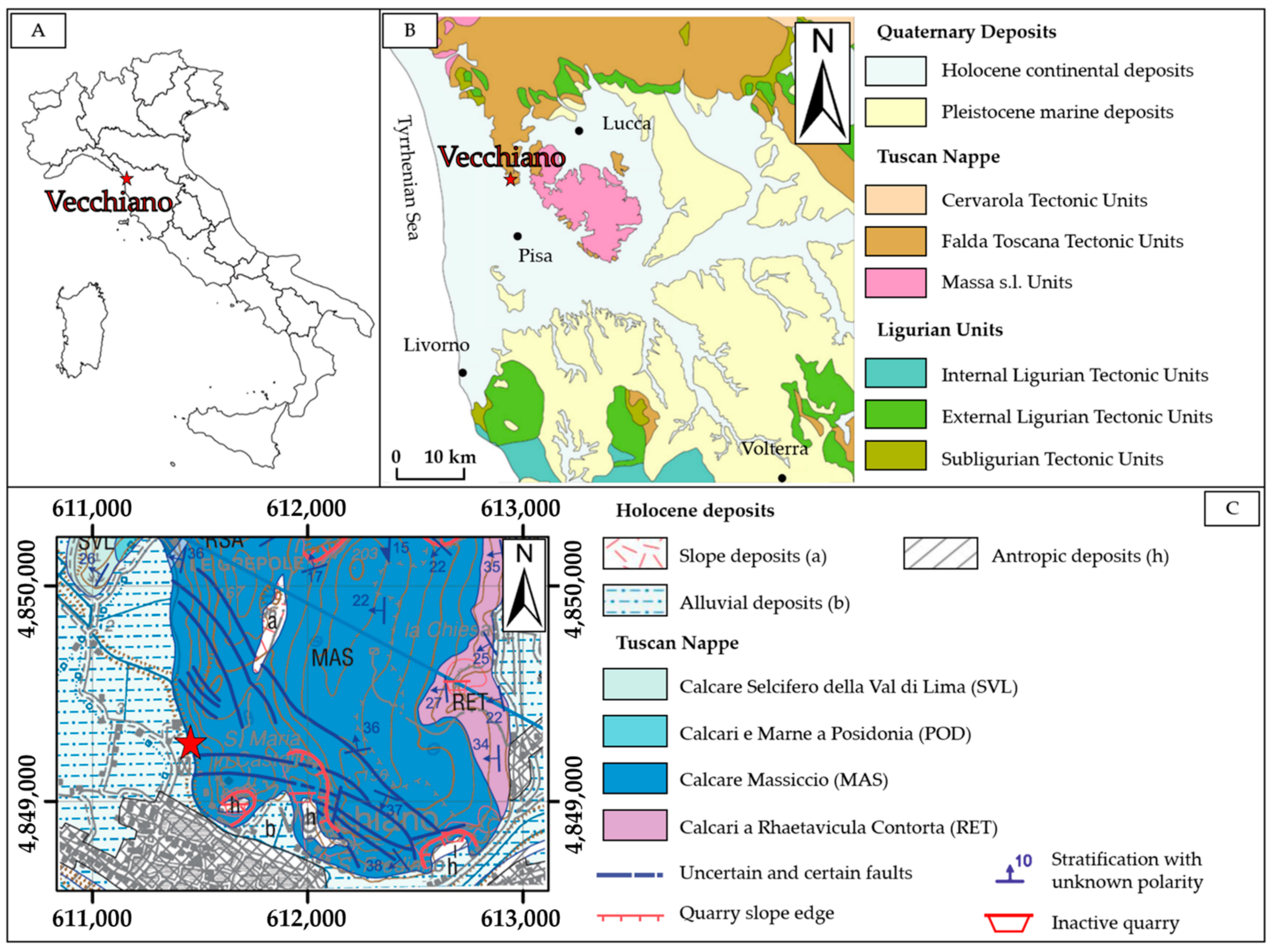
2. Geological Setting
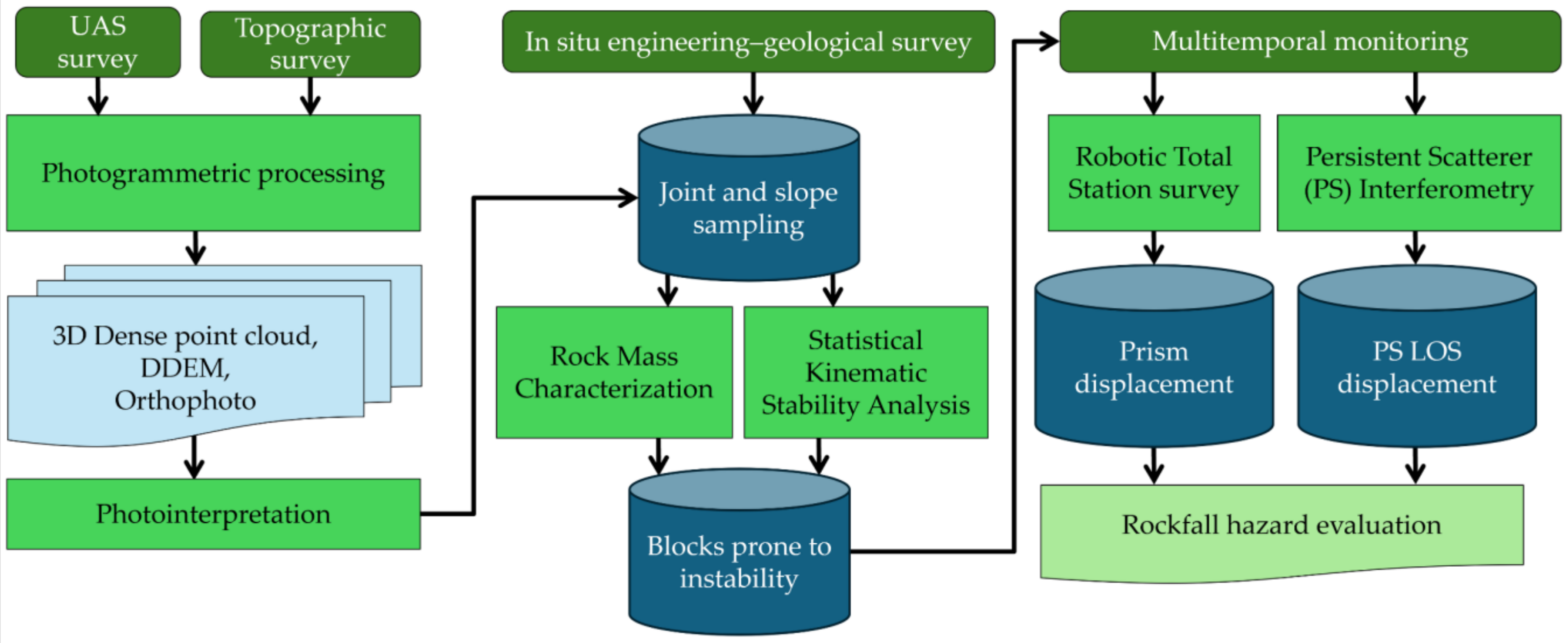
3. Materials and Methods
3.1. Topographic Survey
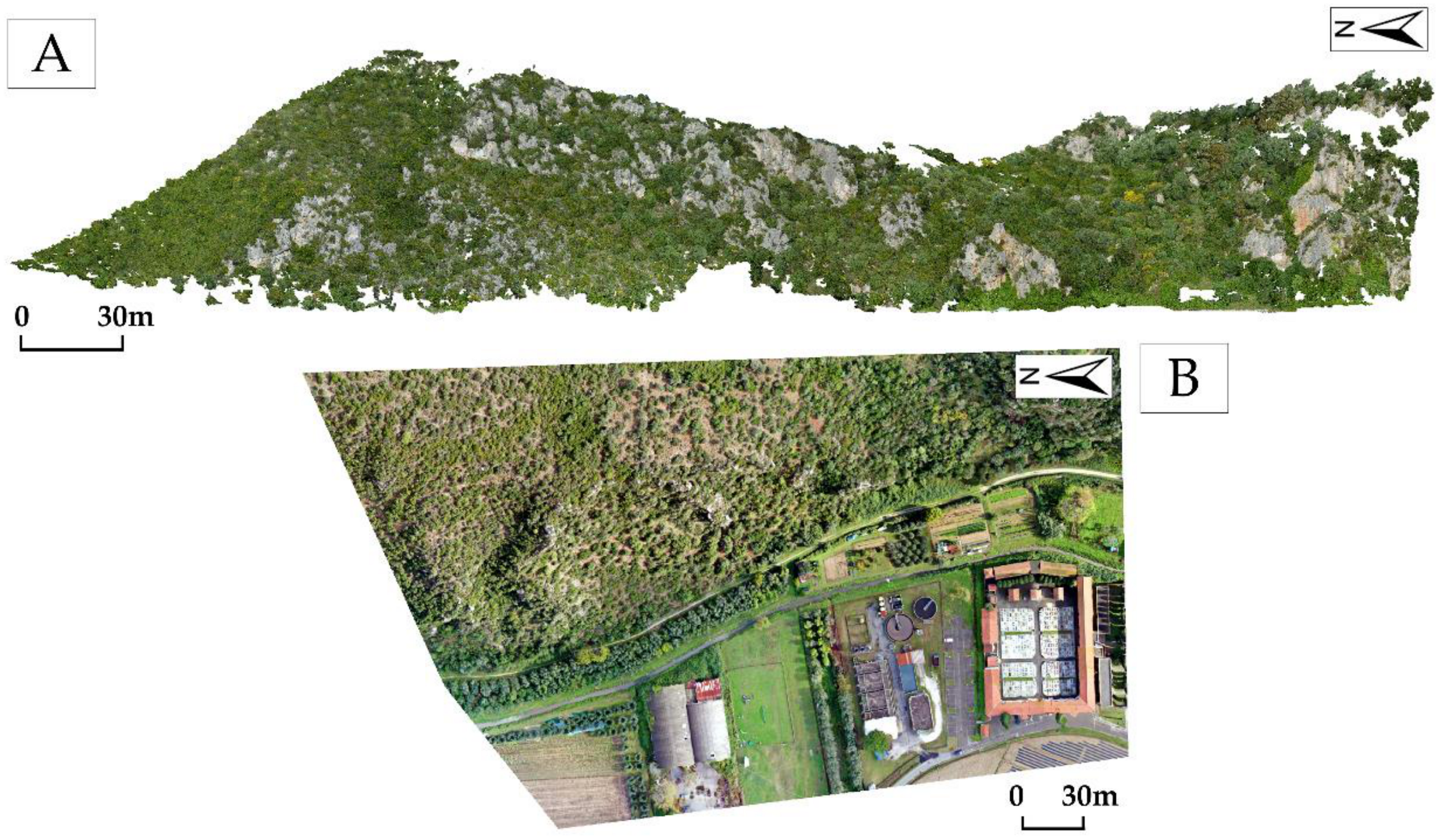
3.2. UAS Photogrammetric Survey
3.3. Engineering–Geological Survey and Rock Mass Characterization
3.4. Statistical Kinematic Stability Analysis
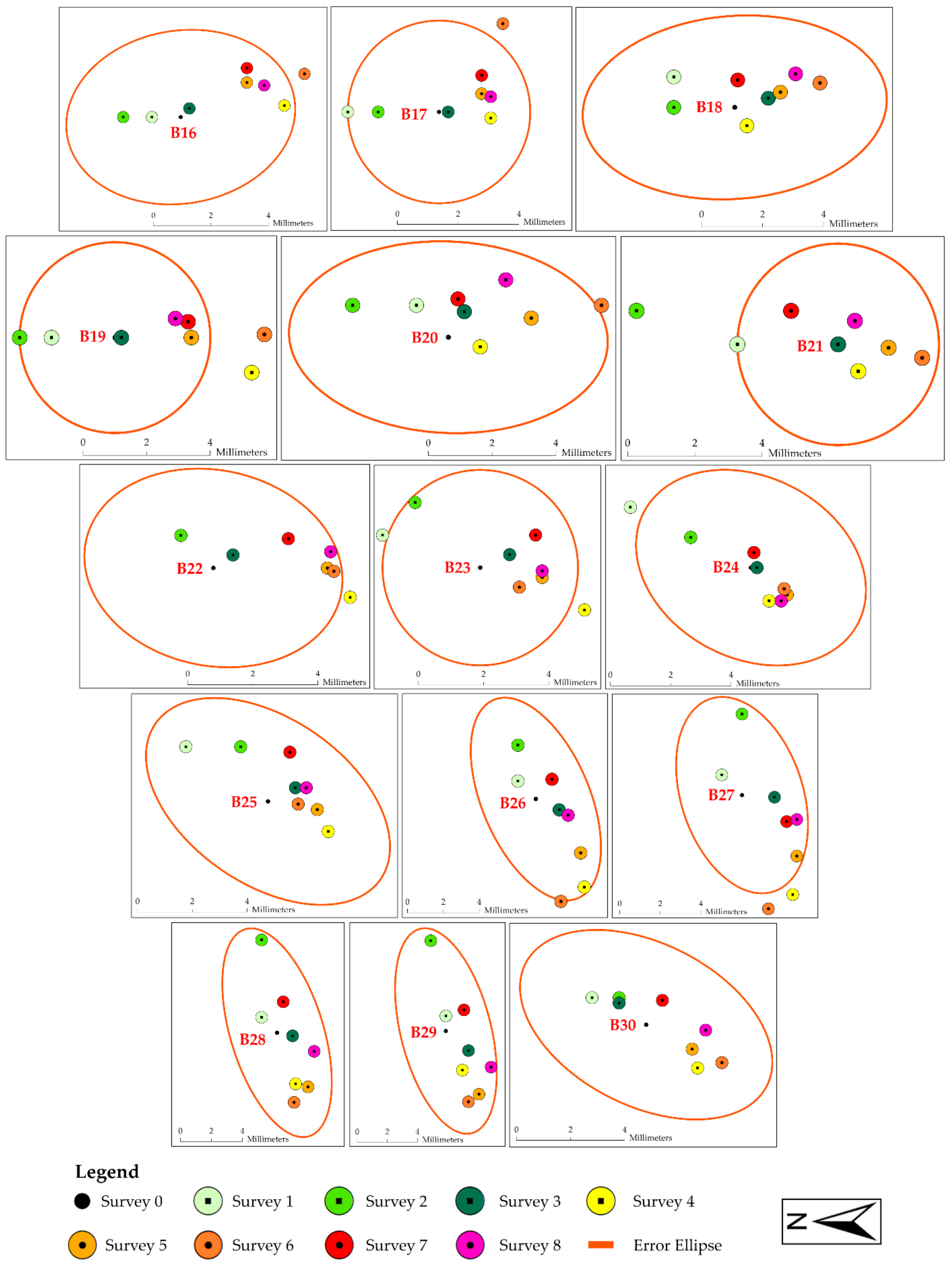
3.5. Multitemporal Monitoring through RTS
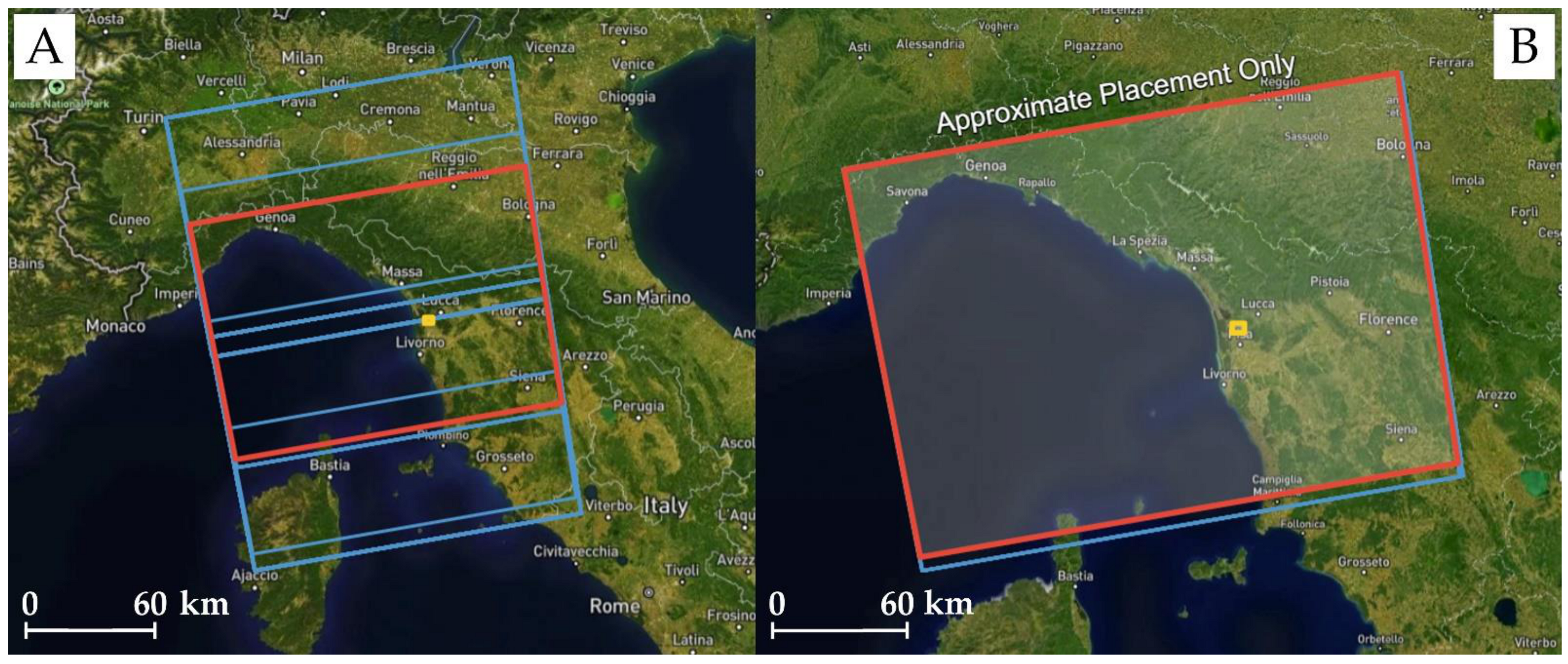
3.6. Persistent Scatterer Interferometry
4. Results
4.1. UAS Photogrammetry
4.2. Engineering–Geological Survey
4.3. Rock Mass Classification
4.3.1. RMR Method
4.3.2. Romana Method
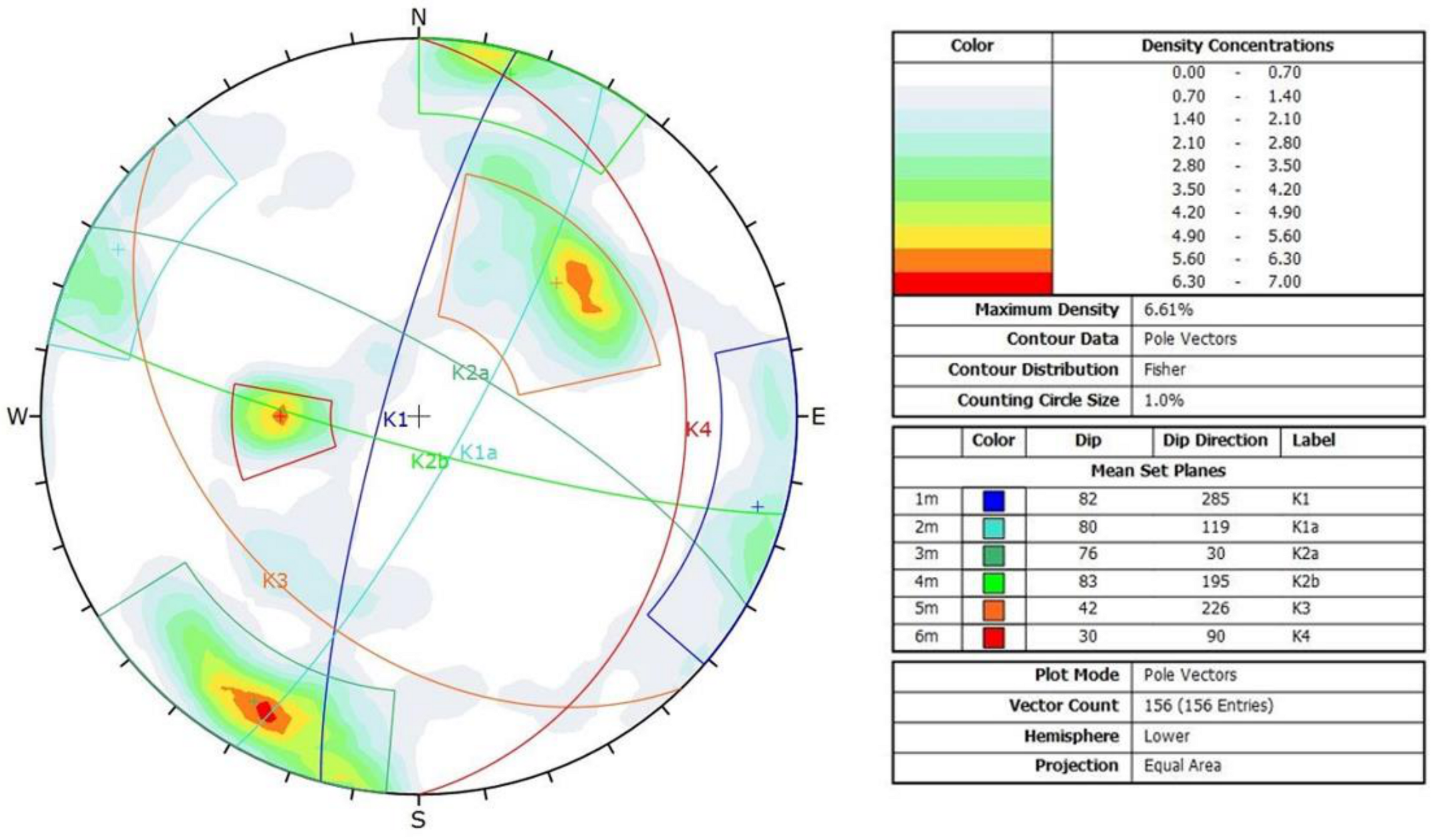
4.4. Statistical Kinematic Stability Analysis
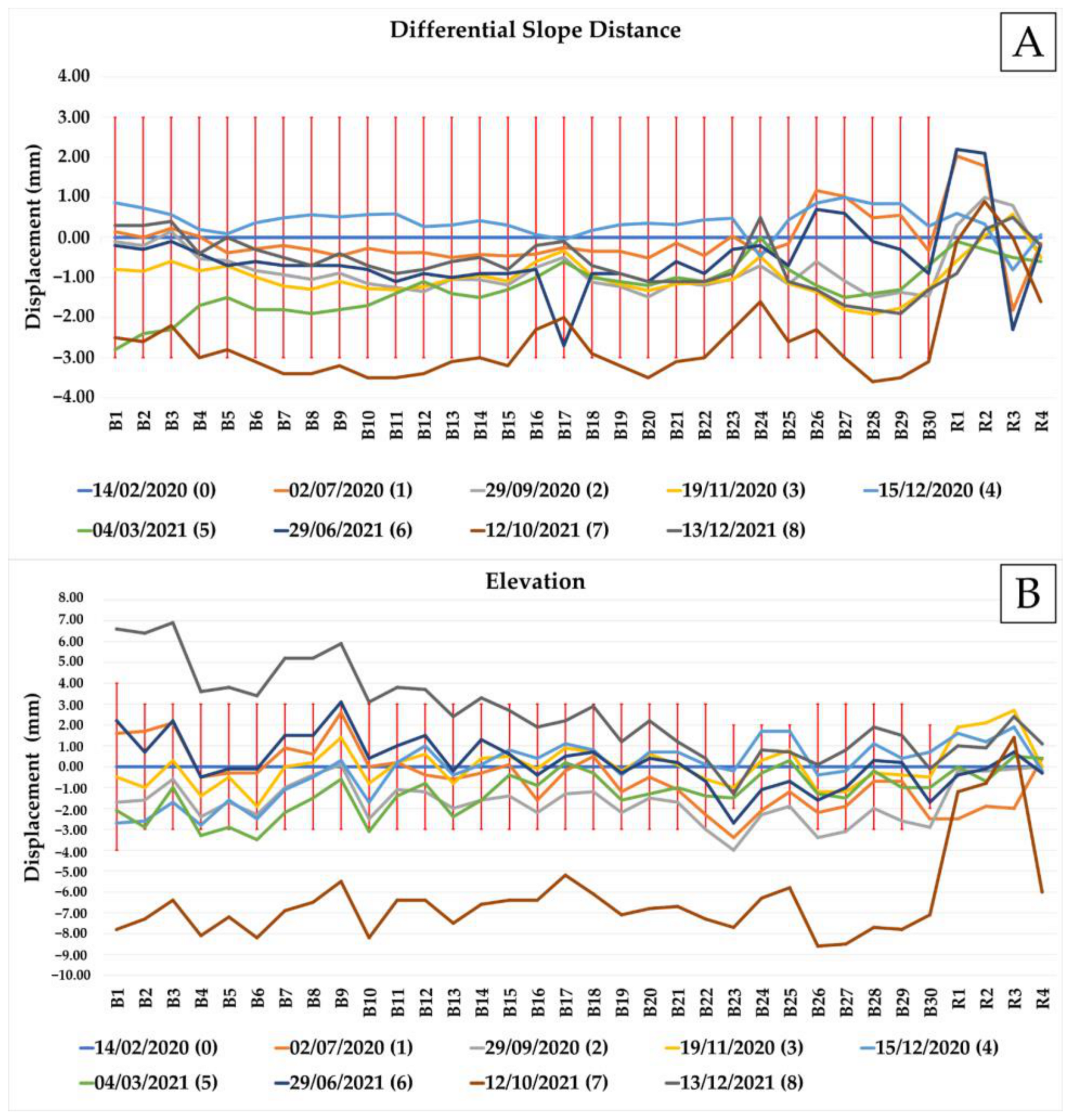
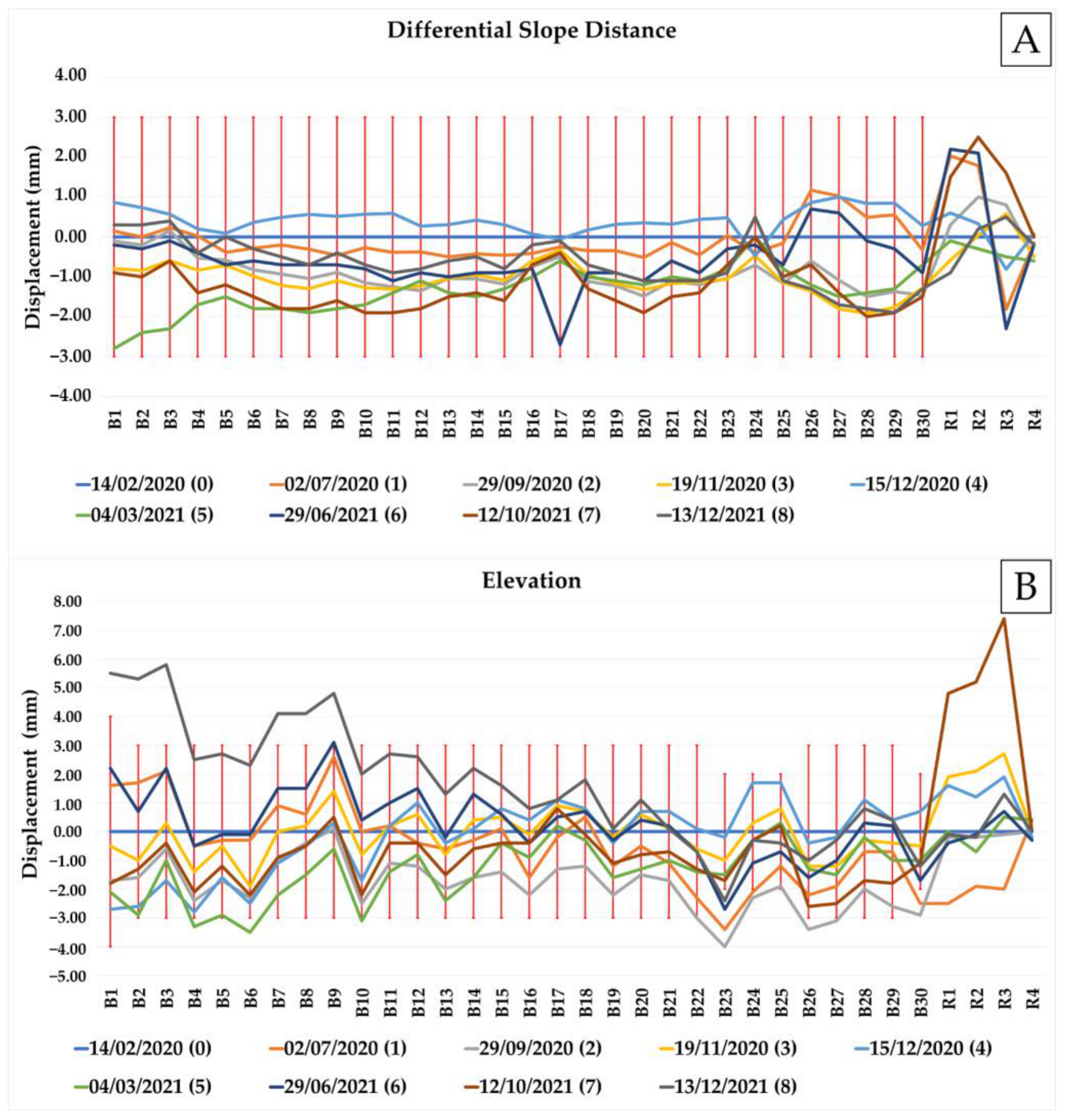
4.5. Multitemporal Monitoring through RTS
4.6. Persistent Scatterer Interferometry
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Varnes, D.J. Slope movement types and processes. In Special Report 176: Landslides: Analysis and Control; Schuster, R.L., Krizek, R.J., Eds.; TRB, National Research Council: Washington, DC, USA, 1978; pp. 11–33. [Google Scholar]
- Cruden, D.M.; Varnes, D.J. Landslide types and processes. In Landslides, Investigation and Mitigation; Turner, A.K., Schuster, R.L., Eds.; Transport Research Board, National Research Council: Washington, DC, USA, 1996. [Google Scholar]
- Hungr, O.; Leroueil, S.; Picarelli, L. The Varnes classification of landslide types, an update. Landslides 2014, 11, 167–194. [Google Scholar] [CrossRef]
- Briones-Bitar, J.; Carrión-Mero, P.; Montalván-Burbano, N.; Morante-Carballo, F. Rockfall Research: A Bibliometric Analysis and Future Trends. Geosciences 2020, 10, 403. [Google Scholar] [CrossRef]
- Wang, M.; Cao, X.; Qiao, L. Comprehensive analysis of hazardous rock mass and simulation of potential rockfall processes using 3D terrain model: A case study of the high cut slope near damsite of a hydropower station in southern China. Chin. J. Geol. Hazard Control. 2023, 34, 86–96. [Google Scholar]
- Konsolaki, A.; Vassilakis, E.; Kotsi, E.; Diakakis, M.; Mavroulis, S.; Petrakis, S.; Filis, C.; Lekkas, E. A Time-Series Analysis of Rockfall Evolution in a Coastal Region Using Remote Sensing Data. In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. [Google Scholar] [CrossRef]
- Caliò, D.; Mineo, S.; Pappalardo, G. Digital Rock Mass Analysis for the Evaluation of Rockfall Magnitude at Poorly Accessible Cliffs. Remote Sens. 2023, 15, 1515. [Google Scholar] [CrossRef]
- Schilirò, L.; Robiati, C.; Smeraglia, L.; Vinci, F.; Iannace, A.; Parente, M.; Tavani, S. An Integrated Approach for the Reconstruction of Rockfall Scenarios from UAV and Satellite-Based Data in the Sorrento Peninsula (Southern Italy). Eng. Geol. 2022, 308, 106795. [Google Scholar] [CrossRef]
- Notti, D.; Guenzi, D.; Lasaponara, R.; Giordan, D. Merging Historical Archives with Remote Sensing Data: A Methodology to Improve Rockfall Mitigation Strategy for Small Communities. Land 2022, 11, 1951. [Google Scholar] [CrossRef]
- Zhan, J.; Yu, Z.; Lv, Y.; Peng, J.; Song, S.; Yao, Z. Rockfall Hazard Assessment in the Taihang Grand Canyon Scenic Area Integrating Regional-Scale Identification of Potential Rockfall Sources. Remote Sens. 2022, 14, 3021. [Google Scholar] [CrossRef]
- Vanneschi, C.; Rindinella, A.; Salvini, R. Hazard Assessment of Rocky Slopes: An Integrated Photogrammetry—GIS Approach Including Fracture Density and Probability of Failure Data. Remote Sens. 2022, 14, 1438. [Google Scholar] [CrossRef]
- Robiati, C.; Eyre, M.; Vanneschi, C.; Francioni, M.; Venn, A.; Coggan, J. Application of Remote Sensing Data for Evaluation of Rockfall Potential within a Quarry Slope. ISPRS Int. J. Geo-Inf. 2019, 8, 367. [Google Scholar] [CrossRef]
- Pasternak, G.; Zaczek-Peplinska, J.; Pasternak, K.; Jóźwiak, J.; Pasik, M.; Koda, E.; Vaverková, M.D. Surface Monitoring of an MSW Landfill Based on Linear and Angular Measurements, TLS, and LIDAR UAV. Sensors 2023, 23, 1847. [Google Scholar] [CrossRef]
- Carlà, T.; Gigli, G.; Lombardi, L.; Nocentini, M.; Meier, L.; Schmid, L.; Wahlen, S.; Casagli, N. Real-Time Detection and Management of Rockfall Hazards by Ground-Based Doppler Radar. Landslides 2024, 21, 155–163. [Google Scholar] [CrossRef]
- Miles, C.; Gomez, F.; Rosenblad, B.L.; Fulks, J.; Loehr, J.E. Quantifying Measurement Capabilities of Ground-Based Interferometric Radar for Rockfall Hazard Applications. Geotech. Test. J. 2020, 43, 985–1002. [Google Scholar] [CrossRef]
- Janeras, M.; Lantada, N.; Núñez-Andrés, M.A.; Hantz, D.; Pedraza, O.; Cornejo, R.; Guinau, M.; García-Sellés, D.; Blanco, L.; Gili, J.A.; et al. Rockfall Magnitude-Frequency Relationship Based on Multi-Source Data from Monitoring and Inventory. Remote Sens. 2023, 15, 1981. [Google Scholar] [CrossRef]
- Romeo, S.; Cosentino, A.; Giani, F.; Mastrantoni, G.; Mazzanti, P. Combining Ground Based Remote Sensing Tools for Rockfalls Assessment and Monitoring: The Poggio Baldi Landslide Natural Laboratory. Sensors 2021, 21, 2632. [Google Scholar] [CrossRef]
- Chen, J.; Li, H.; Jiang, N.; Chen, Q.; Zhou, J. A Method for Automatic Assessment of Rockfall Susceptibility Based on High-Resolution Point Clouds. Rock Mech. Rock Eng. 2024, 57, 1717–1733. [Google Scholar] [CrossRef]
- Giacomini, A.; Thoeni, K.; Santise, M.; Diotri, F.; Booth, S.; Fityus, S.; Roncella, R. Temporal-Spatial Frequency Rockfall Data from Open-Pit Highwalls Using a Low-Cost Monitoring System. Remote Sens. 2020, 12, 2459. [Google Scholar] [CrossRef]
- Minardo, A.; Coscetta, A.; Porcaro, G.; Giannetta, D.; Bernini, R.; Zeni, L. Distributed optical fiber sensors for integrated monitoring of railway infrastructures. Struct. Monit. Maint. 2014, 1, 173–182. [Google Scholar] [CrossRef]
- Lalam, N.; Ng, W.P.; Dai, X.; Wu, Q.; Fu, Q. Analysis of Brillouin Frequency Shift in Distributed Optical Fiber Sensor System for Strain and Temperature Monitoring. In Proceedings of the 4th International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS), Rome, Italy, 27–29 February 2016. [Google Scholar]
- Barrias, A.; Casas, J.R.; Villalba, S. A Review of Distributed Optical Fiber Sensors for Civil Engineering Applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef] [PubMed]
- Carlino, S.; Mirabile, M.; Troise, C.; Sacchi, M.; Zeni, L.; Minardo, A.; Caccavale, M.; Darányi, V.; De Natale, G.; Mcgonigle, A.; et al. Distributed-Temperature-Sensing Using Optical Methods: A First Application in the Offshore Area of Campi Flegrei Caldera (Southern Italy) for Volcano Monitoring. Remote Sens. 2016, 8, 674. [Google Scholar] [CrossRef]
- Minardo, A.; Catalano, E.; Coscetta, A.; Zeni, G.; Zhang, L.; Di Maio, C.; Vassallo, R.; Coviello, R.; Macchia, G.; Picarelli, L.; et al. Distributed Fiber Optic Sensors for the Monitoring of a Tunnel Crossing a Landslide. Remote Sens. 2018, 10, 1291. [Google Scholar] [CrossRef]
- Zhenglin, Z.; Gao, L.; Sun, Y.; Zhang, Q.; Zeng, P. Strain Transfer Law of Distributed Optical Fiber Sensor. Chin. J. Lasers 2019, 46, 0410001. [Google Scholar] [CrossRef]
- Lanciano, C.; Salvini, R. Monitoring of Strain and Temperature in an Open Pit Using Brillouin Distributed Optical Fiber Sensors. Sensors 2020, 20, 1924. [Google Scholar] [CrossRef] [PubMed]
- Lanciano, C.; Vanneschi, C.; Tufarolo, E.; Salvini, R. Distributed Optical Fiber Sensors and Terrestrial Laser Scanner Surveys for the Monitoring of an Underground Marble Quarry. Ital. J. Eng. Geol. Environ. 2021, 1, 117–125. [Google Scholar] [CrossRef]
- Salvini, R.; Vanneschi, C.; Riccucci, S.; Francioni, M.; Gullì, D. Application of an Integrated Geotechnical and Topographic Monitoring System in the Lorano Marble Quarry (Apuan Alps, Italy). Geomorphology 2015, 241, 209–223. [Google Scholar] [CrossRef][Green Version]
- Racek, O.; Blahůt, J.; Hartvich, F. Observation of the Rock Slope Thermal Regime, Coupled with Crackmeter Stability Monitoring: Initial Results from Three Different Sites in Czechia (Central Europe). Geosci. Instrum. Methods Data Syst. 2021, 10, 203–218. [Google Scholar] [CrossRef]
- Auflič, M.J.; Herrera, G.; Mateos, R.M.; Poyiadji, E.; Quental, L.; Severine, B.; Peternel, T.; Podolszki, L.; Calcaterra, S.; Kociu, A.; et al. Landslide Monitoring Techniques in the Geological Surveys of Europe. Landslides 2023, 20, 951–965. [Google Scholar] [CrossRef]
- Blahůt, J.; Racek, O. Modern Methods of Rock Mass Characterisation and Rockfall Monitoring: A Review. In Landslides: Detection, Prediction and Monitoring; Springer eBooks: Berlin/Heidelberg, Germany, 2023; pp. 1–38. [Google Scholar] [CrossRef]
- Souza, B.; Benoît, J. Rockfall Motion Using a Smart Rock Sensor. Can. Geotech. J. 2024, 61, 802–819. [Google Scholar] [CrossRef]
- Dematteis, N.; Wrzesniak, A.; Allasia, P.; Bertolo, D.; Giordan, D. Integration of Robotic Total Station and Digital Image Correlation to Assess the Three-Dimensional Surface Kinematics of a Landslide. Eng. Geol. 2022, 303, 106655. [Google Scholar] [CrossRef]
- Çelik, M.A.; Gülersoy, A.E. Evaluation of Rock Fall Risk in Kilis (Turkey) City by Using GIS and Remote Sensing. Int. J. Comput. Exp. Sci. Eng. 2017, 3, 1–4. [Google Scholar]
- Castelli, M.; Torsello, G.; Vallero, G. Preliminary Modeling of Rockfall Runout: Definition of the Input Parameters for the QGIS Plugin QPROTO. Geosciences 2021, 11, 88. [Google Scholar] [CrossRef]
- Depountis, N.; Nikolakopoulos, K.; Kavoura, K.; Sabatakakis, N. Description of a GIS-Based Rockfall Hazard Assessment Methodology and Its Application in Mountainous Sites. Bull. Eng. Geol. Environ. 2019, 79, 645–658. [Google Scholar] [CrossRef]
- Wang, X.; Liu, H.; Sun, J. A New Approach for Identification of Potential Rockfall Source Areas Controlled by Rock Mass Strength at a Regional Scale. Remote Sens. 2021, 13, 938. [Google Scholar] [CrossRef]
- Wohlers, A.; Damm, B. Rockfall Vulnerability of a Rural Road Network—A Methodological Approach in the Harz Mountains, Germany. Geosciences 2022, 12, 170. [Google Scholar] [CrossRef]
- Pinto Santos, P.; Reyes-Carmona, C.; Pereira, S.; Sarro, R.; Martínez-Corbella, M.; Coll-Ramis, M.A.; Zêzere, J.L.; Mateos, R.M. Seasonal Rockfall Risk Analysis in a Touristic Island: Application to the Tramuntana Range (Mallorca, Spain). Int. J. Disaster Risk Reduct. 2024, 101, 104264. [Google Scholar] [CrossRef]
- El Miloudi, Y.; El Kharim, Y.; Bounab, A.; El Hamdouni, R. Effect of Rockfall Spatial Representation on the Accuracy and Reliability of Susceptibility Models (The Case of the Haouz Dorsale Calcaire, Morocco). Land 2024, 13, 176. [Google Scholar] [CrossRef]
- Mahmood, S.; Atique, F.; Rehman, A.; Mayo, S.M.; Ahamad, M.I. Rockfall Susceptibility Assessment along M-2 Motorway in Salt Range, Pakistan. J. Appl. Geophys. 2024, 222, 105312. [Google Scholar] [CrossRef]
- Peng, H.; Xie, Q.; Chen, B.; Tan, K.; Cao, Z.; Wu, B. Failure Mode of the Hazardous Diaozui Rock Mass of the Qutang Gorge in the Three Gorges Reservoir Area Based on a Three-Dimensional Numerical Analysis. Bull. Eng. Geol. Environ. 2024, 83, 100. [Google Scholar] [CrossRef]
- Massaro, L.; Forte, G.; De Falco, M.; Rauseo, F.; Santo, A. Rockfall Source Identification and Trajectory Analysis from UAV-Based Data in Volcano-Tectonic Areas: A Case Study from Ischia Island, Southern Italy. Bull. Eng. Geol. Environ. 2024, 83, 75. [Google Scholar] [CrossRef]
- Noël, F.; Nordang, S.F.; Jaboyedoff, M.; Digout, M.; Guerin, A.; Locat, J.; Matasci, B. Comparing Flow-R, Rockyfor3D and RAMMS to Rockfalls from the Mel de la Niva Mountain: A Benchmarking Exercise. Geosciences 2023, 13, 200. [Google Scholar] [CrossRef]
- Yuen, T.Y.P.; Weng, M.-C.; Fu, Y.-Y.; Lu, G.-T.; Shiu, W.-J.; Lu, C.-A.; Liu, C.-Y.; Chiu, C.-C.; Wen, T.-H. Assessing the impact of rockfall on a bridge by using hybrid DEM/FEM analysis: A case study in Central Taiwan. Eng. Geol. 2023, 314, 107000. [Google Scholar] [CrossRef]
- Angın, Z.; Karahasan, O.Ş. Evaluation of the Performance of Gabion Walls as a High-Energy Rockfall Protection System Using 3D Numerical Analysis: A Case Study. Appl. Sci. 2024, 14, 2360. [Google Scholar] [CrossRef]
- Agliardi, F.; Frattini, P.; Stock, G.M.; Tosi, T.; Lanfranconi, C.; Collins, B.D. Probabilistic rockfall hazard and risk analysis along the El Portal Road in Yosemite National Park (California, USA). In Proceedings of the EGU General Assembly 2024, Vienna, Austria, 14–19 April 2024. EGU24-9085. [Google Scholar] [CrossRef]
- Liu, G.; Zhong, Z.; Ma, K.; Bo, W.; Zhao, P.; Li, Y.; Zhang, Z.; Zhang, P. Field Experimental Verifications of 3D DDA and Its Applications to Kinematic Evolutions of Rockfalls. Int. J. Rock Mech. Min. Sci. 2024, 175, 105687. [Google Scholar] [CrossRef]
- Merla, G. Geologia dell’Appennino Settentrionale. Boll. Soc. Geol. Ital. 1952, 70, 95–382. [Google Scholar]
- Giannini, E.; Nardi, R. Geologia della zona nord—occidentale del Monte Pisano e dei Monti d’Oltre Serchio (prov. di Pisa e Lucca). Boll. Soc. Geol. Ital. 1965, 84, 198–270. [Google Scholar]
- Rau, A.; Tongiorgi, M. Il lembo mesozoico di Caprona- Uliveto Treme sul margine meridionale dei Monti Pisani: Tettonica e cenni di stratigrafia. Mem. Soc. Geol. Ital. 1969, 7, 1–24. [Google Scholar]
- Boccaletti, M.; Ficcarelli, G.; Manetti, P.; Turi, A. Analisi stratigrafiche, sedimentologiche e petrografiche delle formazioni mesozoiche della Val di Lima (Prov. di Lucca). Mem. Soc. Geol. Ital. 1969, 8, 847–922. [Google Scholar]
- Rau, A.; Tongiorgi, M. Geologia dei Monti Pisani a Sud-Est della valle del Guappero. Mem. Soc. Geol. Ital. 1974, 13, 227–408. [Google Scholar]
- Carosi, R.; Montomoli, C.; Pertusati, P.C.; Sarti, G.; Frassi, C.; Leoni, L. Note Illustrative della Carta Geologica d’Italia alla scala 1:50.000 Foglio 273—Pisa; LAC: Florence, Italy, 2021. (In Italian) [Google Scholar]
- D’Amato Avanzi, G.; Nardi, I. Indizi di neotettonica nei Monti d’Oltre Serchio: Faglie distensive recenti al bordo della pianura pisana e depositi ciottolosi a quota 170 metri. Boll. Soc. Geol. Ital. 1993, 112, 601–614. [Google Scholar]
- CISIS. ConveRgo, Version 2.04; CISIS: Rome, Italy, 2012; Available online: https://www.cisis.it/?page_id=3214 (accessed on 31 May 2024).
- Leica Geosystems AG. Leica Infinity, Version 3.4.2; Leica Geosystems AG—Part of Hexagon. 2021. Available online: https://leica-geosystems.com/products/gnss-systems/software/leica-infinity (accessed on 31 May 2024).
- SPH Engineering. UgCSTM Professional Desktop Drone Flight Planning Software, Version 4.18; Latvia. 2023. Available online: https://www.sphengineering.com/support (accessed on 31 May 2024).
- Agisoft LLC. Agisoft Metashape ProfessionalTM, Version 2.0.; Agisoft LLC: St. Petersburg, Russia, 2023; Available online: https://www.agisoft.com/ (accessed on 31 May 2024).
- CloudCompare. Version 2. 2021. Available online: http://www.cloudcompare.org/ (accessed on 31 May 2024).
- Bieniawski, Z.T. Engineering Rock Mass Classification; John Wiley and Sons: New York, NY, USA, 1989; p. 251. [Google Scholar]
- Romana, M. New adjustment ratings for application of Bieniawski classification to slopes. In Proceedings of the International Symposium on the Role of Rock Mechanics in Excavations for Mining and Civil Works. International Society of Rock Mechanics, Zacatecas, Mexico, 2–4 September 1985; pp. 49–53. [Google Scholar]
- Markland, J.T. A Useful Technique for Estimating the Stability of Rock Slopes When the Rigid Wedge Slide Type of Failure Is Expected; Interdepartmental Rock Mechanics Project, Imperial College of Science and Technology: London, UK, 1972; Volume 19, p. 10. [Google Scholar]
- Hoek, E.; Bray, J.W. Rock Slope Engineering, 3rd ed.; The Institution of Mining and Metallurgy: London, UK, 1981; pp. 257–270. [Google Scholar]
- Rocscience DipsTM: Graphical and Statistical Analysis of Orientation Data, Version 8.022. Available online: https://www.rocscience.com/software/dips (accessed on 31 May 2024).
- Crosetto, M.; Monserrat, O.; Cuevas-González, M.; Devanthéry, N.; Crippa, B. Persistent Scatterer Interferometry: A Review. ISPRS J. Photogramm. Remote Sens. 2016, 115, 78–89. [Google Scholar] [CrossRef]
- Garthwaite, M.C.; Nancarrow, S.; Hislop, A.; Thankappan, M.; Dawson, J.H.; Lawrie, S. The Design of Radar Corner Reflectors for the Australian Geophysical Observing System: A Single Design Suitable for InSAR Deformation Monitoring and SAR Calibration at Multiple Microwave Frequency Bands; Geoscience Australia: Symonston, ACT, Australia, 2015. [CrossRef]
- Hooper, A.; Zebker, H.; Segall, P.; Kampes, B. A New Method for Measuring Deformation on Volcanoes and Other Natural Terrains Using InSAR Persistent Scatterers. Geophys. Res. Lett. 2004, 31, L23611. [Google Scholar] [CrossRef]
- Foumelis, M.; Delgado Blasco, J.M.; Desnos, Y.-L.; Engdahl, M.; Fernandez, D.; Veci, L.; Lu, J.; Wong, C. Esa Snap—Stamps Integrated Processing for Sentinel-1 Persistent Scatterer Interferometry. In Proceedings of the IGARSS 2018—2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018. [Google Scholar] [CrossRef]
- SNAP-ESA Sentinel Application Platform, Version v7.0.0. Available online: http://step.esa.int (accessed on 22 January 2022).
- Hooper, A. A Multitemporal InSAR Method Incorporating Both Persistent Scatterer and Small Baseline Approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Zhao, C.; Lu, Z.; Zhang, Q.; de la Fuente, J. Large-Area Landslide Detection and Monitoring with ALOS/PALSAR Imagery Data over Northern California and Southern Oregon, USA. Remote Sens. Environ. 2012, 124, 348–359. [Google Scholar] [CrossRef]
- Scaioni, M.; Longoni, L.; Melillo, V.; Papini, M. Remote Sensing for Landslide Investigations: An Overview of Recent Achievements and Perspectives. Remote Sens. 2014, 6, 9600–9652. [Google Scholar] [CrossRef]
- Fárová, K.; Jelének, J.; Kopačková-Strnadová, V.; Kycl, P. Comparing DInSAR and PSI Techniques Employed to Sentinel-1 Data to Monitor Highway Stability: A Case Study of a Massive Dobkovičky Landslide, Czech Republic. Remote Sens. 2019, 11, 2670. [Google Scholar] [CrossRef]
- ASF Data Search. search.asf.alaska.edu. Available online: https://search.asf.alaska.edu/#/ (accessed on 31 May 2024).
- Consorzio LaMMA. Geoportale della Difesa del Suolo della Regione Toscana. Available online: https://geoportale.lamma.rete.toscana.it/difesa_suolo/#/viewer/326 (accessed on 31 May 2024).
- Artese, S.; Perrelli, M. Monitoring a Landslide with High Accuracy by Total Station: A DTM Based Model to Correct for the Atmospheric Effects. Geosciences 2018, 8, 46. [Google Scholar] [CrossRef]
- Carvill, J. Mechanical Engineer’s Data Handbook; Butterworth-Heinemann: Oxford, UK, 1993. [Google Scholar]
- Afeni, T.B.; Cawood, F.T. Slope Monitoring using Total Station: What are the Challenges and How Should These be Mitigated? S. Afr. J. Geomat. 2013, 2, 41–53. [Google Scholar]
- Strozzi, T.; Teatini, P.; Tosi, L.; Wegmüller, U.; Werner, C. Land subsidence of natural transitional environments by satellite radar interferometry on artificial reflectors. J. Geophys. Res. Earth Surf. 2013, 118, 1177–1191. [Google Scholar] [CrossRef]
- Ferretti, A.; Savio, G.; Barzaghi, R.; Borghi, A.; Musazzi, S.; Novali, F.; Prati, C.; Rocca, F. Submillimeter accuracy of InSAR time series: Experimental validation. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1142–1153. [Google Scholar] [CrossRef]
- Garthwaite, M.C. On the Design of Radar Corner Reflectors for Deformation Monitoring in Multi-Frequency InSAR. Remote Sens. 2017, 9, 648. [Google Scholar] [CrossRef]
- Czikhardt, R.; Van Der Marel, H.; van Leijen, F.J.; Hanssen, R.F. Estimating Signal-To-Clutter Ratio of InSAR Corner Reflectors from SAR Time Series. IEEE Geosci. Remote Sens. Lett. 2022, 19, 4012605. [Google Scholar] [CrossRef]
- Zerbini, S.; Richter, B.; Rocca, F.; Bordas, S.; Matonti, F. A Combination of Space and Terrestrial Geodetic Techniques to Monitor Land Subsidence: Case Study, the Southeastern Po Plain, Italy. J. Geophys. Res. Solid Earth 2007, 112, B05401. [Google Scholar] [CrossRef]
- Cigna, F.; Esquivel Ramírez, R.; Tapete, D. Accuracy of Sentinel-1 PSI and SBAS InSAR Displacement Velocities against GNSS and Geodetic Leveling Monitoring Data. Remote Sens. 2021, 13, 4800. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, S.; Jiang, M.; Pei, Y.; Qu, T.; Xu, J.; Yang, C. Spatial and Temporal Subsidence Characteristics in Wuhan (China), during 2015–2019, Inferred from Sentinel-1 Synthetic Aperture Radar (SAR) Interferometry. Nat. Hazards Earth Syst. Sci. 2021, 21, 2285–2297. [Google Scholar] [CrossRef]



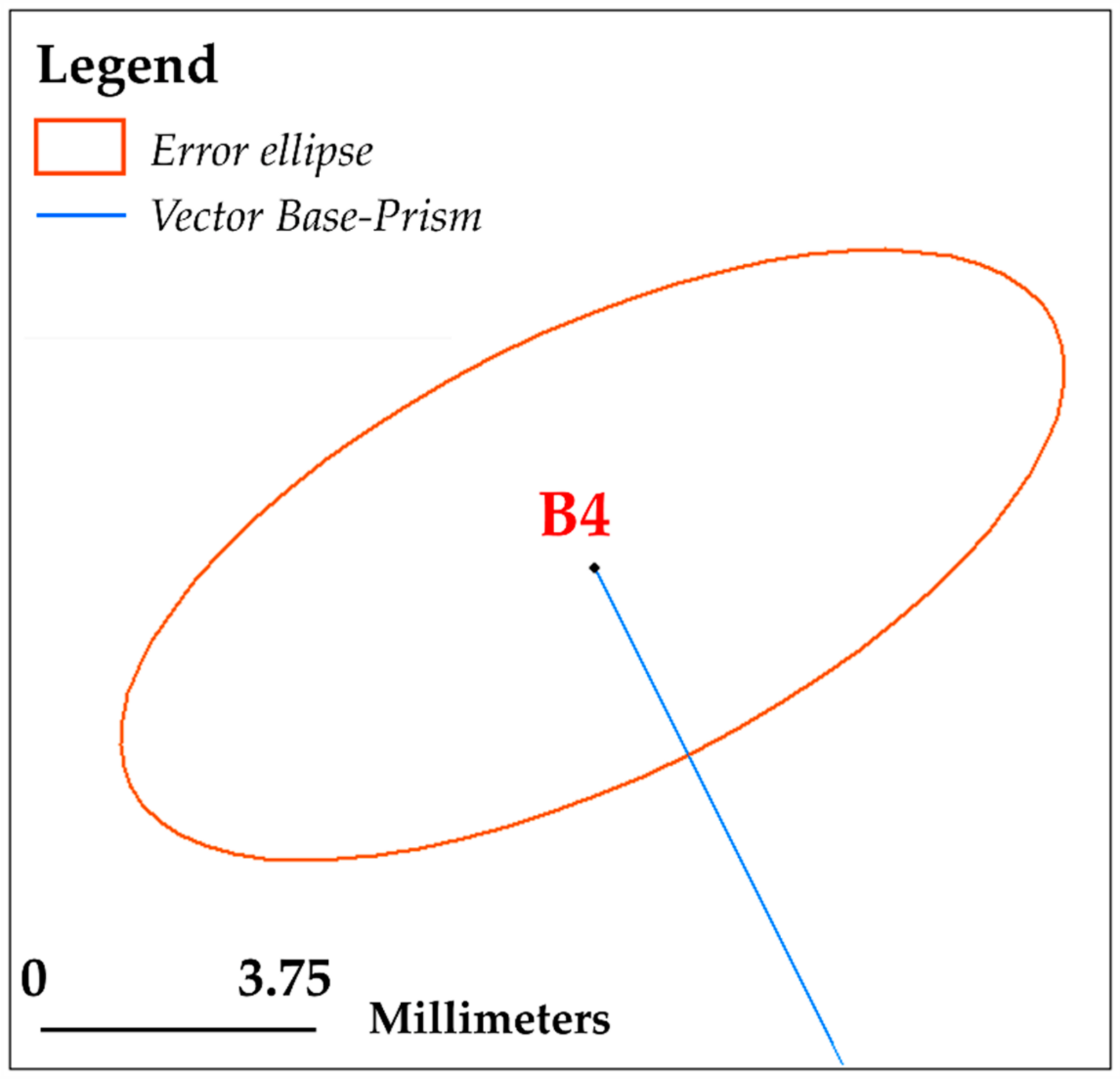



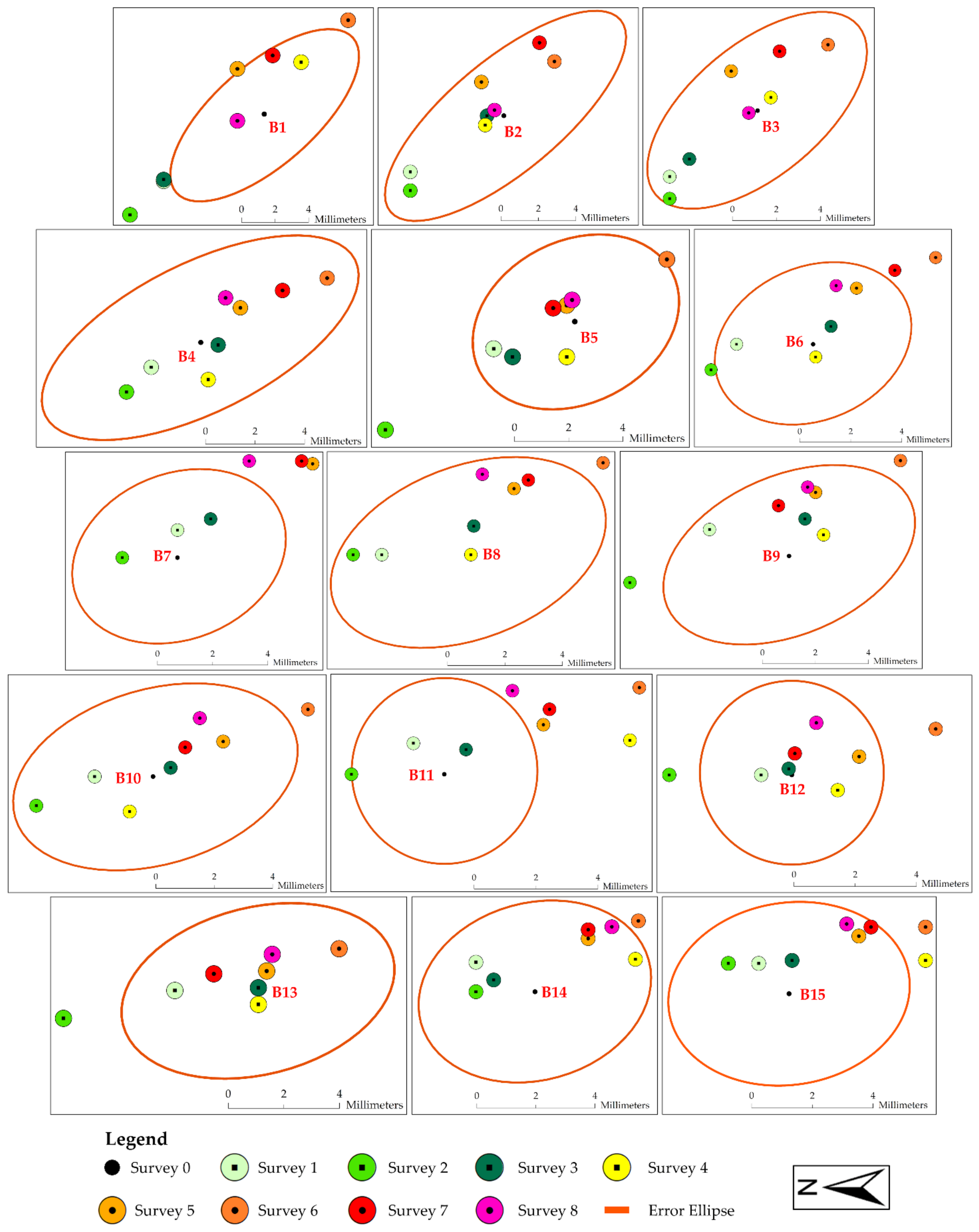

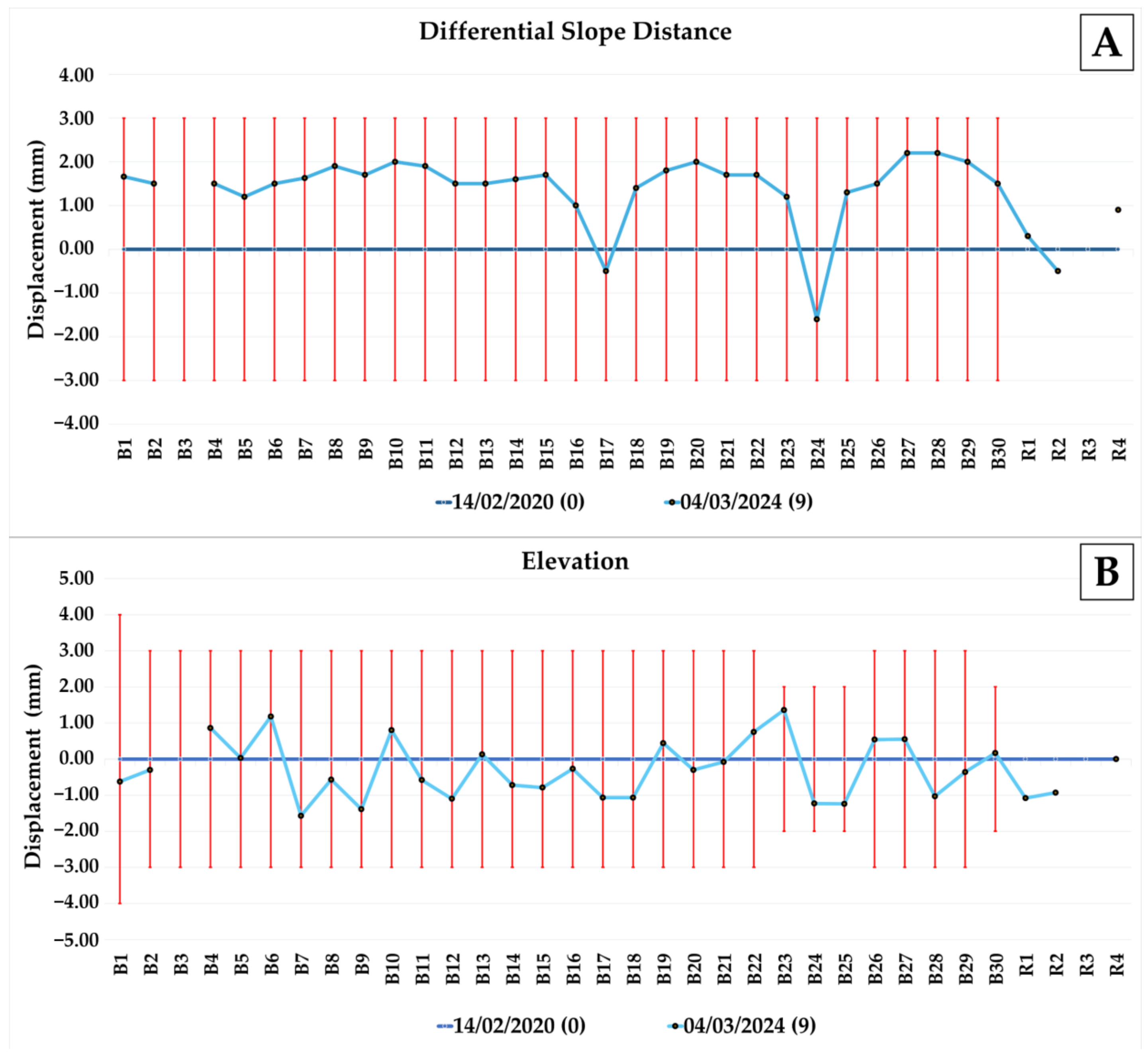
| Prism ID | RTS to Prism Distance (m) | Distance Uncertainty (±mm) | Azimuthal Uncertainty (±mm) | Elevation Uncertainty (±mm) |
|---|---|---|---|---|
| B1 | 257 | 3 | 7 | 4 |
| B2 | 252 | 3 | 8 | 3 |
| B3 | 235 | 3 | 6 | 3 |
| B4 | 212 | 3 | 7 | 3 |
| B5 | 207 | 3 | 4 | 3 |
| B6 | 209 | 3 | 4 | 3 |
| B7 | 213 | 3 | 4 | 3 |
| B8 | 207 | 3 | 5 | 3 |
| B9 | 200 | 3 | 5 | 3 |
| B10 | 203 | 3 | 5 | 3 |
| B11 | 186 | 3 | 3 | 3 |
| B12 | 167 | 3 | 3 | 3 |
| B13 | 171 | 3 | 5 | 3 |
| B14 | 172 | 3 | 4 | 3 |
| B15 | 153 | 3 | 4 | 3 |
| B16 | 133 | 3 | 4 | 3 |
| B17 | 128 | 3 | 3 | 3 |
| B18 | 143 | 3 | 5 | 3 |
| B19 | 149 | 3 | 3 | 3 |
| B20 | 152 | 3 | 5 | 3 |
| B21 | 135 | 3 | 3 | 3 |
| B22 | 119 | 3 | 4 | 3 |
| B23 | 98 | 3 | 3 | 2 |
| B24 | 99 | 3 | 4 | 2 |
| B25 | 100 | 3 | 5 | 2 |
| B26 | 149 | 3 | 6 | 3 |
| B27 | 159 | 3 | 5 | 3 |
| B28 | 164 | 3 | 7 | 3 |
| B29 | 167 | 3 | 7 | 3 |
| B30 | 103 | 3 | 5 | 2 |
| Satellite | First and Last Scene Date | Acquisition Orbit | Path nr. | Frame nr. | Utilized Images |
|---|---|---|---|---|---|
| Sentinel-1A | 30 July 2020–21 January 2022 | Ascending | 15 | 139 | 44 |
| Sentinel-1B | 5 August 2020–22 December 2021 | Ascending | 15 | 137 | 37 |
| System | K1 | K1a | K2a | K2b | K3 | K4 |
|---|---|---|---|---|---|---|
| Dip direction/Dip (°) | 288/82 | 124/78 | 32/79 | 203/82 | 227/40 | 69/30 |
| Aperture (mm) | >5 | >5 | >5 | >5 | 1–5 | 1–5 |
| Length (m) | 3–10 | 3–10 | 1–3 | 1–3 | <1 | <1 |
| Spacing (m) | 1.2 | 1.2 | <1 | <1 | 0.80 | 0.50/1 |
| Surface weathering | Slightly weathered | Slightly weathered | Un-weathered | Un-weathered | Slightly weathered | Un-weathered |
| Filling (type) | Clean | Clean | Clean | Clean | Clean | Soft filling |
| Roughness | Rough | Rough | Rough | Rough | Rough | Slightly rough |
| JRC | 16–18 | 16–18 | 10–12 | 14–16 | 10–12 | 6–8 |
| Humidity | Dry | Dry | Dry | Dry | Dry | Dry |
| R-value (intact rock) | 47 | 47 | 49 | 49 | 53 | 54 |
| Discontinuity System | V1 | V2 | V3 | ||||||
| Failure Type | P | W | T | P | W | T | P | W | T |
| K1 288/82 | 45 * | 78 | 83 | 80 | 80 | 83 | 67 | 80 | 83 |
| K1a 124/78 | 80 | 78 | 77 | 80 | 78 | 83 | 80 | 86 | 66 |
| K2a 32/79 | 80 | 78 | 83 | 80 | 78 | 83 | 80 | 78 | 83 |
| K2b 203/82 | 80 | 80 | 83 | 80 | 80 | 83 | 80 | 80 | 83 |
| K3 227/40 | 79 | 81 | 83 | 67 | 86 | 83 | 79 | 79 | 83 |
| K4 69/30 | 83 | 86 | 86 | 83 | 86 | 81 | 83 | 86 | 86 |
| Discontinuity System | V4 | V5 | V6 | ||||||
| Failure Type | P | W | T | P | W | T | P | W | T |
| K1 288/82 | 80 | 81 | 66 | 87 | 80 | 83 | 87 | 83 | 83 |
| K1a 124/78 | 67 | 63 | 83 | 87 | 78 | 83 | 87 | 81 | 77 |
| K2a 32/79 | 80 | 80 | 83 | 87 | 80 | 83 | 87 | 78 | 83 |
| K2b 203/82 | 80 | 80 | 83 | 87 | 67 | 83 | 87 | 62 | 83 |
| K3 227/40 | 79 | 81 | 83 | 67 | 83 | 87 | 36 * | 79 | 87 |
| K4 69/30 | 83 | 86 | 86 | 83 | 86 | 87 | 63 | 86 | 87 |
| Slope | Planar Sliding | Wedge Sliding | Direct Toppling | Flexural Toppling |
|---|---|---|---|---|
| Critical Plane | Critical Intersection | Critical Intersection | ||
| 280/88 | K1–K2b–K3 | K1/K2b–K1/K2a–K1/K3 (on K3)– K1/K1a (on K1)–K1a/K3 (on K1a) | K1a/K2a–K2a/K4–K2b/K4–K2a/K2b– K1a/K2b (Oblique Toppling) | |
| 250/88 | K1–K2b–K3 | K1/K2b–K1/K3 (on K3)–K1/K1a (on K1a)–K1a/K3 (on K1a) | K1a/K2a– K1/K1a–K1a/K2b (Oblique Topping) | |
| 310/85 | K1–K3 | K1/K2a–K1/K2b–K1/K4 (on K1) | K1a/K2b–K2a/K2b–K2a/K4–K2b/K4–K3/K4– K1a/K2a (Oblique Toppling) | K1a |
| 100/85 | K1a–K2a | K1a/K2a–K1a/K2b–K1a/K4 (on K1a) | K2b/K3– K1/K2a–K1/K2b (Oblique Toppling) | K1 |
| 250/65 | K3 | K1a/K3 (on K1a)–K1/K3–K1/K1a (on K1) | K1a/K2a– K1/K2a–K1a/K2b (Oblique Toppling) | |
| 280/65 | K3 | K1a/K2a–K2a/K2b– K1a/K2b (Oblique Toppling) |
| RTS Survey | Slope Distance Precision (±mm) | Azimuthal Angle Precision (±″) | Zenithal Angle Precision (±″) |
|---|---|---|---|
| 0 | 0.2 | 1.8 | 1.5 |
| 1 | 0.1 | 2.2 | 0.9 |
| 2 | 0.2 | 2.5 | 1.1 |
| 3 | 0.1 | 1.6 | 1.0 |
| 4 | 0.1 | 3.7 | 1.3 |
| 5 | 0.1 | 3.1 | 1.5 |
| 6 | 0.2 | 4.2 | 1.1 |
| 7 | 0.2 | 4.1 | 1.1 |
| 8 | 0.1 | 1.1 | 1.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Beltramone, L.; Rindinella, A.; Vanneschi, C.; Salvini, R. Multitemporal Monitoring of Rocky Walls Using Robotic Total Station Surveying and Persistent Scatterer Interferometry. Remote Sens. 2024, 16, 3848. https://doi.org/10.3390/rs16203848
Beltramone L, Rindinella A, Vanneschi C, Salvini R. Multitemporal Monitoring of Rocky Walls Using Robotic Total Station Surveying and Persistent Scatterer Interferometry. Remote Sensing. 2024; 16(20):3848. https://doi.org/10.3390/rs16203848
Chicago/Turabian StyleBeltramone, Luisa, Andrea Rindinella, Claudio Vanneschi, and Riccardo Salvini. 2024. "Multitemporal Monitoring of Rocky Walls Using Robotic Total Station Surveying and Persistent Scatterer Interferometry" Remote Sensing 16, no. 20: 3848. https://doi.org/10.3390/rs16203848
APA StyleBeltramone, L., Rindinella, A., Vanneschi, C., & Salvini, R. (2024). Multitemporal Monitoring of Rocky Walls Using Robotic Total Station Surveying and Persistent Scatterer Interferometry. Remote Sensing, 16(20), 3848. https://doi.org/10.3390/rs16203848










