Spectral–Spatial Feature Extraction for Hyperspectral Image Classification Using Enhanced Transformer with Large-Kernel Attention
Abstract
:1. Introduction
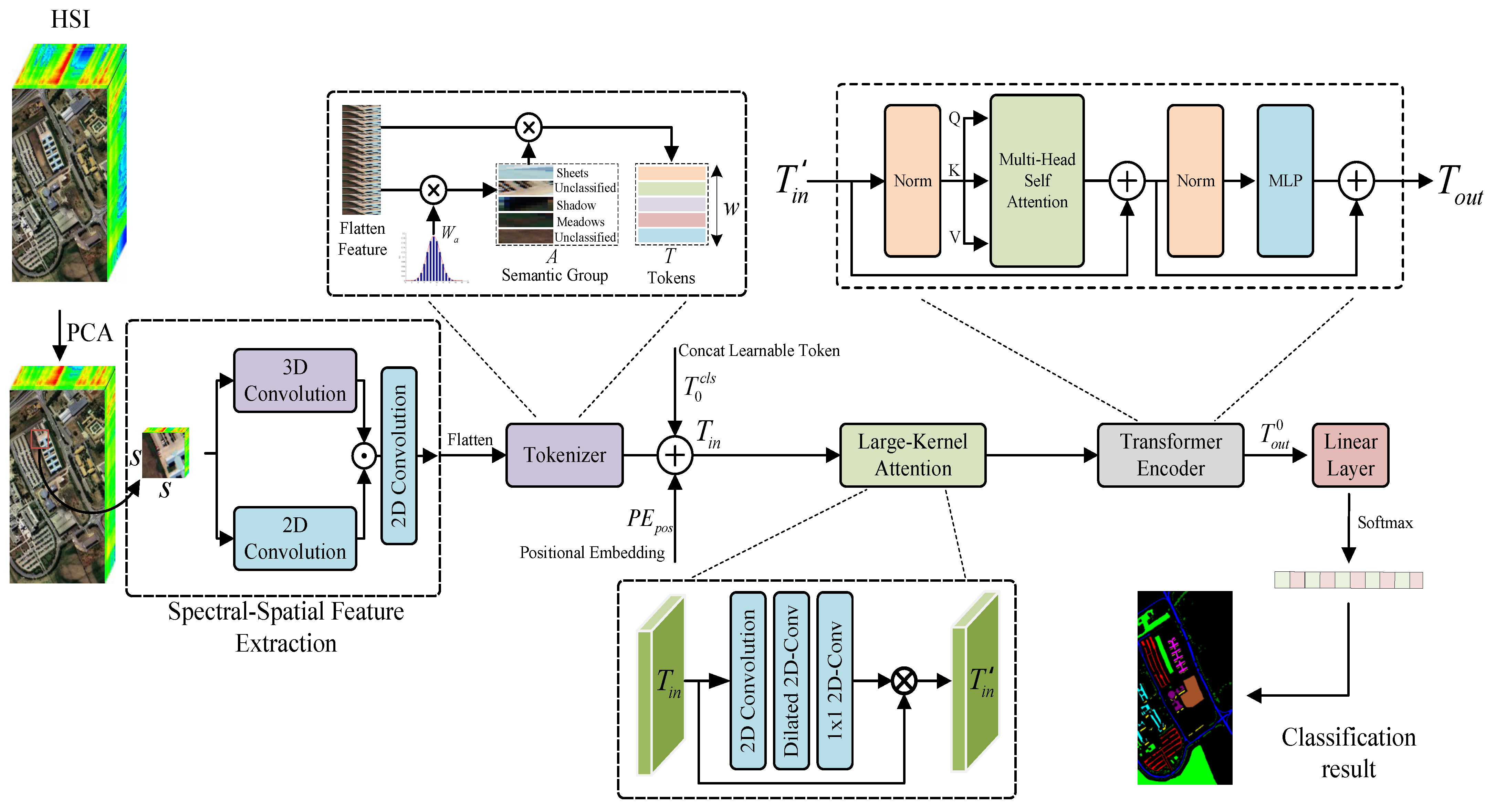
- In order to more comprehensively extract spatial and spectral feature information from HSIs, a high-performance network has been designed that combines a dual-branch CNN with a Transformer framework equipped with a Large-Kernel Attention mechanism. This further enhances the classification performance of the CNN–Transformer combined network;
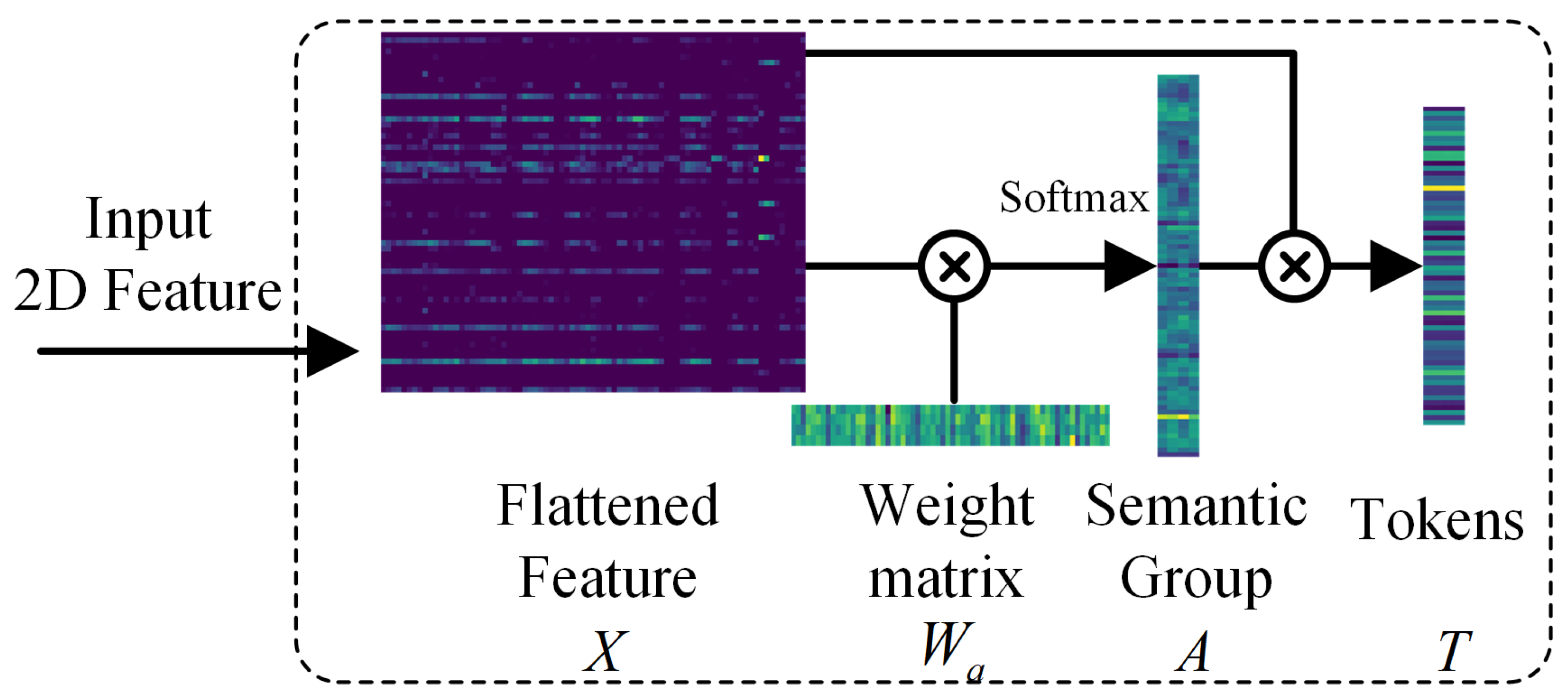
- In the shallow feature extraction module, we designed a dual-branch network that uses 3D convolutional layers to extract spectral features and 2D convolutional layers to extract spatial features. These two discriminative features are then processed by a Gaussian-weighted Tokenizer module to effectively fuse them and generate higher-level semantic tokens;
- From utilizing a CNN network for shallow feature extraction to effectively capturing global contextual information within the image using the Transformer framework, our proposed ETLKA allows for comprehensive learning of spatial–spectral features within HSI, significantly enhancing joint classification accuracy. Experimental validation on three classic public datasets has demonstrated the effectiveness of the proposed network framework.
2. Materials and Methods
2.1. Feature Extraction via Dual-Branch CNNs
2.2. HSI Feature Tokenization
2.3. Large-Kernel Attention
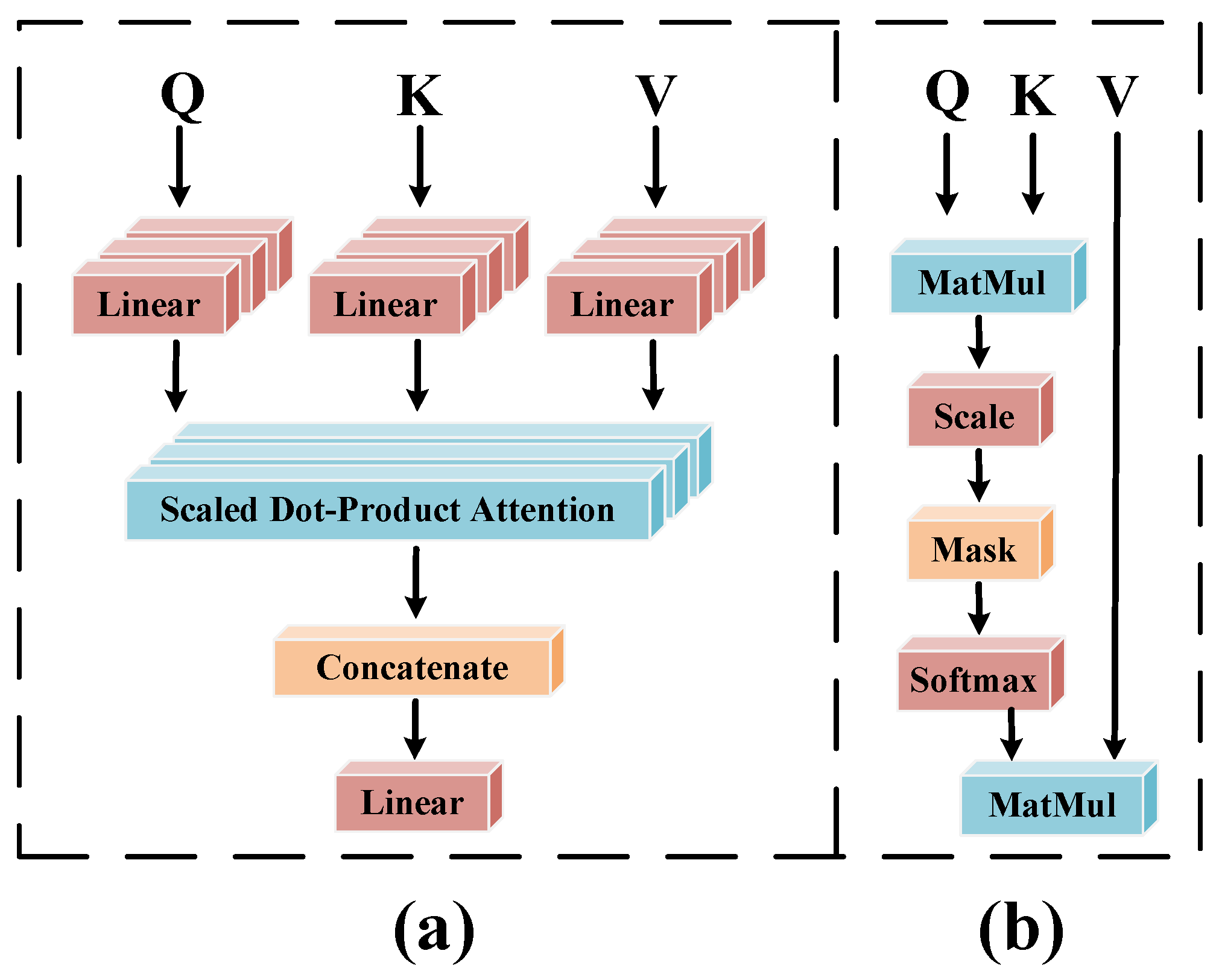
2.4. Transformer Encoder Module
| Algorithm 1 Enhanced Transformer with Large-Kernel Attention Model |
Input: Input HSI data and ground truth labels ; Set the spectral dimension after PCA preprocessing to ; Extract patch size ; and specify the training sample rate as . Output: Predicted labels for the test dataset.
|
3. Results
3.1. Data Description
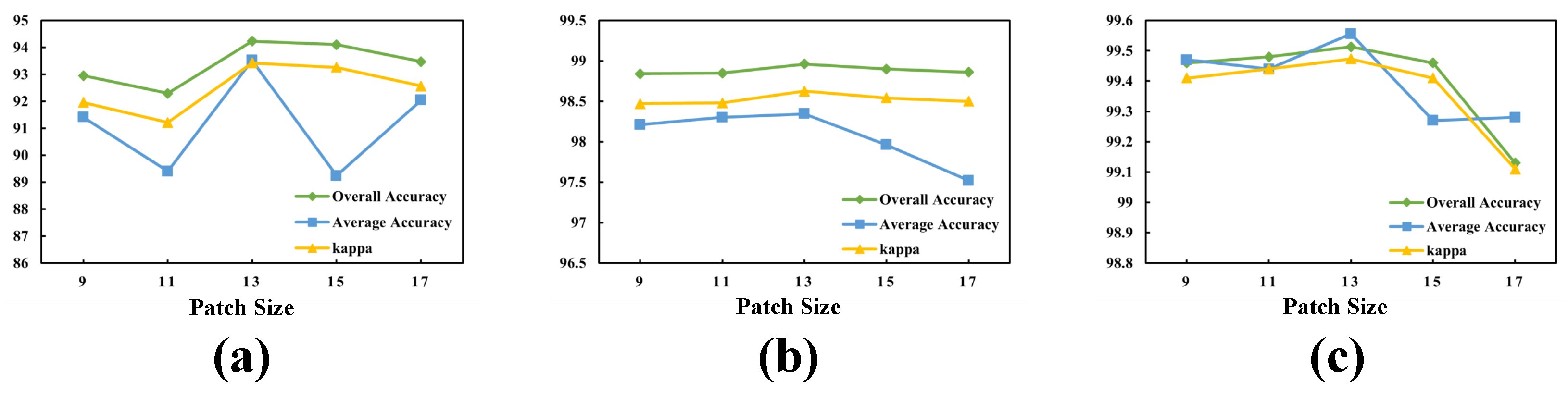
3.2. Parameter Analysis
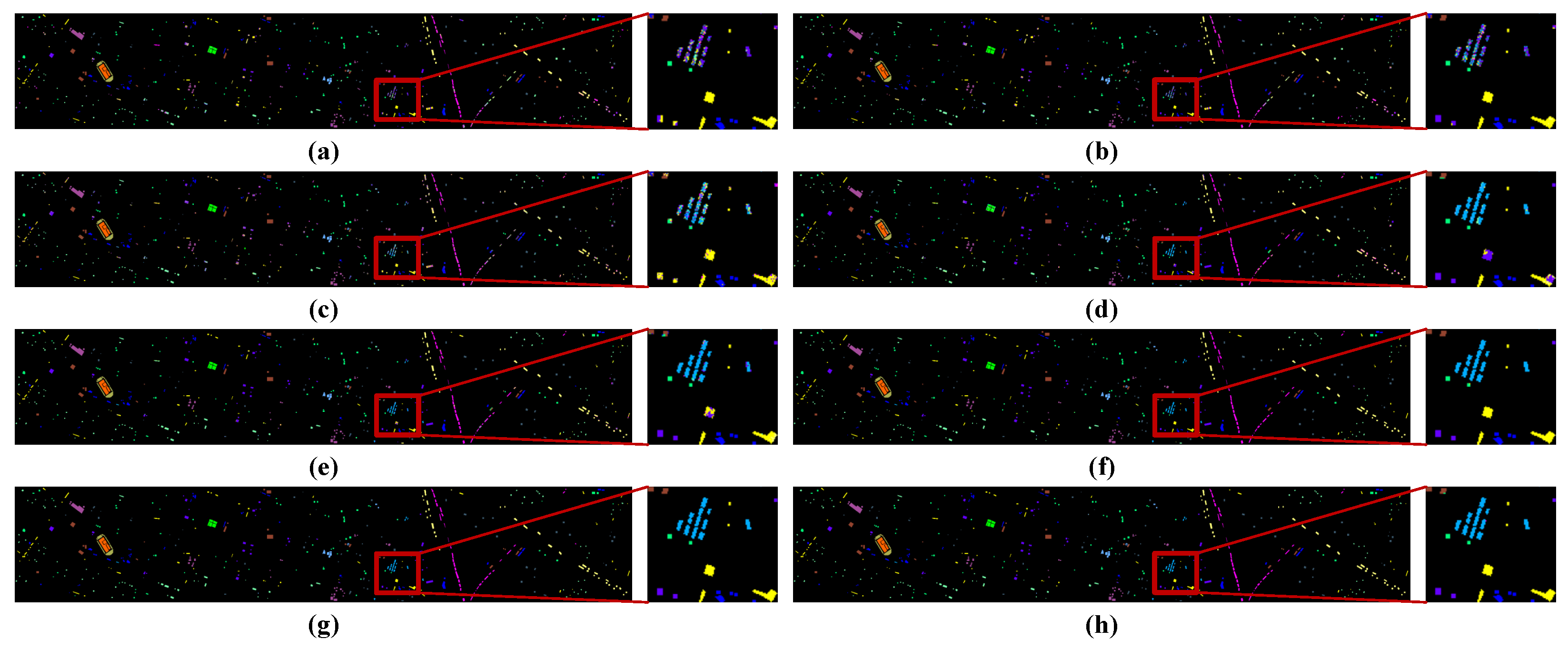
3.3. Classification Results and Analysis
3.4. Inference Speed Analysis
3.5. Ablation Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| AA | Average Accuracy |
| EMAP | Extended Multiple Attribute Profile |
| HSI | Hyperspectral image |
| LKA | Large-Kernal Attention |
| LN | Normalization layers |
| Kappa coefficient | |
| MHSA | Multi-Head Self-Attention |
| OA | Overall Accuracy |
| PCA | Principal Component Analysis |
| SVM | Support Vector Machine |
| TE | Transformer Encoder |
References
- Li, J.; Zheng, K.; Liu, W.; Li, Z.; Yu, H.; Ni, L. Model-Guided Coarse-to-Fine Fusion Network for Unsupervised Hyperspectral Image Super-Resolution. IEEE Geosci. Remote Sens. Lett. 2023, 20, 1–5. [Google Scholar] [CrossRef]
- Li, J.; Zheng, K.; Li, Z.; Gao, L.; Jia, X. X-Shaped Interactive Autoencoders with Cross-Modality Mutual Learning for Unsupervised Hyperspectral Image Super-Resolution. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–17. [Google Scholar] [CrossRef]
- Sun, L.; Cheng, S.; Zheng, Y.; Wu, Z.; Zhang, J. SPANet: Successive pooling attention network for semantic segmentation of remote sensing images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 4045–4057. [Google Scholar] [CrossRef]
- García, J.L.; Paoletti, M.E.; Jiménez, L.I.; Haut, J.M.; Plaza, A. Efficient semantic segmentation of hyperspectral images using adaptable rectangular convolution. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Ben-Ahmed, O.; Urruty, T.; Richard, N.; Fernandez-Maloigne, C. Toward content-based hyperspectral remote sensing image retrieval (CB-HRSIR): A preliminary study based on spectral sensitivity functions. Remote Sens. 2019, 11, 600. [Google Scholar] [CrossRef]
- Sun, L.; Wang, Q.; Chen, Y.; Zheng, Y.; Wu, Z.; Fu, L.; Jeon, B. CRNet: Channel-enhanced Remodeling-based Network for Salient Object Detection in Optical Remote Sensing Images. IEEE Trans. Geosci. Remote Sens. 2023, 61, 5618314. [Google Scholar] [CrossRef]
- Fu, L.; Zhang, D.; Ye, Q. Recurrent thrifty attention network for remote sensing scene recognition. IEEE Trans. Geosci. Remote Sens. 2020, 59, 8257–8268. [Google Scholar] [CrossRef]
- Ren, H.; Du, Q.; Wang, J.; Chang, C.I.; Jensen, J.O.; Jensen, J.L. Automatic target recognition for hyperspectral imagery using high-order statistics. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 1372–1385. [Google Scholar] [CrossRef]
- Matteoli, S.; Diani, M.; Corsini, G. A tutorial overview of anomaly detection in hyperspectral images. IEEE Aerosp. Electron. Syst. Mag. 2010, 25, 5–28. [Google Scholar] [CrossRef]
- Li, L.; Li, W.; Qu, Y.; Zhao, C.; Tao, R.; Du, Q. Prior-based tensor approximation for anomaly detection in hyperspectral imagery. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 1037–1050. [Google Scholar] [CrossRef]
- Pedergnana, M.; Marpu, P.R.; Mura, M.D.; Benediktsson, J.A.; Bruzzone, L. A Novel Technique for Optimal Feature Selection in Attribute Profiles Based on Genetic Algorithms. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3514–3528. [Google Scholar] [CrossRef]
- Song, B.; Li, J.; Dalla Mura, M.; Li, P.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A.; Chanussot, J. Remotely Sensed Image Classification Using Sparse Representations of Morphological Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5122–5136. [Google Scholar] [CrossRef]
- Xia, J.; Dalla Mura, M.; Chanussot, J.; Du, P.; He, X. Random Subspace Ensembles for Hyperspectral Image Classification with Extended Morphological Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 4768–4786. [Google Scholar] [CrossRef]
- Kwan, C.; Gribben, D.; Ayhan, B.; Bernabe, S.; Plaza, A.; Selva, M. Improving Land Cover Classification Using Extended Multi-Attribute Profiles (EMAP) Enhanced Color, Near Infrared, and LiDAR Data. Remote Sens. 2020, 12, 1392. [Google Scholar] [CrossRef]
- Kwan, C.; Ayhan, B.; Budavari, B.; Lu, Y.; Perez, D.; Li, J.; Bernabe, S.; Plaza, A. Deep Learning for Land Cover Classification Using Only a Few Bands. Remote Sens. 2020, 12, 2000. [Google Scholar] [CrossRef]
- Zhang, A.; Sun, G.; Ma, P.; Jia, X.; Ren, J.; Huang, H.; Zhang, X. Coastal Wetland Mapping with Sentinel-2 MSI Imagery Based on Gravitational Optimized Multilayer Perceptron and Morphological Attribute Profiles. Remote Sens. 2019, 11, 952. [Google Scholar] [CrossRef]
- Huang, J.; Liu, K.; Xu, M.; Perc, M.; Li, X. Background Purification Framework With Extended Morphological Attribute Profile for Hyperspectral Anomaly Detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 8113–8124. [Google Scholar] [CrossRef]
- Ye, Q.; Huang, P.; Zhang, Z.; Zheng, Y.; Fu, L.; Yang, W. Multiview learning with robust double-sided twin SVM. IEEE Trans. Cyber. 2021, 52, 12745–12758. [Google Scholar] [CrossRef]
- Fu, L.; Li, Z.; Ye, Q.; Yin, H.; Liu, Q.; Chen, X.; Fan, X.; Yang, W.; Yang, G. Learning Robust Discriminant Subspace Based on Joint L2, p-and L2, s-Norm Distance Metrics. IEEE Trans. Neural Netw. Learn. Syst. 2020, 33, 130–144. [Google Scholar] [CrossRef]
- Ye, Q.; Li, Z.; Fu, L.; Zhang, Z.; Yang, W.; Yang, G. Nonpeaked discriminant analysis for data representation. IEEE Trans. Neural Netw. Learn. Syst. 2019, 30, 3818–3832. [Google Scholar] [CrossRef]
- Baassou, B.; He, M.; Mei, S. An accurate SVM-based classification approach for hyperspectral image classification. In Proceedings of the 2013 21st International Conference on Geoinformatics, Kaifeng, China, 20–22 June 2013; pp. 1–7. [Google Scholar]
- Guo, B.; Gunn, S.R.; Damper, R.I.; Nelson, J.D. Customizing kernel functions for SVM-based hyperspectral image classification. IEEE Trans. Image Proc. 2008, 17, 622–629. [Google Scholar] [CrossRef] [PubMed]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1778–1790. [Google Scholar] [CrossRef]
- Kang, X.; Xiang, X.; Li, S.; Benediktsson, J.A. PCA-based edge-preserving features for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 7140–7151. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, R.; Wu, Q. Hyperspectral image classification based on PCA network. In Proceedings of the 2016 8th Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Los Angeles, CA, USA, 21–24 August 2016; pp. 1–4. [Google Scholar]
- Villa, A.; Benediktsson, J.A.; Chanussot, J.; Jutten, C. Hyperspectral image classification with independent component discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2011, 49, 4865–4876. [Google Scholar] [CrossRef]
- Bandos, T.V.; Bruzzone, L.; Camps-Valls, G. Classification of hyperspectral images with regularized linear discriminant analysis. IEEE Trans. Geosci. Remote Sens. 2009, 47, 862–873. [Google Scholar] [CrossRef]
- Su, Y.; Gao, L.; Jiang, M.; Plaza, A.; Sun, X.; Zhang, B. NSCKL: Normalized Spectral Clustering With Kernel-Based Learning for Semisupervised Hyperspectral Image Classification. IEEE Trans. Cybern. 2023, 53, 6649–6662. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going Deeper With Contextual CNN for Hyperspectral Image Classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Sun, L.; Fang, Y.; Chen, Y.; Huang, W.; Wu, Z.; Jeon, B. Multi-structure KELM with attention fusion strategy for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–17. [Google Scholar] [CrossRef]
- Gao, H.; Yang, Y.; Li, C.; Gao, L.; Zhang, B. Multiscale residual network with mixed depthwise convolution for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3396–3408. [Google Scholar] [CrossRef]
- Gao, H.; Chen, Z.; Xu, F. Adaptive spectral-spatial feature fusion network for hyperspectral image classification using limited training samples. Int. J. Appl. Earth Obs. Geoinf. 2022, 107, 102687. [Google Scholar] [CrossRef]
- Hu, W.; Huang, Y.; Wei, L.; Zhang, F.; Li, H. Deep convolutional neural networks for hyperspectral image classification. J. Sens. 2015, 2015, 1–12. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, Y.Q.; Chan, J.C.W. Learning and transferring deep joint spectral–spatial features for hyperspectral classification. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4729–4742. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep feature extraction and classification of hyperspectral images based on convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Wang, J.; Song, X.; Sun, L.; Huang, W.; Wang, J. A novel cubic convolutional neural network for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4133–4148. [Google Scholar] [CrossRef]
- Roy, S.K.; Hong, D.; Kar, P.; Wu, X.; Liu, X.; Zhao, D. Lightweight heterogeneous kernel convolution for hyperspectral image classification with noisy labels. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Dosovitskiy, A.; Beyer, L.; Kolesnikov, A.; Weissenborn, D.; Zhai, X.; Unterthiner, T.; Dehghani, M.; Minderer, M.; Heigold, G.; Gelly, S.; et al. An image is worth 16x16 words: Transformers for image recognition at scale. arXiv 2020, arXiv:2010.11929. [Google Scholar]
- Carion, N.; Massa, F.; Synnaeve, G.; Usunier, N.; Kirillov, A.; Zagoruyko, S. End-to-end object detection with transformers. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2020; pp. 213–229. [Google Scholar]
- Liu, Z.; Lin, Y.; Cao, Y.; Hu, H.; Wei, Y.; Zhang, Z.; Lin, S.; Guo, B. Swin transformer: Hierarchical vision transformer using shifted windows. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 10012–10022. [Google Scholar]
- Strudel, R.; Garcia, R.; Laptev, I.; Schmid, C. Segmenter: Transformer for semantic segmentation. In Proceedings of the IEEE/CVF International Conference on Computer Vision (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 7262–7272. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Proc. Adv. Neural Inf. Process. Syst. (NIPS) 2017, 30, 1–11. [Google Scholar]
- Yang, X.; Cao, W.; Lu, Y.; Zhou, Y. Hyperspectral Image Transformer Classification Networks. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Hong, D.; Han, Z.; Yao, J.; Gao, L.; Zhang, B.; Plaza, A.; Chanussot, J. SpectralFormer: Rethinking hyperspectral image classification with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Sun, L.; Zhao, G.; Zheng, Y.; Wu, Z. Spectral–spatial feature tokenization transformer for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Xue, Z.; Xu, Q.; Zhang, M. Local transformer with spatial partition restore for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2022, 15, 4307–4325. [Google Scholar] [CrossRef]
- Huang, X.; Dong, M.; Li, J.; Guo, X. A 3-d-swin transformer-based hierarchical contrastive learning method for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–15. [Google Scholar] [CrossRef]
- Fang, Y.; Ye, Q.; Sun, L.; Zheng, Y.; Wu, Z. Multi-Attention Joint Convolution Feature Representation with Lightweight Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–14. [Google Scholar]
- Xu, Y.; Xie, Y.; Li, B.; Xie, C.; Zhang, Y.; Wang, A.; Zhu, L. Spatial-Spectral 1DSwin Transformer with Group-wise Feature Tokenization for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar]
- Zhang, S.; Zhang, J.; Wang, X.; Wang, J.; Wu, Z. ELS2T: Efficient Lightweight Spectral–Spatial Transformer for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Zhang, K.; Zhu, D.; Min, X.; Zhai, G. Implicit Neural Representation Learning for Hyperspectral Image Super-Resolution. In Proceedings of the 2022 IEEE International Conference on Multimedia and Expo (ICME), Taipei, Taiwan, 18–22 July 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Dong, W.; Wang, H.; Wu, F.; Shi, G.; Li, X. Deep Spatial–Spectral Representation Learning for Hyperspectral Image Denoising. IEEE Trans. Comput. Imaging 2019, 5, 635–648. [Google Scholar] [CrossRef]
- Tulczyjew, L.; Kawulok, M.; Nalepa, J. Unsupervised Feature Learning Using Recurrent Neural Nets for Segmenting Hyperspectral Images. IEEE Geosci. Remote Sens. Lett. 2021, 18, 2142–2146. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Imai, Y.; Honda, K.I.; Takeda, T.; Antoniak, M. Unsupervised Segmentation of Hyperspectral Images Using 3-D Convolutional Autoencoders. IEEE Geosci. Remote Sens. Lett. 2020, 17, 1948–1952. [Google Scholar] [CrossRef]
- Sellami, A.; Tabbone, S. Deep neural networks-based relevant latent representation learning for hyperspectral image classification. Pattern Recognit. 2022, 121, 108224. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, X.; Li, T.; Meng, H.; Cao, X.; Wang, L. Adversarial Representation Learning for Hyperspectral Image Classification with Small-Sized Labeled Set. Remote Sens. 2022, 14, 2612. [Google Scholar] [CrossRef]






| NO. | India Pines | Pavia University | Houston2013 | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Class | Training | Test | Class | Training | Test | Class | Training | Test | |
| #1 | Alfalfa | 1 | 45 | Asphalt | 199 | 6432 | Healthy Grass | 125 | 1126 |
| #2 | Corn-notill | 43 | 1385 | Meadows | 559 | 18,090 | Stressed Grass | 125 | 1129 |
| #3 | Corn-mintill | 25 | 805 | Gravel | 63 | 2036 | Synthetis Grass | 70 | 627 |
| #4 | Corn | 7 | 230 | Trees | 92 | 2972 | Tree | 124 | 1120 |
| #5 | Grass-pasture | 14 | 469 | Metal Sheets | 40 | 1305 | Soil | 124 | 1118 |
| #6 | Grass-tree | 22 | 708 | Bare soil | 151 | 4878 | Water | 33 | 292 |
| #7 | Grass-pasture-mowed | 1 | 27 | Bitumen | 40 | 1290 | Residential | 127 | 1141 |
| #8 | Hay-windrowed | 14 | 464 | Bricks | 111 | 3571 | Commercial | 124 | 1120 |
| #9 | Oats | 1 | 19 | Shadows | 28 | 919 | Road | 125 | 1127 |
| #10 | Soybean-notill | 29 | 943 | Highway | 123 | 1104 | |||
| #11 | Soybean-mintill | 73 | 2382 | Railway | 123 | 1112 | |||
| #12 | Soybean-clean | 18 | 575 | Parking Lot 1 | 123 | 1110 | |||
| #13 | wheat | 6 | 199 | Parking Lot 2 | 47 | 422 | |||
| #14 | woods | 38 | 1227 | Tennis Court | 43 | 385 | |||
| #15 | Buildings-Grass-Trees | 12 | 374 | Running Track | 66 | 594 | |||
| #16 | Stone-Steel-Towers | 3 | 90 | ||||||
| Total | 307 | 9942 | Total | 1283 | 14,493 | Total | 1502 | 13,527 | |
| NO. | SVM [21] | EMAP [17] | 1D-CNN [33] | 2D-CNN [34] | 3D-CNN [36] | HybridSN [37] | SSFTT [50] | Proposed |
|---|---|---|---|---|---|---|---|---|
| 1 | 22.22 | 17.07 | 11.68 | 17.46 | 46.13 | 34.09 | 48.00 | 78.67 |
| 2 | 62.31 | 70.55 | 81.87 | 68.46 | 75.84 | 91.96 | 92.74 | 91.89 |
| 3 | 49.68 | 70.01 | 19.41 | 66.54 | 63.50 | 79.59 | 86.55 | 93.90 |
| 4 | 17.82 | 66.19 | 20.39 | 40.18 | 44.37 | 64.00 | 88.96 | 98.35 |
| 5 | 44.77 | 74.25 | 77.13 | 66.67 | 96.51 | 94.12 | 88.32 | 84.14 |
| 6 | 86.58 | 61.34 | 94.04 | 97.54 | 98.86 | 90.62 | 98.80 | 99.00 |
| 7 | 88.89 | 60.00 | 46.67 | 67.04 | 70.37 | 85.19 | 94.81 | 97.04 |
| 8 | 95.04 | 82.32 | 97.29 | 98.37 | 99.45 | 97.80 | 98.15 | 97.16 |
| 9 | 10.53 | 20.45 | 11.76 | 15.26 | 26.32 | 68.42 | 88.42 | 97.37 |
| 10 | 47.08 | 71.89 | 32.92 | 84.06 | 85.36 | 84.72 | 95.26 | 88.12 |
| 11 | 71.99 | 80.99 | 83.76 | 85.71 | 93.48 | 96.78 | 95.54 | 96.56 |
| 12 | 30.98 | 63.11 | 48.61 | 48.67 | 64.65 | 78.15 | 87.43 | 90.19 |
| 13 | 94.97 | 93.46 | 93.10 | 98.97 | 98.97 | 95.38 | 99.85 | 96.68 |
| 14 | 92.75 | 87.09 | 91.63 | 89.09 | 96.92 | 98.92 | 97.47 | 98.22 |
| 15 | 15.77 | 64.84 | 42.07 | 55.04 | 70.57 | 85.83 | 93.50 | 94.97 |
| 16 | 93.33 | 69.05 | 72.15 | 71.26 | 74.71 | 85.23 | 96.44 | 94.11 |
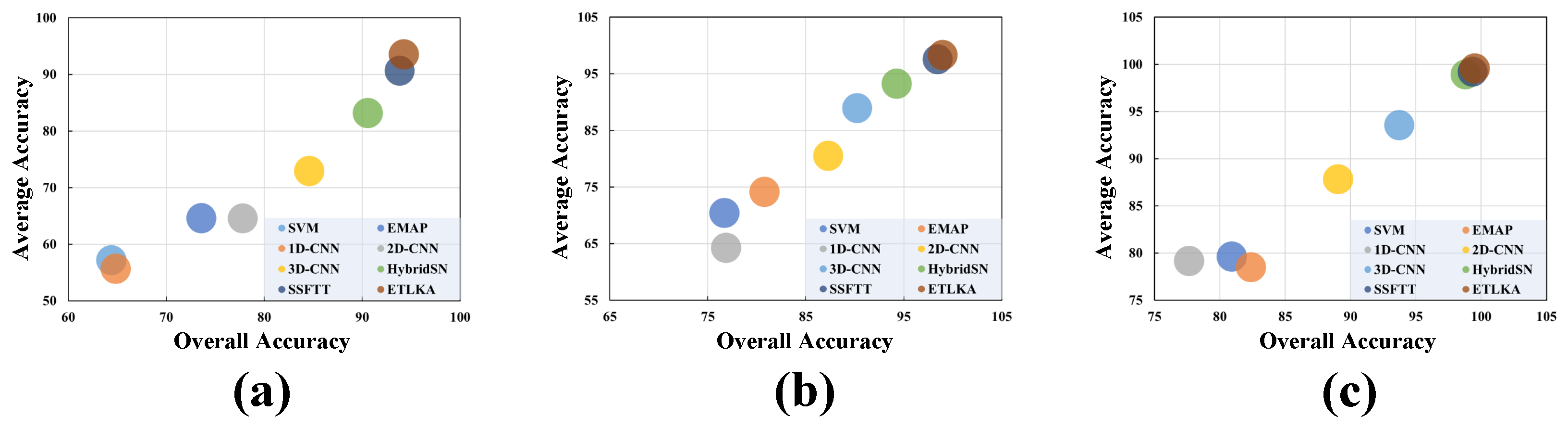
| OA (%) | 64.39 | 73.58 | 64.83 | 77.81 | 84.59 | 90.57 | 93.81 | 94.23 |
| AA (%) | 57.17 | 64.61 | 55.66 | 64.57 | 72.95 | 83.18 | 90.64 | 93.52 |
| × 100 | 59.07 | 69.87 | 62.74 | 74.56 | 82.26 | 89.17 | 92.94 | 93.43 |
| NO. | SVM [21] | EMAP [17] | 1D-CNN [33] | 2D-CNN [34] | 3D-CNN [36] | HybridSN [37] | SSFTT [50] | Proposed |
|---|---|---|---|---|---|---|---|---|
| 1 | 83.05 | 87.50 | 79.27 | 88.64 | 92.95 | 87.84 | 97.39 | 99.26 |
| 2 | 87.36 | 93.35 | 89.33 | 97.75 | 97.85 | 99.87 | 99.89 | 99.78 |
| 3 | 42.59 | 55.97 | 47.99 | 42.97 | 82.45 | 85.08 | 94.47 | 96.67 |
| 4 | 81.47 | 85.36 | 79.10 | 92.98 | 95.37 | 91.38 | 94.86 | 97.84 |
| 5 | 95.17 | 97.47 | 98.92 | 99.32 | 95.63 | 91.50 | 98.67 | 99.74 |
| 6 | 40.15 | 48.54 | 76.42 | 76.14 | 79.59 | 93.93 | 99.77 | 99.88 |
| 7 | 14.92 | 28.39 | 20.70 | 63.78 | 76.44 | 89.38 | 99.38 | 99.53 |
| 8 | 71.23 | 85.13 | 74.19 | 72.13 | 88.08 | 90.33 | 96.25 | 95.21 |
| 9 | 87.54 | 96.84 | 71.47 | 98.93 | 99.78 | 96.12 | 97.48 | 97.17 |
| OA (%) | 76.68 | 80.76 | 76.85 | 87.28 | 90.23 | 94.26 | 98.44 | 98.96 |
| AA (%) | 70.43 | 74.15 | 64.27 | 80.52 | 88.95 | 93.27 | 97.57 | 98.34 |
| × 100 | 74.87 | 79.11 | 69.15 | 82.84 | 89.72 | 93.73 | 97.94 | 98.62 |
| NO. | SVM [21] | EMAP [17] | 1D-CNN [33] | 2D-CNN [34] | 3D-CNN [36] | HybridSN [37] | SSFTT [50] | Proposed |
|---|---|---|---|---|---|---|---|---|
| 1 | 95.65 | 87.85 | 86.20 | 94.02 | 93.75 | 98.85 | 99.66 | 99.42 |
| 2 | 97.52 | 92.53 | 95.13 | 96.30 | 94.91 | 99.73 | 99.14 | 99.81 |
| 3 | 99.84 | 99.84 | 100.00 | 89.73 | 95.54 | 99.84 | 99.68 | 99.79 |
| 4 | 93.66 | 92.63 | 95.43 | 98.31 | 94.91 | 96.07 | 99.34 | 98.40 |
| 5 | 98.30 | 97.26 | 98.98 | 97.88 | 100.00 | 100.00 | 99.99 | 100.00 |
| 6 | 84.25 | 82.16 | 95.15 | 73.46 | 89.86 | 100.00 | 98.15 | 99.73 |
| 7 | 82.65 | 80.47 | 76.60 | 89.63 | 91.84 | 97.63 | 99.11 | 99.56 |
| 8 | 56.61 | 70.51 | 58.12 | 80.96 | 80.36 | 97.95 | 98.61 | 99.26 |
| 9 | 73.91 | 72.69 | 63.16 | 70.98 | 93.58 | 98.67 | 98.74 | 99.26 |
| 10 | 83.51 | 86.78 | 55.57 | 84.65 | 94.28 | 99.00 | 99.99 | 99.84 |
| 11 | 68.97 | 64.59 | 70.16 | 90.96 | 92.64 | 99.28 | 99.82 | 99.94 |
| 12 | 60.72 | 59.18 | 54.74 | 91.46 | 94.37 | 99.46 | 99.60 | 99.19 |
| 13 | 25.69 | 45.29 | 41.93 | 85.65 | 90.97 | 98.10 | 96.49 | 99.43 |
| 14 | 93.25 | 96.48 | 97.05 | 73.71 | 94.58 | 100.00 | 100.00 | 100.00 |
| 15 | 99.66 | 98.45 | 99.04 | 99.52 | 99.65 | 99.49 | 100.00 | 99.70 |
| OA (%) | 80.92 | 82.39 | 77.64 | 89.05 | 93.73 | 98.80 | 99.34 | 99.51 |
| AA (%) | 79.61 | 78.49 | 79.15 | 87.82 | 93.56 | 98.93 | 99.22 | 99.56 |
| × 100 | 79.33 | 80.64 | 75.81 | 88.15 | 93.63 | 98.71 | 99.28 | 99.47 |
| Dataset | India Pines | Pavia University | Houston2013 | |||
|---|---|---|---|---|---|---|
| Train | Test | Train | Test | Train | Test | |
| Time (s) | 8.09 | 71.85 | 26.92 | 276.65 | 32.01 | 100.31 |
| Cases | Components | Trainable | Indicators | ||||||
|---|---|---|---|---|---|---|---|---|---|
| SSFE | Tokenizer | LKA | TE | Parameters (MB) | OA (%) | AA (%) | p(t-Test) | ||
| 1 | Only 2D | √ | √ | √ | 0.14 | 92.81 | 91.91 | 91.81 | 0.4834 |
| 2 | √ | √ | √ | × | 0.71 | 91.59 | 85.10 | 90.41 | 0.4780 |
| 3 | 3D-Conv+2D-Conv | √ | × | √ | 0.56 | 93.81 | 90.64 | 92.94 | 0.4846 |
| 4 | √ | × | × | × | 0.70 | 90.02 | 86.12 | 89.56 | 0.4727 |
| 5 | √ | √ | √ | √ | 0.77 | 94.23 | 93.52 | 93.43 | 0.4926 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, W.; Wang, X.; Sun, L.; Zheng, Y. Spectral–Spatial Feature Extraction for Hyperspectral Image Classification Using Enhanced Transformer with Large-Kernel Attention. Remote Sens. 2024, 16, 67. https://doi.org/10.3390/rs16010067
Lu W, Wang X, Sun L, Zheng Y. Spectral–Spatial Feature Extraction for Hyperspectral Image Classification Using Enhanced Transformer with Large-Kernel Attention. Remote Sensing. 2024; 16(1):67. https://doi.org/10.3390/rs16010067
Chicago/Turabian StyleLu, Wen, Xinyu Wang, Le Sun, and Yuhui Zheng. 2024. "Spectral–Spatial Feature Extraction for Hyperspectral Image Classification Using Enhanced Transformer with Large-Kernel Attention" Remote Sensing 16, no. 1: 67. https://doi.org/10.3390/rs16010067
APA StyleLu, W., Wang, X., Sun, L., & Zheng, Y. (2024). Spectral–Spatial Feature Extraction for Hyperspectral Image Classification Using Enhanced Transformer with Large-Kernel Attention. Remote Sensing, 16(1), 67. https://doi.org/10.3390/rs16010067








