Abstract
Research on high-temporal-resolution rock slope monitoring has tended to focus on scenarios where spatial resolution is also high. Accordingly, there is a lack of understanding of the implications for rock slope monitoring results in cases with high temporal resolution but low spatial resolution, which is the focus of this study. This study uses automatically captured photos taken at a daily frequency by five fixed-base cameras in conjunction with multi-epoch Structure-from-Motion (SfM) photogrammetric processing techniques to evaluate changes in a rock slope in Majes, Arequipa, Peru. The results of the monitoring campaign demonstrate that there are potential issues with the common notion that higher frequency change detection is always superior. For lower spatial resolutions or when only large changes are of concern, using a high-frequency monitoring method may cause small volume changes that eventually aggrade into larger areas of change to be missed, whereas most of the total volume change would be captured with lower-frequency monitoring intervals. In this study, daily change detection and volume calculation resulted in a cumulative rockfall volume of 4300 m3 over about 14 months, while change detection and volume calculation between dates at the start and end of the 14-month period resulted in a total rockfall volume of 12,300 m3. High-frequency monitoring is still the most accurate approach for evaluating slope evolution from a rockfall frequency and size distribution perspective, and it allows for the detection of short accelerations and pre-failure deformations, but longer-term comparison intervals may be required in cases where spatial resolution is low relative to temporal resolution to more accurately reflect the total volume change of a given rock slope over a long period of time.
1. Introduction
Monitoring of natural, modified, and engineered rock slopes is sometimes necessary to provide an indication of slope activity that can be used to assess hazard, inform land use or hazard mitigation decisions, and possibly provide early warning of a destructive or life-threatening event [1,2,3]. With continued population growth and increased traffic and development in steep and mountainous regions, there has been exponential growth in the number of publications focused on rockfall since the 1980s, with a notable increase in the early 2000s [4]. Given that rockfall can cause extensive property damage, injury, loss of life, and disruptions to human activities (particularly transportation), it is important to further the understanding of rockfall in a variety of environments. Changes associated with the failure stage of rockfall can occur in quick succession, making temporal resolution a key consideration with regard to detecting individual rockfalls rather than accumulated changes. An increased understanding of the importance of rockfall monitoring frequency, monitoring method limitations, and, more directly, rock slope evolution can lead to improved hazard assessment. Structure-from-Motion (SfM) photogrammetry is a convenient tool for the development of three-dimensional models of natural scenes, and it has frequently been used for rock slope characterization and monitoring in recent years [5,6,7,8].
In this study, terrestrial fixed-base SfM photogrammetry is used to monitor regularly occurring rockfall at a landslide head scarp located near Majes, Peru. The primary aim of this study is to examine the impacts of low spatial resolution relative to the temporal resolution on long-term slope monitoring results. Previous studies have considered the influence of temporal resolution on rockfall inventories but have either used monthly or less frequent surveys [9,10,11], consist primarily of spatially independent rockfalls [12], or have been able to detect very small volume changes [13,14,15,16]. This study is unique in that the temporal resolution is high (daily data capture) but the spatial resolution is low relative to the temporal resolution such that the minimum detectable change magnitude is over an order of magnitude larger than typical daily slope changes. Understanding the implications of this type of configuration on change detection results is crucial, as monitoring systems with these types of practical limitations are expected to be implemented increasingly often in the future as cost reduction and improvements to automation encourage the use of such systems in practical (non-ideal) conditions.
Several studies have explored ground-based lidar and photogrammetric rockfall monitoring solutions with relatively high spatial resolution, thus allowing rockfalls smaller than 1 m3 to be identified. For example, Hartmeyer et al. [17] performed 78 terrestrial lidar scans between 2011 and 2017 of a rock slope that was buttressed by a thinning glacier. They found spatial correlations between the location of rockfalls and the recently exposed active layer (freeze–thaw) where glacial thinning had occurred. Birien and Gauthier [15] performed 17 lidar surveys scheduled based on forecasted weather events and recorded weather data over a total study period of 554 days to make connections between rockfall magnitude, rockfall frequency, and different weather conditions. Specific to photogrammetric monitoring, there have been a few studies that monitored at daily or sub-daily frequencies or used systems capable of monitoring at sub-daily frequencies [5,6,16]. Kromer et at. [5] performed daily close-range SfM change detection for rockfall monitoring using photos from a system of five fixed cameras, showing that precision similar to lidar can be achieved for some applications and that using a combination of photos (multi-imagery) with slightly different lighting conditions can improve point cloud precision. Giacomini et al. [16] used stereophotogrammetry and semi-automated change detection procedures to monitor for rockfall in an open pit mine, showing that their system could effectively be used to build rockfall inventories including details about size, shape, frequency, and geology. Blanch et al. [6] used a similar camera setup to Kromer et al. [5] but implemented a multi-epoch image alignment procedure to increase precision and aid in georeferencing. These studies that used photogrammetric monitoring provide important methods of evaluation to optimize the setup and processing efficiency of photogrammetric monitoring, but there has been limited evaluation of long-term, high-frequency photogrammetric monitoring results in the literature. Furthermore, these studies, both lidar- and photogrammetry-based, do not fully evaluate the importance of spatial resolution with respect to temporal resolution using examples where the combination of resolutions is less than ideal.
The exact monitoring setups and frequencies used in each of these previous studies were generally chosen based the site-specific requirements, data processing abilities, cost considerations, as well as considerations of precision based on geological models for the monitoring sites. For rockfall monitoring applications, there have been several recent efforts to more closely evaluate the implications of monitoring system selection, specifically with regard to monitoring frequency and spatial resolution, on rock slope evolution. Rockfall volume–frequency relationships are well-documented in the literature [18]. Specific to evaluating the impact of temporal resolution on detected rockfall volume and frequency, van Veen et al. [9] captured seven lidar scans of a rock slope with high rockfall activity over the course of 15 months and used four different subsets of the scans with different monitoring intervals to show that at longer intervals, information is lost regarding small rockfalls because the extents of small rockfalls begin to overlap over time and cannot be distinguished as individual rockfalls. They also noted that the impact of monitoring frequency on overall magnitude–frequency relationships was minimal. Williams et al. [13] showed a similar loss of information at longer intervals as van Veen et al. [9], but they found that volume–frequency relationships are most sensitive to monitoring frequency over much shorter monitoring intervals (less than 12 h). While these studies have made significant contributions toward monitoring program design and rockfall analysis, understanding rock slope evolution, and showing the implications of different monitoring frequencies, they have all had spatial resolutions that were relatively high compared to the monitoring frequencies used. The goal of this study is to explore the limitations of using a high-temporal-resolution monitoring approach with a relatively low spatial resolution. This investigation aims to provide insights for slope monitoring system design where near-slope monitoring is not possible or where sensor quality is poor but short-term slope changes are of interest.
2. Study Site
The rock slope considered in this study is in the Siguas River Valley near the Majes District in Arequipa, Peru (Figure 1).
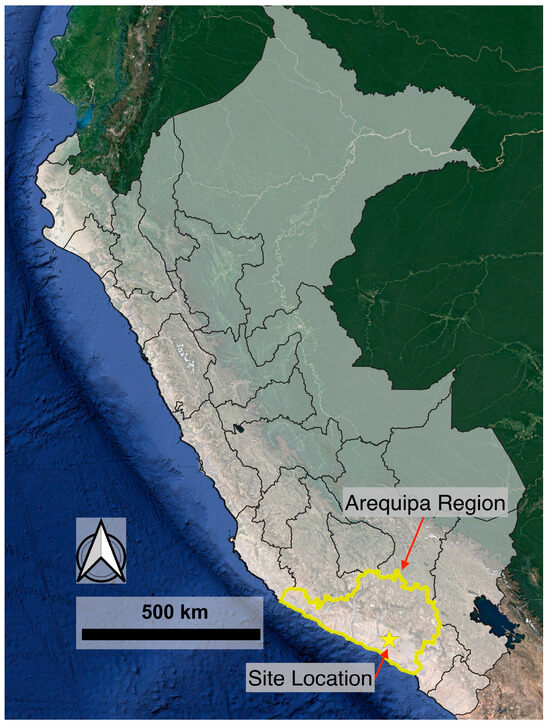
Figure 1.
Site location map showing the project site location in southern Arequipa Region, Peru.
Landslides are a common occurrence in the river valley, with most activity occurring on the northern valley wall [19]. There are a few publications related to landslides in this valley and neighboring valleys that have investigated groundwater conditions [19,20], analyzed geophysical survey data [21], monitored landslide activity with satellite remote sensing and GPS [22,23], and conducted detailed investigations of existing landslides [24]. All of these publications point to increased groundwater levels due to irrigation as a major contributing factor to landslide activity. Similar relationships between landslide activity and irrigation can be seen in several other regions globally [25]. These landslides often leave steep exposed head scarps that exhibit high levels of rockfall activity.
The Siguas River Valley incises into a relatively flat-lying mesa (or pampas). Local to the study site, the main geological unit of interest is the Moquegua Formation. The Moquegua Formation is composed of a series of sub-horizontally bedded conglomerates and sandstones with weak layers of volcanic tuff, clay, poorly cemented gravels, and occasional carbonate marine deposits [24]. The upper 20–30 m is sometimes considered separately as the Millo Formation, which is predominantly conglomerate [19,21]. The Moquequa Formation generally has higher strength than the rocks of the Millo formation, making the Moquequa more of a cliff-forming unit compared to the Millo, which erodes quickly when over-steepened. A schematic cross section of the rock slope is shown in Figure 2.
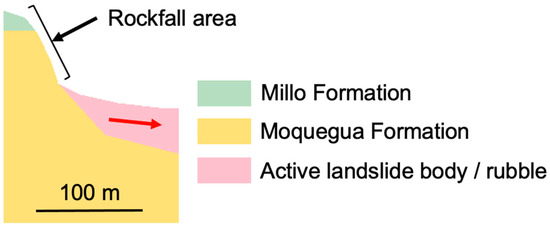
Figure 2.
Schematic cross section of the monitored rock slope (scale is approximate, with no vertical exaggeration).
The site (lat: −16.41951, lon: −72.16939) includes a roughly 700 m long and 600 m wide landslide that can be further classified as a rockslide-debris-slide. The slide is locally referred to as Pachaqui Grande, which is a nearby annex. The location for this study was selected after the identification of a large tension crack at the top of the slope during a site visit in 2019, suggesting that a large-scale scarp retrogression event was likely imminent. The presence of a road on the opposite side of the valley where fixed cameras could be easily installed was also a consideration. Prior to initialization of the photogrammetric monitoring system (in December 2020), the anticipated large-scale displacement did occur, and material from the head scarp moved up to 70 m over the course of five months based on satellite imagery from Planet Labs [26]. While the major event was not captured, the freshly exposed head scarp contributes to the suitability of this site for research as there is consistent rockfall activity, with several individual events over 100 m3 in volume occurring. Although parts of the landslide body were imaged as part of the conducted monitoring campaign, evaluation of the landslide movement is a complex problem in and of itself and is outside the scope of this study.
3. Materials and Methods
3.1. Fixed Camera System
The camera system consisted of five Canon EOS 5D Mark IV 30-megapixel cameras with 85 mm fixed-zoom lenses that were manually focused. Still-image monitoring was chosen over video monitoring because lower-cost, higher-resolution still-image options are available and because the amount of data to transfer and store is much more manageable compared to video for long monitoring periods. The locations of the cameras were chosen on the basis of accessibility (located on a road bench), proximity to the landslide (the toe of which was only 100 m from the cameras), having a viewing angle that allowed for a large portion of the landslide body as well as the head scarp to be captured, and not being easily visible from roads in the area to limit the potential of tampering or theft. Each camera was placed in waterproof housing that was mounted on a metal pole and anchored into the ground with epoxy (Figure 3). The cameras were installed roughly 50 m apart from each other and oriented such that the final image network was convergent. The approximate look angle of the cameras was an azimuth of 297 degrees, which is the same approximate look angle used for all subsequent photos and SfM models of the slope in this paper unless otherwise specified. The ground sampling distance (GSD) at the head scarp for each camera was roughly between 6 and 7 cm. The camera locations and the total field of view for all five cameras is shown in Figure 3. For georeferencing, six Metashape standard 12-bit circular coded targets (sometimes referred to as markers) served as ground control points (GCPs) and were installed on the middle and lower portions of the slope (Figure 3). Each target had a diameter of 1 m. The targets were installed on the landslide body because there was no stable or accessible area of the slope within the field of view where they could be placed. To the northwest of the depicted targets and on the landslide body, the slope was either occluded from the view of the cameras or was not accessible for target placement, resulting in a somewhat confined distribution of GCPs relative to the size of the monitored area.
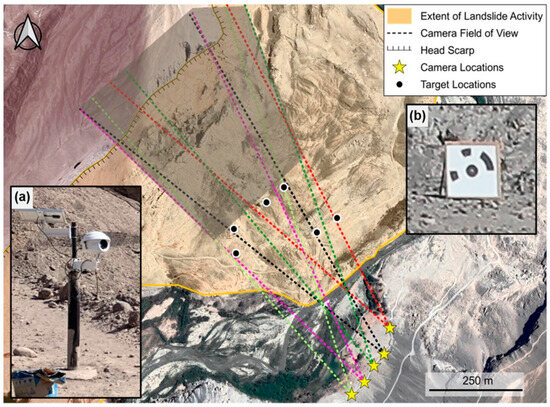
Figure 3.
Photogrammetry system aerial overview with inset photos of a typical fixed camera station (a) and one of the ground control point (GCP) targets (b) at the project site. The horizontal field of view extents are shown with unique colors for each camera. The area shaded in grey was unsuitable for target placement.
3.2. Data Acquisition and Quality Control
Once all five cameras were fully operational (24 December 2020), three photos were captured from each camera twice a day—once at 8 a.m., and once at 2 p.m. The choice to capture three photos per epoch was a compromise between increased model precision (see Section 3.3) and practical limitations, such as data storage, telemetry data transfer speeds, and system power usage. Having multiple camera triggers also allows for redundancy should a camera fail to trigger or if an image is corrupted or temporarily obstructed. The cameras were triggered six minutes apart during both the morning and afternoon epochs using Digisnap camera controllers that are a part of the Cyclapse timelapse system produced by Harbortronics [27]. During the first few months of system operation, photos were automatically uploaded to a remote storage location via a cellular-enabled data logger, but issues with signal quality ultimately led to the decision to collect the photos manually once per month. Regarding the reliability of the camera triggering system itself, there were a few extended periods where camera 1 was non-operational, a few periods where camera 3 was non-operational, and a brief period of 5 days in March where all cameras failed to trigger. There was also a brief period in December 2020 where cameras 3 and 4 were out of focus due to a faulty connector in the timelapse system.
Poor-quality photos can lead to poor-quality photogrammetric models, so to mitigate this, photos below 12 megabytes (MB) (15–20 MB was found to be typical in more ideal conditions) were removed from the dataset. Some of the photos removed during this step were corrupted, some were out of focus, and some were a low file size due to image compression resulting from atmospheric conditions, such as clouds and haze, having caused large areas of the images to be similar in color. There were still photos over 12 MB that were captured in poor atmospheric conditions. These photos were manually identified and excluded from subsequent processing steps. The most common cause of poor atmospheric conditions for higher-quality photos was dust, haze, and fog in the later afternoon, particularly in the winter months (June–September). This initial rejection process left the acceptable photo count at 9417 compared to the original count of 11,209, a roughly 16% reduction. Overall, 83% of days (350/424) had at least one epoch of remaining photos from four or five cameras.
3.3. Workflows for Multi-Epoch Photogrammetric Model Construction
Agisoft Metashape v.1.6.6 and v.1.8.3 [28] were used to create 3D point cloud models using the site photos. Only photos captured in the morning are further considered in this paper because the number of usable morning photos is higher than for afternoon photos and because comparisons between models developed using morning and afternoon photos were not typically successful due to dramatic differences in lighting. Processing was automated using scripts in Python v.3.9 [29] in conjunction with the Metashape Python API. The steps to produce a point cloud include image alignment (or sparse point cloud construction), alignment optimization, and dense point cloud construction.
Following a check to ensure that the dates being processed all had photos from at least four cameras, image alignment in Metashape v.1.8.3 was performed using the highest accuracy setting, an upper key point limit of 200,000, and no tie point limit. Generic preselection was enabled, while reference preselection, adaptive fitting, and guided image matching were disabled. The camera positions and orientations solved during alignment were then optimized using an iterative process of gradual tie point selection, deleting the selected tie points, and then performing optimization with all default fitting parameters enabled. “Fit additional corrections” was not enabled. The first iteration selected tie points down to a reconstruction uncertainty ratio of 10. The second iteration selected tie points down to a projection accuracy of 3. The final three iterations selected tie points down to a maximum reprojection error of 0.3 key point units (~1 pixel). In each iteration, a maximum of 20% of tie points were selected, and the process was stopped if the tie point count dropped below 60,000. Only one iteration was performed for both reconstruction uncertainty and projection accuracy, as performing multiple iterations was found to consistently cause the tie point count to drop below 60,000 before the reprojection error filtering could be performed. Following alignment, photos with fewer than 300 total projections were disabled.
Metashape 1.8.3 was the latest version when these methods were established, but it was found that the dense point clouds in versions 1.7 and 1.8 had large gaps and holes, which was interpreted to be a consequence of stricter filtering in the depth map calculations. Performing the dense point cloud construction in v.1.6.6 avoided this issue. Metashape v.1.8.3 was still used for earlier steps due to its ability to automatically sort cameras into appropriate calibration folders based on camera serial number.
Accordingly, dense point cloud construction was performed in Metashape v.1.6.6 using the medium density setting and aggressive depth filtering to produce point clouds between three and six million points. The point spacing at the head scarp (where rockfall occurs) was generally around 0.25 m. Figure 4 shows the portion of the head scarp considered for rockfall detection in both a site photo and a resulting dense point cloud from the workflow described above.

Figure 4.
Areal extent of rockfall change detection shown and outlined in black in one of the site photos (a) and a dense point cloud (b) resulting from the SfM workflow. This area is the head scarp of the landslide, while the areas not included to this extent either correspond to the landslide body or poor camera overlap.
For SfM-based point cloud change detection to be effective, the compared point clouds need to have consistent geometry and georeferencing such that all features and changes are aligned appropriately. A multi-epoch image alignment approach can be used to achieve this consistent georeferencing and model geometry [7,30,31,32], which can be improved further with multi-imagery, as demonstrated by Blanch et al. [6] and termed Multi-Epoch and Multi-Imagery (MEMI). A multi-imagery workflow implies that for each camera in each epoch, multiple photos are captured within a short time frame (seconds to minutes) and then used for all subsequent processing steps that involve that epoch. The theory is that the slight variations in lighting result in the identification of additional features (i.e., key points), thus leading to a larger number of tie points from the image alignment step. Using a multi-imagery workflow has been shown to improve model precision [6]. A multi-epoch workflow implies that two or more epochs of photos are used during the image alignment processing such that dense point clouds for each epoch can then be created from a single set of tie points (shared between each epoch). According to results shown by Blanch et al. [6], multi-epoch workflows that also use multi-imagery offer further improvements in precision.
We chose to implement a MEMI workflow for this study not necessarily because of the possibility of improved model precision (although it was a consideration) but because models created with single-epoch image alignment were geometrically dissimilar enough that alternative scaling and registration techniques were not sufficient to closely register the point clouds for subsequent change detection, which is similar to results shown by Cook and Dietze [31]. Recently developed multi-sensor, non-rigid registration methods [33] were not applicable given that no additional sensors or remote sensing surveys other than the fixed cameras were used for this research. Fixing camera calibration parameters across multiple epochs (i.e., solving external calibration parameters initially with the reference epoch and then using the same calibration parameters to build models for subsequent epochs) was also not effective as the cameras did experience some movement throughout the course of this study due to opening of the camera housing for manual data transfer, wind, and, potentially, other factors. The reason the multi-epoch approach was found to work is that the tie points found between epochs are generally only in areas where effectively no change has occurred (in this case, unchanged portions of the head scarp) [34]. This does limit the application of this method to sites where there is some sufficiently large portion of the scene that is relatively stable (in the absence of stable GCPs or repeated surveys of unstable GCPs). For the study site in this research, roughly 15 percent of the 2D image area in any given photo can be considered globally stable over the course of the monitoring period. The vast majority of the stable area corresponds to the head scarp of the landslide.
Implementation of the MEMI workflow involved including one reference epoch in every MEMI set. The reference epoch date was set to be 24 December 2020, which was the first day that the setup was completed. The coded targets (GCPs) on the slope, which were surveyed at the beginning of the monitoring period, were marked in all of the images from the reference epoch for initial georeferencing purposes. The GCPs were only used in the one epoch because there was no accessible stable ground and there were no additional ground surveys completed after targets had moved with the slide body. For rockfall monitoring, three epochs in total were included in the image alignment step. This included the reference epoch (with surveyed GCPs) and two comparison epochs. Rockfall detection was performed between the comparison epochs, which resulted in ~24 h day-to-day comparisons (in most cases). Under ideal conditions, a MEMI set for rockfall monitoring contained 35 photos (2 comparison epochs × 5 cameras × 3 photos + 1 reference epoch × 5 cameras × 1 photo). The maximum number of photos was rarely achieved, as the cameras sometimes failed to trigger, and many photos were removed during preliminary quality control (Section 3.2). For each three-epoch set of photos, image alignment (with no pre-calibration) and optimization were performed, and then three separate dense clouds were constructed by only selecting photos from one epoch, building the dense cloud, exporting the dense cloud, and then selecting only the photos from the next epoch and repeating the sequence until all three dense point clouds were constructed and saved. A schematic of the described MEMI workflow as implemented in this study is shown in Figure 5.
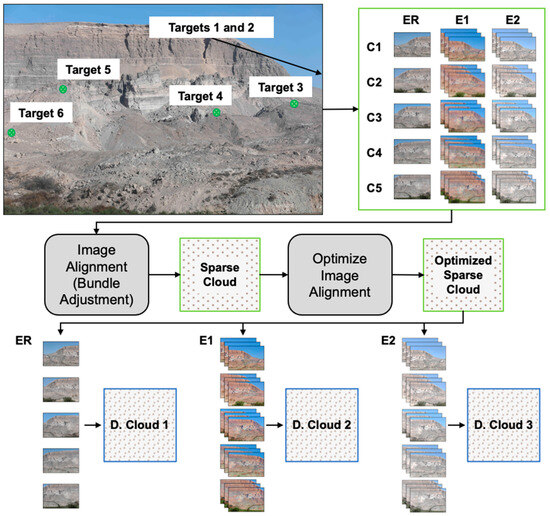
Figure 5.
Full multi-epoch and multi-imagery (MEMI) workflow for rockfall monitoring. Cameras labeled C1–C5. Individual epochs are labeled ER (for the reference epoch) and E1, E2 (for comparison epochs). Dense point clouds are labeled D. Clouds 1–3. Figure after Blanch et al. [6].
3.4. Change Detection, Clustering, and Volume Estimation
Methods originally developed for rockfall detection using lidar point clouds were applied to point clouds developed using the photogrammetric workflow [35,36,37,38,39]. Rockfall monitoring in this study consisted of a processing workflow that included initial masking (i.e., cropping) of the dense point clouds to an area of interest relevant for rockfall detection, computing Multiscale Model to Model Cloud Comparison (M3C2) change [35] in the forward and reverse directions, merging and filtering the M3C2 results, and applying the DBSCAN clustering algorithm [37]. Similar to other studies [6,16,36,38], the full workflow was implemented in Python, with masking, merging, and filtering being executed using CloudComPy and DBSCAN being executed from the machine learning Python module scikit-learn [40].
The created mask was consistent with the head scarp outline in Figure 4. The mask ensured that areas of talus and loose material both above and below the main rock slope face were not included. The mask also excluded about 80 m of the leftmost (southern) extent of the models and about 40 m of the rightmost (northern) extent. These portions of the point clouds were consistently noisier than the central part of the scarp, particularly for point clouds built using photos from only four cameras. The mask also excluded an approximately vertical sliver of the right side of the largest gully near the north extent of the head scarp, because this section almost always had severe shadowing and the local slope trend was roughly parallel to the look direction of the cameras, leading to a large hole in the point cloud at this location.
The change detection portion of the rockfall monitoring workflow consisted of performing M3C2 twice: once forward in time (projected onto the earlier-in-time dense point cloud) and once in reverse (projected onto the later-in-time dense point cloud). The input parameters for M3C2 consisted of a normal diameter of 1.5 m, a projection diameter of 1.5 m, a max depth of 50 m, and point cloud normals computed for all points with a preferred orientation approximately perpendicular to the overall head scarp. The current state of practice when using M3C2 to compare lidar point clouds is to use a projection diameter equal to or slightly greater than the point spacing [41], but because this rule of thumb is for point clouds where each point is an individual measurement, it does not necessarily translate directly to photogrammetry tie point clouds and even less so to dense point clouds. We used a diameter of 1.5 m, which is roughly five times larger than the typical dense point spacing, as a means of filtering out some of the noise in the point clouds. M3C2 results were then filtered such that only points with a change magnitude above 0.40 m remained. This value was chosen to be slightly larger than the average M3C2 standard deviation of 0.35 over the full monitoring period and is therefore below the two-standard-deviation “limit of detection” for many change calculations; this relatively low filter threshold value was selected to ensure the detectability of relatively small rockfalls, although it necessitated extensive manual validation efforts to discard regions of false change (see Section 3.6). Overall, change filter application ensured that large-scale real change was captured while simultaneously limiting the amount of noise and low magnitude change that was carried through to subsequent processing steps. The filtered change point clouds were then merged such that the front and back faces of the change regions were grouped together in a single point cloud.
The final step to produce change clusters was to run the filtered and merged change point cloud through the DBSCAN clustering algorithm. The two input parameters for DBSCAN are epsilon and a minimum point count value. Epsilon is the maximum distance between two points such that they are considered part of the same neighborhood. The minimum point count is the total number of points required to define a cluster. In some cases, these two parameters can be estimated based on point cloud characteristics, such as point spacing and k nearest neighbor relationships [42], but for our photogrammetric point clouds, where there can be large spatial and temporal variations in point density, distortion, and noise (compared to lidar point clouds), we opted to manually test and choose the epsilon and minimum point values. At higher values of minimum points, some small but visually identifiable rockfalls were not clustered. At higher values of epsilon, it was increasingly common for small, close-together areas of change to be grouped into single clusters. Several combinations of parameters were initially tested with epsilon not exceeding 2.0 and minimum points parameter not exceeding 400 points. The final selected parameters for epsilon and minimum points were 0.8 and 80, respectively.
Cluster volumes were calculated using an iterative Alpha-shape procedure that iterates through the Alpha volumes that result in unique shapes and “finds the smallest Alpha-radius that produces a watertight manifold surface mesh” [36]; this is equivalent to the smallest Alpha-radius that results in a single-volume closed shape that can exist in real 3D space. This was performed on a cluster-by-cluster basis so that a single enclosed Alpha-shape was produced for each cluster.
3.5. Identification and Removal of High-Noise Point Clouds and Anomalous M3C2 Results
Because lighting conditions and, ultimately, the amount of noise in the dense point clouds from the Majes site were highly variable, there was a tendency for large numbers of false positive clusters (i.e., erroneously identified rockfalls) to be produced in some cases. To reduce the number of false positives resulting from less-than-optimal point cloud comparisons and correspondingly limit the manual effort needed for cluster validation, clustering results and change detection metrics were used as criteria for point cloud rejection. The two metrics used were the number of clusters of 10 m3 or greater and the M3C2 standard deviation. If there were more than 10 clusters greater than 10 m3 and M3C2 standard deviation was above 0.5 m, the comparison was flagged and manually evaluated to make sure the large clusters did not represent real rockfall, and then those comparisons were rejected and new comparisons were performed to span the dates of the rejected comparisons by modifying a comparison adjacent in time (whichever had a lower M3C2 standard deviation). This rejection procedure was not iterative, and the rejection criteria were only evaluated once. Prior to comparison rejection, there were 348 comparisons over a total time span of 399 days. After comparison rejection, there were 330 remaining comparisons.
3.6. Manual Cluster Validation
Using the cluster database created after the data rejection procedure described in Section 3.5, clusters with calculated volumes over 5 m3 were manually confirmed using site photos. To accomplish this, photos from the same camera and different epochs were spatially aligned in 2D, and then one of the two photo layers was activated and deactivated repeatedly to see if changes were apparent in the photos within the vicinity of the identified changes in the point clouds. In the photos, much smaller changes were evident than in the dense point clouds because the pixel spacing is finer than the point spacing, but, more critically, because the noise (i.e., point location imprecision) in the dense point clouds made interpretations of small changes impractical, if not impossible. Clusters with volumes below 5 m3 were not assessed to limit the amount of manual cluster validation required due to excessive numbers of false positive clusters below this volume as well as to exclude the smallest clusters, which were visually observed to exhibit the largest discrepancies between apparent areal extent of change (per the point clouds) and actual rockfall (per the photos). If there was no change consistent with rockfall identified in the photos within the extent of a cluster, the cluster was marked as a false positive. Regardless of apparent discrepancies in the overall areal extent, for clusters above 5 m3, if there was any change identified in the photos that was visually consistent with rockfall and was at all within the extent of a point cloud change cluster, the cluster was marked as validated (i.e., real) change. The changes were further manually classified as block falls, block falls with areal extent agreement (AEA), and non-block-fall changes (slope ravel). These classifications were assigned through manual evaluation of site photos. Blocks were considered to have AEA if the areal extent of the clusters (as viewed in the look direction of the cameras) was estimated to be less than two times the extent of change evident In the site photos or if the extent in the photos was less than two times larger than the cluster extent. At decreasing volumes, AEA became less common, and the relative error (percent difference) between cluster and photo areal extents was often greater. While errors near the minimum volume limit were a concern, the overall impact of these errors is limited because the full range of rockfall volumes spans several orders of magnitude. A breakdown of the classifications of detected change is shown in Figure 6.
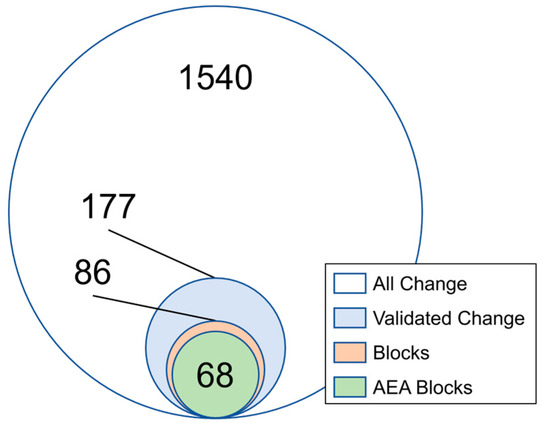
Figure 6.
Number of clusters over 5 m3 categorized by all clusters (prior to manual validation); only clusters that were validated manually using site photos; validated clusters that were identified as rock blocks; and validated clusters that were identified as blocks and also had areal extent agreement (AEA) between cluster and site photos.
Figure 7 shows all false positive clusters identified from the high-frequency workflow, which cover the majority of the area of interest. Areas with concentrated clusters correspond to consistently shadowed regions or regions where point density was particularly inconsistent. These clusters correspond to the difference between “validated change” and “all change”, as shown in Figure 6.

Figure 7.
False positive clusters over 5 m3 identified over the full monitoring period using the high-frequency workflow. The area of interest (AOI) where change detection was performed is outlined in green.
3.7. Magnitude–Cumulative Frequency Curves
The two primary components of rockfall activity that go into evaluation of a given site are rockfall frequency and rockfall volume. These measurements can be used to create magnitude–cumulative frequency (MCF) plots. A power law distribution can be fit to rockfall MCF data. MCF curves were only fit to datasets with five or more rockfalls for this paper. These fitted MCF curves can be used to estimate the recurrence interval for a rockfall of a given volume. The power law distribution in terms of these two measurements is shown in Equation (1), where V is rockfall volume and the constants a and b are fitting parameters.
F(V) = aV−b,
MCF curves typically have a “roll-over” at low volumes below which the power law relationship is no longer representative of the data [11]. The roll-over is typically attributed to spatial resolution because low volumes begin to be under-sampled toward the minimum detectable rockfall volume (i.e., small-volume rockfalls are less likely to be identified) [10,18]. No signs of such a phenomenon were seen in the MCF plots for volumes over 5 m3, suggesting that the transition from complete to incomplete sampling would occur in this case at a volume below the volume selected for manual cluster validation.
3.8. Single Start-to-End Comparison
To evaluate the influence of high-temporal-resolution rockfall monitoring with spatial resolution being a limiting factor in terms of total rockfall volume, a separate, single start-to-end comparison (SSEC) was performed between the monitoring start and end dates of 24 December 2020 and 27 January 2022 (399 days), thus producing a single set of clusters representative of the total rock slope changes over the course of the monitoring period. The clusters were validated in the same way as described in Section 3.6 through manual evaluation of photos from the two compared dates. Evaluation of the enclosed volumes produced by the Alpha-shape algorithm (as described in Section 3.4) revealed that substantial regions unassociated with observed change were being included in the calculated volumes (compare Figure 8a,b). This was found to be a result of the clustering procedure creating very large clusters with irregular and tortuous geometries associated with overlapping or adjoining rockfall regions as opposed to individual rockfall blocks (for which the applied procedure was designed). To mitigate this, the large clusters were manually split up to produce clusters with less large-scale concavity, and cluster volumes were re-calculated. As a primary criterion for this manual splitting process, if a single cluster had multiple regions joined by a small number of points relative to the number of points in the individual regions, the cluster was divided. Additionally, if an otherwise blocky/uniform cluster had localized regions that were tortuous or protruding, these regions were extracted as separate clusters. The result of manual cluster splitting can be seen in Figure 8b, and the associated outlines of the corresponding Alpha-shapes used to calculate volumes are shown in Figure 8c.
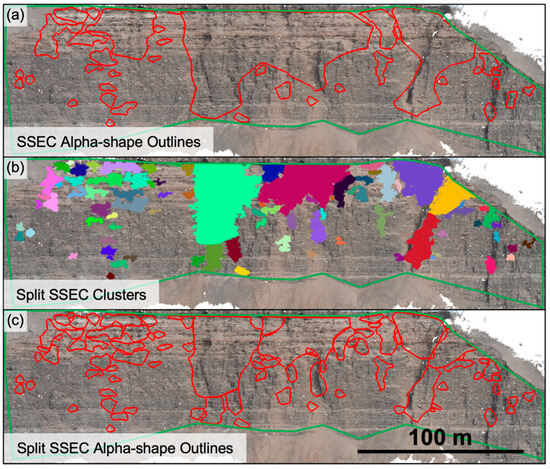
Figure 8.
Visualization of manual cluster splitting process showing (a) outlines of Alpha-shapes prior to cluster splitting, (b) manually split-up clusters, and (c) the resulting Alpha-shape outlines of the divided clusters. The colors used to show individual clusters are a visual aid and have no additional meaning.
4. Results
4.1. Point Cloud Model Quality
The MEMI method allowed for generally consistent quality and alignment of point clouds between different dates, although there was some degree of remaining variability depending on the exact combination of photos being used for the comparisons. Figure 9 shows M3C2 distance for a typical comparison as well as end-member cases. For the typical case where the M3C2 standard deviation was 0.40 m as well as the higher-quality result where the standard deviation was 0.22 m, the compared models were in good agreement, as indicated by the predominance of green and yellow colors corresponding to low-magnitude change. The lower quality result, where the standard deviation was 0.70 m, had many local areas of higher-magnitude change, which, in this case, were not associated with obvious rockfall but can rather be attributed to local variations in point density (i.e., holes in the dense point clouds), possibly due to lighting and shadowing differences between the photos from the compared dates. The total distribution of M3C2 standard deviation results for the full monitoring period is shown in Figure 10.

Figure 9.
Multiscale model-to-model cloud comparison (M3C2) change point cloud results where the standard deviation was (a) 0.22 m between dates 6 January 2021 and 7 January 2021, (b) 0.40 m between dates 29 March 2021 and 30 March 2021, and (c) 0.70 m between dates 7 November 2021 and 8 November 2021. Note the slight change in overall color, from green to a more yellowish hue, indicative of the shift toward higher change values overall.
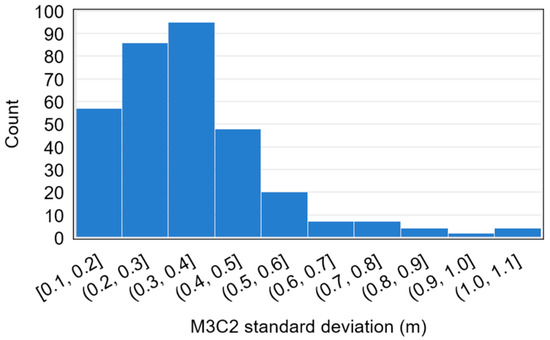
Figure 10.
Distribution of comparison multiscale model-to-model cloud comparison (M3C2) standard deviations over the course of the monitoring period.
4.2. MCF Curves
MCF results for the whole monitoring period were relatively consistent regardless of the specific change classification or monitoring frequency classification (Figure 11), although there were some minor but notable variations. The slope of the MCF curve becomes less steep when only considering blocks and even less steep when only considering AEA blocks. This shows that validated changes classified as slope ravel as well as blocks that did not have AEA were generally small in magnitude (closer to the 5 m3 minimum volume limit), so excluding them causes the MCF curve to be more heavily weighted toward larger-magnitude changes. There was also a slight reduction in slope when shifting from considering all comparisons to only one-day comparisons (see Figure 11).
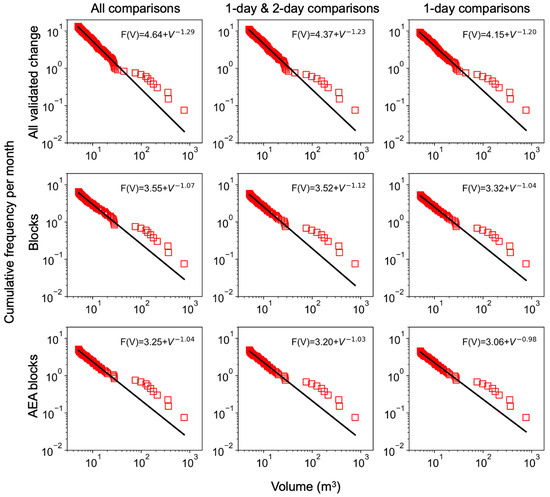
Figure 11.
Magnitude-cumulative-frequency (MCF) plots for the full 14-month monitoring period for three classifications of change and three temporal resolution classifications.
MCF results separated by month show the high degree of variability in block fall MCF relationships over the course of the 14-month monitoring period (Figure 12 and Figure 13 for all blocks and AEA blocks, respectively). Monthly block fall frequencies were highest in January and February of 2021, with June 2021, December 2021, and January 2022 showing moderate frequencies of block fall, while the remaining months showed little or no block fall activity. Except for a 136 m3 block in March 2021 and a 354 m3 block in December 2021, most of the large block falls occurred in January and February 2021.
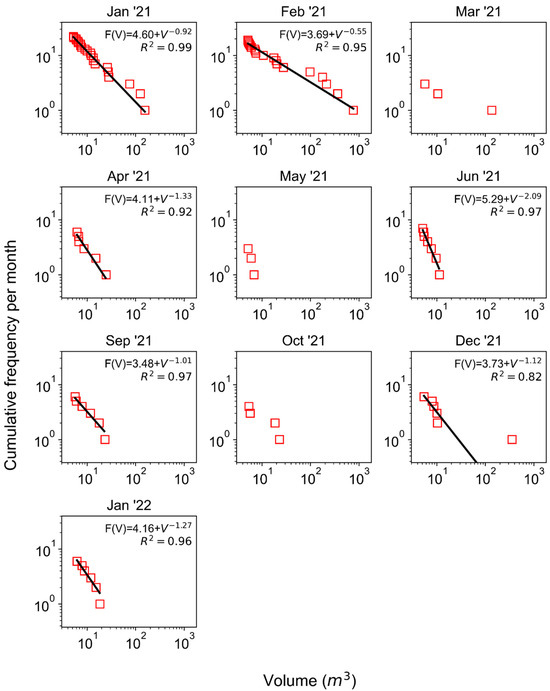
Figure 12.
Magnitude-cumulative-frequency (MCF) plots created using all validated block falls. Months not shown had no clusters corresponding to validated block fall (July 2021, August 2021, November 2021). MCF curves were only fit to the data if there were more than five clusters.
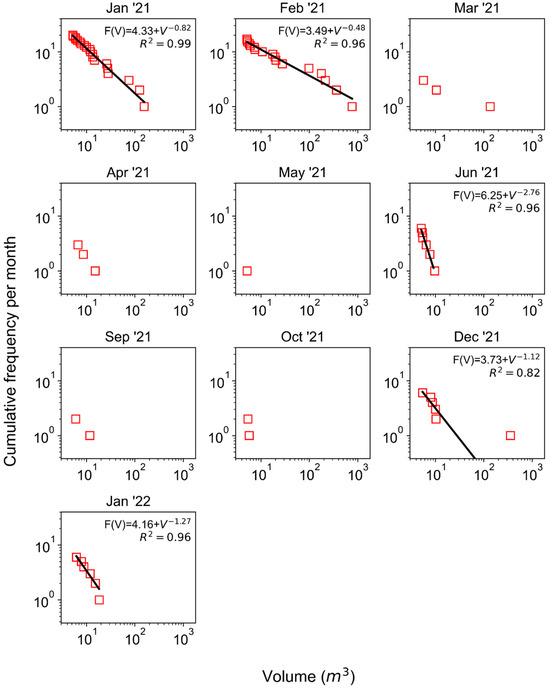
Figure 13.
Magnitude-cumulative-frequency (MCF) plots created using all validated areal extent agreement (AEA) block falls. Months not shown had no clusters corresponding to validated AEA block fall (July 2021, August 2021, November 2021). MCF curves were only fit to the data if there were more than five clusters.
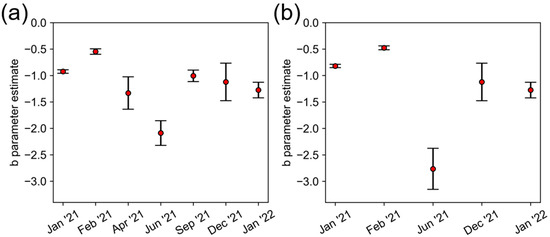
The standard errors of the ‘b’ parameter (slope) estimates for the MCF fits from both Figure 12 and Figure 13 are shown in Figure 14. The standard error was of course higher with fewer data points, but, overall, the differences in slope between months were significant, even when considering the error of each slope estimate. The slope was generally between −1 and −1.5 during the monitoring period, with January and February having notably lower magnitude slopes and June having a notably high-magnitude slope.
4.3. Comparison between High-Temporal-Resolution Monitoring Results and Single Start-to-End Change
For high-temporal-resolution rockfall monitoring where spatial resolution is relatively low, it is important to consider the volume missed by high-frequency workflows that detect rockfall only over short time spans (typically daily in this study). The true positive clusters for the high-frequency workflow as well as the clusters from the SSEC workflow are shown in Figure 15. This shows the areal extent disagreement between the two workflows viewed from an approximately slope-normal orientation. This difference can be attributed to daily changes of less than 5 m3 that accumulate to larger changes over time, which were captured in the single start-to-end comparison.
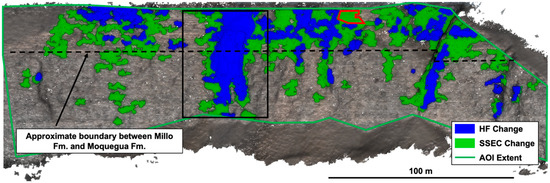
Figure 15.
Comparison of the extent of change (validated clusters over 5 m3) identified using the high-frequency (HF) workflow and a single start-to-end comparison (SSEC). The area of interest (AOI) where change detection was performed is outlined in green. The black outline is showing a large portion of the slope that failed through progression of large-volume block falls and the red outline is showing an area where the HF workflow failed to identify an area of real change.
Much of the volume discrepancy was in the weaker Millo Formation, which can be seen in the upper 1/3 of the rock slope. As a point of comparison (and to avoid potential influences of the applied Alpha-shape volume estimation algorithm), total volumes were estimated based on 2D areal extents and average cluster M3C2 change distances; based on this calculation, the total volume for the high-frequency workflow was 3200 m3, and for SSEC it was 8500 m3. In comparison, based on the Alpha-shape approach, the total volume of all validated change with the high-frequency workflow was 4300 m3, while the total volume with the single start-to-end comparison workflow was 12,300 m3. Figure 16 shows the total Alpha-shape volume of all clusters from two workflows: the high-frequency workflow, where clusters detected over short time spans are all added together, and the SSEC workflow, where the total volume of clusters produced from a single start-to-end comparison is shown. The idea behind comparing the two workflows was to evaluate the sensitivity of the workflows to the minimum cluster volume considered (as representative of the effective spatial resolution). This allows for rough extrapolation to lower volumes below 5 m3, and it also shows the impacts of using an even lower spatial resolution system (i.e., larger minimum volume thresholds).
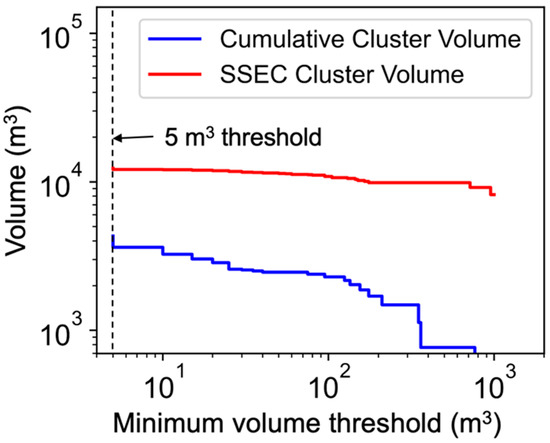
Figure 16.
Total cluster volume with respect to the minimum cluster size considered for both the results from the high-frequency workflow as well as from a single start-to-end comparison (SSEC).
The “minimum volume threshold” in Figure 16 was the smallest volume cluster considered in the volume summation (i.e., for a minimum volume threshold of 10 m3, the corresponding total volume was only calculated from clusters over 10 m3). These results show that there was a large total volume discrepancy between the two workflows. There was a notable trend in terms of total volume as a function of minimum volume threshold for the high-frequency workflow, while the SSEC showed a relatively constant total volume with different minimum volume thresholds. Given that SSEC clusters were manually split prior to filtering, what trend is seen may artificially reduce the volume at any given minimum volume threshold; with that in mind, the lack of sensitivity to minimum volume threshold for the SSEC results is especially clear, as the degree of variation in total SSEC volume as a function of the minimum volume threshold presented can be considered to be an upper bound. The reason for the relative lack of a trend in the case of the SSEC results is that most of the volume can be attributed to the large areas of spatially correlated change that are captured in single, large clusters, so filtering out small-volume clusters negligibly affects the total volume.
To illustrate the different results obtained from the two different temporal resolutions (the high-frequency workflow and SSEC), an example for a small portion of the slope where the two approaches were in disagreement as to the extent of rock slope changes is shown in Figure 17. In this example, a portion of the scarp is shown where there was an area of change that was detected with the SSEC approach but missed using the high-frequency workflow. This particular section was chosen because it was a relatively large area with clear areal extent and an area where the photos were typically good enough in quality that small changes were readily apparent during manual validation. Figure 18 shows the progression of rockfall activity in this same section of the slope at an approximately monthly interval. Even at the monthly frequency, it is apparent that the changes between the images were relatively small between any two months, but the total change over the course of the year was quite significant.
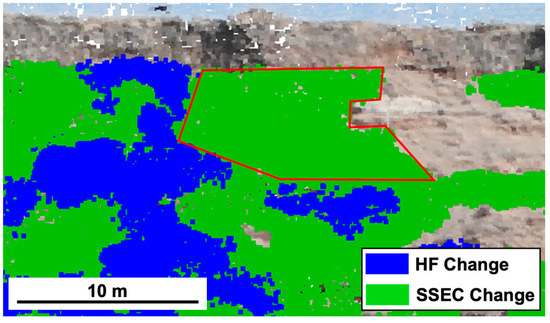
Figure 17.
Example of an area of change (outline in red, see Figure 15) that was included in a cluster over 5 m3 in the single start-to-end comparison (SSEC) but was not detected using the high-frequency (HF) workflow because the long-term change was the result of many changes less than 5 m3 that accumulated over time. The approximate area of the section outlined in red is 70 m2.

Figure 18.
Photos for the area of change in Figure 15 at different times (yyyy-mm-dd) throughout the monitoring period. The arrows show the general locations of the largest change(s) since the previous date. The solid red square in the upper left panel is approximately 1 m2 at the rock slope.
The aggradation of change that occurred at a relatively small scale in Figure 17 and Figure 18 also occurs at larger scales that are captured by the high-frequency workflow. Figure 19 shows this large-scale aggradation as a series of large rockfalls that are spatially correlated and contribute to a significant proportion of the total volume identified using the high-frequency workflow. All of these large-volume rockfalls occurred toward the end of January and the beginning of February, with the exception of the one rockfall in March.
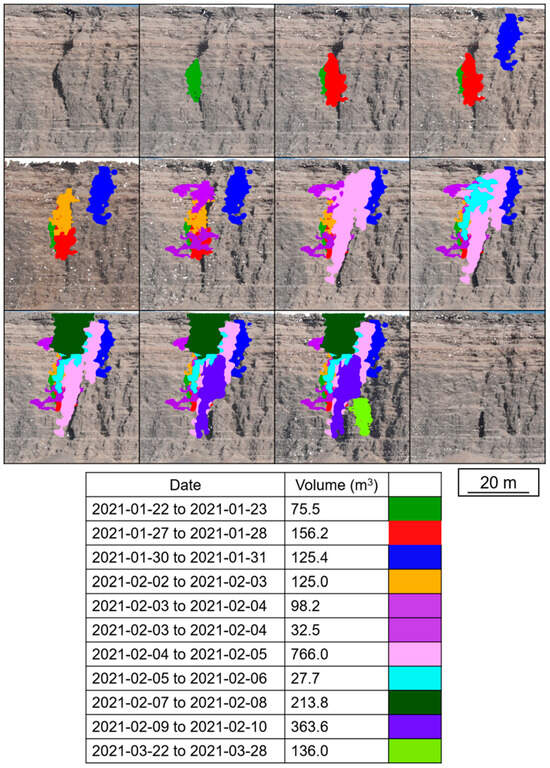
Figure 19.
Large block falls in the center of the head scarp (see Figure 15 for location) that occurred progressively over the course of the first few months of the monitoring period. Dates given in yyyy-mm-dd format.
5. Discussion
A five-sensor, ground-based camera system captured daily photos that were used in a MEMI SfM workflow to reconstruct surface topography over time. Topographic models in the form of point clouds were then compared to extract clusters of topographic change consistent with rockfall. The camera system and the basic SfM workflow have been previously evaluated in detail by Kromer et al. [5], although the range from the cameras to the rock slope is much larger at our research site in Majes. The MEMI step of the photogrammetric workflow has been proven to be effective for constructing point clouds of consistent geometry between comparison epochs by Blanch et al. [6], and the change detection workflows are closely based off of previous work [35,36,37,38,39]. The MEMI approach is relatively new and has yet to see wide implementation [6,30], so this study serves as a unique application of the method where MEMI was critical for ensuring consistent model geometry because there were no stable GCPs (GCPs were only marked in images from one initial epoch separate from the epochs being used for any given comparison), and when models for different dates were created separately, slight geometrical distortions between models precluded the use of standard rigid transformation approaches for point cloud registration. Given that the photogrammetric and change detection methods used for this research have already been established, the primary novel contribution of this paper is the consideration of the balance between spatial and temporal resolution when spatial resolution is relatively low in comparison to a relatively high temporal resolution.
5.1. Volume Calculation Uncertainty
Separate from implications related to temporal resolution, the volume calculations for this study have some uncertainties. One uncertainty is that depending on the magnitudes of M3C2 change and the spatial extents of individual areas of change on the rock slope, DBSCAN did not always successfully isolate individual areas of change that were close together. This may have occasionally caused a given comparison to have a slightly misrepresentative MCF relationship where the MCF scaling parameter would be slightly lower than it would be with better isolation of change areas. This uncertainty was likely not an issue at high frequencies, but in the SSEC, it was more of an issue because so much of the slope had experienced change and the gaps between areas of change were sometimes small. There is also some level of uncertainty associated with the smoothing effect that M3C2 and the subsequent M3C2 change filter threshold had on which points were included with a given cluster. M3C2 smooths the cluster in that the distances are not calculated from individual points but rather from the average point location within a defined search diameter. Regardless of smoothing, a larger uncertainty in calculated volumes comes from the “halo” of small-magnitude change around a rockfall that is below the change filter threshold [43]. This effect would be limited for large clusters relative to their overall magnitude but may significantly affect smaller clusters where the size of the excluded “halo” represents a large proportion of the overall rockfall extent.
Specific to the SSEC workflow, the use of a change filter threshold that was typically below the two-standard-deviation limit of detection caused some merging of independent change areas that were near one another. This effect was mostly mitigated by manually segmenting SSEC clusters where this occurred (Section 3.8). The effectiveness of manual cluster splitting was checked by calculating change volumes via an alternate method (see Section 4.3). The ratio of volumes between the two temporal resolutions was in agreement for both volume calculation methods, suggesting that the manual cluster segmentation reduced the amount of excess volume associated with geometric irregularities by a reasonable amount.
5.2. Comparison of MCF Scaling Parameter to Literature Values
The overall power law scaling exponent (b parameter in Equation (1)) for rock blocks was found to be approximately 1 regardless of whether blocks without AEA were considered (Figure 11). By comparing this value to values reported in the literature, connections can be drawn between overall site geology, rockmass quality, and monitoring methods. Graber and Santi [18] conducted a thorough review of MCF relationships in the literature, and their analysis of variance between different site conditions and the scaling exponent can be used to make comparisons to the results of this study. Regarding general site geology (i.e., igneous, metamorphic, and sedimentary), Graber and Santi [18] found that sedimentary rock slopes had the highest average scaling parameter of around 0.9, and igneous slopes had the lowest average scaling parameter of about 0.6. For rockmass conditions, they found that the scaling exponent tends to decrease with decreasing rockmass quality. For “good-quality” rockmasses, an average scaling parameter of about 1 was found, while for “poor-quality” rockmasses, the average was closer to 0.6. Regarding the method of data collection, there was a wide range of average scaling exponent values, but for terrestrial lidar scanning, which is the closest method to terrestrial photogrammetry as applied in this study, the scaling exponent interquartile range was from about 0.5 to 0.8. The overall ranges of scaling parameter values for each of these categories were shown to be quite large, from about 0.2 to 1.4 over all three variables. Given the actual site conditions in this study of poor to medium rockmass quality, a rock slope of predominantly sedimentary rock, and a monitoring method similar to terrestrial lidar, the scaling exponent of 1 in this study is consistent with trends in the literature [18].
There was a limited amount of variation in the scaling parameter, with differences in temporal resolution and the type of change considered (Figure 11). For all comparisons, where temporal frequency ranged from daily to six days, the scaling parameter had a variation of 0.03 between results that included all blocks and only AEA blocks (see Section 3.6). For results including all blocks, the scaling parameter had a variation of 0.08 for results considering comparisons of all temporal resolutions, one-day and two-day comparisons, and only one-day comparisons. These slope variations are slightly larger than those obtained with method differences, such as the volume reconstruction method [44], and are similar to the slope variation seen with different data quality and filtering decisions [43]. The variations in scaling parameter as a function of temporal resolution are larger than those found by van Veen et al. [9] when considering four temporal resolutions ranging from a few months to a single 461-day comparison, but they are significantly smaller than the variation found by Williams et al. [13] when considering temporal resolutions ranging from 30 days to 1 h. Note that the results of this study are not directly comparable to either of these previous studies because the three variations of temporal resolution that we considered were only slightly different, and they were all dominated by daily temporal resolution comparisons.
5.3. High Temporal Resolution and SSEC Volume Discrepancy
This study shows that in photogrammetric monitoring system design, it is critical to account for the effects of combining low spatial resolution with high temporal resolution, which causes low-magnitude changes to be missed. At a highway rock slope monitoring site, for example, it may be important to have high enough temporal resolution to trigger response teams to check the road conditions after a rockfall occurs, but it is also important to be able to evaluate the long-term changes at the slope to be able to schedule maintenance, such as removing loose rock from rockfall containment features. Where issues might arise is when changes are missed because a significant portion of the change occurs as very low-volume rockfalls that are spatially correlated and accumulate to large-volume changes over time. With daily monitoring in this study, there was often not enough change between days to be detectable, either because the change magnitudes were too small (as measured by M3C2) or because the total cluster volumes fell below the minimum volume threshold used. Comparisons and change detection between dates that are further apart can be performed to capture these changes that would otherwise be missed with the high-frequency change detection.
At volumes below 5 m3 in this study, the error (difference between estimated and actual rockfall volume) was expected to be relatively large (Section 3.6), and the number of false positive clusters was high, so a minimum volume threshold of 5 m3 was used. The decision to use 5 m3 was not directly related to a limit of detection. Rather, it was selected to achieve a balance between spatial resolution (minimum rockfall volume detected), manual validation effort required, and volume estimate accuracy for individual clusters. A smaller volume cutoff could have been used, but that would have led to significant increases in the manual validation effort required and provided a larger number of volume results with low reliability. For example, the 5 m3 threshold led to around 1500 clusters that had to be manually validated, while a 1 m3 threshold resulted in almost 16,000 clusters (the vast majority of which would undoubtedly be false positive or highly erroneous in volume); manual validation of this many clusters was not practical for this study.
While the 5 m3 volume was larger than what was able to be captured in change detection and what was manually identifiable in site photos, by roughly extrapolating the cumulative cluster volume results in Figure 16, the required minimum volume threshold (i.e., volume limit of detection) to match the SSEC total volume would be in the order of 0.5 m3. Extrapolation of the MCF curves (Figure 11) suggests a similar minimum volume would be required. This required detectable volume was below what could be reliably detected using the methods applied in this study. Rockfalls with an areal extent in the photos less than about 1 m2 (~15 × 15 pixels) were difficult to distinguish from lighting variations and image distortion. Using the change filter threshold of 0.4 m as described in Section 3.4 and an area of 1 m2 gives a rough approximation of the best case scenario minimum volume limit for detectable rockfalls of 0.4 m3. If smaller clusters were considered and validated, the discrepancy between the high-frequency workflow and SSEC would be smaller, but it would not be eliminated.
5.4. Spatiotemporal Resolution Considerations for Rockfall Monitoring
While it is important to be able to accurately measure the long-term, cumulative volume change of a given rock slope, it is also important to have high enough temporal resolution monitoring to identify the most accurate MCF relationships. High-temporal-resolution monitoring allows for a higher number of individual rockfalls to be detected rather than the detection of accumulated changes from multiple rockfalls. This is especially critical when material characteristics are such that large portions of the slope change over relatively short periods of time, which is the case for the Millo Formation in this study. The Moquegua Formation, while still showing similar rockfall spatial trends as in the Millo, has less aggregated change and more areas of small-magnitude individual changes, which can be attributed to its higher strength in comparison to the Millo Formation. This difference is expected to be more distinct if material strengths differ more significantly. The high temporal resolution of this study also allows for evaluation of changes in MCF relationships through time (Figure 11, Figure 12 and Figure 13). We observed variations in the scaling exponent from 0.5 to 1.3 on a month-to-month basis, with one anomalous value over 2.5. This variability is generally consistent with the findings of Janeras et al. [45], who showed a fluctuation of the scaling exponent from about 0.25 to 0.81 at one location and from about 0.38 to 0.78 at another location, although their rockfall database monitoring intervals were in the order of a year rather than monthly. Both of these findings show that rockfall hazard is not constant through time over all time intervals. There are certainty benefits to developing an overall rock slope characterization that can be used in practical applications where repeat monitoring may not be planned, but to develop such a characterization, an understanding of the potential variability in MCF relationships through time is needed, as shown by the results of this study. In addition to concerns of temporal variability, the rockfall frequency at a given site partly dictates the required temporal resolution, as the monitoring frequency should be high enough that there are a sufficient number of detected changes that an MCF curve can be fit in a statistically significant manner.
Future work could consider a wider array of site conditions and spatial–temporal resolution combinations to better outline monitoring system recommendations. In cases where spatial resolution is the limiting factor, a multi-temporal change detection approach could be used, where high-frequency (e.g., daily) comparisons allow for the most accurate detection of individual changes and supplemental lower-frequency (e.g., monthly) comparisons allow for the total volume change to be accurately measured.
5.5. Prevalence of False Positive Clusters and Monitoring Method Limitations
While it was not the focus of this study, it is important to consider the prevalence of false positive clusters with the presented change detection workflow (Figure 7). Many of these false positives were a result of shadows or other lighting differences between dates being compared. Reliable methods of cluster identification and classification are required for the methods presented in this study to be fully automated and applicable to real-world scenarios where rigorous manual validation is not practical [46,47]. Relatedly, almost half of the validated changes over 5 m3 corresponded to slope-ravel-type processes where there was no identifiable or coherent rock block that moved. It is important to distinguish between blocks and ravel because blocks are generally capable of causing more damage compared to ravel processes, and while the volumes of ravel events at the study site tended to follow MCF trends consistent with block fall, this may not be the case at other sites. Fully automating the workflow shown in this study is critical not only to reduce manual efforts, but also to enable on-site processing to limit the data that have to be transferred off-site, which, in turn, will allow for higher monitoring frequencies.
6. Conclusions
Fixed-base terrestrial SfM can be used for topographic reconstruction and change detection with relatively high temporal resolution. In this study, five cameras were used to automatically capture photos of a rock slope in the Arequipa Region of Peru. The photos were used in a semi-automated processing workflow that implemented a MEMI approach for image alignment, which was required to ensure consistent point cloud model geometry between comparisons.
The findings of this study show that with limited spatial resolution, high-temporal-resolution (daily) monitoring leads to a large discrepancy in total long-term rock slope volume loss compared to a single comparison spanning nearly the full monitoring period (399 days). At the study site, the total rockfall volume identified using a daily monitoring frequency was less than one fourth of the total rockfall volume identified in the 399-day comparison, suggesting that much of the total slope volume loss occurs as high-frequency, low-magnitude events that were not able to be effectively captured by the monitoring system that was used at this study site. While high-frequency monitoring was not ideal for capturing overall volume loss, it was well-suited for establishing MCF relationships that were true to the actual slope evolution. High-frequency monitoring allowed for the identification of progressive, spatially correlated rockfalls that would have otherwise been detected as single, larger-volume rockfalls if a lower monitoring frequency was used. The implications of these findings are that when selecting a monitoring system for a given site, spatial and temporal resolution specifications should be selected based on the importance of identifying MCF relationships as well as identifying overall volume loss. For systems that are limited in spatial resolution but not necessarily limited in temporal resolution, it may be beneficial to institute a multi-temporal change detection workflow where high-frequency comparisons are made in conjunction with longer-term, rolling window comparisons, possibly of multiple sizes (e.g., weekly, monthly, yearly).
Author Contributions
Conceptualization, B.B., G.W. and R.K.; methodology, B.B., G.W. and R.K; software, B.B.; validation, B.B., G.W. and R.K.; formal analysis, B.B.; investigation, B.B.; resources, G.W. and E.G.; data curation, B.B., A.M. and J.T.; writing—original draft preparation, B.B.; writing—review and editing, B.B., G.W., R.K., E.G., A.M. and J.T.; visualization, B.B.; supervision, G.W. and R.K.; project administration, G.W.; funding acquisition, G.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by The National University of Saint Augustine (UNSA) via the Colorado School of Mines Center for Mining Sustainability under grant number A19-0224 and the Colorado Department of Transportation under grant number IAA 20-HAA-ZH-03024.
Data Availability Statement
The data presented in this study are available upon request from the corresponding author.
Acknowledgments
We would like to acknowledge the Colorado School of Mines Center for Mining Sustainability for their support of collaboration with colleagues at the Universidad Nacional de San Agustín de Arequipa (UNSA), who helped facilitate the research presented in this study. We would also like to thank Carlos Contreras and Bryan Gray for assistance in designing and installing the photogrammetry system used for this research. A final thanks to Luke Weidner, who helped with method automation and provided general guidance related to point cloud analysis.
Conflicts of Interest
The authors declare no conflicts of interest. The funders had no role in the design of this study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Royán, M.; Abellán, A.; Jaboyedoff, M.; Vilaplana, J.; Calvet, J. Spatio-temporal analysis of rockfall pre-failure deformation using Terrestrial LiDAR. Landslides 2014, 11, 697–709. [Google Scholar] [CrossRef]
- Gabrieli, F.; Corain, L.; Vettore, L. A low-cost landslide displacement activity assessment from time-lapse photogrammetry and rainfall data: Application to the Tessina landslide site. Geomorphology 2016, 269, 56–74. [Google Scholar] [CrossRef]
- Vanneschi, C.; Di Camillo, M.; Aiello, E.; Bonciani, F.; Salvini, R. SFM-MVS photogrammetry for rockfall analysis and hazard assessment along the ancient roman via Flaminia road at the Furlo gorge (Italy). ISPRS Int. J. Geo-Inf. 2019, 8, 325. [Google Scholar] [CrossRef]
- Briones-Bitar, J.; Carrión-Mero, P.; Montalván-Burbano, N.; Morante-Carballo, F. Rockfall research: A bibliometric analysis and future trends. Geosciences 2020, 10, 403. [Google Scholar] [CrossRef]
- Kromer, R.; Walton, G.; Gray, B.; Lato, M.; Group, R. Development and optimization of an automated fixed-location time lapse photogrammetric rock slope monitoring system. Remote Sens. 2019, 11, 1890. [Google Scholar] [CrossRef]
- Blanch, X.; Eltner, A.; Guinau, M.; Abellan, A. Multi-Epoch and Multi-Imagery (MEMI) Ohotogrammetric Workflow for Enchanced Change Detection Using Time-Lapse Cameras. Remote Sens. 2021, 13, 1460. [Google Scholar] [CrossRef]
- Parente, L.; Chandler, J.; Dixon, N. Optimising the quality of an SfM-MVS slope monitoring system using fixed cameras. Photogramm. Rec. 2019, 34, 408–427. [Google Scholar] [CrossRef]
- Yakar, M.; Ulvi, A.; Yiğit, A.; Alptekin, A. Discontinuity set extraction from 3D point clouds obtained by UAV Photogrammetry in a rockfall site. Surv. Rev. 2022, 55, 416–428. [Google Scholar] [CrossRef]
- van Veen, M.; Hutchinson, D.J.; Kromer, R.; Lato, M.; Edwards, T. Effects of sampling interval on the frequency—Magnitude relationship of rockfalls detected from terrestrial laser scanning using semi-automated methods. Landslides 2017, 14, 1579–1592. [Google Scholar] [CrossRef]
- Barlow, J.; Lim, M.; Rosser, N.; Petley, D.; Brain, M.; Norman, E.; Geer, M. Modeling cliff erosion using negative power law scaling of rockfalls. Geomorphology 2012, 139–140, 416–424. [Google Scholar] [CrossRef]
- Strunden, J.; Ehlers, T.; Brehm, D.; Nettesheim, M. Spatial and temporal variations in rockfall determined from TLS measurements in a deglaciated valley, Switzerland. J. Geophys. Res. Earth Surf. 2015, 120, 1251–1273. [Google Scholar] [CrossRef]
- D’Amato, J.; Hantz, D.; Guerin, A.; Jaboyedoff, M.; Baillet, L.; Mariscal, A. Influence of meteorological factors on rockfall occurrence in a middle mountain limestone cliff. Nat. Hazards Earth Syst. Sci. 2016, 16, 719–735. [Google Scholar] [CrossRef]
- Williams, J.; Rosser, N.; Hardy, R.; Brain, M. The Importance of Monitoring Interval for Rockfall Magnitude-Frequency Estimation. J. Geophys. Res. Earth Surf. 2019, 124, 2841–2853. [Google Scholar] [CrossRef]
- Williams, J.; Rosser, N.; Hardy, R.; Brain, M.; Afana, A. Optimising 4-D surface change detection: An approach for capturing rockfall magnitude-frequency. Earth Surf. Dyn. 2018, 6, 101–119. [Google Scholar] [CrossRef]
- Birien, T.; Gauthier, F. Assessing the relationship between weather conditions and rockfall using terrestrial laser scanning to improve risk management. Nat. Hazards Earth Syst. Sci. 2023, 23, 343–360. [Google Scholar] [CrossRef]
- Giacomini, A.; Thoeni, K.; Santise, M.; Diotri, F.; Booth, S.; Fitvus, S.; Roncella, R. Temporal-spatial frequency rockfall data from open-pit highwalls using a low-cost monitoring system. Remote Sens. 2020, 12, 2459. [Google Scholar] [CrossRef]
- Hartmeyer, I.; Delleske, R.; Keuschnig, M.; Krautblatter, M.; Lang, A.; Otto, J.C.; Schrott, L. Current glacier recession causes significant rockfall increase: The immediate paraglacial response of deglaciating cirque walls. Earth Surf. Dyn. 2020, 8, 729–775. [Google Scholar] [CrossRef]
- Graber, A.; Santi, P. Power law models for rockfall frequency-magnitude distributions: Review and identification of factors that influence the scaling exponent. Geomorphology 2022, 418, 108463. [Google Scholar] [CrossRef]
- Graber, A.; Santi, P.; Arestegui, P.M. Constraining the critical groundwater conditions for initiation of large, irrigation-induced landslides, Siguas River Valley, Peru. Landslides 2021, 18, 3753–3767. [Google Scholar] [CrossRef]
- Wei, X.; Garcia-Chevesich, P.; Alejo, F.; García, V.; Martínez, G.; Daneshvar, F.; Bowling, L.; Gonzáles, E.; Krahenbuhl, R.; McCray, J. Hydrologic analysis of an intensively irrigated area in southern peru using a crop-field scale framework. Water 2021, 13, 318. [Google Scholar] [CrossRef]
- Flamme, H.; Krahenbuhl, R.; Li, Y.; Dugan, B.; Shragge, J.; Graber, A.; Sirota, D.; Wilson, G.; Gonzales, E.; Ticona, J.; et al. Integrated geophysical investigation for understanding agriculturally induced landslides in southern Peru. Environ. Earth Sci. 2022, 81, 309. [Google Scholar] [CrossRef]
- Lacroix, P.; Araujo, G.; Hollingsworth, J.; Taipe, E. Self-Entrainment Motion of a Slow-Moving Landslide Inferred From Landsat-8 Time Series. J. Geophys. Res. Earth Surf. 2019, 124, 1201–1216. [Google Scholar] [CrossRef]
- Lacroix, P.; Dehecq, A.; Taipe, E. Irrigation-triggered landslides in a Peruvian desert caused by modern intensive farming. Nat. Geosci. 2019, 13, 56–60. [Google Scholar] [CrossRef]
- Araujo, G.; Taipe, E.; Miranda, R.; Valderrama, P. Dinamica y Monitoreo Del Deslizamiento De Siguas; Instituto Geólgico, Minero y Metalúrgico: Arequipa, Peru, 2017. [Google Scholar]
- Garcia-Chevesich, P.; Wei, X.; Ticona, J.; Martínez, G.; Zea, J.; García, V.; Alejo, F.; Zhang, Y.; Flamme, H.; Graber, A.; et al. The impact of agricultural irrigation on landslide triggering: A review from Chinese, English, and Spanish literature. Water 2020, 13, 10. [Google Scholar] [CrossRef]
- Planet Team, Planet Application Program Interface: In Space for Life on Earth. 2023. Available online: https://api.planet.com (accessed on 21 April 2023).
- Harbortronics Cyclapse Time Lapse Camera System. 2018. Available online: https://cyclapse.com (accessed on 12 March 2023).
- Agisoft Metashape Professional Edition. 2022. Available online: http://www.agisoft.com/downloads/installer (accessed on 12 November 2023).
- Python Core Team, Python: A Dynamic, Open Source Programming Language. Python Software Foundation. 2022. Available online: https://www.python.org/ (accessed on 7 February 2022).
- Feurer, D.; Vinatier, F. Joining multi-epoch archival aerial images in a single SfM block allows 3-D change detection with almost exclusively image information. ISPRS J. Photogramm. Remote Sens. 2018, 146, 495–506. [Google Scholar] [CrossRef]
- Cook, K.; Dietze, M. Short Communication: A simple workflow for robust low-cost UAV-derived change detection without ground control points. Earth Surf. Dyn. 2019, 7, 1009–1017. [Google Scholar] [CrossRef]
- Zhang, L.; Rupnik, E.; Pierrot-Deseilligny, M. Feature matching for multi-epoch historical aerial images. ISPRS J. Photogramm. Remote Sens. 2021, 182, 176–189. [Google Scholar] [CrossRef]
- Li, J.; Yang, B.; Chen, C.; Habib, A. NRLI-UAV: Non-rigid registration of sequential raw laser scans and images for low-cost UAV LiDAR point cloud quality improvement. ISPRS J. Photogramm. Remote Sens. 2019, 158, 123–145. [Google Scholar] [CrossRef]
- Butcher, B. Rockslope And Landslide Monitoring Using High Temporal Resolution Terrestrial Structure From Motion Photogrammetry: A Case Study of a Landslide in Majes Zone, Peru Using Multi-Epoch Photogrammetric Techniques; Colorado School of Mines: Golden, CO, USA, 2023. [Google Scholar]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]
- Bonneau, D.; DiFrancesco, P.; Hutchinson, D.J. Surface reconstruction for three-dimensional rockfall volumetric analysis. ISPRS Int. J. Geo-Inf. 2019, 8, 548. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.; Sander, J.; Xu, X. A Density-Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise. In Proceedings of the 2nd International Conference on Knowledge Discovery and Data Mining, Portland, OR, USA, 2–4 August 1996; pp. 226–231. [Google Scholar]
- Tonini, M.; Abellan, A. Rockfall detection from terrestrial lidar point clouds: A clustering approach using R. J. Spat. Inf. Sci. 2013, 8, 95–110. [Google Scholar] [CrossRef]
- Guerin, A.; Rossetti, J.; Hantz, D.; Jaboyedoff, M. Estimating rock fall frequency in a limestone cliff using LIDAR measurements. In Proceedings of the First International Conference Landslides Risk, Tabarka, Tunisia, 14–16 March 2013; pp. 293–301. Available online: https://hal.archives-ouvertes.fr/hal-00808577 (accessed on 4 December 2022).
- Pedregosa, F.; Thirion, B.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; Vanderplas, J.; Passos, A.; Cournapeau, D.; Brucher, M.; et al. Scikit-learn: Machine Learning in {P}ython. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- DiFrancesco, P.; Bonneau, D.; Hutchinson, D. The implications of M3C2 projection diameter on 3D semi-automated rockfall extraction from sequential terrestrial laser scanning point clouds. Remote Sens. 2020, 12, 1885. [Google Scholar] [CrossRef]
- Wang, C.; Ji, M.; Wang, J.; Wen, W.; Li, T.; Sun, Y. An improved DBSCAN method for LiDAR data segmentation with automatic Eps estimation. Sensors 2019, 19, 172. [Google Scholar] [CrossRef] [PubMed]
- Walton, G.; Weidner, L. Accuracy of Rockfall Volume Reconstruction from Point Cloud Data—Evaluating the Influences of Data Quality and Filtering. Remote Sens. 2022, 15, 165. [Google Scholar] [CrossRef]
- DiFrancesco, P.; Bonneau, D.; Hutchinson, D. Computational geometry-based surface reconstruction for volume estimation: A case study on magnitude-frequency relations for a LiDAR-derived rockfall inventory. ISPRS Int. J. Geo-Inf. 2021, 10, 157. [Google Scholar] [CrossRef]
- Janeras, M.; Lantada, N.; Núñez-Andrés, M.; Hantz, D.; Pedraza, O.; Cornejo, R.; Guinau, M.; García-Sellés, D.; Blanco, L.; Blanco, J.; et al. Rockfall Magnitude-Frequency Relationship Based on Multi-Source Data from Monitoring and Inventory. Remote Sens. 2023, 15, 1981. [Google Scholar] [CrossRef]
- Zoumpekas, T.; Puig, A.; Salamo, M.; Garcia-Selles, D.; Nunez, L.; Guinau, M. An intelligent framework for end-to-end rockfall detection. Int. J. Intell. Syst. 2021, 36, 6471–6502. [Google Scholar] [CrossRef]
- Farmakis, I.; DiFrancesco, P.; Hutchinson, D.; Vlachopoulos, N. Rockfall detection using LiDAR and deep learning. Eng. Geol. 2022, 309, 106836. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).