Abstract
The first coastal acoustic tomography (CAT) experiment site of the Neko-Seto Channel was revisited to elucidate the propagation and generation characteristics of the M2 and M4 tidal currents with a second CAT experiment, which was conducted from 3–6 April 2018 (local time). Two-dimensional flow fields of the M2 and M4 tidal currents and the residual current were reconstructed using a coast-fitting inversion model with the reciprocal travel-time data of five acoustic stations. The M2 tidal current is a progressive-type wave that propagates eastward at a speed of 0.7 ms−1, much slower than expected for free progressive tides in this region (19 ms−1). The M4 nonlinear current constructed an out-of-phase relationship between the western and eastern halves of the tomography domain, implying the generation of standing-type waves. Such nonlinear processes led to flood- and ebb-dominant tidal current asymmetries for the western and eastern halves of the model domain, respectively. The two-day mean residual currents constructed a northeastward current with a maximum speed of 0.3 ms−1 in the western half of the model domain and a clockwise rotation in the eastern half. The averaged inversion errors were 0.03 ms−1, significantly smaller than the amplitude of the aforementioned currents.
1. Introduction
In coastal seas, tidal currents are often characterized by obvious nonlinearities due to the interactions of diurnal and semi-diurnal tides and their interaction with bottom friction and coastal geometry [1,2]. Tidal currents become distorted as they propagate nearshore and have a remarkable impact on coastal ecosystems and ship traffic [3]. Although there have been past studies on tides and associated nonlinear tides [4,5,6,7], these were based on elevation data or ocean model simulations because of the difficulties in the synchronous observation of tidal currents over a wide horizontal area. Thus, it is crucial to observe the spatiotemporal variations of tidal currents and the associated nonlinear currents for better coastal sea assessment and management. Coastal acoustic tomography (CAT) is an innovative oceanographic method for coastal-sea environment monitoring and management over a wide area [8]. It has been applied to coastal seas in Japan [9,10,11], China [12,13,14,15], and Indonesia [16] and has served to quickly map varying flow fields of tidal and nonlinear currents and coastal upwelling, and to elucidate the relevant fluid dynamics. The sufficient accuracy of the velocity measurements from CAT has been validated with data obtained by shipboard and moored acoustic Doppler current profilers [17,18].
The Neko-Seto Channel, located in the Seto Inland Sea, Japan, is characterized by the generation of tidal vortex pairs synchronized to M2 tides. An elongated trough with a maximum depth of 90 m was constructed along the axis of the channel by scouring due to strong tidal jets [19]. The first CAT experiment in the Neko-Seto Channel was conducted in March 1999 and focused on the growth, movement, and decay of tidal vortex pairs [20,21].
We conducted a second CAT experiment in April 2018. In the current study, the generation and propagation of nonlinear tidal currents are investigated by adopting a coast-fitting inversion model. The proposed method was originally developed for interpolating and filtering current field data obtained using a high-frequency ocean radar [22,23]. The method decomposes a two-dimensional current field into solenoidal and irrotational components with specific boundary conditions. Unlike the conventional inverse method used by Yamaoka et al. [21], the coast-fitting inversion model automatically considers the kinematic constraints imposed on the current field by the coastlines.
This paper is organized as follows: Section 2 presents the observations and model used to reconstruct the current fields. Section 3 describes the inverted current fields, with a focus on the M2 tidal current, M4 nonlinear current, and residual current. Section 4 discusses the relevant dynamic properties. Finally, Section 5 presents the conclusions.
2. Model and Observation Data
2.1. Observation
Figure 1 shows the location of the experimental site and a bathymetric chart of the area. In this region, tidal waves are dominated by the semidiurnal constituent M2. The tidal current can reach a maximum speed of 2.5 ms−1 and is directed eastward at the flood tide and westward at the ebb tide. Owing to strong tidal mixing, the temperature and salinity were well homogenized in the channel, as seen from the conductivity–temperature–depth (CTD) data at a nearby station available monthly from the Hiroshima Prefecture Research Institute. Five acoustic stations were set up on the north (S1, S2) and south shores (S3, S4, S5) to configure five transmission paths (gray lines in Figure 1c) that cover the major region of the Neko-Seto Channel. The lengths of the transmission paths ranged from 4.4 km for S1S4 to 8.0 km for S2S5 as determined by the global positioning system (GPS). During the experiment, 5 kHz acoustic signals, modulated by the 10th order M-sequence, were transmitted simultaneously every 5 min from the five stations from broadband acoustic transducers (Neptune T170) and were received by the counter stations. The 10th order M sequence is a pseudo-random sequence with 1023 digits with discretized values of −1 and 1. In this experiment, the one-digit width of the M sequence was set to include three waves of the carrier; thus, the transmitted signal had a time width of 0.61 s. The source level at full resonance was estimated as 192 dB re 1 µPa at 1 m. The acoustic transducers were deployed 2 m below the mean sea surface height.
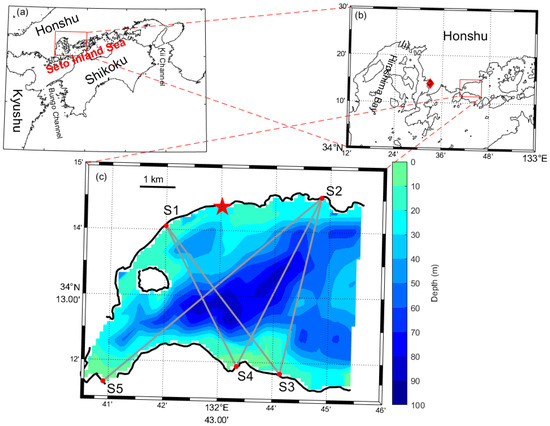
Figure 1.
Location map of (a) Seto Inland Sea and (b) Neko-Seto Channel encircled with red rectangles. (c) The model domain with the bathymetric chart, accompanied by the color bar on the right side. The five acoustic stations (S1–S5) and the transmission paths connecting them are indicated with red dots and grey lines, respectively. The red star and diamond indicate the location of Koyo with the predicted sea-level data and the Kure tide gauge station, respectively. The 1 km scale is illustrated near the upper left corner.
Figure 2 shows stack diagrams of the correlation patterns for the received data for all transmission paths. The threshold of the signal-to-noise ratio (SNR) was set to 30 dB to detect the first arrival peaks. The identified peaks of each transmission path showed good continuity, especially for the transmission path of S2S5; the semidiurnal periods of the first arrival peak were visible during the observation. The ray simulations using the monthly CTD data demonstrated that the ray corresponding to the first arrival peak propagated in the upper 20 m. Data acquisition along S2S3, S2S4, and S2S5 was better than that for S1S3 and S1S4 because the CAT system at the S1 station stopped working on the last day of the experiment. There were also instances of missing data on all the transmission lines owing to sudden GPS signal loss or the barrier effect of the body of traffic ships.
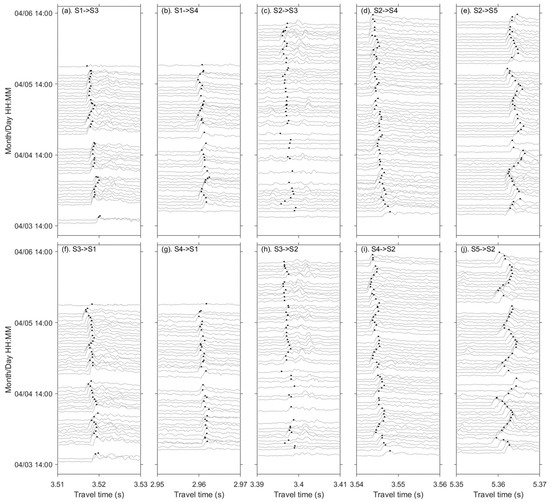
Figure 2.
Stack diagrams (gray lines) constructed by the 10 min interval reciprocal correlation patterns for the transmission paths S1S3 (a), S1S4 (b), S2S3 (c), S2S4 (d), S2S5 (e), S3S1 (f), S4S1 (g), S3S2 (h), S4S2 (i), and S5S2 (j). The first arrival peaks are indicated with black dots.
2.2. Model
As described by Munk et al. [24], the differential travel time of the ith acoustic ray is related to the depth-averaged current at the jth grid along the ith ray, projected onto the horizontal slice as follows:
where and are the total and segmented lengths of the ith projected ray, respectively. is the reference sound speed obtained from CTD measurements. Taking the reference horizontal distance between each station pair as an approximation of , the range-average current (RAC) along the ith acoustic ray is represented as follows:
The horizontal-slice inversion based on the coast fitting method (CFM) was adopted to improve the results from a conventional inversion with no coast fitting. In CFM, a non-normal current is considered at the coasts surrounding the tomography domain [12,25]. The two-dimensional flow field was decomposed into a series of Dirichlet, Neumann, and open-boundary mode functions using the following equation:
where , , and denote the mth mode of the stream, potential, and open-boundary functions, respectively. is a unit vector orthogonal to the horizontal plane.
Substituting Equation (3) in (1), we obtain:
where (, ) represents the position of the acoustic station pair (S1, S2). The expansion coefficients were then calculated by inversion, in which the observed data of the differential travel times were satisfied in collaboration with all three modes (Dirichlet, Neumann, and open-boundary). A detailed explanation of this inversion can be found in Chen et al. [25]. According to Munk et al. [24], Neumann modes do not contribute to the distribution of inverted current. However, an effect was found to be significant in constructing the inverted current. Finally, harmonic analysis was applied to the inverted currents to extract the M2, M4, and residual currents.
The flow patterns of the first six Dirichlet modes (Figure 3a–f), the first three Neumann modes (Figure 3g–i), and the open-boundary modes (Figure 3j–l) are shown in Figure 3 with the vector plots. For the Dirichlet modes, the number of circulations varied from one to three, except for the fourth mode, which had four circulations. For the Neumann modes, the first mode showed an eastward flow pattern, whereas the second and third modes constructed flow patterns diverging from the north coast and converging to the eastern side of the small island near the inlet. The first open-boundary mode constructed an inflow from the western and eastern open boundaries. In contrast, the second open-boundary mode constructed an inflow from the western open boundary and the northern edge of the eastern open boundary and then flowed out through the major part of the eastern open boundary. For the third open-boundary mode, the currents became very weak in the middle of the model domain, and the strong currents were confined near the eastern open boundary.
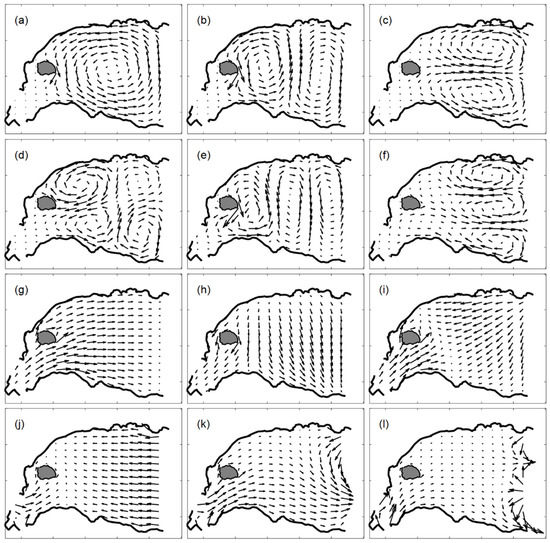
Figure 3.
Flow patterns for (a–f) the first six Dirichlet modes, (g–i) the first three Neumann modes, and (j–l) the first three open-boundary modes.
The RACs for the first arrival peak of received signals with SNR > 30 measured along the five transmission paths—S1S3, S1S4, S2S3, S2S4, and S2S5—are shown in Figure 4 with the time plots. The M2 tidal current was most pronounced along S2S5 (Figure 4e), close to the east–west axis of the channel, and the maximum negative (eastward) current of 0.9 ms−1 surpassed the maximum positive (westward) current of 0.2 ms−1, implying a significant eastward residual current. The M2 tidal currents were also visible along the other four transmission paths but were modulated by the variations with periods shorter than 6 h.
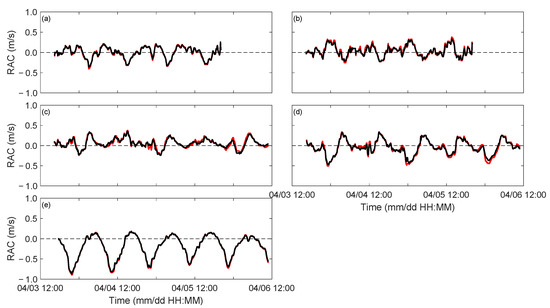
Figure 4.
Comparison of range-average currents from the coastal acoustic tomography observation data (red lines) and coast-fitting method inversion results (black lines) for the transmission paths: (a) S1S3, (b) S1S4, (c) S2S3, (d) S2S4, and (e) S2S5. The positive current is taken in the direction from small to large station number.
Figure 5 compares the RACs along the five transmission paths before and after the inversion with the root mean square difference (RMSD) for all the transmission path data. The five-path averaged RMSDs are plotted against the number of Dirichlet modes, with the numbers of Neumann and open-boundary modes varying from 1–4. The three curves (black, red, and blue) dropped down at higher levels, except for the green one, which corresponded to the case in which four Neumann and open-boundary modes were used. Thus, the optimal number of Neumann and open-boundary modes was 3 for the variation range of the Dirichlet mode number from 1–15. The minimum of the average RMSD was 2.5 cm s−1 when the first six Dirichlet modes were used, with RMSDs of 1.6, 2.9, 3.2, 3.5, and 1.4 cm s−1 for S1S3, S1S4, S2S3, S2S4, and S2S5, respectively.
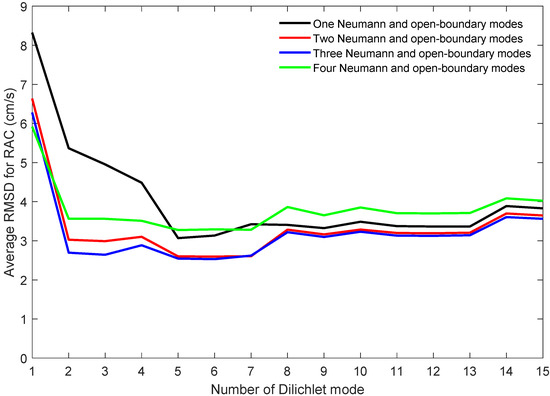
Figure 5.
Five-path averaged RMSDs for RAC, plotted against the number of Dirichlet modes. The number of Neumann modes and open-boundary modes changes from 1–4, corresponding to the black, red, blue, and green lines, respectively.
3. Results
The horizontal distributions of the M2 inverted tidal currents are shown in Figure 6, with hourly vector plots from 00:00 to 11:00 on 4 April 2018. During the second half of the flood tide, the eastward current was strengthened, constructing a jet flow directed from southwest to northeast (Figure 6k,l), reaching a maximum velocity of 0.6 ms−1 at the axis. On the northwest and southeast sides of the jet flow, there was a confined region with a weak velocity of 0.2 ms−1. A pair of tidal vortices with counterclockwise rotation in the western half and an opposite one in the eastern half formed at high water (Figure 6a). A pair of tidal vortices with a reverse rotation to that at the high water formed in low water (Figure 6g). The westward currents were pronounced during the ebb tide with maximum velocities of 0.3–0.4 ms−1, significantly weaker than the eastward currents during the flood tide (Figure 6c–f).
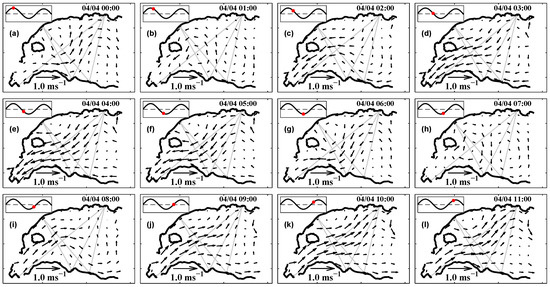
Figure 6.
Hourly distributions of the inverted M2 tidal current from 00:00 to 11:00 (a–l) on 4 April 2018. The corresponding sea level heights were plotted with a red dot in the sub-figures at the upper-left corner.
Figure 7 shows the horizontal distributions of the M4 nonlinear current field at hourly intervals during one cycle of M4 current from 00:00 to 05:00 on 4 April 2018. The central area of the model domain was occupied with a meandering pattern of counterclockwise rotation in the first two hours (00:00 and 01:00) of the M4 current (Figure 7a,b). However, at 02:00, no such current was observed (Figure 7c), and its phase corresponded to the first half of the ebb tide. The current structure at 03:00 and 04:00 showed a meandering pattern in the opposite rotation (clockwise; Figure 7d,e). However, at 05:00, the current was diminished (Figure 7f), and its phase corresponded to the end of the ebb tide (Figure 7f). The maximum absolute velocities in the meandering patterns reached 0.3 ms−1 for both the two-hour durations.
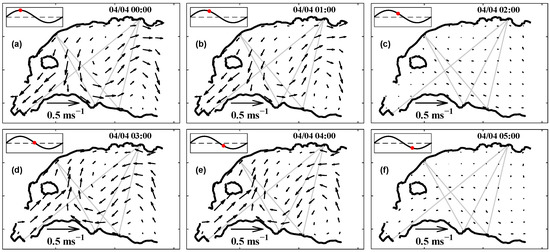
Figure 7.
Hourly distributions of the inverted M4 nonlinear current during the ebb tide from 00:00 to 05:00 (a–f) on 4 April 2018.
The two-day mean residual current is shown in Figure 8 with a vector plot. For the residual currents, the northeast current flowed along the elongated trough (see Figure 1c), running from southwest to northeast in the western half of the model domain and changing to a clockwise rotation in the eastern half. The pattern of northeast current was analogous to that for the M2 tidal current at one hour before the high water (Figure 6l). On the left side of this northeast current, there was a weak vortex with a counterclockwise rotation. The maximum velocity reached 0.3 ms−1 for the northeast current.
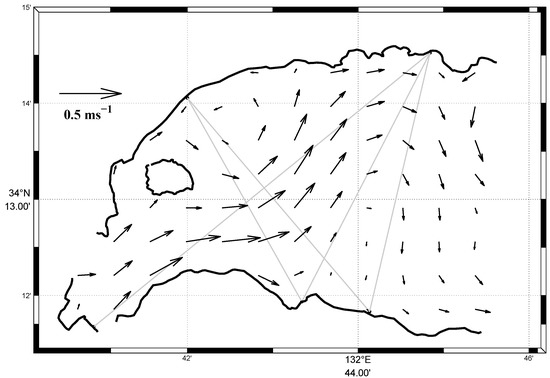
Figure 8.
Distribution of the residual current calculated from 4 to 5 April.
4. Discussion
The flow pattern with a tidal jet and two vortices (Figure 6a,l) was the noticeable feature of this region and followed previous studies [19,20,21]. The tidal ellipses and phases for the M2 and M4 currents and the residuals are plotted in Figure 9. The M2, M4, and residual currents contributed 87.1% of the energy to the observed currents. In the western half of the model domain, the tidal ellipses for the M2 current showed major axes along the coasts, and the ellipticities were large (Figure 9a). The ellipticity became smaller around the center of the model domain, and the lineation of the major axes branched into the northeastward and southeastward axes. The lineation pattern of the major axes was similar to the flow pattern of the M2 current, as seen in the flood tide (Figure 6k,l). The rotation of the tidal ellipses was counterclockwise near the center of the domain and clockwise in the other regions. The tidal phases for the M2 current relative to the western inlet lagged by 0.9 h from west to east in the model domain, implying an eastward propagation of 0.7 ms−1 (Figure 9b), much lower than the phase speed (19 ms−1) of the free progressive tides expected in this region. This remarkably reduced phase speed may be caused by a geometrical constraint owing to the narrow inlet of the strait and north–south coasts. The residuals were smaller than 0.04 ms−1 (Figure 9c).
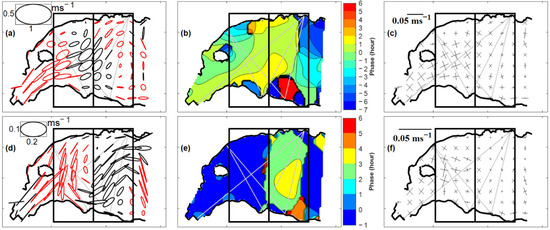
Figure 9.
Tide ellipses and phases and the residuals for M2 (a–c) and M4 (d–f). The red and black circles indicate that the ellipse rotates in the clockwise and counterclockwise directions, respectively. The degree unit for the phase of M2 and M4 currents are converted into hour units.
For the M4 tidal current, the length of the major axes was approximately 0.2 ms−1. The tidal ellipses were directed from north to south in the western half with a clockwise rotation of phase and transited to the northeast to southwest direction with a counterclockwise rotation of phase. The meandering pattern of the major axes was similar to that observed in the vector plots of the M4 current (Figure 7a,b,d,e). The rotation phase of the tidal ellipses showed an out-of-phase relationship with a 3 h time lag between the western and eastern halves of the model domain, implying the generation of a standing-type wave between both halves. The residuals were less than 0.03 ms−1.
In coastal seas, tides become distorted as they intrude into coastal seas and produce asymmetric variations in tidal current velocities. This distortion is caused by the nonlinear interaction between principal astronomical tidal components and compound constituents [26,27,28]. To identify the asymmetry of tidal currents in the Neko-Seto Channel, we examined the horizontal structure of the phase difference ( and are the phases of the M2 and M4 currents, respectively; Figure 10a). In addition, the east–west and north–south components of the sum (M2 + M4) of the M2 and M4 currents were examined with time plots at the representative points W (Figure 10b) and E (Figure 10c) for the western and eastern halves of the model domain, respectively. The variation range of the phase difference was −30–70° in the western half of the tomography domain and 150–250° in its eastern half, constructing an out-of-phase relationship between both halves. The average phase differences of 20° and 200° were slightly over the central phase of the flood and ebb tides, respectively (Figure 10a). At point W, the summed current in the north–south component was asymmetric, whereas the summed current was symmetric in the east–west component. Both components constructed an in-phase relationship during the flood tide and an out-of-phase relationship during the ebb tide. The peak height of the north–south component was much larger during the flood tide than during the ebb tide (Figure 10b). At point E, the variation was coincident for the east–west and north–south components. During the flood tide, the positive peak split into two peaks with a sequence of small and large peaks, while the ebb tide featured a large negative peak (Figure 10c). The large positive peaks for both components coexisted in the flood tides at point W, and the large negative peaks coexisted in the ebb tides at point E. Based on these phase and amplitude relationships, the tidal currents, made up of M2 and M4 currents in the western and eastern halves of the model domain, can be characterized by flood- and ebb-dominant tidal asymmetries, respectively [28].
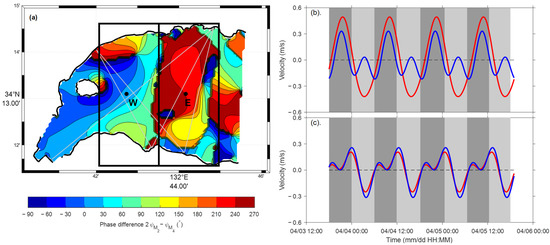
Figure 10.
(a) Contour map of phase difference . (b,c) Time plots of the east–west (red lines) and north–south (blue lines) components of the summed current M2 + M4 for points W and E, respectively. The dark and light shaded zones indicate flood and ebb tides, respectively.
5. Conclusions
The tidal current in the Neko-Seto Channel was studied by focusing on the M2 tidal current and M4 nonlinear current using CFM inversion of differential travel time data obtained along five transmission paths between five acoustic stations. The spatiotemporal variations of the M2 and M4 tidal currents were well reconstructed at 5 min intervals over two cycles of M2 current, leading to new findings on the generation and propagation characteristics of M2 and M4 tidal currents. The M2 tidal current was a progressive-type wave propagating eastward at a speed of 0.7 ms−1, much slower than the phase speed (19 ms−1) of free progressive tides expected in this region. In contrast, the M4 nonlinear current had an out-of-phase relationship between the western and eastern halves of the model domain, implying that the M4 tidal current was initiated as a standing-type wave. The two-day mean residual current field showed that the northeast current developed in the western half of the model domain and changed to a clockwise rotation in its eastern half, reaching a maximum speed of 0.3 ms−1. The phase difference and the sum of the M2 and M4 tidal currents at the representative points W and E inside the model domain were calculated. The results showed that the western and eastern halves of the model domain were characterized by flood- and ebb-dominant tidal asymmetries, respectively. The average inversion errors were both 0.03 ms−1, significantly smaller than the amplitude of the M2 and M4 currents and residual current.
Author Contributions
Conceptualization, M.C., A.D.H., N.T., H.M., X.Z. and A.K.; Methodology, M.C., J.L. and A.K.; Writing—original draft, M.C., A.K.; Writing—review and editing, A.D.H., N.T., H.M., X.Z., Z.Z., C.Z. and J.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (grants 52101394 and 41920104006), the Scientific Research Fund of the Second Institute of Oceanography, MNR (JZ2001), the Project of State Key Laboratory of Satellite Ocean Environment Dynamics, Second Institute of Oceanography (SOEDZZ2106 and SOEDZZ2207), and the Innovation Group Project of the Southern Marine Science and Engineering Guangdong Laboratory, Zhuhai (No. 311020004).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from Chen (E-mail: mmchen_t9@163.com).
Acknowledgments
We express sincere thanks to Noriaki Gohda for his unlimited support in the field work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Speer, P.; Aubrey, D. A study of non-linear tidal propagation in shallow inlet/estuarine systems Part II: Theory. Estuarine Coast. Shelf Sci. 1985, 21, 207–224. [Google Scholar] [CrossRef]
- Davies, A.M.; Jones, J.E. Sensitivity of Tidal Bed Stress Distributions, Near-Bed Currents, Overtides, and Tidal Residuals to Frictional Effects in the Eastern Irish Sea. J. Phys. Oceanogr. 1996, 26, 2553–2575. [Google Scholar] [CrossRef][Green Version]
- Blanton, J.O.; Lin, G.; A Elston, S. Tidal current asymmetry in shallow estuaries and tidal creeks. Cont. Shelf Res. 2002, 22, 1731–1743. [Google Scholar] [CrossRef]
- Dong, L.; Su, J. Tide response and wave distortion in Xiangshan Bay, I, observation and analysis. Acta Oceanol. Sin. 1991, 21, 1–10. [Google Scholar]
- Dong, L.; Su, J. Tide response and wave distortion in Xiangshan Bay, II, numerical modeling study in the Xiangshan Bay. Acta Oceanol. Sin. 1991, 21, 1–8. [Google Scholar]
- Nidzieko, N.J. Tidal asymmetry in estuaries with mixed semidiurnal/diurnal tides. J. Geophys. Res. Earth Surf. 2010, 115. [Google Scholar] [CrossRef]
- Sheng, J.; Wang, L. Numerical study of tidal circulation and nonlinear dynamics in Lunenburg Bay, Nova Scotia. J. Geophys. Res. Earth Surf. 2004, 109, C10018. [Google Scholar] [CrossRef]
- Kaneko, A.; Zhu, X.-H.; Lin, J. Coastal Acoustic Tomography; Elsevier: Amsterdam, The Netherlands, 2020. [Google Scholar] [CrossRef]
- Lin, J.; Kaneko, A.; Gohda, N.; Yamaguchi, K. Accurate imaging and prediction of Kanmon Strait tidal current structures by the coastal acoustic tomography data. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Chen, M.; Kaneko, A.; Lin, J.; Zhang, C. Mapping of a Typhoon-Driven Coastal Upwelling by Assimilating Coastal Acoustic Tomography Data. J. Geophys. Res. Oceans 2017, 122, 7822–7837. [Google Scholar] [CrossRef]
- Taniguchi, N.; Takahashi, T.; Yoshiki, K.; Yamamoto, H.; Hanifa, A.D.; Sakuno, Y.; Mutsuda, H.; Huang, S.-W.; Huang, C.-F.; Guo, J.-H. A reciprocal acoustic transmission experiment for precise observations of tidal currents in a shallow sea. Ocean Eng. 2020, 219, 108292. [Google Scholar] [CrossRef]
- Chen, M.; Zhu, Z.-N.; Zhang, C.; Zhu, X.-H.; Zhang, Z.; Wang, M.; Zheng, H.; Zhang, X.; Chen, J.; He, Z.; et al. Mapping of tidal current and associated nonlinear currents in the Xiangshan Bay by coastal acoustic tomography. Ocean Dyn. 2021, 71, 811–821. [Google Scholar] [CrossRef]
- Huang, H.; Xu, S.; Xie, X.; Guo, Y.; Meng, L.; Li, G. Continuous Sensing of Water Temperature in a Reservoir with Grid Inversion Method Based on Acoustic Tomography System. Remote Sens. 2021, 13, 2633. [Google Scholar] [CrossRef]
- Zhu, Z.-N.; Zhu, X.-H.; Guo, X. Coastal tomographic mapping of nonlinear tidal currents and residual currents. Cont. Shelf Res. 2017, 143, 219–227. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhu, X.; Zhang, C.; Chen, M.; Wang, M.; Dong, M.; Liu, W.; Zheng, H.; Kaneko, A. Dynamics of Tidal and Residual Currents Based on Coastal Acoustic Tomography Assimilated Data Obtained in Jiaozhou Bay, China. J. Geophys. Res. Oceans 2021, 126, e2020JC017003. [Google Scholar] [CrossRef]
- Hanifa, A.D.; Syamsudin, F.; Zhang, C.; Mutsuda, H.; Chen, M.; Zhu, X.-H.; Kaneko, A.; Taniguchi, N.; Li, G.; Zhu, Z.-N.; et al. Tomographic measurement of tidal current and associated 3-h oscillation in Bali Strait. Estuar. Coast. Shelf Sci. 2020, 236, 106655. [Google Scholar] [CrossRef]
- Zhu, X.-H.; Kaneko, A.; Wu, Q.; Zhang, C.; Taniguchi, N.; Gohda, N. Mapping Tidal Current Structures in Zhitouyang Bay, China, Using Coastal Acoustic Tomography. IEEE J. Ocean. Eng. 2012, 38, 285–296. [Google Scholar] [CrossRef]
- Zhu, X.-H.; Zhu, Z.-N.; Guo, X.; Ma, Y.-L.; Fan, X.; Dong, M.; Zhang, C. Measurement of tidal and residual currents and volume transport through the Qiongzhou Strait using coastal acoustic tomography. Cont. Shelf Res. 2015, 108, 65–75. [Google Scholar] [CrossRef]
- Takasugi, Y.; Fujiwara, T.; Sugimoto, T. Formation of sand banks due to tidal vortices around straits. J. Oceanogr. 1994, 50, 81–98. [Google Scholar] [CrossRef]
- Park, J.-H.; Kaneko, A. Assimilation of coastal acoustic tomography data into a barotropic ocean model. Geophys. Res. Lett. 2000, 27, 3373–3376. [Google Scholar] [CrossRef]
- Yamoaka, H.; Kaneko, A.; Park, J.-H.; Zheng, H.; Gohda, N.; Takano, T.; Zhu, X.-H.; Takasugi, Y. Coastal acoustic tomography system and its field application. IEEE J. Ocean. Eng. 2002, 27, 283–295. [Google Scholar] [CrossRef]
- Lekien, F.; Coulliette, C.; Bank, R.; Marsden, J. Open-boundary modal analysis: Interpolation, extrapolation, and filtering. J. Geophys. Res. Earth Surf. 2004, 109, C12004. [Google Scholar] [CrossRef]
- Kaplan, D.D.; Lekien, F. Spatial interpolation and filtering of surface current data based on open-boundary modal analysis. J. Geophys. Res. Earth Surf. 2007, 112, C12007. [Google Scholar] [CrossRef]
- Munk, W.; Worcestor, P.F.; Wunsch, C. Ocean Acoustic Tomography; Cambridge University Press: Cambridge, UK, 1995. [Google Scholar]
- Chen, M.; Zhu, Z.-N.; Zhang, C.; Zhu, X.-H.; Wang, M.; Fan, X.; Zhao, R.; Lin, J.; Kaneko, A. Mapping Current Fields in a Bay Using a Coast-Fitting Tomographic Inversion. Sensors 2020, 20, 558. [Google Scholar] [CrossRef] [PubMed]
- Uncles, R. A note on tidal asymmetry in the severn estuary. Estuar. Coast. Shelf Sci. 1981, 13, 419–432. [Google Scholar] [CrossRef]
- Friedrichs, C.T.; Aubrey, D.G. Non-linear tidal distortion in shallow well-mixed estuaries: A synthesis. Estuar. Coast. Shelf Sci. 1988, 27, 521–545. [Google Scholar] [CrossRef]
- Byun, D.-S.; Cho, Y.-K. Double peak-flood current asymmetry in a shallow-water-constituent dominated embayment with a macro-tidal flat. Geophys. Res. Lett. 2006, 33, L16613. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).