Optimal Planning Approaches under Various Seasonal Variations across an Active Distribution Grid Encapsulating Large-Scale Electrical Vehicle Fleets and Renewable Generation

Abstract

With the emergence of the smart grid, the distribution network is facing various problems, such as power limitations, voltage uncertainty, and many others. Apart from the power sector, the growth of electric vehicles (EVs) is leading to a rising power demand. These problems can potentially lead to blackouts. This paper presents three meta-heuristic techniques: grey wolf optimization (GWO), whale optimization algorithm (WOA), and dandelion optimizer (DO) for optimal allocation (sitting and sizing) of solar photovoltaic (SPV), wind turbine generation (WTG), and electric vehicle charging stations (EVCSs). The aim of implementing these techniques is to optimize allocation of renewable energy distributed generation (RE-DG) for reducing active power losses, reactive power losses, and total voltage deviation, and to improve the voltage stability index in radial distribution networks (RDNs). MATLAB 2022a was used for the simulation of meta-heuristic techniques. The proposed techniques were implemented on IEEE 33-bus RDN for optimal allocation of RE-DGs and EVCSs while considering seasonal variations and uncertainty modeling. The results validate the efficiency of meta-heuristic techniques with a substantial reduction in active power loss, reactive power loss, and an improvement in the voltage profile with optimal allocation across all considered scenarios.

1. Introduction

Due to the drastic increase in power demand, voltage drop and line losses have become a universal challenge at the distribution level [1]. Currently, nearly 75% of total power demand is met by fossil fuels that emit greenhouse gas (GHG) emissions, which cause global warming, decrease natural resources, and increase fuel prices in the global market [2,3]. Therefore, the existing distribution network (DN) faces several financial, environmental, and technical obstructions to fulfilling the load growth [4]. With the load growth of electrical vehicles (EVs) in the radial network (RDN), energy management has become more challenging. Renewable energy (RE)-based distributed generation (DG), such as solar photovoltaic (SPV) and wind turbine generation (WTG) sources, are the foremost contributors to a sustainable, technically feasible, and inexpensive method of generation that mitigates the constraints of load growth [5]. Optimal DG allocation (ODGA) in the DN improves the overall voltage profile, increases system reliability, and reduces network losses [6]. An iterative linear programming algorithm was developed in [7] for decreasing and increasing individual loads for improving the stability of the system. The results were validated using IEEE 9-bus and IEEE 118-bus systems.

Power generation from renewable energy sources (RES) such as SPV and WTG are stochastic in nature; therefore, their generation profile is unlikely to match the load profile. The large-scale EV fleets have significant impacts on the power system because electric vehicle charging stations (EVCSs) draw considerable power from the grid.

Energy management using RES is a vital research dimension in recent years that is targeted at optimizing the allocation of SPV-DG and WTG-DG for fulling the load growth of Grid-to-Vehicle (G2V) demand. In recently published articles, several optimization techniques have been employed to solve ODGA problems in RDN. The objectives include minimizing active power loss (RPL) [2,8,9,10,11], minimizing reactive power loss (QPL) [2,12,13,14], maximizing the voltage stability index (VSI) [9,11,15,16,17], and reducing the total voltage deviation (TVD) [2,9,14,15,16,17,18,19,20,21].

• In this paper, three metaheuristic techniques (GWO, WOA, and DO algorithms) for optimal RE-DG allocation, placement of EVCSs, and optimal allocation of hybrid RE-DGs and EVCSs for both single-objective optimization problems (SOOPs) and multi-objective optimization problems (MOOPs) were used. The contributions of this paper are as follows:
• Three metaheuristic techniques were used: GWO, WOA, DO.
• The optimal allocation of REG (solar and WTG) was determined considering uncertainties with four seasonal impacts: spring, summer, autumn, and winter.
• The impact of optimal EVCS placements in RDNs was analyzed.
• The techniques focused on optimal RE-DG allocation problems for MOOPs, with the aim of optimizing four objectives: RPL, QPL, and TVD minimization and VSI maximization.
• The attained objectives were evaluated with related optimization methods.
• The proficiency of the algorithms was assessed across IEEE 33-bus RDNs.

This article is arranged as follows: the literature review is reported in Section 2. Section 3 contains the problem formulation. Uncertainty modeling of SPV, WTG, EVCSs and load is described in Section 4. Section 5 incorporates three metaheuristic techniques: GWO, WOA, and DO. Section 6 comprises the results and discussions. The conclusion and numerical values are presented in Section 7.

2. Literature Review

From the objective perspective, the optimal allocation of RE-DGs is considered a multi-dimensional problem. Various statistical methods based on mathematical expression have been applied to integrate the RE-DG problems [22], GAMS theory [9], integrated operational planning [23], games theoretical algorithm [24], and others presented in the reported literature. A two-stage framework reported in [25] shows that in the first stage, the suitable location of DG is defined based on the voltage stability (VS) and loss sensitivity factor (LSF). In the second stage, the size of the DG is determined based on the DG location. However, it is easy to solve the mathematical expression due to the assumption and relative nature of the problem. The previous techniques have various problems in defining the multiple objective functions, type of DG, and sizing of DG. The optimal RE-DG allocation problems are directed using SOOPs and MOOPs such as power loss (PL) and the number of objectives simultaneously.

Using both SOOPs and MOOPs for optimal sitting and sizing of RE-DG, respectively, optimization algorithms are widely implemented. For SOOPs, particle swarm optimization (PSO) is executed for minimizing the real power losses (RPL) to optimize the sitting and sizing of DG units [26]. Novel metaheuristic techniques have been proposed for the optimal allocation of RE-DG units by reducing the real and reactive power losses in radial distribution networks (RDNs). The optimization techniques incorporate the whale optimization algorithm (WOA), sine cosine algorithm (SCA), multi-verse optimization algorithm (MVOA) [10], stud krill herd algorithm (SKHA) [14], and sequential optimization algorithm (SOA) [21]. For increasing the overall voltage profile and minimizing losses, these techniques are utilized to optimally allocate the DG.

For MOOPs, Antlion optimization (ALO), genetic algorithm (GA), and PSO [27] have been proposed for minimizing RPL, total voltage deviation (TVD), and generation cost by optimally allocating the DG in 33-bus RDNs. In [11], PSO is implemented for minimizing the RPL, total cost, and the emission produced from the biogas sources considered by optimal DG allocation in a 51-bus network. The Harris Hawk optimizer (HHO) and PSO [28] were presented for optimal allocation of DG to reduce the RPL, TVD, and to improve the voltage stability index along with economical parameters in 33-bus and 94-bus Portuguese grid. To maximize the economic benefits, the Social Spider Optimizer (SSO) [29] has been proposed for optimal sizing of RE-DGs. The improved whale optimization algorithm (IWOA) [8] was presented for minimizing the power losses while considering the economic constraints by optimally allocating the DG in a 33-bus RDN.

Study [12], proposes the Hybrid Nelder mead-particle swarm optimization (HNM-PSO) to find the optimal sizing of DG deliberating the seasonal variation using MOOPs in a 12- and 84-bus system. For optimal sizing of DG using a sequential optimization algorithm (SOA), study [29] proposed to minimize the losses and increase the voltage stability by considering various seasons using MOOPs. For solving the optimal RE-DG allocation problem while considering the seasonal alterations throughout the year using MOOPs IWOA, study [8] presented a method that improves the VSI and voltage profiles and minimize losses in a 33-bus system. Reinforcement learning [30] has been proposed to minimize the power losses considering the seasonal variation and uncertainty modeling of PV using SOOPs in a 13- and 37-bus distribution network.

The stochastic flow capturing location model (SFCLM) [31] and MILP model, along with the k++ clustering algorithm [32], has been proposed to perceive the optimal placement of EVCSs using SOOPs to minimize the losses and cost of EV charging in the central Ohio distribution system and 54-bus system, respectively. For optimal placement of EVCSs, the genetic algorithm (GA) [33] has been presented to minimize the overall cost and emissions produced by the transportation of common vehicles. A hybrid grey wolf optimizer and particle swarm optimization (HGWOPSO) [15] was introduced for reducing the losses and voltage deviation, and to improve the voltage stability using MOOPs by placing the EVCSs at the optimal location in a 33-bus system. For fulfilling the EV load demand using RES, a time-coupled linearized optimal power flow formulation [34] has been proposed to minimize the GHG emissions in a Glasgow southside network. In [16], the African vulture optimization algorithm (AVOA) was implemented for optimal placement of EVCSs to minimize the power loss and voltage deviation, and to improve in voltage stability using MOOPs in a 33- and 136-bus system. The comparison of various optimization techniques used for optimal allocation of renewable DGs and EVCSs to achieve muti-objectives is presented in Table 1.

Table 1. Summary of optimization techniques used for optimal allocation of DGs and EVCSs.

Ref.	Optimization Methods	Objectives				Seasonal Variations	Uncertainty Modeling of RER
		APL	QPL	TVD	VSI
[35]	Hybrid PV-WT system	X	X	X	X	X	✓
[20]	GOA	✓	X	✓	X	X	X
[13]	PSO	✓	✓	✓	X	X	✓
[27]	ALO	✓	X	✓	X	X	X
[32]	MILP	✓	X	X	X	X	X
[10]	WOA, SCA, MVOA	✓	X	X	✓	X	X
[9]	GAMS Theory	✓	X	✓	X	X	✓
[31]	SFCLM	✓	X	X	X	X	✓
[28]	HHO and PSO	✓	X	✓	✓	X	✓
[15]	HGWOPSO	✓	X	✓	✓	X	✓
[29]	SSO	X	X	X	X	X	✓
[16]	AVOA	✓	X	✓	✓	X	X
[12]	HNM-PSO	✓	✓	X	✓	✓	✓
[21]	SOA	✓	X	✓	X	✓	✓
[8]	IWOA	✓	X	X	✓	✓	✓
[P]	GWO, WOA, DO	✓	✓	✓	✓	✓	✓

Note: [P]—Proposed. The symbol X shows a particular objective was not considered in that specific paper. The symbol ✓ shows a particular objective was considered in that specific paper.

It can be seen from the above table that most of the research studies considered uncertainty modeling while solving the problem of optimal renewable DG allocations in DNs for achieving technical objectives by optimizing single and multiple objective functions. However, in [8,12,21], seasonal variation and uncertainty modeling have been considered to solve problem of optimal allocation for RE-DGs and EVCS placements to achieve technical objectives.

3. Problem Formulations

In in this section, optimal renewable DG (solar and WTG) allocation (sitting and sizing) and EV placement in a radial distribution network (RDN) is presented.

3.1. Objective Functions

The key objective of this research is to allocate RE-DG in an optimal method to reduce the RPL and QPL, minimize the TVD, and maximize the VSI with MOOPs. In the following subsection, mathematical calculations have been depicted.

3.1.1. Real Power Loss (RPL)

Because of the radial structure of the DN, it is crucial to minimize the RPL. The first objective function (OF) is characterized in Equation (1):

$$O{F}_1=Min\left(RPL\right)$$

(1)

The RPL reduction is calculated using the following Equation (2) [36]:

$$RPL={\displaystyle \sum }_{j=1}^{M_{br}}{\left|I_k\right|}^2.R_k$$

(2)

where $k$ represents the branch number, $M_{br}$ is the total number of branches, $\left|I_k\right|$ is the absolute current passing through the branch, and $R_k$ is the resistance of the branch.

3.1.2. Reactive Power Loss (QPL)

Minimization of QPL is equally important as minimizing RPL. The second OF $\left(O{F}_2\right)$ is characterized in Equation (3):

$$O{F}_2=\min \left(QPL\right)$$

(3)

The QPL reduction is calculated using the following Equation (4) [2]:

$$QPL={\displaystyle \sum }_{k=1}^{M_{br}}{\left|I_k\right|}^2{X}_k$$

(4)

where $k$ represents the branch number, $M_{br}$ is the total number of branches, $\left|I_k\right|$ is the absolute current passing through the branch, and $X_k$ is the reactance of the branch.

3.1.3. Total Voltage Deviation Minimization (TVD)

With the increasing demand of the users, it has been observed that under the loading conditions, most of the DN voltages shut down in specific areas. The minimization of TVD helps to improve the voltage profile. The third OF is represented in Equation (5) [37,38]:

$$TVD={\displaystyle \sum }_{i=1}^{m\_bus}\left(V_{ref}-V_i\right)$$

(5)

where $V_{ref}$ is the reference voltage, which is always taken as 1.00 p.u. Therefore, the third OF $\left(O{F}_3\right)$ is represented in Equation (6):

$$O{F}_3=\min \left(TVD\right)$$

(6)

3.1.4. Voltage Stability Index Maximization (VSI)

For ensuring the security level, like VD, VSI is also an important factor for the stable distribution of voltage. When the uncertain voltage on any bus occurs in the distribution network, it causes voltage instability, and the whole distribution system is defined with VSI. VSI must be maintained at the suitable limit across all the distribution systems on each bus for stable operation. Equation (7) shows the VSI for RDN [39]:

$$VS{I}_i={\left|v_j\right|}^2-4{\left(P_i{x}_{ij}-Q_i{r}_{ij}\right)}^2-4{\left|v_j\right|}^2\left(P_i{r}_{ij}-Q_i{x}_{ij}\right)$$

(7)

where $P_i$ and $Q_i$ are the real and reactive power of the load, respectively, $x_{ij}$ is the inductive reactance, and $r_{ij}$ is the resistance of the line. For stable operation, $VS{I}_i$ must be greater than zero. When the $VSI$ on the bus is at its lowest value, voltage will collapse. Thus, the $VS{I}_i$ must be high for improvement of voltage stability [40]. The fourth OF $\left(O{F}_4\right)$ is presented as Equation (8):

$$O{F}_4=\max (\min \left(VS{I}_i\right))$$

(8)

3.2. Formulation of Multi-Objective Function

Each objective is of a different nature. To integrate each objective function (SOF) in a mathematical equation, every SOF is divided by its base value, then the weights are incorporated. The weighted sum of the real power loss reduction, reactive power loss reduction, total voltage deviation, and voltage stability index is expressed by multi-objective functions. The weighted sum is easily applicable to the system, having greater effectiveness, and is used as a starting point for the several methods for non-dominate reasons. The sum of weighted coefficients is comprised of four SOF that are transformed in a single OF and mathematically represented in Equation (9):

$$\begin{gathered} \mathrm{fit}=\min \left({\mathrm{w}}_1\times {\mathrm{f}}_1+{\mathrm{w}}_2\times {\mathrm{f}}_2+{\mathrm{w}}_3\times {\mathrm{f}}_3+{\mathrm{w}}_4\times {\mathrm{f}}_4\right) \\ \mathrm{fit}=\min \left({\mathrm{w}}_1\times \frac{\mathrm{RPL}}{{\mathrm{RPL}}_{\mathrm{base}}}+{\mathrm{w}}_2\times \frac{\mathrm{QPL}}{{\mathrm{QPL}}_{\mathrm{base}}}+{\mathrm{w}}_3\times \frac{\mathrm{TVD}}{{\mathrm{TVD}}_{\mathrm{base}}}+{\mathrm{w}}_4\times \frac{{\mathrm{VSI}}^{-1}}{{\mathrm{VSI}}_{\mathrm{base}}^{-1}}\right) \end{gathered}$$

(9)

where ${\mathrm{RPL}}_{\mathrm{base}},{\mathrm{QPL}}_{\mathrm{base}},{\mathrm{TVD}}_{\mathrm{base}},$ and ${\mathrm{VSI}}_{\mathrm{base}}^{-1}$ are the real power loss, reactive power loss, total voltage deviation, and voltage stability index in the base case, respectively, and ${\mathrm{w}}_1+{\mathrm{w}}_2+{\mathrm{w}}_3+{\mathrm{w}}_4$ are the four weights. The weight is equally divided (i.e., $\frac{1}{4}$ or 0.25) among each function, and every function is considered equally in these MOOPs.

3.3. System Constraints

The problem of DG allocation in the DN is the major constraint discussed below.

3.3.1. Equality Constraints

For energy management, the generation is equal to the sum of power losses as well as the power demand. To avoid the reverse power flow generation problem, balance is vital. Thus, these constraints are stated as:

$${\displaystyle \sum }_{j=1}^{M\_DG}{P}_{Gen,j}=P_{demand}+RPL; j=1\dots M\_DG$$

(10)

$${\displaystyle \sum }_{j=1}^{M\_DG}{Q}_{Gen,j}=Q_{demand}+QPL; j=1\dots M\_DG$$

(11)

where $M\_DG$ is the number of DGs integrated into the system, $P_{Gen}$ is the power generated by the DG, and $P_{demand}$ is the power needed to fulfill the load requirement.

3.3.2. Inequality Constraints

There are two inequality constraints that must be set. Voltage limits must be set by forcing the boundary limits. For technical constraints, size limits and the power factor (PF) are employed on the DG.

Voltage Limits

The maximum and minimum voltage limits are presented as [41,42]:

$$0.95p.u\le V_j\le 1.05p.u$$

(12)

The thermal limits are [41,42]:

$$I_{j ,i} \le I_{j , i}^{max}$$

(13)

where $I_{j,i}^{max}$ is the maximum current flowing through the branch in between the ith bus and jth bus.

DG Capacity Limits

The minimum and maximum power of the DG units are presented below [41,43]:

$$Real Power limit: P_{Gen}^{min}\le P_{Gen}\le P_{Gen}^{max }$$

(14)

$$Reactive Power limit: Q_{Gen}^{min}\le Q_{Gen}\le Q_{Gen}^{max}$$

(15)

DG Power Factor Limit

The power factor (PF) is also set in a specific range for DG units:

$$\mathrm{p}.{\mathrm{f}}_{\mathrm{DG},\mathrm{j}}^{\min }\le \mathrm{p}.{\mathrm{f}}_{\mathrm{DG},\mathrm{j}}\le \mathrm{p}.{\mathrm{f}}_{\mathrm{DG},\mathrm{j}}^{\max };\mathrm{j}=1\dots \mathrm{M}\_\mathrm{DG}$$

(16)

According to [44,45,46], the power factor is set in between [0.7, 1], where PF is represented as:

$$\mathrm{p}.{\mathrm{f}}_{\mathrm{DG},\mathrm{j}}={\mathrm{P}}_{\mathrm{DG},\mathrm{j}}^2/\sqrt{{\mathrm{P}}_{\mathrm{DG},\mathrm{j}}^2+{\mathrm{Q}}_{\mathrm{DG},\mathrm{j}}^2}$$

(17)

4. Uncertainty Modeling

Four uncertainty parameters are studied in the work: solar PV, wind, and EV, sources, including load demand. The solar PV model depends on solar irradiance; however, the wind model depends on the wind speed. The SPV, WTG, load demand, and EV have been modeled based on the location and seasonal hourly variation historical data considered in the research. Historical data on solar, wind, EVs, and load demand for one year was deliberated in this work. The yearly data was divided into four seasons (spring, summer, winter, and autumn). The seasonal statistics were further classified into 24 h for extracting the stochastic performance of SPV, WTG, EVs, and load demand. To consider the data of a day from every season, four probability distribution functions (PDFs) were generated, which collectively became 96 time periods (24 h × 4 seasons). The probabilistic model of SPV, wind, EVs, and load demand are classified below.

4.1. Solar Modeling

The output power of the solar PV ($P_{PV}$) in kWh for a specific period is presented in Equation (18) [47]:

$$P_{PV}=\{\begin{array}{ll}{P}_r\left(\frac{G_s^2}{G_{std}\times X_c}\right)& \mathit{for} 0<G_s\le X_c\\ P_r\left(\frac{G_s}{G_{std}}\right)& \mathit{for} X_c\le G_s\le G_{std}\\ P_r& G_{std}\le G_s\end{array}$$

(18)

where $X_c$ is the standard irradiance point, $G_s$ is the solar irradiance in W/m², and $G_{std}$ is the standard solar irradiance environment, which is 1000 W/m².

Solar Irradiance Modeling

For generating the Beta PDF of a specific hour, solar irradiance data was defined using Equation (19) [48,49]:

$$f_b\left(g_s\right)=\left\{\begin{array}{c}\frac{\mathsf{\Gamma }\left(\alpha +\mathsf{\beta }\right)}{\mathsf{\Gamma }\left(\alpha \right)\times \mathsf{\Gamma }\left(\mathsf{\beta }\right)}{g}_s^{\left(\alpha -1\right)}\times {\left(1-g_s\right)}^{\left(\beta -1\right)}, 0\le g_s\le 1;\alpha ,\beta \ge 0\\ 0, otherwise\end{array}\right.$$

(19)

where $f_b\left(g_s\right)$ represents the Beta PDF of the solar irradiance, $\mathsf{\Gamma }$ represents the gamma function, and $\alpha$ and $\mathsf{\beta }$ are the Beta parameters that can be obtained using Equations (20) and (21), respectively [50,51].

$$\alpha =\frac{\mu \times \beta }{1-\mu }$$

(20)

$$\mathsf{\beta }=\left(1-\mathsf{\mu }\right)\times \left(\frac{\mu \times \left(1+\mu \right)}{{\sigma }^2}-1\right)$$

(21)

In Equation (21), $\sigma$ and $\mu$ are the standard deviation of the solar irradiance for each period.

4.2. Wind Modeling

For the uncertainty modeling of wind, the Weibull PDF shown in Equation (22) was utilized [50,52]:

$$PD{F}_v\left(v\right)=\left(\frac{\beta }{\alpha }\right){\left(\frac{v}{\alpha }\right)}^{\left(\beta -1\right)}exp\left[-{\left(\frac{v}{\alpha }\right)}^{\beta }\right] 0\le v<\infty$$

(22)

where $\alpha$ represents the scale parameters and $\beta$ represents the shape parameters of the Weibull PDF. In terms of wind speed and rated power, the output power of the wind $P_{wg}\left(v\right)$ was determined using Equation (23) [53]:

$$P_{wg}\left(v\right)=\left\{\begin{array}{c}0 for v<v_i\&v>v_o\\ P_{wr}\left(\frac{v-v_{wi}}{v_{wr}-v_{wi}}\right) for \left(v_i\le v\le v_r\right) \\ P_{wr} for \left(v_r<v\le v_o\right) \end{array} \right.$$

(23)

where $P_{wr}$ represents the rated power of the wind turbine, $v_{wi}$ is the cut-in speed, $v_{wr}$ is the rated speed, and $v_{wo}$ is the cut-out speed of the wind turbine.

4.3. Electrical Vehicle Modeling

4.3.1. EVCS Model, EV Population Estimation, and Study Area

The proposed optimization techniques comprise PV and wind sources along with EVCS with a limited number of chargers. For probabilistic seasonal distribution of the EV demand, the first step is to determine the network system on which EVCSs are deployed. In the next phase, charger types, charging ports, and ratings of CS are considered. EVCS is considered as the load (G2V) in the distribution system [54].

From the perspective of the power system, EVs are taken as:

i.

Ordinary loads that absorb continuous power while charging, known as the grid to a vehicle (G2V).

ii.

Storage devices such as batteries are charged (G2V) and then discharged (V2G) based on the system requirement.

The power demand of the IEEE 33-node network and institutional load (EV) [55] is shown in Table 2.

Table 2. IEEE 33-node network and Institutional Load (EV) power demand.

Power Demand	Active Power (kW)	Reactive Power (kVAR)	Apparent Power (kVA)
IEEE 33 node network	3715	2300	4369.35
Institutional Load (EV)	3231.19	2289.56	3960.133

Two types of EVs, i.e., Nissan Leaf 2018 and MG ZS EV with 220 km traveling range were considered in this work. The Nissan Leaf 2018 and MG ZS EV have 36 kWh and 42.5 kWh of battery capacity, respectively. For charging these two types of EVs, two types of EV chargers are needed. These two types of chargers are level 2 and level 3, with 19.2 kW and 50 kW ratings, respectively. These chargers are considered in Table 3.

Table 3. EV models with EV specifications and EV charger type.

EV Model	EV Specifications	Charging Type
		Level 2 (19.2 kW)		Level 3 (50 kW)
		Charging Time	No. of EVs	Charging Time	No. of EVs
Nissan Leaf 2018	40 kWh, 220 km	2 h 5 m	16	48 m	34
MG ZS EV	44.5 kWh, 220 km	2 h 19 m	18	53 m	32
Total number of EVs			34		66

4.3.2. EVCS Characteristics

A total of five EVCSs were optimally placed in the existing network to serve 100 EVs. Both level 2 and level 3 chargers were used with different numbers of charging points (CPs), as shown in Table 4 [56]. Two of the five EVCSs were level 2 chargers, while the other three were level 3 chargers.

Table 4. Rating of charging ports and electric vehicle charging stations.

Charger	Rating of CP (kW)	No CP per EVCS	Rating of EVCS (kW)	No of EVCS	Total Rating (kW)
Level 2	19.2	15	288	2	576
Level 3	50	10	500	3	1500
Total no of EVCSs and power demand				5	2076

4.4. Load Modeling

The load has a variable nature; the power demand changes every hour. For modeling of the load, a normal PDF is applied to each bus. The normal PDF of uncertain load demand is extracted using Equation (24) [47]:

$$f_n\left(l\right)=\frac{1}{{\sigma }_l\sqrt{2\pi }}\times exp\left[-\left(\frac{1-{\mu }_l}{2{\sigma }_l^2}\right)\right]$$

(24)

where $f_n\left(l\right)$ represents the normal PDF of the load demand, l is the limit of the normal PDF, ${\mu }_l$ is the mean, and ${\sigma }_1$ represents the standard deviation of the load demand for each period.

5. Methodology

In the following section, three meta-heuristic techniques, Grey Wolf Optimization (GWO), Whale Optimization Algorithm (WOA) and Dandelion Optimizer (DO), have been presented. These techniques are used for attaining multi-objectives, i.e., RPL, QPL, TVD, and VSI considering seasonal variations and uncertainty modeling.

5.1. Grey Wolf Optimization (GWO)

Grey wolves are the apex predators, also known as top predators (top of the food chain). They live in packs of 8 to 12, and each pack is led by a male and a female known as alphas who were responsible for making decisions such as hunting, sleeping places, etc. The female alpha wolf is called “Luna”, and she is responsible for maintaining discipline and strengthening the pack. Beta wolves are the assistants of alpha wolves. When alpha wolves become old or pass away, beta wolves play the role of alpha and strengthen the group. Position allocation, hunting, and discipline of the pack are the main inspirations of GWO [57]. The grey wolf technique comprises three leader wolves named α, β, and γ that help other wolves adopt their best positions for attacking prey.

The GWO algorithm’s mathematical model is explained below.

5.1.1. Encircling

When wolves find their prey, they pursue, harass, and encircling it [57] in a network that can be developed as shown in Equations (25) and (26):

$$\overrightarrow{X}=\left|\overrightarrow{C}\times {\overrightarrow{X}}_P\left(k\right)-\overrightarrow{X}\left(k\right)\right|$$

(25)

$$\overrightarrow{X}\left(k+1\right)=\overrightarrow{X_P}\left(k\right)-\overrightarrow{A}\times \overrightarrow{D}$$

(26)

where ${\overrightarrow{X}}_P$ represents the location of the prey, $\overrightarrow{X}$ locates the position vector of a grey wolf, and $k$ shows the current iteration. In [58], $\overrightarrow{C}$ and $\overrightarrow{A}$ are the coefficient vectors given in Equations (27) and (28), and r is a random vector.

$$\overrightarrow{A}=2\overrightarrow{a}\times {\overrightarrow{r}}_1-\overrightarrow{a} \left(k\right)$$

(27)

$$\overrightarrow{C}=2\times {\overrightarrow{r}}_2$$

(28)

When the iterations are complete, the vector amounts decrease from 2 to 0 and are represented by ${\overrightarrow{r}}_1$ and ${\overrightarrow{r}}_2$ in Equation (29):

$$\overrightarrow{a }\left(k\right)=2-\left(2\times k\right)/Ma{x}_{iter}$$

(29)

5.1.2. Chasing the Prey

According to their good knowledge and decision-making strategies, α, β, and γ wolves search for their prey. The alpha wolf leads the pack and takes them toward their target before initiating the hunt. Upon reaching their optimum positions, they tighten their positions, and α, β, and γ wolves continue updating their positions. Therefore, the three best solutions are involved in selecting the elite search agents. The hunting technique of grey wolves is described in Equations (30)–(32):

$$\begin{gathered} {\overrightarrow{D}}_{\alpha }=\left|{\overrightarrow{C}}_{\alpha }\times {\overrightarrow{X}}_{\alpha }-\overrightarrow{X} \right| \\ {\overrightarrow{D}}_{\beta }=\left|{\overrightarrow{C}}_{\beta }\times {\overrightarrow{X}}_{\beta }-\overrightarrow{X} \right| \\ {\overrightarrow{D}}_{\gamma }=\left|{\overrightarrow{C}}_{\gamma }\times {\overrightarrow{X}}_{\gamma }-\overrightarrow{X} \right| \end{gathered}$$

(30)

where ${\overrightarrow{C}}_1$, ${\overrightarrow{C}}_2$, and ${\overrightarrow{C}}_3$ are decided by Equations (27) and (28).

$$\begin{gathered} {\overrightarrow{X}}_1={\overrightarrow{X}}_{\alpha }-{\overrightarrow{A}}_{\alpha }\times \left({\overrightarrow{D}}_{\alpha }\right) \\ {\overrightarrow{X}}_2={\overrightarrow{X}}_{\beta }-{\overrightarrow{A}}_{\beta }\times \left({\overrightarrow{D}}_{\beta }\right) \\ {\overrightarrow{X}}_3={\overrightarrow{X}}_{\gamma }-{\overrightarrow{A}}_{\gamma }\times \left({\overrightarrow{D}}_{\gamma }\right) \end{gathered}$$

(31)

$$\overrightarrow{X}\left(k+1\right)=\frac{{\overrightarrow{X}}_1+{\overrightarrow{X}}_2+{\overrightarrow{X}}_3}{3}$$

(32)

5.1.3. Attacking

When the wolves’ prey is trapped within the pack, the wolves attack it. In mathematical form, as wolves approach their prey $\overrightarrow{a }\left(k\right)$ starts decreasing. In this model, $\overrightarrow{a }\left(k\right)$ varies within the range of 2 to 0, as described in Equation (29) [1]. This varying range shows the location of prey and the best place for the hunters (α, β, and γ). In each iteration, the α, β, and γ wolves optimize and update their places in steps including searching, encircling, chasing, and attacking. Through continuous iterations, the α wolf achieves an optimum place before attacking the prey.

5.1.4. Searching for Prey

To search for prey, a pack of wolves takes directions from the α, β, and γ wolves, diverging in different directions and then converging to attack. The α, β and γ wolves decide to attack a specific prey according to their best position and knowledge. While in search of prey, the wolves mathematically diverge at any random values between 1 and -1. When $\left|\overrightarrow{A}\right|>1$, the wolves are forced to diverge to find the prey, and when $\left|\overrightarrow{A}\right|<1$, they converge to attack the prey [59].

5.2. Whale Optimization Algorithm (WOA)

In 2016, Mirajalili and Lewis introduced a novel swarm-based metaheuristic algorithm called the whale optimization algorithm (WOA). The process of this approach is discussed below.

5.2.1. Inspiration

The whale is one of the largest creatures found on the earth, including seven different species of mammals: killer, minke, sei, blue, finback, right, and humpback. The highly intelligent, emotional nature and hunting behavior of humpback whales is the basic inspiration of the WOA [8]. Humpback whales hunt their prey by producing bubbles. There are two strategies for producing bubbles: one is a rising spiral, and the other is double rings. In the rising spiral, the whale dives down approximately 12 m, then spirals to make bubbles around its prey as it moves upward. In the double ring technique, the whale produces recording loops.

The WOA algorithm’s mathematical model is explained below.

5.2.2. Encircling Prey

When a whale finds the position of its prey (krill), it approaches the prey using the best and most concise path. The mathematical model of the WOA algorithm also works on the basis of this strategy. The WOA finds the optimal search agents and continually updates the spot of best search agents. This strategy is demonstrated as follows in Equations (33) and (34) [60,61]:

$$\overrightarrow{D}=\left|\overrightarrow{C}\times \overrightarrow{X^{*}}\left(t\right)-\overrightarrow{X}\left(t\right)\right|$$

(33)

$$\overrightarrow{X}\left(t+1\right)=\overrightarrow{X^{*}}\left(t\right)-\overrightarrow{A}\times \overrightarrow{D}$$

(34)

where t represents the existing iteration, $\overrightarrow{A}$ and $\overrightarrow{D}$ are the vector coefficients, $\overrightarrow{X^{*}}$ represents the position vector, and $\overrightarrow{X}$ is the location vector.

$\overrightarrow{A}$ and $\overrightarrow{C}$ are calculated using Equations (35) and (36):

$$\overrightarrow{A}=2\overrightarrow{a}\times \overrightarrow{r}-\overrightarrow{a}$$

(35)

$$\overrightarrow{C}=2\times \overrightarrow{r}$$

(36)

where $\overrightarrow{r}$ is the random vector varying in between [0, 1] and $\overrightarrow{a}$ represents a linear vector that decreases from 0–2 during iterations.

5.2.3. Rising Bubble Method

Humpback whales attack their prey using the bubble net attacking method that is mathematically explained in Equation (37) [8,60]. A humpback whale dives and rotates in a spiralling, arbitrary path around its prey and assumes an optimum position to attack while producing bubbles.

$$\overrightarrow{X}\left(t+1\right)=\left\{\begin{array}{l}\overrightarrow{X^{*}}\left(t\right)-\overrightarrow{A}\times \overrightarrow{D} if p<0.5\\ \overrightarrow{\acute{D}}\times e^{bl}\times Cos\left(2\pi l\right)+\overrightarrow{X^{*}}\left(t\right) if p>0.5\end{array}\right\}$$

(37)

5.2.4. Seeking Prey

Each humpback whale, $\overrightarrow{A}$ searches for its prey according to their opposition at their present location. The search agent $\overrightarrow{A}$ randomly updates its position after every iteration until reaching the optimum position to attack the prey. The mathematical model is shown in Equations (38) and (39):

$$\overrightarrow{D}=\left|\overrightarrow{C}\times \overrightarrow{X_{rand}}-\overrightarrow{X}\right|$$

(38)

$$\overrightarrow{X}\left(t+1\right)=\overrightarrow{X_{rand}}-\overrightarrow{A}\times \overrightarrow{D}$$

(39)

5.3. Dandelion Optimizer (DO)

The dandelion is a plant scientifically known as Herba taraxaci. It is primarily found in open areas, grassy plots, woodlands, and on alpine slopes, mostly in North America and the Himalayas. Their height is usually between 20 to 24 cm, and their structure is inflorescences in nature. Dandelion seeds are composed of thousands of crested or crown hairs [62]. For seed propagation, the dandelion seeds rely on the wind. This crested hair and structure allows the wind to blow the seed for breeding at a new location.

5.3.1. Inspiration

The dandelion optimizer is a swarm intelligence, bio-inspired optimization technique. DO is known for its growth rate and increasing iterative population. Each of the dandelion seeds is a candidate responsible for the population’s growth in a new place. This candidate technique is stated in mathematical form as shown in Equation (40):

$$population=\left[\begin{array}{ccc}{x}_1^1& \cdots & x_1^{Dim}\\ ⋮& \ddots & ⋮\\ x_{pop}^1& \cdots & x_{pop}^{Dim}\end{array}\right]$$

(40)

where $pop$ is the population size and $Dim$ represents the dimension of the variable.

When the seed of a dandelion lands and starts to sprout, it is considered to be in the optimal position which is represented as $X_{elite}$ written in Equation (41) [62]. $X_i$ is the ith individual seed.

$$X_{elite}=X\left(find\left(f_{best}==f\left(X_i\right)\right)\right)$$

(41)

5.3.2. Rising Stage

Factors such as wind, air humidity, weather, and seasons play an essential role in carrying a dandelion seed to a certain height and blowing it away. Summer and winter seasons affect the height and flourishing position of the seeds. In summers, the wind speed is higher; therefore, the seeds fly for a longer period compared to winters. This is why the seeds are scattered in summers. In mathematical form, summer and winter are represented by Equations (42) and (43), respectively [62]:

$$X_{t+1}=X_t+\alpha \times v_x\times v_y\times lnY\times \left(X_s-X_t\right)$$

(42)

$$X_{t+1}=X_t\times k$$

(43)

where $lnY$ is lognormal distribution and $k$ is the dynamic wave carried out using Equations (44) and (45), respectively.

$$\ln Y=\left\{\begin{array}{c}\frac{1}{y\sqrt{2\pi }}exp\left[-\frac{1}{2{\sigma }^2}{\left(lny\right)}^2\right] y\ge 0\\ 0 y<0\end{array}\right.$$

(44)

$$\begin{gathered} q=\frac{1}{T^2-2T+1}{t}^2-\frac{2}{T^2-2T+1}t+1+\frac{1}{T^2-2T+1}t \\ k=1-rand()\times q \end{gathered}$$

(45)

5.3.3. Descending Stage

After ascending and flying with the wind, the dandelion seeds begin to descend in a specific trajectory. The movement trajectory is known as Brownian motion (${\beta }_t$). After rising, ${\beta }_t$ determines the new location of the seed through iterative updates. The mathematical expression for the descending stage is shown in Equation (46):

$$X_{t+1}=X_t-\alpha \times {\beta }_t\times \left(X_{mea{n}_t}-\alpha \times {\beta }_t\times X_t\right)$$

(46)

where $X_{mean\_t}$ is the average position, which is mathematically determined using Equation (47):

$$X_{mean\_t}=\frac{1}{pop}{\displaystyle \sum }_{i=1}^{pop}{X}_i$$

(47)

5.3.4. Landing Stage

Based on the season, the landing of the dandelion seed is decided during the rising stage. Gradually, the algorithm starts converging towards the global optima through the iteration process. After the seed lands, it starts to grow, which is considered the most optimal position. The behavior of landing is expressed mathematically in Equation (48):

$$X_{t+1}=X_{elite}+levy\left(\lambda \right)\times \alpha \times \left(X_{elite}-X_t\times \delta \right)$$

(48)

where $levy\left(\lambda \right)$ represents the function of levy flight, which is calculated using Equation (49):

$$levy\left(\lambda \right)=s\times \frac{\omega \times \sigma }{{\left|t\right|}^{\frac{1}{\beta }}}$$

(49)

where $\omega$ and $t$ are random variables varying between [0, 1], β is a random variable varying between [0, 2], and $s$ is a fixed constant: 0.01.

The process of optimal allocation of renewable energy resources and placement of electric vehicle charging stations is presented in Figure 1.Figure 2 illustrates the process of optimal allocation of renewable energy resources, including solar photovoltaic and wind turbine generation and electric vehicle charging stations, to achieve multiple objectives simultaneously using different metaheuristic optimization techniques considering seasonal variations.

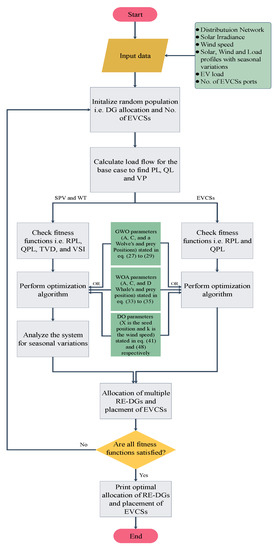
Figure 1. Flow Chart for multiple RE-DG allocations and EVCS placements using GWO, WOA, and DO algorithms.

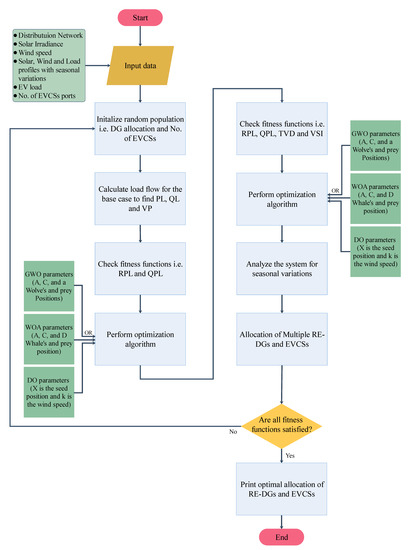
Figure 2. Flow Chart for multiple SPV and EVCS allocations and wind and EVCS allocations using GWO, WOA, and DO algorithms.

6. Simulation Results and Discussions

In this section, three metaheuristic algorithms (GWO, WOA, and DO) were employed on an IEEE 33-bus DN. For GWO, WOA, and DO, the size of population for wolves, whales, and seeds were set to 50, respectively. The stopping criterion was defined by the maximum number of iterations, set at 150. The control parameters of all three algorithms are presented in Table 5. The allocation of RE-based single and multiple DGs was achieved to reduce RPL, QPL, and TVD, and to maximize VSI, which were assessed for the MOOP. To verify the effectiveness of the employed algorithms, the results were compared with other optimization techniques. These three algorithms were coded and simulated in MATLAB 2022a and run-on system HP EliteBook 840 G2 Intel Core i5 with 8GB RAM.

Table 5. Control parameter settings.

Algorithms	Parameters
GWO	Population = 50, max-iter = 150, power factor = 0.9, DG-size (MVA) = 0–2000
WOA	Population = 50, max-iter = 150, power factor = 0.9, DG-size (MVA) = 0–2000
DO	Population = 50, max-iter = 150, power factor = 0.9, DG-size (MVA) = 0–2000

The following scenarios were examined in the 33-bus network by Integrating SPV, WTG, and EVCSs at a 0.9 lagging power factor for multiple DGs.

6.1. IEEE 33-Bus Test System

For analysis of optimization techniques, the IEEE 33-bus system was considered. For the overall description of the 33-bus RDN, line and load data were considered. The single line diagram of the 33-bus RDN is shown in Figure 3. The base values of the 33-bus RDN were kV = 12.66 and MVA = 100.

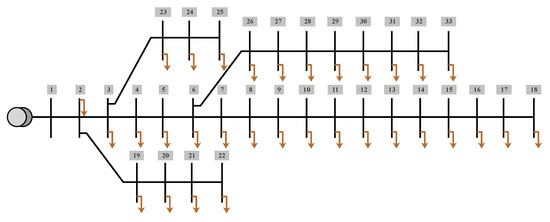
Figure 3. Single-line diagram of IEEE for the 33-bus RDS.

The curves of solar radiation, wind speed, and load demand are shown in Figure 4, Figure 5 and Figure 6, respectively. These profiles change throughout the year; therefore, the average profiles for the four seasons, i.e., spring, summer, autumn, and winter were taken and scaled into 24 h periods. The first 24-h period represents spring, the 24–48th hour represents summer, the 48–72nd hour represents autumn, and the 72–96th hour represents winter.

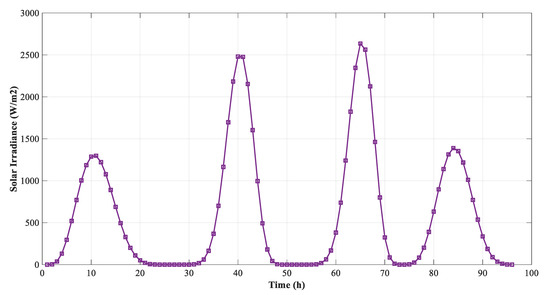
Figure 4. Solar irradiance profile for seasonal variation.

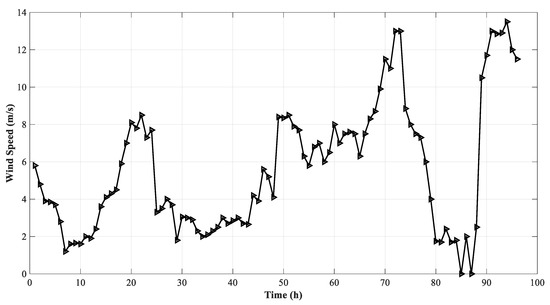
Figure 5. Wind speed profile for seasonal variation.

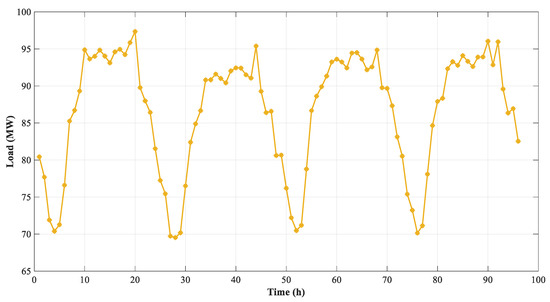
Figure 6. Load profile for seasonal variation.

6.1.1. Multi-Objective Assessment of the 33-Bus RDN

MOOP was applied to the 33-bus RDN to find the optimal allocation of RE-DGs and the optimal placement of the EVCSs. The optimal allocation of RE-DGs helps to reduce the RPL, QPL, and TVD, and to improve the VSI of the 33-bus system. The power flow results show that the baseline value of RPL was 210.05 kW, the QL was 142.44, the TVD was 0.1328, and the VSI was 0.6697 p.u.

6.1.2. RE-DGs and EVCSs Allocation for the 33-Bus RDN

Table 6 presents the various case scenarios that were adopted for the analysis of the muti-objectives involved in this paper using meta-heuristic techniques for optimal allocation of RE-DGs and EVCSs in the 33-bus RDN.

Table 6. Different scenarios adopted for analysis.

Scenarios	SPV	WTG	EVCSs
Scenario 1	✓	X	X
Scenario 2	X	✓	X
Scenario 3	X	X	✓
Scenario 4	✓	X	✓
Scenario 5	X	✓	✓

✓ and X represents the consideration of specific RE-based DG in particular scenario.

6.1.3. Scenario 1: Only SPV

The optimal solar DG allocation at 0.9 PF is presented in Table 7. In the table, the multiple SPV DG locations were 14, 25, and 32 using GWO, the multiple SPV DG locations were 12, 24, and 31 using WOA, and the multiple SPV DG locations were 14, 24, and 30 using DO. The table shows that the RPL obtained from the muti-objective GWO was 65.5066 p.u., the WOA was 56.8897 p.u., and the DO was 61.5987 p.u. The optimal allocation of SPV DGs reduced the RPL by 72.913% from the baseline WOA, which was less than the results of the other two techniques shown in the table. The QPL obtained from the muti-objective GWO was 45.8701 p.u., the WOA was 38.7945 p.u., and the DO was 45.1846 p.u. The optimal allocation of SPV DGs reduced the QPL by 72.764% from the baseline using WOA, which was less than the results of the other two techniques shown in the table. The TVD achieved from the multi-objective GWO was 0.003824, the WOA was 0.002839, and the DO was 0.004336. The voltage deviation of WOA was better than GWO and DO. The voltage stability of WOA was 0.94655, which was better than GWO and DO which were 0.92513 and 0.92127, respectively.

Table 7. Optimal allocation of SPV DGs for the 33-bus network based on multi-objective consideration of various optimization techniques.

Methods	Location	P (MW)	Q (MVAR)	RPL (kW) (%)	QPL (kVAR) (%)	TVD (p.u)	VSI (p.u)
Base case	-	-	-	210.05	142.44	0.1328	0.6697
GWO [P]	14, 25, 32	0.688, 0.793, 1.306	0.246, 0.334, 0.503	65.5066 (68.813%)	45.8701 (67.797%)	0.003824	0.92513
WOA [P]	12, 24, 31	0.816, 0.952, 1.085	0.297 0.303, 0.398	56.8897 (72.913%)	38.7945 (72.764%)	0.002839	0.94655
DO [P]	14, 24, 30	0.809, 0.833, 1.072	0.213, 0.253, 0.477	61.5987 (70.674%)	45.1846 (68.278%)	0.004336	0.92127

[P]—Proposed.

Loss Profiles of SPV DGs

In Figure 7 and Figure 8, the active and reactive power losses were simultaneously considered for SPV DGs using GWO, WOA, and DO.

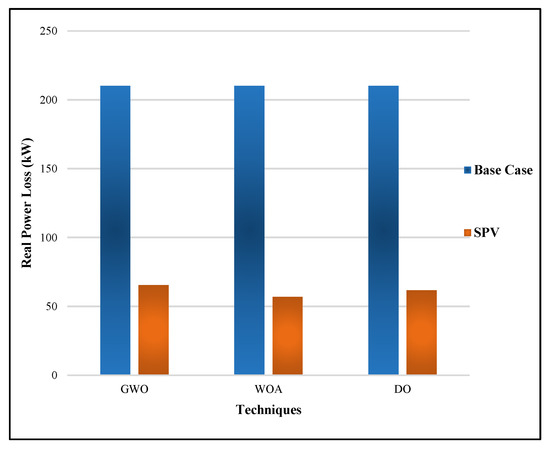
Figure 7. Active power losses of SPV for GWO, WOA, and DO.

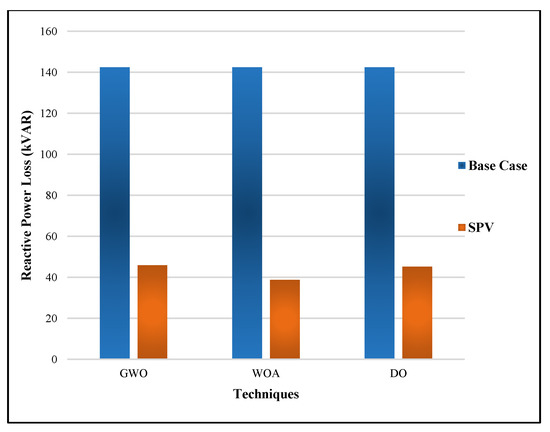
Figure 8. Reactive power losses of SPV for GWO, WOA, and DO.

Voltage Profiles of 33-Bus RDN for SPV DGs

When the TVD and VSI were considered as the muti-objective function, the optimal allocation of WTG DGs improved the voltage profile of the 33-bus system. Figure 9, Figure 10 and Figure 11 show the effect of SPV DGs for GWO, WOA, and DO, respectively, for the MOOPs.

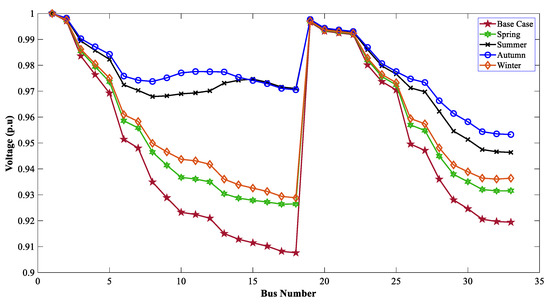
Figure 9. Voltage profiles of 33 buses for seasonal variation with SPV using GWO.

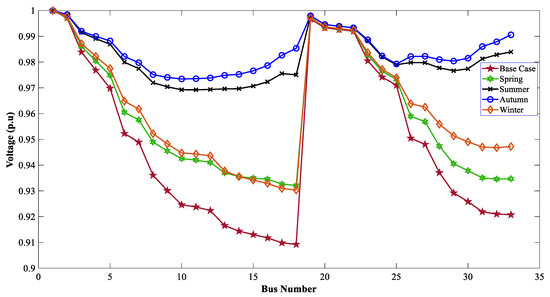
Figure 10. Voltage profiles of 33 buses for seasonal variation with SPV using WOA.

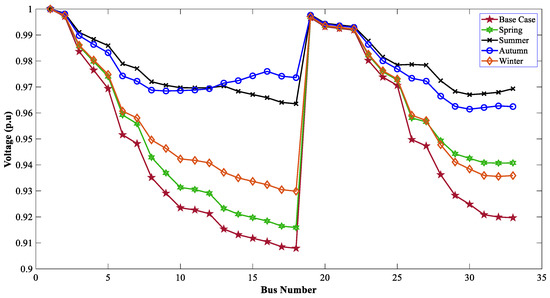
Figure 11. Voltage profiles of 33 buses for seasonal variation with SPV using DO.

6.1.4. Scenario 2: Only WTG

The optimal wind DG allocation at 0.9 PF is presented in Table 8. In the table, the multiple WTG DG locations were 13, 24, and 30 using GWO, the multiple WTG DG locations were 13, 24, and 30 using WOA, and the multiple WTG DG locations were 13, 24, and 30 using DO. The table shows that the RPL obtained from the muti-objective GWO was 49.4825 p.u., the WOA was 54.0478 p.u., and the DO was 54.083 p.u. The optimal allocation of WTG DGs reduced the RPL by 76.44% from the baseline GWO, which was lower than the results obtained using the other two techniques shown in the table. The QPL obtained from the muti-objective GWO was 34.7879 p.u., the WOA was 40.4329 p.u., and the DO was 36.823 p.u. The optimal allocation of WTG DGs reduced the QPL by 75.577% from the baseline using GWO, which was less than the results of the other two techniques shown in the table. The TVD achieved from the multi-objective GWO was 0.004624, the WOA was 0.009322, and the DO was 0.005671. The voltage deviation of GWO was better than WOA and DO. The voltage stability of DO was 0.97896, which was better than the GWO and WOA values of 0.89905 and 0.84611, respectively. Figure 12 and Figure 13 show the active and reactive power losses, which were simultaneously considered for WTG DGs using GWO, WOA, and DO.

Table 8. Optimal allocation of WTG DGs for the 33-bus network based on multi-objective consideration of various optimization techniques.

Methods	Location	P (MW)	Q (MVAR)	RPL (kW) (%)	QPL (kVAR) (%)	TVD (p.u)	VSI (p.u)
Base Case	-	-	-	210.05	142.44	0.1328	0.6697
GWO [P]	13, 24, 30	0.772, 0.922, 1.348	0.258, 0.324, 0.584	49.4825 (76.44%)	34.7879 (75.577%)	0.004624	0.89905
WOA [P]	13, 24, 30	0.765, 0.880, 1.452	0.372, 0.381, 0.643	54.0478 (74.269%)	40.4329 (71.614%)	0.009322	0.84611
DO [P]	13, 24, 30	0.853, 1.006, 1.266	0.425, 0.457, 0.510	54.083 (74.252%)	36.823 (74.148%)	0.005671	0.97896

[P]—Proposed.

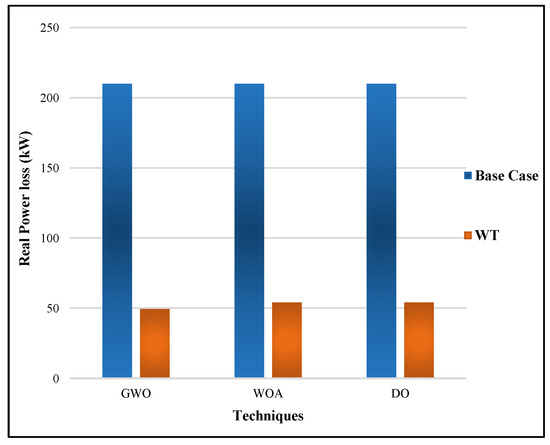
Figure 12. Active power losses of WTG for GWO, WOA, and DO.

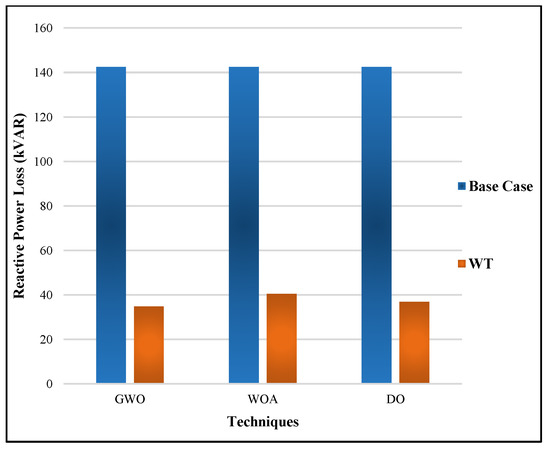
Figure 13. Reactive power losses of WTG for GWO, WOA, and DO.

Voltage Profiles of 33-Bus RDN for WTG DGs

When the TVD and VSI were considered as the muti-objective function, the optimal allocation of WTG DGs improved the voltage profile of the 33-bus network. Figure 14, Figure 15 and Figure 16 show the effect of WTG DGs for GWO, WOA, and DO for the MOOPs.

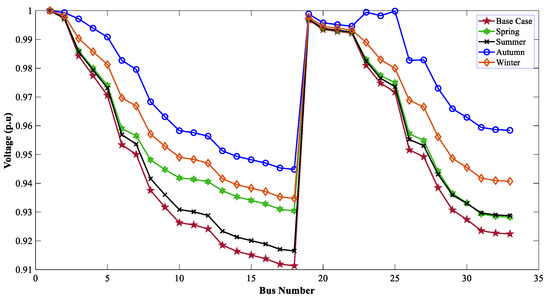
Figure 14. Voltage profiles of 33 buses for seasonal variation with WTG using GWO.

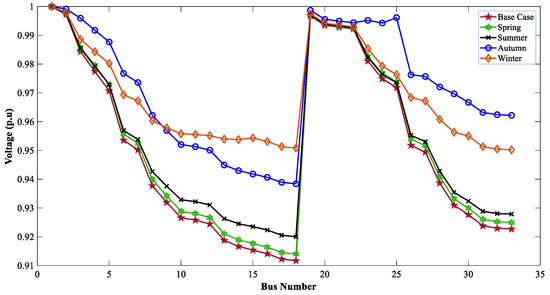
Figure 15. Voltage profiles of 33 buses for seasonal variation with WTG using WOA.

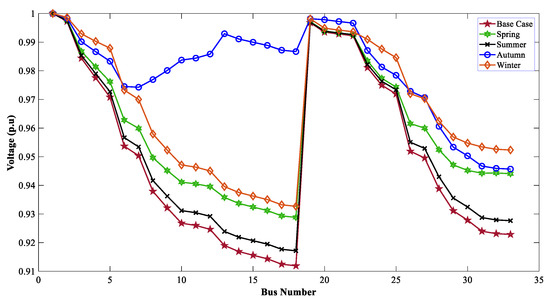
Figure 16. Voltage profiles of 33 buses for seasonal variation with WTG using DO.

6.1.5. Scenario 3: Only EVCSs

EVCSs draw power from the existing 33-bus system to charge the EVs, so they behave as the load on the RDN. These EVCSs charge the vehicles, which is why they act as a grid-to-vehicle (G2V). The optimal EVCS placement at 0.9 PF is presented in Table 9. In the table, the multiple EVCS locations were 4, 12, 13, 22, and 25 using GWO, the multiple EVCS locations were 2, 3, 4, 9, and 13 using WOA, and the multiple EVCS locations were 6, 12, 17, 22, and 25 using DO. The table shows that the RPL obtained from the muti-objective GWO was 267.1758 p.u., the WOA was 262.1438 p.u., and the DO was 280.4705 p.u. In all cases, the real power was more than the baseline real power, but the WOA technique drew less power from the system compared to the other techniques listed in Table 10 to charge the EVs. The QPL obtained from the muti-objective GWO was 181.1311 p.u., the WOA was 177.1492 p.u., and the DO was 189.8264 p.u. Similar to the active power results, the reactive power in the WOA case was less than those obtained by GWO and DO. Figure 17 and Figure 18 active and reactive power losses that were simultaneously considered for EVCSs executing GWO, WOA, and DO algorithms.

Table 9. Optimal placement of EVCSs for the 33-bus network based on single-objective consideration of various optimization techniques.

Methods	Location	P (MW)	Q (MVAR)	RPL (kW) (%)	QPL (kVAR) (%)	TVD (p.u)	VSI (p.u)
Base Case	-	-	-	210.05	142.44	0.1328	0.6697
GWO [P]	4, 12, 13, 22, 25	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82	267.1758 (27.187%)	181.1311 (27.166%)	-	-
WOA [P]	2, 3, 4, 9, 13	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82	262.1438 (24.792%)	177.1492 (24.371%)	-	-
DO [P]	6, 12, 17, 22, 25	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82	280.4705 (33.516%)	189.8264 (33.271%)	-	-

[P]—Proposed.

Table 10. Optimal allocation of SPV DGs and EVCSs for the 33-bus network based on muti-objective consideration of various optimization techniques.

Methods	SPV and EVCSs	Location	P (MW)	Q (MVAR)	RPL (kW) (%)	QPL (kVAR) (%)	TVD (p.u)	VSI (p.u)
Base Case		-	-	-	210.05	142.44	0.1328	0.6697
GWO [P]	SPV	9, 23, 29	0.725, 0.939, 1.159	0.281, 0.292, 0.491	79.4624 (62.170%)	62.3089 (56.256%)	0.005726	0.94724
	EVCSs	4, 12, 13, 22, 25	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82
WOA [P]	SPV	8, 22, 29	0.690, 0.973, 1.099	0.231, 0.392, 0.495	54.0478 (74.269%)	40.4329 (71.614%)	0.009322	0.84611
	EVCSs	2, 3, 4, 9, 13	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82
DO [P]	SPV	13, 22, 29	0.768, 0.977, 1.330	0.331, 0.391, 0.571	63.8158 (69.619%)	45.4183 (68.114%)	0.005419	0.94821
	EVCSs	6, 12, 17, 22, 25	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82

[P]—Proposed.

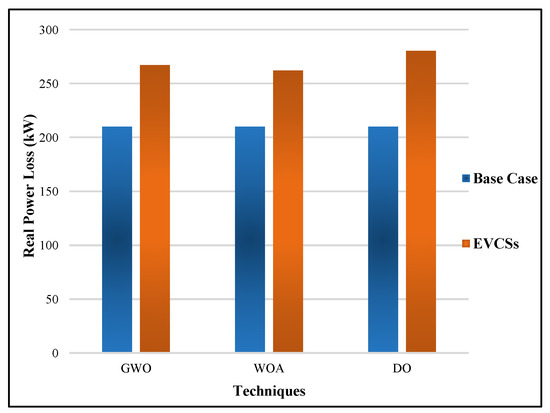
Figure 17. Active power losses of EVCSs for GWO, WOA, and DO.

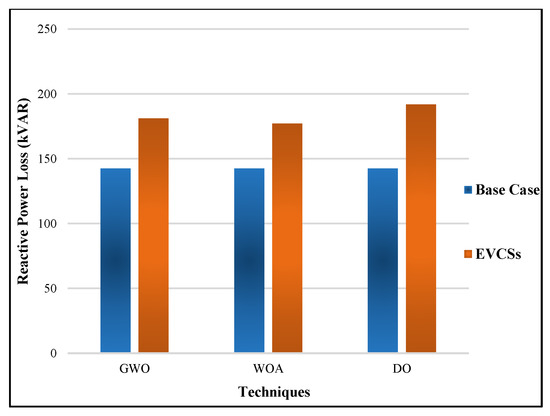
Figure 18. Reactive power losses of EVCSs for GWO, WOA, and DO.

6.1.6. Scenario 4: SPV-DGs and EVCSs

Optimal solar DG and EVCS allocations at 0.9 PF are presented in Table 10. In the table, the multiple solar DG locations were 9, 23, and 29, and the EVCS locations were 4, 12, 13, 22, and 25 using GWO. The multiple solar DG locations were 8, 22, and 29, and the EVCS locations were 2, 3, 4, 9, and 13 using WOA. The multiple solar DG locations were 13, 22, and 29, and the EVCS locations were 6, 12, 17, 22, and 25 using DO. The table shows that the RPL obtained from the muti-objective GWO was 79.4624 p.u., the WOA was 63.8158 p.u., and the DO was 82.7109 p.u. The RPL was reduced by 69.619% compared to its baseline using WOA, which was less than the results of the other two techniques listed in the table. The QPL obtained from the muti-objective GWO was 62.3089 p.u., the WOA was 45.4183 p.u., and the DO was 58.9258 p.u. The QPL was reduced by 68.114% compared to its baseline by applying WOA, which was less than the results of the other two techniques listed in the table. The TVD achieved from the multi-objective GWO was 0.005726, the WOA was 0.005419, and the DO was 0.007747. The voltage deviation of WOA was better than the other two optimization techniques. The voltage stability of WOA was 0.94821, which was better than GWO and DO, which were 0.94724 and 0.89273, respectively. Figure 19 and Figure 20 show the active and reactive power losses, which were considered simultaneously for SPV DGs and EVCSs using GWO, WOA, and DO.

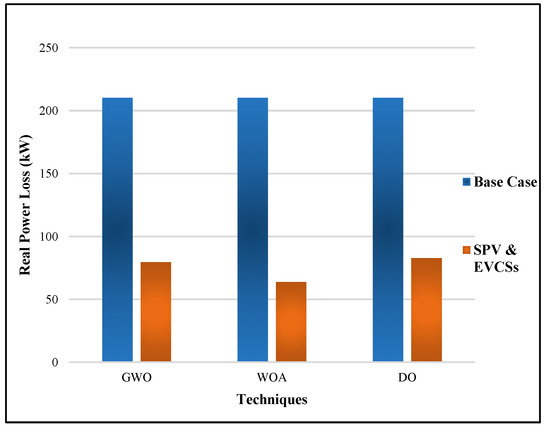
Figure 19. Active power losses of SPV and EVCSs for GWO, WOA, and DO.

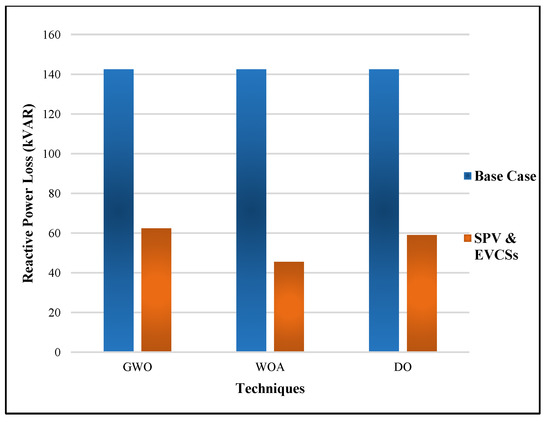
Figure 20. Reactive power losses of SPV and EVCSs for GWO, WOA, and DO.

Voltage Profiles of the 33-Bus RDN with SPV-DGs and EVCSs

When the TVD and VSI were considered as the muti-objective function, the optimal allocation of the WTG DGs improved the voltage profile of the 33-bus system. Figure 21, Figure 22 and Figure 23 show the effect of the WTG DGs for GWO, WOA, and DO, respectively, for the MOOPs. Due to the involvement of EVCSs in these profiles, a slight drop in voltage was observed compared to scenario 1.

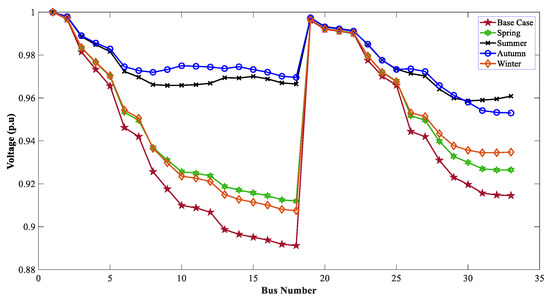
Figure 21. Voltage profiles of 33 buses for seasonal variation with SPV & EVCSs using GWO.

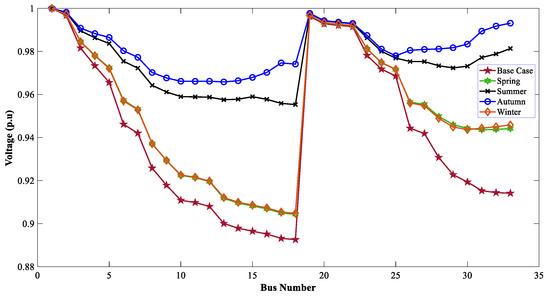
Figure 22. Voltage profiles of 33 buses for seasonal variation with SPV & EVCSs using WOA.

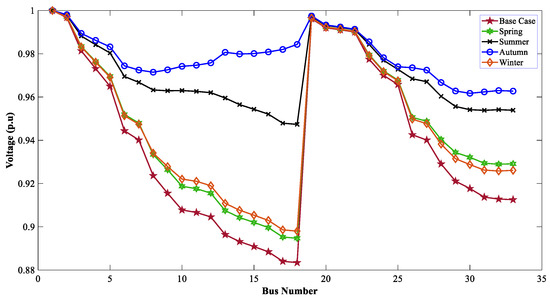
Figure 23. Voltage profiles of 33 buses for seasonal variation with SPV & EVCSs using DO.

6.1.7. Scenario 5: WTG-DGs and EVCSs

The optimal solar DG and EVCS allocations at 0.9 PF are presented in Table 11. In table, the multiple solar DG locations were 6, 14, and 28, and the EVCS locations were 4, 12, 13, 22, and 25 using GWO. The multiple solar DG locations were 11, 18, and 29, and the EVCS locations were 2, 3, 4, 9, and 13 using WOA. The multiple solar DG locations were 9, 20, and 2, and the EVCS locations were 6, 12, 17, 22, and 25 using DO. The table shows that the RPL obtained from the muti-objective GWO was 76.4404 p.u., the WOA was 89.6694 p.u., and the DO was 90.207 p.u. The RPL was reduced by 63.608% compared to its baseline by applying GWO, which was less than the results of the other two techniques listed in the table. The QPL obtained from the muti-objective GWO was 57.8867 p.u., the WOA was 69.5078 p.u., and the DO was 65.3175 p.u.

Table 11. Optimal allocation of WTG DGs and EVCSs for the 33-bus network based on muti-objective consideration of various optimization techniques.

Methods	SPV and EVCSs	Location	P (MW)	Q (MVAR)	RPL (kW) (%)	QPL (kVAR) (%)	TVD (p.u)	VSI (p.u)
Base Case		-	-	-	210.05	142.44	0.1328	0.6697
GWO [P]	WTG	6, 14, 28	0.604, 1.015, 1.324	0.235, 0.344, 0.507	76.4404 (63.608%)	57.8867 (59.361%)	0.009827	0.92341
	EVCSs	4, 12, 13, 22, 25	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82
WOA [P]	WTG	11, 18, 29	0.577, 1.167, 1.173	0.166, 0.248, 0.543	89.6694 (57.310%)	69.5078 (51.202%)	0.005515	0.92139
	EVCSs	2, 3, 4, 9, 13	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82
DO [P]	WTG	9, 20, 28	0.746, 0.912, 0.951	0.228, 0.418, 0.426	90.207 (57.055%)	65.3175 (54.144%)	0.02631	0.79254
	EVCSs	6, 12, 17, 22, 25	1.332, 0.546, 1.497, 0.546, 1.299	0.841, 0.345, 0.945, 0.345, 0.82

[P]—Proposed.

The QPL was reduced by 59.361% compared to its baseline by applying GWO, which was less than the results of the other two techniques listed in the table. The TVD achieved from multi-objective GWO was 0.009827, the WOA was 0.005515, and the DO was 0.02631. The voltage deviation of WOA was better than the other two optimization techniques. The voltage stability of GWO was 0.92341, which was better than the WOA and DO, which produced results of 0.92139 and 0.79254, respectively. In Figure 24 and Figure 25, the active and reactive power losses were considered simultaneously for WTG DGs and EVCSs for GWO, WOA, and DO.

Figure 24. Active power losses of WTG and EVCSs for GWO, WOA, and DO.

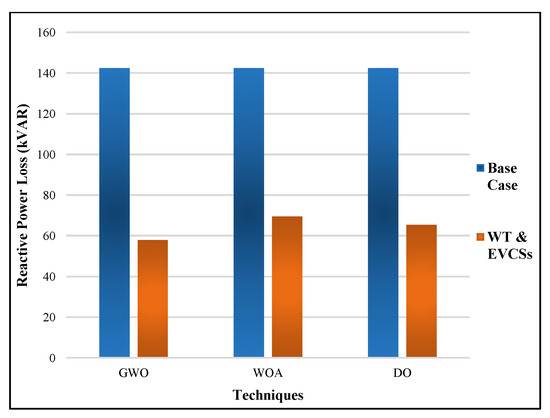
Figure 25. Reactive power losses of WTG and EVCSs for GWO, WOA, and DO.

Voltage Profiles of the 33-Bus RDN for WTG, DGs, and EVCSs

When the TVD and VSI were considered as the muti-objective function for optimal allocation of WTG, DGs improved the voltage profile of the 33-bus network. Figure 26, Figure 27 and Figure 28 show the effect of WTG DGs for GWO, WOA, and DO, respectively, for the MOOPs. Due to the involvement of EVCSs in these profiles, a slight drop in voltage was observed compared to scenario 2.

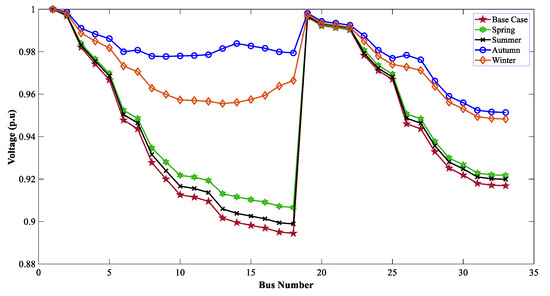
Figure 26. Voltage profiles of 33 buses for seasonal variation with WTG & EVCSs using GWO.

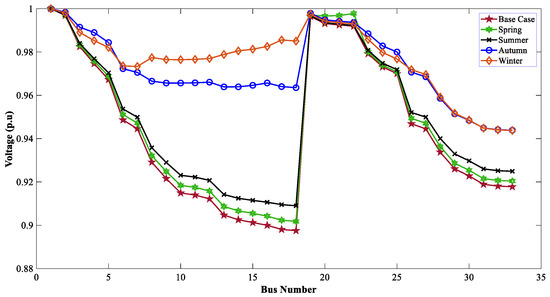
Figure 27. Voltage profiles of 33 buses for seasonal variation with WTG & EVCSs using WOA.

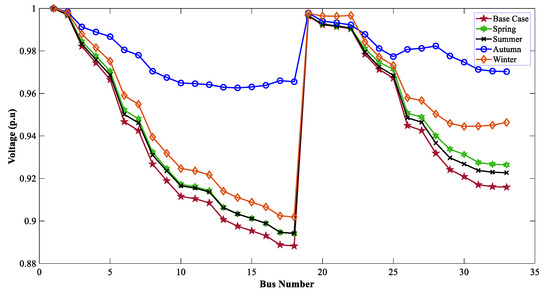
Figure 28. Voltage profiles of 33 buses for seasonal variation with WTG & EVCSs using DO.

7. Conclusions

In this paper, three metaheuristic techniques have been proposed to optimally allocate EVCSs and RE-DGs, incorporating single and multiple objective functions, respectively. The objective functions include total voltage deviation, active power losses, reactive power losses, and voltage stability index. The multi-objective function comprises the objective functions by exploiting weights. These metaheuristic techniques (GWO, WOA, and DO) present effective solutions for optimal allocation of RE-DGs and EVCSs in RDNs. The proposed metaheuristic techniques are implemented and evaluated across 33 bus radial distribution networks. Uncertainty modeling and seasonal variations were also considered in this study. MATLAB 2022a was used to simulate the meta-heuristic techniques and to evaluate the results. The obtained results were presented in various scenarios for SPV, WTG, and EVCSs. These scenarios demonstrated a significant reduction in active and reactive power losses, minimum voltage deviation, and an enhanced voltage stability index. For only SPV allocation, the RPL and QPL were reduced by 72.913% and 72.764% from their baselines, respectively, using the WOA technique, which was then compared to the other two techniques. The RPL and QPL were reduced by almost 76.44% and 75.577% from their baselines, respectively, in scenario 2 using the GWO technique. The RPL and QPL values for scenario 2 using the other two techniques were inferior to the results obtained using the GWO technique. Placement of EVCSs in RDN gained power from the grid; therefore, the RPL and QPL values increased from their respective baselines. SPV-DGs and EVCSs allocation the RPL and QPL was reduced by 69.619% and 68.114% from their respective baselines using the WOA technique, which was compared to the other two techniques. WTG-DGs and EVCSs allocation of the RPL and QPL was reduced by 63.608% and 59.361% from their respective baselines using the GWO technique, which was compared to the other two techniques.