A Novel Decision-Making Framework to Evaluate Rail Transport Development Projects Considering Sustainability under Uncertainty

Abstract

One of the constant concerns in public and private organizations is choosing a project from among the multitude of potential projects to be implemented. Due to the limited resources in different sectors, projects should be prioritized in order to obtain the maximum benefit. In national and government projects, it is not necessarily important to pay attention to financial components, and more dimensions should be considered. Sustainability is a component that considers various economic, environmental, and social aspects in the evaluation of projects. In this regard, in this study, the main goal is to evaluate and select rail transportation projects according to sustainability criteria. In general, 15 indicators were identified in three economic, environmental, and social sectors, which were weighted using the best–worst fuzzy method (FBWM). The most important indicators in the evaluation of projects are the investment cost, the rate of internal return from a national perspective, and the lesser impact of the plan on environmental destruction. According to the weighted indicators, the stochastic VIKOR approach is developed for the first time in this article, which was evaluated according to two scenarios of demand changes and cost changes of candidate projects. In the stochastic VIKOR approach, to deal with uncertainty, different scenarios are defined, through which it is possible to respond to different conditions and evaluate projects more realistically. Validation of this method is compared to other multi-criteria decision-making methods. The main contribution of this study is presenting the stochastic VIKOR approach for the first time and considering the uncertainty in project evaluation. The findings show that the projects that have the most economic gains from the national and environmental aspects are selected as the best projects.

1. Introduction

In recent decades, the transportation industry has attracted a lot of attention as one of the basic foundations of economic and social development at the global level [1]. Due to the increasing population and the growing needs of cities, the development of transportation infrastructure in countries has been considered as a critical issue [2,3]. The railway network design problem is one of the critical issues in the transportation sector due to its significance and variety of necessary applications [4]. Many extensive projects are often potentially defined by the limitations of various financial, human, and resource constraints, which do not allow all projects to be implemented at the same time. In this regard, one of the concerns in organizations is the evaluation and selection of worthy projects among a large number of projects [5,6].

Projects should be evaluated according to various criteria, and paying attention to specific financial, time, human, and other aspects increases the error of choosing the optimal project [7]. In different studies, various criteria are considered in the evaluation of projects, but in today’s world, the concept of sustainability is considered as a vital and key factor in many fields and industries [4,8]. Sustainability means the ability to maintain balance and continuity in the face of environmental, economic and social challenges, needs, and limitations [9,10]. In the transportation industry as well, the importance of sustainability has been given much attention [11,12].

One of the main reasons why sustainability is important in evaluating projects is that transportation plays an important role in all aspects of our lives. From public transportation to the transportation of personal belongings, any deficiency and inefficiency in the transportation system can have a direct impact on our daily life as well as on the economy, environment, and social issues [13,14]. As a result, choosing transportation projects with an emphasis on sustainability can improve the performance of the transportation system and improve the quality of life of the community. In addition, it is important to pay attention to sustainability in the evaluation of projects from an economic point of view since sustainable transportation projects can lead to reduced costs and improved productivity [15,16]. For example, the use of sustainable public transportation systems can reduce traffic and air pollution and, thus, reduce traffic-related costs [17,18]. Also, the use of sustainable technologies in vehicles can lead to fuel and energy savings and prevent the loss of natural resources [11]. Therefore, in the assessment of transportation projects, the importance of sustainability is very important because of the wide-ranging effects on various aspects of our lives and society. The use of sustainability criteria in the selection process of transportation projects can lead to better and more optimal decisions in the structure and development of the transportation system and ultimately lead to improvements in the quality of life of society and the preservation of natural resources.

Numerous studies evaluated different projects in various industries, most of which were based on multi-criteria decision-making methods and expert opinions [19]. One of the important issues in project evaluation is uncertainty; uncertainty shows itself in various financial, time, and operational aspects and project results. In the field of transportation, factors, such as changes in cost, time, and demand, can have a significant impact on the performance of projects, which should be included in the selection of projects. Price changes in raw materials, market fluctuations, and structural changes can increase costs and delay implementation. These issues can have a serious negative impact on the financial constraints of the projects and, as a result, lead to the failure of the successful completion of the projects or a reduction in their quality and performance [20]. Also, the uncertainty in the demand for projects can have a significant effect on the evaluation of transportation projects and cause fundamental changes in the amount of revenue generation of projects [9,21]. For this reason, by involving uncertainty in the evaluation of projects, a more accurate choice can be made. In this regard, according to the notes mentioned before, the present study motivations are as follows:

• Designing a new stochastic multi-criteria decision-making approach to include uncertainty in the evaluation of projects; such an approach has not been observed in other studies. By presenting this method, it is possible to define any number of scenarios for the evaluation of projects without limitation, which can include uncertainty in the evaluation of projects by considering different scenarios.
• Providing comprehensive sustainability indicators to evaluate transportation industry projects; this study is the first study that evaluates large-scale rail transport projects by considering all sustainability criteria in economic, social, and environmental categories.
• Designing a model to evaluate transportation projects considering sustainability indicators and involving uncertainty. This study is the first research that deals with the evaluation of rail transportation projects considering uncertainty. So, considering uncertainty at the same time along with involving sustainability criteria in the evaluation of projects is a new contribution, which is addressed in this study.

In general, the proposed study is innovative from the aspect of the solution method due to providing a new multi-criteria decision-making approach and also considering uncertainty and sustainability criteria in the evaluation of rail transportation projects. In this regard, in Section 2, an overview of the research articles is presented; then, in Section 3, the solution method is presented; and in Section 4, the case study and the evaluation indicators are presented. In Section 5, the findings are explained, and, finally, in Section 6, conclusions and management insights are presented.

2. Literature Review

In the domain of project evaluation and project selection, various studies have been conducted that focused on various industries. For instance, Hamurcu et al. [22] presented a study on the selection of rail transport projects with the process of hierarchical analysis and ideal planning. In their study, it is stated that the Istanbul Municipality intends to develop the rail transportation system of the city according to different goals. In this regard, taking into account various indicators that were weighted with multi-criteria decision-making approaches, various goals were considered as the ideal goals of the project. The important evaluation indicators of railway projects in their study include security, capacity, speed, cost, and credit. According to the mentioned criteria and different scenarios, the target projects were evaluated. In their study, a Financial Computable General Equilibrium (FCGE) model was presented, which simultaneously considered macroeconomic indicators with financial flows. The model was designed to analyze the economic effects of fiscal policies, such as transportation investment expenditure and alternative procurement approaches, on economic growth and distribution across socioeconomic classes, and it relates investment expenditure to specific financial resources. Hamurcu and Eren [23] presented a framework to evaluate and select rail system projects according to the fuzzy network analysis process. In their study, 15 indicators were presented in four categories: technology, environment, economy, and transportation. According to the results obtained from their study, it can be seen that the cost required for the implementation of railway projects, the rate of return on investment, the comfort of passengers, the ability to implement and help employment, and the response to transportation demand were the most important indicators. According to these indicators and the ANP approach, the studied projects were weighted and prioritized. Yücel and Taşabat [24] presented a study on the selection of railway system projects with multi-criteria decision-making methods in the city of Istanbul. In their study, it is stated that transportation projects are usually evaluated and selected based on indicators, such as net present value analysis (NPVA), benefit–cost analysis (BCA), and internal efficiency analysis (IEA); but, there is a point that various indicators and components are effective in the evaluation of projects. In this regard, multi-criteria decision-making (MCDM) methods were used in their study. This method, along with financial indicators, such as the stated methods, considers various indicators, such as environmental compatibility management, historical context, how to integrate with other transportation networks, etc. Project evaluation indicators were identified in four categories: passenger services, environment, economy, and urban architecture. The solution method used in this study is the use of two approaches, AHP and BWM, comparing their findings, as a result of which, the projects were weighted according to the identified indicators.

Çoban [25] explored the assessment and decision-making processes for selecting a solar power plant project using multi-criteria evaluation methods. Since the selection of projects is very difficult from the point of view of experts, the hesitant fuzzy linguistic approach was used in their study, which can assign weight to the options in a spectral manner in the uncertainty of the experts’ opinion. The methodology used in their study was AHP, with its hierarchical approach, and according to hesitant fuzzy linguistics, experts expressed their desired score to the indicators and projects. The most important project evaluation criteria were system technology, energy policies, and energy price changes. The noteworthy point in the findings of the project was the closeness of the final weight of the projects, which indicated the attention of how decision makers consider the criteria that influence project selection. Mahmoudi et al. [26] presented a large-scale multiple criteria decision-making approach for project selection. The model presented in their study was a refinery equipment manufacturing company with a project-oriented structure, implementing a comprehensive approach for project selection, combining the TOPSIS-OPA method and the K-means clustering algorithm. The study involved clustering projects based on their characteristics using the K-means algorithm. Each cluster was then assessed using eight criteria, including project duration, project delay, number of project items, project manager’s score, physical weight, number of modifications, and project code and level. The TOPSIS approach was employed to prioritize project difficulty. The criteria were weighted based on expert surveys and the OPA approach.

Haseli et al. [27] presented a new group decision-making approach based on the best–worst method (G-BWM). Due to the complexity of real-world multi-criteria decision-making problems, the analysis of different opinions from a decision-making group is required to ensure appropriate decision making. Group decision-making methods collect the opinions of decision makers and provide the best opinions using mathematical equations. So, they developed an innovative approach to group decision-making problems based on the BWM method, called G-BWM, which helps to examine the opinions of decision makers and make democratic decisions using the BWM structure. In order to evaluate the feasibility of the proposed method and its innovation, two numerical examples from the literature with applications in supply chain management (SCM) (i.e., green supplier selection and supplier development/segmentation) were reviewed and discussed. Their results showed that the proposed G-BWM method performs well in group decision making due to the large number of decision makers, ease of use, and achieving democratic decisions in the decision-making process. Tirkolaee et al. [17] presented an integrated decision-making approach to evaluate suppliers in a supply chain context. They proposed a multi-criteria decision-making (MCDM) technique that used the Analytic Hierarchy Process (AHP) and the fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to evaluate and rank suppliers. Then, taking into account resource constraints, criteria weights, and suppliers’ ranking, in a multi-objective mixed linear programming with constraints (MOMILP) method, the optimal order quantity of each supplier was determined under unknown conditions. To deal with the unknown multi-objectives of the proposed model, the roust goal programming (RGP) approach based on Shannon entropy was used. Their proposed method was applied in a real case study of a green food production company in Iran in order to check its applicability with the help of sensitivity analysis at different levels of uncertainty. Furthermore, the reliability of the proposed method was studied using different uncertainty budgets for a green food manufacturing company.

Wan et al. [28] introduced a generalized trapezoidal fuzzy number-based best–worst method for multi-criteria decision making. They proposed a fuzzy best–worst method called GITrF BWM, which utilizes generalized trapezoidal fuzzy numbers for multi-criteria decision making. The comparisons among criteria are presented using GITrFNs, and the criterion weights are also modeled as GITrFNs. The concept of criterion weight vector is presented in the normalized GITrF form, and a novel representation, Generalized Mean of Interval-valued Trapezoidal Fuzzy Data (GMIR), is provided for GITrFNs. A goal programming model is constructed to obtain the optimized criterion weights in normalized GITrF form. Furthermore, the GITrF similarity index and GITrF similarity ratio are introduced. GMIR is calculated to measure the acceptable similarity of all pairwise comparisons among criteria. For unacceptable similarity in pairwise comparisons, an approach to improve the similarity of these comparisons is presented. Finally, GITrF BWM is proposed for multi-criteria decision making. Three real examples are analyzed to demonstrate the performance of the proposed GITrF BWM. Comparative analyses show that the proposed GITrF BWM outperforms existing methods for multi-criteria decision making in GITrF environments. Dong et al. [29] developed a fuzzy best–worst method based on triangular fuzzy numbers. They proposed a novel fuzzy best–worst method (BWM) based on triangular fuzzy numbers for multi-criteria decision making. In this method, fuzzy similarity equations are considered as fuzzy equations to obtain the best vector to others and the worst vector to others in the form of triangular fuzzy numbers. To obtain the optimal weights of criteria, the fuzzy decision-making problem is formulated, and using a mathematical programming model, the optimal fuzzy weights of criteria are derived to create a normalized triangular fuzzy weight vector. Then, four linear programming models are presented for optimistic decision making, pessimistic decision making, and neutral decision making. By selecting appropriate tolerance parameters, each of the linear programming models has a unique optimal global solution. Additionally, this article introduces the concepts of fuzzy similarity index and fuzzy similarity ratio. Several application examples are used to validate the proposed fuzzy BWM, demonstrating that the proposed fuzzy BWM provides a highly useful approach for multi-criteria decision making in fuzzy environments.

Wan and Dong, [30] extended the best–worst method with fuzzy referentiality. In this paper, a novel recognized fuzzy interval-based best–worst method (IFBWM) was proposed for multi-criteria decision making. When a decision maker (DM) makes comparisons, they may have uncertainties. Therefore, referential comparisons are represented as recognized fuzzy interval values (IFVs), and the best-to-others and worst-to-others vectors are also presented as recognized fuzzy vectors. Based on the combined similarity of recognized fuzzy preference relations, the similarity equations are formulated as recognized fuzzy equations. In this regard, deriving the optimal recognized fuzzy weights of criteria is introduced as a fuzzy decision-making problem. The article ensures that the optimal recognized fuzzy weights of criteria form a normalized recognized fuzzy weight vector by constructing a mathematical programming model. To accommodate the decision maker’s risk preferences, four linear programming models are provided to obtain the optimal recognized fuzzy weights based on the mathematical programming model for optimistic DM, pessimistic DM, and neutral DM. Additionally, the article examines the process of improving the similarity. Several application examples are presented to demonstrate the effectiveness of the proposed IFBWM method. Bai et al. [31] focused on a study with the aim of evaluating the factors affecting the selection of the project portfolio. In this study, a list of financial and non-financial influencing factors on project selection in the investment portfolio were created by using a theoretical literature review. Then, using the combined system and complex networks, the relationships between factors and network links were evaluated and analyzed. The evidence obtained in their study was very interesting. Four factors, namely project managers, buyers, development capacity, and tangible resources, were the most important factors affecting the selection of projects. They provided a quantitative model for weighting and analyzing the relationships between factors and identifying the most important factors affecting the selection of projects in each investment portfolio. Mohammed [32] introduced a fuzzy-based multi-criteria approach for project selection, focusing on investment projects in Iraq’s oil industry. The study employed the Fuzzy Analytic Hierarchy Process (AHP) to assign weights to five selection criteria, namely time, cost, quality, safety, and environmental sustainability, with time and cost being the most significant criteria, accounting for over 70% of the overall weight. Subsequently, the projects were prioritized using the fuzzy Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method.

Koohathongsumrit and Luangpaiboon [33] presented a new hybrid FAHP-ZODP approach for the software project selection problem. The FAHP process was used to reflect the preferences of decision makers and zero-one desire planning (ZODP) to maximize the total utility value calculated from the individual utility values of quantitative and qualitative objectives. Their proposed approach was for selecting startup projects during the COVID-19 pandemic, and based on their findings, it could be seen that the presented model had appropriate accuracy. Important criteria in the evaluation of projects in their study were strategic criteria. The evaluation of projects was carried out in two stages; first, it was measured using financial and economic criteria to see if the project had the ability to be implemented in this respect, and then the projects were evaluated using strategic criteria. In the strategic criteria, the profitability and strategic efficiency of the organization were also examined. The approach used was a new multi-criteria method with the THOR method. Tirkolaee and Torkayesh [34] presented a hybrid decision-making model based on clustering under uncertainty. They presented an innovative decision support model based on the K-means algorithm and its combination with the best–worst method, which used MARCOS-CoCoSo to integrate interval fuzzy subsets. Their proposed decision support system took into account the rate of waste generation in medical centers, unpredictable but potential future events, and uncertainty in expert opinions, optimizing the location required for the safe and economical disposal of hazardous health waste. The efficiency of their presented method was compared to several well-known methods to show its high efficiency. A. ForouzeshNejad [9] proposed a data-driven model to evaluate and select projects in the telecoms industry. In the first step, after identifying the project evaluation indicators, he calculated the weight of each indicator with the fuzzy best–worst approach, and then the efficiency label of the projects was identified using the data envelopment analysis (DEA) method. Then, using random forest algorithms and historical data, a prospective model was presented to evaluate and select projects. The results showed that profitability indicators were always important, and along with these indicators, the time of both production and entering the market was also very important. Singh et al. [35] presented a new method for project evaluation and selection based on lean six sigma. In their proposed method, intuitive fuzzy sets based on weighted average were used to aggregate the individual suggestions of decision makers. The weights of the selected criteria were calculated using entropy criteria, and the existing projects were modified using the TOPSIS approach and prioritized with VIKOR. The effectiveness of the proposed method was confirmed through a case study in the Indian manufacturing industry. The most important criterion for evaluating projects in their study was environmental waste and destruction.

Goli et al. [36] provided a comprehensive approach based on the MCDM hybrid method to evaluate the effective factors in the implementation of the cyclical supply chain. Circular economy is one of the most important issues in the optimal use of resources worldwide. The combination of the circular economy and the supply chain created a new concept called the circular supply chain, which aimed to increase the efficiency of the supply chain through the optimal use of resources. At first, they identified the effective factors in the cyclical supply chain and determined the weights of these factors using the Analytical Hierarchy Process (AHP) method. Then, the impact intensity of each factor was calculated. In addition, by using the laboratory method of decision making and evaluation (DEMATEL), the correlation between the effective factors in the cyclical supply chain and their effectiveness was analyzed. Finally, using the simple additive weighting (SAW), the most important factors in implementing a cyclical supply chain were identified. The main results of their research showed that the quality of final products was the most important factor in the implementation of the cyclical supply chain. In addition, adopting a circular economy approach contributed to the goal of zero waste production and could increase the efficiency of supply chains. Chen et al. [37] proposed an intuitive fuzzy approach for assessing the risk of epidemic resurgence in the COViD-19 prevention period. In their paper, the objective was to provide an integrated Interval-Valued Intuitionistic Fuzzy (IVIF) method for intelligent risk assessment based on DEMATEL (Decision-Making Trial and Evaluation Laboratory), BWM (best–worst Method), and SPA (Set Pair Analysis). This integrated technique is named IVIF-DBWM-SPA, where IVIF-DEMATEL and IVIF-BWM are used to determine the overall weights of dimensions and criterion weights in each dimension. In the IVIF-BWM method, two bi-objective programming models are developed considering the perspectives of both pessimistic and optimistic experts. By simultaneously considering the intrapersonal and interpersonal uncertainties of experts, a bi-objective programming model is proposed to determine the dynamic weights of experts. Using the determined weights for experts and criteria, an IVIF-SPA is developed to assess the risk levels of all alternatives. The validity of the proposed method is demonstrated with a real case of risk assessment for the resurgence of a university during the COVID-19 period. Additionally, sensitivity and comparative analyses are presented to illustrate the advantages of the proposed approach. A summary of the literature review is shown in Table 1.

Table 1. Literature review. Note. The asterisk-marked items indicate the use of the component utilized in the table.

Author	Aim	Dimensions			Uncertainty	Methods	Case Study
		Economic	Environmental	Social impacts
[22]	Evaluation and selection of transportation projects	*	*			AHP/Goal Programming	Rail systems
[23]	Evaluation and selection of transportation projects	*	*			ANP	Rail systems
[24]	Evaluation and selection of transportation projects	*	*			AHP/BWM	Istanbul Railway
[25]	Evaluation and selection of projects according to sustainability criteria	*				AHP/hesitant fuzzy linguistic	Solar power plant
[26]	Project evaluation and selection	*				TOPSIS-OPA/K-means	Refinery
[32]	Project evaluation and selection	*				Fuzzy AHP/Fuzzy TOPSIS	Iraq oil industry
[27]	A new multi-criteria group decision-making approach		*			G-BWM	supply chain
[17]	A hybrid multi-criteria decision-making approach		*		*	AHP-TOPSIS- MOMILP	supply chain
[28]	Development of best–worst trapezoidal fuzzy method					GITrF BWM	---
[29]	Development of best–worst triangular fuzzy method					Novel Fuzzy BWM	---
[30]	Development of best–worst triangular fuzzy method					IFBWM	---
[33]	Evaluating and selecting startup projects with digital transformation	*				FAHP—ZODP	Thailand software projects
[38]	Evaluation and strategic selection of projects in technology consulting organization	*			*	THOR	Software projects
[31]	Identifying the most important factors affecting the selection of the project portfolio	*				Mathematical Models	---
[34]	Designing a hybrid decision support model under uncertainty		*	*	*	K-means—BWM	Choosing a landfill site
[9]	Data-driven evaluation and selection of telecom industry projects	*		*		FBWM-DEA-Random Forest	Telecom industry
[35]	Evaluation of production industry projects with lean six sigma approach	*	*			Antropi—TOPSIS—VIKOR	Indian manufacturing industries
[36]	Evaluation of factors affecting the cyclical supply chain	*	*			AHP- DEMATEL-SAW	supply chain
[37]	Assessing the risk of epidemic resumption during the period of prevention of COVID-19					IVIF-BWM—IVIF-DEMATEL—IVIF-SPA	COVID-19
This Study	Evaluation of plans and mega-projects of rail development at the national level	*	*	*	*	Fuzzy BWM—Stochastic VIKOR	Rail transportation projects

According to the studies carried out in the research literature, a summary of which is shown in Table 1, it is observed that there is a study that evaluates the national macro projects in the field of rail transportation, taking into account the three economic, social, and environmental dimensions, which are the dimensions of sustainability. Therefore, simultaneous consideration of these dimensions in the evaluation of projects has innovation. On the other hand, considering that the amount of demand of projects in the completion stage and also the costs of implementing projects have uncertainty and are different under different scenarios, considering this uncertainty has not been found in any study. Therefore, considering uncertainty in the evaluation of projects is also innovative, which is addressed in this study, and a new method is presented. In general, the contributions of the current research can be summarized as follow:

• Simultaneously considering the dimensions of sustainability, including economic, social, and environmental aspects in the evaluation of projects: in studies related to the evaluation of projects related to rail transportation, financial and environmental indicators are often considered, but social indicators are also important, especially in national macro-projects that examine the amount of job creation and contribution to the local economy.
• Considering the uncertainty of demand and cost in the evaluation of project: in the evaluation of projects, due to the existence of various conditions and various uncertainties, the amount of spending and income generation of projects varies, which can greatly affect the evaluation of projects that has been addressed in this study.
• Providing a new stochastic multi-criteria decision-making approach to deal with uncertainty.

3. Methods

The present study consists of several steps, which are explained in this section. First, using the fuzzy best–worst method (FBWM), the weight of project evaluation indicators is identified. Then, using the stochastic VIKOR approach, the projects will be evaluated and analyzed in different scenarios, and, finally, the final prioritization of the projects will be presented. It should be noted that the stochastic VIKOR method is presented for the first time in this study.

3.1. Fuzzy Best–Worst Method (FBWM)

The fuzzy best–worst method (FBWM) is a fuzzy decision-making method, in which alternatives are evaluated based on the opinions of users or experts [39]. This method is useful for analyzing and prioritizing elements when detailed information is not available or the elements are fuzzy and ambiguous [39,40]. FBWM is a practical and suitable method for analysis and decision making when the elements are fuzzy and ambiguous and users’ opinions about the importance and performance of the elements are needed [29]. In this research, we employ the FBWM proposed [29] that has the following steps.

Step 1:

Determining a set of decision criteria ($C=\left\{c1,c2,c3,...,cn\right\}$).

Step 2:

Determining the best criterion (CB) and the worst criterion (Cw).

Step 3:

Forming the fuzzy comparison vectors between best criterion and other criteria that is denoted by ${\tilde{A}}_B=\left[{\tilde{a}}_{B1},{\tilde{a}}_{B2},\dots , {\tilde{a}}_{Bn}\right]$ where ${\tilde{a}}_{B\mathrm{j}}=\left(a_{Bj}^l,a_{Bj}^m,a_{Bj}^u\right)$ and ${\tilde{a}}_{B\mathrm{B}}=\left(\mathrm{1,1},1\right)$.

Step 4:

Forming the fuzzy comparison vectors between worst criterion and other criteria that is denoted by ${\tilde{A}}_w=\left[{\tilde{a}}_{1w},{\tilde{a}}_{2w},\dots , {\tilde{a}}_{nw}\right]$ where ${\tilde{a}}_{\mathrm{j}\mathrm{w}}=\left(a_{jw}^l,a_{jw}^m,a_{jw}^u\right)$ and ${\tilde{a}}_{ww}=\left(\mathrm{1,1},1\right)$.

Step 5:

Determining the tolerance parameters ($d_j^t \mathrm{and} q_j^t$) based on preference of the decision maker (DM) and characteristics of the problem.

Step 6:

Based on the risk attitude of the DM, solve one of the optimistic, pessimistic, or mixed approaches. The mathematical model of each model presented in [29].

Step 7:

Calculating the fuzzy deviation denoted by ${\tilde{\xi }}^{*}=\left({\xi }^{*l},{\xi }^{*m},{\xi }^{*u}\right)$ (see [29] to understand the calculation process).

Step 8:

Obtaining the fuzzy consistency index (FCI) based on procedure explained in [29].

Step 9:

Computing the GMIR (graded mean integration representation) based on procedure explained in [12].

Step 10:

Check the consistency. In this step, there are several principles provided in [29] that should be examined.

3.2. Stochastic VIKOR

The VIKOR method is a consensus solution and multi-criteria optimization. VIKOR was first introduced by Aprikovich in 1998 to solve multi-criteria decision problems and achieve the best possible solution. This method is used to rank and select options according to a set of different indicators. The main goal of the VIKOR method is to bring most of the options closer to the ideal answer in each index so that the options are ranked based on this goal [41].

Various approaches have been presented for the VIKOR method, for example, the fuzzy VIKOR approach, gray VIKOR, and various other examples of these cases. In this study, the stochastic VIKOR approach is presented for the first time. In this method, different scenarios are designed, each scenario has a specific weight, and based on different scenarios, the final weight of the options is determined. In other words, choosing the optimal option is based on different conditions and scenarios ahead, and this way, we will be closer to the optimal solution in the real world. The steps of the stochastic VIKOR method are as follows:

• Forming the decision matrix: At this stage, the decision matrix of the stochastic VIKOR method is formed. In this regard, it should be noted that the nature of the stochastic VIKOR method is based on the evaluation of options in different scenarios. Therefore, the decision matrix is also formed based on the scenario. Suppose $Sr=\left\{{sr}_1, {sr}_2, \dots , {sr}_s\right\}$ represents the set of scenarios of the desired problem, where ${Ps}_s$ is the probability of the occurrence of scenario s. On the other hand, suppose $C=\{c_1, c_2, \dots , c_i\}$ is the set of criteria of the desired problem and $A=\{a_1, a_2, \dots , a_j\}$ is also the set of studied options. Considering $x_{jis}$ as the score of option $j$ in criterion $i$ under scenario $s$, the decision matrix of the stochastic VIKOR method can be defined as follows. It should be noted that if there are several decision makers, the decision matrices can be averaged considering Table 2.
  Table 2. Decision matrix of VIKOR.

  	${\mathit{c}}_1$			${\mathit{c}}_2$			$\dots$	${\mathit{c}}_{\mathit{i}}$
  	${\mathit{s}\mathit{r}}_1$	$\dots$	${\mathit{s}\mathit{r}}_{\mathit{s}}$	${\mathit{s}\mathit{r}}_1$	$\dots$	${\mathit{s}\mathit{r}}_{\mathit{s}}$		${\mathit{s}\mathit{r}}_1$	$\dots$	${\mathit{s}\mathit{r}}_{\mathit{s}}$
  $a_1$	$x_{111}$	$\dots$	$x_{11s}$	$x_{121}$	$\dots$	$x_{12s}$	$\dots$	$x_{1i1}$	$\dots$	$x_{1is}$
  $a_2$	$x_{211}$	$\dots$	$x_{21s}$	$x_{221}$	$\dots$	$x_{22s}$	$\dots$	$x_{2i1}$	$\dots$	$x_{2is}$
  $⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$	$⋮$
  $a_j$	$x_{j11}$	$\dots$	$x_{j1s}$	$x_{j21}$	$\dots$	$x_{j2s}$	$\dots$	$x_{ji1}$	$\dots$	$x_{jis}$

2.

Normalize the decision matrix

In the second step, the formed decision matrix is normalized or unscaled. Normalizing the decision matrix can be performed in different ways; the present research used the following method.

$$n_{jis}=\frac{x_{jis}}{\sqrt{x_{jis}^2}}$$

(1)

3.

Forming the weighted normalized decision matrix: At this stage, in order to calculate the weighted normalized matrix, each column of the scenario is multiplied by the probability of its similar occurrence (${Ps}_s$) and by the weight of the corresponding criterion. Assuming $W=\left\{{w_1,w_2, \dots ,w}_i\right\}$ as the set of criteria weights, the weighted normalized decision matrix is calculated as follows.

$$f_{jis}={Ps}_s\times n_{jis}\times w_i$$

(2)

4.

Determining the positive and negative ideal point: In the fourth step, positive ideal and negative ideal points are identified. For this purpose, if the criterion is a positive criterion (the more the better), the positive ideal value for each scenario is equal to the largest value in the column of that scenario. On the other hand, if the criterion is a negative criterion (the lower the better), the positive ideal value for each scenario is equal to the smallest value in the column for that scenario. This process is opposite for the negative ideal answer. For example, if the criterion is positive, the ideal positive and negative answers can be calculated as follows.

$$f_s^{+}=\max \left\{f_{ijs}\right\}$$

(3)

$$f_s^{-}=\min \left\{f_{ijs}\right\}$$

(4)

5.

Calculation of utility (${SS}_j$) and regret ($R_j$) values for each indicator: In this step, the values of usefulness and regret are calculated using the following relationships.

$$L_{js}={\sum }_i\frac{f_s^{+}-f_{ijs}}{f_s^{+}-f_s^{-}}$$

(5)

$${SS}_j={\sum }_s{Ps}_s\times L_{js}$$

(6)

$$T_{js}=\underset{i}{\max }\left\{\frac{f_s^{+}-f_{ijs}}{f_s^{+}-f_s^{-}}\right\}$$

(7)

$$R_j=\sum _s{Ps}_s\times T_{js}$$

(8)

6.

Calculation of VIKOR index values ($Q_j$): In this step, the value of the $Q_j$ index is calculated according to the following relationship. It should be noted that $v$ is collective utility.

$$Q_j=v\times \left[\frac{{SS}_j-{SS}^{*}}{{SS}^{-}-{SS}^{*}}\right]+\left(1-v\right)\times \left[\frac{R_j-R^{*}}{R^{-}-R^{*}}\right]$$

(9)

$${SS}^{-}=\max \left\{{SS}_j\right\},{SS}^{*}=\min \left\{{SS}_j\right\}$$

(10)

$$R^{-}=\max \left\{R_j\right\},R^{*}=\min \left\{R_j\right\}$$

(11)

The important thing is to calculate the $Q_j$ index in summing up all the scenarios, the value of the $Q_j$ index is multiplied by the probability of occurrence of each scenario, and the final $Q_j$ value is calculated by their sum.

7.

Sort options by $Q_j$, $R_j$, and ${SS}_j$ values: The alternatives are sorted in descending order based on their ${SS}_j$, $R_j$, and $Q_j$ values. Alternative $a^{\prime }$ is proposed as a compromise solution, ranked as the best according to the value of $Q_j$ (minimum) and considering the following two conditions. The first condition is an acceptable advantage according to the following formula.

$$Q\left(a^{″}\right)-Q\left(a^{\prime }\right)\ge \frac{1}{i-1},i:number of alternatives$$

(12)

$a^{″}$ alternative with the second position in the $Q_j$ ranking list.

The second condition is acceptance of acceptable stability in decision making. Alternative $a^{\prime }$ must also have the highest rank in the ranking list S and R or both. Such an agreement remains constant in the decision-making process.

If one of the two conditions is not met, a set of agreed solutions is proposed:

Alternatives $a^{\prime }$ and $a^{″}$ if only the second condition is not fulfilled.

Alternatives $a^{\prime },a^{″},a^{‴},\dots ,a^m$ if the first condition is not met.

$a^m$ is determined using the following equation for the maximum value of m.

$$Q\left(a^m\right)-Q\left(a^{\prime }\right)\left(\frac{1}{i-1}\right)$$

(13)

3.3. Hybrid Method

In order to specify the method used in this study, the steps of the research are shown in Figure 1.

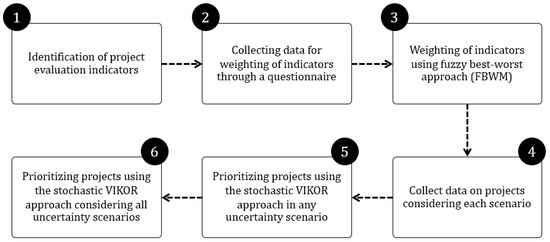
Figure 1. Proposed steps.

The main advantages of the proposed combined method include the following:

• Considering the uncertainty in the evaluation process, which causes things, like cost changes, demand changes, and time changes, to be involved in evaluating.
• No limitation of scenario definition in the proposed method is one of its advantages. In the defined method, it is possible to define scenarios and evaluate projects based on them.
• Combining this method with Fuzzy BWM makes the weight of the indicators more accurately identified to be used in the evaluation of projects in each scenario.

4. Case Study

The present study is about the evaluation of national rail transportation projects in Iran. These projects are in the form of railway line development in different regions of the country, construction of new railways, electrification and updating of existing railways, and development of existing railway technologies. In general, there have been 11 projects evaluated according to the desired research indicators. The project evaluation indicators are categorized into three, economic, social, and environmental, for the case study, and there are 15 indicators in total, as described in Table 3, Table 4 and Table 5. These indicators were finalized using the literature review and expert opinions.

Table 3. Economic criteria.

Row	Criterion	Description	Reference
C1	Investment cost	The cost of studying and implementing the infrastructure, pavement, signs and communications and building stations of a railway project	[22,23]
C2	National Internal Rate of Return (IRR)	IRR or “Internal Rate of Return” is an index in financial analysis. This index is used to estimate the profitability of investment from a national perspective.	[23]
C3	Reducing casualties and road accidents	Transferring cargo and passengers from the road to the railway will reduce road accidents and casualties.	[23,24]
C4	Strengthening the country’s international status and transit	Considering the geopolitical position of our country, it is important to create rail corridors in order to strengthen the country’s transit position.	[23]
C5	Internal rate of return (IRR) from the perspective of the private sector	IRR or “Internal Rate of Return” is an index in financial analysis. This index is used to estimate the profitability of investment from the perspective of the private sector.	[31,32]
C6	Fuel consumption saving	Transporting cargo and passengers from the road to the railway will save fuel consumption.	[23,24]
C7	The amount of traffic	The amount of traffic of each railway axis and the average amount of traffic expected in the rail network	[23,24]

Table 4. Social criteria.

Row	Criterion	Description	Reference
C8	Creating social justice and removing deprivation	Creating social justice and satisfaction in the proportional distribution of transportation infrastructure in order to benefit the members of the society and regions of the country from the railway.	[35]
C9	Providing employment, especially in deprived areas	The construction of transportation infrastructure will create employment in the period of construction and operation directly and create and develop other jobs indirectly.	[9]
C10	The possibility of developing the plan to cover other regions of the country	The feasibility of extending the route of a railway project to cover other parts of the country prone to the rail network (such as the Isfahan-Shiraz railway, which enables the extension of Shiraz to Bushehr port)	[15]
C11	Facilitating people’s rail travel	Facilitating the movement of passengers, especially in areas with limited transportation network	[9]
C12	Improving the correlation between the economic and social centers of the country	Connection and solidarity and synergy of economic and social centers to each other and increasing national solidarity	[9]

Table 5. Environmental criteria.

Row	Criterion	Description	Reference
C13	Reducing environmental pollutants	As green transportation, rail transportation will cause less environmental pollution in exchange for transporting cargo or passengers per unit length.	[24,35]
C14	Less effect on environmental change and destruction	The lower level of environmental destruction and the ecosystem of the region according to the region and the climate of the implementation of the project	[23]
C15	Creating pollution in the implementation of the project	It expresses the amounts of environmental pollutants produced during the implementation of the project.	[23,24]

The criteria tree is also shown in Figure 2.

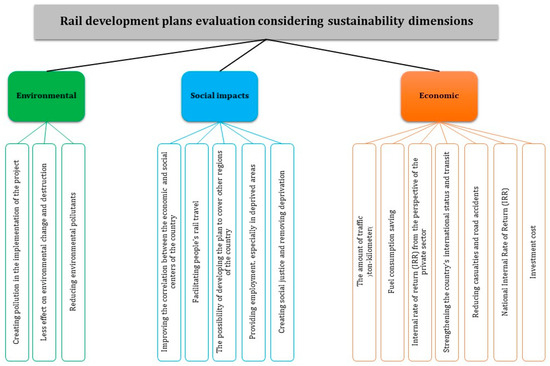
Figure 2. Decision tree.

5. Results

5.1. Calculating the Indicators’ Weights

This section is dedicated to computing the weights of the indicators using the FBWM. In this regard, we consider three groups of experts, dispatch the pairwise comparison questionnaire among them, and use the average of the gathered data to implement the FBWM. For example, Table 6 shows the pairwise comparison vector between the best criteria and other ones, and Table 7 demonstrates the pairwise comparison vector between the worst criteria and other ones. The comparison vectors for other indicators are provided in the Supplementary Materials. The FBWM method was implemented; the weights of the criteria and sub-criteria are presented in Table 8. In addition, Table 9 shows the values of CR for each step. Based on this table, for all steps, the value of CR is close to zero, demonstrating the reliability of the outputs.

Table 6. The best-to-others vector.

Expert	Best Criteria	Economic			Social			Environmental
1	Economic	1	1	1	2.5	3	3.5	3.5	4	4.5
2		1	1	1	2.5	3	3.5	2.5	3	3.5
3		1	1	1	0.67	1	1.5	1.5	2	2.5

Table 7. The others-to-worst vector.

		Worst Criteria: Environmental
	Expert	1	2	3
Critreia
Economic		2.5	3	3.5
		1.5	2	2.5
		1.5	2	2.5
Social		1	1	1
		1	1	1
		1	1	1
Environmental		1	1	1
		1	1	1
		1.5	2	2.5

Table 8. The weights of the criteria and sub-criteria.

Criteria	Weight of Criteria	Sub-Criteria	Initial Weight of Sub-Criteria	Final Weight	Sub-Criteria Code
Economic	0.54925	Investment cost	0.26295	0.14443	C1
		National Internal Rate of Return (IRR)	0.22775	0.12509	C2
		Reducing casualties and road accidents	0.09613	0.05280	C3
		Strengthening the country’s international status and transit	0.10106	0.05551	C4
		Internal rate of return (IRR) from the perspective of the private sector	0.07169	0.03938	C5
		Fuel consumption saving	0.10075	0.05534	C6
		The amount of traffic (ton-kilometer)	0.13967	0.07671	C7
Social	0.24176	Creating social justice and removing deprivation	0.28659	0.06929	C8
		Providing employment, especially in deprived areas	0.12064	0.02917	C9
		The possibility of developing the plan to cover other regions of the country	0.18764	0.04536	C10
		Facilitating people’s rail travel	0.19397	0.04689	C11
		Improving the correlation between the economic and social centers of the country	0.21115	0.05105	C12
Environmental	0.20897	Reducing environmental pollutants	0.31120	0.06503	C13
		Less effect on environmental change and destruction	0.43389	0.09067	C14
		Creating pollution in the implementation of the project	0.25492	0.05327	C15

Table 9. The values of the CR.

Step	CR
Criteria	0.022435
Economic sub-criteria	0.003542
Social sub-criteria	0.006541
Environmental sub-criteria	0.003547

It can be seen that among the indicators, economic index is by far the most important index, followed by social and, finally, environmental indicators. Among the sub-indices, the investment cost, internal return rate from the national perspective, the impact on the damage of the plan area, and the amount of traffic are the most important indicators. According to this weighting, in the next step, the projects are prioritized according to different scenarios and collectively.

5.2. Ranking the Projects

In this section, potential projects are prioritized using a random Vikor approach. In this regard, it should be mentioned that in order to prioritize these items and according to the environmental conditions of the projects, different scenarios are considered in the evaluations. Considering the economic challenges, one of the important scenarios is cost changes. The approach is that, due to various reasons, the prices and costs of the project may be overestimated, which increases the costs, and, vice versa, there is a possibility that the implementation costs may be reduced. By examining the opinions of experts, a frequency range of 30% of costs is considered to cover the scenario of cost changes, and the probability of project implementation in a critical state is 50%, project implementation with 30% less than the estimated cost is 15%, and project implementation with 30% more than the estimated cost is 35%. Therefore, in summary, in Table 9, the sub-scenarios of cost increase can be examined. Table 10 shows the scenario of cost changes.

Table 10. Cost change scenarios.

Scenario	Probability	Scenario of Cost Changes
S1-1	15%	Optimistic: project implementation with 30% lower cost than estimated
S1-2	50%	Probable: implementation of the project with the estimated cost
S1-3	35%	Pessimistic: Project implementation with 30% more cost than estimated

Another influential scenario in decision making for the selection of railway development projects and plans is the level of demand. This amount of demand is based on passenger and cargo demand. In this regard, three sub-scenarios were considered for this scenario to be realized, with a probability of 50% of the estimated demand. With a probability of 25%, about 30% more than the fulfilled demand is realized, and with a probability of 25%, about 30% less than the fulfilled demand is realized. According to the explanations given in Table 10, the specifications of the scenario of demand changes can be seen. Table 11 shows the scenario of demand changes.

Table 11. Demand changes scenarios.

Scenario	Probability	Scenario Demand Changes
S2-1	25%	Optimistic: project implementation with 30% lower demand than estimated
S2-2	50%	Probable: implementation of the project with the estimated demand
S2-3	25%	Pessimistic: Project implementation with 30% more demand than estimated

5.2.1. Scenario of Cost Changes

Table 12 shows the decision matrix for the SVIKOR method. Also, Table 13 shows the ranking of the alternative based on the SVIKOR outputs. According to this table, alternatives P4, P10, and P3 were selected as the best ones. It should be noted that the calculation process, such as normalized decision matrix, values of f+ and f−, etc., is provided in the Supplementary Materials in Tables SB.1–SB.5.

Table 12. The decision matrix of cost-changing scenario.

	S1-1	S1-2	S1-3	S1-1	S1-2	S1-3	S1-1	S1-2	S1-3
	C1			C2			C3
P1	0.0090416	0.0063291	0.0048685	0.16	0.12	0.09	122,268	122,268	122,268
P2	0.0255102	0.0178571	0.0137363	0.20	0.16	0.13	77,539	77,539	77,539
P3	0.0048426	0.0033898	0.0026076	0.10	0.07	0.05	136,877	136,877	136,877
P4	0.0086580	0.0060606	0.0046620	0.22	0.17	0.14	186,397	186,397	186,397
P5	0.0144300	0.0101010	0.0077700	0.18	0.14	0.11	90,842	90,842	90,842
P6	0.0051948	0.0036364	0.0027972	0.10	0.07	0.05	124,293	124,293	124,293
P7	0.0034758	0.0024331	0.0018716	−0.01	−0.02	−0.03	39,828	39,828	39,828
P8	0.0062383	0.0043668	0.0033591	0.16	0.12	0.09	202,564	202,564	202,564
P9	0.0160514	0.0112360	0.0086430	0.12	0.08	0.06	51,538	51,538	51,538
P10	0.0039032	0.0027322	0.0021017	0.10	0.07	0.05	152,209	152,209	152,209
P11	0.0017507	0.0012255	0.0009427	0.18	0.13	0.10	667,207	667,207	667,207
	C4			C5			C6
P1	1465	1465	1465	−0.05	−0.06	−0.06	2170.18	2170.18	2170.18
P2	366	366	366	−0.05	−0.05	−0.05	1376.26	1376.26	1376.26
P3	448	448	448	−0.05	−0.05	−0.06	2429.48	2429.48	2429.48
P4	1465	1465	1465	−0.01	−0.02	−0.03	3308.44	3308.44	3308.44
P5	61	79	61	−0.06	−0.06	−0.06	1612.38	1612.38	1612.38
P6	49	49	49	−0.06	−0.06	−0.06	2206.12	2206.12	2206.12
P7	733	733	733	−0.06	−0.06	−0.06	706.92	706.92	706.92
P8	692	692	692	−0.05	−0.05	−0.06	3595.38	3595.38	3595.38
P9	33	33	33	−0.06	−0.06	−0.06	914.77	914.77	914.77
P10	1465	1465	1465	−0.03	−0.04	−0.04	2701.61	2701.61	2701.61
P11	529	529	529	−0.03	−0.04	−0.05	11,842.49	11,842.49	11,842.49
	C7			C8			C9
P1	658.13	658.13	658.13	1.00	1.00	1.00	195.00	195.00	195.00
P2	781.30	781.30	781.30	5.00	5.00	5.00	312.00	312.00	312.00
P3	2025.00	2025.00	2025.00	6.00	6.00	6.00	540.00	540.00	540.00
P4	3769.60	3769.60	3769.60	10.00	10.00	10.00	729.60	729.60	729.60
P5	495.60	495.60	495.60	3.00	3.00	3.00	201.60	201.60	201.60
P6	1380.00	1380.00	1380.00	4.00	4.00	4.00	414.00	414.00	414.00
P7	715.00	715.00	715.00	4.00	4.00	4.00	660.00	660.00	660.00
P8	1680.00	1680.00	1680.00	5.00	5.00	5.00	268.80	268.80	268.80
P9	563.50	563.50	563.50	4.00	4.00	4.00	386.40	386.40	386.40
P10	4725.00	4725.00	4725.00	10.00	10.00	10.00	1080.00	1080.00	1080.00
P11	10,793.00	10,793.00	10,793.00	8.00	8.00	8.00	602.40	602.40	602.40
	C10			C11			C12
P1	7.00	7.00	7.00	130	130	130	5.00	5.00	5.00
P2	6.00	6.00	6.00	572	572	572	5.00	5.00	5.00
P3	8.00	8.00	8.00	630	630	630	8.00	8.00	8.00
P4	6.00	6.00	6.00	699	699	699	8.00	8.00	8.00
P5	4.00	4.00	4.00	50	50	50	4.00	4.00	4.00
P6	6.00	6.00	6.00	863	863	863	6.00	6.00	6.00
P7	4.00	4.00	4.00	385	385	385	5.00	5.00	5.00
P8	2.00	2.00	2.00	448	448	448	4.00	4.00	4.00
P9	2.00	2.00	2.00	209	209	209	2.00	2.00	2.00
P10	7.00	7.00	7.00	1305	1305	1305	7.00	7.00	7.00
P11	5.00	5.00	5.00	828	828	828	7.00	7.00	7.00
	C13			C14			C15
P1	6255.33	6255.33	6255.33	1.00	1.00	1.00	2.00	2.00	2.00
P2	3966.94	3966.94	3966.94	6.00	6.00	6.00	5.00	5.00	5.00
P3	7002.72	7002.72	7002.72	6.00	6.00	6.00	5.00	5.00	5.00
P4	9536.23	9536.23	9536.23	9.00	9.00	9.00	9.00	9.00	9.00
P5	4647.53	4647.53	4647.53	5.00	5.00	5.00	5.00	5.00	5.00
P6	6358.92	6358.92	6358.92	5.00	5.00	5.00	5.00	5.00	5.00
P7	2037.63	2037.63	2037.63	5.00	5.00	5.00	4.00	4.00	4.00
P8	10,363.33	10,363.33	10,363.33	4.00	4.00	4.00	5.00	5.00	5.00
P9	2636.73	2636.73	2636.73	5.00	5.00	5.00	4.00	4.00	4.00
P10	7787.12	7787.12	7787.12	9.00	9.00	9.00	8.00	8.00	8.00
P11	34,134.78	34,134.78	34,134.78	5.00	5.00	5.00	5.00	5.00	5.00

Table 13. The outputs of the SVIKOR method for the cost-changing scenario.

	Qj	Rank
P1	0.9103212	8
P2	0.7132548	5
P3	0.4625487	3
P4	0	1
P5	0.9658451	9
P6	0.8132564	6
P7	0.9789854	10
P8	0.8654845	7
P9	1	11
P10	0.3232516	2
P11	0.5235154	4

5.2.2. Demand Changes Scenario

Table 14 shows the decision matrix of this scenario. Also, Table 15 shows the ranking of the alternative based on the SVIKOR outputs. According to Table 15, alternatives P4, P3, and P10 were selected as the best ones. It should be noted that the calculation process, such as normalized decision matrix, values of f+ and f−, etc., is provided in the Supplementary Materials in Tables SC.1–SC.5.

Table 14. The decision matrix of demand-changing scenario.

	S2-1	S2-2	S2-3	S2-1	S2-2	S2-3	S2-1	S2-2	S2-3
	C1			C2			C3
P1	0.0057816	0.0044474	0.0057816	0.08	0.09	0.15	105,281	150,402	195,523
P2	0.0163125	0.0125481	0.0163125	0.12	0.13	0.19	66,766	95,380	123,994
P3	0.0034759	0.0026738	0.0034759	0.04	0.05	0.09	135,107	193,010	250,913
P4	0.0055364	0.0042587	0.0055364	0.12	0.14	0.20	197,035	281,479	365,922
P5	0.0092273	0.0070979	0.0092273	0.10	0.11	0.17	78,221	111,744	145,268
P6	0.0033218	0.0025552	0.0033218	0.04	0.05	0.09	107,025	152,893	198,761
P7	0.0025112	0.0019317	0.0025112	−0.03	−0.03	−0.01	31,507	45,010	58,513
P8	0.0039891	0.0030685	0.0039891	0.09	0.09	0.15	174,422	249,174	323,926
P9	0.0102640	0.0078954	0.0102640	0.05	0.06	0.11	44,378	63,397	82,416
P10	0.0024959	0.0019199	0.0024959	0.04	0.05	0.09	131,062	187,232	243,402
P11	0.0011195	0.0008611	0.0011195	0.09	0.10	0.16	574,512	820,731	106,6950
	C4			C5			C6
P1	1058.46048	1512.0864	1965.71232	−0.06	−0.06	−0.05	1606.32407	2294.74867	2983.17327
P2	264.61512	378.0216	491.42808	−0.06	−0.05	−0.04	1018.68208	1455.26011	1891.83814
P3	332.82018	475.4574	618.09462	−0.06	−0.06	−0.05	1849.26975	2641.81393	3434.35811
P4	1161.02448	1658.6064	2156.18832	−0.04	−0.03	−0.01	2680.42877	3829.18395	4977.93914
P5	81.90468	63.0036	81.90468	−0.06	−0.06	−0.06	1193.4526	1704.93228	2216.41196
P6	35.282016	50.40288	65.523744	−0.06	−0.06	−0.06	1632.92726	2332.75322	3032.57919
P7	554.87124	792.6732	1030.47516	−0.06	−0.06	−0.06	528.198374	754.569106	980.939838
P8	499.82856	714.0408	928.25304	−0.06	−0.06	−0.05	2661.23207	3801.7601	4942.28813
P9	23.521344	33.60192	43.682496	−0.07	−0.06	−0.06	677.092767	967.275382	1257.458
P10	1058.46048	1512.0864	1965.71232	−0.05	−0.04	−0.03	1999.67718	2856.68169	3713.68619
P11	382.22184	546.0312	709.84056	−0.05	−0.05	−0.04	8765.57424	12522.2489	16278.9236
	C7			C8			C9
P1	470.362	671.946	873.529	1.00	1.00	1.00	195	195	195
P2	558.395	797.707	1037.019	5.00	5.00	5.00	312	312	312
P3	1447.268	2067.525	2687.783	6.00	6.00	6.00	540	540	540
P4	2694.133	3848.762	5003.390	10.00	10.00	10.00	730	730	730
P5	3.157	4.510	5.863	3.00	3.00	3.00	202	202	202
P6	8.791	12.558	16.325	4.00	4.00	4.00	414	414	414
P7	4.555	6.507	8.458	4.00	4.00	4.00	660	660	660
P8	10.702	15.288	19.874	5.00	5.00	5.00	269	269	269
P9	3.589	5.128	6.666	4.00	4.00	4.00	386	386	386
P10	30.098	42.998	55.897	10.00	10.00	10.00	1080	1080	1080
P11	68.751	98.216	127.681	8.00	8.00	8.00	602	602	602
	C10			C11			C12
P1	8	8	8	91	130	169	5.00	5.00	5.00
P2	7	7	7	400	572	744	5.00	5.00	5.00
P3	9	9	9	441	630	819	8.00	8.00	8.00
P4	7	7	7	489	699	909	8.00	8.00	8.00
P5	4	4	4	35	50	66	4.00	4.00	4.00
P6	7	7	7	604	863	1121	6.00	6.00	6.00
P7	4	4	4	270	385	501	5.00	5.00	5.00
P8	2	2	2	314	448	582	4.00	4.00	4.00
P9	2	2	2	147	209	272	2.00	2.00	2.00
P10	8	8	8	914	1305	1697	7.00	7.00	7.00
P11	6	6	6	580	828	1077	7.00	7.00	7.00
	C13			C14			C15
P1	4033	5761	7490	1.00	1.00	1.00	2.00	2.00	2.00
P2	2557	3654	4750	6.00	6.00	6.00	5.00	5.00	5.00
P3	4662	6660	8657	6.00	6.00	6.00	5.00	5.00	5.00
P4	6615	9450	12,286	9.00	9.00	9.00	9.00	9.00	9.00
P5	2996	4280	5564	5.00	5.00	5.00	5.00	5.00	5.00
P6	4100	5857	7614	5.00	5.00	5.00	5.00	5.00	5.00
P7	1314	1877	2440	5.00	5.00	5.00	4.00	4.00	4.00
P8	6681	9545	12,408	4.00	4.00	4.00	5.00	5.00	5.00
P9	1700	2428	3157	5.00	5.00	5.00	4.00	4.00	4.00
P10	5020	7172	9324	9.00	9.00	9.00	8.00	8.00	8.00
P11	22,007	31,438	40,870	5.00	5.00	5.00	5.00	5.00	5.00

Table 15. The outputs of the SVIKOR method for the demand-changing scenario.

	Qj	Rank
P1	0.9232151	8
P2	0.5951321	4
P3	0.2032154	2
P4	0.1325411	1
P5	0.9352132	9
P6	0.8651423	6
P7	0.9523251	10
P8	0.906854	7
P9	1	11
P10	0.5565411	3
P11	0.6032151	5

5.2.3. Integration of Scenarios

In this, the alternatives are ranked based on the integrated scenarios. Since the probability of occurrence of each of the scenarios is 50%, the value of the VIKOE index ($Q$) was calculated for the projects in Table 16. According to the obtained results, alternatives P4, P3, P10, and P11 are the best ones.

Table 16. Ranking of the alternative in the integrated scenario.

	Cost Changes Scenario		Demand Changes Scenario		Integration of Scenarios
	Qj	Rank	Qj	Rank	Qj	Rank
P1	0.9103212	8	0.9232151	8	0.916768	8
P2	0.7132548	5	0.5951321	4	0.654193	5
P3	0.4625487	3	0.2032154	2	0.332882	2
P4	0	1	0.1325411	1	0.066271	1
P5	0.9658451	9	0.9352132	9	0.950529	9
P6	0.8132564	6	0.8651423	6	0.839199	6
P7	0.9789854	10	0.9523251	10	0.965655	10
P8	0.8654845	7	0.906854	7	0.886169	7
P9	1	11	1	11	1	11
P10	0.3232516	2	0.5565411	3	0.439896	3
P11	0.5235154	4	0.6032151	5	0.563365	4

5.3. Comparison of the Fuzzy Best–Worst Method in this Article

As stated in Section 3.1, this study utilized the extended fuzzy best–worst method [29]. In this section, this method is compared with fuzzy best–worst methods [42] and the simple best–worst method [40]. All three methods were applied to 10 different samples, and the results indicate that the obtained weights for various issues are almost similar (a sample is shown in Table 17). However, the CR in the method [29] is lower (shown in Figure 3), demonstrating its higher accuracy.

Table 17. Weighting of indicators using three methods in one of the examples.

Criteria	[40]	[42]	[29]
C1	0.26584	0.27170	0.26295
C2	0.22285	0.22776	0.22775
C3	0.09641	0.09439	0.09613
C4	0.09671	0.09884	0.10106
C5	0.07626	0.07093	0.07169
C6	0.09990	0.09884	0.10075
C7	0.14204	0.13761	0.13967

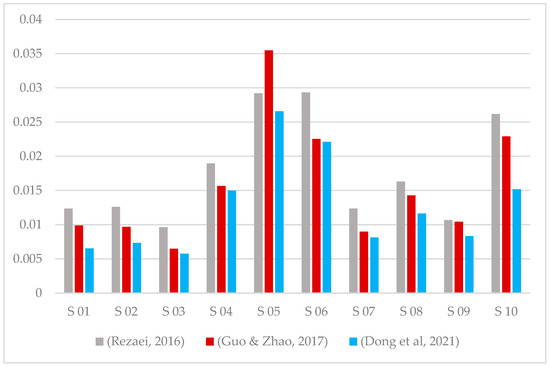
Figure 3. Comparison of CR in different examples using the three methods [29,40,42].

5.4. Validation of the Proposed Method

In order to validate the proposed random VIKOR method, the projects of this article were compared with VIKOR, Fuzzy VIKOR, and Fuzzy TOPSIS approaches so that the validity of the outputs of this method can be examined. Table 18 shows the ranking of projects in each method.

Table 18. Ranking projects based on different methods.

	Stochastic VIKOR	VIKOR	Fuzzy VIKOR	Fuzzy TOPSIS
P1	8	8	8	8
P2	5	5	5	5
P3	2	3	2	2
P4	1	1	1	1
P5	9	9	9	9
P6	6	6	6	6
P7	10	11	10	10
P8	7	7	7	7
P9	11	10	11	11
P10	3	2	3	3
P11	4	4	4	4

It can be seen that the findings of the Fuzzy VIKOR and Fuzzy TOPSIS methods are exactly the same as the SVIKOR method. However, the VIKOR approach has a slight difference in the evaluation of the two projects, which does not have a great impact on the final result. Therefore, in general, it can be seen that the results of SVIKOR are correct and accurate, and because it has the ability to define many scenarios, it is much more efficient than other approaches. In fuzzy or simple methods, necessarily, one number or finally a spectrum of three or four numbers (triangular and trapezoidal fuzzy numbers) can be provided for each index, which does not exist in SVIKOR.

5.5. Sensitivity Analysis for SVIKOR

An important parameter to analyze the sensitivity of the random Vikor method, which is presented for the first time, is the probability of the scenarios. In this regard, in this section, sensitivity analysis for different scenarios of cost changes and demand changes is examined. The most important component in the ranking of projects is the Q value of each project, which is observed for changes in the probability of scenarios. In the cost change scenario, the probability of occurrence of scenarios is 15%, 50%, and 35% for pessimistic, probable, and optimistic scenarios, respectively. In the other two cases, where the probability of the scenarios are equal, and in another case, where the scenarios are 80%, 10%, and 10%, respectively, for pessimistic, probable, and optimistic, it is checked, and the comparison of different cases is seen. In Figure 4, the value of Q is seen for different scenarios.

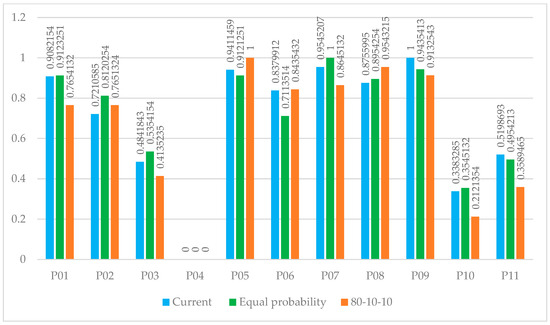
Figure 4. Sensitivity analysis on the probability of cost change scenarios.

It can be seen that by changing the probability of occurrence in each scenario for cost changes, the value of Q for the projects will change, and, with this approach, the ranking of the projects will also change. This problem shows that the presented method is sensitive to the possibility of scenarios and the ranking of projects will change with their change. Another considered mode is demand changes. In the scenario of demand changes, the probability of occurrence of the scenarios is 25%, 50%, and 25%, respectively, for pessimistic, probable, and optimistic scenarios. In two other cases, where the probability of occurrence of the scenarios is equal, and in the other case, where the scenarios are 10%, 10%, and 80% for pessimistic, probable, and optimistic respectively, the comparison of different cases is seen. In Figure 5, the value of Q is seen for different scenarios.

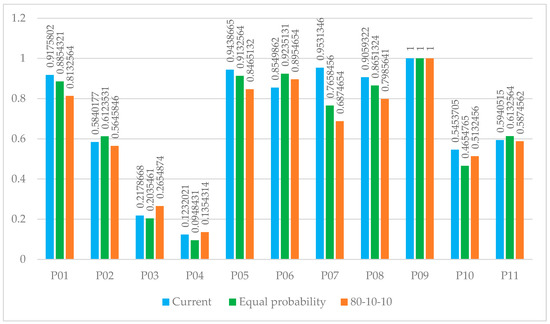
Figure 5. Sensitivity analysis on the probability of occurrence of demand change scenarios.

It can be seen that by changing the probability of occurrence of each scenario of demand changes, the value of Q for the projects will change, and, with the same approach, the ranking of the projects will also change. This problem shows that the presented method is sensitive to the possibility of scenarios, and the ranking of projects will change with their change.

6. Conclusions and Managerial Implications

This study presented a new approach to the evaluation and selection of rail transportation projects considering uncertainty. In various reviewed studies, multi-criteria decision-making approaches were used in project evaluation, but these approaches are based on expert opinions and sometimes fuzzy data [9,43]. In this study, the stochastic VIKOR approach is presented for the first time, so that uncertainty can be taken into account by considering different scenarios in the evaluation of projects. In this regard, due to the uncertainty in the implementation costs and also in the demand for the use of different selected projects, the scenarios of demand changes and cost changes are involved in the evaluation of the projects. The approach means that, by taking into account the changes in demand and the cost of the projects, the evaluations were carried out, and, finally, the ranking of the projects was presented. The presented stochastic VIKOR approach has an advantage over other methods in that it has the ability to define unlimited scenarios in the evaluation of projects. For this reason, it is more efficient than VIKOR, fuzzy VIKOR, and gray VIKOR approaches.

In terms of thematic aspects and evaluation criteria, economic, environmental, and social dimensions were integrated in the evaluation of projects, which were generally evaluated within the paradigm of project sustainability. Studies were conducted in the field of the evaluation of transportation projects that considered the economic and environmental components in an integrated manner [22,24], but a study that also examined the social dimension in the evaluation of transportation projects was not found in studies. Also, it is essential to consider uncertainty along with these dimensions in the evaluation of projects in today’s world, which is not considered in this study.

According to the findings of the article, it was observed that the most important indicators in the evaluation of rail transport projects are financial indicators. The main reason for this problem is the challenging economic conditions in Iran, in which, of course, the importance of financial indicators in the evaluation of projects in most developing countries has a stronger role than other dimensions [9]. For this reason, managers of organizations in developing countries should always emphasize the financial components of selected projects, through which they can provide more economic income for the country and organizations. After the economic dimension, the social dimension is important in developing countries. Since the problem of employment is abundant in these countries, large projects that have the power to generate employment for many groups are placed at higher priority. After the economic and social indicators, it is the turn of the environmental indicators to choose projects with minimum environmental destruction or having a better perspective of helping the environment as much as possible. In addition to the aspects of sustainability in the evaluation of projects, in today’s world, due to the extensive changes in the business environment, there are many uncertainties and risks in the context of projects [44]. These uncertainties are caused by economic changes, including inflation and exchange rates, political changes, changes in laws and regulations, and also the amount of demand for projects. For this reason, it is important to be able to identify the uncertainties in the evaluation of the projects before selecting them, and considering them, proceeding to examine the projects. In this regard, managers of organizations can use the approach developed in this study to evaluate projects by defining different scenarios. Since the presented random VIKOR method has no limit in defining the number of scenarios, managers can define different numbers of scenarios according to the conditions of the organization and evaluate projects based on them. Finally, it should be mentioned that evaluating rail transport projects using sustainability criteria and considering uncertainty in it help us to make better decisions in the field of project implementation. Considering that rail transport has significant effects on the environment, economy, and society, these assessments can provide a path for the sustainable development of rail transport.

In summarizing the findings of this study, it is suggested that due to the existence of wide uncertainties, especially in the field of project implementation costs, scenario-based approaches should always be used to choose a better project [45]. From the findings and the approach presented in this study, the managers of different organizations, especially project-oriented organizations, can use them well in evaluating potential projects. Multidimensionally evaluate your projects by defining multiple scenarios and also estimating the values of indicators in each scenario, as well as by determining the probability of the occurrence of each scenario. In the continuation of this research, it is suggested that this structure should be combined with data-oriented algorithms and approaches, and scenario-oriented models based on inference systems and machine learning algorithms will be presented with the aim of prospective evaluation.