Intelligent PV Panels Fault Diagnosis Method Based on NARX Network and Linguistic Fuzzy Rule-Based Systems

Abstract

The expanding use of photovoltaic (PV) systems as an alternative green source for electricity presents many challenges, one of which is the timely diagnosis of faults to maintain the quality and high productivity of such systems. In recent years, various studies have been conducted on the fault diagnosis of PV systems. However, very few instances of fault diagnostic techniques could be implemented on integrated circuits, and these techniques require costly and complex hardware. This work presents a novel and effective, yet small and implementable, fault diagnosis algorithm based on an artificial intelligent nonlinear autoregressive exogenous (NARX) neural network and Sugeno fuzzy inference. The algorithm uses Sugeno fuzzy inference to isolate and classify faults that may occur in a PV system. The fuzzy inference requires the actual sensed PV system output power, the predicted PV system output power, and the sensed surrounding conditions. An artificial intelligent NARX-based neural network is used to obtain the predicted PV system output power. The actual output power of the PV system and the surrounding conditions are obtained in real-time using sensors. The algorithm is proven to be implementable on a low-cost microcontroller. The obtained results indicate that the fault diagnosis algorithm can detect multiple faults such as open and short circuit degradation, faulty maximum power point tracking (MPPT), and conditions of partial shading (PS) that may affect the PV system. Moreover, radiation and temperature, among other non-linear associations of patterns between predictors, can be captured by the proposed algorithm to determine the accurate point of the maximum power for the PV system.

1. Introduction

During the previous decade, there has been an expanding enthusiasm for photovoltaic (PV) systems because of the numerous favorable circumstances resulting from these systems. Among such favorable circumstances are the unpolluted operation, the unlimited power resources, the overall simplicity of establishment, and the noiseless operation. Therefore, the size and number of PV systems has expanded quickly around the word [1]. PV panels produce electrical power that is proportional to the total amount of solar radiation received on their surface from the sun. This is normally denoted by the Global Horizontal Irradiance (GHI). Other factors, such as temperature, also affect the power produced from the photovoltaic panel. Nevertheless, during the operation of photovoltaic systems under evolving and complex climate conditions, faults have always been among the critical factors affecting the performance of a PV system’s power generation. Faults due to shading, open-circuits, and short-circuits are often hard to avoid. Such faults can lead to a reduced PV system lifespan, loss in system-generated energy, or even serious safety-related issues. Therefore, it is particularly important to develop fault detection methods for a PV system. Such fault detection and diagnosis methods would provide benefits in terms of a longer PV system lifespan, improvement in the energy conversion efficiency, and reduction in maintenance cost.

Some methods for detecting faults in PV systems have been built previously. These methods can be classified into time domain-based methods, mathematical model analysis-based methods, thermal infrared detection-based methods, and artificial-intelligence-based methods.

The time-domain-based methods need to send a signal pulse into the PV array circuit, which is then used to identify the PV system’s fault status by comparing the feedback output signal to the pulse input signal. The authors in [2,3] apply the time-domain method to detect PV array degradation faults by changing the response waveform. If we use the time-domain approach to detect faults, however, the PV system needs to be turned off, and this will have a crucial effect on the efficiency of the system.

Further, the mathematical model approach contrasts computing performance analytically with measuring output to detect a PV array’s fault status. For instance, the authors in [4,5] use a one-diode model method to detect PV array faults. Silvestre et al. [6] present an automated fault detection technique in photovoltaic systems based on voltage assessment and current indicators. However, this method cannot distinguish between partial shading (PS) abnormalities and degradation failures. Kang et al. [7] propose a method based on the Kalman filter algorithm to diagnose the reduction of output power in a PV array. Nevertheless, the usefulness of these mathematical modeling approaches depends greatly on the accuracy of the models.

On the other hand, the thermal infrared detection method uses an infrared scanner to identify and detects faults by measuring the body temperature of the PV panel for irregular heat. Peizhen and Shicheng [8] used infrared image analysis to recognize and analyze the working status of PV arrays. While their approach can recognize the shading and deterioration status of the PV panel, it focuses mainly on the identification of hot spot defects within the PV array. Nian et al. [9] designed a tool to obtain infrared images of PV panels; their approach can sense faults such as fragmentation, black pieces, and cracks in PV panels.

Artificial intelligence techniques have demonstrated over the last decade their usefulness to control, model, predict and forecast many aspects related to the PV system [10,11,12,13,14,15]. The authors in [16,17,18,19,20] used the artificial neural network to forecast different parameters such as power consumption solar radiation and PV power generation. On the other hand, in [21], the author used the artificial neural network to manage the power flow within standalone hybrid power systems. However, recently, a few papers have been published in Fuzzy Logic (FL) and Artificial Neural Network (ANN) applications for the identification and diagnosis of PV faults [22,23,24,25,26,27]. For example, in [28,29], the authors used a multi-layer perceptron neural network to identify faults related to PS and short circuits in a PV array. Dhimish et al. [30] proposed FL control to differentiate PS faults in PV array from short-circuit faults. Boukenoui et al. [31] utilized an FL controller with scanning and storing algorithms to implement an intelligent tracker to determine the maximum power point in a standalone PV system.

Furthermore, the authors in [32,33] used the Mamdani FL classification to detect a number of PV system faults, such as PS and short-circuit PV panels. China et al. [34] implemented an ANN for detecting PV array faults on the DC side of a PV system, which included diodes to bypass faulty PV panels. Yagi et al. [35] build a learning strategy using expert systems to distinguish two kinds of fault. Polo et al. [36] proposed an energy harvesting and failure mode prediction of a PV system to support dynamic task maintenance using ANN.

From the previous research, we can find that various studies have been conducted on the fault diagnosis of PV systems; however, there are very few instances of fault diagnostic techniques that could be implemented on integrated circuits, and these techniques require costly and complex hardware [37]. Nevertheless, hardware implementation for fault diagnosis techniques is necessary for real-life and Internet of Things (IoT) applications. An IoT-enabled application is an application that can be managed and monitored over the Internet. Thus, the key contribution of this paper is to introduce a novel and effective, yet small and implementable, algorithm based on a nonlinear autoregressive exogenous (NARX) neural network as well as Sugeno fuzzy inference. The proposed algorithm aims to isolate and classify faults occurring in PV systems. Under a set of real-time sensed output and surrounding conditions of a PV system, the NARX network is used to predict the PV system’s maximum output power, which is subsequently used by the fuzzy inference algorithm to diagnose and categorize faults that may occur in the PV system. The algorithm is proven to be implementable on a low-cost microcontroller. The proposed algorithm will be able to detect multiple faults such as open and short-circuit deterioration, flawed MPPT, and PS problems which may impact the PV system. Moreover, radiation and temperature, among other non-linear associations of patterns between predictors, can be captured by the proposed algorithm to determine the accurate point of maximum power for the PV system.

2. PV System Fault Types

Most of the faults that occur in the PV system are mostly associated with the PV array, inverters, MPPT, storage units, and the electrical grid. In this work, as shown in Table 1, sixteen different PV faults are investigated. It will be discussed in more detail in subsequent sections, as they will be categorized into minor, moderate, and major PV faults.

Table 1. Type of faults that may appear in the photovoltaic (PV) system under examination. PS: partial shading; G: Solar radiation.

Fault Type	Fault Type
One faulty panel	Two faulty panels + low PS in PV
Two faulty panels	Two faulty panels + high PS in PV
Three faulty panels	One faulty panel in G and low PS in other G
Low PS in PV	One faulty panel in G and high PS in other G
High PS in PV	One faulty panel + low PS in G and high PS in other G
One faulty panel + low PS in G	One faulty panel + low PS in G and one faulty panel + high PS in other G
One faulty panel + low PS in PV	Three faulty panels and low PS
One faulty panel + high PS in PV	Two faulty panels in G and high PS + one faulty panel in other G

3. Methodology

This section describes the proposed structure, the hypothetical PV model, the algorithm for fault detection, and the full design of the proposed NARX network with the Sugeno fuzzy inference system.

3.1. System Structure and Dataset Collection

The PV system architecture introduced in this work comprises one string of PV panels logically divided into two groups. Each group comprises two polycrystalline PV panels with a nominal power of 225 W for each PV panel. The PV panel nominal power is denoted as the maximum power that can be obtained from the PV panel within a group of standard test conditions (STCs). The STC normally mean a temperature of 25°C, an air mass (AM) of 1.5, and 1000 W/m² solar radiation. The string PV panels are connected in series. A NARX MPPT with an output effectiveness of not less than 98.2% [38] is connected to the PV string. The overall PV system architecture is illustrated in Figure 1.

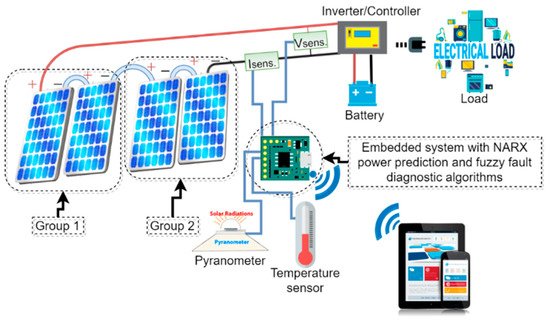
Figure 1. Overall system structure. NARX: nonlinear autoregressive exogenous neural network.

The fuzzy diagnostic algorithm is implemented using a low-cost embedded system that employs the ATmega2560 microcontroller. The embedded system uses a current sensor (denoted by Isens. in Figure 1) and voltage sensor (denoted by Vsens. in Figure 1) to provide the PV string voltage and power needed for the fuzzy diagnostic algorithm.

The embedded system uses the ESP8266 to facilitate WiFi connectivity. This allows the embedded system to send the PV string’s diagnosis status, notifications, and related data over the Internet to a monitoring system. The embedded system also collects the meteorological data needed for the fuzzy diagnostic algorithm.

Meteorological data consisting of temperature and solar radiation were assembled in real-time by the Energy Research Centre [39] at An-Najah National University. The apparatus used to assemble the dataset consists of a PV panel body temperature sensor (namely the WE710 sensor with a precision of ±0.25 °C), and a solar radiation sensor with high accuracy (namely the WE300 sensor with a precision of ±1%). Regardless of the accuracy of the used sensors, the captured data are occasionally noisy, incomplete, or unreliable. This is mainly due to the noise ratio in the connections or the sensor error. Thus, a moving average filter [38] was used to resolve the noise in the obtained data. By averaging 60 samples, the measurements are collected at a rate of 1 Hz over a 1 min period. The tests for voltage and current obtained are thus measured at intervals of 1 min. The manufacturer specifications of the PV panel are shown in Table 2.

Table 2. Electrical characteristics of the Astronergy CHSM6610P-225 PV panel.

PV Panels Specification	Value	PV Panels Specification	Value
Power at maximum (Pm)	225W	How many cells are in series	60
Current at Pm (Iamp)	7.55A	How many cells are in parallel	1
Voltage at Pm (Vamp)	29.76V	Isc Temp. coefficient	0.052 %/°C
Short-circuit current (Isc)	8.27A	Voc Temp. coefficient	−0.129 V/°C
Open-circuit voltage (Voc)	36.88V

The case study used in this work consists of one string of 4 PV panels. However, more PV strings can be added in parallel. In general, the PV string may consist of more than four panels, but the used FS will analyze them into two groups.

3.2. PV Theoretical Modeling and Characteristics Analysis

To assess the PV panel’s performance under different operating conditions, a precise model is used to forecast the power-voltage (P-V) characteristic curve. The dynamic PV model utilized in this study is based on a model introduced in our previous work [34,35,36,37,38,39,40,41,42,43]. Figure 2 shows the single diode equivalent circuit, consisting of a diode, a photocurrent, one parallel, and one series resistor.

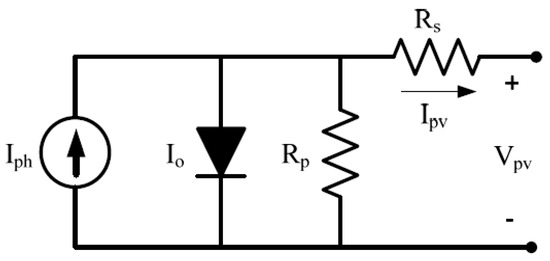
Figure 2. Solar cell equivalent circuit.

The equivalent single diode circuit is inferred from the physical principles and defines a cell’s entire I-V curve as a continuous function for a particular set of operating conditions [44].

In Equation (1) [40], the mathematical relation between the current of a PV panel and the other related parameters is shown:

$$Ipv=Iph-Io\left[\exp \left(\frac{\left(Vpv+Ipv Rs\right)q}{a KBTc Ns}\right)-1\right]-\frac{Vpv+Ipv Rs}{Rp}$$

(1)

where Rs is the series resistance (U), Io is the diode saturation currents (A), Iph is the photocurrent (A), Rp is the shunt resistance (U), Tc is the cell temperature (K), KB is Boltzmann’s constant (1.38065 × 10⁻²³ J/K), q is the electron charge (1.60217 × 10⁻¹⁹ C), a is ideality factor of the diode that represents the diffusion current of the components, and Ns is the number of the PV panel cells that are in series.

To reduce the hot spot effect successfully, a bypass diode is connected in parallel with respect to the solar cells, which are connected in series in a PV panel under the PS condition [45]. The proposed model [40] is implemented as shown in Figure 3.

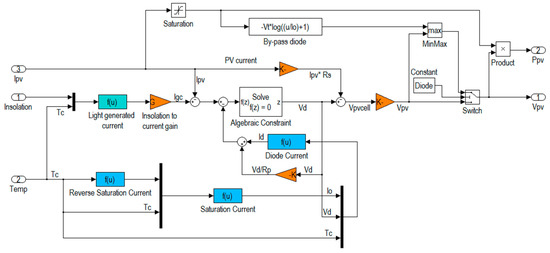
Figure 3. Implementation of the PV model using MATLAB/ Simulink.

In this work, the enhanced PV panels are linked in series to create two PV string groups, as illustrated in Figure 4. Also, a bypass diode is connected in parallel with respect to each PV panel to model the actual bypass diode in the actual PV panel. When a PV panel experiences shading, its resistivity becomes very high, causing its temperature to rise, and this causes a hot spot effect. The bypass diode helps to overcome this effect.

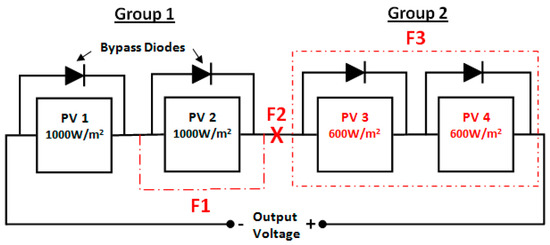
Figure 4. The structural configuration of the PV system under common fault conditions.

There are three well-known faults that may occur in the PV system’s DC side [46], which are open-circuit, short-circuit, and PS. The main cause of a short-circuit fault is the vibration and the abrasion of PV panels. In addition, the bad wiring of the PV string is a significant source for short-circuit faults. Faults of the short-circuit type are indicated by the label F1 in Figure 4. On the other hand, wire breaks between the solar cells in series may cause an open-circuit fault. Faults of the open-circuit type are indicated by the label F2 in Figure 4. PS may occur when the PV string receives uneven temperature and irradiation due to adjacent buildings, passing clouds, trees and so on [47]; F3 stands for the PS fault in the string of PV panels in Figure 4.

The output characteristics of the PV string are entirely different when faults occur. Figure 5 represents the output characteristic curves of the PV string under the faults set in Figure 4. As shown in Figure 5, the voltage of the PV string is reduced when a fault of the short-circuit type happens; when an open-circuit fault appears, there will be no current. Further, under PS faults, there are multi-peak characteristics of the PV string. Consequently, in order to implement an algorithm to detect faults, the current and voltage at the MPP, and the PV string open-circuit voltage are chosen as fault characteristic quantities in this work.

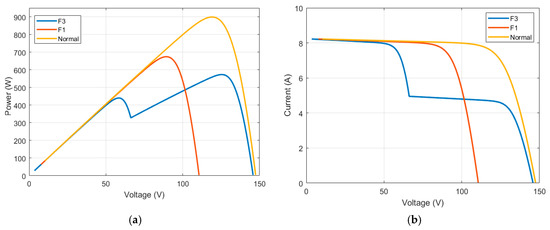
Figure 5. The PV system output characteristic curves under common faults: (a) P-V curves (b) I-V curves.

It is worth mentioning here that, in this paper, various scenarios will be covered regarding short-circuit and PS faults. Moreover, in the PS condition, the radiation level is assumed to equally affect all PV panels belonging to the same group. However, the used algorithm takes into account the fact that different groups in the string may have different radiation levels.

3.3. Algorithm for Fault Detection in PV Panels

Two ratios have been established to decide which type of fault occurred in our PV system. These are the voltage ratio (VR) and the power ratio (PR). The two ratios change in a manner that makes them suitable for classifying the region of the fault during faulty conditions.

The VR and PR are given as in Equations (2) and (3):

$$VR=\frac{V_t}{V_r}$$

(2)

$$PR=\frac{P_t}{P_r}$$

(3)

where Vt and Pt are the maximum theoretical (predicted) output voltage and power the PV system should have produced, respectively. Vt and Pt are calculated in real-time using the NARX neural network algorithm. Vr and Pr are the measured output voltage and power from the PV system, respectively.

The MPPT used in this paper has a conversion accuracy rate of 98.2%, which has been validated in the author’s previous work [38]. Therefore, the calculated power ratios are calculated within ±2% error tolerance. Hence, we can define the maximum and the minimum voltage and power ratios, respectively, as shown in Equations (4)–(7):

$$VR\min =\frac{V_t}{V_r}$$

(4)

$$VR\max =\frac{V_t}{V_r\times \mathrm{MPPT}\mathrm{Tolerance}\mathrm{Rate}}$$

(5)

$$PR\min =\frac{P_t}{P_r}$$

(6)

$$PR\max =\frac{P_t}{P_r\times \mathrm{MPPT}\mathrm{Tolerance}\mathrm{Rate}}$$

(7)

Under the normal operation mode (standard test condition), the maximum and minimum value of PR can be calculated using Equations (8) and (9) as follows:

$$PR{\min }_{STC}=\frac{P_t}{P_r}=\frac{900}{900}=1$$

(8)

$$PR{\max }_{STC}=\frac{P_t}{P_r\times \mathrm{MPPT}\mathrm{Tolerance}\mathrm{Rate}}=\frac{900}{900\times 98.2\%}=1.02$$

(9)

In this work, the detected maximum PS condition by the radiation sensor is 95% of the total shading; hence, the maximum PR is measured as

$$PR{\max }_{PS}=\frac{P_t}{P_r\times \mathrm{MPPT}\mathrm{Tolerance}\mathrm{Rate}}=\frac{900}{18.17\times 98.2\%}=50.4$$

(10)

Figure 6 shows the developed fault detection algorithm. If the value of PR is not higher than the maximum PR and not within the scope of the normal operation mode, then the algorithm based on the fuzzy system will determine the type of fault and whether it is a minor or moderate fault. Furthermore, the algorithm can classify, based on a PR value larger than 50, whether there is a major fault in a PV string, or if the fault is in the MPPT unit.

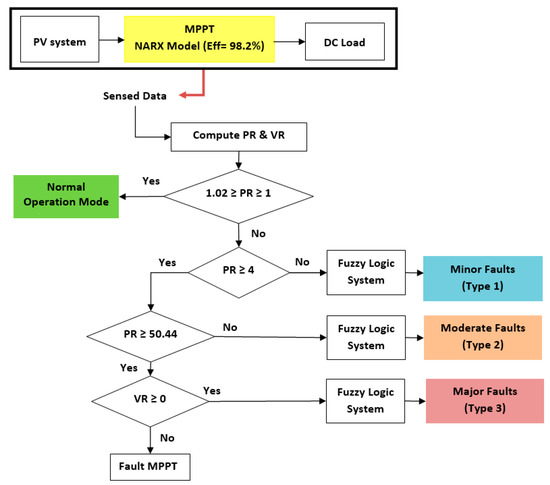
Figure 6. The proposed fault detection algorithm. MPPT: maximum power point tracking; PR: power ratio; VR: voltage ratio.

3.4. NARX MPPT Reference Model

An essential part of a PV system is monitoring the MPP of a PV string. As such, several MPPT techniques have been developed and put into practice [48]. In this model, the MPPT controller is implemented using a NARX network to increase tracking efficiency by increasing the tracking response. NARX is a recurrent neural network that has been successfully used, especially for applications of the time-series type [49]. The key variance between multi-layer perceptron and NARX is that NARX permits a feedback connection among layers, and that makes it suitable for time-series analysis because it enables the network to operate with past period values of variables.

There are two architectures of the NARX neural network [50]: the open-loop and the closed-loop. In this work, the open-loop architecture is used because of the accessibility of former accurate values of the time series and the pure feed-forward network architecture. The NARX network behavior can be mathematically modeled by Equation (11):

$$y\left(t\right)=f\left(y\left(t-1\right),y\left(t-2\right),\dots ,y\left(t-n_y\right),x\left(t-1\right),x\left(t-2\right),\dots ,x\left(t-n_x\right)\right)$$

(11)

where f(.) is the mapping function of the network, y(t) is the output of the NARX at time t, (y(t−1), y(t−2), …, y(t−n_y)) are the NARX past output values, (x(t−1), x(t−2), …, x(t−n_x)) are the NARX exterior data, n_y is the number of output delay, and n_x is the number of input delays.

In the proposed work, NARX uses its former measured values and some external data to estimate the current and voltage at their optimum values for the PV system. As an input, NARX uses four inputs with exterior data and two previous outputs, which represent time-series inputs at time t-1. Figure 7 shows the structure of the presented MPPT controller.

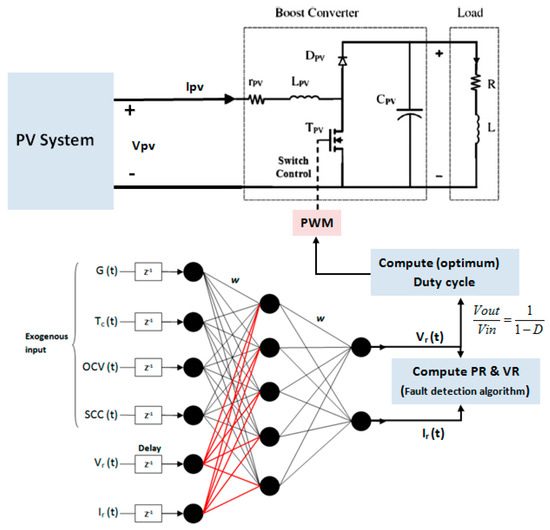
Figure 7. The structure of the MPPT controller. PWM: pulse width modulation.

As illustrated in Figure 7, the six input nodes in the first layer are the solar radiation, the temperature of the panel, the open-circuit voltage of the panel, the short-circuit current of the panel, and the two output values of the time series previously achieved. There are five nodes in the hidden layer with an activation function for hyperbolic tangent sigmoid transfer. The last layer is composed of two nodes; each has an activation function of a linear type. These two nodes produce the optimum operating current and the optimum operating voltage of the PV system.

After constructing the NARX network model and feeding the collected data, the targeted output current and voltage are gathered by executing a code in MATLAB that analyzes the characteristics of the output to the validated PV model. The module validation and the results for different PV panel types (under a diversity of temperature and solar radiation conditions) can be found in the published previous work of the author [38]. Using the Levenberg–Marquardt (LM) training algorithm, the network is trained to understand the relevance between the parameters of input and output. Figure 8 illustrates the state diagram for the training algorithm.

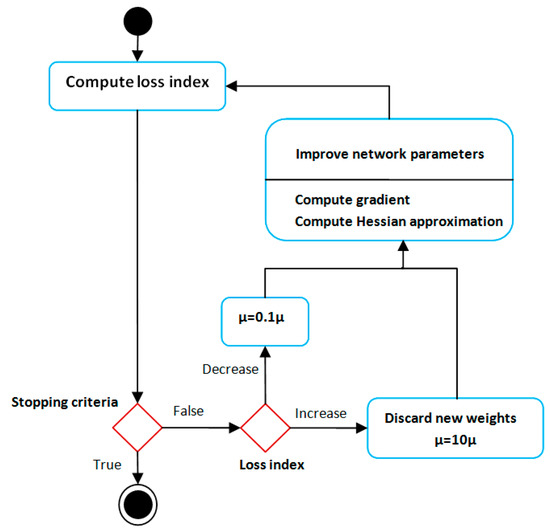
Figure 8. Levenberg–Marquardt state diagram.

A training set of 5880 cases was obtained from three different PV panels before performing the network training using the LM algorithm, namely Astronergy-CHSM6610P, Sharp’s-NUS0E3E, and Lorentz mono-crystalline. The open circuit voltage (OCV) and short circuit current (SCC) are chosen from the three PV panels as the reference variables. This dataset covers the various temperatures and solar radiation conditions that would normally take place. More detail regarding the NARX network validation can be found in the author’s previous work [38].

3.5. Sugeno Fuzzy Reference Model

A single spike (singleton) of the consequent rule is used as a membership function to shorten the time of the fuzzy inference single spike (singleton). Sugeno inference is very similar to the Mamdani method, but a mathematical function of the input variable is used as a result of the rule instead of a fuzzy set. The Sugeno method has different features, such as the following:

• It is computationally efficient;
• It works well with adaptive techniques and optimization methods;
• It has certain output interface surface continuity;
• It is best suited for linear techniques.

In the present work, the Sugeno fuzzy model with zero-order is used as shown by the fuzzy rule:

IF x is A AND y is B THEN z is K

where K is a constant; A and B are fuzzy sets on the universe of discourses x and y, respectively; and x, y, and z are linguistic variables.

For the proposed fault diagnosis system, three zero-order Sugeno fuzzy models have been developed for the minor, moderate, and major faults of the PV system, as illustrated in Figure 6. Table 3 classifies the 16 faults, shown in Table 1, into minor, moderate, and major faults.

Table 3. PV system fault classification.

Mode	Symbol	Fault Scenario
Minor	F1L	One faulty panel
	F2L	Low PS in PV
	F3L	One faulty panel + low PS in G
	F4L	One faulty panel in G and low PS in other G
	F5L	Two faulty panels
	F6L	One faulty panel + low PS in PV
	F7L	Two faulty panels + low PS in PV
Moderate	F1M	Three faulty panels
	F2M	One faulty panel in G and high PS in other G
	F3M	Three faulty panels and low PS
	F4M	One faulty panel + low PS in G and one faulty panel + high PS in other G
	F5M	One faulty panel + low PS in G and high PS in other G
Major	F1H	High PS in PV
	F2H	One faulty panel + high PS in PV
	F3H	Two faulty panels + high PS in PV
	F4H	Two faulty panels in G and high PS + one faulty panel in other G

For the three models, PR and VR are utilized as input linguistic variables for classification in the fuzzy system. The PR and VR regions are shown in Table 4, where PR and VR are calculated using Equations (4)–(7).

Table 4. Fuzzy logic input regions.

Fault Symbol	Fuzzy Classification Region	Partial Shading %	Max VR (V)	Min VR (V)	Max PR (W)	Min PR (W)
F1L	1	-	1.359	1.335	1.359	1.335
F2L	2	up to 35%	1.014	0.996	1.587	1.559
F3L	3	up to 35%	1.27	1.24	1.91	1.88
F4L	4	up to 35%	1.315	1.29	2.0216	1.98
F5L	5	-	2.039	2.003	2.039	2.003
F6L	6	up to 35%	1.352	1.328	2.117	2.079
F7L	7	up to 35%	2.048	1.99	3.208	3.118
F1M	8	-	4.078	4.005	4.079	4.005
F2M	9	up to 95%	4.23	4.159	4.254	4.17
F3M	10	up to 35%	4.055	3.98	6.35	6.237
F4M	11	Low up to 35%	4.138	4.064	6.48	6.36
F5M	12	High up to 95%	4.226	4.15	6.618	6.49
F1H	13	up to 95%	1.4	1.37	50.44	49.5
F2H	14		1.868	1.834	67.29	66.07
F3H	15		2.801	2.75	100.93	99.11
F4H	16		5.604	5.503	201.87	198.23

Noting the preceding table, a selection of the 16 different regions has been used. Regions from 13–16 are used for a major fault in the PV system with high PS conditions (up to 95%). The maximum and minimum voltage and power ratios for each region are also shown in Table 4.

The fuzzy subsets and the shape of the membership functions for the three fuzzy models are shown in Figure 9, Figure 10 and Figure 11.

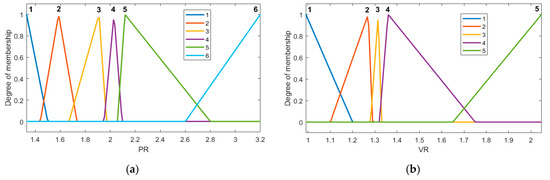
Figure 9. Membership functions of the minor fault model: (a) power rate, (b) voltage rate.

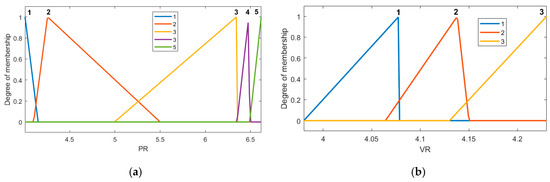
Figure 10. Membership functions of the moderate fault model: (a) power rate, (b) voltage rate.

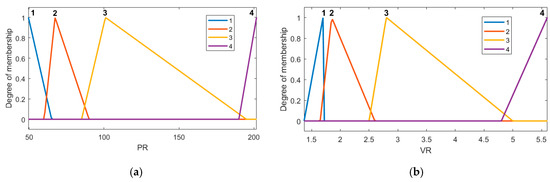
Figure 11. Membership functions of the major fault model: (a) power rate, (b) voltage rate.

After regions of the input variables are identified, the fuzzy system sets the rules which are required to be set. The primary rule sets for the three fuzzy models are illustrated in Table 5. The system’s Sugeno-based architecture takes the product as an intersection method with a weighted average defuzzification method.

Table 5. Fuzzy logic rules.

Mode	#	Rules
Minor	1	If PR is 1 and VR is 4 then fault is 1
	2	If PR is 2 and VR is 1 then fault is 2
	3	If PR is 3 and VR is 2 then fault is 3
	4	If PR is 4 and VR is 3 then fault is 4
	5	If PR is 4 and VR is 5 then fault is 5
	6	If PR is 5 and VR is 4 then fault is 6
	7	If PR is 6 and VR is 5 then fault is 7
Moderate	1	If PR is 1 and VR is 1 then fault is 8
	2	If PR is 2 and VR is 3 then fault is 9
	3	If PR is 3 and VR is 1 then fault is 10
	4	If PR is 4 and VR is 2 then fault is 11
	5	If PR is 5 and VR is 3 then fault is 12
Major	1	If PR is 1 and VR is 1 then fault is 13
	2	If PR is 2 and VR is 2 then fault is 14
	3	If PR is 3 and VR is 3 then fault is 15
	4	If PR is 4 and VR is 4 then fault is 16

It is worth pointing out that a large number of fuzzy rules can cause an over-parameterized system, which reduces the ability to generalize and the accuracy of detecting the type of fault in the PV system being examined. Thus, as shown in Table 5, the three core rule sets have been chosen with regard to a sensitivity examination as follows:

• Reviewing the model input and output variables;
• Reviewing the fuzzy groups;
• Reviewing the standing rules;
• Revising the shapes of the fuzzy groups.

Using the three-dimensional output surface from the MATLAB Fuzzy Logic Toolbox, a satisfactory level of performance was reached following the tuning process; i.e., starting from a faulty PV panel only and progressively modifying the fuzzy system to detect all possible faults that may occur in the PV according to the fault types listed in Table 3.

4. Results and Discussion

4.1. Evaluation of the Proposed MPPT

To determine the NARX network configuration, several trials have been performed, as explained previously by the authors in [38]. The mean square error for training with this structure was 0.006415.

Once the training of the neural network was done, as shown in [38], the subsequent step was to test the proposed MPPT algorithm to determine whether the actual results agreed with the prediction results and to test its performance. Hence, to test the proposed MPPT algorithm, seven different P-V characteristic curves were used. Table 6 presents a performance evaluation between the developed method and the P-V characteristic curve. Figure 12 illustrates graphically the results of power tracking through the developed algorithm compared to the maximum power from the P-V curve. The results have been taken from the Astronergy CHSM6610P-225 PV panel. The panel STC electrical characteristics can be found in Table 2.

Table 6. Performance evaluation between the developed method and the P-V characteristic carve.

#	Input				MATLAB Simulation		Hardware Implementation
#	Solar Radiation (W/m2)	Temperature (°C)	Open-Circuit Voltage (V)	Short-Circuit Current (A)	MPPT Output Power (W)	Maximum Power from the P-V Curve (W)	MPPT Output Power (W)	Tracking Time (ms)
1	125	5	36.88	8.27	24.754623	24.89109345	24.3828	30.912
2	235	10	36.88	8.27	52.164364	51.85359312	51.843	31.36
3	325	15	36.88	8.27	72.581871	72.41724493	72.3528	31.168
4	420	20	36.88	8.27	92.913429	92.66318971	92.8236	30.912
5	530	25	36.88	8.27	114.95480	114.7404373	114.6934	32.192
6	650	30	36.88	8.27	137.14440	137.0608187	136.9548	31.936
7	745	35	36.88	8.27	151.63885	151.7050295	151.51	31.872

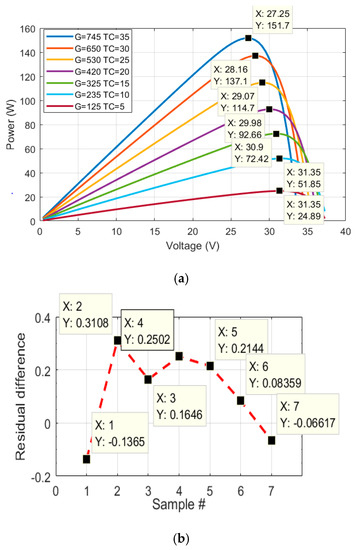
Figure 12. (a) P-V characteristic curves outcomes through the use of the developed MPPT algorithm; (b) residual difference between the proposed method and the P-V characteristic curve.

4.2. Implementation of NARX and the Fuzzy Diagnostic Algorithm on a Low-Cost Microcontroller

The NARX neural network MPPT algorithm and the fuzzy diagnostic algorithm were implemented on a low-cost embedded system employing the Atmega2560 microcontroller. The running frequency of the used embedded system was 16 MHz. The embedded system was connected to the PV system through sensors, as shown in Figure 1.

As shown by the rightmost two columns of Table 6, the embedded system (hardware implementation) finds the Pt (MPP output power) of the PV system in a fairly fast time using the implemented NARX neural network algorithm. The used NARX algorithm predicts what should be the maximum output power of a PV system with regard to the surrounding conditions with an accuracy of 98.2%. The predicted output power is found by the algorithm in about 31 ms. The predicted output power is used by the fuzzy diagnostic algorithm to diagnose the PV system.

Table 7 shows the running time and the output of the fuzzy algorithm using some test cases. It is important to note that the running time here denotes the running time for the fuzzy algorithm providing that the value of Pt is already available. The fuzzy algorithm has an average running time of 1.6 ms.

Table 7. Fuzzy diagnosis test cases outputs and running time.

Test Case #	PR	VR	Fault Type	Diagnosis Time in ms	Test Case #	PR	VR	Fault Type	Diagnosis Time in ms
1	1.41	1.35	1	1.472	7	6.06	4.06	10	1.248
2	1.84	1.24	3	1.504	8	6.58	4.17	12	1.36
3	1.98	1.31	4	1.52	9	82.3	2.25	14	1.152
4	2.56	1.63	6	1.696	10	116	3.79	15	1.232
5	2.83	1.83	7	1.664	11	193	5.49	16	1.44
6	4.5	4.17	9	1.28

The meaning of each fault type is discussed in the previous sections. From the previous results, we see that the used embedded system requires about 33 ms to diagnosis a PV system for possible faults.

4.3. Evaluation of the Developed Fault Detection Algorithm

Several experiments were conducted to test the performance of the developed fault detection algorithm. Figure 13 shows the circuit diagram of how the developed fault algorithm is examined. As illustrated, the proposed algorithm was applied on a PV array with two PV strings in parallel. Each string had its own fuzzy fault system. Table 8 shows the test cases which were applied to the PV array shown in Figure 13. Each scenario contained different conditions and lasted for half an hour. Readings were taken after 5 min of installation.

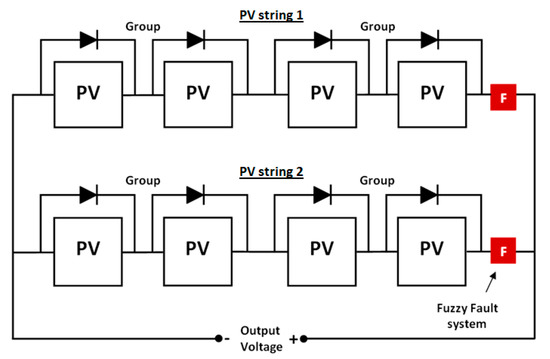
Figure 13. Experiment setup for the PV array circuit diagram.

Table 8. Fault test cases.

Test Case	Start Time	End Time	Fault Condition	Applied
1	7:00	7:29	Normal operation mode	-
2	7:30	7:59	One faulty panel	PV string 1
3	8:00	8:29	Two faulty panels	PV string 1+ PV string 2
4	8:30	8:59	Three faulty panels	PV string 1
5	9:00	9:29	30% PS in PV	PV string 1
6	9:30	9:59	95% PS in PV	PV string 2
7	10:00	10:29	One faulty panel + 35% PS in G	PV string 1+ PV string 2
8	10:30	10:59	Normal operation mode	-
9	11:00	11:29	One faulty panel + 35% PS in G and 95% PS in other G	PV string 1 + PV string 2
10	11:30	11:59	35% PS in PV	PV string 1
11	12:00	12:29	One faulty panel + 95% PS in PV	PV string 2
12	12:30	12:59	Two faulty panels + 95% PS in PV	PV string 1
13	13:00	13:29	One faulty panel in G and 35% PS in other G	PV string 1+ PV string 2
14	13:30	13:59	One faulty panel + 30% PS in PV	PV string 2
15	14:00	14:29	One faulty panel + 35% PS in G and one faulty panel + 95% PS in other G	PV string 2
16	14:30	14:59	Three faulty panels and 34% PS	PV string 1
17	15:00	15:29	Normal operation mode	-

The set of samples for the operational normal mode is not involved in the assessment process of the fuzzy logic because it is detectable using the mathematical regions described in Figure 6.

Figure 14 and Figure 15 show the faulty samples versus the output membership function for the Sugeno fuzzy system. For instance, case 11 is an example of a fault in one PV panel and high PS condition influencing the second PV string; for this case, the fuzzy system output is equal to 14 (F2H), which is the same region shown in Figure 15 and Figure 16. Similarly, cases 5 and 10 present a low PS in PV with 30% and 35% PS, respectively. These two cases lie in the same fuzzy region because of the low PS condition influencing the first PV string; this situation is labeled as region 2 (FL2) in both Figure 14 and Figure 16. In conclusion, all examined faulty conditions were accurately detected.

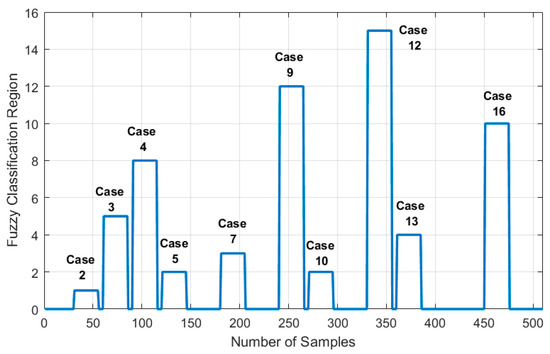
Figure 14. The Sugeno fuzzy logic system output results attained for PV string 1.

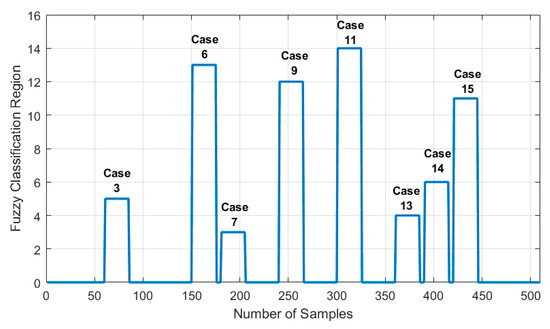
Figure 15. The Sugeno fuzzy logic system output results attained for PV string 2.

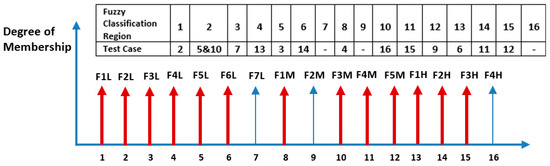
Figure 16. Singleton values mapped to the test cases.

5. Conclusions

This work presented a novel and effective, yet small and implementable, fault diagnosis algorithm based on an artificial intelligent nonlinear autoregressive exogenous neural network and Sugeno fuzzy inference. The NARX neural network predicted the maximum output power of a PV system under a set of surrounding conditions with an accuracy of 98.2%. The predicted output power was used subsequently by the fuzzy diagnosis algorithm to identify the type of fault in a PV system if there was one. The diagnostic algorithm was implemented on a low-cost embedded system. The algorithm was able to diagnose many faults that may occur in a PV system, such as open and short-circuit degradation, faulty MPPT, and partial shading conditions with an average running time of about 33 ms. The presented fault diagnosis algorithm is an important step toward a complete system that can diagnose faults in large PV systems such as PV plants.